Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings
Abstract
:1. Introduction
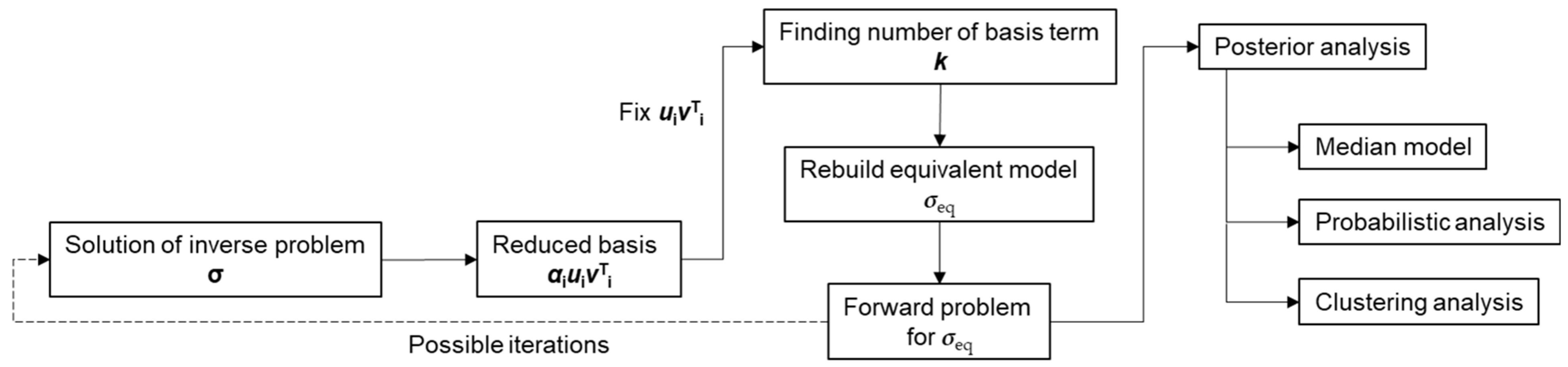
2. Inverse Problem and Uncertainty Analysis on Reduced Basis
2.1. Inverse Problem
2.2. Uncertainty Analysis in Reduced Specter Basis
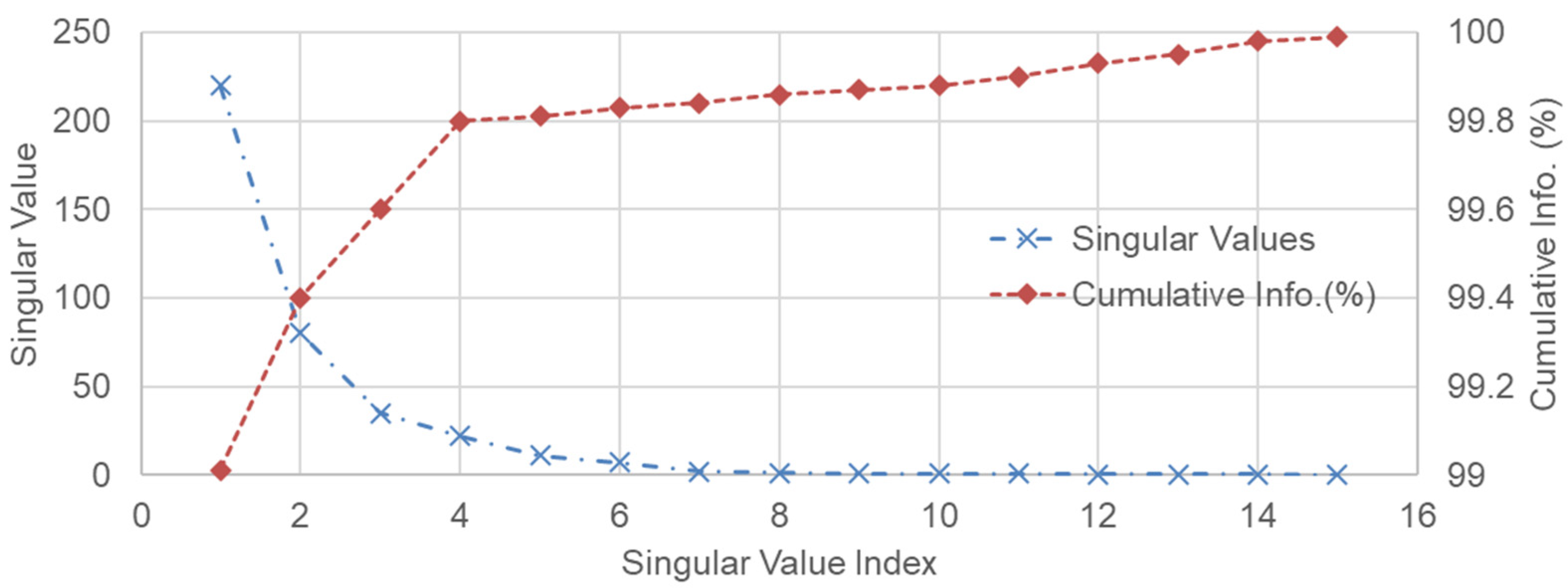
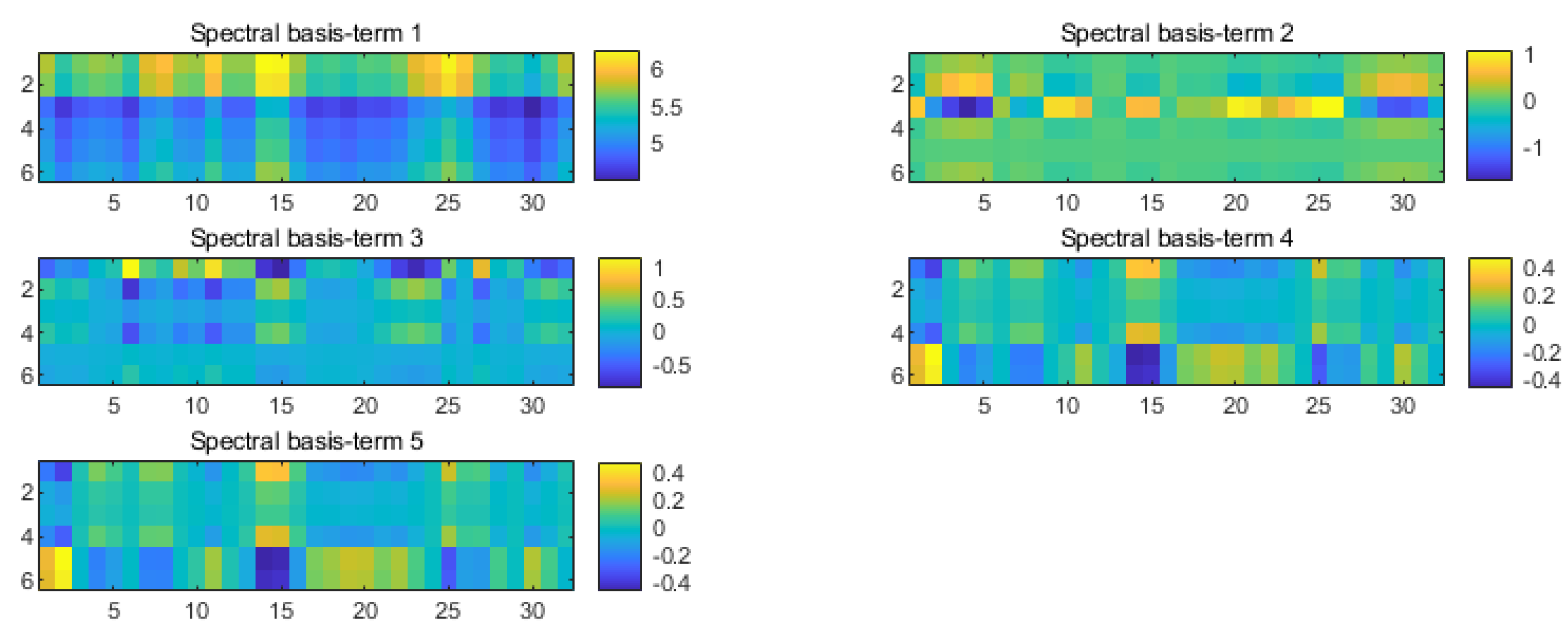
2.2.1. Spectral Decomposition of the Inverse Model
2.2.2. Model Sampling in Non-Linear Equivalence Region
2.2.3. Uncertainty Analysis in a Chosen Space
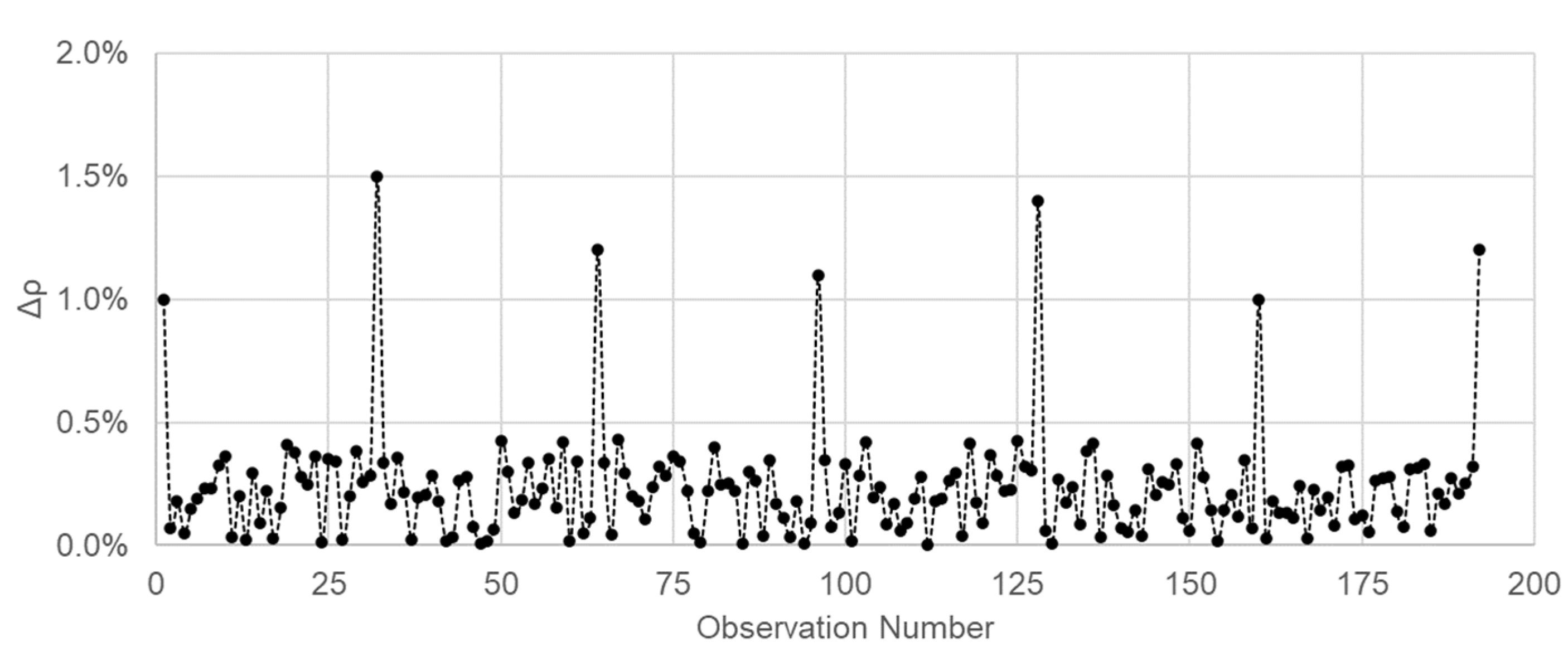
3. Results
3.1. Design of Field Survey
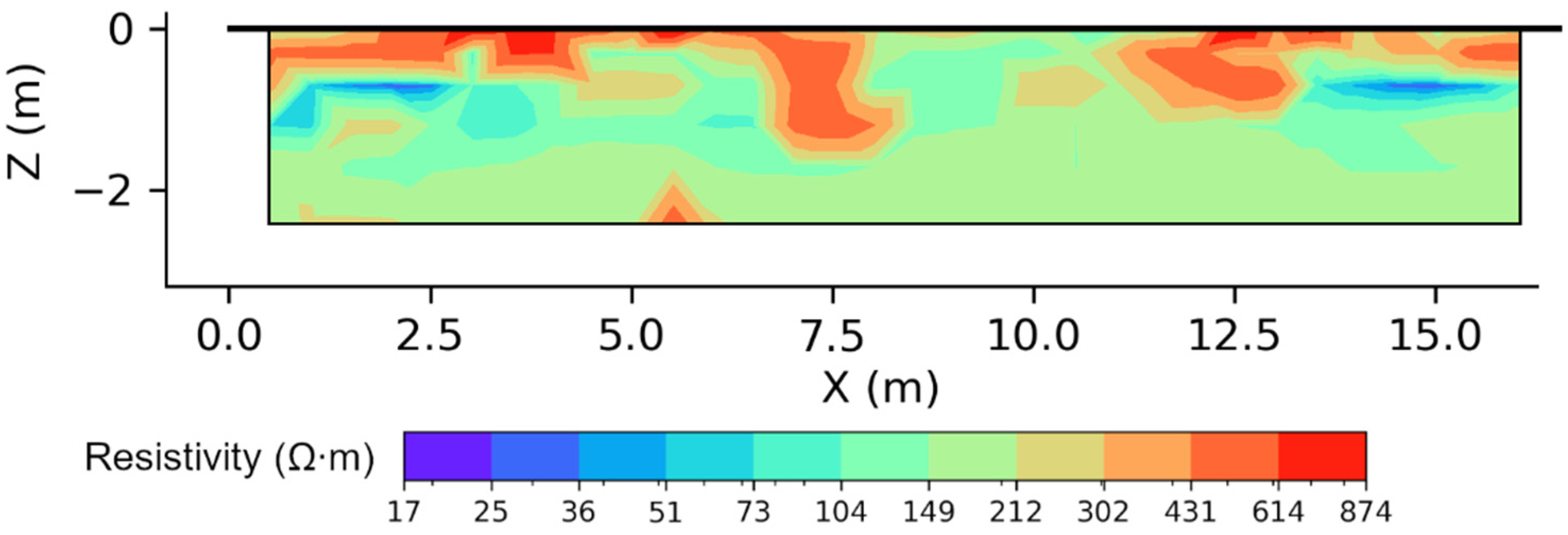
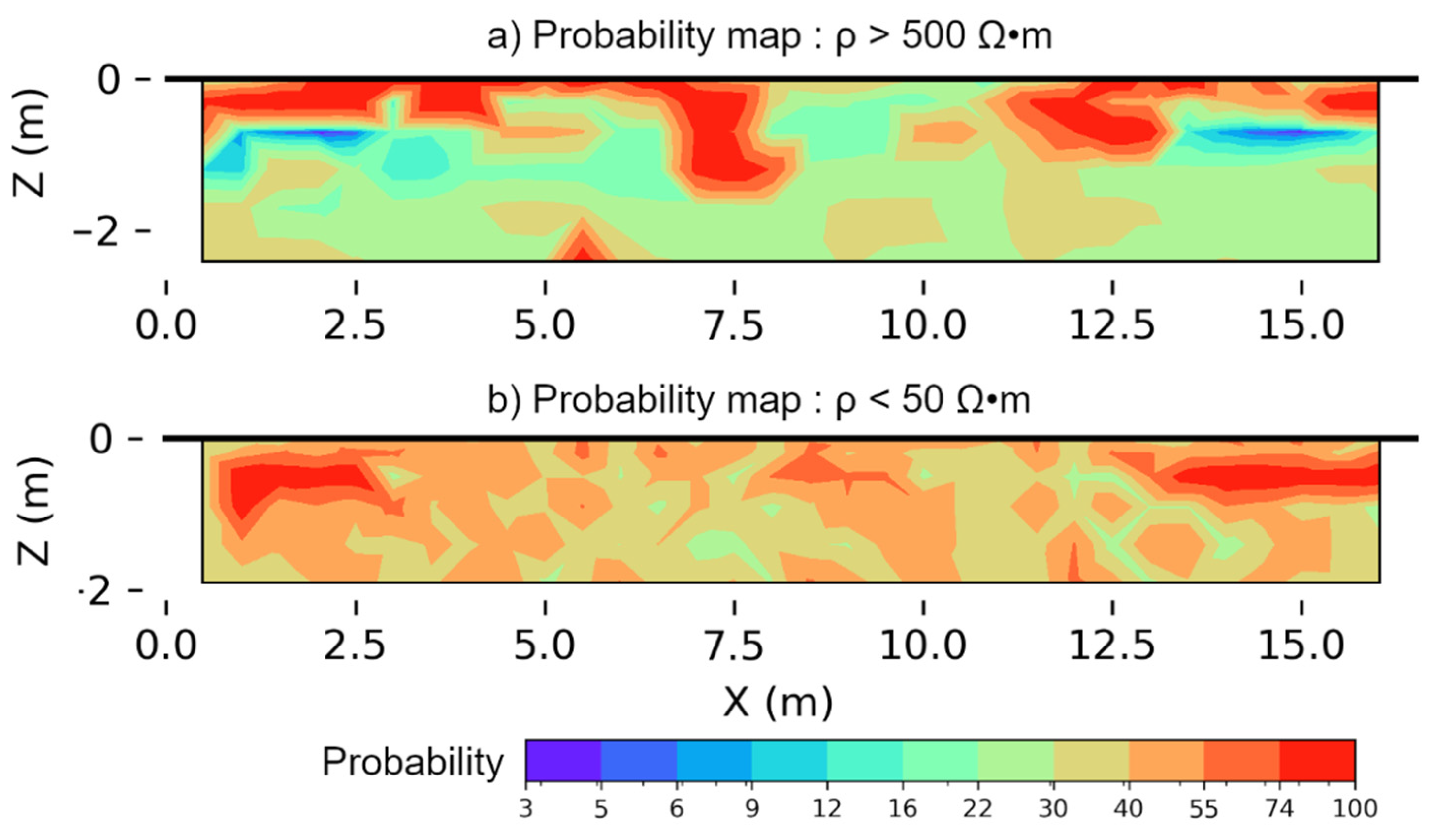
- The shadow part of the model (less than 0.6 m) is composed of the most resistant blocks. The average value of resistivity equals 300 Ω∙m and can reach 875 Ω∙m. A heterogeneity could be observed between 8 and 11 m, corresponding to an erosion part caused by the weathering of the stone.
- Under the shadow part, the resistivity values are stable, and the average value is 178 Ω∙m; however, between 6.5 and 8 m, an abnormally resistant area is identified, which corresponds to a mechanical fissure, verified by a geotechnical test.
- Two conductive layers are located on the left and right sides (between 0.5 to 2.5 m and 13 to 15.5 m). The average value of resistivity is 35 Ω∙m and the lowest value could attain 22 Ω∙m. This part could be the fissure filled with moisture, which caused the erosion of the wall.
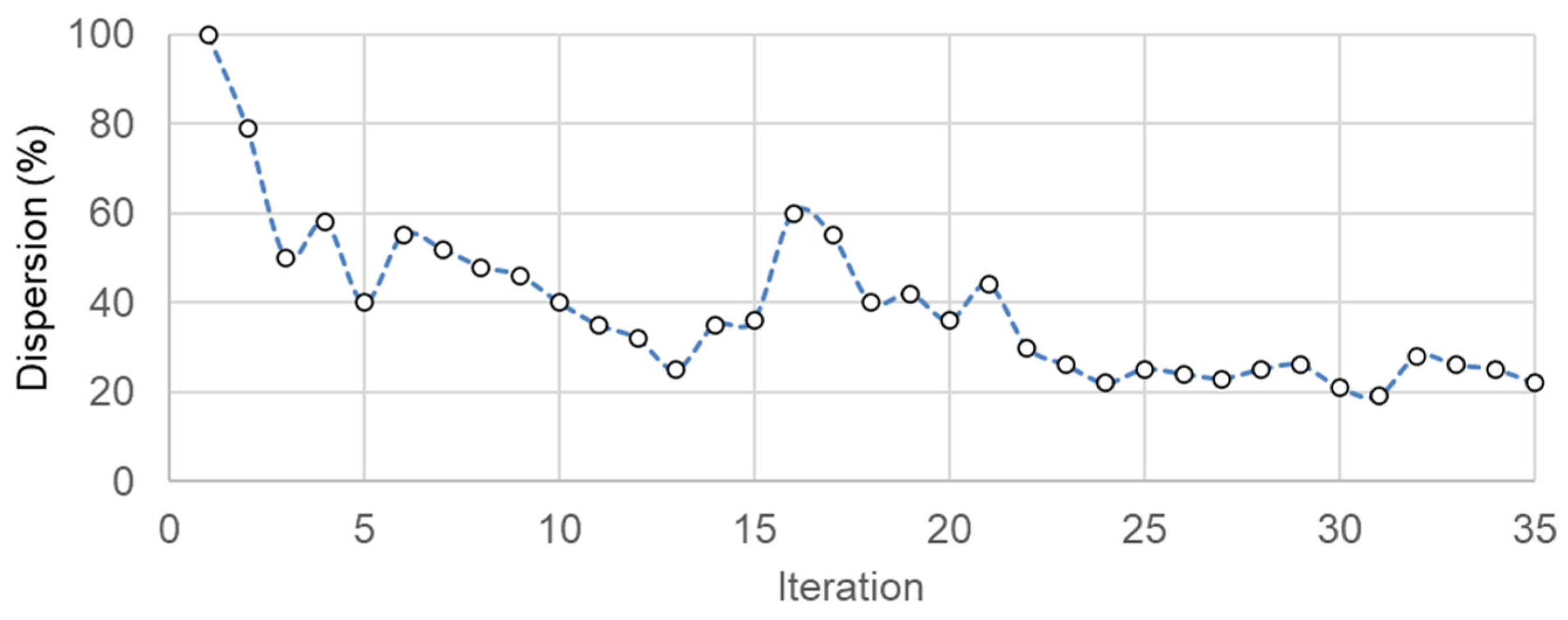
3.2. Model Sampling
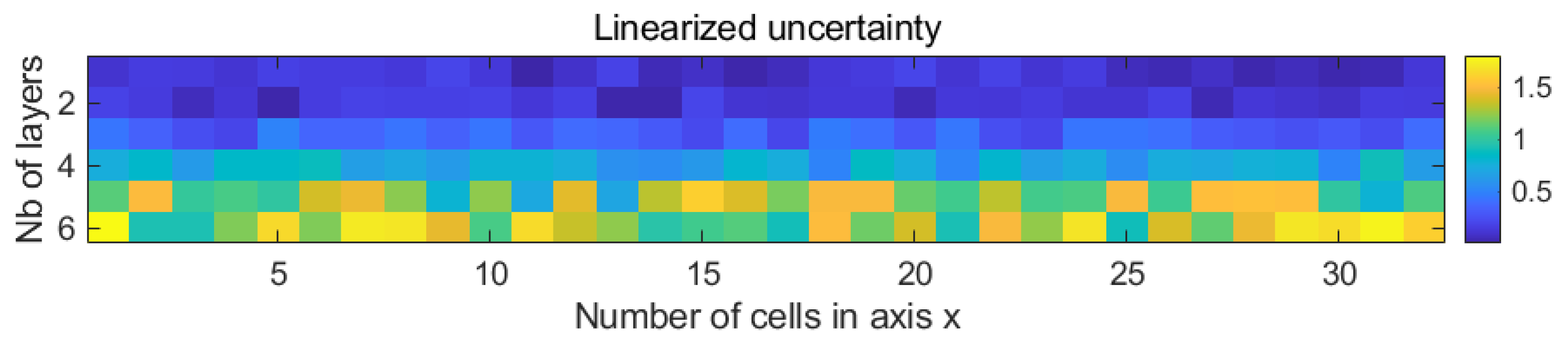
3.3. Results of Uncertainty Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garrido, I.; Solla, M.; Lagüela, S.; Fernández, N. IRT and GPR Techniques for Moisture Detection and Characterisation in Buildings. Sensors 2020, 20, 6421. [Google Scholar] [CrossRef] [PubMed]
- Vinha, J.; Salminen, M.; Salminen, K.; Kalamees, T.; Kurnitski, J.; Kiviste, M. Internal moisture excess of residential buildings in Finland. J. Build. Phys. 2018, 42, 239–258. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P.; Sun, Y.; Wang, W. Study on breaking concrete structures by pulse power technology. Buildings 2022, 12, 274. [Google Scholar] [CrossRef]
- Ortega-Ramírez, J.; Bano, M.; Villa Alvarado, L.A.; Medellín Martínez, D.; Rivero-Chong, R.; Motolinía-Temol, C.L. High-resolution 3-D GPR applied in the diagnostic of the detachment and cracks in pre-Hispanic mural paintings at “Templo Rojo”, Cacaxtla, Tlaxcala, Mexico. J. Cult. Herit. 2021, 50, 61–72. [Google Scholar] [CrossRef]
- Parracha, J.; Pereira, M.; Maurício, A.; Faria, P.; Lima, D.F.; Tenório, M.; Nunes, L. Assessment of the density loss in anobiid infested pine using X-ray micro-computed tomography. Buildings 2021, 11, 173. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. Instantaneous spectral entropy: An application for the online monitoring of multi-storey frame structures. Buildings 2022, 12, 310. [Google Scholar] [CrossRef]
- Garrido, I.; Barreira, E.; Almeida, R.M.S.F.; Lagüela, S. Introduction of active thermography and automatic defect segmentation in the thermographic inspection of specimens of ceramic tiling for building façades. Infrared Phys. Technol. 2022, 121, 104012. [Google Scholar] [CrossRef]
- Tejedor, B.; Barreira, E.; Almeida, R.M.S.F.; Casals, M. Automated data-processing technique: 2D Map for identifying the distribution of the U-value in building elements by quantitative internal thermography. Autom. Constr. 2021, 122, 103478. [Google Scholar] [CrossRef]
- Pang, G.; Wang, N.; Fang, H.; Liu, H.; Huang, F. Study of damage quantification of concrete drainage pipes based on point cloud segmentation and reconstruction. Buildings 2022, 12, 213. [Google Scholar] [CrossRef]
- Munawar, H.S.; Ullah, F.; Shahzad, D.; Heravi, A.; Qayyum, S.; Akram, J. Civil infrastructure damage and corrosion detection: An application of machine learning. Buildings 2022, 12, 156. [Google Scholar] [CrossRef]
- Stałowska, P.; Suchocki, C.; Rutkowska, M. Crack detection in building walls based on geometric and radiometric point cloud information. Autom. Constr. 2022, 134, 104065. [Google Scholar] [CrossRef]
- Jeon, D.; Kim, M.K.; Jeong, Y.; Oh, J.E.; Moon, J.; Kim, D.J.; Yoon, S. High-accuracy rebar position detection using deep learning–based frequency-difference electrical resistance tomography. Autom. Constr. 2022, 135, 104116. [Google Scholar] [CrossRef]
- Ren, H.; Tian, K.; Hong, S.; Dong, B.; Xing, F.; Qin, L. Visualized investigation of defect in cementitious materials with electrical resistance tomography. Constr. Build. Mater. 2019, 196, 428–436. [Google Scholar] [CrossRef]
- Valero, L.R.; Sasso, V.F.; Vicioso, E.P. In situ assessment of superficial moisture condition in façades of historic building using non-destructive techniques. Case Stud. Constr. Mater. 2019, 10, e00228. [Google Scholar] [CrossRef]
- Hola, A. Measuring of the moisture content in brick walls of historical buildings—The overview of methods. Presented at the IOP Conference Series: Materials Science and Engineering. 2017. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/251/1/012067 (accessed on 31 March 2022).
- Hoła, A. Methodology for the in situ testing of the moisture content of brick walls: An example of application. Archiv. Civ. Mech. Eng. 2020, 20, 114. [Google Scholar] [CrossRef]
- Di Tommaso, A.; Cianfrone, F.; Pascale, G. Detection of internal fissures on rock structural elements of historical buildings. Eng. Fract. Mech. 1990, 35, 473–492. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, Y.; Chen, X.; Xiong, W. Seismic behavior of underground station and surface building interaction system in earth fissure environment. Tunn. Undergr. Space Technol. 2021, 110, 103778. [Google Scholar] [CrossRef]
- Kłosowski, G.; Rymarczyk, T.; Gola, A. Increasing the Reliability of Flood Embankments with Neural Imaging Method. Appl. Sci. 2018, 8, 1457. [Google Scholar] [CrossRef] [Green Version]
- Verdet, C.; Sirieix, C.; Marache, A.; Riss, J.; Portais, J.-C. Detection of undercover karst features by geophysics (ERT) Lascaux cave hill. Geomorphology 2020, 360, 107177. [Google Scholar] [CrossRef]
- Xu, S.; Sirieix, C.; Riss, J.; Malaurent, P. A clustering approach applied to time-lapse ERT interpretation—Case study of Lascaux cave. J. Appl. Geophys. 2017, 144, 115–124. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G.; Hoła, A.; Hoła, J.; Sikora, J.; Tchórzewski, P.; Skowron, Ł. Historical buildings dampness analysis using electrical tomography and machine learning algorithms. Energies 2021, 14, 1307. [Google Scholar] [CrossRef]
- Netto, L.G.; Filho, W.M.; Moreira, C.A.; Donato, F.T.; Helene, L.P.I. Delineation of necroleachate pathways using electrical resistivity tomography (ERT): Case study on a cemetery in Brazil. Environ. Chall. 2021, 5, 100344. [Google Scholar] [CrossRef]
- Ray, A.; Sekar, A.; Hoversten, G.M.; Albertin, U. Frequency domain full waveform elastic inversion of marine seismic data from the Alba field using a Bayesian trans-dimensional algorithm. Geophys. J. Int. 2016, 205, 915–937. [Google Scholar] [CrossRef]
- Carter, S.; Xie, X.; Zhou, L.; Yan, L. Hybrid Monte Carlo 1-D joint inversion of LOTEM and MT. J. Appl. Geophys. 2021, 194, 104424. [Google Scholar] [CrossRef]
- Athens, N.D.; Caers, J.K. Gravity inversion for geothermal exploration with uncertainty quantification. Geothermics 2021, 97, 102230. [Google Scholar] [CrossRef]
- Karolczuk, A.; Kurek, M. Fatigue life uncertainty prediction using the Monte Carlo and Latin hypercube sampling techniques under uniaxial and multiaxial cyclic loading. Int. J. Fatigue 2022, 160, 106867. [Google Scholar] [CrossRef]
- Gnewuch, M.; Wnuk, M. Explicit error bounds for randomized Smolyak algorithms and an application to infinite-dimensional integration. J. Approx. Theory 2020, 251, 105342. [Google Scholar] [CrossRef] [Green Version]
- Li, P.P.; Lu, Z.H.; Zhao, Y.G. An effective and efficient method for structural reliability considering the distributional parametric uncertainty. Appl. Math. Model. 2022, 106, 507–523. [Google Scholar] [CrossRef]
- Liu, S.; Jia, J.; Zhang, Y.D.; Yang, Y. Image reconstruction in electrical impedance tomography based on structure-aware sparse Bayesian learning. IEEE Trans. Med. Imaging 2018, 37, 2090–2102. [Google Scholar] [CrossRef] [Green Version]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E. A non-destructive system based on electrical tomography and machine learning to analyze the moisture of buildings. Sensors 2018, 18, 2285. [Google Scholar] [CrossRef] [Green Version]
- Rymarczyk, T.; Kłosowski, G.; Hoła, A.; Sikora, J.; Wołowiec, T.; Tchórzewski, P.; Skowron, S. Comparison of machine learning methods in electrical tomography for detecting moisture in building walls. Energies 2021, 14, 2777. [Google Scholar] [CrossRef]
- Pidlisecky, A.; Knight, R. FW2_5D: A MATLAB 2.5-D electrical resistivity modeling code. Comput. Geosci. 2008, 34, 1645–1654. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Günther, T.; Rücker, C.; Spitzer, K. Three-dimensional modelling and inversion of dc resistivity data incorporating topography—II. Inversion. Geophys. J. Int. 2006, 166, 506–517. [Google Scholar] [CrossRef] [Green Version]
- Watkins, D.S. Fundamentals of Matrix Computations, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Arboleda-Zapata, M.; Guillemoteau, J.; Tronicke, J. A comprehensive workflow to analyze ensembles of globally inverted 2D electrical resistivity models. J. Appl. Geophys. 2022, 196, 104512. [Google Scholar] [CrossRef]
- Wolke, R.; Schwetlick, H. Iteratively reweighted least Squares: Algorithms, Convergence Analysis, and Numerical Comparisons. SIAM J. Sci. Stat. Comput. 1988, 9, 907–921. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Fernández-Muñiz, Z. The curse of dimensionality in inverse problems. J. Comput. Appl. Math. 2020, 369, 112571. [Google Scholar] [CrossRef]
- Jafadideh, A.T.; Asl, B.M. A new data covariance matrix estimation for improving minimum variance brain source localization. Comput. Biol. Med. 2022, 143, 105324. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Wang, X.; Zhu, R.; Wang, D. Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings. Buildings 2022, 12, 622. https://doi.org/10.3390/buildings12050622
Xu S, Wang X, Zhu R, Wang D. Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings. Buildings. 2022; 12(5):622. https://doi.org/10.3390/buildings12050622
Chicago/Turabian StyleXu, Shan, Xinran Wang, Ruiguang Zhu, and Ding Wang. 2022. "Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings" Buildings 12, no. 5: 622. https://doi.org/10.3390/buildings12050622
APA StyleXu, S., Wang, X., Zhu, R., & Wang, D. (2022). Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings. Buildings, 12(5), 622. https://doi.org/10.3390/buildings12050622






