Investigation of Pedestrian-Level Wind Environment with Skyline Quantitative Factors
Abstract
1. Introduction
2. Materials and Methods
2.1. Evaluation Index
2.1.1. Evaluation Index of the Skyline Quantitative
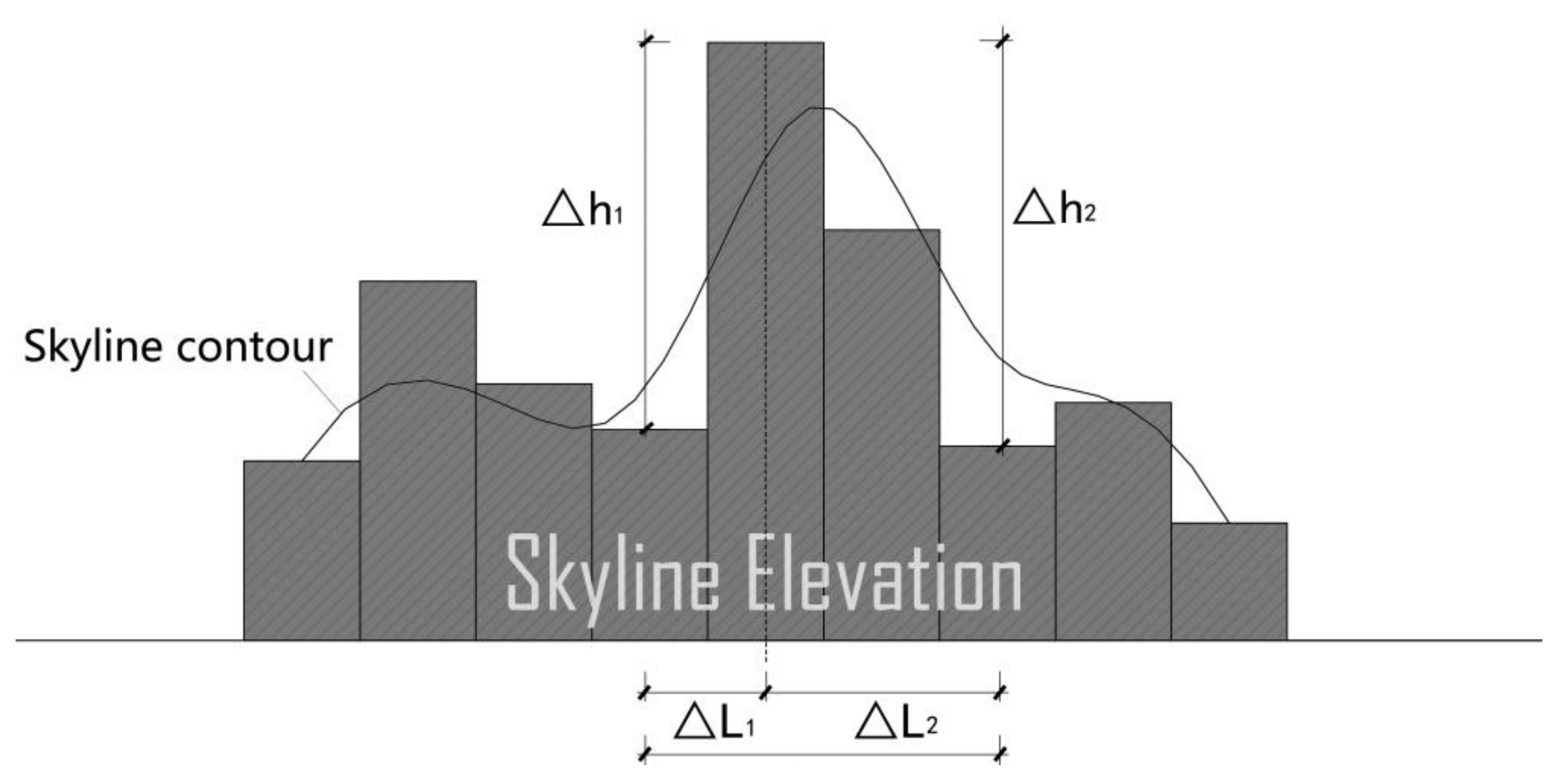
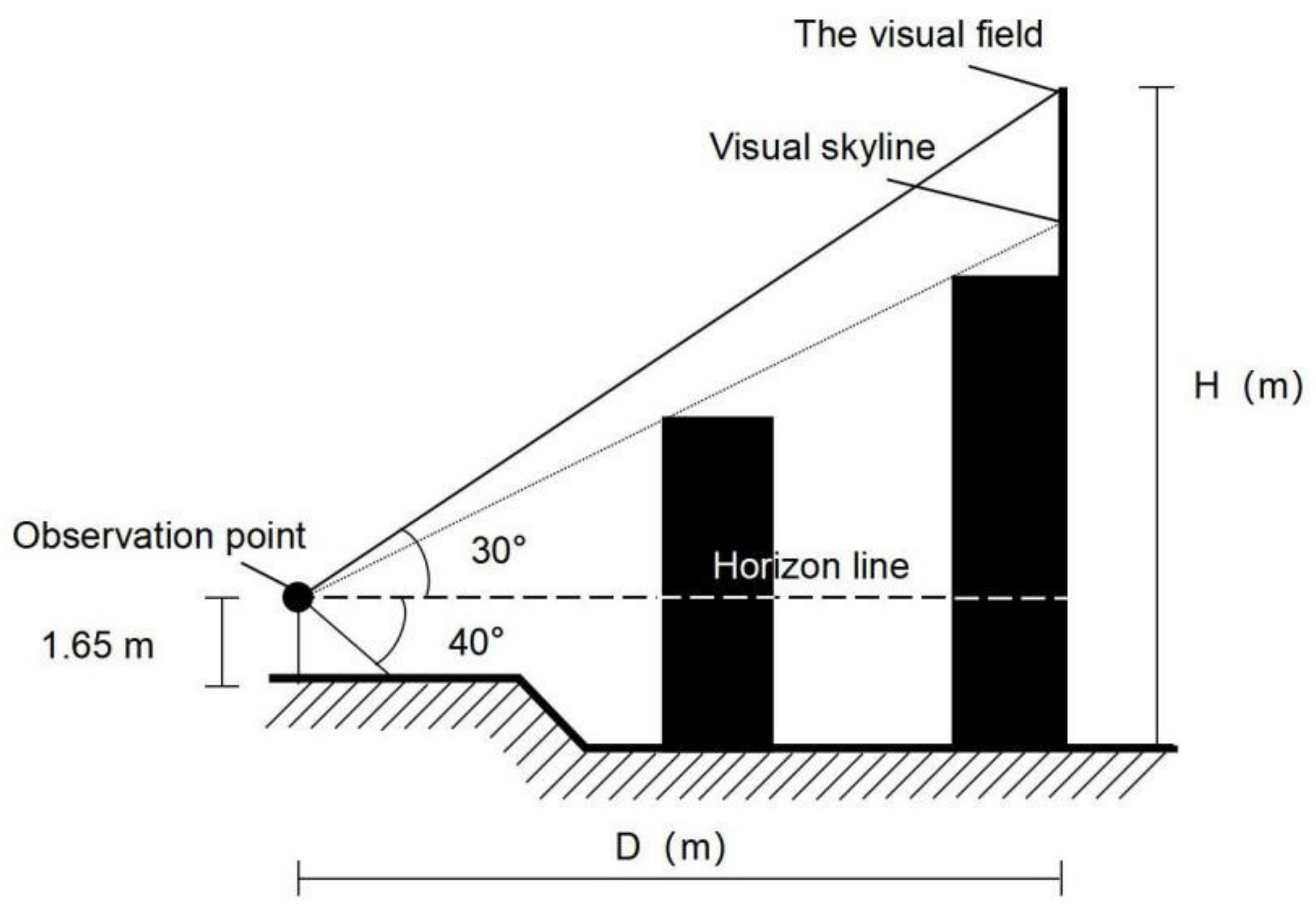
- Contour tortuosity: it represents the wave of the skyline (Figure 1). The contour tortuosity is defined by Equation (1). is contour tortuosity of the whole skyline, is single band of contour tortuosity, is the sum of differences of each band between the low and high points, and refers to the horizontal distance of each band [27].
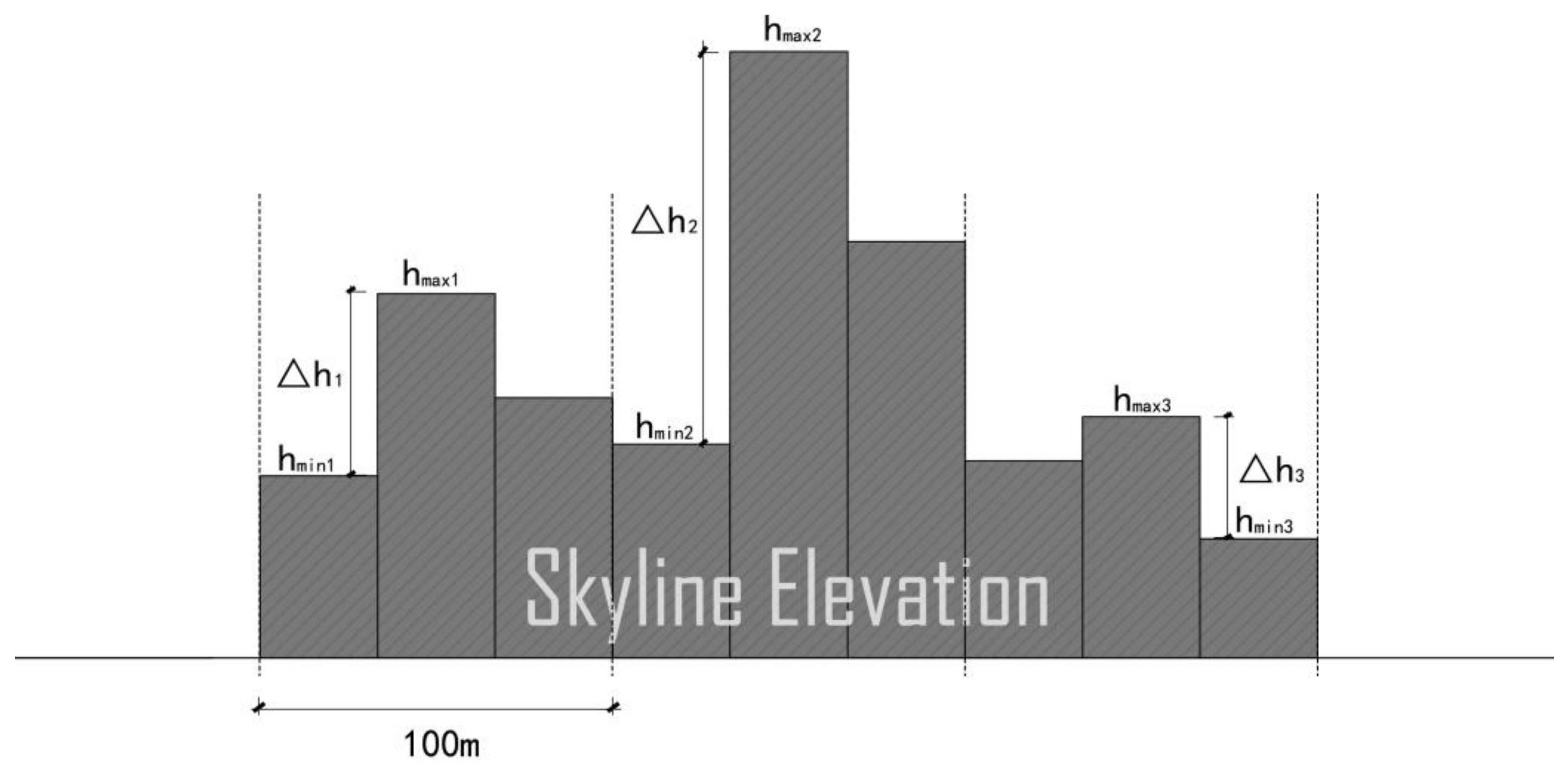
- Building undulation: it represents the lengthwise rhythm of the skyline (Figure 2). It is calculated the percentage of elevation difference between the tallest building and the shortest building (except the podium) in all units according to each 100m horizontal distance as a unit. The building undulation is defined by Equation (2). is building undulation of the whole skyline, is the degree of unit building undulation, which means the difference between the highest building and the lowest building in every 100 m units [28].
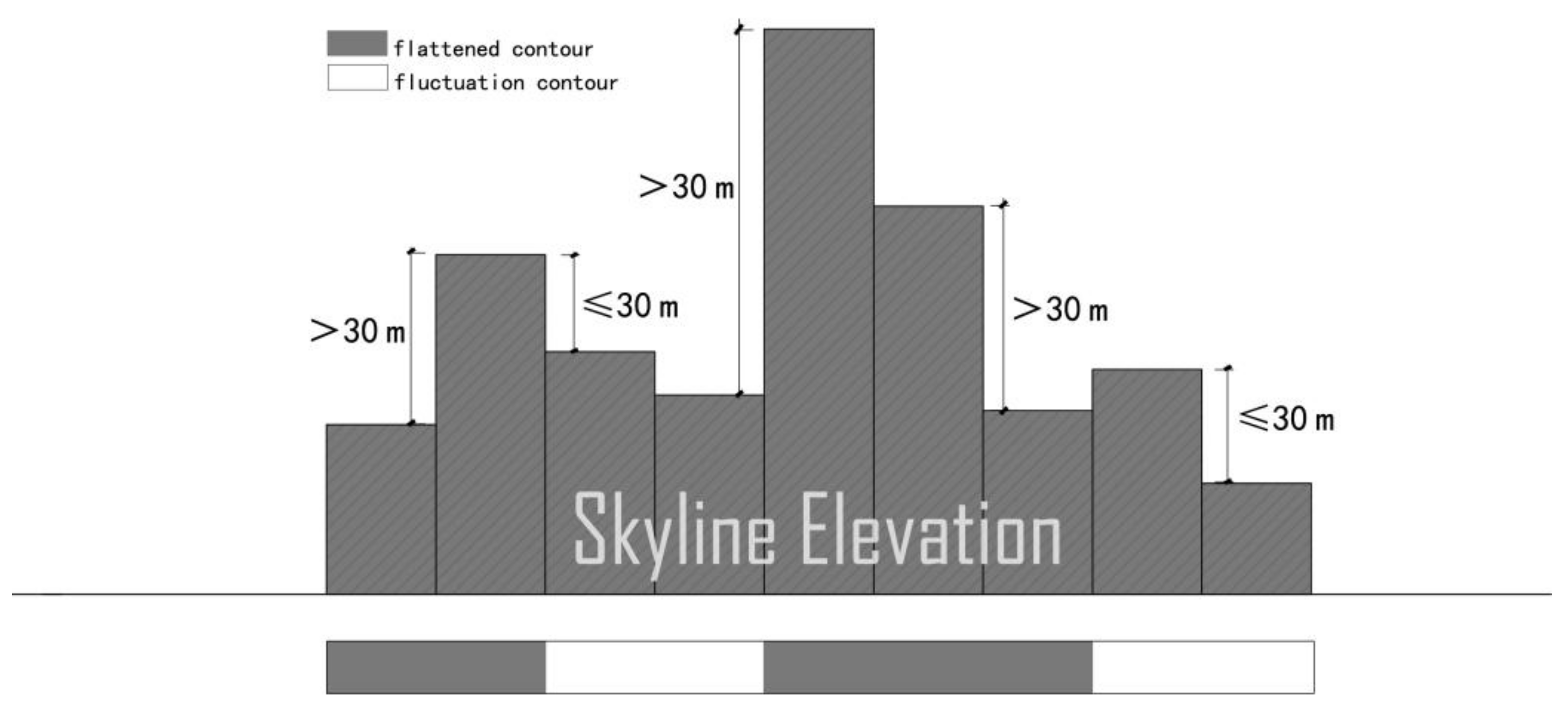
- Skyline rhythm index: it represents the transverse rhythm of the skyline (Figure 3). The contour whose elevation difference between adjacent buildings does not exceed 30 m is defined as a flattened contour, and vice versa as a fluctuation contour. The ratio of the flattened contour length to the total skyline length is calculated. The skyline rhythm index is defined by Equation (3). is skyline rhythm index of the whole skyline, is the length of flattened contour, and is the whole length of the skyline [28].
2.1.2. Evaluation Index of the Wind Environment
- Wind speed ratio: it represents an index to evaluate the comfort level of wind environment comfort. The wind speed ratio is generated according to Equation (4). Rw is the wind speed ratio, Vs is the absolute value of wind speed at the measuring point at the pedestrian height, and v means the absolute value of initial wind speed at the pedestrian height. Previous studies have shown that the wind speed ratio is more comfortable for pedestrians in the range of 0.5–2.0 [29] (Table 1) The evaluation method of wind speed ratio is more objective and is used in current research. However, its disadvantage is that the evaluation of wind speed ratio is difficult to complete the detection of wind environment in the areas for different measuring points.
- Therefore, researchers introduce the average wind speed ratio index to evaluate the regional wind environment. The overall ventilation level of urban scope is reflected by comparing the ratio of average wind speed at pedestrian height to initial wind speed. The average wind speed ratio is generated according to Equation (5). RM is the average wind speed ratio index, Vi is the absolute value of average wind speed at pedestrian height, vr is the absolute value of initial wind speed at the same height [30].
- Wind speed ratio dispersion: it is an important index to evaluate the stability of wind speed. The change in the wind speed is calculated to obtain the dispersion of each district’s wind speed. The high dispersion will cause the unstable distribution of wind speed [31]. Wind speed ratio dispersion is calculated according to Equation (6). is the wind speed ratio dispersion, n means the number of data, and is the average of all values.
2.2. Computational Fluid Dynamics Model
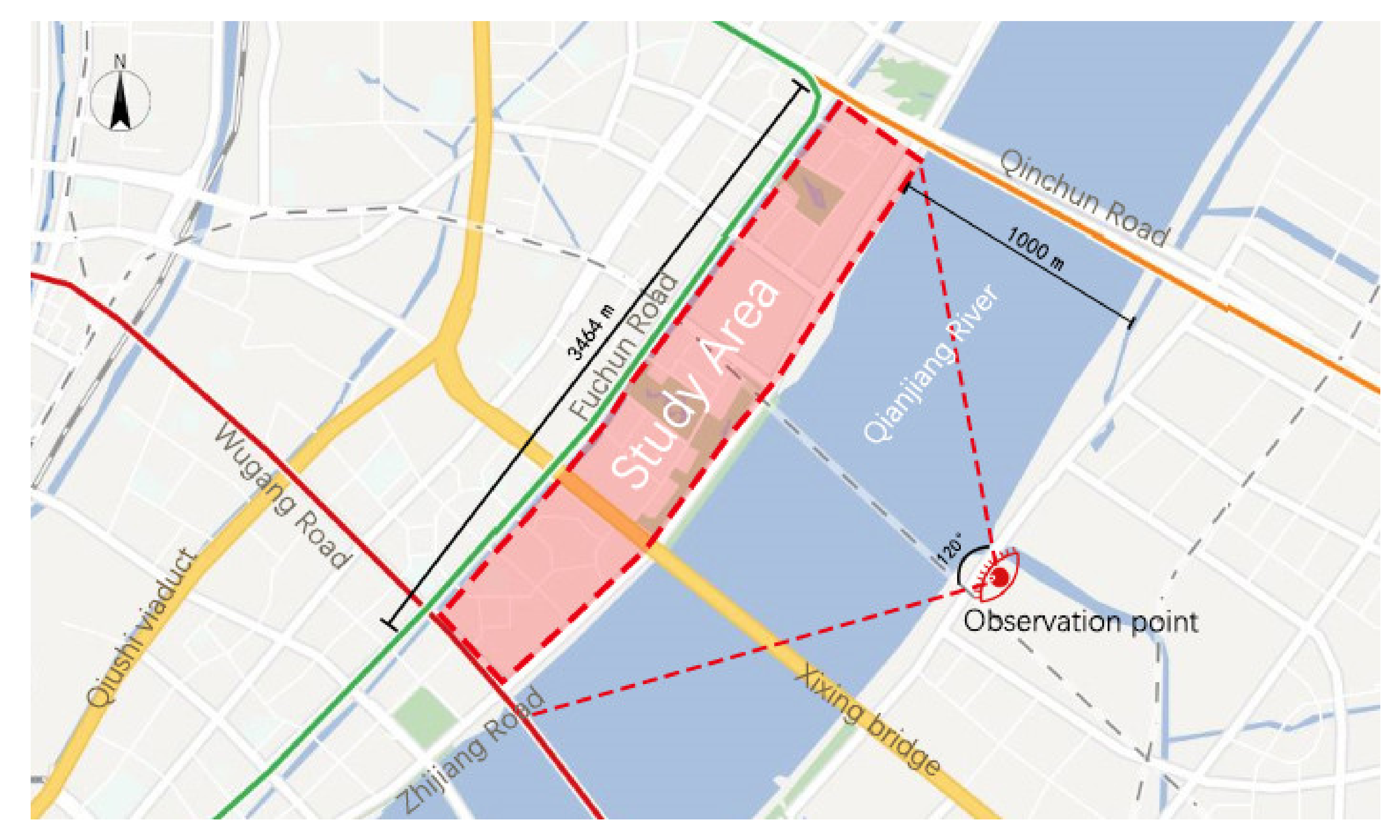
2.2.1. Study Area
2.2.2. Skyline Model
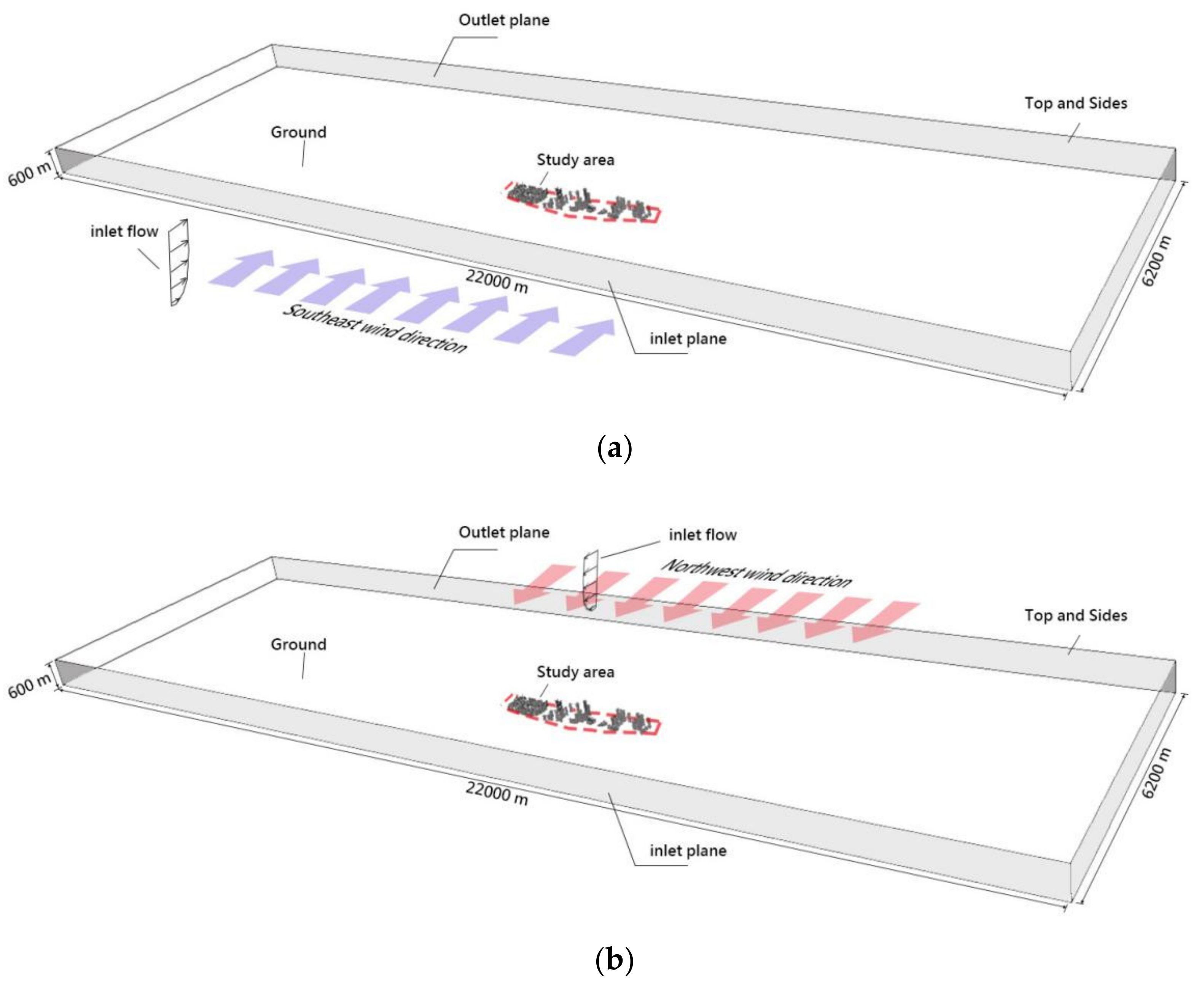
2.2.3. Computational Domain
2.2.4. Boundary Conditions
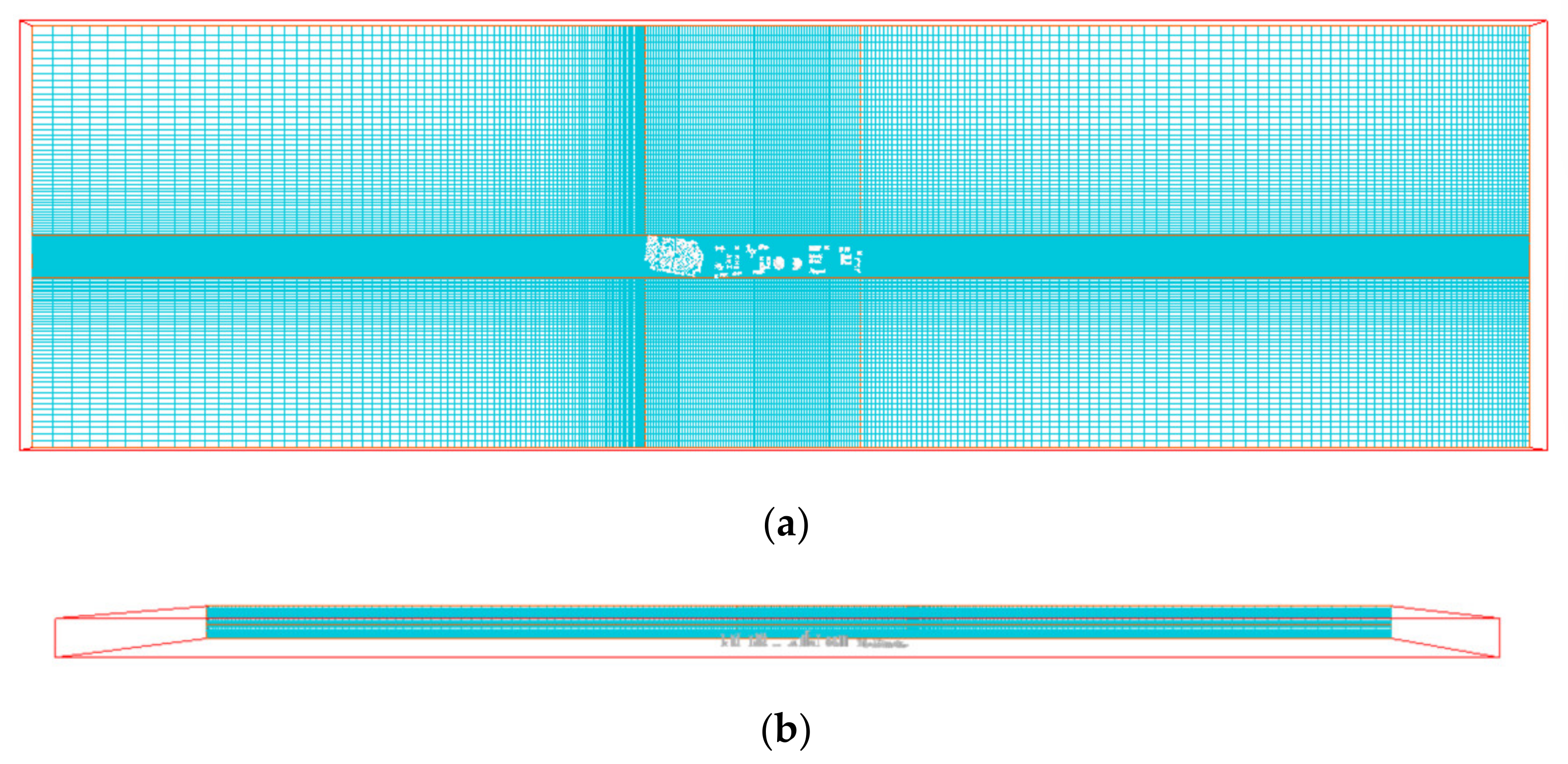
2.2.5. Grid Discretization
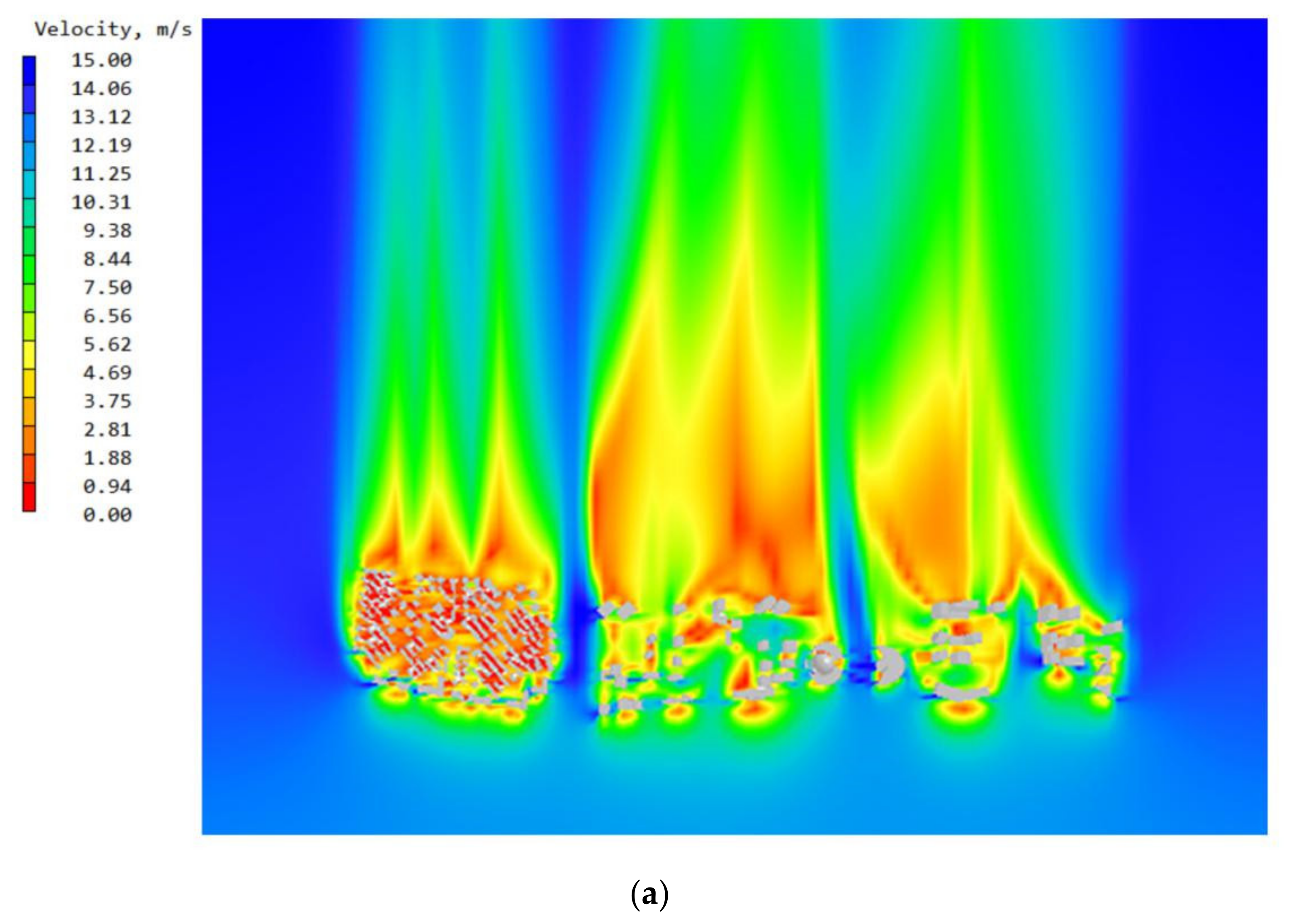
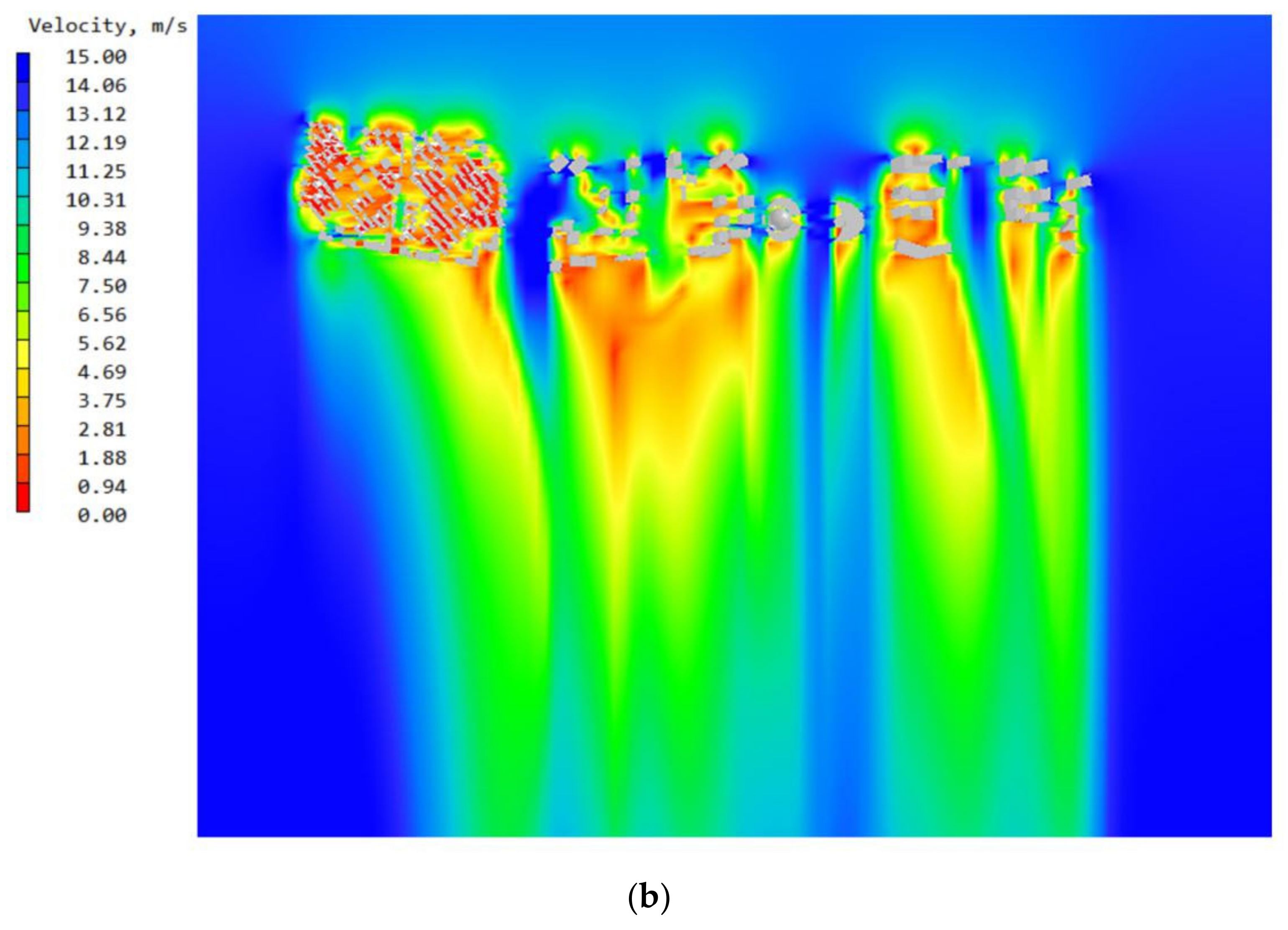
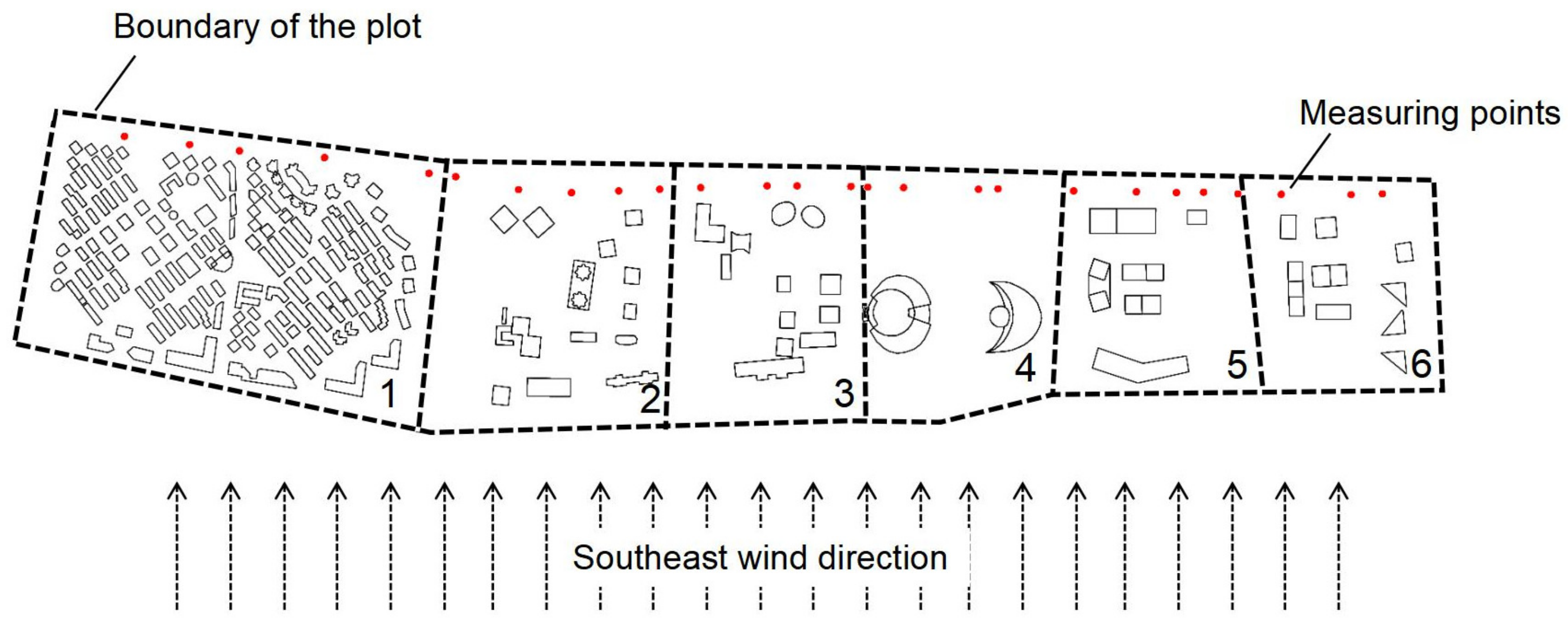
2.2.6. Measuring Points
2.3. Validation of the CFD Simulation
3. Results
3.1. Skyline Morphological Characteristics
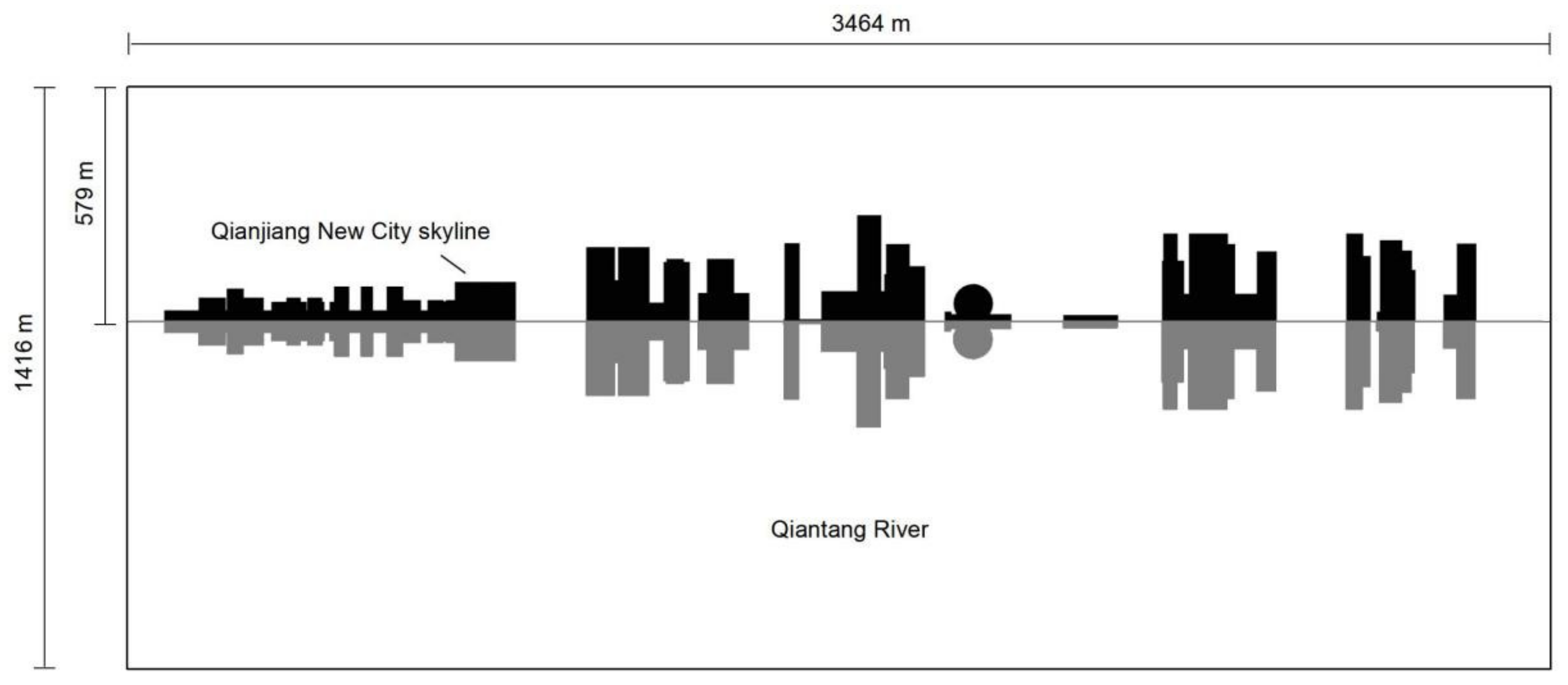
3.1.1. The Virtual Viewing Field of Hangzhou Qianjiang New City Skyline
3.1.2. The Contour Tortuosity of Hangzhou Qianjiang New City Skyline
3.1.3. The Building Undulation of Hangzhou Qianjiang New City Skyline
3.1.4. The Skyline Rhythm Index of Hangzhou Qianjiang New City Skyline
3.2. Analysis of Wind Environment Results
3.2.1. Data Processing
3.2.2. Correlation Test
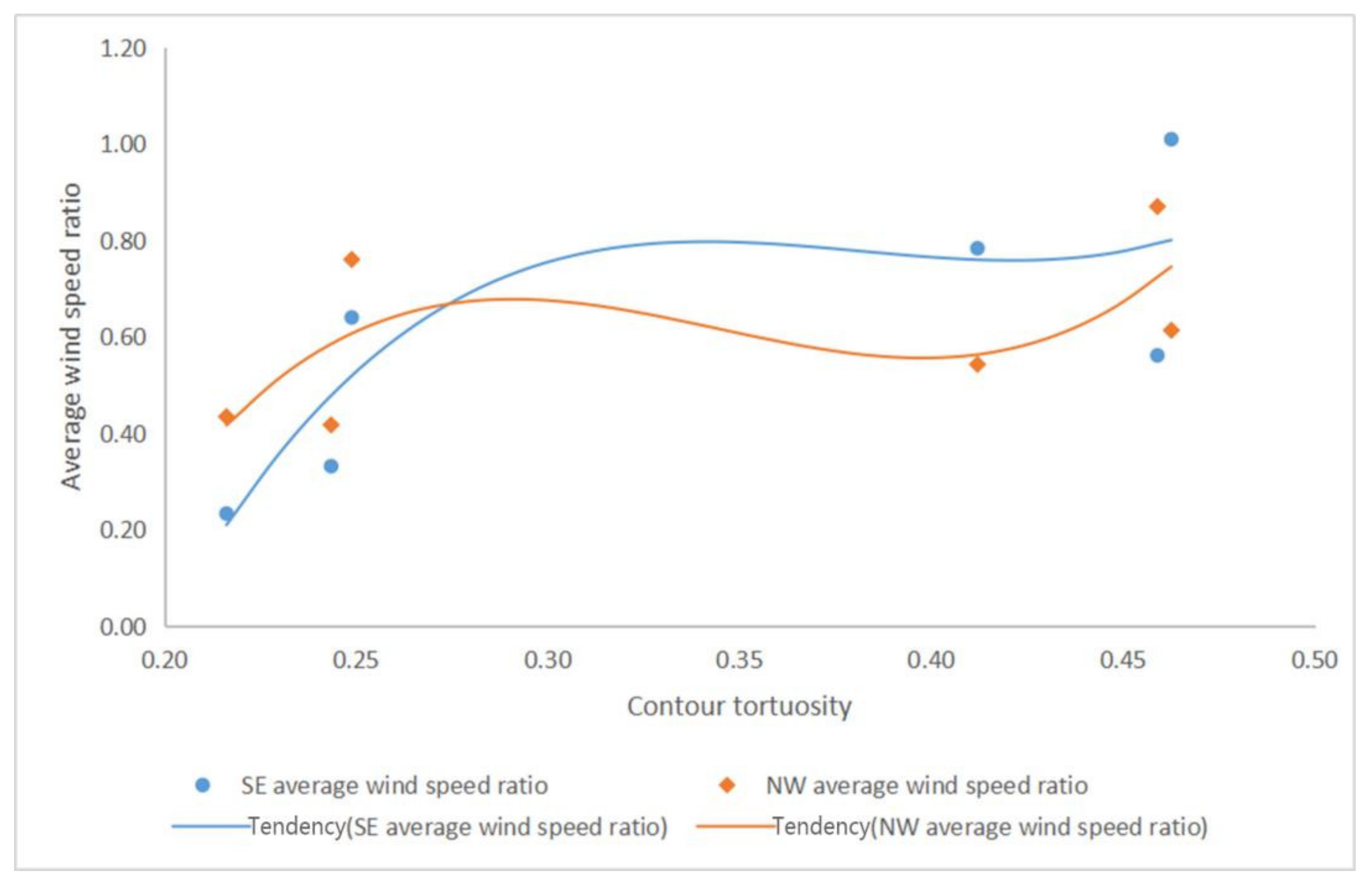
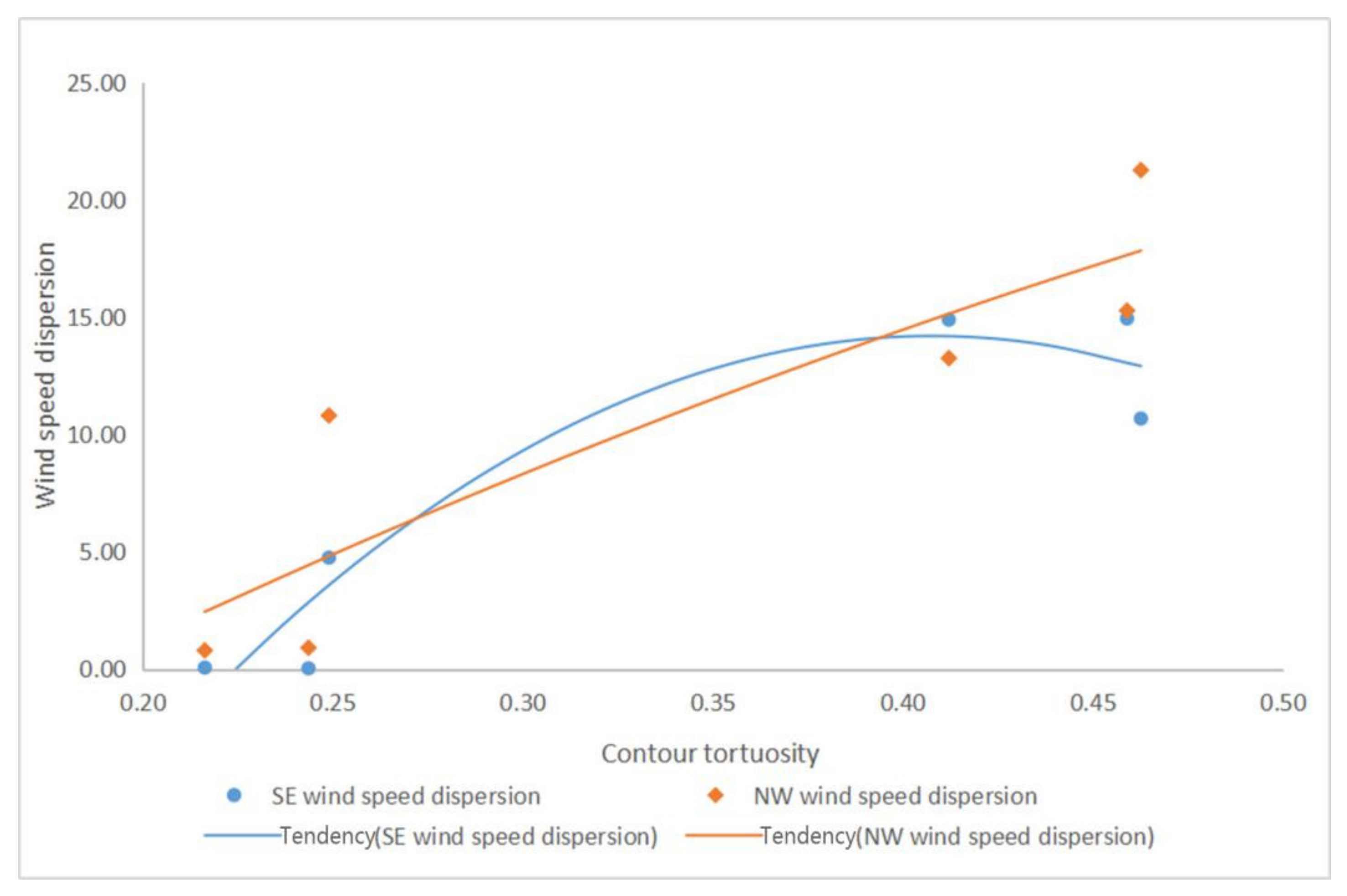
3.2.3. The Relationship between Wind Environment and Contour Tortuosity
The Relationship between the Average Wind Speed Ratio and Contour Tortuosity
The Relationship between the Wind Speed Dispersion and Contour Tortuosity
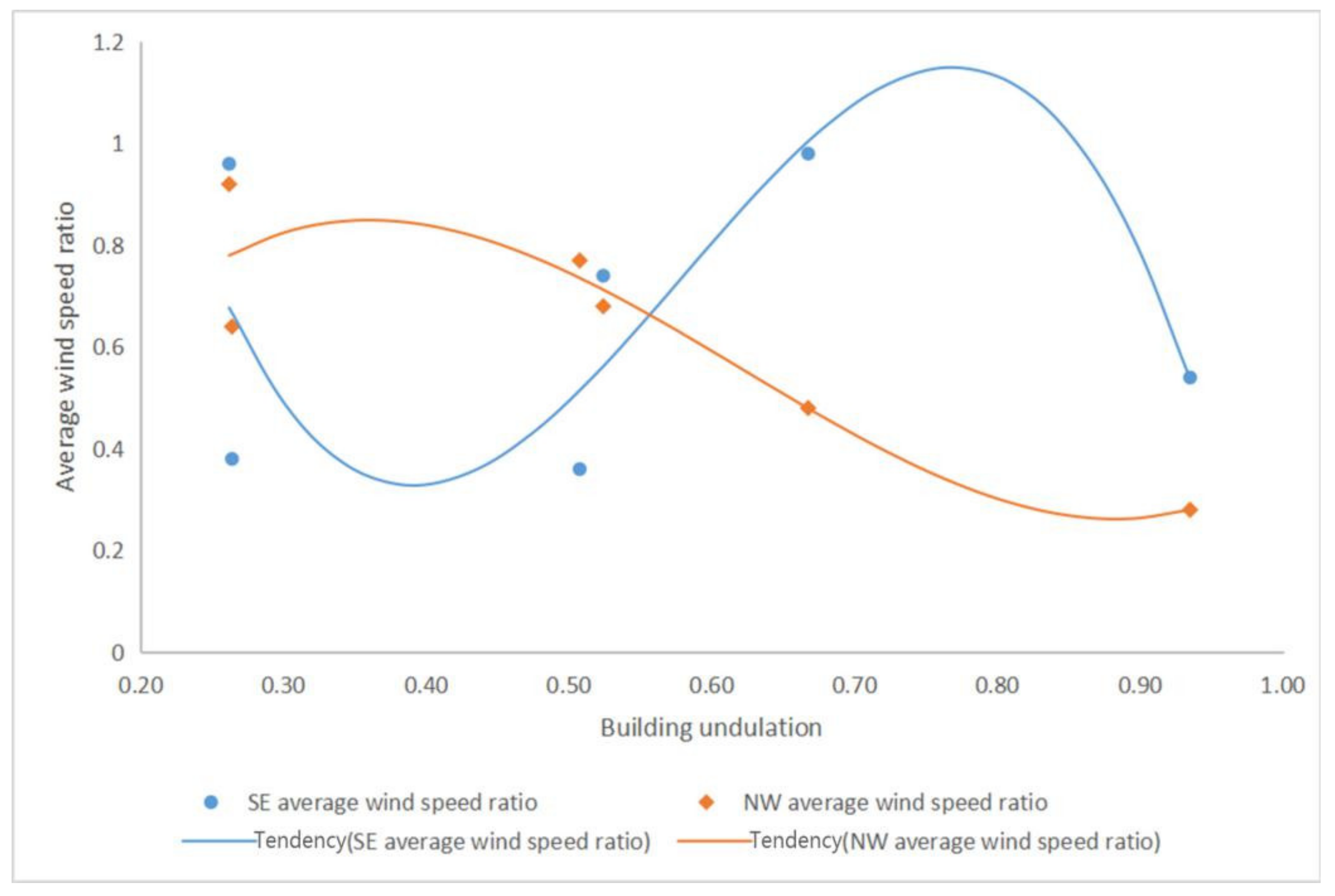
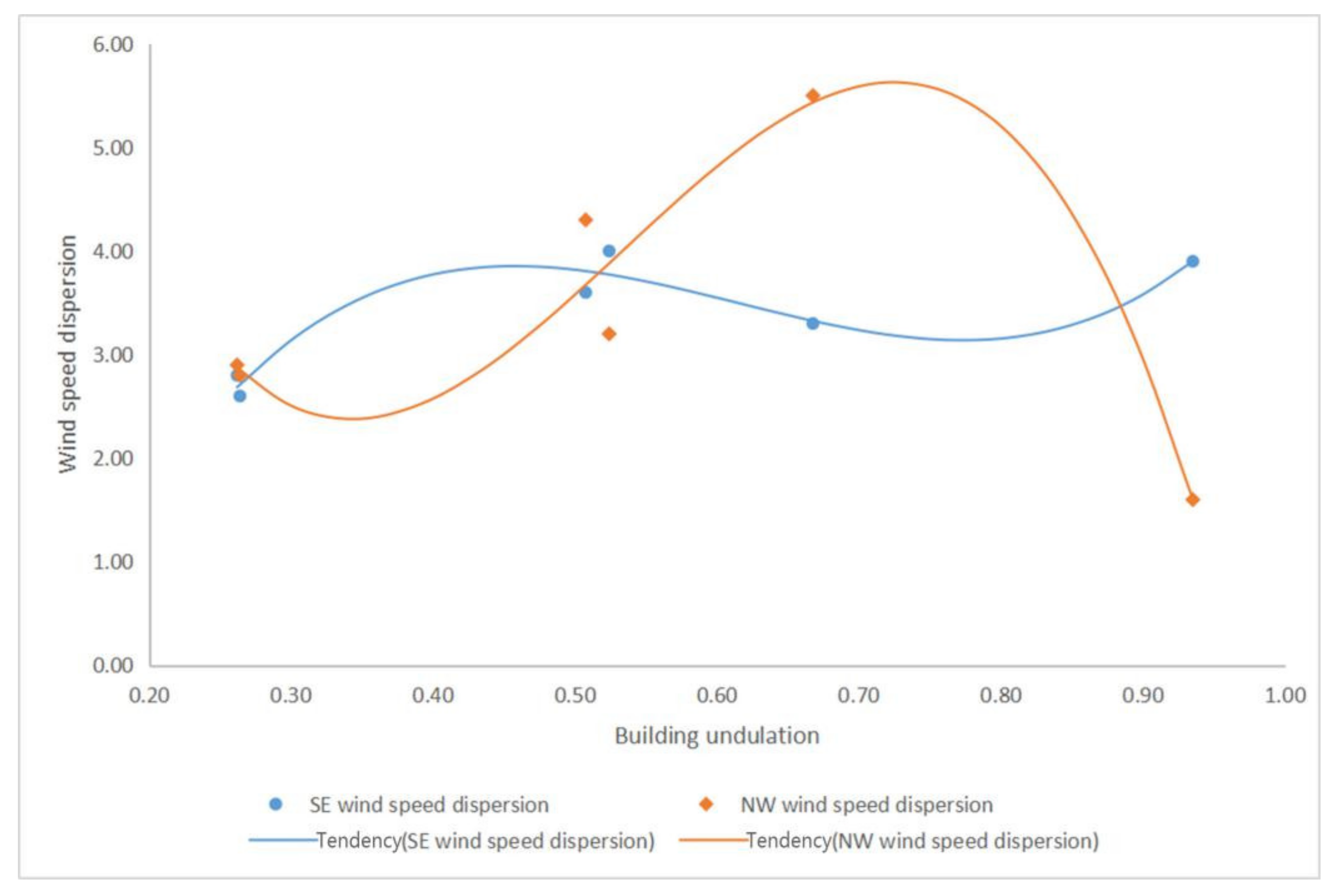
3.2.4. The Relationship between Wind Environment and Building Undulation
The Relationship between the Average Wind Speed Ratio and Building Undulation
The Relationship between the Wind Speed Dispersion and Building Undulation
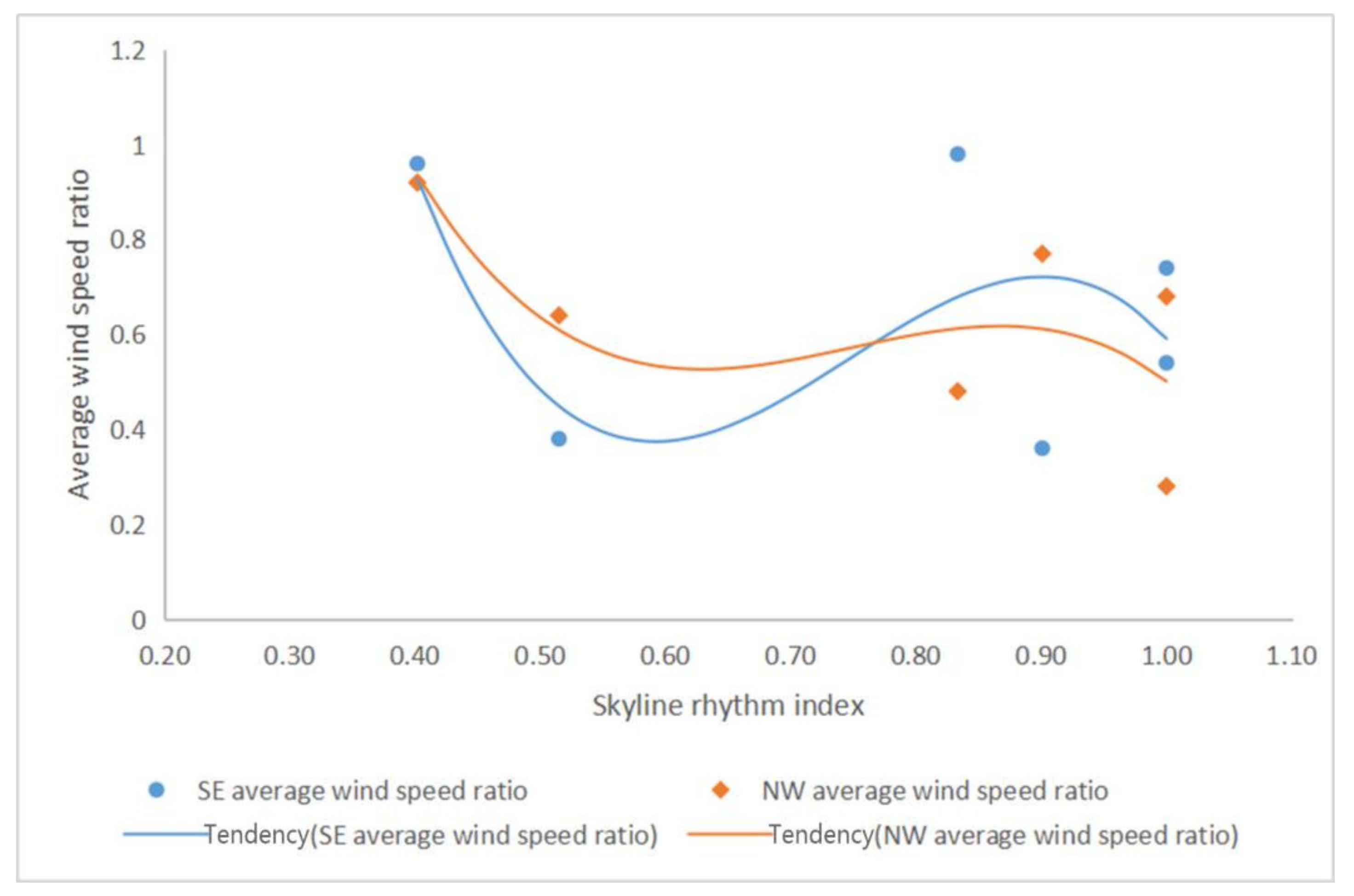
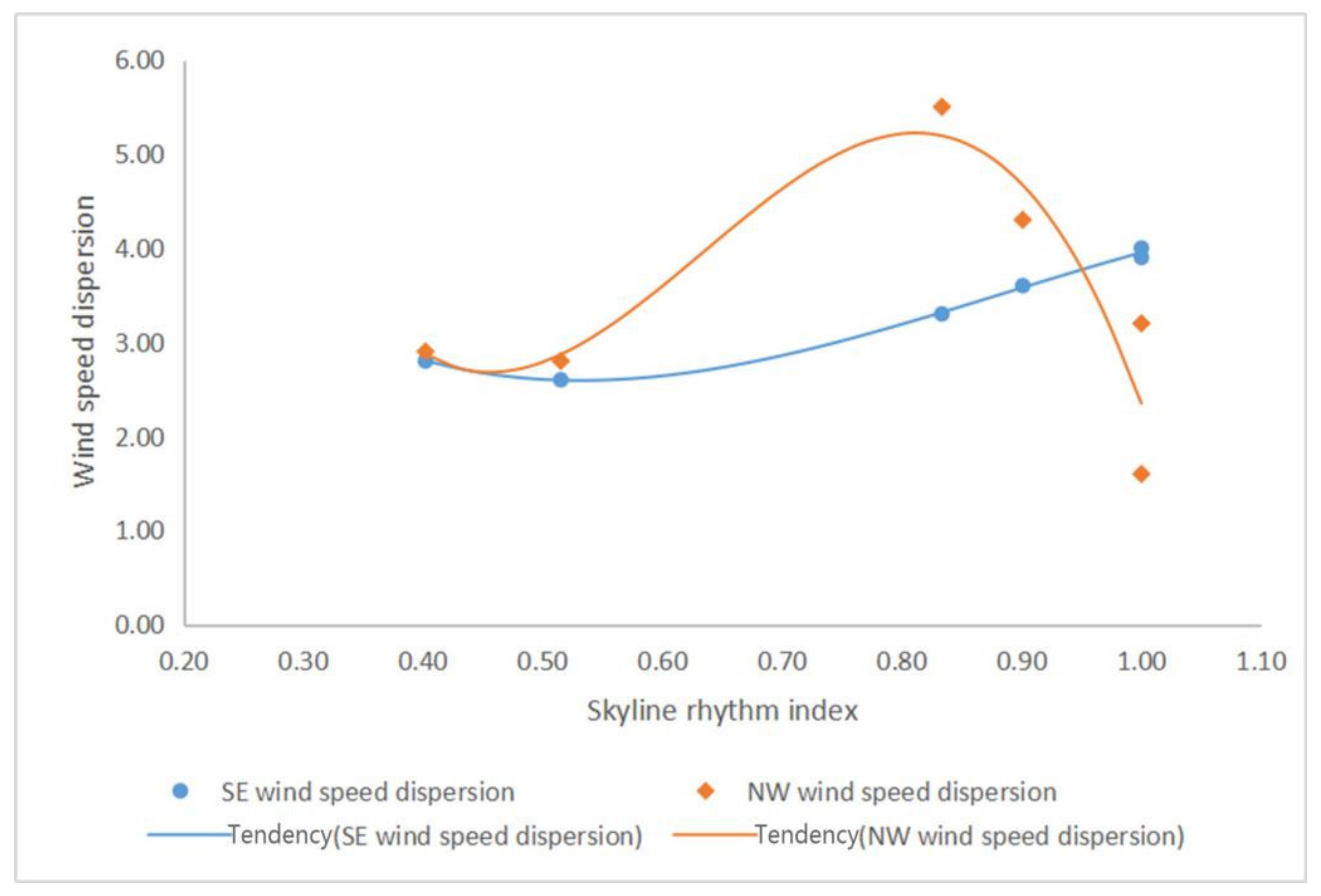
3.2.5. The Relationship between Wind Environment and Skyline Rhythm Index
The Relationship between the Average Wind Speed Ratio and Skyline Rhythm Index
The Relationship between the Wind Speed Dispersion and Skyline Rhythm Index
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics | ||
| CBD | Central business districts | ||
| SPSS | Statistical product and Service Solutions | ||
| SE | Southeast | ||
| NW | Northwest | ||
| F | Fluctuations | ||
| D | Districts | ||
| S | Segments | ||
| ELC | European Landscape Convention | ||
| KC | Contour tortuosity | ||
| kn | Single band of contour tortuosity | ||
| △H | The sum of differences of each band between the low and high points | meter/meters | m |
| △L | The horizontal distance of each band | meter/meters | m |
| U | building undulation | ||
| △hn | The degree of unit building undulation | meter/meters | m |
| n | The units of building undulation | ||
| Rf | Skyline rhythm index | ||
| w | The length of fluctuation contour | meter/meters | m |
| L | The whole length of the skyline | meter/meters | m |
| Rw | Wind speed ratio | ||
| Vs | The absolute value of wind speed at the measuring point at the pedestrian height | meters per second | m/s |
| v | the absolute value of initial wind speed at The pedestrian height | meters per second | m/s |
| RM | The average wind speed ratio index | ||
| Vi | The absolute value of average wind speed at pedestrian height | meters per second | m/s |
| vr | The absolute value of initial wind speed at the same height | meters per second | m/s |
| σ | Wind speed ratio dispersion | ||
| n | The number of data | ||
| μ | The average of all values | meters per second | m/s |
| L | The width of the visual viewing field | meter/meters | m |
| D | The visual viewing range | meter/meters | m |
| H | The height of viewing field | meter/meters | m |
| U(z) | The average wind speed at height | meters per second | m/s |
| Z | Height | meter/meters | m |
| UG | The average wind speed at the standard height ZG | meters per second | m/s |
| ZG | The standard height | meter/meters | m |
| α | a parameter to describe the surface roughness | ||
| P | The significance value | ||
| R | The correlation values | ||
References
- Fisher-Gewirtzman, D.; Burt, M.; Tzamir, Y. A 3-d visual method for comparative evaluation of dense built-up environments. Environ. Plan. B Plan. Des. 2003, 30, 575–587. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, L. Arrangement and creation of urban horizon landscape in coastal city around mountains—Case study on the coastal skyline of Yantai City. Urban Stud. 2010, 17, 77–84. [Google Scholar]
- Niu, X.; Li, K. A quantitative to visual impact analysis of city skyline. Urban Plan. Forum 2013, 3, 99–105. [Google Scholar]
- Shi, Y.; Cao, J.; Zhu, X. City skyline aesthetic analysis based on evaluation model. Mod. Urban Res. 2018, 10, 67–74. [Google Scholar]
- Stamps, A.; Nasar, J.L.; Hanyu, K. Using pre-construction validation to regulate urban skylines. J. Am. Plan. Assoc. 2005, 71, 73–91. [Google Scholar] [CrossRef]
- Imamoglu, Ç. Complexity, liking and familiarity: Architecture and non-architecture Turkish students’ assessments of traditional and modern house facades. J. Environ. Psychol. 2000, 20, 5–16. [Google Scholar] [CrossRef]
- Stamps, A. Fractals, skylines, nature and beauty. Landsc. Urban Plan. 2002, 60, 163–184. [Google Scholar] [CrossRef]
- Nasar, J.; Terzano, K. The desirability of views of city skylines after dark. J. Environ. Psychol. 2010, 30, 215–225. [Google Scholar] [CrossRef]
- Le, D.; Li, N.; Su, L.; .Li, J.; Wei, X. Numerical simulation of wind environment in the urban areas. Saf. Environ. 2012, 12, 257–262. [Google Scholar]
- Zhou, X.; Chen, H. A research on the impact of different city development models on climates in central urban areas: A case study of Wuhan. Archit. Pract. 2019, 2, 27–28. [Google Scholar]
- Zhao, Q.; Zhang, T. A preliminary study on the integration of evaluation methods and strategies for urban outdoor wind environment. In Proceedings of the 2015 China Urban Planning Annual Conference, Guiyang, China, 19–21 September 2015; pp. 215–229. [Google Scholar]
- Van Hove, L.W.A.; Jacobs, C.M.J.; Heusinkveld, B.G.; Elbers, J.A.; van Driel, B.L.; Holtslag, A.A.M. Temporal and spatial variability of urban heat island and thermal comfort within the Rotterdam agglomeration. Build. Environ. 2015, 83, 91–103. [Google Scholar] [CrossRef]
- Adamek, K.; Vasan, N.; Elshaer, A.; English, E.; Bitsuamlak, G. Pedestrian level wind assessment through city development: A study of the financial district in Toronto. Sustain. Cities Soc. 2017, 35, 178–190. [Google Scholar] [CrossRef]
- Zhuang, A.; Gao, C.; Ling, Z. Numerical simulation of the wind field around different building arrangements. Wind Eng. Ind. Aerodyn. 2005, 93, 891–904. [Google Scholar] [CrossRef]
- Chen, H. The effect of building shape and its arrangement on ventilation efficiency in urban area. J. Wuhan Univ. Technol. 2002, 7, 44–46. [Google Scholar]
- Blocken, B.; Persoon, J. Pedestrian wind comfort around a large football stadium in an urban environment: CFD simulation validation and application of the new Dutch wind nuisance standard. Wind Eng. Ind. Aerodyn. 2008, 96, 621–639. [Google Scholar] [CrossRef]
- Ying, X.; Wang, Y.; Li, W.; Liu, Z.; Ding, G. Group layout pattern and outdoor wind environment of enclosed office buildings in Hangzhou. Energies 2020, 13, 406. [Google Scholar] [CrossRef]
- Takebayashi, H.; Moriyama, M.; Miyake, K. Analysis on the relationship between properties of urban block and wind path in the street canyon for the use of the wind as the climate resources. J. Environ. Eng. 2009, 74, 77–82. [Google Scholar] [CrossRef][Green Version]
- Shan, Y.; Cai, X.; Zhang, D. Research on comfortable spatial pattern of microclimate in waterfront residential areas of cold regions: A case study of Tianjiahu Residential Area in Tianjin. Build. Sci. 2022, 38, 82–88. [Google Scholar]
- Zhang, H.; Yang, W. The application of natural ventilation in the traditional dwelling. Archit. Cult. 2016, 2, 164–165. [Google Scholar]
- Chang, C.-H.; Meroney, R.N. Concentration and flow distributions in urban street canyons: Wind tunnel and computational data. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1141–1154. [Google Scholar] [CrossRef]
- Ma, J.; Chen, S. Numerical study of plan arrangement effect on wind environment around tall buildings. J. Zhejiang Univ. 2007, 9, 1477–1481. [Google Scholar]
- Blocken, B.; Carmeliet, J. Guidelines for the required time resolution of meteorological input data for wind-driven rain calculations on buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 621–639. [Google Scholar] [CrossRef]
- Chen, L.; Hang, J.; Sandberg, M.; Claesson, L.; Di Sabatino, S.; Wigo, H. The impacts of building height variations and building packing densities on flow adjustment and city breathability in idealized urban models. Build. Environ. 2017, 118, 344–361. [Google Scholar] [CrossRef]
- Jian, H.; Yu, G. Ventilation strategy and air change rates in idealized high-rise compact urban areas. Build. Environ. 2010, 45, 2754–2767. [Google Scholar]
- Kono, T.; Tamura, T.; Ashie, Y. Numerical investigations of mean winds within canopies of regularly arrayed cubical buildings under neutral stability conditions. Bound. Layer Meteorol. 2009, 134, 131–155. [Google Scholar] [CrossRef]
- Yang, J.; Pan, Y.; Shi, B. Evaluation of overlooking views of city central district:the case of Hong Kong. Urban Plan. Forum 2013, 5, 106–112. [Google Scholar]
- Lyu, S.; Yan, T.; Li, L. Comparison of the studies on quantitative index evaluation of urban skyline aesthetics. Hous. Sci. 2019, 39, 27–31. [Google Scholar]
- Kubota, T.; Miura, M.; Tominaga, Y.; Mochida, A. Wind tunnel tests on the relationship between building density and pedestrian-level wind velocity: Development of guidelines for realizing acceptable wind environment in residential neighborhoods. Build. Environ. 2008, 43, 1699–1708. [Google Scholar] [CrossRef]
- Xie, Z.; Lu, Y.; Yu, X. Experimental investigation on pedestrian-level wind environment around a high-rise building. J. Tongji Univ. 2020, 48, 1726–1732. [Google Scholar]
- Ye, Z. Wind environment oriented urban block spatial design-a case study of CAUP area Tongji University. In Proceedings of the 2010 Urban Development and Planning International Conference, Qinhuangdao, China, 22 June 2010; pp. 301–305. [Google Scholar]
- Niu, X.; Xu, F. Quantitative evaluation of spatial openness of built environment using visual impact analysis. Urban Plan. Forum 2011, 1, 91–97. [Google Scholar]
- Zhuang, Z.; Yu, Y.; Ye, H.; Tan, H.; Xie, J. Review on CFD simulation technology of wind environment around buildings. Build. Sci. 2014, 30, 108–114. [Google Scholar]
- Franke, J.; Hellsten, A.; Schlunzen, K.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419. [Google Scholar] [CrossRef]
- Yu, B.; He, X.; Wei, L.; Chen, L.; Zhou, W. Primary exploration for construction of urban multilevel ventilation corridors system in Hangzhou. J. Meteorol. Sci. 2018, 38, 625–636. [Google Scholar]
- Davenport, A.G. An approach to human comfort criteria for environment wind conditions. In Proceedings of the the Colloquium on Building Climatology, Stockholm, Sweden, 4–6 September 1972. [Google Scholar]
- Yoshie, R.; Mochida, A.; Tominaga, Y.; Kataoka, H.; Harimoto, K.; Nozu, T.; Shirasawa, T. Cooperative project for CFD prediction of pedestrian wind environment in the Architectural Institute of Japan. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1551–1578. [Google Scholar] [CrossRef]
- Franke, J.; Hirsch, C.; Jensen, A.G.; Krüs, H.W.; Schatzmann, M.; Westbury, P.S.; Miles, S.D.; Wisse, J.A.; Wright, N.G. Recommendations on the use of CFD in wind engineering. In COST Action C14, Impact of Windand Storm on City Life Built Environment, Proceedings of the International Conference on Urban Wind Engineeringand Building Aerodynamics, Rhode-St-Genèse, Belgium, 5–7 May 2004; Van Beeck, J.P.A.J., Ed.; von Karman Institute: Sint-Genesius-Rode, Belgium, 2004. [Google Scholar]
- Jones, M.; Stenseke, M. The European Landscape Convention; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Zhu, B. Skyline aesthetics. Urban Plan. Overseas 1987, 03, 35–43. [Google Scholar]





| Wind Speed Ratio | Human Comfort |
|---|---|
| >2 | Too strong wind |
| 0.5–2 | Comfortable |
| <0.5 | No air circulation |
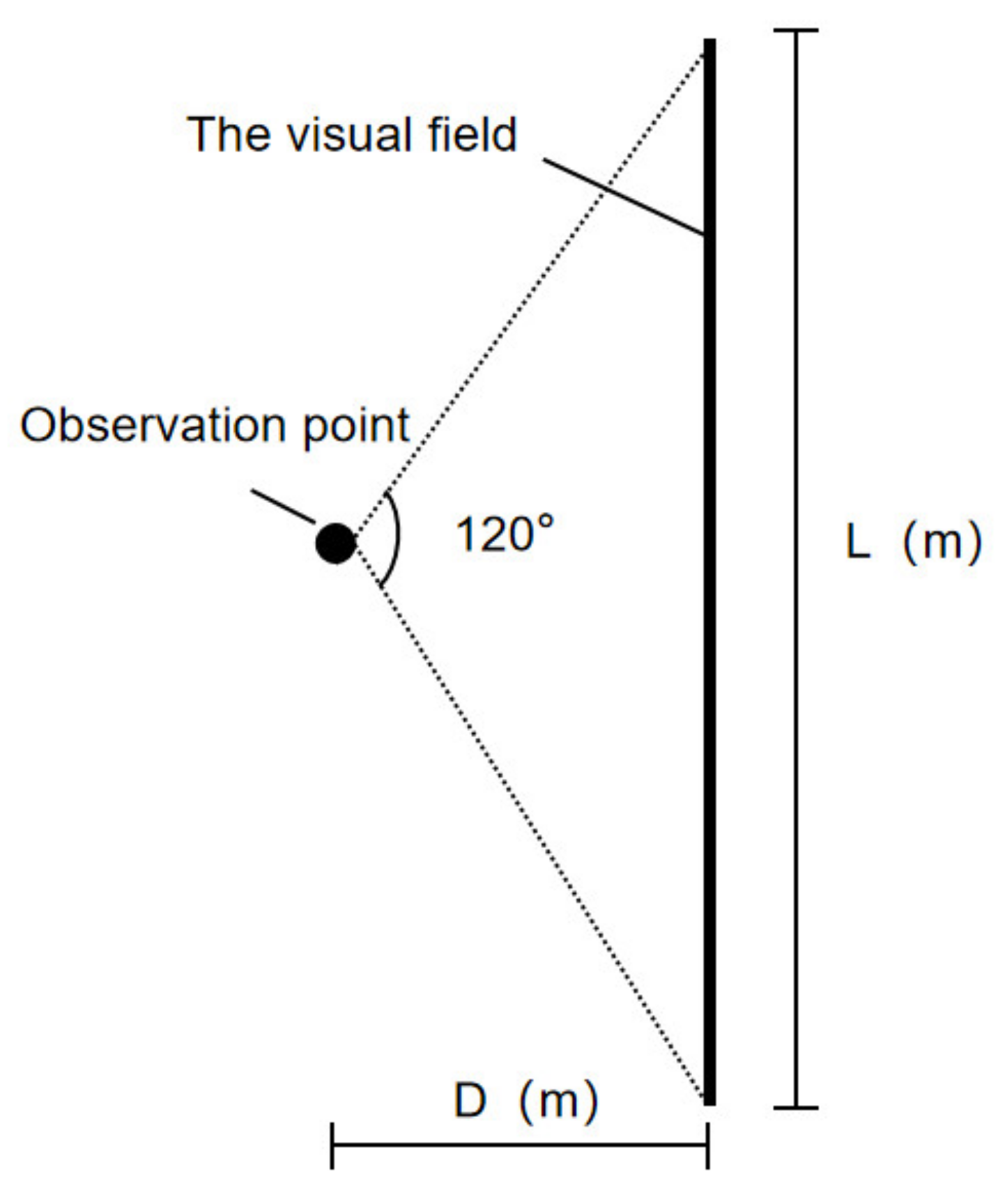
| Hierarchical Classification | Viewing Distance (m) | Viewing Range |
|---|---|---|
| The front skyline | <300 | Architectural details |
| The middle skyline | 500–1000 | Overall skyline |
| The far part skyline | 1000–4000 | The whole skyline including background |
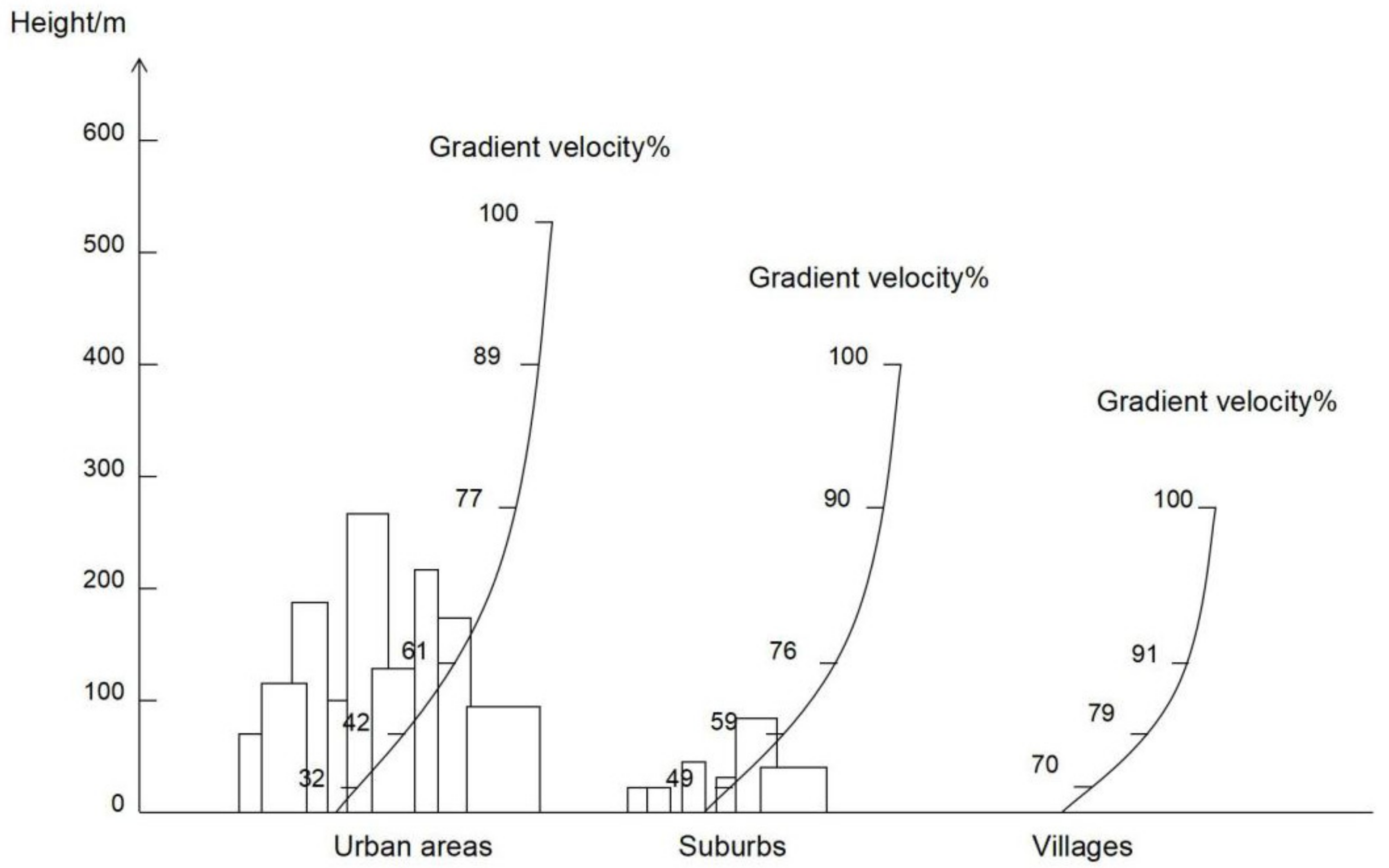
| Classification | Properties of Underlying Surface | α | ZG(m) |
|---|---|---|---|
| A | Offshore sea surface and island, coast, lakeshore, and desert areas | 0.12 | 300 |
| B | Fields, villages, jungles, hills, towns, and suburbs with sparse houses | 0.16 | 350 |
| C | Urban areas with dense buildings | 0.22 | 400 |
| D | Urban areas with dense buildings and high housing | 0.30 | 450 |
| Computational Condition | Settings |
|---|---|
| Computational domain | 22,000 m × 6200 m × 600 m |
| Turbulence model | Standard k-ε turbulence model |
| Convergence criteria | ≤10−4 |
| Time step | 1 |
| Flow boundary | summer-southeast wind, winter-northwest wind; v = 10 m/s |
| Outflow boundary | Natural outflow |
| Boundary condition | Top and sides-Free-slip wall; Ground-No-slip wall |
| Grid resolution | 260 (x) × 148 (y) × 31 (z) = 1,192,880 cells |
| Fluctuations | F1 | F2 | F3 | F4 | F5 | F6 |
|---|---|---|---|---|---|---|
| Kc | 0.24 | 0.22 | 0.25 | 0.41 | 0.46 | 0.46 |
| Districts | D1 | D2 | D3 | D4 | D5 | D6 |
|---|---|---|---|---|---|---|
| U | 2.64 | 5.24 | 9.35 | 2.62 | 6.68 | 5.08 |
| Segments | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|
| Rf | 0.52 | 1.00 | 1.00 | 0.40 | 0.83 | 0.90 |
| Wind Environment Evaluation Index | RM | σ | ||
|---|---|---|---|---|
| Wind Direction | SE | NW | SE | NW |
| F1 | 0.33 | 0.42 | 0.04 | 0.92 |
| F2 | 0.23 | 0.43 | 0.07 | 0.80 |
| F3 | 0.64 | 0.76 | 4.76 | 10.82 |
| F4 | 0.78 | 0.54 | 14.90 | 13.26 |
| F5 | 1.01 | 0.61 | 10.69 | 21.28 |
| F6 | 0.56 | 0.87 | 14.96 | 15.29 |
| Wind Environment Evaluation Index | RM | σ | ||
|---|---|---|---|---|
| Wind Direction | SE | NW | SE | NW |
| D1 | 0.38 | 0.64 | 2.60 | 2.80 |
| D2 | 0.74 | 0.68 | 4.00 | 3.20 |
| D3 | 0.54 | 0.28 | 3.90 | 1.60 |
| D4 | 0.96 | 0.92 | 2.80 | 2.90 |
| D5 | 0.98 | 0.48 | 3.30 | 5.50 |
| D6 | 0.36 | 0.77 | 3.60 | 4.30 |
| Wind Environment Evaluation Index | RM | σ | ||
|---|---|---|---|---|
| Wind Direction | SE | NW | SE | NW |
| S1 | 0.38 | 0.64 | 2.60 | 2.80 |
| S2 | 0.74 | 0.68 | 4.00 | 3.20 |
| S3 | 0.54 | 0.28 | 3.90 | 1.60 |
| S4 | 0.96 | 0.92 | 2.80 | 2.90 |
| S5 | 0.98 | 0.48 | 3.30 | 5.50 |
| S6 | 0.36 | 0.77 | 3.60 | 4.30 |
| Variables | Wind Directions | P | |
|---|---|---|---|
| Kc | 0.15 | ||
| U | 0.20 | ||
| Rf | 0.17 | ||
| F1–F6 | RM | SE | 0.20 |
| σ | NW | 0.20 | |
| D1–D6 | RM | SE | 0.20 |
| σ | NW | 0.20 | |
| S1–S6 | RM | SE | 0.20 |
| σ | NW | 0.20 | |
| R | RM | σ | ||
|---|---|---|---|---|
| SE | NW | SE | NW | |
| Kc | 0.67 | 0.44 | 0.92 | 0.78 |
| U | 0.43 | 0.83 | 0.93 | 0.91 |
| Rf | 0.34 | 0.50 | 0.83 | 1.00 |
| Fluctuations | F1 | F2 | F3 | F4 | F5 | F6 | |
|---|---|---|---|---|---|---|---|
| Kc | 0.24 | 0.22 | 0.25 | 0.41 | 0.46 | 0.46 | |
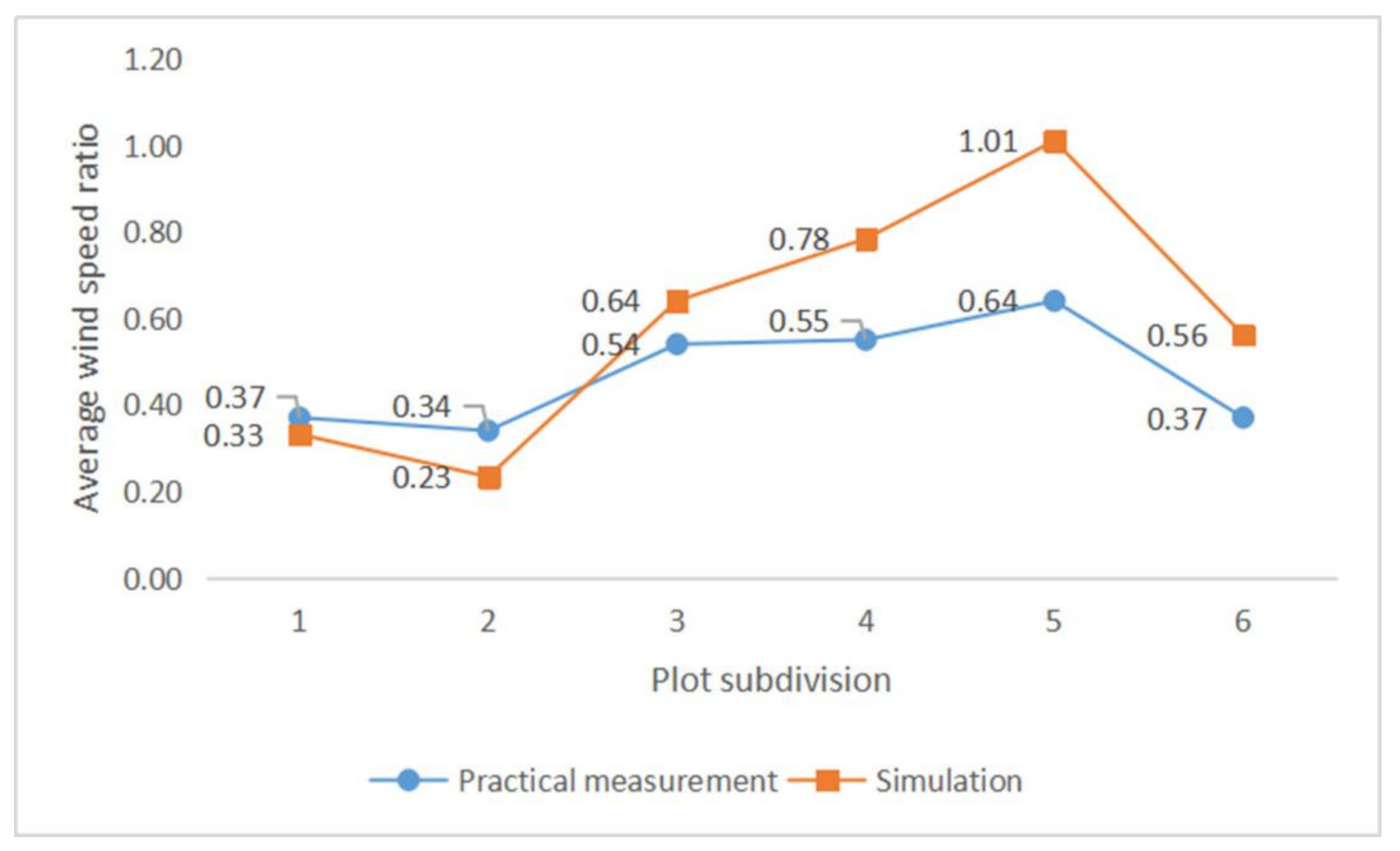
| RM | SE | 0.33 | 0.23 | 0.64 | 0.78 | 1.01 | 0.56 |
| NW | 0.42 | 0.43 | 0.76 | 0.54 | 0.61 | 0.87 | |
| Fluctuations | F1 | F2 | F3 | F4 | F5 | F6 | |
|---|---|---|---|---|---|---|---|
| Kc | 0.24 | 0.22 | 0.25 | 0.41 | 0.46 | 0.46 | |
| σ | SE | 0.04 | 0.07 | 4.76 | 14.90 | 10.69 | 14.96 |
| NW | 0.92 | 0.80 | 10.82 | 13.26 | 21.28 | 15.29 | |
| Districts | D1 | D2 | D3 | D4 | D5 | D6 | |
|---|---|---|---|---|---|---|---|
| U | 0.26 | 0.52 | 0.94 | 0.26 | 0.67 | 0.51 | |
| RM | SE | 0.38 | 0.74 | 0.54 | 0.96 | 0.98 | 0.36 |
| NW | 0.64 | 0.68 | 0.28 | 0.92 | 0.48 | 0.77 | |
| Districts | D1 | D2 | D3 | D4 | D5 | D6 | |
|---|---|---|---|---|---|---|---|
| U | 26.40 | 52.40 | 93.50 | 26.20 | 66.75 | 50.75 | |
| σ | SE | 2.60 | 4.00 | 3.90 | 2.80 | 3.30 | 3.60 |
| NW | 2.80 | 3.20 | 1.60 | 2.90 | 5.50 | 4.30 | |
| Segments | S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|---|
| Rf | 0.52 | 1.00 | 1.00 | 0.40 | 0.83 | 0.90 | |
| RM | SE | 0.38 | 0.74 | 0.54 | 0.96 | 0.98 | 0.36 |
| NW | 0.64 | 0.68 | 0.28 | 0.92 | 0.48 | 0.77 | |
| Segments | S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|---|
| Rf | 0.52 | 1.00 | 1.00 | 0.40 | 0.83 | 0.90 | |
| σ | SE | 2.60 | 4.00 | 3.90 | 2.80 | 3.30 | 3.60 |
| NW | 2.80 | 3.20 | 1.60 | 2.90 | 5.50 | 4.30 | |
| Skyline Quantification Factors | Wind Direction | Equation | Factors Comfort Range | Wind Environment Comfort Range |
|---|---|---|---|---|
| Kc | SE | y = 152.95x3 − 174.97x2 + 65.992x − 7.425 | [0.25, 0.59] | (0.5, 2) |
| NW | y = 199.73x3 − 206.29x2 + 69.307x − 6.9439 | [0.23, 0.55] | ||
| U | SE | y = -30.298x3 + 52.706x2 − 27.307x + 4.7582 | [0.13, 0.30] ∪ [0.50, 0.93] | |
| NW | y = 8.1804x3 − 15.259x2 + 7.8053x − 0.3648 | [0.15, 0.65] ∪ [1.06, 1.3] | ||
| Rf | SE | y = -23.513x3 + 52.649x2 − 37.611x + 9.0669 | [0.29, 0.49] ∪ [0.72, 1.03] | |
| NW | y = -13.481x3 + 30.269x2 − 22.082x + 5.7951 | [0.24, 1] |
| Skyline Quantification Factors | Wind Direction | Equation | Wind Environment Comfort Range |
|---|---|---|---|
| Kc | SE | y = −421.98x2 + 343.96x − 55.884 | Relativity judgments based on changes in factors |
| NW | y = −47.147x2 + 94.499x − 15.777 | ||
| U | SE | y = 45.601x3 − 84.188x2 + 48.407x − 5.0382 | |
| NW | y = −116.2x3 + 186x2 − 86.501x + 14.853 | ||
| Rf | SE | y = −112.16x3 + 213.18x2 − 124.36x + 25.697 | |
| NW | y = −10.473x3 + 27.796x2 − 20.669x + 7.2992 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, X.; Gao, J.; Liu, Z.; Qin, X.; Chen, J.; Shen, L.; Han, X. Investigation of Pedestrian-Level Wind Environment with Skyline Quantitative Factors. Buildings 2022, 12, 792. https://doi.org/10.3390/buildings12060792
Ying X, Gao J, Liu Z, Qin X, Chen J, Shen L, Han X. Investigation of Pedestrian-Level Wind Environment with Skyline Quantitative Factors. Buildings. 2022; 12(6):792. https://doi.org/10.3390/buildings12060792
Chicago/Turabian StyleYing, Xiaoyu, Jing Gao, Ziqiao Liu, Xiaoying Qin, Jiahui Chen, Liying Shen, and Xinyu Han. 2022. "Investigation of Pedestrian-Level Wind Environment with Skyline Quantitative Factors" Buildings 12, no. 6: 792. https://doi.org/10.3390/buildings12060792
APA StyleYing, X., Gao, J., Liu, Z., Qin, X., Chen, J., Shen, L., & Han, X. (2022). Investigation of Pedestrian-Level Wind Environment with Skyline Quantitative Factors. Buildings, 12(6), 792. https://doi.org/10.3390/buildings12060792





