Gediminas Hill Slopes Behavior in 3D Finite Element Model
Abstract
:1. Introduction
2. Input Data
2.1. Computational Resources
2.2. Geodetic Data
2.3. Engineering Geological and Geotechnical Conditions
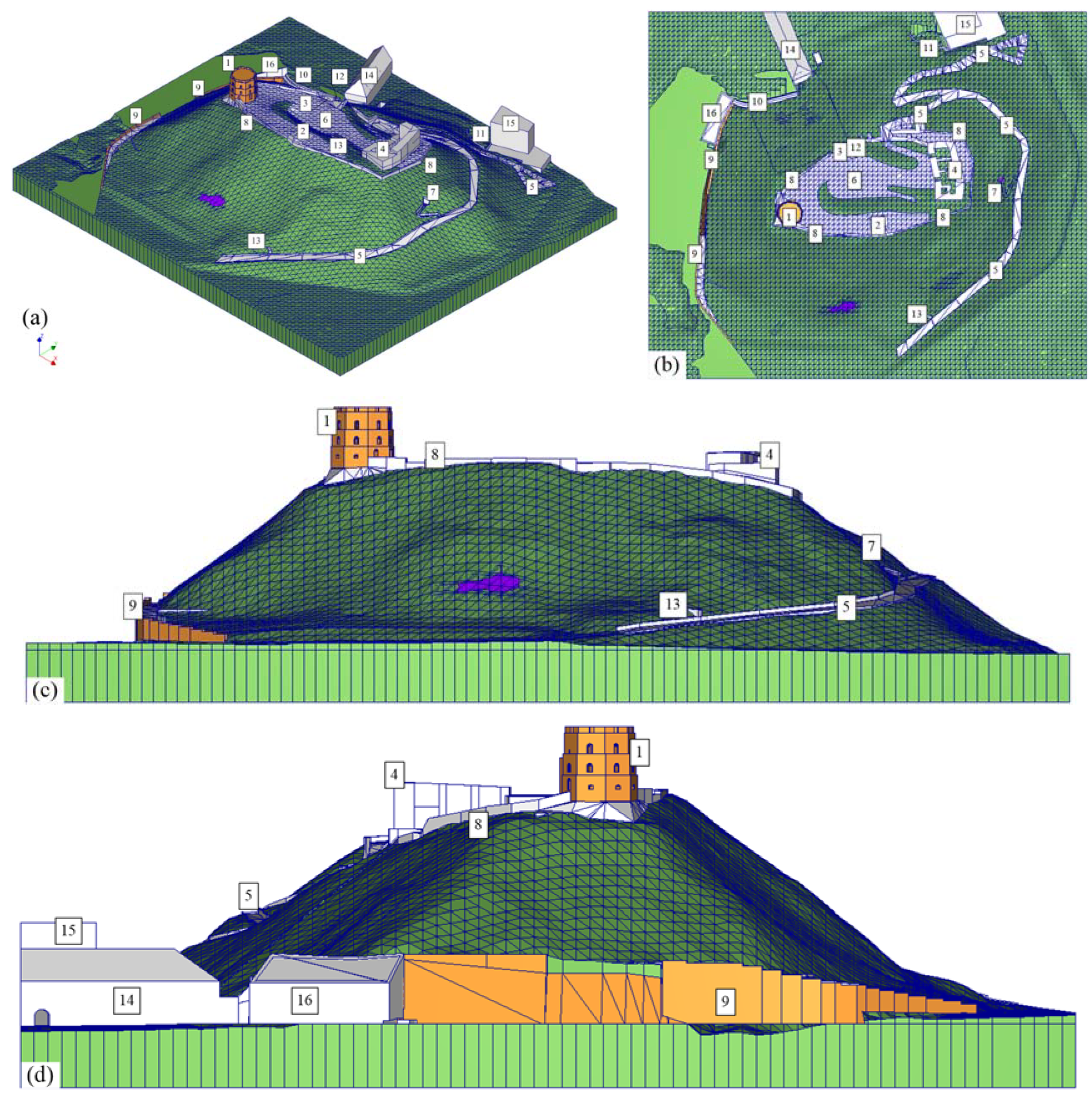
2.4. Buildings and Structures Remains, Path, Funicular and Tunnels
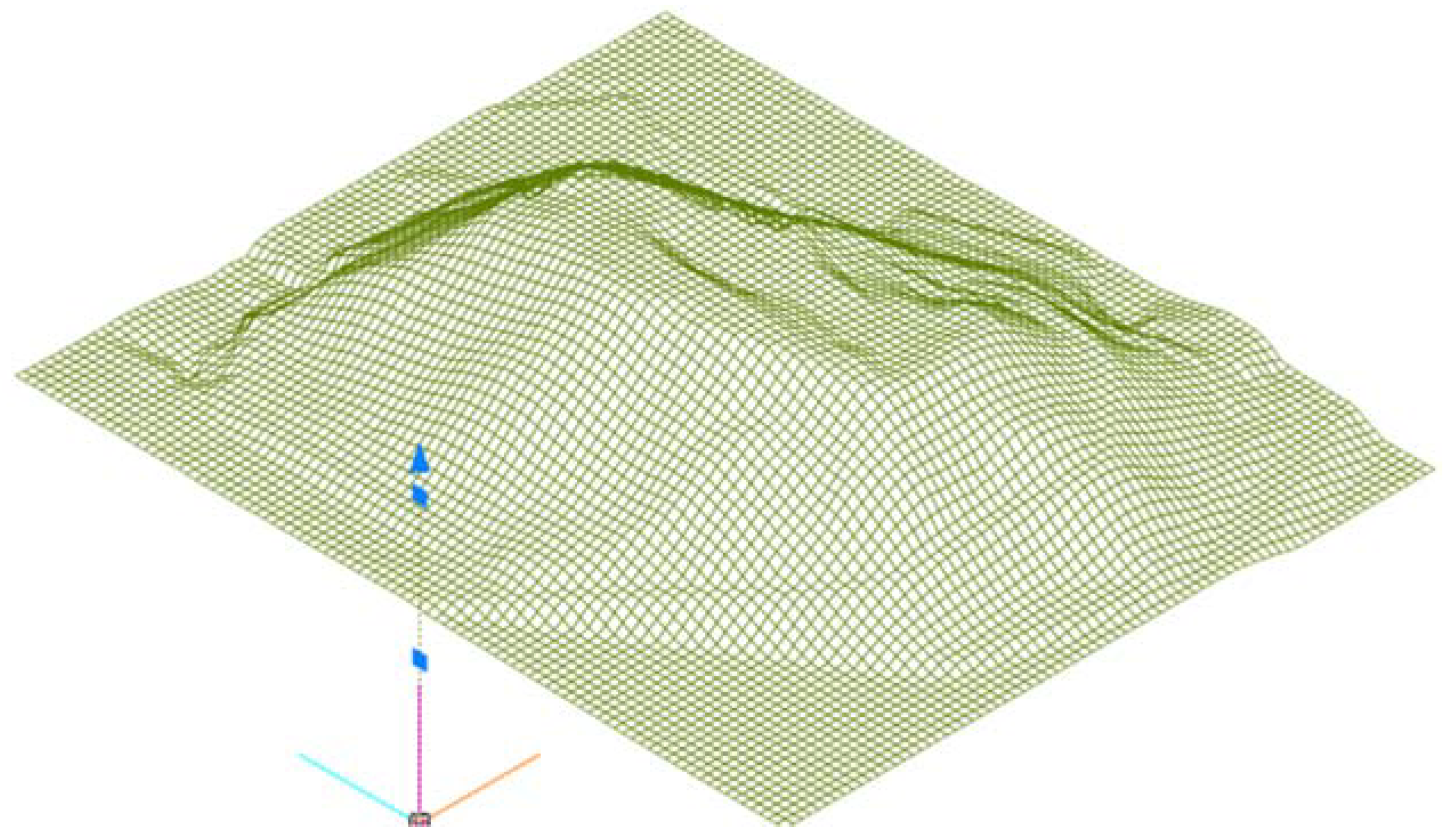
3. Development of a Numerical Three-Dimensional Model of Gediminas Hill
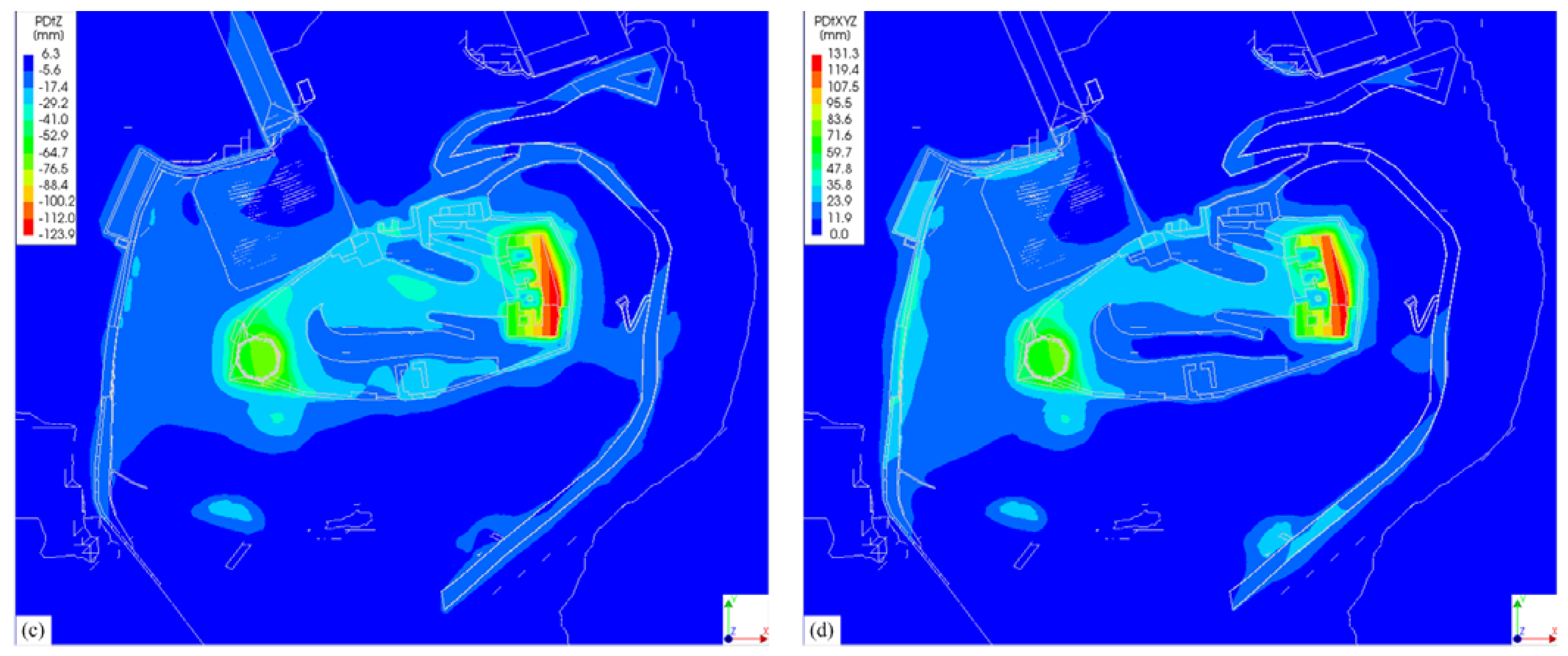
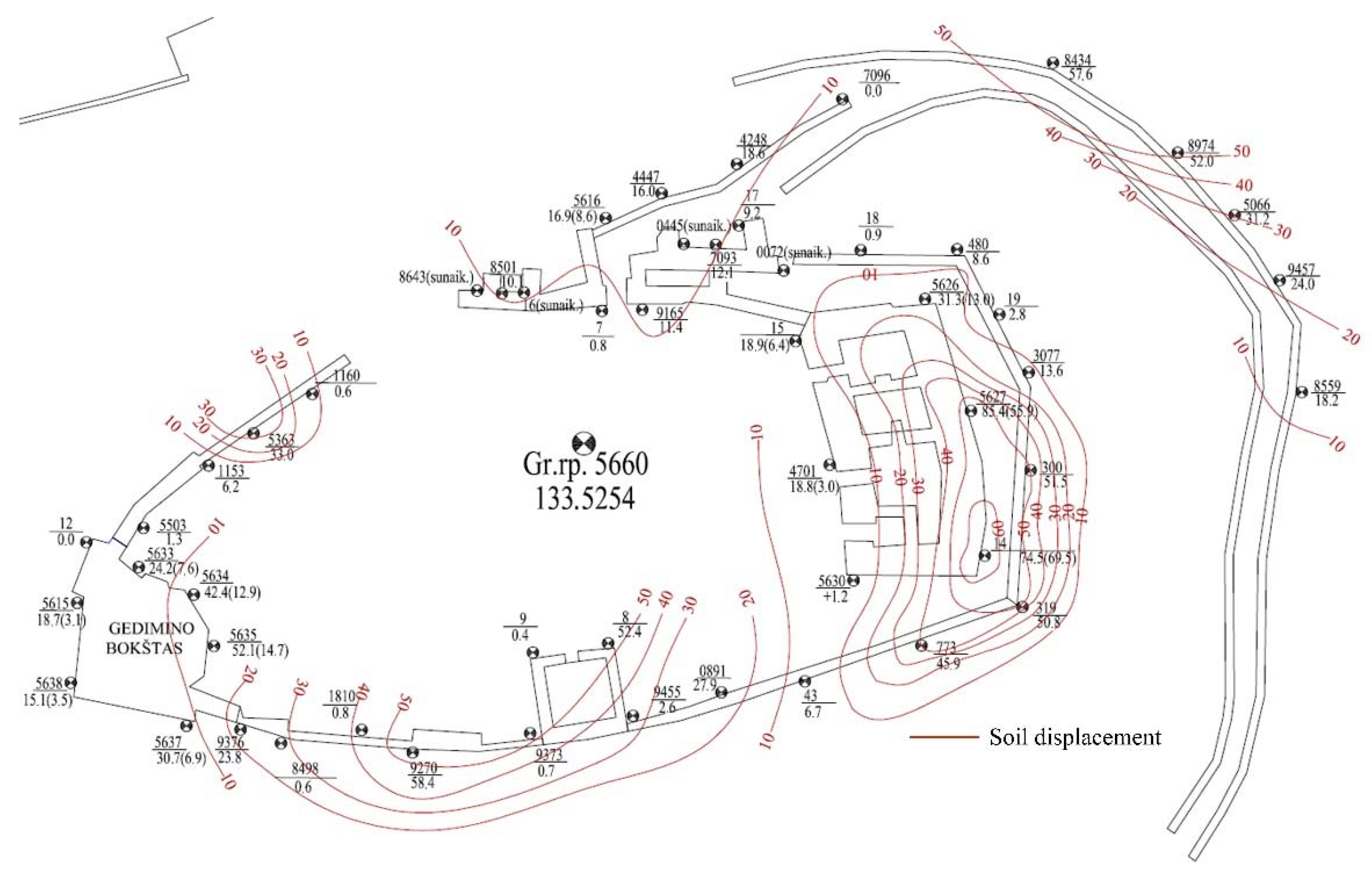
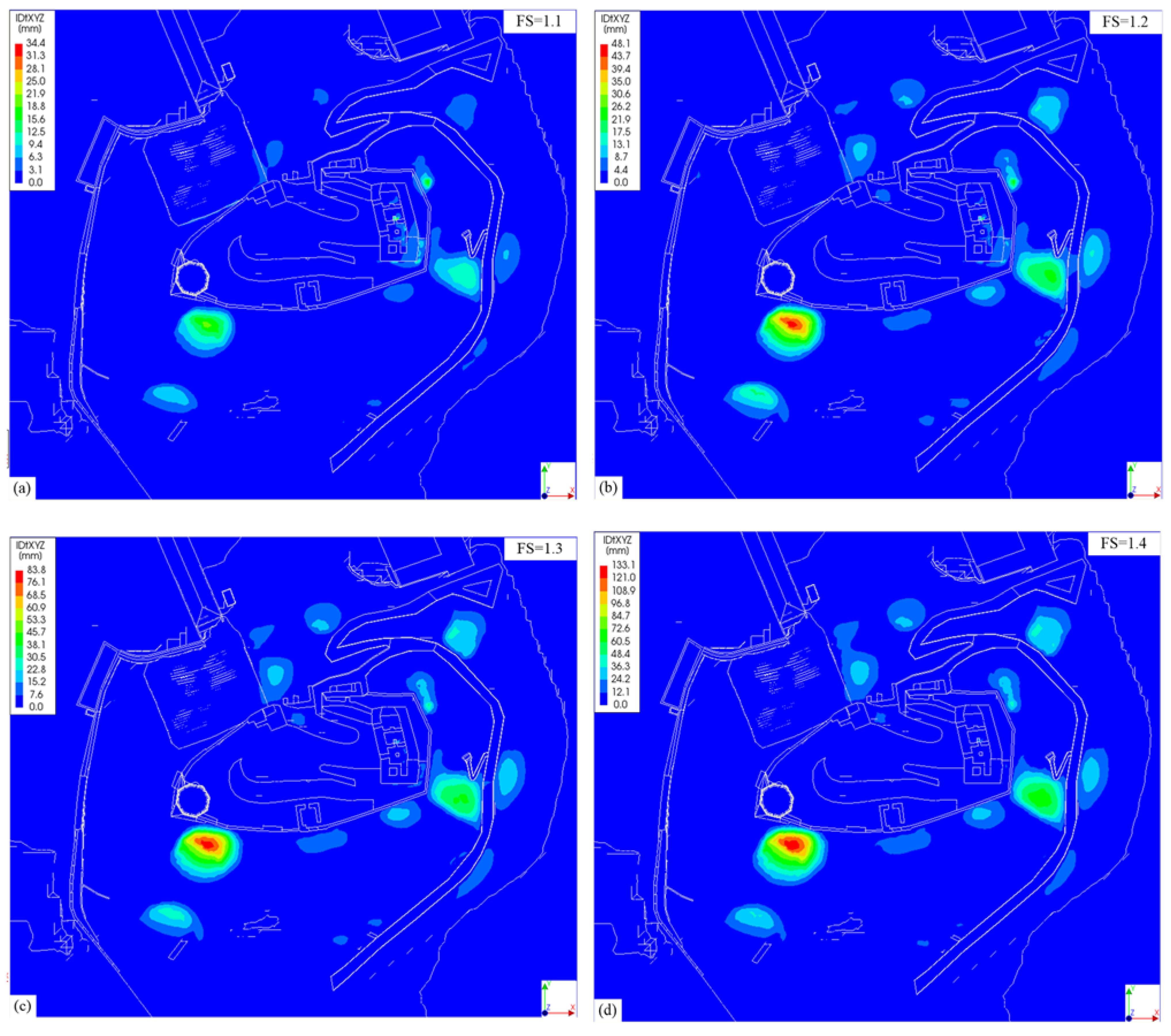
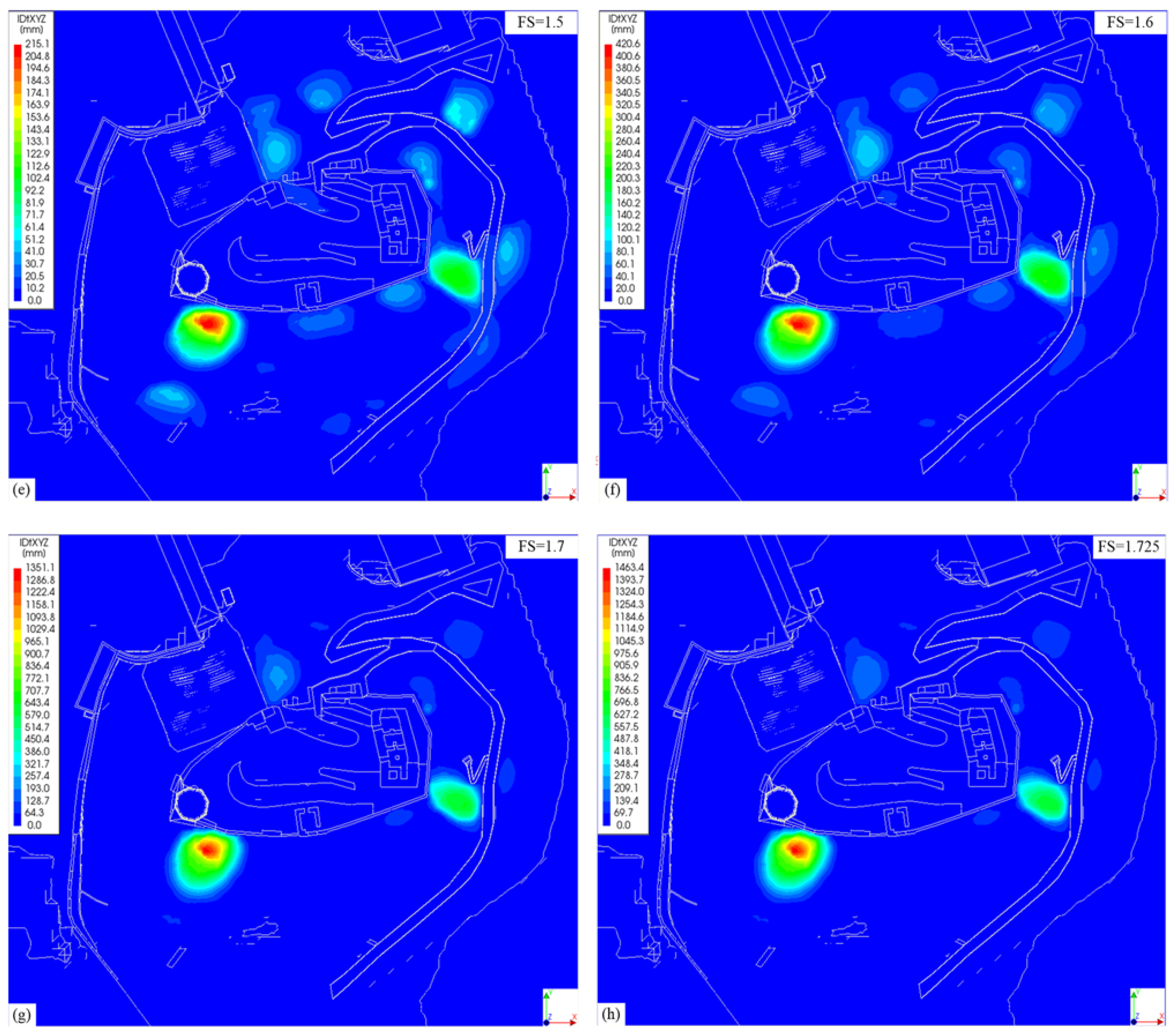
4. Behavior of Numerical Model
5. Conclusions
- Constructions, buildings, and additional loads increased soil displacement, mostly in the technogenic (tIV-dIV) soil layer. The analyzed monitoring data, including recent and historical investigation reports on the constructions, as well as the numerical model behavior, allowed us to assume that the deformation of building remains depends on technogenic (tIV-dIV) soil layer displacements. The influence of the climate (i.e., precipitation) on slope stability was also evaluated, considering strength reductions, which demonstrated that the slope stability depends on the technogenic soil layer height and the inclination of undisturbed soil layers.
- The surface inclination of natural soil layers at the point of contact with the technogenic (tIV-dIV) soil layer in some areas is higher than that of the technogenic soil layers. In these areas, the biggest deformation zones may form. Numerical model analysis allowed for us to make the conclusion that technogenic (tIV-dIV) soil layer shallow landslide occurrence depends on the layer height, changes in mechanical parameters, and the surface inclination of the natural soil layers.
- The numerical Gediminas Hill 3D model allowed for us to assess the soil–building interaction behaviors. The results of non-linear analysis of the created model corresponded to the tendencies observed in direct geodetic measurements and were in agreement with the relevant landslide history.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hovland, H.J. Three-Dimensional Slope Stability Analysis Method. J. Geotech. Eng. Div. 1977, 103, 971–986. [Google Scholar] [CrossRef]
- Kausel, E. Early History of Soil–Structure Interaction. Soil Dyn. Earthq. Eng. 2010, 30, 822–832. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Park, J.; Seo, J. Geotechnical Property Modeling and Construction Safety Zoning Based on GIS and BIM Integration. Appl. Sci. 2021, 11, 4004. [Google Scholar] [CrossRef]
- Weir, F.; Fowler, M.; Sullivan, T.; Kobler, M.; Bu, J. Evolution of a Geotechnical Model for Slope Design in an Active Volcanic Environment. In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Australian Centre for Geomechanics, Perth, Australia, 12–14 May 2022; pp. 455–472. [Google Scholar]
- Andersen, T.R.; Poulsen, S.E.; Pagola, M.A.; Medhus, A.B. Geophysical Mapping and 3D Geological Modelling to Support Urban Planning: A Case Study from Vejle, Denmark. J. Appl. Geophys. 2020, 180, 104130. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, J.; Chen, C.; Tang, R.; Zhu, S.; Luo, X. Analytical Reliability Evaluation Framework of Three-Dimensional Engineering Slopes. Buildings 2022, 12, 268. [Google Scholar] [CrossRef]
- Savvides, A.A.; Papadrakakis, M. A Computational Study on the Uncertainty Quantification of Failure of Clays with a Modified Cam-Clay Yield Criterion. SN Appl. Sci. 2021, 3, 1–26. [Google Scholar] [CrossRef]
- Wang, M.-Y.; Liu, Y.; Ding, Y.-N.; Yi, B.-L. Probabilistic Stability Analyses of Multi-Stage Soil Slopes by Bivariate Random Fields and Finite Element Methods. Comput. Geotech. 2020, 122, 103529. [Google Scholar] [CrossRef]
- Aery, B. Recent Advances in Geotechnical Infrastructure. In Lecture Notes in Civil Engineering; Patel, S., Solanki, C.H., Reddy, K.R., Shukla, S.K., Eds.; Springer: Singapore, 2021; Volume 140, pp. 31–40. ISBN 978-981-33-6589-6. [Google Scholar]
- Jostad, H.P.; Sivasithamparam, N.; Lacasse, S.; Degago, S.A.; Le, T.M.H.; Giese, S.; Rosenquist af Åkershult, A.; Johansen, T.; Aabøe, R. 3D Stability Analyses of Skjeggestad Landslide. IOP Conf. Ser. Earth Environ. Sci. 2021, 710, 1–12. [Google Scholar] [CrossRef]
- Rohmer, O.; Bertrand, E.; Mercerat, E.D.; Régnier, J.; Pernoud, M.; Langlaude, P.; Alvarez, M. Combining Borehole Log-Stratigraphies and Ambient Vibration Data to Build a 3D Model of the Lower Var Valley, Nice (France). Eng. Geol. 2020, 270, 105588. [Google Scholar] [CrossRef]
- Erharter, G.H.; Tschuchnigg, F.; Poscher, G. Stochastic 3D Modelling of Discrete Sediment Bodies for Geotechnical Applications. Appl. Comput. Geosci. 2021, 11, 100066. [Google Scholar] [CrossRef]
- Hemeda, S. 3D Finite Element Coupled Analysis Model for Geotechnical and Complex Structural Problems of Historic Masonry Structures: Conservation of Abu Serga Church, Cairo, Egypt. Herit. Sci. 2019, 7, 6. [Google Scholar] [CrossRef]
- Lin, H.-D.; Wang, W.-C.; Li, A.-J. Investigation of Dilatancy Angle Effects on Slope Stability Using the 3D Finite Element Method Strength Reduction Technique. Comput. Geotech. 2020, 118, 103295. [Google Scholar] [CrossRef]
- Morkunaite, R.; Česnulevičius, A. Recent Investigations of the Peculiarities of Vilnius Relief Dynamics. Proc. Est. Acad. Sci. Geol. 2005, 54, 191–203. [Google Scholar]
- Jonaitis, B.; Antonovič, V.; Šneideris, A.; Boris, R.; Zavalis, R. Analysis of Physical and Mechanical Properties of the Mortar in the Historic Retaining Wall of the Gediminas Castle Hill (Vilnius, Lithuania). Materials 2018, 12, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skuodis, Š.; Kelevišius, K.; Žaržojus, G. Vibrations Measurement of the Funicular Generated Vibrations on Gediminas Hill North Part Slope. In Proceedings of the 10th International Conference ‘Environmental Engineering’, VGTU Technika, Vilnius, Lithuania, 27–28 April 2017; pp. 1–8. [Google Scholar]
- Skuodis, Š.; Ng, P.L. Slope Restoration and Topographical Monitoring for Heritage Preservation of Gediminas Hill and Castle Tower in Lithuania. In Proceedings of the 38th Annual Seminar, Geotechnical Division, Geotechnical Engineering for Infrastructure Development, Hong Kong, China, 18 May 2018; pp. 121–133. [Google Scholar]
- Šadzevičius, R.; Vyčius, Ž.; Damulevičius, V. Modeling of Gediminas Hill Western-North Slope Stability. Eng. Educ. Technol. 2018, 1, 114–122. (In Lithuanian) [Google Scholar]
- Vaičiūnas, G. Evaluation of Gediminas Hill’s Slopes Stability. Liet. Pilys Lith. 2010, 6, 65–75. [Google Scholar]
- Markelionis, M.; Miltinytė, G.; Popovas, D.; Aksamitauskas, V.Č. Investigation of Vilnius Upper Castle Vertical Defor-mations. In Proceedings of the 10th International Conference ‘Environmental Engineering’. VGTU Technika, Vilnius, Lithuania, 27–28 April 2017; pp. 1–7. [Google Scholar]
- Baubinienė, A.; Morkūnaitė, R.; Bauža, D.; Vaitkevičius, G.; Petrošius, R. Aspects and Methods in Reconstructing the Medieval Terrain and Deposits in Vilnius. Quat. Int. 2015, 386, 83–88. [Google Scholar] [CrossRef]
- Antanavičiūtė, R. Urban Development in Vilnius during the Second World War. In Art and Artistic Life during the Two World Wars; Lithuanian Culture Research Institute: Vilnius, Lithuania, 2012; pp. 319–350. [Google Scholar]
- TNO Diana 2022a. Available online: https://Manuals.Dianafea.Com/D103/Diana.Html (accessed on 11 April 2022).
- Bentley 2022. Available online: https://Www.Bentley.Com/En/Products/Brands/Contextcapture (accessed on 11 April 2022).
- Guobytė, R. Lietuvos Geomorfologinės Sritys Ir Rajonai. Available online: https://Www.Vle.Lt/Straipsnis/Lietuvos-Geomorfologines-Sritys-Ir-Rajonai/ (accessed on 10 June 2022). (In Lithuanian).
- Skuodis, Š.; Michelevičius, D.; Damušytė, A.; Valivonis, J.; Medzvieckas, J.; Šneideris, A.; Jokubaitis, A.; Daugevičius, M. The Engineering Geological and Geotechnical Conditions of Gediminas Hill (Vilnius, Lithuania): An Update. Geol. Q. 2021, 65, 1–11. [Google Scholar] [CrossRef]
- Guobytė, R.; Satkūnas, J. Pleistocene Glaciations in Lithuania. In Developments in Quaternary Science; Elsevier: Amsterdam, The Netherlands, 2011; Volume 15, pp. 231–246. ISBN 9780444534477. [Google Scholar]
- JSC Geobaltic. JSC Geobaltic, 2020. III Geotechninės Kategorijos Projektinių IGG Tyrimų Visoje Gedimino Kalno Teritorijoje Ataskaita; JSC Geobaltic: Vilnius, Lithuania, 2020. (In Lithuanian) [Google Scholar]
- Bolton, M.D. The Strength and Dilatancy of Sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Hong, L.; Chen, L.; Wang, X. Reliability Analysis of Serviceability Limit State for Braced Excavation Considering Multiple Failure Modes in Spatially Variable Soil. Buildings 2022, 12, 722. [Google Scholar] [CrossRef]
- EN ISO 14688-1:2018; Geotechnical Investigation and Testing—Identification and Classification of Soil-Part 1: Identification and Description (ISO 14688-1:2017). European Committee for Standardization: Brussels, Belgium, 2018.
- Milkulėnas, V.; Minkevičius, V.; Satkūnas, J. Gediminas’s Castle Hill (in Vilnius) Case: Slopes Failure Through Historical Times Until Present. In Advancing Culture of Living with Landslides; Springer International Publishing: Cham, Switzerland, 2017; pp. 69–76. [Google Scholar]
- Vitkauskienė, B.R. Pilininko Namo (Unik. KVR k. 24707) Su Gretima Vakarų Atraminės Sienos Dalimi (TRP), Arsenalo g. 1, Vilniuje, Taikomieji Tyrimai. Dalis: Istoriniai Tyrimai. (2021); Report No 2019-11-26/1. 2020. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwjf2_ar0Jr5AhXIq1YBHQnjDuAQFnoECAIQAQ&url=https%3A%2F%2Fkvr.kpd.lt%2FKvrWcf%2FLabbisServiceKvr.svc%2FGetDocument%2F95CB0422-8F29-4861-A24B-0B320534EFB8&usg=AOvVaw1ib9nGcwGtgtE3UKHF1_c- (accessed on 20 June 2022). (In Lithuanian).
- Mair, L.R. A Review of Earthworks Management; Network Rail: London, UK, 2021. [Google Scholar]
- Dyson, A.P.; Tolooiyan, A. Prediction and Classification for Finite Element Slope Stability Analysis by Random Field Comparison. Comput. Geotech. 2019, 109, 117–129. [Google Scholar] [CrossRef]
- Li, L.; Chu, X. Failure Mechanism and Factor of Safety for Spatially Variable Undrained Soil Slope. Adv. Civ. Eng. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Chatterjee, P.; Elkadi, A. Strength Reduction Analysis. Available online: https://dianafea.com/sites/default/files/2018-04/StrengthReductionAnalysis.pdf (accessed on 11 April 2022).
- TNO Diana 2022b. Available online: https://Manuals.Dianafea.Com/D101/Analys/Node578.Html (accessed on 11 April 2022).
- Su, Z.; Shao, L. A Three-Dimensional Slope Stability Analysis Method Based on Finite Element Method Stress Analysis. Eng. Geol. 2021, 280, 105910. [Google Scholar] [CrossRef]
- Sobhey, M.; Shahien, M.; El Sawwaf, M.; Farouk, A. Analysis of Clay Slopes with Piles Using 2D and 3D FEM. Geotech. Geol. Eng. 2021, 39, 2623–2631. [Google Scholar] [CrossRef]
- KVR 2022. Available online: https://Kvr.Kpd.Lt/#/Static-Heritage-Search (accessed on 12 April 2022).
- Guilhot, D.; Martinez del Hoyo, T.; Bartoli, A.; Ramakrishnan, P.; Leemans, G.; Houtepen, M.; Salzer, J.; Metzger, J.S.; Maknavicius, G. Internet-of-Things-Based Geotechnical Monitoring Boosted by Satellite InSAR Data. Remote Sens. 2021, 13, 2757. [Google Scholar] [CrossRef]





| Stratigraphy Index | Soil Layer Identification | Soil Type | γ, kN/m3 | ρ, Mg/m3 | ρs, Mg/m3 | w, % | wP, % | wL, % | k, m/d | φ’ (Degrees) | c’, kPa | cu, kPa | E, 1 MPa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tIV-dIV | tIV | Sa; Si;Cl | 17.76 | 1.81 | 2.67 | 9.7 | 13.4 | 16.9 | 1.94 | 35.3 | 13.5 | - | 3.6 |
| gdIImd | 31 | Cl | 21.49 | 2.19 | 2.69 | 12.1 | 11.0 | 20.3 | - | - | - | 71.0 | 21.4 |
| 32 | 21.76 | 2.22 | 2.69 | 11.4 | 12.1 | 19.9 | - | 33.8 | 15.3 | - | 33.1 | ||
| 33 | 22.30 | 2.27 | 2.69 | 11.0 | 12.1 | 21.7 | - | 32.4 | 48.8 | - | 93.2 | ||
| 34 | 20.51 | 2.09 | 2.69 | 10.3 | 12.8 | 18.2 | - | 44.6 | 21.1 | - | 7.3 | ||
| fIImd | 41 | Sa | 17.46 | 1.78 | 2.66 | 3.7 | - | - | 8.94 | 31.6 | 24.0 | - | 30.8 |
| 42 | 19.02 | 1.94 | 2.66 | 10.7 | - | - | 7.35 | 38.1 | 34.1 | - | 56.8 | ||
| 43 | 19.85 | 2.02 | 2.67 | 14.4 | - | - | 5.91 | 36.7 | 36.7 | - | 96.9 | ||
| 44 | 16.56 | 1.69 | 2.66 | 3.2 | - | - | 12.1 | 32.8 | 11.5 | - | - | ||
| lgIIžm | 51 | 20.12 | 2.05 | 2.68 | 14.9 | 14.4 | 18.0 | 0.11 | 35.8 | 30.2 | - | 79.2 | |
| 52 | Cl-Si | 21.16 | 2.16 | 2.68 | 14.3 | 14.6 | 19.9 | - | 35.1 | 46.2 | - | 110.7 | |
| 53 | Cl | 20.09 | 2.05 | 2.72 | 21.2 | 20.9 | 38.9 | - | 14.5 | 107.0 | - | 79.9 | |
| 54 | Sa | 20.15 | 2.05 | 2.67 | 15.3 | - | - | 4.9 | 39.2 | 40.9 | - | 112.0 | |
| gdIIžm | 61 | Cl | 22.11 | 2.24 | 2.69 | 11.5 | 22.0 | 12.2 | - | 28.1 | 76.9 | - | 74.2 |
| 62 | 21.78 | 2.22 | 2.69 | 10.9 | 21.0 | 10.8 | - | - | - | 115.0 | 29.0 | ||
| 63 | 21.59 | 2.20 | 2.69 | 15.0 | 25.8 | 13.0 | - | - | - | 81.6 | 17.5 | ||
| 64 | 21.39 | 2.18 | 2.70 | 14.8 | 26.4 | 12.2 | - | - | - | 28.8 | 6.2 | ||
| lgIIdn | 71 | Sa | 19.71 | 2.01 | 2.67 | 16.5 | 19.9 | 15.7 | 0.39 | 37.5 | 41.7 | - | 119.9 |
| 72 | Si | 20.00 | 2.04 | 2.68 | 15.7 | 20.0 | 15.8 | 0.08 | 33.1 | 73.1 | - | 186.1 | |
| 73 | Sa | 17.19 | 1.75 | 2.66 | 3.3 | - | - | 1.56 | 30.4 | 29.0 | - | - | |
| 74 | Sa | 19.86 | 2.03 | 2.67 | 15.7 | - | - | 1.68 | 36.9 | 37.4 | - | 139.2 |
| Stratigraphy Index | Soil Name 1 | E, MPa | ν | ρ, t/m3 | e | c, kPa | φ’ (Degrees) | Ψ (Degrees) |
|---|---|---|---|---|---|---|---|---|
| tIV-dIV | Mg | 3.6 | 0.30 | 1.81 2.04 ** | 0.61 | 13.5 | 35.3 | 0.0 |
| gdIImd | saCIL | 33.1 | 0.35 | 2.22 | 0.35 | 15.3 | 33.8 | 3.0 |
| fIImd | Sa | 56.8 | 0.30 | 1.94 | 0.53 | 34.1 | 38.1 | 8.0 |
| gdIImd | saCIL | 33.1 | 0.35 | 2.22 | 0.35 | 15.3 | 33.8 | 3.0 |
| lgIIžm | siSa | 110.7 | 0.35 | 2.16 | 0.43 | 46.2 | 35.1 | 5.0 |
| lgIIžm | saCIL-SiL | 79.2 | 0.35 | 2.05 | 0.49 | 30.2 | 35.8 | 6.0 |
| gdIIžm | saCIL | 74.2 | 0.35 | 2. 24 | 0.34 | 76.9 | 28.1 | 2.0 |
| lgIIdn | siSa | 119.9 | 0.30 | 2.01 | 0.55 | 41.7 | 37.5 | 7.5 |
| tIV *** | siSaW | 12.0 | 0.35 | 1.74 | 0.65 | 12.3 | 35.8 | 0.1 |
| Layer | E, MPa | ν | ρ, t/m3 | e | c, kPa | φ’, (Degrees) | Ψ, (Degrees) |
|---|---|---|---|---|---|---|---|
| Gabions surrounding soil | 40 | 0.33 | 1.85 | 0.6 | 2 | 39.98 | 9.99 |
| Gabions | 120 | 0.22 | 2.50 | 0.6 | 5 | 44.98 | 14.99 |
| Element | E, MPa | ν | ρ, t/m3 |
|---|---|---|---|
| Remains of Upper castle pitch (Figure 3) | 1300 | 0.2 | 2.5 |
| Pedestrian path (Figure 3) | 1300 | 0.2 | 2.5 |
| Rest of all construction remains (Figure 3) | 2600 | 0.2 | 2.9 |
| Remains of Old Arsenal (Figure 3) | 2600 | 0.2 | 0.532 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skuodis, Š.; Daugevičius, M.; Medzvieckas, J.; Šneideris, A.; Jokūbaitis, A.; Rastenis, J.; Valivonis, J. Gediminas Hill Slopes Behavior in 3D Finite Element Model. Buildings 2022, 12, 1113. https://doi.org/10.3390/buildings12081113
Skuodis Š, Daugevičius M, Medzvieckas J, Šneideris A, Jokūbaitis A, Rastenis J, Valivonis J. Gediminas Hill Slopes Behavior in 3D Finite Element Model. Buildings. 2022; 12(8):1113. https://doi.org/10.3390/buildings12081113
Chicago/Turabian StyleSkuodis, Šarūnas, Mykolas Daugevičius, Jurgis Medzvieckas, Arnoldas Šneideris, Aidas Jokūbaitis, Justinas Rastenis, and Juozas Valivonis. 2022. "Gediminas Hill Slopes Behavior in 3D Finite Element Model" Buildings 12, no. 8: 1113. https://doi.org/10.3390/buildings12081113
APA StyleSkuodis, Š., Daugevičius, M., Medzvieckas, J., Šneideris, A., Jokūbaitis, A., Rastenis, J., & Valivonis, J. (2022). Gediminas Hill Slopes Behavior in 3D Finite Element Model. Buildings, 12(8), 1113. https://doi.org/10.3390/buildings12081113







