Blast Resistance in Sandwich Structures Based on TPMS
Abstract
:1. Introduction
2. TPMS Explosion Experiment
2.1. TPMS Unit Design
2.2. Explosion Experiment System
2.3. Experimental Model Design
2.4. TPMS Sandwich Panel Anti-Explosion Effect
3. Model Building and Validation
3.1. Simulation Model Introduction
3.2. Material Model
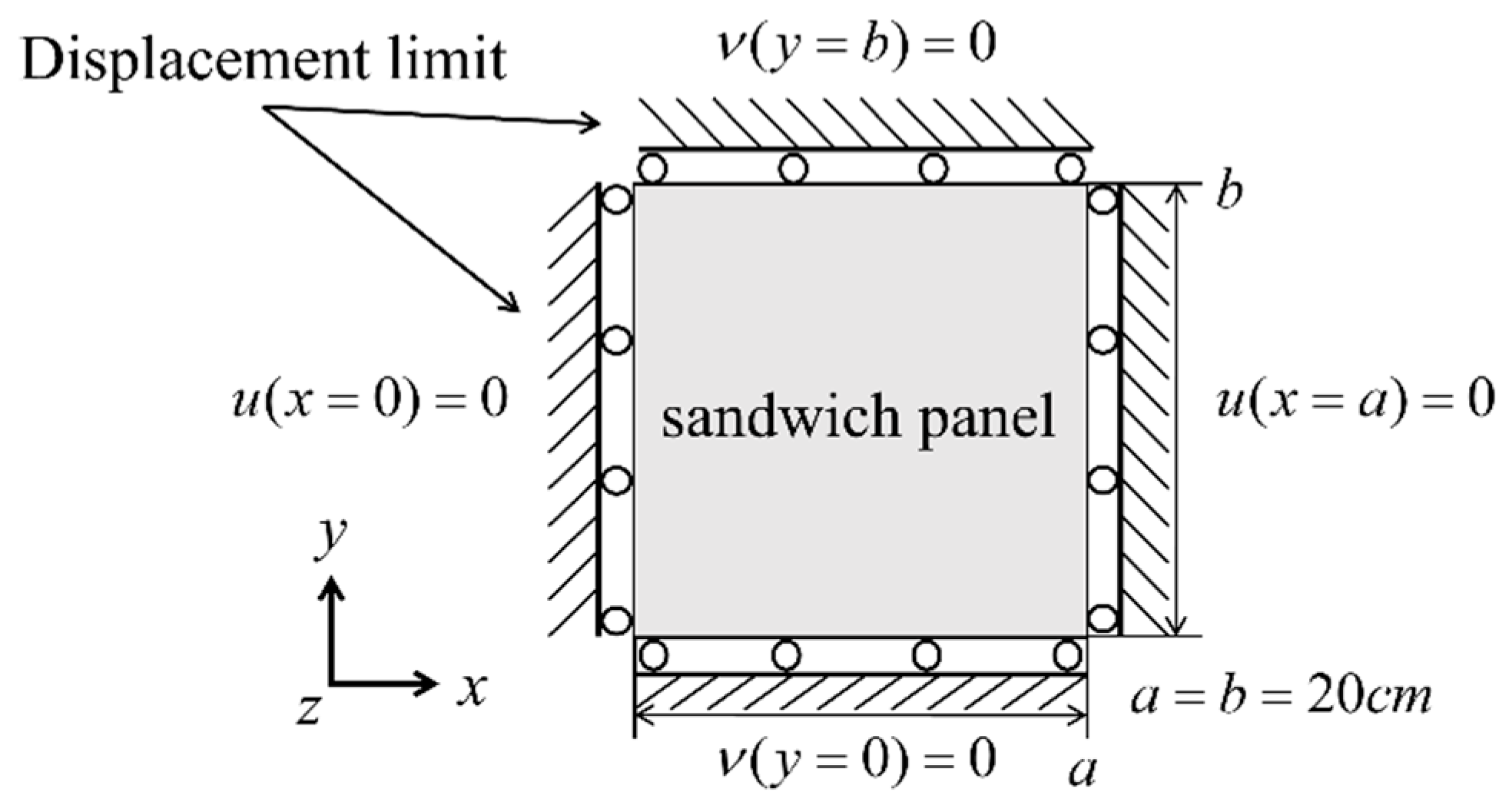
3.3. Explosive Loads and Boundary Conditions
3.4. Structural Blast Resistance Parameters
4. Results and Discussion
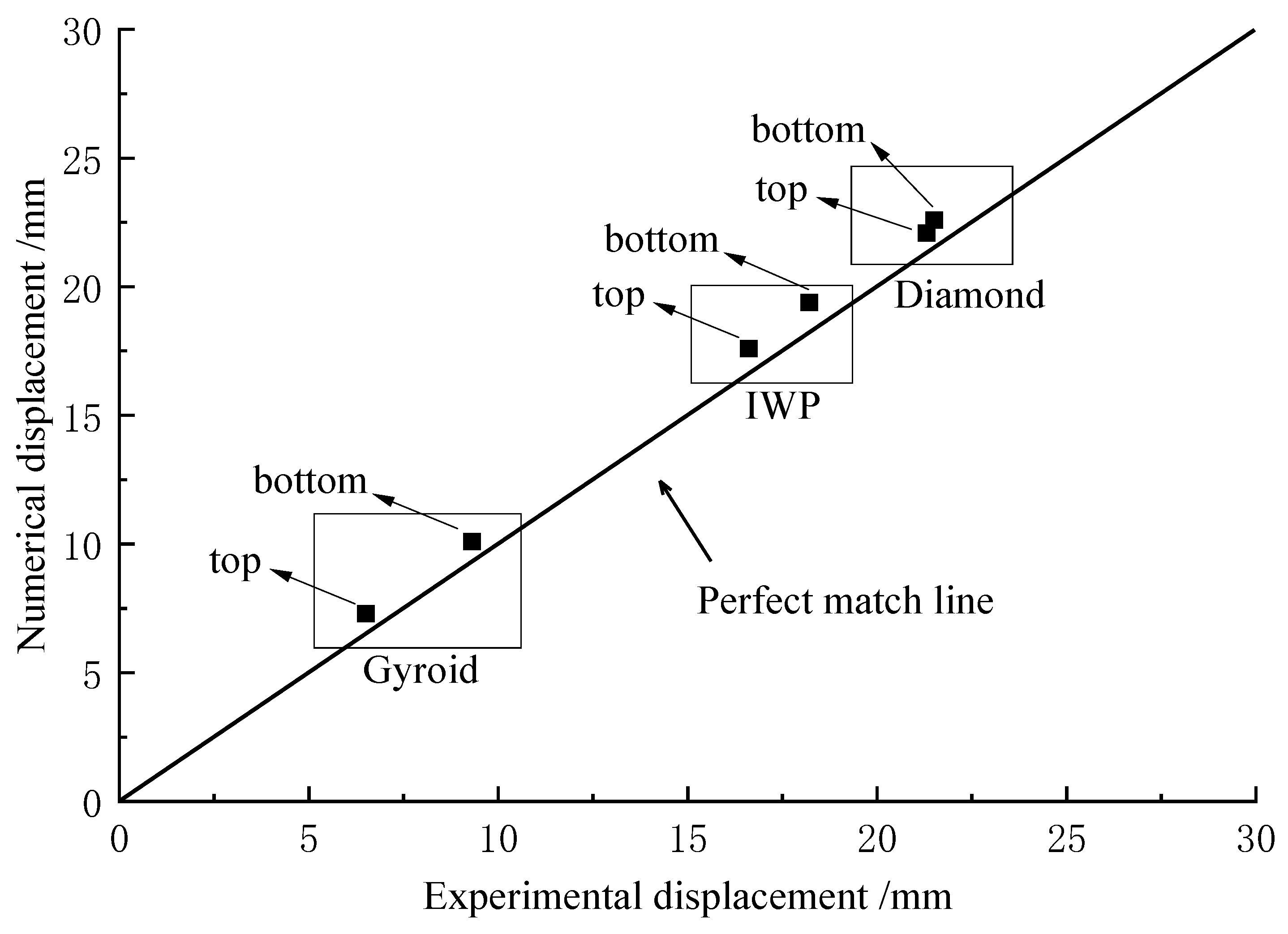
4.1. Simulation Model Validation
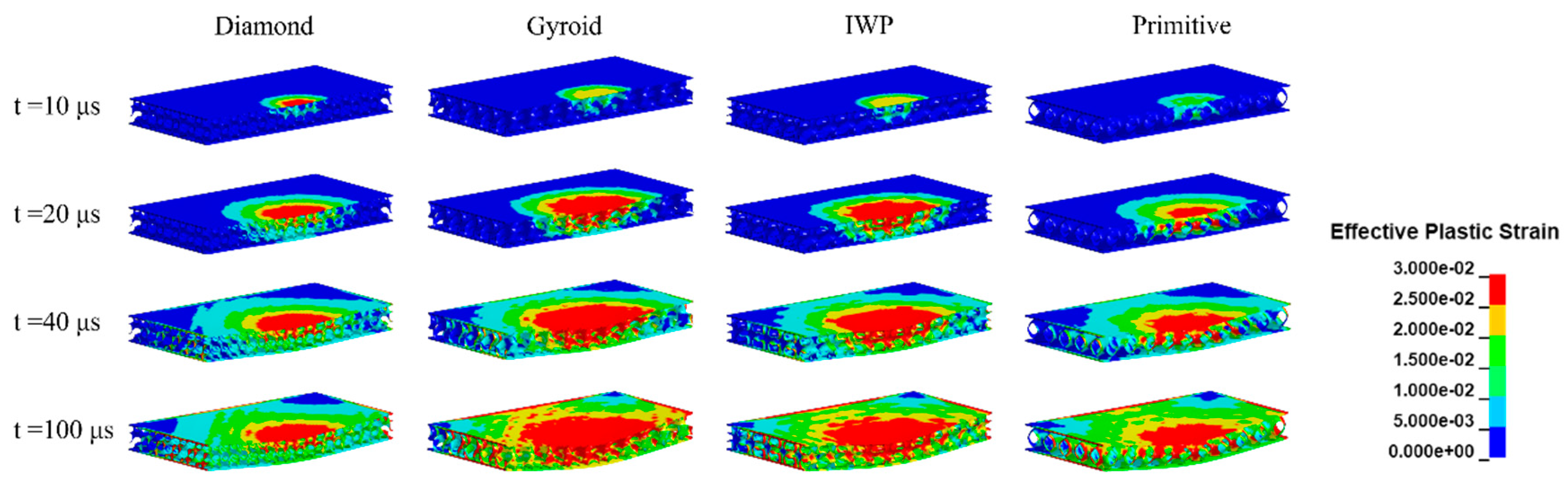
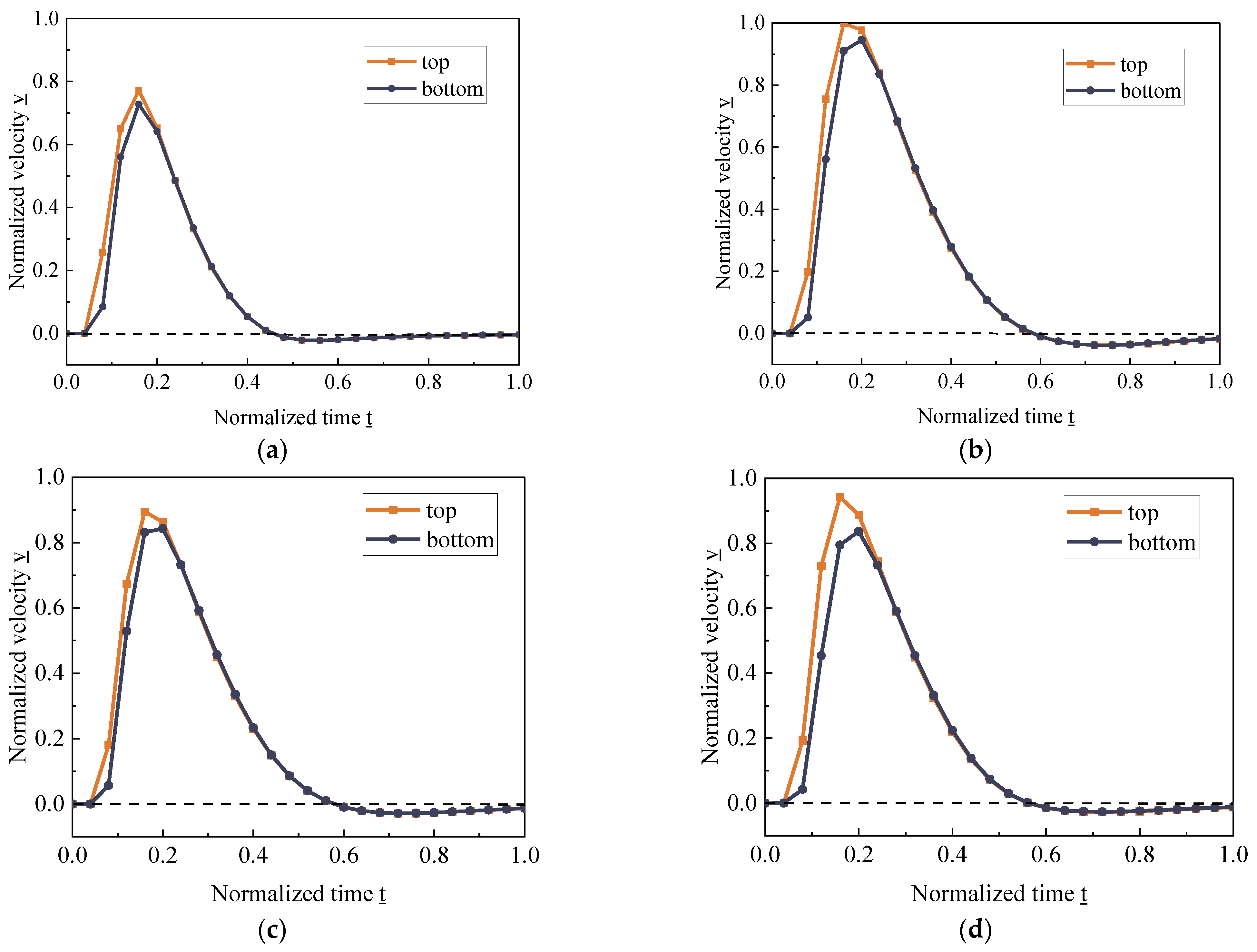
4.2. TPMS Dynamic Response Process
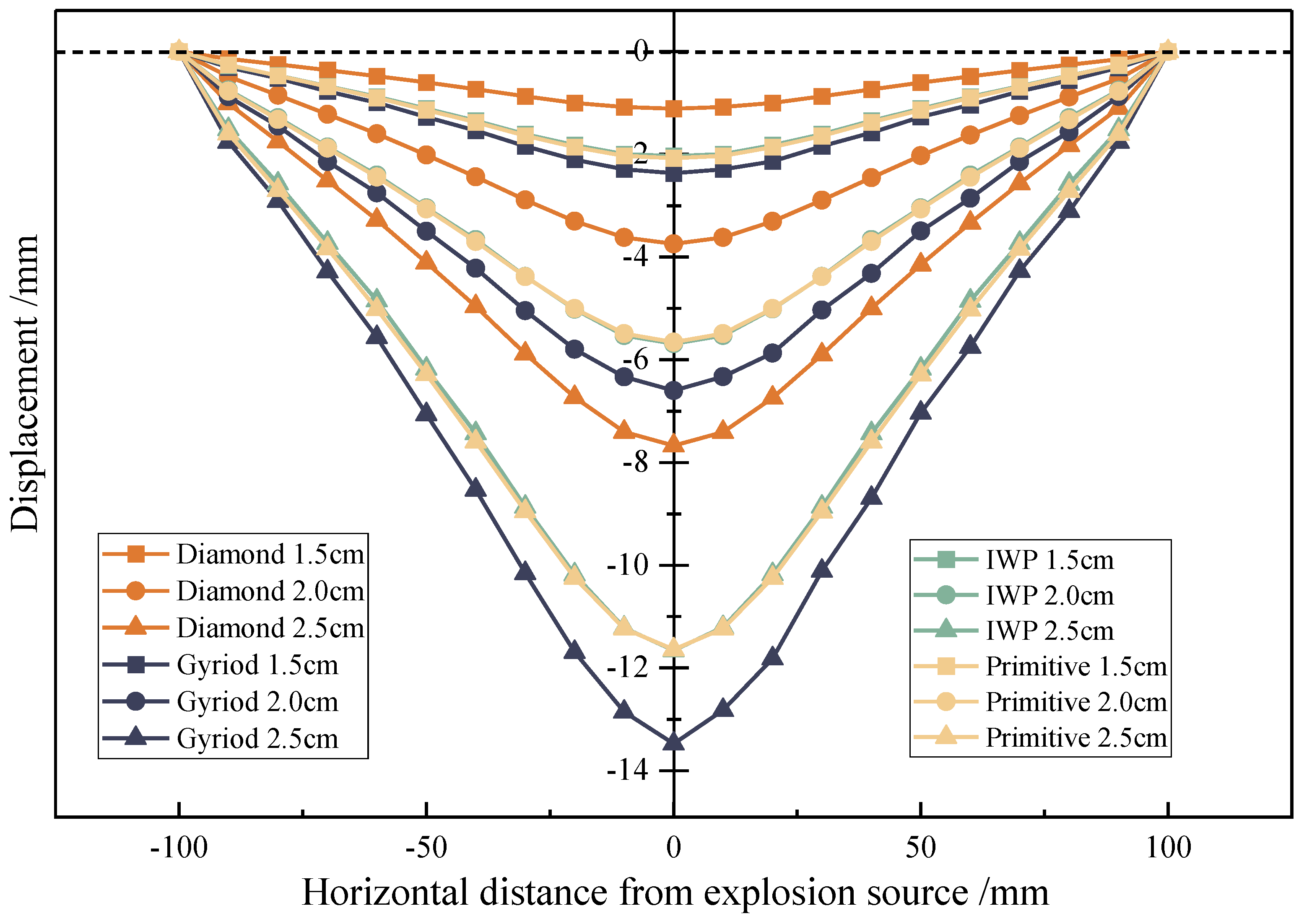
4.3. Influence of Sheet Thickness
4.4. Influence of the Amount of Explosives
4.5. Multivariate Optimization
5. Conclusions
- The anti-explosion performance of four TPMS structures is studied, which provides a new direction for the research of TPMS sandwich structures, which can be applied to the anti-explosion protection of buildings.
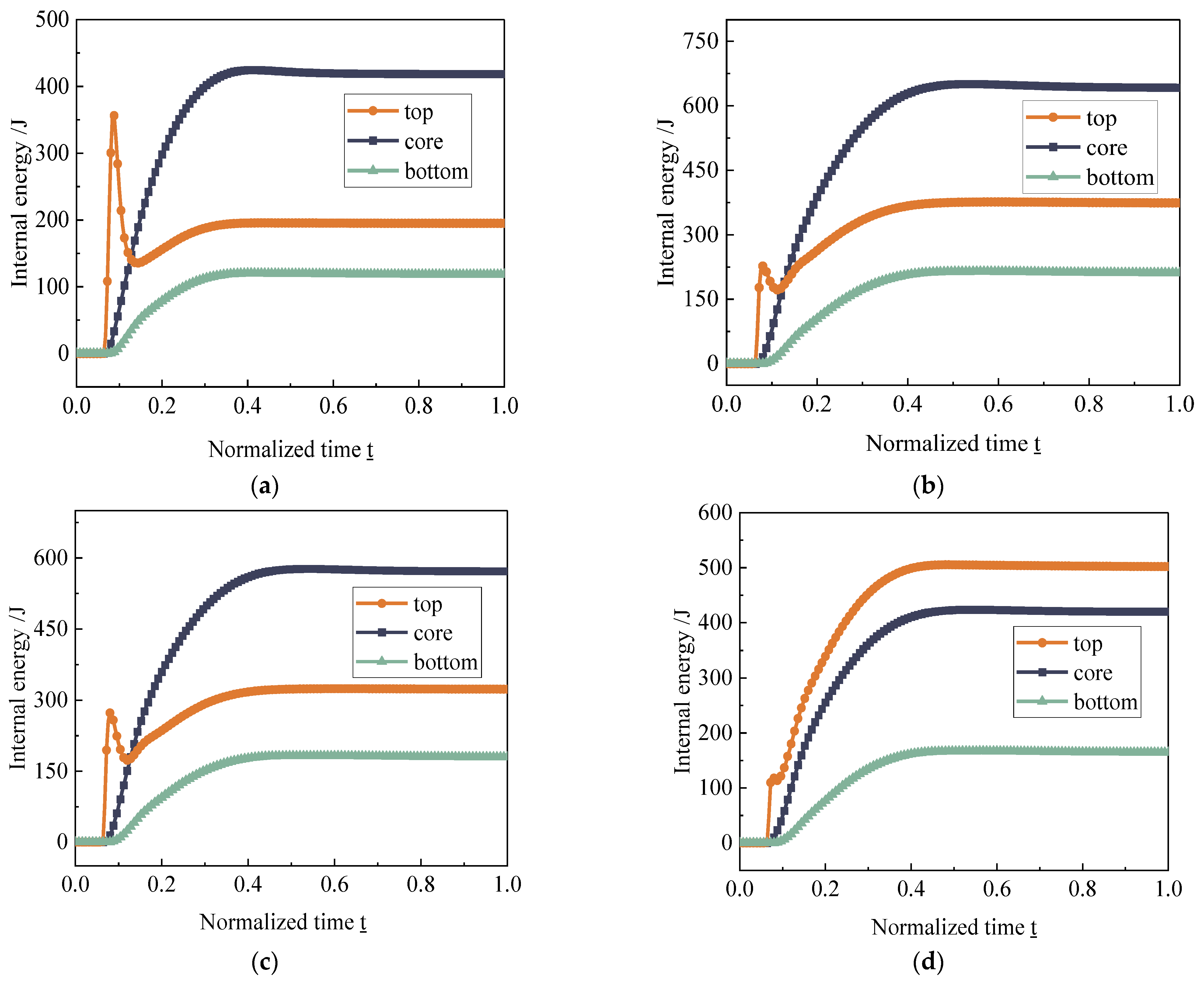
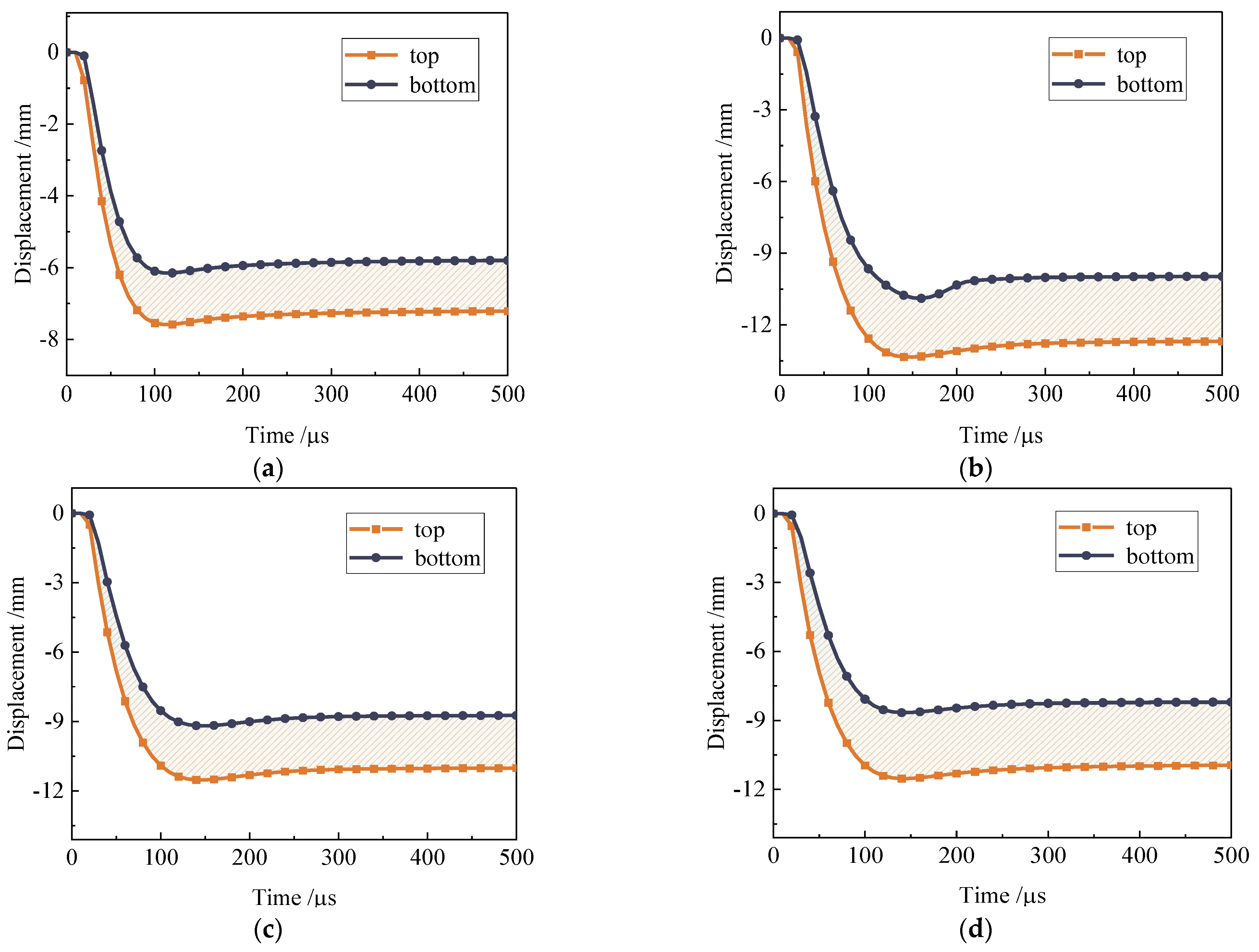
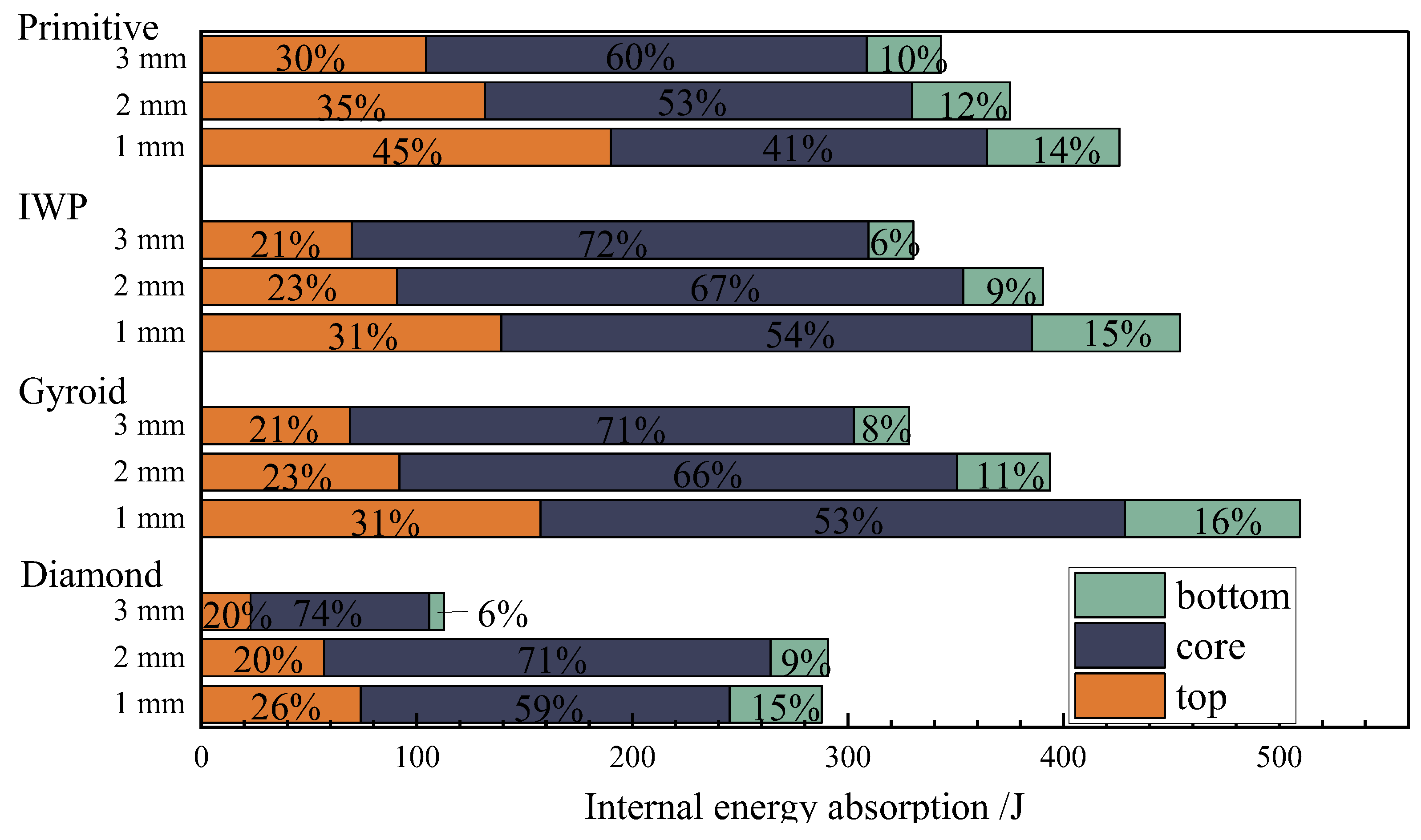
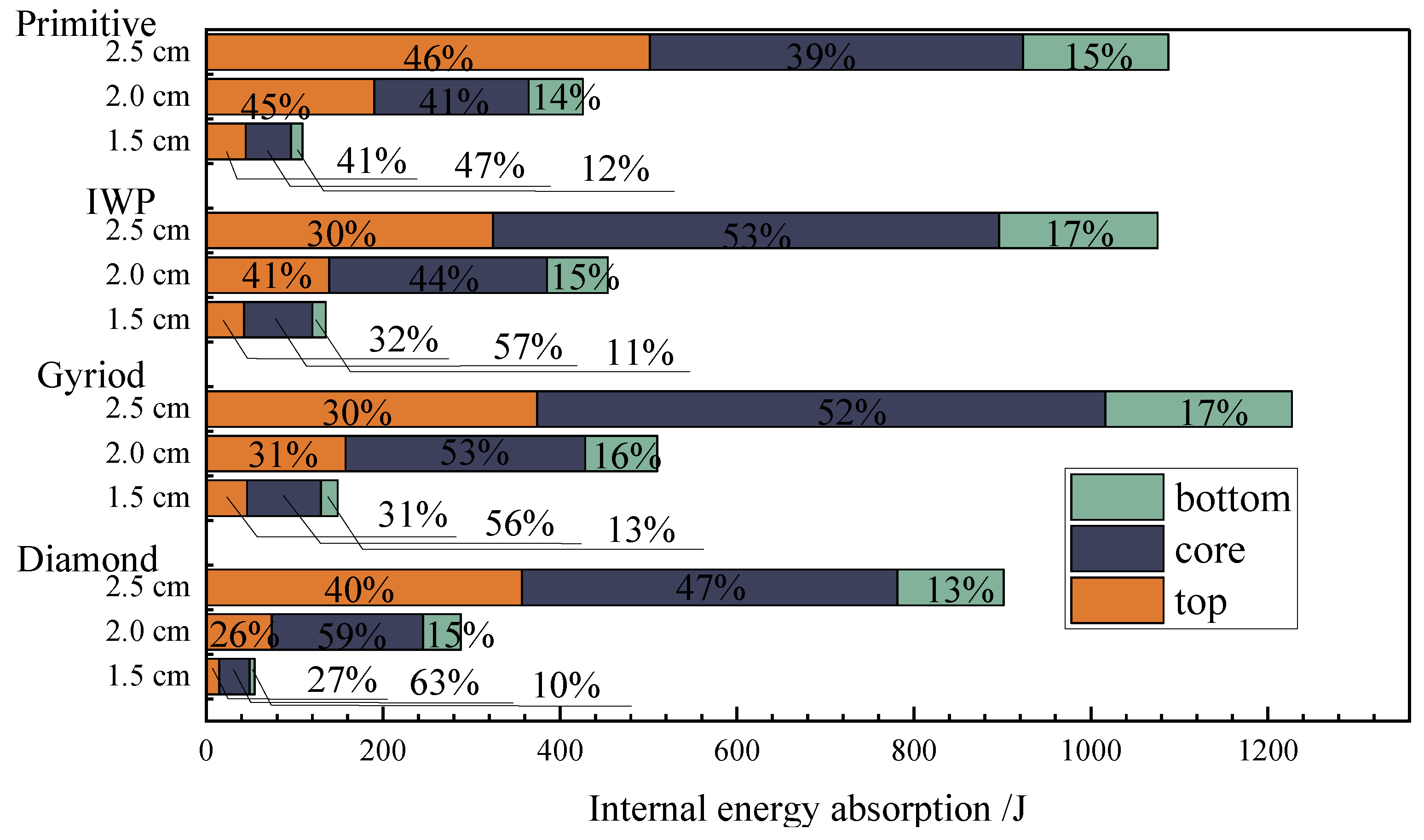
- Under the action of an explosion load, the absorption of energy of the top plate and the sandwich layer accounted for the main part, the sandwich layer had an obvious compression deformation process, and the structure had a compression densification process. In an actual application process, the thickness of the sandwich layer can be increased to achieve the purpose of protecting the building.
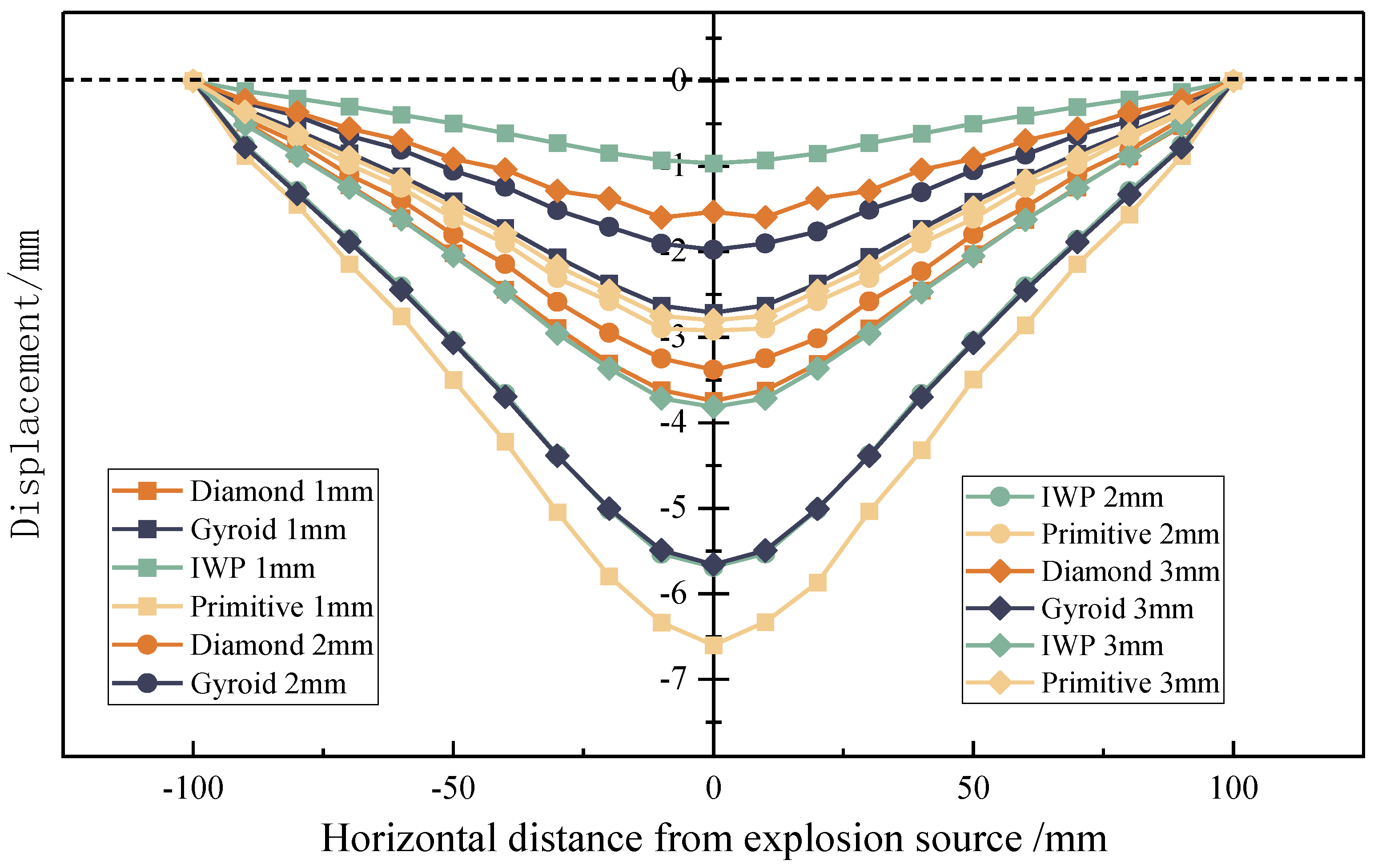
- When four Diamond, Gyroid, IWP, and Primitive TPMS sandwich panel structures were under the action of explosion load, the Diamond structure had better resistance to deformation, the Gyroid had better energy absorption effect, and the Diamond structure in actual use could avoid structural damage, and Gyroid structure can protect the material of the building.
- Parametric studies have shown that the TPMS configuration and the corresponding different panel thicknesses play an important role in energy absorption during the explosion, and the increase in panel thickness can enhance the deformation resistance in the sandwich panel during the explosion.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D. Cushioning Properties of Multi-layer Corrugated Sandwich Structures. J. Sandw. Struct. Mater. 2009, 11, 57–66. [Google Scholar] [CrossRef]
- Li, M.; Wu, L.; Ma, L.; Wang, B.; Guan, Z. Mechanical Response of All-composite Pyramidal Lattice Truss Core Sandwich Structures. J. Mater. Sci. Technol. 2011, 27, 570–576. [Google Scholar] [CrossRef]
- Dogan, A. Low-velocity impact, bending, and compression response of carbon fiber/epoxy-based sandwich composites with different types of core materials. J. Sandw. Struct. Mater. 2020, 23, 1956–1971. [Google Scholar] [CrossRef]
- Kalubadanage, D.; Remennikov, A.; Ngo, T.; Qi, C. Close-in blast resistance of large-scale auxetic re-entrant honeycomb sandwich panels. J. Sandw. Struct. Mater. 2020, 23, 4016–4053. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Wang, C.; Zhou, G.; Karamoozian, A.; Zhao, W. On the out-of-plane ballistic performances of hexagonal, reentrant, square, triangular and circular honeycomb panels. Int J Mech Sci. 2020, 173, 2–11. [Google Scholar] [CrossRef]
- Tan, P.; Lee, B.; Tsangalis, C. Finite element analysis of sandwich panels subjected to shock tube blast loadings. J. Sandw. Struct. Mater. 2010, 13, 263–278. [Google Scholar] [CrossRef]
- Sun, G.; Huo, X.; Chen, D.; Li, Q. Experimental and numerical study on honeycomb sandwich panels under bending and in-panel compression. Mater. Des. 2017, 133, 154–168. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, Q.; Li, J.; Li, K.; Poh, L.H.; Li, Y.; Zhang, J.; Xie, S.; Chen, H.; Zhao, J. Deformation and failure of hybrid composite sandwich beams with a metal foam core under quasi-static load and low-velocity impact. Comp. Struct. 2020, 242, 112175. [Google Scholar] [CrossRef]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Li, J.; Qin, Q.; Zhang, J. Internal blast resistance of sandwich cylinder with lattice cores. Int. J. Mech. Sci. 2021, 191, 106107. [Google Scholar] [CrossRef]
- Boonkong, T.; Shen, Y.O.; Guan, Z.W.; Cantwell, W.J. The low velocity impact response of curvilinear-core sandwich structures. Int. J. Impact Eng. 2016, 93, 28–38. [Google Scholar] [CrossRef]
- Baba, B.O. Curved sandwich composites with layer-wise graded cores under impact loads. Compos. Struct. 2017, 159, 1–11. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, Q.; Li, K.; Li, J.; Wang, Q. Effect of stepwise gradient on dynamic failure of composite sandwich beams with metal foam core subject to low-velocity impact. Int. J. Solids Struct. 2021, 228, 111125. [Google Scholar] [CrossRef]
- Li, X.; Zhang, P.; Wang, Z.; Wu, G.; Zhao, L. Dynamic behavior of aluminum honeycomb sandwich panels under air blast: Experiment and numerical analysis. Compos. Struct. 2014, 108, 1001–1008. [Google Scholar] [CrossRef]
- Neuberger, A.; Peles, S.; Rittel, D. Scaling the response of circular plates subjected to large and close-range spherical explosions. Part I: Air-blast loading. Int. J. Impact Eng. 2007, 34, 859–873. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, L.; Lu, G.; Wang, Z. Deformation and failure of blast-loaded metallic sandwich panels—Experimental investigations. Int. J. Impact Eng. 2008, 35, 937–951. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Y.; Xu, P. Blast resistance of metallic sandwich panels subjected to proximity underwater explosion. Int. J. Impact Eng. 2016, 93, 128–135. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Li, Y.; Wang, Z.; Wang, J. A Simplified Method for Evaluating the Dynamic Response of the Metal Sandwich Structure under Explosion Load. Metals 2022, 12, 1933. [Google Scholar] [CrossRef]
- Patel, S.; Patel, M. The efficient design of hybrid and metallic sandwich structures under air blast loading. J. Sandw. Struct. Mater. 2022, 24, 1706–1725. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Han, L.; Che, S. An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems. Adv. Mater. 2018, 30, e1705708. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Lei, H.; Wang, P.; Meng, J.; Li, C.; Zhou, H.; Zhang, X.; Fang, D. An experimental and numerical investigation of compressive response of designed Schwarz Primitive triply periodic minimal surface with non-uniform shell thickness. Extreme Mech. Lett. 2020, 37, 100671. [Google Scholar] [CrossRef]
- Novak, N.; Kytyr, D.; Rada, V.; Doktor, T.; Al-Ketan, O.; Rowshan, R.; Vesenjak, M.; Ren, Z. Compression behaviour of TPMS-filled stainless steel tubes. Mater. Sci. Eng. A 2022, 852, 143680. [Google Scholar] [CrossRef]
- Ramos, H.; Santiago, R.; Soe, S.; Theobald, P.; Alves, M. Response of gyroid lattice structures to impact loads. Int. J. Impact Eng. 2022, 164, 104202. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Gao, T.; Shi, C. Mechanical behavior and deformation mechanism of triply periodic minimal surface sheet under compressive loading. Mech. Adv. Mater. Struct. 2021, 28, 2057–2069. [Google Scholar] [CrossRef]
- Wei, S.; Song, B.; Zhang, Y.; Zhang, L.; Shi, Y. Mechanical Response of Triply Periodic Minimal Surface Structures Manufactured by Selective Laser Melting with Composite Materials. Acta Metall. Sin. (Engl. Lett.) 2021, 35, 397–410. [Google Scholar] [CrossRef]
- Yin, H.; Tan, D.; Wen, G.; Tian, W.; Wu, Q. Crashworthiness analysis and optimization design of TPMS-filled structure. Int. J. Crashworthiness. 2021, 27, 1481–1498. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Li, L.; Han, B.; He, S.-Y.; Zhao, Z.-Y.; Zhang, R.; Zhang, Q.-C.; Lu, T.J. Shock loading simulation using density-graded metallic foam projectiles. Mater. Design 2019, 164, 107546. [Google Scholar] [CrossRef]
- Kapfer, S.C.; Hyde, S.T.; Mecke, K.; Arns, C.H.; Schroder-Turk, G.E. Minimal surface scaffold designs for tissue engineering. Biomaterials 2011, 32, 6875–6882. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, C.; Wang, J.; Wang, P.; Bi, S.; Abbas, C.A. Design and Simulation of Flow Field for Bone Tissue Engineering Scaffold Based on Triply Periodic Minimal Surface. Chin. J. Mech. Eng. 2019, 32, 19. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, P.; Wei, D.; Si, J.; Wu, Y. Energy absorption of diamond lattice cylindrical shells under axial compression loading. Thin-Walled Struct. 2022, 181, 110131. [Google Scholar] [CrossRef]
- Yin, H.; Liu, Z.; Dai, J.; Wen, G.; Zhang, C. Crushing behavior and optimization of sheet-based 3D periodic cellular structures. Comp. Part B Eng. 2020, 182, 107565. [Google Scholar] [CrossRef]
- Yin, H.; Wang, X.; Wen, G.; Zhang, C.; Zhang, W. Crashworthiness optimization of bio-inspired hierarchical honeycomb under axial loading. Int. J. Crashworth. 2021, 26, 26–37. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Soliman, A.; AlQubaisi, A.M.; Abu Al-Rub, R.K. Nature-Inspired Lightweight Cellular Co-Continuous Composites with Architected Periodic Gyroidal Structures. Adv. Eng. Mater. 2018, 20, 1700549. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Palazotto, A.N.; Abu Al-Rub, R.K. On Mechanical Properties of Cellular Steel Solids With Shell-Like Periodic Architectures Fabricated by Selective Laser Sintering. J. Eng. Mater. Technol. 2019, 141, 021009. [Google Scholar] [CrossRef]
- Lin, C.; Wen, G.; Yin, H.; Wang, Z.-P.; Liu, J.; Xie, Y.M. Revealing the sound insulation capacities of TPMS sandwich panels. J. Sound Vibr. 2022, 540, 117303. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Jasiuk, I.; Sobh, N.A. Acoustic band gaps and elastic stiffness of PMMA cellular solids based on triply periodic minimal surfaces. Mater. Des. 2018, 145, 20–27. [Google Scholar] [CrossRef]
- Novak, N.; Borovinšek, M.; Al-Ketan, O.; Ren, Z.; Vesenjak, M. Impact and blast resistance of uniform and graded sandwich panels with TPMS cellular structures. Comp. Struct. 2022, 300. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Krstulovic-Opara, L.; Rowshan, R.; Vesenjak, M.; Ren, Z. Bending behavior of triply periodic minimal surface foam-filled tubes. Mech. Adv. Mater. Struct. 2022, 30, 3061–3074. [Google Scholar] [CrossRef]
- Yoo, D.-J. Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces. Int. J. Precis. Eng. Manuf. 2011, 12, 61–71. [Google Scholar] [CrossRef]
- Duan, Y.; Du, B.; Shi, X.; Hou, B.; Li, Y. Quasi-static and dynamic compressive properties and deformation mechanisms of 3D printed polymeric cellular structures with Kelvin cells. Int. J. Impact Eng. 2019, 132, 103303. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.-S.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical properties of 3D printed polymeric Gyroid cellular structures: Experimental and finite element study. Mater. Design 2019, 165, 107597. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, R.; Liu, J.; Armstrong, J.; Zhao, R.; Zhou, C. Continuous stereolithography 3d printing of multi-network hydrogels in triply periodic minimal structures (tpms) with tunable mechanical strength for energy absorption. J. Manufact. Sci. Eng. 2023, 86656, 1–25. [Google Scholar] [CrossRef]
- Mohamed, G.G.; Shinichi, O. 3D-printed triply periodic minimal surface (TPMS) structures: Towards potential application of adsorption-based atmospheric water harvesting. Energy Conver. Manag. 2023, 297, 117729. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Z.; Ning, J.; Xiao, G.; Liu, E.; Shu, X. Dynamic response of sandwich structures with graded auxetic honeycomb cores under blast loading. Compos. Part B Eng. 2016, 106, 206–217. [Google Scholar] [CrossRef]
- Zhang, C.; Gholipour, G.; Mousavi, A.A. Nonlinear dynamic behavior of simply-supported RC beams subjected to combined impact-blast loading. Eng. Struct. 2019, 181, 124–142. [Google Scholar] [CrossRef]
- Suazo, G.; Villavicencio, G. Numerical simulation of the blast response of cemented paste backfilled stopes. Comput. Geotech. 2018, 100, 1–14. [Google Scholar] [CrossRef]
- Sun, G.; Xu, F.; Li, G.; Li, Q. Crashing analysis and multiobjective optimization for thin-walled structures with functionally graded thickness. Int. J. Impact Eng. 2014, 64, 62–74. [Google Scholar] [CrossRef]
- Firouzi, M.; Niknejad, A.; Ziaee, S.; Hematiyan, M.R. Optimization of H-shaped thin-walled energy absorber by Taguchi method and a new theoretical estimation for its energy absorption. Thin-Walled Struct. 2018, 131, 33–44. [Google Scholar] [CrossRef]
- Nalbant, M.; Gökkaya, H.; Sur, G. Application of Taguchi method in the optimization of cutting parameters for surface roughness in turning. Mater. Des. 2007, 28, 1379–1385. [Google Scholar] [CrossRef]
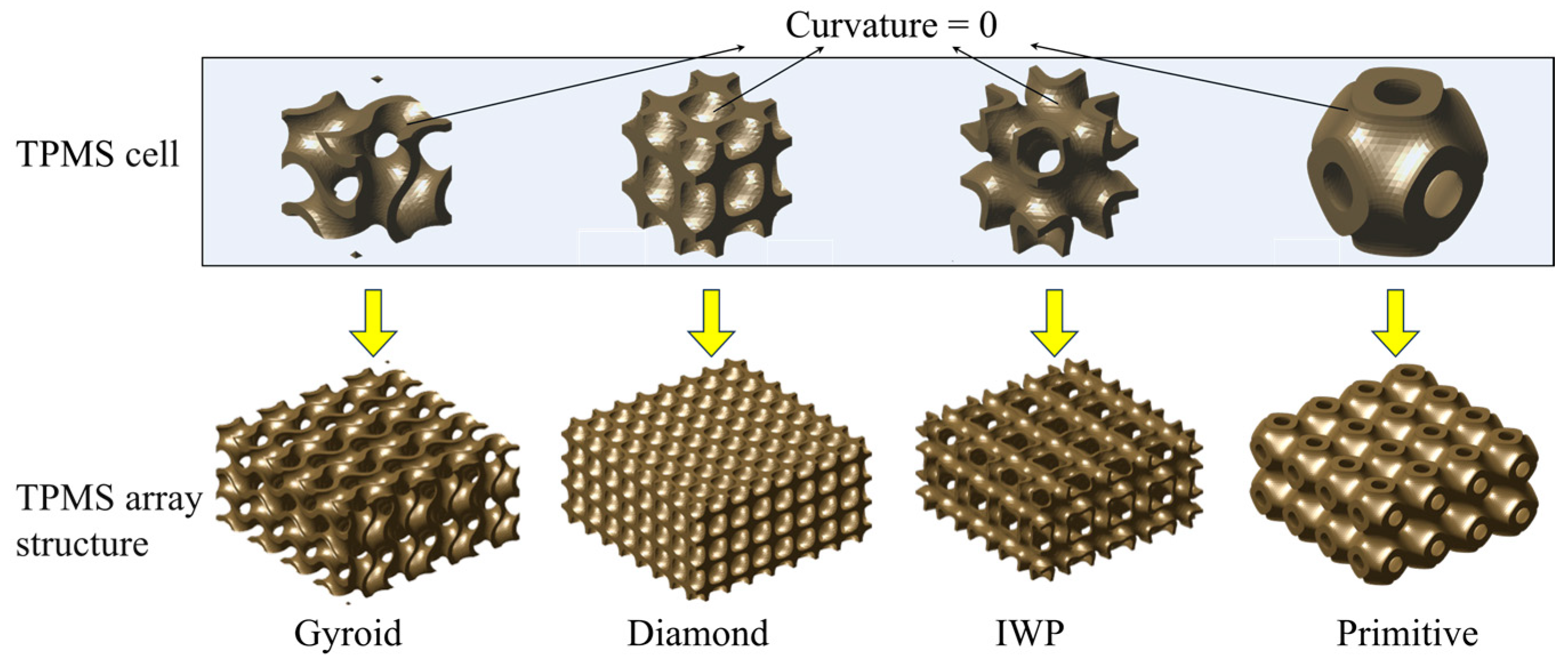
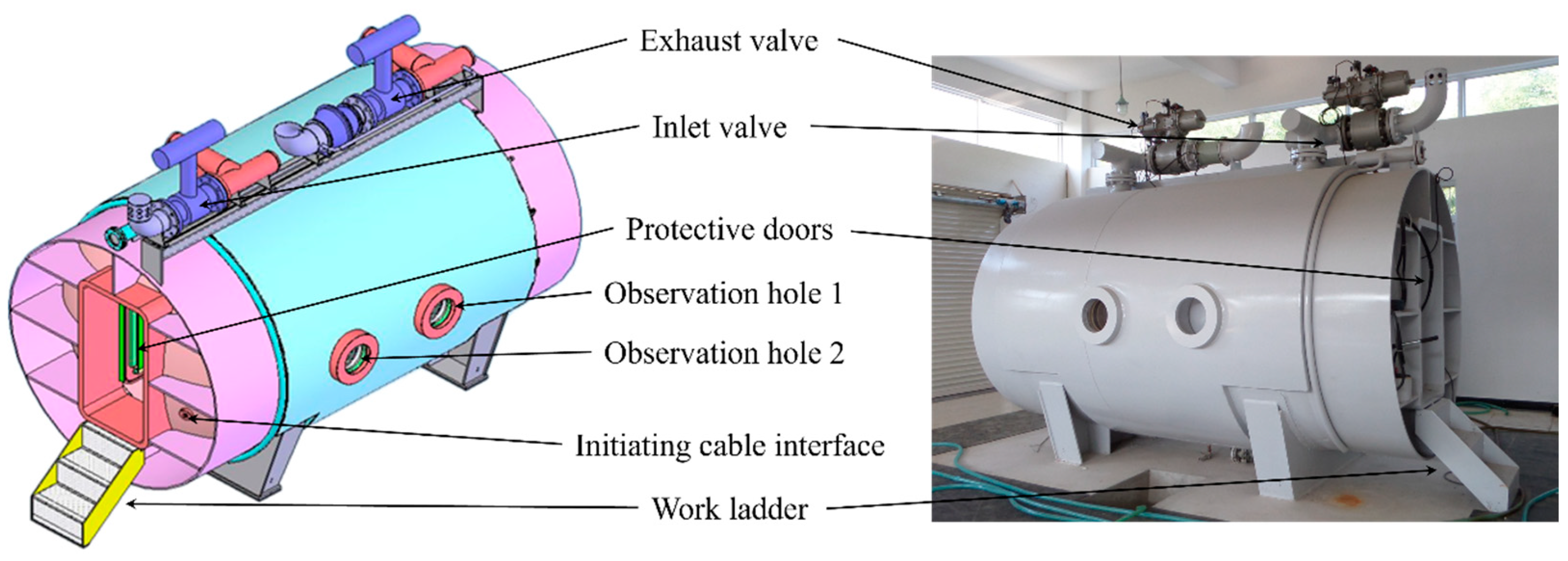
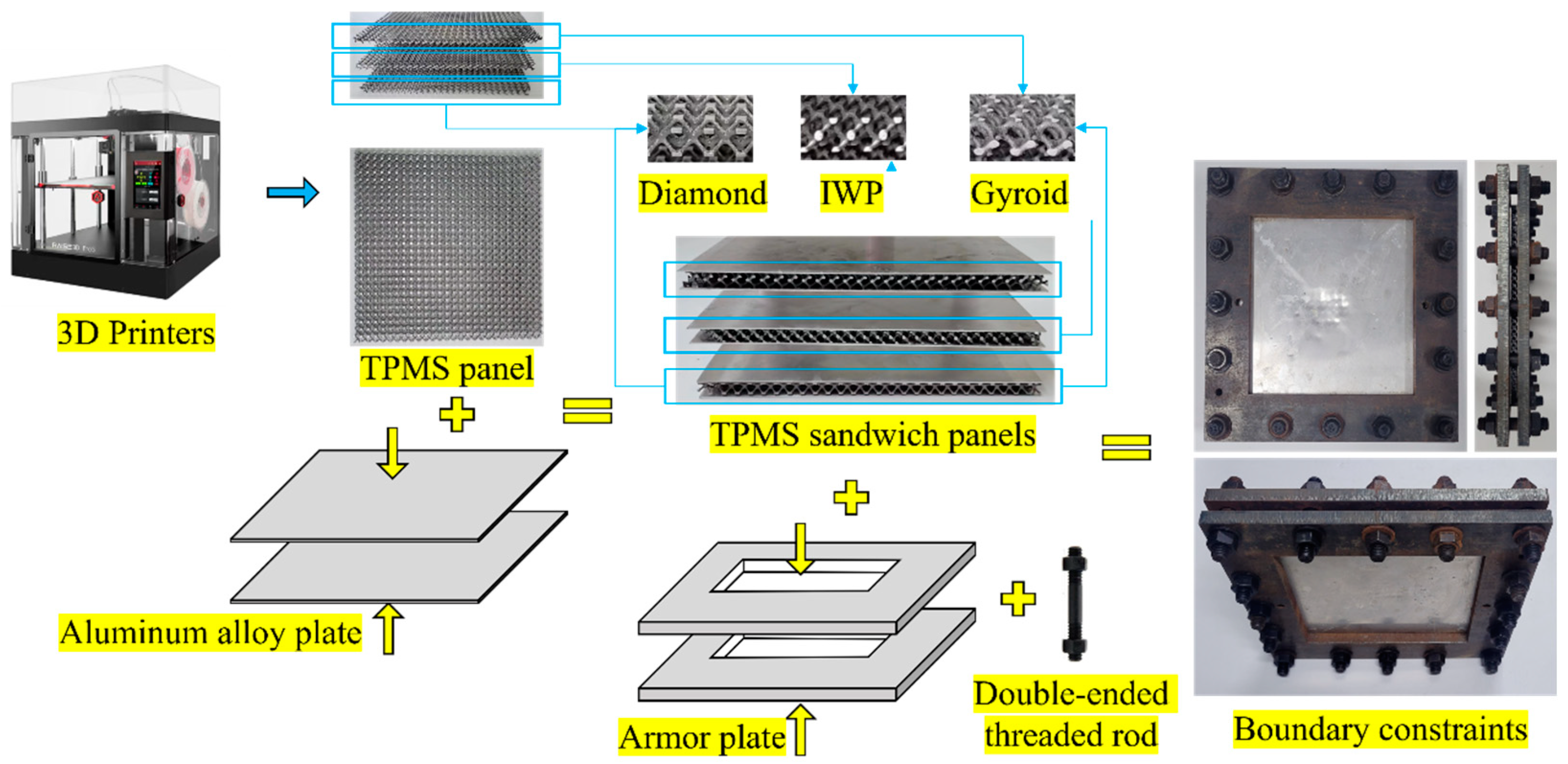



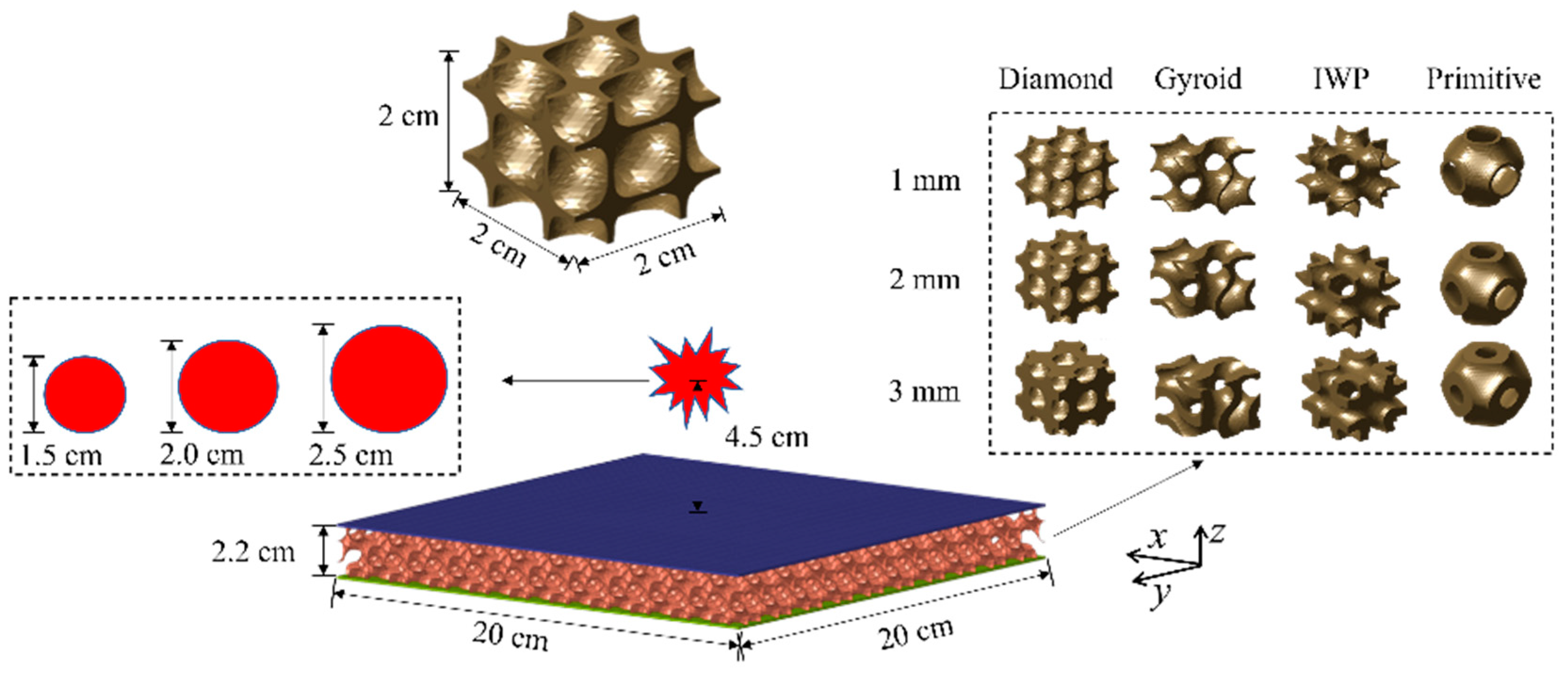



| No. | Types of TPMS | Thickness/mm | TNT Charge Diameter/cm |
|---|---|---|---|
| 1 | Gyroid | 1 | 2.5 |
| 2 | Diamond | 1 | 2.5 |
| 3 | IWP | 1 | 2.5 |
| 4 | Primitive | 1 | 2.5 |
| 5 | Gyroid | 1 | 2.0 |
| 6 | Diamond | 1 | 2.0 |
| 7 | IWP | 1 | 2.0 |
| 8 | Primitive | 1 | 2.0 |
| 9 | Gyroid | 2 | 2.0 |
| 10 | Diamond | 2 | 2.0 |
| 11 | IWP | 2 | 2.0 |
| 12 | Primitive | 2 | 2.0 |
| 13 | Gyroid | 3 | 2.0 |
| 14 | Diamond | 3 | 2.0 |
| 15 | IWP | 3 | 2.0 |
| 16 | Primitive | 3 | 2.0 |
| 17 | Gyroid | 1 | 1.5 |
| 18 | Diamond | 1 | 1.5 |
| 19 | IWP | 1 | 1.5 |
| 20 | Primitive | 1 | 1.5 |
| AISI 4340 Aluminum alloy | ||||
| Density (kg/m3) | Modulus of elasticity (GPa) | Shear modulus (GPa) | Poisson’s ratio | Yield stress (MPa) |
| 2680 | 72 | 0.737 | 0.33 | 75.8 |
| TNT explosives | ||||
| Density (kg/m3) | Explosive speed (m/s) | PCJ (GPa) | A (GPa) | B (GPa) |
| 1650 | 6930 | 2.1 | 366 | 6.75 |
| ω | R1 (GPa) | R2 (GPa) | V | |
| 0.32 | 4.8 | 1.4 | 1.0 | |
| Air | ||||
| Density (kg/m3) | Cut-off pressure (Pa) | |||
| 1.293 | −0.1 | |||
| C0, C1, C2, C3, C6 | C4, C5 | E0 (Gpa) | ||
| 0 | 0.4 | 2.5 × 10−4 | ||
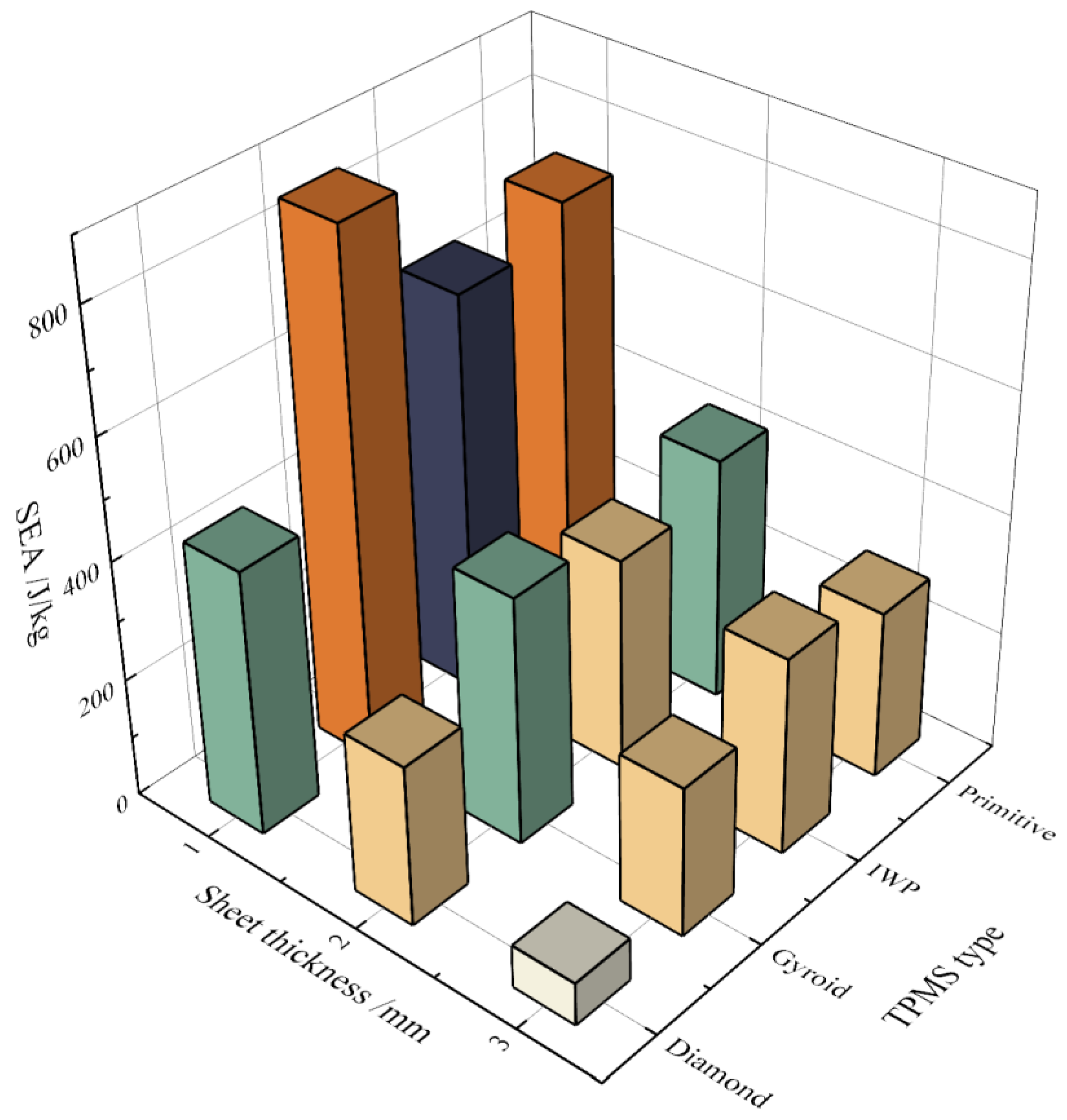
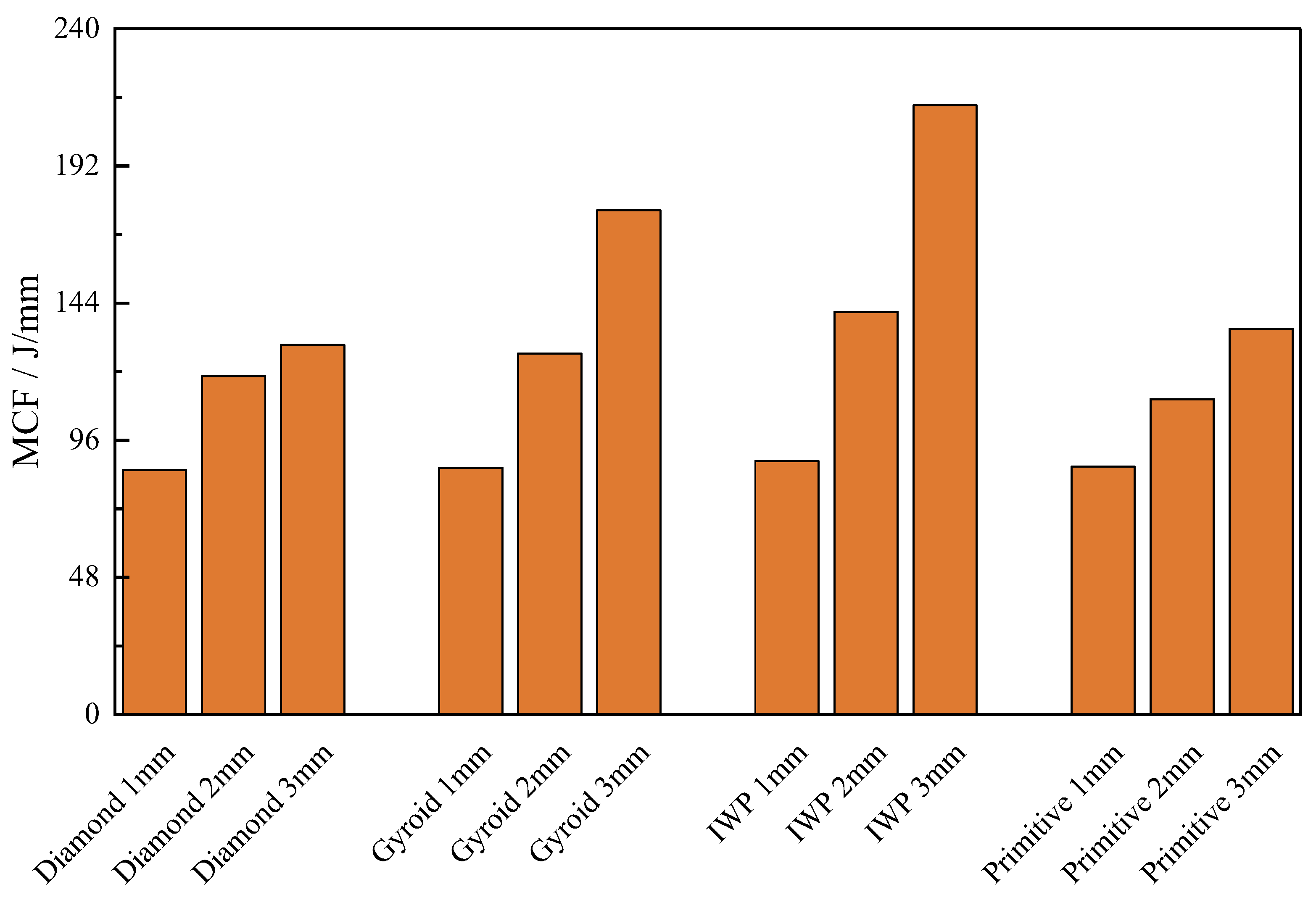
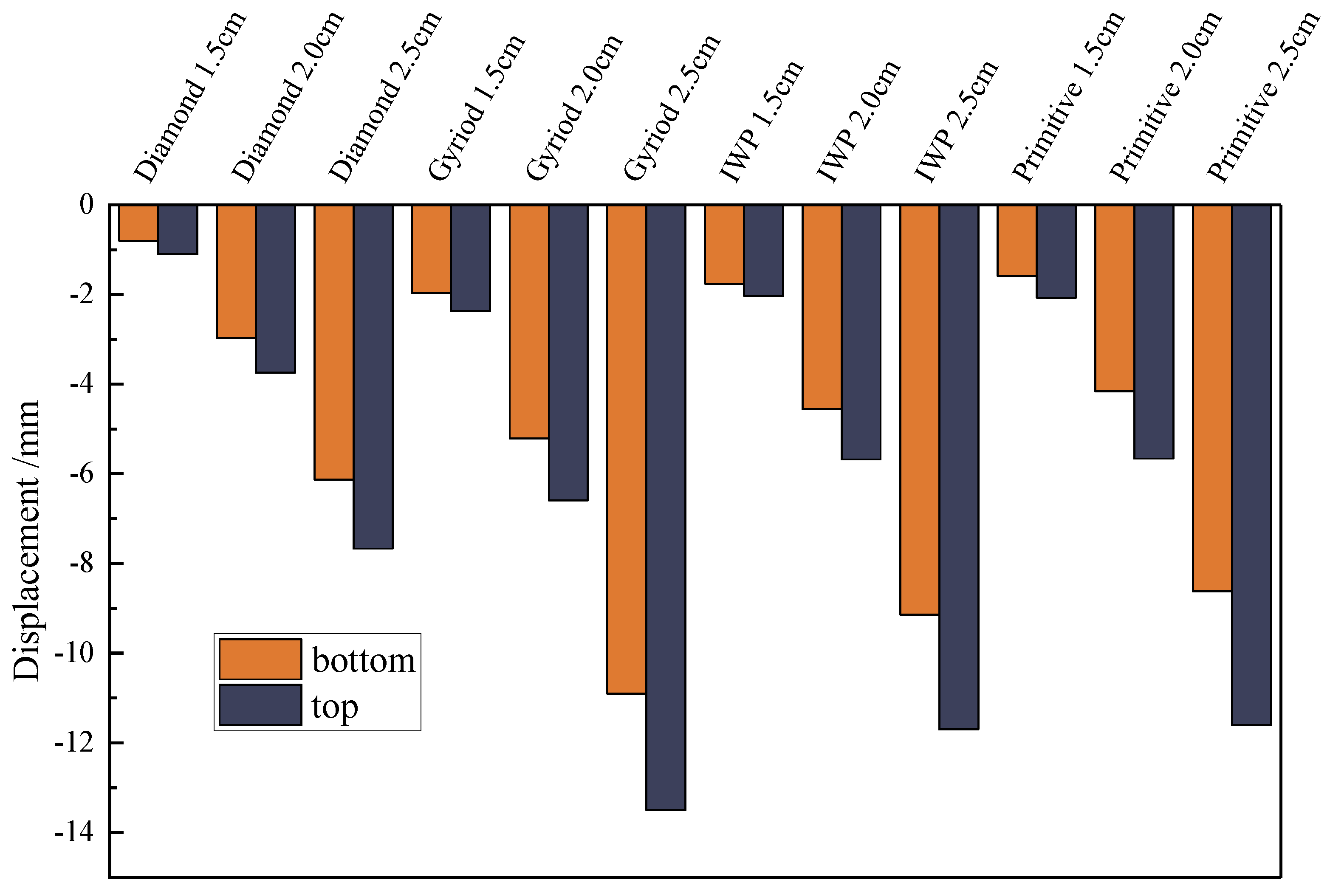
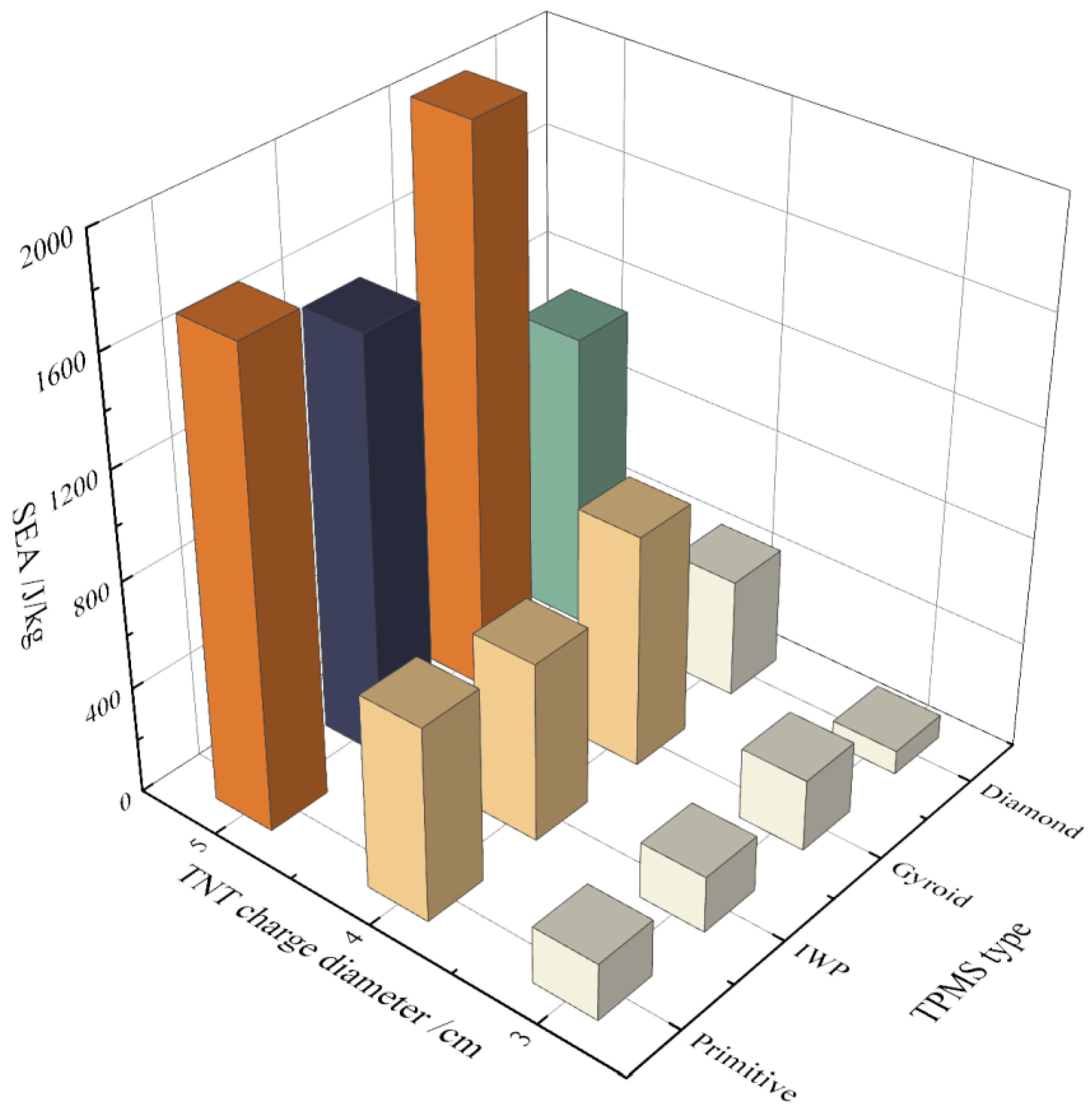
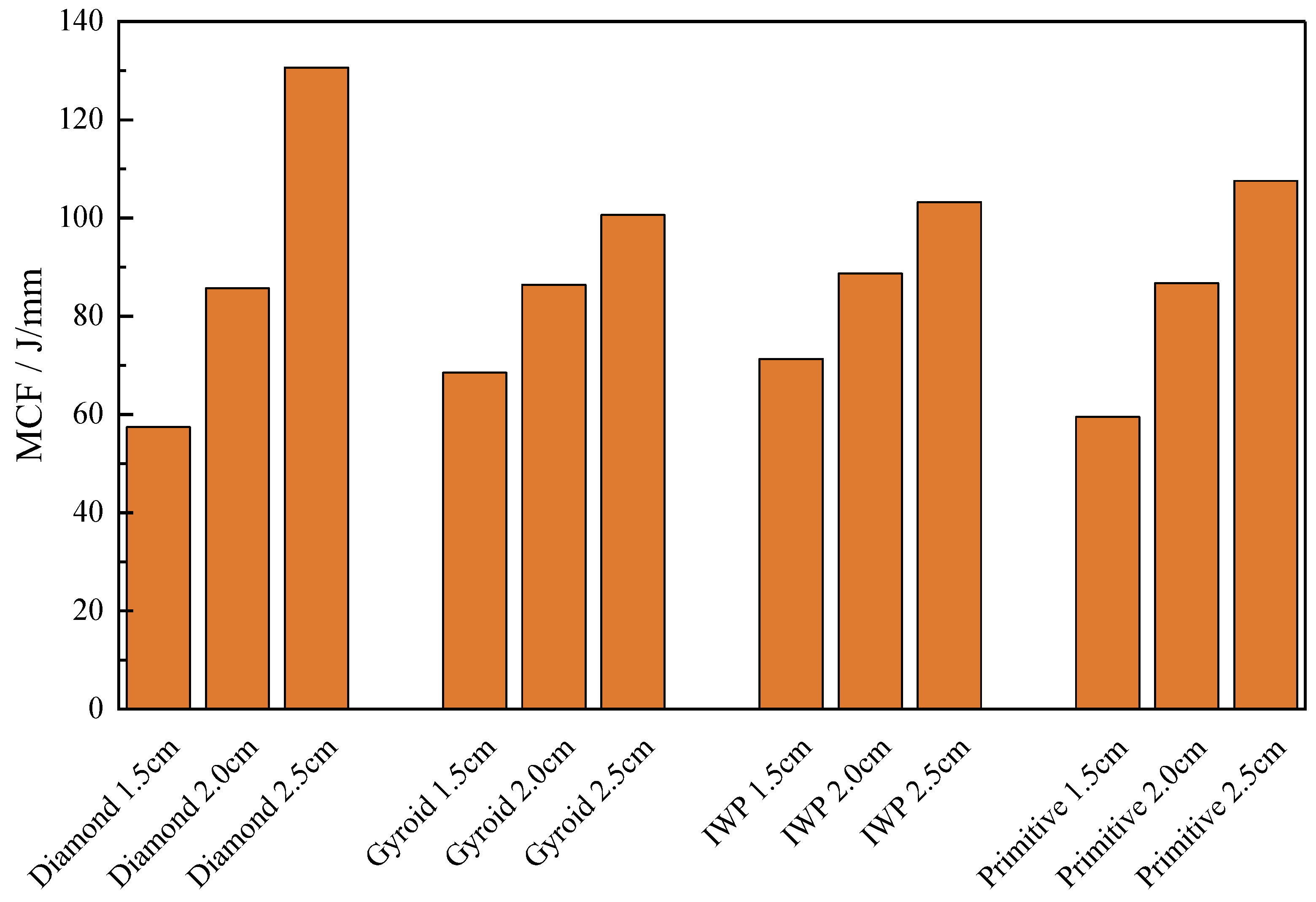
| Configuration | No. | Thickness/mm | Displacement/mm | EA/J | SEA/J/kg | MCF/J/mm |
|---|---|---|---|---|---|---|
| Diamond | 1 | 0.001 | 1.10 | 54.825 | 89.65357 | 57.41 |
| 2 | 0.001 | 3.74 | 287.86 | 444.6431 | 85.67 | |
| 3 | 0.002 | 2.71 | 290.815 | 269.1842 | 118.46 | |
| 4 | 0.003 | 0.96 | 112.655 | 71.75474 | 129.41 | |
| 5 | 0.001 | 7.67 | 901.41 | 1103.007 | 130.64 | |
| Gyroid | 6 | 0.001 | 2.37 | 148.639 | 268.8357 | 68.50 |
| 7 | 0.001 | 6.59 | 509.757 | 872.0952 | 86.40 | |
| 8 | 0.002 | 3.38 | 393.771 | 416.1870 | 126.41 | |
| 9 | 0.003 | 1.97 | 328.385 | 250.9451 | 176.55 | |
| 10 | 0.001 | 13.50 | 1227.32 | 2068.043 | 100.60 | |
| IWP | 11 | 0.001 | 2.03 | 135.087 | 210.3183 | 71.29 |
| 12 | 0.001 | 5.68 | 453.974 | 670.1660 | 88.67 | |
| 13 | 0.002 | 2.92 | 390.376 | 357.6279 | 140.93 | |
| 14 | 0.003 | 1.58 | 330.474 | 331.0945 | 213.21 | |
| 15 | 0.001 | 11.70 | 1075.59 | 1557.8030 | 103.22 | |
| Primitive | 16 | 0.001 | 2.07 | 108.902 | 213.0182 | 59.51 |
| 17 | 0.001 | 5.66 | 425.986 | 722.8856 | 86.76 | |
| 18 | 0.002 | 3.81 | 375.208 | 410.7380 | 110.36 | |
| 19 | 0.003 | 2.80 | 343.133 | 282.5041 | 135.09 | |
| 20 | 0.001 | 11.60 | 1087.400 | 1748.4660 | 107.56 |
| Energy Absorption Index | TPMS | Thickness/mm |
|---|---|---|
| Displacement | Diamond | 3 |
| EA | Gyroid | 2 |
| SEA | Gyroid | 2 |
| MCF | IWP | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Li, T.; Zhong, D.; Tao, H.; Peng, Y.; Chen, S. Blast Resistance in Sandwich Structures Based on TPMS. Buildings 2023, 13, 2835. https://doi.org/10.3390/buildings13112835
He L, Li T, Zhong D, Tao H, Peng Y, Chen S. Blast Resistance in Sandwich Structures Based on TPMS. Buildings. 2023; 13(11):2835. https://doi.org/10.3390/buildings13112835
Chicago/Turabian StyleHe, Li, Tengfei Li, Dongwang Zhong, Haohao Tao, Yuesen Peng, and Shasha Chen. 2023. "Blast Resistance in Sandwich Structures Based on TPMS" Buildings 13, no. 11: 2835. https://doi.org/10.3390/buildings13112835
APA StyleHe, L., Li, T., Zhong, D., Tao, H., Peng, Y., & Chen, S. (2023). Blast Resistance in Sandwich Structures Based on TPMS. Buildings, 13(11), 2835. https://doi.org/10.3390/buildings13112835








