Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints
Abstract
1. Introduction
2. Experimental Overview
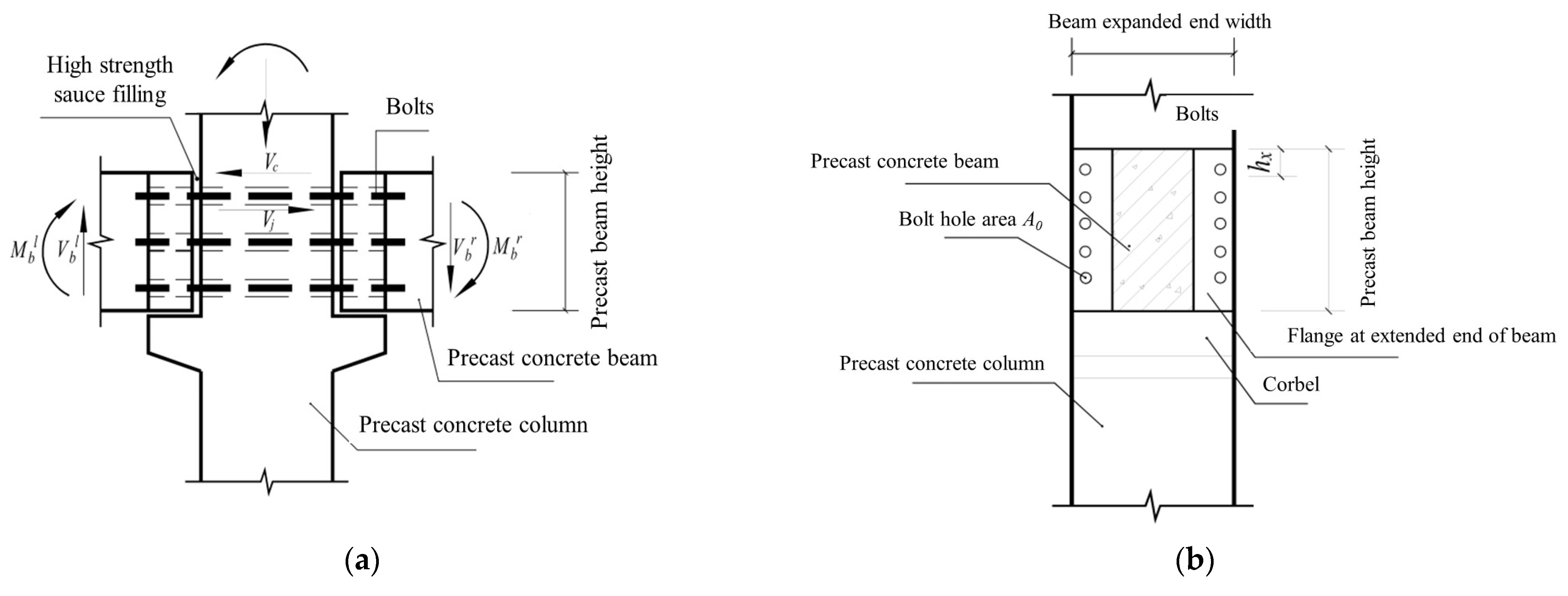
2.1. Design Principles of Joints
2.2. Sizing and Reinforcement of Test Specimens
2.3. Material Properties
2.3.1. Mechanical Properties of Concrete
2.3.2. Mechanical Properties of Steel
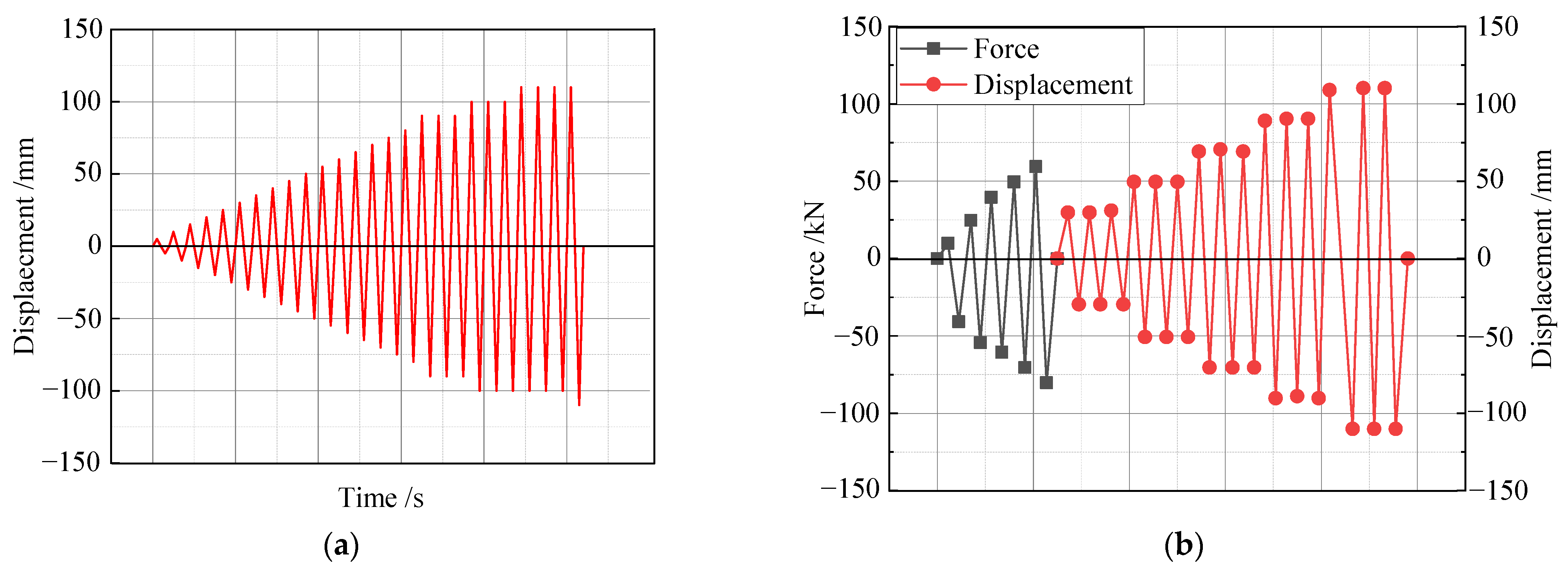
2.4. Loading Devices and Loading Regimes
3. Experimental Phenomena and Their Analysis
3.1. Main Experimental Phenomena
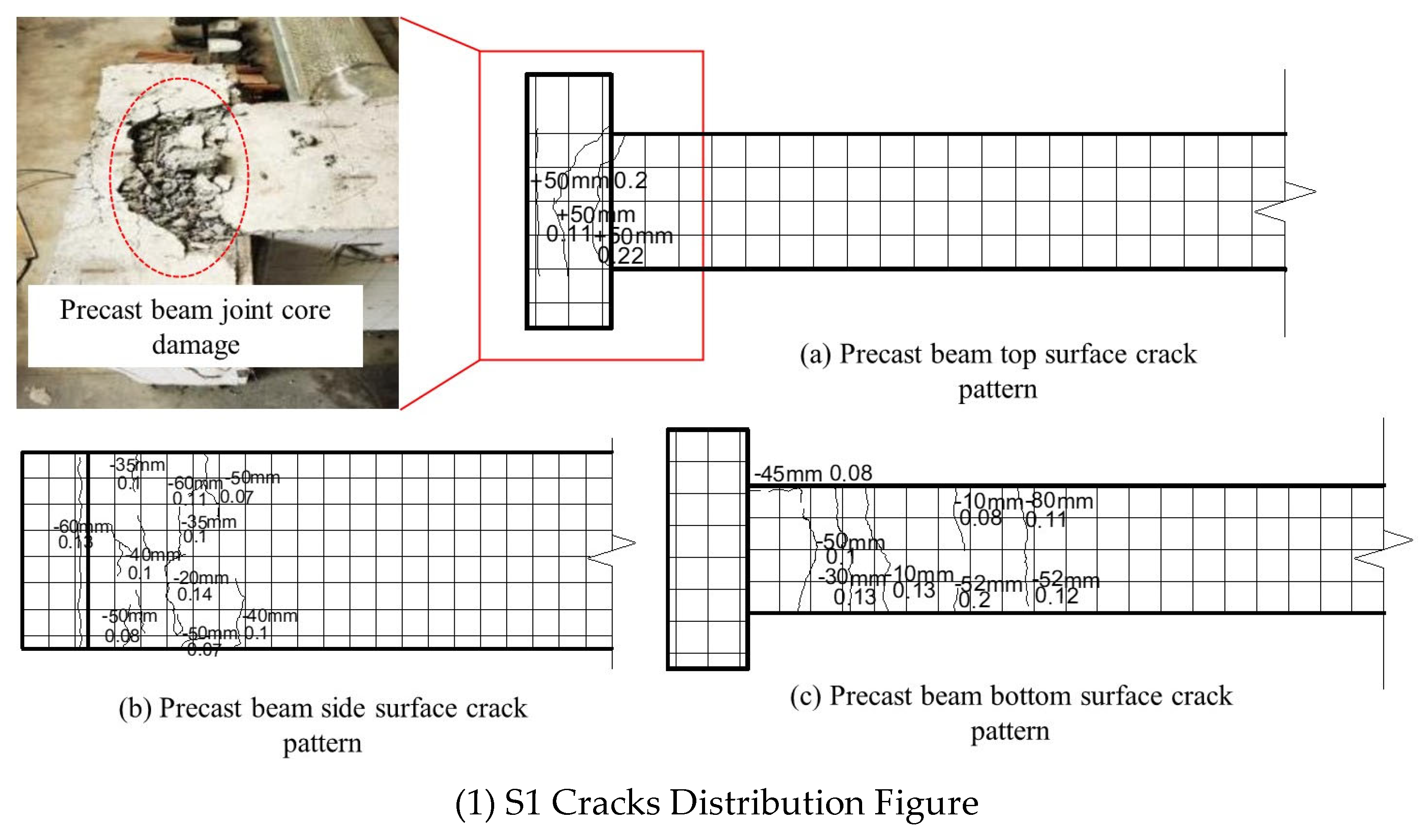
3.1.1. Crack Development in Specimen S1
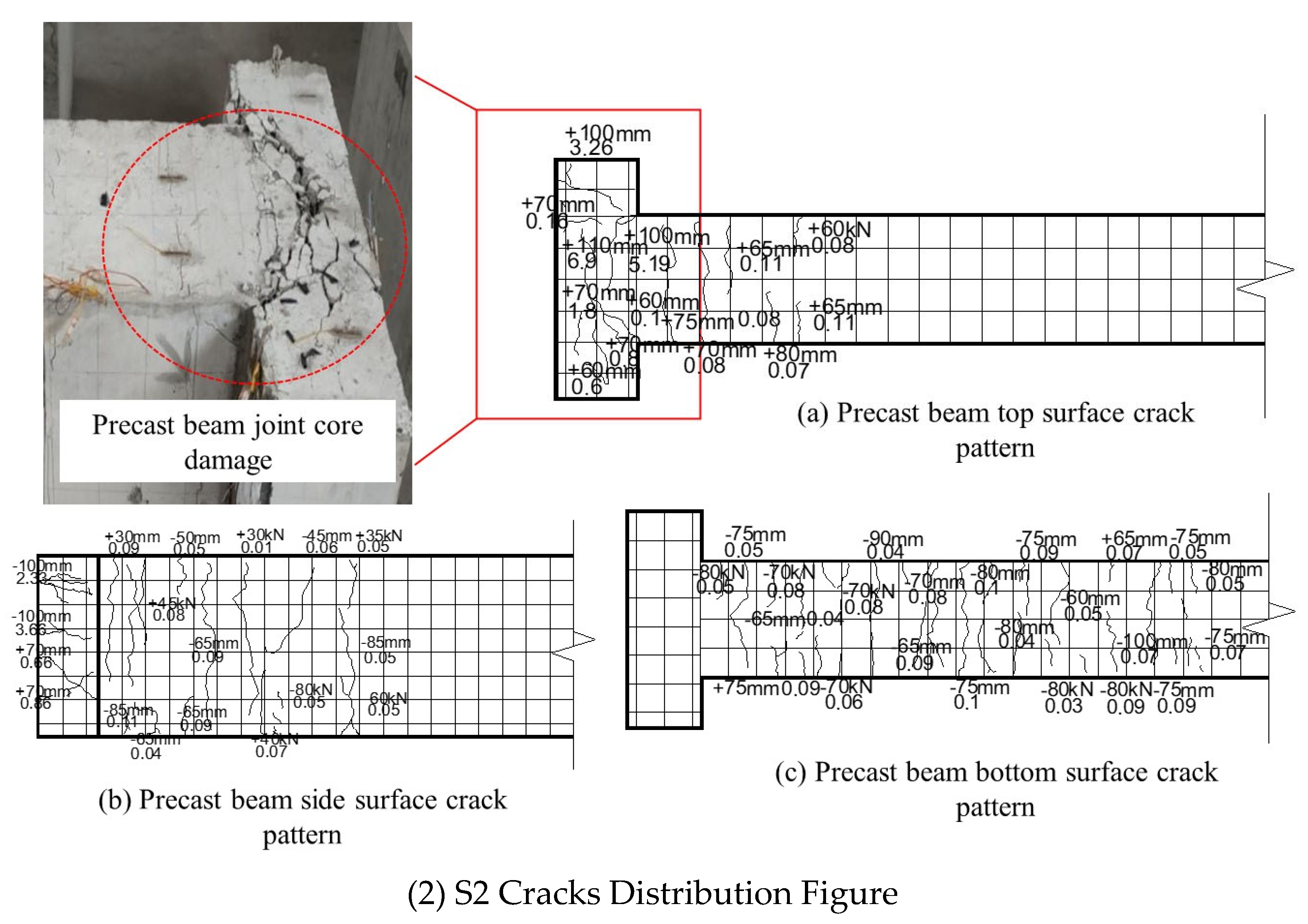
3.1.2. Crack Development in Specimen S2
3.2. Analysis of Experimental Phenomena
3.3. Experimental Results
3.3.1. Load Displacement Curves
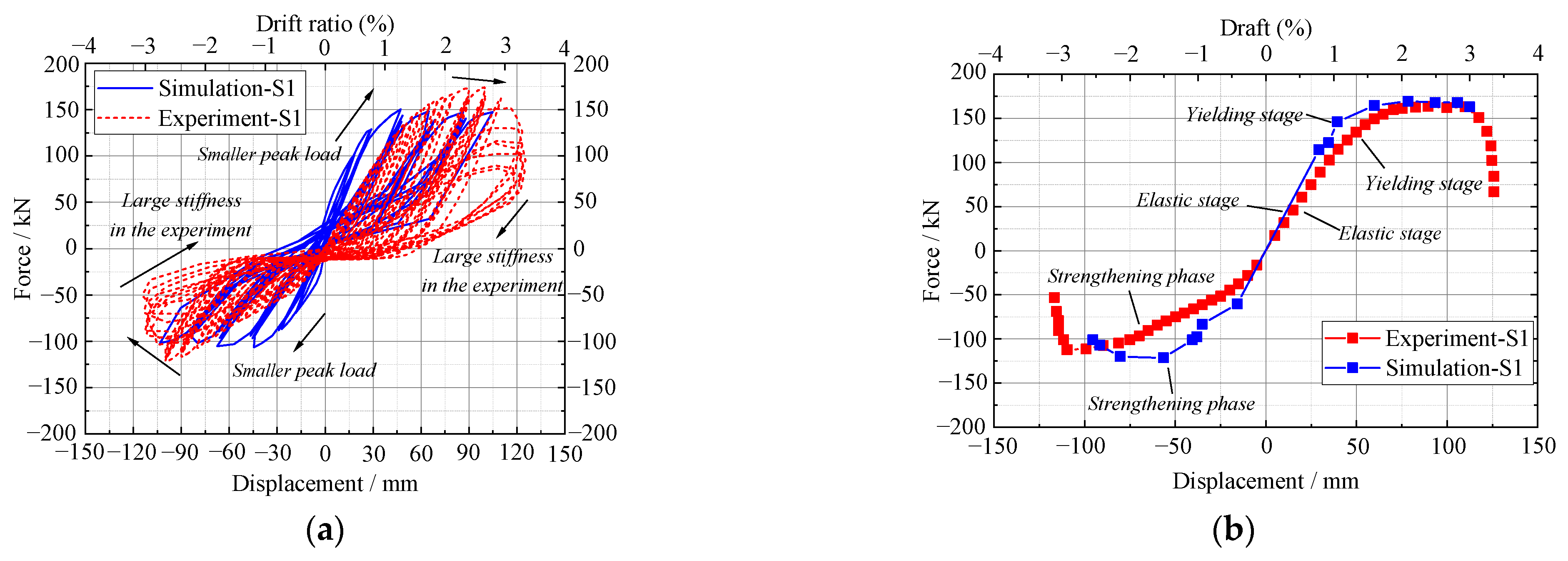
- Comparing the hysteresis curves of S1 and S2, the hysteresis curves are bowed, generally smooth and full. The area of the hysteresis curve increases with the increase in displacement load, which indicates that both S1 and S2 have some plastic deformation capacity and a good energy dissipation capacity. At the same time, the loading force and displacement of the two new joints are approximately linear at the beginning of the loading, when the joints did not crack; with the increase in force, they gradually became non-linear.
- The hysteresis circle of S2 is significantly larger than that of S1. The ultimate displacements of S2 and S1 are 115.8 mm and 126.6 mm, respectively, and the ultimate displacement of S2 is 9.32% higher than that of S1. This indicates that S2 bolt deformation in the energy dissipation phase is greater than S1, enhancing the energy dissipation performance of the joint. It can be seen that an increase in the bolt diameter of the connector increases the energy dissipation performance of the joint.
- The hysteresis curves of both S1 and S2 are asymmetrical during reciprocating loading. This is due to the corbel limiting the rotation of the precast beam during negative loading, increasing the stiffness of the joints, decreasing the bolt deformation and reducing the energy dissipation capacity.
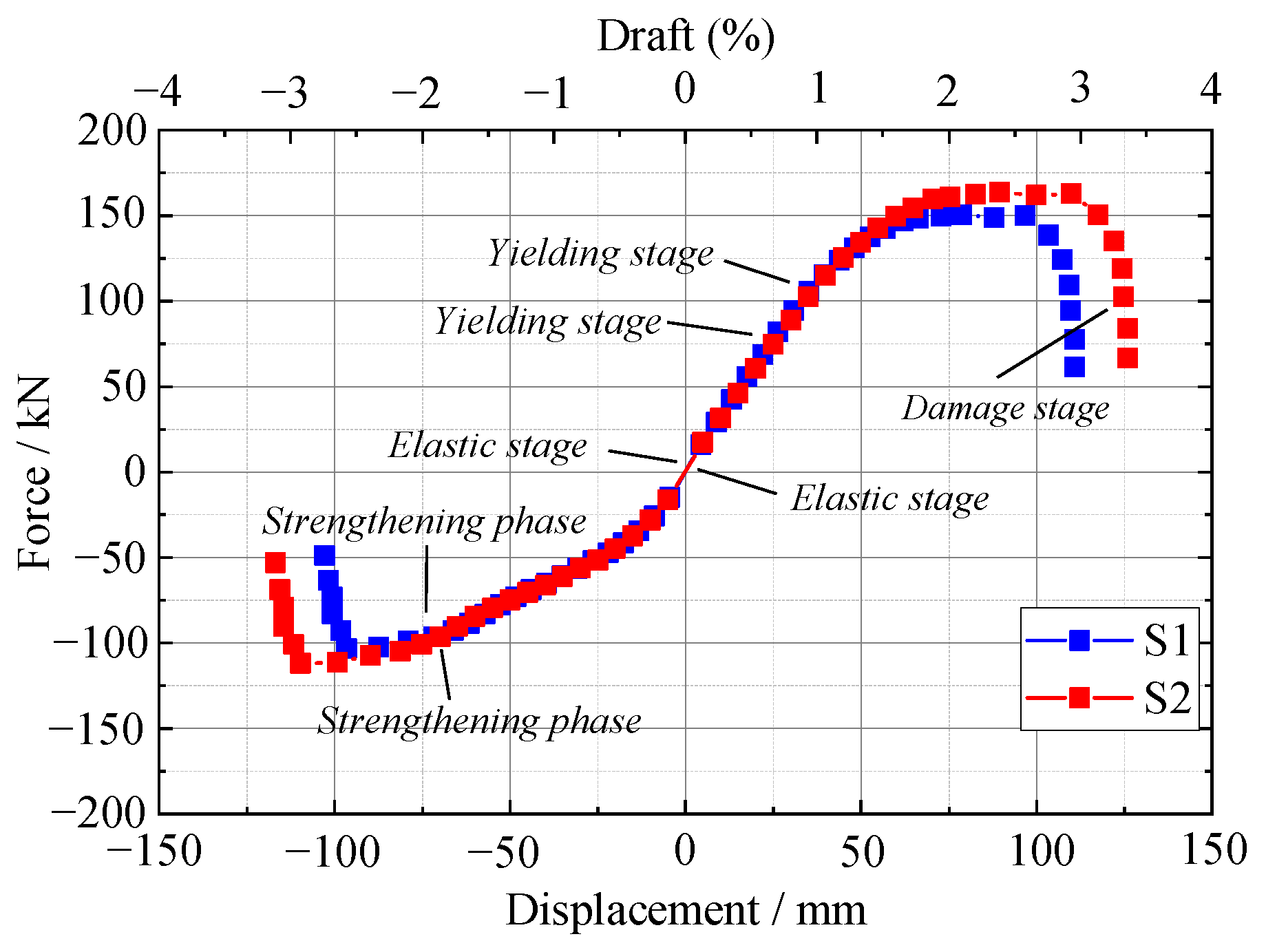
3.3.2. Skeleton Curves
- The two joints in the experimental state go through the elastic phase, the yield phase, the strengthening phase and the damage phase. All maintain good stiffness in the early stages of loading, and the skeleton curves of the specimens all tend to be approximately straight lines, indicating that the components are in the elastic stage with little change in stiffness and displacement. As the load continues to increase, the reinforcement of the precast beam starts to deform and yield and the bolt deformation of specimens S1 and S2 increases. The specimens begin to develop elastoplastic, their skeleton curves gradually shift towards the displacement axis and no longer change linearly, and the stiffness of the specimens gradually degrades.
- The yield load was Py = 98 kN, ultimate load was Pmax = 148 kN and ultimate damage load was Pu = 151 kN for S1. The yield load was Py = 113 kN, ultimate load was Pmax = 165 kN and ultimate damage load was Pu = 178 kN for S2. It can be seen that the S2 yield load is 39.4% higher, the ultimate load is 11.5% higher and the damage load is 13.2% higher than S1 for the same working conditions. The reason for this is that the S2 bolt diameter is larger than S2, allowing the cracks in the beam to crack and move back, increasing the stiffness and load-carrying capacity of the enlarged end of the precast beam, thus increasing the load-carrying capacity.
- Specimen S1 has a positive peak load of 151 kN and a negative peak load of 113 kN, a difference of 25.2%. Specimen S2 has a positive peak load of 178 kN and a negative peak load of 121 kN, a difference of 32.02%. The corbel acts as a support for the beam and was not subjected to forces, the load capacity being determined by the structure of the beam itself. The final damage to both S1 and S2 was due to the bolts yielding and cracks in the beam end surfaces, but the load-bearing reinforcement did not yield. It can be seen that the energy consumption of the new joints is primarily based on bolts and cracks produced in the core zone of the joints. No damage occurred to the corbel and columns, compounded by the new joints’ design concept.
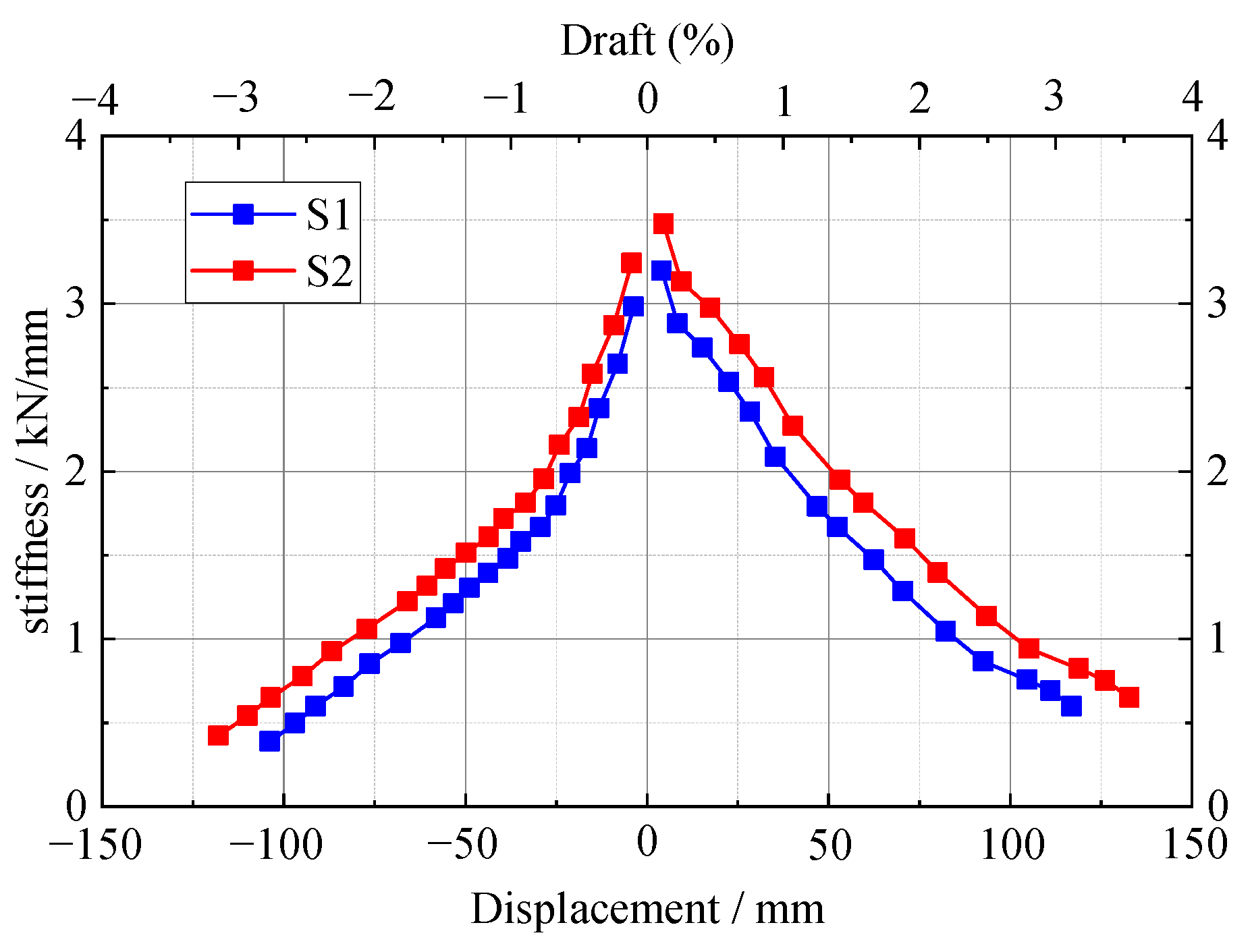
3.3.3. Stiffness Degradation Curves
4. Finite Element Simulation Analysis
4.1. Concrete Damage Model Theory
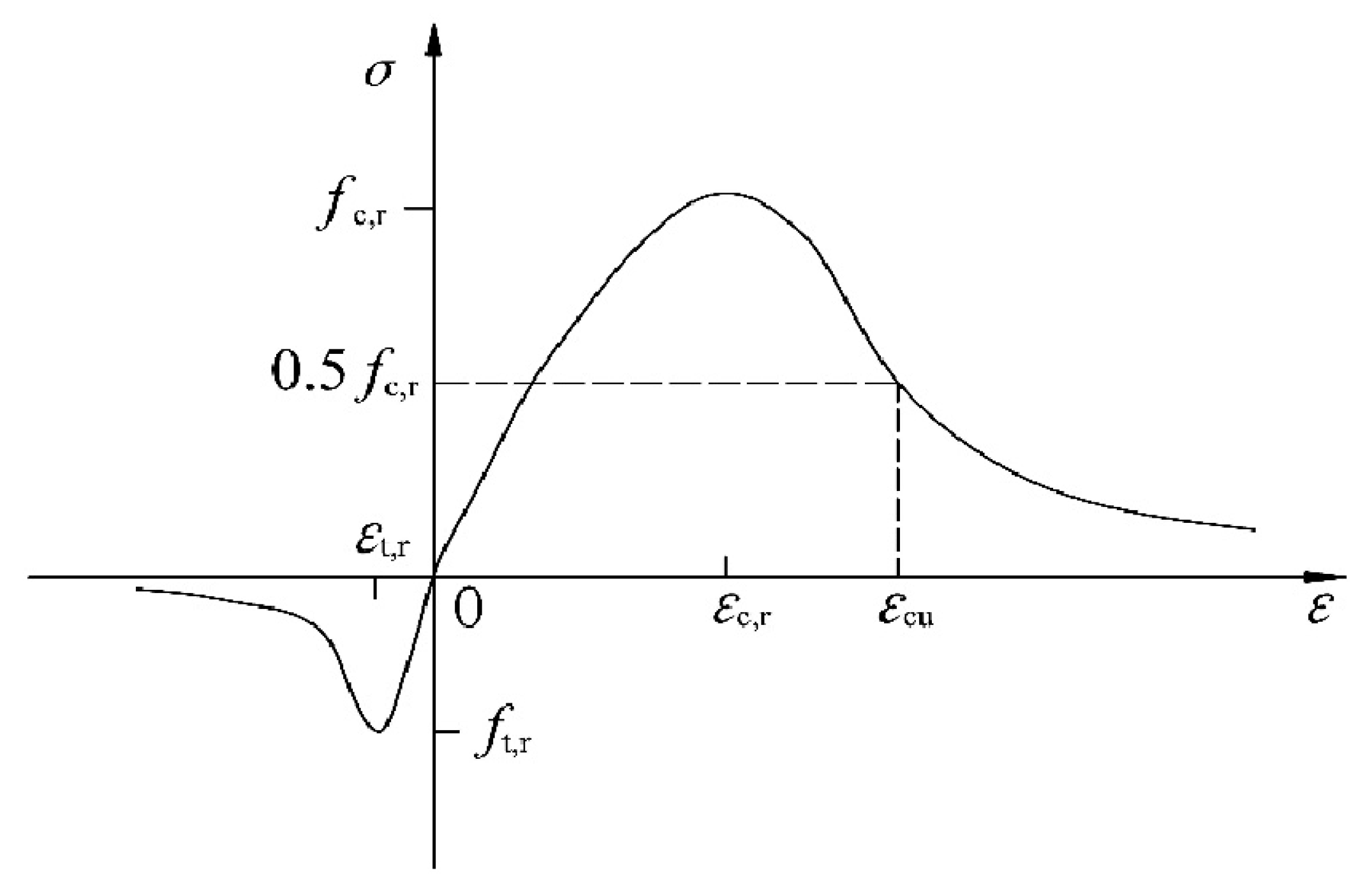
4.1.1. Concrete Material Constitutive Relationships
4.1.2. Hysteresis Rules
4.1.3. Yield Criterion and Law of Flow
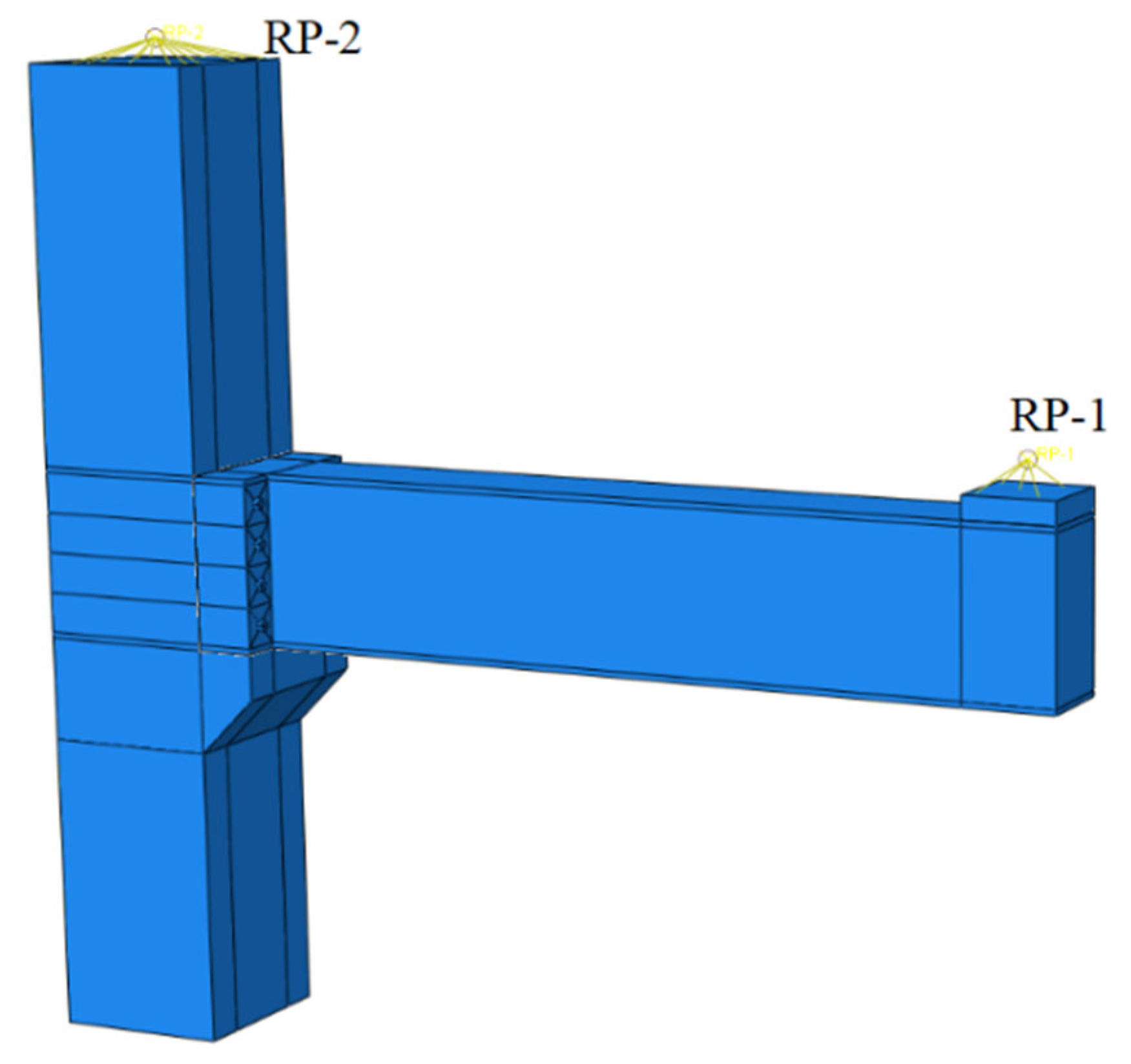
4.2. Finite Element Model
4.3. Material Properties
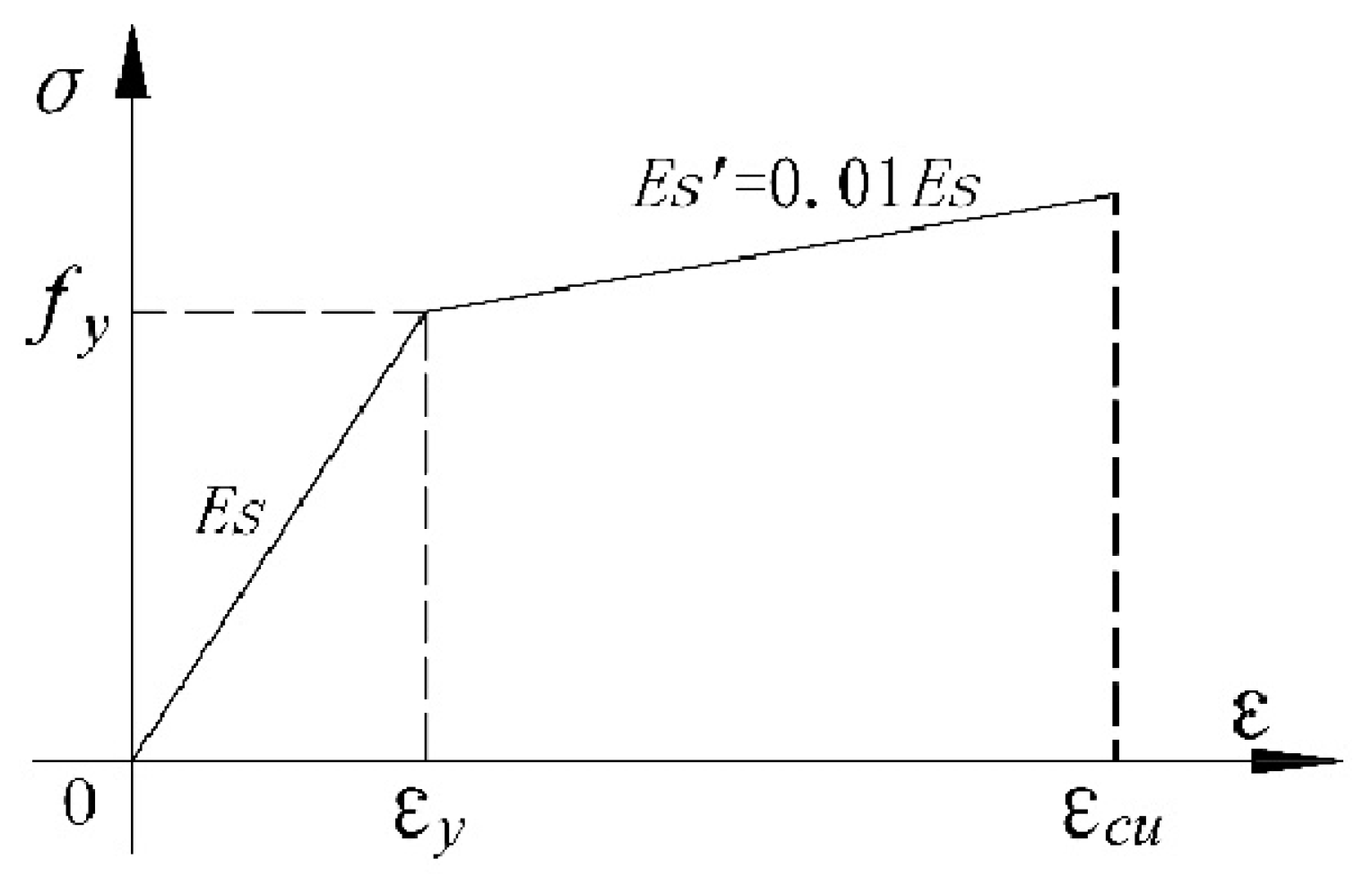
Material Stress–Strain Curves
4.4. Interaction
4.5. Boundary Conditions and Load Loading
4.6. Validation of Finite Element Results
4.7. Hysteresis Performance
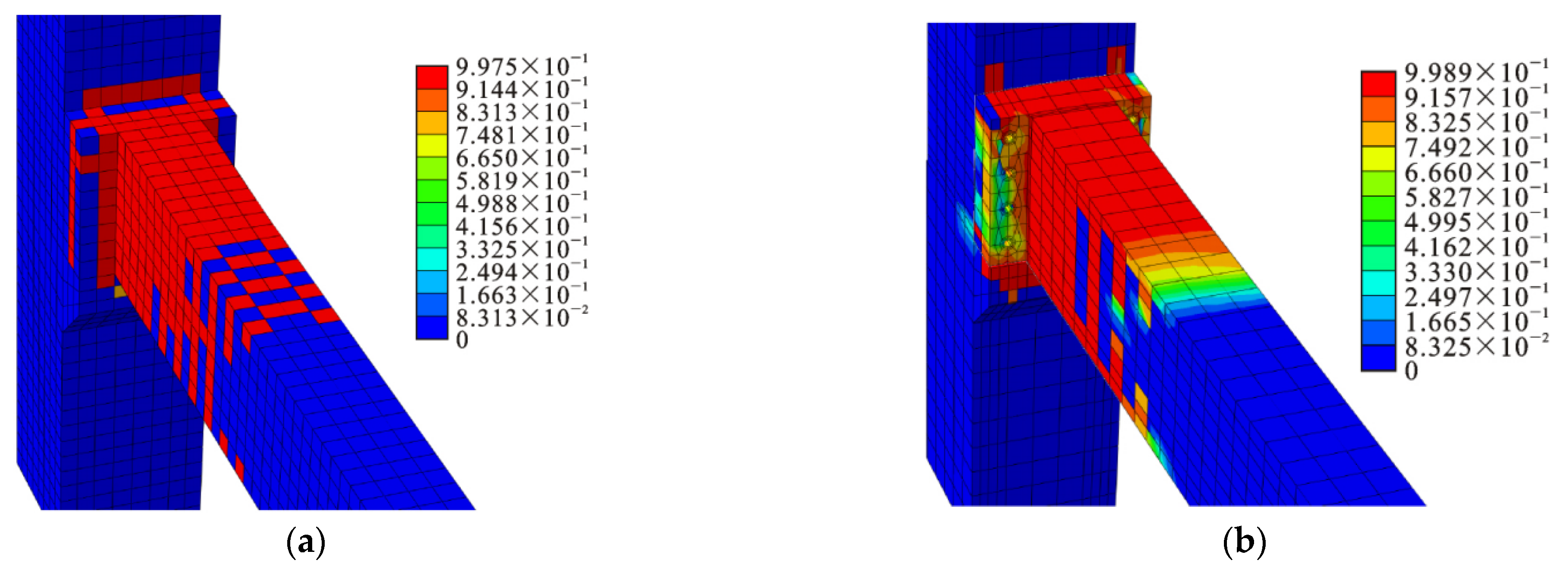
4.8. Concrete Plastic Damage Model
5. Research on the Design Method of New Assembled Beam–Column Joints
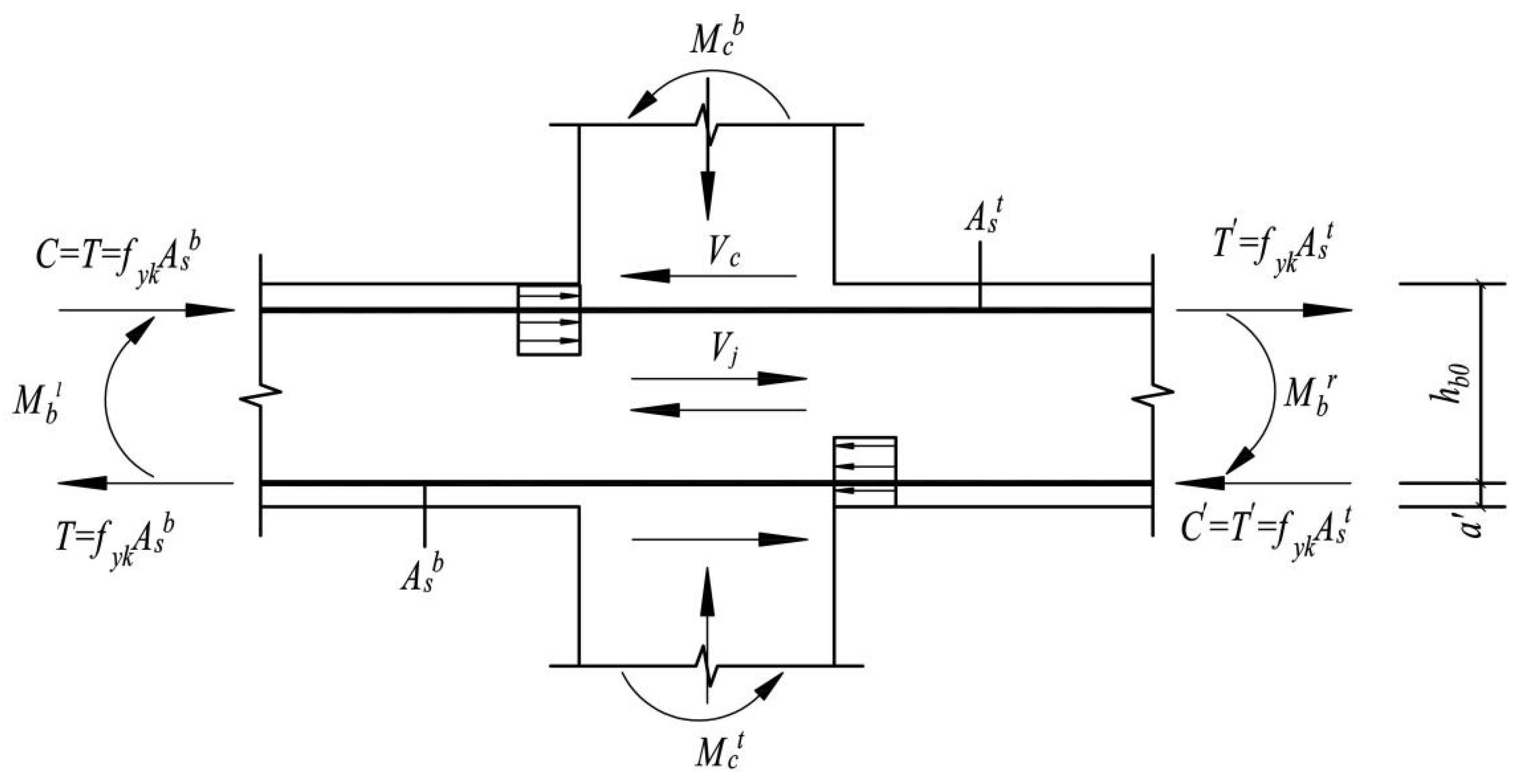
5.1. Calculation of Internal Forces in New Assembly Joints
5.1.1. Calculation of Internal Forces in Joints for Existing Standards
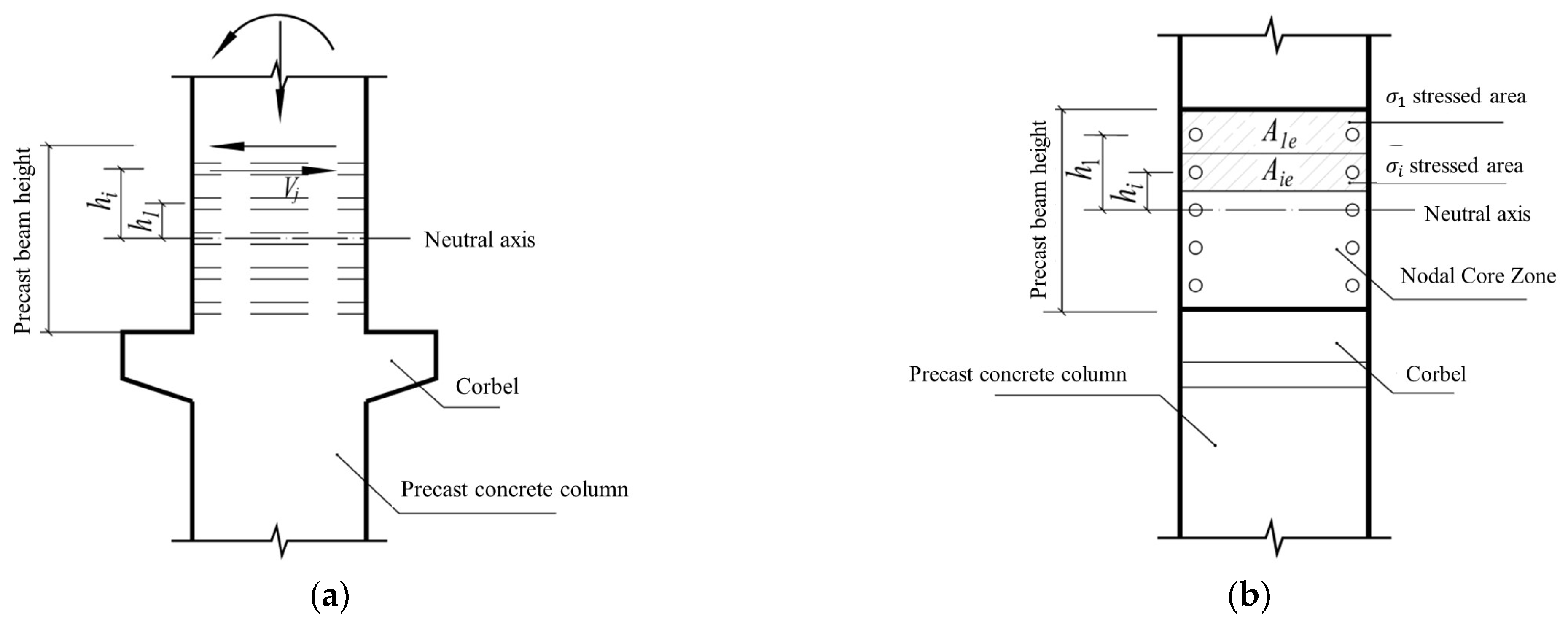
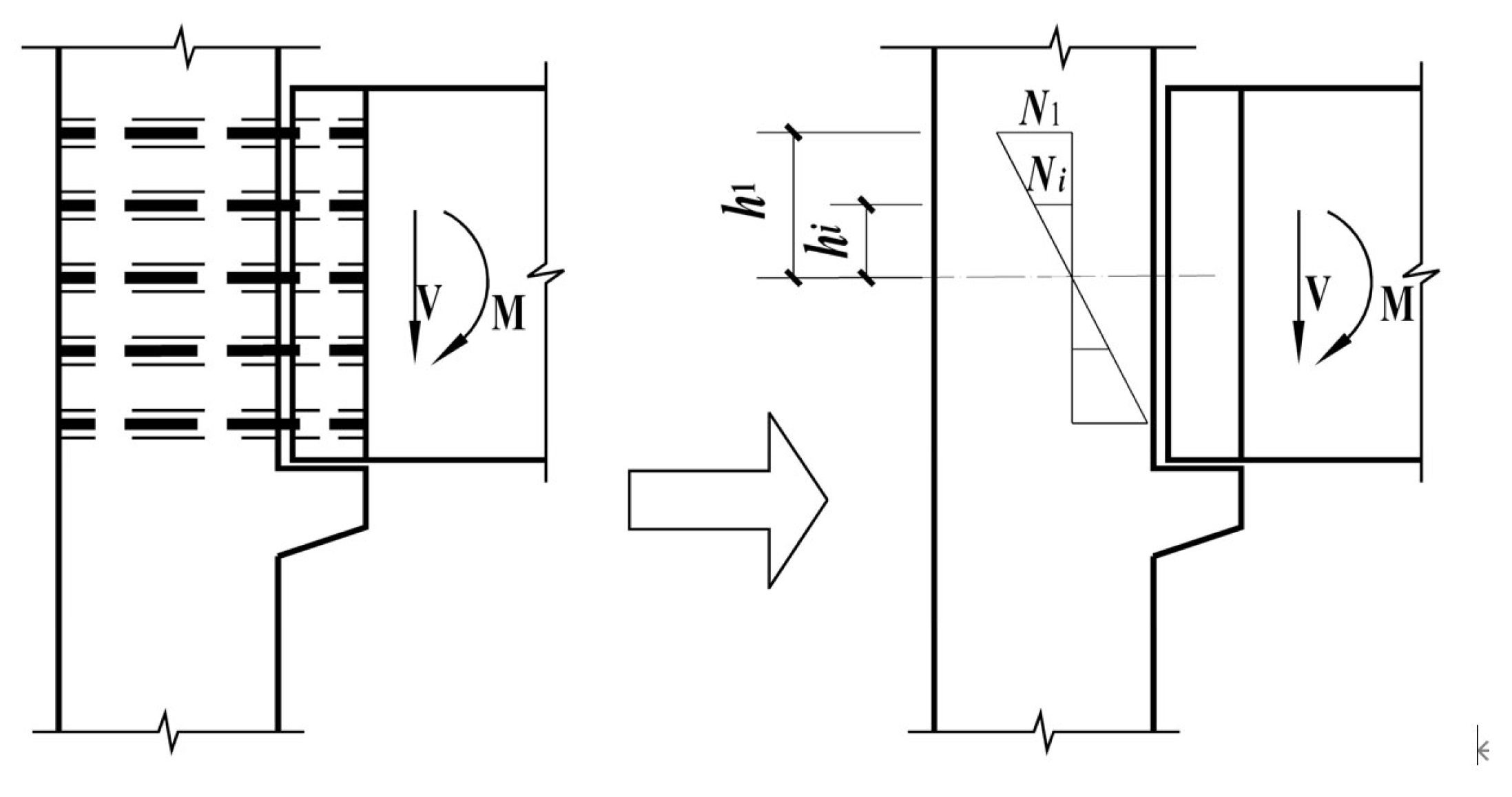
5.1.2. Requirements to Prevent Oblique Compression Damage in the Nodal Core Zone
5.1.3. Shear Bearing Capacity Check of the Nodal Core Zone
5.2. New Assembled Beam–Column Joint Design Method
- (1)
- A rigid connection state, in which, during the stress process, the beam end and the column are in close contact without separation. Due to the reaction force between the precast concrete beam end on the precast concrete column, extrusion occurs and there is compressive stress between the two.
- (2)
- A semi-rigid connection state, in which, under the action of the bending moment, the bolt deformation increases, which makes the beam end and the column have a tendency to separate, and the compression force between the upper part of the two is 0.
5.2.1. Node Rigid Connection State
5.2.2. Semi-Rigid Connection of Joints
6. Conclusions
- (1)
- The two new joints have good seismic performance and energy dissipation performance, the bolts and precast beams are the main load-bearing elements, and the new joints can be repaired by replacing the bolts and precast beams, meeting the seismic design concepts of “strong columns and weak beams” and “strong joints and weak elements”.
- (2)
- The hysteresis curves of the two new joints are bowed, and the hysteresis curves are generally smooth and full, with a large hysteresis loop area, indicating that the new joints have a strong energy dissipation capacity. The hysteresis curves of both joints show an obvious “pinching” phenomenon under the action of low cyclic loads, which is caused by the relative slip between the bolts and the bolt holes, which also makes the energy dissipation capacity of the two joints not fully developed.
- (3)
- The diameter of the connecting bolt has an effect on the seismic performance of the new joint. S2 increases the yield load by 39.4%, the ultimate load by 11.5% and the damage load by 13.2% compared to S1. This shows that when the bolt diameter increases, the yield load capacity and ultimate load capacity of the joint will increase.
- (4)
- According to the stiffness degradation curve, the rate of stiffness degradation of S2 at each displacement stage is slightly less than that of specimen S1, and the stiffness at each displacement stage is greater than that of specimen S1, indicating that increasing the bolt diameter reduces the node stiffness degradation rate.
- (5)
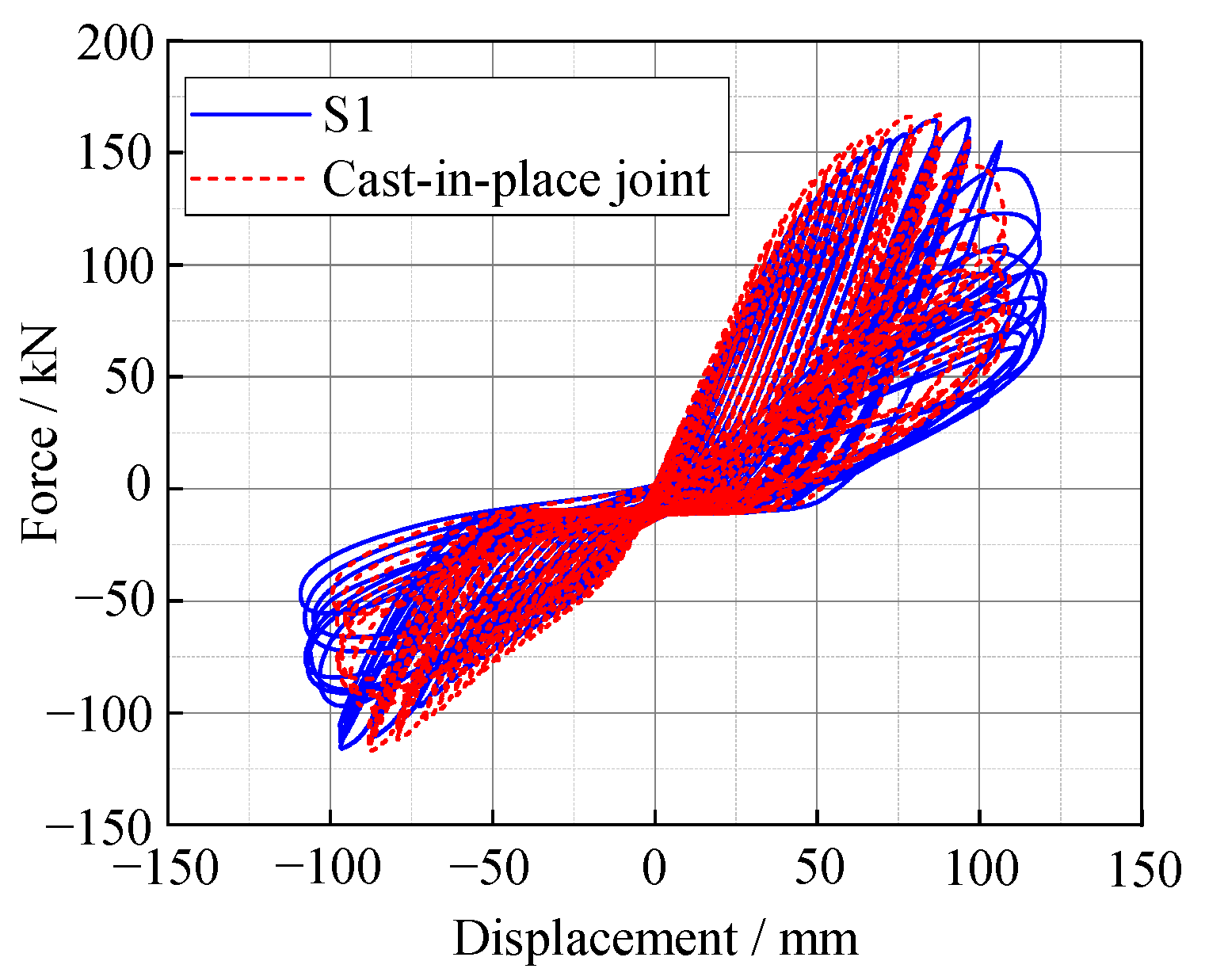
- The test joint is inferior to the cast-in-place joint in terms of energy consumption capacity, but superior to the cast-in-place joint in terms of load-bearing capacity. The presence of the explicit corbel solves the problems of accuracy and assembly efficiency of the bolted joint installation, while also avoiding the additional costs associated with temporary supports.
- (6)
- Based on the experimental and numerical simulation of the force characteristics of the nodal core zone, a nodal core zone mechanical analysis model of the new assembled concrete beam–column joint is proposed, and the nodal core zone shear force calculation formulae of the new assembled concrete beam–column rigid joints and semi-rigid joints are derived.
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, C.; Ge, B.W. Research on Assembled Building Structure in Farmland Amland Hydraulic Structure. Fresen. Environ. Bull. 2020, 29, 4430–4436. [Google Scholar]
- Shu, X.; He, R.; Zhang, Z.; Yao, Y.; Leonard, J. Experimental Study on the Mechanical Properties of a New Long-Span Prefabricated Truss Composite Floor System. Rev. DYNA 2019, 94, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.Y.; Feng, D.C.; Wang, Z.; Wu, W. Parametric investigation of the assembled bolt-connected buckling-restrained brace and performance evaluation of its application into the structural retrofit. J. Build. Eng. 2022, 48, 103998. [Google Scholar] [CrossRef]
- The Journal. The accelerated development of assembled buildings. Architectural 2022, 10, 14–17. (In Chinese) [Google Scholar]
- Pantelides, C.P.; Hansen, J.; Ameli, M.J.; Reaveley, L.D. Seismic performance of reinforced concrete building exterior joints with substandard details. J. Struct. Integr. Main. 2017, 2, 34–47. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.K.; Kim, J. Nonlinear finite element model for the novel mechanical beam-column joints of precast concrete-based frame. Comput. Struct. 2017, 189, 31–48. [Google Scholar] [CrossRef]
- Bruno, D.L.; Paolo, N.; Alberto, D.L. Seismic design and performance of dry-assembled precast structures with adaptable joints. Soil. Dyn. Earthq. Eng. 2018, 106, 182–195. [Google Scholar] [CrossRef]
- Pan, Z.H.; Si, Q.; Zhou, Z.B.; Zhang, Y.B.; Zhu, Y.Z.; Chen, X.D. Experimental and numerical investigations of seismic performance of hybrid joints with bolted connections. J. Constr. Steel. Res. 2017, 138, 867–886. [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ma, W.; Liu, Y.L. Experimental study on the seismic performance of new assembled semi-rigid joints. China Civ. Eng. J. 2021, 54, 1–7, 56. (In Chinese) [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ren, J.W.; Ma, W. Dynamic Responses of Cellular Metal-Filled Steel Beam-Column Joint under Impact Loading. J. Shanghai Jiaotong Univ. Sci. 2020, 25, 384–393. [Google Scholar] [CrossRef]
- Ding, K.W.; Zong, D.; Liu, Y.L.; He, S.L.; Shen, W.Y. Experimental and Finite Element Analysis of ALC Panel Steel Frames with New Semi-Rigid External Connector. Appl. Sci. 2021, 11, 1099. [Google Scholar] [CrossRef]
- Ding, K.W.; Ye, Y.; Ma, W. Seismic performance of precast concrete beam-column joint based on the bolt connection. Eng. Struct. 2021, 232, 111884. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, K.W. Study on seismic behavior of fabricated beam-column bolted joint. Struct. Eng. Mech. 2022, 82, 801–812. [Google Scholar] [CrossRef]
- Guan, D.Z.; Tian, W.H.; Chen, Z.X.; Liu, J.B.; Guo, Z.X. Research on the seismic performance of assembled concrete beam-column connections based on UHPC shells. China Civ. Eng. J. 2022, 1–7. (In Chinese) [Google Scholar] [CrossRef]
- Fan, W.; Su, H.X.; He, Y.B.; Sun, W.B.; Shao, X.D. Experimental investigation on UHPC-based gravity-type half-grouted sleeve connections under tensile and cyclic loadings. J. Build. Eng. 2022, 61, 105284. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Ding, R.; Nie, X.; Fan, J.S. Seismic performance of a novel interior precast concrete beam-column joint using ultra-high performance concrete. Eng. Struct. 2020, 222, 111145. [Google Scholar] [CrossRef]
- Xiong, X.Y.; Xie, Y.F.; Yao, G.F.; Liu, J.; Yan, L.Z.; He, L. Experimental Study on Seismic Performance of Precast Pretensioned Prestressed Concrete Beam-Column Interior Joints Using UHPC for Connection. Materials 2022, 15, 5791. [Google Scholar] [CrossRef]
- Tang, L.; Tian, W.H.; Guan, D.Z.; Chen, Z.X. Experimental Study of Emulative Precast Concrete Beam-to-Column Connections Locally Reinforced by U-Shaped UHPC Shells. Materials 2022, 15, 4066. [Google Scholar] [CrossRef]
- Wang, H.S.; Marino, E.M.; Hang, P.P.; Nie, L.X. Experimental study of a novel precast prestressed reinforced concrete beam-to-column joint. Eng. Struct. 2018, 156, 68–81. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, J.M.; Hong, W.K. Material nonlinear finite element analysis of hybrid hollow concrete beams encasing steel sections. Structure 2020, 25, 500–519. [Google Scholar] [CrossRef]
- Yang, T.Y.; Dashlejeh, A.A.; Arabzadeh, A.; Hizaji, R. New model for prediction of ultimate load of prestressed RC deep beams. Structure 2020, 23, 509–527. [Google Scholar] [CrossRef]
- Oliveira, J.L.A.; Araújo, D.L.; El Debs, M.K.; Diógenes, H.J.F. Precast Beam–Column Connection Subjected to Cyclic and Dynamic Loadings. Struct. Eng. Int. 2018, 27, 114–126. [Google Scholar] [CrossRef]
- Dai, E.-L.; Jin, G.-J.; Dai, S.-P. Study on the application of C80 high strength and high performance pumped concrete in practical engineering. Concrete 2013, 1, 97–101, 104. (In Chinese) [Google Scholar]
- Liu, Y.L.; Zhu, S.T. Finite element analysis on the seismic behavior of side joint of a Prefabricated Cage System in a prefabricated concrete frame. Front. Struct. Civ. Eng. 2019, 13, 1095–1104. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, C.; Pan, H.; Fu, J.L.; Huang, J.Q.; Hong, J.Q. Experimental and numerical investigation on seismic performance of a semi-precast concrete sandwich shear wall. Adv. Struct. Eng. 2022, 25, 2772–2784. [Google Scholar] [CrossRef]
- Liu, Y.L.; Huang, J.Q.; Chong, X.; Ye, X.G. Experimental investigation on flexural performance of semi-precast reinforced concrete one-way slab with joint. Struct. Concrete 2021, 22, 2243–2257. [Google Scholar] [CrossRef]
- Du, H.X.; Zhang, M.L. Experimental investigation of thermal pore pressure in reinforced C80 high-performance concrete slabs at elevated temperatures. Constr. Build. Mater. 2020, 260, 120451. [Google Scholar] [CrossRef]
- Lohaus, L.; Oneschkow, N.; Wefer, M. Design model for the fatigue behavior of normal-strength, high-strength and ultra-high-strength concrete. Struct. Concrete 2012, 3, 189–192. [Google Scholar]
- Wu, H.M.; Shen, B.; Ma, K.J.; Xuan, D.X. Assessment of mechanical properties of C80 concrete prepared with different stone powder contents by a statistical analysis. J. Build. Eng. 2022, 56. [Google Scholar] [CrossRef]
- GB50010-2010 (2015 Edition); Code for the Design of Concrete Structures. Ministry of Construction of the People’s Republic of China: Beijing, China, 2015. (In Chinese)
- GB50010-2010 (2016 Edition); Code for Seismic Resistance of Building Structures. China Construction Industry Press: Beijing, China, 2016. (In Chinese)
- JGJ55-2011; Specification for the Design of Ordinary Concrete Proportions. China Construction Industry Press: Beijing, China, 2011. (In Chinese)
- El-Sabbagh, A.; Sharaf, T.; Nagy, S.; El-Ghandour, M. Behavior of extended end-plate bolted connections subjected to monotonic and cyclic loads. Eng. Struct. 2019, 190, 142–159. [Google Scholar] [CrossRef]
- Liu, Y.B.; Guo, Z.; Ding, J.H.; Wang, X.G.; Liu, Y. Experimental study on seismic behaviour of plug-in assembly concrete beam-column connections. Eng. Struct. 2020, 211, 111049. [Google Scholar] [CrossRef]
- Brunesia, E.; Nascimbeneb, R.; Rassatic, G.A. Response of partially-restrained bolted beam-to-column connections under cyclic loads. J. Constr. Steel Res. 2014, 97, 24–38. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, X.; Pei, E.L.; Hwang, H.G.; Chen, T.P.; Yi, W.G.; Deng, L. Dynamic load test on progressive collapse resistance of fully assembled precast concrete frame structures. Eng. Struct. 2020, 2014, 110675. [Google Scholar] [CrossRef]
- Aksoylu, C.; Özkılıç, Y.O.; Arslan, M.H. Damages on prefabricated concrete dapped-end purlins due to snow loads and a novel reinforcement detail. Eng. Struct. 2020, 225, 111–225. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Experimental and numerical investigations of steel fiber reinforced concrete dapped-end purlins. J. Build. Eng. 2021, 36, 10499. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Yazman, Ş.; Aksoylu, C.; Arslan, M.H.; Gemi, L. Numerical investigation of the parameters influencing the behavior of dapped end prefabricated concrete purlins with and without CFRP strengthening. Constr. Build. Mater. 2021, 275, 122–173. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Numerical evaluation of effects of shear span, stirrup spacing and angle of stirrup on reinforced concrete beam behaviour. Struct. Eng. Mech. Int. J. 2021, 79, 309–326. [Google Scholar]
- Yasin, O.O.; Ceyhun, A.; Şakir, Y.; Lokman, G.; Musa, H.A. Behavior of CFRP-strengthened RC beams with circular web openings in shear zones: Numerical study. Structure 2022, 41, 1369–1389. [Google Scholar]
- Aksoylu, C.; Özkılıç, Y.O.; Yazman, Ş.; Gemi, L.; Arslan, M. İnceltilmiş Uçlu Önüretimli Aşık Kirişlerinin Yük Taşıma Kapasitelerinin Deneysel ve Numerik Olarak İrdelenmesi ve Çözüm Önerileri. Teknik Dergi. 2021, 32, 10823–10858. [Google Scholar]
- Wu, C.X.; Zhou, Y.; Zhang, C.; Deng, X.S.; Lai, W.S. Experimental study on the seismic performance of cast-in-place and precast assembled frame beam-column assemblies with the deployment of dampers. J. Build. Struct. 2015, 33, 61–68. (In Chinese) [Google Scholar]
- Mi, S.K. Application Analysis of a New Type of Assembled Concrete Frame Joints; Anhui Jianzhu University: Hefei, China, 2020. (In Chinese) [Google Scholar]
- Gemi, L.; Madenci, E.; Özkılıç, Y.O. Experimental, analytical and numerical investigation of pultruded GFRP composite beams infilled with hybrid FRP reinforced concrete. Eng. Struct. 2021, 244, 103699. [Google Scholar] [CrossRef]
- Yao, Z.; Xia, Z.B. Principles of Steel Construction; China Construction Industry Press: Beijing, China, 2020. (In Chinese) [Google Scholar]

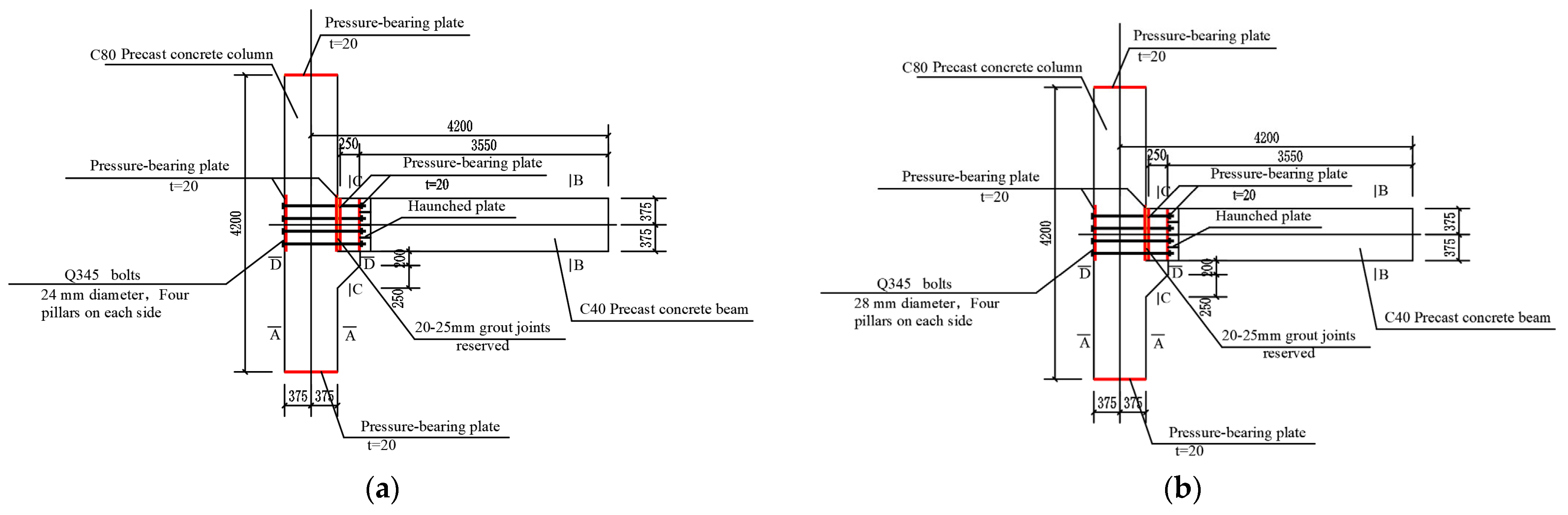
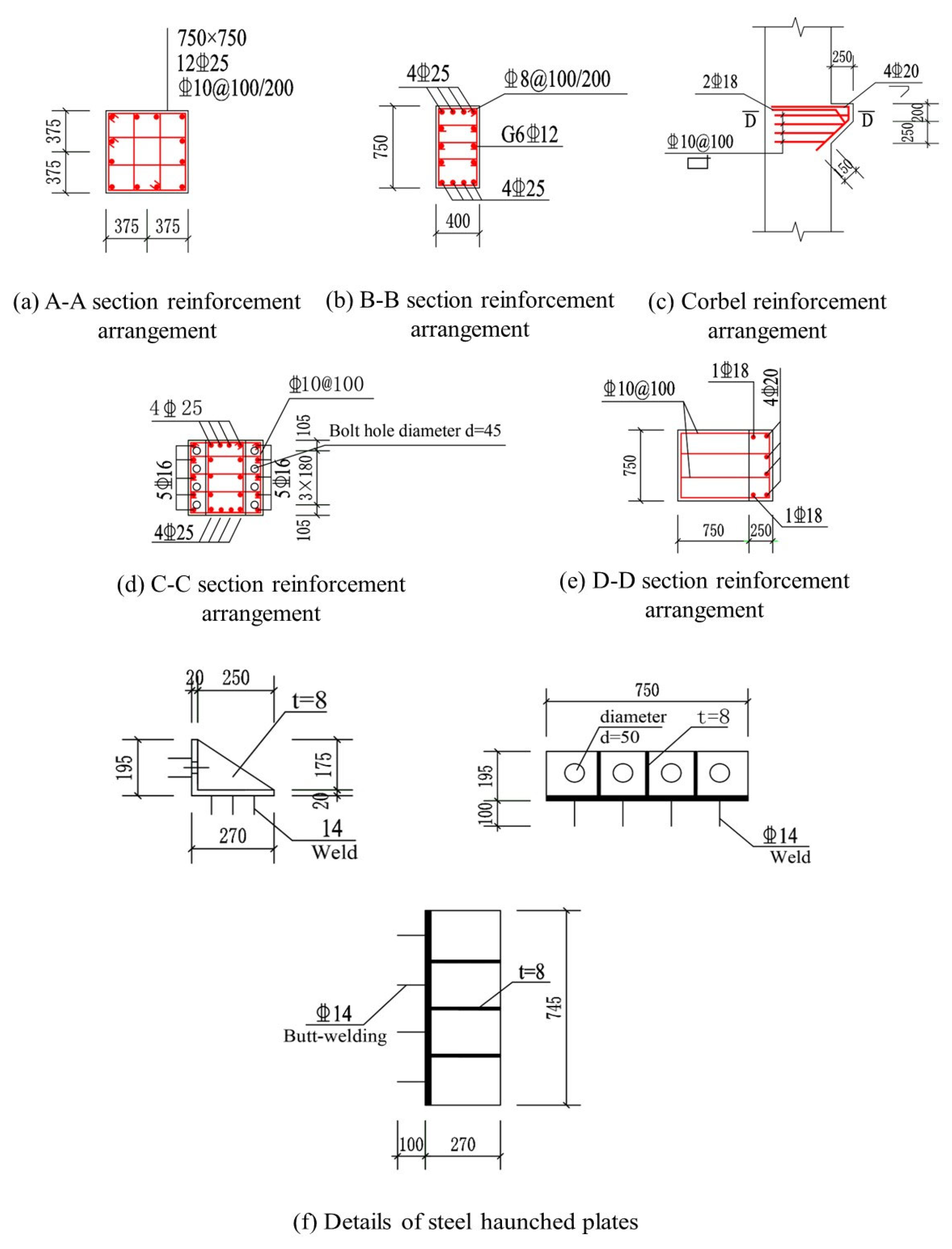

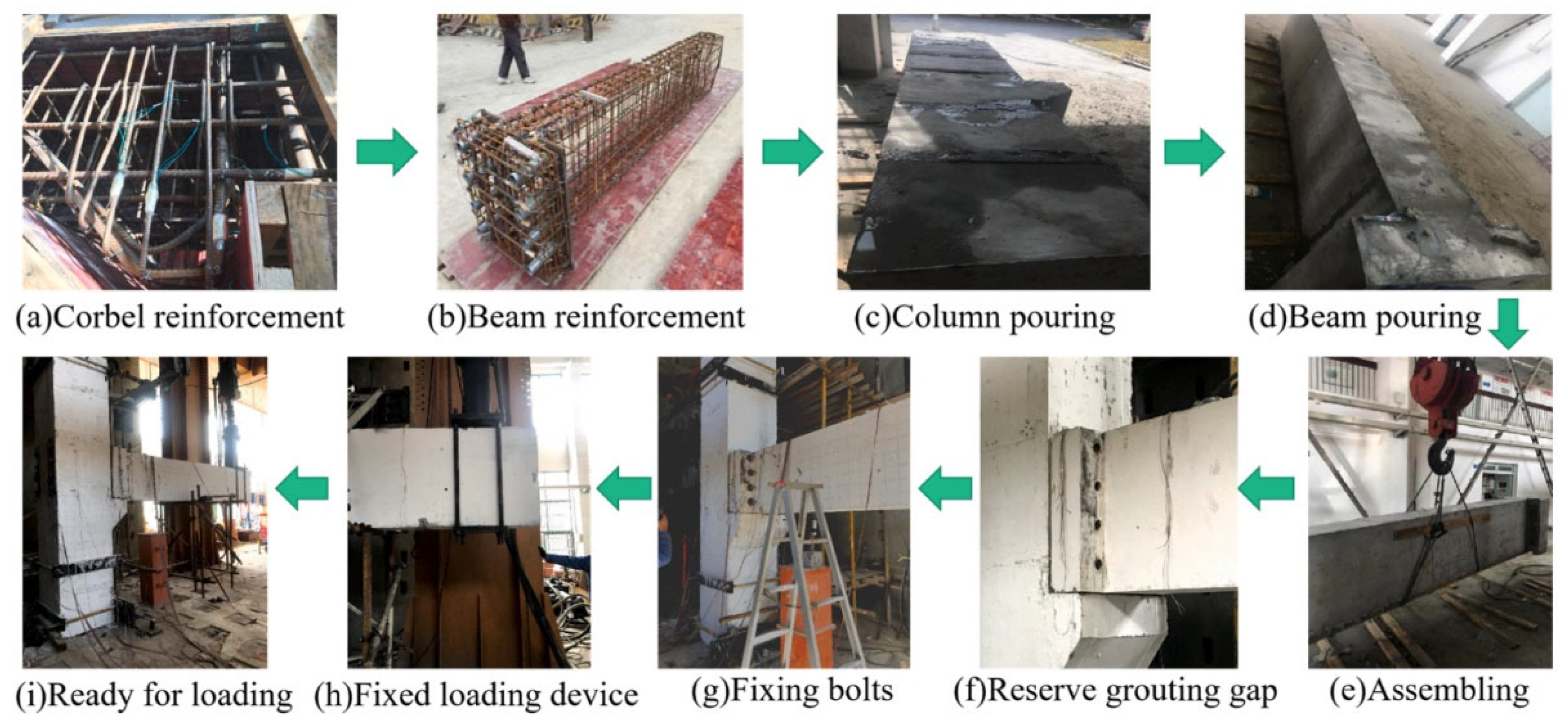
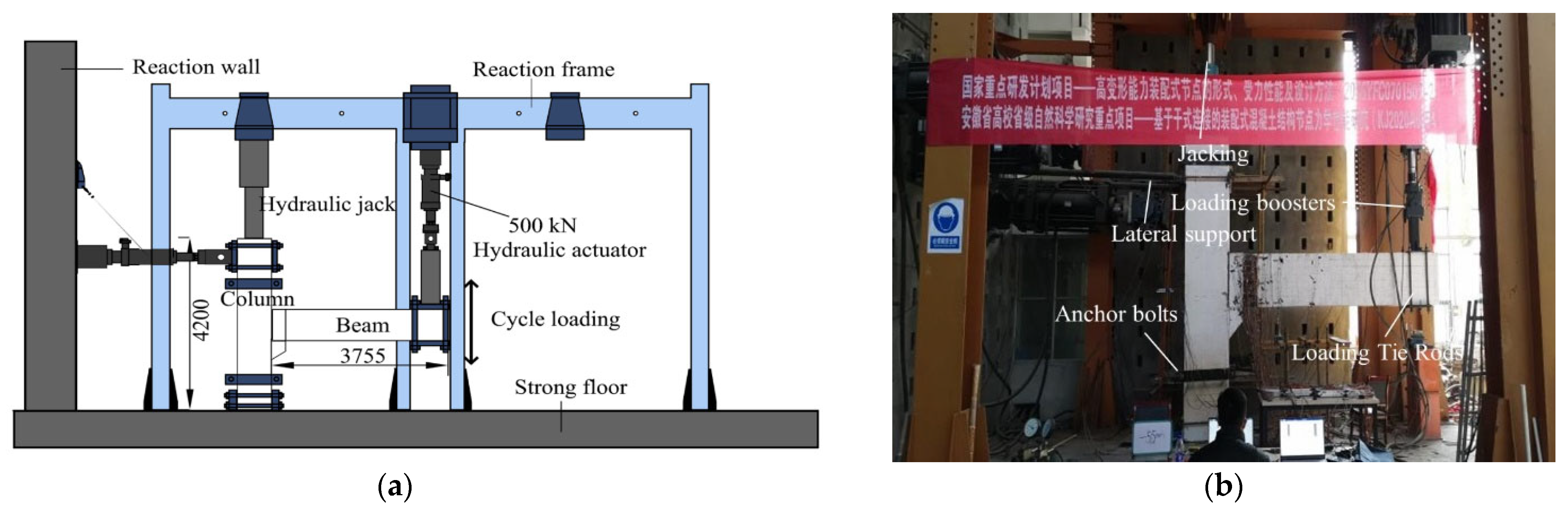






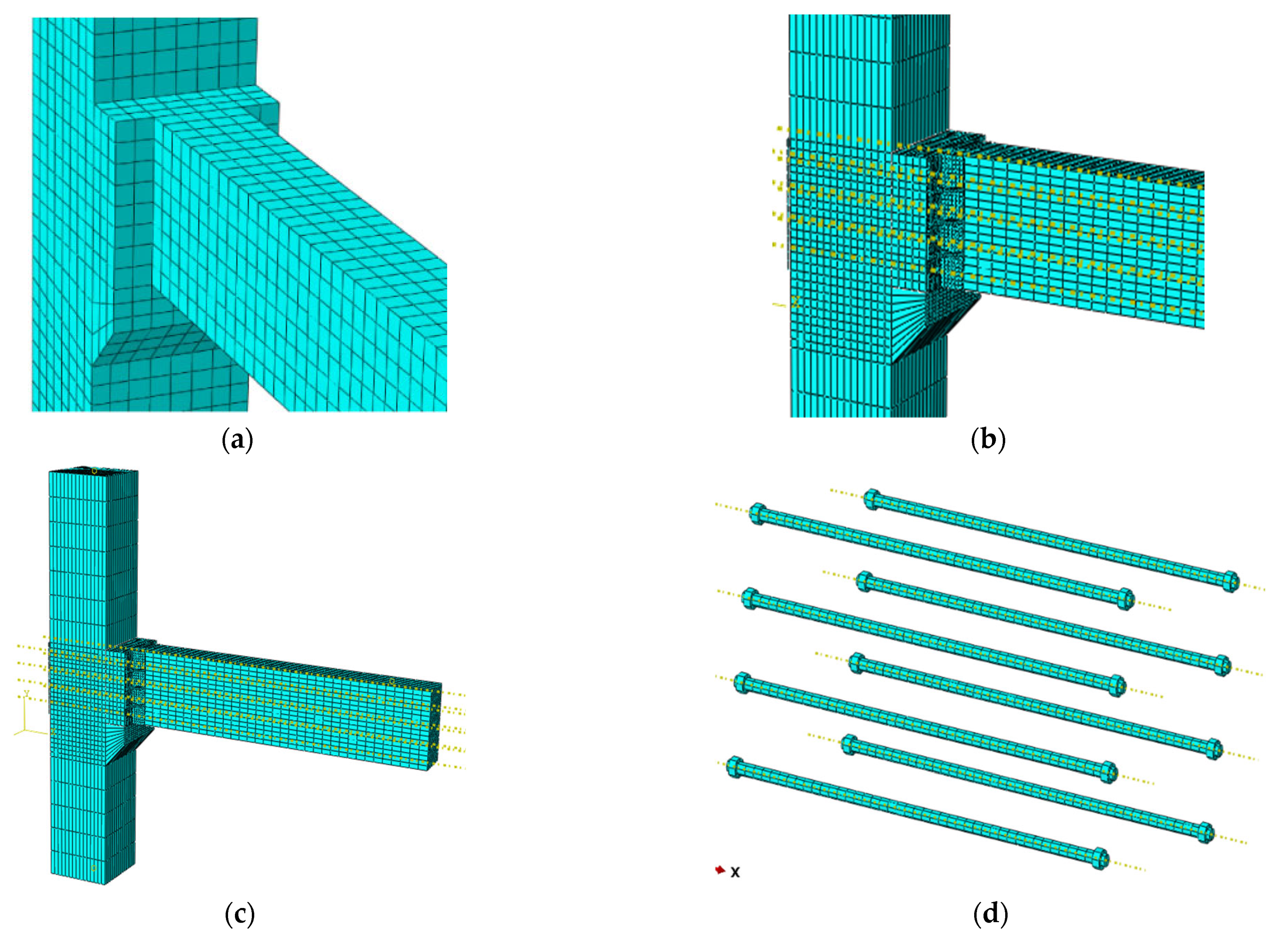


| Specimen Name | Concrete Grade | Thickness of the Concrete Protection Layer (mm) | Cross-Sectional Dimensions (mm) | Length (mm) |
|---|---|---|---|---|
| Precast concrete beam | C40 | 25 | 400 × 750 (Extended end 750 × 750) | 3800 |
| Precast concrete column | C80 | 25 | 750 × 750 | 4200 |
| Number | Type of Joint Construction | Bolt Grades | Bolt Diameter (mm) |
|---|---|---|---|
| S1 | with haunched plates | Q345 | 24 |
| S2 | with haunched plates | Q345 | 28 |
| Concrete Strength | Cube Compressive Strength (N/mm2) | Standard Values for Axial Compressive Strength (N/mm2) | Modulus of Elasticity (×104 N/mm2) |
|---|---|---|---|
| C40 | 28.28 | 18.34 | 3.25 |
| C40 | 28.68 | 18.25 | 3.25 |
| C40 | 28.13 | 18.32 | 3.25 |
| C80 | 77.30 | 50.20 | 3.80 |
| C80 | 78.20 | 52.30 | 3.80 |
| C80 | 77.90 | 51.40 | 3.80 |
| Category | Diameter (mm) | Yield Strength (N/mm2) | Ultimate Strength (N/mm2) | Modulus of Elasticity (×105 N/mm2) | Elongation/% |
|---|---|---|---|---|---|
| HRB400 | 8 | 427.60 | 637.10 | 2.10 | 16.30 |
| HRB400 | 10 | 437.90 | 568.30 | 2.10 | 15.60 |
| HRB400 | 12 | 465.20 | 577.30 | 2.00 | 16.60 |
| HRB400 | 14 | 447.40 | 547.60 | 2.00 | 16.20 |
| HRB400 | 16 | 437.60 | 640.40 | 2.10 | 23.20 |
| HRB400 | 22 | 487.50 | 635.90 | 2.11 | 21.60 |
| HRB400 | 25 | 456.60 | 605.70 | 2.06 | 17.80 |
| Q345 | 20 (Plate thickness) | 425.20 | 570.40 | 2.07 | 31.90 |
| Bolt Grades | Diameter (mm) | Yield Strength (N/mm2) | Ultimate Strength (N/mm2) | Modulus of Elasticity (×105 N/mm2) |
|---|---|---|---|---|
| Q345 | 24 | 432 | 761 | 2.12 |
| Q345 | 28 | 436 | 764 | 2.06 |
| Type of Material | Density (t × mm3) | Elasticity Model/Mpa | Poisson’s Ratio |
|---|---|---|---|
| Steel | 7.89 × 10−9 | 20,600 | 0.3 |
| C40 | 2.5 × 10−9 | 32,500 | 0.2 |
| C80 | 2.5 × 10−9 | 38,000 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, Y.; Yu, D. Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints. Buildings 2023, 13, 329. https://doi.org/10.3390/buildings13020329
Liu J, Liu Y, Yu D. Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints. Buildings. 2023; 13(2):329. https://doi.org/10.3390/buildings13020329
Chicago/Turabian StyleLiu, Jianhua, Yunlin Liu, and Dehu Yu. 2023. "Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints" Buildings 13, no. 2: 329. https://doi.org/10.3390/buildings13020329
APA StyleLiu, J., Liu, Y., & Yu, D. (2023). Experimental and Numerical Studies on the Seismic Performance of New Assembled Concrete Frame Beam–Column Joints. Buildings, 13(2), 329. https://doi.org/10.3390/buildings13020329





