Investigation of Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals
Abstract
1. Introduction
2. Experimental Program
2.1. Material Selection and Properties
2.1.1. Concrete
2.1.2. Reinforcements
2.2. Preparation of Specimens
2.3. Test Setup and Instrumentation
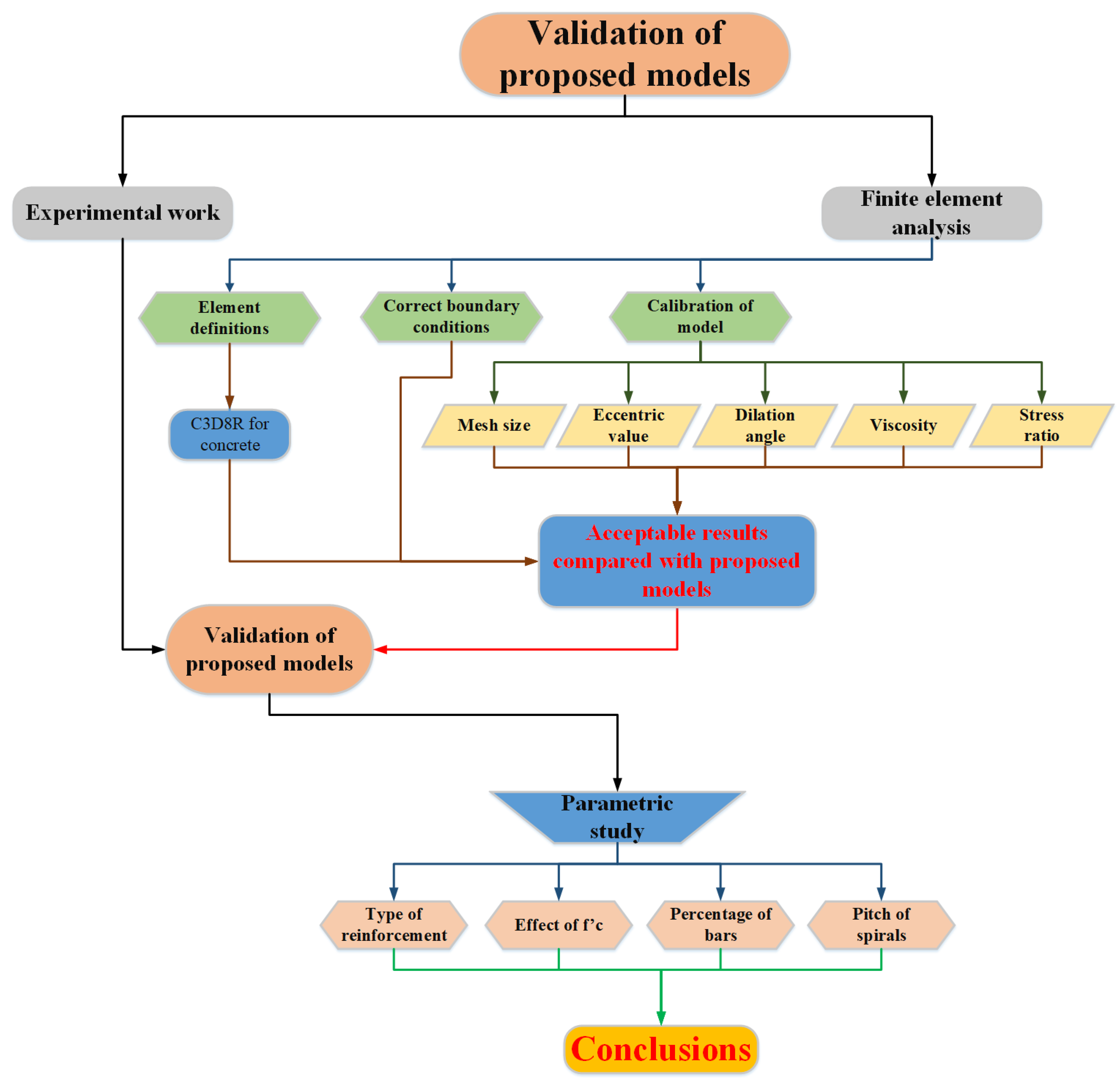
3. FEA
3.1. Overview
3.2. Simulation of Concrete (CDP Model)
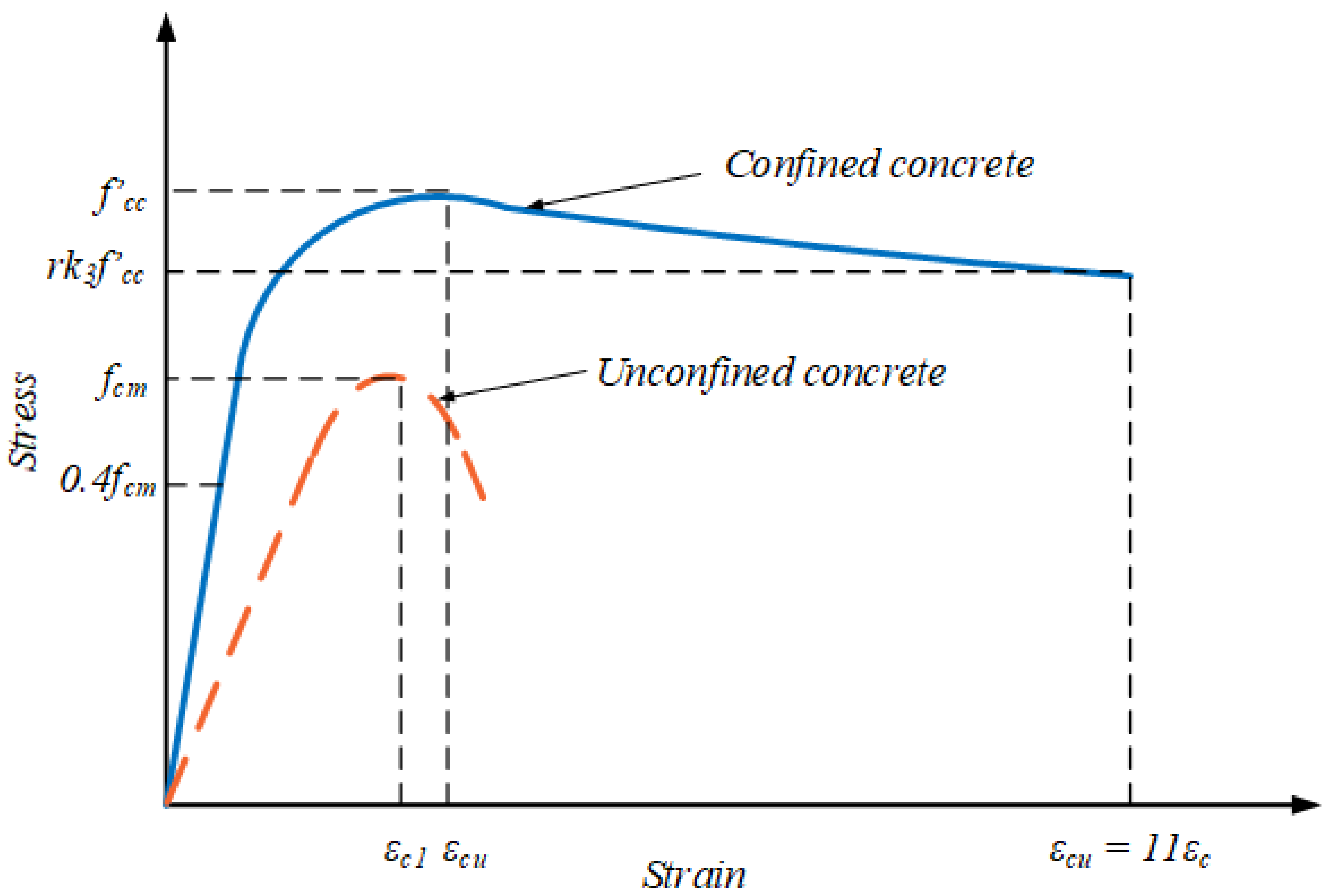
3.2.1. Concrete Plasticity Models
3.2.2. Computation of Compressive and Tensile Stresses
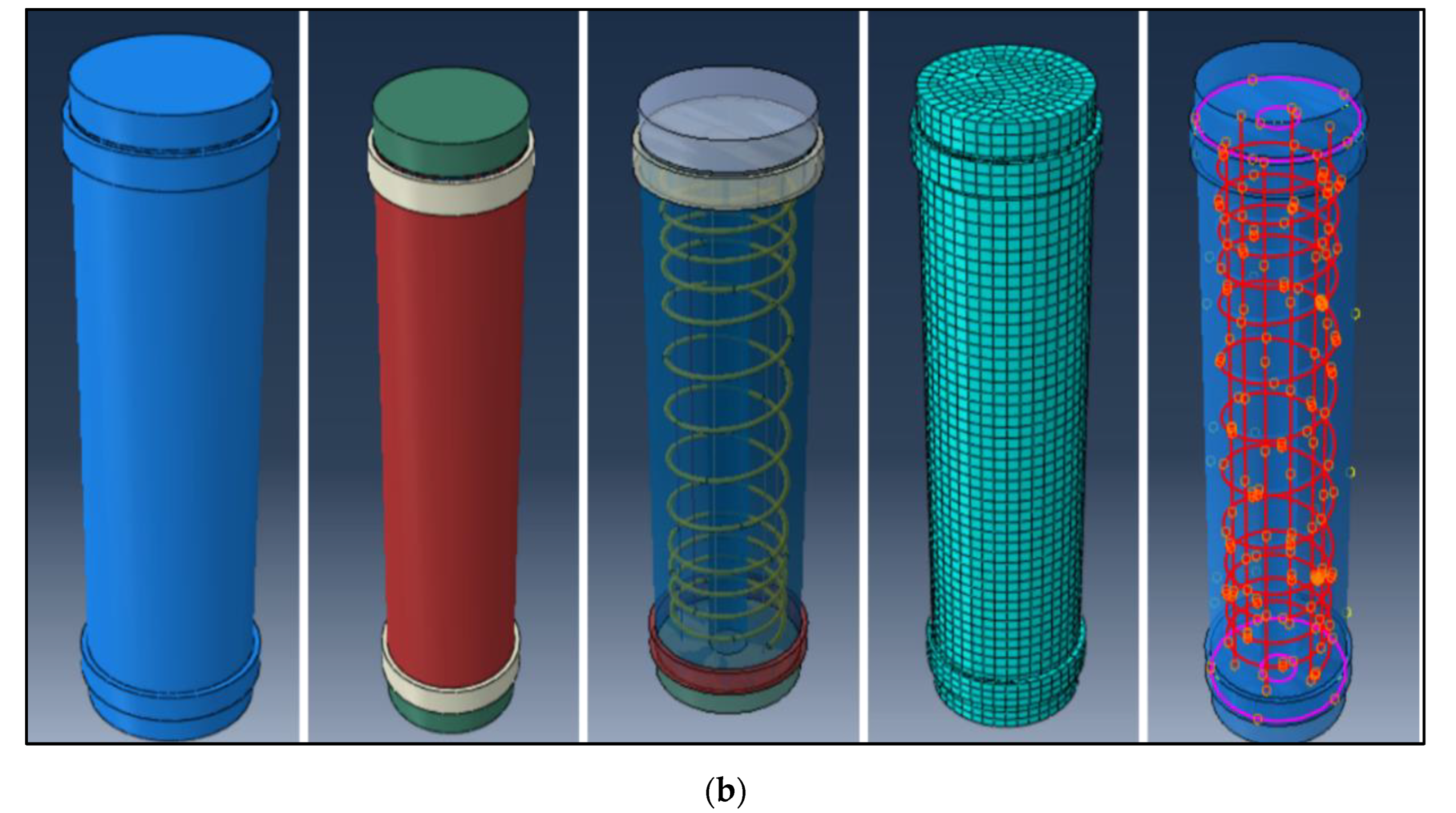
3.3. Finite Element Modeling
3.3.1. Geometric and Material Properties
3.3.2. Finite Element Mesh
3.3.3. Constraints and Interactions
3.4. Calibration of Control Model
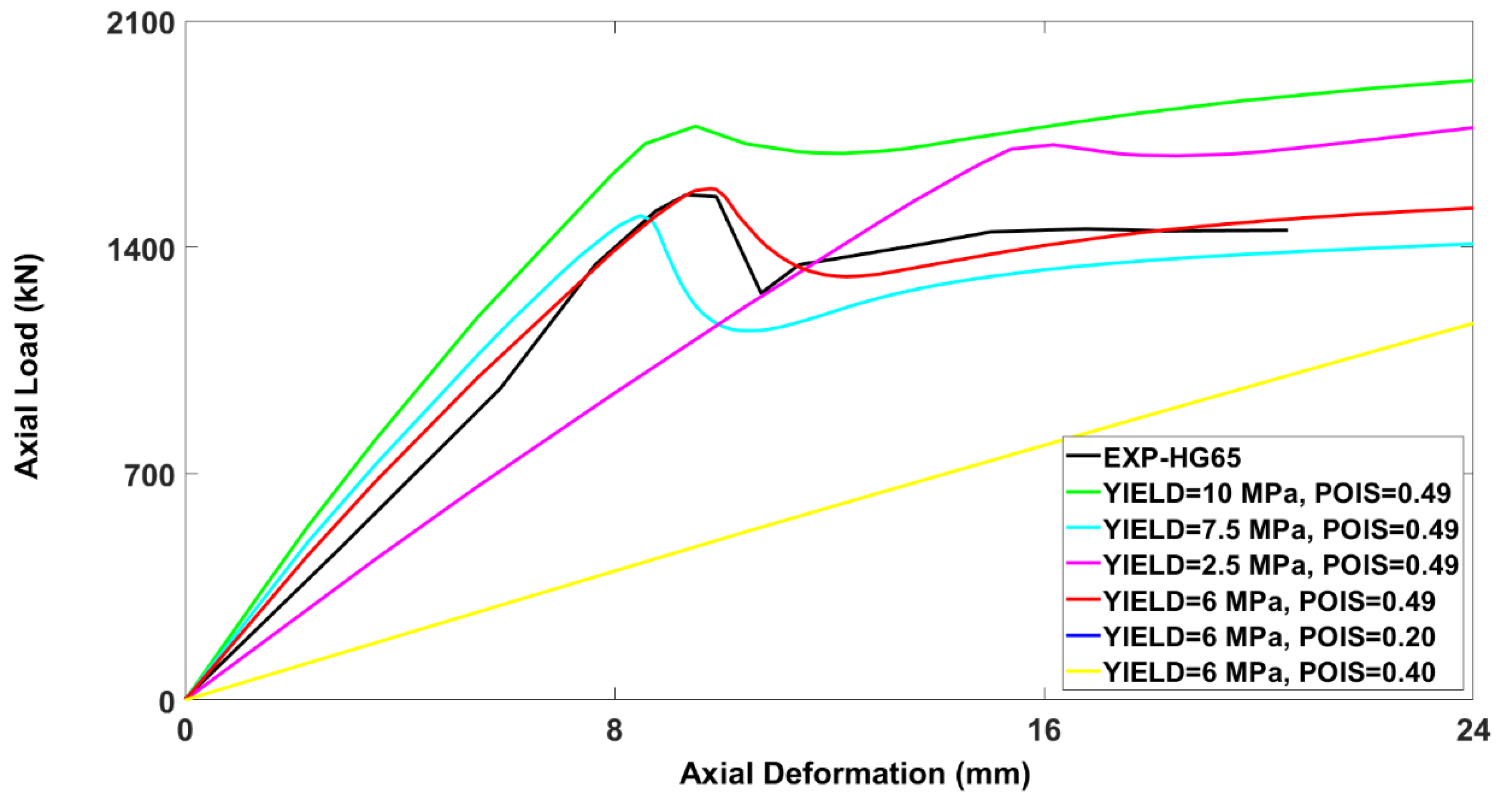
3.4.1. Parameters for Calibration
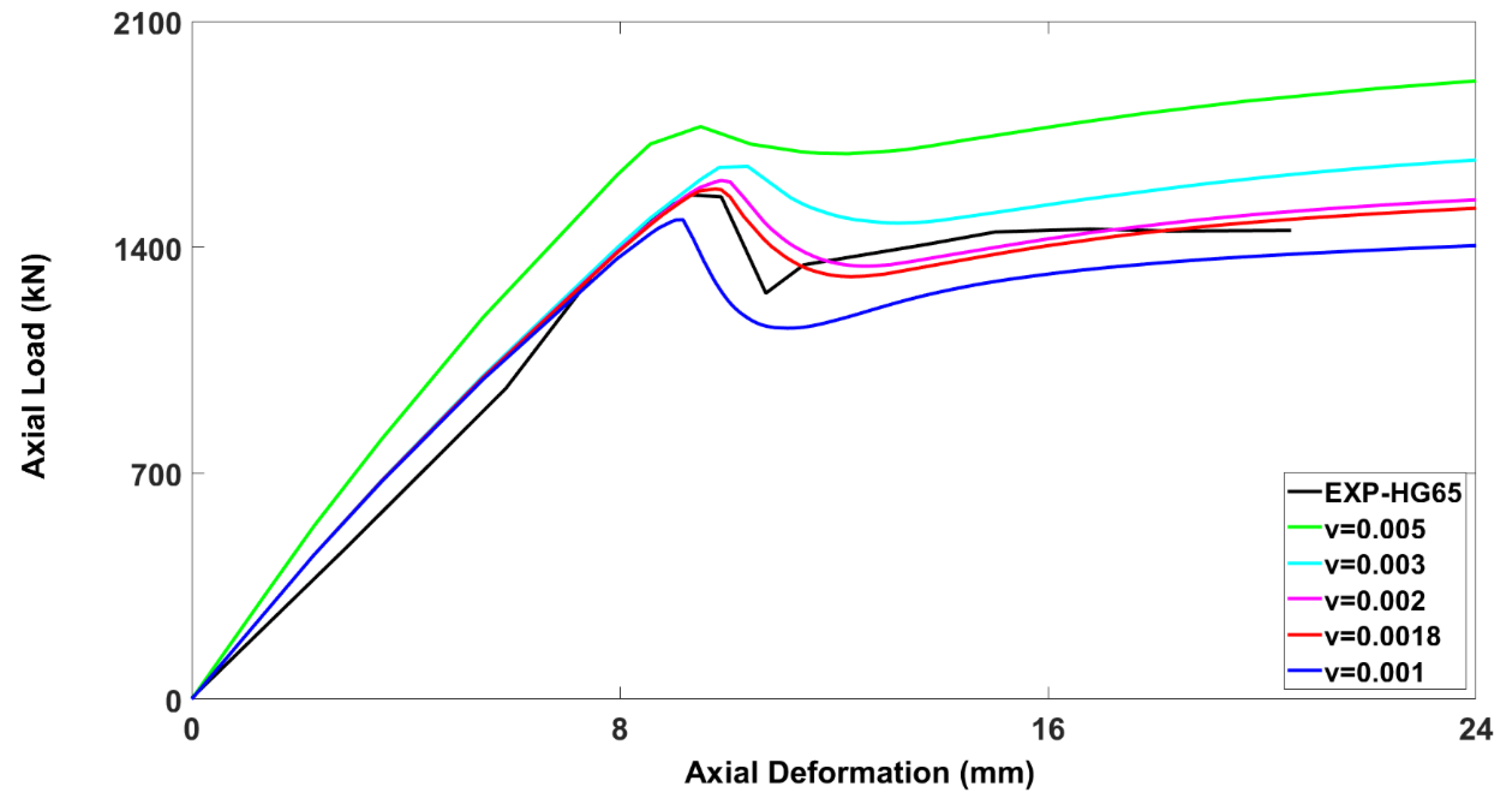
3.4.2. Viscosity Parameter (ν)
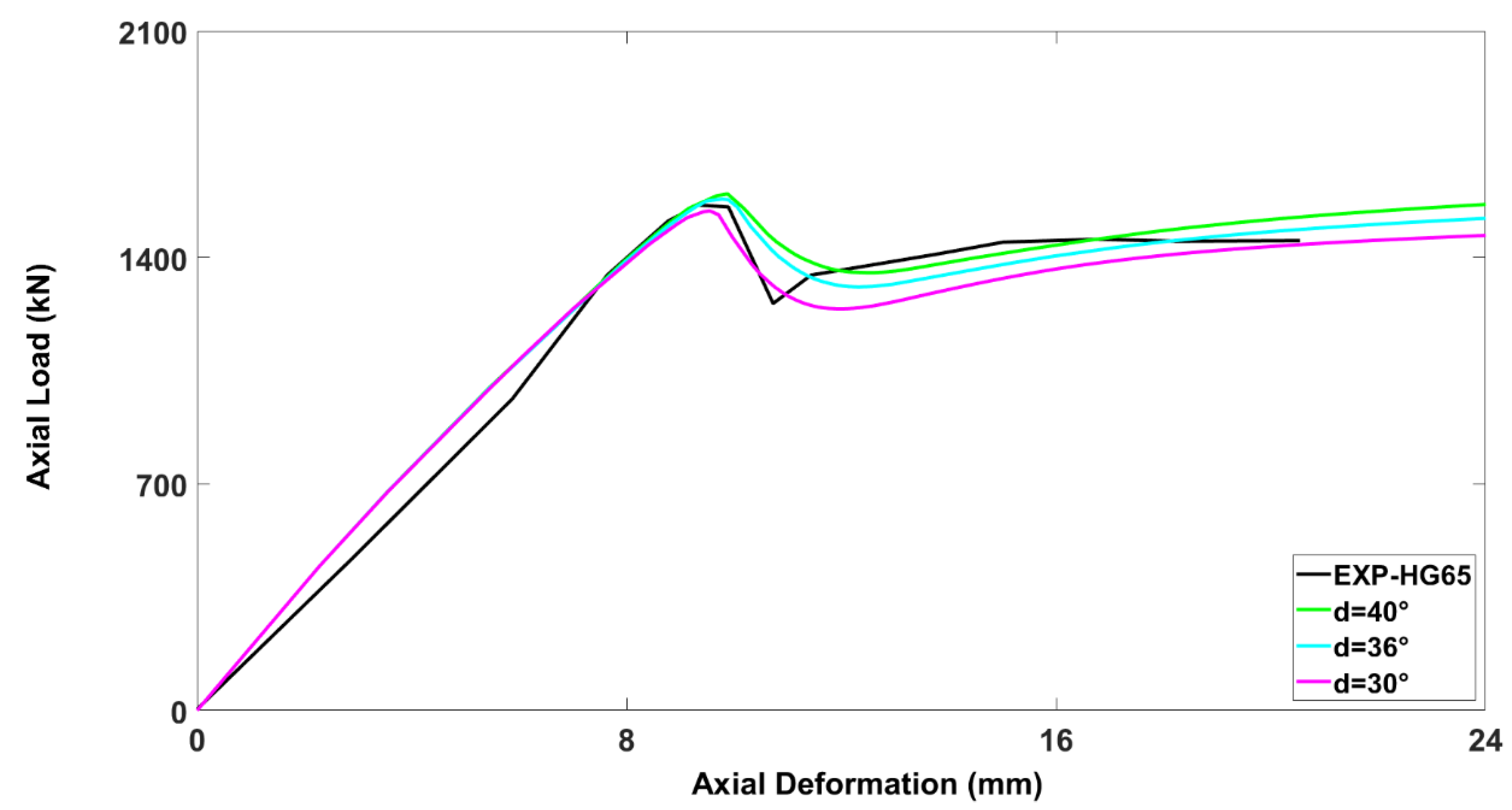
3.4.3. Dilation Angle (d)
3.4.4. Shape Factor (Kc)
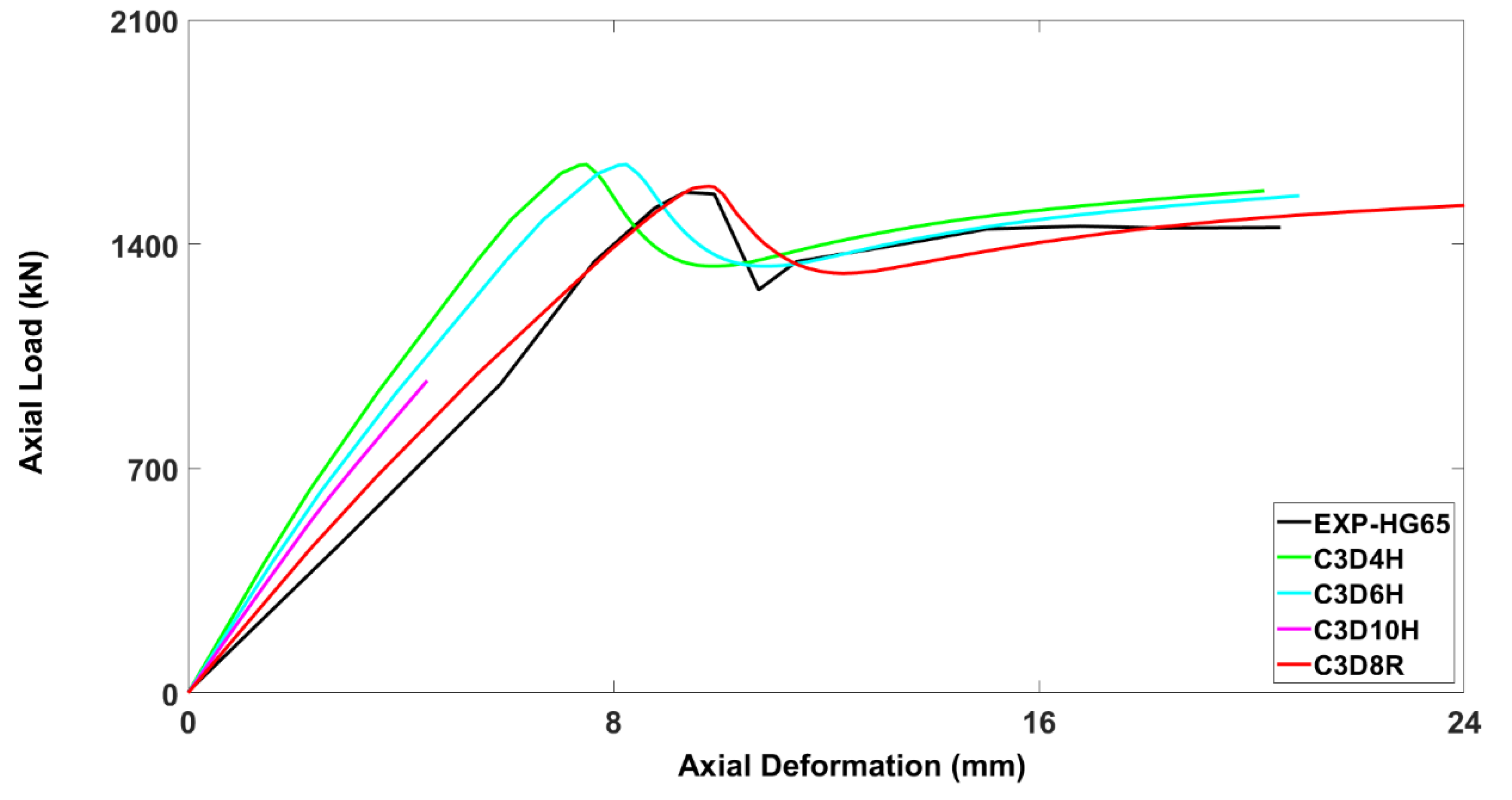
3.4.5. Mesh Size
3.4.6. Mesh Element Type
3.4.7. Properties of Rubber Pads
4. Comparisons of Numerical Results and Experimental Result
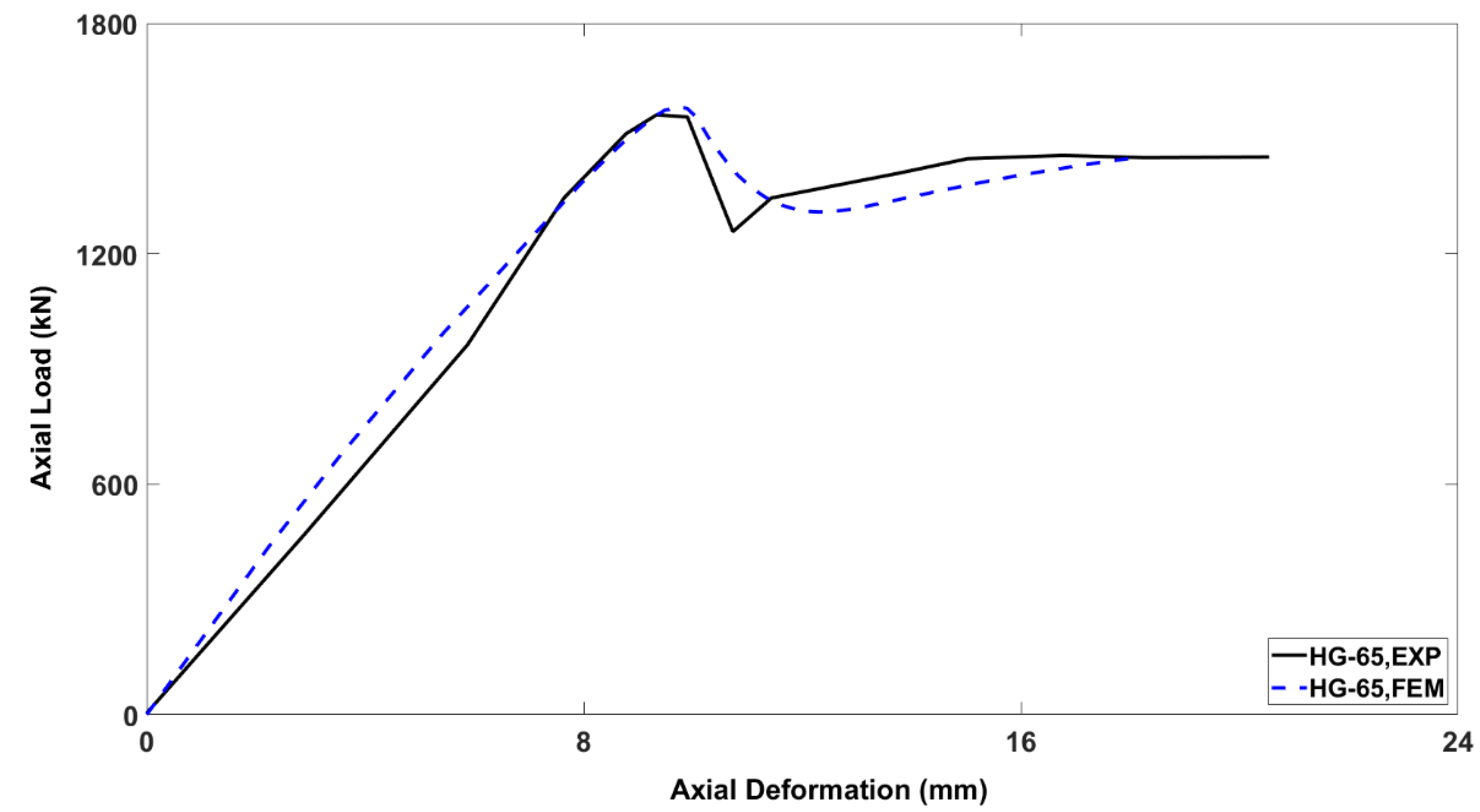
4.1. Control Finite Element Model (HG-65)
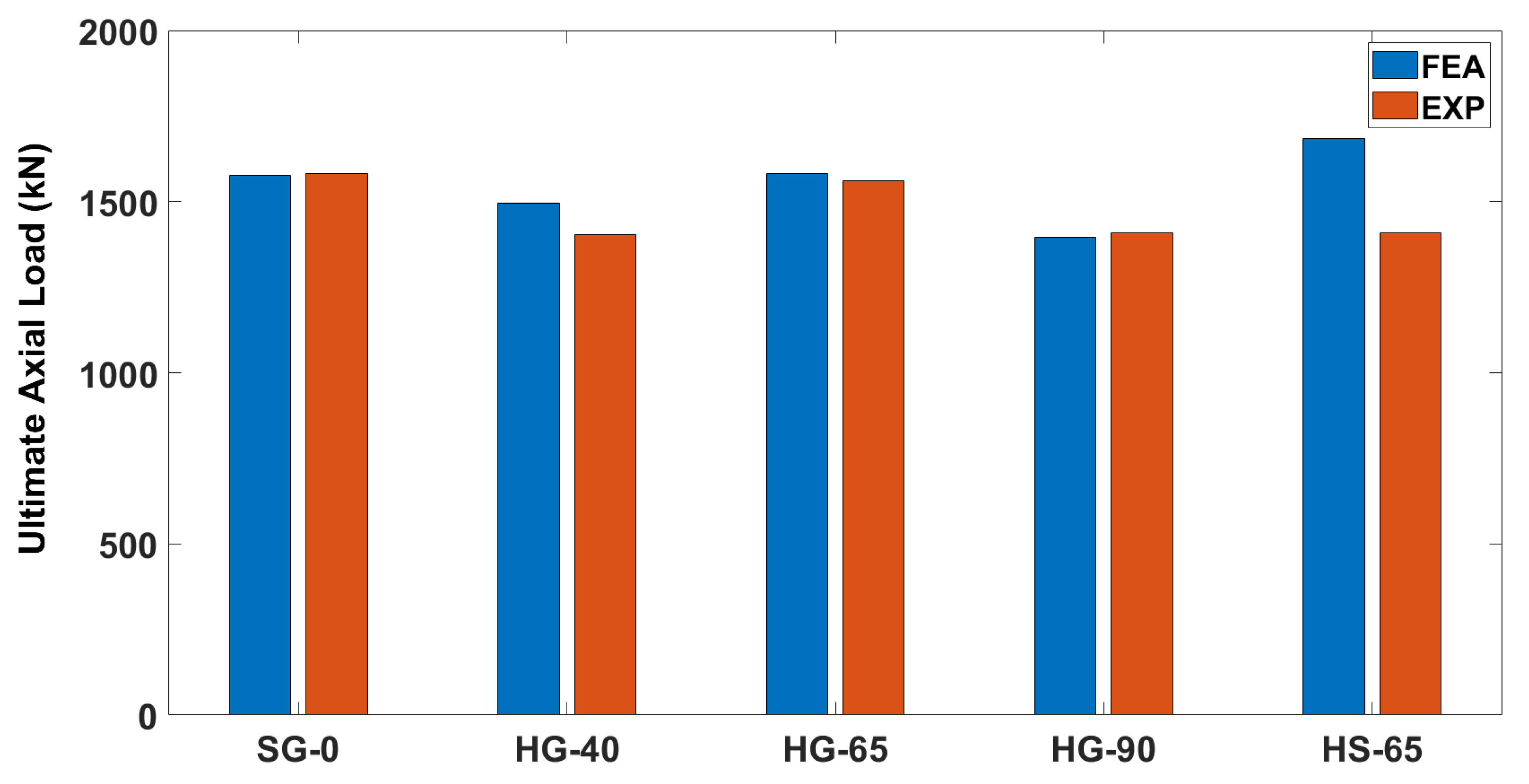
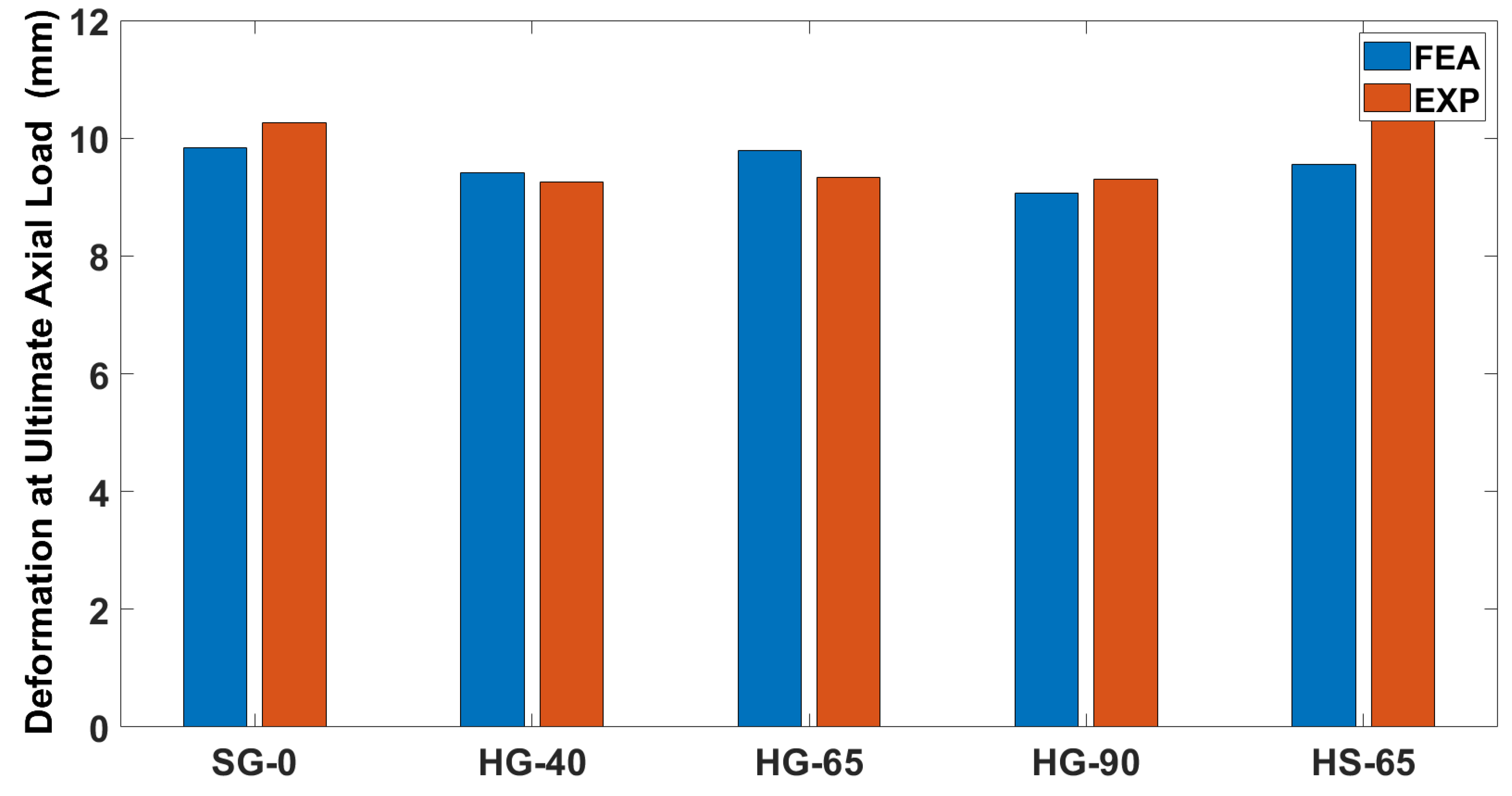
4.2. Ultimate Axial Load-Carrying Capacity and Corresponding Axial Deformation
4.3. Axial Load–Axial Deformation Behavior
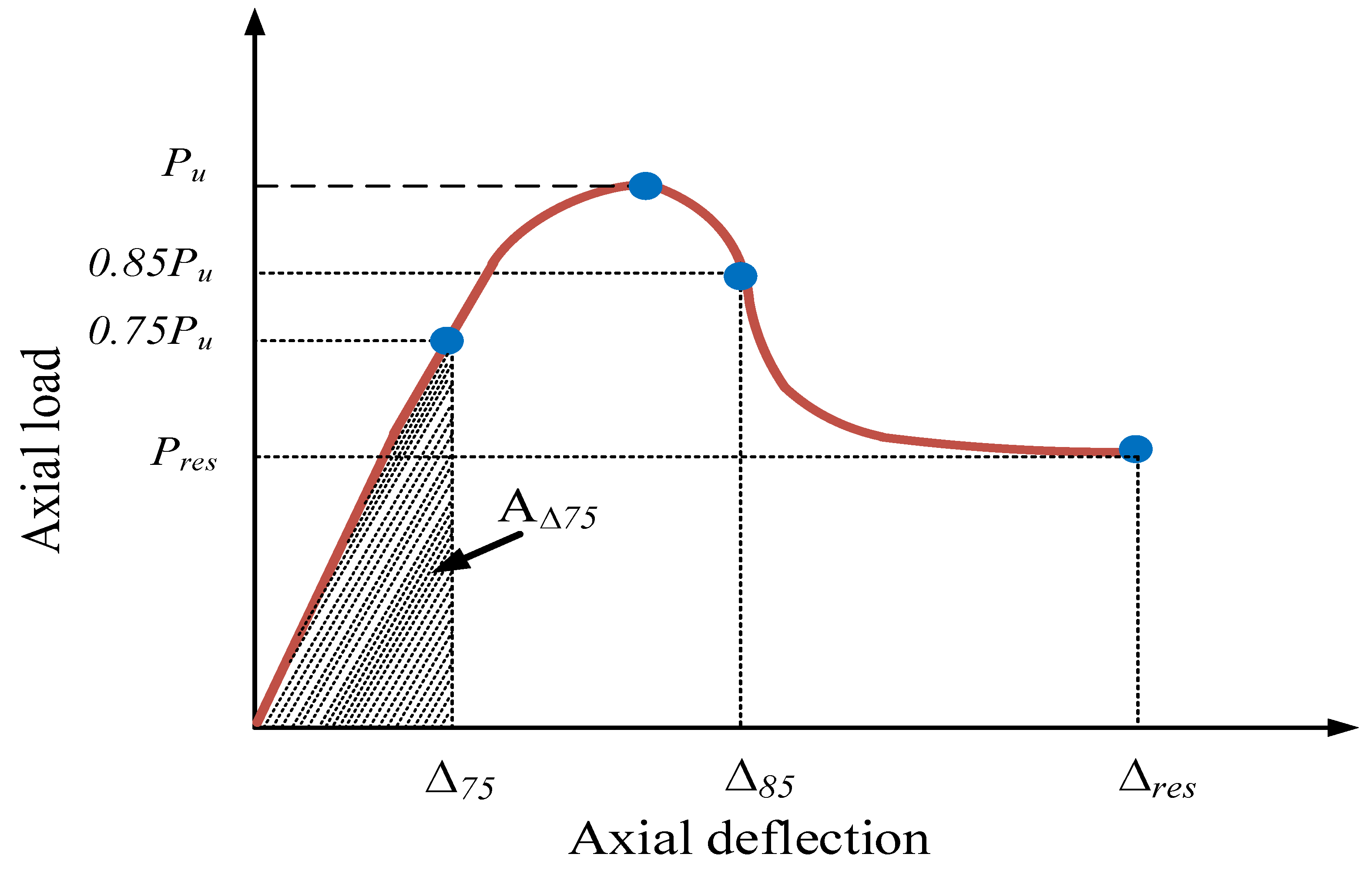
4.4. Ductility of Columns
4.5. Crack Development and Failure Pattern
- a.
- Failure Mode of SG-0
- b.
- Failure Mode of HG-40
- c.
- Failure Mode of HG-65
- d.
- Failure Mode of HG-90
- e.
- Failure Mode of HS-65
4.6. Summary of Validity of Calibrated Model
5. Parametric Study
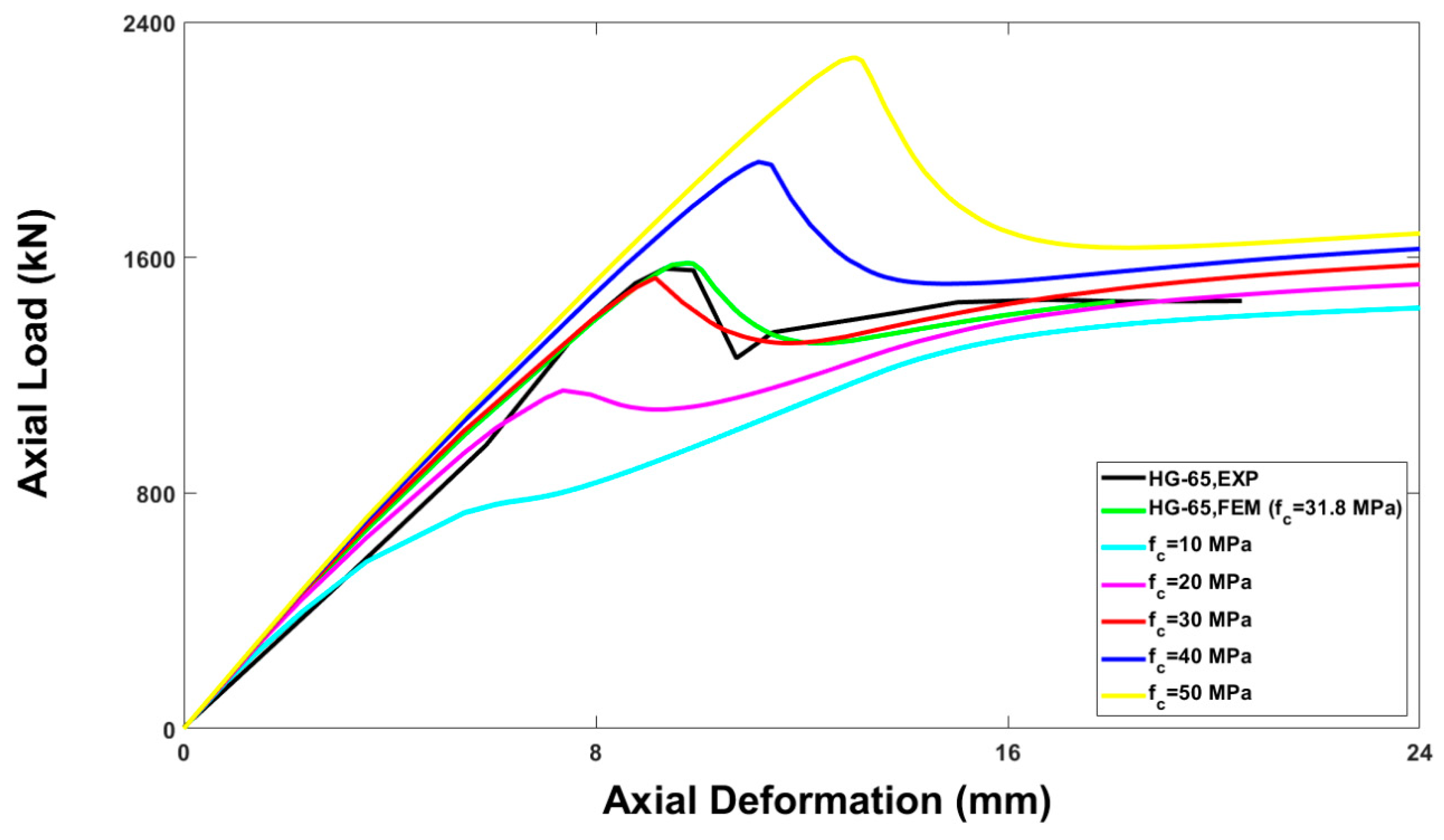
5.1. Effect of Concrete Compressive Strength (f’c)
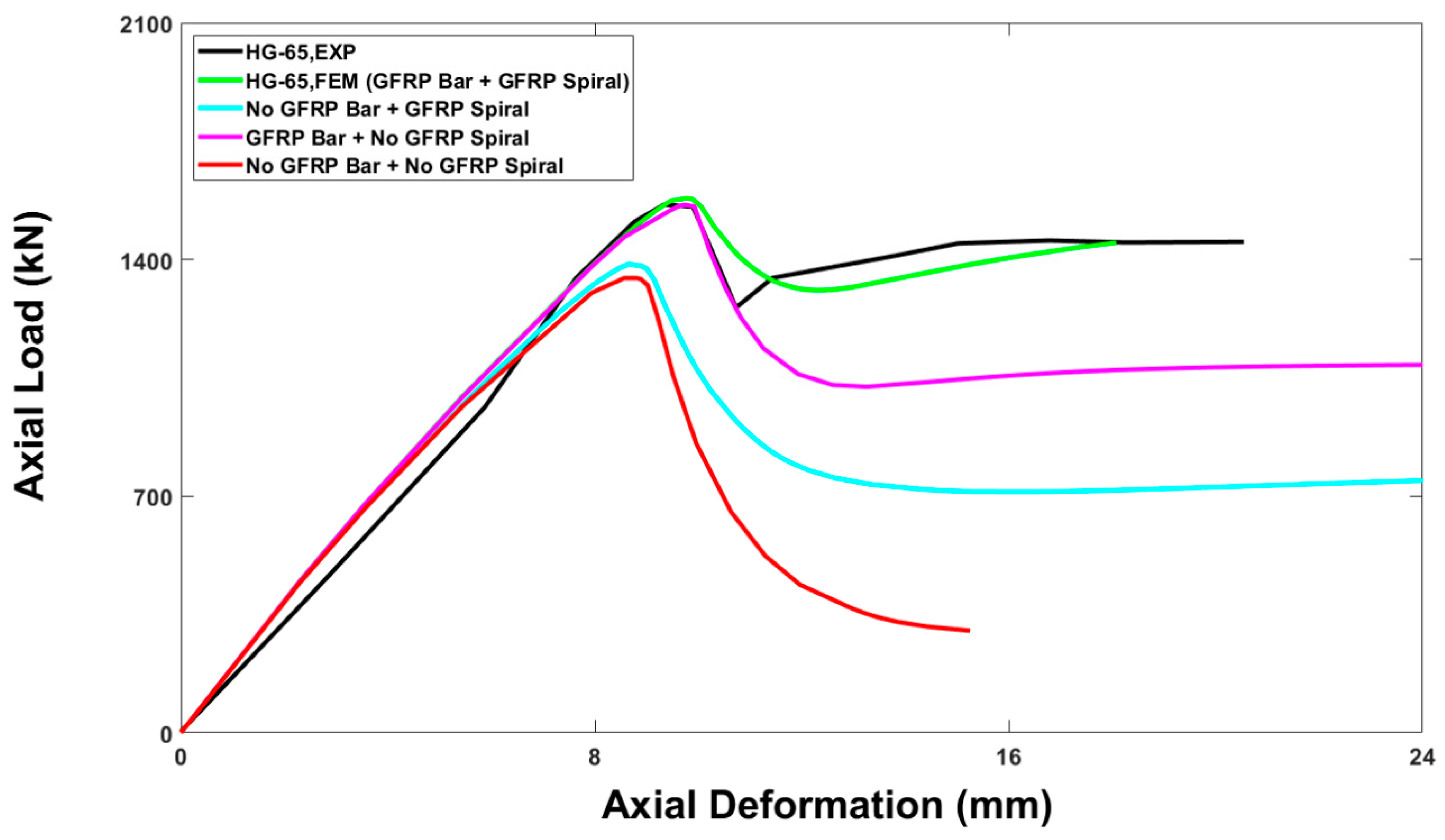
5.2. Effect of Provision of Reinforcements
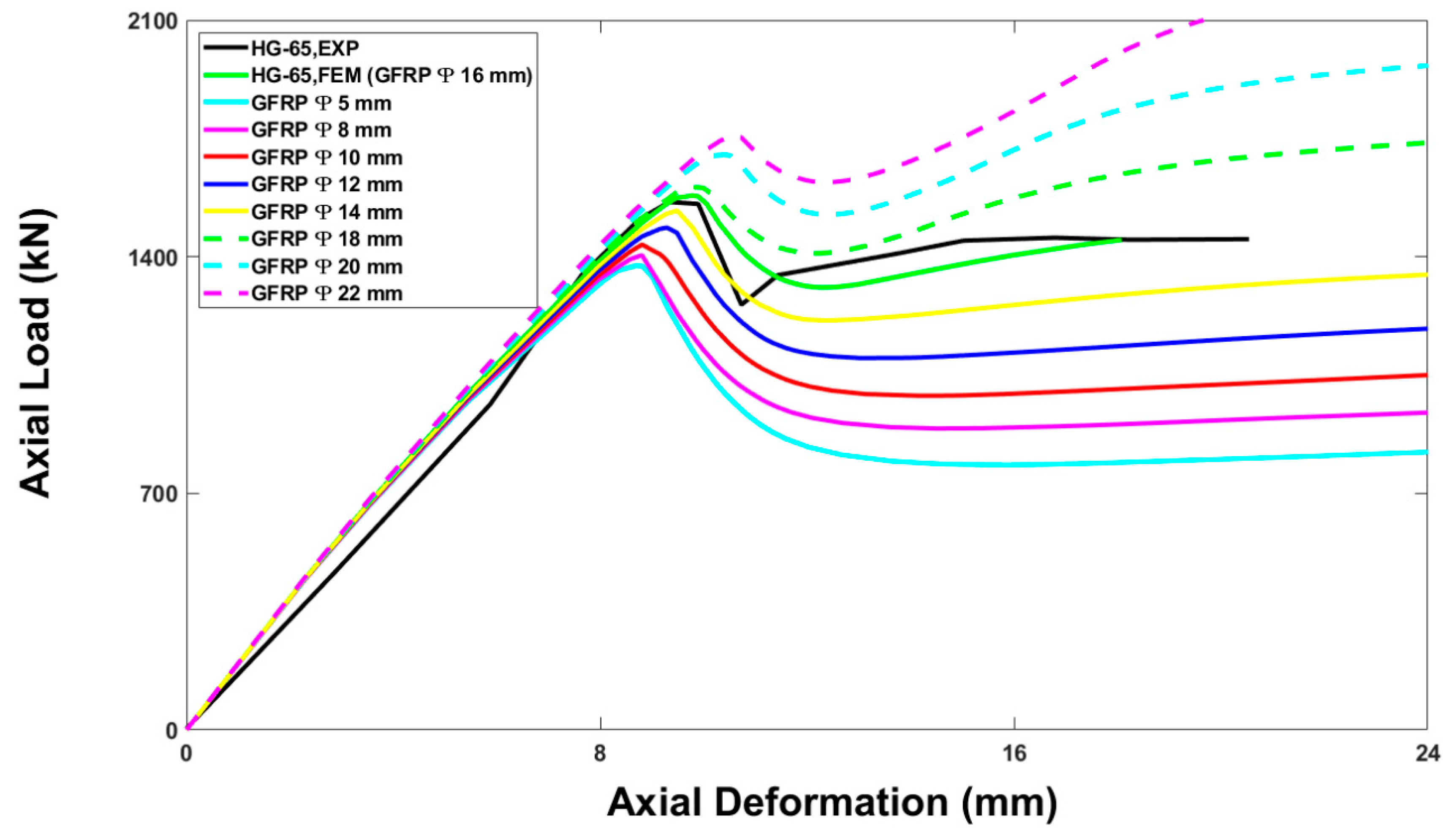
5.3. Effect of Longitudinal Reinforcement Ratio (ρl)
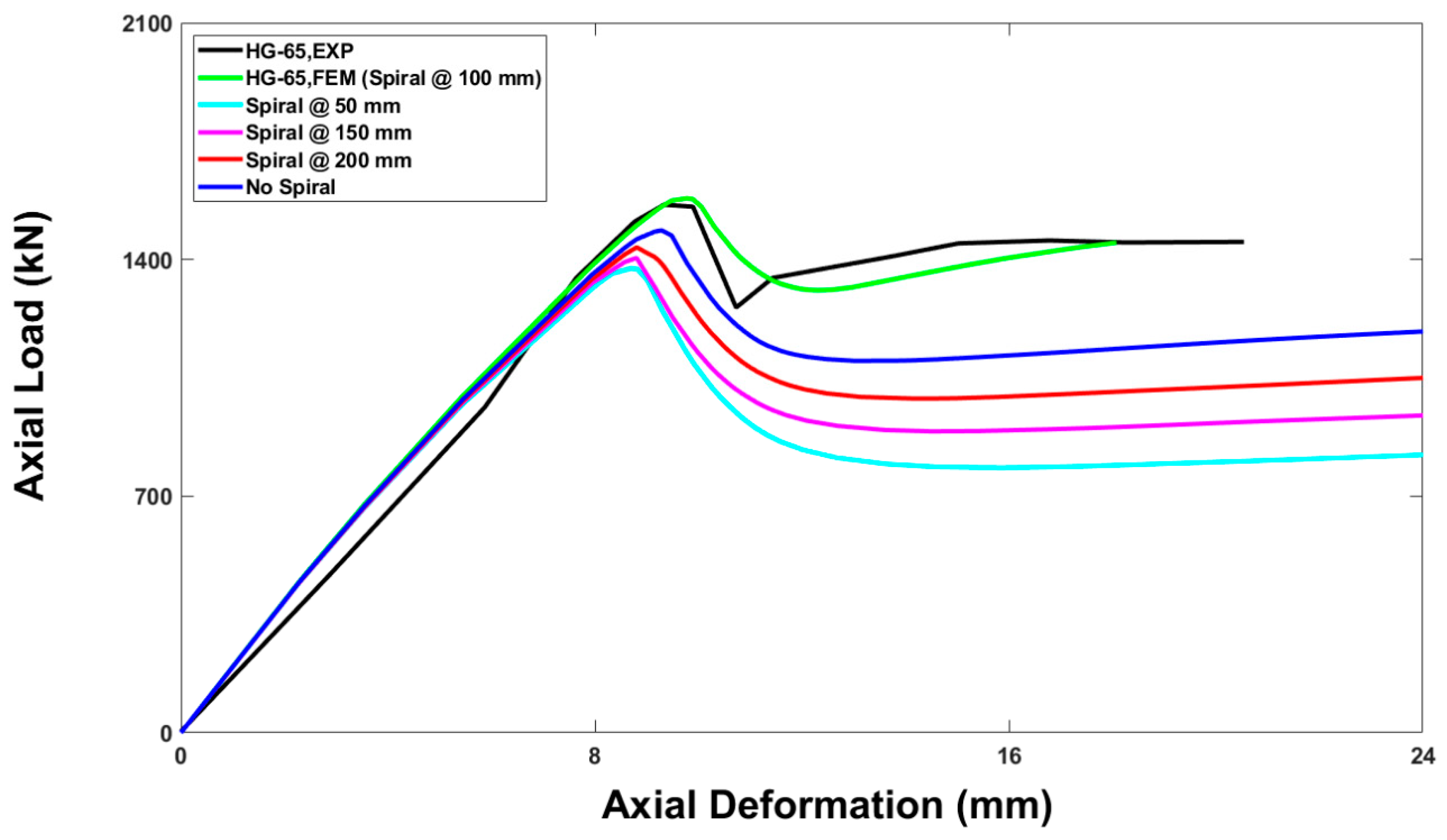
5.4. Effect of Pitch of Spiral Reinforcement
6. Compatibility of Equations for Axial Load-Carrying Capacity
7. Conclusions
- The results indicated that the axial load-carrying capacity of the hollow RC columns reinforced with GFRP was affected by certain input parameters. The most critical of these parameters were the mesh size and viscosity parameter. Other variables affecting ultimate axial load-carrying capacity of the columns were the shape factor, dilation angle, and mesh type. Thus, any finite element model should be calibrated for these variables before using it for numerical study.
- The FEA analysis yielded close results with those earlier concluded by experimental work. The axial load-axial deformation responses of the finite element models of all the columns coincided with a reasonable accuracy to the experimental curve, particularly in the pre-peak phase.
- The post-peak behavior of the axial load–axial deformation curves which employed the GFRP bars and spirals, could be accurately simulated by Abaqus. However, the ultimate failure of the GFRP reinforcements could not be predicted by the curve. This was probably due to the fact that the damage parameters of the GFRP were not as defined as that of concrete. Therefore, further study is required to define the damage pattern of the GFRP reinforcements.
- The average variation in the ultimate axial load-carrying capacities of the experimental results, from that of FEA values, was noted to be only 3.87%, while the average difference in their corresponding deformations was 7.08%. This nominal difference in the results revealed that the numerical model was suitable for implementation in further study on the hollow GFRPRC columns.
- The numerical analysis confirmed the results of the experimental work regarding the effects of inner-to-outer diameter ratios, hollowness, and confinement efficiency on the hollow RC columns reinforced with GFRP.
- The cracking pattern in the hollow RC columns was visualized through PEEQs. A satisfactory comparison was obtained between the crack development behavior attained through the FEA and actual experimental cracks. This substantiated the idea that the FEA analysis of structural members can be performed using Abaqus, instead of undergoing costly experimental investigations.
- The average variations between numerically obtained ultimate axial load-carrying capacities and the results of Equations (8)–(10) were 31.368%, 3.383%, and 3.378%, respectively.
- The numerical parametric study of HG-65 (selected model column) revealed that the ultimate axial load-carrying capacity of the column was enhanced by increasing the concrete compressive strength and longitudinal reinforcement ratio or by reducing the spiral pitch.
Recommendation
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deitz, D.; Harik, I.E.; Gesund, H. Physical properties of glass fiber reinforced polymer rebars in compression. J. Compos. Constr. 2003, 7, 363–366. [Google Scholar] [CrossRef]
- Ephraim, M.; Adetiloye, A.; Harcourt, P. Mechanical properties of glass fibre reinforced polymer based on resin from recycled plastic. IJSER 2015, 6, 145–152. [Google Scholar]
- ACI Committee. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars (ACI 440. 1R-15); American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Jabbar, S.A.; Farid, S.B. Replacement of steel rebars by GFRP rebars in the concrete structures. Karbala Int. J. Mod. Sci. 2018, 4, 216–227. [Google Scholar] [CrossRef]
- Afifi, M.Z.; Mohamed, H.M.; Benmokrane, B. Axial capacity of circular concrete columns reinforced with GFRP bars and spirals. J. Compos. Constr. 2014, 18, 04013017. [Google Scholar] [CrossRef]
- Afifi, M.Z.; Mohamed, H.M.; Benmokrane, B. Theoretical stress–strain model for circular concrete columns confined by GFRP spirals and hoops. Eng. Struct. 2015, 102, 202–213. [Google Scholar] [CrossRef]
- Ali, M.A.; El-Salakawy, E. Seismic performance of GFRP-reinforced concrete rectangular columns. J. Compos. Constr. 2016, 20, 04015074. [Google Scholar] [CrossRef]
- El Refai, A.; Abed, F.; Al-Rahmani, A. Structural performance and serviceability of concrete beams reinforced with hybrid (GFRP and steel) bars. Constr. Build. Mater. 2015, 96, 518–529. [Google Scholar] [CrossRef]
- Hadhood, A.; Mohamed, H.M.; Ghrib, F.; Benmokrane, B. Efficiency of glass-fiber reinforced-polymer (GFRP) discrete hoops and bars in concrete columns under combined axial and flexural loads. Compos. Part B Eng. 2017, 114, 223–236. [Google Scholar] [CrossRef]
- Hadi, M.N.; Karim, H.; Sheikh, M.N. Experimental investigations on circular concrete columns reinforced with GFRP bars and helices under different loading conditions. J. Compos. Constr. 2016, 20, 04016009. [Google Scholar] [CrossRef]
- Hadi, M.N.; Youssef, J. Experimental investigation of GFRP-reinforced and GFRP-encased square concrete specimens under axial and eccentric load, and four-point bending test. J. Compos. Constr. 2016, 20, 04016020. [Google Scholar] [CrossRef]
- Hales, T.A.; Pantelides, C.P.; Reaveley, L.D. Experimental evaluation of slender high-strength concrete columns with GFRP and hybrid reinforcement. J. Compos. Constr. 2016, 20, 04016050. [Google Scholar] [CrossRef]
- Karim, H.; Sheikh, M.N.; Hadi, M.N. Axial load-axial deformation behaviour of circular concrete columns reinforced with GFRP bars and helices. Constr. Build. Mater. 2016, 112, 1147–1157. [Google Scholar] [CrossRef]
- Khan, Q.S.; Sheikh, M.N.; Hadi, M.N. Axial-flexural interactions of GFRP-CFFT columns with and without reinforcing GFRP bars. J. Compos. Constr. 2017, 21, 04016109. [Google Scholar] [CrossRef]
- Khorramian, K.; Sadeghian, P. Experimental and analytical behavior of short concrete columns reinforced with GFRP bars under eccentric loading. Eng. Struct. 2017, 151, 761–773. [Google Scholar] [CrossRef]
- Mohamed, H.M.; Benmokrane, B. Design and performance of reinforced concrete water chlorination tank totally reinforced with GFRP bars: Case study. J. Compos. Constr. 2014, 18, 05013001. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Gibbons, M.E.; Reaveley, L.D. Axial load behavior of concrete columns confined with GFRP spirals. J. Compos. Constr. 2013, 17, 305–313. [Google Scholar] [CrossRef]
- Sun, L.; Wei, M.; Zhang, N. Experimental study on the behavior of GFRP reinforced concrete columns under eccentric axial load. Constr. Build. Mater. 2017, 152, 214–225. [Google Scholar] [CrossRef]
- Tabatabaei, A.; Eslami, A.; Mohamed, H.M.; Benmokrane, B. Strength of compression lap-spliced GFRP bars in concrete columns with different splice lengths. Constr. Build. Mater. 2018, 182, 657–669. [Google Scholar] [CrossRef]
- Tavassoli, A.; Sheikh, S.A. Seismic resistance of circular columns reinforced with steel and GFRP. J. Compos. Constr. 2017, 21, 04017002. [Google Scholar] [CrossRef]
- Raza, A.; Khan, Q.u.Z.; Ahmad, A. Prediction of axial compressive strength for FRP-confined concrete compression members. KSCE J. Civ. Eng. 2020, 24, 2099–2109. [Google Scholar] [CrossRef]
- Raza, A.; Khan, Q.u.Z.; Ahmad, A. Investigation of HFRC columns reinforced with GFRP bars and spirals under concentric and eccentric loadings. Eng. Struct. 2021, 227, 111461. [Google Scholar] [CrossRef]
- Ahmad, A.; Aljuhni, A.; Arshid, U.; Elchalakani, M.; Abed, F. Prediction of columns with GFRP bars through Artificial Neural Network and ABAQUS. Structures 2022, 40, 247–255. [Google Scholar] [CrossRef]
- AlAjarmeh, O.; Manalo, A.; Benmokrane, B.; Schubel, P.; Zeng, X.; Ahmad, A.; Hassanli, R.; Sorbello, C.-D. Compression behavior of GFRP bars under elevated In-Service temperatures. Constr. Build. Mater. 2022, 314, 125675. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Concrete columns reinforced longitudinally and transversally with glass fiber-reinforced polymer bars. ACI Struct. J. 2012, 109, 551–558. [Google Scholar]
- Raval, R.; Dave, U. Behavior of GFRP wrapped RC columns of different shapes. Procedia Eng. 2013, 51, 240–249. [Google Scholar] [CrossRef]
- Guo, Y.-C.; Gao, W.-Y.; Zeng, J.-J.; Duan, Z.-J.; Ni, X.-Y.; Peng, K.-D. Compressive behavior of FRP ring-confined concrete in circular columns: Effects of specimen size and a new design-oriented stress-strain model. Constr. Build. Mater. 2019, 201, 350–368. [Google Scholar] [CrossRef]
- Elmessalami, N.; El Refai, A.; Abed, F. Fiber-reinforced polymers bars for compression reinforcement: A promising alternative to steel bars. Constr. Build. Mater. 2019, 209, 725–737. [Google Scholar] [CrossRef]
- El Gamal, S.; Alshareedah, O. Experimental study on the performance of circular concrete columns reinforced with GFRP under axial load. In Proceedings of the International Conference on Civil Infrastructure and Construction, Doha, Qatar, 2–5 February 2020. [Google Scholar] [CrossRef]
- Lignola, G.P.; Nardone, F.; Prota, A.; De Luca, A.; Nanni, A. Analysis of RC hollow columns strengthened with GFRP. J. Compos. Constr. 2011, 15, 545–556. [Google Scholar] [CrossRef]
- Hadhood, A.; Mohamed, H.M.; Benmokrane, B. Strength of circular HSC columns reinforced internally with carbon-fiber-reinforced polymer bars under axial and eccentric loads. Constr. Build. Mater. 2017, 141, 366–378. [Google Scholar] [CrossRef]
- Liang, X.; Sritharan, S. Effects of confinement in square hollow concrete column sections. Eng. Struct. 2019, 191, 526–535. [Google Scholar] [CrossRef]
- Wayghan, A.R.T.; Mofid, M.; Ravandi, B.B.; Yazdi, S.M.Z. Increasing the contribution of gfrp bars on the compressive strength of concrete columns with circular cross section. Civ. Eng. J. 2019, 5, 1850–1862. [Google Scholar] [CrossRef]
- Al-Rubaye, M.; Manalo, A.; Alajarmeh, O.; Ferdous, W.; Lokuge, W.; Benmokrane, B.; Edoo, A. Flexural behaviour of concrete slabs reinforced with GFRP bars and hollow composite reinforcing systems. Compos. Struct. 2020, 236, 111836. [Google Scholar] [CrossRef]
- AlAjarmeh, O.S.; Manalo, A.C.; Benmokrane, B.; Vijay, P.V.; Ferdous, W.; Mendis, P. Novel testing and characterization of GFRP bars in compression. Constr. Build. Mater. 2019, 225, 1112–1126. [Google Scholar] [CrossRef]
- AlAjarmeh, O.S.; Manalo, A.C.; Benmokrane, B.; Karunasena, K.; Ferdous, W.; Mendis, P. Hollow concrete columns: Review of structural behavior and new designs using GFRP reinforcement. Eng. Struct. 2020, 203, 109829. [Google Scholar] [CrossRef]
- AlAjarmeh, O.S.; Manalo, A.C.; Benmokrane, B.; Karunasena, W.; Mendis, P. Effect of spiral spacing and concrete strength on behavior of GFRP-reinforced hollow concrete columns. J. Compos. Constr. 2020, 24, 04019054. [Google Scholar] [CrossRef]
- Raza, A.; Khan, Q.u.Z.; Ahmad, A. Numerical investigation of load-carrying capacity of GFRP-reinforced rectangular concrete members using CDP model in ABAQUS. Adv. Civ. Eng. 2019, 2019, 1745341. [Google Scholar] [CrossRef]
- Havlásek, P. Numerical modeling of axially compressed circular concrete columns. Eng. Struct. 2021, 227, 111445. [Google Scholar] [CrossRef]
- Bahrami, A.; Mahmoudi Kouhi, A. Compressive behaviour of circular, square, and rectangular concrete-filled steel tube stub columns. Civ. Eng. Arch. 2020, 8, 1119–1126. [Google Scholar] [CrossRef]
- He, K.; Chen, Y.; Yan, Y. Axial mechanical properties of concrete-filled GFRP tubular hollow composite columns. Compos. Struct. 2020, 243, 112174. [Google Scholar] [CrossRef]
- Rashid, S.M.P.; Bahrami, A. Structural performance of infilled steel–concrete composite thin-walled columns combined with FRP and CFRP: A comprehensive review. Materials 2023, 16, 1564. [Google Scholar] [CrossRef]
- ASTM C143/C143M; Standard Test Method for Slump of Hydraulic-Cement Concrete. ASTM: West Conshohocken, PA, USA, 2020.
- ASTM C39/C39M; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2018.
- AS 1012.9; Methods of Testing Concrete, Method 9: Compressive Strength Tests—Concrete, Mortar and Grout Specimens. Standards Australia: Sydney, Australia, 2014.
- Abaqus. ABAQUS 6.14 Documentation: Simulia, Dassault Systemes, RI, USA. 2014. Available online: https://130.149.89.49:2080/v6.14/ (accessed on 25 February 2023).
- Amiri, G.G.; Jahromi, A.J.; Mohebi, B. Effect of transverse reinforcing on circular columns confined with FRP. In Challenges, Opportunities and Solutions in Structural Engineering and Construction; CRC Press: Las Vegas, NV, USA, 2009; pp. 251–256. [Google Scholar]
- Afifi, M.Z.; Mohamed, H.M.; Benmokrane, B. Strength and axial behavior of circular concrete columns reinforced with CFRP bars and spirals. J. Compos. Constr. 2014, 18, 04013035. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Strength model for concrete columns reinforced with fiber-reinforced polymer bars and ties. ACI Struct. J. 2014, 111, 789–798. [Google Scholar] [CrossRef]


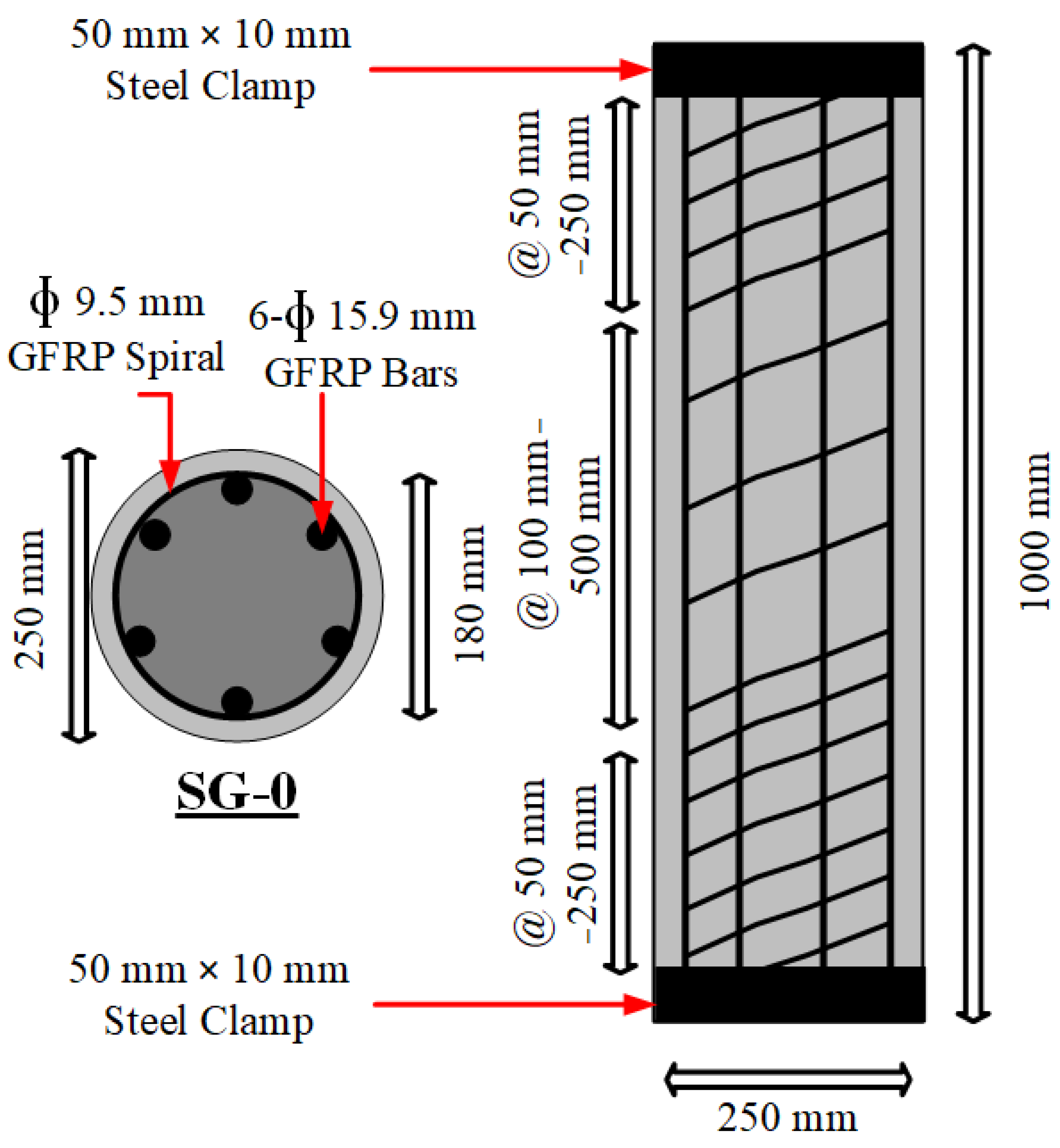





| Type of Reinforcement | Nominal Diameter (mm) | Area (mm2) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Ultimate Strain (%) |
|---|---|---|---|---|---|
| GFRP spiral No. 3 | 9.5 | 70.8 | 1315 | 62.5 | 2.3 |
| GFRP bar No. 5 | 15.9 | 198.5 | 1237 | 60 | 2.1 |
| Steel bar No. 5 | 16 | 200.96 | 500 | 200 | 2.1 |
| Specimen | Inner Diameter (mm) | Inner-to-Outer Diameter Ratio (i/o) | Reinforcement Ratio (%) | Volumetric Ratio (%) |
|---|---|---|---|---|
| SG-0 | 00 | 0 | 2.41 | 1.49 |
| HG-40 | 40 | 0.16 | 2.47 | 1.56 |
| HG-65 | 65 | 0.26 | 2.59 | 1.69 |
| HG-90 | 90 | 0.36 | 2.78 | 1.92 |
| HS-65 | 65 | 0.26 | 2.59 | 1.60 |
| Parameter | Concrete | GFRP | Steel | Rubber Pad |
|---|---|---|---|---|
| Density (ton/mm3) | 2.4 × 10−9 | 2.1 × 10−9 | 7.58 × 10−9 | 1.25 × 10−9 |
| Poisson’s ratio | 0.2 | 0.25 | 0.3 | 0.49 |
| Elastic modulus (N/mm2) | 24,435 | 60,000 | 200,000 | 6000 |
| Concrete cover of specimen (mm) | - | 20 | 40 | - |
| Sr. No. | Specimen | Ultimate Axial Load-Carrying Capacity (kN) | Deformation at Ultimate Axial-Load Carrying Capacity (mm) | ||||
|---|---|---|---|---|---|---|---|
| FEA | EXP | Percentage Difference | FEA | EXP | Percentage Difference | ||
| 1 | SG-0 | 1577.13 | 1582.48 | 0.34 | 9.84 | 10.27 | 4.17 |
| 2 | HG-40 | 1494.80 | 1403.51 | −6.5 | 9.41 | 9.26 | −1.64 |
| 3 | HG-65 | 1580.82 | 1561.91 | −1.21 | 9.78 | 9.33 | −4.8 |
| 4 | HG-90 | 1395.91 | 1410.14 | 1.01 | 9.07 | 9.30 | 2.41 |
| 5 | HS-65 | 1684.64 | 1409.07 | −19.56 | 9.56 | 11.65 | 17.95 |
| Column Specimen | Percentage Difference (Equation vs. Exp) | Percentage Difference (Equation vs. FEA) | ||||
|---|---|---|---|---|---|---|
| Equation (8) | Equation (9) | Equation (10) | Equation (8) | Equation (9) | Equation (10) | |
| SG-0 | 28.78 | 3.79 | 3.79 | 29.22 | 3.47 | 3.46 |
| HG-40 | 42.36 | −5.63 | −5.63 | 42.49 | −5.72 | −5.73 |
| HG-65 | 23.73 | 9.28 | 9.28 | 22.25 | 10.36 | 10.36 |
| HG-90 | 30.18 | 6.37 | 6.37 | 31.51 | 5.42 | 5.42 |
| Average | 31.263 | 3.453 | 3.453 | 31.368 | 3.383 | 3.378 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, A.; Bahrami, A.; Alajarmeh, O.; Chairman, N.; Yaqub, M. Investigation of Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals. Buildings 2023, 13, 1056. https://doi.org/10.3390/buildings13041056
Ahmad A, Bahrami A, Alajarmeh O, Chairman N, Yaqub M. Investigation of Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals. Buildings. 2023; 13(4):1056. https://doi.org/10.3390/buildings13041056
Chicago/Turabian StyleAhmad, Afaq, Alireza Bahrami, Omar Alajarmeh, Nida Chairman, and Muhammad Yaqub. 2023. "Investigation of Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals" Buildings 13, no. 4: 1056. https://doi.org/10.3390/buildings13041056
APA StyleAhmad, A., Bahrami, A., Alajarmeh, O., Chairman, N., & Yaqub, M. (2023). Investigation of Circular Hollow Concrete Columns Reinforced with GFRP Bars and Spirals. Buildings, 13(4), 1056. https://doi.org/10.3390/buildings13041056









