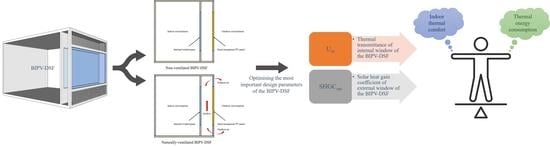
Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia
Abstract
1. Introduction
2. Methods
2.1. Design Parameters to Be Optimised
2.2. Optimisation Methods
2.2.1. Design Parameters for Optimisation
2.2.2. Mathematical Model
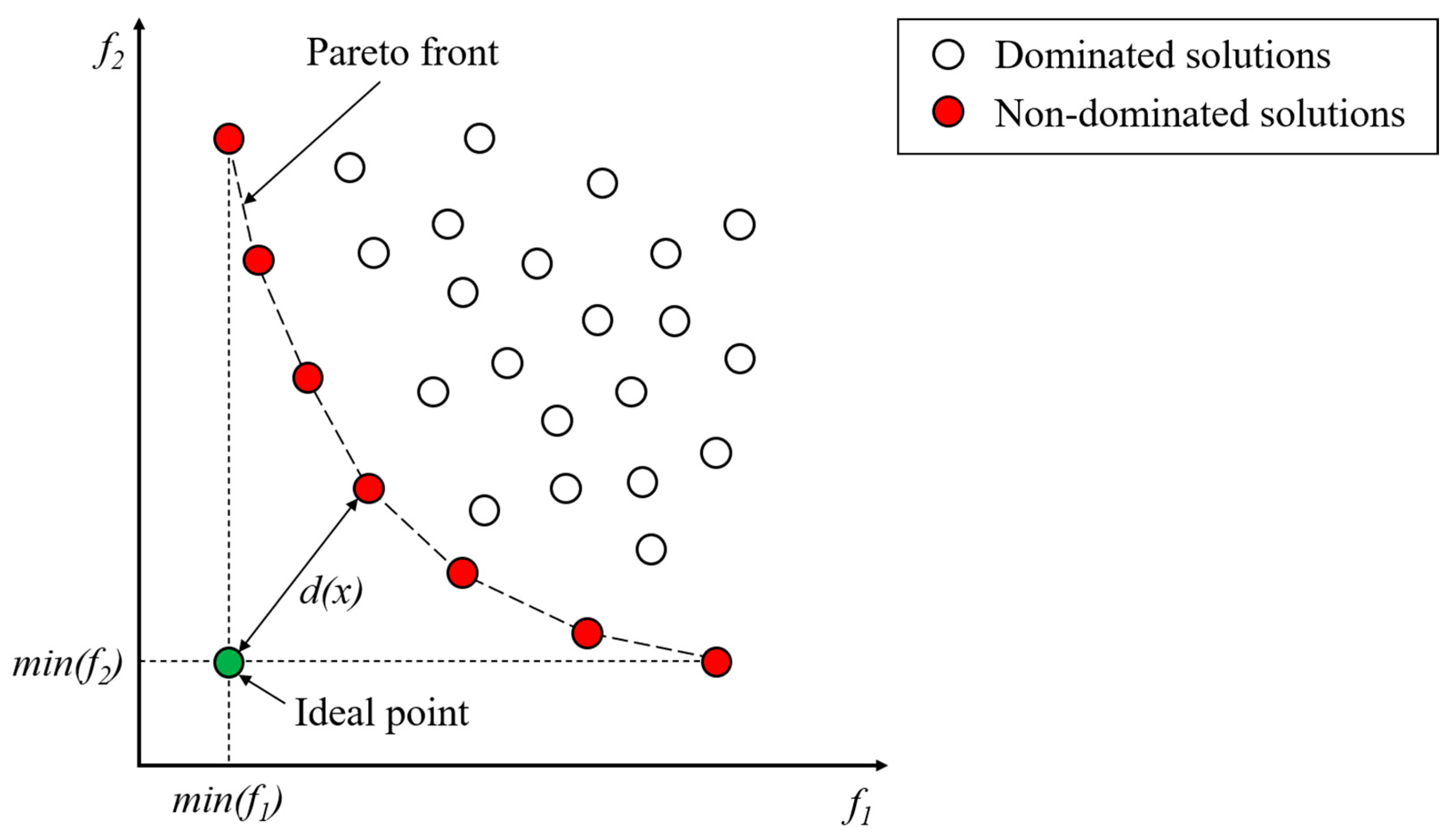
2.2.3. Pareto Optimality Method
2.3. BIPV-DSF Model
3. Results and Discussion
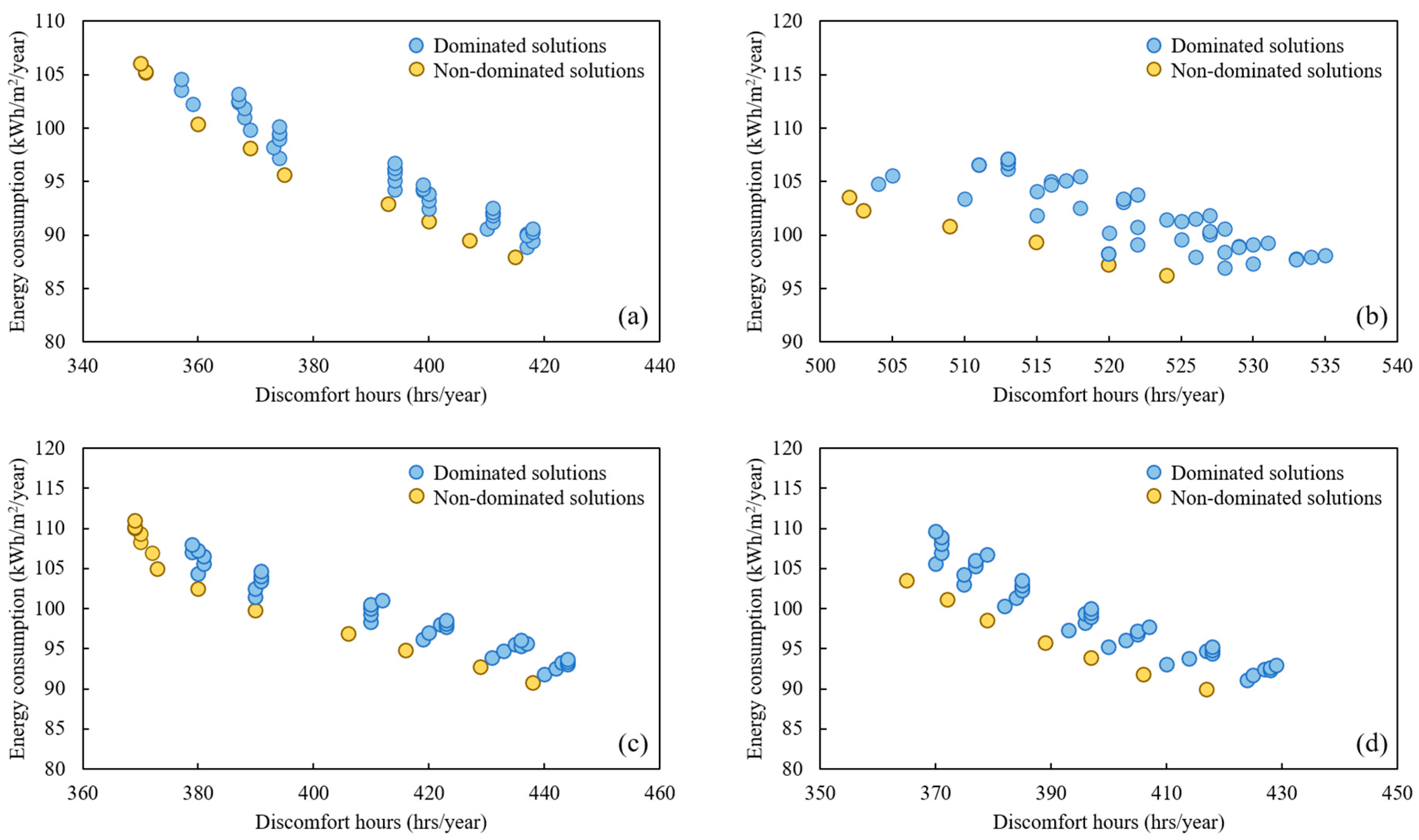
3.1. Optimising BIPV-DSF for High-Humidity Summer and Warm Winter Climate (Darwin)
3.2. Optimising BIPV-DSF for Warm Temperate Climate (Sydney)
3.3. Optimising BIPV-DSF for Cool Temperate Climate (Canberra)
4. Conclusions
- Thermal transmittance of internal window of the BIPV-DSF (Uin);
- Solar heat gain coefficient of external window of the BIPV-DSF (SHGCout).
- In the high-humidity summer and warm winter climate zone (Darwin): naturally-ventilated BIPV-DSF with a semi-transparent perovskite-based PV glazing either facing north, south or west being utilised throughout the year. In this case, a Uin of 5.16 W/m2K and a SHGCout of 0.81 are optimum; while the Uin and SHGCout should be 5.53 W/m2K and 0.81, respectively, when the BIPV-DSF is east-oriented.
- In the warm temperate climate zone (Sydney): a semi-transparent perovskite-based PV glazed BIPV-DSF facing north, east and west should be non-ventilated and naturally-ventilated during the cold and hot months, respectively. In this case, a Uin of 5.87 W/m2K and SHGCout of 0.81 are optimum. However, the Uin and SHGCout should be 5.16 W/m2K and 0.81, respectively, when the BIPV-DSF is south-oriented.
- In the cool temperate climate (Canberra): a semi-transparent perovskite-based PV glazed BIPV-DSF facing north, east and west should be operated as non-ventilated and naturally-ventilated modes, respectively, during the cold and hot months. In this case, a Uin of 5.87 W/m2K and SHGCout of 0.81 are optimum, while the respective Uin and SHGCout should be 5.16 W/m2K and 0.81 when the BIPV-DSF is facing south.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| A | PV panel exposed area [m2] |
| d(x)min | shortest distance of non-dominated solution to the “ideal point” [-] |
| EH | exceedance hours or total discomfort hours [-] |
| f1(x) | objective function 1 [hrs/year] |
| f2(x) | objective function 2 [kWh/m2/year] |
| GT | total incident solar radiation on PV panel surface [kW/m2] |
| Hdisc | a discomfort hour [-] |
| IAM | incidence angle modifier [-] |
| min(f1) | minimum value of objective function 1 [hrs/year] |
| min(f2) | minimum value of objective function 2 [kWh/m2/year] |
| PPV | PV electric power production [kW] |
| qcomb,s,i | combined convective and radiative heat flux in the space [kW] |
| qcomb,s,o | combined convective and radiative heat flux to the surface [kW] |
| qs,i | conductive heat flux from the wall at the inside surface [kW] |
| qs,o | conductive heat flux into the wall at the outside surface [kW] |
| Ss,i | solar radiation and long-wave radiation generated from internal objects [kW] |
| Ss,o | solar radiation from external surfaces [kW] |
| SHGC | solar heat gain coefficient [-] |
| SHGCout | solar heat gain coefficient of external window of BIPV-DSF [-] |
| U-value | thermal transmittance [W/m2K] |
| Uin | thermal transmittance of internal window of BIPV-DSF [W/m2K] |
| Uout | thermal transmittance of external window of BIPV-DSF [W/m2K] |
| Wallgain | user defined energy flow to inside wall or window surfaces [kW] |
| x | a design variable [-] |
| Greek symbols | |
| ηPV | PV power conversion efficiency [%] |
| τα | product of PV panel’s transmittance and absorptance [-] |
| Subscripts | |
| n | normal incidence angle of solar radiation |
| Abbreviations | |
| BIPV | building-integrated photovoltaic |
| BIPV-DSF | building-integrated photovoltaic double-skin facade |
| CdTe | cadmium telluride |
| CIGS | copper indium gallium selenide |
| DSF | double-skin facade |
| NatVent-DSF | naturally-ventilated BIPV-DSF |
| NoVent-DSF | non-ventilated BIPV-DSF |
| PMV | Predicated Mean Vote |
| PV | photovoltaic |
| SCoP | seasonal coefficient of performance |
| STC | standard test condition |
References
- Al-Humaiqani, M.M.; Al-Ghamdi, S.G. The built environment resilience qualities to climate change impact: Concepts, frameworks, and directions for future research. Sustain. Cities Soc. 2022, 80, 103797. [Google Scholar] [CrossRef]
- Moncaster, A. The Impact of the Built Environment on Climate Change—And of Climate Change on the Built Environment. Design for Sustainability. 2021. Available online: http://www.open.ac.uk/blogs/design/the-impact-of-the-built-environment-on-climate-change-and-of-climate-change-on-the-built-environment/#:~:text=Why%20is%20the%20built%20environment,than%20any%20other%20individual%20sector (accessed on 5 June 2022).
- Ritchie, H.; Roser, M.; Rosado, P. CO2 and Greenhouse Gas Emissions. 2020. Available online: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions (accessed on 5 June 2022).
- Malyan, S.K.; Kumar, A.; Baram, S.; Kumar, J.; Singh, S.; Kumar, S.S.; Yadav, A.N. Role of Fungi in Climate Change Abatement through Carbon Sequestration, in Recent Advancement in White Biotechnology through Fungi; Springer: Berlin/Heidelberg, Germany, 2019; pp. 283–295. [Google Scholar]
- Tricoire, J.-P. Rethinking Buildings is a Climate Imperative: Here’s What to Focus on. 2022. Available online: https://www.weforum.org/agenda/2022/05/rethinking-buildings-is-a-climate-imperative-here-s-what-to-focus-on/ (accessed on 5 June 2022).
- Jafarpur, P.; Berardi, U. Effects of climate changes on building energy demand and thermal comfort in Canadian office buildings adopting different temperature setpoints. J. Build. Eng. 2021, 42, 102725. [Google Scholar] [CrossRef]
- Yang, L.; Yan, H.; Lam, J.C. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Holmes, M.J.; Hacker, J.N. Climate change, thermal comfort and energy: Meeting the design challenges of the 21st century. Energy Build. 2007, 39, 802–814. [Google Scholar] [CrossRef]
- Mirrahimi, S.; Mohamed, M.F.; Haw, L.C.; Ibrahim, N.L.N.; Yusoff, W.F.M.; Aflaki, A. The effect of building envelope on the thermal comfort and energy saving for high-rise buildings in hot–humid climate. Renew. Sustain. Energy Rev. 2016, 53, 1508–1519. [Google Scholar] [CrossRef]
- Ghaffarianhoseini, A.; Ghaffarianhoseini, A.; Berardi, U.; Tookey, J.; Li, D.H.W.; Kariminia, S. Exploring the advantages and challenges of double-skin façades (DSFs). Renew. Sustain. Energy Rev. 2016, 60, 1052–1065. [Google Scholar] [CrossRef]
- Bui, D.-K.; Nguyen, T.N.; Ghazlan, A.; Ngo, N.T.; Ngo, T.D. Enhancing building energy efficiency by adaptive façade: A computational optimization approach. Appl. Energy 2020, 265, 114797. [Google Scholar] [CrossRef]
- Attia, S.; Bilir, S.; Safy, T.; Struck, C.; Loonen, R.; Goia, F. Current trends and future challenges in the performance assessment of adaptive façade systems. Energy Build. 2018, 179, 165–182. [Google Scholar] [CrossRef]
- Attia, S.; Lioure, R.; Declaude, Q. Future trends and main concepts of adaptive facade systems. Energy Sci. Eng. 2020, 8, 3255–3272. [Google Scholar] [CrossRef]
- Attia, S.; Bertrand, S.; Cuchet, M.; Yang, S.; Tabadkani, A. Comparison of Thermal Energy Saving Potential and Overheating Risk of Four Adaptive Façade Technologies in Office Buildings. Sustainability 2022, 14, 6106. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Prasad, D.; Sproul, A. Numerical Simulation Modelling of Building-Integrated Photovoltaic Double-Skin Facades. In Recent Advances in Numerical Simulations; Bulnes, F., Hessling, J.P., Eds.; IntechOpen: London, UK, 2021; pp. 61–75. [Google Scholar]
- Xu, C.; Ma, X.; Francis Yu, C.W. Photovoltaic double-skin façade: A combination of active and passive utilizations of solar energy. Indoor Built Environ. 2019, 28, 1013–1017. [Google Scholar] [CrossRef]
- Bloem, J.J.; Lodi, C.; Cipriano, J.; Chemisana, D. An outdoor Test Reference Environment for double skin applications of Building Integrated PhotoVoltaic Systems. Energy Build. 2012, 50, 63–73. [Google Scholar] [CrossRef]
- Gaillard, L.; Giroux-Julien, S.; Ménézo, C.; Pabiou, H. Experimental evaluation of a naturally ventilated PV double-skin building envelope in real operating conditions. Sol. Energy 2014, 103, 223–241. [Google Scholar] [CrossRef]
- Saadon, S.; Gaillard, L.; Giroux-Julien, S.; Ménézo, C. Simulation study of a naturally-ventilated building integrated photovoltaic/thermal (BIPV/T) envelope. Renew. Energy 2016, 87, 517–531. [Google Scholar] [CrossRef]
- Peng, J.; Lu, L.; Yang, H. An experimental study of the thermal performance of a novel photovoltaic double-skin facade in Hong Kong. Sol. Energy 2013, 97, 293–304. [Google Scholar] [CrossRef]
- Peng, J.; Curcija, D.C.; Lu, L.; Selkowitz, S.E.; Yang, H.; Zhang, W. Numerical investigation of the energy saving potential of a semi-transparent photovoltaic double-skin facade in a cool-summer Mediterranean climate. Appl. Energy 2016, 165, 345–356. [Google Scholar] [CrossRef]
- Ioannidis, Z.; Buonomano, A.; Athienitis, A.K.; Stathopoulos, T. Modeling of double skin façades integrating photovoltaic panels and automated roller shades: Analysis of the thermal and electrical performance. Energy Build. 2017, 154, 618–632. [Google Scholar] [CrossRef]
- Fatnassi, S.; Abidi-Saad, A.; Ben Maad, R.; Polidori, G. Numerical study of spacing and alternation effects of parietal heat sources on natural convection flow in a DSF-channel: Application to BIPV. Heat Mass Transf. 2018, 54, 3617–3629. [Google Scholar] [CrossRef]
- Wang, C.; Peng, J.; Li, N.; Wang, M.; Li, X. Study on the operation strategy of ventilated photovoltaic windows in hot-summer and cold-winter zone in China. Procedia Eng. 2017, 205, 2092–2099. [Google Scholar] [CrossRef]
- Shakouri, M.; Ghadamian, H.; Noorpoor, A. Quasi-dynamic energy performance analysis of building integrated photovoltaic thermal double skin façade for middle eastern climate case. Appl. Therm. Eng. 2020, 179, 115724. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Sproul, A.; Prasad, D. Studies on Optimal Application of Building-Integrated Photovoltaic/Thermal Facade for Commercial Buildings in Australia. In Proceedings of the SWC2017/SHC2017, Abu Dhabi, United Arab Emirates, 29 October–2 November 2017; pp. 1–10. [Google Scholar]
- Yang, S.; Fiorito, F.; Sproul, A.; Prasad, D. Study of building integrated photovoltaic/thermal double-skin facade for commercial buildings in Sydney, Australia. In Proceedings of the Final Conference of COST TU1403 “Adaptive Facades Network”, Lucerne, Switzerland, 26–27 November 2018. [Google Scholar]
- Yang, S.; Cannavale, A.; Prasad, D.; Sproul, A.; Fiorito, F. Numerical simulation study of BIPV/T double-skin facade for various climate zones in Australia: Effects on indoor thermal comfort. Build. Simul. 2018, 12, 51–67. [Google Scholar] [CrossRef]
- Yang, S.; Cannavale, A.; Di Carlo, A.; Prasad, D.; Sproul, A.; Fiorito, F. Performance assessment of BIPV/T double-skin façade for various climate zones in Australia: Effects on energy consumption. Sol. Energy 2020, 199, 377–399. [Google Scholar] [CrossRef]
- Roberts, F.; Yang, S.; Du, H.; Yang, R. Effect of semi-transparent a-Si PV glazing within double-skin façades on visual and energy performances under the UK climate condition. Renew. Energy 2023, 207, 601–610. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Prasad, D.; Sproul, A.; Cannavale, A. A sensitivity analysis of design parameters of BIPV/T-DSF in relation to building energy and thermal comfort performances. J. Build. Eng. 2021, 41, 102426. [Google Scholar] [CrossRef]
- Elsharkawy, H.; Zahiri, S. The significance of occupancy profiles in determining post retrofit indoor thermal comfort, overheating risk and building energy performance. Build. Environ. 2020, 172, 106676. [Google Scholar] [CrossRef]
- Kumar, A.; Suman, B.M. Experimental evaluation of insulation materials for walls and roofs and their impact on indoor thermal comfort under composite climate. Build. Environ. 2013, 59, 635–643. [Google Scholar] [CrossRef]
- Liu, M.; Heiselberg, P.K.; Antonov, Y.I.; Mikkelsen, F.S. Parametric analysis on the heat transfer, daylight and thermal comfort for a sustainable roof window with triple glazing and external shutter. Energy Build. 2019, 183, 209–221. [Google Scholar] [CrossRef]
- Song, B.; Bai, L.; Yang, L. Analysis of the long-term effects of solar radiation on the indoor thermal comfort in office buildings. Energy 2022, 247, 123499. [Google Scholar] [CrossRef]
- Stiglitz, J.E. Pareto optimality and competition. J. Financ. 1981, 36, 235–251. [Google Scholar] [CrossRef]
- Maltais, L.-G.; Gosselin, L. Daylighting ‘energy and comfort’ performance in office buildings: Sensitivity analysis, metamodel and pareto front. J. Build. Eng. 2017, 14, 61–72. [Google Scholar] [CrossRef]
- Bre, F.; Fachinotti, V.D. A computational multi-objective optimization method to improve energy efficiency and thermal comfort in dwellings. Energy Build. 2017, 154, 283–294. [Google Scholar] [CrossRef]
- Ameur, M.; Kharbouch, Y.; Mimet, A. Optimization of passive design features for a naturally ventilated residential building according to the bioclimatic architecture concept and considering the northern Morocco climate. Build. Simul. 2020, 13, 677–689. [Google Scholar] [CrossRef]
- Chi, F.A.; Xu, Y. Building performance optimization for university dormitory through integration of digital gene map into multi-objective genetic algorithm. Appl. Energy 2022, 307, 118211. [Google Scholar] [CrossRef]
- Wijeratne, W.M.P.U.; Samarasinghalage, T.I.; Yang, R.J.; Wakefield, R. Multi-objective optimisation for building integrated photovoltaics (BIPV) roof projects in early design phase. Appl. Energy 2022, 309, 118476. [Google Scholar] [CrossRef]
- Pal, S.K.; Alanne, K.; Jokisalo, J.; Siren, K. Energy performance and economic viability of advanced window technologies for a new Finnish townhouse concept. Appl. Energy 2016, 162, 11–20. [Google Scholar] [CrossRef]
- Chen, F.; Wittkopf, S.K.; Ng, P.K.; Du, H. Solar heat gain coefficient measurement of semi-transparent photovoltaic modules with indoor calorimetric hot box and solar simulator. Energy Build. 2012, 53, 74–84. [Google Scholar] [CrossRef]
- Lie, S.; Bruno, A.; Wong, L.H.; Etgar, L. Semitransparent Perovskite Solar Cells with >13% Efficiency and 27% Transperancy Using Plasmonic Au Nanorods. ACS Appl. Mater. Interfaces 2022, 14, 11339–11349. [Google Scholar] [CrossRef]
- ASHRAE. Standard 55. In Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2017. [Google Scholar]
- TRNSYS. TRNSYS 17—Volume 5—Multizone Building Modelling with Type56 and TRNBuild; Solar Energy Laboratory, University of Wisconsin-Madison: Madison, WI, USA, 2005. [Google Scholar]
- Thermal Energy System Specialists. TESSLibs 17 Component Libraries for the TRNSYS Simulation Environment; HVAC Library Mathematical Reference, Ed.; Thermal Energy System Specialists, LLC: Madison, WI, USA, 2013. [Google Scholar]
- Australian Building Codes Board. Building Code of Australia, in National Construction Code Volume One; Australian Building Codes Board: Canberra, Australia, 2019. [Google Scholar]
- Amasuomo, T.; Amasuomo, J. Perceived Thermal Discomfort and Stress Behaviours Affecting Students’ Learning in Lecture Theatres in the Humid Tropics. Buildings 2016, 6, 18. [Google Scholar] [CrossRef]

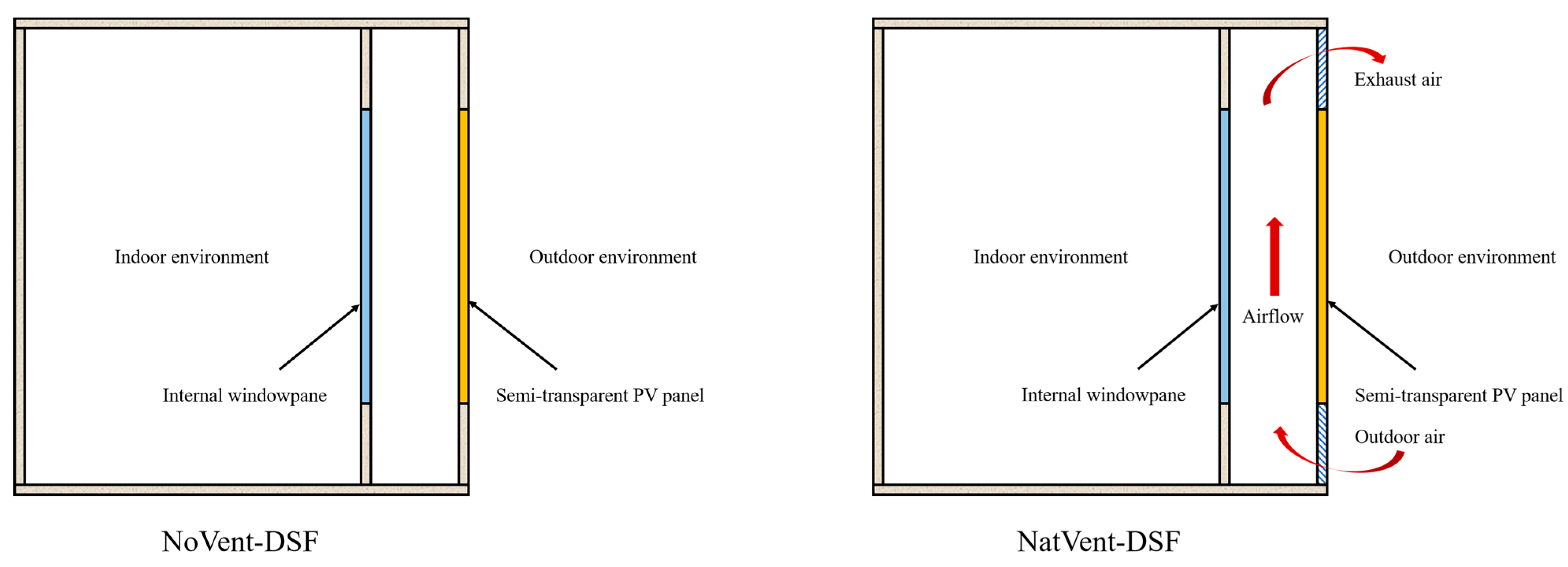


| Design Parameter | Abbreviation | Type of Parameter |
|---|---|---|
| Thermal transmittance (U-value) of internal window of the BIPV-DSF | Uin | Material-based |
| Solar heat gain coefficient (SHGC) of external window of the BIPV-DSF | SHGCout | Material-based |
| High Humidity Summer and Warm Winter Climate (Represented by Darwin) | Warm Temperate Climate (Represented by Sydney) | Cool Temperate Climate (Represented by Canberra) | |
|---|---|---|---|
| Ventilation mode | Natural ventilation (whole year) | Natural ventilation (hot months) Non ventilation (cold months) | Natural ventilation (hot months) Non ventilation (cold months) |
| Parameter | Unit | Original Value | Variation Range/Values |
|---|---|---|---|
| Uin | W/m2K | 5.68 | 5.16, 5.39, 5.53, 5.68, 5.73, 5.8, 5.87 |
| SHGCout | - | 0.624 | 0.432, 0.495, 0.557, 0.624, 0.683, 0.747, 0.811 |
| Operation Mode for Ventilation | Characteristics |
|---|---|
| NoVent-DSF |
|
| NatVent-DSF |
|
| Parameter | Value | Reference |
|---|---|---|
| Operating hours | 8 a.m.~6 p.m. | Typical setting for offices |
| Heat gain from occupant (assuming there was one person in the room) | 150 W/person | Typical value for offices |
| Heat gain from computer | 25 W/m2 | Typical value for offices |
| Heat gain from lights | 5 W/m2 | Typical value for offices |
| U-value of external wall | 0.51 W/m2K | Building Code of Australia for office buildings [48] |
| U-value of roof | 0.24 W/m2K | Building Code of Australia for office buildings [48] |
| Slab on ground | Adiabatic | Deemed as an adiabatic surface |
| Heating (reversible heat pump system) | SCoP: 3.5 Setpoint temperature: 22 °C | Previous research [29] |
| Cooling (reversible heat pump system) | SCoP: 2.5 Setpoint temperature: 26 °C | Previous research [29] |
| Parameter | Values |
|---|---|
| Visible light transmittance | 37.5% |
| Visible light reflectance (front) | 4.0% |
| Visible light reflectance (back) | 4.0% |
| Solar transmittance (front) | 33.2% |
| Solar transmittance (back) | 33.2% |
| Solar reflectance (front) | 3.5% |
| Solar reflectance (back) | 3.5% |
| U-value | 5.59 W/m2K |
| Emissivity | 0.89 |
| PV efficiency (under STC) | 6.64% |
| Temperature coefficient of power | −0.3%/°C |
| f1(x), Hours | min(f1), Hours | f2(x), kWh/m2 | min(f2), kWh/m2 | d(x)min | Uin, W/m2K | SHGCout | |
|---|---|---|---|---|---|---|---|
| North | 360 | 350 | 100.37 | 87.9 | 15.99 | 5.16 | 0.81 |
| South | 502 | 502 | 103.54 | 96.24 | 152.8 | 5.16 | 0.81 |
| East | 370 | 369 | 108.31 | 90.78 | 28.58 | 5.53 | 0.81 |
| West | 365 | 365 | 103.5 | 89.95 | 21.64 | 5.16 | 0.81 |
| f1(x), Hours | min(f1), Hours | f2(x), kWh/m2 | min(f2), kWh/m2 | d(x)min | Uin, W/m2K | SHGCout | |
|---|---|---|---|---|---|---|---|
| North | 4002 | 4002 | 46.51 | 28.92 | 3652.23 | 5.87 | 0.81 |
| South | 4281 | 4281 | 51.41 | 46.78 | 3931.17 | 5.16 | 0.81 |
| East | 4015 | 4015 | 47.11 | 34.72 | 3665.23 | 5.87 | 0.81 |
| West | 3809 | 3809 | 49.9 | 36.41 | 3459.21 | 5.87 | 0.81 |
| f1(x), Hours | min(f1), Hours | f2(x), kWh/m2 | min(f2), kWh/m2 | d(x)min | Uin, W/m2K | SHGCout | |
|---|---|---|---|---|---|---|---|
| North | 5277 | 5277 | 51.71 | 38.65 | 4927.13 | 5.87 | 0.81 |
| South | 5855 | 5855 | 64.47 | 62.88 | 5505.05 | 5.16 | 0.81 |
| East | 5539 | 5539 | 56.59 | 47.27 | 5189.09 | 5.87 | 0.81 |
| West | 5127 | 5127 | 55.04 | 46.27 | 4777.11 | 5.87 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Fiorito, F.; Sproul, A.; Prasad, D. Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia. Buildings 2023, 13, 1096. https://doi.org/10.3390/buildings13041096
Yang S, Fiorito F, Sproul A, Prasad D. Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia. Buildings. 2023; 13(4):1096. https://doi.org/10.3390/buildings13041096
Chicago/Turabian StyleYang, Siliang, Francesco Fiorito, Alistair Sproul, and Deo Prasad. 2023. "Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia" Buildings 13, no. 4: 1096. https://doi.org/10.3390/buildings13041096
APA StyleYang, S., Fiorito, F., Sproul, A., & Prasad, D. (2023). Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia. Buildings, 13(4), 1096. https://doi.org/10.3390/buildings13041096