Functionality Loss and Recovery Time Models for Structural Elements, Non-Structural Components, and Delay Times to Estimate the Seismic Resilience of Mexican School Buildings
Abstract
1. Introduction
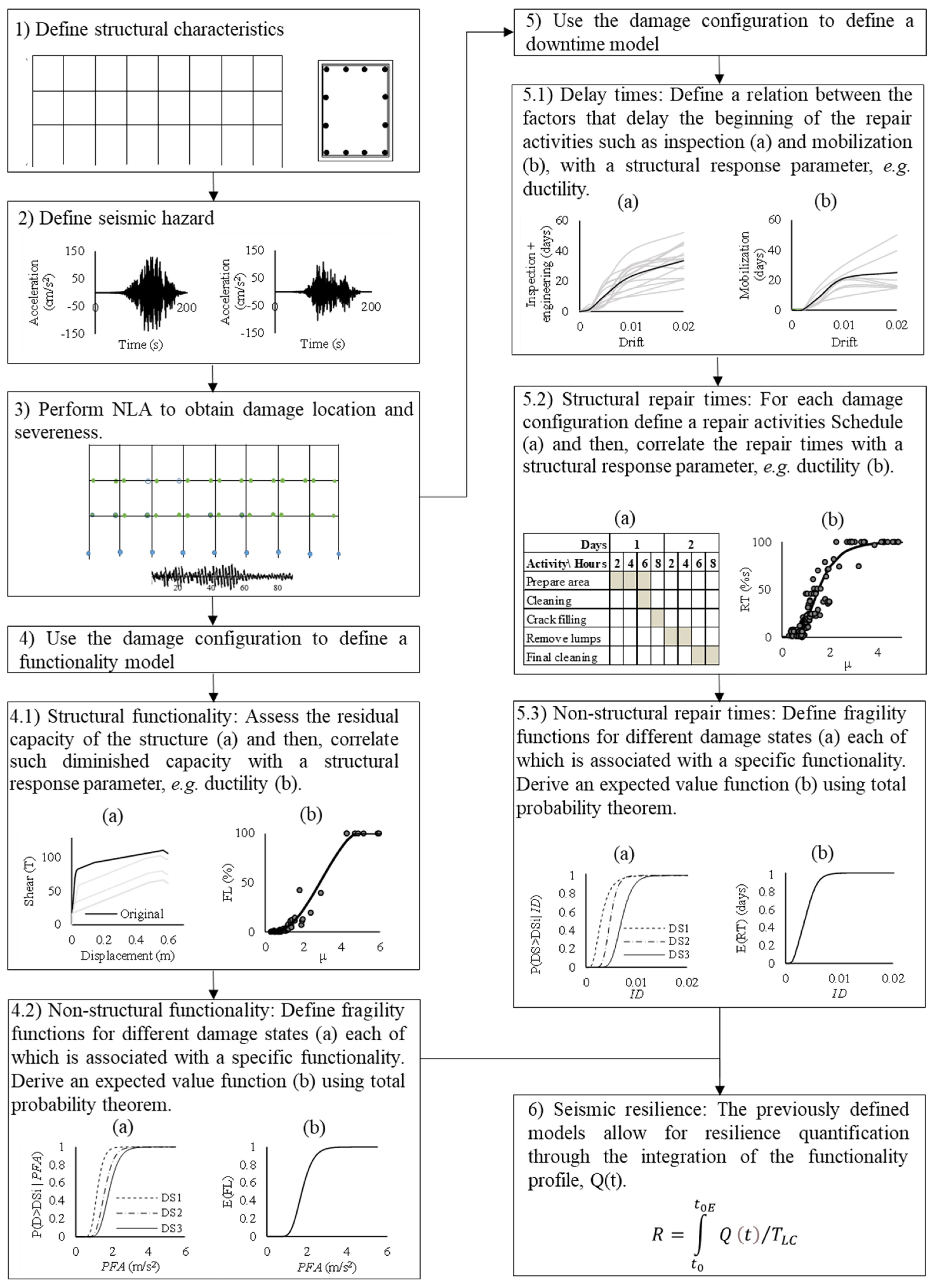
2. Methodology
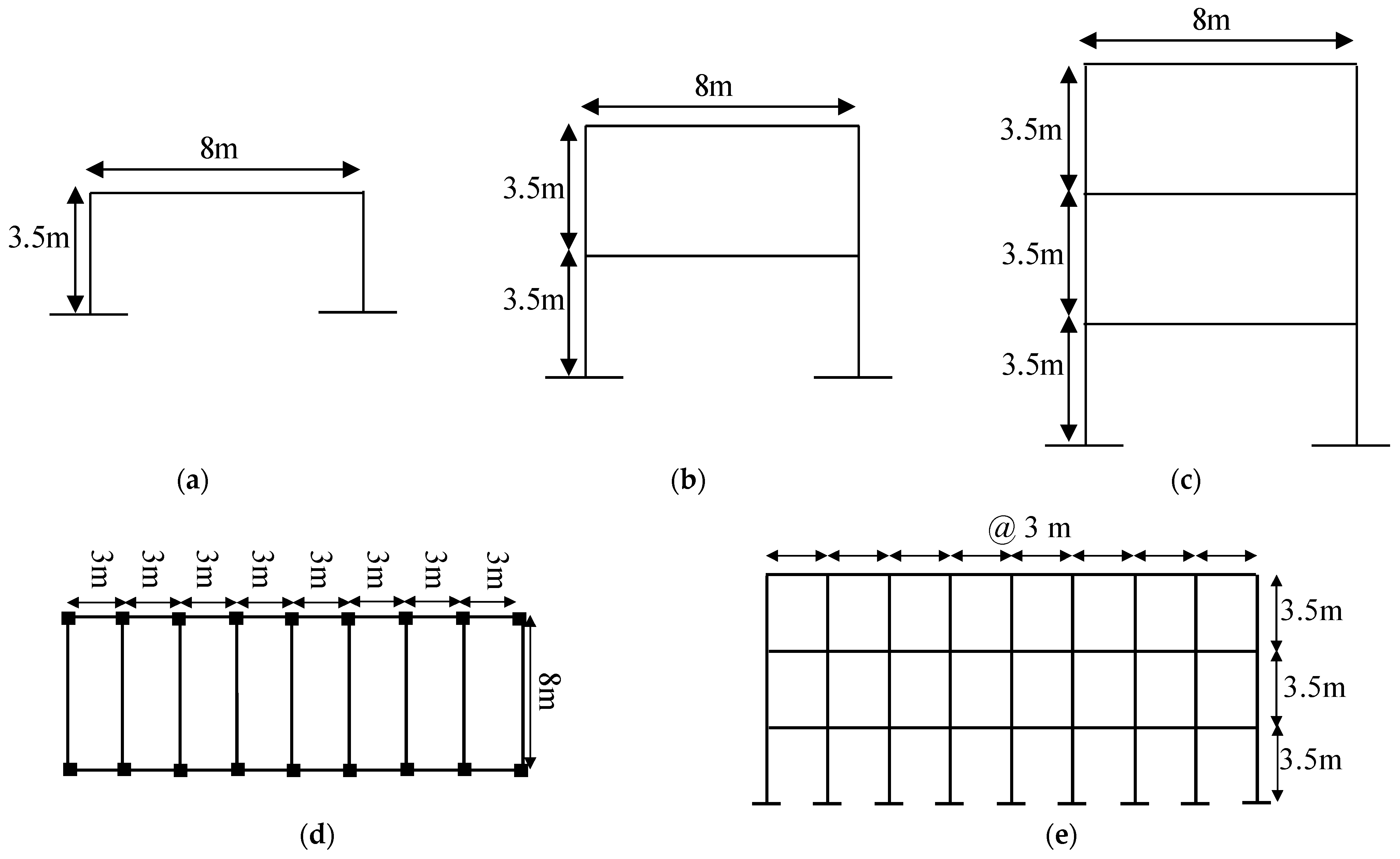
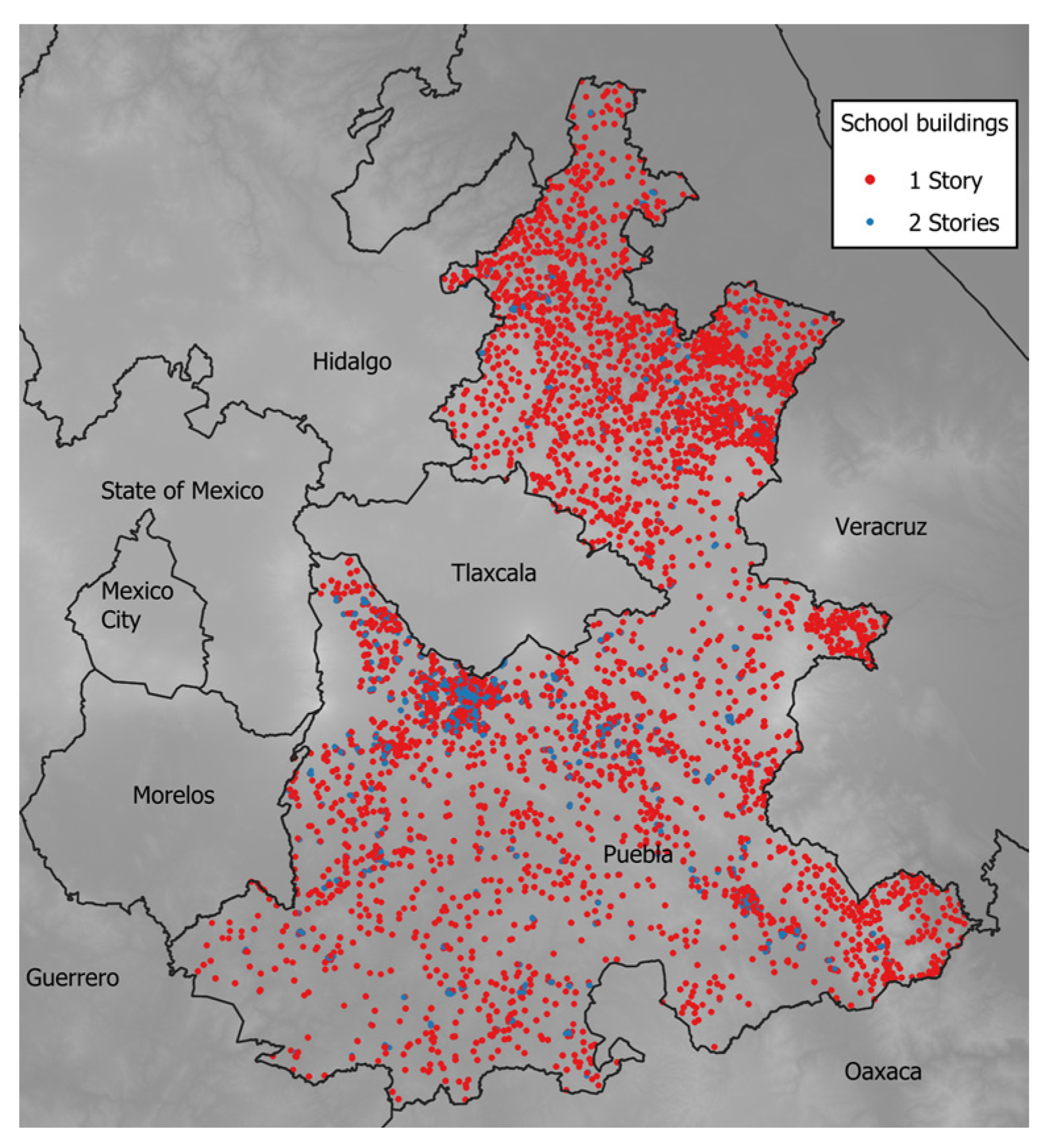
2.1. Structural Characteristics
2.2. Seismic Hazard
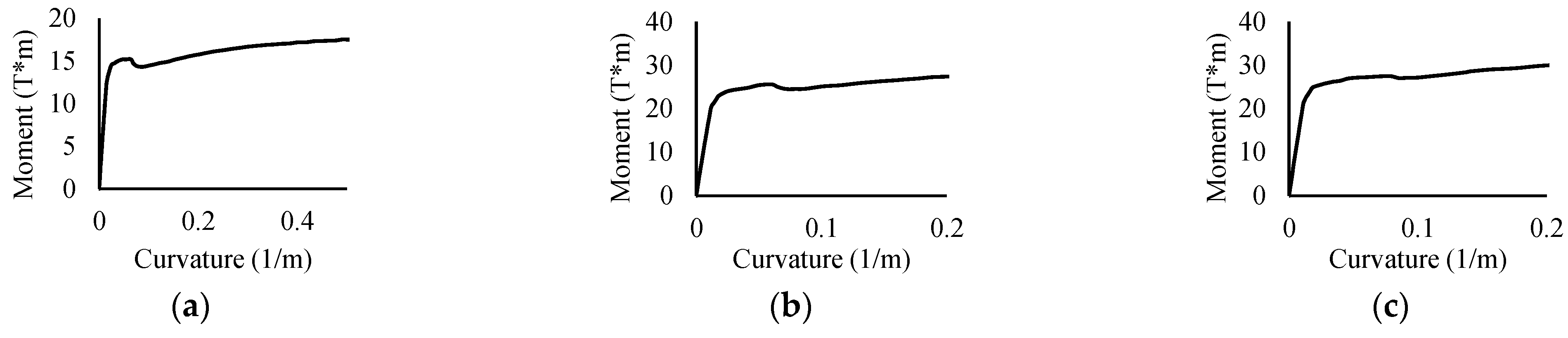
2.3. Structural Analysis
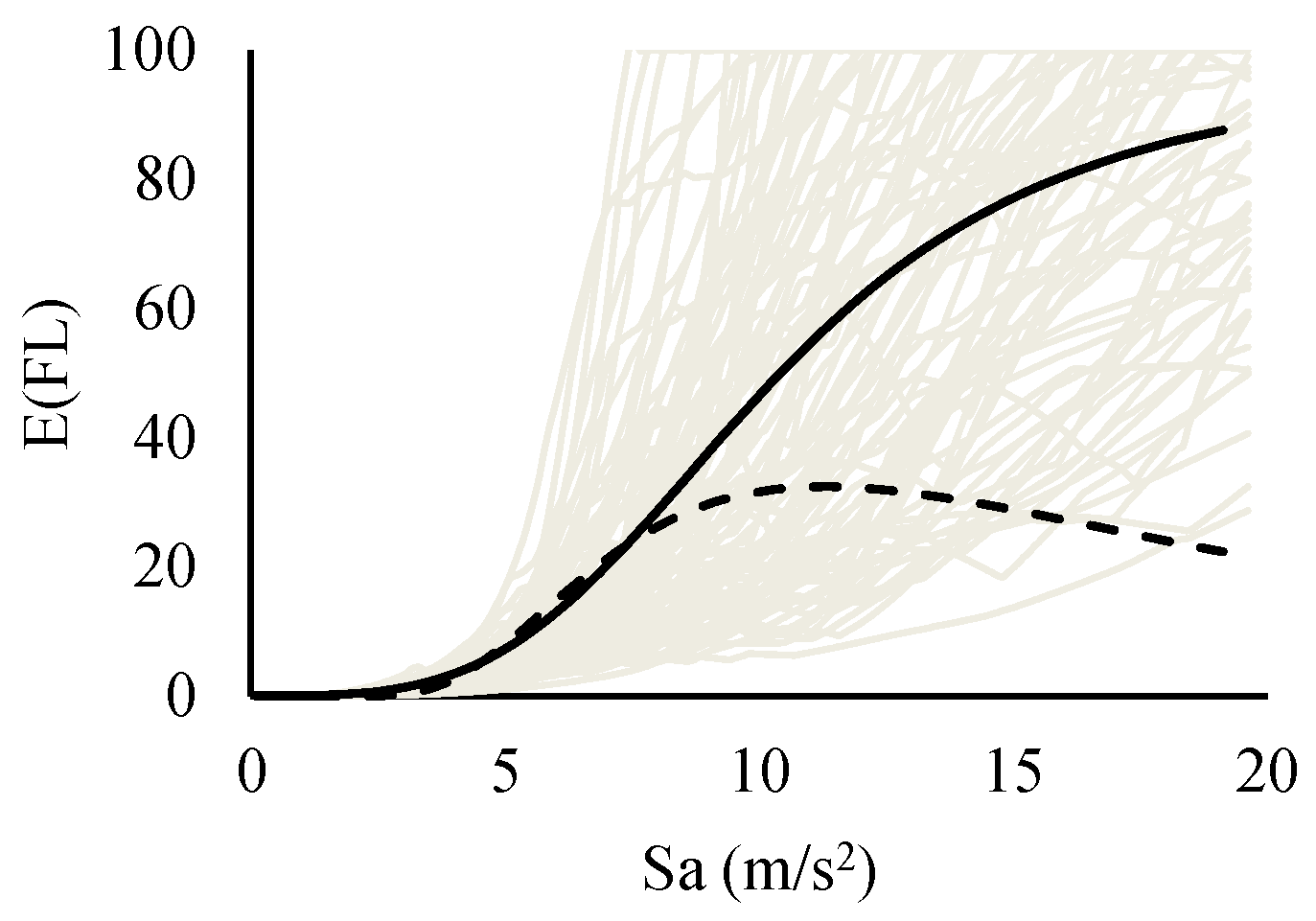
2.4. Functionality Loss
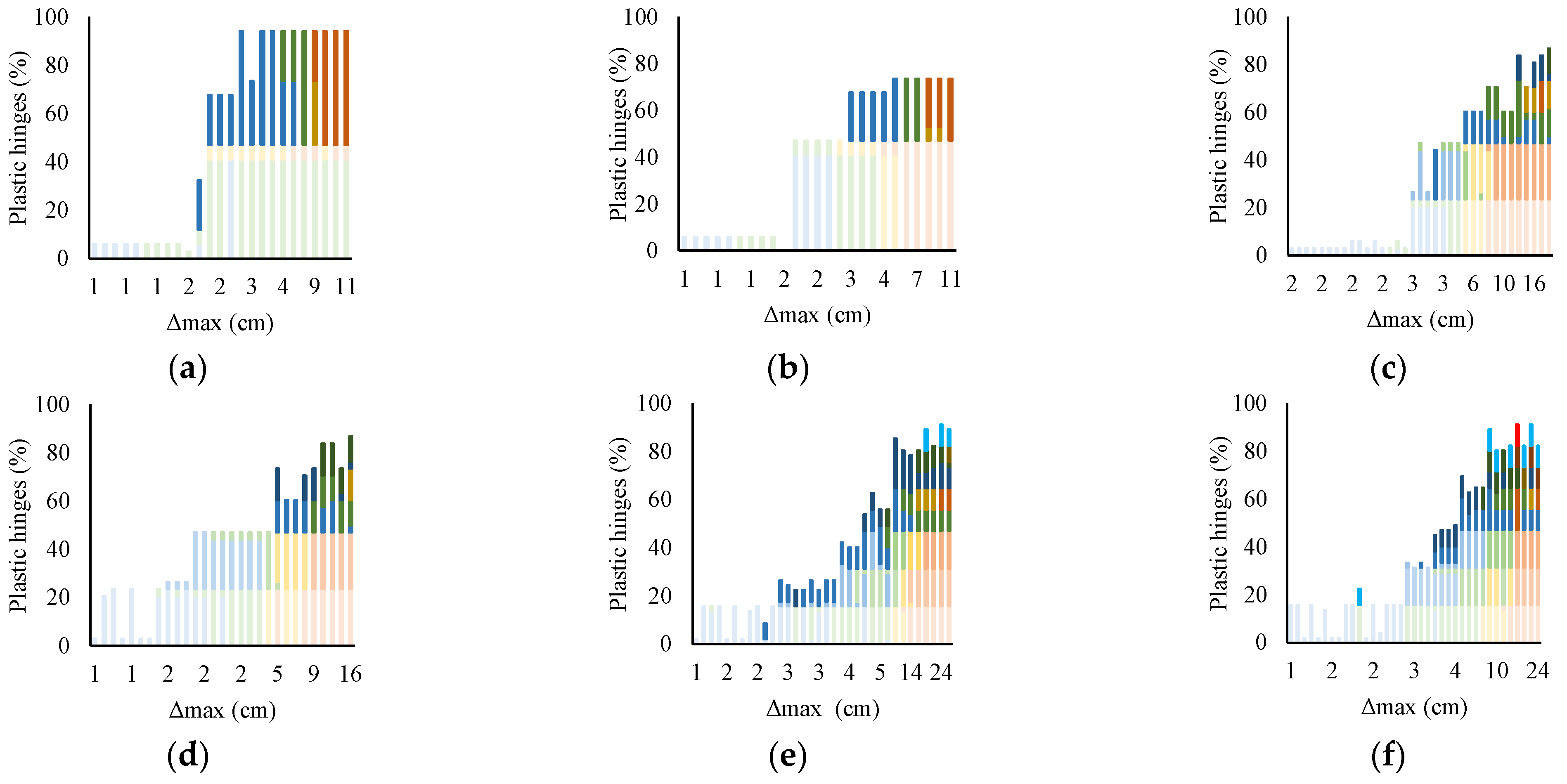
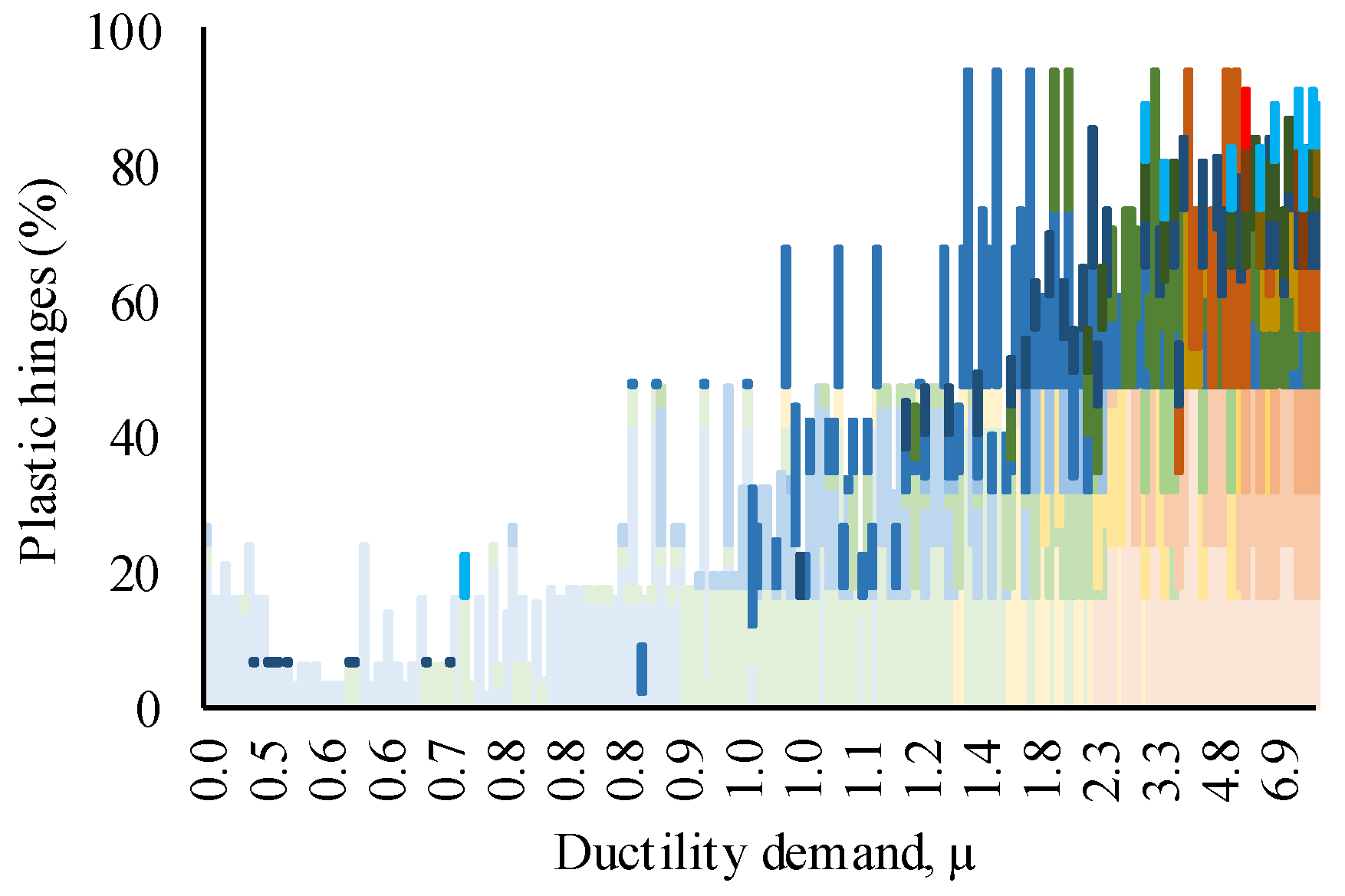
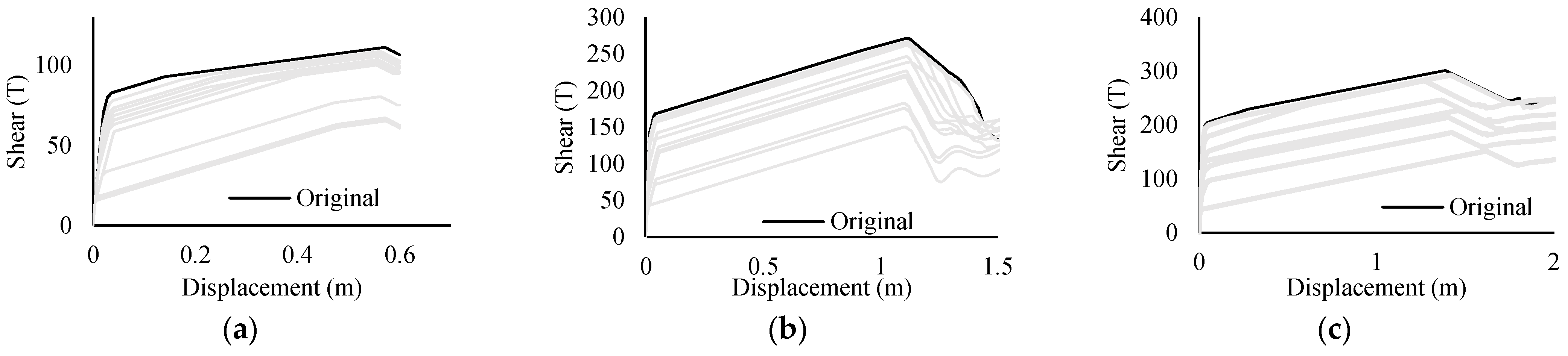
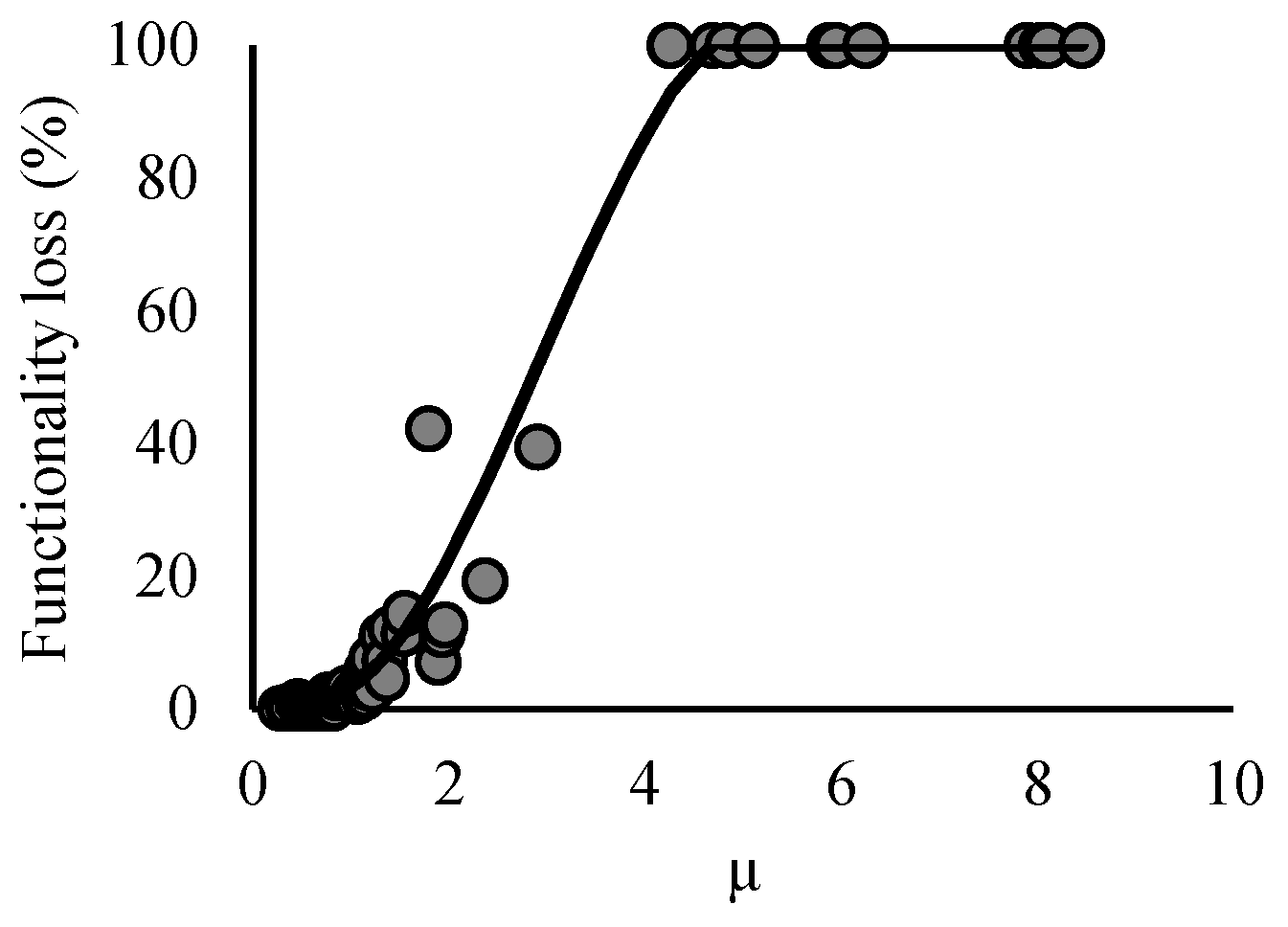
2.4.1. Structural Elements
2.4.2. Non-Structural Elements and Contents
- Define the relevant non-structural elements and contents.
- Define models that correlate functionality loss and damage state.
- Generate fragility curves for all the damage states in each element.
- Obtain E(FL) curves from the fragility functions.
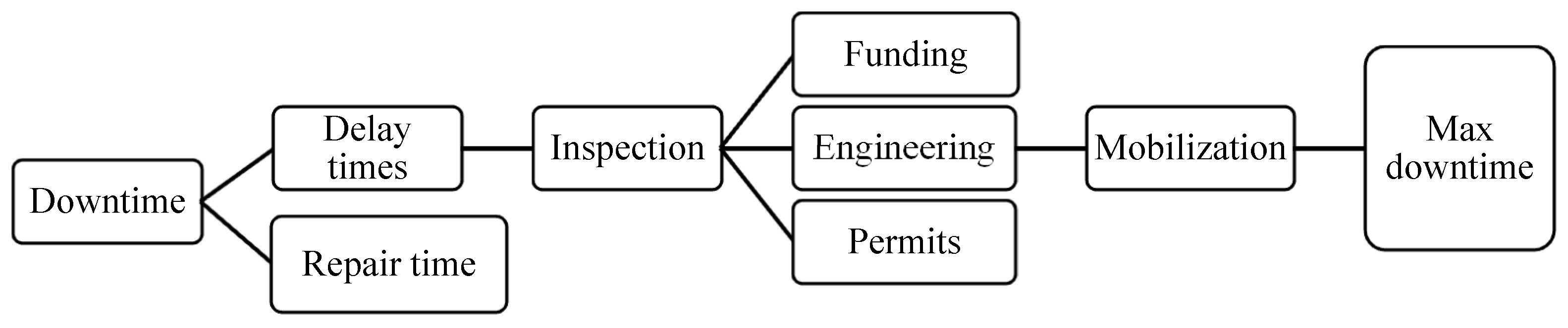
2.5. Downtime
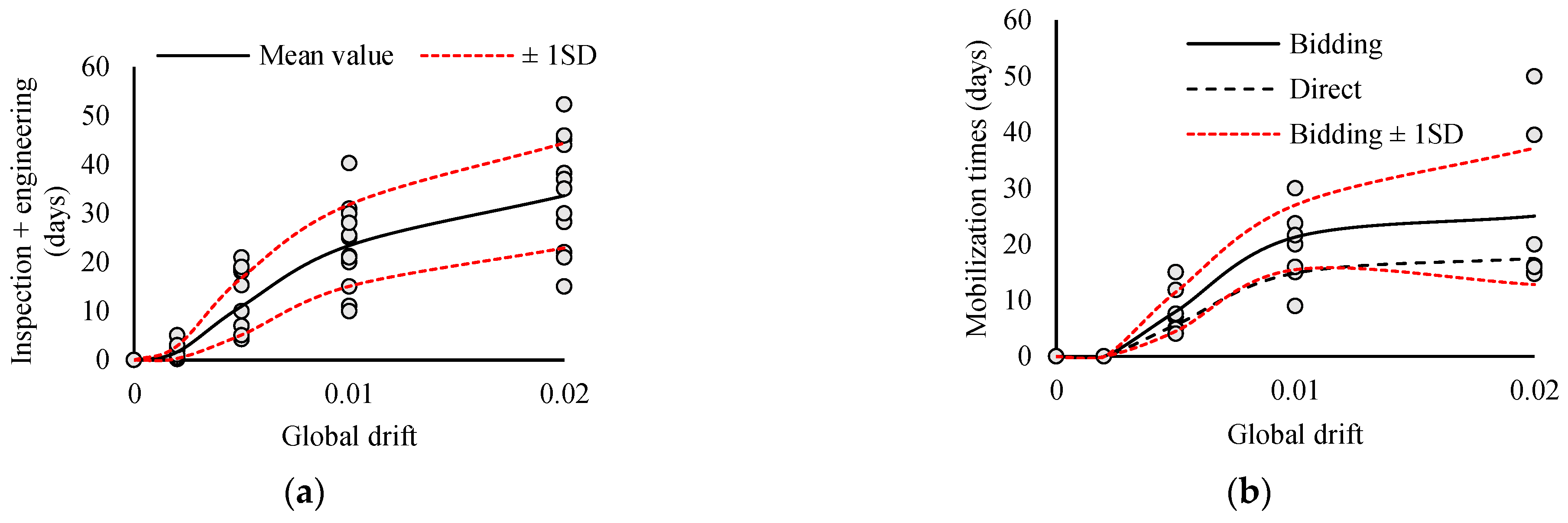
2.5.1. Delay Time Factors
- Visual inspection: after the occurrence of an earthquake, structures require an inspection, which may be superficial in the case of light or no damage or deep in the case of severe damage.
- Engineering: if the structure is moderately or severely damaged, it is necessary to carry out an engineering process to ensure that safety and functionality are recovered by means of the repairing actions.
- Permits: Permit approval from the local building jurisdiction would likely be required for buildings that exhibit structural damage. Repairs of certain non-structural components may also require permits, but these may usually be obtained “over the counter” and do not account for significant delays.
- Financing: Significant delays may occur due to the inability to obtain financing to fund the necessary repairs. Financing may be procured through loans or insurance payments. Federal or other government grants should not be considered a viable financing option due to the uncertainty in securing these funds.
- Contractor mobilization: there are several factors that are critical contributors to the overall time required to mobilize a contractor, including a shortage of contractors, the severity of damage, bidding, essential facilities, and building height.
2.5.2. Repair Times in Structural Elements
2.5.3. Repair Times in Non-Structural Elements
- Define the relevant non-structural elements and contents.
- Define models that correlate repair time and damage state.
- Generate fragility curves for all the damage states in each element.
- Create E(RT) curves.
2.6. Seismic Resilience
3. Results
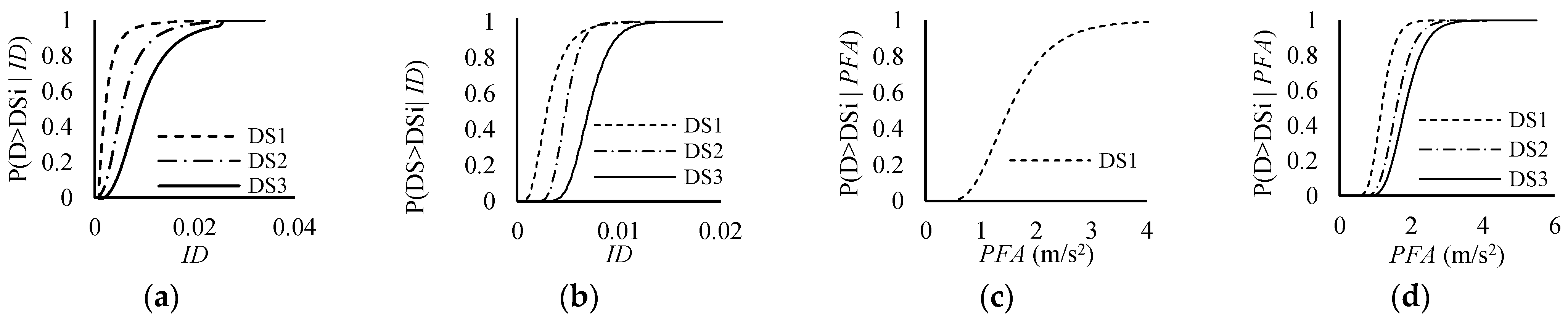
3.1. Expected Functionality Loss Curves
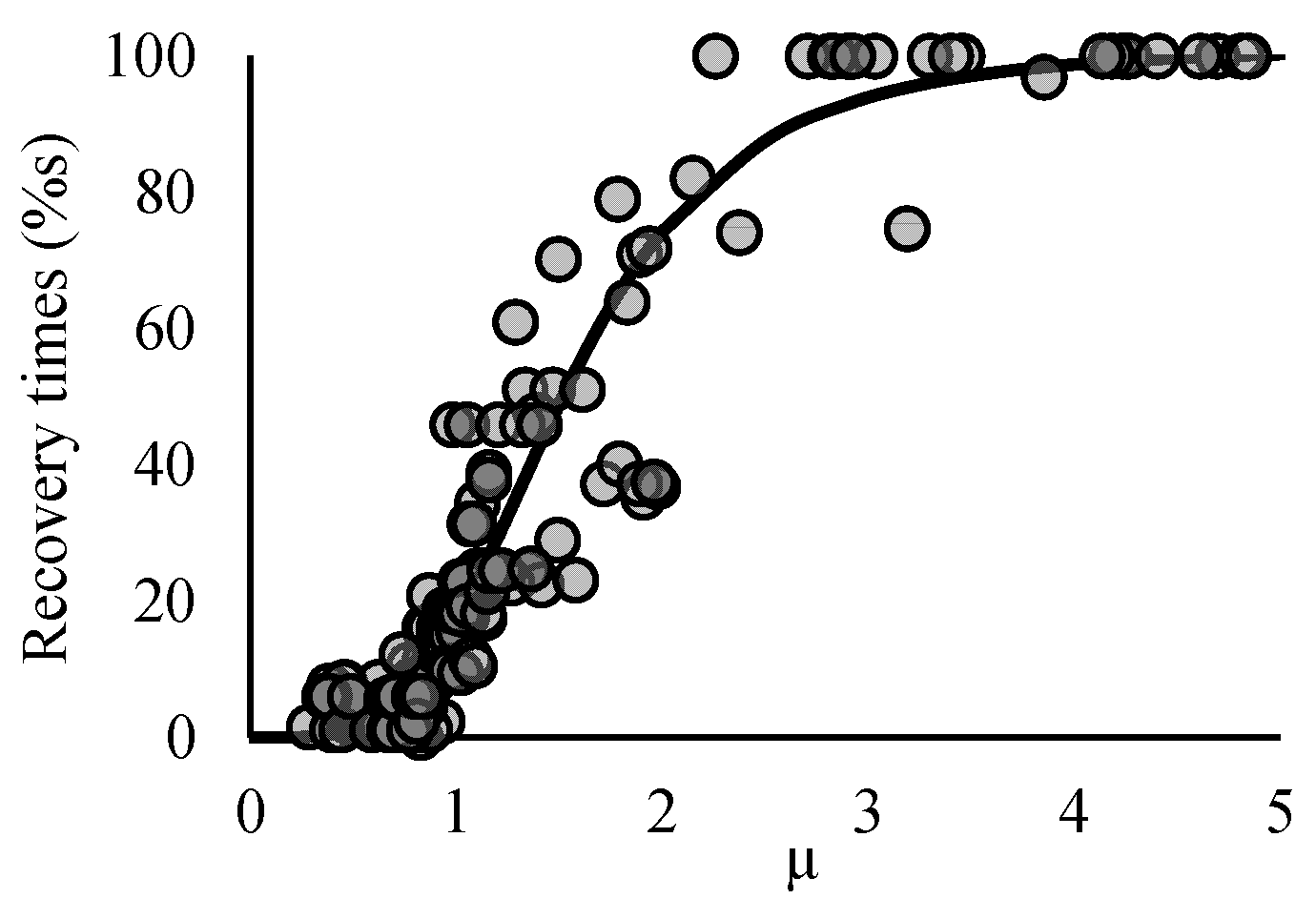
3.2. Downtimes: Delay Time Estimation
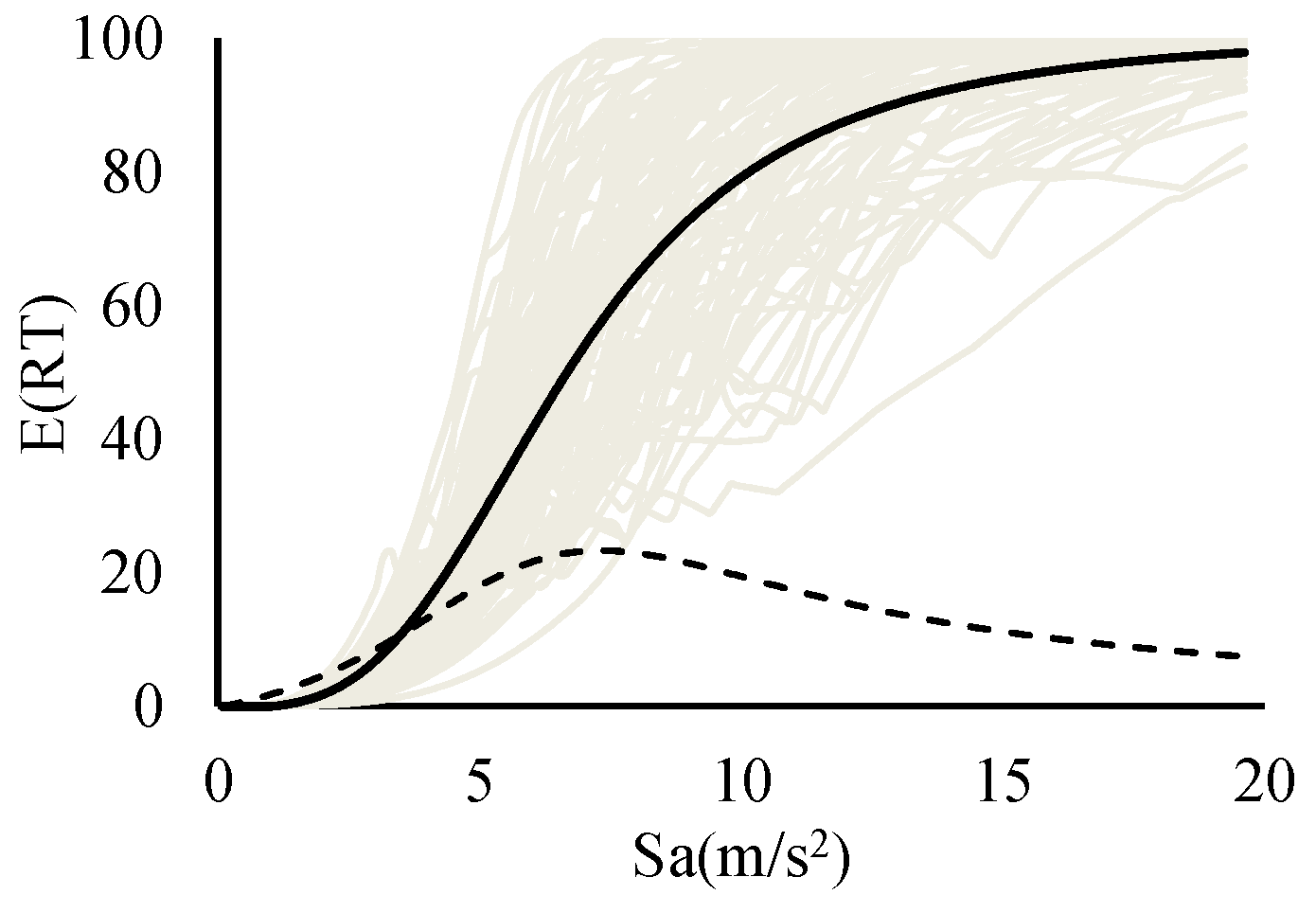
3.3. Expected Repair Time Curves
3.4. Non-Structural Elements
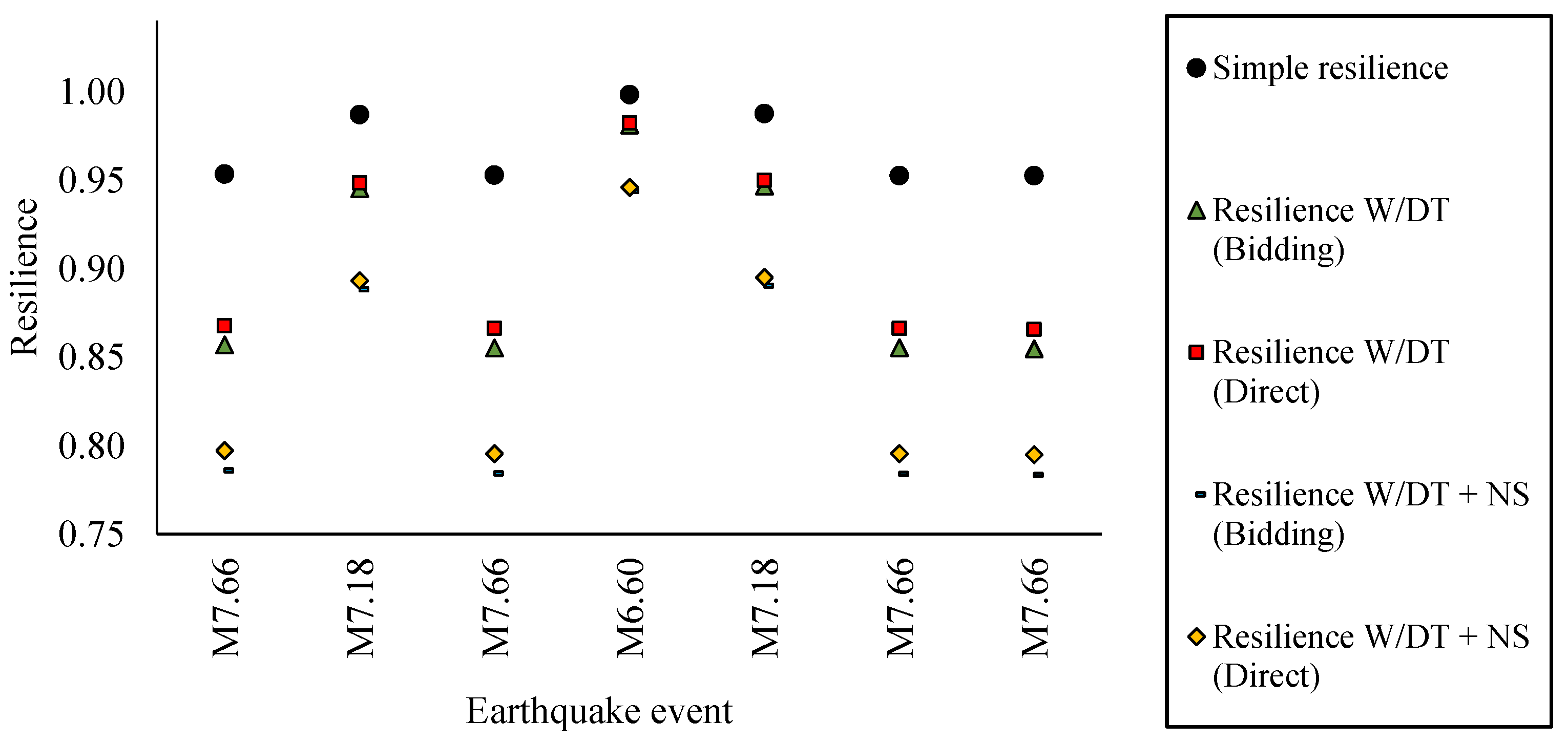
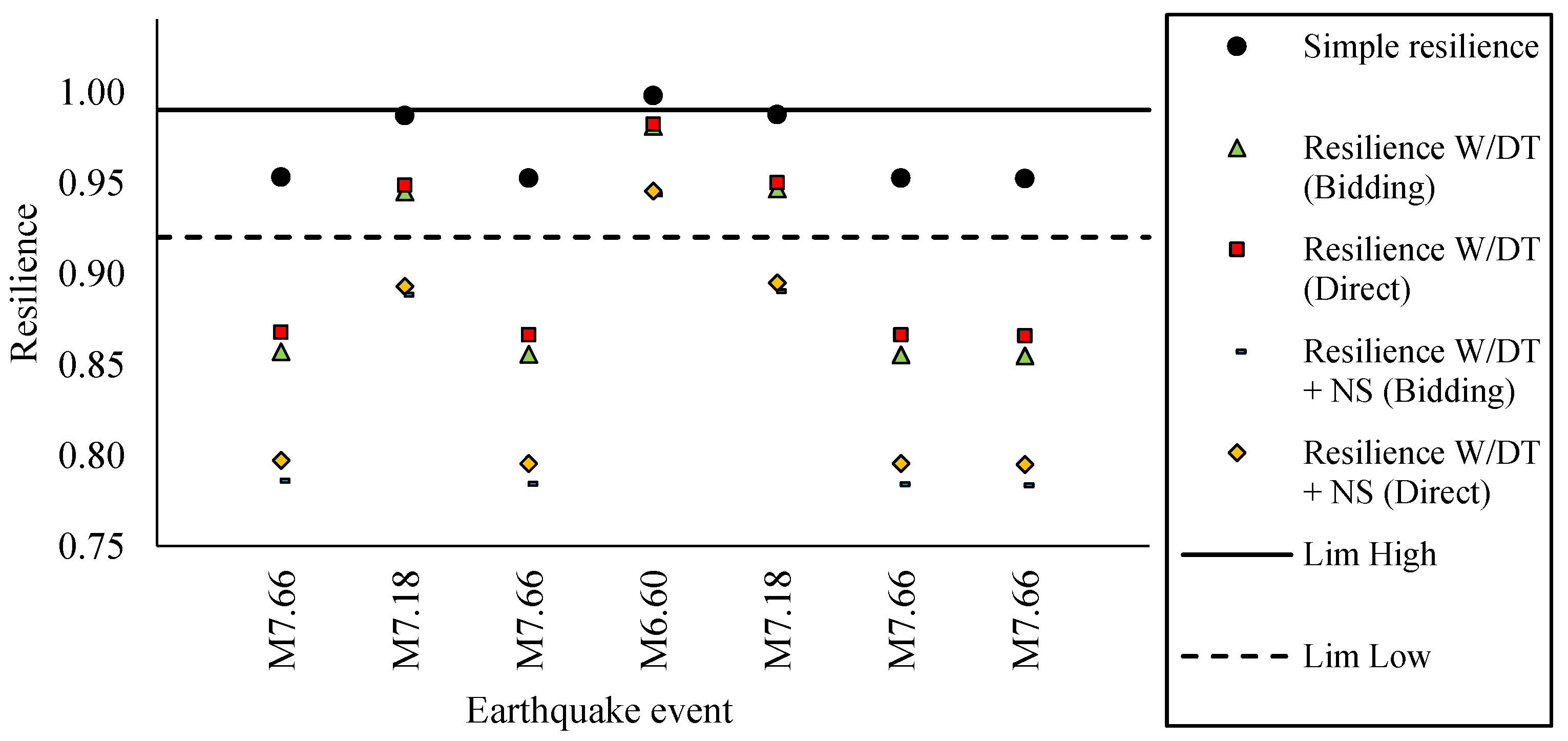
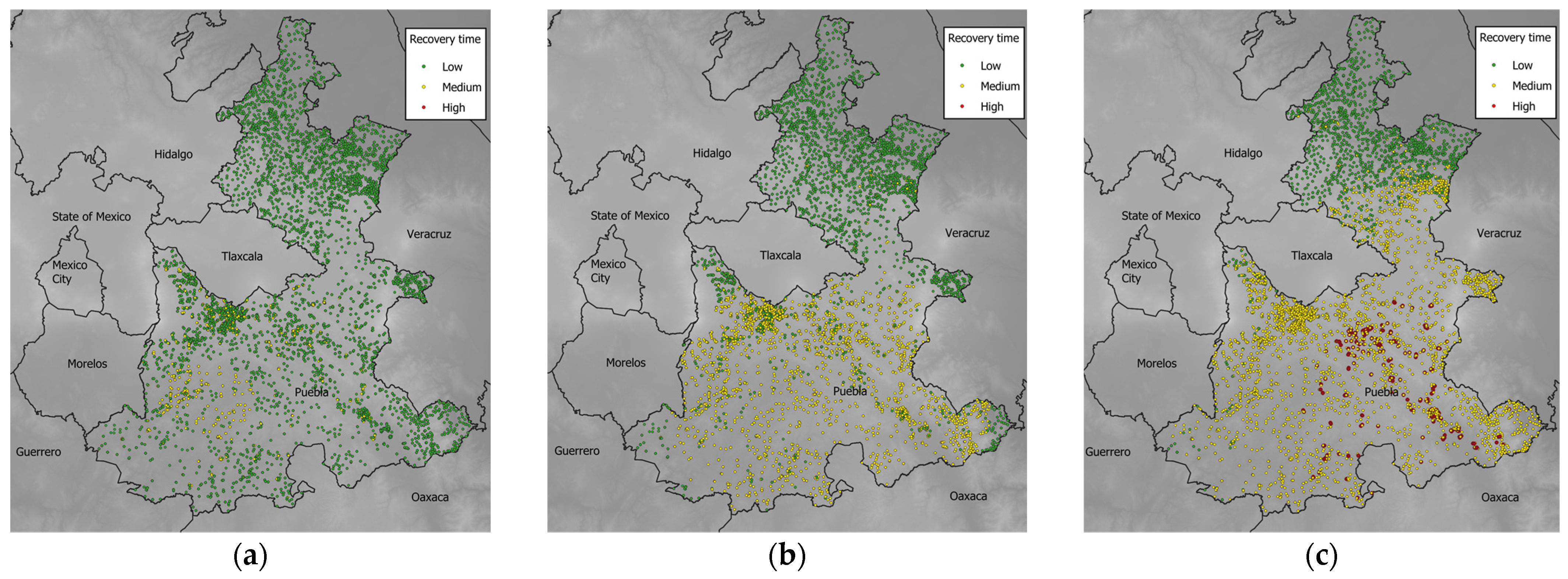
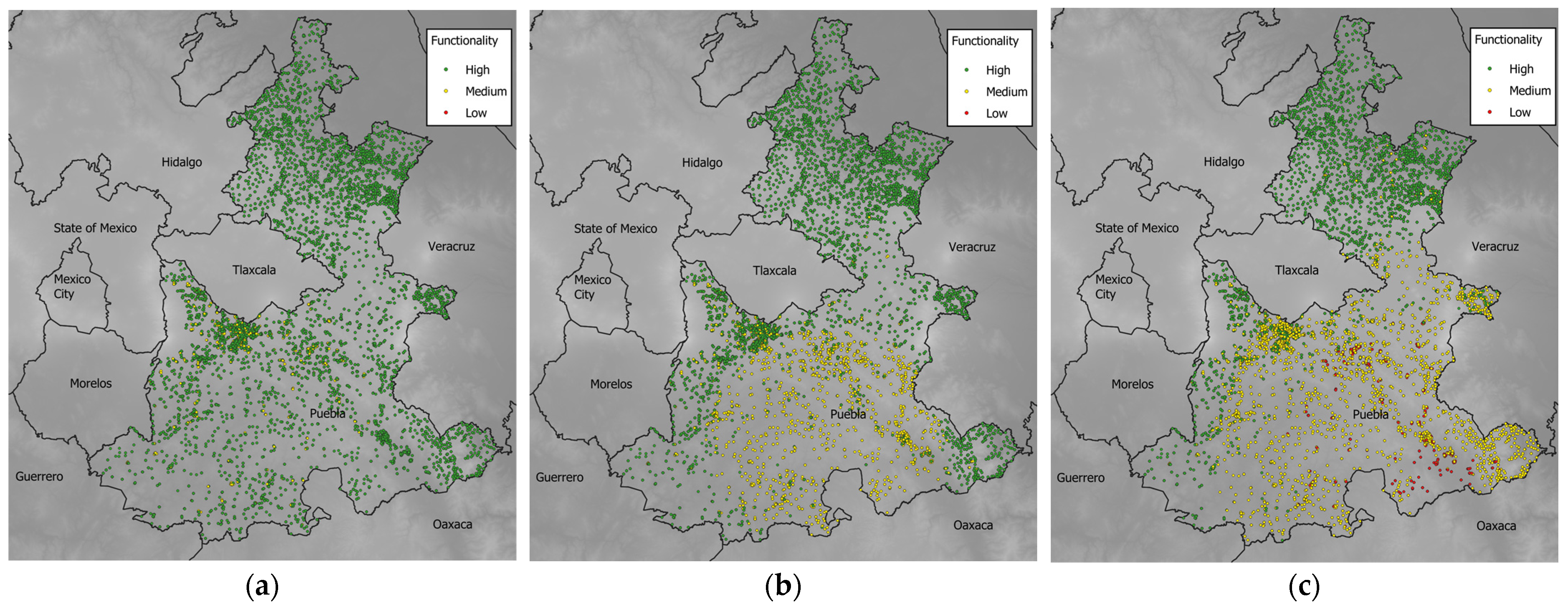
3.5. Seismic Resilience
4. Discussion
4.1. Application of the Expected Times and Functionality Curves
4.2. Acceptable Resilience Values
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ortiz, D.; Reinoso, E. Tiempo de interrupción de negocios en la ciudad de México por daños directos y efectos indirectos en edificios a causa del sismo del 19s de 2017. Rev. De Ing. Sísmica 2020, 104, 1–31. (In Spanish) [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.; Eguchi, R.; Lee, G.; O’Rourke, T.; Reinhorn, A.; Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Bruneau, M.; Reinhorn, A. Exploring the concept of seismic resilience for acute care facilities. Earthq. Spectra 2007, 23, 41–62. [Google Scholar] [CrossRef]
- Cimellaro, G.; Reinhorn, A.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Anwar, G.; Dong, Y.; Zhai, C. Performance-based probabilistic framework for seismic risk, resilience, and sustainability assessment of reinforced concrete structures. Adv. Struct. Eng. 2019, 23, 1454–1472. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Titi, A. Seismic resilience of concrete structures under corrosion. Earthq. Eng. Struct. Dyn. 2015, 44, 2445–2466. [Google Scholar] [CrossRef]
- González, C.; Niño, M.; Jaimes, M. Event-based assessment of seismic resilience in Mexican school buildings. Bull. Earhtq. Eng. 2020, 18, 6313–6336. [Google Scholar] [CrossRef]
- Rojahn, C.; Johnson, L.; O’Rourke, T.; Cedillos, V.; McAllister, T.; McCabe, S. Increasing Community Resilience Through Improved Lifeline Infrastructure Performance. Bridge. 2019. Available online: https://www.nae.edu/212179/Increasing-Community-Resilience-through-Improved-Lifeline-Infrastructure-Performance (accessed on 28 January 2023).
- Feng, K.; Wang, N.; Li, Q.; Lin, P. Measuring and enhancing resilience of building portfolios considering the functional interdepence among community sectors. Struct. Saf. 2017, 66, 118–126. [Google Scholar] [CrossRef]
- Fontana, C.; Cianci, E.; Moscatelli, M. Assessing Seismic Resilience of School Educational Sector. An attempt to establish the initial conditions in Calabria Region, Southern Italy. Int. J. Disaster Risk Reduct. 2020, 51, 101936. [Google Scholar] [CrossRef]
- Ruggieri, S.; Perrone, D.; Leone, M.; Uva, G.; Aiello, M.A. A prioritization RVS methodology for the seismic risk assessment of RC school buildings. Int. J. Disaster Risk Reduct. 2020, 51, 101807. [Google Scholar] [CrossRef]
- Ruggieri, S.; Porco, F.; Uva, G.; Vamvatsikos, D. Two frugal options to assess class fragility and seismic safety for low-rise reinforced concrete school buildings in Southern Italy. Bull. Earthq. Eng. 2021, 19, 1415–1439. [Google Scholar] [CrossRef]
- Samadian, D.; Ghafoy-Ashtiany, M.; Naderpour, H.; Eghbali, M. Seismic resilience evaluation based on vulnerability curves for existing and retrofitted typical RC school buildings. Soil Dyn. Earthq. Eng. 2019, 127, 105844. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Ayala, G. Análisis de la resiliencia sísmica de edificios. Ing. Sísmica 2022, 107, 47–73. [Google Scholar] [CrossRef]
- Almufti, I.; Willford, M. Resilience-based Earthquake Design Initiative fot the Next Generation of Buildings; Arup: San Francisco, CA, USA, 2013. [Google Scholar] [CrossRef]
- Mieler, M.; Stojadinovic, B.; Budnitz, R.; Comerio, M.; Mahin, S. A framework for linking community-resilience goals to specific performance targets for the built environment. Earthq. Spectra 2015, 31, 1267–1283. [Google Scholar] [CrossRef]
- Hall, D.; Giglio, N. Architectural Graphic Standards, 12th ed.; American Institute of Architects: Washington, DC, USA, 2016. [Google Scholar]
- Yang, T.Y.; Tung, D.P.; Li, Y. Equivalent Energy Design Procedure for Earthquake Resilient Fused Structures. Earthq. Spectra 2018, 34, 795–815. [Google Scholar] [CrossRef]
- Tena-Colunga, A.; Nangullasmú-Hernández, H. Resilient seismic design of reinforced concrete framed buildings with metallic fuses including soil-structure interaction effects. Soil Dyn. Earthq. Eng. 2023, 164, 137. [Google Scholar] [CrossRef]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Engng. Struct. Dyn. 2005, 34, 1489–1511. [Google Scholar] [CrossRef]
- Tsionis, G. Seismic Resilience: Concept, Metrics and Integration with Other Hazards; Joint Research Center: Luxembourg, 2014. [Google Scholar]
- Taghavi, S.; Miranda, E. Response Assessment of Nonstructural Building Elements, 1st ed.; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2003; pp. 57–66. [Google Scholar]
- Ghorawat, S. Rapid Loss Modeling of Death and Downtime Caused by Earthquake Induced Damage to Structures. Master’s Thesis, Texas A&M University, College Station, TX, USA, May 2011. [Google Scholar]
- Comerio, M.C. Estimating Downtime in Loss Modeling. Earthq. Spectra 2006, 22, 349–365. [Google Scholar] [CrossRef]
- Alcocer, S.; Bautista, R.; Martínez, Y.; Valencia, G. Desarrollo de capacidades nacionales para aumentar la resiliencia de edificios de concreto y mampostería con un enfoque de diseño por desempeño. In Revisión de la Literatura y del Estado del Arte de Metodologías de Evaluación Post-Sísmica, 1st ed.; Instituto de Ingeniería UNAM: Ciudad de México, México, 2019; pp. 3–58. [Google Scholar]
- Alcocer, S.; Muria, D.; Abarca, J.; Bautista, R.; Bogoya, G.; Cruz, V.; Martínez, Y.; Moctezuma, B.; Ramírez, D.; Valencia, G. Guía técnica para la Rehabilitación Sísmica de Edificios Escolares de la Ciudad de México, 1st ed.; Instituto de Ingeniería UNAM: Ciudad de México, México, 2019; pp. 55–169. [Google Scholar]
- Alcocer, S.; Muria, D.; Fernández, L.; Ordaz, M.; Arce, J. Observed damage in public school buildings during the 2017 Mexico earthquakes. Earthq. Spectra 2020, 36, 110–129. [Google Scholar] [CrossRef]
- McKenna, F.; Mazzooni, S.; Scott, M.; Fenves, G. Open System for Earthquake Engineering Simulation Version 3.2.0.; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2016. [Google Scholar]
- Newmark, N.M.; Hall, W.J. Seismic Design Criteria for Nuclear Reactor Facilities. Rep. No. 46; Building Practices for Disaster Mitigation National Bureau of Standards: Washington, DC, USA, 1973; pp. 209–236. [Google Scholar]
- Hidalgo, P.A.; Arias, A. New Chilean code for earthquake resistant design of buildings. In Proceedings of the 4th US National Conference on Earthquake Engineering, Palm Springs, CA, USA, 20–24 May 1990; Volume 2, pp. 927–936. [Google Scholar]
- Tanik, B.; Inel, M.; Ozer, E. Effect of Soil-Structure interaction on seismic behavior of mid- and low-rise buildings. ASCE Int. J. Geomech. 2021, 21, 04021009. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, A. Incremental Dynamic Analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Forte, A.; Santini, S.; Lavorato, D.; Fiorentino, G. Influence of material knowledge on the assessment of shear strength characteristic value on existing RC beams. In Proceedings of the 12th fib International PhD Symposium in Civil Engineering, Prague, Czech Republic, 29–31 August 2018. [Google Scholar]
- Gobierno Ciudad de México. Normas para la Rehabilitación Sísmica de Edificios de Concreto Dañados por el Sismo del 19 de Septiembre de 2017; Gaceta Oficial de la Ciudad de México: Ciudad de México, México, 2017; pp. 6–17. [Google Scholar]
- FEMA-P-58. Seismic Performance Assessment of Buildings, 1 Methodology, 2nd ed.; Federal Emergency Management Agency: Redwood City, CA, USA, 2018; pp. 3.1–3.38. [Google Scholar]
- Baggio, C.; Bernardini, A.; Colozza, R.; Corazza, L.; Della Bella, M.; Di Paaquele, G.; Dolce, M.; Orsini, G.; Papa, F.; Zuccaro, G. Field Manual for Post-Earthquake Damage and Safety Assessment and Short-Term Countermeasures; EUR 22868 EN. JRC37914; Office for Official Publications of the European Communities: Luxembourg, 2007. [Google Scholar]
- INIFED. Estrategias y Mecanismos de Coordinación para la Evaluación y Validación de Daños; SEP-INIFED: Ciudad de México, México, 2017. [Google Scholar]
- Noyola, V.; Soca, J.; Aguilera, M.; Martínez, O. Infraestructura, Mobiliario y Materiales de Apoyo Educativo en las Escuelas Primarias ECEA 2014, 1st ed.; INEE: Ciudad de México, México, 2016; pp. 21–82. [Google Scholar]
- FEMA-P-58-2. Seismic Performance Assessment of Buildings, 2 Implementation Guide, 2nd ed.; Federal Emergency Management Agency: Redwood City, CA, USA, 2018; pp. 2.11–2.15. [Google Scholar]
- Jaimes, M.; Candia, G. Seismic risk of sliding ground-mounted rigid equipment. Eng. Struct. 2020, 204, 110066. [Google Scholar] [CrossRef]
- Jaimes, M.; Niño, M. Cost-Benefit analysis to assess seismic mitigation options in Mexican public-school buildings. Bull. Earthq. Eng. 2017, 15, 3919–3942. [Google Scholar] [CrossRef]
- Cardona, O.; Ordaz, M.; Reinoso, E.; Yamín, L.B.; Barbat, A.H. CAPRA- Comprehensive approach to probabilistic risk assessment: International initiative for risk management effectiveness. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisabon, Portugal, 24–28 September 2012. [Google Scholar]
- González, C.; Niño, M.; Jaimes, M. Seismic resilience estimation in public school buildings. In Proceedings of the XXI National Congress on Structural Engineering, Campeche, México, 19–21 May 2018. [Google Scholar]

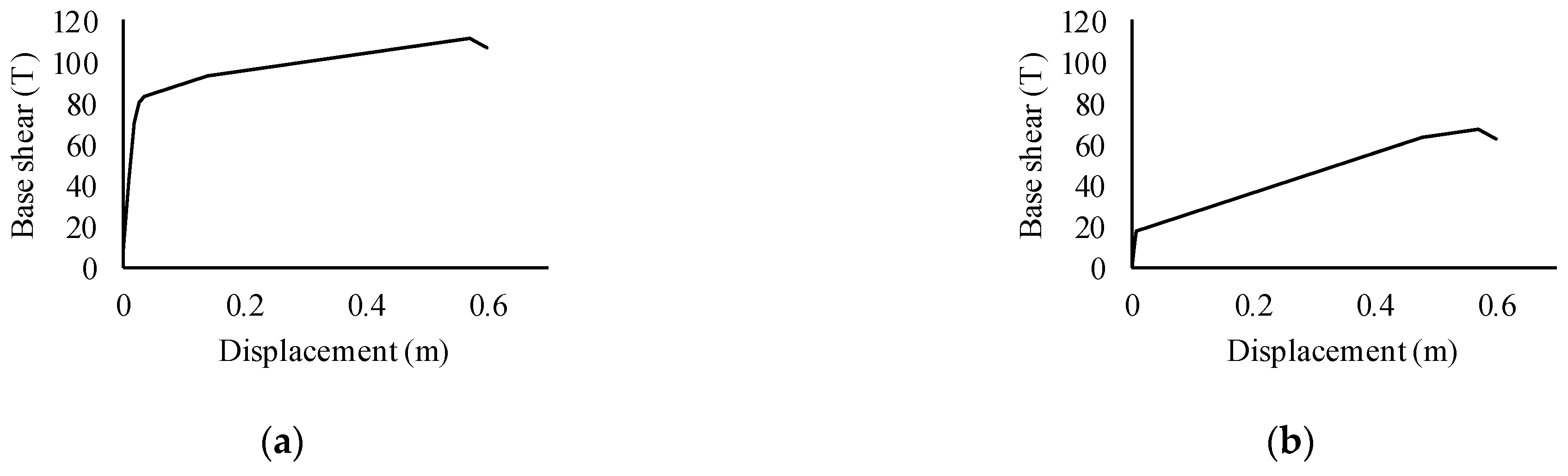


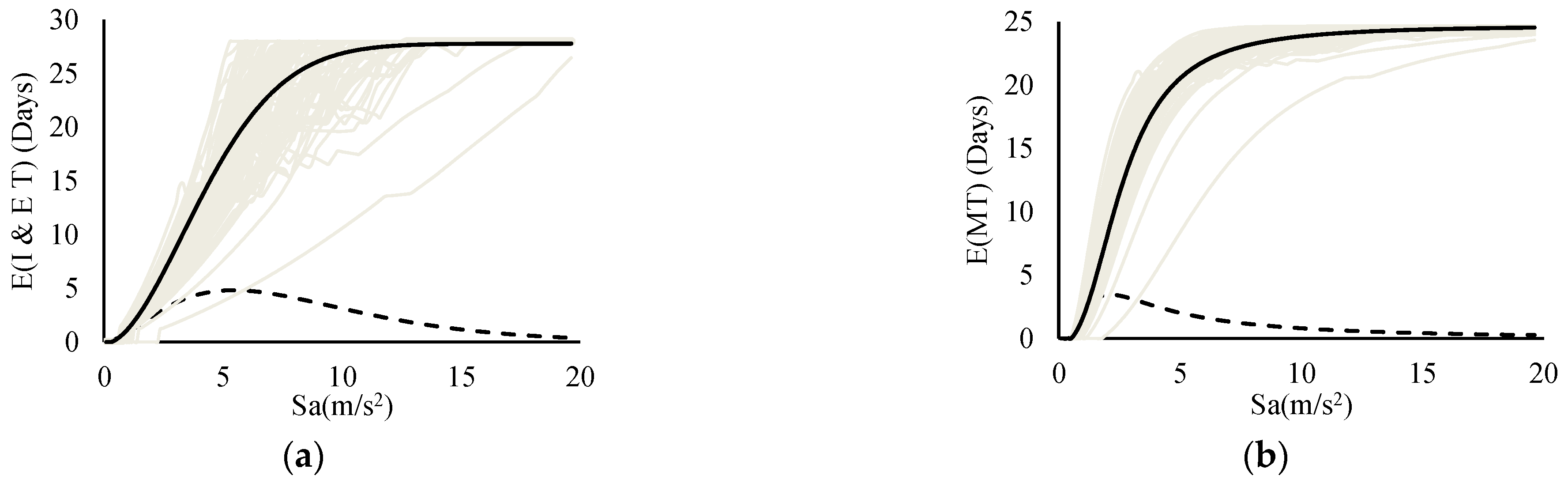

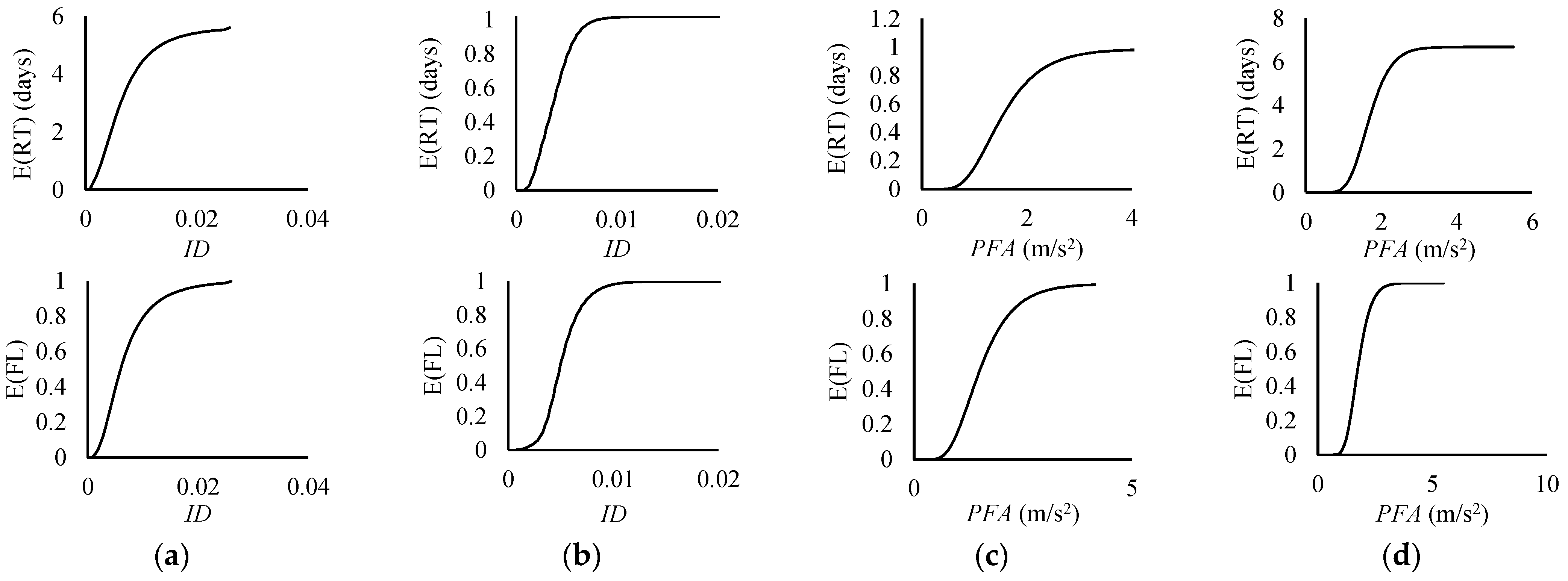



| Station | Date (d/m/y) | Direction | Epicenter | Mw | Station | Date (d/m/y) | Direction | Epicenter | Mw | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat(°) | Lon(°) | Lat(°) | Lon(°) | ||||||||
| ARTG | 14/01/91 | EW-NS | 17.86 | 101.8 | 5.2 | COYC | 19/07/97 | EW-NS | 15.86 | 98.26 | 6.7 |
| ARTG | 11/06/86 | EW-NS | 15.14 | 93.51 | 5.8 | COYC | 19/09/85 | EW-NS | 18.41 | 102.4 | 8.1 |
| ARTG | 05/01/90 | EW-NS | 18.71 | 107.0 | 5.8 | COYC | 20/09/85 | EW-NS | 17.82 | 101.6 | 7.6 |
| ARTG | 30/04/86 | EW-NS | 18.36 | 103.0 | 7.0 | COYC | 22/03/97 | EW-NS | 17.04 | 99.76 | 4.7 |
| CALE | 11/01/97 | EW-NS | 18.34 | 102.5 | 7.1 | COYC | 25/04/89 | EW-NS | 16.58 | 99.46 | 6.9 |
| CALE | 19/09/85 | EW-NS | 18.41 | 102.4 | 8.1 | COYC | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 |
| CALE | 22/05/97 | EW-NS | 18.41 | 101.8 | 6.0 | CSER | 15/05/93 | EW-NS | 16.47 | 98.72 | 6.0 |
| CALE | 05/01/90 | EW-NS | 18.71 | 107.0 | 5.8 | CSER | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 |
| CALE | 30/04/86 | EW-NS | 18.36 | 103.0 | 7.0 | CSER | 16/09/89 | EW-NS | 16.21 | 94.01 | 5.9 |
| CENA | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 | CSER | 23/02/94 | EW-NS | 17.82 | 97.30 | 5.4 |
| CENA | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 | CSER | 25/04/89 | EW-NS | 16.58 | 99.46 | 6.9 |
| COPL | 14/09/95 | EW-NS | 17.00 | 99.00 | 7.3 | CSER | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 |
| COPL | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 | CUER | 10/12/94 | EW-NS | 18.02 | 101.56 | 6.2 |
| COPL | 21/01/97 | EW-NS | 16.44 | 98.15 | 5.6 | CUER | 14/09/95 | EW-NS | 17.00 | 99.00 | 7.3 |
| COPL | 24/10/93 | EW-NS | 16.76 | 98.76 | 6.6 | CUER | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 |
| COPL | 25/04/89 | EW-NS | 16.58 | 99.46 | 6.9 | CUER | 23/05/94 | EW-NS | 17.97 | 100.6 | 5.8 |
| COPL | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 | CUER | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 |
| COYC | 07/06/98 | EW-NS | 15.82 | 94.07 | 6.2 | RIPC | 14/09/95 | EW-NS | 17.00 | 99.00 | 7.3 |
| COYC | 05/07/98 | EW-NS | 16.83 | 100.1 | 5.2 | RIPC | 23/02/94 | EW-NS | 17.82 | 97.30 | 5.4 |
| COYC | 08/05/97 | EW-NS | 17.32 | 100.4 | 5.1 | SXPU | 19/09/85 | EW-NS | 18.41 | 102.4 | 8.1 |
| COYC | 11/01/97 | EW-NS | 18.34 | 102.5 | 7.1 | SXPU | 20/09/85 | EW-NS | 17.82 | 101.6 | 7.6 |
| COYC | 14/09/95 | EW-NS | 17.00 | 99.00 | 7.3 | YAIG | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 |
| COYC | 15/06/99 | EW-NS | 18.13 | 97.53 | 7.0 | YAIG | 30/09/99 | EW-NS | 16.05 | 97.0 | 7.4 |
| Color | Location Beams | Color | Location Beams | Color | Location Beams | Color | Location Columns | Color | Location Columns | Color | Location Columns | DS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Floor 1 | Floor 2 | Floor 3 | Floor 1 | Floor 2 | Floor 3 | DS1 | ||||||||||||||||||
| Floor 1 | Floor 2 | Floor 3 | Floor 1 | Floor 2 | Floor 3 | DS2 | ||||||||||||||||||
| Floor 1 | Floor 2 | Floor 3 | Floor 1 | Floor 2 | Floor 3 | DS3 | ||||||||||||||||||
| Floor 1 | Floor 2 | Floor 3 | Floor 1 | Floor 2 | Floor 3 | DS4 | ||||||||||||||||||
| Damage State | Physical Damage | Recommended Repair | Repair Time (Days) |
|---|---|---|---|
| DS1—Light damage | Sealer failure | Remove the glass piece to repair the sealer. | 0.68 |
| DS2—Moderate damage | Window cracking | Replace the cracked glass piece. | 1.02 |
| DS3—Severe damage/Collapse | Window collapse | Replace the glass piece and temporarily cover the gap. | 1.5 |
| Magnitude | Frequency | RTS | FLS | RTM | FLM | RTV | FLV | RTL | FLL | RTP | FLP | I&ET | MT(B) | MT(D) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.66 | 0.000306 | 0.27 | 0.19 | 0.23 | 0.07 | 0.04 | 0.01 | 0.03 | 0.01 | 0.02 | 0.08 | 0.04 | 0.09 | 0.06 |
| 7.18 | 0.000655 | 0.19 | 0.09 | 0.27 | 0.04 | 0.05 | 0.01 | 0.04 | 0.00 | 0.00 | 0.04 | 0.04 | 0.10 | 0.07 |
| 7.66 | 0.000309 | 0.28 | 0.19 | 0.23 | 0.07 | 0.04 | 0.01 | 0.03 | 0.01 | 0.01 | 0.08 | 0.04 | 0.09 | 0.06 |
| 6.69 | 0.001375 | 0.08 | 0.04 | 0.33 | 0.03 | 0.06 | 0.00 | 0.04 | 0.00 | 0.01 | 0.02 | 0.04 | 0.10 | 0.08 |
| 7.18 | 0.000642 | 0.18 | 0.09 | 0.27 | 0.04 | 0.05 | 0.01 | 0.04 | 0.00 | 0.00 | 0.04 | 0.04 | 0.10 | 0.07 |
| 7.66 | 0.000300 | 0.27 | 0.19 | 0.23 | 0.07 | 0.04 | 0.01 | 0.03 | 0.01 | 0.01 | 0.08 | 0.04 | 0.10 | 0.06 |
| 7.66 | 0.000299 | 0.27 | 0.19 | 0.23 | 0.07 | 0.04 | 0.01 | 0.03 | 0.01 | 0.01 | 0.08 | 0.04 | 0.10 | 0.06 |
| Class | Resilience (R) | Time (RT) | Functionality (F) |
|---|---|---|---|
| High | R ≥ 99% | RT ≤ 3% | F ≥ 97.5% |
| Medium | 99% > R > 92% | 3% < RT < 35% | 97.5% > F > 88% |
| Low | R ≤ 92% | RT ≥ 35% | F ≤ 88% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, C.; Niño, M.; Ayala, G. Functionality Loss and Recovery Time Models for Structural Elements, Non-Structural Components, and Delay Times to Estimate the Seismic Resilience of Mexican School Buildings. Buildings 2023, 13, 1498. https://doi.org/10.3390/buildings13061498
González C, Niño M, Ayala G. Functionality Loss and Recovery Time Models for Structural Elements, Non-Structural Components, and Delay Times to Estimate the Seismic Resilience of Mexican School Buildings. Buildings. 2023; 13(6):1498. https://doi.org/10.3390/buildings13061498
Chicago/Turabian StyleGonzález, Carlos, Mauro Niño, and Gustavo Ayala. 2023. "Functionality Loss and Recovery Time Models for Structural Elements, Non-Structural Components, and Delay Times to Estimate the Seismic Resilience of Mexican School Buildings" Buildings 13, no. 6: 1498. https://doi.org/10.3390/buildings13061498
APA StyleGonzález, C., Niño, M., & Ayala, G. (2023). Functionality Loss and Recovery Time Models for Structural Elements, Non-Structural Components, and Delay Times to Estimate the Seismic Resilience of Mexican School Buildings. Buildings, 13(6), 1498. https://doi.org/10.3390/buildings13061498





