Optimizing Truss Structures Using Composite Materials under Natural Frequency Constraints with a New Hybrid Algorithm Based on Cuckoo Search and Stochastic Paint Optimizer (CSSPO)
Abstract
:1. Introduction
- The study compared truss structures made of various materials (i.e., CFRP, GFRP, and steel).
- The study used composite material for the optimization of truss design for the first time.
- A novel hybrid of the SPO algorithm called the CSSPO was created, and its strength and robustness were validated by optimizing through the optimization of four different truss structures.
- The CSSPO algorithm was shown to outperform the original SPO algorithm.
- Truss structures made of composite materials resulted in a lighter weight.
2. Composite Materials
2.1. Glass Fiber Reinforced Polymer (GFRP)
2.2. Carbon Fiber Reinforced Polymer (CFRP)
2.3. FRP Properties
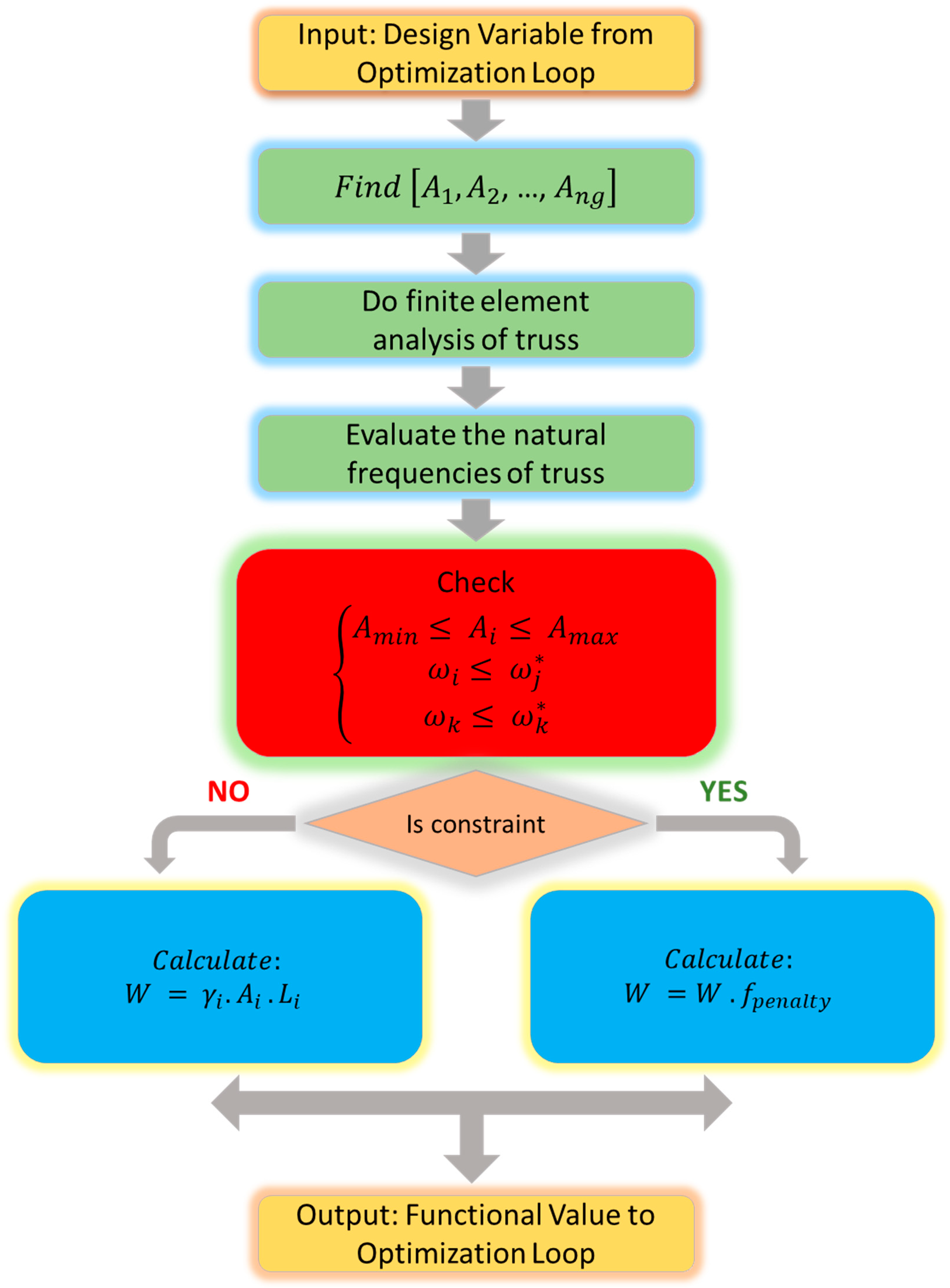
3. Definition of Truss Structures Optimization
4. Methodology
4.1. Cuckoo Search (CS)
4.2. Stochastic Paint Optimizer (SPO)
4.2.1. Analogous Combination Technique
4.2.2. Complementary Combination Technique
4.2.3. Triadic Combination Technique
4.2.4. Tetradic Combination Technique
4.3. The Hybrid of Cuckoo Search-Stochastic Paint Optimizer (CSSPO)
| Algorithm 1: Pseudo-code of CSSPO |
| Inputs: The number of colors (pop size) Outputs: The best location of colors and their objective values 1. Initialize the random colors 2. Find the objective values 3. For (it<itMax) Do 4. Divide colors into three groups randomly 5. for every color 6. Create new colors (combine colors) 7. Sort the fitness of all colors 8. Find the best colors 9. Build new nests at new locations using Levy flight 10. Retain the best solutions (nests with quality solutions) 11. Rank the solutions and find the current best solution 12. End for 13. End For (Termination criteria are satisfied) 14. Return the best solution |
5. Structural Examples
5.1. A 37-Member Planar Truss
5.2. A 72-Member Space Truss
5.3. A 120-Member Dome Truss
5.4. A 200-Member Planar Truss
6. Statistical Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EEl-Kenawy, E.S.M.; Mirjalili, S.; Khodadadi, N.; Abdelhamid, A.A.; Eid, M.M.; El-Said, M.; Ibrahim, A. Feature selection in wind speed forecasting systems based on meta-heuristic optimization. PLoS ONE 2023, 18, e0278491. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, M.; Ye, Z.; Cao, L. Improved particle swarm optimization algorithm and its application in text feature se-lection. Appl. Soft Comput. 2015, 35, 629–636. [Google Scholar] [CrossRef]
- Atteia, G.; El-Kenawy, E.-S.M.; Samee, N.A.; Jamjoom, M.M.; Ibrahim, A.; Abdelhamid, A.A.; Azar, A.T.; Khodadadi, N.; Ghanem, R.A.; Shams, M.Y. Adaptive Dynamic Dipper Throated Optimization for Feature Selection in Medical Data. Comput. Mater. Contin. 2023, 75, 1883–1900. [Google Scholar] [CrossRef]
- Dhiman, G. MOSHEPO: A hybrid multi-objective approach to solve economic load dispatch and micro grid problems. Appl. Intell. 2019, 50, 119–137. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; El-Kenawy, E.-S.M.; Alrowais, F.; Ibrahim, A.; Khodadadi, N.; Lim, W.H.; Alruwais, N.; Khafaga, D.S. Deep Learning with Dipper Throated Optimization Algorithm for Energy Consumption Forecasting in Smart Households. Energies 2022, 15, 9125. [Google Scholar] [CrossRef]
- Khodadadi, N.; Abualigah, L.; El-Kenawy, E.-S.M.; Snasel, V.; Mirjalili, S. An Archive-Based Multi-Objective Arithmetic Optimization Algorithm for Solving Industrial Engineering Problems. IEEE Access 2022, 10, 106673–106698. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Abdelhamid, A.A.; Towfek, S.K.; Khodadadi, N.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; Ibrahim, A. Waterwheel Plant Algorithm: A Novel Metaheuristic Optimization Method. Processes 2023, 11, 1502. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2022, 259, 110011. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Gao, H.; Zhan, Z.-H.; Li, J.; Zhang, H. Growth Optimizer: A powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl. -Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021, 38, 3025–3056. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics 2022, 10, 1626. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain Gazelle Optimizer: A new Nature-inspired Metaheuristic Algorithm for Global Optimization Problems. Adv. Eng. Softw. 2022, 174, 103282. [Google Scholar] [CrossRef]
- Khodadadi, N.; Talatahari, S.; Gandomi, A.H. ANNA: Advanced neural network algorithm for optimization of structures. Proc. Inst. Civ. Eng.-Struct. Build. 2023, 176, 1–23. [Google Scholar] [CrossRef]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K.; Mirjalili, S. Truss optimization with natural frequency bounds using improved symbiotic organisms search. Knowl.-Based Syst. 2018, 143, 162–178. [Google Scholar] [CrossRef] [Green Version]
- Farshchin, M.; Camp, C.V.; Maniat, M. Optimal design of truss structures for size and shape with frequency constraints using a collaborative optimization strategy. Expert Syst. Appl. 2016, 66, 203–218. [Google Scholar] [CrossRef]
- Nanni, A.; De Luca, A.; Zadeh, H.J. Reinforced Concrete with FRP Bars: Mechanics and Design; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Khodadadi, N.; Mirjalili, S. Truss optimization with natural frequency constraints using generalized normal distribution optimization. Appl. Intell. 2022, 52, 10384–10397. [Google Scholar] [CrossRef]
- Tinkov, D.V.; Safonov, A.A. Design optimization of truss bridge structures of composite materials. J. Mach. Manuf. Reliab. 2017, 46, 46–52. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B.; Kamalinejad, M. Improved slime mould algorithm with elitist strategy and its application to structural optimization with natural frequency constraints. Comput. Struct. 2022, 264, 106760. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, H.; Chen, Z.; Cao, H. Frequency-constrained truss optimization using the fruit fly optimization algorithm with an adaptive vision search strategy. Eng. Optim. 2019, 52, 777–797. [Google Scholar] [CrossRef]
- Millan-Paramo, C.; Filho, J.E.A. Size and Shape Optimization of Truss Structures with Natural Frequency Constraints Using Modified Simulated Annealing Algorithm. Arab. J. Sci. Eng. 2019, 45, 3511–3525. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Nguyen-Thoi, T.; Truong-Khac, T.; Le-Anh, L.; Vo-Duy, T. An improved differential evolution based on roulette wheel selection for shape and size optimization of truss structures with frequency constraints. Neural Comput. Appl. 2016, 29, 167–185. [Google Scholar] [CrossRef]
- Wei, L.; Tang, T.; Xie, X.; Shen, W. Truss optimization on shape and sizing with frequency constraints based on parallel genetic algorithm. Struct. Multidiscip. Optim. 2010, 43, 665–682. [Google Scholar] [CrossRef]
- Pyone, E.C.; Tangaramvong, S.; Van, T.; Bui, L.; Gao, W. Comprehensive learning phasor particle swarm opti-mization of structures under limited natural frequency conditions. Acta Mech. Sin. 2023, 39, 722386. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural opti-mization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S.; Khodadadi, N. Stochastic paint optimizer: Theory and application in civil engineering. Eng. Comput. 2020, 38, 1921–1952. [Google Scholar] [CrossRef]
- Liu, T.; Liu, X.; Feng, P. A comprehensive review on mechanical properties of pultruded FRP composites subjected to long-term environmental effects. Compos. Part B Eng. 2020, 191, 107958. [Google Scholar] [CrossRef]
- Bai, J. Advanced Fibre-Reinforced Polymer (FRP) Composites for Structural Applications; Woodhead Publishing: Sawston, UK, 2013. [Google Scholar] [CrossRef]
- GangaRao, H.V.S.; Prachasaree, W. FRP Composite Structures: Theory, Fundamentals, and Design; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic Arithmetic Optimization Algorithm for Truss Optimization Under Natural Frequency Constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S.; Mirjalili, S. Optimal Design of Truss Structures with Continuous Variable Using Moth-Flame Optimization. In Handbook of Moth-Flame Optimization Algorithm; CRC Press: Boca Raton, FL, USA, 2022; pp. 265–280. [Google Scholar]
- Yang, X.-S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S.; Mirjalili, S.; Mirjalili, S. Chaotic Stochastic Paint Optimizer (CSPO). In Lecture Notes on Data Engineering and Communications Technologies, Proceedings of the 7th International Conference on Harmony Search, Soft Computing and Applications, 23–24 February 2022, Seoul, Republic of Korea; Springer: Berlin/Heidelberg, Germany, 2022; pp. 195–205. [Google Scholar]
- Kaveh, A.; Zolghadr, A. Truss optimization with natural frequency constraints using a hybridized CSS-BBBC algorithm with trap recognition capability. Comput. Struct. 2012, 102–103, 14–27. [Google Scholar] [CrossRef]


































| Material | Density | Modulus of Elasticity | ||
|---|---|---|---|---|
| lb/ft3 | Kg/m3 | GPa | Ksi | |
| GFRP | 97 | 1550 | 55 | 8000 |
| CFRP | 109 | 1750 | 160 | 23,000 |
| Steel | 490 | 7850 | 207 | 30,000 |
| Test Problem | Cross-Sectional A (cm2) | Natural Frequency Constraints ω (Hz) |
|---|---|---|
| 37-member planar bridge | ||
| 72-member space truss | ||
| 120-member dome truss | ||
| 200-member planar truss |
| Materials | GFRP | CFRP | Steel | |||
|---|---|---|---|---|---|---|
| Member Group | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| (Y3-Y19) m | 1.5184 | 1.0011 | 1.0001 | 1.0000 | 1.0048 | 1.0000 |
| (Y5-A17) m | 1.8947 | 1.3657 | 1.6809 | 1.3292 | 1.3652 | 1.3728 |
| (Y7-A15) m | 2.0950 | 1.5189 | 1.6850 | 1.5813 | 1.5746 | 1.5405 |
| (Y9-Y13) m | 2.2646 | 1.6556 | 1.8538 | 1.7402 | 1.7213 | 1.6485 |
| (Y11) m | 2.3462 | 1.7209 | 1.9387 | 1.8052 | 1.8217 | 1.7231 |
| (A1-A27) cm2 | 5.0000 | 4.2428 | 1.0000 | 1.0002 | 3.6223 | 2.9181 |
| (A2-A26) cm2 | 1.9234 | 1.4950 | 1.0000 | 1.0000 | 1.6336 | 1.0191 |
| (A3-A24) cm2 | 1.0002 | 1.2581 | 1.0000 | 1.0000 | 1.0013 | 1.0009 |
| (A4-A25) cm2 | 2.0466 | 3.9872 | 1.8513 | 1.0451 | 3.2354 | 2.6357 |
| (A5-A23) cm2 | 1.9483 | 1.8549 | 1.0002 | 1.0001 | 3.2649 | 1.2225 |
| (A6-A21) cm2 | 2.3951 | 2.0886 | 1.0000 | 1.0000 | 1.0807 | 1.2106 |
| (A7-A22) cm2 | 2.3431 | 3.7248 | 1.0181 | 1.1791 | 1.7398 | 2.6363 |
| (A8-A20) cm2 | 2.1990 | 2.1120 | 2.0736 | 1.0000 | 1.0324 | 1.4348 |
| (A9-A18) cm2 | 2.5342 | 2.2236 | 1.5062 | 1.0000 | 1.2940 | 1.5293 |
| (A10-A19) cm2 | 2.0994 | 3.9553 | 1.0272 | 1.2119 | 2.0527 | 2.7911 |
| (A11-A17) cm2 | 4.3423 | 1.8406 | 1.0015 | 1.0000 | 1.5098 | 1.2057 |
| (A12-A15) cm2 | 2.8011 | 1.9479 | 1.8380 | 1.0000 | 1.4822 | 1.2726 |
| (A13-A16) cm2 | 3.1363 | 3.8760 | 1.0000 | 1.2400 | 3.4292 | 2.4663 |
| (A14-A16) cm2 | 1.0045 | 1.0035 | 1.0000 | 1.0000 | 1.0014 | 1.0004 |
| Best weight | 80.8917 | 76.3119 | 79.0690 | 76.8983 | 370.8402 | 363.2729 |
| Average weight | 140.6229 | 77.3588 | 85.0605 | 76.9032 | 434.8858 | 364.4259 |
| Standard deviation | 49.6651 | 1.1125 | 7.6528 | 0.0058 | 57.8664 | 1.1706 |
| No. Analyses | 13,150 | 10,500 | 5400 | 4400 | 6150 | 4600 |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| Frequency No. | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 20.000 | 20.0000 | 20.0024 | 20.0001 | 20.0000 | 20.0000 | |
| 42.9544 | 40.0000 | 47.3363 | 42.2966 | 40.0049 | 40.0000 | |
| 60.0000 | 60.0000 | 67.8965 | 66.0972 | 60.0000 | 60.0000 | |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| Member Group | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 1 (A1-A4) cm2 | 13.3972 | 4.7702 | 1.4932 | 1.4932 | 1.4932 | 1.1560 |
| 2 (A5-A12) cm2 | 9.4481 | 9.9981 | 3.4486 | 3.4486 | 3.4486 | 2.6751 |
| 3 (A13-A16) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| 4 (A17-A18) cm2 | 0.6724 | 0.7181 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| 5 (A19-A22) cm2 | 12.0096 | 10.5253 | 3.4111 | 3.4111 | 3.4111 | 2.6876 |
| 6 (A23-A30) cm2 | 11.3740 | 10.0562 | 3.5042 | 3.5042 | 3.5042 | 2.6555 |
| 7 (A31-A34) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| 8 (A35-A36) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6453 |
| 9 (A37-A40) cm2 | 13.6289 | 16.9763 | 5.7274 | 5.7274 | 5.7274 | 4.2783 |
| 10 (A41-A48) cm2 | 8.6208 | 10.0865 | 3.5086 | 3.5086 | 3.5086 | 2.6824 |
| 11 (A49-A52) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| 12 (A53-A54) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6452 |
| 13 (A55-A58) cm2 | 20.0000 | 20.0000 | 7.3112 | 7.3112 | 7.3112 | 5.6892 |
| 14 (A59-A66) cm2 | 11.2354 | 9.9604 | 3.4397 | 3.4397 | 3.4397 | 2.7112 |
| 15 (A67-A70) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| 16 (A71-A72) cm2 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 | 0.6450 |
| Best weight (kg) | 236.0334 | 227.2641 | 103.4361 | 94.8585 | 356.0184 | 337.7553 |
| Average weight (kg) | 268.0583 | 227.3044 | 129.3833 | 94.8953 | 472.1857 | 337.8333 |
| Standard deviation | 23.0932 | 0.0311 | 18.6853 | 0.0271 | 65.8768 | 0.0600 |
| No. Analyses | 19,100 | 6900 | 6800 | 4900 | 4150 | 4050 |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| Frequency No. | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 4.0000 | 4.0000 | 4.0000 | 4.0000 | 4.0000 | 4.0000 | |
| 4.0001 | 4.0001 | 4.0000 | 4.0000 | 4.0001 | 4.0001 | |
| 6.0000 | 6.0000 | 6.0002 | 6.0000 | 6.0000 | 6.0000 | |
| 6.0023 | 6.0049 | 8.5403 | 8.2394 | 8.9257 | 9.0087 | |
| 8.7654 | 8.6107 | 10.6718 | 9.7387 | 9.2840 | 9.8549 | |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| No. Group | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 1 | 79.2113 | 80.0669 | 24.3782 | 24.5554 | 20.9089 | 19.8347 |
| 2 | 129.2908 | 129.3000 | 47.8216 | 46.4722 | 39.1228 | 42.1216 |
| 3 | 39.9363 | 38.0518 | 10.7601 | 11.3803 | 11.4432 | 11.4296 |
| 4 | 75.7910 | 75.1591 | 20.9776 | 21.0117 | 21.0978 | 21.6645 |
| 5 | 34.4651 | 33.3149 | 9.1935 | 9.3981 | 11.0651 | 10.0670 |
| 6 | 40.1374 | 41.8914 | 13.3115 | 12.3117 | 10.6454 | 12.9819 |
| 7 | 47.0609 | 47.8410 | 11.8182 | 11.9763 | 19.7014 | 15.2824 |
| Best weight | 5943.8442 | 5939.8775 | 1968.0971 | 1965.5323 | 9245.8842 | 8885.6721 |
| Average weight | 6749.4283 | 5942.1393 | 2169.862 | 1966.1123 | 10,457.864 | 8889.385 |
| Standard deviation | 719.3279 | 4.2971 | 279.4734 | 0.7860 | 1500.93 | 3.13777 |
| No. Analyses | 4400 | 4150 | 4850 | 4550 | 4100 | 4400 |
| Materials | CFRP | GFRP | STEEL | |||
|---|---|---|---|---|---|---|
| No. Frequency | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 9.0000 | 9.0000 | 9.0000 | 9.0000 | 9.0000 | 9.0000 | |
| 11.0000 | 11.0000 | 11.0000 | 11.0000 | 11.0000 | 11.0000 | |
| 11.0052 | 11.0000 | 11.0000 | 11.0000 | 11.0603 | 11.0000 | |
| 11.0075 | 11.0075 | 11.0033 | 11.0032 | 11.0890 | 11.0096 | |
| 11.0524 | 11.0522 | 11.0530 | 11.0535 | 11.1581 | 11.0494 | |
| Group | Member Number | Group | Member Number |
|---|---|---|---|
| 1 | 1,2,3,4 | 16 | 82,83,85,88,89,91,92,103,104,106,107,109,110,112,113 |
| 2 | 5,8,11,14,17 | 17 | 115,116,117,118 |
| 3 | 19,20,21,22,23,24 | 18 | 119,122,125,128,131 |
| 4 | 18,25,56,63,94,101,132,139,170,177 | 19 | 133,134,135,136,137,138 |
| 5 | 26,29,32,35,38 | 20 | 140,143,146,149,152 |
| 6 | 6,7,9,10,12,13,15,16,27,28,30,31,33,34,36,37 | 21 | 120,121,123,124,126,127,129,130,141,142,144,145,147,148,150,151 |
| 7 | 39,40,41,42 | 22 | 153,154,155,156 |
| 8 | 43,46,49,52,55 | 23 | 157,160,163,166,169 |
| 9 | 57,58,59,60,61,62 | 24 | 171,172,173,174,175,176 |
| 10 | 64,67,70,73,76 | 25 | 178,181,184,187,190 |
| 11 | 44,45,47,48,50,51,53,54,65,66,68,69,71,72,74,75 | 26 | 158,159,161,162,164,165,167,168,179,180,182,183,185,186,188,189 |
| 12 | 77,78,79,80 | 27 | 191,192,193,194 |
| 13 | 81,84,87,90,93 | 28 | 195,197,198,200 |
| 14 | 95,96,97,98,99,100 | 29 | 196,199 |
| 15 | 102,105,108,111,114 |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| Member Group | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 1 | 2.4229 | 2.5728 | 4.9125 | 0.7093 | 1.2342 | 0.5002 |
| 2 | 2.3958 | 2.1358 | 0.1000 | 0.8604 | 0.1000 | 0.4979 |
| 3 | 0.1000 | 0.1000 | 6.5239 | 0.1016 | 0.1369 | 0.1019 |
| 4 | 0.2973 | 0.1912 | 0.1000 | 0.1000 | 0.1055 | 0.1003 |
| 5 | 2.2152 | 1.9297 | 0.1923 | 0.8845 | 0.2325 | 0.4506 |
| 6 | 3.9470 | 4.0269 | 2.3523 | 1.4840 | 2.1007 | 0.8848 |
| 7 | 0.1000 | 0.3803 | 1.9255 | 0.1024 | 7.3151 | 0.1000 |
| 8 | 5.7238 | 6.2060 | 0.9830 | 2.1670 | 1.0079 | 1.4102 |
| 9 | 2.2937 | 0.1000 | 0.1000 | 0.1008 | 12.9035 | 0.1000 |
| 10 | 7.0010 | 7.1127 | 0.7830 | 2.3657 | 0.3016 | 1.5747 |
| 11 | 6.2874 | 5.0863 | 2.1217 | 1.6194 | 1.9754 | 1.1112 |
| 12 | 0.6026 | 0.7847 | 4.6294 | 0.1198 | 0.1000 | 0.1381 |
| 13 | 12.0973 | 13.7674 | 1.4760 | 3.9790 | 3.1709 | 2.9040 |
| 14 | 0.1811 | 0.1875 | 0.1000 | 0.1019 | 10.6532 | 0.1008 |
| 15 | 12.8618 | 15.9121 | 6.7499 | 4.0400 | 3.7011 | 3.1706 |
| 16 | 7.7501 | 7.6639 | 1.8909 | 1.8853 | 2.8960 | 1.5698 |
| 17 | 0.9657 | 1.9940 | 5.9667 | 0.2114 | 0.1000 | 0.2814 |
| 18 | 30.0000 | 26.7505 | 3.5944 | 5.6836 | 6.9783 | 5.0985 |
| 19 | 30.0000 | 0.3966 | 0.2184 | 0.1149 | 0.1013 | 0.1073 |
| 20 | 30.0000 | 30.0000 | 4.4254 | 5.6443 | 10.8546 | 5.2830 |
| 21 | 12.2261 | 12.2957 | 1.7639 | 2.0817 | 3.4605 | 2.0484 |
| 22 | 30.0000 | 13.6074 | 0.7094 | 0.6481 | 0.1130 | 0.4935 |
| 23 | 30.0000 | 30.0000 | 13.7444 | 7.9415 | 12.5323 | 7.7323 |
| 24 | 30.0000 | 21.3507 | 1.9093 | 0.1193 | 2.1160 | 0.2046 |
| 25 | 29.9999 | 30.0000 | 7.8694 | 7.6309 | 13.7618 | 8.1349 |
| 26 | 29.9970 | 30.0000 | 1.0521 | 2.4493 | 3.0577 | 2.6627 |
| 27 | 30.0000 | 30.0000 | 15.5103 | 9.1655 | 10.8998 | 10.2624 |
| 28 | 29.9985 | 30.0000 | 25.3566 | 18.5299 | 27.1305 | 21.3333 |
| 29 | 30.0000 | 30.0000 | 29.6547 | 10.3016 | 26.2179 | 10.2026 |
| Best weight | 6245.0062 | 5645.5521 | 713.0536 | 483.5991 | 3632.2153 | 2136.1284 |
| Average weight | 10,483.24 | 5646.58 | 945.4095 | 486.1037 | 6300.8391 | 2153.1362 |
| Standard deviation | 2068.484 | 2.971819 | 131.2423 | 7.5141 | 1273.747 | 36.1414 |
| No. Analyses | 13,150 | 6300 | 15,050 | 6700 | 7250 | 7150 |
| Materials | GFRP | CFRP | STEEL | |||
|---|---|---|---|---|---|---|
| No. Frequency | SPO | CSSPO | SPO | CSSPO | SPO | CSSPO |
| 5.0038 | 5.0057 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | |
| 14.3882 | 14.9355 | 14.8533 | 16.0865 | 14.7750 | 13.0865 | |
| 15.0000 | 16.0203 | 19.1823 | 16.2436 | 19.0460 | 15.0000 | |
| 19.1034 | 18.9980 | 19.5299 | 25.2140 | 19.5141 | 20.0789 | |
| 22.7452 | 22.2454 | 25.9642 | 32.3189 | 25.8055 | 22.0192 | |
| 25.3107 | 23.9112 | 26.4719 | 36.9720 | 26.2873 | 25.4215 | |
| Examples | Algorithms | GFRP | STEEL | CFRP |
|---|---|---|---|---|
| 37-Member truss | SPO vs. CSSPO | 4.37 × 10−9 | 1.85 × 10−7 | 1.06 × 10−8 |
| 73-Member truss | SPO vs. CSSPO | 1.08 × 10−13 | 2.07 × 10−14 | 4.38 × 10−16 |
| 120-Member truss | SPO vs. CSSPO | 7.79 × 10−8 | 1.86 × 10−4 | 3.87 × 10−7 |
| 200-Member truss | SPO vs. CSSPO | 1.50 × 10−18 | 9.73 × 10−27 | 3.29 × 10−25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodadadi, N.; Harati, E.; De Caso, F.; Nanni, A. Optimizing Truss Structures Using Composite Materials under Natural Frequency Constraints with a New Hybrid Algorithm Based on Cuckoo Search and Stochastic Paint Optimizer (CSSPO). Buildings 2023, 13, 1551. https://doi.org/10.3390/buildings13061551
Khodadadi N, Harati E, De Caso F, Nanni A. Optimizing Truss Structures Using Composite Materials under Natural Frequency Constraints with a New Hybrid Algorithm Based on Cuckoo Search and Stochastic Paint Optimizer (CSSPO). Buildings. 2023; 13(6):1551. https://doi.org/10.3390/buildings13061551
Chicago/Turabian StyleKhodadadi, Nima, Ehsan Harati, Francisco De Caso, and Antonio Nanni. 2023. "Optimizing Truss Structures Using Composite Materials under Natural Frequency Constraints with a New Hybrid Algorithm Based on Cuckoo Search and Stochastic Paint Optimizer (CSSPO)" Buildings 13, no. 6: 1551. https://doi.org/10.3390/buildings13061551
APA StyleKhodadadi, N., Harati, E., De Caso, F., & Nanni, A. (2023). Optimizing Truss Structures Using Composite Materials under Natural Frequency Constraints with a New Hybrid Algorithm Based on Cuckoo Search and Stochastic Paint Optimizer (CSSPO). Buildings, 13(6), 1551. https://doi.org/10.3390/buildings13061551










