Numerical Simulation of Pressure Wave Propagation and Its Effect on Damage to the Reactor Cavity under TNT Detonation for Steam Explosion
Abstract
1. Introduction
2. Methodologies
2.1. Material Models
2.1.1. Material Models for Concrete and Steel
2.1.2. Material Models for TNT, Water and Air
2.2. Numerical Modeling
2.2.1. Arbitrary Lagrangian–Eulerian and Fluid–Structure Interaction Methods
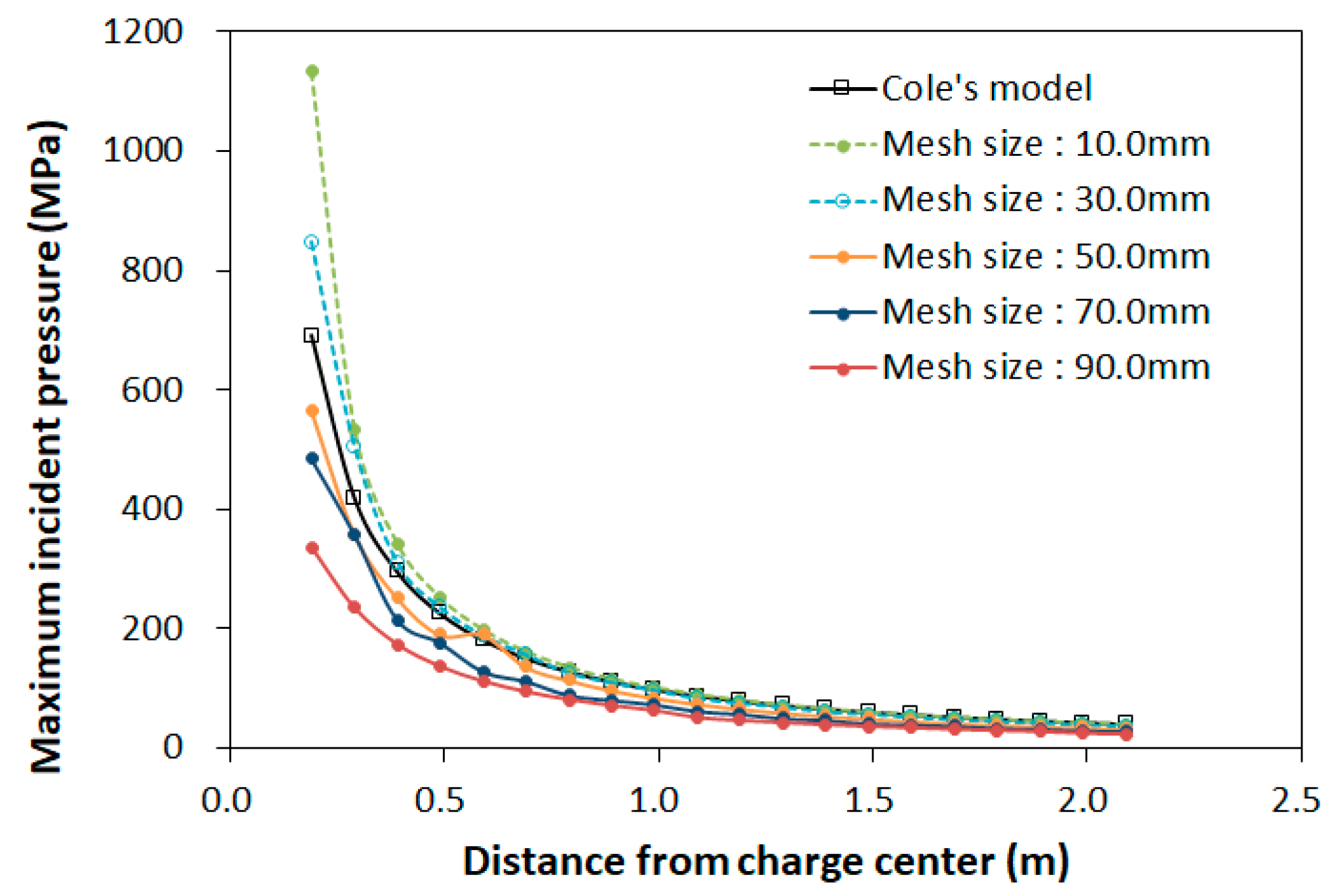
2.2.2. Mesh Sensitivity of Fluid Model Using 1D ALE Method
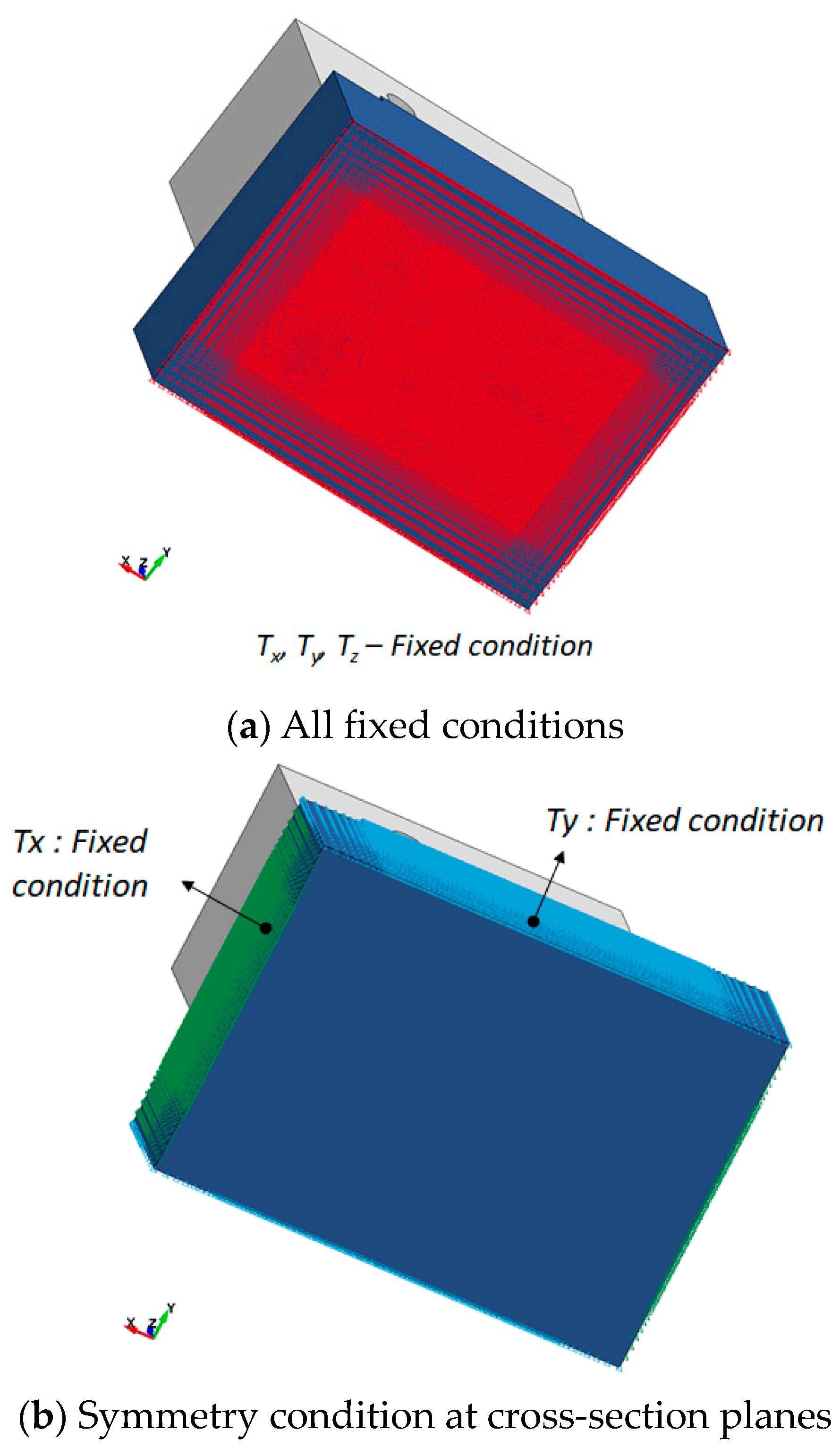
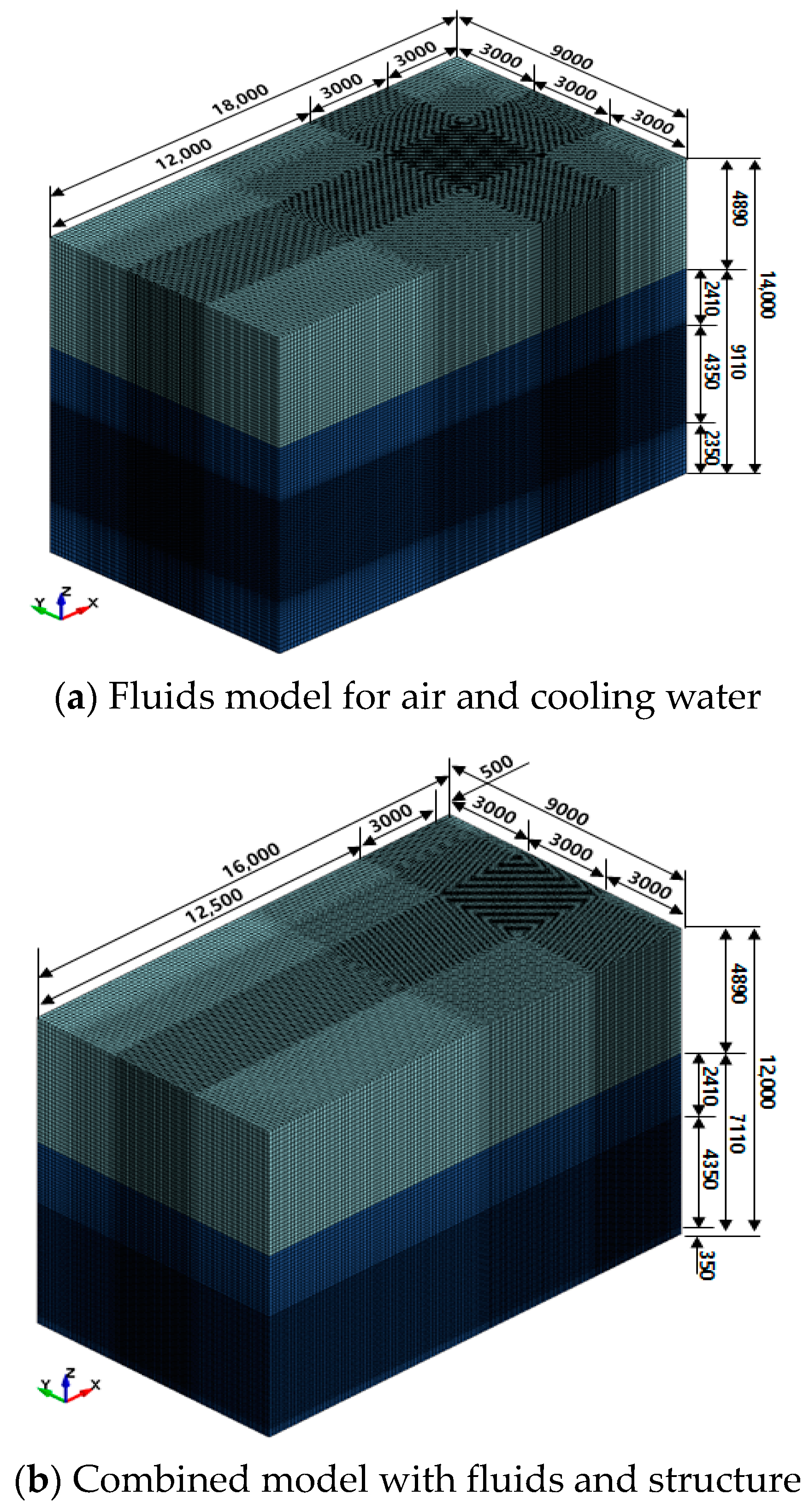
2.2.3. FE Modeling
3. Results and Discussion
3.1. Characteristics of the Pressure and Stress Waves Propagation
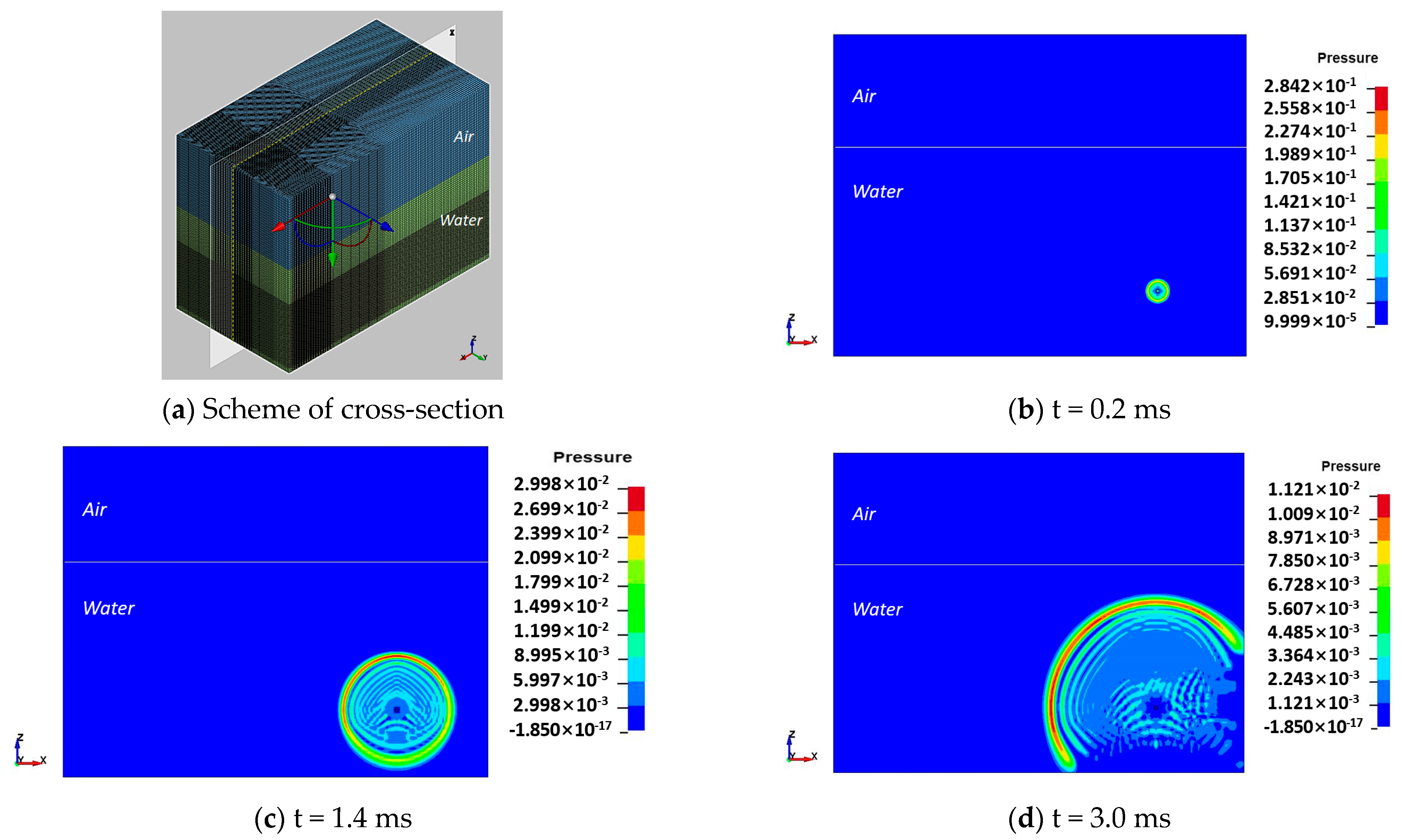
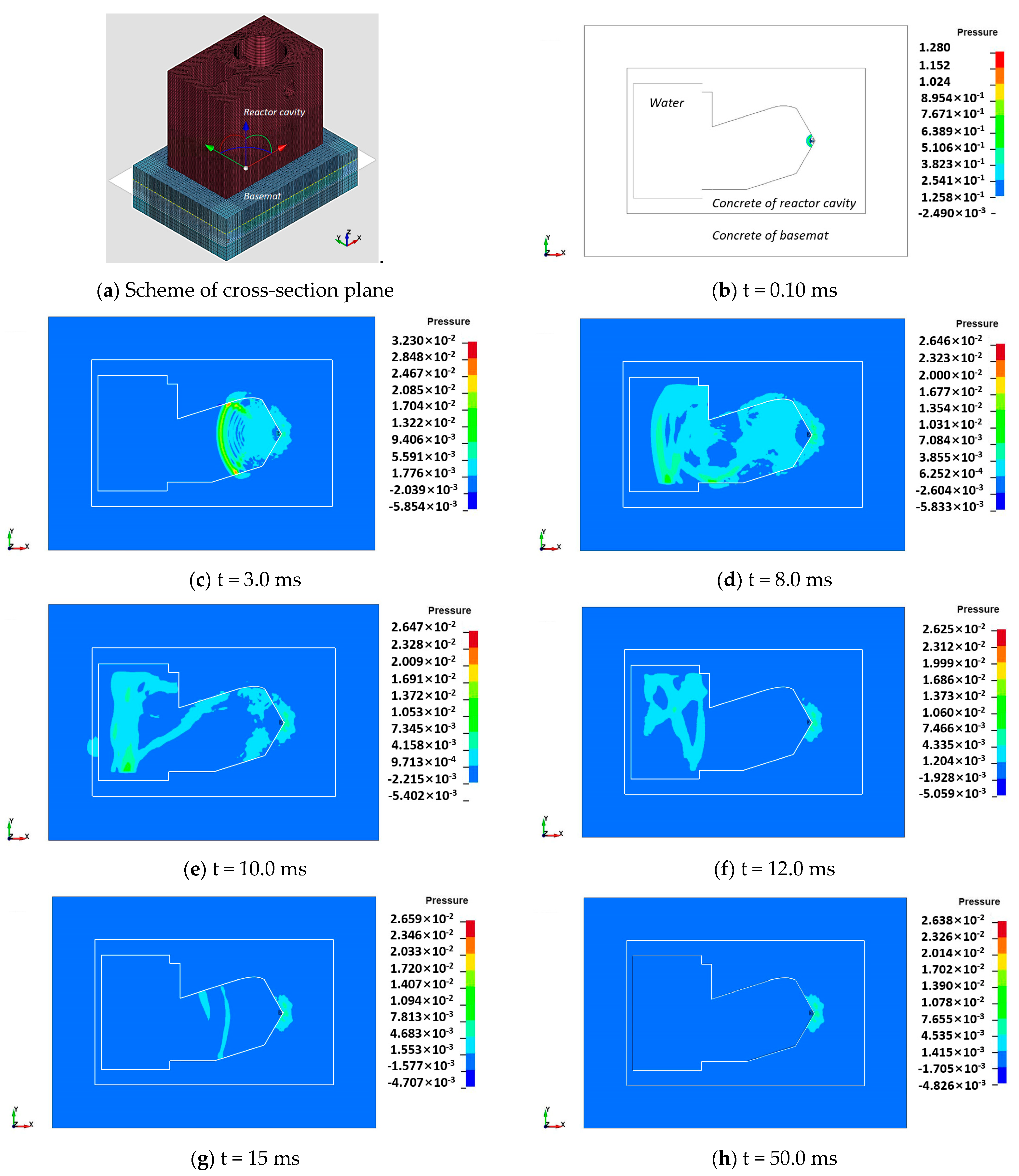
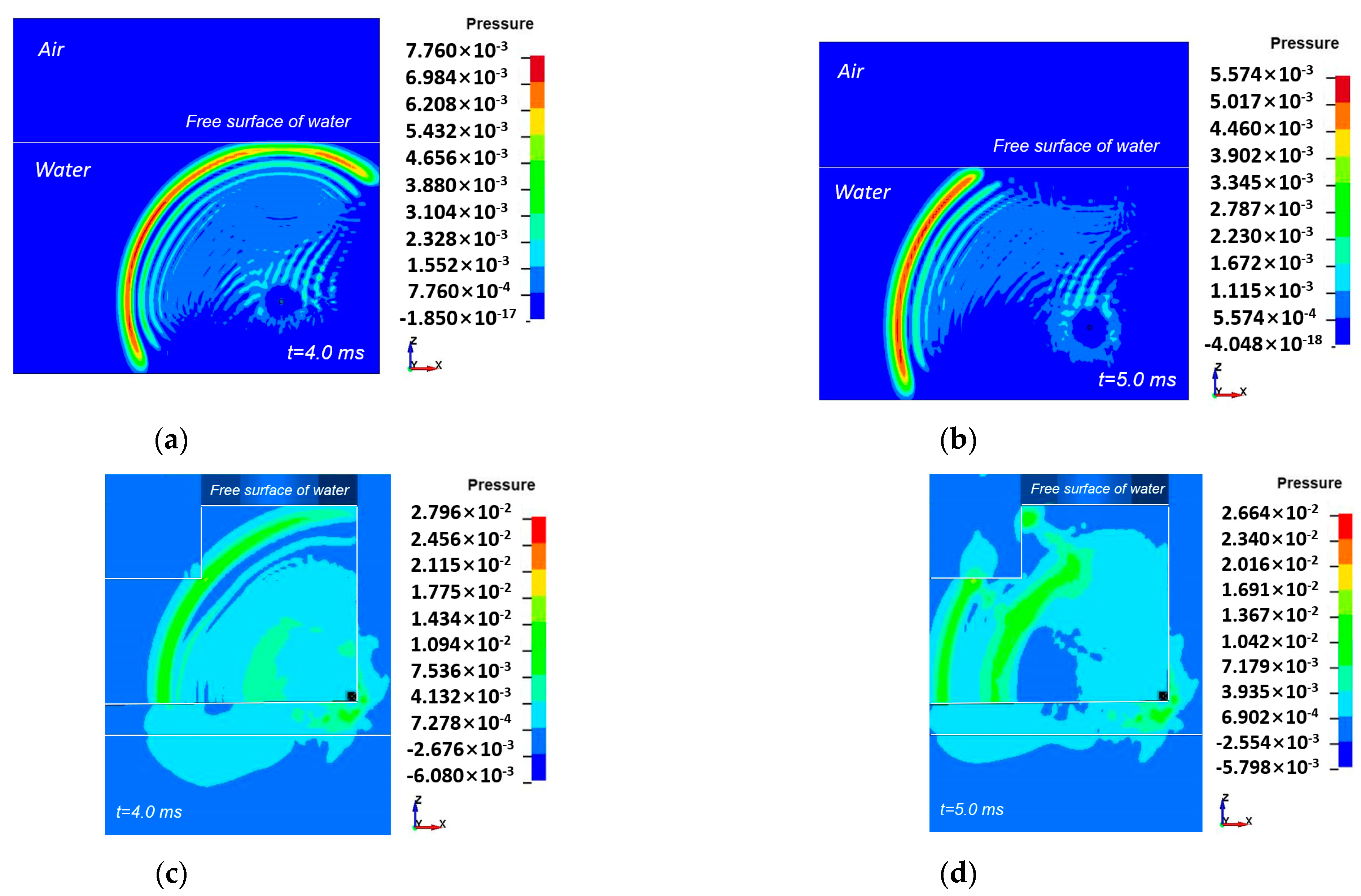
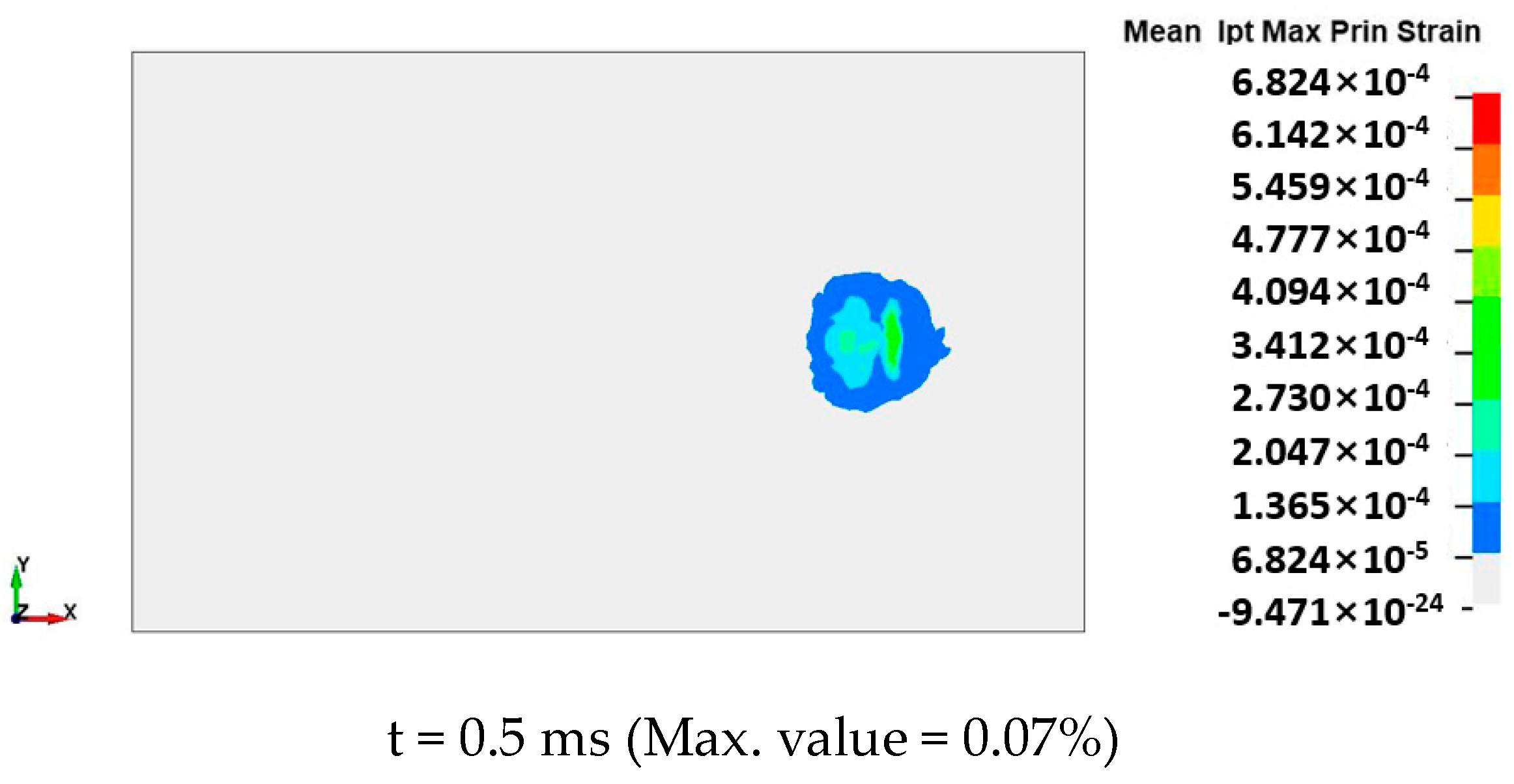
3.1.1. Pressure Wave Propagation
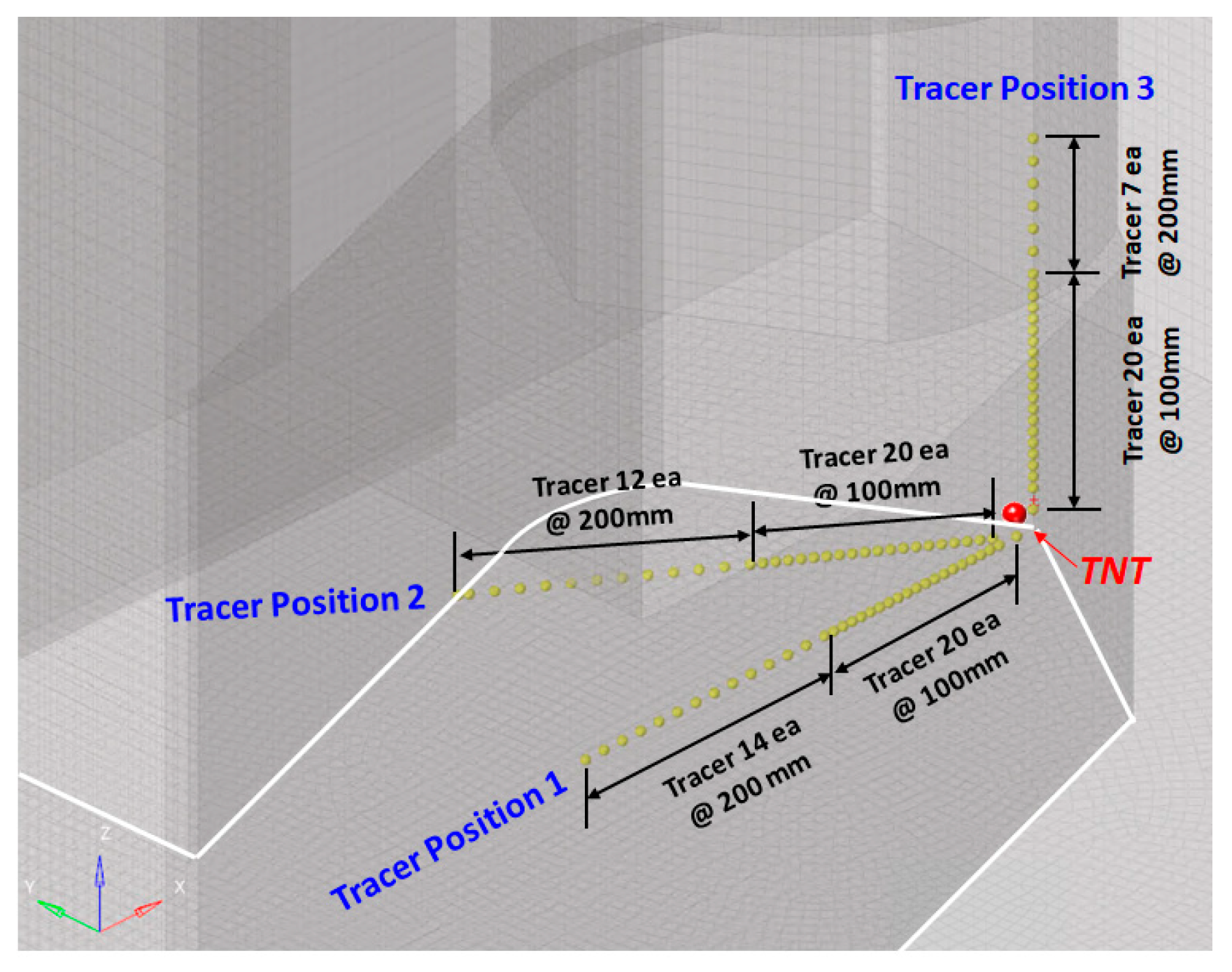
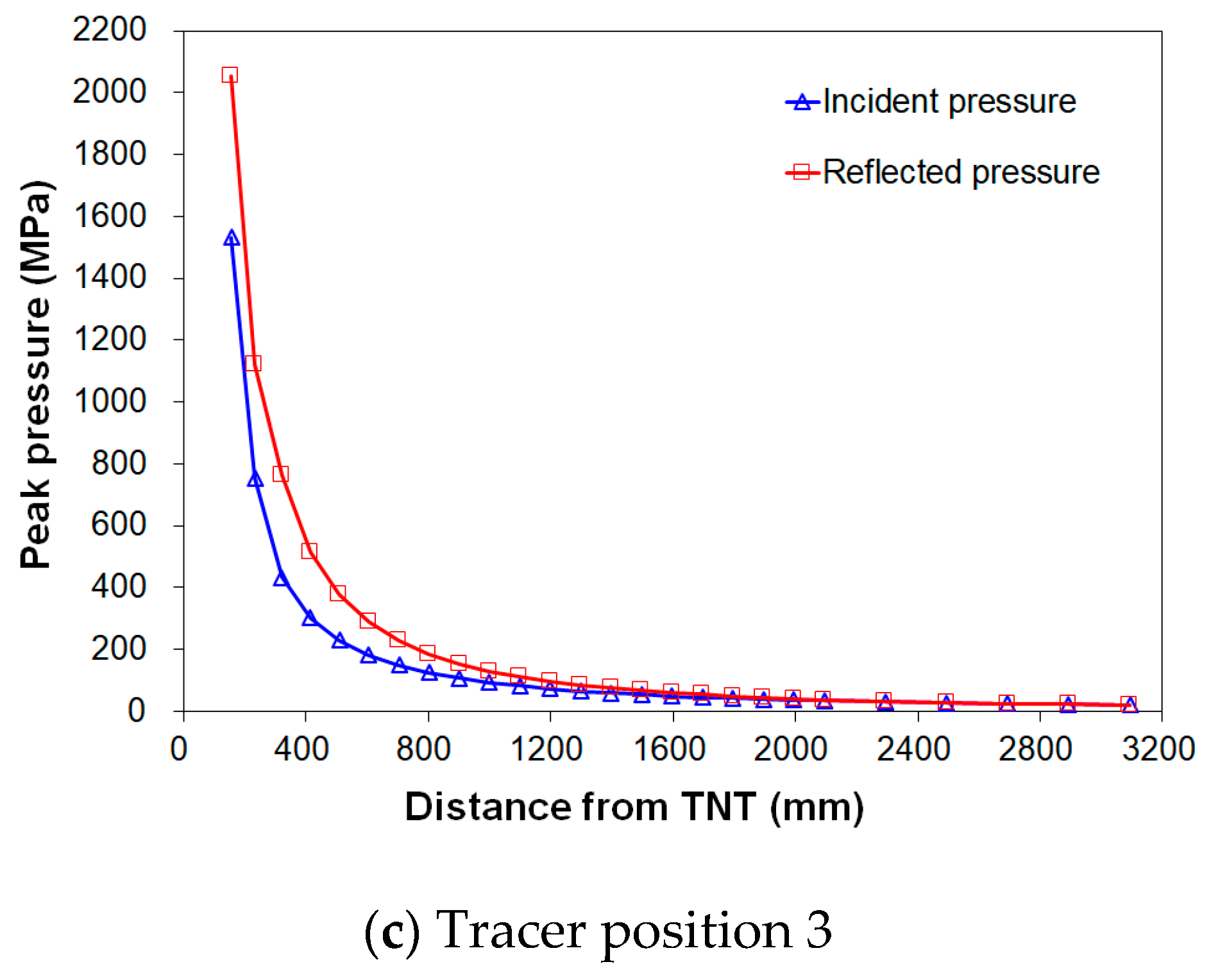
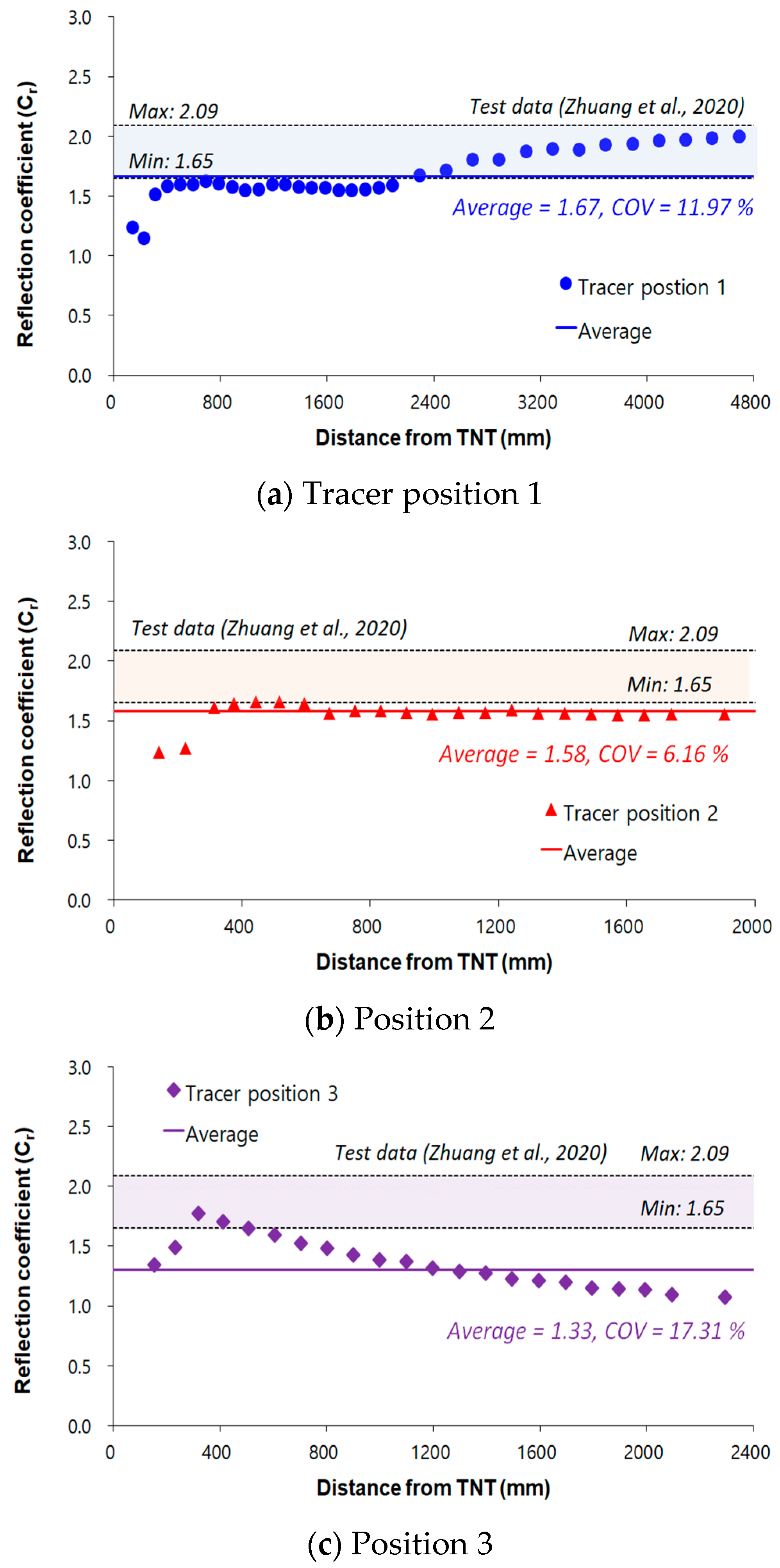
3.1.2. Attenuation and Amplification of the Pressure Waves
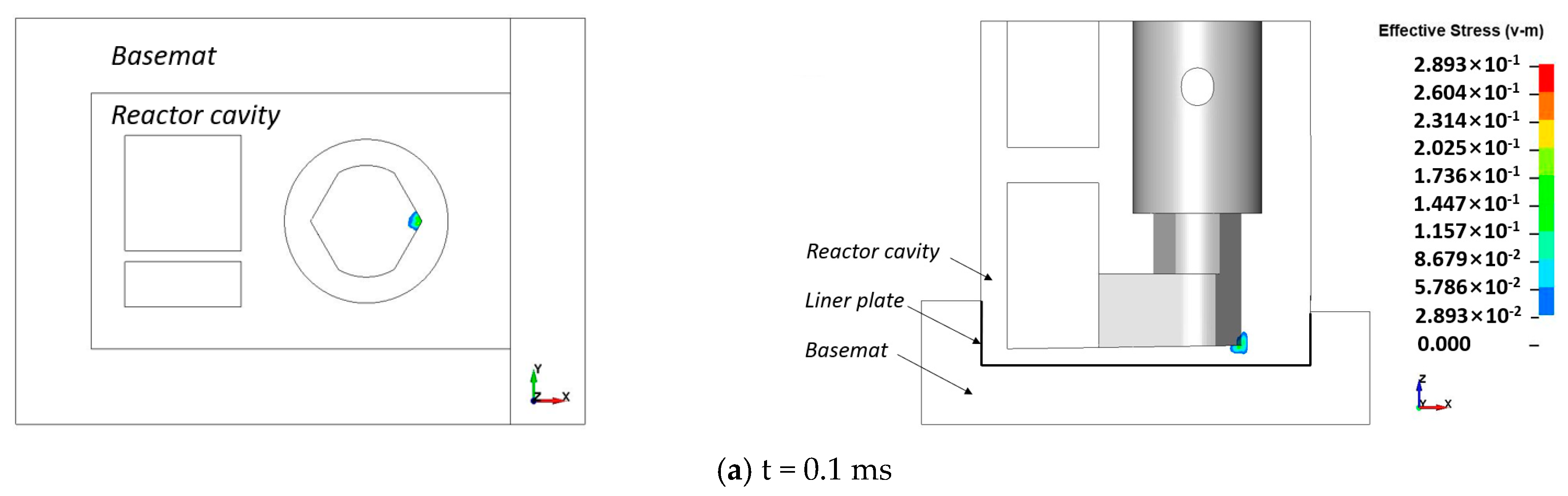
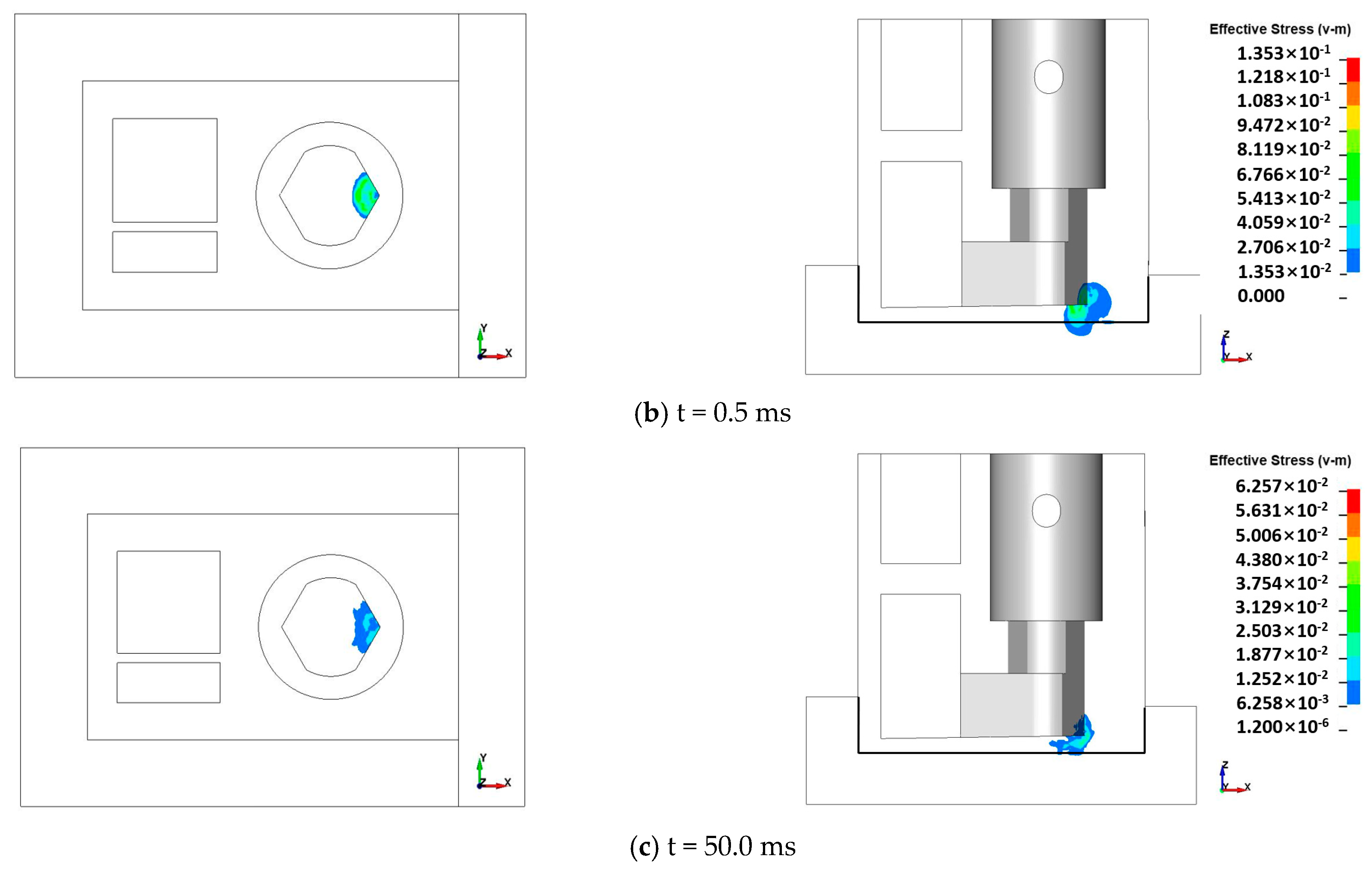
3.1.3. Effective Stress Wave Propagation
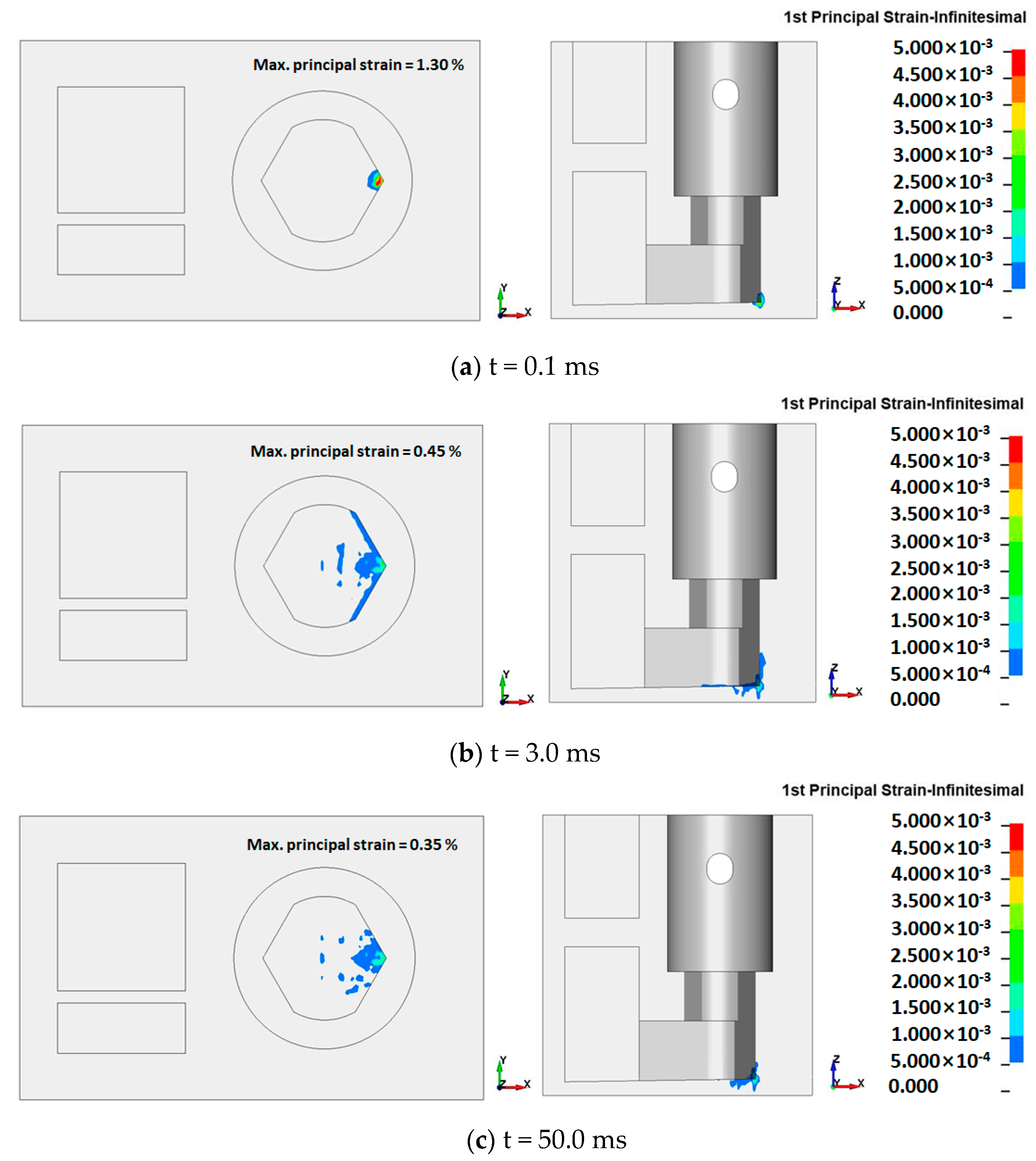
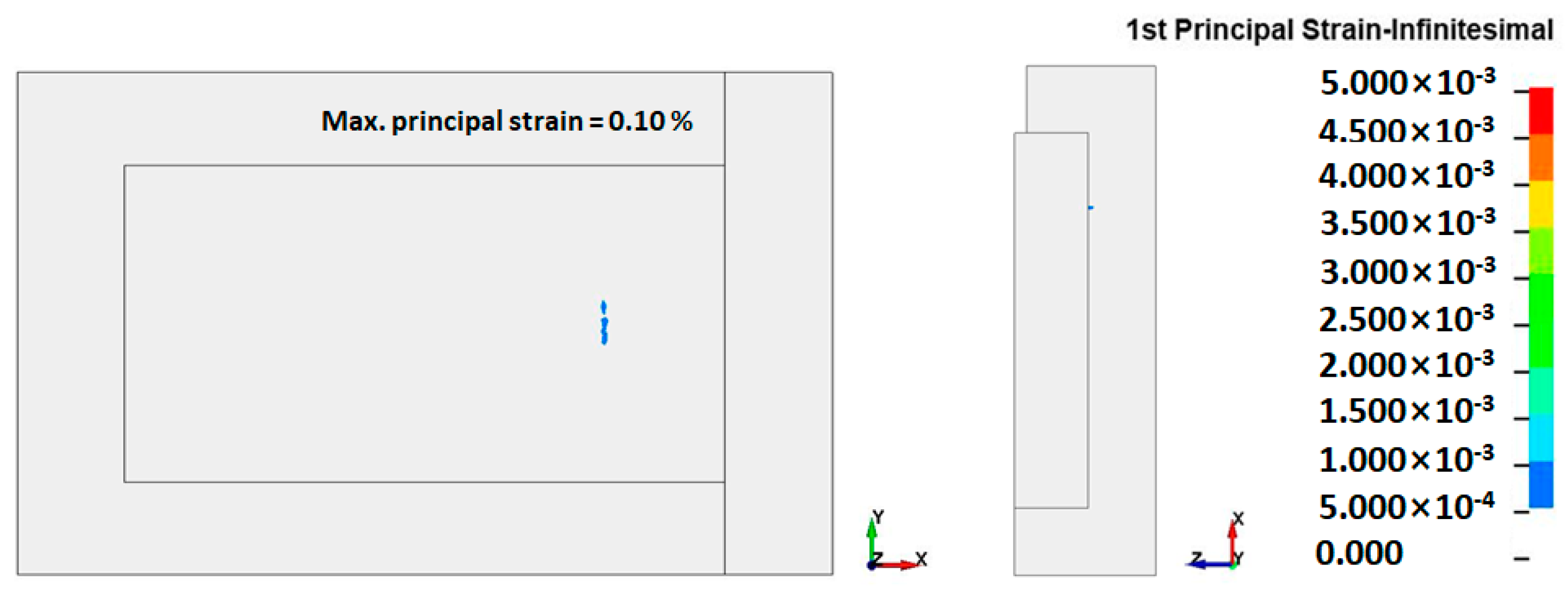
3.2. Damage Assessments
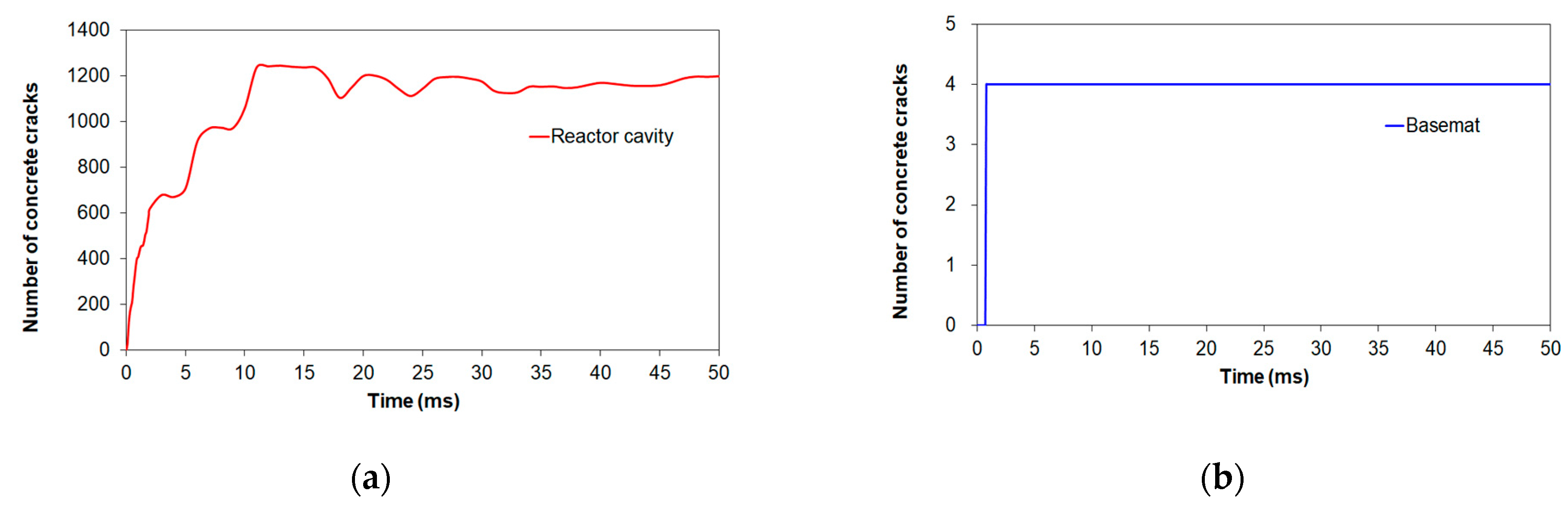
3.2.1. Damage Assessment of the Concrete
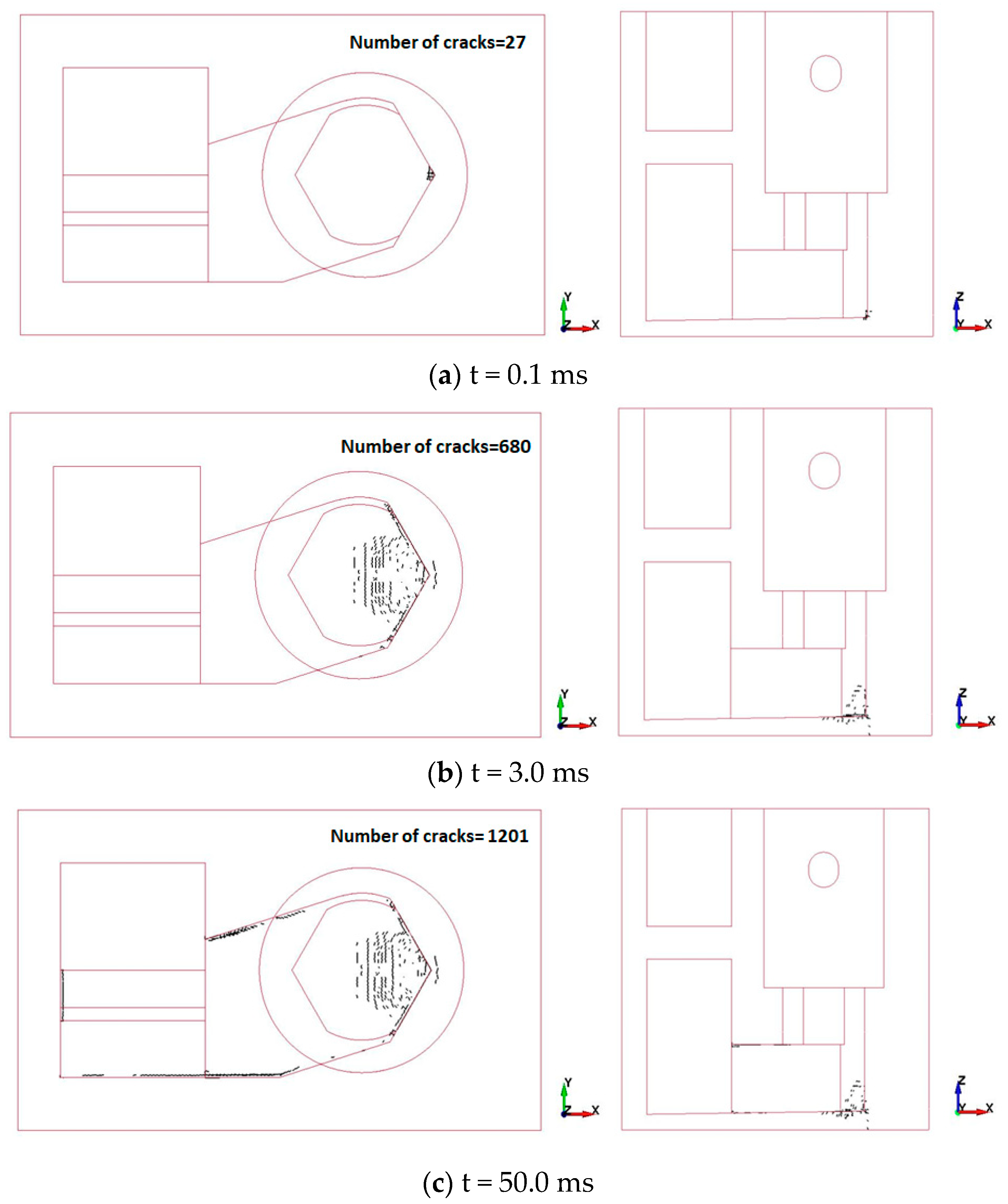
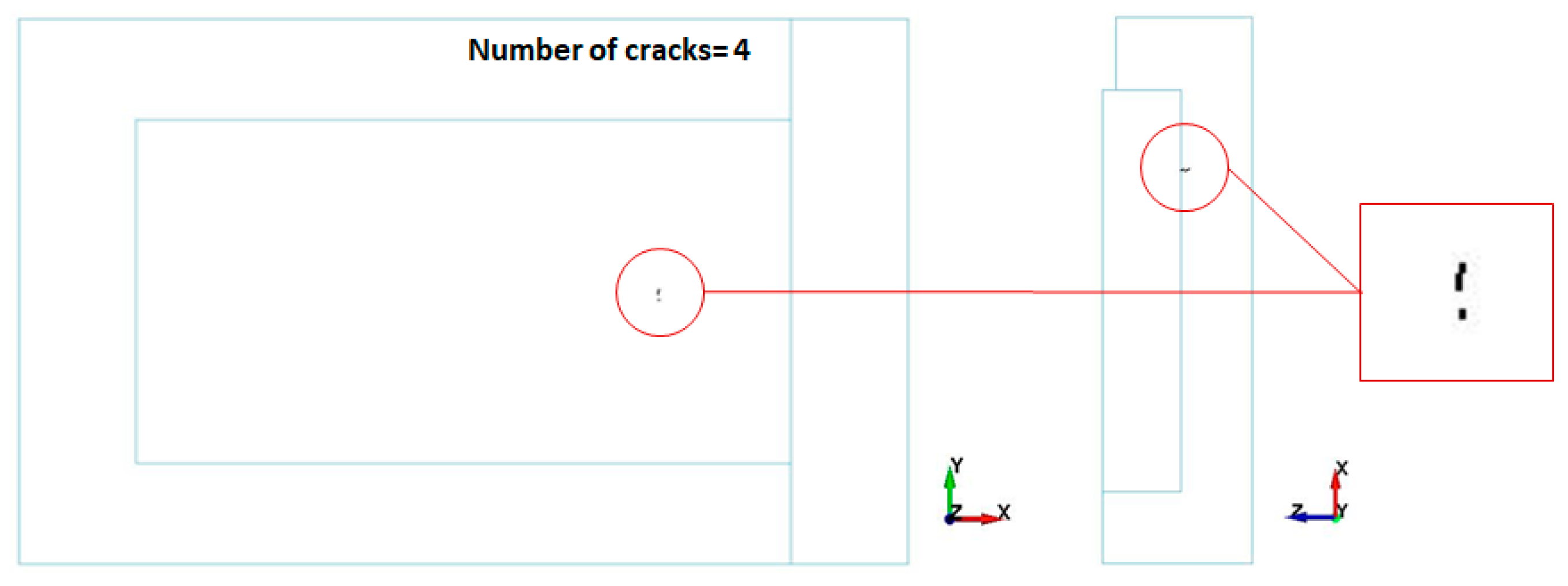
3.2.2. Damage Assessment of the Liner Plate and Reinforcement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- OECD/NEA. OECD Research Programme on Fuel-Coolant Interaction: SERENA Final Report; Organisation for Economic Co-operation and Development: Paris, France, 2007. [Google Scholar]
- Leskovar, M.; Uršič, M. Estimation of ex-vessel steam explosion pressure loads. Nucl. Eng. Des. 2009, 239, 2444–2458. [Google Scholar] [CrossRef]
- Kim, S.H.; Chang, Y.S.; Song, S.C.; Cho, Y.J. Structural assessment of fully flooded reactor cavity and penetration piping under steam explosion conditions. Int. J. Press. Vessels Pip. 2015, 131, 36–44. [Google Scholar] [CrossRef]
- Jung, J.H.; An, S.M.; Ha, K.S.; Kim, H.Y. Evaluation of heat-flux distribution at the inner and outer reactor cavity walls under the in-vessel retention through external reactor vessel. Nucl. Eng. Technol. 2015, 47, 66–73. [Google Scholar] [CrossRef]
- Kim, S.H.; Chang, Y.S.; Cho, Y.J.; Jhung, M.J. Modeling of reinforced concrete for reactor cavity analysis under energetic steam explosion condition. Nuc. Eng. Technol. 2016, 48, 218–227. [Google Scholar] [CrossRef][Green Version]
- Cizelj, L.; Končar, B.; Leskovar, M. Vulnerability of a partially flooded PWR reactor cavity to a steam explosion. Nucl. Eng. Des. 2006, 236, 1617–1627. [Google Scholar] [CrossRef]
- Chunyu, Z.; Pengb, C.; Juanhuab, Z.; Jimingb, L.; Yulanc, L.; Shishunb, Z.; Biao, W. Evaluation of the structural integrity of the CPR1000 PWR containment under steam explosion accidents. Nucl. Eng. Des. 2014, 278, 632–643. [Google Scholar]
- Corradini, M.L.; Murphy, J.; Nilsuwankosit, S. User’s Manual for TEXAS-V One Dimensional Transient Fluid Model; University of Wisconsin: Madison, WI, USA, 2002. [Google Scholar]
- Turland, B.D.; Dobson, G.P. Molten Fuel Coolant Interactions: A State-of-the-Art Report; EUR 16874 EN; European Commission: Luxembourg, 1996. [Google Scholar]
- Taleyarkhan, R.P. Vapor explosion studies for nuclear and non-nuclear industries. Nucl. Eng. Des. 2005, 235, 1061–1077. [Google Scholar] [CrossRef]
- Park, S.H.; Bang, K.H.; Cho, J.R. Structural Integrity Evaluation of a Reactor Cavity during a Steam Explosion for External Reactor Vessel Cooling. Energies 2021, 14, 3605. [Google Scholar] [CrossRef]
- IAEA. Safety Aspects of Nuclear Power Plants in Human Induced External Events: Assessment of Structures; Safety Reports Series. No. 87; International Atomic Energy Agency: Vienna, Austria, 2018. [Google Scholar]
- NEI (Nuclear Energy Institute). Methodology for Performing. Aircraft Impact Assessments for New Plant Designs; NEI 07-13, Rev. 8; Nuclear Energy Institute: Washington, DC, USA, 2011. [Google Scholar]
- Broadhouse, B.J.; Neilson, A.J. Modeling reinforced concrete structures in DYNA3D. In Proceedings of the DYNA3D User Group Conference, London, UK, 24 September 1987. [Google Scholar]
- Broadhouse, B.J.; Attwood, G.J. Finite Element Analysis of the Impact Response of Reinforced Concrete Structures using DYNA3D. In Proceedings of the Structural Mechanics in Reactor Technology (SMiRT) 12, Stuttgart, Germany, 15–20 August 1993. [Google Scholar]
- Athanasiou, E.; Teixeira-Dias, F.; Coghe, F.; Desmaret, L. Response of reinforced concrete structural elements to near-field and contact explosions. Int. J. Saf. Secur. Eng. 2016, 6, 418–426. [Google Scholar] [CrossRef]
- Schwer, L. Modeling Rebar: The forgotten sister in reinforced concrete modeling. In Proceedings of the 13th-International-LSDyna-Conference, Wien, Austria, 8–10 June 2014. [Google Scholar]
- Kral, P.; Husek, M. Concrete in Uniaxial and Triaxial Compression—Experimental and Numerical Analysis in Interaction with Material Parameter Optimization (Conference paper). In Proceedings of the Juniorstav 2017, Brno, Czech Republic, 26 January 2017; pp. 1–6. [Google Scholar]
- Hokes, F.; Kral, P.; Krnavek, O.; Husek, M. Improved Sensitivity Analysis in the Inverse Identification of the Parameters of a Nonlinear Material Model. Procedia Eng. 2017, 172, 347–354. [Google Scholar] [CrossRef]
- Dubec, B.; Maňas, P.; Štoller, J.; Zezulová, E.; Dvořák, P.; Hejmal, Z. Numerical Identification of Material Model Parameters of UHPFRC Slab under Blast Loading. Appl. Sci. 2023, 13, 70. [Google Scholar] [CrossRef]
- Jayasinghe, L.B.; Thambiratnam, D.P.; Perera, N.; Jayasooriya, J.H.A.R. Blast response of reinforced concrete pile using fully coupled computer simulation techniques. Comput. Struct. 2014, 135, 40–49. [Google Scholar] [CrossRef]
- CEB. Bullettin D’information 213/214 CEB-FIP Model Code 1990; Thomas Telford: London, UK, 1993. [Google Scholar]
- LS-DYNA. Keyword User’s Manual: Volume II, Material Models; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2017. [Google Scholar]
- Yin, H.; Ouyang, Y. Experimental and Numerical Study on Steel Fiber Concrete under Blast Loading. Buildings 2022, 12, 2119. [Google Scholar] [CrossRef]
- Dobratz, B.M.; Crawford, P.C. Properties of Chemical Explosives and Explosive Simulants; Lawrence Livemore National Laboratory: Livermore, CA, USA, 1985; pp. 8–23. [Google Scholar]
- Trevino, T. Applications of Arbitrary Lagrangian Eulerian (ALE) Analysis Approach to Underwater and Air Explosive Problems. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2000. [Google Scholar]
- Webster, K.G. Investigation of Close Proximity Underwater Explosion Effects on a Ship-Like Structure Using the Multi-Material Arbitrary Lagrangian Eulerian Finite Element Method. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 2007. [Google Scholar]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Yang, G.; Wang, G.; Lu, W.; Zhao, X.; Yan, P.; Chen, M. Cross-section shape effects on anti-knock performance of RC columns subjected to air and underwater explosion. Ocean Eng. 2019, 181, 252–266. [Google Scholar] [CrossRef]
- Olovsson, L.; Souli, M. ALE and fluid-structure interaction capabilities in LS-DYNA. In Proceedings of the 7th International LS-DYNA Users Conferences, Dearborn, MI, USA, 19–21 May 2002. [Google Scholar]
- Cole, R.H. Underwater Explosions; Princeton University Press: Princeton, NI, USA, 1948. [Google Scholar]
- Kinney, G.F.; Graham, K.J. Explosive Shocks in the Air, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Hwang, M.K.; Park, S.Y.; Park, I.K. Assessment of Steam Explosion Impact on KNGR Plant; KAERI/TR-1303/99; KAERI: Daejeon, Republic of Korea, 1999. [Google Scholar]
- OECD/NEA. OECD Research Programme on Fuel-Coolant Interaction Steam Explosion Resolution for Nuclear Applications—SERENA; OECD: Danvers, MA, USA, 2007. [Google Scholar]
- Bottin, M. Molten Corium Concrete Interaction: Investigation of convective heat transfer in a pool with gas sparging. In Proceedings of the 7th European Review Meeting on Severe Accident Research (ERMSAR-2015), Marseille, France, 24–26 March 2015. [Google Scholar]
- Park, H.S.; Chapman, R.; Corradini, M.L. Vapor Explosions in a One-Dimensional Large Scale Geometry with Simulant Melts; NUREG/CR-6623; University of Wisconsin: Madison, WI, USA, 1999. [Google Scholar]
- Rajendran, R.; Narasimhan, K. Deformation and Fracture Behavior of Plate Specimens Subjected to Underwater Explosion: A Review. Int. J. Impact Eng. 2006, 32, 1945–1963. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Kong, Y.; Li, H. Comparative study of the dynamic response of concrete gravity dams subjected to underwater and air explosions. J. Perform. Constr. Facil. 2014, 29, 04014092. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Wang, C.; Cui, W.; Cao, K.; Fang, X. Blast-induced damage and evaluation method of concrete gravity dam subjected to near-field underwater explosion. Eng. Struct. 2020, 209, 109996. [Google Scholar] [CrossRef]
- Wood, S.L. Cavitation Effects on a Ship-Like Box Structure Subjected to an Underwater Explosion, in Mechanical Engineering. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 1998. [Google Scholar]
- Zhuang, T.S.; Wang, M.Y.; Wu, J.; Yang, C.Y.; Zhang, T.; Gao, C. Experimental investigation on dynamic response and damage models of circular RC columns subjected to underwater explosions. Def. Technol. 2020, 16, 856–875. [Google Scholar] [CrossRef]



| Property | Reactor Cavity and Basemat |
|---|---|
| Density (kg/m3) | 2400 |
| Poisson’s ratio | 0.18 |
| Compressive strength () (MPa) | 57.2 |
| Initial tangent modulus (TM) (GPa) | 40 |
| Uniaxial tensile strength (UTS) (MPa) | 4.86 |
| Coefficient as a function of maximum aggregate diameter (GF0) (N/m) | 32 |
| Fracture energy (GF) (GPa-mm) | 1.186 × 10−4 |
| Property | Reinforcement | Liner Plate |
|---|---|---|
| Density (kg/m3) | 7840 | 7840 |
| Modulus of Elasticity (GPa) | 200 | 200 |
| Poisson’s Ratio | 0.3 | 0.3 |
| Yield Stress (MPa) | 469 | 310 |
| Ultimate Tensile Strength (MPa) | 510 | 372 |
| Tangent Modulus (MPa) | 864 | 325 |
| Tracer Position | Reflection Coefficient (Cr) | ||||
|---|---|---|---|---|---|
| Number of Tracers | Minimum | Average | Maximum | Coefficient of Variation (%) | |
| 1 | 34 | 1.14 | 1.67 | 1.99 | 11.97 |
| 2 | 32 | 1.24 | 1.58 | 1.72 | 6.16 |
| 3 | 27 | 0.95 | 1.30 | 1.77 | 17.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, S.-K.; Yoon, Y.-H. Numerical Simulation of Pressure Wave Propagation and Its Effect on Damage to the Reactor Cavity under TNT Detonation for Steam Explosion. Buildings 2023, 13, 2152. https://doi.org/10.3390/buildings13092152
Ha S-K, Yoon Y-H. Numerical Simulation of Pressure Wave Propagation and Its Effect on Damage to the Reactor Cavity under TNT Detonation for Steam Explosion. Buildings. 2023; 13(9):2152. https://doi.org/10.3390/buildings13092152
Chicago/Turabian StyleHa, Seong-Kug, and Yeo-Hoon Yoon. 2023. "Numerical Simulation of Pressure Wave Propagation and Its Effect on Damage to the Reactor Cavity under TNT Detonation for Steam Explosion" Buildings 13, no. 9: 2152. https://doi.org/10.3390/buildings13092152
APA StyleHa, S.-K., & Yoon, Y.-H. (2023). Numerical Simulation of Pressure Wave Propagation and Its Effect on Damage to the Reactor Cavity under TNT Detonation for Steam Explosion. Buildings, 13(9), 2152. https://doi.org/10.3390/buildings13092152







