State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections
Abstract
:1. Introduction
1.1. History of Cold-Formed Steel (CFS) Sections
1.2. Overview of Cold-Formed Steel (CFS) Structures
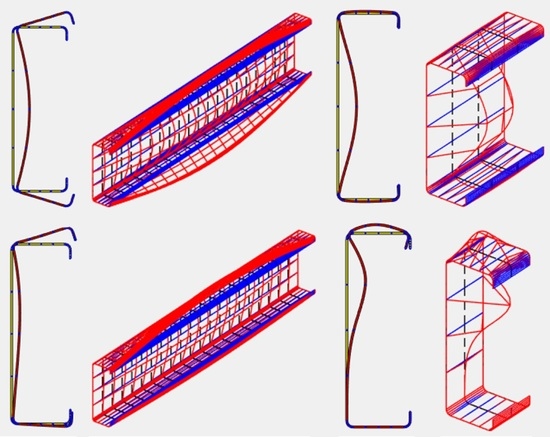
2. Buckling Phenomena in Cold-Formed Steel (CFS) Members
2.1. Local Buckling Behavior
2.2. Distortional Buckling Behavior
2.3. Global Buckling Characteristics
- Flexural Buckling: This mode occurs when a compression element (column) laterally flexes without changing or twisting its cross-sectional shape. It typically happens when the column is slender and subjected to axial compression forces.
- Torsional Buckling: In this mode, a compression member simultaneously bends and twists without changing the form of its cross-section. It occurs in columns that are slender and have significant axial torsional forces acting on them.
- Flexural-Torsional Buckling: This mode is a combination of flexural and torsional buckling, where both bending and twisting occur simultaneously in a compression member without altering its cross-sectional shape.
- Lateral-Torsional Buckling: This mode occurs in flexural members like beams when they are subjected to combined lateral bending and torsional moments. The beam twists about its shear center while also deflecting out of the plane of bending.
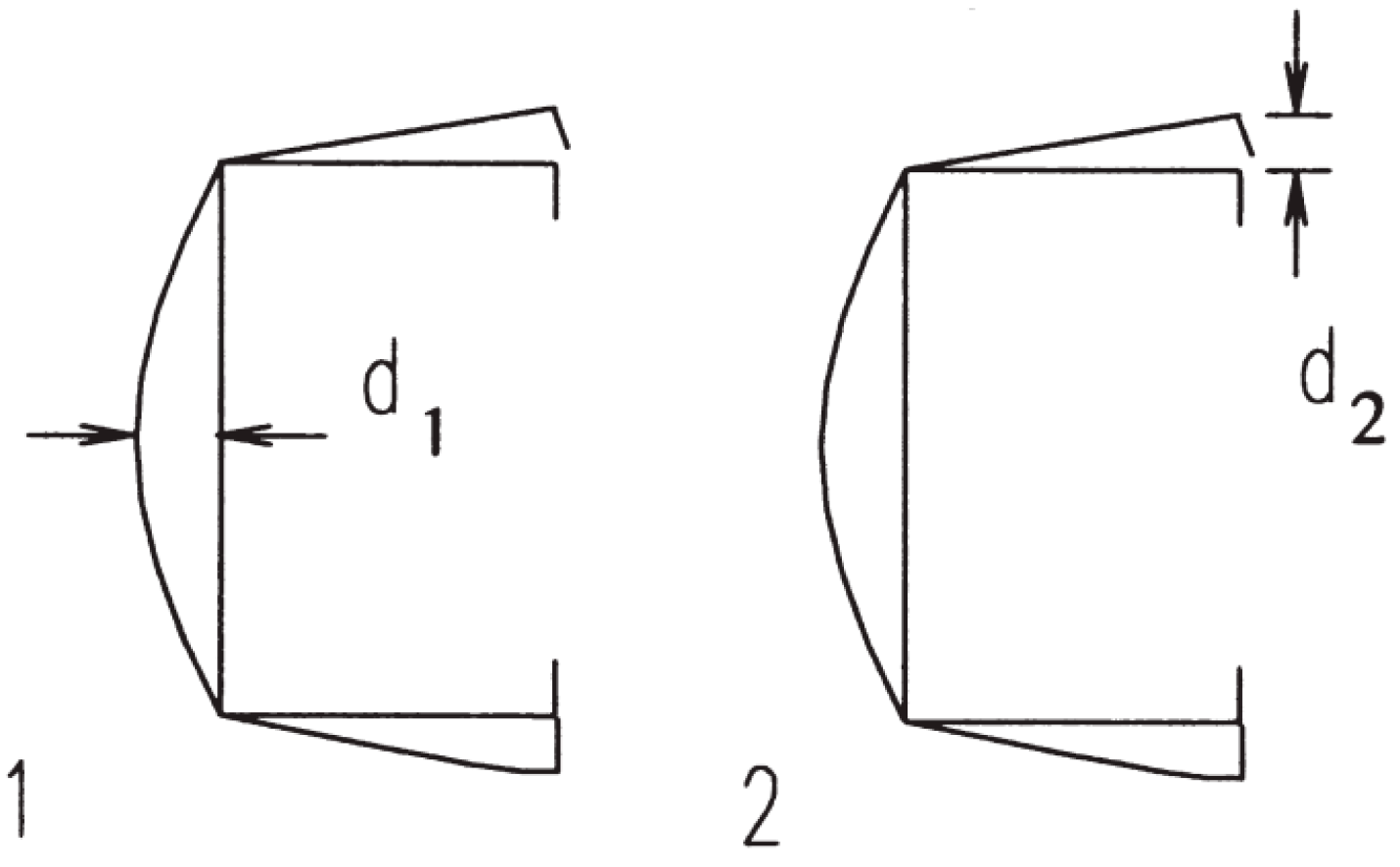
3. Behavior of Cold-Formed Steel (CFS) Members with Web Holes
3.1. Bending Response of CFS Members
3.2. Web Crippling Phenomenon in CFS Elements
3.3. Shear Behavior of CFS Sections
4. Design Considerations for Strength and Stability in Cold-Formed Steel (CFS) Structures
4.1. Effective Width Method (EWM) in CFS
4.2. Direct Strength Method (DSM) in CFS
4.3. Factors Affecting the Strength of CFS Members
4.4. Effect of Contact between CFS Sections in Assemblies
4.5. Influence of End Conditions and End Fastener Groups (EFGs)
4.6. Effects of Different Geometric Shapes on CFS Performance
4.7. Temperature Effects on CFS Behavior
4.8. Impact of Connectors on CFS Structural Performance
4.9. Influence of Connector Spacing on Composite Action in CFS Systems
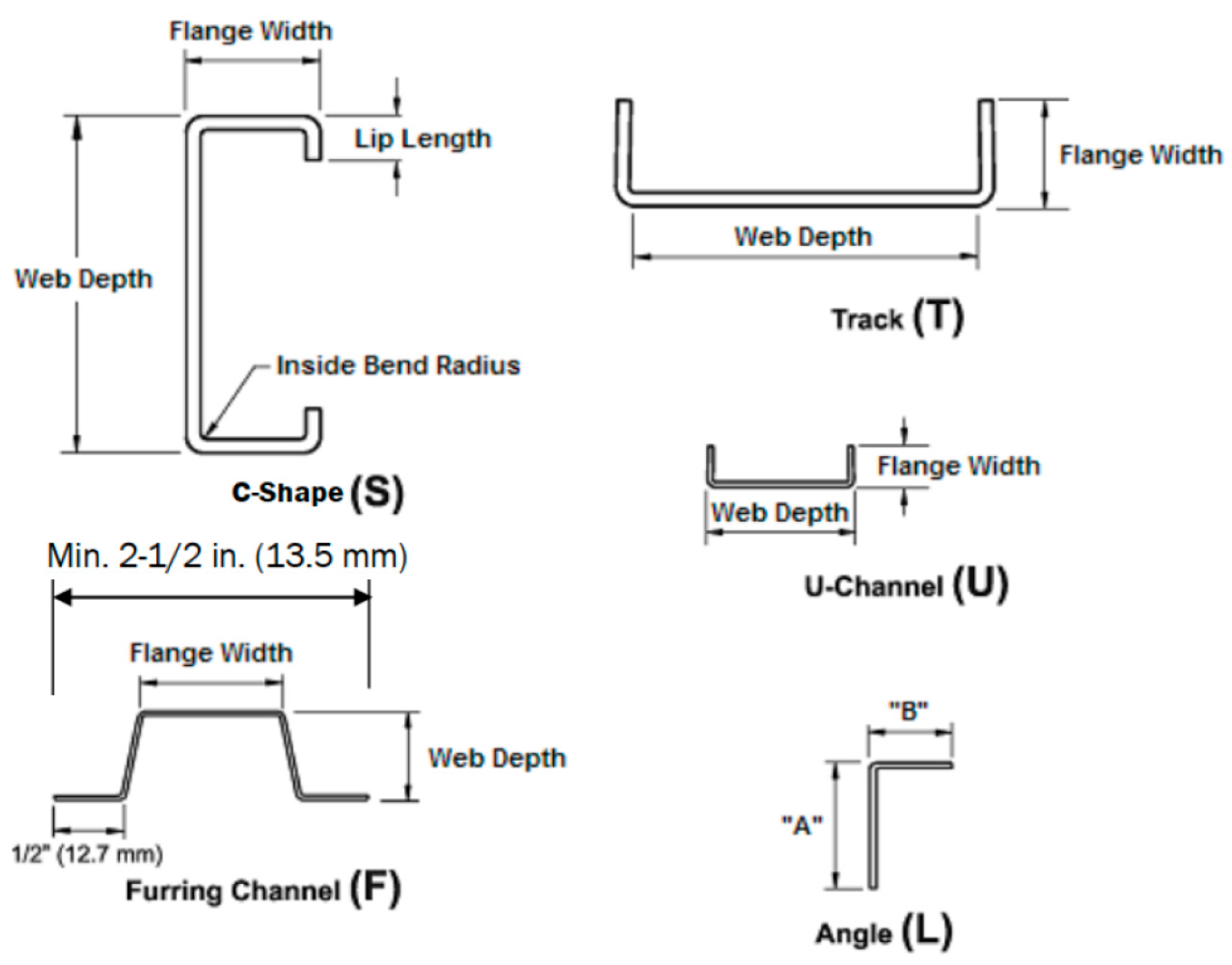
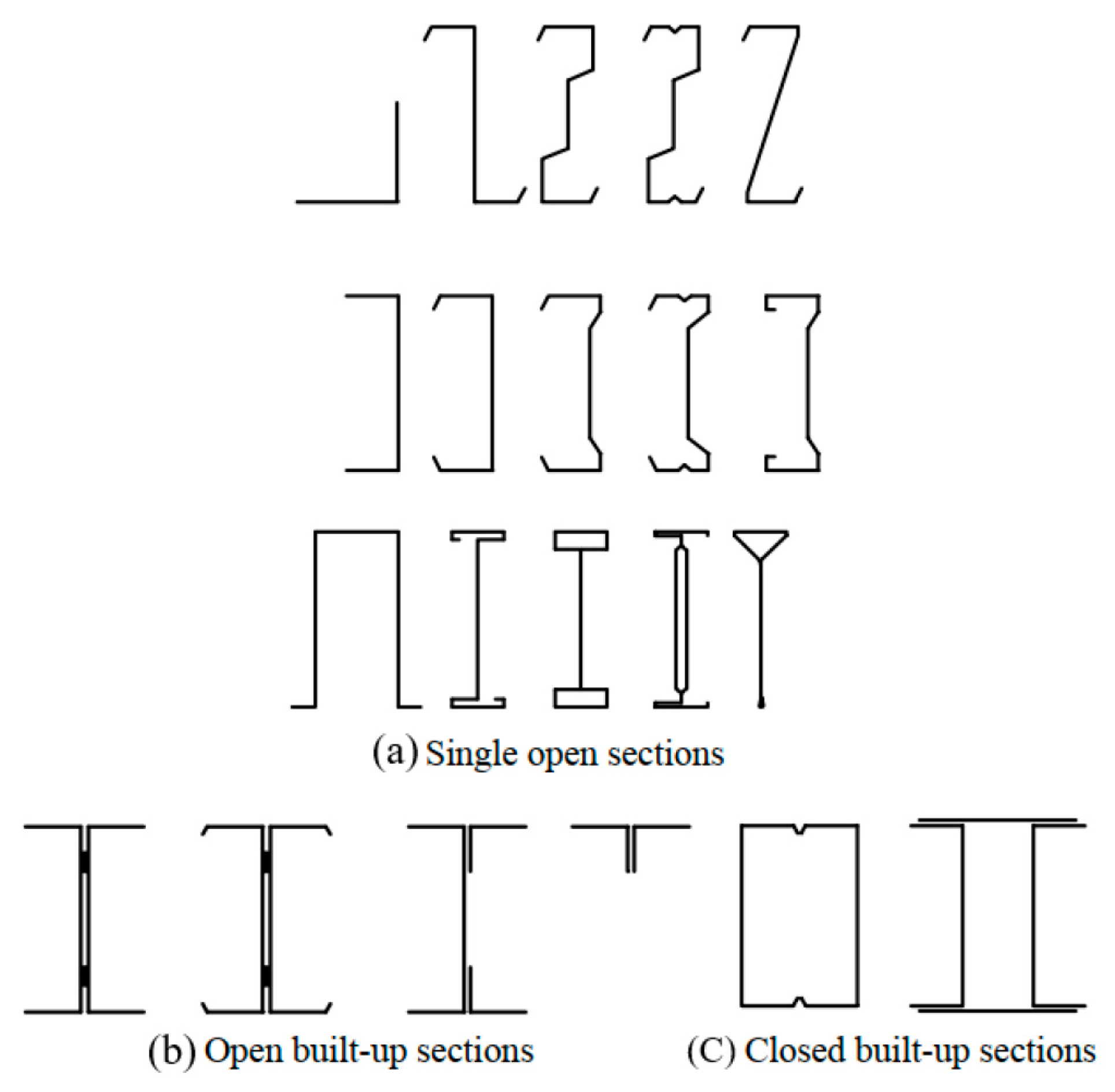
5. Types and Configurations of Cold-Formed Steel (CFS) Sections
5.1. Advantages of Cold-Formed Steel (CFS) Sections in Structural Applications
- High Ratio of Strength to Weight: Cold-formed steel sections have a great ratio of strength to weight, ensuring the integrity of the structure whilst reducing the weight of the overall construction. This advantage is crucial in applications where lightweight materials are desired to reduce foundation requirements, transportation costs, and assembly time [3,14,49,54,58,59].
- Sustainability: CFS members are environmentally friendly and sustainable. They might be recycled indefinitely without losing their structural properties, reducing waste and conserving natural resources. Additionally, their lightweight composition contributes to lower carbon emissions during transportation and construction processes [3,58,59,60,61].
- At room temperature, there is neither shrinkage nor creep, resulting in more accurate detailing [3].
5.2. Disadvantages of Cold-Formed Steel (CFS) Sections in Construction
- Reduced Ductility: Sections made of cold-formed steel generally exhibit lower ductility as compared to sections made of hot-rolled steel. This reduced ductility may limit their ability to absorb energy during seismic events or high-impact loads, requiring careful design and detailing to ensure structural performance [20,64,65].
- Sensitivity to Corrosion: In particular, cold-formed steel sections can corrode in moist or corrosive situations. The adequate use of safeguards like coatings, galvanization, or corrosion-resistant materials must be employed to enhance their durability and longevity [62].
- Thermal Conductivity: In comparison with some other types of building materials, cold-formed steel sections have a higher heat conductivity. This property can lead to increased heat transfer through the building envelope, necessitating additional insulation to maintain energy efficiency [53].
- Limited Availability of Design Codes: In some regions, design codes and standards specifically tailored for CFS elements may be limited as opposed to traditional steel sections made of hot-rolled. Designers must carefully navigate existing codes and ensure proper implementation of relevant design provisions [46,66,67].
5.3. Manufacturing Process of Cold-Formed Steel (CFS) Elements
- Material selection: The first step in the manufacturing process is selecting the appropriate steel material. Cold-formed steel sections are typically made from low-carbon steel, which can be easily cold-formed without cracking or breaking.
- Strip preparation: The selected steel material is first cleaned and processed into strips of the required thickness and width. The strips are then straightened to ensure they are perfectly flat.
- Roll forming: The next step is roll forming, the process involves the passage of steel strips through a sequence of rollers in order to obtain the desired configuration. The rollers apply pressure to the steel strips, causing them to bend and form into the desired shape.
- Cut-to-length: Once the steel sections have been formed, the materials are trimmed to the specified dimensions with a cutter or other cutting equipment.
- Post-processing: After the steel sections have been cut to length, they may undergo additional processing, such as punching or drilling holes, bending, or welding, depending on the specific requirements of the application.
- Quality control: Throughout the manufacturing process, quality control checks are performed to ensure that the steel sections meet the required specifications for strength, dimensions, and surface finish.
- Packaging and shipping: Finally, the finished steel sections are packaged and shipped to the customer, ready for use in construction or other applications.
5.4. Material Properties of Cold-Formed Steel (CFS) Materials
- Yield Strength: CFS members have a high yield strength; this denotes the amount of stress the steel can withstand without permanent deformation. The yield strength of CFS sections typically varies between 230 and 550 N/, depending on the kind and thickness (t) of steel used.
- Tensile Strength: The tensile strength of CFS elements concerns the stress levels the steel can withstand before breaking. The tensile strength of CFS members varies between 310 and 700 N/, depending on the type and thickness of the steel used.
- Elastic modulus is a measure of the steel’s stiffness. It refers to the stress quantity necessary to induce a predetermined strain amount in the steel. The elastic modulus for CFS members varies between 190 and 210 GPa.
- Ductility: it is the steel’s ability to deform without fracturing. Cold-formed steel sections have good ductility, which allows them to absorb energy during loading and reduce the risk of catastrophic failure.
- Fatigue Strength: CFS members’ fatigue strength refers to their ability to withstand repeated loading without failure. CFS sections’ static strength is often higher than their fatigue strength, and it depends on numerous variables, including loading types, the section’s geometry, and the surface conditions.
- Corrosion Resistance: CFS members are susceptible to corrosion, which can reduce their strength and durability. To mitigate this, coatings and surface treatments are often applied to the steel.
- Fire Resistance: Cold-formed steel sections have relatively low thermal conductivity, which means they are slow to heat up and transfer heat. This makes them a good choice for structures that require fire resistance.
6. Composite Action in Cold-Formed Steel (CFS) Structures
6.1. Filling and Sheathing of CFS Sections
6.2. Challenges of Inadequate Guidelines for CFS Composite Elements
6.3. Stiffeners in CFS Assemblies
6.4. Conservative
7. Connection Types and Methods Used in Cold-Formed Steel (CFS) Sections
7.1. Screw Connections in CFS Components
7.2. Welded Connections for CFS Members
7.3. Riveted Connections in CFS Structures
7.4. Bolted Connections for CFS Applications
7.5. Clip Connections in Cold-Formed Steel (CFS) Systems
8. Design Considerations for Screw Spacing and Fastener Restrictions
8.1. Effects of Fastener Spacing on Compression Strength and Buckling
8.2. Impact of Screw Spacing on CFS Built-Up Column Capacities
8.3. Screw End Distance Impact
9. Failure Modes and Design Considerations for Built-Up CFS Columns and Bolted Connections
10. Methodology Employed in the Study of CFS Structures
- Global Buckling (GB): The critical buckling load, , can be found using the formula . The formula may be used to calculate the critical buckling load, which is denoted by the letter . Next, calculate the slenderness ratio using the formula . If is greater than 1.5, then the nominal compressive strength, , is equal to times . If is less than or equal to 1.5, then is equal to times . The design strength, represented by the variable , is commonly determined through the multiplication of the factors and . The final step is to apply the capacity-reducing ratio to using a formula: = 0.85 times .
- Local Buckling (LB): The nominal strength in compression refers to the maximum amount of compressive stress that a material can withstand before failure occurs, is equal to . The design strength, denoted as , might have determined by multiplying the product of and . Next, calculate the slenderness ratio using the formula . If the value of is equal to or below 0.776, then the nominal strength, denoted as , is equivalent to . If is greater than 0.776, then is equal to times times . Finally, the capacity-reducing ratio is multiplied to using a formula: = 0.85 times .
- Distortional Buckling (DB): Calculate the slenderness ratio using the formula . If is equal to or below 0.561, then the nominal strength, , is equal to . If is greater than 0.561, then is equal to times times . Finally, the capacity reduction factor is multiplied to using a formula: = 0.85 times .
- The initial type of buckling under consideration pertains to global buckling. In the determination of the critical load, (buckling resistance), the following steps are undertaken. Firstly, the critical moment, denoted as , is ascertained, along with the section modulus, , specific to the structural element in question. Subsequently, the critical axial force, , is computed as the ratio of to . Additionally, is established as the product of the shape factor, , and the yield strength, , of the material.To evaluate , a set of conditions is established based on the relationship between and . If exceeds or equals 2.78 times , is assigned a value equal to . Conversely, if is less than or equal to 0.56 times , is determined as equal to . In cases where falls between 0.56 times and 2.78 times , is calculated as 10/9 times times .Once is determined, the nominal moment strength, , is computed as the product of the shape factor, , and . To finalize the assessment, if is less than or equal to , is adopted as the nominal strength. Subsequently, the resistance factor, , is applied to derive , with the expression = 0.90 * .
- The subsequent category of buckling under consideration pertains to local buckling phenomena. To determine the nominal moment strength, , our initial step involves determining the length factor that is effective, denoted as . The value of is obtained by taking the square root of the ratio between and . If is equal to or below 0.776, then is the LB’s nominal strength with respect to bending, is equal to . If is greater than 0.776, then is equal to times times . After obtaining the , the resistance factor () is then used to calculate , which represents 0.90 times the value of
- The subsequent kind of buckling that will be analyzed is distortional buckling. In order to ascertain the nominal moment strength, denoted as , the first step involves calculating the slenderness ratio by the use of the formula . If is equal to or below 0.673, then the DB’s nominal strength with respect to bending , is equal to . If is greater than 0.673, then is equal to times times . Finally, the resistance factor is applied to using the formula is equal to 0.90 times .
10.1. Example 1: Determining Nominal Axial Strength in Cold-Formed Steel Members
- = 50 KSi (34,473.8 MPa).
- = 48.891 Kips (217,478 N),
- or
- where: .
- = 0.85 * 25.552 = 21.719 Kips (96,611 N).
- = 43.622 Ksi (300.76 Mpa)
- = 0.978 * 43.622 = 42.662 Kips (189,770 N).
- = 0.85 * 42.662 = 36.263 Kips (161,305.9 N)
- = = 1.89
- If then , but = 1.89
- If , then
- = 23.323 Kips (103,745.9 N)
- where: .
- = 0.85 * 23.323= 19.824 Kips (88,181.6 N)
- = = 1.645
- If , then , but
- When , then
- = 23.193 Kips (103,167.6 N)
- = 0.85 * 23.193 = 19.714 Kips (87,692.2 N).
- is the minimum of ( = 36.263 Kips (161,305.9 N), = 19.824 Kips (88,181.6 N), = 19.714 Kips (87,692.2 N)).
- Distortional Buckling controls the member, then = 19.714 Kips (87,692.2 N).
10.2. Example 2: Calculating Nominal Flexural Strength in Cold-Formed Steel Elements
- = 55 Ksi (379.2 Mpa).
- = 48.891 Kips (217,478 N), or
- = = 256.576 Kips*in. (28,989,195.5 N*mm),
- or
- = 221.184 Kips*in (24,990,436.42 N*mm)
- Where: .
- = 0.90 * 221.184 = 199.066 Kips*in (22,491,392 N*mm).
- = 254.65 Kips*in (28,771,587 N*mm)
- = 0.90 * 166.194= 149.575 Kips * in (16,899,706 N*mm)
- = = .
- = = 0.785
- For , then , but
- When ,
- = 164.980 Kips*in (18,640,237 N*mm)
- Where: .
- = 0.90 * 164.980 = 148.482 Kips*in (16,776,213.4 N*mm)
- = = 1.078
- If , then , but = 1.078 > 0.673
- When > 0.673,
- = 188.047 Kips*in (21,246,458.2 N*mm).
- = 0.90 * 188.047 = 169.242 Kips*in (19,121,778.4 N*mm)
- is the minimum of ( = 149.575 Kips * in (16,899,706 N*mm), = 148.482 Kips*in (16,776,213.4 N*mm), = 169.242 Kips*in (19,121,778.4 N*mm)).
- Local Buckling controls the member, then = 148.482 Kips*in (16,776,213.4 N*mm).
11. Discussion of Findings and Results
12. Conclusions and Key Takeaways from the Study
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | Definitions |
| LB | Local buckling |
| DB | Distortional buckling |
| FB | Flexural buckling |
| FT | Flexural-Tortional buckling |
| DL | Distortional-Lateral buckling |
| LF | Lateral-Flexural buckling |
| DF | Distortional-Flexural buckling |
| FTL | Flexural-Tortional + Lateral buckling |
| FTD | Flexural-Tortional + Distortional buckling |
| FFT | Flexural + Flexural-Tortional buckling |
| cross-sectional area in gross | |
| area of the flange | |
| area of the hole | |
| the opening’s area | |
| area of the web | |
| b | rectangular opening’s horizontal dimension |
| the net member’s warping stiffness | |
| d | the diameter of a round hole or the size of a square hole |
| E | Young’s elasticity modulus |
| web’s flexural stiffness | |
| the flange’s rectangular opening’s torsional stiffness | |
| h | the web’s flat depth |
| depth of the web stiffener | |
| the gross cross-section’s moment of inertia | |
| net cross-sectional moment of inertia at a hole | |
| the torsional constant of St. Venant, includes the effect of openings | |
| coefficient of shear buckling of the section without the opening | |
| coefficient of shear buckling of the section with the opening | |
| L | span or length of the section ( |
| length of the column member with no openings | |
| length of the column part with openings | |
| Global Buckling’s (GB) Half-Wavelength | |
| Distortional Buckling’s (DB) Half-Wavelength | |
| Local Buckling’s (LB) Half-Wavelength | |
| DB’s critical elastic moment | |
| DB’s critical elastic moment with holes’ impact | |
| DB’s critical elastic moment with no holes’ impact | |
| LTB’s critical elastic moment with openings’ impact | |
| LTB’s Critical elastic moment | |
| LB’s critical elastic moment with openings’ impact | |
| , | LB’s critical elastic moment with no openings’ impact |
| DB’s nominal flexural strength | |
| LTB’s nominal flexural strength | |
| is the LB’s Critical elastic moment | |
| LB’s nominal flexural strength | |
| the bottom or top segment below or above the holes’ (with the lips and the flanges) plastic flexure moment capability | |
| Member plastic moment | |
| , | nominal flexural strength |
| ) | |
| , | Positive flexural strengths are required |
| flexural strengths that are available around centroidal axes | |
| The flexural strengths pertaining to centroidal axis that are currently accessible with or | |
| Required bimoment strength [bimoment due to factored loads] taken as positive | |
| available bimoment strength [factored resistance] | |
| the greatest longitudinal fastener spacing | |
| Moment of yielding for net cross-sectional | |
| Plastic section modulus | |
| Modulus of elasticity of the whole, unreduced fiber segment under very high compression | |
| Full unreduced cross-sectional elastic modulus in relation to the extreme fiber in the initial yield | |
| yielding stress | |
| Compressive stress | |
| Elastic global (FTB, or TB, FB) stress | |
| N | bearing plate’s length |
| n | the load (support) plate’s effective length |
| Column force critical for elastic DB | |
| DB’s critical elastic load for a section with opening | |
| DB’s critical elastic load for a section with no opening | |
| GB’s critical elastic load for a section with opening | |
| GB’s critical elastic load of the column | |
| LB’s critical elastic load of the column | |
| LB’s critical elastic load for a section with opening | |
| LB’s critical elastic load for a section with no opening | |
| Theoretical estimates of web-holed section compression resistance [95] | |
| DB’s nominal axial strength | |
| GB’s nominal axial strength | |
| , | LB’s nominal axial strength |
| the section’s compression resistance with web opening | |
| axial compressive strength measured in a positive direction | |
| Nominal Axial Strength | |
| axial strength available | |
| ) | |
| net cross-section’s yield strength | |
| the web hole’s edge-stiffener’s length | |
| factor for reducing shear strength | |
| proposed reduction factor for web crippling strength | |
| The inner corner radius refers to the curvature between the web and the edge-stiffener of an opening | |
| spacing of the opening | |
| s | clear spacing of the opening |
| t | thickness of the web |
| thickness equivalence | |
| thickness of the flange | |
| The shear forces acting at each opening’s edge | |
| a web’s nominal resistance to shear [96,97] | |
| The shear capacity of a section is diminished when it has an opening. | |
| element’s shear capability with no opening | |
| shear that was performed over the hole using the Vierendel mechanism | |
| shear that was performed over the hole using the Vierendel mechanism for the member characterized by the ratio of hole diameter (d) to section height (h) equal to 0.6. | |
| shear that was performed over the hole using the Vierendel mechanism for the member characterized by the ratio of dh/h equal to m. | |
| The shear load capacity for the section with no openings. | |
| The shear load capacity for the section with openings. | |
| The horizontal clear space between the web openings and the edge of the bearing plate. | |
| g | The vertical distance refers to the measurement between two rows of connectors that are located closest to the top and bottom flanges. |
| connection’s available tension strength | |
| m | The measurement of the distance between the shear center of a C-section and the mid-plane of its web. |
| q | Determine the longitudinal spacing of fastener based on the intended load on the beam. |
| reduced moment of inertia in determining the global buckling force | |
| I | the built-up component’s Moment of inertia around the flexural buckling axis |
| KL | The length of the built-up part that is effective for the axis of the flexural buckling |
| r | The radius of gyration of the built-up member’s complete unreduced cross-sectional area around the axis of flexural buckling. |
| a | spacing between sections for shear-bearing welds or intermediate fasteners |
| Minimum radius of gyration of an individual shape’s complete unreduced cross-sectional area in a built-up member | |
| Flexural strength that is available for a built-up part around the axis of buckling with | |
| Q | For the gross built-up cross-section, the initial moment of area of linked shapes around the buckling axis |
| Gross built-up cross-section moment of inertia around the buckling axis |
Appendix A
| References | Rules | Comments |
|---|---|---|
| [7] | Yielding and Global (FB, TB, or FTB) | |
where | Yielding and Global Buckling Interacting with LB | |
where | Distortional Buckling | |
| [98] | ||
| [95] | (F, T, or FT) buckling | |
| LB | ||
| distortional buckling | ||
| [99] | (F, T, or FT) buckling | |
| local buckling | ||
| distortional buckling | ||
| [100] | ||
| [101] | global flexural buckling | |
| flexural–torsional buckling | ||
| distortional buckling | ||
| local buckling |
| References | Rules | Comments |
|---|---|---|
| [7] | Where: , where: , where: , | Yielding and Global (LTB). Capability till the first yield |
| For ; | Yielding and Global (LTB). Reserve capacity that is inelastic. | |
Where: , Where: , | LB Interacting with GB. | |
Where: 0, Where: > 0.6730, | Distortional Buckling | |
| [23] | built-up sections, local buckling | |
| [102] | local buckling | |
; | distortional buckling | |
| [101] | lateral–torsional buckling | |
| distortional buckling | ||
| [103] | local buckling |
| References | Rules | Comments |
|---|---|---|
| [104] | ❶ ❷ | ITF |
| [105] | ❸ ❹ | ITF |
| [106] | ❸ ❹.0 | ITF |
| [107] | ❺: | (ITF) |
| ❸ ❹ | ||
| ❻: | ||
| ❸ ❹ | ||
| [108] | ❺ ❻ | ITF, edge–stiffened holes |
| [109] | IOF | |
| [110] | IOF | |
| [110] | ❺: | IOF |
| ❸: ❹: | ||
| ❻: | ||
| ❸: ❹: | ||
| [110] | EOF | |
| [111] | ❺: | EOF |
| ❸ ❹ | ||
| ❻: | ||
|
❸ ❹ | ||
| [106] | ❸ ❹ | ETF |
| [112] | ❸ ❹ | ETF |
| [113] | ❺ ❻ | ETF, openings with stiffening edges |
References
- Yu, W.-W. Scholars’ Mine Scholars’ Mine AISI-Specifications for the Design of Cold-Formed Steel Structural Members. 2009. Available online: https://scholarsmine.mst.edu/ccfss-aisi-spechttps://scholarsmine.mst.edu/ccfss-aisi-spec/159 (accessed on 9 August 2023).
- Živaljević, V.; Jovanović, Đ.; Kovačević, D.; Džolev, I. The Influence of Web Holes on the Behaviour of Cold-Formed Steel Members: A Review. Buildings 2022, 12, 1091. [Google Scholar] [CrossRef]
- Yu, W.-W.; LaBoube, R.A.; Chen, H. Cold-Formed Steel Design, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Dubina, D.; Ungureanu, V.; Landolfo, R. Eurocode 3: Part 1-3, 1st ed.; ECCS—European Convention for Constructional Steelwork: Brussels, Belgium, 2012. [Google Scholar]
- Manual, A. AISI D100-08. 2008. Available online: https://scholarsmine.mst.edu/ccfss-aisi-spec/159/ (accessed on 9 August 2023).
- ANSI/AISC 360-22; Specification for Structural Steel Buildings. AISC: Chicago, IL, USA, 2022.
- AISI S100-16 (R2020) w/S3-22; North American Specification for the Design of Cold-Formed Steel Structural Members. AISI: Washington, DC, USA, 2016; Volume 3.
- AISI S100-16 (2020) w/S2-20; North American Specification for the Design of Cold-Formed Steel Structural Members. AISI: Washington, DC, USA, 2016; Volume 2.
- AS/NZS 4600:2018; Cold-Formed Steel Structures. Standards New Zealand: Wellington, New Zealand, 2018. Available online: www.standards.govt.nz (accessed on 9 August 2023).
- AISI S240-20; North American Standard for Cold-Formed Steel Structural Framing. AISI: Washington, DC, USA, 2020.
- Dubina, D. Chapter 2: Peculiar Problems in Cold-formed Steel Design Parti 2.1 Elements 2.2.1. Cold-formed steel sections: Linear profiles, cladding and sheeting panels. In Light Gauge Metal Structures Recent Advances; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Beulah, G.; Ananthi, G. State-of-the-Art Review on Cold-Formed Steel Channel Sections under Compression. J. Struct. Eng. 2017, 44, 23–38. Available online: https://www.researchgate.net/publication/318261977 (accessed on 9 August 2023).
- Lu, Y.; Zhou, T.; Li, W.; Wu, H. Experimental investigation and a novel direct strength method for cold-formed built-up I-section columns. Thin-Walled Struct. 2017, 112, 125–139. [Google Scholar] [CrossRef]
- Mathews, D.P.K.M. Web Buckling Analysis of Cold Formed Built-Up I Section. GRD J.-Glob. Res. Dev. J. Eng. 2017, 2, 177–182. Available online: www.grdjournals.com (accessed on 9 August 2023).
- Wald, F.; Wald, F.; Jandera, M. Numerical investigation of steel built-up columns composed of track and channel cold-formed sections. In Stability and Ductility of Steel Structures 2019: Proceedings of the International Colloquia on Stability and Ductility of Steel Structures, Prague, Czech Republic, 11–13 September 2019; CRC Press: Boca Raton, FL, USA, 2019; pp. 370–373. Available online: https://www.researchgate.net/publication/336286611_Numerical_Investigation_of_Steel_Built-up_Columns_Composed_of_Track_and_Channel_Cold-Formed_Sections (accessed on 2 June 2023).
- Schafer, B.W.; Peköz, T. Computational modeling of cold-formed steel: Characterizing geometric imperfections and residual stresses. J. Constr. Steel Res. 1998, 47, 193–210. [Google Scholar] [CrossRef]
- Liao, F.; Wu, H.; Wang, R.; Zhou, T. Compression test and analysis of multi-limbs built-up cold-formed steel stub columns. J. Constr. Steel Res. 2016, 128, 405–415. [Google Scholar] [CrossRef]
- Ting, T.C.H.; Roy, K.; Lau, H.H.; Lim, J.B.P. Effect of screw spacing on behavior of axially loaded back-to-back cold-formed steel built-up channel sections. Adv. Struct. Eng. 2017, 21, 474–487. [Google Scholar] [CrossRef]
- Post, B. Fastener Spacing Study of Cold-Formed Steel Wall Studs Using Finite Strip and Finite Element Methods; Johns Hopkins University: Baltimore, MD, USA, 2012. [Google Scholar]
- Landolfo, R. Material Ductility and Buckling Behaviour of Eurocode-compliant Cold-formed Steel Hollow Columns. ce/papers 2022, 5, 1–8. [Google Scholar] [CrossRef]
- Laboube, R.A.; Yu, W.W.; Deshmukh, S.U.; Uphoff, C.A. Crippling capacity of web elements with openings. J. Struct. Eng. 1999, 125, 137–141. [Google Scholar] [CrossRef]
- Fang, Z.; Roy, K.; Chen, B.; Xie, Z.; Ingham, J.; Lim, J.B.P. Effect of the web hole size on the axial capacity of back-to-back aluminium alloy channel section columns. Eng. Struct. 2022, 260, 114238. [Google Scholar] [CrossRef]
- Wang, L.; Young, B. Design of cold-formed steel built-up sections with web perforations subjected to bending. Thin-Walled Struct. 2017, 120, 458–469. [Google Scholar] [CrossRef]
- Hancock, G.J. Cold-formed steel structures. J. Constr. Steel Res. 2003, 59, 473–487. [Google Scholar] [CrossRef]
- Young, B.; Hancock, G.J. Design of cold-formed channels subjected to web crippling. J. Struct. Eng. 2001, 127, 1137–1144. [Google Scholar] [CrossRef]
- He, J.; Young, B. Web crippling design of cold-formed steel built-up I-sections. Eng. Struct. 2022, 252, 113731. [Google Scholar] [CrossRef]
- Matthew, R.; Roger, E.; LaBoube, A.; Yu, W. Behavior of Web Elements with Openings Subjected to Linearly Varying Shear. 1997. Available online: https://scholarsmine.mst.edu/ccfss-libraryhttps://scholarsmine.mst.edu/ccfss-library/149 (accessed on 9 August 2023).
- Rasmussen, K.J.R.; Khezri, M.; Schafer, B.W.; Zhang, H. The mechanics of built-up cold-formed steel members. Thin-Walled Struct. 2020, 154, 106756. [Google Scholar] [CrossRef]
- von Kármán, T.; Sechler, E.E.; Donnell, L.H. The strength of thin plates in compression. Trans. Am. Soc. Mech. Eng. 1932, 54, 53–56. [Google Scholar] [CrossRef]
- Winter, G. Strength of thin steel compression flanges. Trans. Am. Soc. Civ. Eng. 1947, 112, 527–554. [Google Scholar] [CrossRef]
- Schafer, B.W. Review: The Direct Strength Method of cold-formed steel member design. J. Constr. Steel Res. 2008, 64, 766–778. [Google Scholar] [CrossRef]
- Bhatti; Hamza, A.; Qadeer, J.; Khan, R.M.A.; Khan, M.A. Design of Cold-form Beams Using Effective Width Method and Direct Strength Method: A Comparative Study. Pak. J. Sci. Ind. Res. Ser. A Phys. Sci. 2023, 66, 120–129. [Google Scholar]
- Schafer, B.W. Advances in the Direct Strength Method of cold-formed steel design. Thin-Walled Struct. 2019, 140, 533–541. [Google Scholar] [CrossRef]
- Camotim, D.; Dinis, P.B.; Martins, A.D. Direct strength method-a general approach for the design of cold-formed steel structures. In Recent Trends in Cold-Formed Steel Construction; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 69–105. [Google Scholar] [CrossRef]
- Wang, L.; Young, B. Behaviour and design of cold-formed steel built-up section beams with different screw arrangements. Thin-Walled Struct. 2018, 131, 16–328. [Google Scholar] [CrossRef]
- Mahar, A.M.; Jayachandran, S.A.; Mahendran, M. Global buckling strength of discretely fastened back-to-back built-up cold-formed steel columns. J. Constr. Steel Res. 2021, 187, 106998. [Google Scholar] [CrossRef]
- Nie, S.F.; Zhou, T.H.; Zhang, Y.; Liu, B. Compressive behavior of built-up closed box section columns consisting of two cold-formed steel channels. Thin-Walled Struct. 2020, 151, 106762. [Google Scholar] [CrossRef]
- Ghannam, M. Behaviour of Axially Loaded Cold-Formed Steel Built-Up Stub Columns. In Proceedings of the 1st International Conference on Structural Engineering Research (iCSER 2017), Sydney, Australia, 20–22 November 2017. [Google Scholar]
- Fratamico, D.C.; Torabian, S.; Rasmussen, K.J.R.; Schafer, B.W. Buckling and Collapse Behavior of Screw-Fastened, Built-Up Cold-Formed Steel Columns of Varying Cross-Section Size: Experimental Investigation. In Proceedings of the Annual Stability Conference Structural Stability Research Council, San Antonio, TX, USA, 21–24 March 2017; Available online: https://www.aisc.org/globalassets/continuing-education/ssrc-proceedings/2017/buckling-and-collapse-behavior-of-screw-fastened-built-up-cold-formed-steel-columns-of-varying-cross-section-size-experimental-investigation.pdf (accessed on 26 June 2023).
- Tawfic, M.; Amoush, E. Compressive Strength of Axially Loaded Built-up Sigma Cold Formed Sections Columns. Future Eng. J. 2020, 1, 2314–7237. Available online: https://digitalcommons.aaru.edu.jo/fej/vol1/iss1/6/ (accessed on 27 July 2023).
- Samuel, J.; Joanna, P.S. Experimental Study and Numerical Modelling on the Behaviour of Built-Up Cold-Formed Steel Beams with Diagonal Web Bars. Int. J. Sci. Technol. Res. 2020, 9, 2. Available online: www.ijstr.org (accessed on 27 July 2023).
- Meza, F.J.; Becque, J.; Hajirasouliha, I. Experimental study of cold-formed steel built-up columns. Thin-Walled Struct. 2020, 149, 106291. [Google Scholar] [CrossRef]
- Vishweswaran, C.K.; Srisanthi, V.G. Experimental Study on Cold-formed Steel Built-up Column Sections. Int. J. Innov. Res. Technol. 2021, 8, 152058. [Google Scholar]
- Fratamico, D.C.; Torabian, S.; Zhao, X.; Rasmussen, K.J.R.; Schafer, B.W. Experimental study on the composite action in sheathed and bare built-up cold-formed steel columns. Thin-Walled Struct. 2018, 127, 290–305. [Google Scholar] [CrossRef]
- Lukačević, I.; Ungureanu, V. Numerical parametric study on corrugated web built-up beams with pinned end supports. In Proceedings of the Cold-Formed Steel Research Consortium Colloquium, Online, 17–19 October 2022; Available online: https://www.researchgate.net/publication/364403581 (accessed on 9 August 2023).
- Mon, T.Y.; Selvam, J. Buckling Behaviors of Cold-Formed Steel Built-Up Columns under Axial Compression Tests: Review Paper. Int. J. Recent Technol. Eng. 2021, 10, 7–11. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Zhao, X.; Rasmussen, K.J.R.; Schafer, B.W. Experiments on the global buckling and collapse of built-up cold-formed steel columns. J. Constr. Steel Res. 2018, 144, 65–80. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Rasmussen, K.J.R.; Schafer, B.; Schafer, B.W. Experimental investigation of the effect of screw fastener spacing on the local and distortional buckling behavior of built-up cold-formed steel columns. In Proceedings of the Wei-Wen Yu International Specialty Conference on Cold-Formed Steel Structures, Baltimore, MD, USA, 9–10 November 2016; Available online: https://scholarsmine.mst.edu/cgi/viewcontent.cgi?article=1914&context=isccss (accessed on 1 June 2023).
- Meza, F.J.; Becque, J.; Hajirasouliha, I. Experimental Study of Cold-Formed Steel Built-Up Beams. J. Struct. Eng. 2020, 146, 04020126. [Google Scholar] [CrossRef]
- Prabhakaran, S.; Kalaiselvi, S. Experimental Study on Load Carrying Capacity of Cold Formed Steel Built-up Column. Int. J. ChemTech Res. 2018, 11, 164–170. [Google Scholar] [CrossRef]
- Nie, S.; Zhou, T.; Liao, F.; Yang, D. Study on axial compressive behavior of quadruple C-channel built-up cold-formed steel columns. Struct. Eng. Mech. 2019, 70, 499–511. [Google Scholar] [CrossRef]
- Phan, D.K.; Rasmussen, K.J.R.; Schafer, B.W. Tests and design of built-up section columns. J. Constr. Steel Res. 2021, 181, 106619. [Google Scholar] [CrossRef]
- Cai, Y.; Young, B. Fire resistance of stainless steel single shear bolted connections. Thin-Walled Struct. 2018, 130, 332–346. [Google Scholar] [CrossRef]
- Kumbhar, S.S.; Jadhav, H.S. Current Research on Cold-Formed Steel Structures: A Review. Int. Res. J. Eng. Technol. 2021, 8, 389–392. [Google Scholar]
- Vy, S.T.; Mahendran, M. Screwed connections in built-up cold-formed steel members at ambient and elevated temperatures. J. Constr. Steel Res. 2022, 192, 107218. [Google Scholar] [CrossRef]
- Fonseca, E.M.M.; Silva, L.; Leite, P.A.S. Numerical model to predict the effect of wood density in wood–steel–wood connections with and without passive protection under fire. J. Fire Sci. 2020, 38, 122–135. [Google Scholar] [CrossRef]
- Craveiro, H.D.; Rahnavard, R.; Laím, L.; Simões, R.A.; Santiago, A. Buckling behavior of closed built-up cold-formed steel columns under compression. Thin-Walled Struct. 2022, 179, 109493. [Google Scholar] [CrossRef]
- Sani, M.; Muftah, F.; Osman, A.R. A Review and Development of Cold-formed Steel Channel Columns with Oriented Strand Board Sections. Mater. Today Proc. 2019, 17, 1078–1085. Available online: www.sciencedirect.com (accessed on 9 August 2023). [CrossRef]
- Halabi, Y.; Alhaddad, W. Manufacturing, Applications, Analysis and Design of Cold-Formed Steel in Engineering Structures: A Review. Int. J. Adv. Eng. Res. Sci. 2020, 7, 11–34. [Google Scholar] [CrossRef]
- Johnston, R.P.; McGrath, T.; Nanukuttan, S.; Lim, J.B.; Soutsos, M.; Chiang, M.C.; Masood, R.; Rahman, M.A. Sustainability of Cold-formed Steel Portal Frames in Developing Countries in the Context of Life Cycle Assessment and Life Cycle Costs. Structures 2018, 13, 79–87. [Google Scholar] [CrossRef]
- Iuorio, O.; Gigante, A.; De Masi, R.F. Life Cycle Analysis of Innovative Technologies: Cold Formed Steel System and Cross Laminated Timber. Energies 2023, 16, 586. [Google Scholar] [CrossRef]
- Roy, K.; Lau, H.H.; Fang, Z.; Masood, R.; Ting, T.C.H.; Lim, J.B.; Lee, V.C.C. Effects of corrosion on the strength of self-drilling screw connections in cold-formed steel structures-Experiments and finite element modeling. Structures 2022, 36, 1080–1096. [Google Scholar] [CrossRef]
- Billah, M.M.; Islam, R.; Bin, A. Cold formed steel structure: An overview. World Sci. News 2019, 118, 59–73. Available online: www.worldscientificnews.com (accessed on 9 August 2023).
- Dubina, D.; Stratan, A.; Alexandru, F.L.; Zsolt, N.; Dubina, D.; Stratan, A. STRENGTH, STIFFNESS AND DUCTILITY OF Cold-Formed Steel Bolted Connections. In Proceedings of the Connections in Steel Structures V, Amsterdam, The Netherlands, 3–4 June 2004; Available online: https://www.researchgate.net/publication/283676582 (accessed on 9 August 2023).
- Aly, E.H.A.H.; Hanna, M.T.; El-Mahdy, G.M. Strength and Ductility of Steel Cold-Formed Section Beam to Column Bolted Connections. In Sustainable Civil Infrastructures; Springer Science and Business Media B.V.: Berlin/Heidelberg, Germany, 2018; pp. 431–445. [Google Scholar] [CrossRef]
- Vy, S.T.; Mahendran, M.; Sivaprakasam, T. Built-up back-to-back cold-formed steel compression members failing by local and distortional buckling. Thin-Walled Struct. 2020, 159, 107224. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Wang, S.; Shen, Z. Ultimate load-carrying capacity of cold-formed thin-walled columns with built-up box and i section under axial compression. Thin-Walled Struct. 2014, 79, 202–217. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Q.Y.; Li, H.; Ren, Q. Loading capacity prediction and optimization of cold-formed steel built-up section columns based on machine learning methods. Thin-Walled Struct. 2022, 180, 109826. [Google Scholar] [CrossRef]
- Bešević, M.; Prokić, A.; Landović, A.; Kasaš, K. The analysis of bearing capacity of axially compressed cold formed steel members. Period. Polytech. Civ. Eng. 2017, 61, 88–97. [Google Scholar] [CrossRef]
- Da Silva, L.S.; Lamas, A.; Jaspart, J.-P.; Bjorhovde, R.; Kuhlmann, U. Design of Steel Structures, 2nd ed.; ECCS—European Convention for Constructional Steelwork: Brussels, Belgium, 2016. [Google Scholar]
- Eurocode. EN 1993-1-8; Eurocode 3: Design of Steel Structures—Part 1-8: Design of Joints. John Wiley & Sons: Hoboken, NJ, USA, 2005.
- Eurocode. EN 1993-1-1; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. John Wiley & Son: Hoboken, NJ, USA, 2005.
- Roy, K.; Lau, H.; Chen, B.; Chui, T.; Ting, H.; Lim, J.B.P. Effect of screw spacing on axial strength of cold-formed steel built-up box sections-numerical investigation and parametric study. In Proceedings of the 2019 World Congress on Advances in Structural Engineering and Mechanics (ASEM19), Jeju Island, Republic of Korea, 17–21 September 2019; Available online: http://www.i-asem.org/publication_conf/asem19/2.SC/XH5B.2.SC1152_5425F1.pdf (accessed on 1 July 2023).
- Kyprianou, C.; Kyvelou, P.; Gardner, L.; Nethercot, D.A. Finite element modelling of sheathed cold-formed steel beam–columns. Thin-Walled Struct. 2023, 183, 110365. [Google Scholar] [CrossRef]
- Kechidi, S.; Fratamico, D.C.; Schafer, B.W.; Castro, J.M.; Bourahla, N. Simulation of screw connected built-up cold-formed steel back-to-back lipped channels under axial compression. Eng. Struct. 2019, 206, 110109. [Google Scholar] [CrossRef]
- Renuka, R.; Kalaiselvi, S. Experimental Investigation on Behaviour of Cold Formed Steel Batten Column with Angles Under Axial Compression. Int. J. Adv. Res. Eng. Technol. 2020, 11, 625–632. [Google Scholar] [CrossRef]
- Portioli, F.; Di Lorenzo, G.; Landolfo, R.; Mazzolani, F. Contact Buckling Effects in Built-Up Cold-Formed Steel Beams. In Proceedings of the 6th International Conference on Coupled Instabilities in Metal Structures, Glasgow, UK, 3–5 December 2012. [Google Scholar]
- Ananthi, G.B.G.; Ashvini, B. Experimental theoretical and numerical studies on cold-formed steel stub channel columns with stiffeners. Asian J. Civ. Eng. 2018, 20, 171–185. [Google Scholar] [CrossRef]
- Selvaraj, S.; Madhavan, M. Design of cold-formed steel built-up columns subjected to local-global interactive buckling using direct strength method. Thin-Walled Struct. 2021, 159, 107305. [Google Scholar] [CrossRef]
- Roy, K.; Ting, T.C.H.; Lau, H.H.; Lim, J.B.P. Nonlinear behavior of axially loaded back-to-back built-up cold-formed steel un-lipped channel sections. Steel Compos. Struct. 2018, 28, 233–250. [Google Scholar] [CrossRef]
- Roy, K.; Ting, T.C.H.; Lau, H.H.; Lim, J.B.P. Effect of thickness on the behaviour of axially loaded back-to-back cold-formed steel built-up channel sections—Experimental and numerical investigation. Structures 2018, 16, 327–346. [Google Scholar] [CrossRef]
- Roy, K.; Lim, J.B.P. Numerical investigation into the buckling behaviour of face-to-face built-up cold-formed stainless steel channel sections under axial compression. Structures 2019, 20, 42–73. [Google Scholar] [CrossRef]
- Roy, K.; Rezaeian, H.; Fang, Z.; Raftery, G.M.; Lim, J.B.P. Experimental and numerical study of a novel cold-formed steel T-Stub connection subjected to tension force. J. Constr. Steel Res. 2022, 197, 107466. [Google Scholar] [CrossRef]
- Khezri, M.; Abbasi, M.; Rasmussen, K.J.R. Application of the compound strip method in buckling analysis of cold-formed steel built-up sections. ce/papers 2017, 1, 1667–1676. [Google Scholar] [CrossRef]
- Meza, F.; Becque, J. Experimental and numerical investigation of cold-formed steel built-up stub columns. ce/papers 2017, 1, 1617–1626. [Google Scholar] [CrossRef]
- Meza, F.J.; Becque, J.; Hajirasouliha, I. Experimental study of the cross-sectional capacity of cold-formed steel built-up columns. Thin-Walled Struct. 2020, 155, 106958. [Google Scholar] [CrossRef]
- Muftah, F.; Sani, H.M.; Muda, M.F.; Mohammad, S. Assessment of Connection Arrangement of built-up cold-formed steel section under axial compression. In Advanced Materials Research; Trans Tech Publications Ltd.: Zurich, Switzerland, 2014; pp. 252–257. [Google Scholar] [CrossRef]
- Vy, S.T.; Mahendran, M.; Sivaprakasam, T. Built-up nested cold-formed steel compression members subject to local or distortional buckling. J. Constr. Steel Res. 2021, 182, 106667. [Google Scholar] [CrossRef]
- Vy, S.T.; Mahendran, M. DSM design of fixed-ended slender built-up back-to-back cold-formed steel compression members. J. Constr. Steel Res. 2021, 189, 107053. [Google Scholar] [CrossRef]
- Ye, J.; Mojtabaei, S.M.; Hajirasouliha, I.; Pilakoutas, K. Efficient design of cold-formed steel bolted-moment connections for earthquake resistant frames. Thin-Walled Struct. 2019, 150, 105926. [Google Scholar] [CrossRef]
- Abbasi, M.; Khezri, M.; Rasmussen, K.J.R.; Schafer, B.W. Elastic buckling analysis of cold-formed steel built-up sections with discrete fasteners using the compound strip method. Thin-Walled Struct. 2018, 124, 58–71. [Google Scholar] [CrossRef]
- Chea, B.; Chaisomphob, T.; Patwichaichote, W.; Yamaguchi, E. Experimental and Numerical Study on Cold-formed Steel Built-up Box Beams. In Proceedings of the Regional Conference in Civil Engineering (RCCE), the Third International Conference on Civil Engineering Research (ICCER), Surabaya, Indonesia, 1–2 August 2017; pp. 300–307. [Google Scholar]
- Akchurin, D.; Li, Z. Development of Design Tables for the Cold-Formed Steel Cross-Sections in AISI D100, RESEARCHREPORTRP21-01; American Iron and Steel Institute: Washington, DC, USA, 2021. [Google Scholar]
- Schafer, B.W.; Ádány, S. Buckling analysis of cold-formed steel members using CUFSM: Conventional and constrained finite strip methods. In Proceedings of the Eighteenth International Specialty Conference on Cold-Formed Steel Structures, Orlando, FL, USA, 26–27 October 2006; pp. 39–54. Available online: www.ce.jhu.edu/bschafer/cufsm (accessed on 9 August 2023).
- Moen, C.D.; Schafer, B.W. Direct Strength Method for Design of Cold-Formed Steel Columns with Holes. J. Struct. Eng. 2011, 137, 559–570. [Google Scholar] [CrossRef]
- Hsiao, L.-E.; Yu, W.-W.; Galambos, T. Load and Resistance Factor Design of Cold-Formed Steel Load and Resistance Factor Design Specification for Cold-Formed Steel Structural Members with Commentary. 1989. Available online: https://scholarsmine.mst.edu/ccfss-libraryhttps://scholarsmine.mst.edu/ccfss-library/142 (accessed on 9 August 2023).
- Galambos, T.V.; Yu, W.-W.; Yu, W. Load and resistance factor design of cold-formed steel structural members. In Proceedings of the International Specialty Conference on Cold-Formed Steel Structures, St. Louis, MO, USA, 13–14 November 1984; Available online: https://scholarsmine.mst.edu/isccss/7iccfss/7iccfss-session10/2 (accessed on 9 August 2023).
- Shanmugam, N.E.; Dhanalakshmi, M. Design for openings in cold-formed steel channel stub columns. Thin-Walled Struct. 2001, 39, 961–981. [Google Scholar] [CrossRef]
- Yao, Z.; Rasmussen, K.J.R. Perforated Cold-Formed Steel Members in Compression. II: Design. J. Struct. Eng. 2017, 143, 04016227. [Google Scholar] [CrossRef]
- Chen, B.; Roy, K.; Uzzaman, A.; Raftery, G.M.; Lim, J.B.P. Parametric study and simplified design equations for cold-formed steel channels with edge-stiffened holes under axial compression. J. Constr. Steel Res. 2020, 172, 106161. [Google Scholar] [CrossRef]
- Grey, C.N.; Moen, C.D. Elastic Buckling Simplified Methods for Cold-Formed Columns and Beams with Edge-Stiffened Holes. In Proceedings of the Annual Stability Conference Structural Stability Research Council, Pittsburgh, PA, USA, 10–14 May 2011; pp. 92–103. [Google Scholar]
- Zhao, J.; Sun, K.; Yu, C.; Wang, J. Tests and direct strength design on cold-formed steel channel beams with web holes. Eng. Struct. 2019, 184, 434–446. [Google Scholar] [CrossRef]
- Yu, C. Cold-formed steel flexural member with edge stiffened holes: Behavior, optimization, and design. J. Constr. Steel Res. 2012, 71, 210–218. [Google Scholar] [CrossRef]
- Davis, C.S. The Structural Behavior of Cold-Formed Steel Members with Perforated Elements. 1972. Available online: https://scholarsmine.mst.edu/doctoral_dissertations/2091 (accessed on 9 August 2023).
- Uzzaman, A.; Lim, J.B.P.; Nash, D.; Rhodes, J.; Young, B. Web crippling behaviour of cold-formed steel channel sections with offset web holes subjected to interior-two-flange loading. Thin-Walled Struct. 2012, 50, 76–86. [Google Scholar] [CrossRef]
- Uzzaman, A.; Lim, J.B.P.; Nash, D.; Rhodes, J.; Young, B. Cold-formed steel sections with web openings subjected to web crippling under two-flange loading conditions—Part II: Parametric study and proposed design equations. Thin-Walled Struct. 2012, 56, 79–87. [Google Scholar] [CrossRef]
- Yousefi, A.M.; Lim, J.B.P.; Clifton, G.C. Cold-formed ferritic stainless steel unlipped channels with web openings subjected to web crippling under interior-two-flange loading condition—Part II: Parametric study and design equations. Thin-Walled Struct. 2017, 116, 342–356. [Google Scholar] [CrossRef]
- Uzzaman, A.; Lim, J.B.P.; Nash, D.; Roy, K. Web crippling behaviour of cold-formed steel channel sections with edge-stiffened and unstiffened circular holes under interior-two-flange loading condition. Thin-Walled Struct. 2020, 154, 106813. [Google Scholar] [CrossRef]
- Sivakumaran, K.S.; Zielonka, K.M. Web Crippling Strength of Thin-Walled Steel Members with Web Opening. Thin-Walled Struct. 1989, 8, 295–319. [Google Scholar] [CrossRef]
- Lian, Y.; Uzzaman, A.; Lim, J.B.P.; Abdelal, G.; Nash, D.; Young, B. Web crippling behaviour of cold-formed steel channel sections with web holes subjected to interior-one-flange loading condition—Part II: Parametric study and proposed design equations. Thin-Walled Struct. 2017, 114, 92–106. [Google Scholar] [CrossRef]
- Lian, Y.; Uzzaman, A.; Lim, J.B.P.; Abdelal, G.; Nash, D.; Young, B. Effect of web holes on web crippling strength of cold-formed steel channel sections under end-one-flange loading condition—Part II: Parametric study and proposed design equations. Thin-Walled Struct. 2016, 107, 489–501. [Google Scholar] [CrossRef]
- Uzzaman, A.; Lim, J.B.P.; Nash, D.; Rhodes, J.; Young, B. Effect of offset web holes on web crippling strength of cold-formed steel channel sections under end-two-flange loading condition. Thin-Walled Struct. 2013, 65, 34–48. [Google Scholar] [CrossRef]
- Uzzaman, A.; Lim, J.B.P.; Nash, D.; Roy, K. Cold-formed steel channel sections under end-two-flange loading condition: Design for edge-stiffened holes, unstiffened holes and plain webs. Thin-Walled Struct. 2019, 147, 106532. [Google Scholar] [CrossRef]
- Pham, C.H. Shear buckling of plates and thin-walled channel sections with holes. J. Constr. Steel Res. 2017, 128, 800–811. [Google Scholar] [CrossRef]
- Keerthan, P.; Mahendran, M. Experimental studies of the shear behaviour and strength of lipped channel beams with web openings. Thin-Walled Struct. 2013, 73, 131–144. [Google Scholar] [CrossRef]
- Pham, S.H.; Pham, C.H.; Hancock, G.J. Design of Cold-Formed Steel Beams with Holes and Transverse Stiffeners in Shear. Ph.D. Thesis, The University of Sydney, Sydney, Australia, 2018. [Google Scholar]
- Pham, D.K.; Pham, C.H.; Pham, S.H.; Hancock, G.J. Experimental investigation of high strength cold-formed channel sections in shear with rectangular and slotted web openings. J. Constr. Steel Res. 2019, 165, 105889. [Google Scholar] [CrossRef]
- Pham, C.H.; Hancock, G.J. Shear tests and design of cold-formed steel channels with central square holes. Thin-Walled Struct. 2020, 149, 106650020. [Google Scholar] [CrossRef]


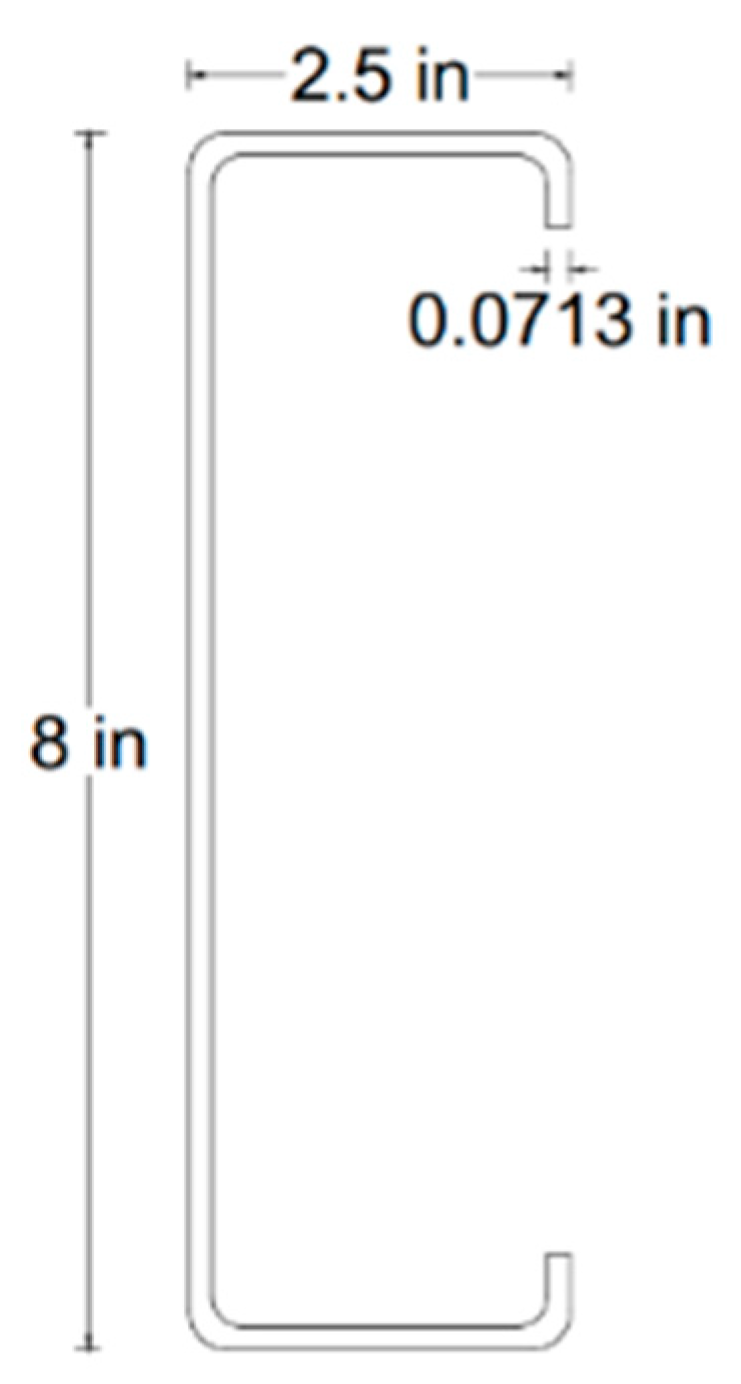
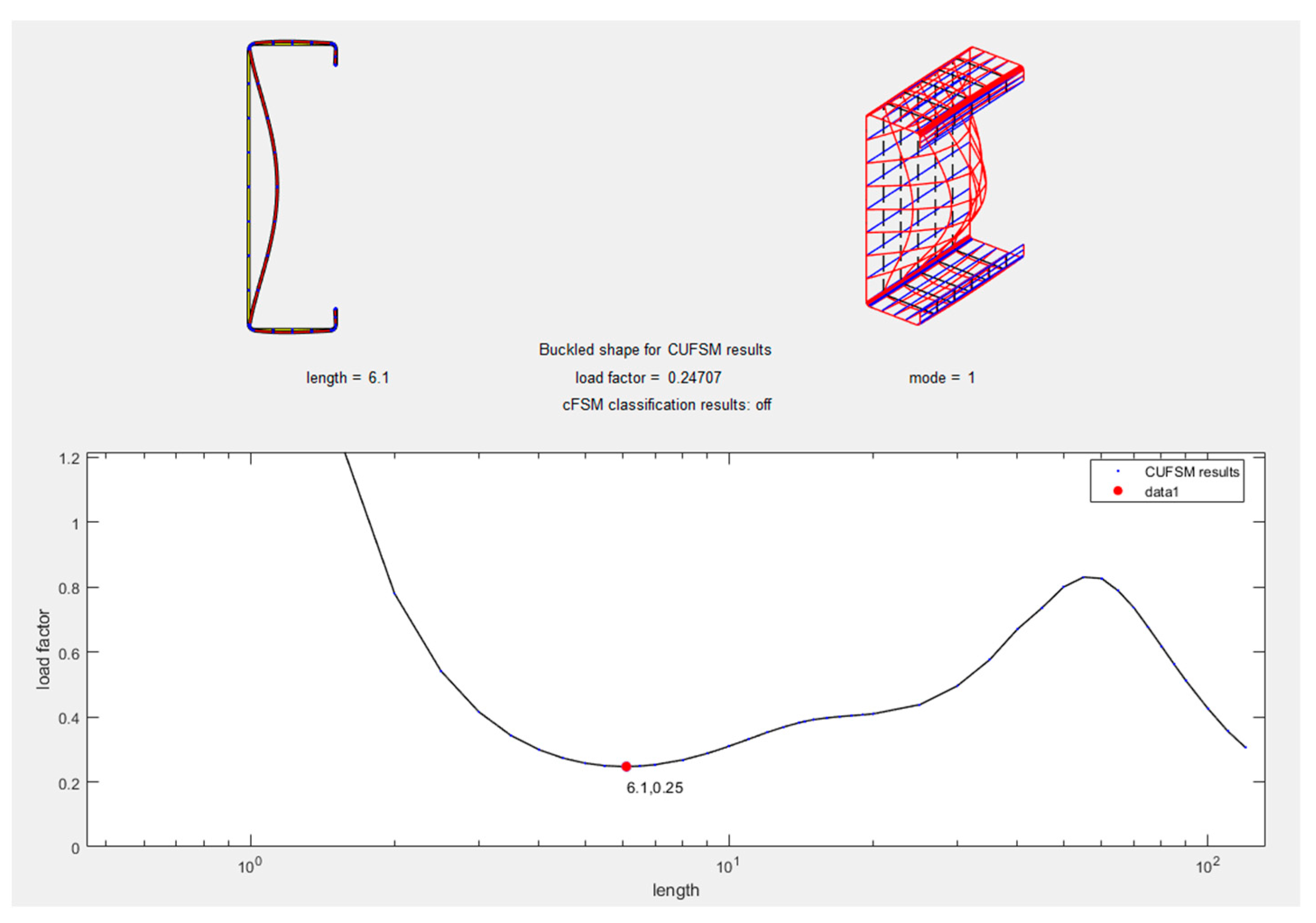
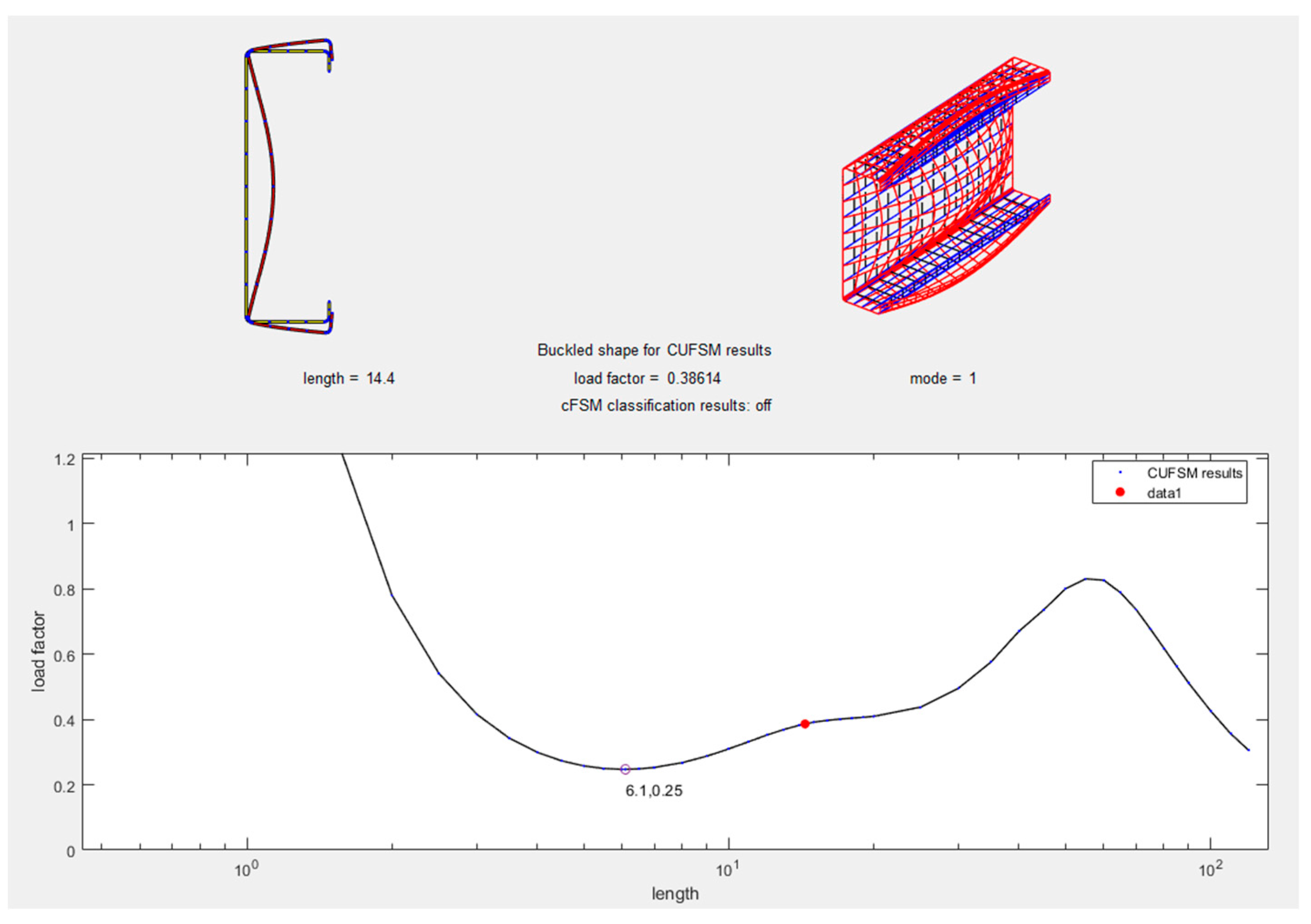

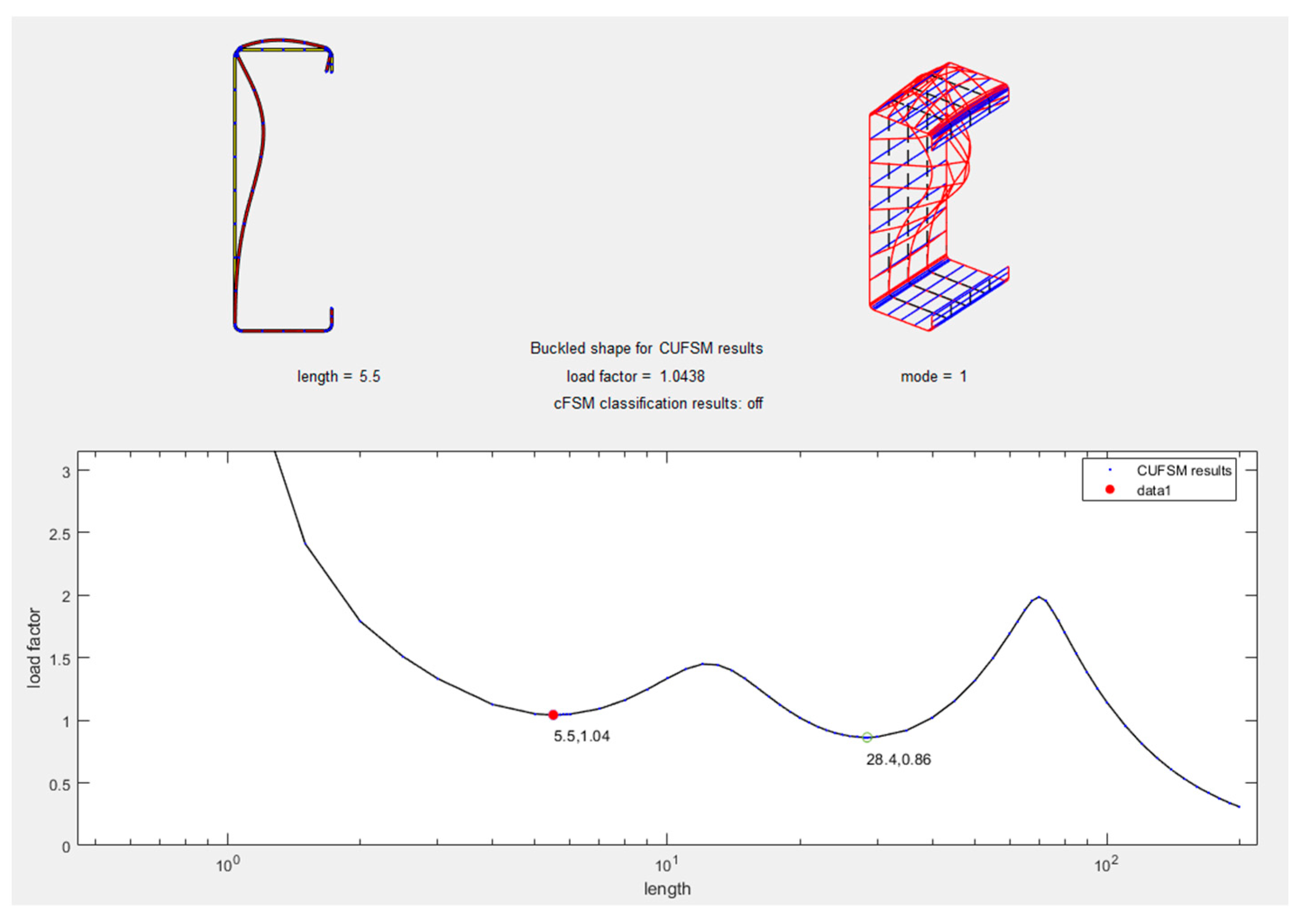
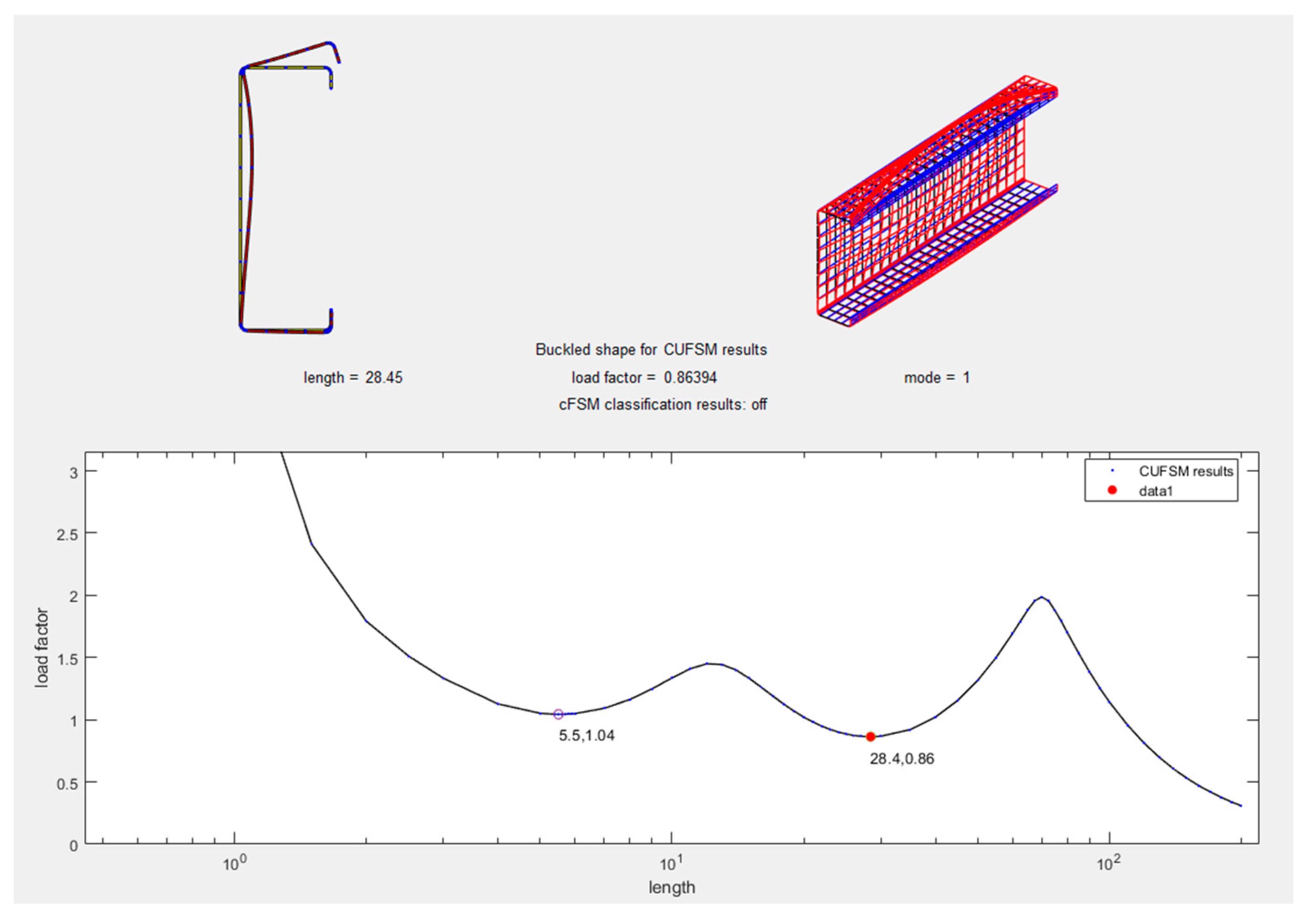
| ABAQUS Kips (N) | CUFSM Kips (N) | |
|---|---|---|
| 23.323 (103,745.9) | 25.552 (113,661) | |
| 23.193 (103,167.6) | 23.722 (105,521) | |
| 42.662 (189,770) | 48.891 (217,478) * Fully braced | |
| 23.193 (103,167.6) | 25.552 (113,661) | |
| % of Error | 10.171% | |
| ABAQUS Kips*in (N*mm) | CUFSM Kips*in (N*mm) | |
|---|---|---|
| 164.980 (1,864,023) | 221.184 (24,990,436.42) | |
| 188.047 (21,246,458.2) | 189.717 (21,435,142.81) | |
| 149.575 (16,899,706) | 256.576 (28,989,195.5) *Fully braced | |
| 149.575 (16,899,706) | 189.717 (21,435,142.81) | |
| % of Error | 14.994% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, A.B.; Papp, F. State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections. Buildings 2023, 13, 2338. https://doi.org/10.3390/buildings13092338
Hussein AB, Papp F. State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections. Buildings. 2023; 13(9):2338. https://doi.org/10.3390/buildings13092338
Chicago/Turabian StyleHussein, Ardalan B., and Ferenc Papp. 2023. "State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections" Buildings 13, no. 9: 2338. https://doi.org/10.3390/buildings13092338
APA StyleHussein, A. B., & Papp, F. (2023). State-of-the-Art: Integrating Fastener Technology and Design Guidelines for Enhanced Performance of Cold-Formed Steel Sections. Buildings, 13(9), 2338. https://doi.org/10.3390/buildings13092338