Effects of Lip Length and Inside Radius-to-Thickness Ratio on Buckling Behavior of Cold-Formed Steel C-Sections
Abstract
:1. Introduction
2. Impact of Lips
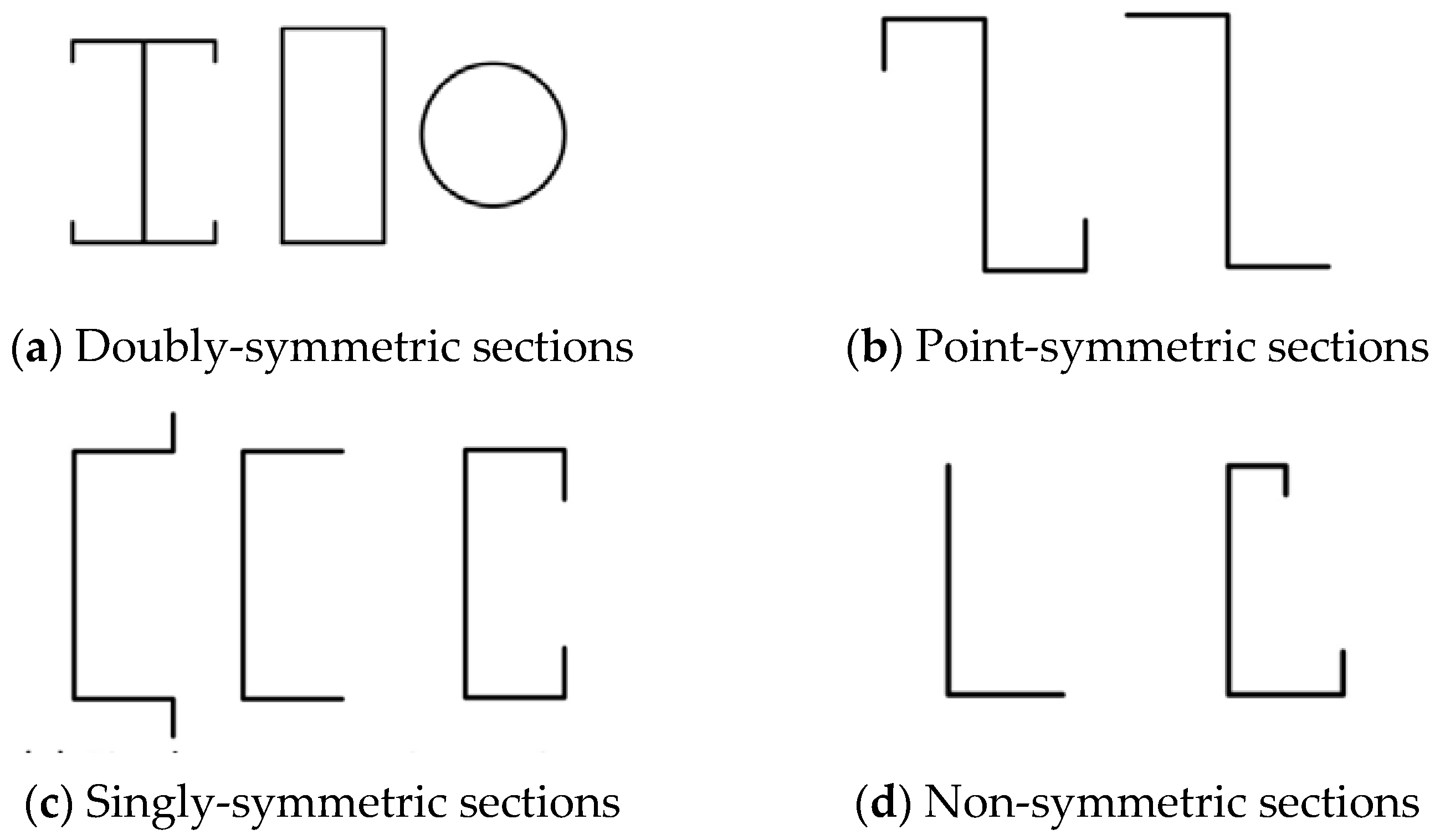
2.1. Shapes of Sections According to Symmetry
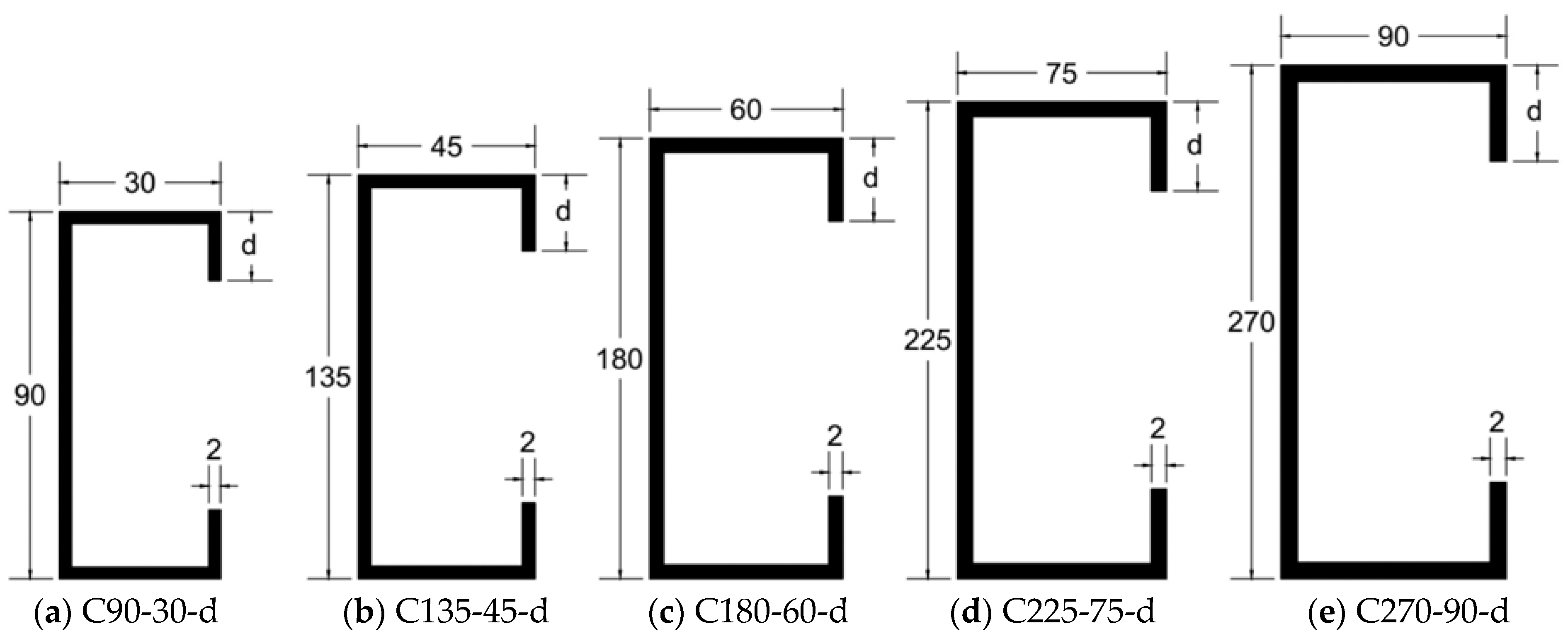
2.2. Single-Steel Member Dimensions
2.3. Major Modes of Buckling
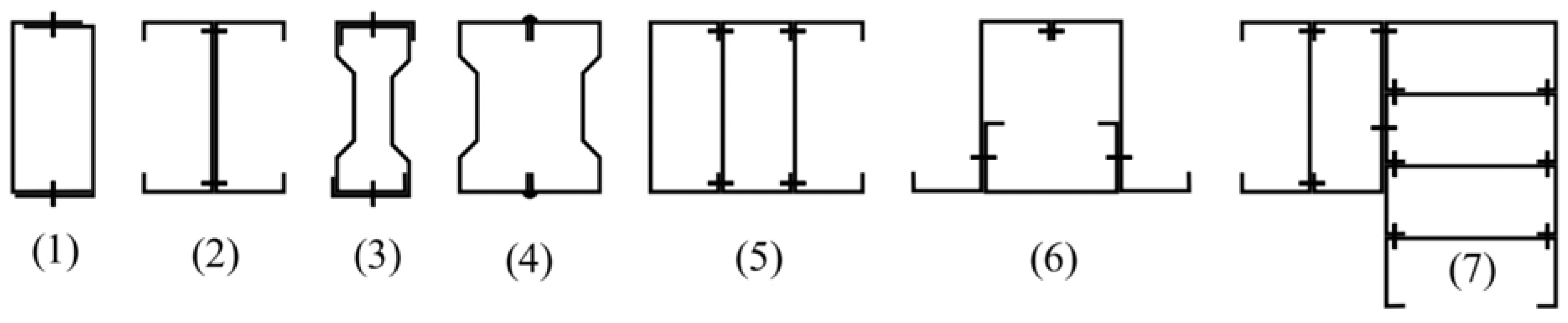
2.4. Factors That Affect Strength
3. Impact of Inside Radius
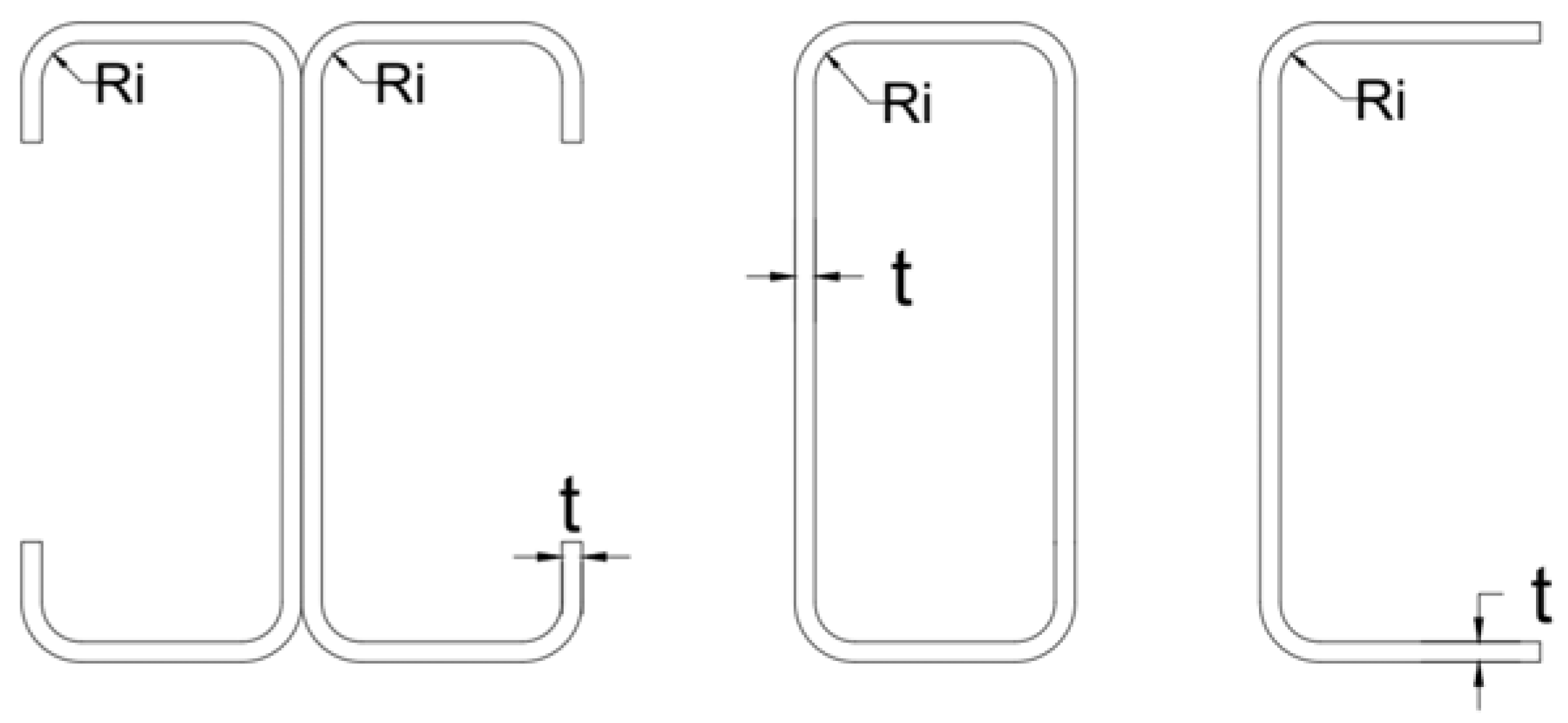
3.1. Effects of Various Geometric Shapes
3.2. Web Crippling and Holes of CFS Elements
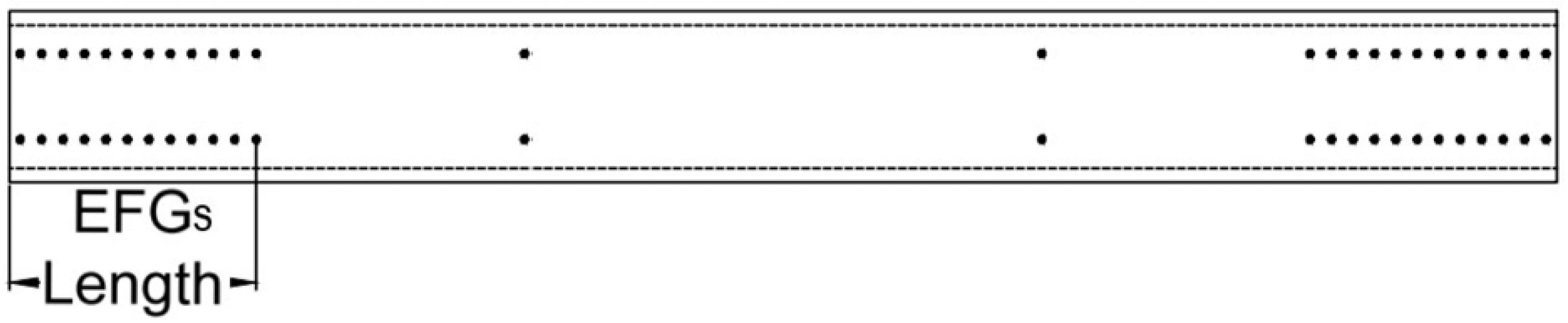
3.3. Impacts of End Fastener Groups (EFGs) and End Conditions on CFS Sections
4. Equations for Determining Various Buckling Modes in Columns and Beams [28,29,30,41]
4.1. Members in Compression
4.1.1. Global Buckling (GB)
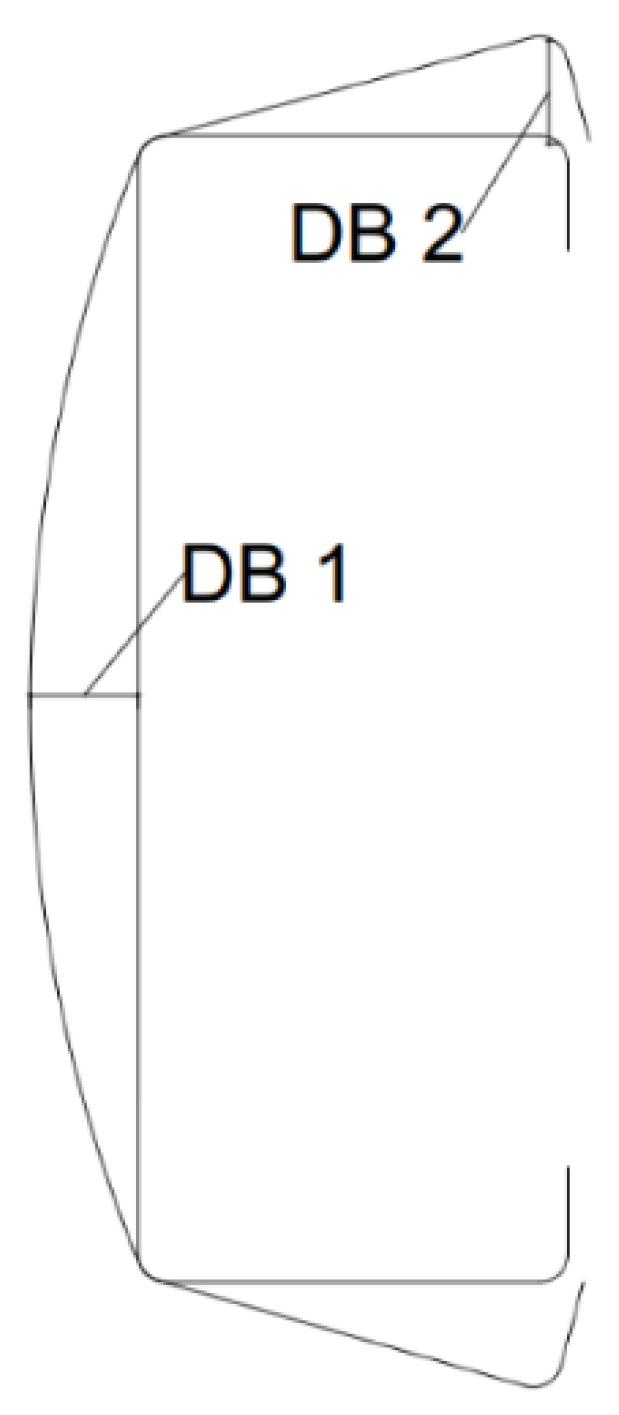
4.1.2. Distortional Buckling (DB)
4.1.3. Local Buckling (LB)
4.2. Members in Flexure
4.2.1. Global Buckling (GB)
4.2.2. Distortional Buckling (DB)
4.2.3. Local Buckling (LB)
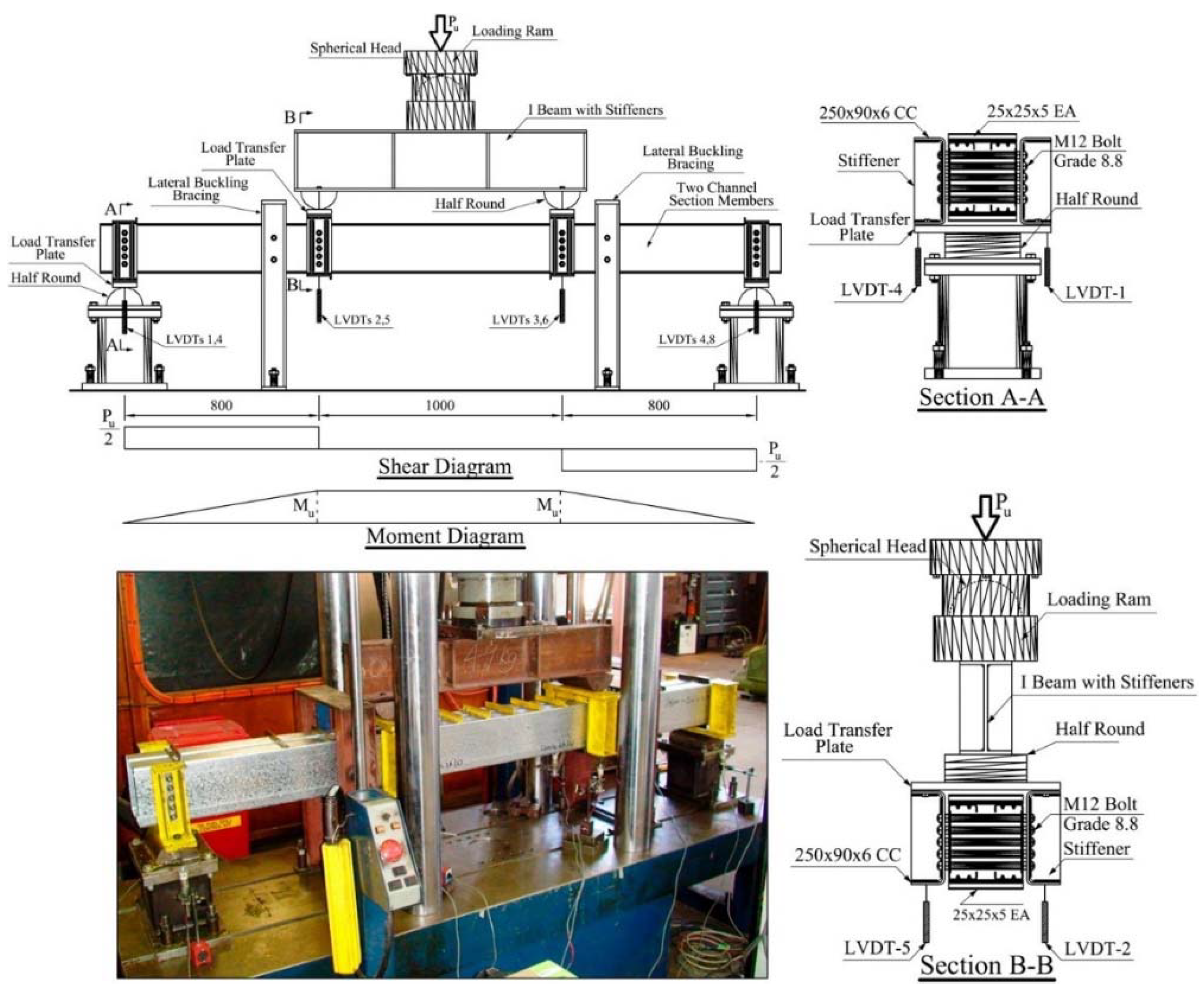
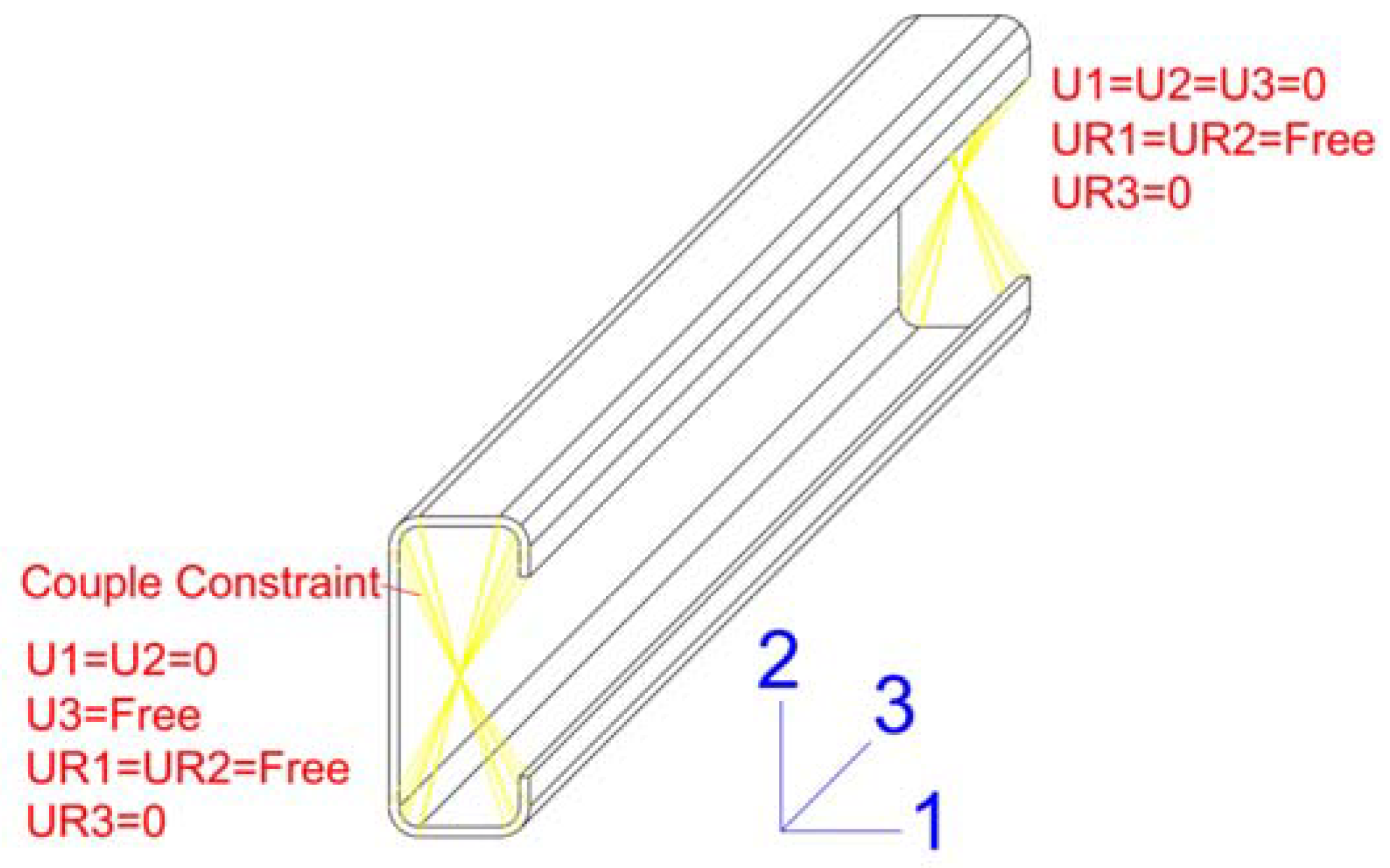
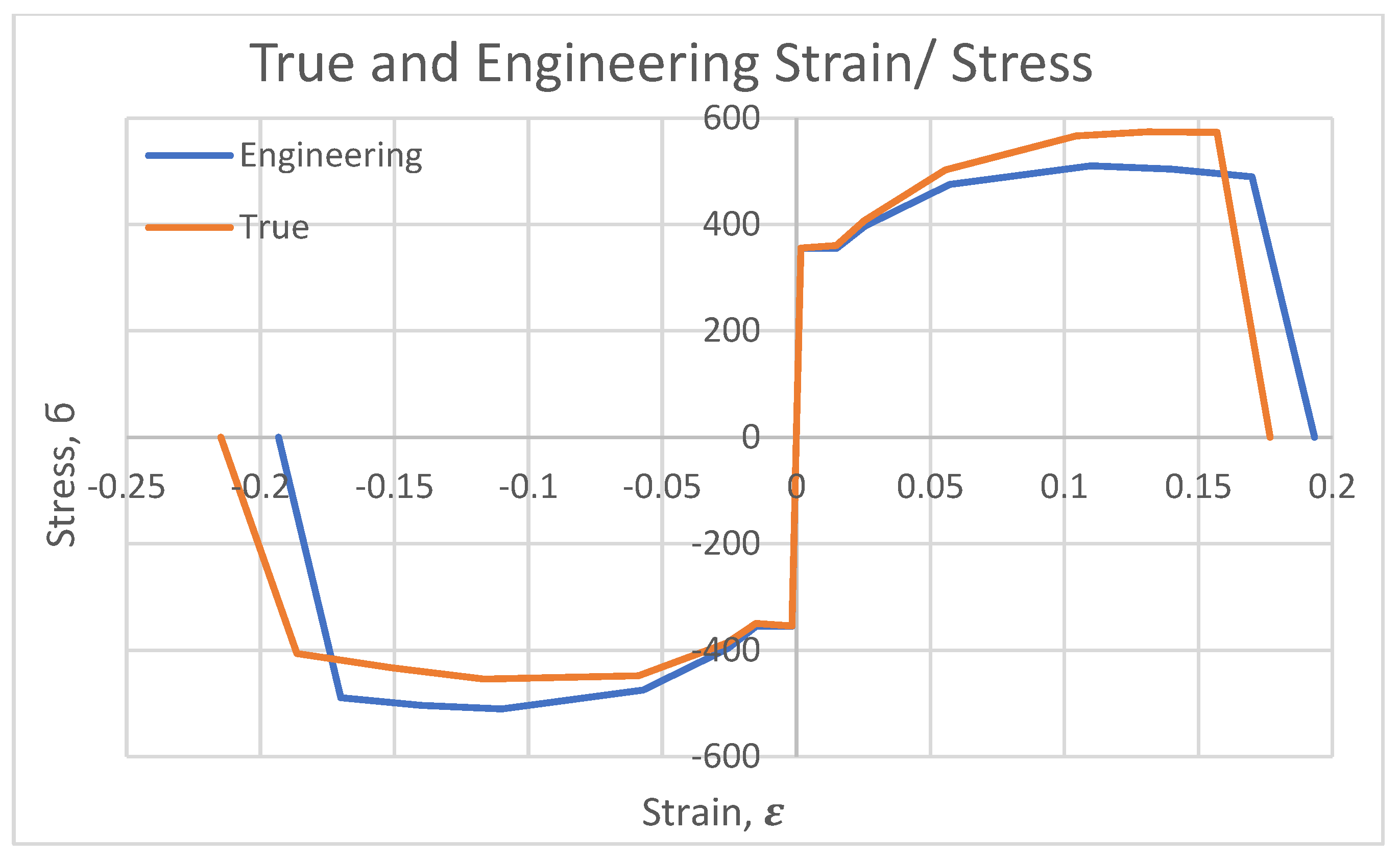
5. Validation of FE Models
6. Numerical Modelling
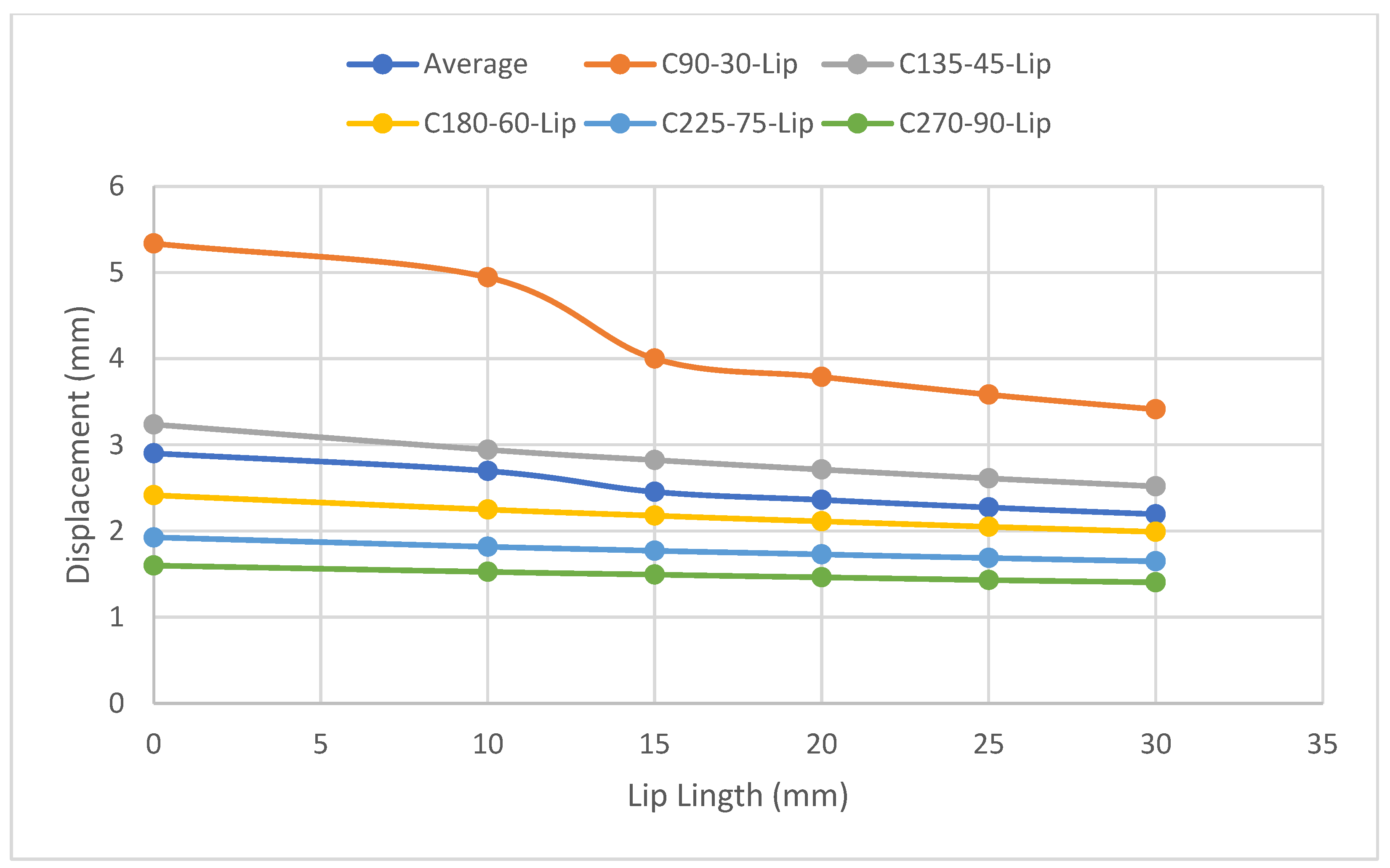
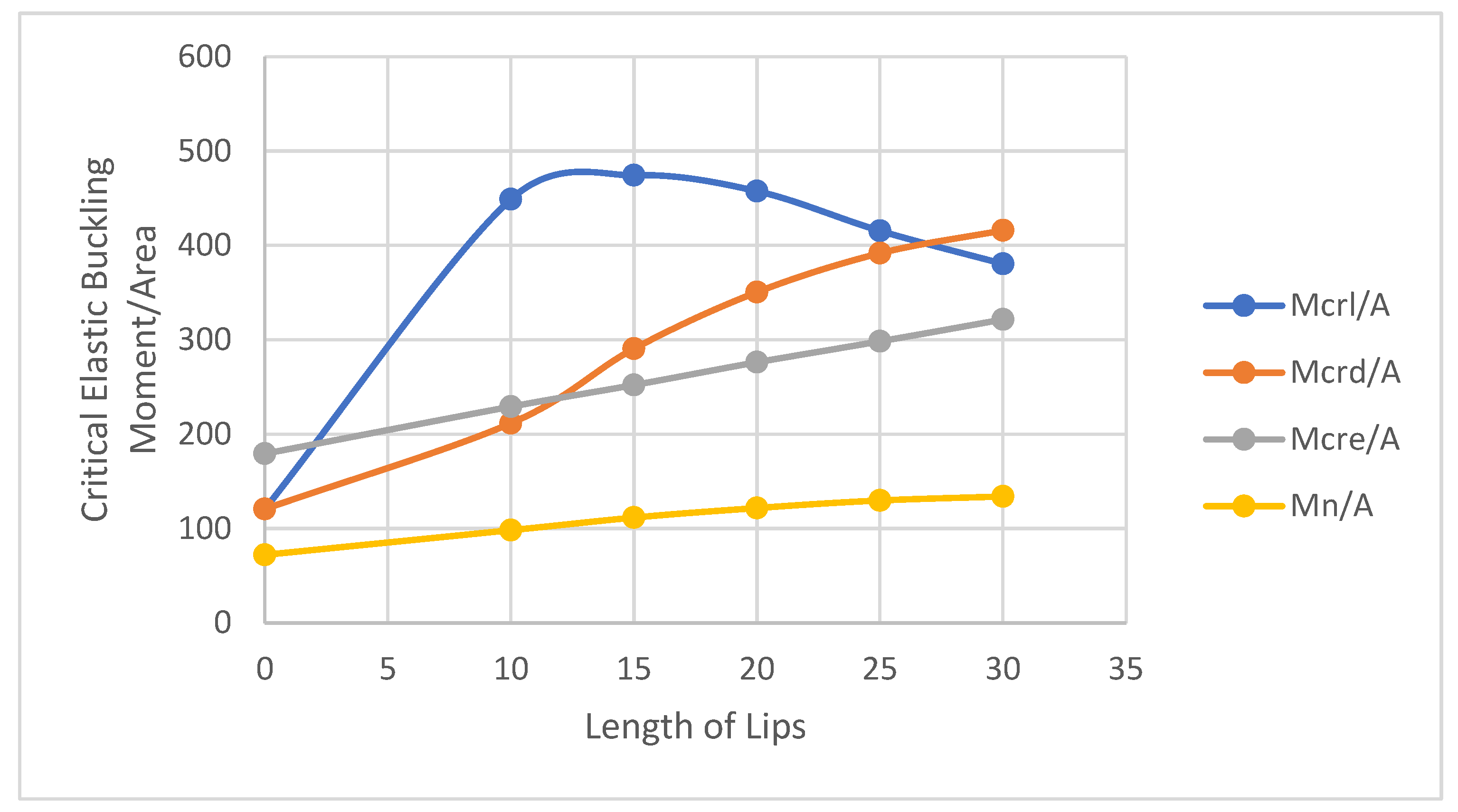
7. An Analysis of the Effects of Lip Length on Various Types of Column and Beam Buckling
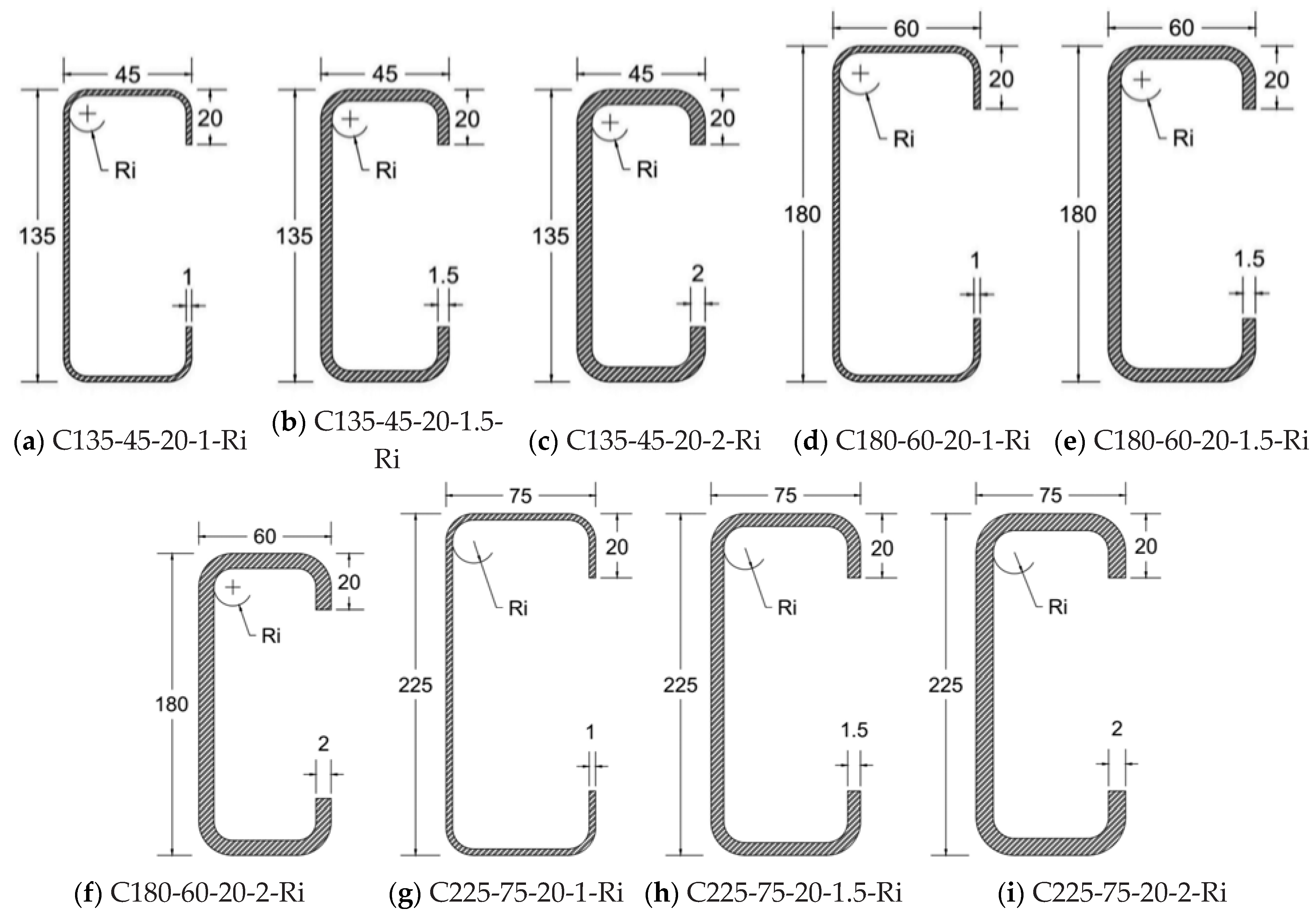
8. Analysis of the Effects of Inside Radius/Thickness on Various Buckling Modes in Columns and Beams
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Recommendations for Future Research
References
- Yuan, W.-B.; Cheng, S.; Li, L.-Y.; Kim, B. Web-flange distortional buckling of partially restrained cold-formed steel purlins under uplift loading. Int. J. Mech. Sci. 2014, 89, 476–481. [Google Scholar] [CrossRef]
- Dhole, P.S.; Bhusare, V. Behaviour of the Cold Form Channel Section with and Without Stiffener under Pure Torsion. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 11766–11774. [Google Scholar]
- Zhao, X.; Tootkaboni, M.; Schafer, B.W. Laser-based cross-section measurement of cold-formed steel members: Model reconstruction and application. Thin-Walled Struct. 2017, 120, 70–80. [Google Scholar] [CrossRef]
- Pham, C.H.; Hancock, G.J. Experimental investigation and direct strength design of high strength complex c-sections in pure bending. J. Struct. Eng. 2013, 139, 1842–1852. [Google Scholar] [CrossRef]
- Laím, L.; Rodrigues, J.P.C.; Craveiro, H.D. Flexural behaviour of beams made of cold-formed steel sigma-shaped sections at ambient and fire conditions. Thin-Walled Struct. 2015, 87, 53–65. [Google Scholar] [CrossRef]
- Keerthan, P.; Mahendran, M. Experimental studies on the shear behaviour and strength of LiteSteel beams. Eng. Struct. 2010, 32, 3235–3247. [Google Scholar] [CrossRef]
- Keerthan, P.; Mahendran, M. Improved shear design rules of cold-formed steel beams. Eng. Struct. 2015, 99, 603–615. [Google Scholar] [CrossRef]
- Steau, E.; Keerthan, P.; Mahendran, M. Web crippling capacities of rivet fastened rectangular hollow flange channel beams under one flange load cases. Steel Constr. 2016, 9, 222–239. [Google Scholar] [CrossRef]
- Siahaan, R.; Mahendran, M.; Keerthan, P. Section moment capacity tests of rivet fastened rectangular hollow flange channel beams. J. Constr. Steel Res. 2016, 125, 252–262. [Google Scholar] [CrossRef]
- Schafer, B.W. Cold-formed steel structures around the world. Steel Constr. 2011, 4, 141–149. [Google Scholar] [CrossRef]
- Wolter, B.; Gabi, Y.; Conrad, C. Nondestructive testing with 3MA-an overview of principles and applications. Appl. Sci. 2019, 9, 1068. [Google Scholar] [CrossRef]
- Doktor, M.S.; Fox, C.; Kurz, W.; Stockis, J.P. Characterization of steel buildings by means of non-destructive testing methods. J. Math. Ind. 2018, 8, 10. [Google Scholar] [CrossRef]
- Quintela, P.; Barral, P.; Gómez, D.; Pena, F.J.; Rodríguez, J.; Salgado, P.; Vázquez-Méndez, M.E. Progress in Industrial Mathematics at ECMI 2016; Springer: Berlin/Heidelberg, Germany, 2018; Volume 26, Available online: http://www.springer.com/series/4650 (accessed on 15 December 2023).
- Landesmann, A.; Camotim, D.; Garcia, R. On the strength and DSM design of cold-formed steel web/flange-stiffened lipped channel columns buckling and failing in distortional modes. Thin-Walled Struct. 2016, 105, 248–265. [Google Scholar] [CrossRef]
- Almatrafi, M.; Theofanous, M.; Dirar, S.; Gkantou, M. Structural response of cold-formed lipped Z purlins—Part 1: Experimental investigation. Thin-Walled Struct. 2021, 161, 107452. [Google Scholar] [CrossRef]
- Nabil, A.; Badawy Abu-Sena, A.; Darwish, E.; El-Tobgy, H. Experimental and Parametric Research on the Behavior of Cfs-Zee Section under Cyclic Load. J. Al-Azhar Univ. Eng.Sector 2022, 17, 895–942. [Google Scholar] [CrossRef]
- Almatrafi, M.; Theofanous, M.; Dirar, S.; Bock, M. Structural response of cold-formed lipped Z purlins—Part 2 numerical modelling and optimisation of lip size. Thin-Walled Struct. 2021, 161, 107453. [Google Scholar] [CrossRef]
- Seah, L.K.; Rhodes, J.; Lim, B.S. Influence of Lips on Thin-Walled Sections. Thin-Walled Struct. 1993, 16, 145–177. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, M. Experimental investigation and finite element analysis of web-stiffened cold-formed lipped channel columns with batten sheets. Thin-Walled Struct. 2018, 125, 38–50. [Google Scholar] [CrossRef]
- Liu, C.; Duan, L. Analytical Prediction of the Distortional Buckling Loads for Cold-Formed Channel Beams with Edge-Stiffened Rectangular Web Openings. Buildings 2023, 13, 101. [Google Scholar] [CrossRef]
- Pham, N.H.; Vu, Q.A. Effects of stiffeners on the capacities of cold-formed steel channel members. Steel Constr. 2021, 14, 270–278. [Google Scholar] [CrossRef]
- Supapurlins® Supazeds® & Supacees®. Design and Installation Guide for Building Professionals. Available online: https://manningriversteel.com.au/wp-content/uploads/pdfs/lysaght-purlins.pdf (accessed on 19 November 2023).
- Venkata, A.; Manoj, P.; Selvan, S.S. Flexural Behaviour of Light Gauge Cold Formed Steel ‘Z’ and ‘Hat’ Sections with and without Lips. Int. J. Civ. Eng. Technol. 2017, 8, 8–11. Available online: http://www.iaeme.com/IJCIET/index.asp662http://www.iaeme.com/IJCIET/issues.asp?JType=IJCIET&VType=8&IType=3 (accessed on 15 December 2023).
- Ye, J.; Hajirasouliha, I.; Becque, J. Experimental investigation of local-flexural interactive buckling of cold-formed steel channel columns. Thin-Walled Struct. 2018, 125, 245–258. [Google Scholar] [CrossRef]
- Feng, Y.; Tong, G.; Zhang, L. Distortional and Lateral Buckling of Z-Purlins with Sloping Lips in Flexure. J. Struct. Eng. 2018, 144, 04018168. [Google Scholar] [CrossRef]
- Beulah, G.; Ananthi, G.; Vishuvardhan, S.; Knight, S. Experimental, theoretical and numerical study on thin walled steel single and compound channel sections in axial compression. Indian J. Eng. Mater. Sci. 2015, 22, 570–580. [Google Scholar]
- Kindmann, R.; Kraus, M. Steel Structures Design Using FEM; Wilhelm Ernst & Sohn: Hoboken, NJ, USA, 2011. [Google Scholar]
- AISI S100-16 (R2020) w/S3-22; North American Specification for the Design of Cold-Formed Steel Structural Members. AISI: Washington, DC, USA, 2016; Volume 3.
- AS/NZS 4600: 2018; Cold-Formed Steel Structures. AS/NZS: Wellington, New Zealand, 2018. Available online: www.standards.govt.nz (accessed on 15 December 2023).
- Yu, W.-W.; LaBoube, R.A.; Chen, H. Cold-Formed Steel Design, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Dubina, D.; Ungureanu, V.; Landolfo, R. Eurocode 3: Part 1–3, 1st ed.; ECCS—European Convention for Constructional Steelwork: Brussels, Belgium, 2012; Available online: www.steelconstruct.com (accessed on 15 December 2023).
- Merrick, J.T.; Hancock, G.J.; Bamach, M.R.; Merrick, J.T.; Hancock, G.J.; Bambach, M.R. Distortional Buckling Formulae for Thin Walled Channel and Z-Sections with Return Lips. In Proceedings of the Fourteenth International Specialty Conference on Cold-Formed Steel Structures, St. Louis, MI, USA, 15–16 October 1998; Available online: https://scholarsmine.mst.edu/isccss/14iccfsss/14iccfsss-session1/3 (accessed on 15 December 2023).
- Ye, J.; Hajirasouliha, I.; Becque, J.; Pilakoutas, K. Development of more efficient cold-formed steel channel sections in bending. Thin-Walled Struct. 2016, 101, 1–13. [Google Scholar] [CrossRef]
- Ye, J.; Mojtabaei, S.M.; Hajirasouliha, I. Local-flexural interactive buckling of standard and optimised cold-formed steel columns. J. Constr. Steel Res. 2018, 144, 106–118. [Google Scholar] [CrossRef]
- AISI S240-20; North American Standard for Cold-Formed Steel Structural Framing. AISI: Washington, DC, USA, 2020.
- Buhagiar, D.; Chapman, J.C.; Dowling, P.J. Design of C-sections Against Deformational Lip Buckling. 1992. Available online: https://scholarsmine.mst.edu/isccss/11iccfss/11iccfss-session2/2 (accessed on 15 December 2023).
- Cava, D.; Camotim, D.; Dinis, P.B.; Madeo, A. Numerical investigation and direct strength design of cold-formed steel lipped channel columns experiencing local-distortional–global interaction. Thin-Walled Struct. 2016, 105, 231–247. [Google Scholar] [CrossRef]
- Peiris, M.; Mahendran, M. Behaviour of cold-formed steel lipped channel sections subject to eccentric axial compression. J. Constr. Steel Res. 2021, 184, 106808. [Google Scholar] [CrossRef]
- Babu, S.S.; Selvan, S.S. State of the art of cold formed steel members. Mater. Today Proc. 2020, 37, 3069–3073. [Google Scholar] [CrossRef]
- Dizdar, Ç.; Baran, E.; Topkaya, C. Strength and stiffness of floor trusses fabricated from cold-formed steel lipped channels. Eng. Struct. 2019, 181, 437–457. [Google Scholar] [CrossRef]
- AISI S100-16 (2020) w/S2-20; North American Specification for the Design of Cold-Formed Steel Structural Members. AISI: Washington, DC, USA, 2016; Volume 2.
- Dubina, D. Chapter 2: Peculiar Problems in Cold-Formed Steel Design Parti 2.1 Elements 2.2.1. Cold-Formed Steel Sections: Linear Profiles, Cladding and Sheeting Panels; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Beulah, G.; Ananthi, G. State-of-The-Art Review on Cold-Formed Steel Channel Sections Under Compression Built-Up Cold-Formed Steel Sections View Project. 2017. Available online: https://www.researchgate.net/publication/318261977 (accessed on 15 December 2023).
- Lu, Y.; Zhou, T.; Li, W.; Wu, H. Experimental investigation and a novel direct strength method for cold-formed built-up I-section columns. Thin-Walled Struct. 2017, 112, 125–139. [Google Scholar] [CrossRef]
- Mathews, D.P.K.M. Web Buckling Analysis of Cold Formed Built-Up I Section. GRD J.-Glob. Res. Dev. J. Eng. 2017, 2, 177–182. Available online: www.grdjournals.com (accessed on 15 December 2023).
- Wald, F.; Wald, F.; Jandera, M. Numerical Investigation of Steel Built-up Columns Composed of Track and Channel Cold-Formed Sections. In Proceedings of the International Colloquia on Stability and Ductility of Steel Structures, (SDSS 2019), Prague, Czech Republic, 11–13 September 2019; pp. 363–370. [Google Scholar]
- Yao, X.; Liu, Y.; Zhang, S.; Guo, Y.; Hu, C. Experiment and Design Method of Cold-Formed Thin-Walled Steel Double-Lipped Equal-Leg Angle under Axial Compression. Buildings 2022, 12, 1775. [Google Scholar] [CrossRef]
- Schafer, B.W.; Peköz, T. Computational modeling of cold-formed steel: Characterizing geometric imperfections and residual stresses. J. Constr. Steel Res. 1998, 47, 193–210. [Google Scholar] [CrossRef]
- Post, B. Fastener Spacing Study of Cold-Formed Steel Wall Studs Using Finite Strip and Finite Element Methods; Core: London, UK, 2012. [Google Scholar]
- Liao, F.; Wu, H.; Wang, R.; Zhou, T. Compression test and analysis of multi-limbs built-up cold-formed steel stub columns. J. Constr. Steel Res. 2017, 128, 405–415. [Google Scholar] [CrossRef]
- Ting, T.C.H.; Roy, K.; Lau, H.H.; Lim, J.B.P. Effect of screw spacing on behavior of axially loaded back-to-back cold-formed steel built-up channel sections. Adv. Struct. Eng. 2018, 21, 474–487. [Google Scholar] [CrossRef]
- Roy, K.; Ting, T.C.H.; Lau, H.H.; Lim, J.B.P. Nonlinear behavior of axially loaded back-to-back built-up cold-formed steel un-lipped channel sections. Steel Compos. Struct. 2018, 28, 233–250. [Google Scholar] [CrossRef]
- Huang, X.-H.; Yang, J.; Liu, Q.-F.; Zhu, J.; Bai, L.; Wang, F.-L.; Wang, J.-H. A simplified flange–lip model for distortional buckling of cold-formed steel channel-sections with stiffened web. Int. J. Mech. Sci. 2018, 136, 451–459. [Google Scholar] [CrossRef]
- Dissanayake, D.M.M.P.; Poologanathan, K.; Gunalan, S.; Tsavdaridis, K.D.; Wanniarachchi, K.S.; Nagaratnam, B. Numerical investigation of cold-formed stainless steel lipped channels with longitudinal stiffeners subjected to shear. Thin-Walled Struct. 2021, 158, 107179. [Google Scholar] [CrossRef]
- Karthik, C.; Anbarasu, M. Cold-formed ferritic stainless steel closed built-up beams: Flexural behaviour and numerical parametric study. Thin-Walled Struct. 2021, 164, 107816. [Google Scholar] [CrossRef]
- Deepak, M.S.; Ananthi, G.B.G.; Mahendran, K. Behaviour of thin-walled intermediate stiffened back-to-back columns under axial compression. Mater. Today Proc. 2020, 37, 2145–2152. [Google Scholar] [CrossRef]
- Waghmare, S.R.; Kulkarni, P.M. Behaviour of Cold Form Steel under Point Loading & Statically Defining Its Limitation. Int. Res. J. Eng. Technol. 2008, 6. [Google Scholar]
- Ghannam, M. Behaviour of Axially Loaded Cold-Formed Steel Built-Up Stub Columns. In Proceedings of the 1st International Conference on Structural Engineering Research (iCSER 2017), Sydney, Australia, 20–22 November 2017. [Google Scholar]
- Rasmussen, K.J.R.; Khezri, M.; Schafer, B.W.; Zhang, H. The mechanics of built-up cold-formed steel members. Thin-Walled Struct. 2020, 154, 106756. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Rasmussen, K.J.R.; Schafer, B.W. Buckling and Collapse Behavior of Screw-Fastened, Built-Up Cold-Formed Steel Columns of Varying Cross-Section Size: Experimental Investigation. In Proceedings of the Annual Stability Conference Structural Stability Research Council, San Antonio, TX, USA, 21–24 March 2017. [Google Scholar]
- Nie, S.; Zhou, T.; Liao, F.; Yang, D. Study on axial compressive behavior of quadruple C-channel built-up cold-formed steel columns. Struct. Eng. Mech. 2019, 70, 499–511. [Google Scholar] [CrossRef]
- Nie, S.F.; Zhou, T.H.; Zhang, Y.; Liu, B. Compressive behavior of built-up closed box section columns consisting of two cold-formed steel channels. Thin-Walled Struct. 2020, 151, 106762. [Google Scholar] [CrossRef]
- Samuel, J.; Joanna, P.S. Experimental Study And Numerical Modelling On The Behaviour Of Built-Up Cold-Formed Steel Beams With Diagonal Web Bars. Int. J. Sci. Technol. Res. 2020, 9, 2. [Google Scholar]
- El Aghoury, M.; Tawfic, M.; Amoush, E. Compressive Strength of Axially Loaded Built-up Sigma Cold Formed Sections Columns. Futur. Eng. J. 2020, 1, 10–21. [Google Scholar] [CrossRef]
- Karren, K.W. Corner properties of cold-formed steel shapes. J. Struct. Div. 1967, 93, 401–433. [Google Scholar] [CrossRef]
- Schafer, B. Direct Strength Method (DSM) Design Guide Committee on Specifications for the Design of Cold-Formed Steel Structural Members; American Iron and Steel Institute: Washington, DC, USA, 2006. [Google Scholar]
- Gatheeshgar, P.; Poologanathan, K.; Gunalan, S.; Nagaratnam, B.; Tsavdaridis, K.D.; Ye, J. Structural behaviour of optimized cold-formed steel beams. Steel Constr. 2020, 13, 294–304. [Google Scholar] [CrossRef]
- Prabhakaran, S.; Kalaiselvi, S. Experimental Study on Load Carrying Capacity of Cold Formed Steel Built-up Column. Int. J. Chemtech Res. 2018, 11, 164–170. [Google Scholar] [CrossRef]
- Lukačević, I.; Ungureanu, V. Numerical Parametric Study on Corrugated Web Built-Up Beams with Pinned End Supports. Available online: https://www.researchgate.net/publication/364403581 (accessed on 15 December 2023).
- Thirunavukkarasu, K.; Kanthasamy, E.; Gatheeshgar, P.; Poologanathan, K.; Rajanayagam, H.; Suntharalingam, T.; Dissanayake, M. Sustainable performance of a modular building system made of built-up cold-formed steel beams. Buildings 2021, 11, 460. [Google Scholar] [CrossRef]
- Phan, D.K.; Rasmussen, K.J.R.; Schafer, B.W. Tests and design of built-up section columns. J. Constr. Steel Res. 2021, 181, 106619. [Google Scholar] [CrossRef]
- Deng, F.; He, Y.; Deng, L.; Zhong, W. Experimental and Numerical Study on the Flexural Behavior of Cold-Formed Steel Multi-Limb Built-Up Section Beams. Buildings 2022, 12, 1639. [Google Scholar] [CrossRef]
- Sujitha, R.; Sunmathi, N.; Manikandan, R.K.; Arunprasad, J.; Rajkumar, S.; Sharma, S.; Sharma, K.; Li, C.; Eldin, E.M.T. Analytical and Experimental Study on Cold-Formed Steel Built-Up Sections for Bending. Materials 2022, 15, 7140. [Google Scholar] [CrossRef] [PubMed]
- Živaljević, V.; Jovanović, Đ.; Kovačević, D.; Džolev, I. The Influence of Web Holes on the Behaviour of Cold-Formed Steel Members: A Review. Buildings 2022, 12, 1091. [Google Scholar] [CrossRef]
- Kanthasamy, E.; Alsanat, H.; Poologanathan, K.; Gatheeshgar, P.; Corradi, M.; Thirunavukkarasu, K.; Dissanayake, M. Web Crippling Behaviour of Cold-Formed High Strength Steel Unlipped Channel Beams. Buildings 2022, 12, 291. [Google Scholar] [CrossRef]
- He, J.; Young, B. Web crippling design of cold-formed steel built-up I-sections. Eng. Struct. 2022, 252. [Google Scholar] [CrossRef]
- Chen, B.; Roy, K.; Fang, Z.; Uzzaman, A.; Chi, Y.; Lim, J.B.P. Web crippling capacity of fastened cold-formed steel channels with edge-stiffened web holes, un-stiffened web holes and plain webs under two-flange loading. Thin-Walled Struct. 2021, 163, 107666. [Google Scholar] [CrossRef]
- Fang, Z.; Roy, K.; Chen, B.; Xie, Z.; Ingham, J.; Lim, J.B.P. Effect of the web hole size on the axial capacity of back-to-back aluminium alloy channel section columns. Eng. Struct. 2022, 260. [Google Scholar] [CrossRef]
- Portioli, F.; Lorenzo, G.D.; Landolfo, R.; Mazzolani, F. Contact buckling effects in built-up cold-formed steel beams. Proceedings of The 6th International Conference on Coupled Instabilities in Metal Structures, Glasgow, UK, 3–5 December 2012. [Google Scholar]
- Vishweswaran, C.K.; Srisanthi, V.G. Experimental Study on Cold-formed Steel Built-up Column Sections. Eng. Struct. 2022, 256, 113954. [Google Scholar]
- Fratamico, D.C.; Torabian, S.; Rasmussen, K.J.R.; Schafer, B.; Schafer, B.W. Experimental Investigation of the Effect of Screw Fastener Spacing on the Local and Distortional Buckling Behavior of Built-Up Cold-Formed Steel Columns. 2016. Available online: https://www.researchgate.net/publication/305568137 (accessed on 15 December 2023).
- Mon, T.Y.; Selvam, J. Buckling Behaviors of Cold-Formed Steel Built-Up Columns under Axial Compression Tests. Int. J. Recent Technol. Eng. 2021, 10, 7–11. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Zhao, X.; Rasmussen, K.J.R.; Schafer, B.W. Experiments on the global buckling and collapse of built-up cold-formed steel columns. J. Constr. Steel Res. 2018, 144, 65–80. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Zhao, X.; Rasmussen, K.J.R.; Schafer, B.W. Experimental study on the composite action in sheathed and bare built-up cold-formed steel columns. Thin-Walled Struct. 2018, 127, 290–305. [Google Scholar] [CrossRef]
- Schafer, B.W.; Adany, S. Buckling Analysis of Cold-formed Steel Members Using CUFSM: Conventional and Constrained Finite Strip Methods. In CCFSS Proceedings of International Specialty Conference on Cold-Formed Steel Structures (1971–2018); University of Missouri: Rolla, MO, USA, 2006; pp. 39–54. Available online: https://scholarsmine.mst.edu/isccss (accessed on 15 December 2023).
- Kankanamge, N.D. Structural Behaviour and Design of Cold-Formed Steel Beams at Elevated Temperatures; QUT ePrints: Queensland, Australia, 2010. [Google Scholar]







| Test [4] | FS | FE | Test/FE | FS/FE | Test [4] | FS | FE | Test/FE | FS/FE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Section | t | D | B | d | |||||||||||
| mm | mm | mm | mm | MPa | kN·m | kN·m | kN·m | kN·m | kN·m | kN·m | |||||
| Mw-C15015 | 1.5 | 152.7 | 64.77 | 16.51 | 541.13 | 10.44 | 10.46 | 10.54 | 0.99 | 0.99 | 8.00 | 8.05 | 8.24 | 0.97 | 0.98 |
| Mw-C15019 | 1.9 | 153.38 | 64.47 | 16 | 534.48 | 20.81 | 20.85 | 21.11 | 0.99 | 0.99 | 12.85 | 12.92 | 12.93 | 0.99 | 1.00 |
| Mw-C15024 | 2.4 | 152.6 | 62.7 | 19.7 | 485.29 | 42.44 | 42.55 | 43.27 | 0.98 | 0.98 | 25.67 | 25.76 | 25.76 | 1.00 | 1.00 |
| Mw-C20015 | 1.5 | 203.7 | 76.08 | 16.42 | 513.40 | 10.31 | 10.35 | 10.35 | 1.00 | 1.00 | 8.70 | 8.75 | 9.15 | 0.95 | 0.96 |
| Mw-C20019 | 1.9 | 202.6 | 77.92 | 17.28 | 510.48 | 20.81 | 20.87 | 20.97 | 0.99 | 1.00 | 14.70 | 14.78 | 15.16 | 0.97 | 0.97 |
| Mw-C20024 | 2.4 | 203.35 | 76.61 | 20.88 | 483.49 | 42.35 | 42.48 | 42.85 | 0.99 | 0.99 | 29.07 | 29.17 | 30.07 | 0.97 | 0.97 |
| Ms-C15015 | 1.5 | 153.46 | 64.53 | 15.02 | 541.13 | 10.37 | 10.39 | 10.48 | 0.99 | 0.99 | 7.36 | 7.41 | 7.52 | 0.98 | 0.99 |
| Ms-C15019 | 1.9 | 153.54 | 65.01 | 16.27 | 534.48 | 20.78 | 20.82 | 21.09 | 0.99 | 0.99 | 12.97 | 13.04 | 13.06 | 0.99 | 1.00 |
| Ms-C15024 | 2.4 | 153.43 | 63.58 | 20.88 | 485.29 | 42.54 | 42.62 | 43.34 | 0.98 | 0.98 | 26.79 | 26.88 | 27.22 | 0.98 | 0.99 |
| Ms-C20015 | 1.5 | 203.74 | 75.88 | 16.16 | 513.40 | 10.29 | 10.33 | 10.33 | 1.00 | 1.00 | 8.59 | 8.64 | 9.00 | 0.95 | 0.96 |
| Ms-C20019 | 1.9 | 203.53 | 79.27 | 17.51 | 510.48 | 20.81 | 20.88 | 20.98 | 0.99 | 1.00 | 14.74 | 14.81 | 15.24 | 0.97 | 0.97 |
| Ms-C20024 | 2.4 | 202.3 | 77.58 | 21.26 | 483.49 | 42.44 | 42.56 | 42.94 | 0.99 | 0.99 | 29.15 | 29.26 | 30.24 | 0.96 | 0.97 |
| Mean | 0.99 | 0.99 | 0.97 | 0.98 | |||||||||||
| COV | 0.42% | 0.53% | 1.70% | 0.43% |
| Dimensions | TEST [86] | FEM | Difference | |||||
|---|---|---|---|---|---|---|---|---|
| Section | D | B | d | t | L | TEST; FEM | ||
| mm | mm | mm | mm | mm | kN·m | kN·m | % | |
| G250-1.95-1500 | 108.56 | 38.37 | 13.57 | 1.943 | 1500 | 3.686 | 3.49 | 5.4 |
| G250-1.95-2000 | 108.52 | 38.23 | 13.51 | 1.943 | 2000 | 3.550 | 3.39 | 4.5 |
| G250-1.95-2500 | 108.42 | 38.15 | 14.49 | 1.943 | 2500 | 3.266 | 3.19 | 2.4 |
| G250-1.95-2900 | 108.55 | 38.00 | 13.79 | 1.943 | 2900 | 2.969 | 2.93 | 1.4 |
| Mean | 3.4% | |||||||
| ID | /A | /A | /A | /A |
|---|---|---|---|---|
| CD-B-d | ||||
| C90-30-0 | 4323 | 4323 | 182 | 135 |
| C90-30-10 | 5484 | 6189 | 292 | 217 |
| C90-30-15 | 5588 | 6498 | 324 | 242 |
| C90-30-20 | 5600 | 7216 | 348 | 260 |
| C90-30-25 | 5637 | 6834 | 366 | 273 |
| C90-30-30 | 5619 | 6028 | 378 | 282 |
| C135-45-0 | 1867 | 1867 | 418 | 311 |
| C135-45-10 | 2387 | 2700 | 602 | 449 |
| C135-45-15 | 2431 | 3579 | 667 | 497 |
| C135-45-20 | 2445 | 4266 | 719 | 536 |
| C135-45-25 | 2450 | 4682 | 762 | 568 |
| C135-45-30 | 2450 | 5487 | 796 | 593 |
| C180-60-0 | 1036 | 1036 | 746 | 548 |
| C180-60-10 | 1324 | 1487 | 1003 | 725 |
| C180-60-15 | 1353 | 2012 | 1099 | 777 |
| C180-60-20 | 1362 | 2396 | 1181 | 818 |
| C180-60-25 | 1365 | 2892 | 1249 | 850 |
| C180-60-30 | 1370 | 3224 | 1304 | 877 |
| C225-75-0 | 658 | 658 | 1153 | 633 |
| C225-75-10 | 842 | 938 | 1471 | 808 |
| C225-75-15 | 862 | 1305 | 1593 | 858 |
| C225-75-20 | 866 | 1627 | 1692 | 891 |
| C225-75-25 | 869 | 1908 | 1770 | 914 |
| C225-75-30 | 870 | 2268 | 1843 | 935 |
| C270-90-0 | 455 | 455 | 1592 | 685 |
| C270-90-10 | 581 | 650 | 1904 | 825 |
| C270-90-15 | 596 | 878 | 2048 | 862 |
| C270-90-20 | 600 | 1128 | 2160 | 886 |
| C270-90-25 | 603 | 1489 | 2216 | 897 |
| C270-90-30 | 603 | 1656 | 2220 | 898 |
| d = 0 | 1668 | 1668 | 818 | 462 |
| d = 10 | 2124 | 2393 | 1054 | 605 |
| d = 15 | 2166 | 2854 | 1146 | 647 |
| d = 20 | 2174 | 3327 | 1220 | 678 |
| d = 25 | 2185 | 3561 | 1272 | 700 |
| d = 30 | 2182 | 3733 | 1308 | 717 |
| ID | /A | /A | /A | A |
|---|---|---|---|---|
| CD-B-d | ||||
| C90-30-0 | 213 | 213 | 22 | 19 |
| C90-30-10 | 793 | 362 | 33 | 28 |
| C90-30-15 | 842 | 457 | 38 | 32 |
| C90-30-20 | 746 | 486 | 43 | 37 |
| C90-30-25 | 549 | 465 | 48 | 41 |
| C90-30-30 | 440 | 421 | 54 | 45 |
| C135-45-0 | 138 | 138 | 59 | 50 |
| C135-45-10 | 516 | 246 | 84 | 72 |
| C135-45-15 | 549 | 340 | 96 | 79 |
| C135-45-20 | 548 | 412 | 108 | 86 |
| C135-45-25 | 534 | 456 | 120 | 90 |
| C135-45-30 | 475 | 473 | 133 | 93 |
| C180-60-0 | 103 | 103 | 132 | 85 |
| C180-60-10 | 373 | 184 | 178 | 125 |
| C180-60-15 | 403 | 264 | 200 | 133 |
| C180-60-20 | 407 | 335 | 221 | 138 |
| C180-60-25 | 405 | 397 | 242 | 142 |
| C180-60-30 | 399 | 442 | 263 | 144 |
| C225-75-0 | 82 | 82 | 252 | 102 |
| C225-75-10 | 327 | 146 | 318 | 132 |
| C225-75-15 | 317 | 213 | 346 | 153 |
| C225-75-20 | 322 | 280 | 382 | 169 |
| C225-75-25 | 323 | 343 | 411 | 181 |
| C225-75-30 | 322 | 393 | 454 | 185 |
| C270-90-0 | 68 | 68 | 432 | 105 |
| C270-90-10 | 235 | 120 | 532 | 136 |
| C270-90-15 | 261 | 179 | 580 | 160 |
| C270-90-20 | 266 | 240 | 627 | 180 |
| C270-90-25 | 267 | 297 | 669 | 195 |
| C270-90-30 | 267 | 352 | 705 | 203 |
| d = 0 | 121 | 121 | 179 | 72 |
| d = 10 | 449 | 212 | 229 | 98 |
| d = 15 | 474 | 291 | 252 | 112 |
| d = 20 | 458 | 351 | 276 | 122 |
| d = 25 | 416 | 392 | 298 | 130 |
| d = 30 | 381 | 416 | 322 | 134 |
| CD-B-d-t-R | /A | /A | /A | /A |
|---|---|---|---|---|
| C135-45-20-1-0 | 605 | 1916 | 724 | 452 |
| C135-45-20-1-1 | 606 | 1905 | 710 | 446 |
| C135-45-20-1-2 | 612 | 1880 | 705 | 445 |
| C135-45-20-1-3 | 618 | 1882 | 699 | 444 |
| C135-45-20-1-4 | 626 | 1831 | 693 | 443 |
| C135-45-20-1-5 | 642 | 1848 | 686 | 444 |
| C135-45-20-1-6 | 660 | 1859 | 679 | 445 |
| C135-45-20-1.5-0 | 1369 | 2909 | 724 | 539 |
| C135-45-20-1.5-1.5 | 1378 | 2896 | 701 | 523 |
| C135-45-20-1.5-3 | 1397 | 2914 | 692 | 516 |
| C135-45-20-1.5-4.5 | 1426 | 2939 | 683 | 509 |
| C135-45-20-1.5-6 | 1470 | 2875 | 672 | 501 |
| C135-45-20-1.5-7.5 | 1512 | 2858 | 667 | 497 |
| C135-45-20-1.5-9 | 1576 | 2889 | 656 | 489 |
| C135-45-20-2-0 | 2445 | 4266 | 719 | 536 |
| C135-45-20-2-2 | 2475 | 4088 | 688 | 513 |
| C135-45-20-2-4 | 2531 | 4063 | 675 | 503 |
| C135-45-20-2-6 | 2521 | 4171 | 707 | 527 |
| C135-45-20-2-8 | 2696 | 4029 | 652 | 486 |
| C135-45-20-2-10 | 2820 | 4029 | 641 | 478 |
| C135-45-20-2-12 | 2990 | 3992 | 625 | 466 |
| C180-60-20-1-0 | 338 | 1101 | 1140 | 497 |
| C180-60-20-1-1 | 339 | 1097 | 1120 | 492 |
| C180-60-20-1-2 | 340 | 1095 | 1113 | 490 |
| C180-60-20-1-3 | 343 | 1099 | 1105 | 490 |
| C180-60-20-1-4 | 346 | 1101 | 1097 | 489 |
| C180-60-20-1-5 | 352 | 1106 | 1088 | 490 |
| C180-60-20-1-6 | 358 | 1109 | 1080 | 490 |
| C180-60-20-1.5-0 | 764 | 1658 | 1174 | 673 |
| C180-60-20-1.5-1.5 | 767 | 1653 | 1143 | 662 |
| C180-60-20-1.5-3 | 774 | 1661 | 1130 | 659 |
| C180-60-20-1.5-4.5 | 785 | 1672 | 1116 | 657 |
| C180-60-20-1.5-6 | 801 | 1687 | 1102 | 656 |
| C180-60-20-1.5-7.5 | 814 | 1699 | 1095 | 657 |
| C180-60-20-1.5-9 | 838 | 1719 | 1080 | 657 |
| C180-60-20-2-0 | 1362 | 2396 | 1181 | 818 |
| C180-60-20-2-2 | 1374 | 2384 | 1137 | 799 |
| C180-60-20-2-4 | 1390 | 2394 | 1119 | 793 |
| C180-60-20-2-6 | 1415 | 2407 | 1106 | 791 |
| C180-60-20-2-8 | 1455 | 2437 | 1086 | 789 |
| C180-60-20-2-10 | 1496 | 2376 | 1070 | 788 |
| C180-60-20-2-12 | 1559 | 2428 | 1049 | 782 |
| C225-75-20-1-0 | 216 | 687 | 1464 | 495 |
| C225-75-20-1-1 | 216 | 687 | 1448 | 492 |
| C225-75-20-1-2 | 217 | 687 | 1442 | 492 |
| C225-75-20-1-3 | 218 | 688 | 1436 | 491 |
| C225-75-20-1-4 | 219 | 690 | 1430 | 491 |
| C225-75-20-1-5 | 222 | 693 | 1405 | 488 |
| C225-75-20-1-6 | 225 | 696 | 1403 | 490 |
| C225-75-20-1.5-0 | 486 | 1117 | 1621 | 709 |
| C225-75-20-1.5-1.5 | 488 | 1084 | 1571 | 697 |
| C225-75-20-1.5-3 | 492 | 1087 | 1563 | 696 |
| C225-75-20-1.5-4.5 | 497 | 1091 | 1552 | 695 |
| C225-75-20-1.5-6 | 504 | 1098 | 1539 | 695 |
| C225-75-20-1.5-7.5 | 510 | 1102 | 1533 | 696 |
| C225-75-20-1.5-9 | 521 | 1111 | 1513 | 696 |
| C225-75-20-2-0 | 866 | 1627 | 1692 | 891 |
| C225-75-20-2-2 | 872 | 1549 | 1637 | 876 |
| C225-75-20-2-4 | 882 | 1555 | 1615 | 872 |
| C225-75-20-2-6 | 891 | 1556 | 1599 | 870 |
| C225-75-20-2-8 | 910 | 1568 | 1576 | 868 |
| C225-75-20-2-10 | 929 | 1582 | 1556 | 867 |
| C225-75-20-2-12 | 956 | 1593 | 1531 | 866 |
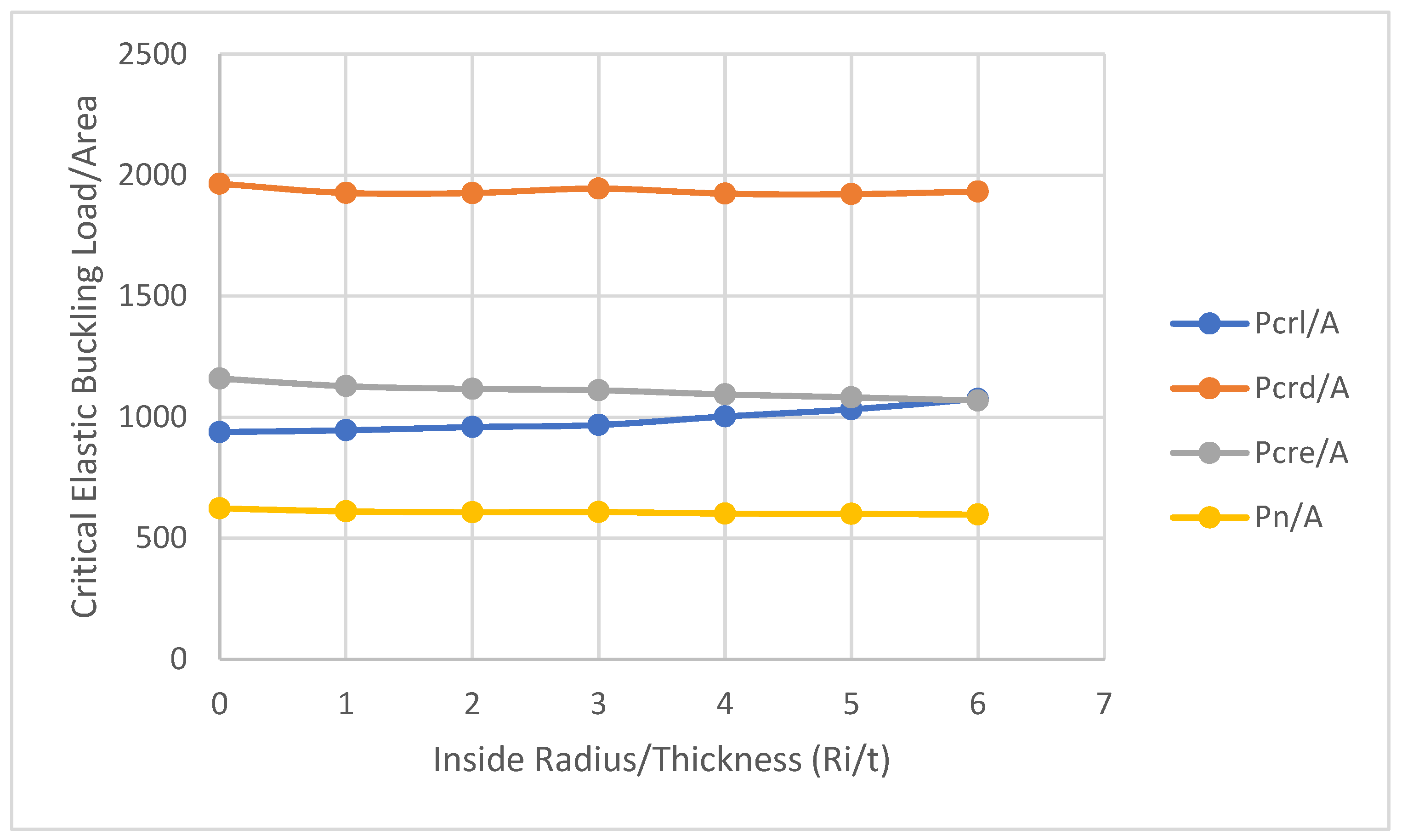
| r/t = 0 | 939 | 1964 | 1160 | 623 |
| r/t = 1 | 946 | 1927 | 1128 | 611 |
| r/t = 2 | 959 | 1926 | 1117 | 608 |
| r/t = 3 | 968 | 1945 | 1111 | 608 |
| r/t = 4 | 1003 | 1924 | 1094 | 602 |
| r/t = 5 | 1033 | 1922 | 1082 | 600 |
| r/t = 6 | 1076 | 1933 | 1068 | 598 |
| CD-B-d-t-R | /A | /A | /A | A |
|---|---|---|---|---|
| C135-45-20-1-0 | 133 | 197 | 107 | 80 |
| C135-45-20-1-1 | 131 | 196 | 105 | 79 |
| C135-45-20-1-2 | 131 | 195 | 104 | 78 |
| C135-45-20-1-3 | 133 | 195 | 103 | 78 |
| C135-45-20-1-4 | 136 | 194 | 102 | 78 |
| C135-45-20-1-5 | 142 | 193 | 101 | 79 |
| C135-45-20-1-6 | 149 | 193 | 100 | 80 |
| C135-45-20-1.5-0 | 304 | 300 | 108 | 86 |
| C135-45-20-1.5-1.5 | 297 | 296 | 104 | 84 |
| C135-45-20-1.5-3 | 299 | 296 | 103 | 83 |
| C135-45-20-1.5-4.5 | 307 | 295 | 101 | 82 |
| C135-45-20-1.5-6 | 322 | 294 | 99 | 81 |
| C135-45-20-1.5-7.5 | 334 | 293 | 98 | 80 |
| C135-45-20-1.5-9 | 356 | 292 | 96 | 78 |
| C135-45-20-2-0 | 548 | 412 | 108 | 86 |
| C135-45-20-2-2 | 532 | 405 | 104 | 83 |
| C135-45-20-2-4 | 540 | 404 | 102 | 82 |
| C135-45-20-2-6 | 547 | 417 | 107 | 84 |
| C135-45-20-2-8 | 587 | 400 | 97 | 79 |
| C135-45-20-2-10 | 624 | 401 | 95 | 77 |
| C135-45-20-2-12 | 673 | 396 | 92 | 75 |
| C180-60-20-1-0 | 100 | 165 | 221 | 100 |
| C180-60-20-1-1 | 99 | 166 | 218 | 99 |
| C180-60-20-1-2 | 99 | 165 | 216 | 99 |
| C180-60-20-1-3 | 99 | 165 | 214 | 99 |
| C180-60-20-1-4 | 101 | 164 | 213 | 99 |
| C180-60-20-1-5 | 103 | 165 | 211 | 100 |
| C180-60-20-1-6 | 107 | 164 | 209 | 101 |
| C180-60-20-1.5-0 | 227 | 247 | 221 | 131 |
| C180-60-20-1.5-1.5 | 223 | 247 | 215 | 129 |
| C180-60-20-1.5-3 | 224 | 248 | 212 | 129 |
| C180-60-20-1.5-4.5 | 227 | 248 | 209 | 129 |
| C180-60-20-1.5-6 | 235 | 247 | 206 | 129 |
| C180-60-20-1.5-7.5 | 240 | 247 | 205 | 130 |
| C180-60-20-1.5-9 | 252 | 246 | 201 | 131 |
| C180-60-20-2-0 | 407 | 335 | 221 | 138 |
| C180-60-20-2-2 | 398 | 335 | 213 | 136 |
| C180-60-20-2-4 | 402 | 336 | 209 | 134 |
| C180-60-20-2-6 | 409 | 335 | 207 | 133 |
| C180-60-20-2-8 | 425 | 335 | 202 | 131 |
| C180-60-20-2-10 | 444 | 336 | 199 | 130 |
| C180-60-20-2-12 | 472 | 334 | 194 | 128 |
| C225-75-20-1-0 | 79 | 140 | 384 | 113 |
| C225-75-20-1-1 | 8 | 140 | 378 | 48 |
| C225-75-20-1-2 | 79 | 139 | 376 | 112 |
| C225-75-20-1-3 | 79 | 140 | 373 | 112 |
| C225-75-20-1-4 | 80 | 140 | 370 | 112 |
| C225-75-20-1-5 | 81 | 140 | 368 | 113 |
| C225-75-20-1-6 | 83 | 140 | 365 | 114 |
| C225-75-20-1.5-0 | 180 | 208 | 389 | 150 |
| C225-75-20-1.5-1.5 | 177 | 208 | 369 | 148 |
| C225-75-20-1.5-3 | 178 | 209 | 371 | 148 |
| C225-75-20-1.5-4.5 | 180 | 209 | 365 | 148 |
| C225-75-20-1.5-6 | 184 | 209 | 362 | 149 |
| C225-75-20-1.5-7.5 | 187 | 209 | 360 | 149 |
| C225-75-20-1.5-9 | 194 | 209 | 356 | 150 |
| C225-75-20-2-0 | 322 | 280 | 382 | 169 |
| C225-75-20-2-2 | 316 | 280 | 373 | 169 |
| C225-75-20-2-4 | 318 | 282 | 369 | 168 |
| C225-75-20-2-6 | 322 | 282 | 366 | 168 |
| C225-75-20-2-8 | 331 | 283 | 360 | 167 |
| C225-75-20-2-10 | 342 | 284 | 355 | 167 |
| C225-75-20-2-12 | 359 | 283 | 349 | 166 |
| r/t = 0 | 256 | 254 | 238 | 117 |
| r/t = 1 | 242 | 253 | 231 | 108 |
| r/t = 2 | 252 | 253 | 229 | 115 |
| r/t = 3 | 256 | 254 | 227 | 115 |
| r/t = 4 | 267 | 252 | 224 | 114 |
| r/t = 5 | 278 | 252 | 221 | 114 |
| r/t = 6 | 294 | 251 | 218 | 114 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, A.B.; Hussein, D.B. Effects of Lip Length and Inside Radius-to-Thickness Ratio on Buckling Behavior of Cold-Formed Steel C-Sections. Buildings 2024, 14, 587. https://doi.org/10.3390/buildings14030587
Hussein AB, Hussein DB. Effects of Lip Length and Inside Radius-to-Thickness Ratio on Buckling Behavior of Cold-Formed Steel C-Sections. Buildings. 2024; 14(3):587. https://doi.org/10.3390/buildings14030587
Chicago/Turabian StyleHussein, Ardalan B., and Diyari B. Hussein. 2024. "Effects of Lip Length and Inside Radius-to-Thickness Ratio on Buckling Behavior of Cold-Formed Steel C-Sections" Buildings 14, no. 3: 587. https://doi.org/10.3390/buildings14030587
APA StyleHussein, A. B., & Hussein, D. B. (2024). Effects of Lip Length and Inside Radius-to-Thickness Ratio on Buckling Behavior of Cold-Formed Steel C-Sections. Buildings, 14(3), 587. https://doi.org/10.3390/buildings14030587






