Developments in Quantifying the Response Factors Required for Linear Analytical and Seismic Design Procedures
Abstract
:1. Introduction
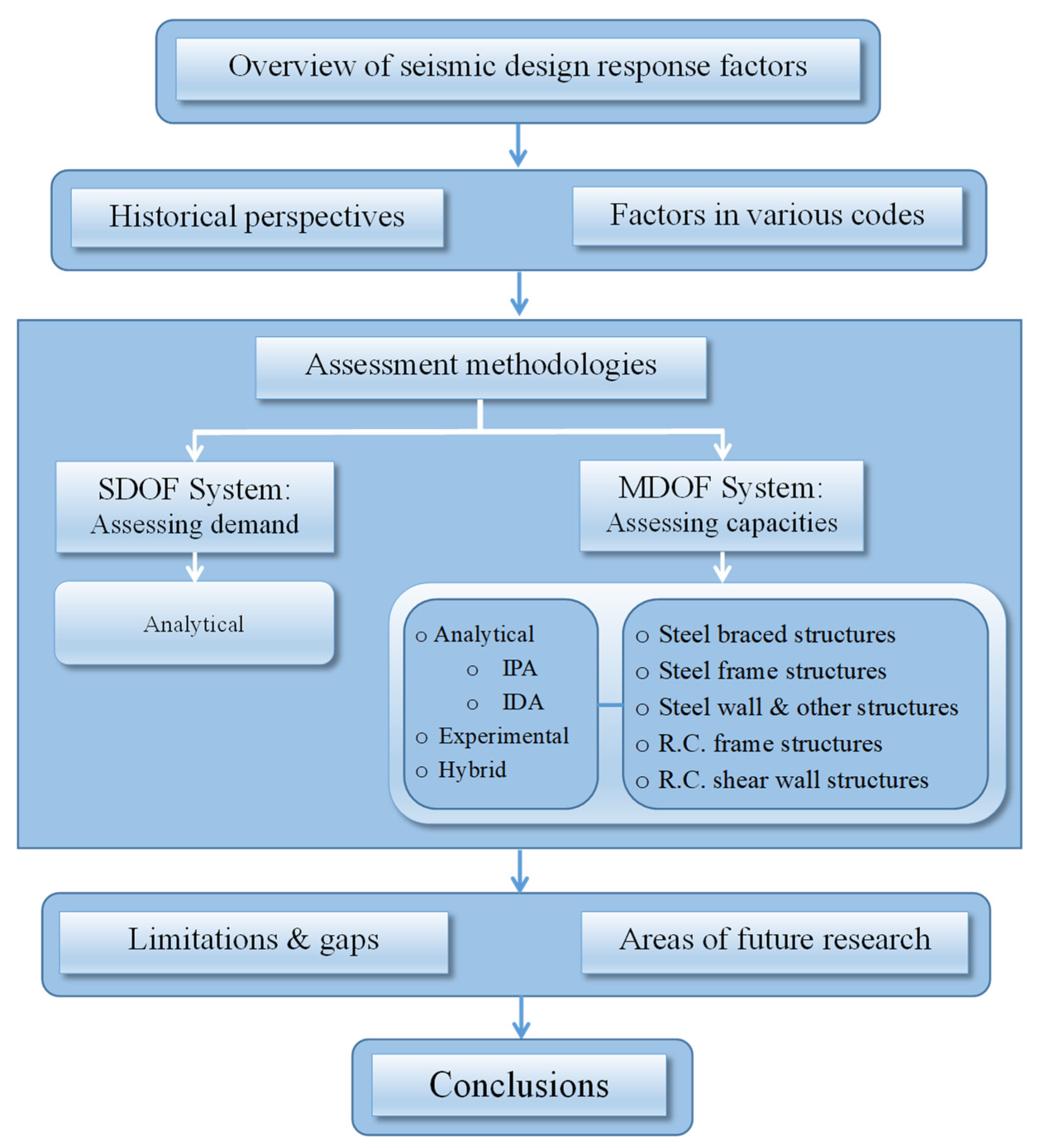
2. Scope and Literature Review Approach
3. Overview of Seismic Design Response Factors
3.1. Historical Perspective of Seismic Response Factors
3.2. Seismic Response Factors in Various Codes
4. Methods of Assessing Seismic Response Factors
- Single degree of freedom (SDOF) systems assessing demands
- Multi-degree of freedom (MDOF) systems assessing capacities
4.1. Single Degree of Freedom (SDOF) Systems: Assessing Demands
4.2. Multi-Degree of Freedom (MDOF) Systems: Assessing the Capacities
- Steel-braced structures.
- Steel frame structures.
- Steel walls and other structures.
- RC frame structures.
- RC shear wall structures.
4.2.1. Steel-Braced Structures
4.2.2. Steel-Framed Structures
4.2.3. Steel Walls and Other Structures
4.2.4. RC Frame Structures
4.2.5. RC Shear Wall Structures
5. Limitations, Gaps, and Future Research
5.1. Limitations and Gaps
5.2. Areas for Future Research
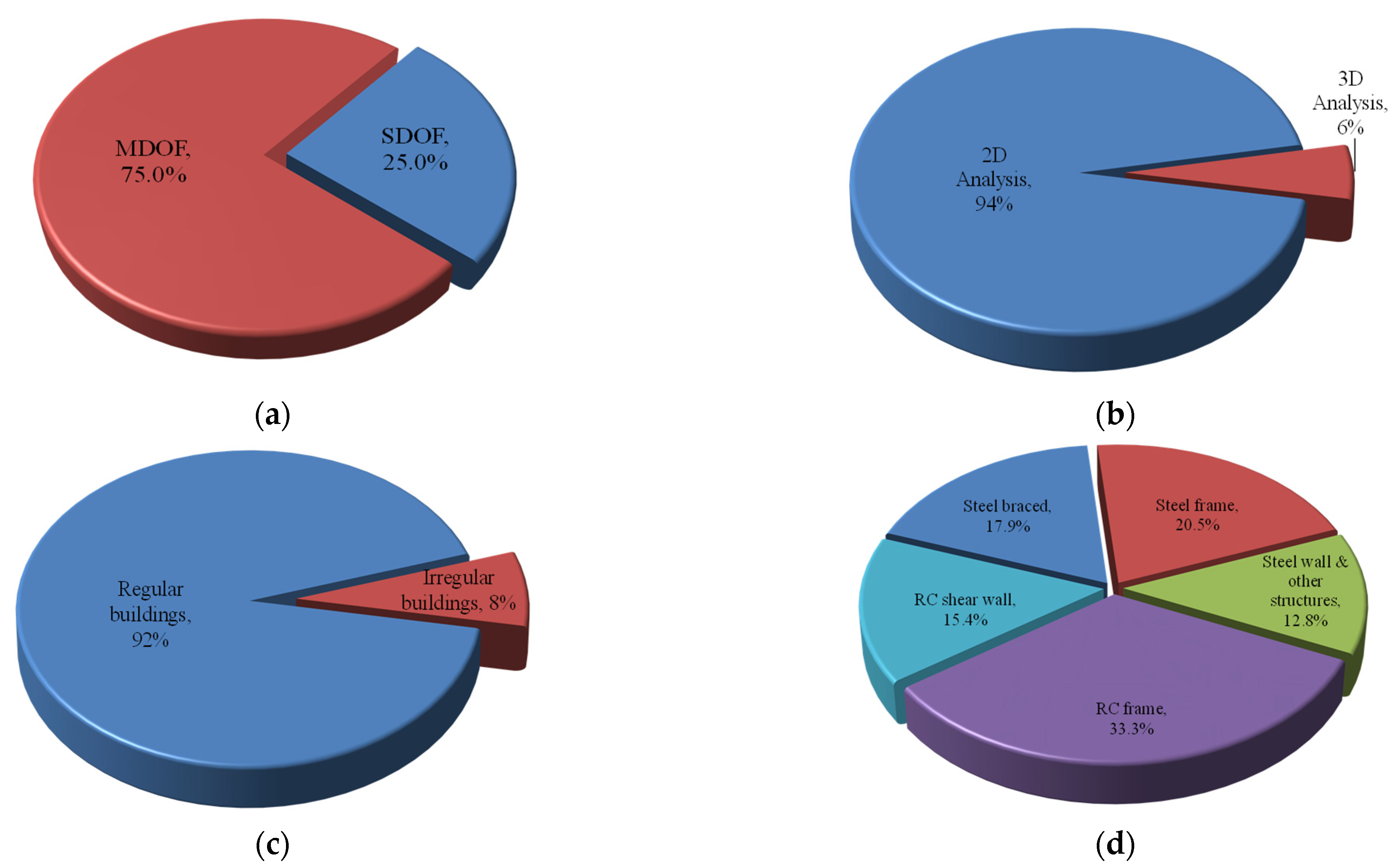
- Limited research (only 8% of previous studies) was conducted to evaluate the seismic response of irregular buildings. This emphasizes the need to investigate practical buildings covering different types of irregularities with various heights;
- Most of the earlier work was based on 2D inelastic analysis with unidirectional seismic loading. Only 6% of research was conducted using 3D inelastic analysis. This presses the need to evaluate the seismic response factors using 3D inelastic analysis under the effect of bi-directional seismic loading;
- Many previous studies did not account for structural overstrength. This shows the need to consider structural overstrength in assessing the seismic response of buildings;
- Studies on regular RC shear wall buildings were limited to 15.4% in the previous investigations. This emphasizes a need to evaluate the seismic behavior of RC shear wall buildings with varying heights;
- Previous studies focused on buildings in seismic zones representing moderate to severe earthquakes. Furthermore, the effects of aftershock events need to be investigated to better evaluate the seismic performance of buildings with post-earthquake events.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDOF | Single degree of freedom |
| MDOF | Multi-degree of freedom |
| Vs | Design base shear |
| Ve | Elastic base shear |
| Vy | Yield base shear |
| R | Response modification factor |
| Rμ | Ductility reduction factor |
| Cd | Deflection amplification factor |
| Ωo | Structural overstrength factor |
| µ | Ductility |
| T | Fundamental period |
| Tg | Characteristic period |
| GM | Ground motion |
| EQ | Earthquake |
| α | Strain hardening coefficient |
| EPP | Elastic perfectly plastic |
| SSP | Shear-slipped |
| BILE | Bilinear elastic |
| R | Strength reduction factor |
| q | Strength reduction factor (termed the behavior factor in EN standards) |
| RD | Damage-based strength reduction factor |
| RR | Redundancy factor |
| Rd | Ductility-related modification factor |
| Ro | Overstrength-related modification factor |
| ASCE | American Society of Civil Engineers |
| AISC | American Institute of Steel Construction |
| NZS | New Zealand Standard |
| UBC | Universal Building Code |
| IBC | International Building Code |
| ENs | European Norms (Eurocode) |
| FEMA | Federal Emergency Management Agency |
| MCBC | Mexico City Building Code |
| NBCC | National Building Code of Canada |
| PEER | Pacific Earthquake Engineering Research Centre |
| ATC | Applied Technology Council |
| CBF | Concentrically braced frame |
| BRBF | Buckling restrained braced frame |
| CKB | Chevron knee brace |
| MRF | Moment-resisting frame |
| CMR | Collapse margin ratio |
| ACMR | Adjusted collapse margin ratio |
| ELFA | Equivalent lateral force analysis |
| MRSA | Modal response spectrum analysis |
| PGA | Peak ground acceleration |
| IPA | Inelastic pushover analysis |
| IDA | Incremental dynamic analysis |
| SAC | SAC steel project |
| THA | Time history analysis |
| APA | Adaptive pushover analysis |
| DAPA | Displacement-based adaptive pushover analysis |
| FAPA | Force-based adaptive pushover analysis |
| ISDR | Inter-story drift ratio |
| SDC | Seismic design category |
| SMA | Shape memory alloy |
References
- Quantification of Building Seismic Performance Factors; FEMA P695; Federal Emergency Management Agency: Washington, DC, USA, 2009.
- NEHRP Recommended Seismic Provisions for New Buildings and Other Structures; FEMA P-1050; Building Seismic Safety Council: Washington, DC, USA, 2015; Volume II, p. 388.
- NBCC. National Building Code of Canada; National Research Council: Ontario, ON, Canada, 2010.
- EN 1998-1; Eurocode 8: DESIGN of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- ASCE. Minimum Design Loads for Buildings and Other Structures ASCE7-16; American Society of Civil Engineers: Reston, Virginia, USA, 2016; p. 608. [Google Scholar]
- MCBC. Mexico City Building Code; Director of Public Works: Mexico City, Mexico, 2004. [Google Scholar]
- Mwafy, A. Assessment of seismic design response factors of concrete wall buildings. Earthq. Eng. Eng. Vib. 2011, 10, 115–127. [Google Scholar] [CrossRef]
- Mwafy, A. Use of overstrength and inelastic response in seismic design. Proc. Inst. Civ. Eng.-Struct. Build. 2013, 166, 282–297. [Google Scholar] [CrossRef]
- Mondal, A.; Ghosh, S.; Reddy, G. Performance-based evaluation of the response reduction factor for ductile RC frames. Eng. Struct. 2013, 56, 1808–1819. [Google Scholar] [CrossRef]
- Mwafy, A.; Hussain, N.; El-Sawy, K. Assessment of Material Strength Implications on Seismic Design of Tall Buildings through Collapse Analysis. Adv. Struct. Eng. 2015, 18, 2017–2033. [Google Scholar] [CrossRef]
- Husain, M.; Tsopelas, P. Measures of structural redundancy in reinforced concrete buildings. I: Redundancy indices. J. Struct. Eng. 2004, 130, 1651–1658. [Google Scholar] [CrossRef]
- Tsopelas, P.; Husain, M. Measures of Structural Redundancy in Reinforced Concrete Buildings. II: Redundancy Response Modification Factor Rr. J. Struct. Eng. 2004, 130, 1659–1666. [Google Scholar] [CrossRef]
- Massumi, A.; Mohammadi, R. Structural redundancy of 3D RC frames under seismic excitations. Struct. Eng. Mech. 2016, 59, 15–36. [Google Scholar] [CrossRef]
- Liao, K.-W.; Wen, Y.-K.; Foutch, D.A. Evaluation of 3D Steel Moment Frames under Earthquake Excitations. II: Reliability and Redundancy. J. Struct. Eng. 2007, 133, 471–480. [Google Scholar] [CrossRef]
- Malley, J.; Cheever, P. History of Structural Response Modification Factors. In Structures Congress: New Horizons and Better Practices. ASCE: Reston, VA, USA, 2007; pp. 1–7. [Google Scholar]
- Diebold, J.; Moore, K.; Hale, T.; Mochizuki, G. SEAOC Blue Book: Seismic Design Recommendations 1959 To 2008. In Proceedings of the 14th World Conference on Earthquake Engineering (14WCEE), Beijing, China, 12–17 October 2008. [Google Scholar]
- SEAOC. Recommended Lateral Force Requirements; Seismology Committee, Structural Engineers Association of California: Sacramento, CA, USA, 1959. [Google Scholar]
- ATC 3-06; Tentative Provisions for the Development of Seismic Regulations for Buildings: A Cooperative Effort with the Design Professions, Building Code Interests and the Research Community. Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1978; 514p.
- ASCE. Seismic Rehabilitation of Existing Buildings, ASCE Standard ASCE/SEI 41-06 “Formerly FEMA 356”; American Society of Civil Engineers: Reston, VA, USA, 2006. [Google Scholar]
- ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers:: Reston, VA, USA, 2022.
- NZS 1170.5:2016; Structural Design Actions—Part 5: Earthquake Actions—New Zealand. 4th ed. Standards New Zealand (SNZ): Wellington, New Zealand, 2016.
- NBCC. National Building Code of Canada; Canadian Commission on Building and Fire Codes, National Research Council: Ontario, ON, Canada, 2020. [Google Scholar]
- UBC. Uniform Building Code, Structural Engineering Design Provisions—Volume 2, International Conference of Building Officials, California; International Conference of Building Officials: Whittier, CA, USA, 1994. [Google Scholar]
- UBC. Uniform Building Code, Structural Engineering Design Provisions—Volume 2, International Conference of Building Officials, California; International Conference of Building Officials: Whittier, CA, USA, 1997. [Google Scholar]
- Borzi, B.; Elnashai, A. Refined force reduction factors for seismic design. Eng. Struct. 2000, 22, 1244–1260. [Google Scholar] [CrossRef]
- Applied Technology Council (ATC). Structural Response Modification Factors; Rep. No. ATC-19; ATC: Redwood City, CA, USA, 1995. [Google Scholar]
- Mwafy, A.M. Seismic Design Response Factors and Vulnerability Functions of Typical UAE Buildings. In Phase I: Response Factors; UAE University: Al Ain, United Arab Emirates, 2009. [Google Scholar]
- Mwafy, A.; Khalifa, S.; El-Ariss, B. Relative Safety Margins of Code-Conforming Vertically Irregular High-Rise Buildings. In Proceedings of the European Conference on Earthquake Engineering and Seismology (2ECEES), Istanbul, Turkey, 24–29 August 2014. [Google Scholar]
- Newmark, N.M.; Hall, W.J. Procedures and criteria for earthquake resistant design. In National Bureau of Standards; No Building Sci. Series No. 46; U.S. Department of Commerce: Washington, DC, USA, 1973. [Google Scholar]
- Newmark, N.M.; Hall, W.J. Earthquake spectra and design. In Earth System Dynamics; Earthquake Engineering Research Institute: Oakland, CA, USA, 1982; Volume 1. [Google Scholar]
- Krawinkler, H.; Nassar, A.A. Seismic design based on ductility and cumulative damage demands and capacities. In Nonlinear Seismic Analysis and Design of Reinforced Concrete Buildings; Fajfar, P., Krawinkler, H., Eds.; Elsevier Applied Science: New York, NY, USA, 1992. [Google Scholar]
- Miranda, E.; Bertero, V.V. Evaluation of strength reduction factors for earthquake-resistant design. Earthq. Spectra 1994, 10, 357–379. [Google Scholar] [CrossRef]
- Vidic, T.; Fajfar, P.; Fischinger, M. Consistent inelastic design spectra: Strength and displacement. Earthq. Eng. Struct. Dyn. 1993, 23, 507–521. [Google Scholar] [CrossRef]
- Cuesta, I.; Aschheim, M.A. Isoductile strengths and strength reduction factors of elasto-plastic SDOF systems subjected to simple waveforms. Earthq. Eng. Struct. Dyn. 2001, 30, 1043–1059. [Google Scholar] [CrossRef]
- Genshu, T.; Yongfeng, Z. Seismic force modification factors for modified-Clough hysteretic model. Eng. Struct. 2007, 29, 3053–3070. [Google Scholar] [CrossRef]
- Cuesta, I.; Aschheim, M.A.; Fajfar, P.; Cuesta, M.A.A.I.; Khose, V.N.; Singh, Y.; Pekoz, H.A.; Pincheira, J.A. Simplified R-factor relationships for strong ground motions. Earthq. Spectra 2003, 19, 25–45. [Google Scholar] [CrossRef]
- Chakraborti, A.; Gupta, V.K. Scaling of strength reduction factors for degrading elasto-plastic oscillators. Earthq. Eng. Struct. Dyn. 2005, 34, 189–206. [Google Scholar] [CrossRef]
- Jalali, R.S.; Trifunac, M.D. A note on strength-reduction factors for design of structures near earthquake faults. Soil Dyn. Earthq. Eng. 2008, 28, 212–222. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G. Behavior factors for nonlinear structures subjected to multiple near-fault earthquakes. Comput. Struct. 2010, 88, 309–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Sun, C. Damage-based strength reduction factor for nonlinear structures subjected to sequence-type ground motions. In Soil Dynamics and Earthquake Engineering; Elsevier: Amsterdam, The Netherlands, 2017; Volume 92, pp. 298–311. [Google Scholar]
- Molazadeh, M.; Saffari, H. The effects of ground motion duration and pinching-degrading behavior on seismic response of SDOF systems. Soil Dyn. Earthq. Eng. 2018, 114, 333–347. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.; Zhang, C.; Zhang, Y. Damage-based strength reduction factor spectra of structures subjected to bidirectional ground motions. Adv. Struct. Eng. 2023, 26, 72–88. [Google Scholar] [CrossRef]
- Calado, L.; Azevedo, J.; Lamas, A. Assessment of q factors for seismic design of low-rise steel buildings. J. Constr. Steel Res. 1995, 35, 1–17. [Google Scholar] [CrossRef]
- Balendra, T.; Huang, X. Overstrength and Ductility Factors for Steel Frames Designed According to BS 5950. J. Struct. Eng. 2003, 129, 1019–1035. [Google Scholar] [CrossRef]
- Asgarian, B.; Shokrgozar, H. BRBF response modification factor. J. Constr. Steel Res. 2009, 65, 290–298. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Zaree, M. Evaluating response modification factors of concentrically braced steel frames. J. Constr. Steel Res. 2010, 66, 1196–1204. [Google Scholar] [CrossRef]
- Farahi, M.; Mofid, M. On the quantification of seismic performance factors of Chevron Knee Bracings, in steel structures. Eng. Struct. 2013, 46, 155–164. [Google Scholar] [CrossRef]
- Moni, M.; Moradi, S.; Alam, M.S. Response modification factors for steel buckling restrained braced frames designed as per the 2010 National Building Code of Canada. Can. J. Civ. Eng. 2016, 43, 702–715. [Google Scholar] [CrossRef]
- Kheyroddin, A.; Mashhadiali, N. Response modification factor of concentrically braced frames with hexagonal pattern of braces. J. Constr. Steel Res. 2018, 148, 658–668. [Google Scholar] [CrossRef]
- Yakhchalian, M.; Asgarkhani, N.; Yakhchalian, M. Evaluation of deflection amplification factor for steel buckling restrained braced frames. J. Build. Eng. 2020, 30, 101228. [Google Scholar] [CrossRef]
- Li, S.; Li, R.; Wang, D.; Pan, X.; Guo, H. Response Modification Factor and Displacement Amplification Factor of Y-Shaped Eccentrically Braced High-Strength Steel Frames. Int. J. Steel Struct. 2021, 21, 1823–1844. [Google Scholar] [CrossRef]
- Mokhtari, M.; Imanpour, A. Proposed seismic design parameters for the moment-resisting knee-braced frame system. Eng. Struct. 2023, 276, 115318. [Google Scholar] [CrossRef]
- Mohammadi, R.K. Approximate Evaluation of Deflection Amplification Factor. J. Struct. Eng. 2002, 128, 179–187. [Google Scholar] [CrossRef]
- Foutch, D.A.; Eeri, M.; Wilcoski, J. A Rational Approach for Determining Response Modification Factors for Seismic Design of Buildings Using Current Code Provisions. Earthq. Spectra 2005, 21, 339–352. [Google Scholar] [CrossRef]
- Stefano, M.D.E.; Marino, E.M.; Rossi, P.P. Effect of Overstrength on the Seismic Behavior of Multi-Story Regularly Asymmetric Buildings. Bull. Earthq. Eng. 2006, 4, 23–42. [Google Scholar] [CrossRef]
- Karavasilis, T.L.; Bazeos, N.; Beskos, D.E. Behavior Factor for Performance-Based Seismic Design of Plane Steel Moment Resisting Frames. J. Earthq. Eng. 2007, 11, 531–559. [Google Scholar] [CrossRef]
- Gupta, A.; Krawinkler, H. Seismic Demands for Performance Evaluation of Steel Moment Resisting Frame Structures; John, A., Ed.; Blume Earthquake Engineering Centre Report No.132; Department of Civil and Environmental Engineering, Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Kang, C.-K.; Choi, B.-J. New approach to evaluate the response modification factors for steel moment resisting frames. Int. J. Steel Struct. 2011, 11, 275–286. [Google Scholar] [CrossRef]
- Izadinia, M.; Rahgozar, M.A.; Mohammadrezaei, O. Response modification factor for steel moment-resisting frames by different pushover analysis methods. J. Constr. Steel Res. 2012, 79, 83–90. [Google Scholar] [CrossRef]
- Ferraioli, M.; Lavino, A.; Mandara, A. Behavior factor of code-designed steel moment-resisting frames. Int. J. Steel Struct. 2014, 14, 243–254. [Google Scholar] [CrossRef]
- Reyes-Salazar, A.; Bojórquez, E.; Bojorquez, J.; Valenzuela-Beltran, F.; Llanes-Tizoc, M.D. Energy Dissipation and Local, Story, and Global Ductility Reduction Factors in Steel Frames under Vibrations Produced by Earthquakes. Shock. Vib. 2018, 2018, 19. [Google Scholar] [CrossRef]
- Macedo, L.; Silva, A.; Castro, J.M. A more rational selection of the behavior factor for seismic design according to Eurocode 8. Eng. Struct. 2019, 188, 69–86. [Google Scholar] [CrossRef]
- Rofooei, F.R.; Seyedkazemi, A. Evaluation of the seismic performance factors for steel diagrid structural systems using FEMA P-695 and ATC-19 procedures. Bull. Earthq. Eng. 2020, 18, 4873–4910. [Google Scholar] [CrossRef]
- Samadi, M.; Jahan, N. Comparative study on the effect of outrigger on seismic response of tall buildings with braced and Wall Core. II: Determining seismic design parameters. Struct. Des. Tall Spéc. Build. 2021, 30, e1855. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Broderick, B.M. Seismic response of composite frames—II. Calculation of behavior factors. Eng Struct. 1996, 18, 707–723. [Google Scholar] [CrossRef]
- Moroni, B.M.O.; Astroza, M.; Guzman, R. Establishing Rw and Cd Factors for Confined Masonry Buildings. J. Struct. Eng. 1996, 122, 1208–1215. [Google Scholar] [CrossRef]
- Mitchell, D.; Tremblay, R.; Karacabeyli, E.; Paultre, P.; Saatcioglu, M.; Anderson, D.L. Seismic force modification factors for the proposed 2005 edition of the National Building Code of Canada. Can. J. Civ. Eng. 2005, 30, 308–327. [Google Scholar] [CrossRef]
- Kurban, C.O.; Topkaya, C. A numerical study on response modification, overstrength, and displacement amplification factors for steel plate shear wall systems. Earthq. Eng. Struct. Dyn. 2008, 38, 497–516. [Google Scholar] [CrossRef]
- Fiorino, L.; Shakeel, S.; Macillo, V.; Landolfo, R. Behavior factor (q) evaluation the CFS braced structures according to FEMA P695. J. Constr. Steel Res. 2017, 138, 324–339. [Google Scholar] [CrossRef]
- Reza Salimbahrami, S.; Gholhaki, M. Effects of Higher Modes and Degrees of Freedom (DOF) on Strength Reduction Factor in Reinforced Concrete Frames Equipped With Steel Plate Shear Wall. Structures 2019, 19, 234–247. [Google Scholar] [CrossRef]
- Kappos, A.J. Evaluation of behavior factors on the basis of ductility and overstrength studies. Eng. Struct. 1999, 21, 823–835. [Google Scholar] [CrossRef]
- Chryssanthopoulos, M.K.; Dymiotis, C.; Kappos, A.J. Probabilistic evaluation of behavior factors in EC8-designed R/C frames. Eng. Struct. 2000, 22, 1028–1041. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Mwafy, A.M. Overstrength and force reduction factors of multistorey reinforced-concrete buildings. Struct. Des. Tall Build. 2002, 11, 329–351. [Google Scholar] [CrossRef]
- Maheri, M.R.; Akbari, R. Seismic behaviour factor, R, for steel X-braced and knee-braced RC buildings. Eng. Struct. 2003, 25, 1505–1513. [Google Scholar] [CrossRef]
- Mwafy, A.M.; Elnashai, A.S. Calibration of force reduction factors of RC buildings. J. Earthq. Eng. 2002, 6, 239–273. [Google Scholar] [CrossRef]
- Maheri, M.; Kousari, R.; Razazan, M. Pushover tests on steel X-braced and knee-braced RC frames. Eng. Struct. 2003, 25, 1697–1705. [Google Scholar] [CrossRef]
- AlHamaydeh, M.; Abdullah, S.; Hamid, A.; Mustapha, A. Seismic design factors for RC special moment resisting frames in Dubai, UAE. Earthq. Eng. Eng. Vib. 2011, 10, 495–506. [Google Scholar] [CrossRef]
- Alam, M.S.; Moni, M.; Tesfamariam, S. Seismic overstrength and ductility of concrete buildings reinforced with super elastic shape memory alloy rebar. Eng. Struct. 2012, 34, 8–20. [Google Scholar] [CrossRef]
- Van Thuat, D. Strength reduction factor demands for building structures under different seismic levels. Struct. Des. Tall Spéc. Build. 2012, 23, 42–53. [Google Scholar] [CrossRef]
- Akbari, R.; Maheri, M.R. Analytical investigation of response modification (behaviour) factor, R, for reinforced concrete frames rehabilitated by steel chevron bracing. Struct. Infrastruct. Eng. 2013, 9, 507–515. [Google Scholar] [CrossRef]
- Maniatakis, C.A.; Psycharis, I.N.; Spyrakos, C.C. Effect of higher modes on the seismic response and design of moment-resisting RC frame structures. Eng. Struct. 2013, 56, 417–430. [Google Scholar] [CrossRef]
- Hossain, A.; Alam, M.S.; Rteil, A. Seismic Force Reduction Factors for Concrete Buildings Reinforced with Super elastic Shape Memory Alloy Rebars. In Proceedings of the 11th Canadian Conference on Earthquake Engineering, Victoria, BC, Canada, 21–24 July 2015. [Google Scholar]
- Vona, M.; Mastroberti, M. Estimation of the behavior factor of existing RC-MRF buildings. Earthq. Eng. Eng. Vib. 2018, 17, 191–204. [Google Scholar] [CrossRef]
- Mohsenian, V.; Nikkhoo, A.; Hajirasouliha, I. Estimation of seismic response parameters and capacity of irregular tunnel-form buildings. Bull. Earthq. Eng. 2019, 17, 5217–5239. [Google Scholar] [CrossRef]
- Siddiquee, K.N.; Billah, A.M.; Issa, A. Seismic collapse safety and response modification factor of concrete frame buildings reinforced with super elastic shape memory alloy (SMA) rebar. J. Build. Eng. 2021, 42, 102468. [Google Scholar] [CrossRef]
- Fazileh, F.; Fathi-Fazl, R.; Dolati, A.; Ventura, C.E.; Saatcioglu, M.; Lau, D.; Yang, T.; Sadeghian, V.; Erochko, J. Methodology for determination of seismic force modification factors in Canada: Performance-based unified procedure. Earthq. Spectra 2023, 39, 218–241. [Google Scholar] [CrossRef]
- Challal, O.; Gauthier, D. Deformation and ductility considerations of ductile coupled shear walls located in Canadian seismic regions. Can. J. Civ. Eng. 2001, 28, 738–746. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. Canadian Standards Association: Toronto, ON Canada, 2010; p. 132.
- Mwafy, A.; Khalifa, S. Effect of vertical structural irregularity on seismic design of tall buildings. Struct. Des. Tall Spéc. Build. 2017, 26, e1399. [Google Scholar] [CrossRef]
- Zerbin, M.; Aprile, A.; Beyer, K.; Spacone, E. Ductility reduction factor formulations for seismic design of RC wall and frame structures. Eng. Struct. 2018, 178, 102–115. [Google Scholar] [CrossRef]
- Zerbin, M.; Aprile, A.; Spacone, E. New formulation of ductility reduction factor of RC frame-wall dual systems for design under earthquake loadings. Soil Dyn. Earthq. Eng. 2020, 138, 106279. [Google Scholar] [CrossRef]
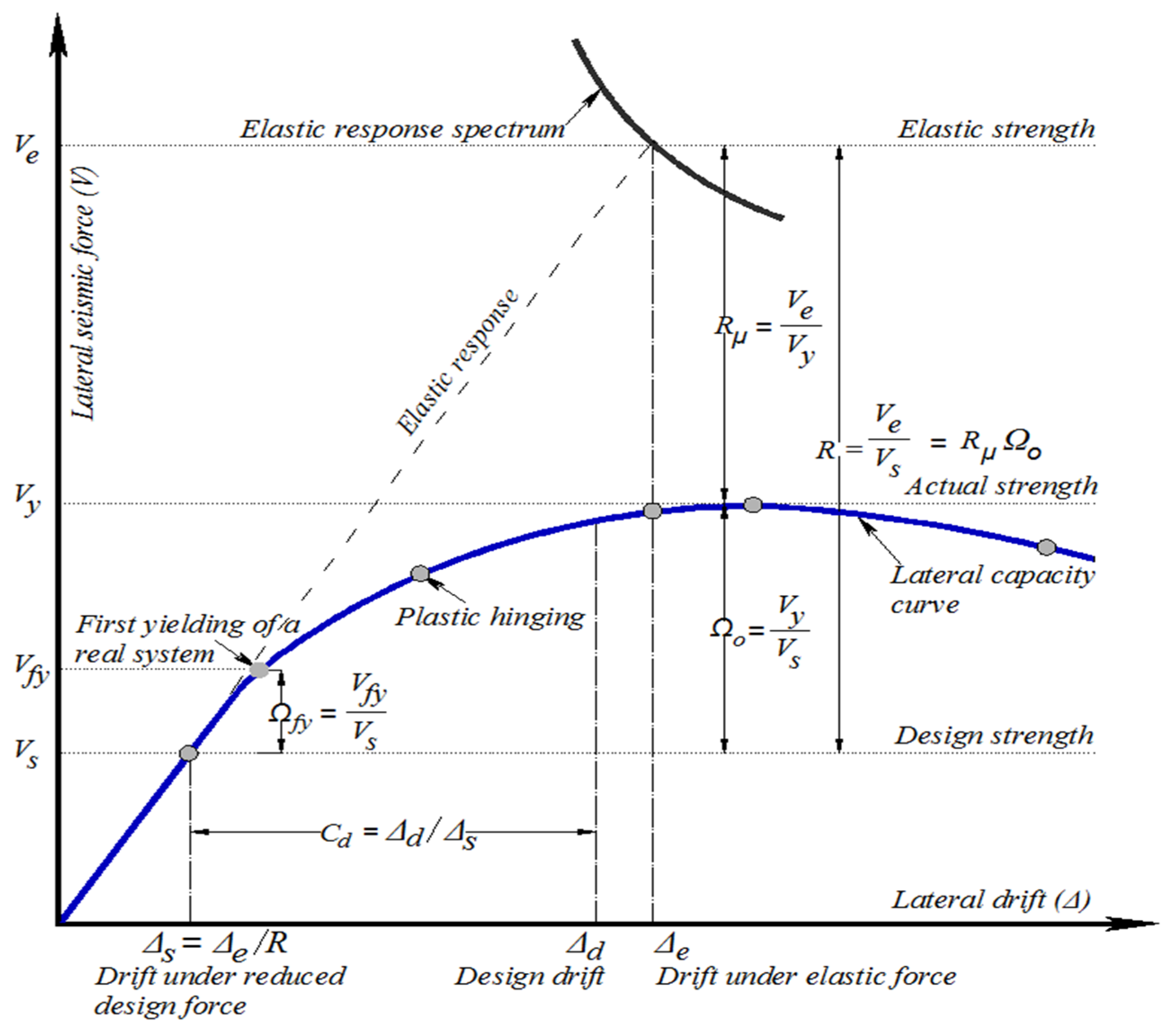
| Seismic Provisions | Applicable Region/ Country | Response Modification Factor | Deflection Amplification Factor | Deflection Amplification Factor/ Response Modification Factor |
|---|---|---|---|---|
| ASCE 7-22 (2022) [20] | U.S. and other countries | R | Cd | 0.50–1.00 |
| Eurocode 8 (2004) [4] | Europe | q a | q | 1.00 c |
| NZS 1170.4 (2016) [21] | New Zealand | µ b | µ | 1.00 c |
| NBCC (2020) [22] | Canada | Rd/Ro | Rd/Ro | |
| MCBC (2015) [6] | Mexico | Q a | Q | 1.00 c |
| UBC | ||||
| UBC (1994) [23] | U.S. and other countries | Rw | (0.375)Rw | 0.375 |
| UBC (1997) [24] | R | 0.7R | 0.70 |
| Author | Equations | Remarks | ||
|---|---|---|---|---|
| Newmark and Hall (1973; 1982) [29,30] | Rμ = 1 Rμ = Rμ = μ | T < 0.2 s 0.2 s < T < 0.5 s T > 1 s | ||
| Krawinkler and Nassar (1992) [31] | Rμ = c (T, α) = + | Hardening Value α | Model Parameters | |
| a | b | |||
| 0% | 1.00 | 0.42 | ||
| 2% | 1.01 | 0.37 | ||
| 10% | 0.80 | 0.29 | ||
| Miranda and Bertero (1994) [32] | = 1 + − exp [−1.5 (ln T − 0.6)2] = 1 + − exp [−2.0 (ln T − 0.2)2] = 1 + − exp Rμ = + 1 ≥ 1 | Rock sites Alluvium sites Soft soil sites Tg is the predominant period of ground motion corresponding to the relative velocity of the linear elastic system with 5% maximum damping for the entire period range | ||
| Vidic et al. (1994) [33] | Rμ ≈μ Rμ = c1 + 1 Rμ = c1 + 1 To = c2 T1 | To is the period range in the two segments related to the predominant period of the ground motion T1 T ≤ To T ≥ To c1, c2, cR, and cT depend on hysteretic behavior and damping | ||
| Borzi and Elnashai (2000) [25] | q = (q1 − 1) + 1 q = q1 + (q2 − q1) q = q2 | T ≤ T1 T1 < T ≤ T2 T > T2 | ||
| Cuesta and Aschheim (2001) [34] | R = R(µ,T) = | |||
| Genshu and Yongfeng (2007) [35] | R = Rμ Rα Rξ | |||
| Author | Analysis Type and Methodology | Type of Structure and Structural System | Seismic Design Factors | Seismic Factor Dependencies | Soil Site Class | Features of Input Ground Motions |
|---|---|---|---|---|---|---|
| Newmark and Hall (1973; 1982) [29,30] | 2D analytical | Long and short period range structures | Rµ | T, µ | Alluvium, very soft, and rock sites | Elastic response spectra for long and short periods |
| Krawinkler and Nassar (1992) [31] | 2D analytical | Short period range structures | Rµ | T, µ, α | Alluvium soil and rock sites | 15 GM with 5.7 to 7.7 EQ magnitude |
| Miranda and Bertero (1994) [32] | 2D analytical | Short period range structures | Rµ | T, Tg, µ | Alluvium, very soft, and rock sites | 124 GM with low shear velocity |
| Vidic et al. (1994) [33] | 2D analytical | Short period range structures | Rµ | T, µ, c | Alluvium and stiff soil sites | 20 strong motion EQ records |
| Borzi and Elnashai (2000) [25] | 2D analytical | Low-rise structures | R (q) | T, µ | Soft, stiff, and rock sites | 43 GM with 5.5 to 7.7 EQ magnitude |
| Cuesta and Aschheim (2001) [34] | 2D analytical | Elastoplastic structures | R | T, µ, Tg | Alluvium and stiff soil sites | 24 simple waveforms linear, triangular, sinusoidal, and quadratic |
| Cuesta et al. (2003) [36] | 2D analytical | Bilinear and stiffness degrading models | R | T, µ, Tg | Alluvium and stiff soil sites | 14 GM of short- and long-duration frequencies |
| Chakraborti and Gupta (2005) [37] | 2D analytical | Short period range structures | R | T, µ, Tg | Alluvium, intermediate, and hard rock sites | Several accelerograms of 3 to 8 EQ magnitude |
| Genshu and Yongfeng (2007) [35] | 2D analytical | Modified Clough hysteretic model | R | T, µ, Tg | Site classes A, B, C, and D | 370 seismic records, different site classes, and 0.2 g acceleration |
| Jalali and Trifunac (2008) [38] | 2D analytical | Short period range structures | R | T, µ | Stiff and soft soil sites | Near-field EQ with EQ magnitude ranging from 4 to 8 |
| Hatzigeorgiou (2010) [39] | 2D analytical | RC structures | R (q) | T, µ | Soft, stiff, dense, and rock sites | 110 near-fault Eqn. with 5.5 to 7.8 magnitude |
| Zhang et al. (2017) [40] | 2D analytical | Elastoplastic structures | Rµ, RD | T, µ | Site classes B and C | Mainshock > 0.10 g PGA and aftershock > 0.05 g |
| Molazadeh and Saffari (2018) [41] | 2D analytical | Short period range structures | Rµ | T, µ | Site class D | Short and long duration records of varying magnitudes |
| Feng Wang et al. (2023) [42] | 2D analytical | Short period range structures | Rb, R | T, µ | All site classes | 178 ground motion records with bi-directional loading |
| Author | Analysis Type and Methodology | Type of Structure and Structural System | No. of Stories | Seismic Design Factors | Remarks |
|---|---|---|---|---|---|
| Calado et al. (1995) [43] | 2D analytical | Regular MRFs, cantilever, and braced | 1, 2, and 3 | R(q) | Adequate margin of safety |
| Balendra and Huang (2003) [44] | 2D analytical and IPA | Regular MRFs, CBFs, and semi-rigid | 3, 6, and 10 | Rμ and Ωo | Adequate margin of safety |
| Asgarian and Shokrgozar (2009) [45] | 2D analytical, IPA, and IDA | BRBFs with diagonal, split X, chevron V, and inverted V bracings | 4, 6, 8, 10, 12, and 14 | Rμ, Ωo, and R | Adequate margin of safety |
| Mahmoudi and Zaree (2010) [46] | 2D analytical and IPA | Regular CBFs and BRBFs with X, chevron V, and inverted V bracings | 3, 5, 7, 10, and 12 | R | Adequate margin of safety |
| Farahi and Mofid (2013) [47] | 2D analytical, IPA, and IDA | Regular chevron knee bracings | 2, 4, 6, 10, and 14 | Rμ, Ωo, and R | Adequate margin of safety |
| Moni et al. (2016) [48] | 2D analytical, IPA, and THA | Regular BRBFs with chevron-inverted V and split X bracings | 4, 6, and 8 | Rμ, Ωo, and R | Adequate margin of safety |
| Kheyroddin and Mashhadiali (2018) [49] | 2D analytical, IPA, and IDA | Regular CBFs with hexagonal patterns and X-frames | 4, 10, and 20 | R | Adequate margin of safety |
| Masood Yakhchalian et al. (2020) [50] | 2D analytical, IPA, and IDA | Regular BRBFs | 2, 4, 6, 8, 10, and 12 | R and Cd | Adequate margin of safety |
| Shen Li et al. (2021) [51] | 2D analytical, IPA, and IDA | Y-shaped eccentrically braced high strength | 4 to 16 | R and Cd | Adequate margin of safety |
| Mahdi Mokhtari and Ali Imanpour (2023) [52] | 2D analytical, IPA, and IDA | Moment-resisting knee brace (MKF) | 6 to 15 | Rd and Ro | Adequate margin of safety |
| Author | Analysis Type and Methodology | Type of Structure and Structural System | No. of Stories | Seismic Design Factors | Remarks |
|---|---|---|---|---|---|
| Mohammadi (2002) [53] | 2D analytical and IDA | Regular MRF buildings | 5, 10, and 15 | Cd | Adequate margin of safety |
| Foutch and Wilcoski (2005) [54] | 2D analytical, experimental, and IDA | Regular MRF buildings | 3, 9, and 20 | R | Adequate margin of safety |
| Stefano et al. (2006) [55] | 2D analytical, IPA, and THA | Plan irregular MRF buildings | 1 and 6 | Ωo | Proposed improvement |
| Karavasilis et al. (2007) [56] | 2D analytical, experimental, and THA | Regular MRF buildings | 3, 6, 9, 12, 15, and 20 | R (q) | Not valid for long duration–high amplitude GMs |
| Kang and Choi (2011) [58] | 2D analytical and IPA | Regular MRF buildings | 4, 8, and 16 | R | Adequate margin of safety |
| Izadinia et al. (2012) [59] | 2D analytical and IPA | Regular MRF buildings | 3, 9, and 20 | Rμ, Ωo, and R | Conservative with CPA and APA |
| Ferraioli et al. (2014) [60] | 2D analytical, IPA, and IDA | Six regular and six irregular MRF | 3, 5, 7, and 9 | Rμ, Ωo, and R (q) | Adequate margin of safety |
| Reyes-Salazar et al. (2018) [61] | 2D analytical and THA | Regular MRF buildings | 3 and 10 | µ, Rμ, and E | More conservative in medium-rise buildings |
| Macedo et al. (2019) [62] | 2D analytical, IPA, and IDA | Five regular MRF frames | 2 to 8 | R (q) | Adequate margin of safety |
| Fayaz Rofooei and Ali Seyedkazemi (2020) [63] | 2D analytical, IPA, and IDA | Regular steel diagrid structures | 6 to 24 | R and Ωo | Adequate margin of safety |
| Maysam Samadi and Norouz Jahan (2021) [64] | 3D analytical, MRS, IPA, and NLTH | Two regular steel-braced buildings with outriggers | 28 and 56 | R, Cd, and Ωo | Adequate margin of safety, R, and Ωo. Inadequate Cd |
| Author | Analysis Type and Methodology | Type of Structure and Structural System | No. of Stories | Seismic Design Factors | Remarks |
|---|---|---|---|---|---|
| Elnashai and Broderick (1996) [65] | 2D analytical and IDA | Steel MRFs and composite buildings | 2, 3, 6, and 10 | R (q) | Adequate margin of safety |
| Moroni et al. (1996) [66] | 3D analytical and THA | Regular confined masonry buildings | 3 and 4 | Rμ, Cd, and R | Reasonable margin of safety |
| Mitchell et al. (2005) [67] | 2D analytical and experimental | Steel, concrete, timber, and masonry building | Buildings up to 12 stories | Rd and Ro | Proposed changes by enhancing R values |
| Kurban and Topkaya (2009) [68] | 3D analytical and THA | SPSW systems | 2, 4, 6, 8, and 10 | Rμ, Ωo, Cd, and R | R increased proportionally with height |
| Fiorino et al. (2017) [69] | 3D analytical and IDA | CFS strap-braced stud wall | 1, 2, 3, and 4 | R (q) | Adequate margin of safety |
| Reza Salimbahrami and Majid Gholhaki (2019) [70] | 2D analytical and IDA | Steel MRFs with steel plate shear walls | 6, 12, and 20 | Rμ, CR, Rυ, and Cd, | Adequate margin of safety |
| Author | Analysis Type and Methodology | Type of Structure and Structural System | No. of Stories | Seismic Design Factors | Remarks |
|---|---|---|---|---|---|
| Kappos (1999) [71] | 2D analytical, IPA, and THA | Regular MRF buildings | 1 to 5 | R (q) | Adequate safety margins |
| Chryssanthopoulos et al. (2000) [72] | 2D analytical and THA | Regular MRF buildings | 10 | R (q) | Adequate safety margins |
| Elnashai and Mwafy; Mwafy and Elnashai (2002) [73,75] | 2D analytical, IPA, and IDA | Regular and irregular MRF buildings | 8 and 12 regular and eight irregular | Ωo and R | Adequate safety margins |
| Maheri and Akbari (2003) [74,76] | 2D analytical, experimental, and IPA | Regular MRF with steel bracing | 4, 8, and 12 | R | Adequate safety margins |
| Husain and Tsopelas (2004) [11] | 2D analytical and IPA | Regular MRF | 3, 5, 7, and 9 | RR | RR increased with an increase in ductility capacity |
| FEMA P695 (2009) [1] | 2D analytical, IPA, and THA | Regular MRF | 1, 2, 4, 8, 12, and 20 | Ωo, Cd, and R | R acceptable for ACMR > collapse probability at the MCE |
| Alhamaydeh et al. (2011) [77] | 2D analytical, IPA, and THA | Regular MRF buildings | 4, 16, and 32 | Ωo, Cd, and R | Adequate margin of safety |
| Alam et al. (2012) [78] | 2D analytical, IPA, and THA | Regular MRF buildings with SMAs | 3, 6, and 8 | µ and Ro | Adequate margin of safety |
| Thuat (2012) [79] | 2D analytical and THA | Regular MRF | 5 and 9 | R (q) | Adequate safety margins |
| Akbari and Maheri (2013) [80] | 2D analytical and IPA | Dual system (frame with steel bracings) | 4, 8, and 12 | Ωo, Cd, and R | Adequate safety margins |
| Maniatakis et al. (2013) [81] | 2D analytical, IPA, and THA | Regular MRF buildings | 9 | R | Adequate safety margins |
| Mondal et al. (2013) [9] | 2D analytical and IPA | Regular MRF buildings | 2, 4, 8, and 12 | R | Adequate margin of safety |
| Hossain et al. (2015) [82] | 2D analytical, IPA, and IDA | Regular MRF buildings with SMAs | 3 and 8 | R | Adequate margin of safety |
| Vona and Mastroberti (2018) [83] | 2D analytical and IDA | Regular MRF buildings retrofit with masonry infill | 2, 4, and 8 | R (q) | Proposed R values for a retrofit building |
| Vahid Mohsenian et al. (2019) [84] | 3D analytical and IDA | Horizontal irregular MRFs | 3, 5, 7, and 10 | R, Ωo, and Cd, | Adequate margin of safety |
| Kader Newaj Siddiquee et al. (2021) [85] | 2D analytical, IPA, and IDA | Regular MRFs with normal rebars and SMA bars | 3, 6, and 8 | R | Adequate margin as per FEMA P695 |
| Farrokh Fazileh et al. (2023) [86] | 2D analytical, IPA, and IDA | Regular SFRS using the PBU procedure | 21 SFRS archetypes | Rd and Ro | Proposed work enhanced performance level |
| Author | Analysis Type and Methodology | Type of Structure and Structural System | No. of Stories | Seismic Design Factors | Remarks |
|---|---|---|---|---|---|
| Challal and Gauthier (2001) [87] | 2D analytical and IDA | Regular coupled shear wall (CSW) system | 6, 10, 15, 20, and 30 | µd | Adequate margin of safety |
| Elnashai and Mwafy; Mwafy and Elnashai (2002) [73,75] | 2D analytical, IPA, and IDA | Regular shear wall building | 8 | Ωo and R | Adequate safety margins |
| Mwafy (2011) [7] | 2D analytical, IPA, and IDA | Regular shear wall buildings | 20 to 60 | Ωo, Cd, and R | Adequate margin of safety |
| Mwafy (2013) [8] | 2D analytical, IPA, and IDA | Regular shear wall buildings | 10 to 60 | Ωo, Cd, and R | Adequate margin of safety |
| Mwafy et al. (2015) [10] | 2D analytical, IPA, and IDA | Regular shear wall buildings with varying material strengths | 60 | Ωo, Cd, and R | Adequate margin of safety |
| Mwafy and Khalifa (2017) [89] | 2D analytical, IPA, and IDA | Regular shear wall buildings with varying vertical irregularities | 50 | Ωo, Cd, and R | Adequate margin of safety |
| Zerbin et al. (2018) [90] | 2D analytical, IPA, and THA | Regular frame and wall buildings | 3 to 12 | Cd, and R | Adequate margin of safety |
| Matteo Zerbin et al. (2020) [91] | 2D analytical, IPA, and THA | Regular RC walls and frames | 4, 8, and 12 | Rμ, | Rμ decrease with an increase in story height with an adequate safety margin |
| Maysam Samadi and Norouz Jahan (2021) [64] | 3D analytical, MRS, IPA, and NLTH | Two regular steel-braced buildings with outriggers | 28 and 56 | R, Cd, and Ωo | Adequate margin of safety, R, and Ωo. Inadequate Cd |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, N.; Alam, S.; Mwafy, A. Developments in Quantifying the Response Factors Required for Linear Analytical and Seismic Design Procedures. Buildings 2024, 14, 247. https://doi.org/10.3390/buildings14010247
Hussain N, Alam S, Mwafy A. Developments in Quantifying the Response Factors Required for Linear Analytical and Seismic Design Procedures. Buildings. 2024; 14(1):247. https://doi.org/10.3390/buildings14010247
Chicago/Turabian StyleHussain, Nadeem, Shahria Alam, and Aman Mwafy. 2024. "Developments in Quantifying the Response Factors Required for Linear Analytical and Seismic Design Procedures" Buildings 14, no. 1: 247. https://doi.org/10.3390/buildings14010247
APA StyleHussain, N., Alam, S., & Mwafy, A. (2024). Developments in Quantifying the Response Factors Required for Linear Analytical and Seismic Design Procedures. Buildings, 14(1), 247. https://doi.org/10.3390/buildings14010247









