Seismic Stability and Sustainable Performance of Diaphragm Walls Adjacent to Tunnels: Insights from 2D Numerical Modeling and Key Factors
Abstract
:1. Introduction
1.1. Related Works
1.2. Conceptual and Practical Contributions
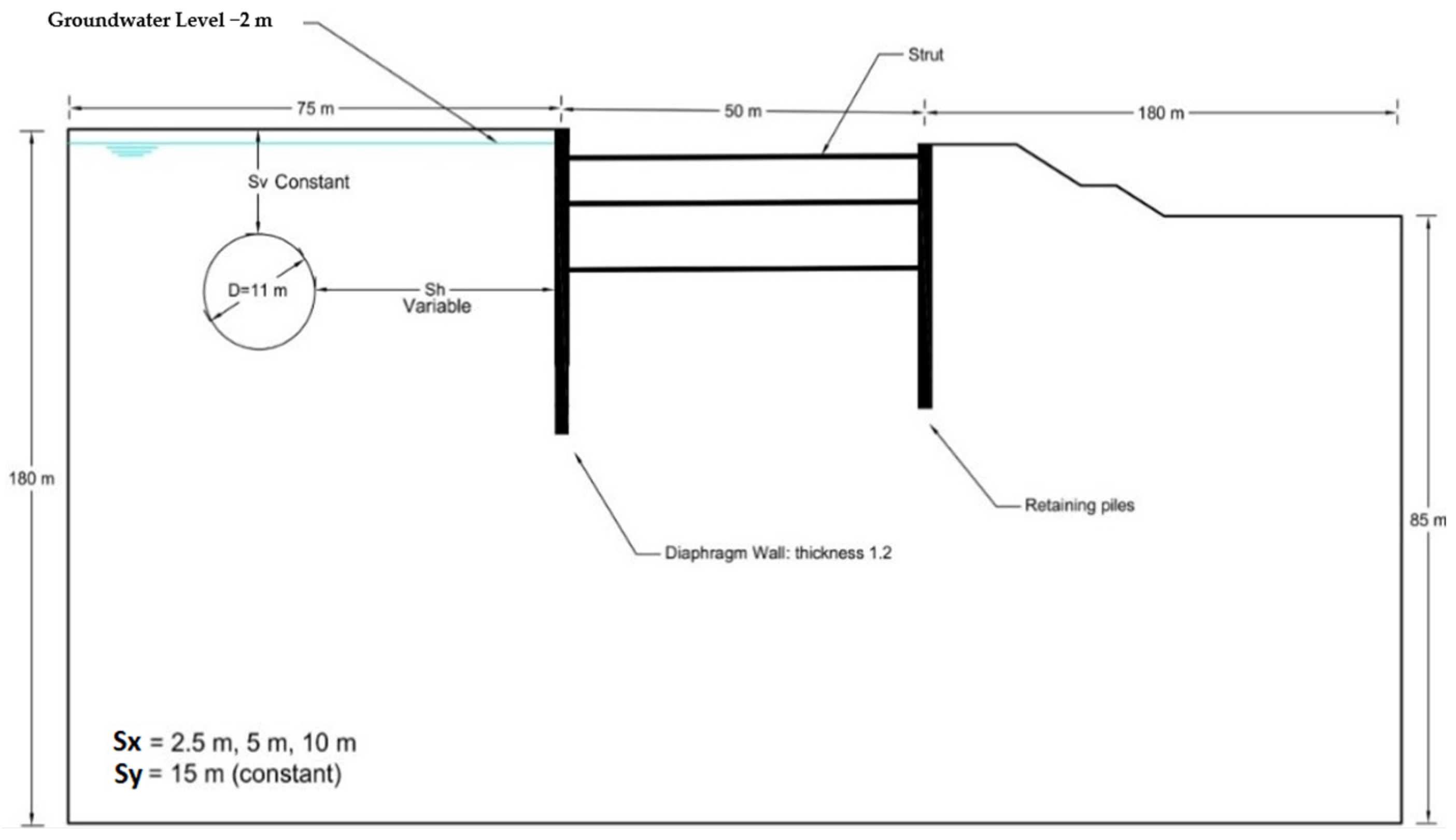
2. Case Study
3. Numerical Modeling and Verification
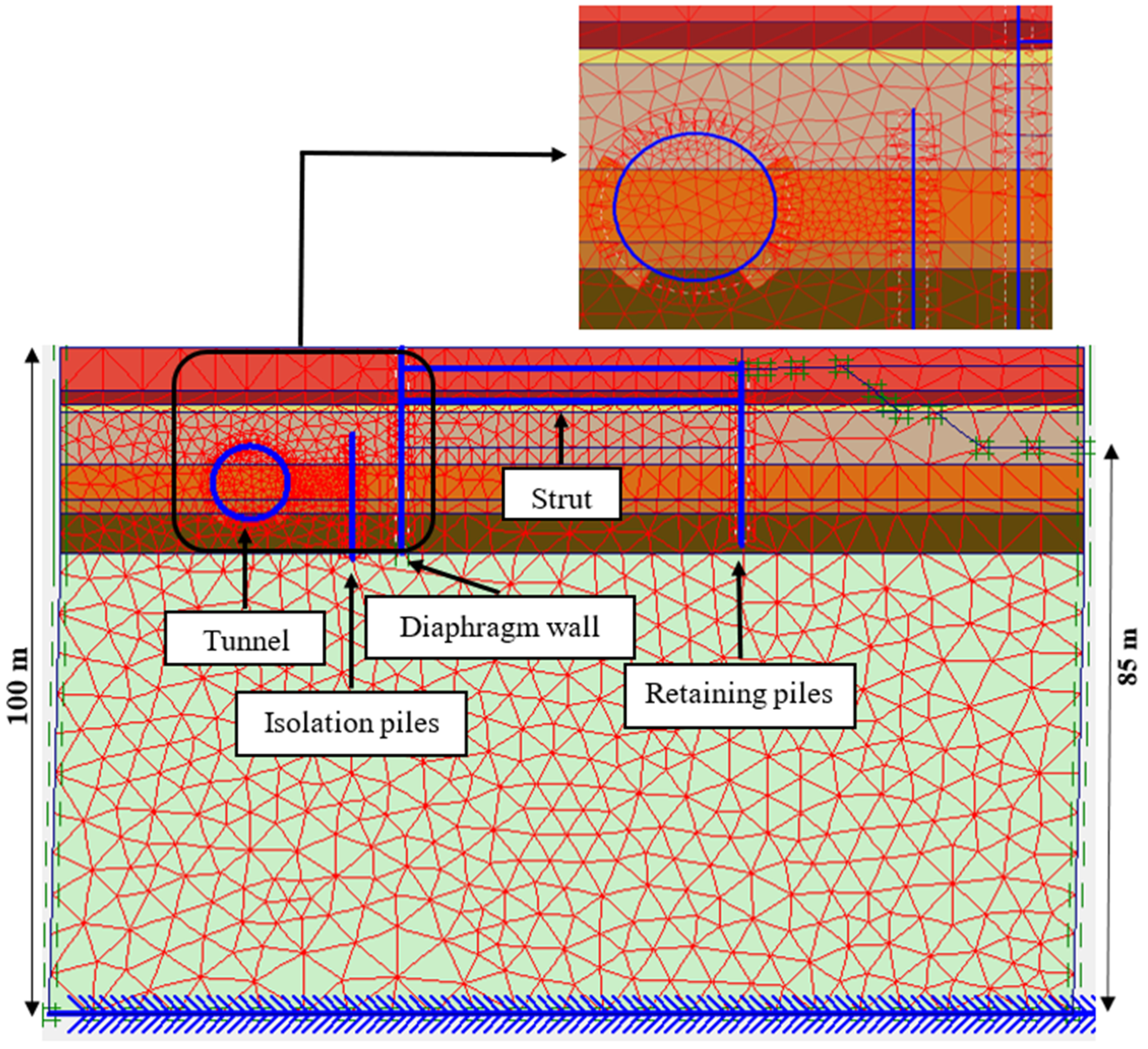
3.1. Geometry and Details of Numerical Model
- Stress is generated at first.
- There is activation of the plate elements of the diaphragm wall, tunnel lining, isolation piles, and contiguous piles.
- It continues until the excavation’s base is dewatered.
- Excavation to a depth of 3.6 m and installation of the first level strut on the excavation’s southern edge.
- The second-level struts are built on the southern excavation side after excavation to a depth of 8.4 m.
- On the northern excavation side, 9.6 m of excavation were completed.
- The northern excavation side is being excavated all the way to the bottom.
- The southern excavation side is being excavated all the way to the bottom.
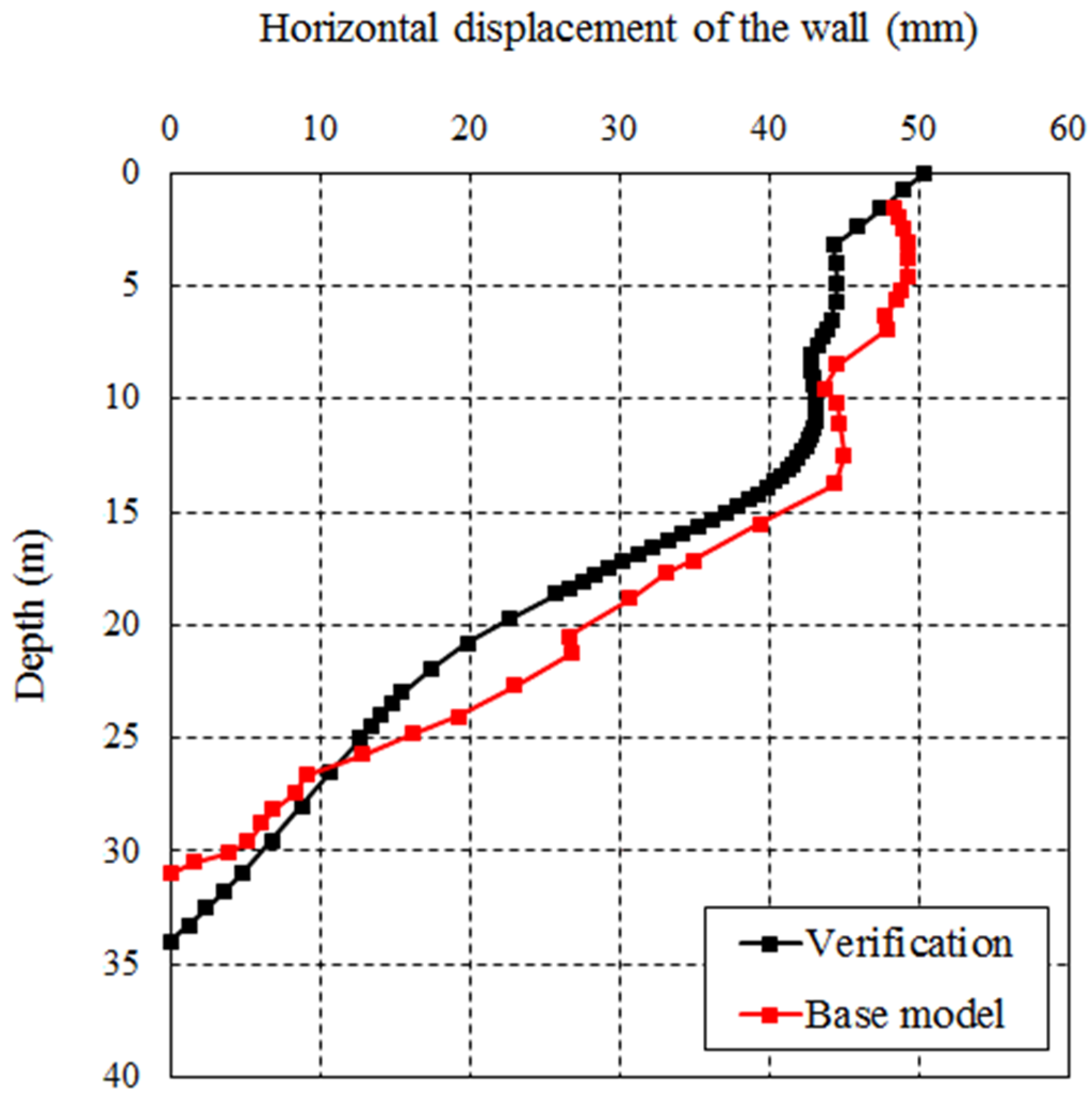
3.2. Verification
4. Parametric Study
5. Results and Discussion
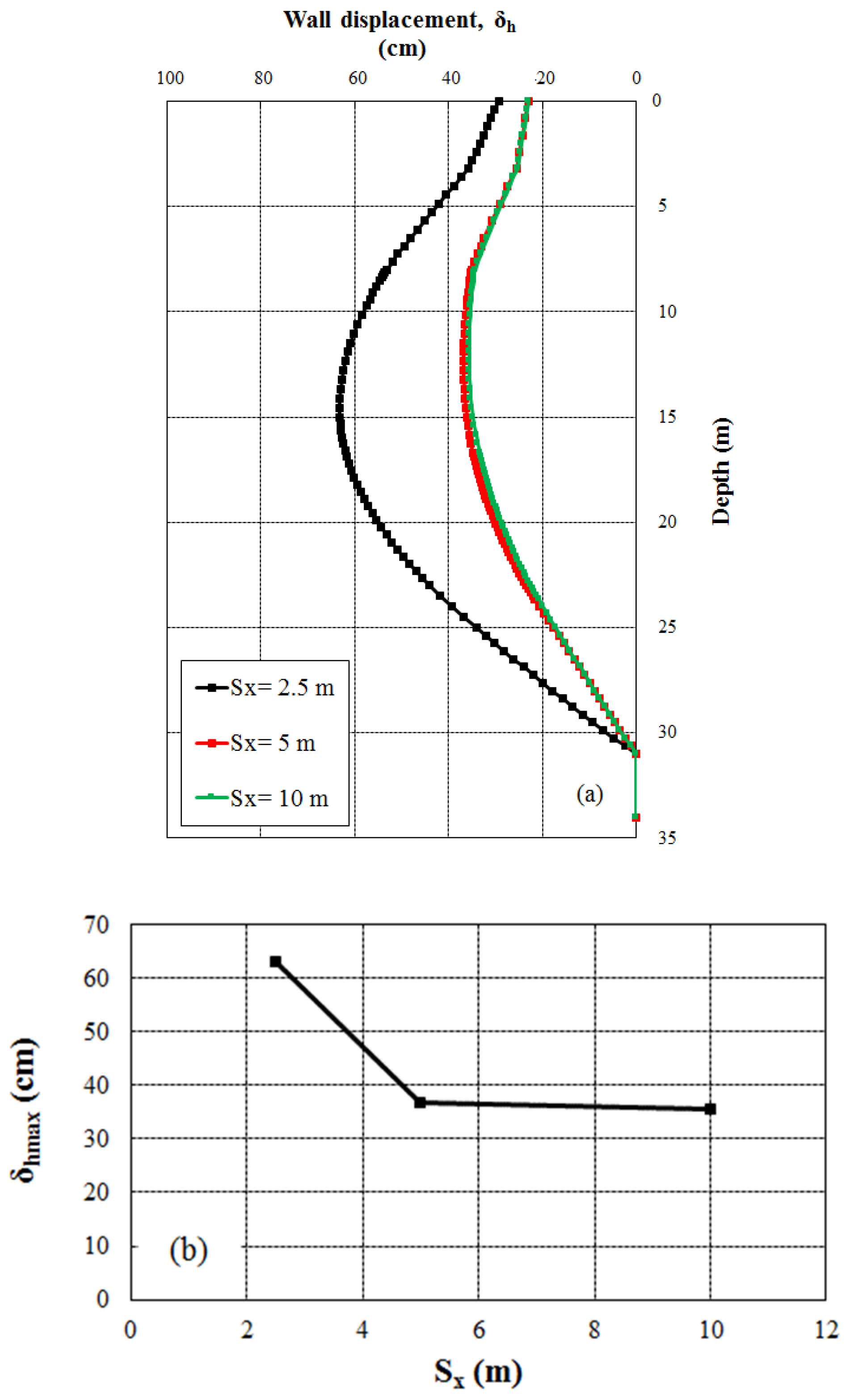
5.1. Wall Displacements
5.2. Plastic Zones
5.3. Displacement of Soil Layers
5.4. Displacement of the Tunnel
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Layer No. | Soil Type | Thickness (m) | γ (kN/m3) | c’ (kPa) | φ (°) |
|---|---|---|---|---|---|
| 1-1 | Miscellaneous fill soil | 6.5 | 18.5 | 12.4 | 16.1 |
| 3-1 | Silty clay | 2 | 18.55 | 5.6 | 2629 |
| 6-3 | Silt | 1.2 | 18.69 | 6 | 27.65 |
| 6-4 | Silty clay | 7.8 | 19.46 | 9.54 | 28.59 |
| 8-1 | Silty clay | 5.5 | 19.78 | 13.95 | 25.66 |
| 8-2 | Silt | 2 | 18.36 | 10 | 32.3 |
| 9-1 | Silty clay | 6 | 19.83 | 21.45 | 21.6 |
| 10-2 | Silty sand | 3 | 20.98 | 10.2 | 36.4 |
| 11 | Silty clay | 66 | 20.28 | 14.62 | 24.66 |
| Element | Specific Weight (kN/m3) | Elasticity Modulus (kPa) | Poisson’s Ratio | Height (m) | Damping Ratio | Thickness (m) |
|---|---|---|---|---|---|---|
| Diaphragm wall | 25 | 3 × 106 | 0.2 | 34 | 10% | 1.2 |
| Piles | 25 | 3 × 106 | 0.2 | 19 | 10% | 0.8 |
| 29.8 | 0.9 | |||||
| Struts | 25 | 3 × 106 | 0.2 | 50 | 10% | - |
References
- Bahrami, M.; Khodakarami, M.I.; Haddad, A. 3D numerical investigation of the effect of wall penetration depth on excavations behavior in sand. Comput. Geotech. 2018, 98, 82–92. [Google Scholar] [CrossRef]
- Bahrami, M.; Khodakarami, M.I.; Haddad, A. Seismic behavior and design of strutted diaphragm walls in sand. Comput. Geotech. 2019, 108, 75–87. [Google Scholar] [CrossRef]
- Liu, W.; Shi, P.; Cai, G.; Cao, C. Seepage on local stability of slurry trench in deep excavation of diaphragm wall construction. Comput. Geotech. 2021, 129, 103878. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M.; Ke, L.; Yi, J. Distributions of lateral earth pressure behind rock-socketed circular diaphragm walls considering radial deflection. Comput. Geotech. 2022, 143, 104604. [Google Scholar] [CrossRef]
- Hashash, Y.M.; Hook, J.J.; Schmidt, B.; Yao, J.I.-C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Haiyang, Z.; Jing, Y.; Su, C.; Jisai, F.; Guoxing, C. Seismic performance of underground subway station structure considering connection modes and diaphragm wall. Soil Dyn. Earthq. Eng. 2019, 127, 105842. [Google Scholar] [CrossRef]
- Kang, G.-C.; Tobita, T.; Iai, S. Seismic simulation of liquefaction-induced uplift behavior of a hollow cylinder structure buried in shallow ground. Soil Dyn. Earthq. Eng. 2014, 64, 85–94. [Google Scholar] [CrossRef]
- Sayed, M.A.; Kwon, O.-S.; Park, D.; Van Nguyen, Q. Multi-platform soil-structure interaction simulation of Daikai subway tunnel during the 1995 Kobe earthquake. Soil Dyn. Earthq. Eng. 2019, 125, 105643. [Google Scholar] [CrossRef]
- Mahmoud, A.O.; Hussien, M.N.; Karray, M.; Chekired, M.; Bessette, C.; Jinga, L. Mitigation of liquefaction-induced uplift of underground structures. Comput. Geotech. 2020, 125, 103663. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, Z.; Fan, J.; Zhao, L.; Lin, D.; Zhao, J. Problems of durability and reinforcement measures for underground structures in China. J. Rock Mech. Geotech. Eng. 2011, 3, 250–259. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Pu, X.; Li, F.; Li, T. Experimental study on the dynamic characteristics of low-angle loess slope under the influence of long- and short-term effects of rainfall before earthquake. Eng. Geol. 2020, 273, 105684. [Google Scholar] [CrossRef]
- Gazetas, G.; Psarropoulos, P.; Anastasopoulos, I.; Gerolymos, N. Seismic behaviour of flexible retaining systems subjected to short-duration moderately strong excitation. Soil Dyn. Earthq. Eng. 2004, 24, 537–550. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, X.; Zhou, H.; Du, Y.; Sun, J.; Yu, X. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations. Comput. Geotech. 2018, 95, 119–128. [Google Scholar] [CrossRef]
- Arai, Y.; Kusakabe, O.; Murata, O.; Konishi, S. A numerical study on ground displacement and stress during and after the installation of deep circular diaphragm walls and soil excavation. Comput. Geotech. 2008, 35, 791–807. [Google Scholar] [CrossRef]
- Segura-Castillo, L.; Aguado, A.; Josa, A. Bi-layer diaphragm walls: Experimental and numerical structural analysis. Eng. Struct. 2013, 56, 154–164. [Google Scholar] [CrossRef]
- Zheng, G.; Du, Y.; Cheng, X.; Diao, Y.; Deng, X.; Wang, F. Characteristics and prediction methods for tunnel deformations induced by excavations. Géoméch. Eng. 2017, 12, 361–397. [Google Scholar] [CrossRef]
- Pomonis, A.; Saito, K.; Siau, F.; Stuart, G.; Katsuichiro, M.; Joshua, M.; Raby, A.; Sammonds, P. The Mw9.0 Tohoku Earthquake and Tsunami of 11th March 2011, A Field Report by EEFIT. 2011. Available online: https://www.semanticscholar.org/paper/The-Mw9.0-Tohoku-Earthquake-and-Tsunami-of-11th-A-Pomonis-Saito/6ee03fa87148c92d3072003895fbf963da1242f3 (accessed on 17 August 2023).
- Yariyan, P.; Zabihi, H.; Wolf, I.D.; Karami, M.; Amiriyan, S. Earthquake risk assessment using an integrated Fuzzy Analytic Hierarchy Process with Artificial Neural Networks based on GIS: A case study of Sanandaj in Iran. Int. J. Disaster Risk Reduct. 2020, 50, 101705. [Google Scholar] [CrossRef]
- Madabhushi, S.P.G.; Zeng, X. Seismic Response of Gravity Quay Walls. II: Numerical Modeling. J. Geotech. Geoenviron. Eng. 1998, 124, 418–427. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Deb, K.; Sengupta, A. Behavior of underground strutted retaining structure under seismic condition. Earthq. Struct. 2015, 8, 1147–1170. [Google Scholar] [CrossRef]
- Wartman, J.; Rondinel-Oviedo, E.A.; Rodriguez-Marek, A. Performance and Analyses of Mechanically Stabilized Earth Walls in the Tecomán, Mexico Earthquake. J. Perform. Constr. Facil. 2006, 20, 287–299. [Google Scholar] [CrossRef]
- Balkaya, C.; Kalkan, E. Nonlinear seismic response evaluation of tunnel form building structures. Comput. Struct. 2003, 81, 153–165. [Google Scholar] [CrossRef]
- Wen, Y.; Yuan, D.; Xie, H.; Su, R.; Su, Q.; Li, Z.; Sun, H.; Si, G.; Yu, J.; Chen, Y.; et al. Typical Fine Structure and Seismogenic Mechanism Analysis of the Surface Rupture of the 2022 Menyuan Mw 6.7 Earthquake. Remote. Sens. 2023, 15, 4375. [Google Scholar] [CrossRef]
- Yu, J.; Kang, Y.; Zhai, Z. Advances in research for underground buildings: Energy, thermal comfort and indoor air quality. Energy Build. 2020, 215, 109916. [Google Scholar] [CrossRef]
- Miao, Y.; Zhong, Y.; Ruan, B.; Cheng, K.; Wang, G. Seismic response of a subway station in soft soil considering the structure-soil-structure interaction. Tunn. Undergr. Space Technol. 2020, 106, 103629. [Google Scholar] [CrossRef]
- Kiryu, S.; Murono, Y.; Morikawa, H. Comparative Study of Retrofit Technique For Cut and Cover Tunnel. Doboku Gakkai Ronbunshuu A 2008, 64, 825–830. [Google Scholar] [CrossRef]
- Fabozzi, S.; Licata, V.; Autuori, S.; Bilotta, E.; Russo, G.; Silvestri, F. Prediction of the seismic behavior of an underground railway station and a tunnel in Napoli (Italy). Undergr. Space 2017, 2, 88–105. [Google Scholar] [CrossRef]
- Yang, C.-S.; Mo, H.-H.; Chen, J.-S.; Wang, Y.-Z. Influence of Seismic Loading on Segment Opening of a Shield Tunnel. Sci. World J. 2014, 2014, 387210. [Google Scholar] [CrossRef]
- Jardine, R.J.; Potts, D.M.; Fourie, A.B.; Burland, J.B. Studies of the influence of non-linear stress–strain characteristics in soil–structure interaction. Géotechnique 1986, 36, 377–396. [Google Scholar] [CrossRef]
- Burland, J.B. Ninth Laurits Bjerrum Memorial Lecture: “Small is beautiful”—The stiffness of soils at small strains. Can. Geotech. J. 1989, 26, 499–516. [Google Scholar] [CrossRef]
- Peiris, T.; Thambiratnam, D.; Gallage, C.; Perera, N. Soil–Pile Interaction of Pile Embedded in Deep-Layered Marine Sediment under Seismic Excitation. Struct. Eng. Int. 2014, 24, 521–531. [Google Scholar] [CrossRef]
- Al-Jeznawi, D.; Jais, I.B.M.; Albusoda, B.S.; Alzabeebee, S.; Al-Janabi, M.A.Q.; Keawsawasvong, S. Response of Pipe Piles Embedded in Sandy Soils Under Seismic Loads. In Transportation Infrastructure Geotechnology; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–27. [Google Scholar] [CrossRef]
- Wu, M.; Li, S.; Fan, S.; Lu, J. Experimental study on soil-structure interaction of steel frame under seismic excitations. Structures 2023, 55, 2280–2294. [Google Scholar] [CrossRef]
- Han, J.; Guo, Z.; El Naggar, M.H.; Li, L.; Wang, X.; Du, X. Response of Buried Pipeline to Non-Uniform Longitudinal and Transverse Ground Motions. J. Earthq. Eng. 2023, 1–20. [Google Scholar] [CrossRef]
- Yusra, A.; Mustafa, A.; Refiyanni, M.; Zakia, Z. Performance Structural Analysis of U2C Building with the Kobe Earthquake Spectrum. Int. J. Eng. Sci. Inf. Technol. 2023, 3, 36–46. [Google Scholar] [CrossRef]
- Hussien, R.S.; Albusoda, B.S. Experimental modeling of a single pile in liquefiable soil under the effect of coupled static-dynamic loads. Innov. Infrastruct. Solutions 2022, 8, 50. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, L.; Niu, Y.; Ma, F.; Lu, S.; Fu, Z. Study on the Surface Settlement of an Overlying Soft Soil Layer under the Action of an Earthquake at a Subway Tunnel Engineering Site. Sustainability 2023, 15, 9484. [Google Scholar] [CrossRef]
- Khamesi, S.O.; Hosseini, S.M.M.M. Numerical investigation of the main factors influencing rocking responses of shallow foundations. Proc. Inst. Civ. Eng.—Geotech. Eng. 2023, 1–16. [Google Scholar] [CrossRef]
- Yang, J.; Zhuang, H.; Zhang, G.; Tang, B.; Xu, C. Seismic performance and fragility of two-story and three-span underground structures using a random forest model and a new damage description method. Tunn. Undergr. Space Technol. 2023, 135, 104980. [Google Scholar] [CrossRef]
- Tong, L.; Wang, D.; Sun, Z.; Chen, L.; Shi, F. Seismic Uplift Effect at End Spans of Long-Span Rigid-Frame Bridges Subjected to Near-Fault and Far-Fault Ground Motions. J. Bridg. Eng. 2023, 28, 5023001. [Google Scholar] [CrossRef]
- Shutong, C.; Kassem, M.M.; Jalilluddin, A.M.; Nazri, F.M.; Wenjun, A. The effect of bridge girder-bearing separation on shear key pounding under vertical earthquake action—A state-of-the-art review. Structures 2023, 55, 2445–2460. [Google Scholar] [CrossRef]
- Pai, L.F.; Wu, H.G.; Sun, H.; Ma, Z.G. Shaking table test of the dynamic response of a tunnel across a main sliding surface. Int. J. Rock Mech. Min. Sci. 2023, 169, 105440. [Google Scholar] [CrossRef]
- Zhang, J. Dynamic analysis of fixed platforms equipped with mass dampers under earthquake loading using crow search algorithm. In Multiscale and Multidisciplinary Modeling, Experiments and Design; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–13. [Google Scholar] [CrossRef]
- Zarinfar, M. Investigating the Effect of Soil Layering on Soil-structure Interaction under Seismic Load. Int. J. Eng. 2022, 35, 1989–2006. [Google Scholar] [CrossRef]
- Moosavi, J.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Supply chain disruption during the COVID-19 pandemic: Recognizing potential disruption management strategies. Int. J. Disaster Risk Reduct. 2022, 75, 102983. [Google Scholar] [CrossRef] [PubMed]
- Gheibi, M.; Eftekhari, M.; Akrami, M.; Emrani, N.; Hajiaghaei-Keshteli, M.; Fathollahi-Fard, A.M.; Yazdani, M. A Sustainable Decision Support System for Drinking Water Systems: Resiliency Improvement against Cyanide Contamination. Infrastructures 2022, 7, 88. [Google Scholar] [CrossRef]


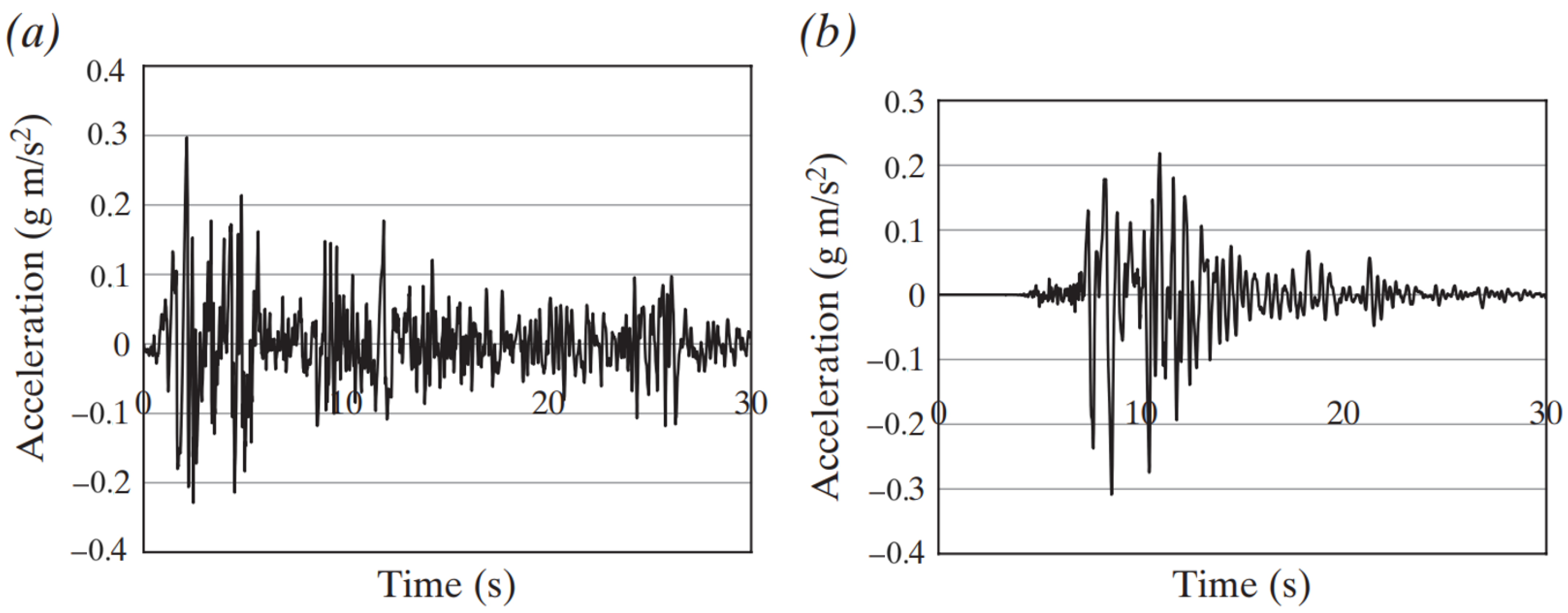
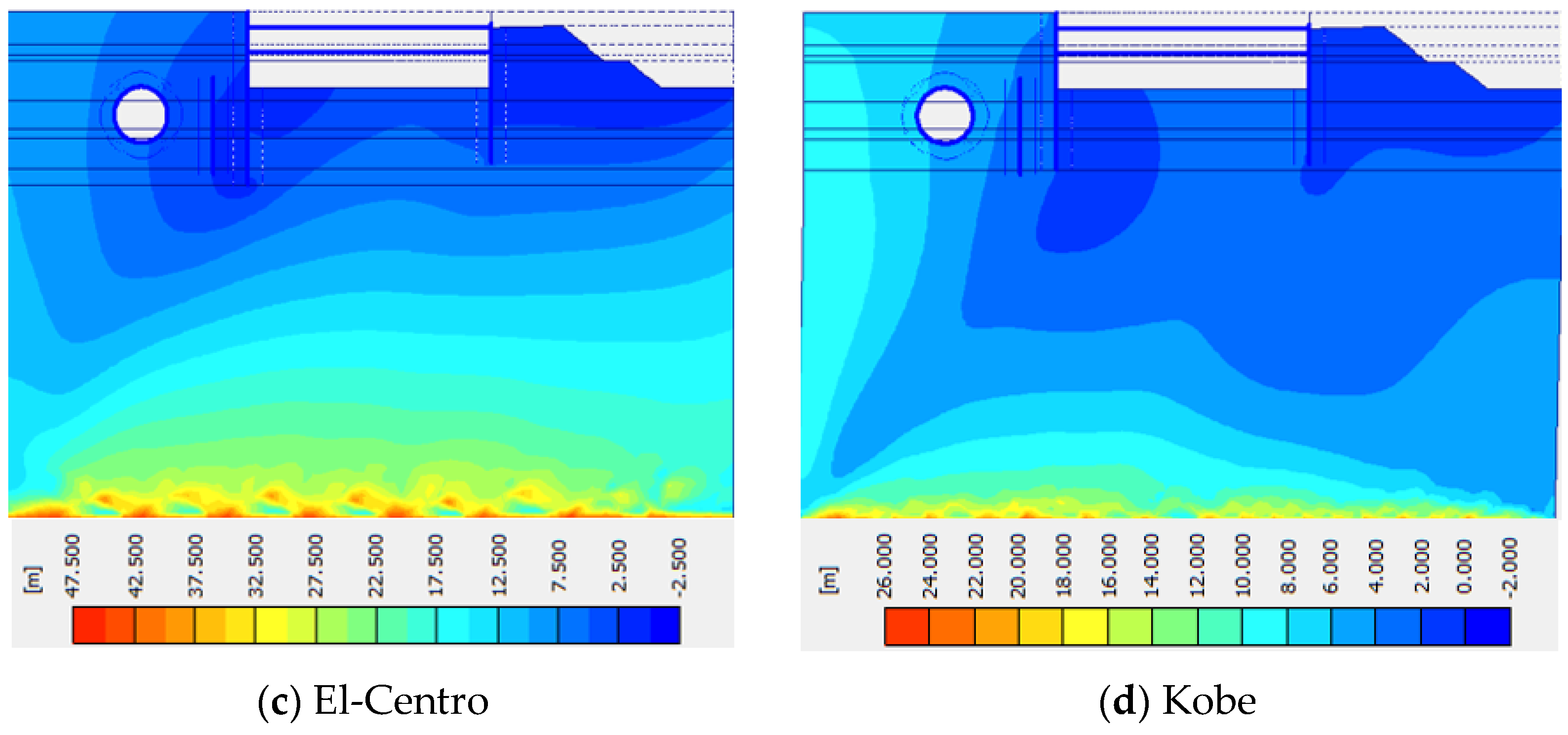
| Earthquake | Magnitude | Duration (sec) | Rjb (km) | Rrup (km) |
|---|---|---|---|---|
| El-Centro (1940) | 6.95 | 41.86 | 6.09 | 6.09 |
| Kobe (1995) | 6.9 | 20 | 0.9 | 0.92 |
| Discussion Aspect | Description | Reference |
|---|---|---|
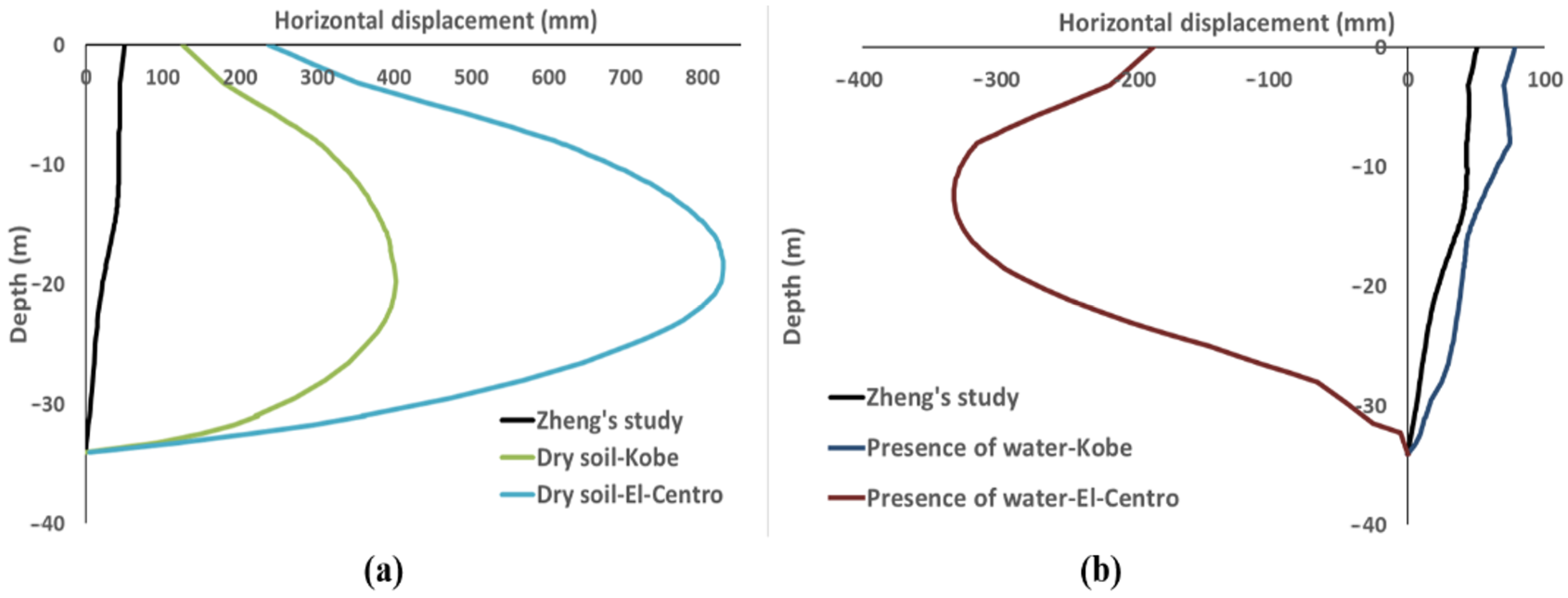
| Effects of Seismic Loading | The study demonstrates that inducing seismic loads, such as the El Centro and Kobe earthquakes, leads to horizontal displacements of the diaphragm wall. This behavior is expected due to the dynamic forces exerted by the earthquakes. However, the differences in the magnitude of displacement between the two earthquakes are intriguing. Despite the similar magnitudes of the Kobe and El Centro earthquakes, their durations differ significantly, which prompts questions about the relationship between earthquake duration and the resulting structural response. | [32] |
| Influence of Water Presence | The diaphragm wall’s response to seismic loads appears to be influenced by the presence or absence of water. The passage notes that the diaphragm wall’s horizontal displacement is different when water is present compared to when it’s absent. This suggests that water may act as a damping or stabilizing factor, affecting the wall’s dynamic behavior. The reasons behind this disparity could be explored, potentially involving the role of water pressure, fluid-structure interaction, and soil mechanics. | [33] |
| Spatial Variation of Displacement | The study presents varying displacement values at different depths from the wall head. This spatial variation indicates that the behavior of the diaphragm wall is not uniform along its length. Investigating the reasons for this variation could involve factors such as soil stratification, lateral spreading, and the distribution of seismic forces within the wall. | [34] |
| Comparison of El Centro and Kobe Earthquakes | Despite the similar magnitudes of the two earthquakes, their effects on the diaphragm wall’s displacement are different. This discrepancy raises questions about how other earthquake characteristics beyond magnitude might influence the structural response. The duration of the seismic event, as mentioned in the passage, could play a role, but other factors such as wave propagation, frequency content, and the distance from the epicenter might also contribute to the observed differences. | [35] |
| Static vs. Dynamic Displacement | The study notes that the diaphragm wall’s displacement is higher under dynamic load conditions compared to static conditions. This distinction between static and dynamic behavior underscores the importance of considering dynamic effects in seismic design and analysis. Exploring the reasons for this increase in displacement could involve examining the amplification of forces during dynamic loading and how structures respond differently to transient and sustained loads. | [36] |
| Implications for Seismic Design | The findings have potential implications for seismic design practices, particularly in regions prone to earthquakes. Understanding how structures behave under specific seismic events and conditions can inform design choices, reinforcement strategies, and mitigation measures. Additionally, the insights gained from this study could contribute to improving the accuracy of numerical simulations and analytical models used in seismic design. | [37] |
| Discussion Aspect | Description | Reference |
|---|---|---|
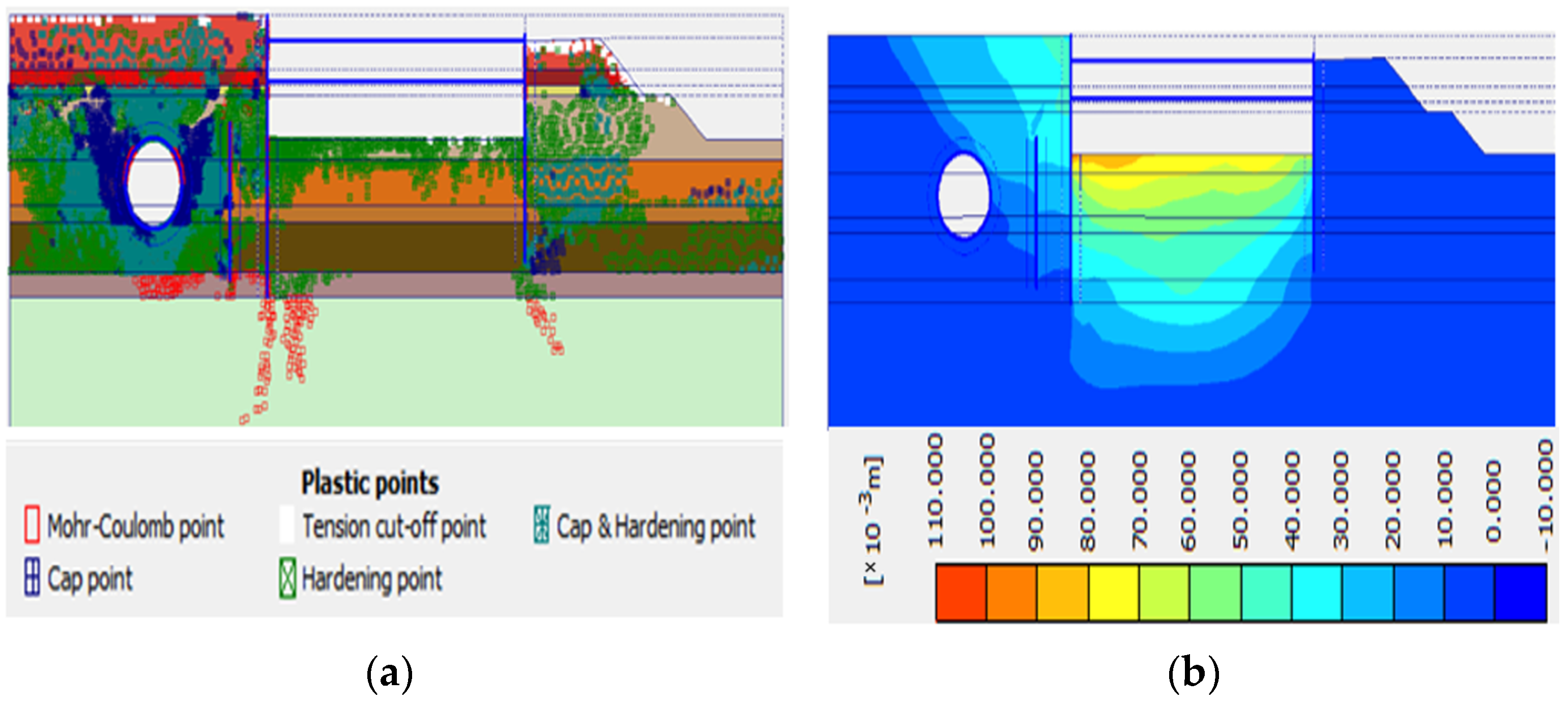
| Mohr-Coulomb Criterion and Failure Envelopes | The use of the red open square to denote the Mohr-Coulomb point is crucial. This point signifies that the stress state of the soil aligns with the failure envelope defined by the Mohr-Coulomb criterion. This criterion is mathematically expressed as τ = c + σn × tan(φ), where τ is the shear stress, c is the cohesion, σn is the normal stress, and φ is the angle of internal friction. When stresses lie on this envelope, it indicates that the soil is on the verge of failure. The visualization of this alignment through the red open square provides an intuitive representation of soil stability and its proximity to failure conditions. | [38] |
| Tension Cut-off Criterion and Negative Stresses | The solid white square representing the tension cut-off point holds significance in terms of mathematical interpretation. The concept of negative stresses in soils, especially in tension, is non-physical due to the inherent cohesion among soil particles. The tension cut-off criterion prevents the calculation of tensile stresses beyond a certain threshold, often defined by tensile strength or cohesion. This is expressed as τ ≤ 0, ensuring that negative shear stresses are not considered in the analysis. Mathematically, this criterion ensures that the soil’s response remains consistent with its mechanical behavior and prevents unrealistic results. | [39] |
| Cap Points and Reconsolidation Stress | The introduction of the blue-crossed square to represent cap points introduces the notion of reconsolidation stress. This concept is pivotal, especially in scenarios involving cyclic loading. Mathematically, the cap point implies that the reconsolidation stress equals the current stress state. In equations, this can be expressed as σ_reconsolidation = σ_current, indicating that the soil is reverting to a state of consolidation. The introduction of cap points provides insights into the soil’s dynamic behavior, capturing its response to cyclic loading and stress reversals. | [40] |
| Hardening Points and Shear Strength Evolution | The significance of the green squares, both with and without a plus sign, goes beyond their visual representation. These points provide a direct link to the evolving shear strength of the soil under cyclic loading. Mathematically, the concept of shear hardening implies an increase in the soil’s shear strength with increasing shear strain. This is often modeled using constitutive equations that capture the evolution of shear strength parameters. The presence of hardening points on the shear hardening envelope illustrates the interplay between soil stiffness, strength, and deformation under varying loading conditions. | [41] |
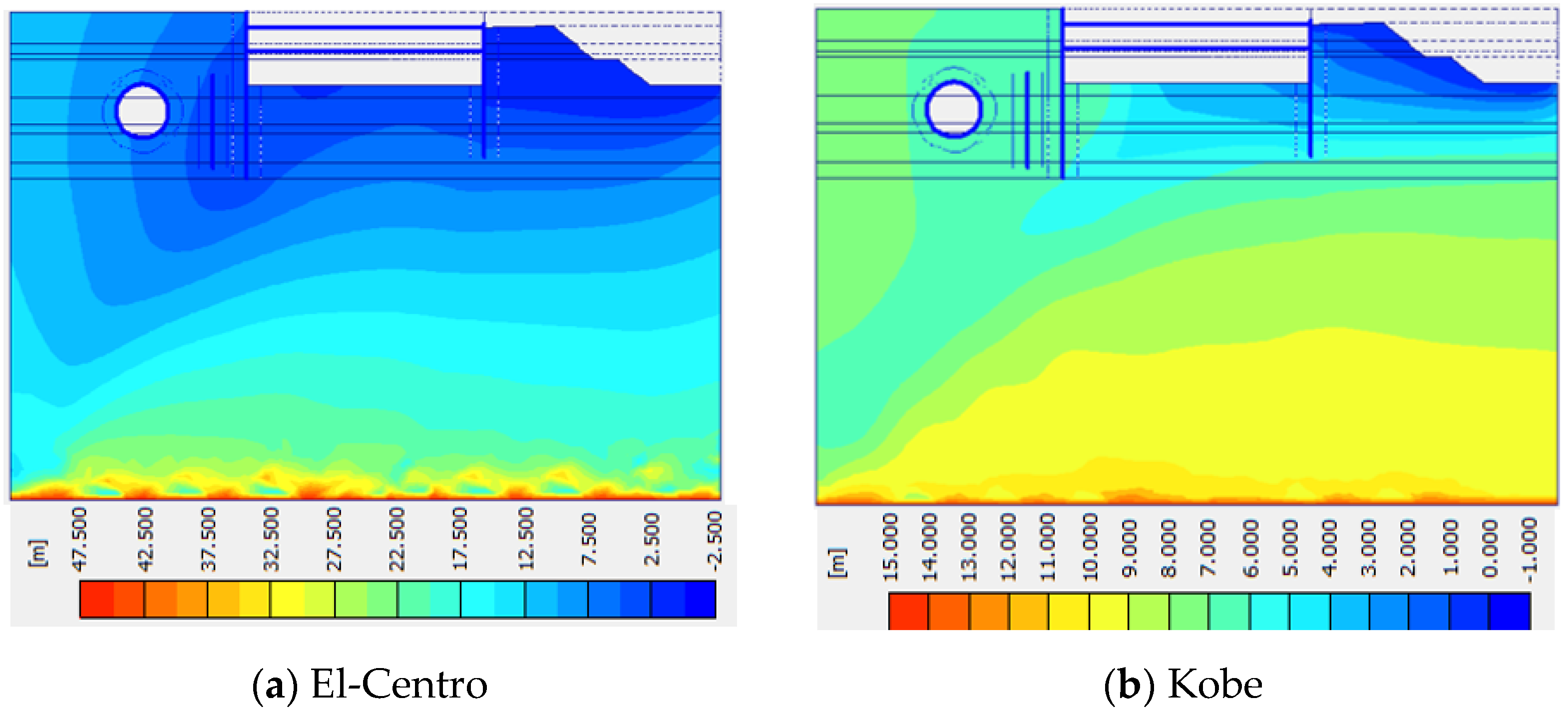
| Effect of Water and Stress Localization | The researchers’ observation that plastic points are more concentrated and compressed in the presence of water opens a pathway for deeper analysis. The mathematical connection between water content, pore pressure, and effective stress is fundamental. Changes in pore pressure due to water can significantly affect effective stress and consequently alter the soil’s shear strength parameters. The concentration of plastic points in specific areas can be attributed to localized changes in shear strength, driven by variations in water content and its distribution. Mathematically, this can be linked to Terzaghi’s effective stress principle, which relates total stress, pore water pressure, and effective stress. | [42] |
| Dynamic Loading Duration and Energy Dissipation | The variation in plastic point distribution with different earthquake load durations is intriguing. Mathematically, this can be correlated to the concept of energy dissipation. Longer-duration seismic loads lead to more cumulative loading cycles, which can result in greater energy dissipation within the soil matrix. This dissipation can influence the soil’s stiffness, shear strength, and deformation characteristics, directly impacting the distribution and density of plastic points. The relationship between loading duration, energy dissipation, and soil behavior can be analyzed using concepts from cyclic loading theories and hysteresis loops. | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bigonah, N.; Khaksar, R.Y.; Fathollahi-Fard, A.M.; Gheibi, M.; Wacławek, S.; Moezzi, R. Seismic Stability and Sustainable Performance of Diaphragm Walls Adjacent to Tunnels: Insights from 2D Numerical Modeling and Key Factors. Buildings 2024, 14, 60. https://doi.org/10.3390/buildings14010060
Bigonah N, Khaksar RY, Fathollahi-Fard AM, Gheibi M, Wacławek S, Moezzi R. Seismic Stability and Sustainable Performance of Diaphragm Walls Adjacent to Tunnels: Insights from 2D Numerical Modeling and Key Factors. Buildings. 2024; 14(1):60. https://doi.org/10.3390/buildings14010060
Chicago/Turabian StyleBigonah, Nafiseh, Reza Yeganeh Khaksar, Amir M. Fathollahi-Fard, Mohammad Gheibi, Stanisław Wacławek, and Reza Moezzi. 2024. "Seismic Stability and Sustainable Performance of Diaphragm Walls Adjacent to Tunnels: Insights from 2D Numerical Modeling and Key Factors" Buildings 14, no. 1: 60. https://doi.org/10.3390/buildings14010060
APA StyleBigonah, N., Khaksar, R. Y., Fathollahi-Fard, A. M., Gheibi, M., Wacławek, S., & Moezzi, R. (2024). Seismic Stability and Sustainable Performance of Diaphragm Walls Adjacent to Tunnels: Insights from 2D Numerical Modeling and Key Factors. Buildings, 14(1), 60. https://doi.org/10.3390/buildings14010060










