Dynamic Compaction of High Groundwater Level Subgrade of Buildings: A Model Test-Based Analysis of Stress Distribution and Reinforcement Mechanisms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Similarity Ratio
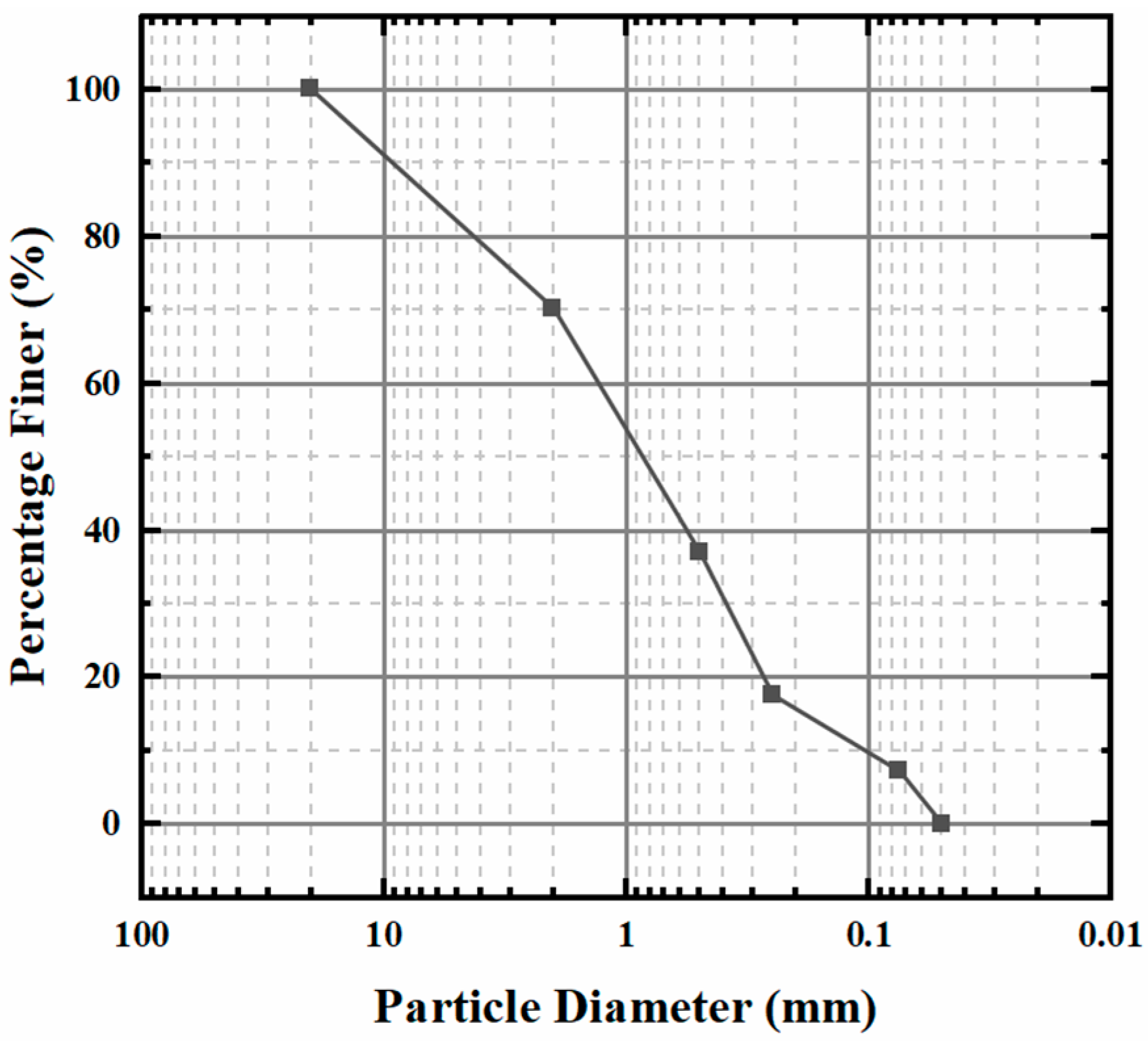
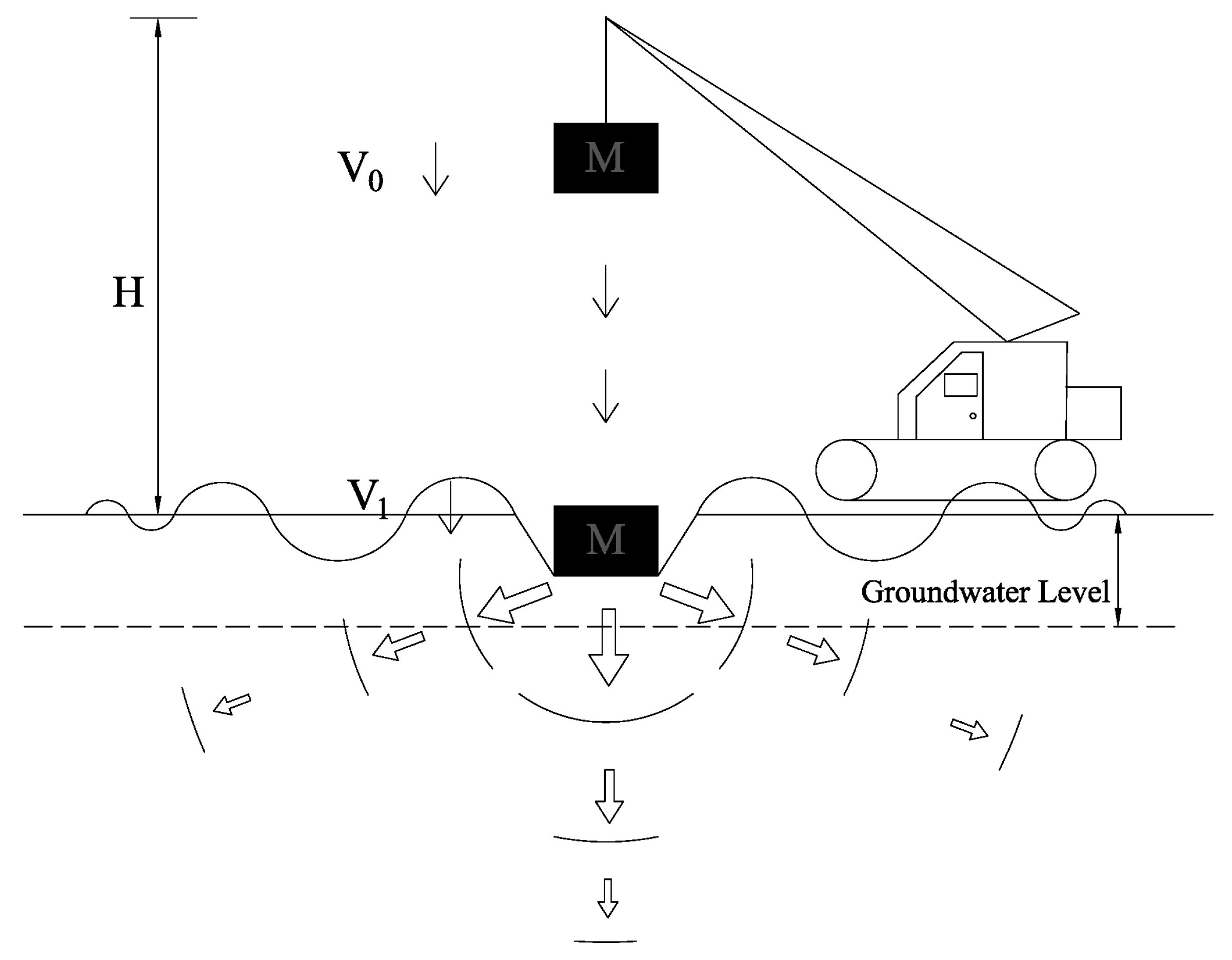
2.2. Materials and Test Equipment
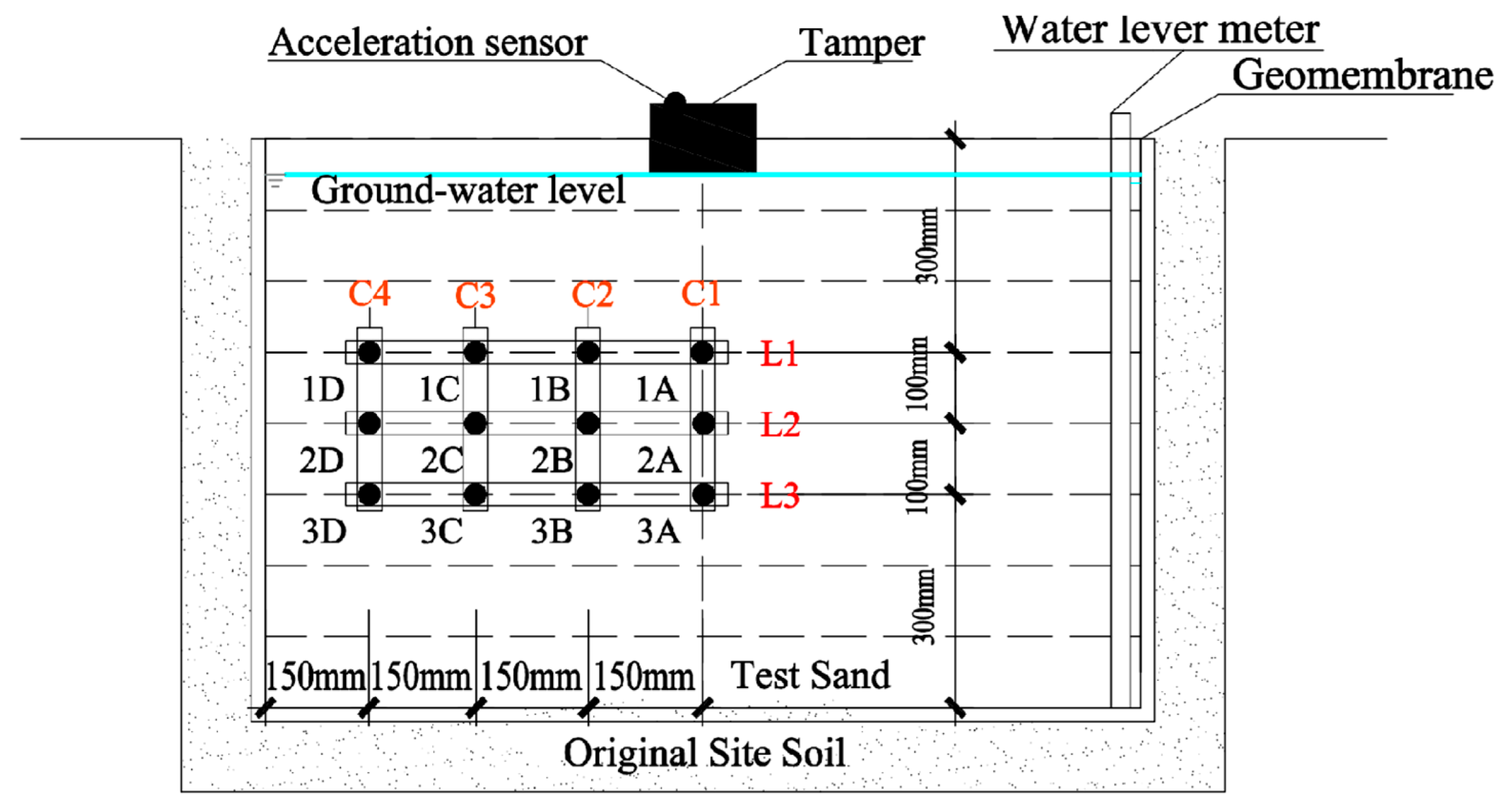
2.3. Test Program and Monitoring Point Arrangement
3. Results
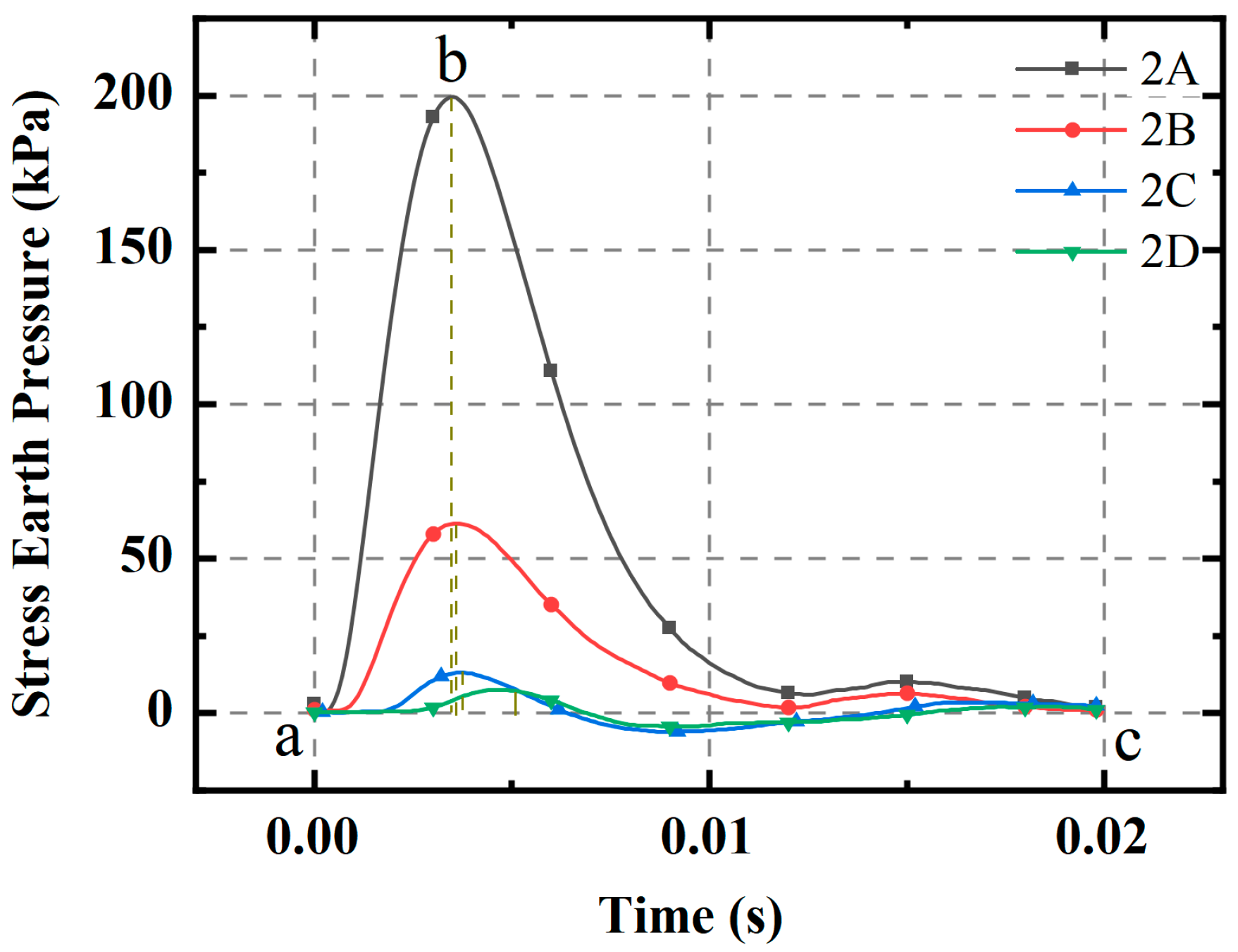
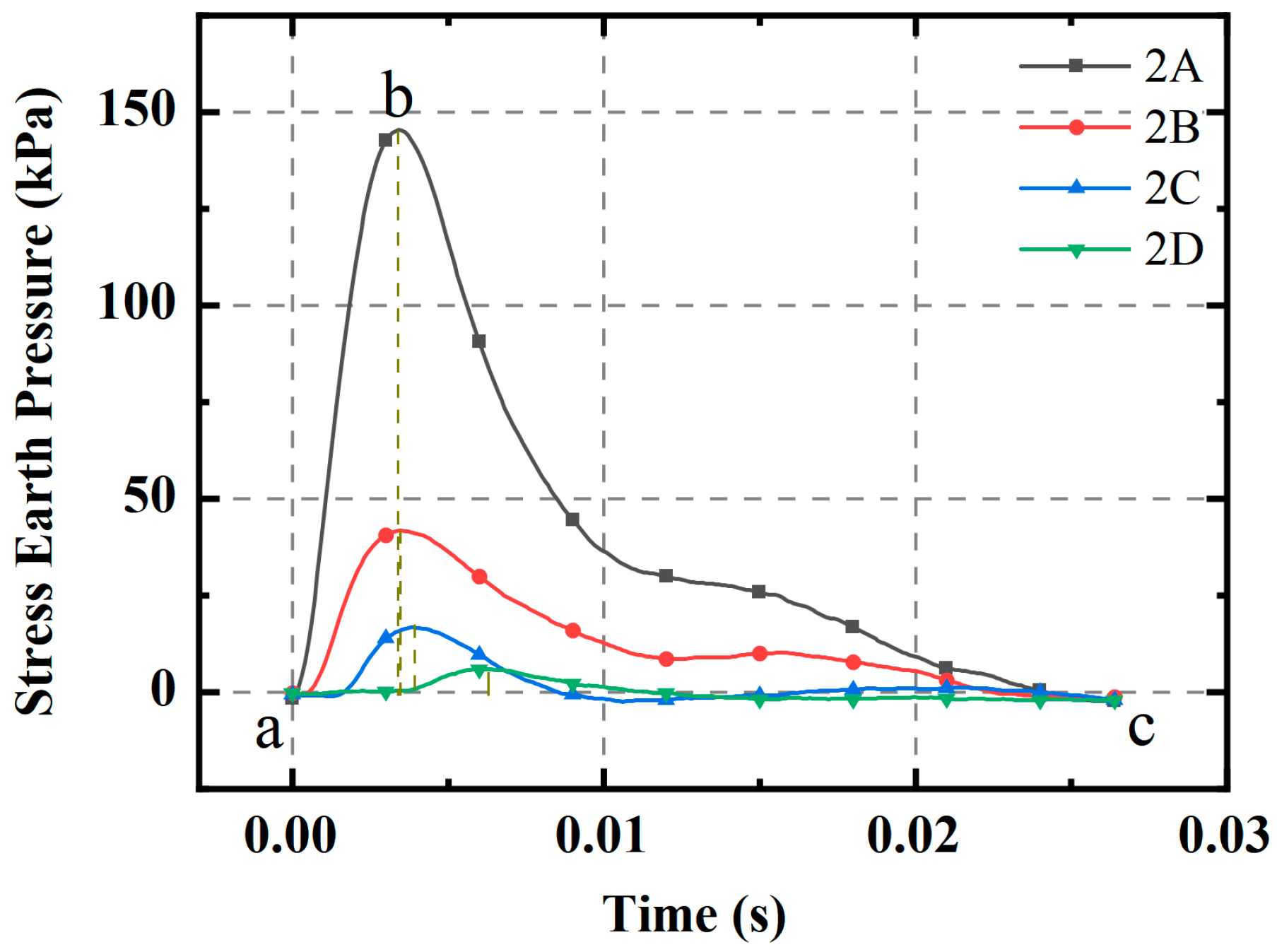
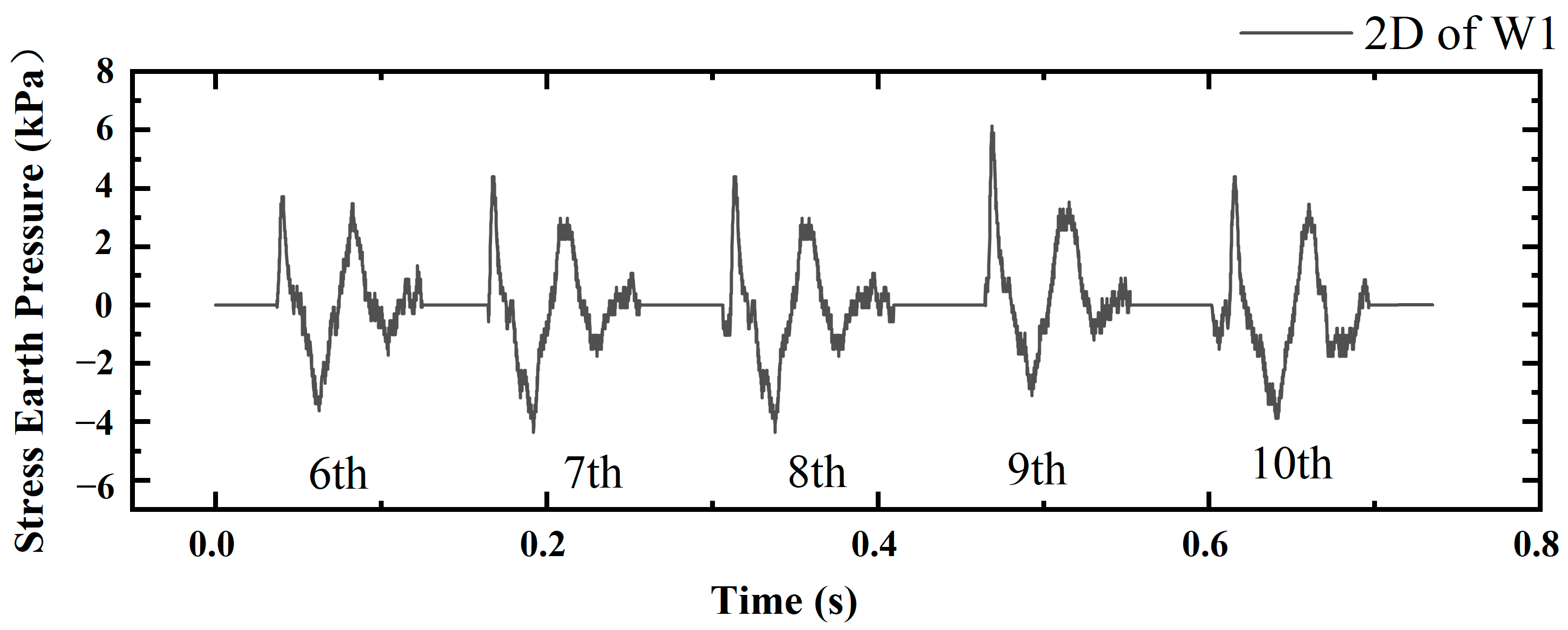
3.1. Dynamic Stress Waveform Analysis
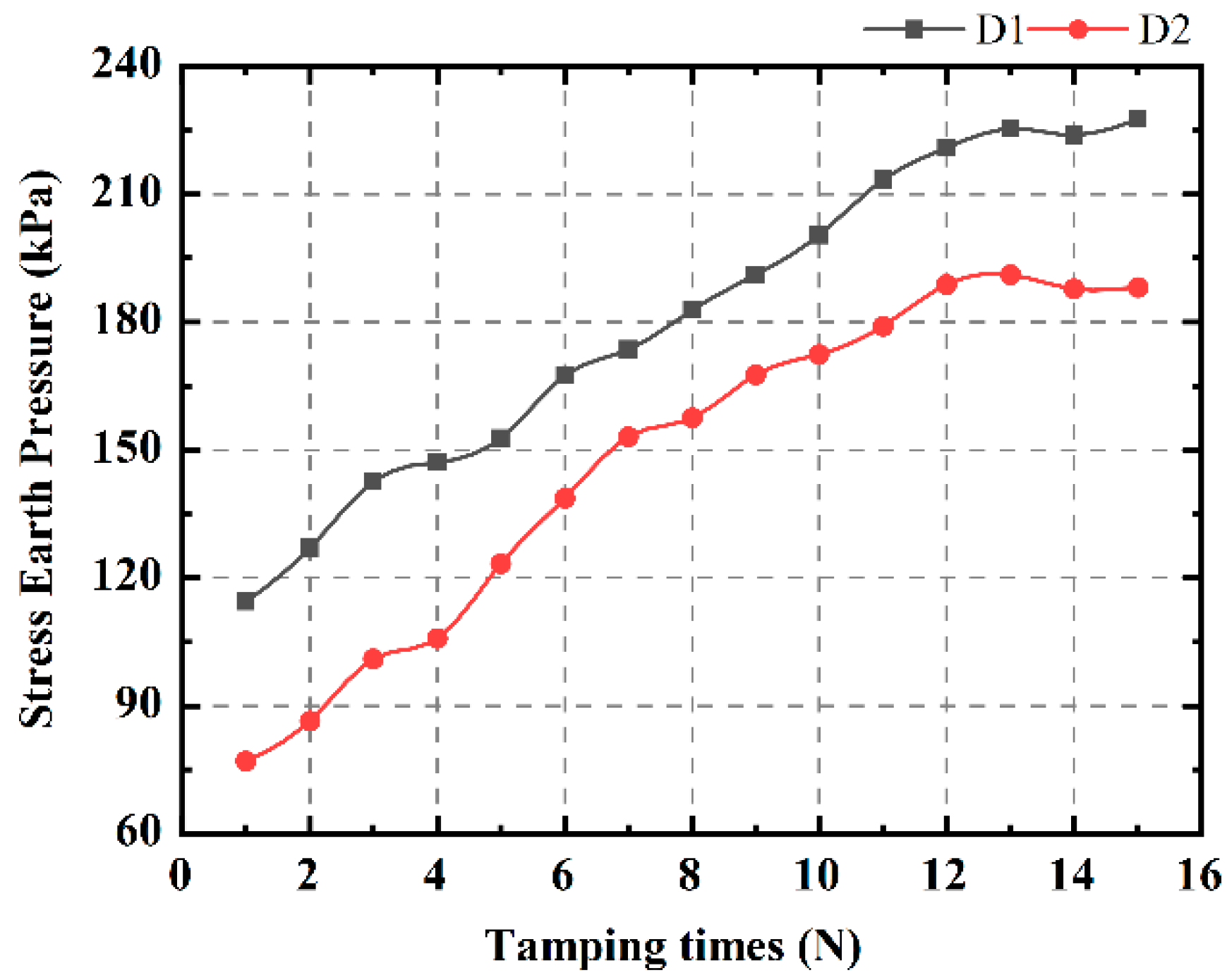
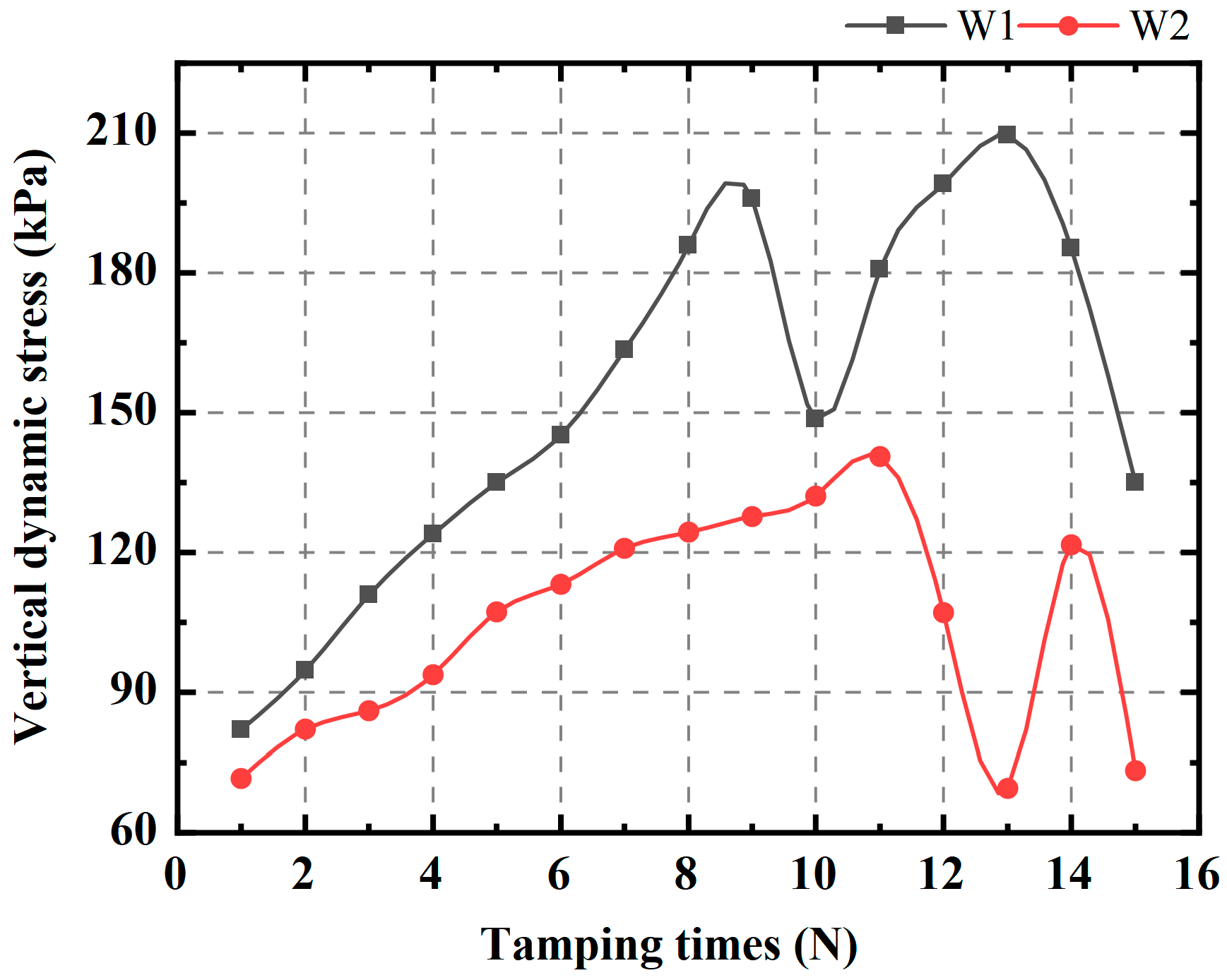
3.2. Peak Dynamic Stress Development Analysis
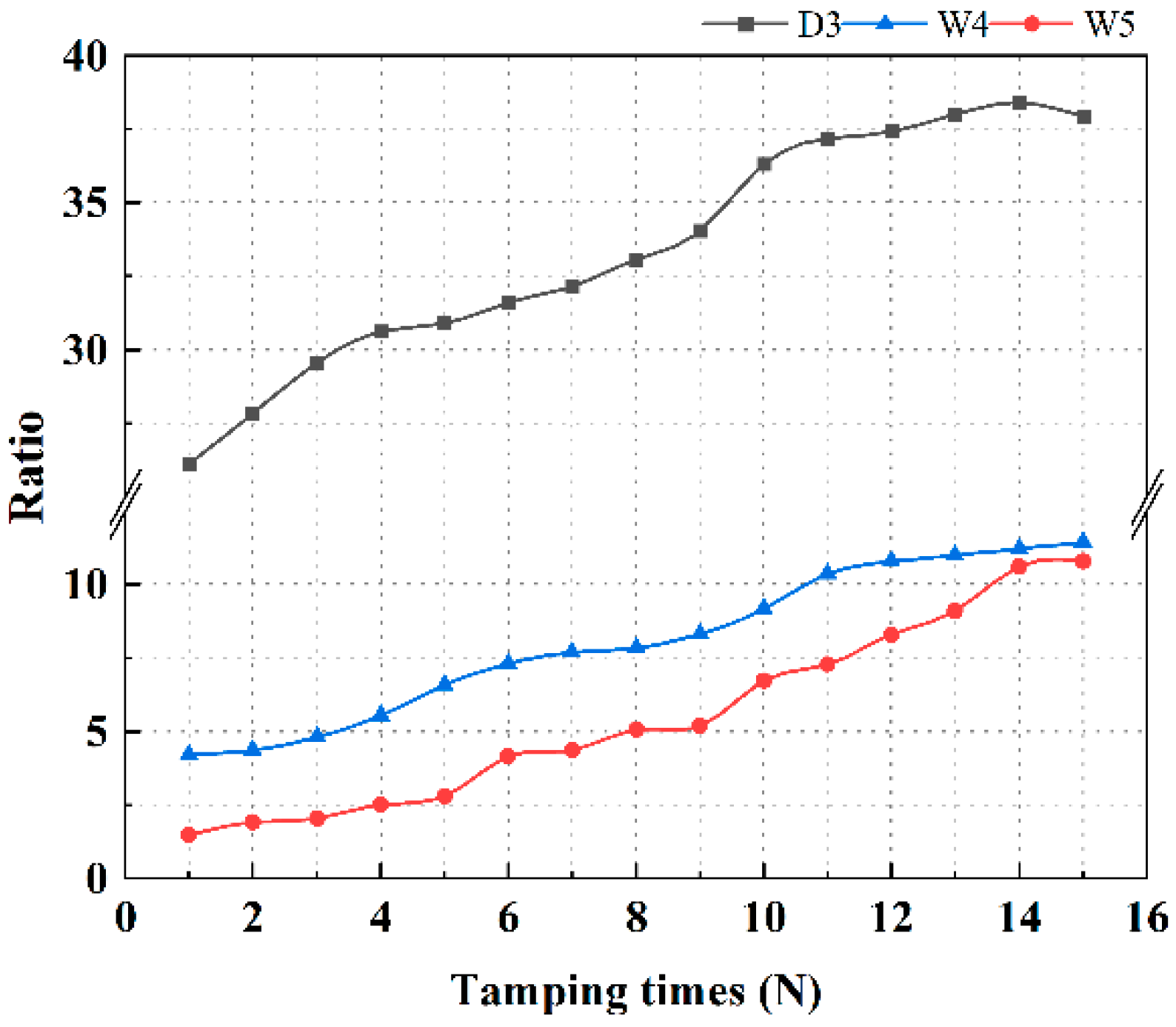
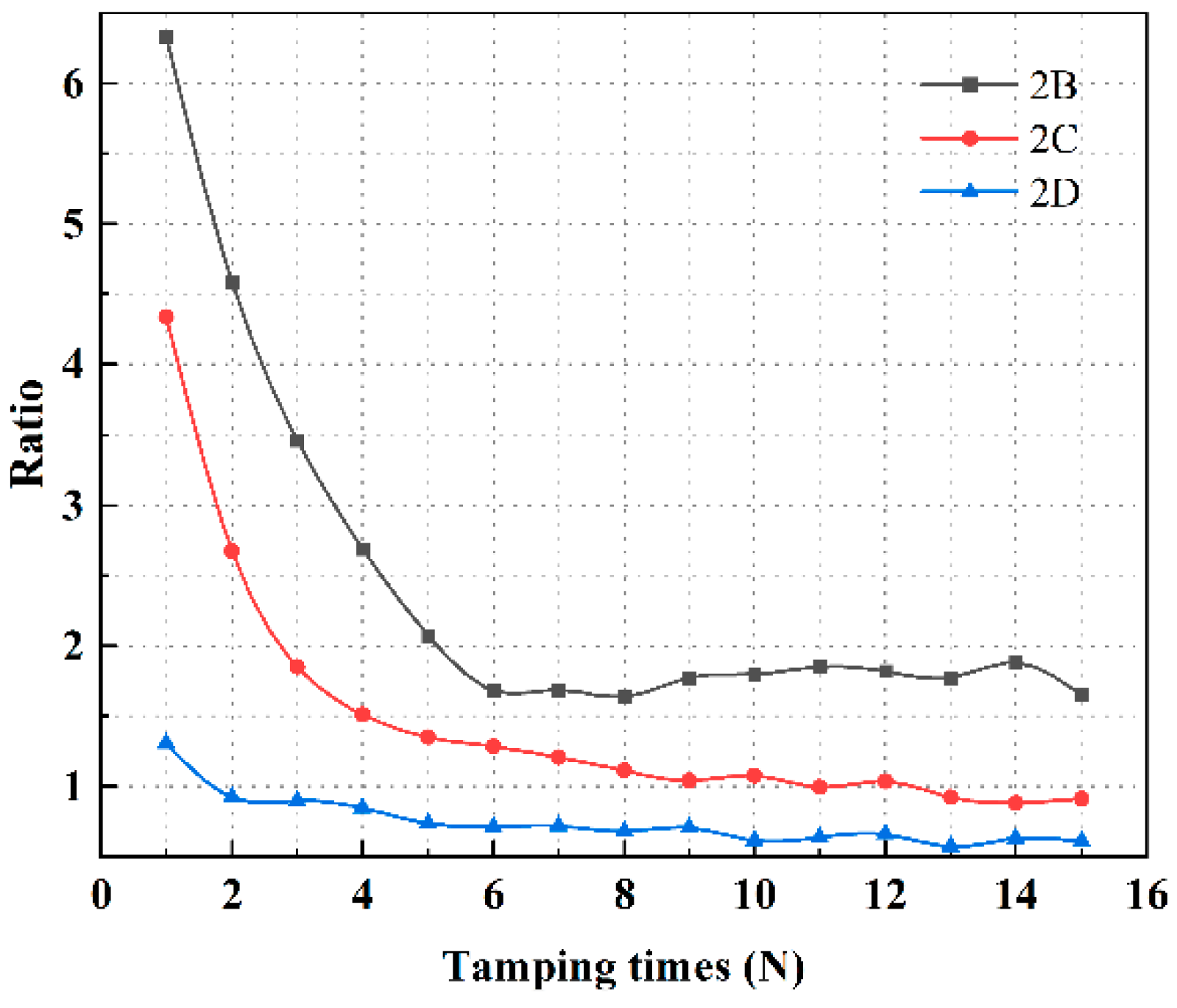
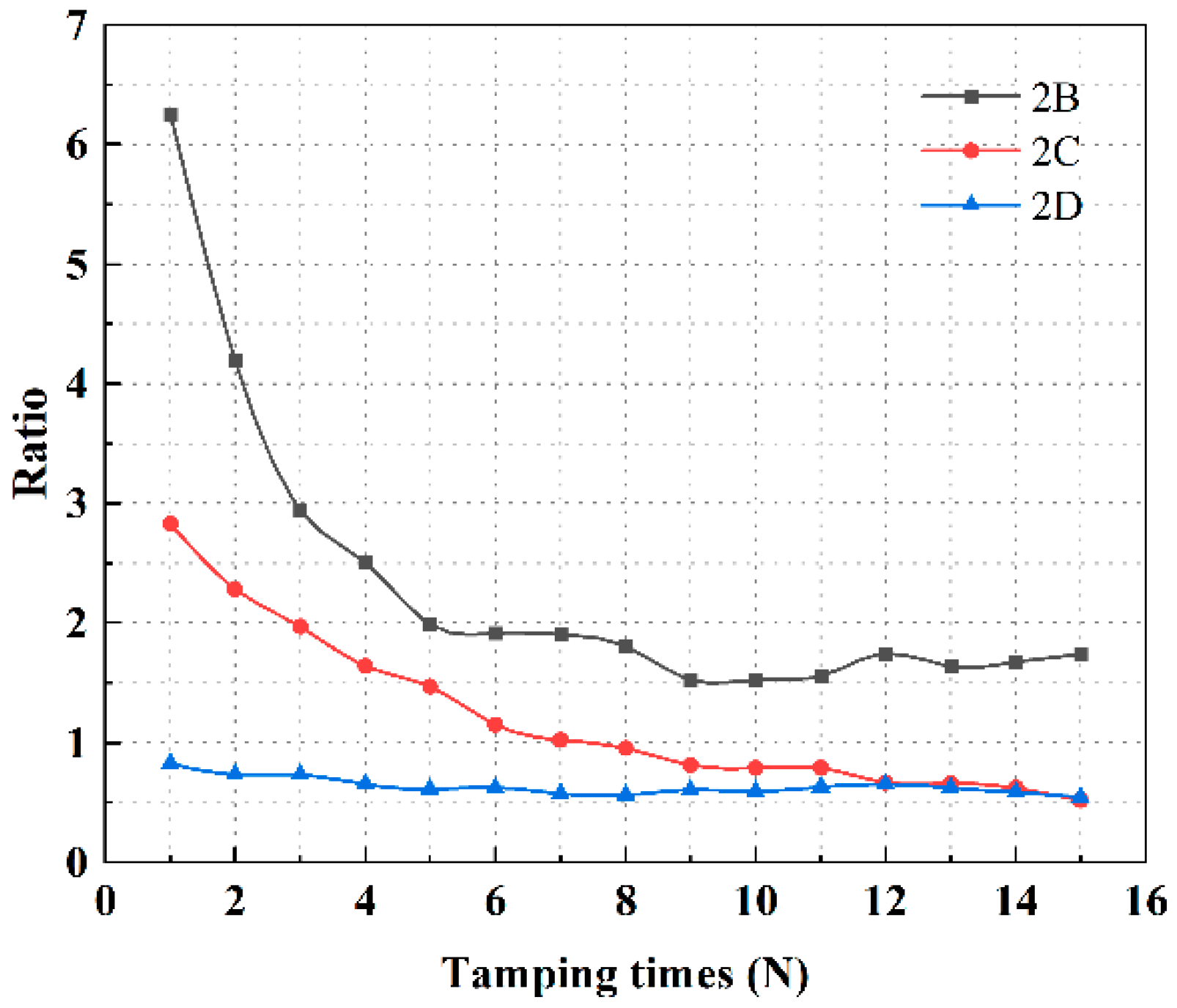
3.3. Two-Way Dynamic Stress Peak Analysis
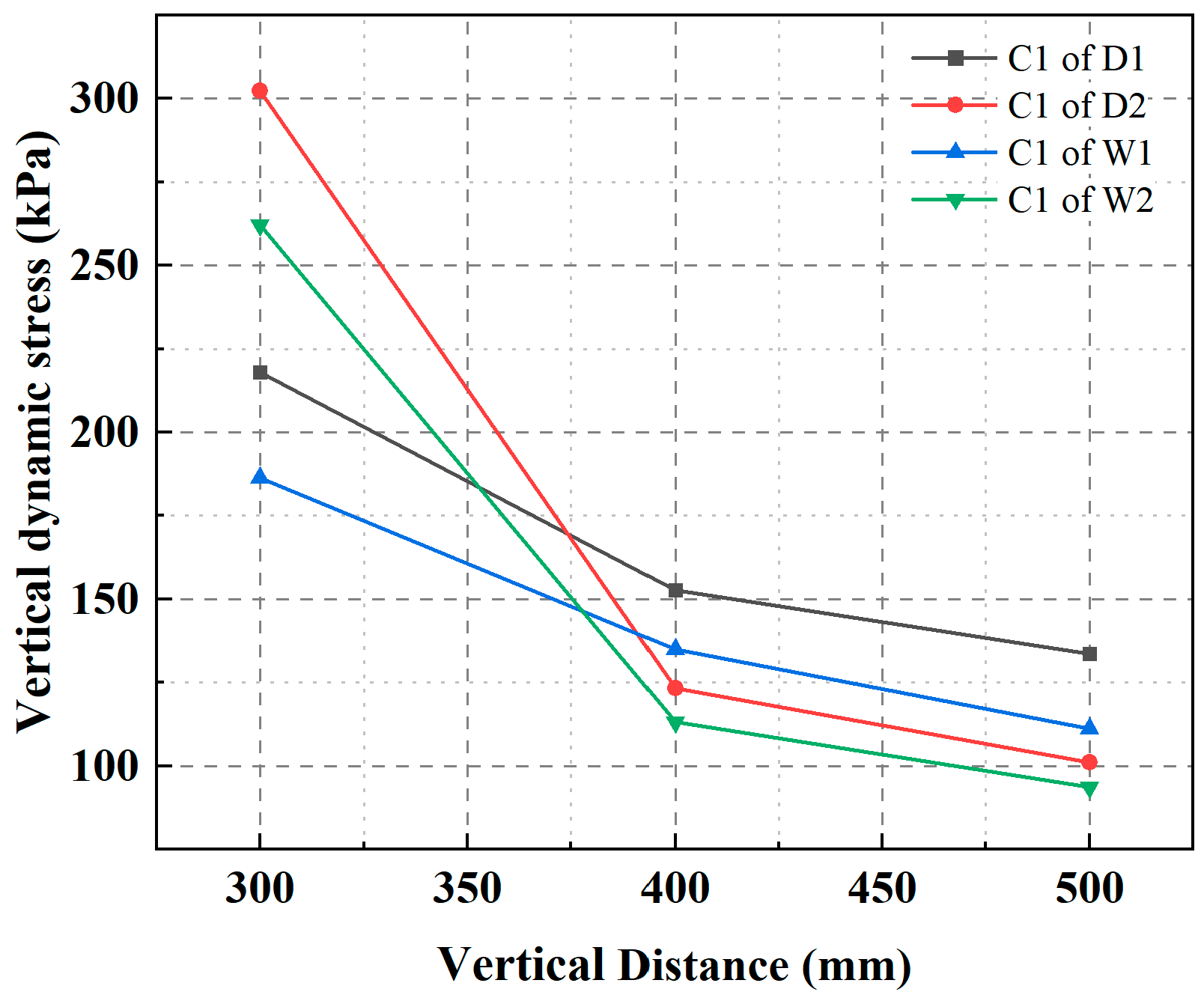
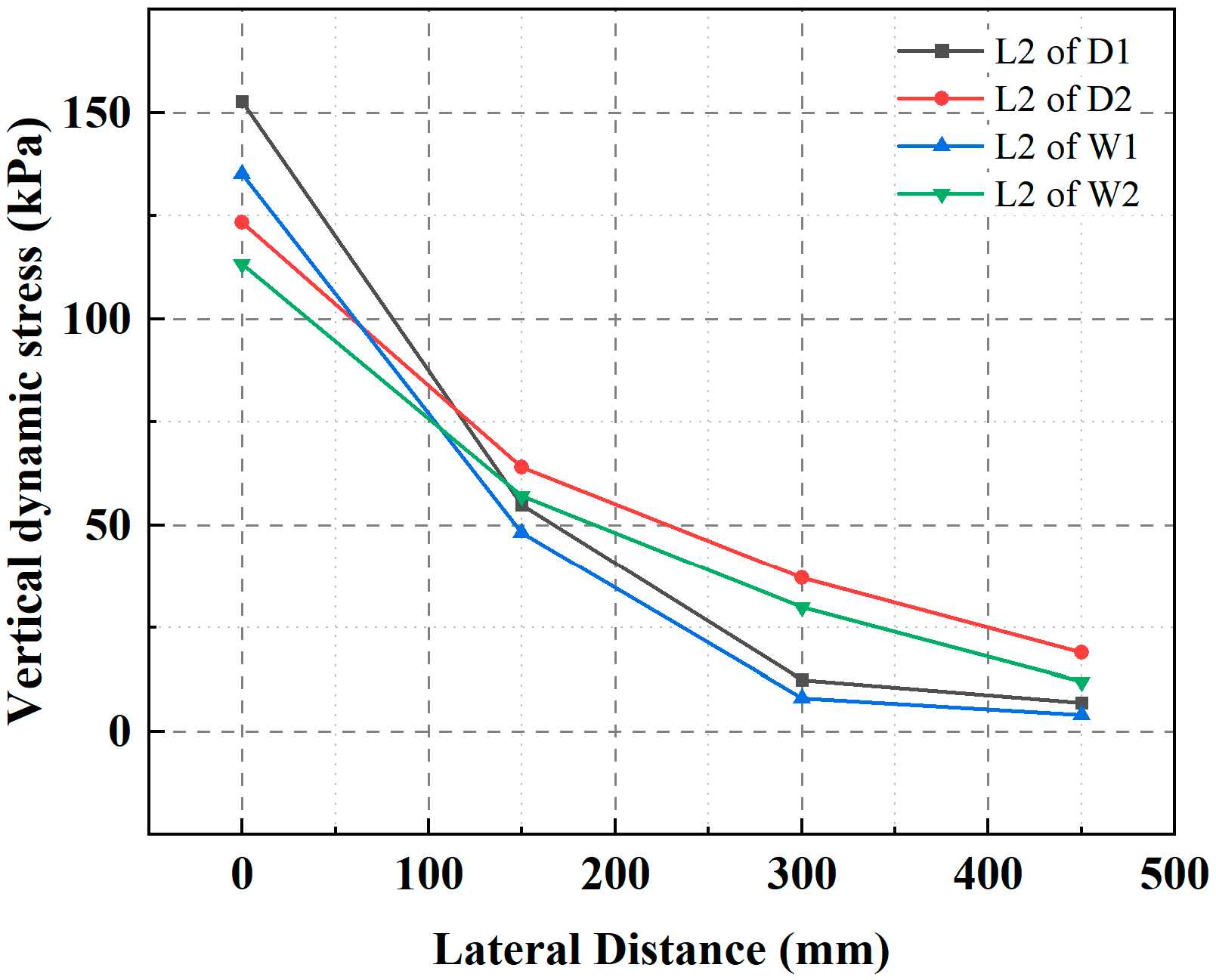
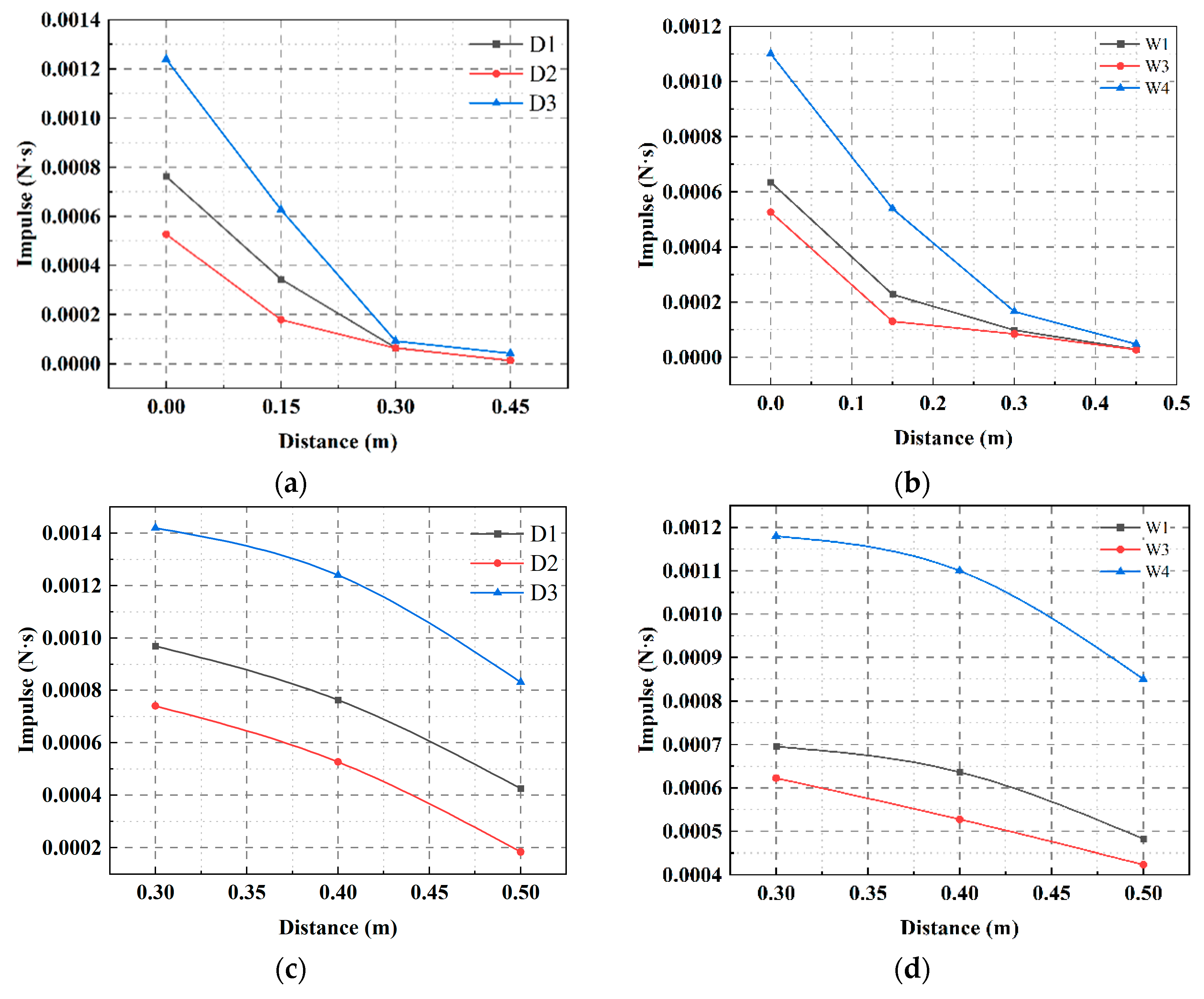
3.4. Attenuation Analysis
3.4.1. Analysis of Water Level Height on Attenuation Rate
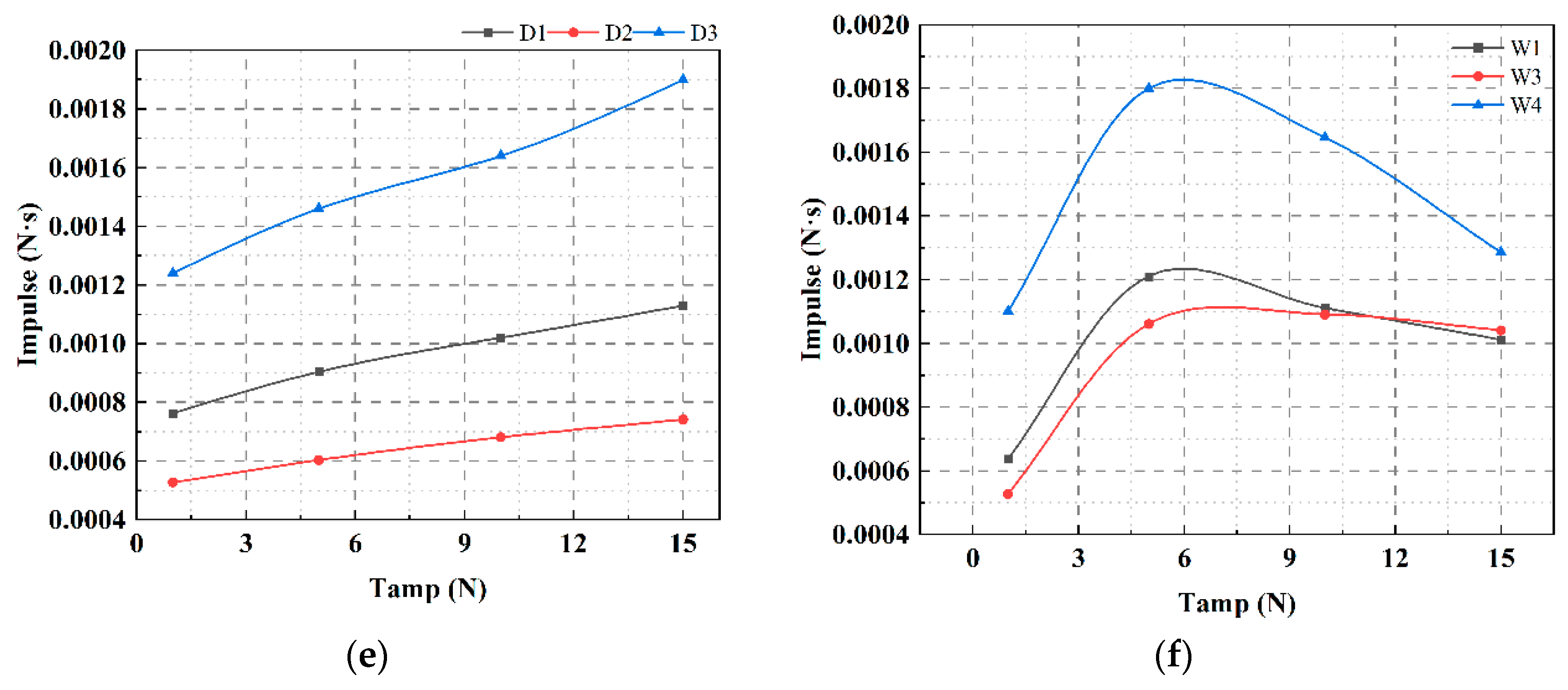
3.4.2. Analysis of Tamper Weight on Attenuation Rate
4. Discussion
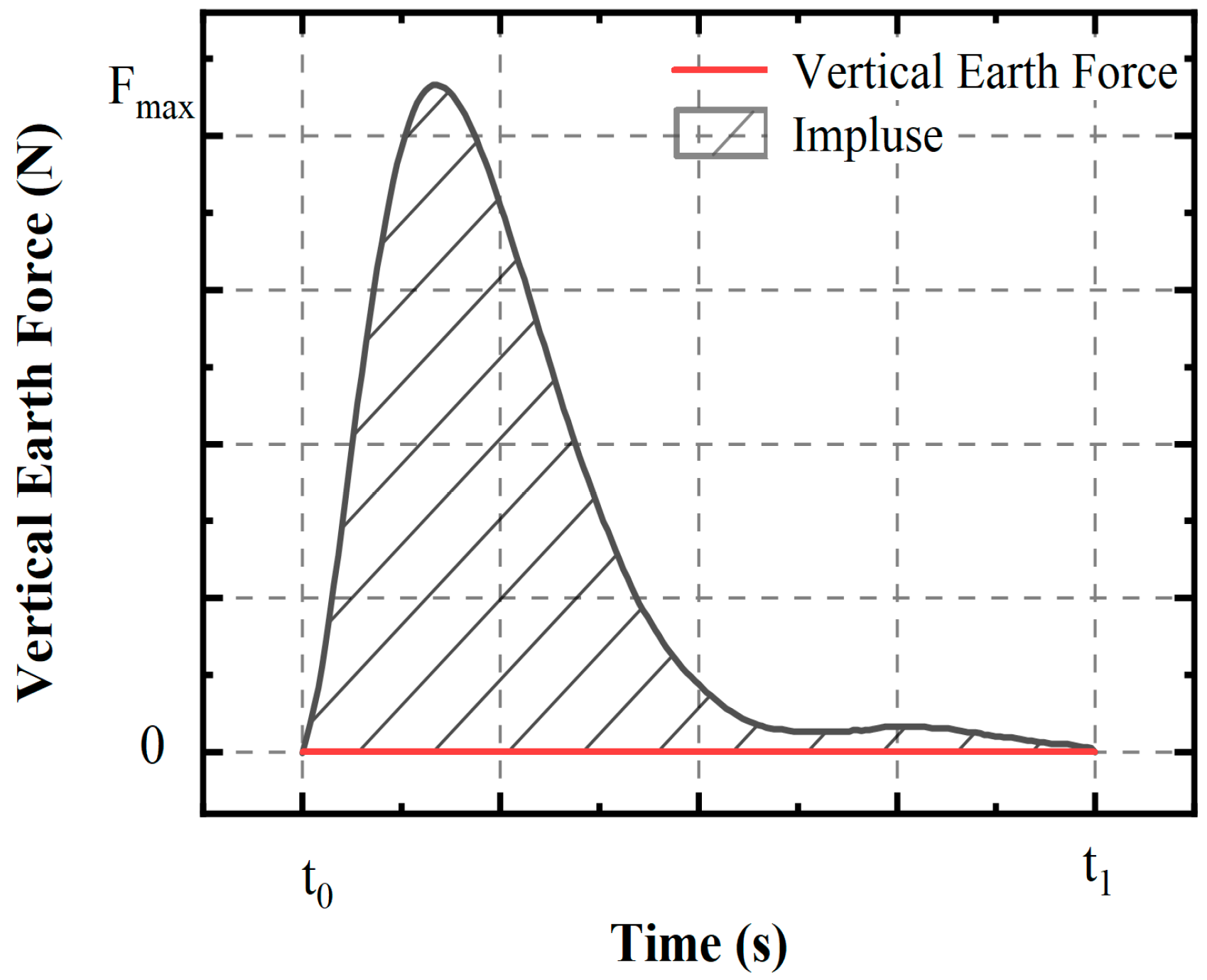
4.1. Energy Input Analysis
4.2. Energy Transfer Analysis
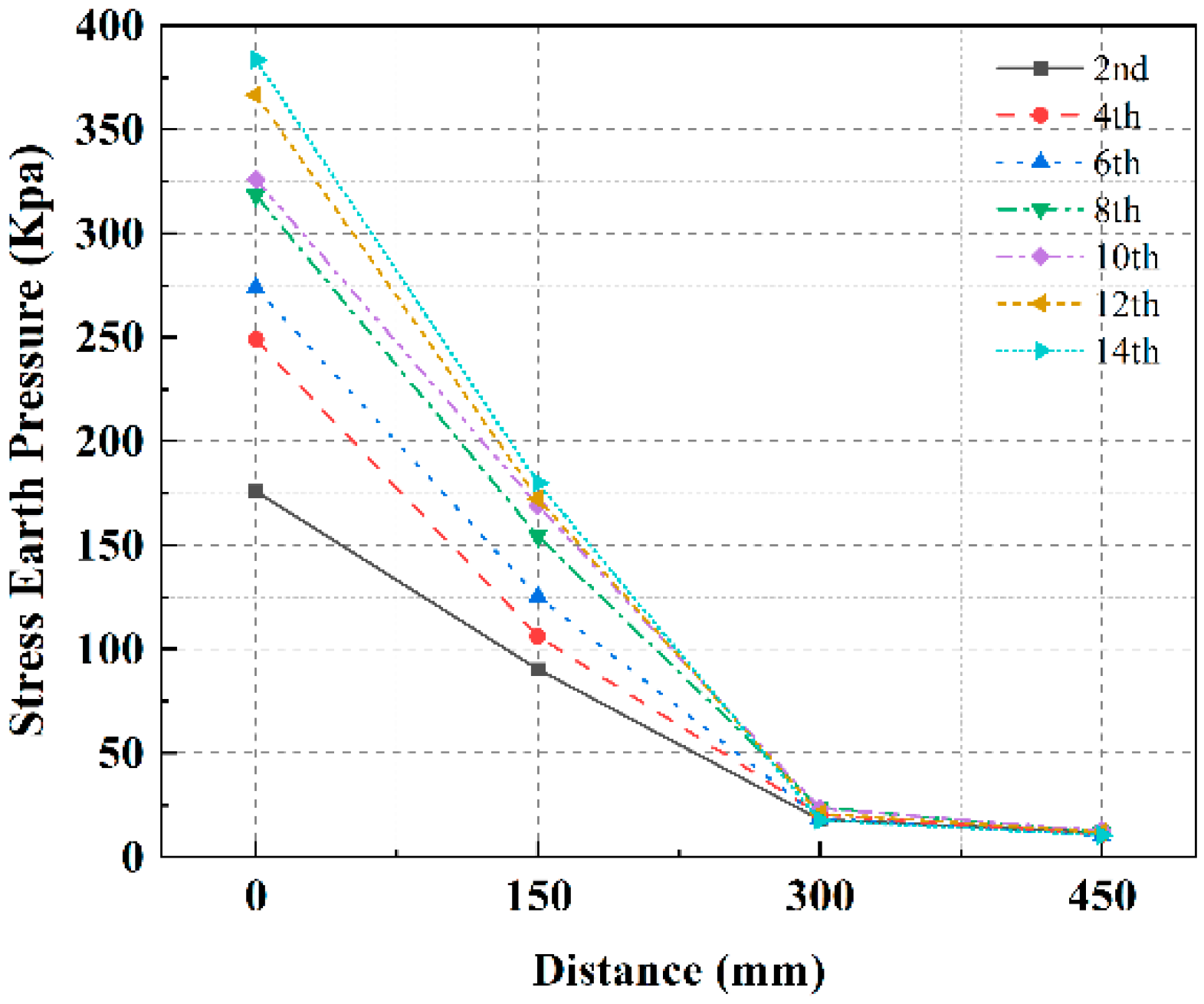
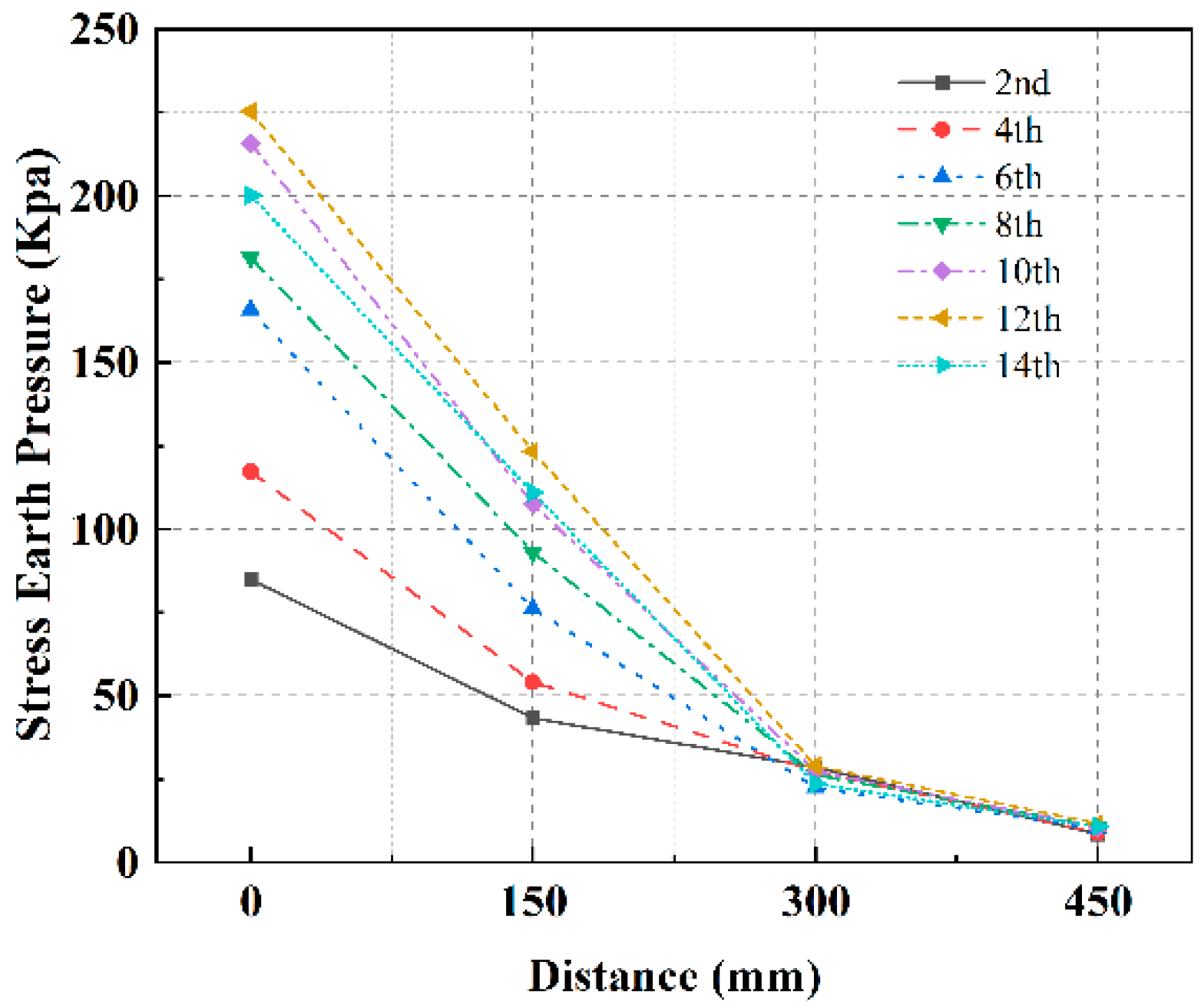
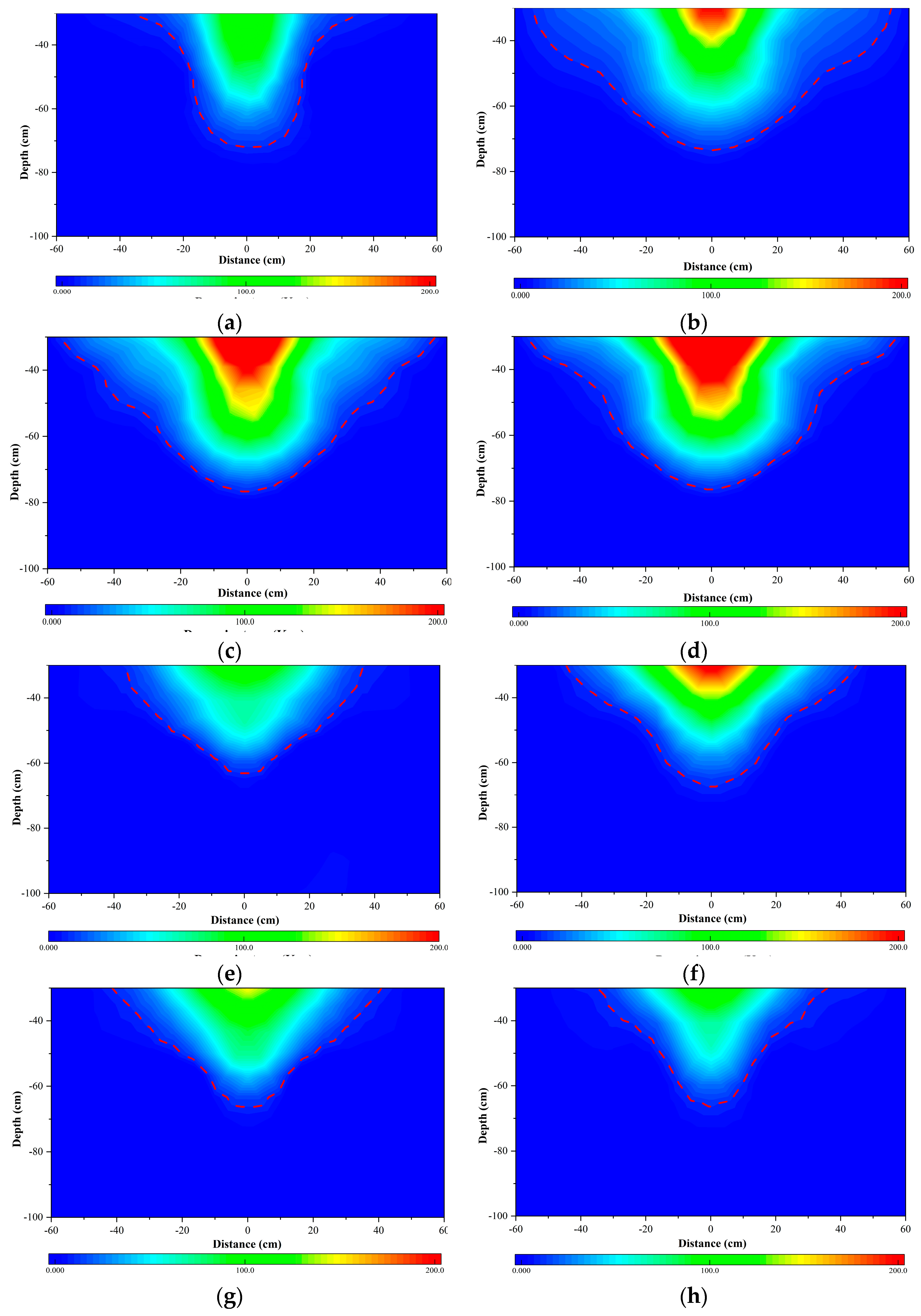
4.3. Spatial Distribution of the Dynamic Stress
5. Limitations
6. Conclusions
- Dynamic compaction has been demonstrated to be an effective method for reinforcing HGL subgrade. The dynamic stress waveform generated by DC was primarily manifested in shock stress waveforms and vibration damping waveforms. A more pronounced transverse effect was observed in HGL subgrade.
- The HGL functions as an obstacle to the energy transfer of DC, both in terms of energy input to the tamper and energy reception by the soil. Compared to the low-water level subgrade, the tamping action time was extended by an average of 1.96 times. The mean reduction in peak dynamic stresses in the DC-strengthened HGL subgrade was 33.05% and the depth of influence was reduced by 14.5%. Furthermore, the time lag and decay rate were observed to increase.
- The impulse was a more accurate representation of the actual energy transmitted to the soil. The loss of tamping impulse per unit of soil went up to 31.5% when the water level was higher than the tamping crater. Lowering the water level, increasing energy levels, and switching to heavy tampers can all significantly increase the impulse of energy received per unit of soil.
- In the construction of HGL subgrade reinforcement by DC, it is essential to comprehensively evaluate both the water level and the reinforcement effect. Increasing the tamper weight and energy level causes the groundwater level to rise more rapidly. To avoid dangerous situations, it is crucial to monitor the water level and adjust accordingly throughout the construction process. It is recommended that the single energy level tamping operation be abandoned in favor of a combination of light and heavy tamper construction methods with multiple rounds and fewer tamps each.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Han, J.; Jia, M.-C.; Lin, X. Laboratory model study on densification of hydraulically-filled fine sands by vibro-compaction. In Proceedings of the GeoCongress 2008: Geosustainability and Geohazard Mitigation New York: Geo-Institute of The American Society of Civil Engineers, New Orleans, LA, USA, 9–12 March 2008; pp. 700–707. [Google Scholar] [CrossRef]
- Bo, M.W.; Na, Y.M.; Arulrajah, A.; Chang, M.F. Densification of granular soil by dynamic compaction. Proc. Inst. Civ. Eng. Ground Improv. 2009, 162, 121–132. [Google Scholar] [CrossRef]
- Feng, S.-J.; Shui, W.-H.; Tan, K.; Gao, L.-Y.; He, L.-J. Field Evaluation of Dynamic Compaction on Granular Deposits. J. Perform. Constr. Facil. 2011, 25, 241–249. [Google Scholar] [CrossRef]
- Asaka, Y. Improvement of fine-grained reclaimed ground by dynamic compaction method. Jpn. Geotech. Soc. Spéc. Publ. 2016, 2, 2038–2042. [Google Scholar] [CrossRef]
- Ménard, L.; Broise, Y. Theoretical and practical aspect of dynamic consolidation. Géotechnique 1975, 25, 3–18. [Google Scholar] [CrossRef]
- Mayne, P.W.; Jones, J.J.S.; Dumas, J.C. Ground Response to Dynamic Compaction. J. Geotech. Eng. 1984, 110, 757–774. [Google Scholar] [CrossRef]
- Lutenegger, A.J. Dynamic compaction in friable loess. J. Geotech. Eng. 1986, 112, 663–667. [Google Scholar] [CrossRef]
- Thilakasiri, H.S.; Gunaratne, M.; Mullins, G.; Stinnette, P.; Jory, B. Investigation of impact stresses induced in laboratory dynamic compaction of soft soils. Int. J. Numer. Anal. Methods Geomech. 1996, 20, 753–767. [Google Scholar] [CrossRef]
- Oshima, A.; Takada, N.; Tanaka, Y. Relation between compacted area and ram momentum by heavy tamping. Doboku Gakkai Ronbunshu 1996, 1996, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Perucho, A.; Olalla, C. Dynamic consolidation of a saturated plastic clayey fill. Proc. Inst. Civ. Eng.—Ground Improv. 2006, 10, 55–68. [Google Scholar] [CrossRef]
- Rollins, K.M.; Kim, J. Dynamic Compaction of Collapsible Soils Based on U.S. Case Histories. J. Geotech. Geoenviron. 2010, 136, 1178–1186. [Google Scholar] [CrossRef]
- Mostafa, K.F.; Liang, R.Y. Numerical Modeling of Dynamic Compaction in Cohesive Soils; ASCE: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Dou, J.; Chen, J.; Wang, W. Method for Estimating the Degree of Improvement in Soil between Adjacent Tamping Locations under Dynamic Compaction. Int. J. Géoméch. 2019, 19, 04019134. [Google Scholar] [CrossRef]
- Kundu, S.; Viswanadham, B. Studies to evaluate the impact of tamper on the depth of improvement in dynamic compaction. Jpn. Geotech. Soc. Spéc. Publ. 2016, 2, 2033–2037. [Google Scholar] [CrossRef]
- El Shamy, U.; Zeghal, M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils. Soil Dyn. Earthq. Eng. 2007, 27, 712–729. [Google Scholar] [CrossRef]
- Devi Priyanka, D.; Rathi, D.; Kumar, G.K. Effect of Dynamic Loading on Properties of Saturated Sand. In Soil Dynamics and Earthquake Geotechnical Engineering: IGC 2016; Springer: Singapore, 2019; Volume 3, pp. 3–12. [Google Scholar] [CrossRef]
- Nashed, R.; Thevanayagam, S.; Martin, G.R. Dynamic compaction of saturated sands and silty sands: Design. Proc. Inst. Civ. Eng.-Ground Improv. 2009, 162, 81–92. [Google Scholar] [CrossRef]
- Martin, B.E.; Chen, W.; Song, B.; Akers, S.A. Moisture effects on the high strain-rate behavior of sand. Mech. Mater. 2009, 41, 786–798. [Google Scholar] [CrossRef]
- Zhang, H.B.; Li, C.; Wu, J.Q. Field Tests of Effects of Underground Water Level on Dynamic Consolidation. Highway 2015, 60, 14–19. [Google Scholar]
- Zhou, C.; Yao, K.; Rong, Y.; Lee, F.H.; Zhang, D.; Jiang, H.; Yang, C.; Yao, Z.; Chen, L. Numerical investigation on zone of improvement for dynamic compaction of sandy ground with high groundwater table. Acta Geotech. 2022, 18, 695–709. [Google Scholar] [CrossRef]
- Jia, M.; Cheng, J.; Liu, B.; Ma, G. Model tests of the influence of ground water level on dynamic compaction. Bull. Eng. Geol. Environ. 2021, 80, 3065–3078. [Google Scholar] [CrossRef]
- Kundu, S.; Viswanadham, B.V.S. Centrifuge Modeling and DIC of Dynamic Compaction on Sandy Soils with Shallow Water Table. J. Geotech. Geoenviron. Eng. 2021, 147, 04021037. [Google Scholar] [CrossRef]
- Poran, C.J.; Rodriguez, J.A. Design of dynamic compaction. Can. Geotech. J. 1992, 29, 796–802. [Google Scholar] [CrossRef]
- Didyk, R.P.; Masakovskii, E.A. Investigation of field of dynamic stresses with impulse loading. Int. Appl. Mech. 1999, 35, 170–174. [Google Scholar] [CrossRef]
- Niu, Z.; Lu, G.; Cheng, D. Dynamic Characteristics of Soils Subject to Impact Loadings. Acta Mech. Solida Sin. 2008, 21, 347–353. [Google Scholar] [CrossRef]
- Omidvar, M.; Iskander, M.; Bless, S. Stress-strain behavior of sand at high strain rates. Int. J. Impact Eng. 2012, 49, 192–213. [Google Scholar] [CrossRef]
- Yuan, H.-P.; Liu, M.; Li, W.; Wang, Y.-X. Dynamic Compaction Model Tests for the Characteristics of Red Clay Under equal Energy Level. Geotech. Geol. Eng. 2017, 36, 1873–1883. [Google Scholar] [CrossRef]
- Chow, Y.K.; Yong, D.M.; Yong, K.Y.; Lee, S.L. Dynamic Compaction Analysis. J. Geotech. Eng. 1992, 118, 1141–1157. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Ali, A.F.; Ahmed, B.A. Impact Induced Responses of Saturated and Dry Dense Sand. Int. J. Geotech. Earthq. Eng. 2018, 9, 63–85. [Google Scholar] [CrossRef]
- Westine, P.; Dodge, F.; Baker, W. Similarity Methods in Engineering Dynamics; Hayden Book Company: Indianapolis, IN, USA, 1973. [Google Scholar]
- GB/T50123-2019; Standard for Soil Method. The Ministry of Water Resources: Beijing, China, 2019.
- Li, Y.-X.; Airey, D.; Feng, W.-Q. Effectiveness of rolling dynamic compaction with a three-sided compactor on unsaturated sand. Transp. Geotech. 2023, 42, 101093. [Google Scholar] [CrossRef]






| Parameters | Energy Level | Tamper Weight | Tamper Diameter | Water Level (from Ground Level) | ||||
|---|---|---|---|---|---|---|---|---|
| Prototype (kN·m) | Model (N·m) | Prototype (t) | Model (kg) | Prototype (m) | Model (cm) | Prototype (m) | Model (mm) | |
| Numerical Value | 4000 | 192.9 | 20 | 11.58 | 2.52 | 21 | 1 | 83.33 |
| 8000 | 385.8 | 40 | 23.15 | 2.52 | 21 | 2 | 166.67 | |
| Soil | Poisson’s Ratio μ | C (Pa) | φ (°) | ρ (kg/m3) | ω (%) | Ip |
|---|---|---|---|---|---|---|
| Test sand | 0.3 | 2500 | 30 | 1780 | 13 | - |
| Original site soil | - | - | - | 1790 | 14.9 | 9.8 |
| Group | Categories | Tamping Energy (kN·m) | Tamper Weight (t) | Falling Height (m) | Diameter (m) | Water Level (m) |
|---|---|---|---|---|---|---|
| D1 | Group D | 4000 | 40 | 10 | 2.52 | none |
| D2 | 4000 | 20 | 20 | 2.52 | none | |
| D3 | 8000 | 40 | 20 | 2.52 | none | |
| W1 | Group W | 4000 | 40 | 10 | 2.52 | 2 |
| W2 | 4000 | 20 | 20 | 2.52 | 2 | |
| W3 | 4000 | 40 | 10 | 2.52 | 1 | |
| W4 | 8000 | 40 | 20 | 2.52 | 2 | |
| W5 | 8000 | 40 | 20 | 2.52 | 1 |
| Point Location | Group D | Group W | ||||
|---|---|---|---|---|---|---|
| 5% Trimmed Mean | Variance | Standard Deviation | 5% Trimmed Mean | Variance | Standard Deviation | |
| 1A–2A | 41.40% | 0.01 | 0.100 | 39.60% | 0.015 | 0.124 |
| 1B–2B | 53.90% | 0.015 | 0.124 | 56.30% | 0.014 | 0.120 |
| 1A–1B | 69.00% | 0.020 | 0.140 | 48.20% | 0.053 | 0.231 |
| 1B–1C | 68.30% | 0.026 | 0.160 | 73.70% | 0.012 | 0.112 |
| 2A–2B | 60.90% | 0.007 | 0.086 | 62.80% | 0.017 | 0.131 |
| 2B–2C | 81.40% | 0.002 | 0.046 | 64.60% | 0.027 | 0.163 |
| 3A–3B | 57.90% | 0.001 | 0.036 | 50.00% | 0.010 | 0.101 |
| 3B–3C | 40.40% | 0.002 | 0.041 | 47.20% | 0.007 | 0.081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Li, P.; Ge, X.; Wang, J.; Liu, Y.; Tian, S. Dynamic Compaction of High Groundwater Level Subgrade of Buildings: A Model Test-Based Analysis of Stress Distribution and Reinforcement Mechanisms. Buildings 2024, 14, 3090. https://doi.org/10.3390/buildings14103090
Sun J, Li P, Ge X, Wang J, Liu Y, Tian S. Dynamic Compaction of High Groundwater Level Subgrade of Buildings: A Model Test-Based Analysis of Stress Distribution and Reinforcement Mechanisms. Buildings. 2024; 14(10):3090. https://doi.org/10.3390/buildings14103090
Chicago/Turabian StyleSun, Jingyuan, Peixuan Li, Xinsheng Ge, Jingyue Wang, Yasheng Liu, and Shiyu Tian. 2024. "Dynamic Compaction of High Groundwater Level Subgrade of Buildings: A Model Test-Based Analysis of Stress Distribution and Reinforcement Mechanisms" Buildings 14, no. 10: 3090. https://doi.org/10.3390/buildings14103090
APA StyleSun, J., Li, P., Ge, X., Wang, J., Liu, Y., & Tian, S. (2024). Dynamic Compaction of High Groundwater Level Subgrade of Buildings: A Model Test-Based Analysis of Stress Distribution and Reinforcement Mechanisms. Buildings, 14(10), 3090. https://doi.org/10.3390/buildings14103090





