A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes
Abstract
:1. Introduction
2. Methodology
3. Building Envelope Thermal Transmittance
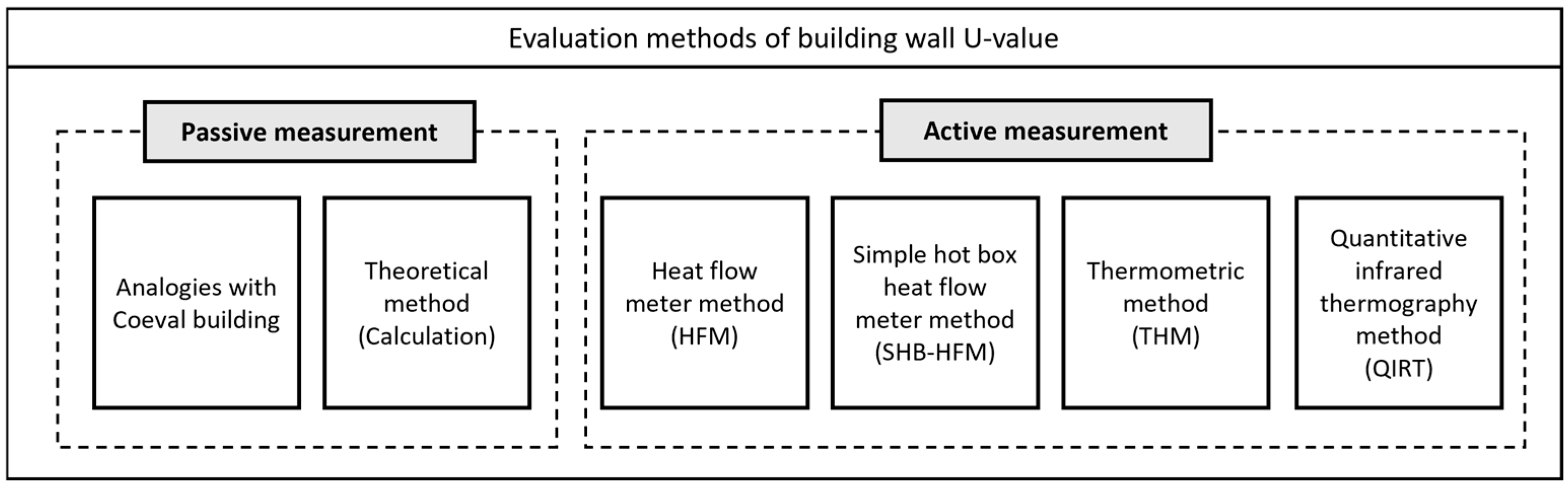
4. Passive Measurement (In-Office)
- Analogies with coeval buildings;
- Theoretical method (calculation).
4.1. Analogies with Coeval Buildings
4.2. Theoretical Method (Calculation)
5. Active Measurement (In Situ)
- Heat flow meter (HFM) method;
- Simple hot box–HFM (SHB-HFM) method;
- Thermometric (THM) method;
- Quantitative infrared thermography (QIRT) method.
5.1. Heat Flow Meter (HFM) Method
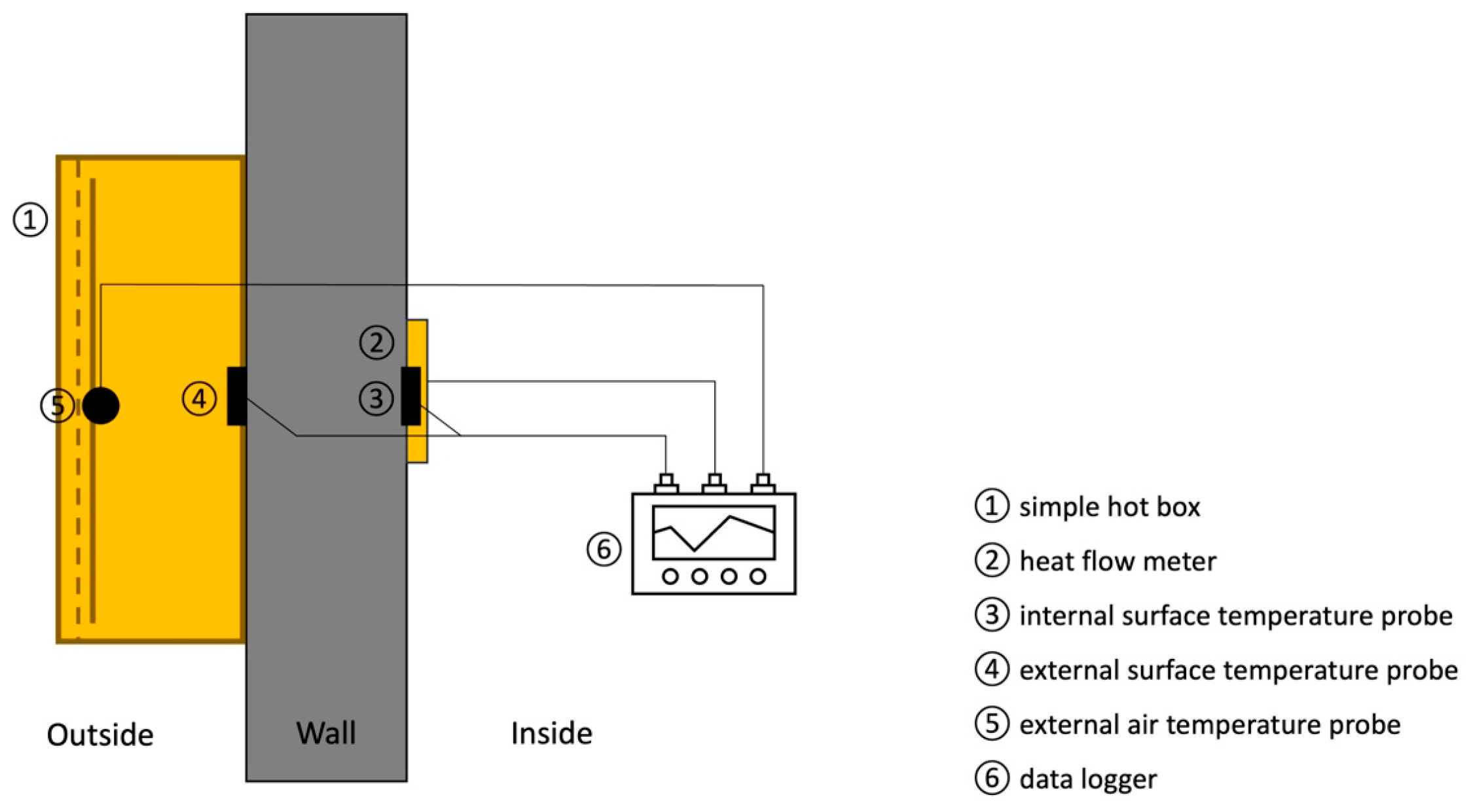
5.2. Simple Hot Box–HFM (SHB-HFM) Method
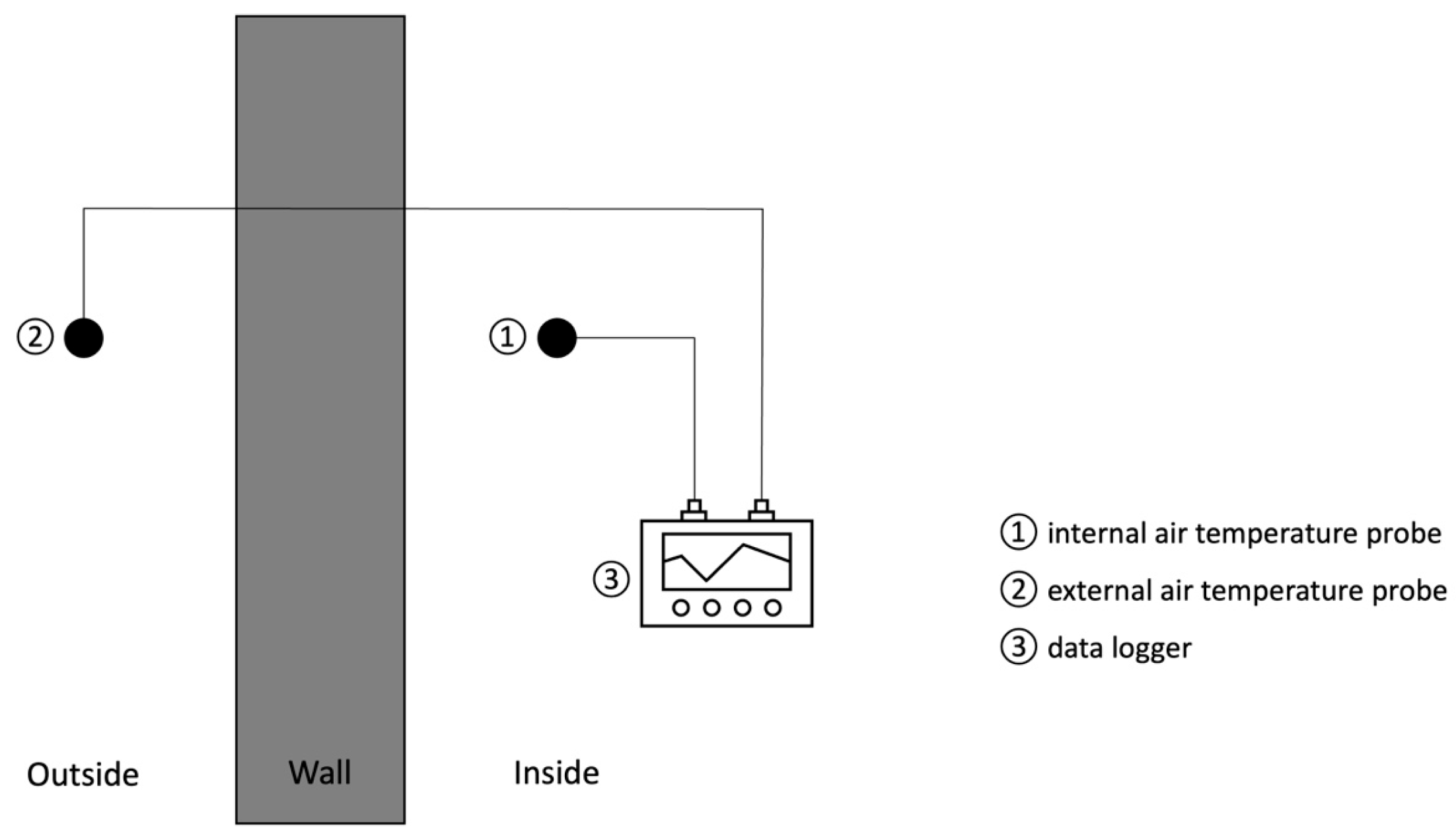
5.3. Thermometric (THM) Method
| Author (Year) | Measurement Method | Comparison Method | Deviation [%] | Test Period | Building Information |
|---|---|---|---|---|---|
| Andújar Márquez et al. (2017) [97] | THM method | HFM method | 2% | Summer and winter, 4 days | - |
| Bienvenido-Huertas et al. (2018) [94] | THM method | Theoretical method: ISO 6946 | Winter: 4–37% Summer:7–62% Autumn: 19–83% | Summer, winter, and autumn | Eight buildings from different architectural periods located in Seville and Cadiz, Spain |
| Kim et al. (2018) [95] | ASTR method | HFM method | 0.3–5% | November to December 2015 7–14 days | Four buildings located in South Korea, constructed in the late 20th century |
| Evangelisti et al. (2019) [100] | ASTR method | HFM method | 37.2~143.7% | Summer | Educational buildings in Italy from the 1960s |
| Evangelisti et al. (2022) [70] | THM method | Theoretical method: ISO 6946 | North: 0.5~32.4% North-west: 76.3~127.4% | January 2019, 4 days (north) April 2019, 7 days (north-west) | Educational buildings in Italy |
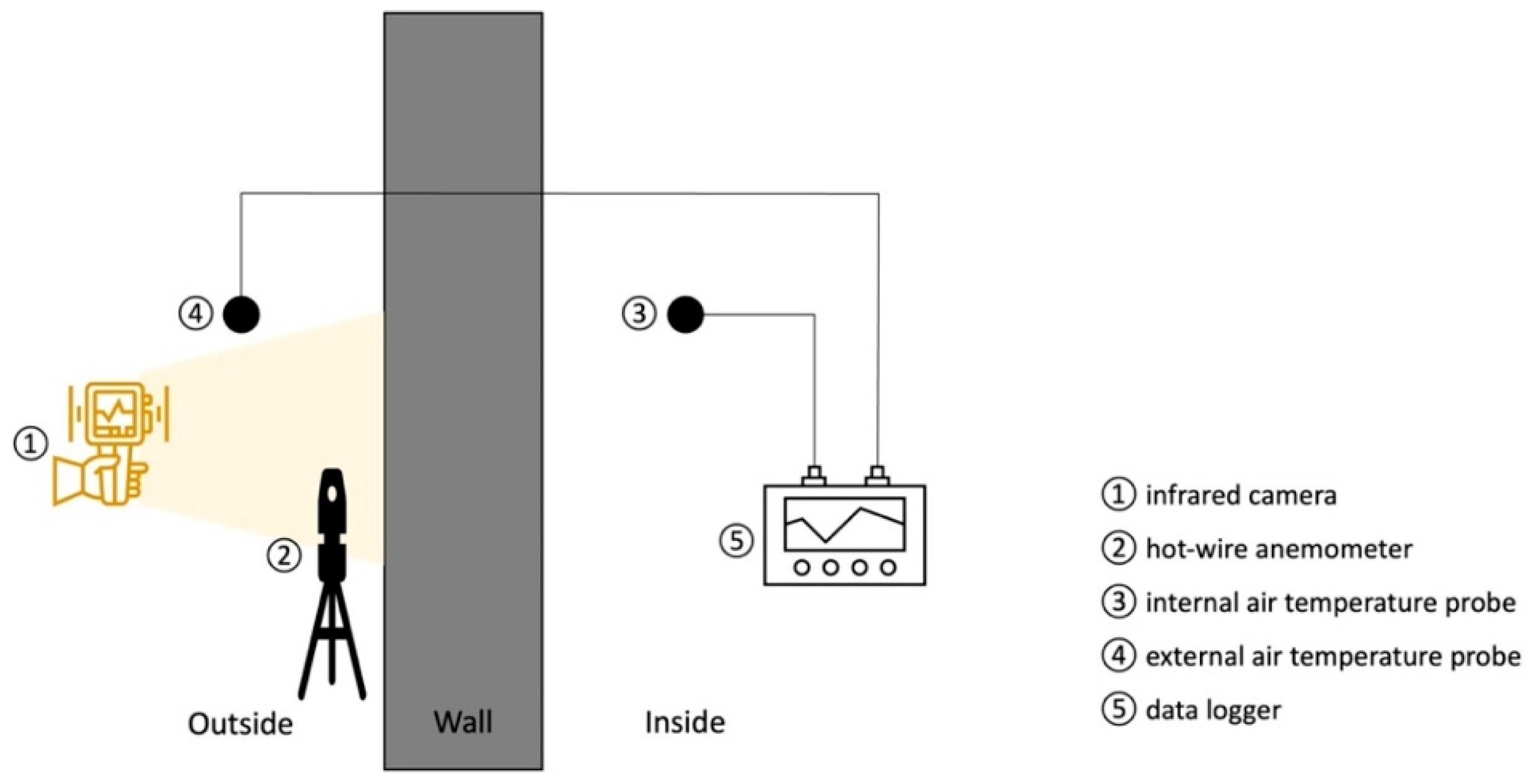
5.4. Quantitative Infrared Thermography (QIRT) Method
| Author (Year) | Measurement Method | Comparison Method | Deviation [%] | Test Period | Building Information |
|---|---|---|---|---|---|
| Dall’O et al. (2013) [123] | QIRT method | Theoretical method | 1.5–154%, average 36% | January 2013 | Fourteen buildings located in Milan, completed between 18,800 and 2009 |
| Tzifa et al. (2014) [103] | QIRT method | Theoretical method: ISO 6946 | Winter 2–68%, average 29% Summer 10–286%, average 97% | January to February 2011 | An educational building located in Athens, Greece |
| Albatici et al. (2015) [124] | QIRT method | Theoretical method: ISO 6946 | 0–43%, average 22% | November 2010 to March 2011 November 2011 to March 2012 November 2012 to March 2013 | Buildings in Italy specifically designed for research, featuring five types of walls |
| QIRT method | HFM method | 5–29%, average 19% | |||
| Nardi et al. (2015) [17] | QIRT method | Theoretical method: ISO 6946 | 4–46%, average 20% | 72–144 h | Buildings in Italy designed for three different purposes |
| QIRT method | HFM method | 1–48%, average 17% | |||
| Nardi et al. (2016) [121] | QIRT method: in a guarded hot box | Theoretical method: ISO 6946 | 0–96%, average 22% | February 2013 7–18 days | Walls reproducing typical 1970s Italian building stock |
| QIRT method: in a guarded hot box | HFM method | 0–77%, average 18% | |||
| Tejedor et al. (2017) [116] | QIRT method | Theoretical method: ISO 6946 | 4–20%, average 12% | January and February 2016 | Two typical types of Spanish walls from different periods |
| QIRT method | HFM method | 13–27%, average 20% | |||
| Tejedor et al. (2018) [125] | QIRT method | Theoretical method: ISO 6946 | 0.2–9%, average 4% | January to February 2017 | An educational building located in Spain |
| Choi and Ko (2017) [126] | QIRT method | Theoretical method: ISO 6946 | 7~44% | January to February 2016 27 days | Residential building in South Korea |
| Bienvenido-Huertas et al. (2019) [127] | QIRT method | Theoretical method: ISO 6946 | 0~150% | Scheduled date for the lowest external temperature | Most representative building in Spain |
| Milad Mahmoodzadeh et al. (2022) [128] | QIRT method | Theoretical method: ISO 6946 | 5.88~12.5% | Different days with varying exterior and interior conditions | Representative of low-rise Canadian west coast construction |
| Rodríguez et al. (2024) [129] | QIRT method | THM method | 4.3~29.1% | Summer and winter 3 days | Educational buildings in Spain built in 2001 |
| Zhang et al. (2024) [130] | QIRT method | HFM method-Average | 20~46% (case 1) 3~24% (case 2) | December 2020 | Residential buildings in Harbin built in 1985 (case 1) and 2014 (case 2) |
| QIRT method | HFM method-Dynamic | 18~45% (case 1) 3~24% (case 2) |
6. Discussion
7. Conclusions
- In situ measurements under summer conditions are limited, and existing seasonal constraints remain to be addressed.
- It is a necessity to provide a shorter test duration to enable more measurements to be performed in a given time.
- The limitations of the measurement time and orientation of the measurement wall were not overcome because field measurements were not performed under conditions affected by solar radiation.
- Most of the studies were conducted in indoor spaces, but further studies are needed on how to determine U-values through outdoor measurements.
- Analysis of factors affecting accuracy in U-value determination by the QIRT method outdoors.
- Development of field application of the QIRT method regardless of an unstable environment through in-depth AI analysis (e.g., seasonal impact, measurement time zone, or solar radiation effect by measurement orientation).
- Development of a rapid and accurate method of determining U-values by photographing the exterior wall using a drone equipped with a thermal imaging camera.
- Verification of field application accuracy of a combination of thermal imaging and drone-mounted cameras.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UN Environment Programme. 2021 Global Status Report for Buildings and Construction: Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector; UN Environment Programme: Nairobi, Kenya, 2021. [Google Scholar]
- Maierhofer, D.; Röck, M.; Saade, M.R.M.; Hoxha, E.; Passer, A. Critical life cycle assessment of the innovative passive nZEB building concept ‘be 2226’ in view of net-zero carbon targets. Build. Environ. 2022, 223, 109476. [Google Scholar] [CrossRef]
- Ebel, R.E.; Croissant, M.P.; Masih, J.R.; Calder, K.E.; Thomas, R.G. International energy outlook: US department of energy. Wash. Q. 1996, 19, 70–99. [Google Scholar] [CrossRef]
- Lucon, O.; Ürge-Vorsatz, D.; Ahmed, A.; Akbari, H.; Bertoldi, P.; Cabeza, L.; Eyre, N.; Gadgil, A.; Harvey, L.; Jiang, Y. Buildings Climate Change 2014: Mitigation of Climate Change IPCC Working Group III Contribution to AR5; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zhang, Y.; Bai, X.; Mills, F.P.; Pezzey, J.C. Rethinking the role of occupant behavior in building energy performance: A review. Energy Build. 2018, 172, 279–294. [Google Scholar] [CrossRef]
- Asif, M. Growth and sustainability trends in the buildings sector in the GCC region with particular reference to the KSA and UAE. Renew. Sustain. Energy Rev. 2016, 55, 1267–1273. [Google Scholar] [CrossRef]
- Coates, G.J. The sustainable urban district of Vauban in Freiburg, Germany. Int. J. Des. Nat. Ecodynamics 2013, 8, 265–286. [Google Scholar] [CrossRef]
- Ismail, A.M.; Ramirez-Iniguez, R.; Asif, M.; Munir, A.B.; Muhammad-Sukki, F. Progress of solar photovoltaic in ASEAN countries: A review. Renew. Sustain. Energy Rev. 2015, 48, 399–412. [Google Scholar] [CrossRef]
- Scarlat, N.; Dallemand, J.-F.; Monforti-Ferrario, F.; Banja, M.; Motola, V. Renewable energy policy framework and bioenergy contribution in the European Union—An overview from National Renewable Energy Action Plans and Progress Reports. Renew. Sustain. Energy Rev. 2015, 51, 969–985. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Quantum computing and quantum artificial intelligence for renewable and sustainable energy: A emerging prospect towards climate neutrality. Renew. Sustain. Energy Rev. 2022, 165, 112493. [Google Scholar] [CrossRef]
- Iwaro, J.; Mwasha, A. The impact of sustainable building envelope design on building sustainability using Integrated Performance Model. Int. J. Sustain. Built Environ. 2013, 2, 153–171. [Google Scholar] [CrossRef]
- Harish, V.; Kumar, A. A review on modeling and simulation of building energy systems. Renew. Sustain. Energy Rev. 2016, 56, 1272–1292. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, L.; Bozlar, M.; Liu, Z.; Guo, H.; Meggers, F. Active building envelope systems toward renewable and sustainable energy. Renew. Sustain. Energy Rev. 2019, 104, 470–491. [Google Scholar] [CrossRef]
- LaFrance, M. Technology Roadmap: Energy Efficient Building Envelopes; IEA: Paris, France, 2013. [Google Scholar]
- Desogus, G.; Mura, S.; Ricciu, R. Comparing different approaches to in situ measurement of building components thermal resistance. Energy Build. 2011, 43, 2613–2620. [Google Scholar] [CrossRef]
- Ficco, G.; Iannetta, F.; Ianniello, E.; Alfano, F.R.d.A.; Dell’Isola, M. U-value in situ measurement for energy diagnosis of existing buildings. Energy Build. 2015, 104, 108–121. [Google Scholar] [CrossRef]
- Nardi, I.; Ambrosini, D.; De Rubeis, T.; Sfarra, S.; Perilli, S.; Pasqualoni, G. A comparison between thermographic and flow-meter methods for the evaluation of thermal transmittance of different wall constructions. J. Phys. Conf. Ser. 2015, 655, 012007. [Google Scholar] [CrossRef]
- Zheng, K.; Cho, Y.K.; Wang, C.; Li, H. Noninvasive Residential Building Envelope R-Value Measurement Method Based on Interfacial Thermal Resistance. J. Archit. Eng. 2016, 22, A4015002. [Google Scholar] [CrossRef]
- Kirimtat, A.; Krejcar, O. A review of infrared thermography for the investigation of building envelopes: Advances and prospects. Energy Build. 2018, 176, 390–406. [Google Scholar] [CrossRef]
- Lucchi, E. Applications of the infrared thermography in the energy audit of buildings: A review. Renew. Sustain. Energy Rev. 2018, 82, 3077–3090. [Google Scholar] [CrossRef]
- Tardy, F. A review of the use of infrared thermography in building envelope thermal property characterization studies. J. Build. Eng. 2023, 75, 106918. [Google Scholar] [CrossRef]
- Teni, M.; Krstić, H.; Kosiński, P. Review and comparison of current experimental approaches for in-situ measurements of building walls thermal transmittance. Energy Build. 2019, 203, 109417. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Moyano, J.; Marín, D.; Fresco-Contreras, R. Review of in situ methods for assessing the thermal transmittance of walls. Renew. Sustain. Energy Rev. 2019, 102, 356–371. [Google Scholar] [CrossRef]
- ISO 7345; Thermal Performance of Buildings and Building Components—Physical Quantities and Definitions. ISO: Geneva, Switzerland, 2018. Available online: https://cdn.standards.iteh.ai/samples/65000/62f3bede7e394297acf7484026c7d505/ISO-7345-2018.pdf (accessed on 5 May 2024).
- ISO 6946:2017; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. European Committee for Standardization: Brussels, Belgium, 2017.
- ASHRAE. ASHRAE Terminology. Available online: https://terminology.ashrae.org/ (accessed on 5 May 2024).
- Snow, D.A. Plant Engineer’s Reference Book; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Muresan, A.A.; Attia, S. Energy efficiency in the Romanian residential building stock: A literature review. Renew. Sustain. Energy Rev. 2017, 74, 349–363. [Google Scholar] [CrossRef]
- Economidou, M.; Atanasiu, B.; Despret, C.; Maio, J.; Nolte, I.; Rapf, O.; Laustsen, J.; Ruyssevelt, P.; Staniaszek, D.; Strong, D. Europe’s buildings under the microscope. In A Country-by-Country Review of the Energy Performance of Buildings; BPIE: Siromanipur, India, 2011. [Google Scholar]
- Ascione, F.; Bianco, N.; De Masi, R.F.; Mauro, G.M.; Musto, M.; Vanoli, G.P. Experimental validation of a numerical code by thin film heat flux sensors for the resolution of thermal bridges in dynamic conditions. Appl. Energy 2014, 124, 213–222. [Google Scholar] [CrossRef]
- Ascione, F.; Ceroni, F.; De Masi, R.F.; de’Rossi, F.; Pecce, M.R. Historical buildings: Multidisciplinary approach to structural/energy diagnosis and performance assessment. Appl. Energy 2017, 185, 1517–1528. [Google Scholar] [CrossRef]
- Nardi, I.; Lucchi, E.; de Rubeis, T.; Ambrosini, D. Quantification of heat energy losses through the building envelope: A state-of-the-art analysis with critical and comprehensive review on infrared thermography. Build. Environ. 2018, 146, 190–205. [Google Scholar] [CrossRef]
- Li, X.; Yao, R.; Liu, M.; Costanzo, V.; Yu, W.; Wang, W.; Short, A.; Li, B. Developing urban residential reference buildings using clustering analysis of satellite images. Energy Build. 2018, 169, 417–429. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; O’Donnell, J.; Finn, D.P. Identification of representative buildings and building groups in urban datasets using a novel pre-processing, classification, clustering and predictive modelling approach. Build. Environ. 2018, 140, 90–106. [Google Scholar] [CrossRef]
- Cesaratto, P.G.; De Carli, M. A measuring campaign of thermal conductance in situ and possible impacts on net energy demand in buildings. Energy Build. 2013, 59, 29–36. [Google Scholar] [CrossRef]
- Aksoezen, M.; Daniel, M.; Hassler, U.; Kohler, N. Building age as an indicator for energy consumption. Energy Build. 2015, 87, 74–86. [Google Scholar] [CrossRef]
- Ballarini, I.; Corgnati, S.P.; Corrado, V. Use of reference buildings to assess the energy saving potentials of the residential building stock: The experience of TABULA project. Energy Policy 2014, 68, 273–284. [Google Scholar] [CrossRef]
- TABULA Database. Available online: https://episcope.eu/welcome (accessed on 24 February 2024).
- Basaglia, A.; Cianchino, G.; Cocco, G.; Rapone, D.; Terrenzi, M.; Spacone, E.; Brando, G. An automatic procedure for deriving building portfolios using the Italian “CARTIS” online database. Structures 2021, 34, 2974–2986. [Google Scholar] [CrossRef]
- Wardhana, K.; Hadipriono, F.C. Study of recent building failures in the United States. J. Perform. Constr. Facil. 2003, 17, 151–158. [Google Scholar] [CrossRef]
- Lucchi, E. Thermal transmittance of historical stone masonries: A comparison among standard, calculated and measured data. Energy Build. 2017, 151, 393–405. [Google Scholar] [CrossRef]
- Lucchi, E. Thermal transmittance of historical brick masonries: A comparison among standard data, analytical calculation procedures, and in situ heat flow meter measurements. Energy Build. 2017, 134, 171–184. [Google Scholar] [CrossRef]
- Siviour, J. Experimental U-values of some house walls. Build. Serv. Eng. Res. Technol. 1994, 15, 35–36. [Google Scholar] [CrossRef]
- Lucchi, E. Diagnosi Energetica Strumentale Degli Edifici; Dario Flaccovio Editore: Palermo, Italy, 2012. [Google Scholar]
- Xu, Y.; Sun, D.a.; Zeng, Z.; Lv, H. Effect of aging on thermal conductivity of compacted bentonites. Eng. Geol. 2019, 253, 55–63. [Google Scholar] [CrossRef]
- Pontinha, A.D.R.; Mäntyneva, J.; Santos, P.; Durães, L. Thermomechanical performance assessment of sustainable buildings’ insulating materials under accelerated ageing conditions. Gels 2023, 9, 241. [Google Scholar] [CrossRef]
- Villarejo, P.; Gámez, R.; Santamaría-López, Á. Building renovation passports in Spain: Integrating exiting instruments for building conservation, renovation and heritage protection. Energy Policy 2021, 157, 112506. [Google Scholar] [CrossRef]
- Jensen, P.A.; Maslesa, E. Value based building renovation–A tool for decision-making and evaluation. Build. Environ. 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Nardi, I.; Lucchi, E. In Situ Thermal Transmittance Assessment of the Building Envelope: Practical Advice and Outlooks for Standard and Innovative Procedures. Energies 2023, 16, 3319. [Google Scholar] [CrossRef]
- Asdrubali, F.; D’Alessandro, F.; Baldinelli, G.; Bianchi, F. Evaluating in situ thermal transmittance of green buildings masonries—A case study. Case Stud. Constr. Mater. 2014, 1, 53–59. [Google Scholar] [CrossRef]
- Pérez-Bella, J.M.; Dominguez-Hernandez, J.; Cano-Sunen, E.; del Coz-Diaz, J.J.; Rabanal, F.P.A. A correction factor to approximate the design thermal conductivity of building materials. Application to Spanish façades. Energy Build. 2015, 88, 153–164. [Google Scholar] [CrossRef]
- ISO 10456; Building Materials and Products—Hygrothermal Properties—Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values. International Organization for Standardization: Geneva, Switzerland, 2007.
- Rodríguez-Soria, B.; Domínguez-Hernández, J.; Pérez-Bella, J.M.; del Coz-Díaz, J.J. Review of international regulations governing the thermal insulation requirements of residential buildings and the harmonization of envelope energy loss. Renew. Sustain. Energy Rev. 2014, 34, 78–90. [Google Scholar] [CrossRef]
- ISO 9869:1994; Thermal Insulation: Building Elements: In-Situ Measurement of Thermal Resistance and Thermal Transmittance. ISO: Geneva, Switzerland, 1994.
- ISO 9869-1:2014; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance: Isolation Thermique—Éléments de Construction—Mesurage In Situ de la Résistance Thermique et du Coefficient de Transmission Thermique. Heat Flow Meter Method. Méthode Du Fluxmètre. ISO: Geneva, Switzerland, 2014.
- Aittomäki, A. Determination of the Overall Heat Transfer Coefficient of Multilayer Structures under Non-Steady-State Conditions; CIB Session Working paper; CIB: Hongkong, China, 1972. [Google Scholar]
- Roulet, C.; Gass, J.; Marcus, I. In-situ U-value measurement: Reliable results in shorter time by dynamic interpretation of measured data. ASHRAE Trans 1987, 108, 1371–1379. [Google Scholar]
- Anderlind, G. Multiple regression analysis of in situ thermal measurements—Study of an attic insulated with 800 mm loose fill insulation. J. Therm. Insul. Build. Envel. 1992, 16, 81–104. [Google Scholar] [CrossRef]
- Norlén, U. Estimating thermal parameters of outdoor test cells. Build. Environ. 1990, 25, 17–24. [Google Scholar] [CrossRef]
- Jiménez, M.J.; Madsen, H.; Andersen, K.K. Identification of the main thermal characteristics of building components using MATLAB. Build. Environ. 2008, 43, 170–180. [Google Scholar] [CrossRef]
- Jiménez, M.; Porcar, B.; Heras, M. Application of different dynamic analysis approaches to the estimation of the building component U value. Build. Environ. 2009, 44, 361–367. [Google Scholar] [CrossRef]
- Gutschker, O. Parameter identification with the software package LORD. Build. Environ. 2008, 43, 163–169. [Google Scholar] [CrossRef]
- Baker, P.H.; Van Dijk, H. PASLINK and dynamic outdoor testing of building components. Build. Environ. 2008, 43, 143–151. [Google Scholar] [CrossRef]
- Naveros, I.; Bacher, P.; Ruiz, D.; Jiménez, M.; Madsen, H. Setting up and validating a complex model for a simple homogeneous wall. Energy Build. 2014, 70, 303–317. [Google Scholar] [CrossRef]
- Walker, R.; Pavía, S. Thermal performance of a selection of insulation materials suitable for historic buildings. Build. Environ. 2015, 94, 155–165. [Google Scholar] [CrossRef]
- Bros-Williamson, J.; Garnier, C.; Currie, J.I. A longitudinal building fabric and energy performance analysis of two homes built to different energy principles. Energy Build. 2016, 130, 578–591. [Google Scholar] [CrossRef]
- Gori, V.; Elwell, C.A. Estimation of thermophysical properties from in-situ measurements in all seasons: Quantifying and reducing errors using dynamic grey-box methods. Energy Build. 2018, 167, 290–300. [Google Scholar] [CrossRef]
- Ahmad, A.; Maslehuddin, M.; Al-Hadhrami, L.M. In situ measurement of thermal transmittance and thermal resistance of hollow reinforced precast concrete walls. Energy Build. 2014, 84, 132–141. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Vollaro, R.D.L.; Asdrubali, F. A methodological approach for heat-flow meter data post-processing under different climatic conditions and wall orientations. Energy Build. 2020, 223, 110216. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Fontana, L.; Vollaro, R.D.L.; Asdrubali, F. On the ageing and weathering effects in assembled modular facades: On-site experimental measurements in an Italian building of the 1960s. J. Build. Eng. 2022, 45, 103519. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. A comparison of standardized calculation methods for in situ measurements of façades U-value. Energy Build. 2016, 130, 592–599. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Kinnane, O.; Lennon, D.; Colclough, S. In-situ U-value monitoring of highly insulated building envelopes: Review and experimental investigation. Energy Build. 2021, 252, 111447. [Google Scholar] [CrossRef]
- Choi, D.-S.; Lee, Y.-J.; Moon, J.-H.; Kim, Y.-S.; Ko, M.-J. Estimating in-situ R-value of highly insulated building walls based on the measurement of temperature and heat flux inside the wall. Energies 2023, 16, 5714. [Google Scholar] [CrossRef]
- Suh, W.D.; Yuk, H.; Park, J.H.; Jo, H.H.; Kim, S. Sustainable use of historic campus buildings: Retrofit technology to improve building energy performance considering preservation of interior finishing material. Energy Build. 2024, 320, 114620. [Google Scholar]
- Deconinck, A.-H.; Roels, S. Comparison of characterisation methods determining the thermal resistance of building components from onsite measurements. Energy Build. 2016, 130, 309–320. [Google Scholar] [CrossRef]
- Naveros, I.; Ghiaus, C.; Ruíz, D.; Castaño, S. Physical parameters identification of walls using ARX models obtained by deduction. Energy Build. 2015, 108, 317–329. [Google Scholar] [CrossRef]
- Biddulph, P.; Gori, V.; Elwell, C.A.; Scott, C.; Rye, C.; Lowe, R.; Oreszczyn, T. Inferring the thermal resistance and effective thermal mass of a wall using frequent temperature and heat flux measurements. Energy Build. 2014, 78, 10–16. [Google Scholar] [CrossRef]
- Gori, V.; Marincioni, V.; Biddulph, P.; Elwell, C.A. Inferring the thermal resistance and effective thermal mass distribution of a wall from in situ measurements to characterise heat transfer at both the interior and exterior surfaces. Energy Build. 2017, 135, 398–409. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. Review of criteria for determining HFM minimum test duration. Energy Build. 2018, 176, 360–370. [Google Scholar] [CrossRef]
- Hoffmann, C.; Geissler, A. The prebound-effect in detail: Real indoor temperatures in basements and measured versus calculated U-values. Energy Procedia 2017, 122, 32–37. [Google Scholar] [CrossRef]
- Atsonios, I.A.; Mandilaras, I.D.; Kontogeorgos, D.A.; Founti, M.A. A comparative assessment of the standardized methods for the in-situ measurement of the thermal resistance of building walls. Energy Build. 2017, 154, 198–206. [Google Scholar] [CrossRef]
- Tadeu, A.; Simoes, N.; Simões, I.; Pedro, F.; Škerget, L. In-situ thermal resistance evaluation of walls using an iterative dynamic model. Numer. Heat Transf. Part A Appl. 2015, 67, 33–51. [Google Scholar] [CrossRef]
- Cesaratto, P.G.; De Carli, M.; Marinetti, S. Effect of different parameters on the in situ thermal conductance evaluation. Energy Build. 2011, 43, 1792–1801. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. Influence of HFM thermal contact on the accuracy of in situ measurements of façades’ U-value in operational stage. Appl. Sci. 2021, 11, 979. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Moon, J.-H.; Choi, D.-S.; Ko, M.-J. Application of the Heat Flow Meter Method and Extended Average Method to Improve the Accuracy of In Situ U-Value Estimations of Highly Insulated Building Walls. Sustainability 2024, 16, 5687. [Google Scholar] [CrossRef]
- Tian, S. Study on In-Situ Measurement Method of Heat Transfer Coefficient of Building Envelop. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2006. [Google Scholar]
- Pan, L.; Chen, B.; Fang, Z.; Han, B.; Zhen, Y. Measurement of thermal resistance of building enclosures by means of the heat box method, Build. Energy Environ. 2005, 2, 74–77. [Google Scholar]
- Pan, L.; Chen, B.; Fang, Z.; Zhen, Y. Field measurement and data processing method of envelope’s thermal resistance, Build. Energy Environ. 2005, 6, e84. [Google Scholar]
- Zhu, X.; Li, L.; Yin, X.; Zhang, S.; Wang, Y.; Liu, W.; Zheng, L. An in-situ test apparatus of heat transfer coefficient for building envelope. Build. Energy Effic. 2012, 256, 57–60. [Google Scholar]
- Meng, X.; Gao, Y.; Wang, Y.; Yan, B.; Zhang, W.; Long, E. Feasibility experiment on the simple hot box-heat flow meter method and the optimization based on simulation reproduction. Appl. Therm. Eng. 2015, 83, 48–56. [Google Scholar] [CrossRef]
- Meng, X.; Luo, T.; Gao, Y.; Zhang, L.; Shen, Q.; Long, E. A new simple method to measure wall thermal transmittance in situ and its adaptability analysis. Appl. Therm. Eng. 2017, 122, 747–757. [Google Scholar] [CrossRef]
- Roque, E.; Vicente, R.; Almeida, R.M.; da Silva, J.M.; Ferreira, A.V. Thermal characterisation of traditional wall solution of built heritage using the simple hot box-heat flow meter method: In situ measurements and numerical simulation. Appl. Therm. Eng. 2020, 169, 114935. [Google Scholar] [CrossRef]
- Nicoletti, F.; Cucumo, M.A.; Arcuri, N. Evaluating the accuracy of in-situ methods for measuring wall thermal conductance: A comparative numerical study. Energy Build. 2023, 290, 113095. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Rodríguez-Álvaro, R.; Moyano, J.J.; Rico, F.; Marín, D. Determining the U-value of façades using the thermometric method: Potentials and limitations. Energies 2018, 11, 360. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, J.-H.; Jeong, H.-G.; Song, K.-D. Reliability field test of the air–surface temperature ratio method for in situ measurement of U-values. Energies 2018, 11, 803. [Google Scholar] [CrossRef]
- Cengel, A. Heat Transfer; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Andújar Márquez, J.M.; Martínez Bohórquez, M.Á.; Gómez Melgar, S. A new metre for cheap, quick, reliable and simple thermal transmittance (U-Value) measurements in buildings. Sensors 2017, 17, 2017. [Google Scholar] [CrossRef] [PubMed]
- Buzatu, G.-C.; Stan-Ivan, F.-E.; Mircea, P.-M.; Manescu, L.-G. Thermal transmittance determination for different components of buildings. In Proceedings of the 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & 2017 Intl Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Brasov, Romania, 25–27 May 2017; pp. 227–232. [Google Scholar]
- ISO 9869-2:2018; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 2: Infrared Method for Frame Structure Dwelling. ISO: Geneva, Switzerland, 2018.
- Evangelisti, L.; Guattari, C.; Asdrubali, F. Comparison between heat-flow meter and Air-Surface Temperature Ratio techniques for assembled panels thermal characterization. Energy Build. 2019, 203, 109441. [Google Scholar] [CrossRef]
- Kato, S.; Kuroki, K.; Hagihara, S. Method of in-situ measurement of thermal insulation performance of building elements using infrared camera. In Proceedings of the 6th International Conference on Indoor Air Quality, Ventilation & Energy Conservation in Buildings-IAQVEC, Sendai, Japan, 28–31 October 2007. [Google Scholar]
- Albatici, R.; Tonelli, A. On site evaluation of U-value of opaque building elements: A new methodology. In Towards Zero Energy Buildings; University College Dublin: Dublin, Ireland, 2008; pp. 1–8. [Google Scholar]
- Tzifa, V.; Papadakos, G.; Papadopoulou, A.G.; Marinakis, V.; Psarras, J. Uncertainty and method limitations in a short-time measurement of the effective thermal transmittance on a building envelope using an infrared camera. Int. J. Sustain. Energy 2017, 36, 28–46. [Google Scholar] [CrossRef]
- Madding, R. Finding R-values of stud frame constructed houses with IR thermography. Proc. InfraMation 2008, 2008, 261–277. [Google Scholar]
- Gonçalves, M.D. Commissioning of exterior building envelopes of large buildings for air leakage and thermal anomalies using infrared thermography and other diagnostic tools. In Proceedings of the Workshop on Building and Ductwork Airtightness Design, Implementation, Control and Durability: Feedback from Practice and Perspectives, Washington, DC, USA, 18–19 April 2013. [Google Scholar]
- Kilic, G. Using advanced NDT for historic buildings: Towards an integrated multidisciplinary health assessment strategy. J. Cult. Herit. 2015, 16, 526–535. [Google Scholar] [CrossRef]
- Kominsky, J.; Luckino, J.; Martin, T. Passive Infrared Thermography—A Qualitative Method for Detecting Moisture Anomalies in Building Envelopes; Tedford & Pond: Hartford, CT, USA, 2007; pp. 1–11. [Google Scholar]
- Barreira, E.; Almeida, R.; Delgado, J. Infrared thermography for assessing moisture related phenomena in building components. Constr. Build. Mater. 2016, 110, 251–269. [Google Scholar] [CrossRef]
- Grinzato, E.; Bison, P.G.; Marinetti, S. Monitoring of ancient buildings by the thermal method. J. Cult. Herit. 2002, 3, 21–29. [Google Scholar] [CrossRef]
- Taylor, T.; Counsell, J.; Gill, S. Energy efficiency is more than skin deep: Improving construction quality control in new-build housing using thermography. Energy Build. 2013, 66, 222–231. [Google Scholar] [CrossRef]
- Hopper, J.; Littlewood, J.R.; Taylor, T.; Counsell, J.A.; Thomas, A.M.; Karani, G.; Geens, A.; Evans, N.I. Assessing retrofitted external wall insulation using infrared thermography. Struct. Surv. 2012, 30, 245–266. [Google Scholar] [CrossRef]
- Taileb, A.; Dekkiche, H. Infrared imaging as a means of analyzing and improving energy efficiency of building envelopes: The case of a LEED gold building. Procedia Eng. 2015, 118, 639–646. [Google Scholar] [CrossRef]
- Kalamees, T. Air tightness and air leakages of new lightweight single-family detached houses in Estonia. Build. Environ. 2007, 42, 2369–2377. [Google Scholar] [CrossRef]
- Lerma, C.; Barreira, E.; Almeida, R.M. A discussion concerning active infrared thermography in the evaluation of buildings air infiltration. Energy Build. 2018, 168, 56–66. [Google Scholar] [CrossRef]
- Kylili, A.; Fokaides, P.A.; Christou, P.; Kalogirou, S.A. Infrared thermography (IRT) applications for building diagnostics: A review. Appl. Energy 2014, 134, 531–549. [Google Scholar] [CrossRef]
- Tejedor, B.; Casals, M.; Gangolells, M.; Roca, X. Quantitative internal infrared thermography for determining in-situ thermal behaviour of façades. Energy Build. 2017, 151, 187–197. [Google Scholar] [CrossRef]
- Fokaides, P.A.; Kalogirou, S.A. Application of infrared thermography for the determination of the overall heat transfer coefficient (U-Value) in building envelopes. Appl. Energy 2011, 88, 4358–4365. [Google Scholar] [CrossRef]
- Lehmann, B.; Wakili, K.G.; Frank, T.; Collado, B.V.; Tanner, C. Effects of individual climatic parameters on the infrared thermography of buildings. Appl. Energy 2013, 110, 29–43. [Google Scholar] [CrossRef]
- Van De Vijver, S.; Steeman, M.; Van Den Bossche, N.; Carbonez, K.; Janssens, A. The influence of environmental parameters on the thermographic analysis of the building envelope. In Proceedings of the 12th International Conference on Quantitative InfraRed Thermography (QIRT 2014), Bordeaux, France, 7–11 July 2014. [Google Scholar]
- Kisilewicz, T.; Wróbel, A. Quantitative infrared wall inspection. In Proceedings of the 10th Edition of the Quantitative InfraRed Thermography—International Conference, Québec, QC, Canada, 27–30 July 2010; pp. 27–30. [Google Scholar]
- Nardi, I.; Paoletti, D.; Ambrosini, D.; De Rubeis, T.; Sfarra, S. U-value assessment by infrared thermography: A comparison of different calculation methods in a Guarded Hot Box. Energy Build. 2016, 122, 211–221. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M. Infrared thermovision technique for the assessment of thermal transmittance value of opaque building elements on site. Energy Build. 2010, 42, 2177–2183. [Google Scholar] [CrossRef]
- Dall’O’, G.; Sarto, L.; Panza, A. Infrared screening of residential buildings for energy audit purposes: Results of a field test. Energies 2013, 6, 3859–3878. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M.; Chiogna, M. A comprehensive experimental approach for the validation of quantitative infrared thermography in the evaluation of building thermal transmittance. Appl. Energy 2015, 141, 218–228. [Google Scholar] [CrossRef]
- Tejedor, B.; Casals, M.; Gangolells, M. Assessing the influence of operating conditions and thermophysical properties on the accuracy of in-situ measured U-values using quantitative internal infrared thermography. Energy Build. 2018, 171, 64–75. [Google Scholar] [CrossRef]
- Choi, D.S.; Ko, M.J. Comparison of various analysis methods based on heat flowmeters and infrared thermography measurements for the evaluation of the in situ thermal transmittance of opaque exterior walls. Energies 2017, 10, 1019. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Bermúdez, J.; Moyano, J.; Marín, D. Comparison of quantitative IRT to estimate U-value using different approximations of ECHTC in multi-leaf walls. Energy Build. 2019, 184, 99–113. [Google Scholar] [CrossRef]
- Mahmoodzadeh, M.; Gretka, V.; Lee, I.; Mukhopadhyaya, P. Infrared thermography for quantitative thermal performance assessment of wood-framed building envelopes in Canada. Energy Build. 2022, 258, 111807. [Google Scholar] [CrossRef]
- Rodríguez, M.V.; Melgar, S.G.; Márquez, J.M.A. Evaluation of aerial thermography for measuring the thermal transmittance (U-value) of a building façade. Energy Build. 2024, 324, 114874. [Google Scholar] [CrossRef]
- Zhang, D.; Zhan, C.; Chen, L.; Wang, Y.; Li, G. An in-situ detection method for assessing the thermal transmittance of building exterior walls using unmanned aerial vehicle–infrared thermography (UAV-IRT). J. Build. Eng. 2024, 91, 109724. [Google Scholar] [CrossRef]
- European Commission. A Roadmap for Moving to a Competitive Low Carbon Economy in 2050: Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar]
- Sadhukhan, D.; Peri, S.; Sugunaraj, N.; Biswas, A.; Selvaraj, D.F.; Koiner, K.; Rosener, A.; Dunlevy, M.; Goveas, N.; Flynn, D. Estimating surface temperature from thermal imagery of buildings for accurate thermal transmittance (U-value): A machine learning perspective. J. Build. Eng. 2020, 32, 101637. [Google Scholar] [CrossRef]
- Patel, D.; Estevam Schmiedt, J.; Röger, M.; Hoffschmidt, B. A Model Calibration Approach to U-Value Measurements with Thermography. Buildings 2023, 13, 2253. [Google Scholar] [CrossRef]


| Author (Year) | Measurement Method | Comparison Method | Deviation [%] | Test Period | Building Information |
|---|---|---|---|---|---|
| Asdrubali et al. (2014) [50] | HFM, average method | Theoretical method: ISO 6946 | 14–43%, average 23% | Heating season 2010 and 2013 At least 7 days | Six buildings constructed using green architecture techniques |
| Ficco et al. (2015) [16] | HFM, average method | Theoretical method: ISO 6946 | winter 1–70%, average 24% summer 45–142%, average 90% | Winter and Summer 3–168 h | Six different buildings in Italy completed between 1965 and 2015 |
| HFM, average method | Endoscopic analysis and core samplings | winter 2–55%, average 13% summer 62–264%, average 152% | |||
| Walker and Pavia (2015) [65] | HFM, average method | Theoretical method: provider values | 13–25% | June 2014 to April 2015 | Brick building in Dublin completed in 1805 |
| Gaspar et al. (2016) [71] | HFM, average method | Theoretical method: ISO 6946 | 2–20%, average 9% | December 2015 to April 2016 72 h | Three buildings in Catalonia, Spain, completed in 1960, 1992, and 2007 |
| HFM, dynamic method | Theoretical method: ISO 6946 | 1–10%, average 3% | |||
| Bros Williamson et al. (2016) [66] | HFM method | Theoretical method: ISO 6946 | 10–65%, average 27% | First winter in 2012 and 2014 14–21 days | A residential building in the UK completed in 2012 |
| Lucchi (2017) [42] | HFM, average method | Tabulated design method: Standard UNI TS 11300-1:2014 | 7.7–46.5% | Two winter seasons 7–14 days | Fourteen old brick buildings in Italy |
| Lucchi (2017) [41] | HFM, average method | Theoretical method: ISO 6946 | 3–54% | Two winter seasons 7–14 days | Ten brick buildings in the Lombardy region, representing northern Italy |
| Evangelisti et al. (2020) [69] | HFM, average method | Theoretical method: ISO 6946 | 2–60%, average 1–11% | February 2019 7–18 days | Buildings in Italy characterized by high-insulation walls and solar-shading systems |
| Gaspar et al. (2021) [84] | HFM, dynamic method | Theoretical method: ISO 6946 | 1–6% | June and October 2016 144–168 h | Buildings in Spain completed in 1960 and 2005 |
| Richard O’Hegarty et al. (2021) [72] | HFM, average method | Theoretical method: ISO 6946 | 10~297% | August 2019~February 2021 more than 72 h | A total of 13 tests at 7 different sites in Ireland |
| Evangelisti et al. (2022) [70] | HFM, average method | Theoretical method: ISO 6946 | 10.45% (north), 92.14% (north-west) | January 2019, 4 days (north) April 2019, 7 days (north-west) | Educational buildings in Italy from the 1960s |
| Choi et al. (2023) [73] | HFM, average method | Theoretical method: ISO 6946 | 9.12% | November to December 2021 13 days | Specially designed and constructed for this research in May 2021 |
| Lee et al. (2024) [85] | HFM, average method | Theoretical method: ISO 6946 | 5.63~9.97% average 7.01% | June 2022~May 2023 7 days, 86 sets | Specially designed and constructed for this research in May 2021 |
| HFM, dynamic method | Theoretical method: ISO 6946 | 5.85~37.83% average 12.81% | |||
| HFM method, extended average | Theoretical method: ISO 6946 | 2.57~6.86% average 4.02% | |||
| Suh et al. (2024) [74] | HFM, average method | Theoretical method: DesignBuilder | 1.52% | 72 h | Campus buildings in Seoul, South Korea, constructed in 1924 |
| Author (Year) | Measurement Method | Comparison Method | Deviation [%] | Test Period | Building Information |
|---|---|---|---|---|---|
| Meng et al. (2015) [90] | SHB–HFM method | Theoretical method | 4–7%, average 5.97% | August 2013 192 h | A newly built two-story rural building located in China |
| Meng et al. (2017) [91] | SHB–HFM method | Theoretical method | 4.4–7.5% | August 2013 192 h | A newly built two-story rural building located in China |
| Roque et al. (2020) [92] | SHB–HFM method | Endoscopic analysis and core samplings | 1.4–4.3% | Winter 120 h | Tabique buildings located in the northern region of Portugal, constructed in late 19th century or early 20th century |
| Francesco Nicoletti et al. (2023) [93] | SHB–HFM method | Theoretical method | 0.3~7.5% (winter) 1.9~13% (summer) | January 2019, 5~7 days (winter) July 2019, 4~9 days (summer) | A total of eight masonry walls, which are differentiated by various thermal characteristics |
| Method | Accuracy | Test Period | Measurement Parameter | Equipment Required for Measurement |
|---|---|---|---|---|
| HFM | Winter 1–70% Summer 45–264% | Min. 3 days Max. 21 days | Heat flux Air temperature (internal and external) | Heat flow meter Air temperature probe Data logger |
| SHB-HFM | 0.3–13% | Min. 3 days | Heat flux Surface temperature (internal and external) Air temperature (external) | Simple hot box Heat flow meter Surface temperature probe Air temperature probe Data logger |
| THM | Winter 0.3–37% Summer 7–143.7% | Less than 1 day | Air temperature (internal and external) Surface temperature (internal) | Air temperature probe Data logger |
| QIRT | Winter 0–154% Summer 10–286% | Min. 3 nights | Air temperature (internal and external) Surface temperature (internal or external) Emissivity Wind speed | Infrared camera Hot wire anemometer Air temperature probe Data logger |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, A.; Kim, Y.; Hwang, S.; Shin, M.; Lee, S. A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes. Buildings 2024, 14, 3304. https://doi.org/10.3390/buildings14103304
Song A, Kim Y, Hwang S, Shin M, Lee S. A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes. Buildings. 2024; 14(10):3304. https://doi.org/10.3390/buildings14103304
Chicago/Turabian StyleSong, Ahhyun, Yeeun Kim, Sangjun Hwang, Minjae Shin, and Sanghyo Lee. 2024. "A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes" Buildings 14, no. 10: 3304. https://doi.org/10.3390/buildings14103304
APA StyleSong, A., Kim, Y., Hwang, S., Shin, M., & Lee, S. (2024). A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes. Buildings, 14(10), 3304. https://doi.org/10.3390/buildings14103304







