Systematic Calculation of Yield and Failure Curvatures of Reinforced Concrete Cross-Sections
Abstract
1. Introduction
2. Column Limit States
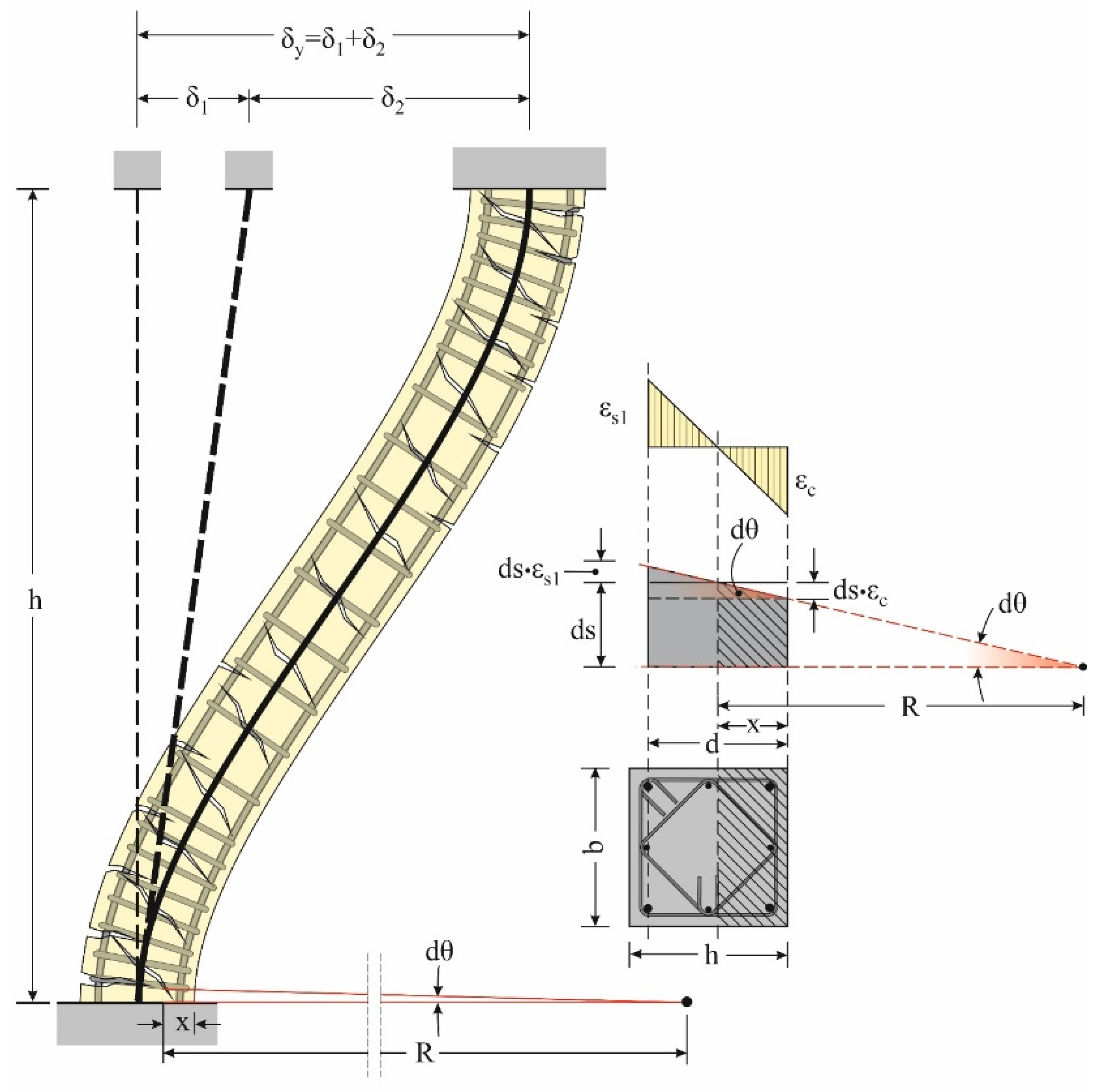
2.1. Column in Yield Limit State
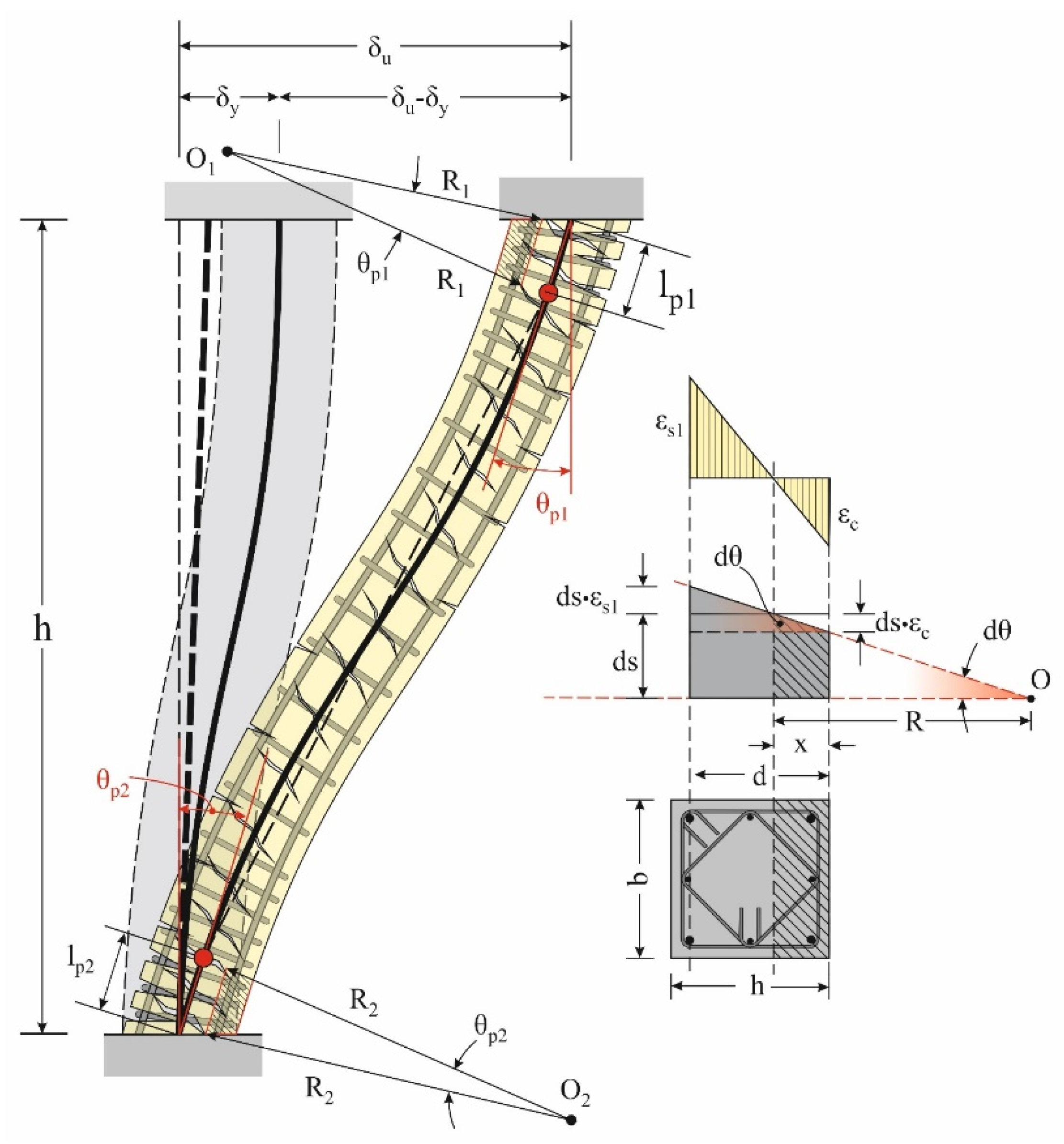
2.2. Column in the Failure Limit State
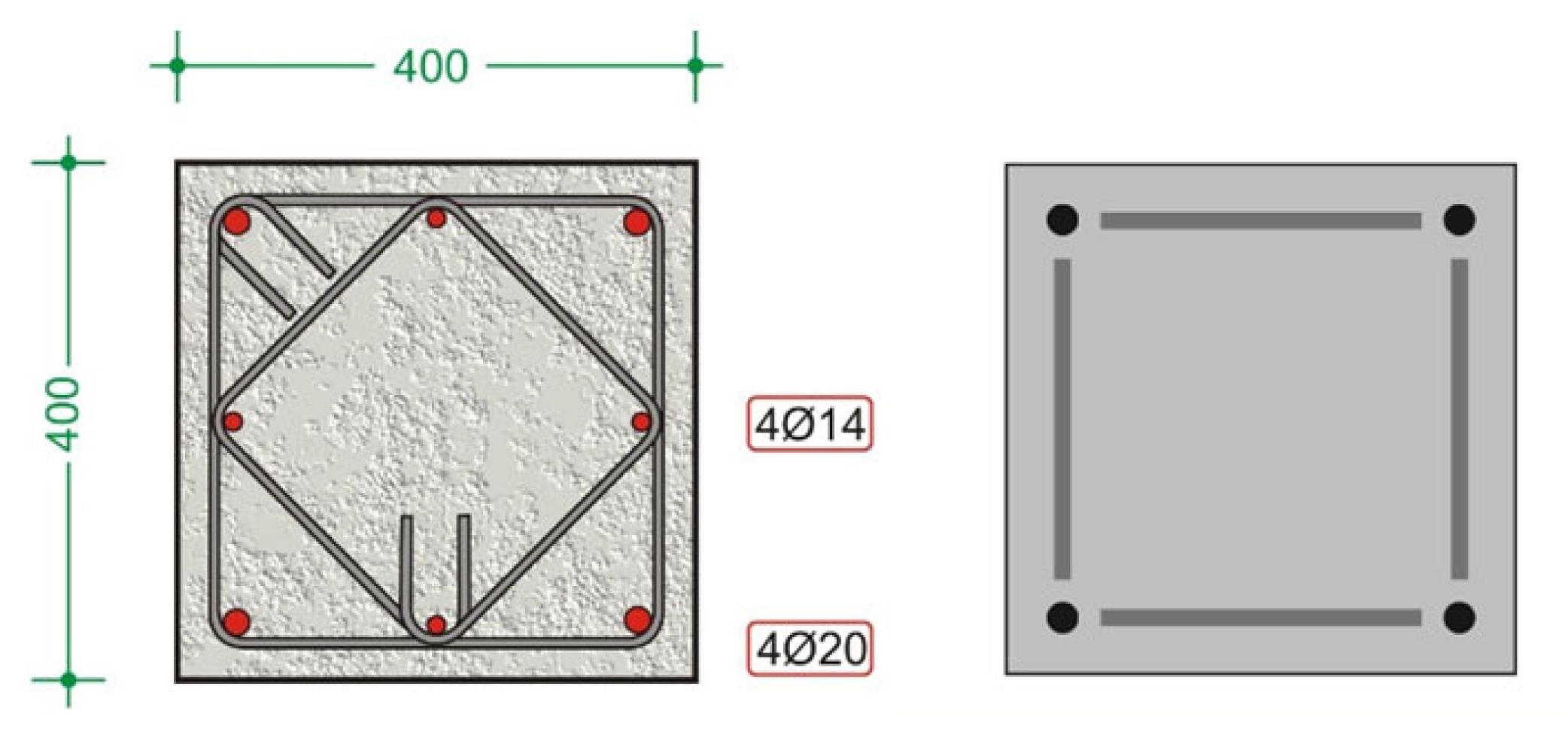
2.3. Example: Calculation of Limit State Curvatures
- (1)
- Yield limit y.
- (2)
- Failure limit u.
2.3.1. Calculation of Yield Curvature
2.3.2. Calculation of Failure Curvature
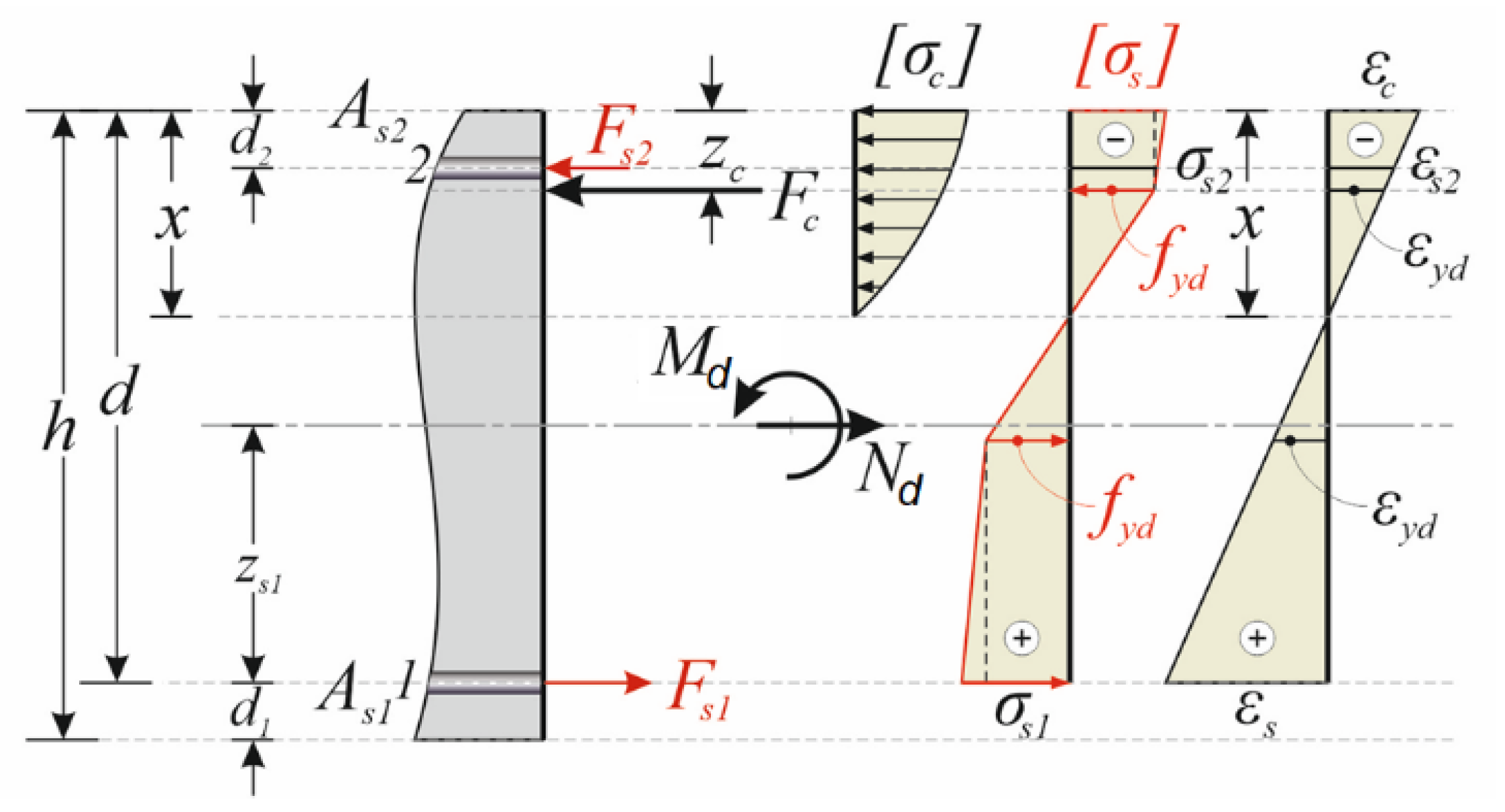
3. Equilibrium of Internal and External Forces
- (a)
- Equilibrium equation of the forces Fs1, Fc, and Fs2 with the axial force Nd
- (b)
- Equilibrium equation of the moments of the forces Fc and Fs2 with the bending moment Md in the cross-section center and the moment of axial force Nd
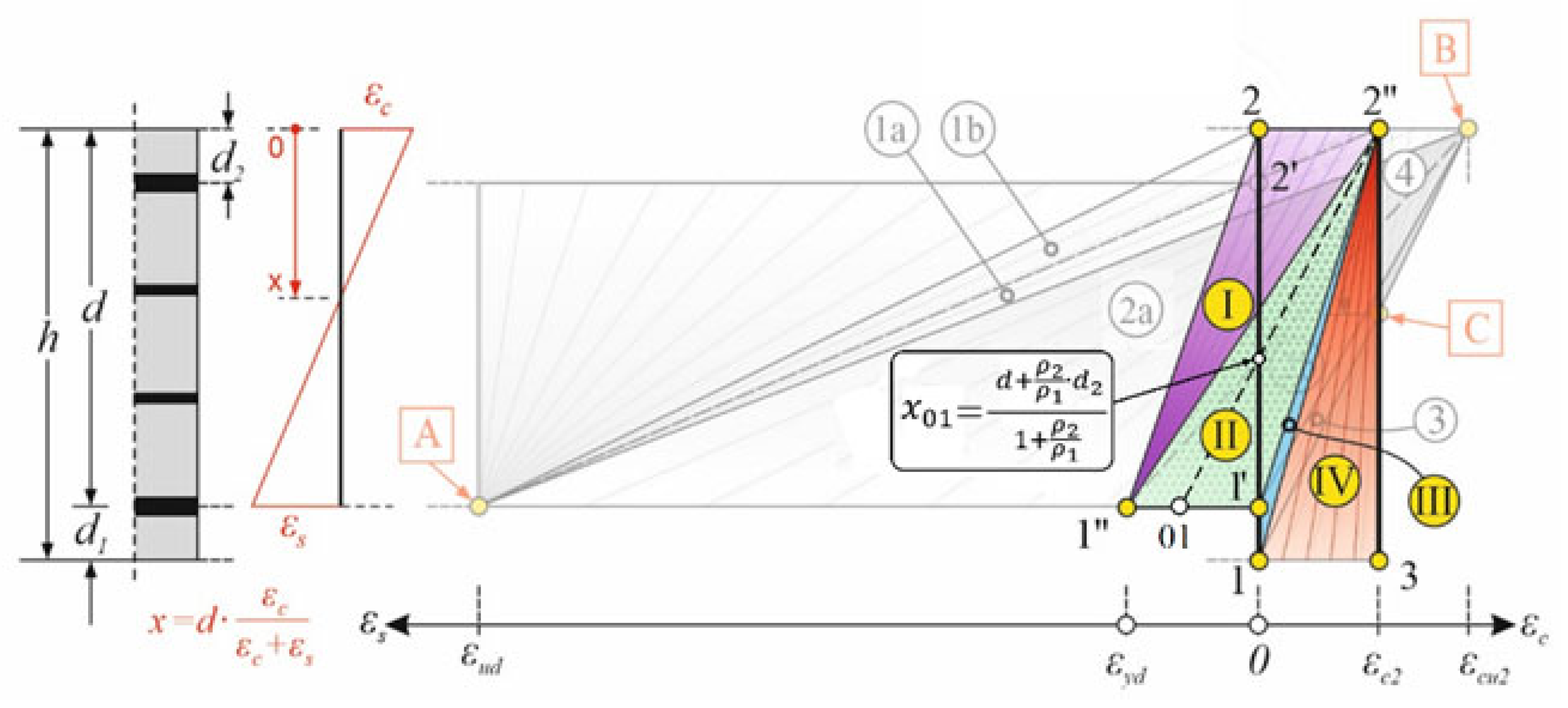
- First condition: the reinforcement ratio ρ2/ρ1 is provided.
- Second condition: either εc or εs should be in the limit state.
4. Solution Regions in the Yield Limit State
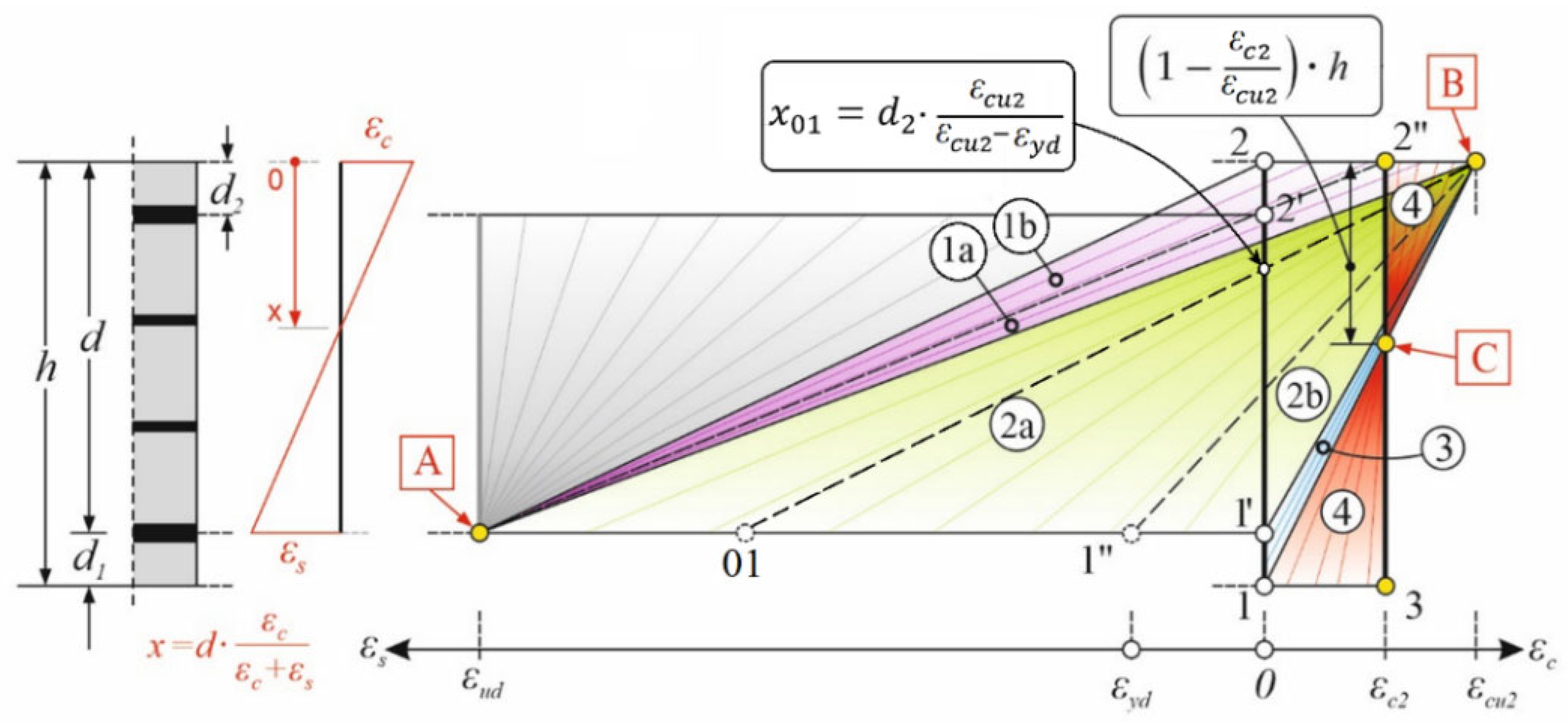
5. Solution Regions in the Failure Limit State
- (1)
- The boundary 1″B of the subregions 2a and 2b, has εs1 = εyd → σs1 = fyd and εc = εcu2. Since it is usually εs2 ≥ εyd → σs2 = fyd, we have dσ = σs1 − σs2 = fyd − fyd = 0.
- (2)
- To the left of location 1″B will continue to be dσ = 0 until the specific location 01 with εs1 = εs2.
6. Application: The “Typical Rectangular Section” in Limit States
6.1. Yield Limit State
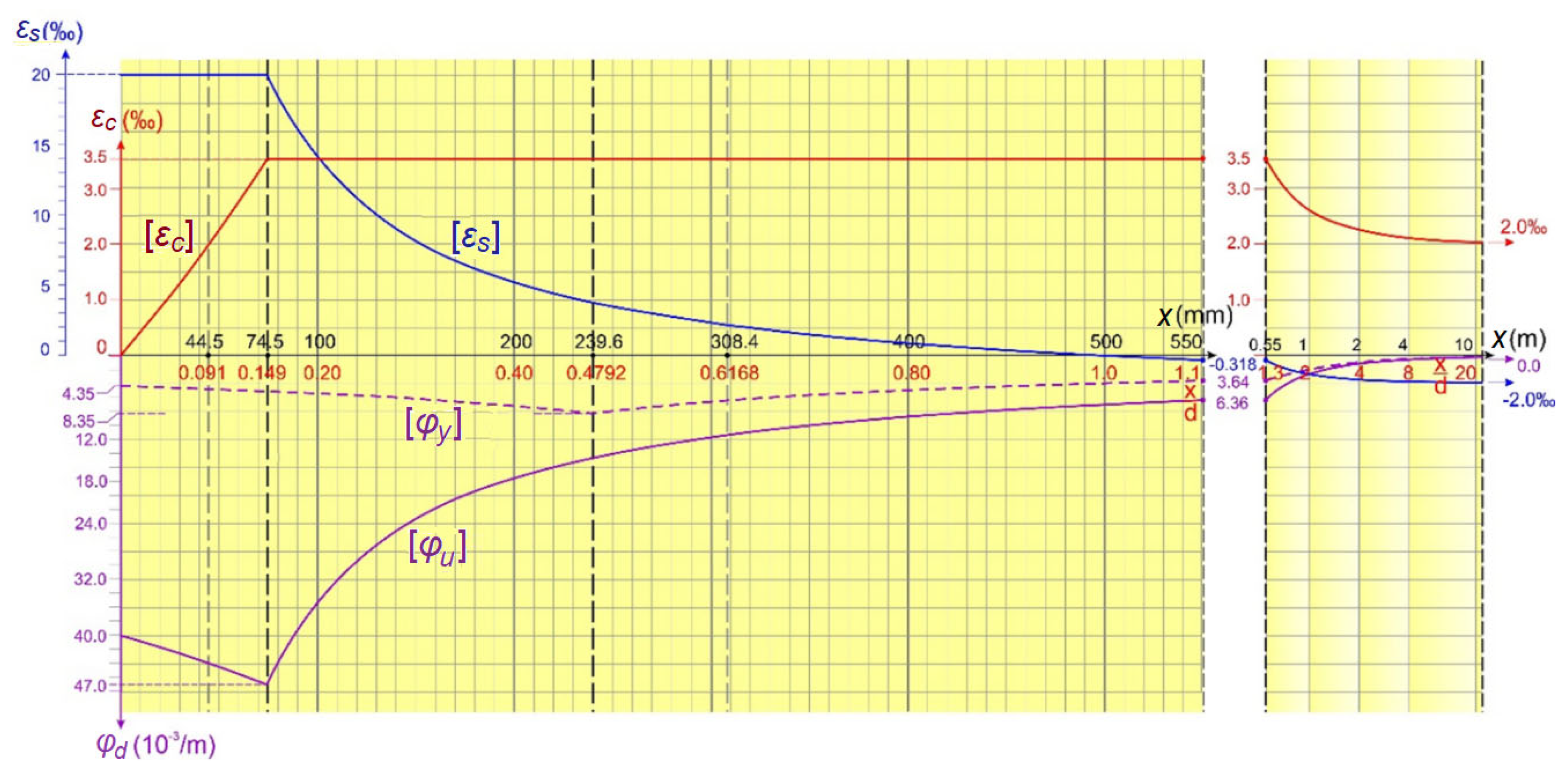
6.1.1. Strain and Curvature Diagrams in the Yield Limit State
6.1.2. Asymptotic Location in Yield Limit State for ρ2/ρ1 = 1
6.1.3. Solution Nomogram in Yield Limit State for ρ2/ρ1 = 1
6.2. Failure Limit State
6.2.1. Strain and Curvature Diagrams in the Failure Limit State
6.2.2. Asymptotic Region in Failure Limit State for ρ2/ρ1 = 1
6.2.3. Solution Nomogram in Failure Limit State for ρ2/ρ1 = 1
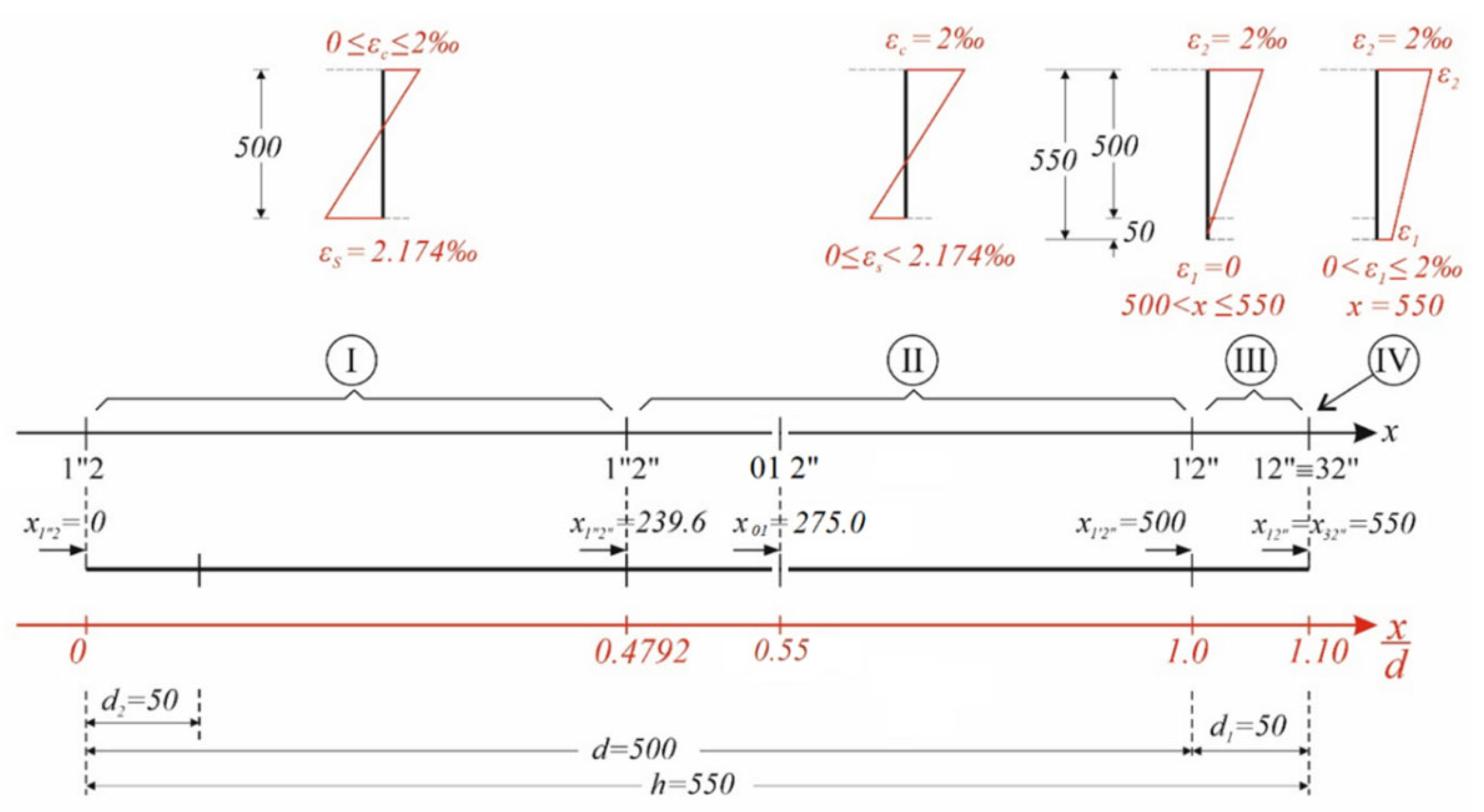
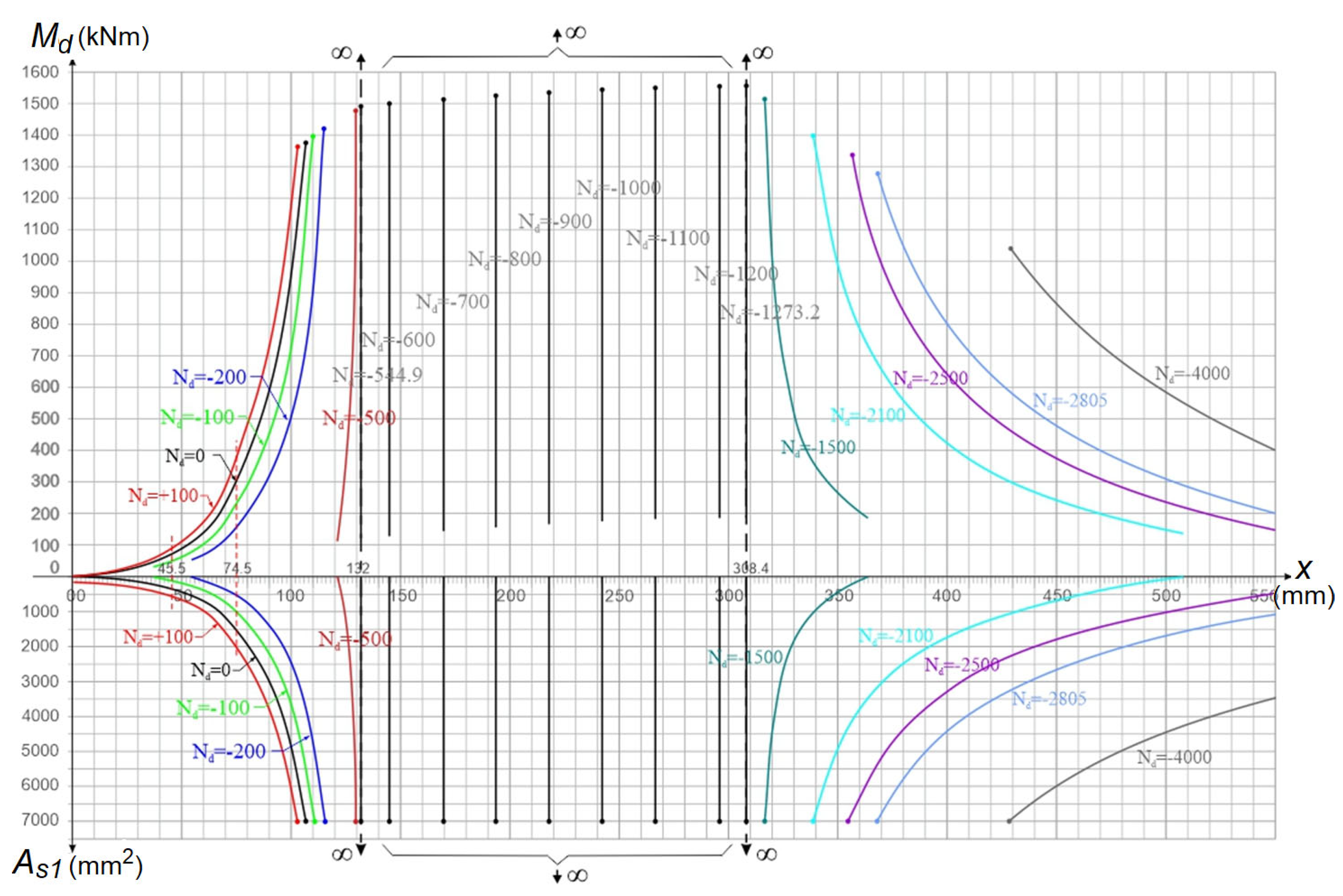
6.2.4. Indeterminacy or Multiple Solution Region in Failure Limit State
6.2.5. Application in Failure Limit State for ρ2/ρ1 = 1 and Nd = −1000 kN
7. Conclusions
- The influence of cracking on the curvature of RC elements is significant in relation to the corresponding elastic curvature, even in the yield state, so the corresponding yield stiffness is significantly smaller than the elastic stiffness.
- For specific flexural reinforcement, the yield curvature is much smaller than the failure curvature, while the yield moment of resistance is of the same order of magnitude as the failure moment of resistance.
- During the bending design of a cross-section in the failure limit state, there is an extended region of compressive axial forces where the curvature is practically constant regardless of the acting moment. Then, for any given axial force, the necessary flexural reinforcement is derived from the acting moment based on a first-order equation.
- It is proposed that the design process should take place in the following order:
- (a)
- Calculate reinforcement in the failure state.
- (b)
- Choose and apply reinforcement.
- (c)
- Calculate failure curvatures φu, yield curvatures φy, and elastic curvatures φe.
- (d)
- Estimate curvature ductilities from the ratios φu/φy and/or φu/φe.
- (e)
- Determine effective stiffness and resolve.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| As | total reinforcement |
| As1 | tensile reinforcement |
| As2 | compressive reinforcement |
| αcc | long-term effects factor |
| b | beam width |
| c | ratio of compressive reinforcement to tensile reinforcement |
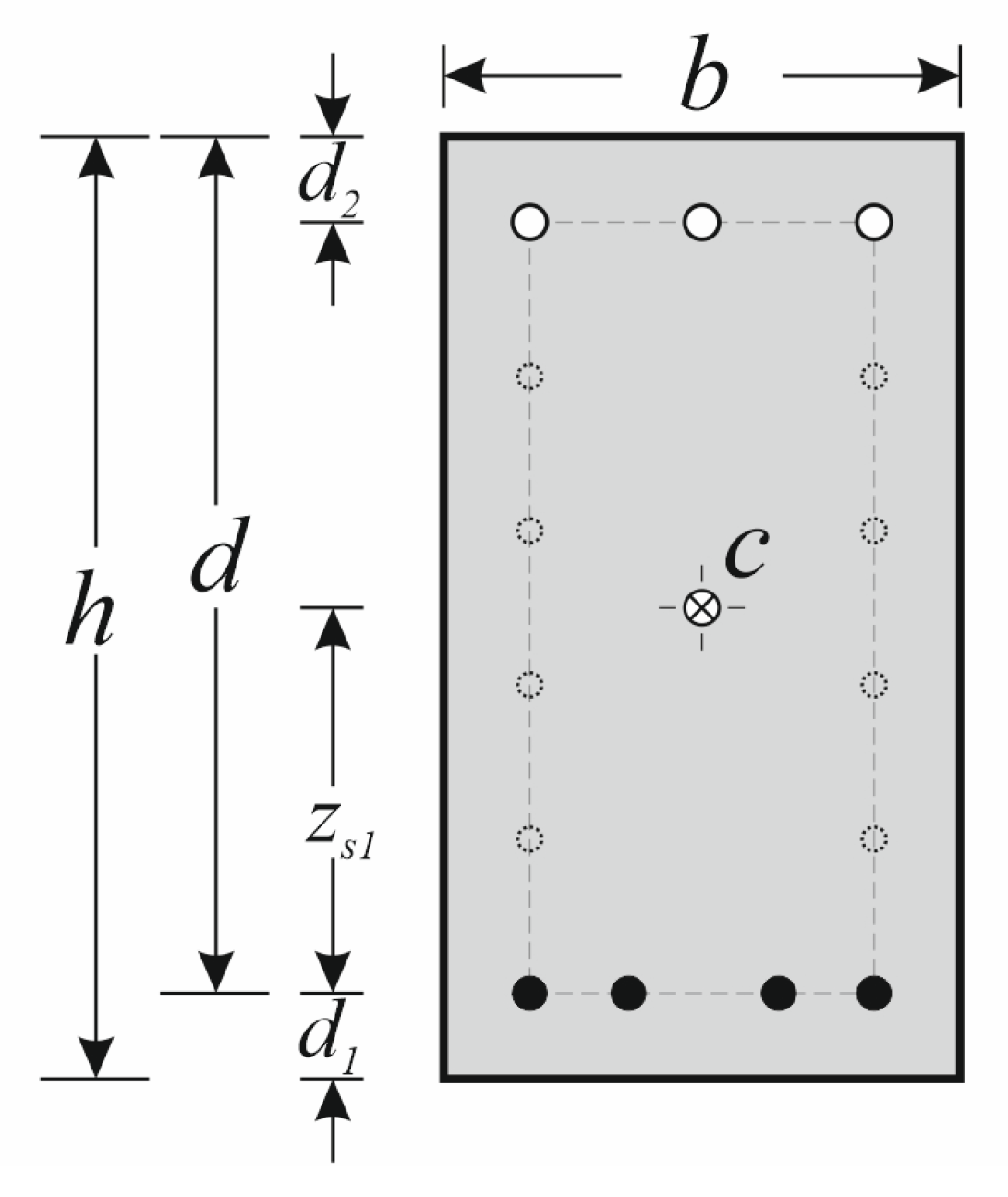
| d | beam effective depth |
| d1 | tensile reinforcement cover |
| d2 | compressive reinforcement cover |
| E | concrete modulus of elasticity |
| Es | steel modulus of elasticity |
| Fc | concrete compressive force |
| Fs1 | tensile reinforcement force |
| Fs2 | compressive reinforcement force |
| fck | concrete compressive strength |
| fcm | concrete mean compressive strength |
| fyk | steel yield strength |
| fcd | concrete design strength |
| fyd | steel design strength |
| h | beam height |
| I | cross-section moment of inertia |
| K | strain hardening coefficient (ductility property) |
| kF | concrete compressive force coefficient |
| Md | bending moment acting in the cross-section center |
| Msd | bending moment acting in the tensile reinforcement position |
| Nd | axial force acting in the cross-section center |
| Re | radius of elastic curvature |
| Ry | radius of yield curvature |
| Ru | radius of failure curvature |
| x | compressive zone depth distance of the outermost upper fiber from the neutral axis |
| xij | compressive zone depth corresponding to the “ij” location |
| x01 | compressive zone depth corresponding to the asymptotic location |
| zc | distance of the outermost upper fiber from the concrete compression center |
| zs1 | distance of the tensile reinforcement position from the cross-section center |
| α | distribution factor of concrete compressive force |
| γc | concrete safety factor |
| γs | steel safety factor |
| δ1 | yield state displacement due to shear |
| δ2 | yield state displacement due to bending |
| εc | concrete strain |
| εc2 | concrete yield strain |
| εcu2 | concrete ultimate strain |
| εs | steel strain |
| εs1 | tensile reinforcement strain |
| εs2 | compressive reinforcement strain |
| εsu | steel ultimate strain |
| εud | steel design ultimate strain |
| κ | position factor of concrete compressive force |
| ρ1 | tensile reinforcement percentage |
| ρ2 | compressive reinforcement percentage |
| σs1 | tensile reinforcement stress |
| σs2 | compressive reinforcement stress |
| φe | elastic curvature |
| φy | yield curvature |
| φu | failure curvature |
References
- Chen, C.C.; Hsu, S.M. Formulas for Curvature Ductility Design of Doubly Reinforced Concrete Beams. J. Mech. 2004, 20, 257–265. [Google Scholar] [CrossRef]
- Hernández-Montes, E.; Aschheim, M.; Gil-Martín, L.M. Impact of Optimal Longitudinal Reinforcement on the Curvature Ductility Capacity of Reinforced Concrete Column Sections. Mag. Concr. Res. 2004, 56, 499–512. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Nunziante, L.; Serino, G.; Carannante, F. Curvature Ductility of RC Sections Based on Eurocode: Analytical Procedure. KSCE J. Civ. Eng. 2010, 15, 131–144. [Google Scholar] [CrossRef]
- Arslan, G.; Cihanli, E. Curvature Ductility Prediction of Reinforced High-strength Concrete Beam Sections. J. Civ. Eng. Manag. 2010, 16, 462–470. [Google Scholar] [CrossRef]
- Lee, H.-J. Predictions of Curvature Ductility Factor of Doubly Reinforced Concrete Beams with High Strength Materials. Comput. Concr. 2013, 12, 831–850. [Google Scholar] [CrossRef]
- Laterza, M.; D’Amato, M.; Thanthirige, A.P.; Braga, F.; Gigliotti, R. Comparisons of Codal Detailing Rules for Curvature Ductility and Numerical Investigations. Open Constr. Build. Technol. J. 2014, 8, 132–141. [Google Scholar] [CrossRef]
- Zhou, J.; He, F.; Liu, T. Curvature Ductility of Columns and Structural Displacement Ductility in RC Frame Structures Subjected to Ground Motions. Soil. Dyn. Earthq. Eng. 2014, 63, 174–183. [Google Scholar] [CrossRef]
- Baji, H.; Ronagh, H.R. Probabilistic Models for Curvature Ductility and Moment Redistribution of RC Beams. Comput. Concr. 2015, 16, 191–207. [Google Scholar] [CrossRef]
- Breccolotti, M.; Materazzi, A.L.; Regnicoli, B. Curvature Ductility of Biaxially Loaded Reinforced Concrete Short Columns. Eng. Struct. 2019, 200, 109669. [Google Scholar] [CrossRef]
- Kollerathu, J.A. Curvature Ductility of Reinforced Masonry Walls and Reinforced Concrete Walls. In Sustainability Trends and Challenges in Civil Engineering: Select Proceedings of CTCS 2020; Lecture Notes in Civil Engineering; Springer: Singapore, 2021; pp. 9–23. [Google Scholar] [CrossRef]
- Foroughi, S.; Yuksel, S.B. A New Approach for Determining the Curvature Ductility of Reinforced Concrete Beams. Slovak. J. Civ. Eng. 2022, 30, 8–20. [Google Scholar] [CrossRef]
- Karayannis, C.G. Design and Behavior of Reinforced Concrete Structures for Seismic Actions: Chapter 8—Element Ductility; Editions SOFIA: Sofia, Bulgaria, 2019; (In Greek). ISBN 978-960-633-005-6. [Google Scholar]
- Konstantinides, A. Earthquake Resistant Buildings Made of Reinforced Concrete: The Art of Construction and the Detailing According to Eurocodes; Alta Grafico SA: Ano Liossia, Greece, 2010; Volume A, ISBN 978-960-85506-3-6. [Google Scholar]
- EN 1992-1-1: 2004; Eurocode 2: Design of Concrete Structures. Part 1-1: General Rules and Rules for Buildings. British Standard Institution: London, UK, 2005.
- EN 1998-1: 2004; Eurocode 8: Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Konstantinides, A.; Bellos, J. Earthquake Resistant Buildings Made of Reinforced Concrete: Static and Dynamic Analysis According to Eurocodes; Alta Grafico SA: Ano Liossia, Greece, 2013; Volume B, ISBN 978-960-85506-4-3. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, J.; Konstantinidis, A. Systematic Calculation of Yield and Failure Curvatures of Reinforced Concrete Cross-Sections. Buildings 2024, 14, 826. https://doi.org/10.3390/buildings14030826
Bellos J, Konstantinidis A. Systematic Calculation of Yield and Failure Curvatures of Reinforced Concrete Cross-Sections. Buildings. 2024; 14(3):826. https://doi.org/10.3390/buildings14030826
Chicago/Turabian StyleBellos, John, and Apostolos Konstantinidis. 2024. "Systematic Calculation of Yield and Failure Curvatures of Reinforced Concrete Cross-Sections" Buildings 14, no. 3: 826. https://doi.org/10.3390/buildings14030826
APA StyleBellos, J., & Konstantinidis, A. (2024). Systematic Calculation of Yield and Failure Curvatures of Reinforced Concrete Cross-Sections. Buildings, 14(3), 826. https://doi.org/10.3390/buildings14030826








