The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method
Abstract
1. Introduction
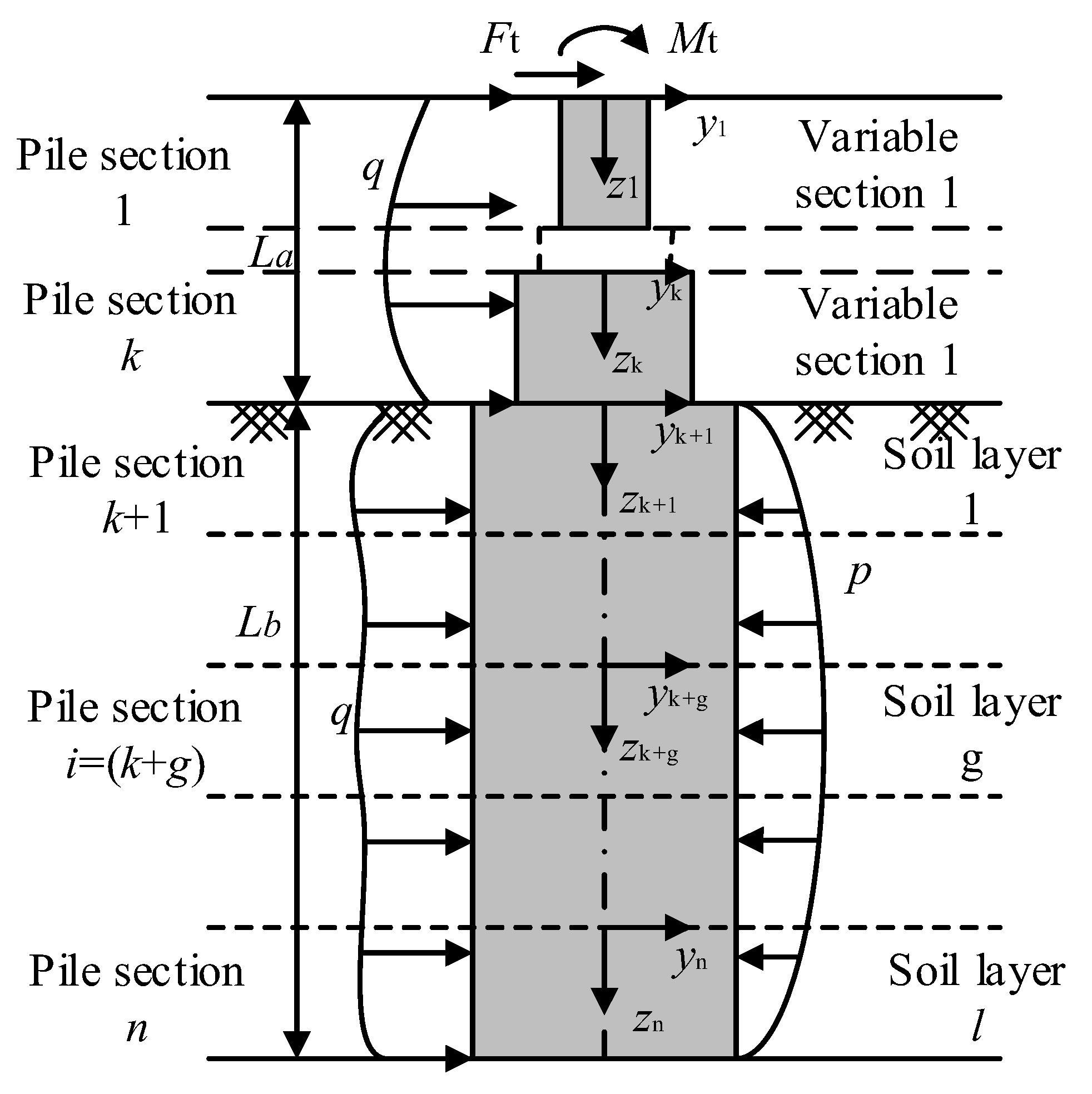
2. Analytical Models and Solution Methods
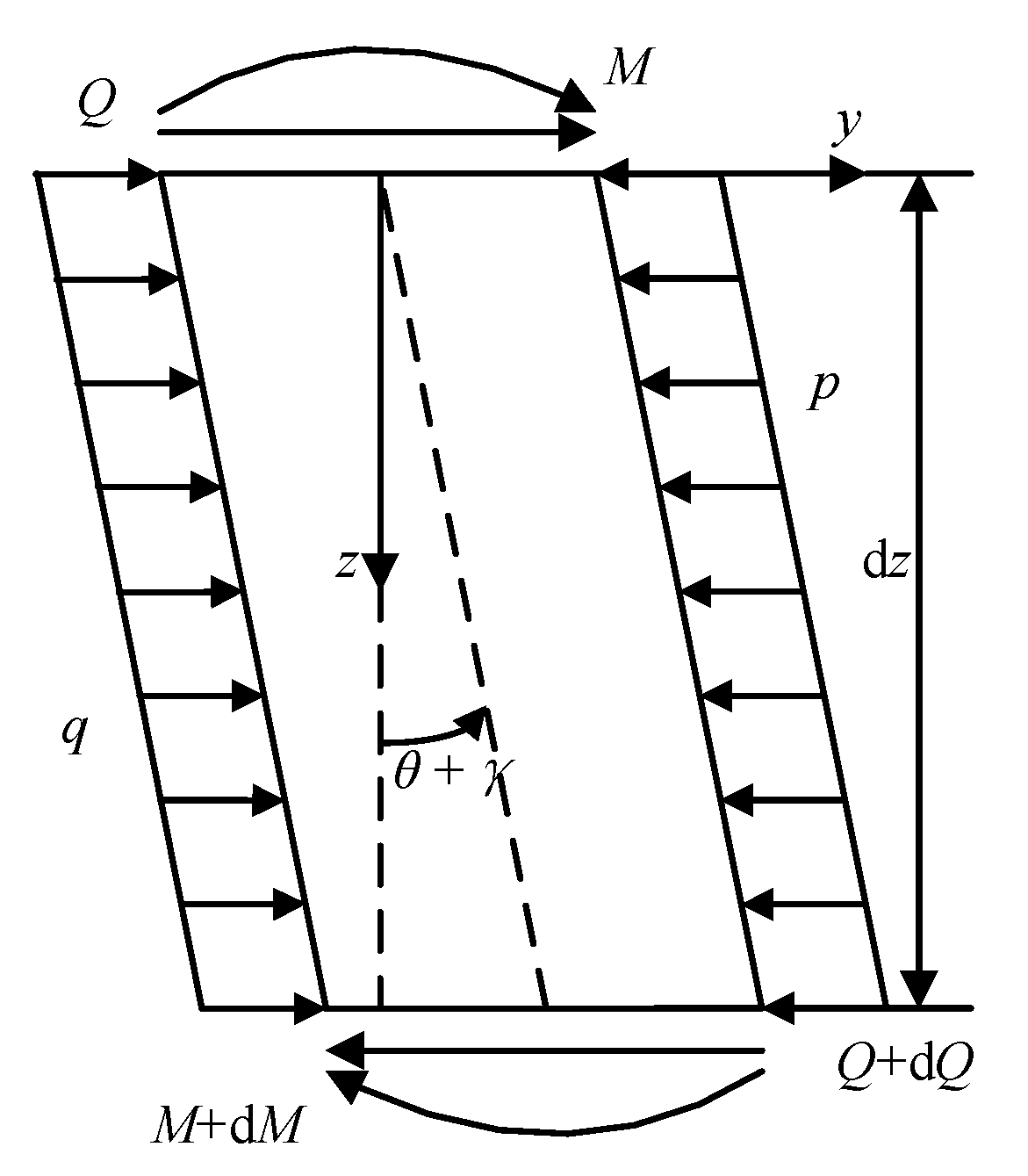
2.1. Differential Element Equilibrium Equations
2.2. The Relationship between Internal Force and Deformation of the Pile Body
2.3. Solving the Coefficient of the Free-Segment Transfer Matrix on the Mud Surface
2.4. Solution of the Transfer Matrix Coefficient of the Elastic Segment under the Mud Surface
2.5. Solution of the Transfer Matrix Coefficient of the Plastic Segment under the Mud Surface
2.6. Boundary Conditions and Calculation Process
2.6.1. Boundary Conditions
- (1)
- Pile-top free constraint: M0 = Mt, Q0 = Fh;
- (2)
- Pile-top fixed constraint: θ0 = 0, Q0 = Fh;
- (3)
- Free constraint at the pile end: Mn = 0, Qn = 0;
- (4)
- Pile-end fixed constraint: yn = 0, θn = 0.
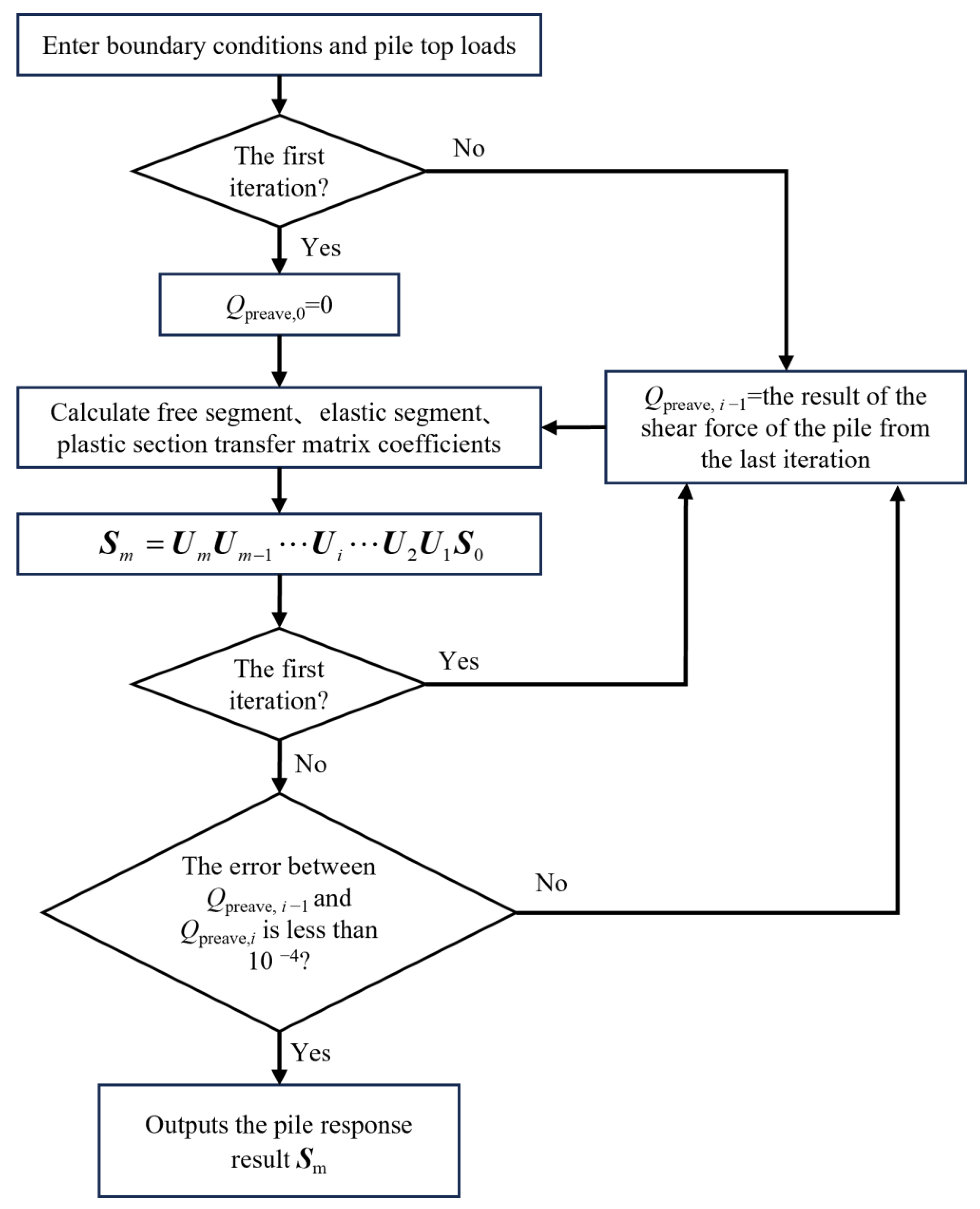
2.6.2. Calculation Process
- (1)
- For the initial calculation, Qpreave = 0 is set, and assuming that the mud surface below is in the elastic stage, the initial calculation result is obtained according to the pile-bearing response transfer matrix.
- (2)
- After the first step of calculation, the pile-body shear force value can be obtained. The pile-body shear force is taken as a constant term Qpreave, and then substituted into the previous process for iterative calculation. At the same time, according to the calculation results of the first step, the method to judge whether the points under the mud surface are in the elastic stage or the plastic stage is as follows: if they are in the elastic stage, the elastic-segment transfer matrix formula continues to be used in the second step of iterative calculation; if they are in the plastic stage, the corresponding unit is calculated by using the plastic-segment transfer matrix formula when the second step is iteratively calculated, and the calculation result of the second step is obtained.
- (3)
- After repeating the above steps until the Qpreave calculated in the last two steps meets the convergence error (10−4 in this paper), the iterative calculation is over, at which time the result is the final result.
3. Case Comparison
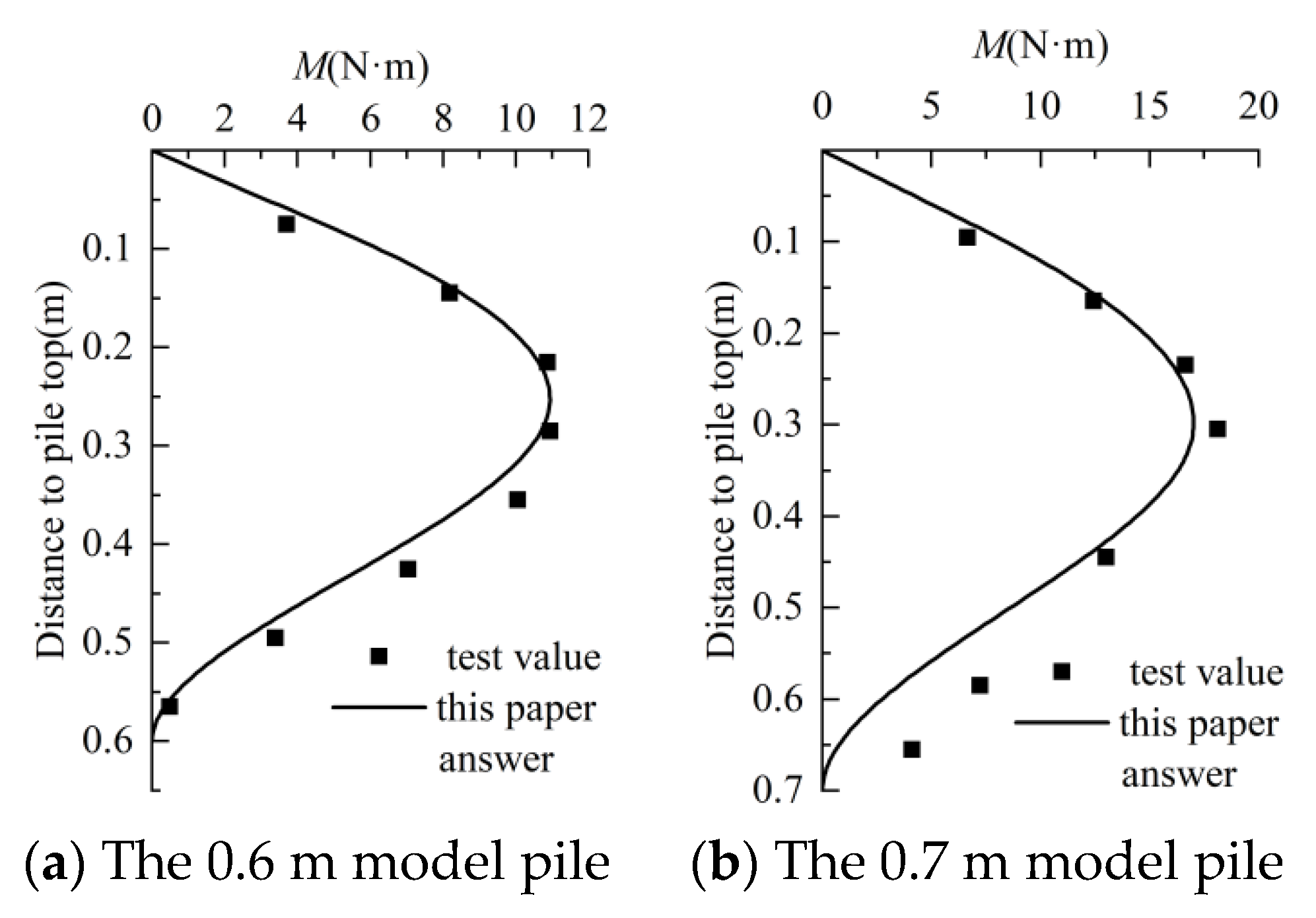
3.1. Case 1
3.2. Case 2
4. Comparative Analysis of the Timoshenko Beam and Euler–Bernoulli Beam
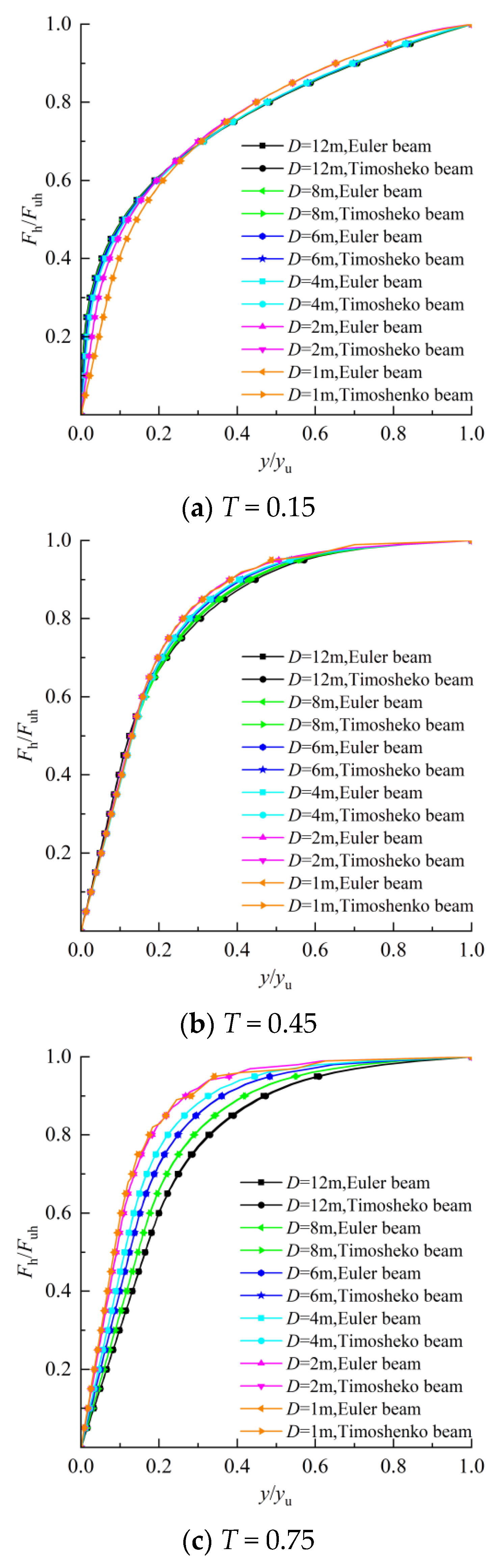
4.1. Comparison of Load–Displacement Curves of Timoshenko Beams and Euler–Bernoulli Beams
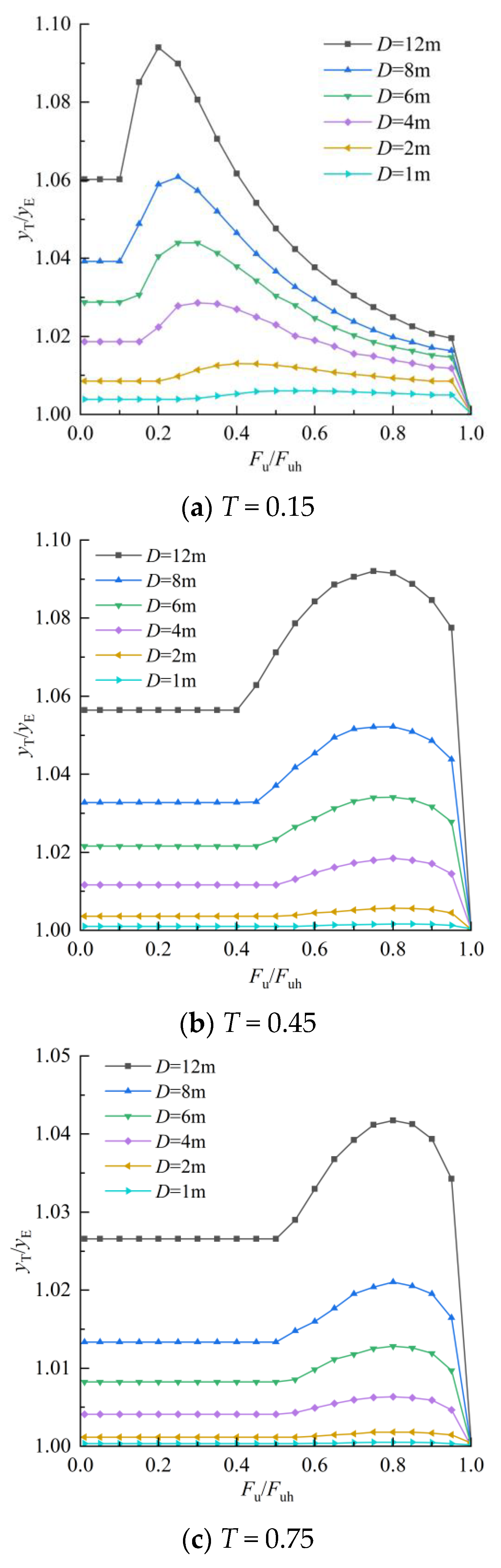
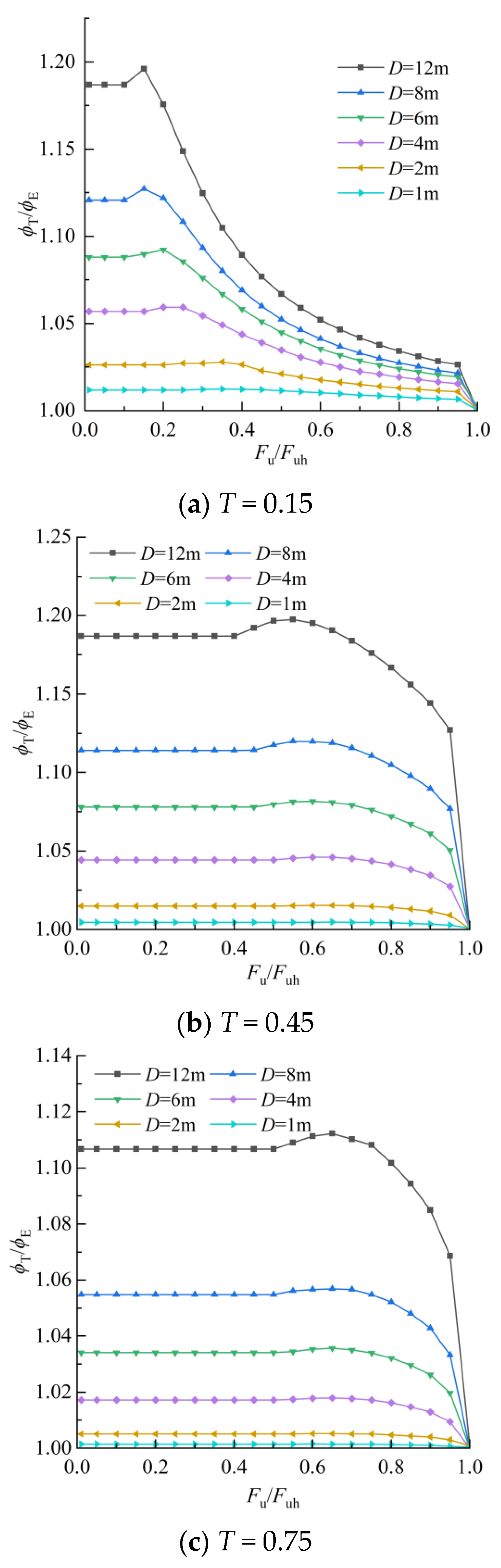
4.2. Deformation Analysis of Timoshenko Beams and Euler–Bernoulli Beams
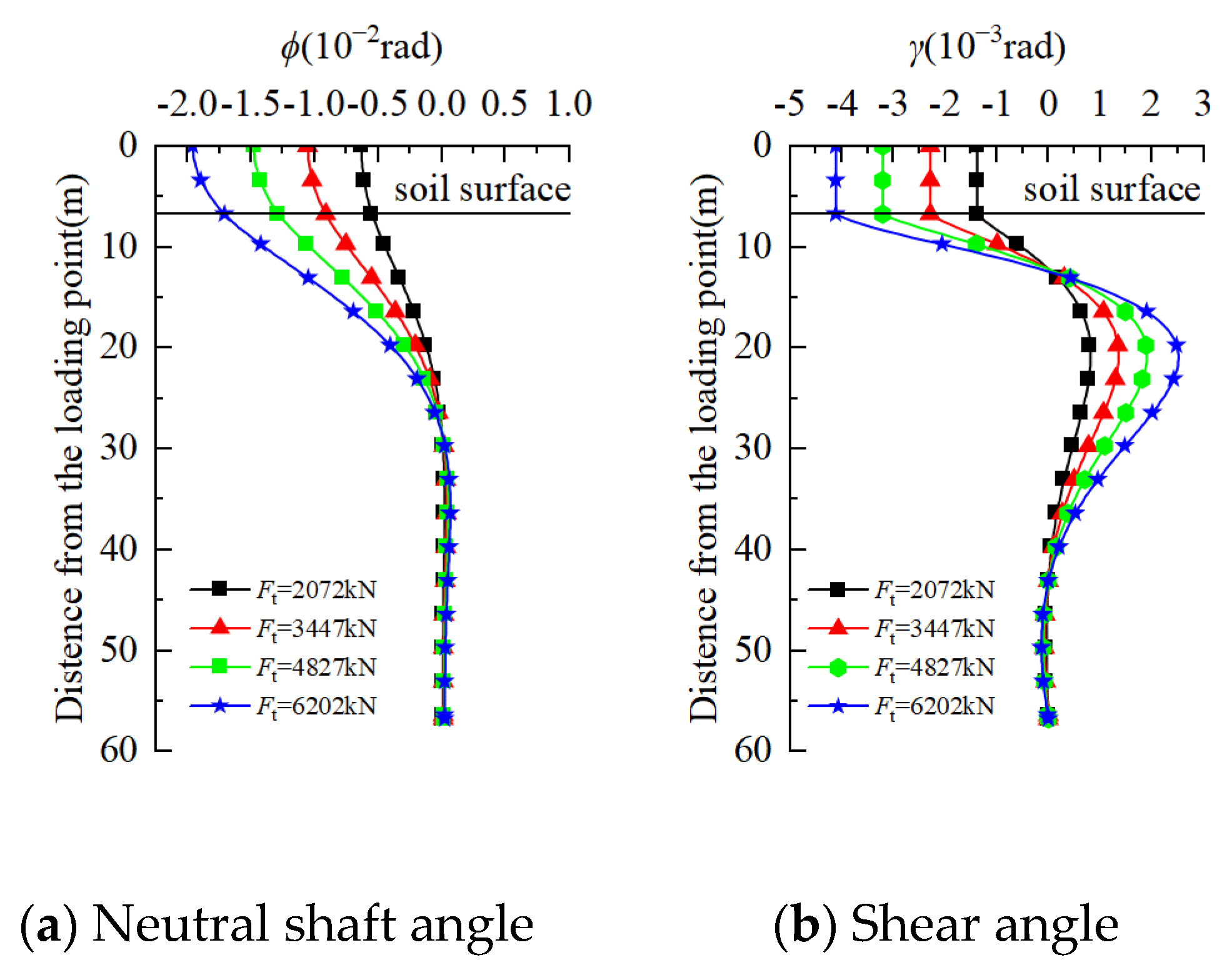
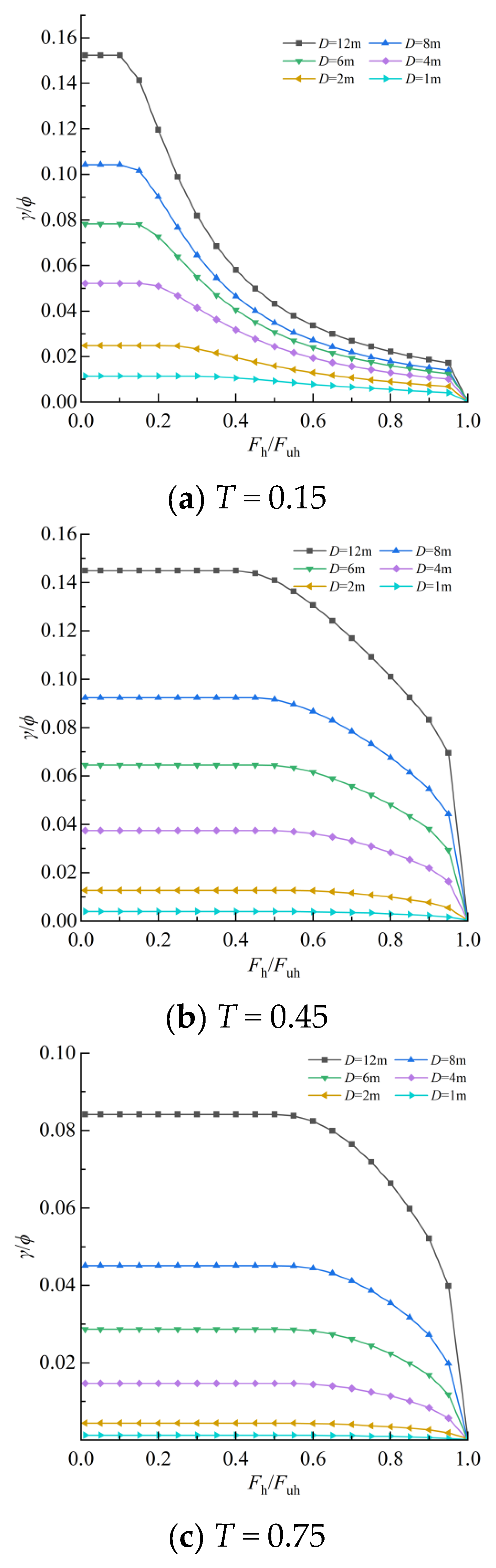
4.3. Analysis of the Relationship between the Shear Angle and Total Rotation of the Timoshenko Beam
5. Conclusions
- (1)
- Firstly, based on the Timoshenko beam theory, the transfer matrix coefficient and pile-body response equation derived from the idea of variable constantization, which greatly reduces the difficulty of programming and calculation, was introduced in this paper. Then, several sets of case studies were used to verify the correctness of the method and programming process used in this paper.
- (2)
- It is observed that the load–displacement curves of laterally loaded piles based on Timoshenko beam theory and Euler–Bernoulli beam theory basically overlap, which means that considering the effect of shear deformation has limited influence on the lateral capacity of large-diameter piles.
- (3)
- Under a non-limiting load, with the increase in pile diameter, the influence of shear deformation of the pile body on the response of the pile body to the lateral load becomes more and more non-negligible; for flexible piles, ϕT is only 0.5% higher than ϕE when the pile diameter D = 1 m, and is 19.7% higher than ϕE when the pile diameter increases to 12 m. Also, the overall deformation of the pile body is influenced more by shear deformation in flexible pile and semi-rigid pile bodies than it is in rigid pile bodies; ϕT is 19.8% higher than ϕE for a semi-rigid pile with a pile diameter of 12 m, while ϕT is only 11.2% higher than ϕE for a rigid pile with a pile diameter of 12 m. However, when the load is close to the ultimate load, the pile deformation calculated based on the Timoshenko beam and Euler–Bernoulli beam theories tends to be consistent, and the influence of pile shear deformation can be ignored.
- (4)
- Under a non-limiting load, the proportion of the shear angle in the neutral shaft angle obtained based on Timoshenko beam theory is increased with the increase in pile-body diameter; for flexible piles, the ratio is only 1.2% when D = 1 m, and the ratio is 15.2% when the diameter is increased to 12 m. However, when the load is close to the ultimate load, the proportion of the shear angle in the neutral shaft angle tends to be 0, that is, the influence of the shear deformation of the pile body on the overall deformation of the pile body can be ignored.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Qin, W.; Gao, J.; Chang, K.; Dai, G.; Wei, H. Set-up effect of large-diameter open-ended thin-walled pipe piles driven in clay. Comput. Geothecnics 2023, 159, 105459. [Google Scholar] [CrossRef]
- Wang, J.; Wu, X.; Qin, W.; Chang, K. Negative skin friction of piles installed in dredged slurry after being reinforced by the vacuum preloading method. Acta Geotech. 2023, 18, 6159–6174. [Google Scholar] [CrossRef]
- Irving, S.; Dym, C. Energy and Finite Element Methods in Structural Mechanics; Taylor and Francis: New York, NY, USA, 1985. [Google Scholar]
- Klinkvort, R.T.; Hededal, O. Effect of load eccentricityand stress level on monopile support for offshore wind turbines. Can. Geotech. J. 2014, 51, 966–974. [Google Scholar] [CrossRef]
- Byrne, B.W.; McAdam, R.A.; Burd, H.J.; Houlsby, G.T.; Martin, C.M.; Zdravković, L.; Taborda, D.M.G.; Potts, D.M.; Jardine, R.J.; Sideri, M.; et al. New design methods for large diameter piles under lateral loading for offshore wind applications. In Frontiers in Offshore Geotechnics III; Meyer, V., Ed.; CRC Press/Balkema (Taylor & Francis Group): Leiden, The Netherlands, 2015; pp. 705–710. [Google Scholar]
- Gupta B K, Basu D Applicability of Timoshenko, Euler–Bernoulli and rigid beam theories in analysis of laterally loaded monopiles and piles. Géotechnique 2018, 68, 772–785. [CrossRef]
- Ansari, A.; Rao, K.S.; Jain, A.K. Seismic microzonation of the himalayan region considering site characterization: Application toward seismic risk assessment for sustainable tunneling projects. Nat. Hazards Rev. 2024, 25. [Google Scholar] [CrossRef]
- Han, J.; Frost, J.D. Load–Deflection response of transversely isotropic piles under lateral loads. Int. J. Numer. Anal. Methods Geomech. 2000, 24, 509–529. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhao, H.P.; Liu, S.W.; Wan, J.H.; Bai, R. Innovative Timoshenko soil-pile integrated element for lager diameter laterally-loaded piles considering soil-pile interactions. Comput. Geotech. 2022, 152, 105020. [Google Scholar] [CrossRef]
- Li, X.; Dai, G.; Zhu, M.; Zhu, W.; Zhang, F. Investigation of the soil deformation around late-rally loaded deep foundations with large diameters. Acta Geotech. 2023, 19, 2293–2314. [Google Scholar] [CrossRef]
- Li, X.J.; Dai, G.L.; Zhu, M.X.; Wang, L.Y.; Liu, H.Y. A Simplified Method for Estimating the Initial Stiffness of Monopile—Soil Interaction Under Lateral Loads in Offshore Wind Turbine Systems. China Ocean Eng. 2023, 37, 165–174. [Google Scholar] [CrossRef]
- Li, X.J.; Zhu, M.X.; Dai, G.L.; Wang, L.Y.; Liu, J. Interface Mechanical Behavior of Flexible Piles Under Lateral Loads in OWT Systems. China Ocean Eng. 2023, 37, 484–494. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Timoshenko beam theory-based dynamic analysis of laterally loaded piles in multilayered viscoelastic soil. J. Eng. Mech. 2018, 144, 04018091. [Google Scholar] [CrossRef]
- Zheng, C.; Luan, L.; Qin, H.; Zhou, H. Lateral Dynamic Response of a Combined Loaded Large-Diameter Pipe Pile Simulated by the Timoshenko Beam Theory. Int. J. Struct. Stab. Dyn. 2020, 20, 2071003. [Google Scholar] [CrossRef]
- Zhu, T. Matrix analysis method for interaction between lateral load pile and soil. Sichuan Build. Sci. Res. China 1979, 4. [Google Scholar]
- Gong, W. Dynamic Response Analysis of Pile Foundation. Master’s Thesis, Tongji University, Shanghai, China, 1987. [Google Scholar]
- Liu, Q.; Ni, G. Transfer Matrix Method in Structural Analysis; China Railway Press: Beijing, China, 1997. [Google Scholar]
- Ai, Z.; Gu, G.; Li, P. Interaction analysis of fractional viscoelastic saturated foundation and laterally loaded piles. Rock Soil Mech. 2022, 43, 2933–2940. [Google Scholar]
- Jiang, J.; Chai, W. Analysis of lateral dynamic response of a single pile in layered foundations based on the Timoshenko–Pasternak model. Adv. Civ. Eng. 2022, 2022, 6913977. [Google Scholar] [CrossRef]
- Zhang, L.; Yue, Z.; Zhao, M.; Peng, W. Force deformation analysis of pile-type piers based on improved Pastornak foundation model. Chin. J. Geotech. Eng. 2022, 44, 10. [Google Scholar]
- Zhu, X.; Li, X. Application of Transfer Matrix Method in Pile Foundation Engineering; Southeast University Press: Nanjing, China, 2022. [Google Scholar]
- Zhao, M. The calculation of piles under simultaneous axial and lateral loading. J. Hunan Univ. (Nat. Sci.) 1987, 14, 68–81. [Google Scholar]
- Cowper, G.R. The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Zhu, M.; Gong, W.; He, X.; Xu, G. Matrix transfer solutions to deformation and internal forces of piles under combined vertical and lateral loads. Rock Soil Mech. 2014, 35, 3281–3288. [Google Scholar]
- Zhu, B.; Xiong, G.; Liu, J.; Sun, Y.; Chen, R. Centrifuge modelling of a large-diameter single pile under lateral loads in sand. Chin. J. Geotech. Eng. 2013, 35, 1807–1815. [Google Scholar]
- Li, X. Study on Large-Diameter Steel Pipe Pile-Soil Interaction of Offshore Wind Power under Lateral Loading. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Byrne, B.W.; McAdam, R.A.; Burd, H.J.; Houlsby, G.T.; Martin, C.M.; Gavin, K.; Doherty, P.; Igoe, E.; Zdravković, L.; Taborda, D.M.G.; et al. Field testing of large diameter piles under lateral loading for offshore wind applications. In Proceedings of the XVI ECSMGE, Geotechnical Engineering for Infrastructure and Development, Edinburgh, UK, 13–17 September 2015; pp. 1255–1260. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Offshore wind turbine monopile foundations: Design perspectives. Ocean. Eng. 2020, 213, 107514. [Google Scholar] [CrossRef]
- Gupta, B.K. Dynamics pile-head stiffness of laterally loaded end-bearing pile in linear viscoelastic soil-a comparative study. Comput. Geotech. 2022, 145, 104654. [Google Scholar] [CrossRef]

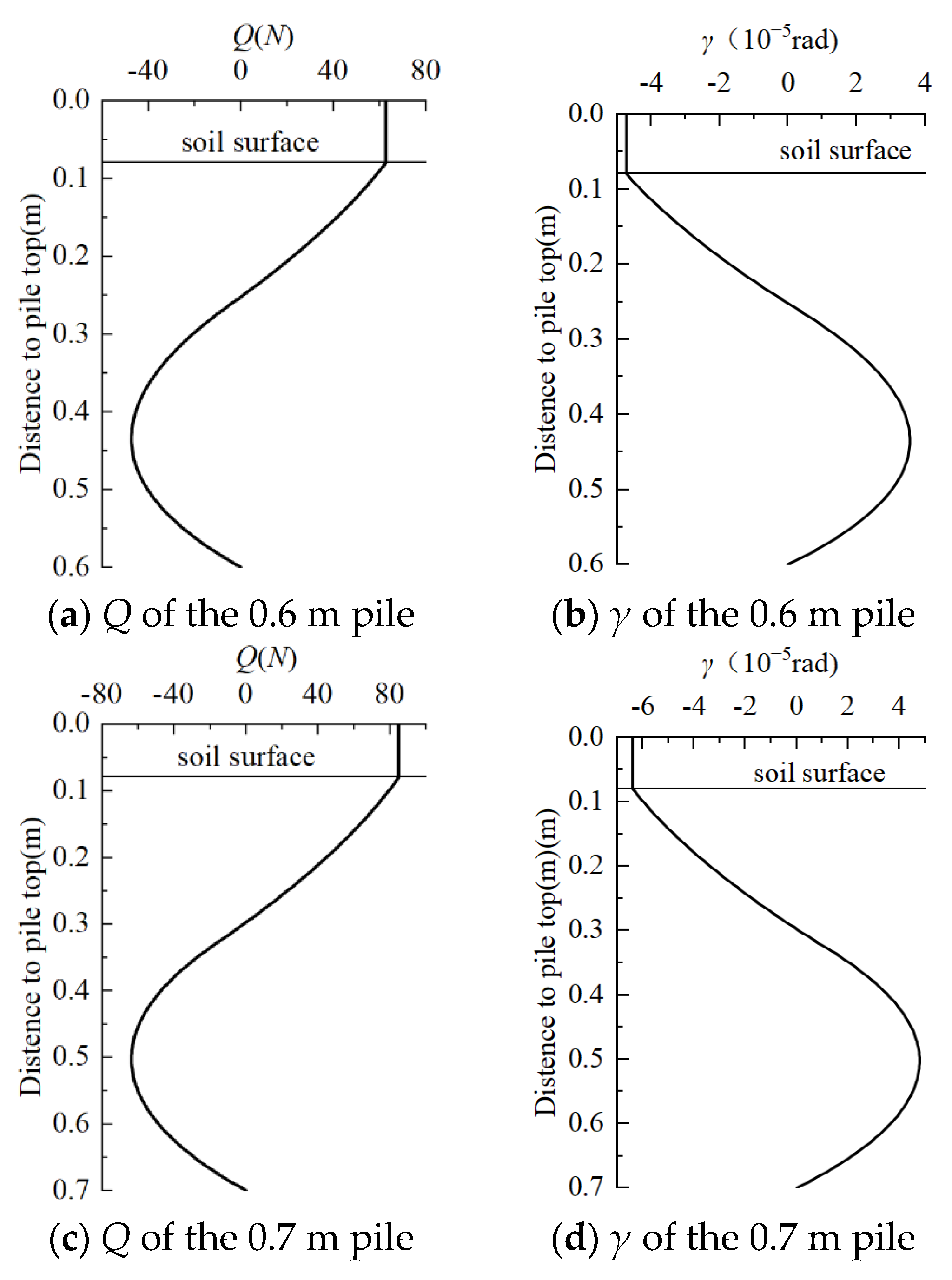
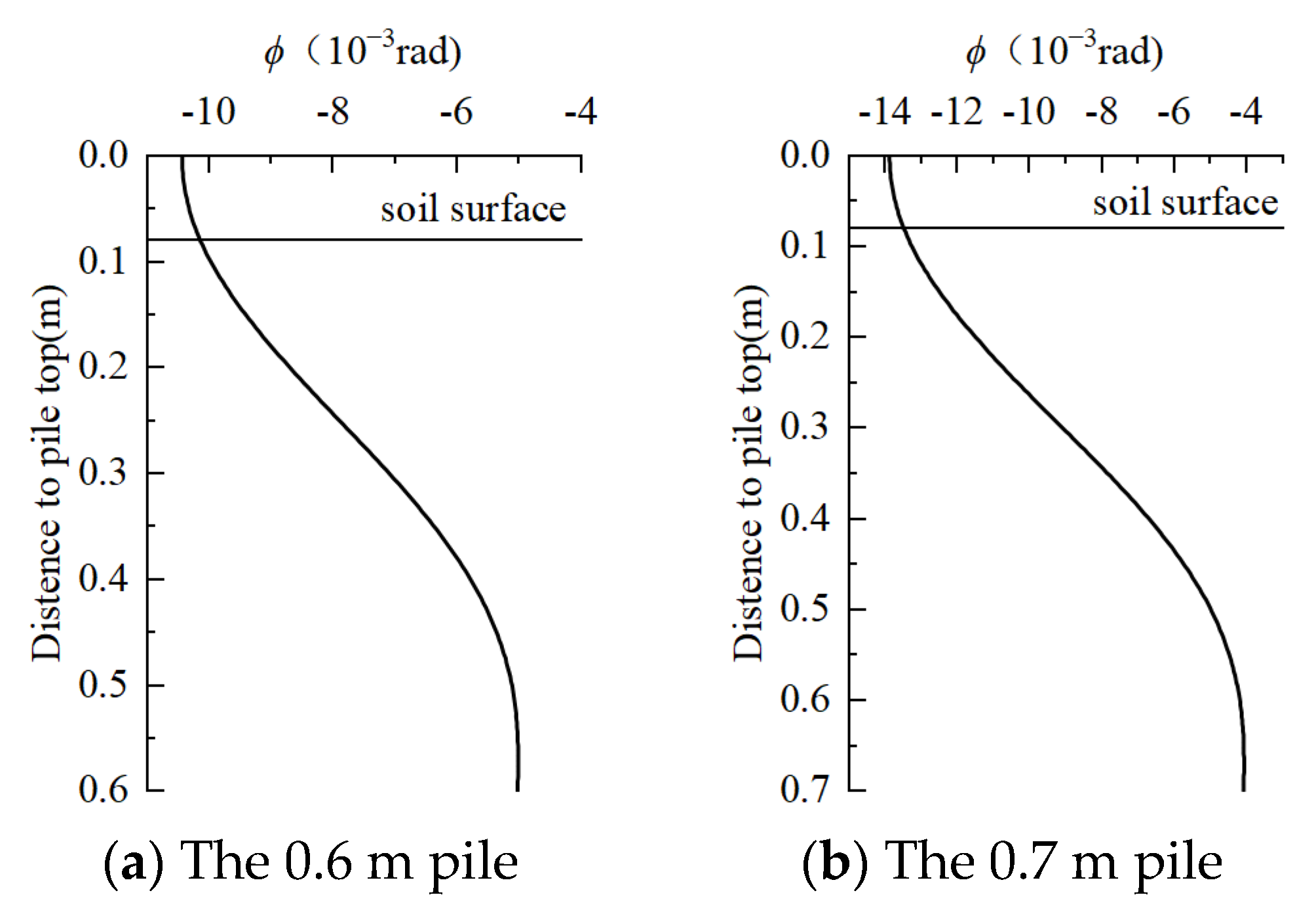
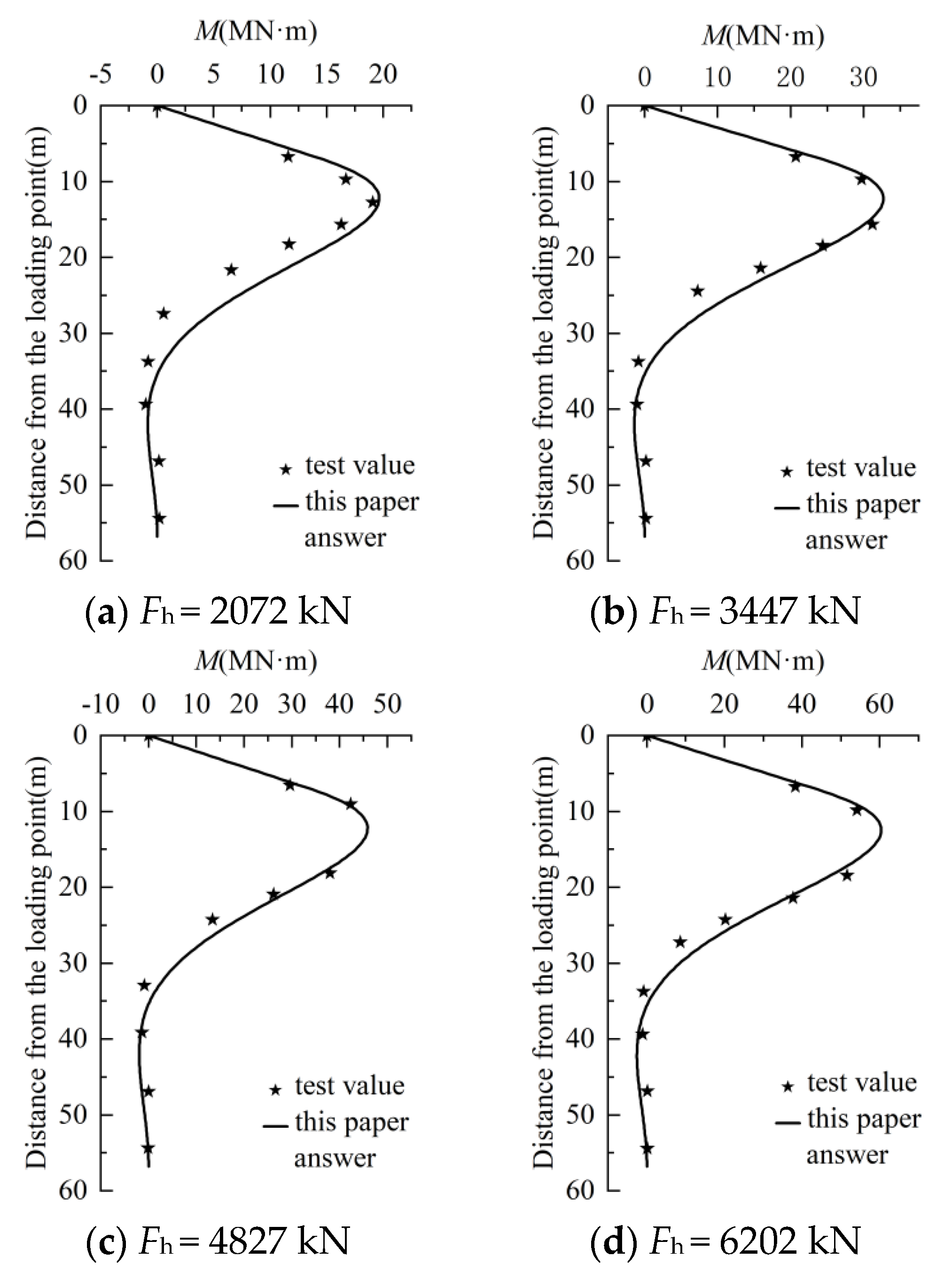
| Mode Pile | L (m) | La (m) | t (m) | EI (kN·m2) | Fh (kN) |
|---|---|---|---|---|---|
| A | 0.6 | 0.08 | 0.001 | 0.684 | 0.0628 |
| B | 0.7 | 0.08 | 0.001 | 0.684 | 0.0849 |
| T | 0.15 | 0.45 | 0.75 | |||||||||||||||
| Pile length/m | 190 | 140 | 110 | 80 | 45 | 25 | 63 | 46 | 37 | 27 | 15.4 | 8.5 | 38 | 27.7 | 22.3 | 16.2 | 9.2 | 5.1 |
| Pile diameter/m | 12 | 8 | 6 | 4 | 2 | 1 | 12 | 8 | 6 | 4 | 2 | 1 | 12 | 8 | 6 | 4 | 2 | 1 |
| L/D ratio | 15.83 | 17.5 | 18.3 | 20 | 22.5 | 25 | 5.25 | 5.75 | 6.17 | 6.75 | 7.7 | 8.5 | 3.17 | 3.46 | 3.72 | 4.05 | 4.6 | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhu, M.; Li, X.; Ling, C.; Wang, T.; Li, X. The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method. Buildings 2024, 14, 1448. https://doi.org/10.3390/buildings14051448
Liu J, Zhu M, Li X, Ling C, Wang T, Li X. The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method. Buildings. 2024; 14(5):1448. https://doi.org/10.3390/buildings14051448
Chicago/Turabian StyleLiu, Jing, Mingxing Zhu, Xiaojuan Li, Chen Ling, Tengfei Wang, and Xuan Li. 2024. "The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method" Buildings 14, no. 5: 1448. https://doi.org/10.3390/buildings14051448
APA StyleLiu, J., Zhu, M., Li, X., Ling, C., Wang, T., & Li, X. (2024). The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method. Buildings, 14(5), 1448. https://doi.org/10.3390/buildings14051448









