Numerical Simulation and Calculation Method Study on Seamless Construction of Super-Length Raft Structures Based on Novel Magnesium Oxide Expansive Strengthening Band Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Establishment
2.1.1. Material Constitutive Relations
2.1.2. Element Type
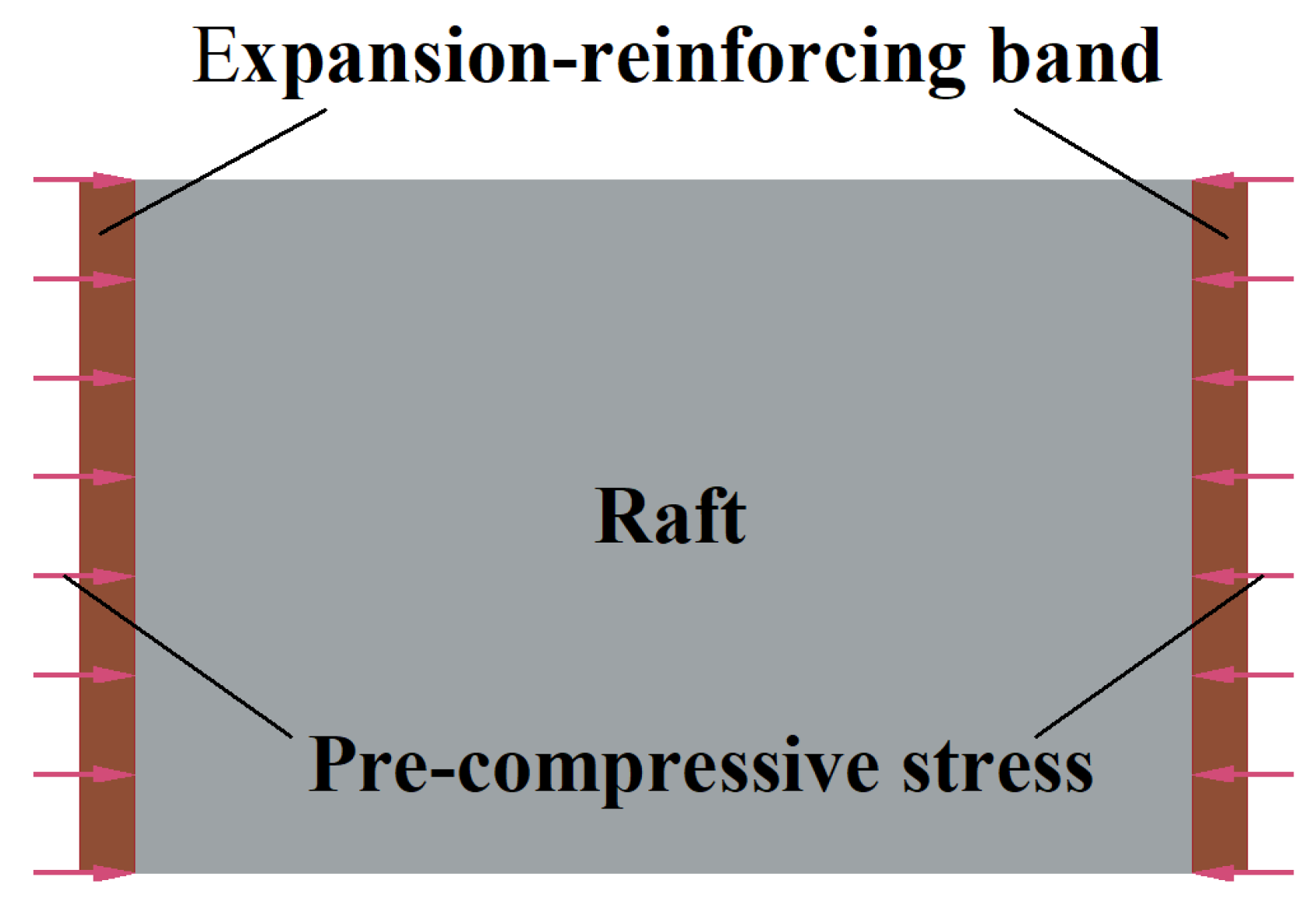
2.1.3. Boundary Conditions
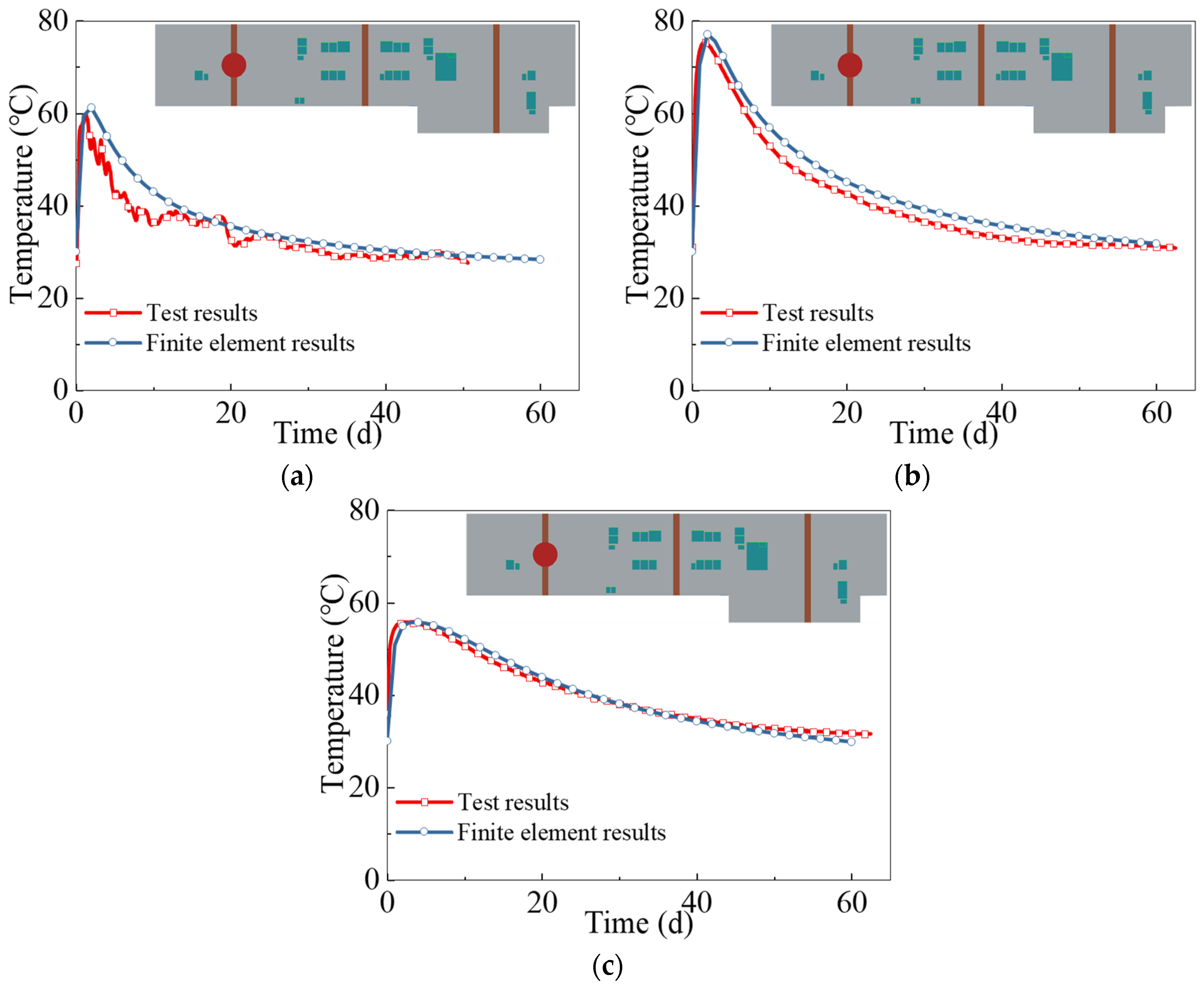
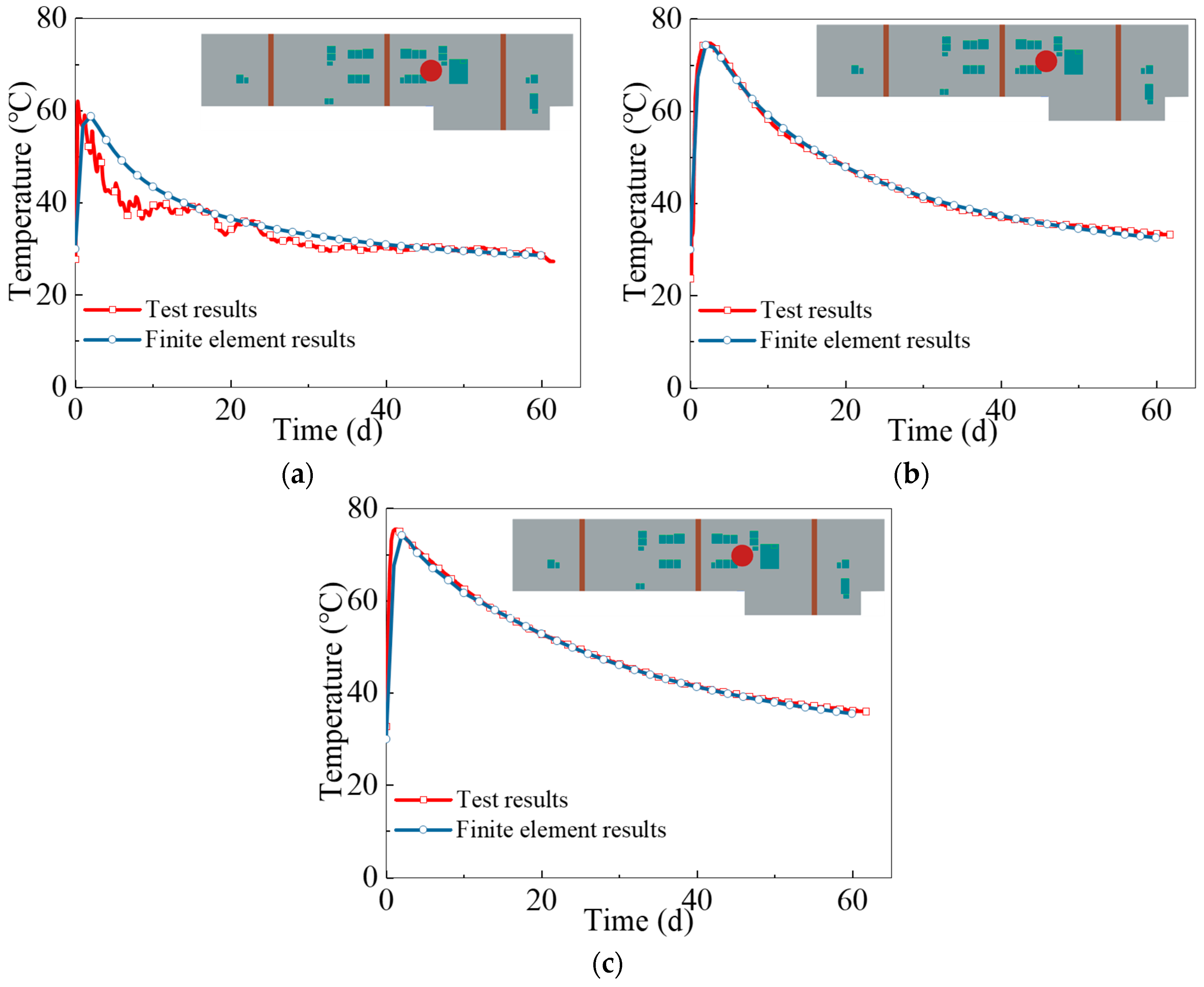
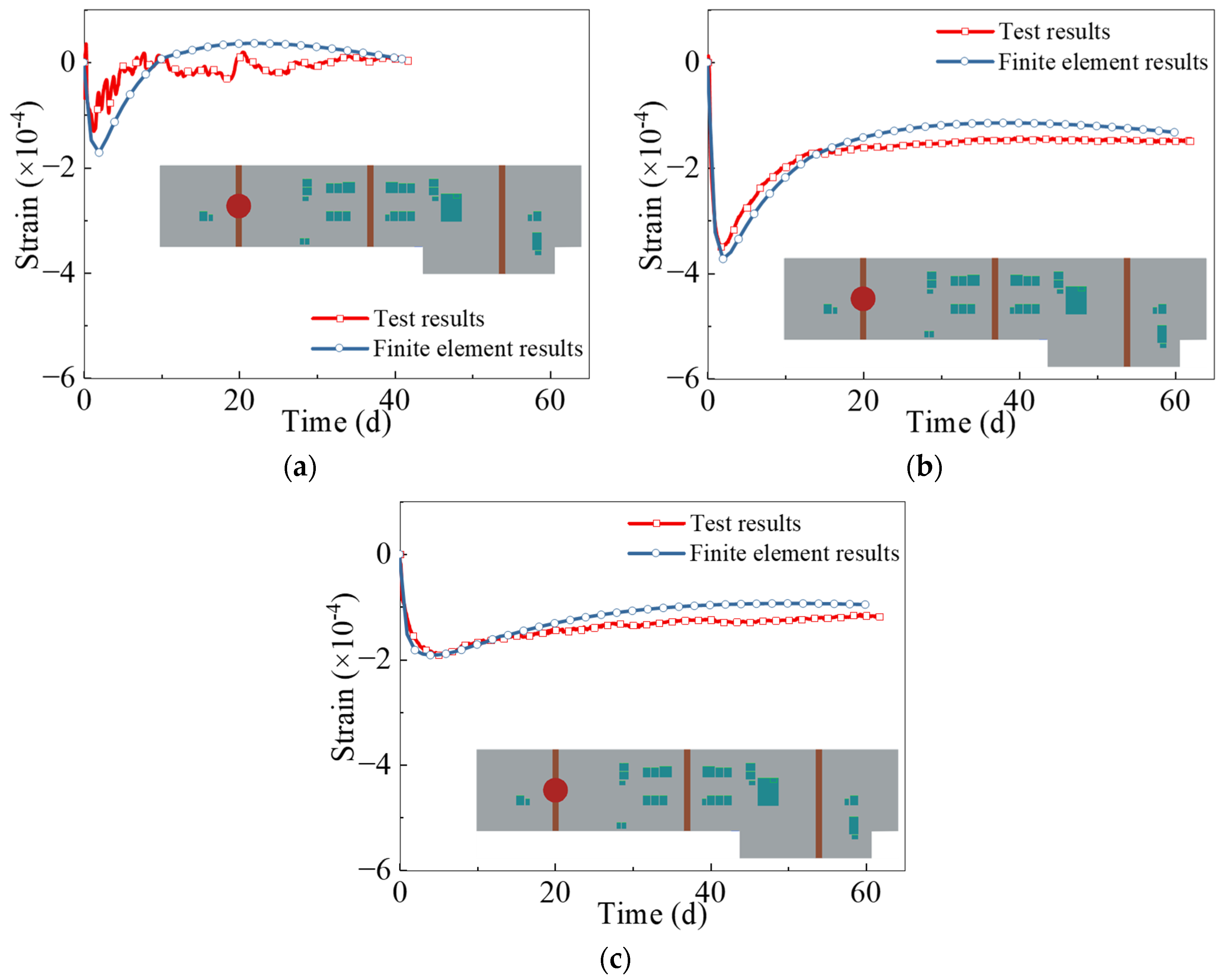
2.2. Numerical Simulation Results and Validation
2.2.1. Principle of Temperature Distribution
2.2.2. Principle of Strain Distribution
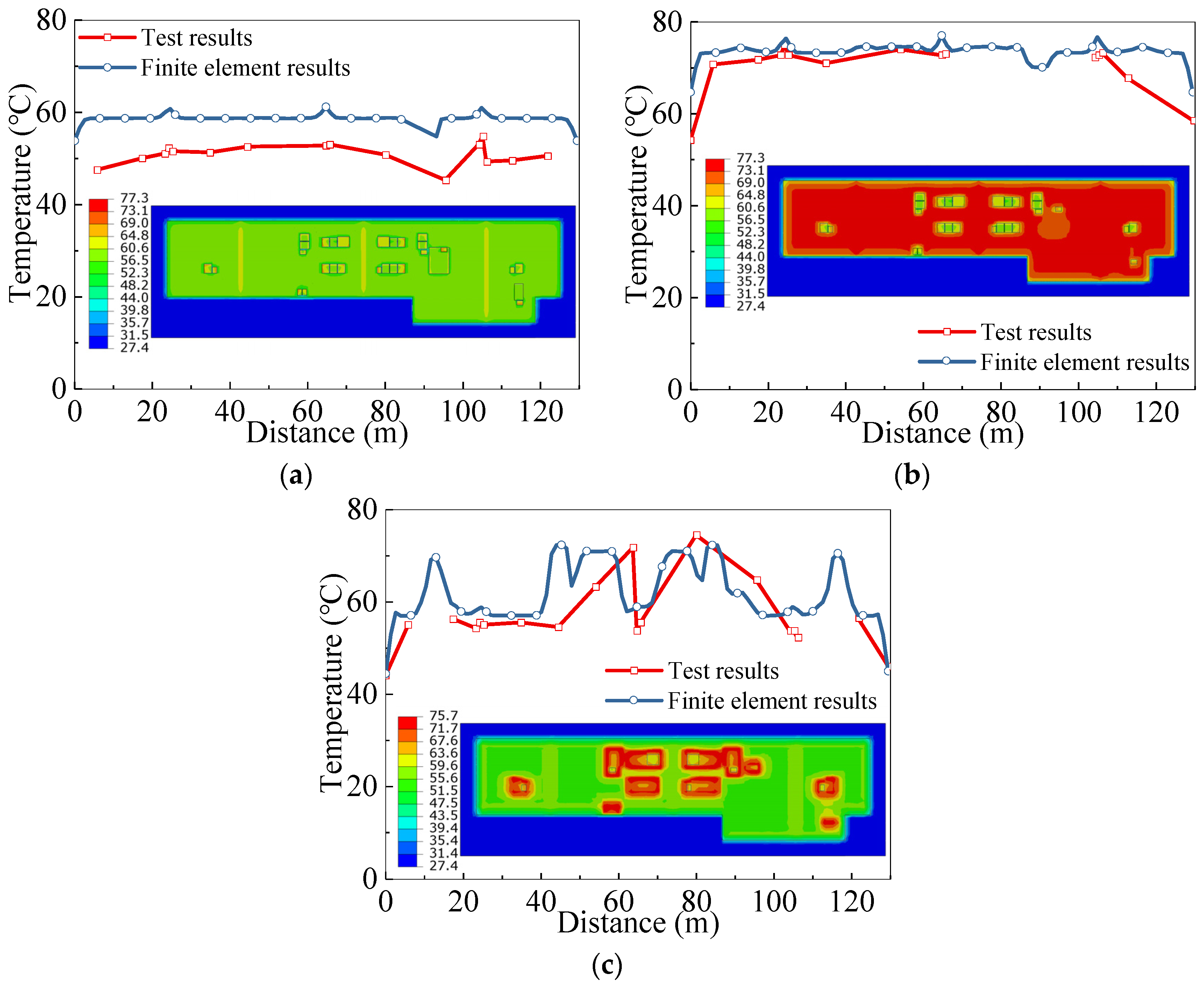
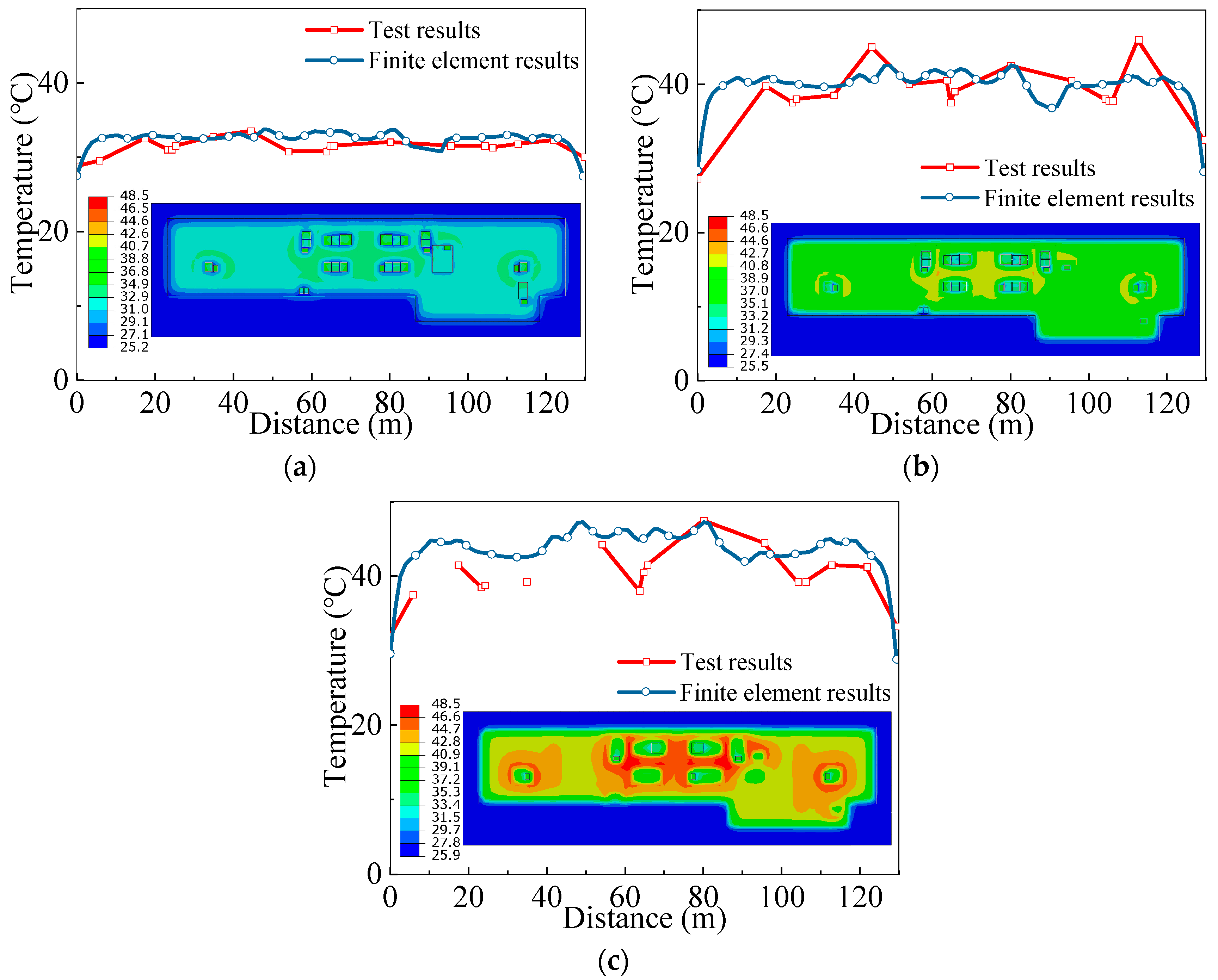
2.2.3. Temperature–Time Characteristic
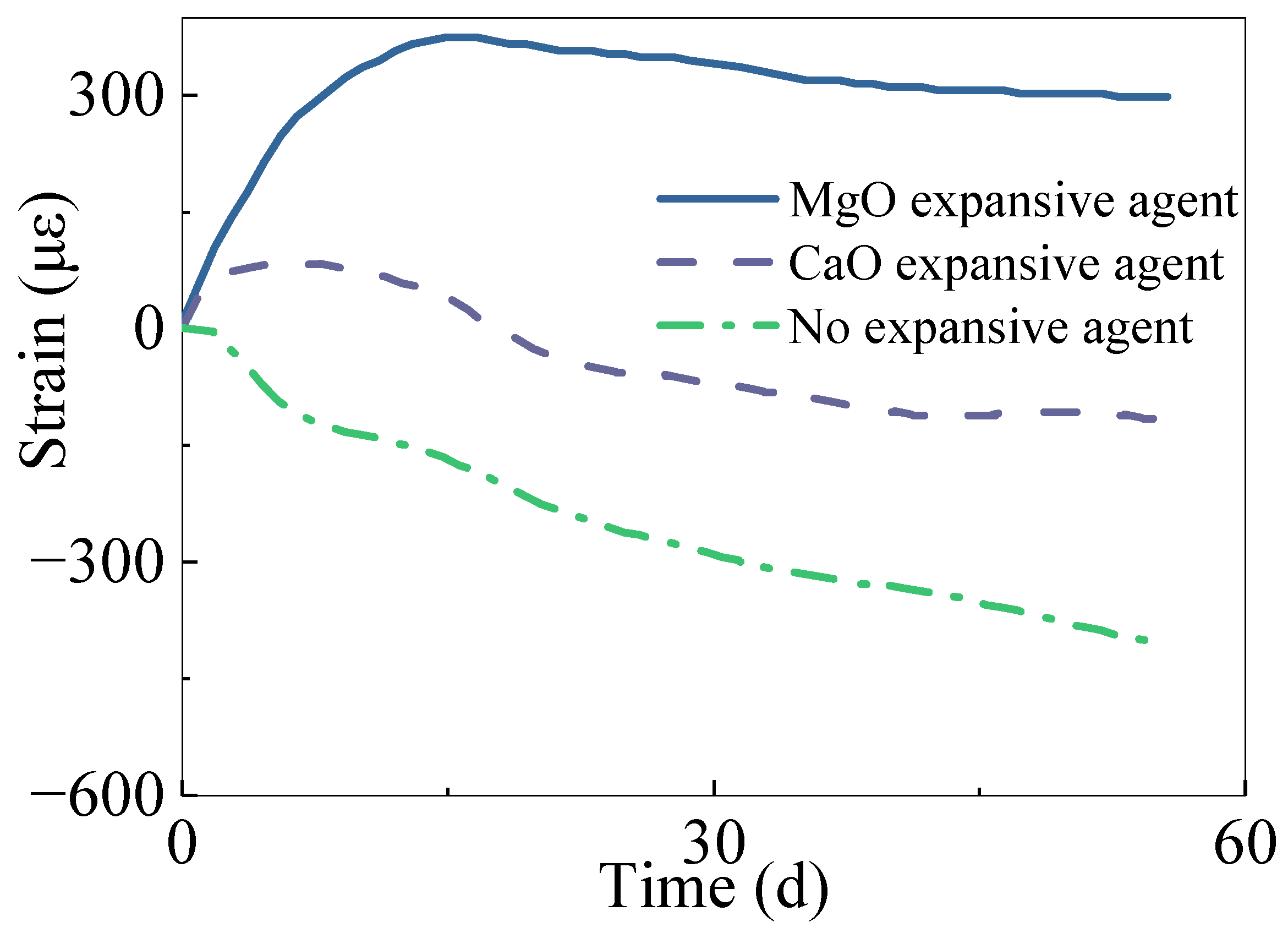
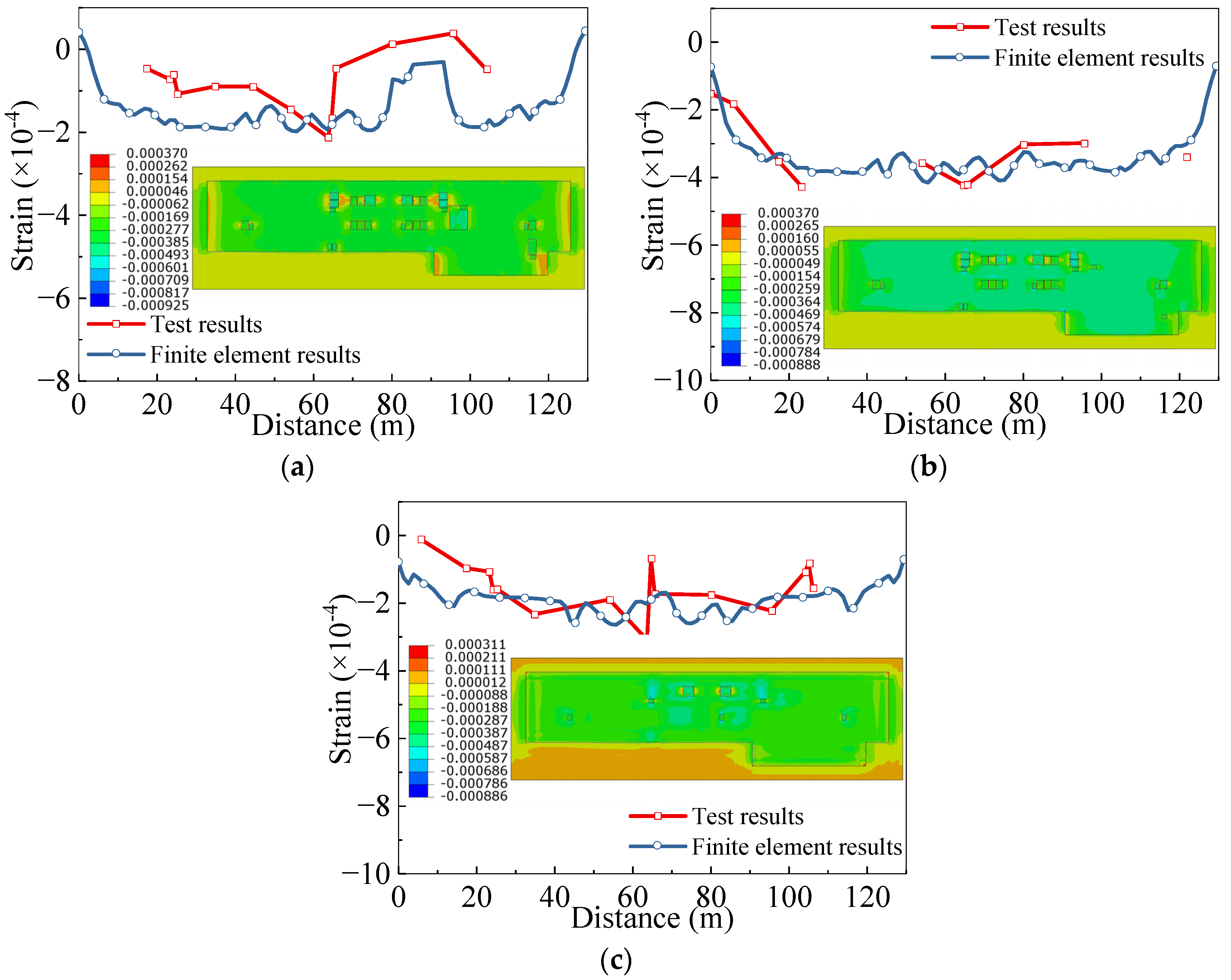
2.2.4. Strain–Time Characteristic
3. Parameter Analysis
3.1. Parameter Analysis Model
3.2. Parameter Analysis Results
3.2.1. The ESB-to-Raft-Width Ratio r
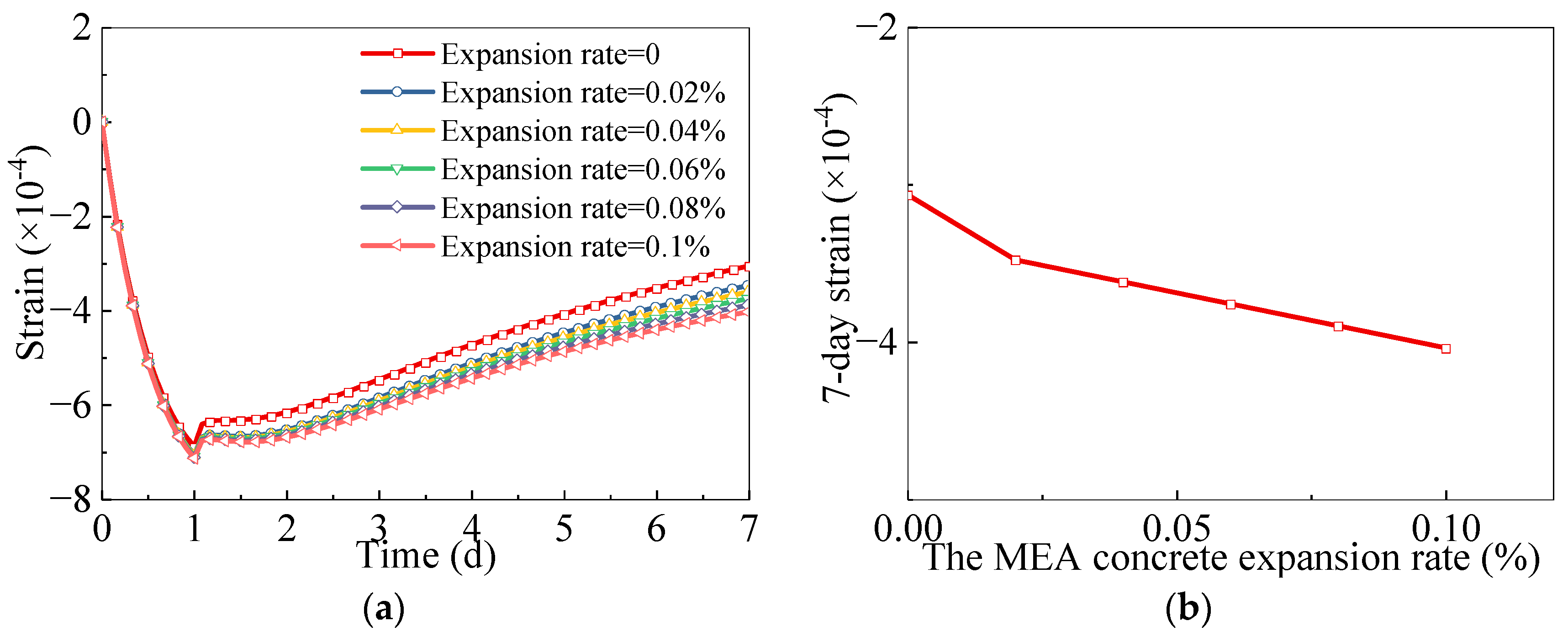
3.2.2. The MEA Concrete Expansion Rate e
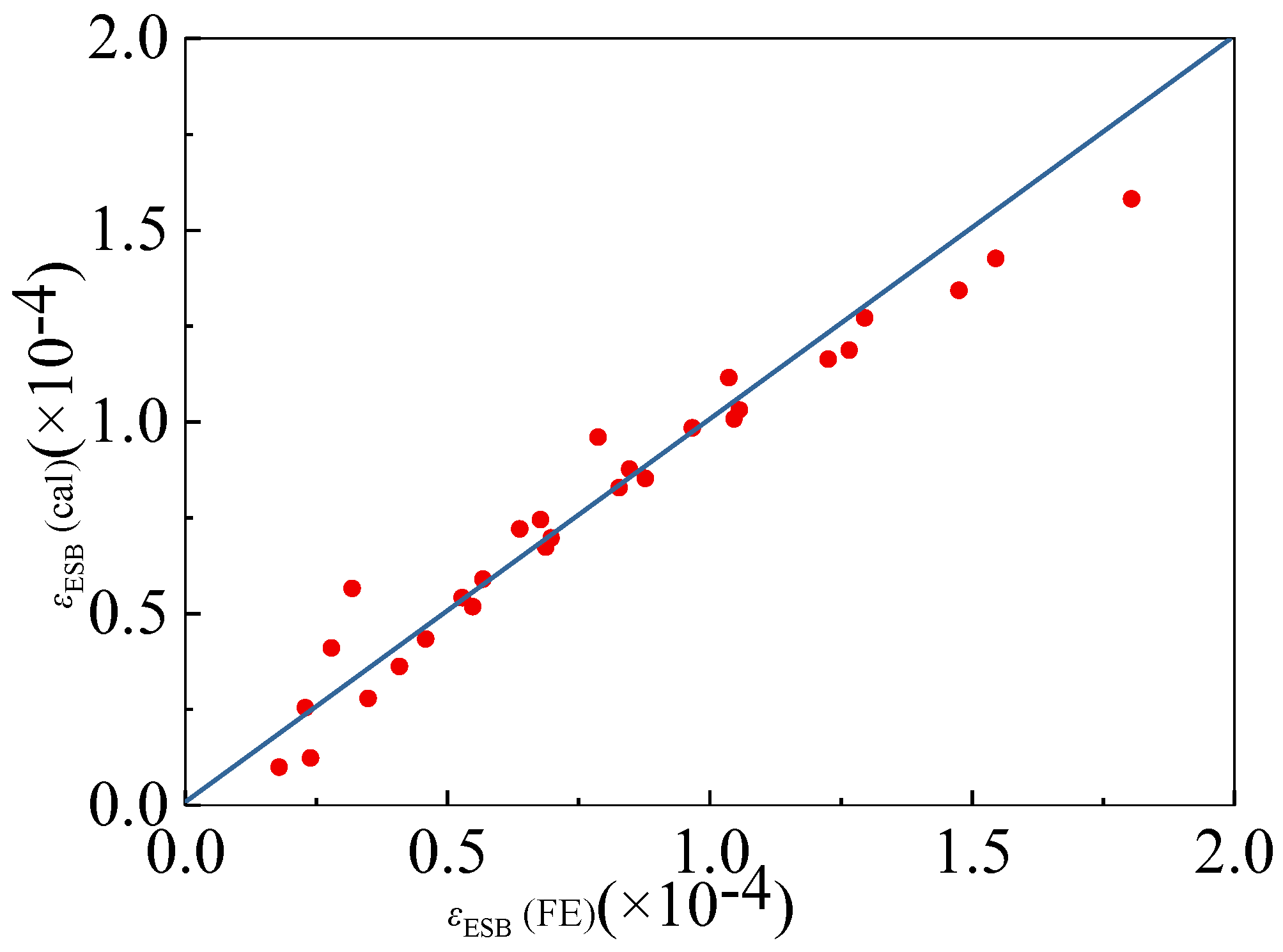
4. Computational Formula
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- You, B.K.; Wu, W.C.; Han, L.L.; Zhang, L.J.; Dong, T.G.; Chen, F.Y. A New Design Method for the Cancellation of Expansion Joints. Build. Struct. 1993, 1, 44–45. [Google Scholar] [CrossRef]
- Zhang, Y.M. Study on Crack Control of Over-Long Concrete Frame Structures. Ph.D. Thesis, Southeast University, Nanjing, China, 2007. [Google Scholar]
- You, B.K.; Li, G.M.; Wang, D.M.; Fang, R.L. Super-length Reinforced Concrete Structures: UEA Continuous Design and Construction Methodologies. Build. Struct. 1998, 6, 21–23. [Google Scholar] [CrossRef]
- Yang, J.; Yang, P.; Wan, Y. Xinfei Sales Building Structural Design. Build. Struct. 2009, 39 (Suppl. 1), 327–330. [Google Scholar] [CrossRef]
- Zhang, J.G.; Li, S.H.; Wang, L.B. Application of UEA Concrete Expansive Strengthening Band Seamless Design in Engineering. Coal Eng. 2003, 10, 20–21. [Google Scholar]
- Jin, J.M. Design Suggestion about Crack Precaution and Reduction Caused by Temperature and Shrinkage Jointly in Over-long Concrete Structures. Ind. Archit. 2002, 6, 57–59. [Google Scholar]
- Li, W.B.; Zhong, W.P.; Song, C.Y. The Technical Measures of Crack Control for Bed Plate Engineering. Ind. Archit. 2005, S1, 908–910. [Google Scholar]
- Dong, P.; Lin, B.X. Seismic Analysis and Crack Control of the Superlong and Superwide Structure with Multi-Tower Buildings. J. Hefei Univ. Technol. Nat. Sci. 2001, 1, 106–111. [Google Scholar]
- Zhou, Q.; Lachowski, E.E.; Glasser, F.P. A Decomposition Product of Ettringite. Cem. Concr. Res. 2004, 34, 703–710. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhang, S.Z.; Tian, Q.; Guo, F.; Wang, Y. Deformation Behavior of High Performance Concrete Containing MgO Composite Expansive Agent. J. Southeast Univ. Nat. Sci. Ed. 2010, 40 (Suppl. 2), 150–154. [Google Scholar]
- Mo, L.W.; Deng, M.; Tang, M.S. Effects of calcination condition on expansion property of MgO-type expansive agent used in cement-based materials. Cem. Concr. Res. 2010, 40, 437–446. [Google Scholar] [CrossRef]
- Mo, L.W.; Liu, M.; Al-Tabbaa, A.; Deng, M.; Lau, W.Y. Deformation and mechanical properties of quaternary blended cements containing ground granulated blast furnace slag, fly ash, and magnesia. Cem. Concr. Res. 2015, 71, 7–13. [Google Scholar] [CrossRef]
- Mo, L.W.; Liu, M.; Al-Tabbaa, A.; Deng, M. Deformation and mechanical properties of the expansive cements produced by inter-grinding cement clinker and MgOs with various reactivities. Constr. Build. Mater. 2015, 80, 1–8. [Google Scholar] [CrossRef]
- Mo, L.W.; Fang, J.W.; Hou, W.H.; Ji, X.K.; Yang, J.B.; Fan, T.T.; Wang, H.L. Synergetic effects of curing temperature and hydration reactivity of MgO expansive agents on their hydration and expansion behaviours in cement pastes. Constr. Build. Mater. 2019, 207, 206–217. [Google Scholar] [CrossRef]
- Mo, L.W.; Deng, M.; Wang, A. Effects of MgO-based expansive additive on compensating the shrinkage of cement paste under non-wet curing conditions. Cem. Concr. Compos. 2012, 34, 377–383. [Google Scholar] [CrossRef]
- Mo, L.W.; Fang, J.W.; Huang, B.; Wang, A.G.; Deng, M. Combined effects of biochar and MgO expansive additive on the autogenous shrinkage, internal relative humidity, and compressive strength of cement pastes. Constr. Build. Mater. 2019, 229, 116877. [Google Scholar] [CrossRef]
- Jiao, M.P.; Wang, P.G.; Tian, L.; Cui, D.B.; Zhao, T.J.; Sun, X.G. Influence of S-type Magnesia Expansive Agent on Micro-structure, Shrinkage and Durability of Concrete. J. Chin. Ceram. Soc. 2023, 51, 2905–2913. [Google Scholar] [CrossRef]
- Li, P.; Miao, M.; Miao, F.; Jiang, H.W.; Ma, X.J. Research progress of deformation performance of shrinkage-compensated concrete. Bull. Chin. Ceram. Soc. 2016, 35, 192–197, 208. [Google Scholar] [CrossRef]
- Li, P.; Miao, M.; Ma, X. Effect of expansive agent on the performance of shrinkage-compensated concrete. Bull. Chin. Ceram. Soc. 2016, 35, 167–173. [Google Scholar] [CrossRef]
- Klemczak, B.; Żmij, A. Reliability of standard methods for evaluating the early-age cracking risk of thermal-shrinkage origin in concrete walls. Constr. Build. Mater. 2019, 226, 651–661. [Google Scholar] [CrossRef]
- Jędrzejewska, A.; Kanavaris, F.; Zych, M.; Schlicke, D.; Azenha, M. Experiences on early age cracking of wall-on-slab concrete structures. Structures 2020, 27, 2520–2549. [Google Scholar] [CrossRef]
- ACI 207.2R-07; Report on Thermal and Volume Change Effects on Cracking of Mass Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2007; ACI Committee 207.
- EN 1992-1-1; Eurocode 2–Design of Concrete Structures–Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2008.
- EN 1992-3; Eurocode 2–Design of Concrete Structures–Part 3: Liquid Retaining and Containment Structures. European Committee for Standardization: Brussels, Belgium, 2006.
- Japanese Concrete Institute. Guidelines for Control of Cracking of Mass Concrete 2016; Japanese Concrete Institute: Tokyo, Japan, 2017. [Google Scholar]
- EN 1991-4; Eurocode 1: Actions on structures–Part 4: Silos and Tanks. European Committee for Standardization: Brussels, Belgium, 2006.
- Bamforth, P.B. CIRIA C766: Control of Cracking Caused by Restrained Deformation in Concrete; CIRIA: London, UK, 2007. [Google Scholar]
- Smolana, A.; Klemczak, B.; Azenha, M.; Schlicke, D. Early age cracking risk in a massive concrete foundation slab: Comparison of analytical and numerical prediction models with on-site measurements. Constr. Build. Mater. 2021, 301, 124135. [Google Scholar] [CrossRef]
- Klemczak, B.; Flaga, K.; Knoppik-Wróbel, A. Analytical model for evaluation of thermal-shrinkage strains and stresses in RC wall-on-slab structures. Arch. Civ. Mech. Eng. 2017, 17, 75–95. [Google Scholar] [CrossRef]
- Klemczak, B.; Knoppik-Wróbel, A. Reinforced concrete tank walls and bridge abutments: Early-age behaviour, analytic approaches and numerical models. Eng. Struct. 2015, 84, 233–251. [Google Scholar] [CrossRef]
- Li, X.; Yu, Z.; Chen, K.; Deng, C.; Yu, F. Investigation of temperature development and cracking control strategies of mass concrete: A field monitoring case study. Case Stud. Constr. Mater. 2023, 18, e02144. [Google Scholar] [CrossRef]
- Kanavaris, F.; Jędrzejewska, A.; Sfikas, I.P.; Schlicke, D.; Kuperman, S.; Šmilauer, V.; Honório, T.; Fairbairn, E.M.R.; Valentim, G.; de Faria, E.F.; et al. Enhanced massivity index based on evidence from case studies: Towards a robust pre-design assessment of early-age thermal cracking risk and practical recommendations. Constr. Build. Mater. 2021, 271, 121570. [Google Scholar] [CrossRef]
- Azenha, M.; Kanavaris, F.; Schlicke, D.; Jędrzejewska, A.; Benboudjema, F.; Honorio, T.; Šmilauer, V.; Serra, C.; Forth, J.; Riding, K.; et al. Recommendations of RILEM TC 287-CCS: Thermo-chemo-mechanical modelling of massive concrete structures towards cracking risk assessment. Mater. Struct. 2021, 54, 135. [Google Scholar] [CrossRef]
- Han, B.; Wang, H.; Liao, H.; Dai, C.; Zhao, Y.; Xu, W.; Zhou, G.; Shi, C. Investigation into the seamless construction for hundred-meter scale super-length raft structure based on magnesia expansive agent concrete. Front. Mater. 2024, 11, 1367600. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- SL/T 352-2020; Test Code for Hydraulic Concrete. China Water & Power Press: Beijing, China, 2020. (In Chinese)
- CEB-FIP. CEB-FIP Model Code 1990; Thomas Telford: London, UK, 1993. [Google Scholar]
- GB 50496-2018; Standard for Construction of Mass Concrete. China Architecture & Building Press: Beijing, China, 2018. (In Chinese)
- Liu, F.; Shen, S.-L.; Hou, D.-W.; Arulrajah, A.; Horpibulsuk, S. Enhancing behavior of large volume undersubgrade concrete structures using expansive agents. Constr. Build. Mater. 2016, 114, 49–55. [Google Scholar] [CrossRef]
- GB 50119-2013; Code for Concrete Admixture Application. China Construction Publishing Media Co., Ltd.: Beijing, China, 2014. (In Chinese)
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B Methodol. 1951, 13, 1–45. [Google Scholar] [CrossRef]





| Material Name | Density (kg/m3) | Specific Heat (kJ/(kg·K)) | Conductivity ((kJ/(m·s·K)) | 28-Day Cube Compressive Strength (MPa) |
|---|---|---|---|---|
| C35 | 2360 | 0.947 | 9.5506 | 45.9 |
| C40 | 2398 | 0.943 | 9.5399 | 52.1 |
| Condition Identifier | r | e (%) | ε7-day (×10−4) | Condition Identifier | r | e (%) | ε7-day (×10−4) |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | −3.07 | 17 | 0.13 | 0.02 | −3.60 |
| 2 | 0.03 | 0.02 | −3.21 | 18 | 0.13 | 0.04 | −3.77 |
| 3 | 0.03 | 0.04 | −3.25 | 19 | 0.13 | 0.06 | −3.95 |
| 4 | 0.03 | 0.06 | −3.30 | 20 | 0.13 | 0.08 | −4.12 |
| 5 | 0.03 | 0.08 | −3.35 | 21 | 0.13 | 0.1 | −4.30 |
| 6 | 0.03 | 0.1 | −3.39 | 22 | 0.16 | 0.02 | −3.71 |
| 7 | 0.06 | 0.02 | −3.31 | 23 | 0.16 | 0.04 | −3.92 |
| 8 | 0.06 | 0.04 | −3.42 | 24 | 0.16 | 0.06 | −4.13 |
| 9 | 0.06 | 0.06 | −3.53 | 25 | 0.16 | 0.08 | −4.34 |
| 10 | 0.06 | 0.08 | −3.64 | 26 | 0.16 | 0.1 | −4.55 |
| 11 | 0.06 | 0.1 | −3.75 | 27 | 0.2 | 0.02 | −3.86 |
| 12 | 0.1 | 0.02 | −3.48 | 28 | 0.2 | 0.04 | −4.11 |
| 13 | 0.1 | 0.04 | −3.62 | 29 | 0.2 | 0.06 | −4.37 |
| 14 | 0.1 | 0.06 | −3.76 | 30 | 0.2 | 0.08 | −4.62 |
| 15 | 0.1 | 0.08 | −3.90 | 31 | 0.2 | 0.1 | −4.88 |
| 16 | 0.1 | 0.1 | −4.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, H.; Tan, Y.; Dai, C.; Pu, J.; Han, B. Numerical Simulation and Calculation Method Study on Seamless Construction of Super-Length Raft Structures Based on Novel Magnesium Oxide Expansive Strengthening Band Method. Buildings 2024, 14, 1531. https://doi.org/10.3390/buildings14061531
Liao H, Tan Y, Dai C, Pu J, Han B. Numerical Simulation and Calculation Method Study on Seamless Construction of Super-Length Raft Structures Based on Novel Magnesium Oxide Expansive Strengthening Band Method. Buildings. 2024; 14(6):1531. https://doi.org/10.3390/buildings14061531
Chicago/Turabian StyleLiao, Hong, Yuan Tan, Chao Dai, Jie Pu, and Bin Han. 2024. "Numerical Simulation and Calculation Method Study on Seamless Construction of Super-Length Raft Structures Based on Novel Magnesium Oxide Expansive Strengthening Band Method" Buildings 14, no. 6: 1531. https://doi.org/10.3390/buildings14061531
APA StyleLiao, H., Tan, Y., Dai, C., Pu, J., & Han, B. (2024). Numerical Simulation and Calculation Method Study on Seamless Construction of Super-Length Raft Structures Based on Novel Magnesium Oxide Expansive Strengthening Band Method. Buildings, 14(6), 1531. https://doi.org/10.3390/buildings14061531






