Modeling Schemes and Performance Comparisons of Unbonded and Partially Bonded Tendon in Post-Tensioned Concrete Beam
Abstract
:1. Introduction
2. Modeling Schemes for Unbonded and Partially Bonded Tendons
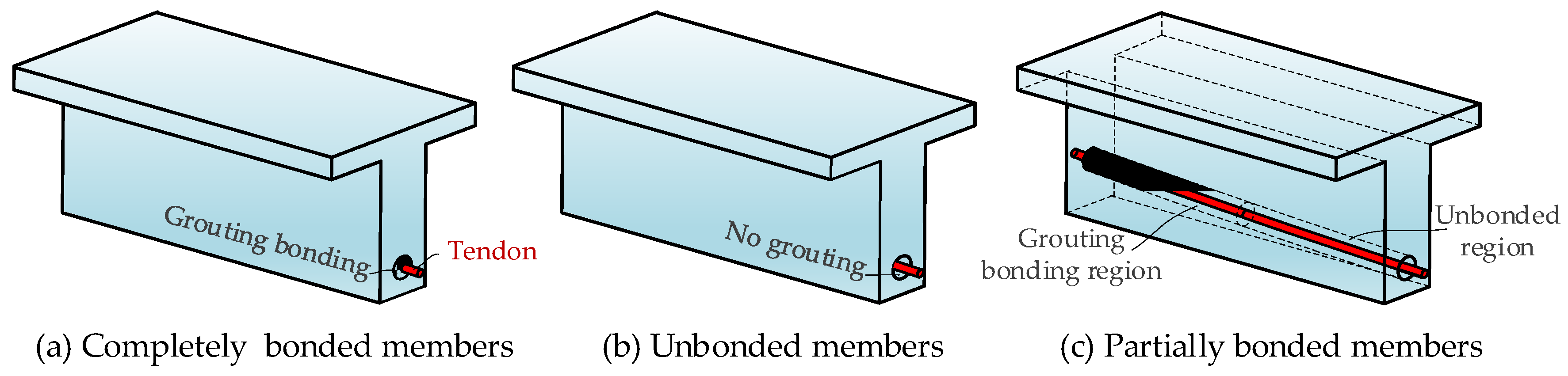
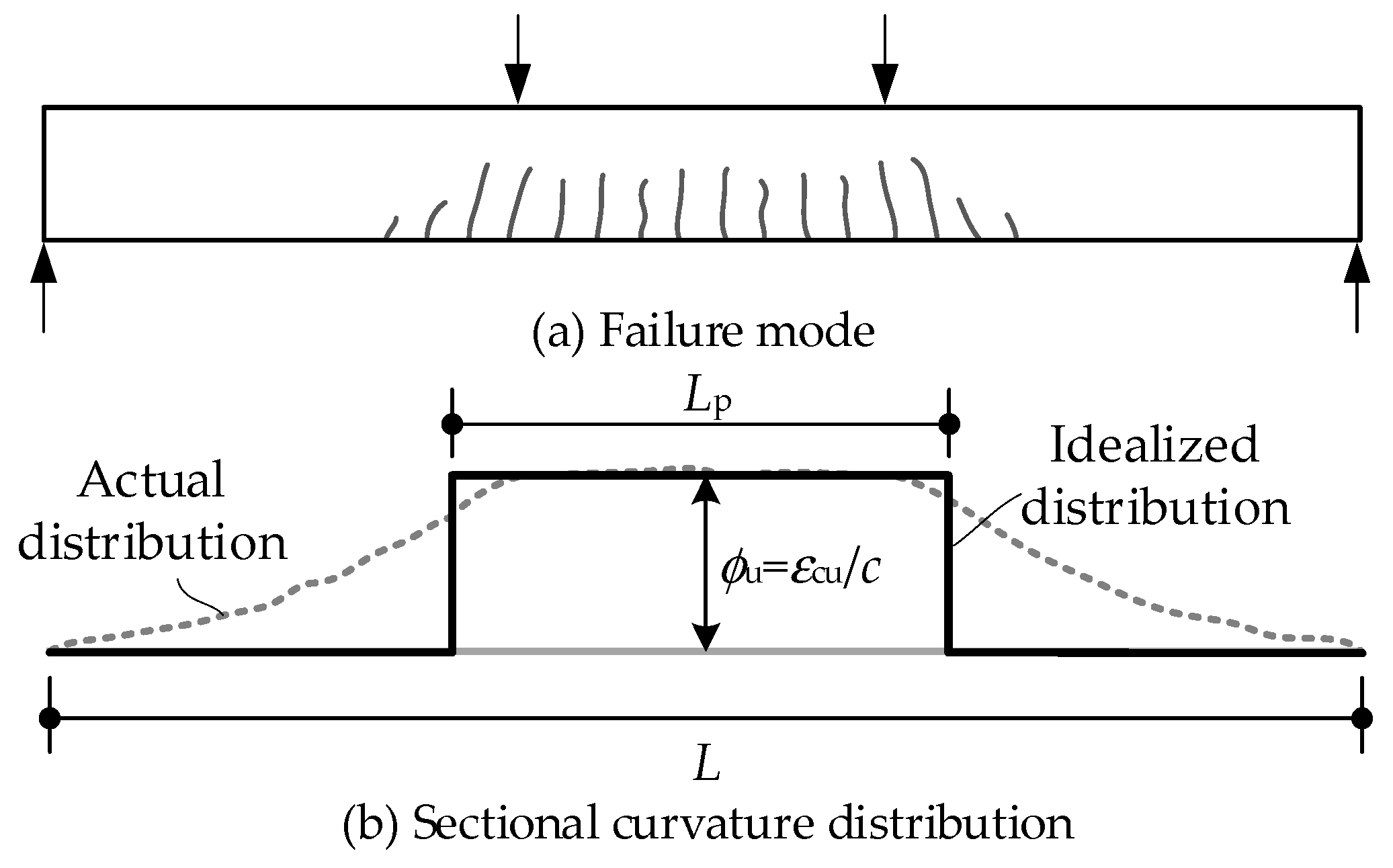
2.1. Mechanical Characteristics of Post-Tensioned Concrete Beams with Different Bonding Conditions
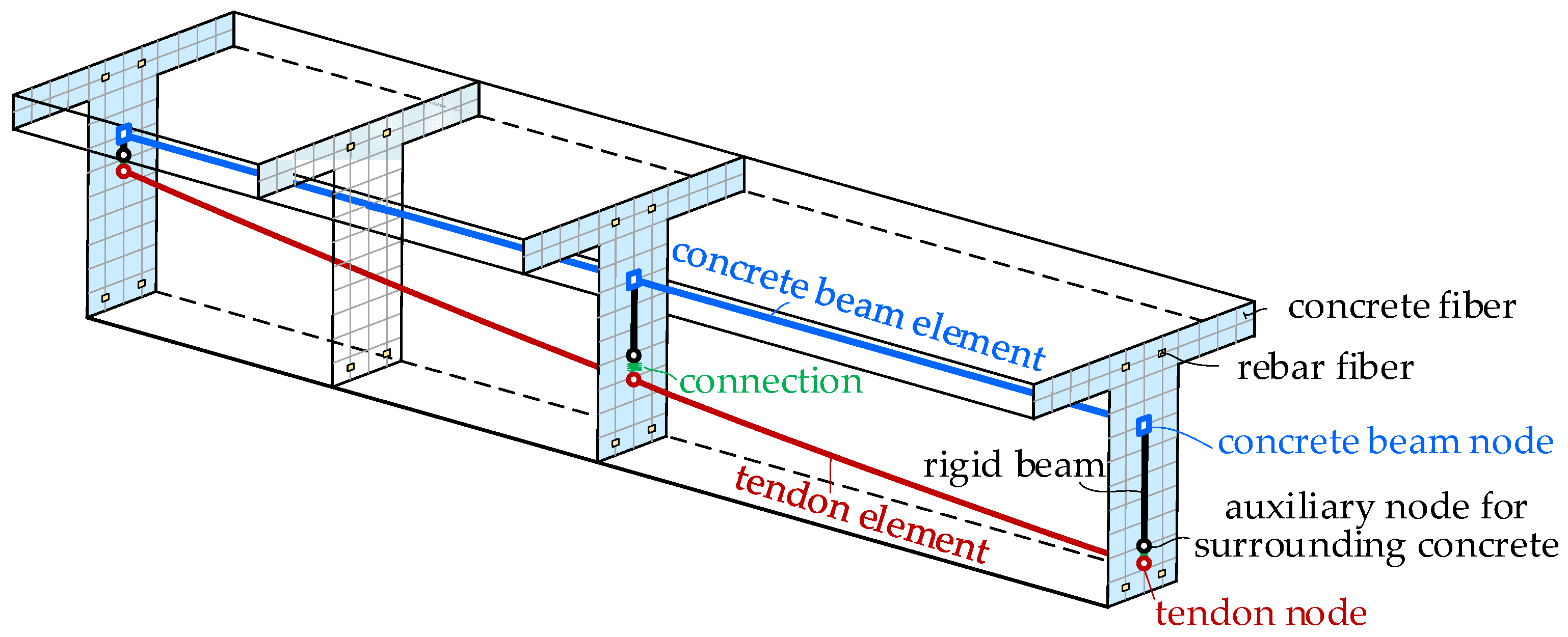
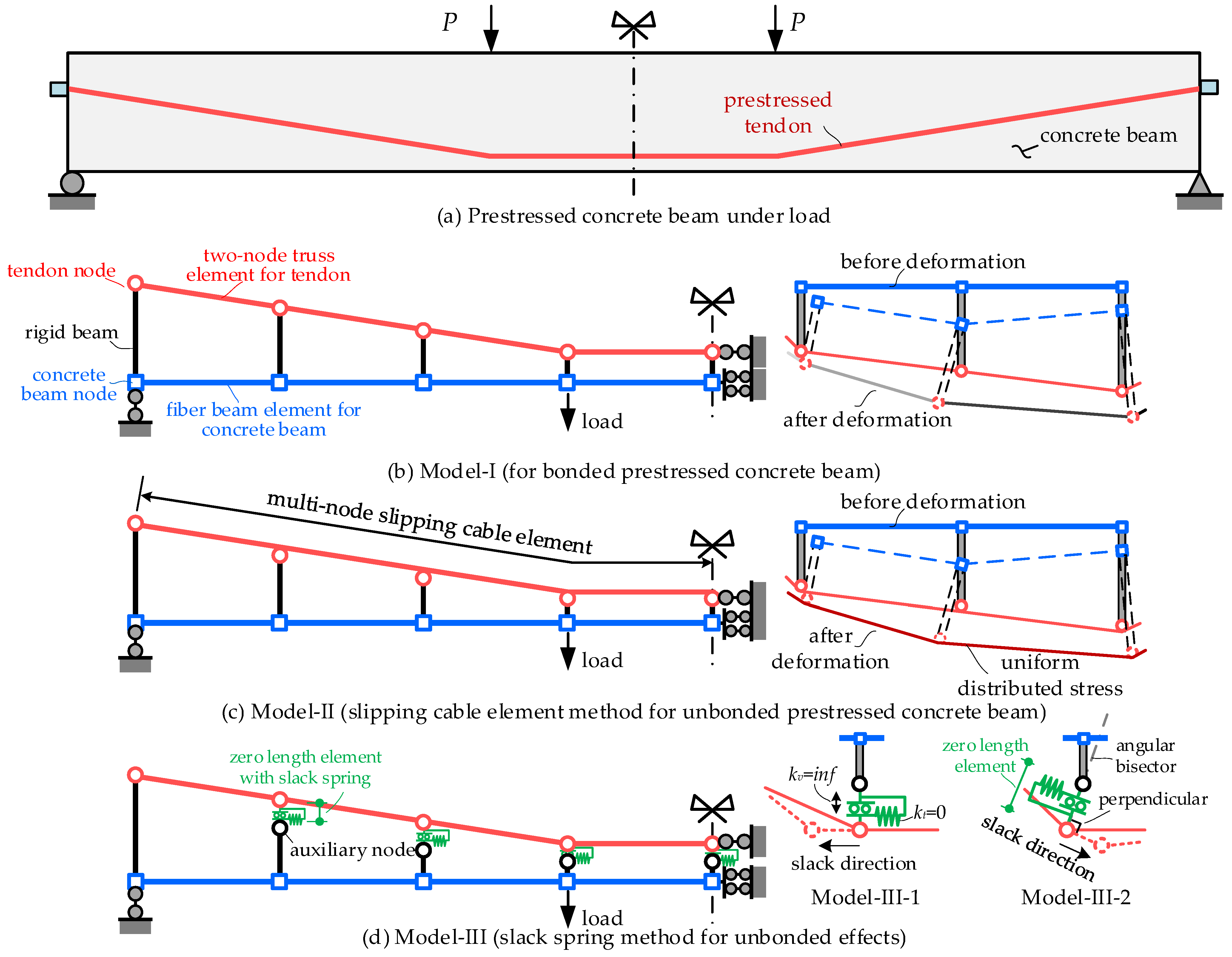
2.2. Modeling Schemes and Applicability Comparisons
2.3. Computational Procedure
3. Model Verification
3.1. Externally Prestressed Concrete Beam
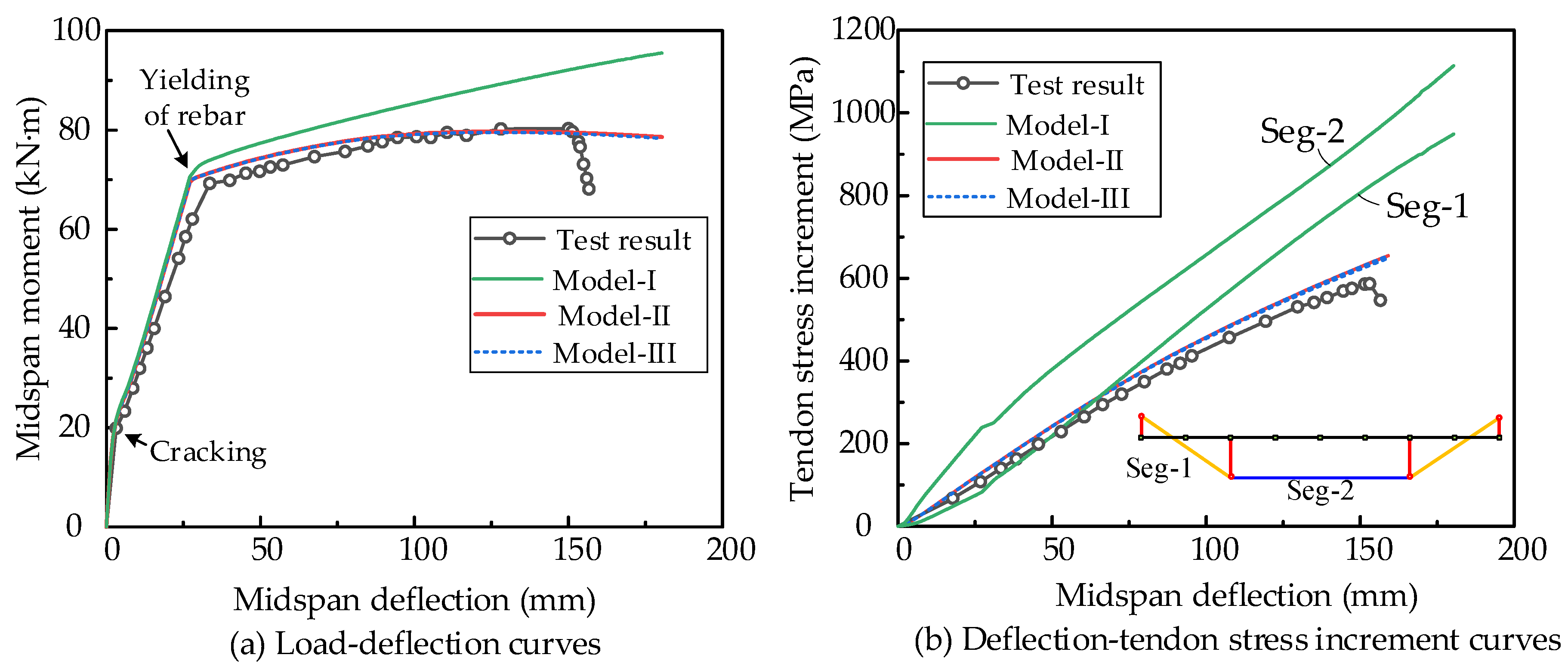
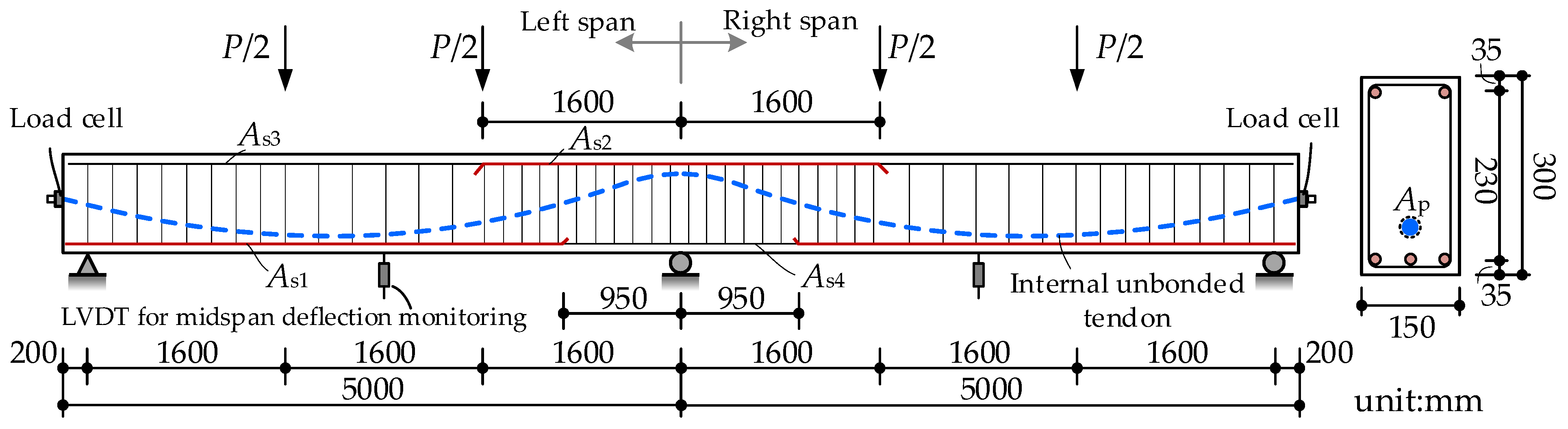
3.2. Internal Unbonded Prestressed Concrete Beam
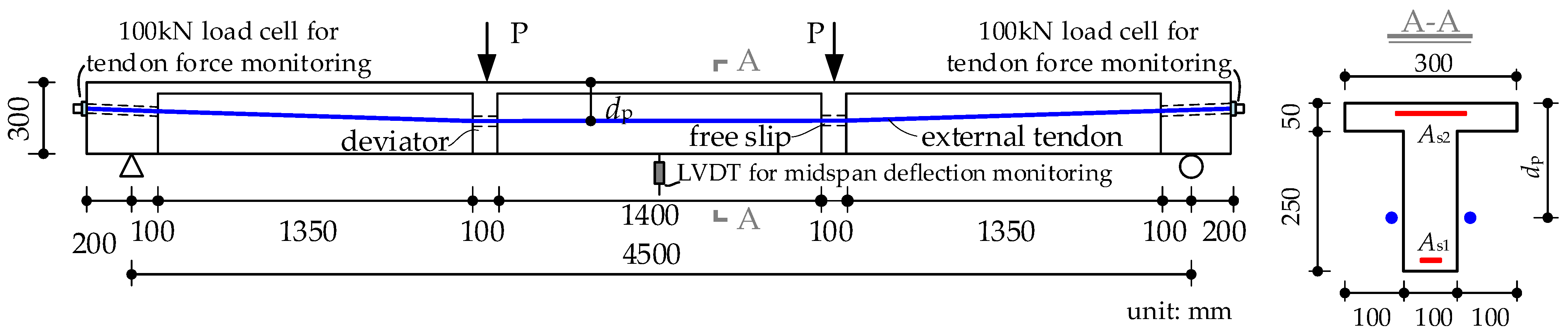
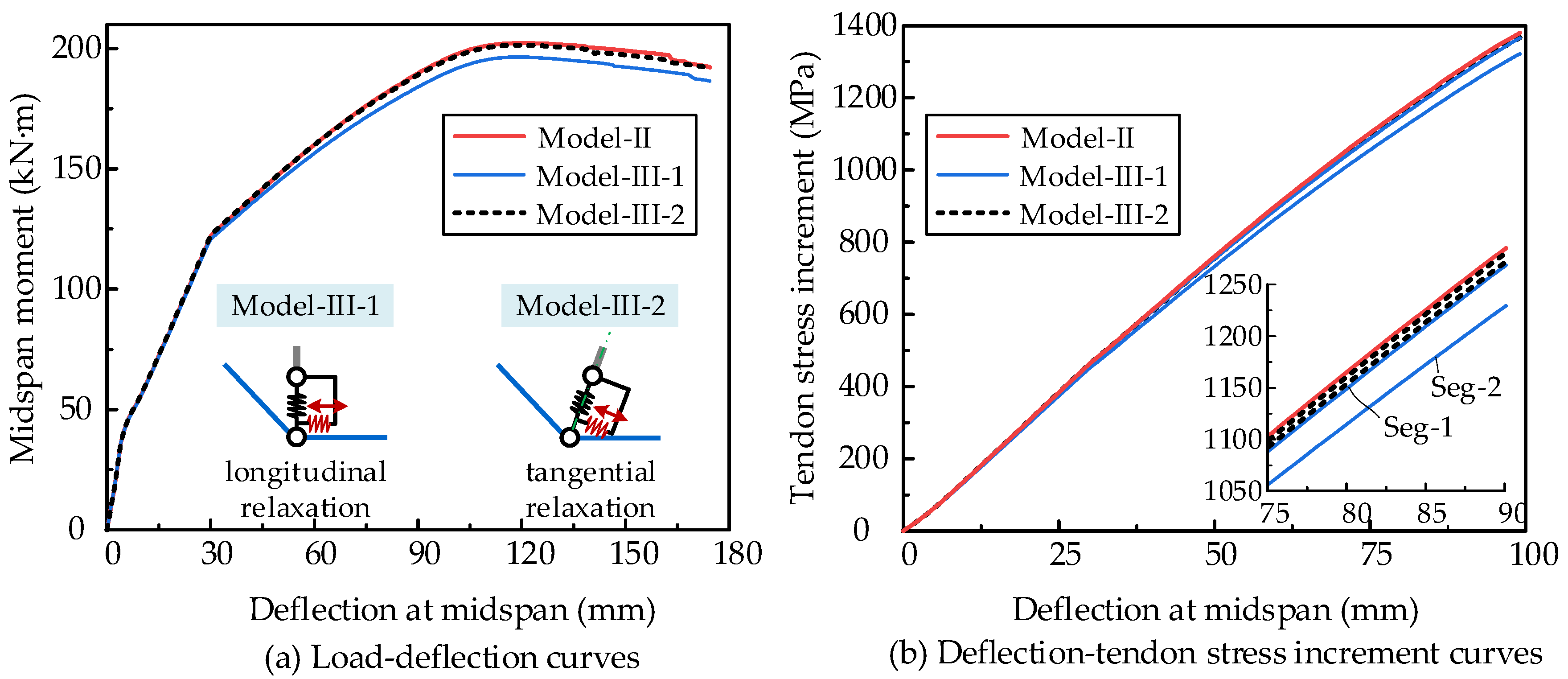
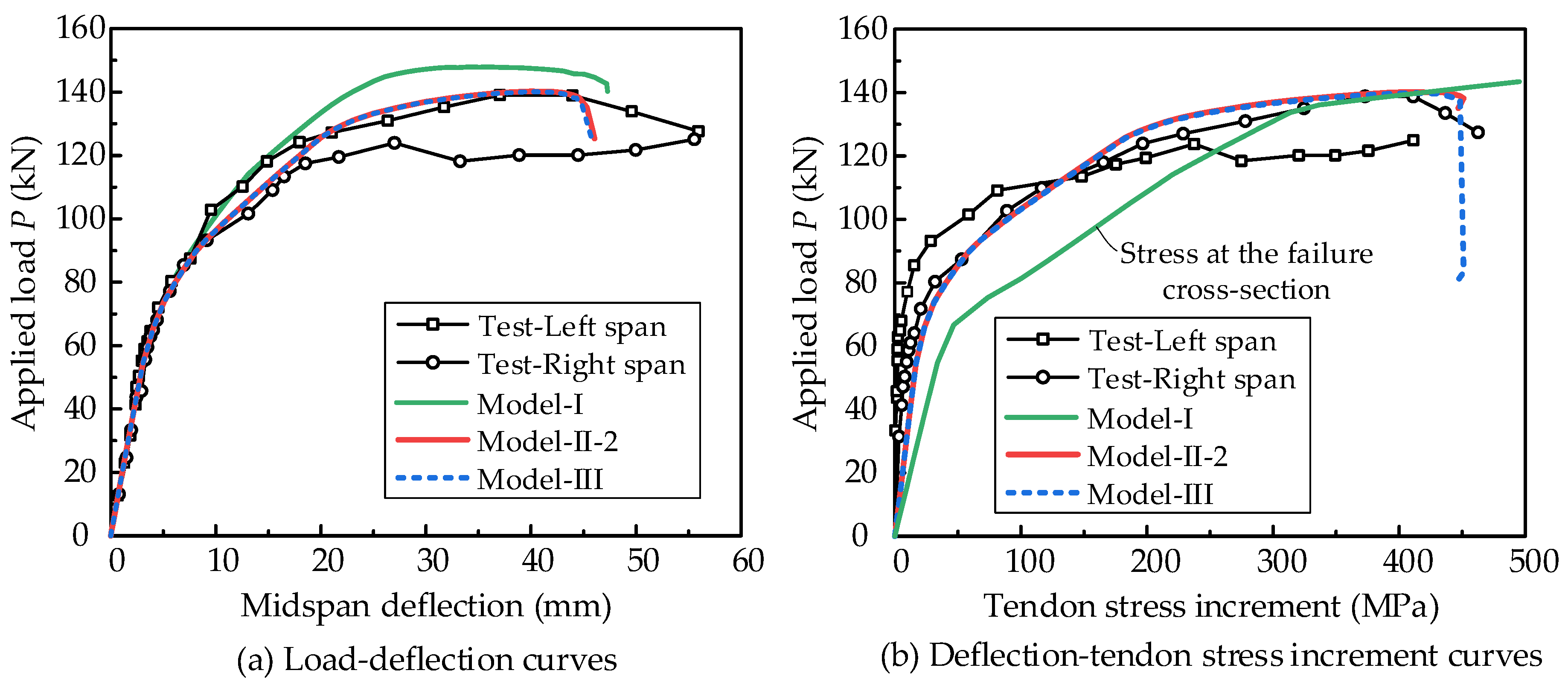
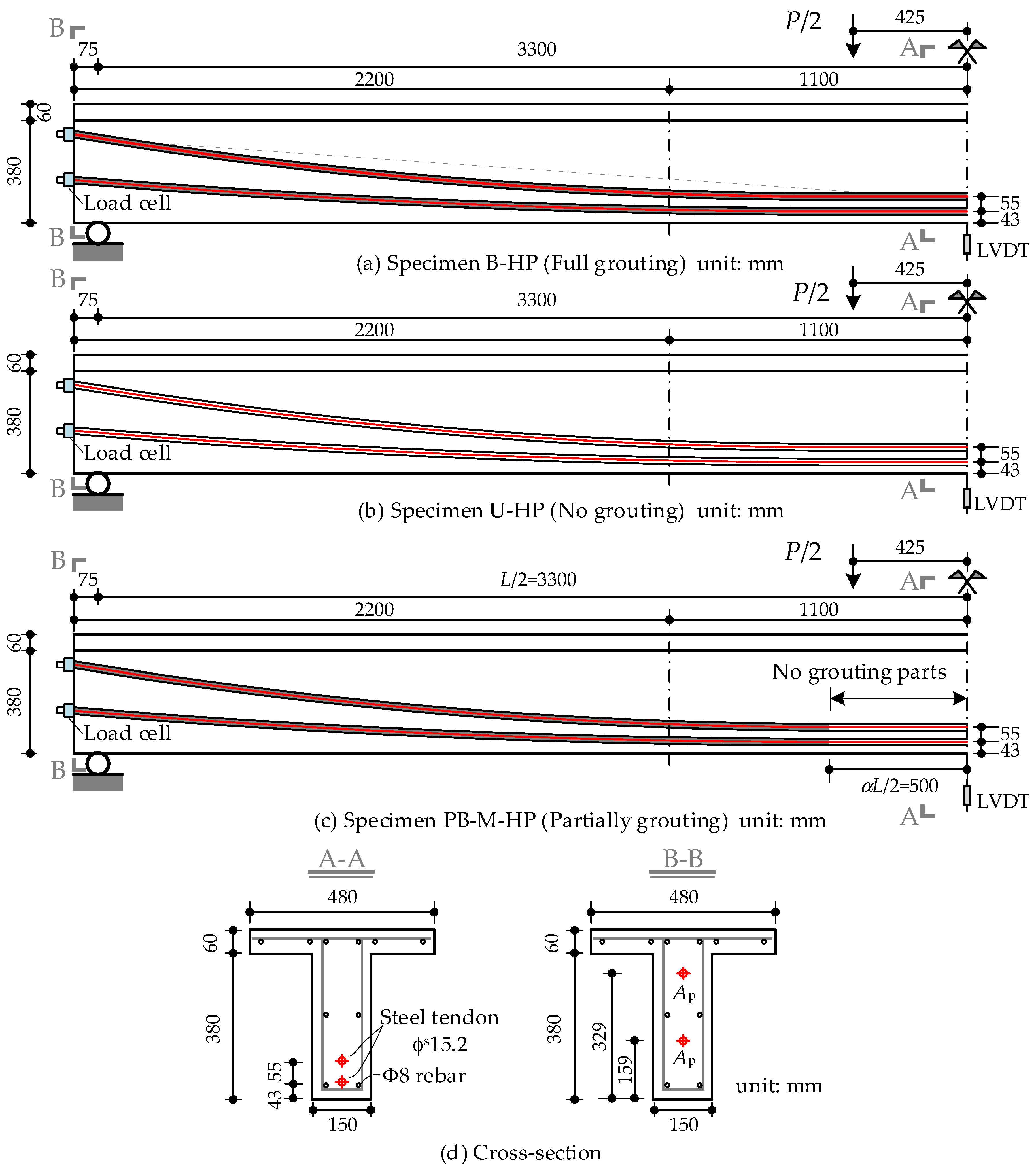
3.3. Partially Bonded Prestressed Concrete Beam
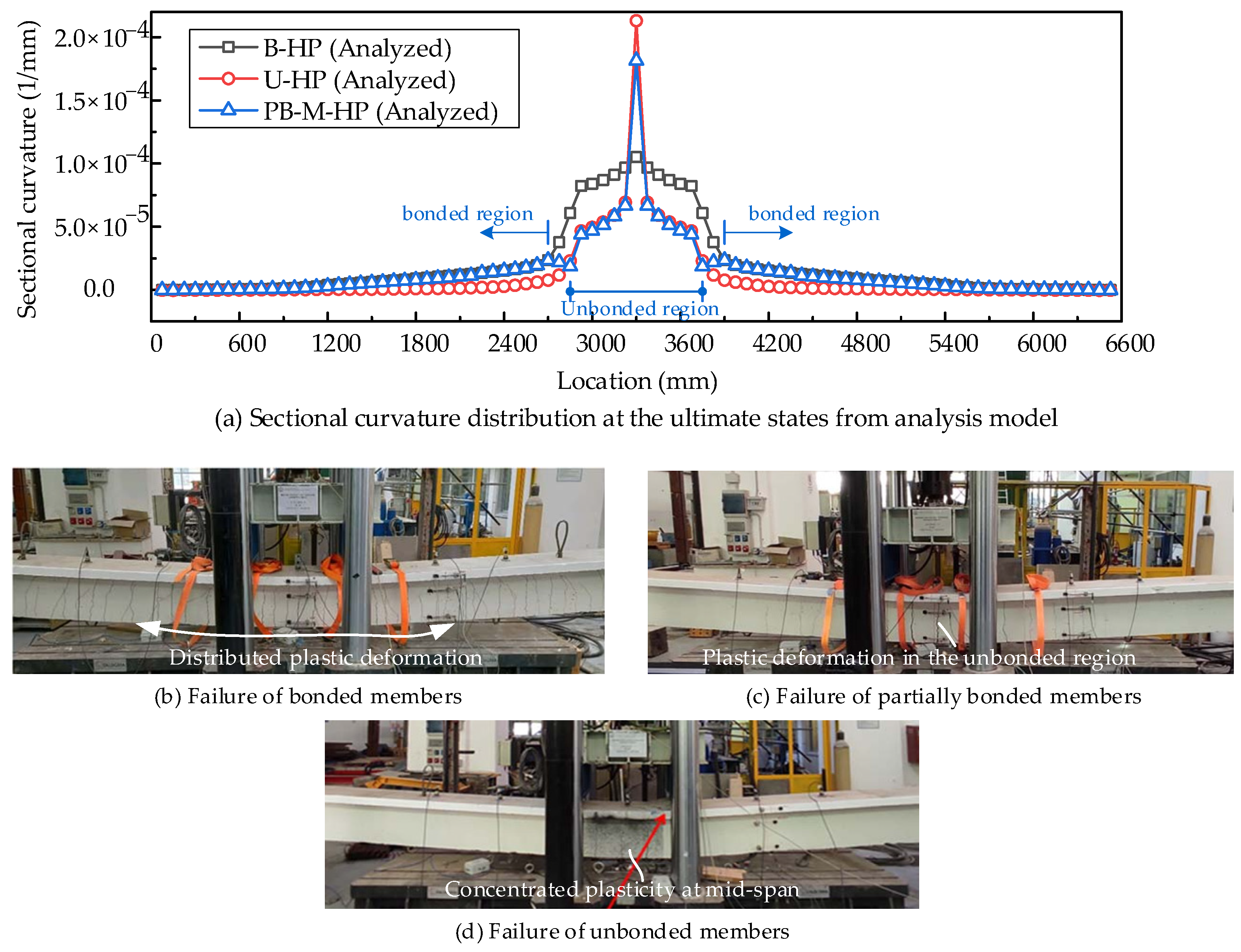
4. Discussion
5. Conclusions
- (1)
- Model I is adequate for the analysis of bonded prestressed members. Model II can capture the flexural behaviors of unbonded members well, but it cannot be used to analyze partially bonded members. Moreover, the application of Model II goes beyond the function of most finite element software, and a self-complied procedure is needed.
- (2)
- Model III is applicable for analyzing prestressed concrete beams with different bonding conditions (bonded, unbonded, and partially bonded members). The prediction accuracy can be improved by setting the orientation of the zero-length element, along with the angular bisector between the adjacent truss elements (Model III-2).
- (3)
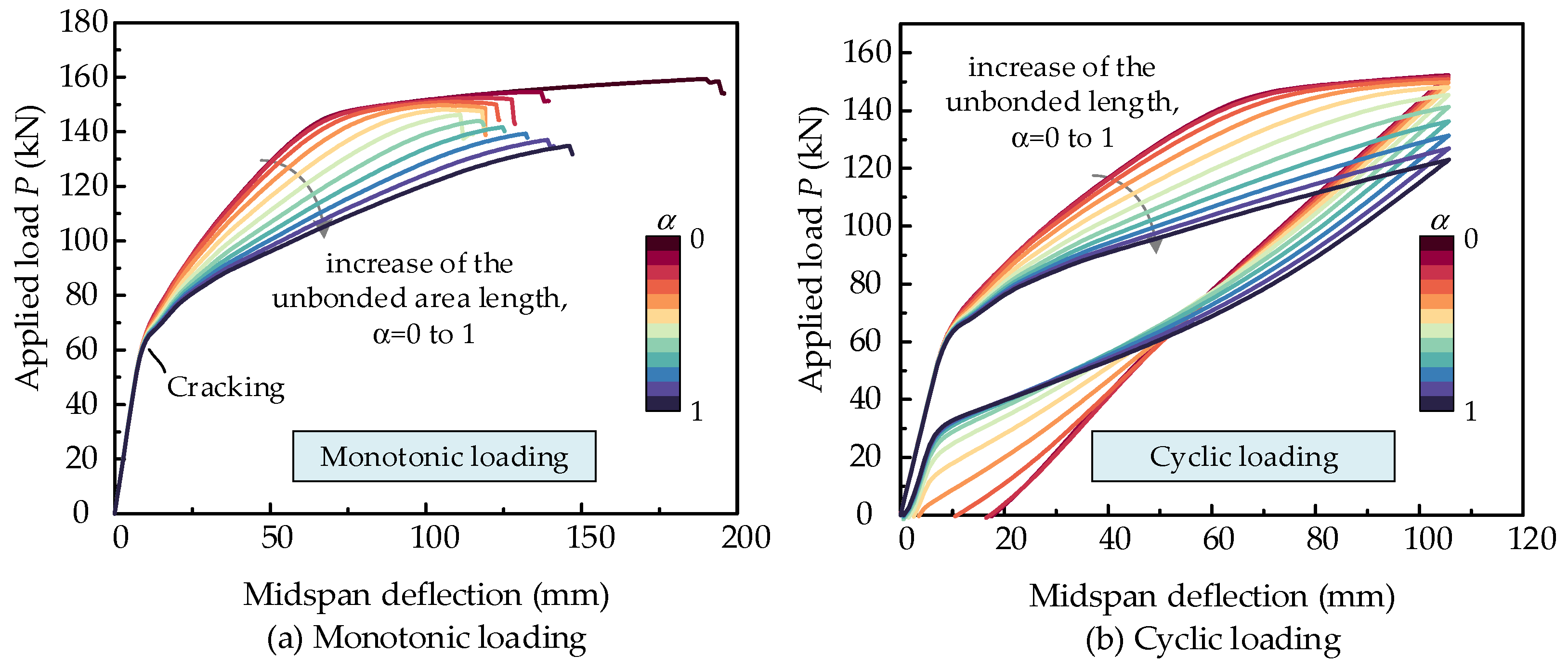
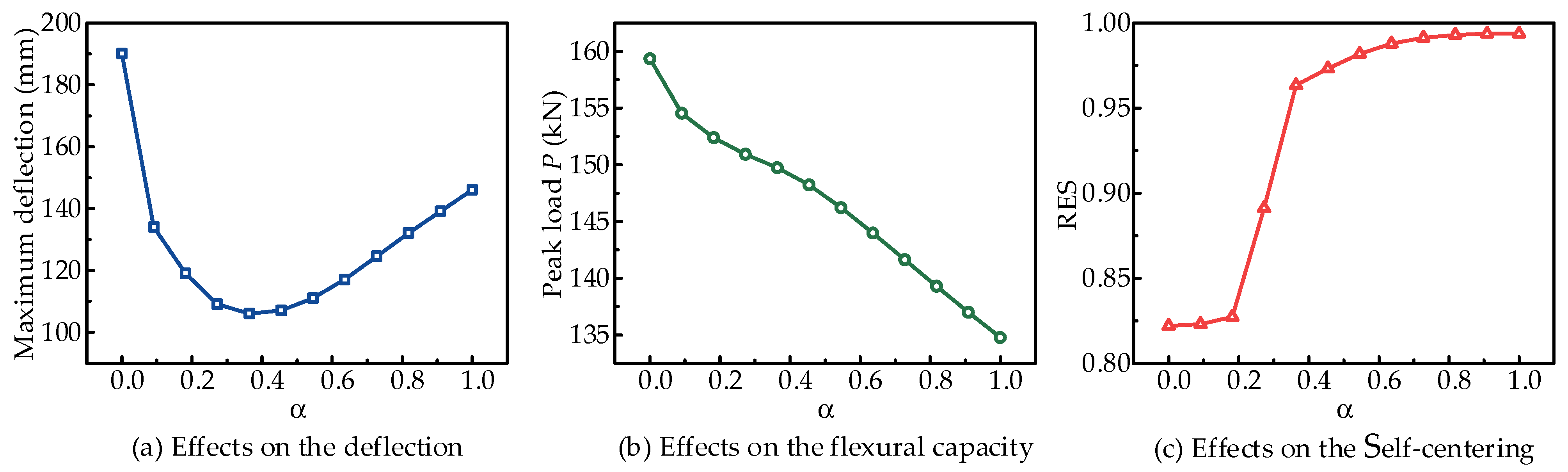
- With increased unbonded length, the flexural capacity decreases, but the self-centering performance is improved. The effects of unbonded length on structural deformability are not monotonic, showing a trend of declining and then rising along with the increase in unbonded length.
- (4)
- An experimental study on the flexural performance of post-tensioned concrete beams with different bonding conditions needs to be conducted in the future to verify the modeling schemes thoroughly. More accurate information on the practicability of the proposed FE models can thus be provided. The influences of unbonded length on flexural capacity, deformability, and self-centering performance will be further experimentally verified.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Asi | Cross-sectional area of steel reinforcement; |
| Ap | Cross-sectional area of tendon; |
| α | Coefficient of unbonded length; |
| α1, α2 | Included angle between the tendon segment and the concrete beam; |
| β | Degree of non-uniform distribution between two truss elements; |
| εcu | Concrete compressive strain at ultimates; |
| Au | Sectional curvature at ultimates; |
| θ | Included angle between axial force N and x direction; |
| δ | Angular deviation of the tendon; |
| cu | Depth of compression zone; |
| dp | Effective height of tendon; |
| Ec | Elasticity modulus of concrete; |
| Es | Elasticity modulus of steel reinforcement; |
| Ep | Elasticity modulus of prestressed tendon; |
| fc | Compressive strength of concrete prisms; |
| fcu | Compressive strength of concrete cube; |
| ft | Tensile strength of concrete; |
| fpe | Effective prestress of tendon; |
| fpy | Nominal yield strength of tendon; |
| fpu | Ultimate tensile strength of tendon; |
| fy | Yield strength of steel reinforcement; |
| Lp | Plastic hinge length; |
| N | Axial force of the zero-length element; |
| kt | Longitudinal stiffness of the slack spring; |
| kv | Vertical stiffness of the slack spring; |
| T1, T2 | Tendon force; |
| vmax | Maximum midspan deflection; |
| LVDT | Linear variable differential transducer; |
| res100 | Residual deformation after unloading from 100 mm midspan deflection. |
References
- Terán-Torres, B.T.; Elías-Chávez, A.A.; Valdez-Tamez, P.L.; Rodríguez-Rodríguez, J.A.; Juárez-Alvarado, C.A. Flexural Stiffness and Crack Width of Partially Prestressed Beams with Unbonded Tendons. Buildings 2023, 13, 2717. [Google Scholar] [CrossRef]
- Havez, A.A.; Al-Mayah, A. Flexural Strengthening of Concrete Structures Using Externally Bonded and Unbonded Prestressed CFRP Laminates-A Literature Review. J. Compos. Constr. 2023, 27, 03123001. [Google Scholar] [CrossRef]
- He, Z.Q.; Liu, Z. Stresses in External and Internal Unbonded Tendons_ Unified Methodology and Design Equations. J. Struct. Eng. 2010, 136, 1055–1065. [Google Scholar] [CrossRef]
- Oukaili, N.; Peera, I. Behavioral nonlinear modeling of prestressed concrete flexural members with internally unbonded steel strands. Results Eng. 2022, 14, 100411. [Google Scholar] [CrossRef]
- Mossor, K. Differences in moment redistribution in concrete beams prestressed with bonded and unbonded tendons. PCI J. 2022, 67, 23–34. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, Y.; Wang, Y. Stiffness assessment of cracked post-tensioned concrete beams with unbonded tendons based on the cracking pattern. Eng. Struct. 2020, 214, 110599. [Google Scholar] [CrossRef]
- Alqam, M.; Alkhairi, F. Numerical and Analytical Behavior of Beams Prestressed with Unbonded Internal or External Steel Tendons: A State-of-the-Art Review. Arab. J. Sci. Eng. 2019, 44, 8149–8170. [Google Scholar] [CrossRef]
- Nakari, T.; Tulonen, J.; Asp, O.; Kytoelae, U.; Laaksonen, A. Experimental study of moment redistribution in continuous concrete beams prestressed with unbonded tendons. Struct. Concr. 2024, EA, 1–18. [Google Scholar] [CrossRef]
- Dogu, M.; Menkulasi, F. Flexural response of UHPC beams post-tensioned with internal unbonded tendons: Experimental study. Eng. Struct. 2023, 296, 116895. [Google Scholar] [CrossRef]
- Yuan, A.; He, Y.; Dai, H.; Cheng, L. Experimental Study of Precast Segmental Bridge Box Girders with External Unbonded and Internal Bonded Posttensioning under Monotonic Vertical Loading. J. Bridge Eng. 2015, 20, 04014075. [Google Scholar] [CrossRef]
- Heo, S.; Shin, S.; Lee, C. Flexural Behavior of Concrete Beams Internally Prestressed with Unbonded Carbon-Fiber-Reinforced Polymer Tendons. J. Compos. Constr. 2013, 17, 167–175. [Google Scholar] [CrossRef]
- Bonopera, M.; Liao, W.C.; Perceka, W. Experimental-theoretical investigation of the short-term vibration response of uncracked prestressed concrete members under long-age conditions. Structures 2022, 35, 260–273. [Google Scholar] [CrossRef]
- Nakari, T.; Laaksonen, A. Determination of the Stress Increase of the Unbonded Tendon in a Continuous Concrete Beam at Ultimate Capacity Using Nonlinear Analysis. Nord. Concr. Res. 2021, 64, 109–128. [Google Scholar] [CrossRef]
- Alqam, M.; Alkhairi, F.M.; Naaman, A.E. Stress at Ultimate in Prestressed Unbonded Tendons: Assessment of Code Equations and Recommendation. ACI Struct. J. 2021, 118, 177–187. [Google Scholar]
- Alqam, M.; Alkhairi, F.; Naaman, A. An Improved Methodology for the Prediction of the Stress at Ultimate in Unbonded Internal and External Steel Tendons. Arab. J. Sci. Eng. 2020, 45, 7915–7954. [Google Scholar] [CrossRef]
- Peng, F.; Xue, W. Calculating Method for Ultimate Tendon Stress in Internally Unbonded Prestressed Concrete Members. ACI Struct. J. 2019, 116, 225–234. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, T.; Liu, X.; Zhang, B. Failure mode and flexural capacity of concrete beams prestressed with unbonded FRP tendons. Compos. Struct. 2022, 283, 114956. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, T.; Liu, X. Design of concrete beams reinforced and unbonded prestressed with FRP bars based on serviceability requirements. Compos. Struct. 2022, 300, 116133. [Google Scholar] [CrossRef]
- Raiyan, E.; Khorgade, P.; Hueckler, A.; Schlaich, M. Nonlinear analysis of the stress increase in the CFRP tendon of a unbonded prestressed beam. Beton-Und Stahlbetonbau 2022, 118, 57–68. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Yuan, C. Performance of precast segmental concrete beams posttensioned with carbon fiber-reinforced polymer (CFRP) tendons. Compos. Struct. 2019, 208, 56–69. [Google Scholar] [CrossRef]
- Zheng, H.; Chen, D.; Ou, M.; Liang, X.; Luo, Y. Flexural Behavior of Precast UHPC Segmental Beams with Unbonded Tendons and Epoxy Resin Joints. Buildings 2023, 13, 1643. [Google Scholar] [CrossRef]
- Halder, R.; Yuen, T.Y.P.; Chen, W.-W.; Zhou, X.; Deb, T.; Zhang, H.; Wen, T.-H. Tendon stress evaluation of unbonded post-tensioned concrete segmental bridges with two-variable response surfaces. Eng. Struct. 2021, 245, 112984. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, G.H.; Wu, Y.F.; Zhang, Y. Effect of strand debonding on the shear strength of existing pretensioned PC hollow slab. Eng. Struct. 2023, 291, 116417. [Google Scholar] [CrossRef]
- Losanno, D.; Galano, S.; Parisi, F.; Pecce, M.R.; Cosenza, E. Experimental Investigation on Nonlinear Flexural Behavior of Post-Tensioned Concrete Bridge Girders with Different Grouting Conditions and Prestress Levels. J. Bridge Eng. 2024, 29, 04023121. [Google Scholar] [CrossRef]
- Hu, X.Y.; Xue, W.C.; Zheng, R.G. Hysteretic performance of prestressed concrete beams with AFRP tendons under cyclic loading. Struct. Concr. 2024, 25, 620–636. [Google Scholar] [CrossRef]
- Janet, M.L.; Chris, J.B. Experimental Study of Influence of Bond on Flexural Behavior of Concrete Beams Pretensioned with Aramid Fiber Reinforced Plastics. ACI Struct. J. 1999, 96, 377–385. [Google Scholar]
- Yuen, T.Y.P.; Halder, R.; Chen, W.-W.; Zhou, X.; Deb, T.; Liu, Y.; Tseng, Y.; Wen, T.-H. DFEM of a post-tensioned precast concrete segmental bridge with unbonded external tendons subjected to prestress changes. Structures 2020, 28, 1322–1337. [Google Scholar] [CrossRef]
- Tran, D.T.; Pham, T.M.; Hao, H.; Chen, W. Numerical investigation of flexural behaviours of precast segmental concrete beams internally post-tensioned with unbonded FRP tendons under monotonic loading. Eng. Struct. 2021, 249, 113341. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H. Numerical study on the flexural performance of precast segmental concrete beams with unbonded internal steel tendons. Constr. Build. Mater. 2020, 248, 118362. [Google Scholar] [CrossRef]
- Jaiswal, O.R. Effect of prestressing on the first flexural natural frequency of beams. Struct. Eng. Mech. 2008, 28, 515–524. [Google Scholar] [CrossRef]
- Yan, W.; Jiang, F.; Chen, L.; Sun, Y. Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons. Appl. Sci. 2023, 13, 6652. [Google Scholar] [CrossRef]
- Yan, W.T.; Chen, L.J.; Han, B.; Xie, H.B.; Sun, Y. Flexural Analysis Model of Externally Prestressed Steel-Concrete Composite Beam with Nonlinear Interfacial Connection. Appl. Sci. 2022, 12, 4699. [Google Scholar] [CrossRef]
- Yan, W.; Chen, L.; Han, B.; Xie, H.; Sun, Y. Numerical Model for Flexural Analysis of Precast Segmental Concrete Beam with Internal Unbonded CFRP Tendons. Materials 2022, 15, 4105. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Lu, X. Modelling unbonded prestressing tendons in self-centering connections through improved sliding cable elements. Eng. Struct. 2019, 180, 809–828. [Google Scholar] [CrossRef]
- Moreira, L.S.; Sousa, J.B.M.; Parente, E. Nonlinear finite element simulation of unbonded prestressed concrete beams. Eng. Struct. 2018, 170, 167–177. [Google Scholar] [CrossRef]
- Brenkus, N.R.; Tatar, J.; Hamilton, H.R.; Consolazio, G.R. Simplified finite element modeling of post-tensioned concrete members with mixed bonded and unbonded tendons. Eng. Struct. 2019, 179, 387–397. [Google Scholar] [CrossRef]
- Chen, D.; Zeng, B.; Xu, Q.; Xu, X.; Xu, M. Effects of Prestressing Magnitude and Position on Seismic Performance of Unbonded Prestressed Concrete Beams. Buildings 2024, 14, 431. [Google Scholar] [CrossRef]
- Ayinde, O.O.; Zuo, X.-B.; Yin, G.-J. Numerical analysis of concrete degradation due to chloride-induced steel corrosion. Adv. Concr. Constr. 2019, 7, 203–210. [Google Scholar]
- Markou, G.; AlHamaydeh, M. Computationally-efficient high-fidelity nonlinear FEA of seismically isolated post-tensioned RC bridges. Structures 2024, 60, 105816. [Google Scholar] [CrossRef]
- Parente, L.; Addessi, D.; Spacone, E. A fiber beam element based on plastic and damage models for prestressed concrete structures. Eng. Struct. 2023, 292, 116501. [Google Scholar] [CrossRef]
- Pang, M.; Liu, X.; Dong, Y.; Lou, T. Numerical Assessment on Bonded and Unbonded Prestressed Concrete Beams. Buildings 2022, 12, 1658. [Google Scholar] [CrossRef]
- Mckenna, F.; Fenves, G. Opensees, version 2.5.0. Computer Software. UC Berkeley: Berkeley, CA, USA, 2015.
- Yan, W.-T.; Han, B.; Xie, H.-B.; Li, P.-F.; Zhu, L. Research on numerical model for flexural behaviors analysis of precast concrete segmental box girders. Eng. Struct. 2020, 219, 110733. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Y.; Wang, J.-J.; Fan, J.-S.; Tao, M.-X.; Mo, Y.L. Biaxial reinforced concrete constitutive models for implicit and explicit solvers with reduced mesh sensitivity. Eng. Struct. 2020, 219, 110880. [Google Scholar] [CrossRef]
- Au, F.T.K.; Su, R.K.L.; Tso, K.; Chan, K.H.E. Behaviour of partially prestressed beams with external tendons. Mag. Concr. Res. 2008, 60, 455–467. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Nonlinear and time-dependent analysis of continuous unbonded prestressed concrete beams. Comput. Struct. 2013, 119, 166–176. [Google Scholar] [CrossRef]



| Modeling Schemes | Applicability | Element Type | Can It Be Used in General FE Software? | Validation | |||
|---|---|---|---|---|---|---|---|
| Bonded Members | Unbonded Members | Partially Bonded Members | Concrete Beam | Tendon | |||
| Model I | Yes | No | No | Beam | Truss | Yes | Yes |
| Model II | No | Yes | No | Beam | Slipping cable element | No | Yes |
| Model III-1 | Yes | Yes | Yes | Beam | Truss | Yes | No |
| Model III-2 | Yes | Yes | Yes | Beam | Truss | Yes | No |
| Specimen | Bottom Rebar | Top Rebar | Concrete | Tendon | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| As1 (mm2) | fy (MPa) | As2 (mm2) | fy (MPa) | fc (MPa) | ft (MPa) | Ec (GPa) | Ap (mm2) | fpe (MPa) | Ep (GPa) | |
| SSS1 | 402 | 549 | 317 | 492 | 58.3 | 3.0 | 50.7 | 198 | 357 | 201.9 |
| Specimen | As1 (mm2) | As2 (mm2) | As3 (mm2) | As4 (mm2) | fc (MPa) | ft (MPa) | Ec (GPa) | Ap (mm2) | fpe (MPa) | Ep (GPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| YLA2 | 452.4 (4Φ12) | 226.2 (2Φ12) | 226.2 (2Φ12) | 226.2 (2Φ12) | 36.7 | 3.85 | 36.2 | 140 | 1196 | 197 |
| Specimen | Concrete | Steel Reinforcement A8 | Tendon As 15.2 | |||||
|---|---|---|---|---|---|---|---|---|
| fcu (MPa) | Es (GPa) | fy (MPa) | Ap (mm2) | Ep (GPa) | fpe (MPa) | fpy (MPa) | fpu (MPa) | |
| B-HP | 33.8 | 200 | 450 | 140 | 203.4 | 716.5 | 1782 | 1969 |
| U-HP | 33.8 | 200 | 450 | 140 | 203.4 | 773.5 | 1782 | 1969 |
| PB-M-HP | 33.8 | 200 | 450 | 140 | 203.4 | 740.0 | 1782 | 1969 |
| α | Maximum Deflection (mm) | Peak Load P (kN) | Residual Deformation res100 | RES Index |
|---|---|---|---|---|
| 0.0 | 190.1 | 159.3 | 17.800 | 0.822 |
| 0.1 | 134.1 | 154.5 | 17.700 | 0.823 |
| 0.2 | 119.1 | 152.4 | 17.270 | 0.827 |
| 0.3 | 109.1 | 150.9 | 10.890 | 0.891 |
| 0.4 | 106.1 | 149.7 | 3.660 | 0.963 |
| 0.5 | 107.1 | 148.2 | 2.679 | 0.973 |
| 0.5 | 111.1 | 146.2 | 1.817 | 0.982 |
| 0.6 | 117.1 | 144.0 | 1.215 | 0.988 |
| 0.7 | 124.6 | 141.6 | 0.872 | 0.991 |
| 0.8 | 132.1 | 139.3 | 0.707 | 0.993 |
| 0.9 | 139.1 | 137.0 | 0.626 | 0.994 |
| 1.0 | 146.1 | 134.8 | 0.630 | 0.994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Jiang, F.; Sun, Y.; Yan, W. Modeling Schemes and Performance Comparisons of Unbonded and Partially Bonded Tendon in Post-Tensioned Concrete Beam. Buildings 2024, 14, 1682. https://doi.org/10.3390/buildings14061682
Chen S, Jiang F, Sun Y, Yan W. Modeling Schemes and Performance Comparisons of Unbonded and Partially Bonded Tendon in Post-Tensioned Concrete Beam. Buildings. 2024; 14(6):1682. https://doi.org/10.3390/buildings14061682
Chicago/Turabian StyleChen, Shangzhi, Fangxin Jiang, Yue Sun, and Wutong Yan. 2024. "Modeling Schemes and Performance Comparisons of Unbonded and Partially Bonded Tendon in Post-Tensioned Concrete Beam" Buildings 14, no. 6: 1682. https://doi.org/10.3390/buildings14061682
APA StyleChen, S., Jiang, F., Sun, Y., & Yan, W. (2024). Modeling Schemes and Performance Comparisons of Unbonded and Partially Bonded Tendon in Post-Tensioned Concrete Beam. Buildings, 14(6), 1682. https://doi.org/10.3390/buildings14061682





