Finite Element Investigation of a Novel Cold-Formed Steel Shear Wall
Abstract
1. Introduction
2. Design and Experimental Program of CCS-CFS Shear Wall Configuration
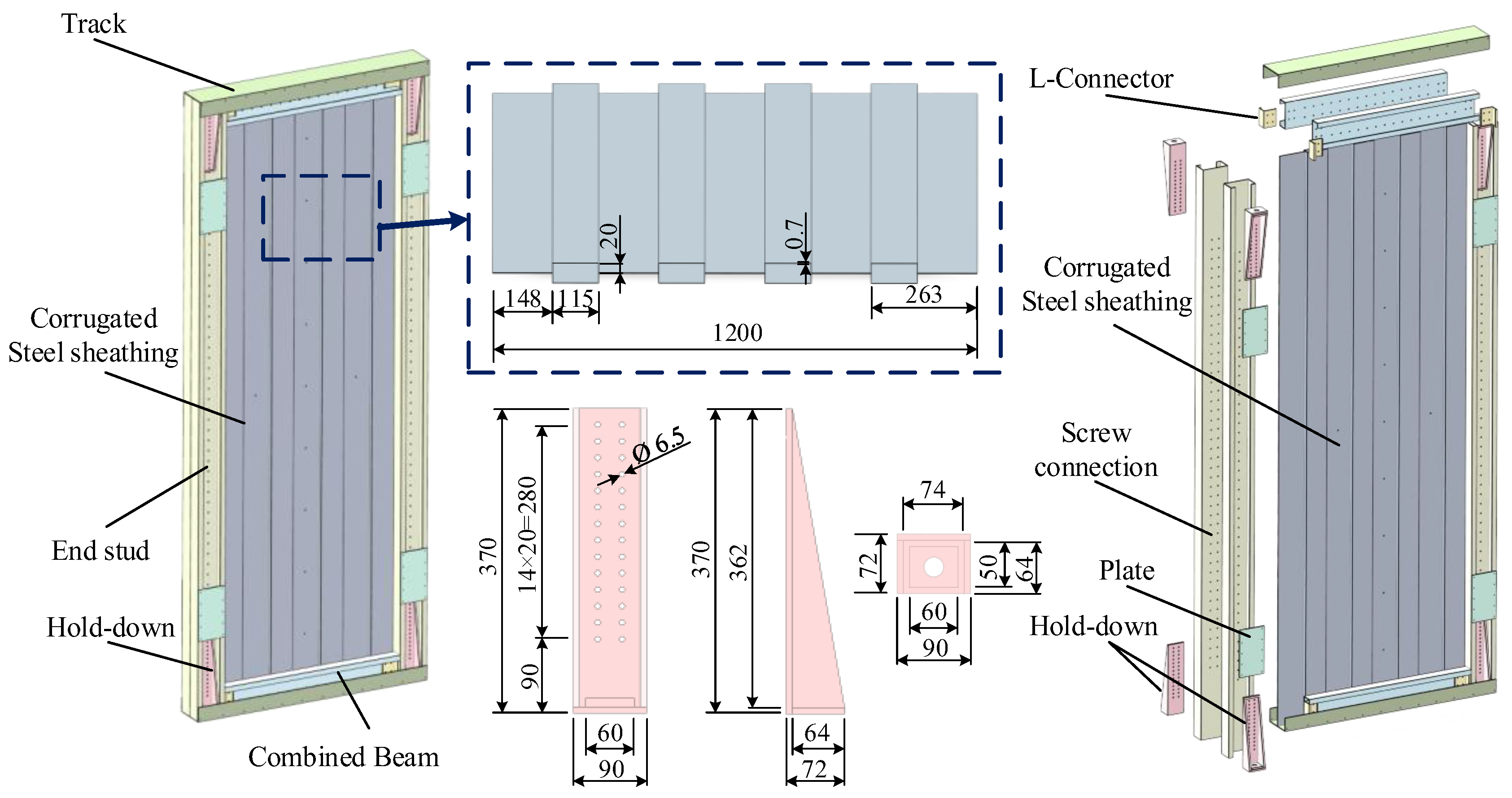
2.1. Innovative Configuration of the CCS-CFS Shear Wall
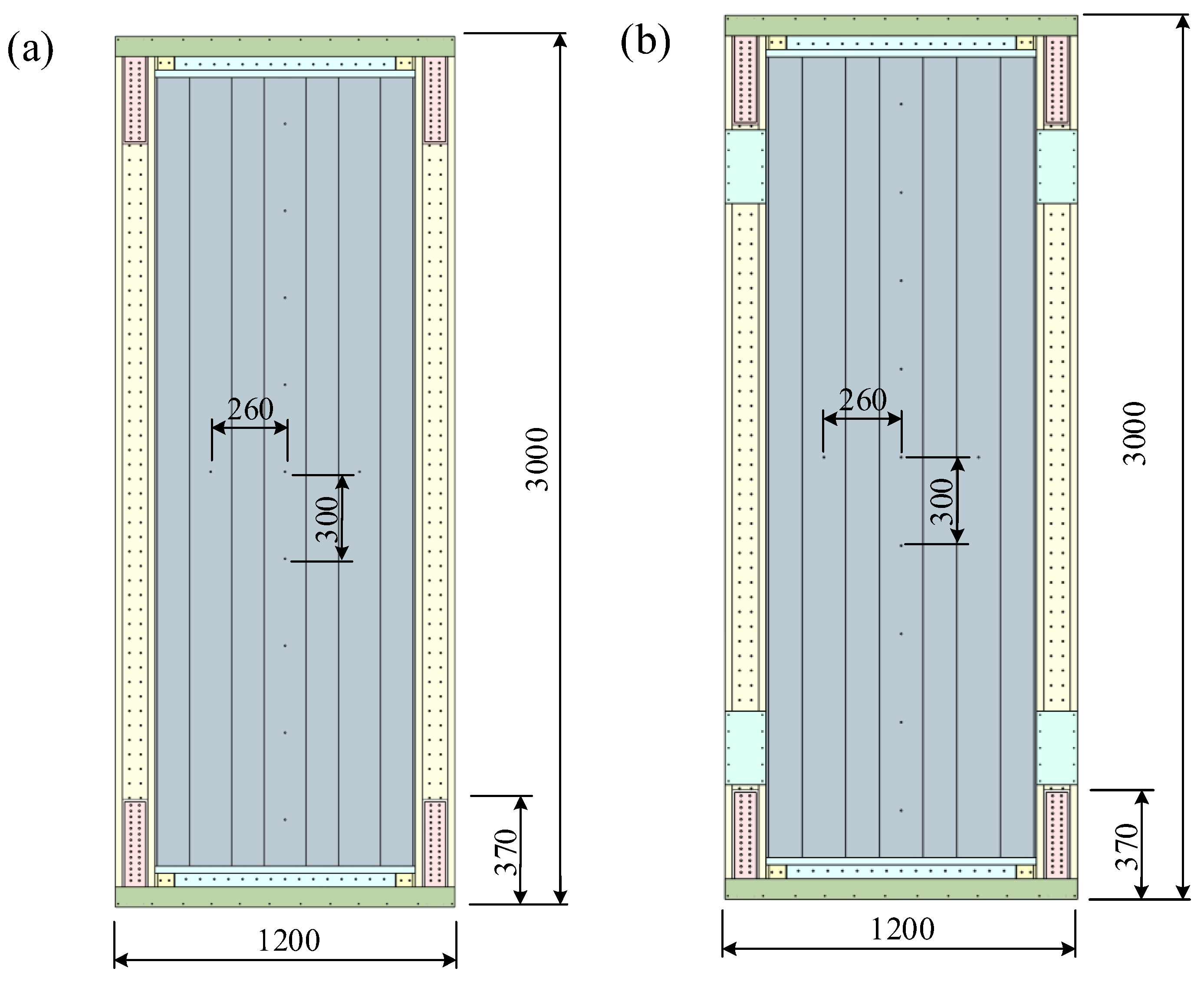
2.2. Specimen Design
2.3. Material Properties
2.4. Test Results Analysis
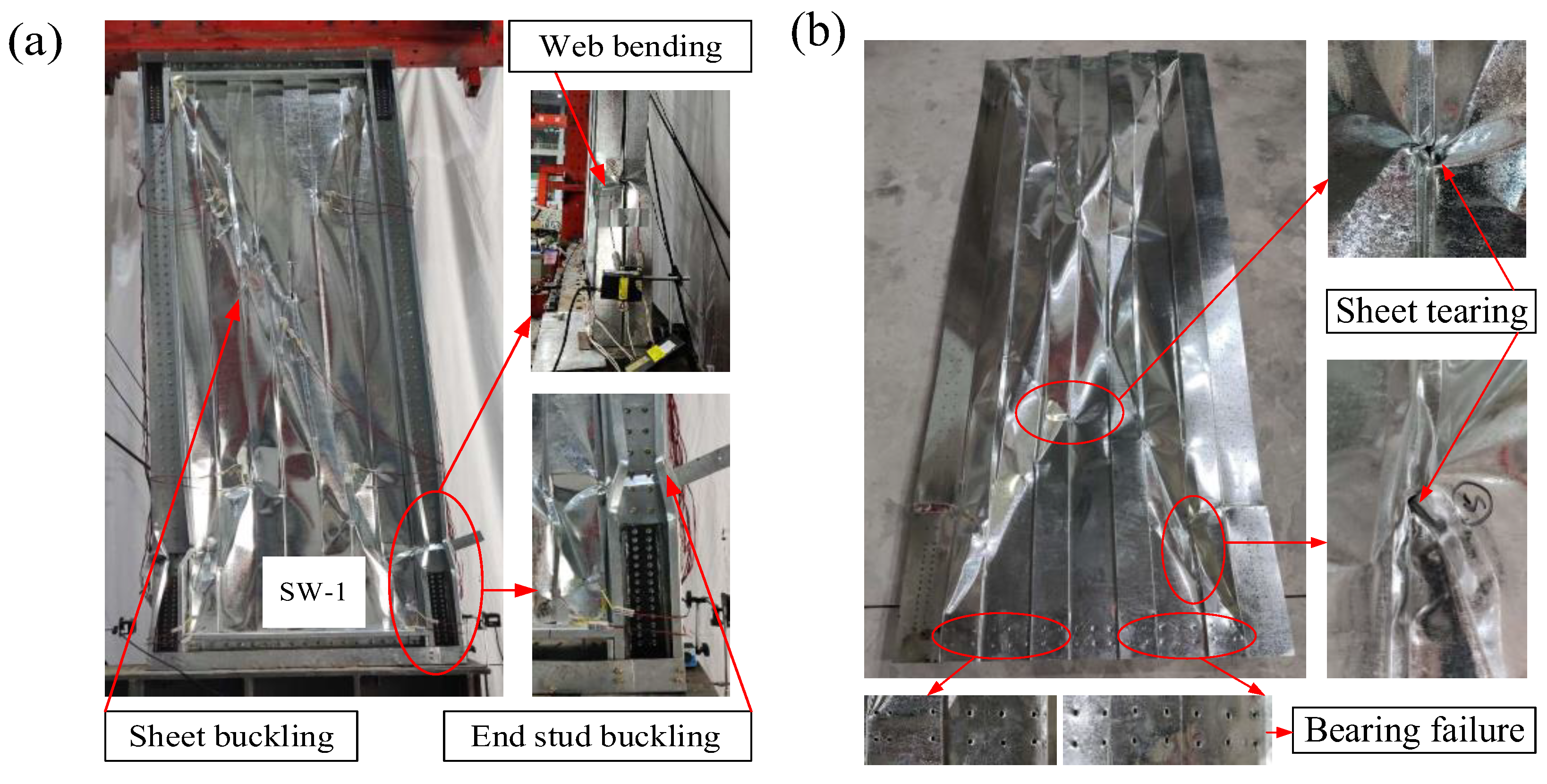
2.4.1. Failure Modes
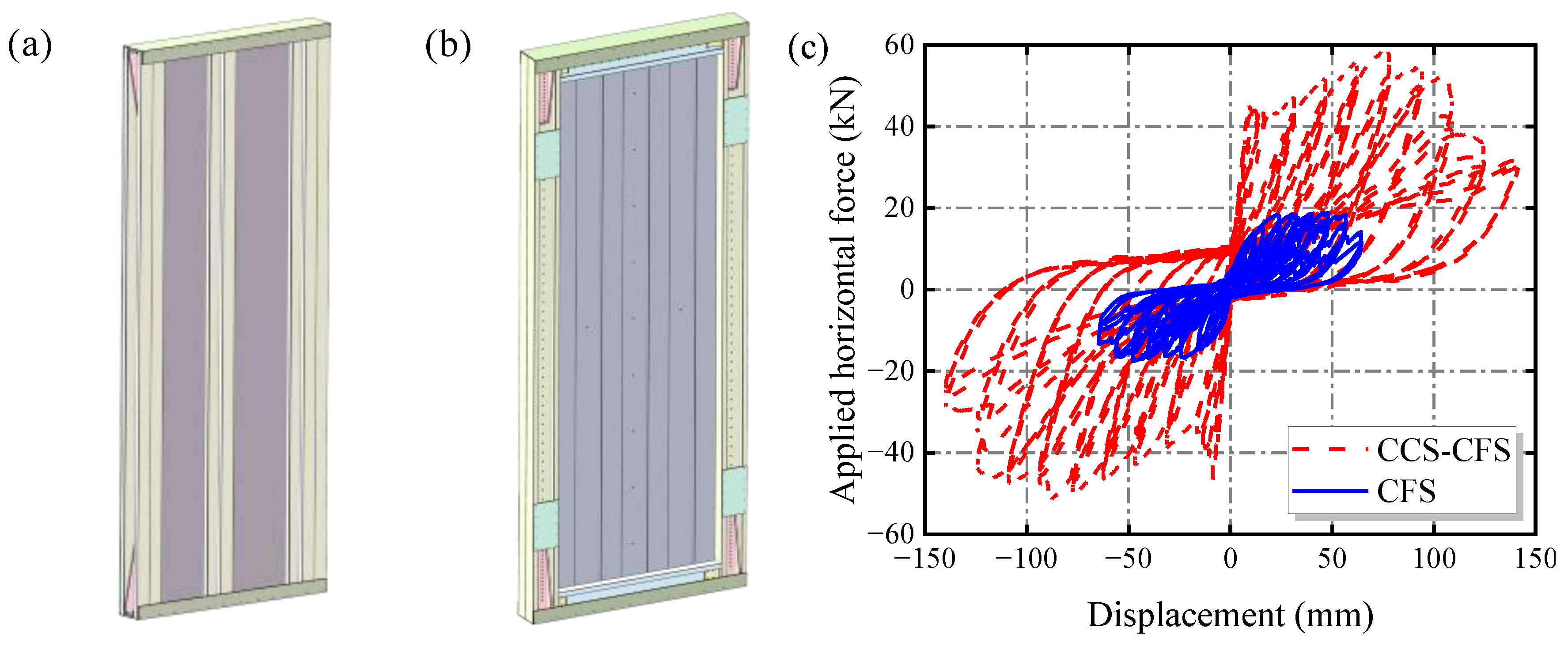
2.4.2. Hysteresis Curves
2.4.3. Comparison with the Conventional CFS Shear Wall
3. Numerical Methodology
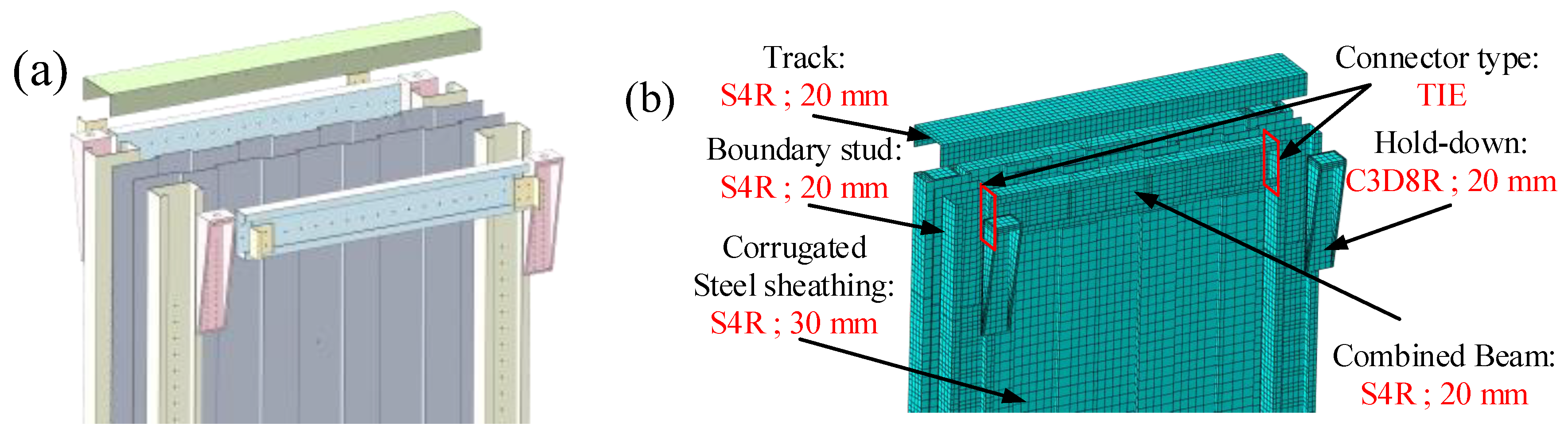
3.1. Modeling of Shear Walls
3.1.1. Element Choice and Mesh Size
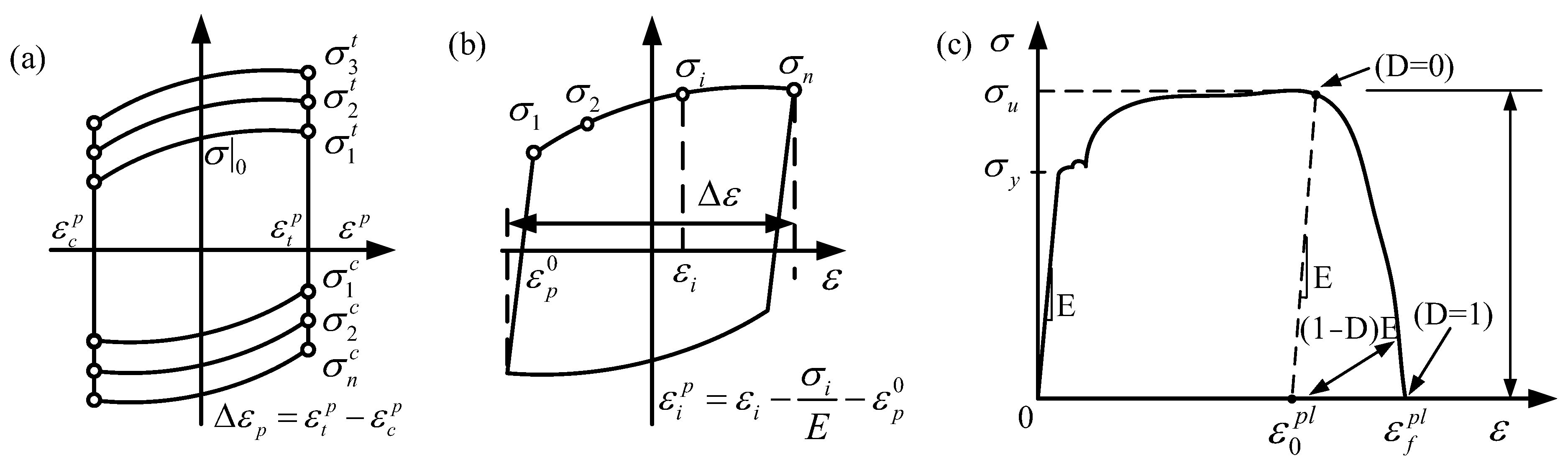
3.1.2. Material Modeling
3.1.3. Geometric Nonlinearity
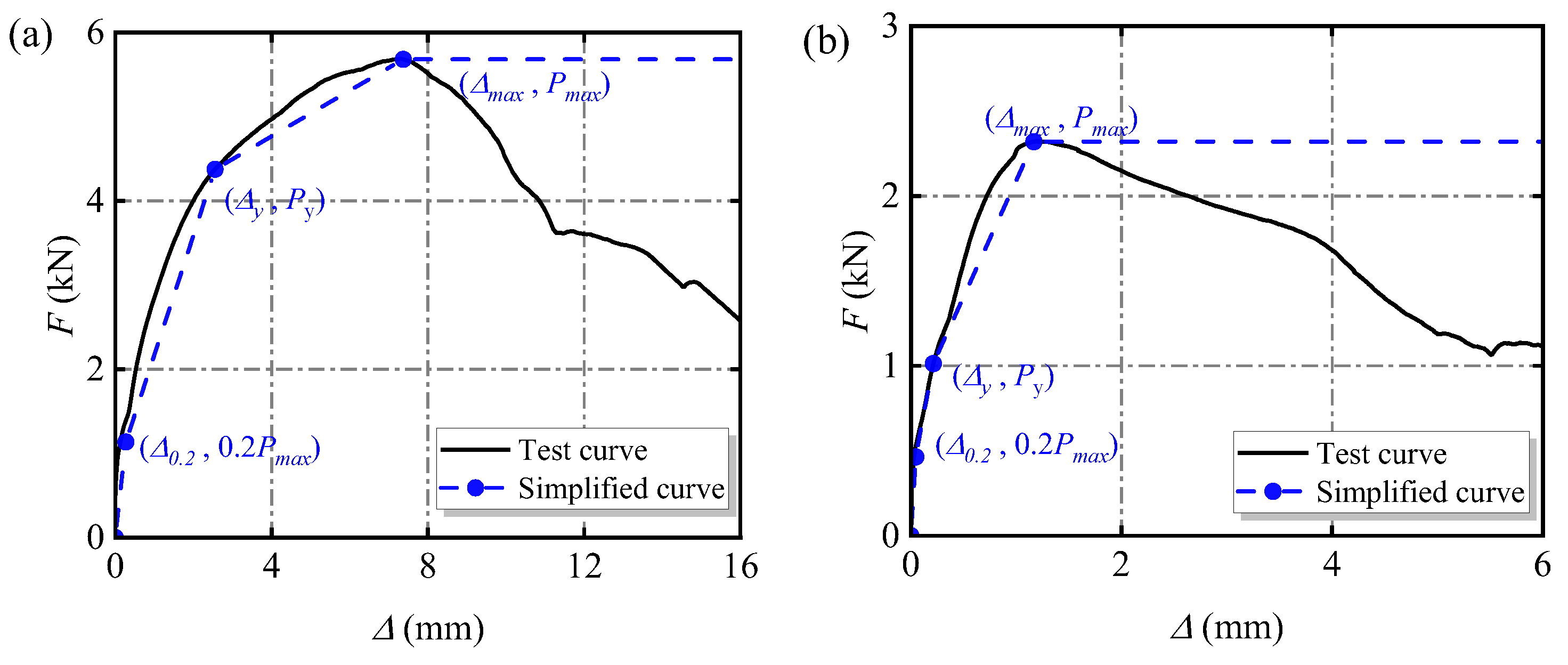
3.1.4. Modeling of the Screw Connection
3.1.5. Boundary Conditions and Loading Mode
3.2. Model Validation
3.2.1. Comparison of Failure Mode
3.2.2. Comparison of Load–Displacement Curve
4. Parametric Analyses
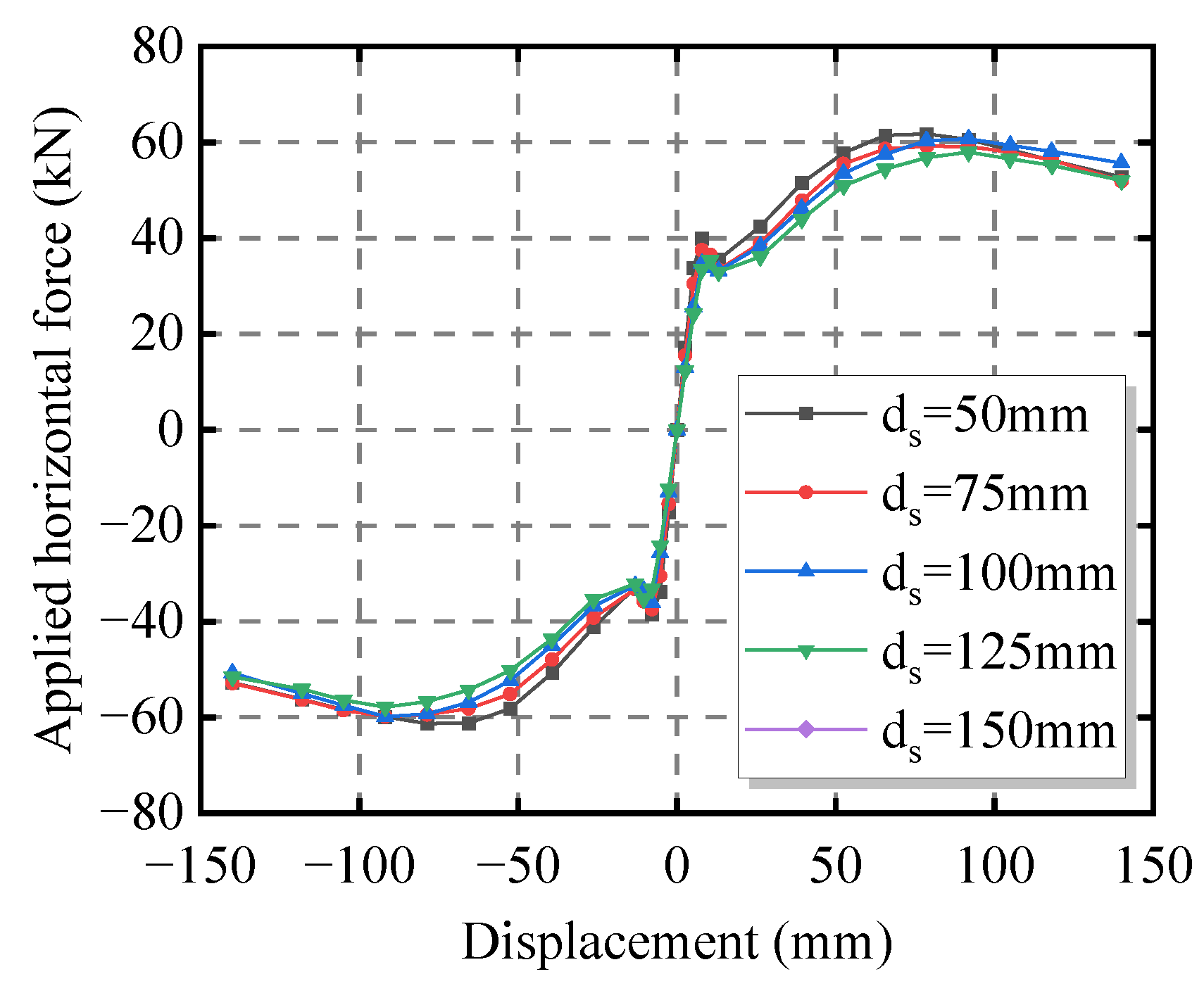
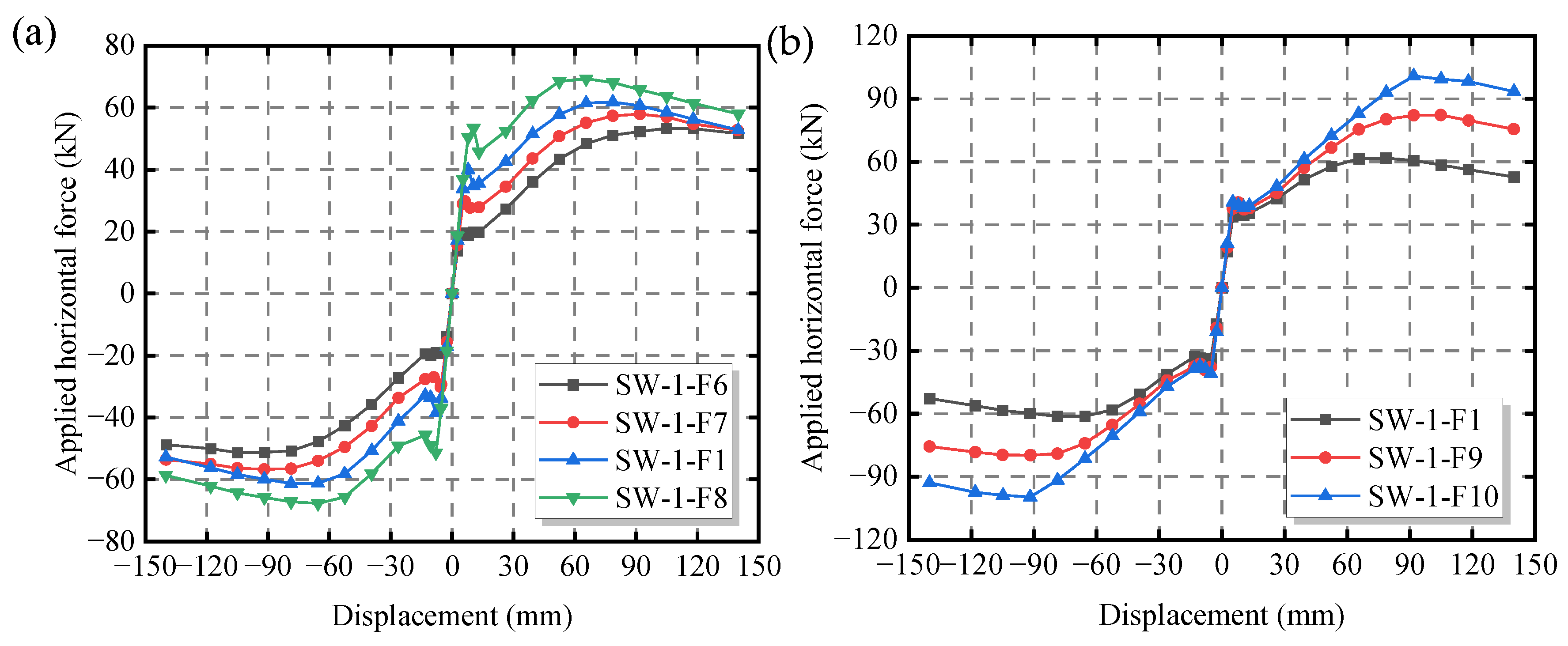
4.1. Influence of Screw Spacing on the Seismic Performance of the CCS-CFS Shear Wall
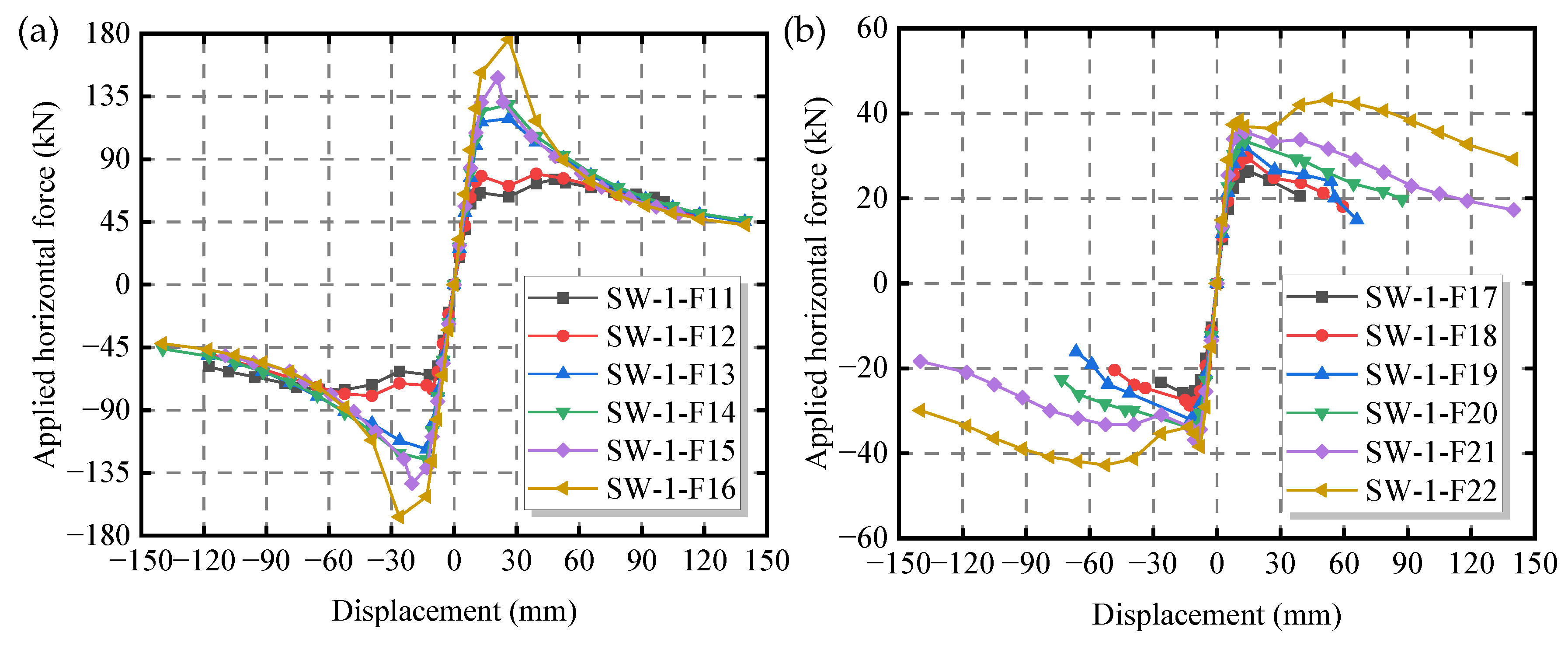
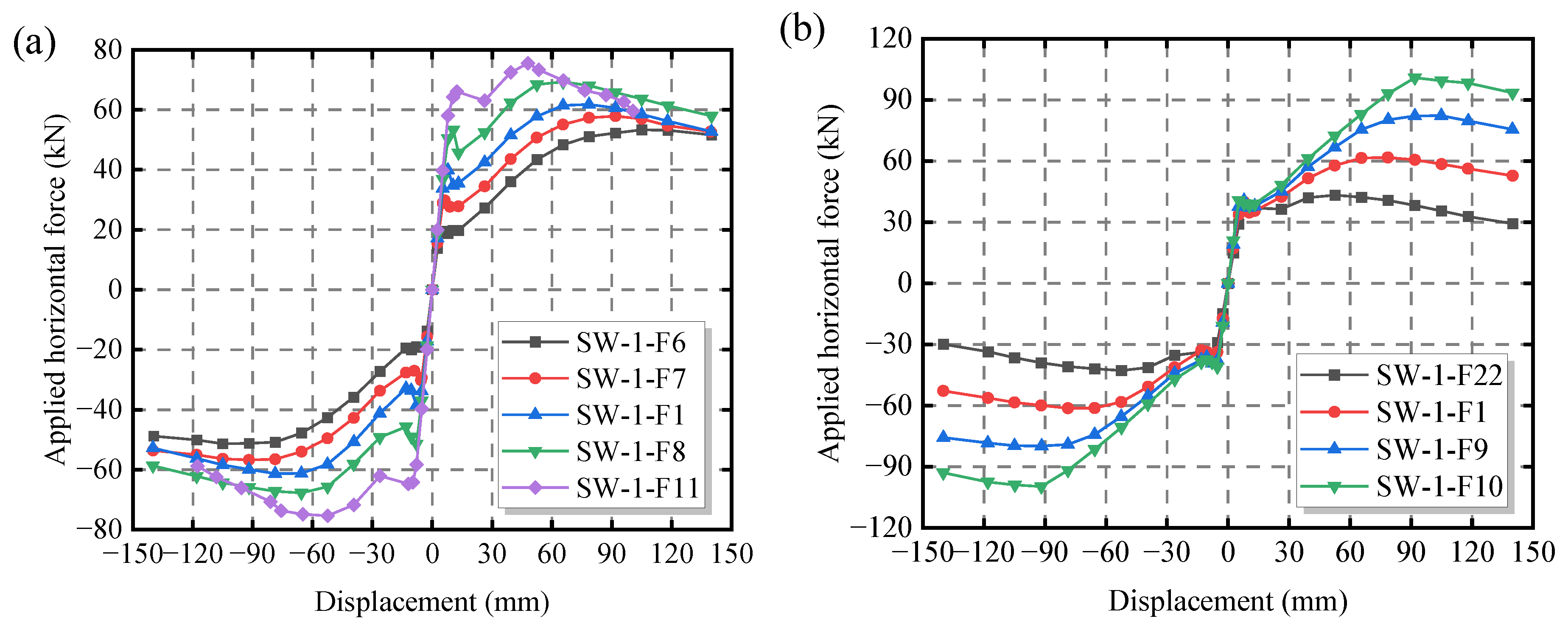
4.2. Influence of Sheet Thickness Ratio on the Seismic Performance of the CCS-CFS Shear Wall
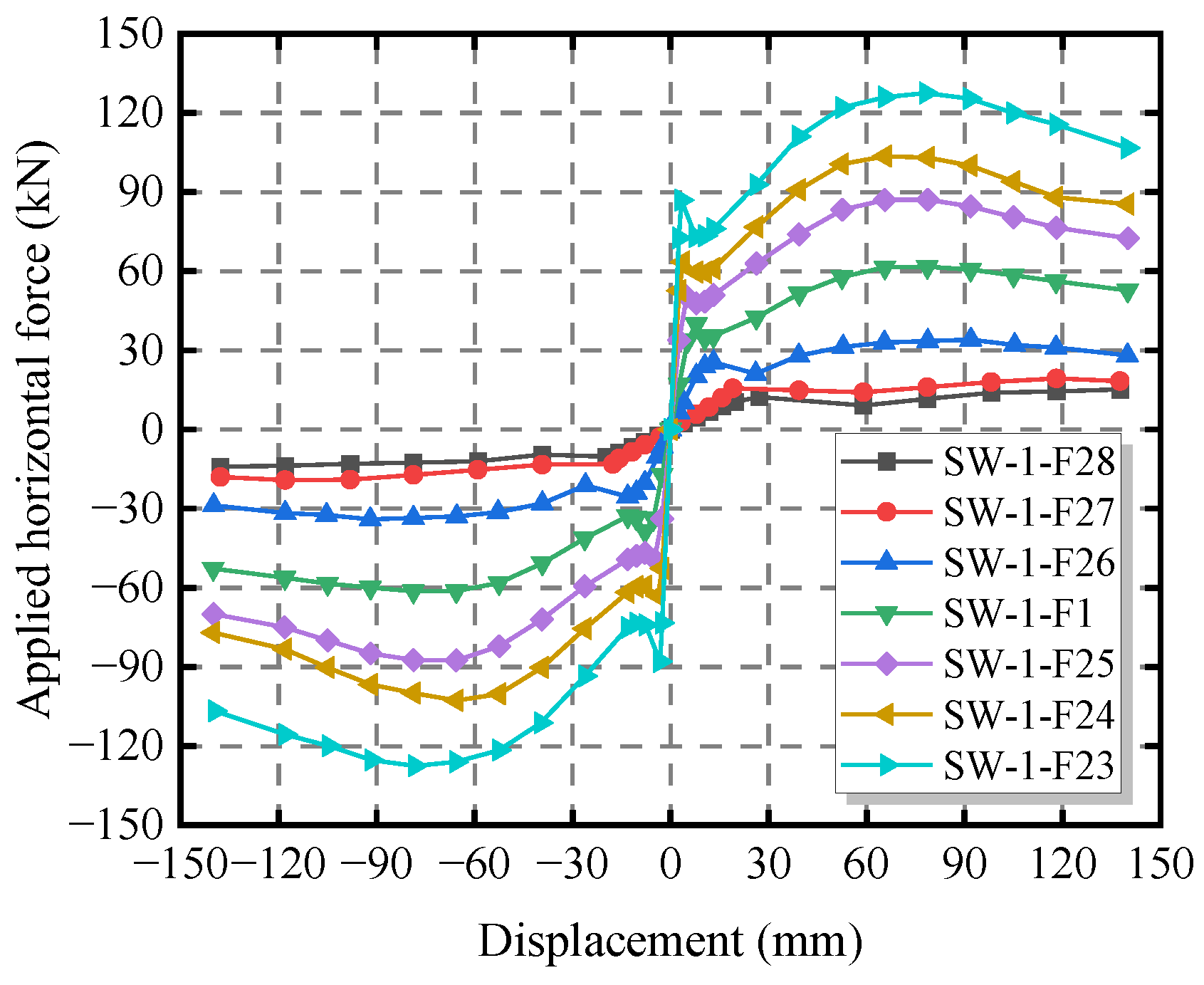
4.3. Influence of Aspect Ratio on the Seismic Performance of the CCS-CFS Shear Wall
5. Conclusions
- (1)
- The CCS-CFS shear wall effectively solved the problem of a connection failure between frame and sheet. Under cyclic load, the main failure modes were the plastic buckling of the corrugated steel sheet and the distortional buckling of the end stud. The method of adding a plate to the side stud considerably improved the deformation ability of the shear wall but had limited influence on its shear strength and stiffness.
- (2)
- Compared with the conventional CFS shear wall, the shear strength, cumulative energy consumption and shear stiffness of the CCS-CFS shear wall were increased by 208%, 175%, and 267%, respectively. Therefore, it is recommended that the CCS-CFS shear wall be employed as a potential lateral force resistance scheme in a multi-layer CFS structure system.
- (3)
- By considering the characteristics of steel mixed strengthening and metal damage criteria, the detailed numerical simulation of the CCS-CFS shear wall developed in this paper can simulate the real failure mode of a shear wall. Furthermore, the finite element analysis results were in good agreement with the test results.
- (4)
- The influence of screw spacing on the seismic performance of the shear wall was relatively limited. Thus, it is highly recommended that the screw spacing be set at 100 mm to ensure the seismic performance of the shear wall and facilitate construction.
- (5)
- To prevent brittle damage to the wall, it is recommended that the sheet thickness ratio of the CCS-CFS shear wall exceed 2.0. Additionally, increasing the frame thickness can effectively enhance the shear strength of the shear wall, while significantly improving the shear stiffness and ductility of the shear wall can be achieved by increasing the sheet thickness.
- (6)
- The aspect ratio exerted a significant influence on both the shear strength and maximum displacement of the CCS-CFS shear wall. The impact on the shear strength of the shear wall can be directly assessed by referencing the North American code AISI S400, but its aspect ratio limit can be relaxed to 10:4.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Yao, Y.; Liang, C.; Ye, Y. Experimental study on the cyclic performance of steel-hollow core partially encased composite spliced frame beam. Soil Dyn. Earthq. Eng. 2022, 163, 107499. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, X.; Huang, B.; Wu, Z.; Chen, H. Static homotropy response analysis of structure with random variables of arbitrary distributions by minimizing stochastic residual error. Comput. Struct. 2023, 288, 107153. [Google Scholar] [CrossRef]
- Deng, E.; Wang, Y.; Zong, L.; Zhang, Z.; Zhang, J. Seismic behavior of a novel liftable connection for modular steel buildings: Experimental and numerical studies. Thin-Walled Struct. 2024, 197, 111563. [Google Scholar] [CrossRef]
- Yang, L.; Ye, M.; Huang, Y.; Dong, J. Study on Mechanical Properties of Displacement-Amplified Mild Steel Bar Joint Damper. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023. [Google Scholar] [CrossRef]
- Wei, J.; Ying, H.; Yang, Y.; Zhang, W.; Yuan, H.; Zhou, J. Seismic performance of concrete-filled steel tubular composite columns with ultra-high performance concrete plates. Eng. Struct. 2023, 278, 115500. [Google Scholar] [CrossRef]
- Hasanali, M.; Roy, K.; Mojtabaei, S.M.; Hajirasouliha, I.; Clifton, G.C.; Lim, J.B.P. A critical review of cold-formed steel seismic resistant systems: Recent developments, challenges and future directions. Thin-Walled Struct. 2022, 180, 109953. [Google Scholar] [CrossRef]
- Hasanali, M.; Mojtabaei, S.M.; Clifton, G.C.; Hajirasouliha, I.; Torabian, S.; Lim, J.B.P. Capacity and design of cold-formed steel warping-restrained beam–column elements. J. Constr. Steel Res. 2022, 190, 107139. [Google Scholar] [CrossRef]
- Deng, R.; Ye, L.; Wang, Y.H.; Li, P.; Shi, Y. Lateral performance of cold-formed steel framed shear walls using slitted sheathing with stiffeners. Eng. Struct. 2024, 302, 117385. [Google Scholar] [CrossRef]
- Wu, J.; Rogers, C. Cold-formed steel centre-sheathed (mid-ply) shear walls of intermediate resistance. Thin-Walled Struct. 2023, 188, 110834. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Yu, C.; Li, Y.; Jiang, Z.; Yu, S. Experimental study on cold-formed steel shear walls with different corrugated steel sheathings. J. Constr. Steel Res. 2022, 199, 107639. [Google Scholar] [CrossRef]
- Niari, S.E.; Rafezy, B.; Abedi, K. Seismic behavior of steel sheathed cold-formed steel shear wall: Experimental investigation and numerical modeling. Thin-Walled Struct. 2015, 96, 337–347. [Google Scholar] [CrossRef]
- Feng, R.Q.; Zhu, B.; Xu, P.; Qiu, Y. Seismic performance of cold-formed steel framed shear walls with steel sheathing and gypsum board. Thin-Walled Struct. 2019, 143, 106238. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, W.; Chen, T.; Zhou, D.; Shi, L.; Tang, Y.; Yu, C. Comparative analysis and design method of shear strength for hybrid SPR-SDS joints in thin-walled steel structures. Structures 2021, 33, 4313–4329. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, A.; Yan, W.; Zhang, Y.; Mu, T.; Yu, C. Study on shear performance and calculation method for self-pierce riveted joints in galvanized steel sheet. Thin-Walled Struct. 2021, 161, 107490. [Google Scholar] [CrossRef]
- Rizk, R. Cold-Formed Steel Frame-Steel Sheathed Shear Walls: Improved Range of Shear Strength Values Accounting for Effect of Full Frame Blocking and Thick Sheathing/Framing Members. Master’s Thesis, McGill University, Montreal, QC, Canada, 2017. [Google Scholar]
- DaBreo, J.; Balh, N.; Ong-Tone, C.; Rogers, C.A. Steel sheathed cold-formed steel framed shear walls subjected to lateral and gravity loading. Thin-Walled Struct. 2014, 74, 232–245. [Google Scholar] [CrossRef]
- Santos, V. Higher Capacity Cold-Formed Steel Sheathed and Framed Shear Walls for Mid-Rise Buildings. Master’s Thesis, McGill University, Montreal, QC, Canada, 2017. [Google Scholar]
- Wang, Y.; Gu, C.; Tang, Q.; Shi, Y.; Zhang, H.; Ye, L. Experimental study on seismic behavior of buckling-restrained steel plate shear wall panel element by cold-formed steel with hat-section under pure shear load. J. Build. Struct. 2020, 41, 49–57+64. (In Chinese) [Google Scholar]
- Brière, V.; Santos, V.; Rogers, C.A. Cold-formed steel centre-sheathed (mid-ply) shear walls. Soil Dyn. Earthq. Eng. 2018, 114, 253–266. [Google Scholar] [CrossRef]
- Yu, C.; Yu, G.; Wang, J. Optimization of Cold-Formed Steel Framed Shear Wall Sheathed with Corrugated Steel Sheets: Experiments and Dynamic Analysis. In Proceedings of the 2015 ASCE Structures Congress, Portland, OR, USA, 23–25 April 2015; pp. 1008–1020. [Google Scholar]
- Zhang, W.; Mahdavian, M.; Li, Y.; Yu, C. Experiments and simulations of cold-formed steel wall assemblies using corrugated steel sheathing subjected to shear and gravity loads. J. Struct. Eng. 2016, 143, 04016193. [Google Scholar] [CrossRef]
- Ngo, H.H. Numerical and Experiment Studies of Wood Sheathed Cold-Formed Steel Framed Shear Walls; Johns Hopkins University: Baltimore, MD, USA, 2014. [Google Scholar]
- Xu, P. Seismic Performance Investigation of New-Type Cold-Formed Steel Framed Sheer Walls with Steel Sheathing; Southeast University: Nanjing, China, 2017. (In Chinese) [Google Scholar]
- Yi, J.; Gil, H.; Youm, K.; Lee, H. Interactive shear buckling behavior of trapezoidally corrugated steel webs. Eng. Struct. 2008, 30, 1659–1666. [Google Scholar] [CrossRef]
- GB/T228.1-2010; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. China Standards Press: Beijing, China, 2010. (In Chinese)
- AISI S100-16; North American Specification for the Design of Cold-Formed Steel Structural Members. American Iron and Steel Institute: Washington, DC, USA, 2016.
- Xie, Z.; Yan, W.; Yu, C.; Mu, T.; Song, L. Experimental investigation of cold-formed steel shear walls with self-piercing riveted connections. Thin-Walled Struct. 2018, 131, 1–15. [Google Scholar] [CrossRef]
- Dassault System Simulia Corp. ABAQUS Analysis User’s Manual Version 6.10; Dassault System Simulia Corp.: Providence, RI, USA, 2010. [Google Scholar]
- Schafer, B.W.; Li, Z.; Moen, C.D. Computational modeling of cold-formed steel. Thin-Walled Struct. 2010, 48, 752–762. [Google Scholar] [CrossRef]
- Chaboche, J.L. Time independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Wang, M.; Shi, Y.; Wang, Y. Equivalent constitutive model of steel with degradation and damage. J. Constr. Steel Res. 2012, 79, 101–114. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, M.; Wang, Y. Experimental and constitutive model study of structural steel under cyclic loading. J. Constr. Steel Res. 2011, 67, 1185–1197. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS/Standard User’s Manual. Version 2019; Dassault Systemes Simulia Corp.: Johnston, RI, USA, 2019. [Google Scholar]
- JGJ 227-2011; Technical Specification for Construction of Low-Rise Cold-Formed Thin-Walled Steel Buildings. China Architecture and Building Press: Beijing, China, 2011. (In Chinese)
- JGJ/T 421-2018; Technical Standard for Cold-Formed Thin-Walled Steel Multi-Storey Residential Buildings. China Architecture and Building Press: Beijing, China, 2018. (In Chinese)
- AISI S400-20; North American Standard for Seismic Design of Cold-Formed Steel Structural Systems. American Iron and Steel Institute: Washington, DC, USA, 2020.


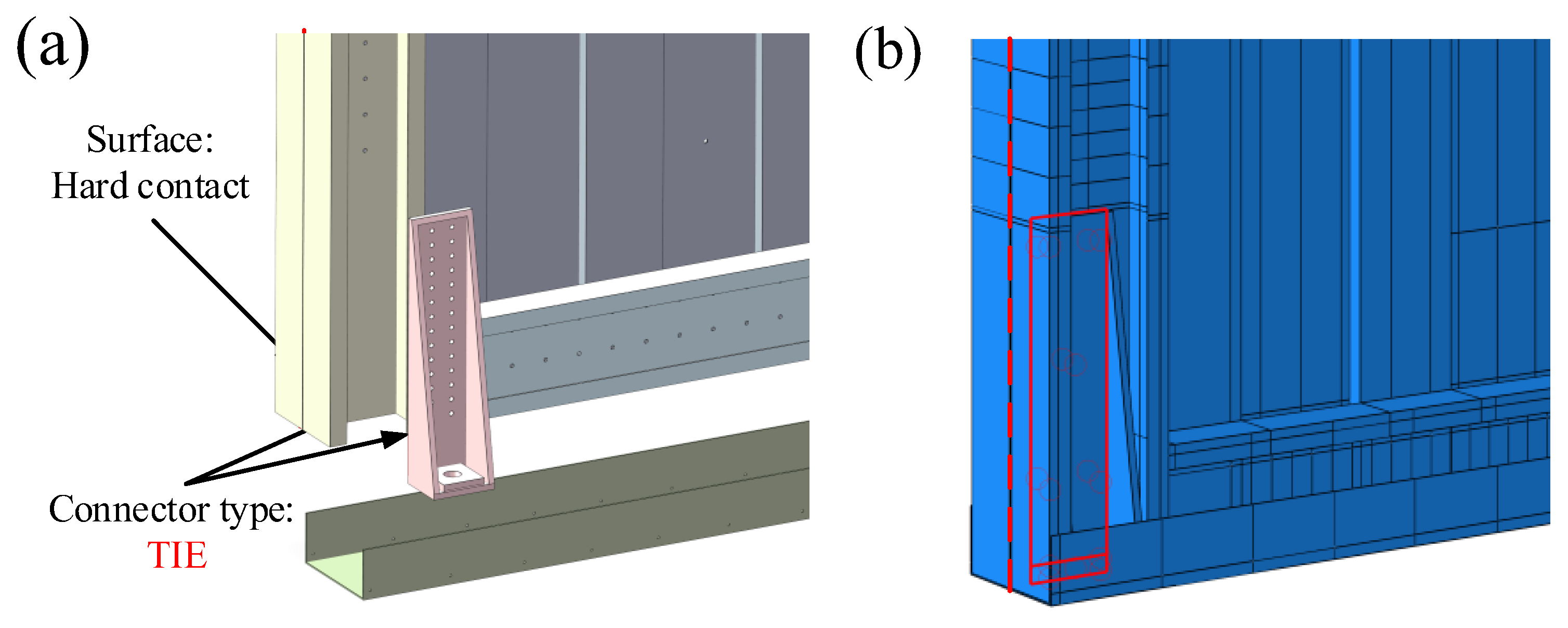
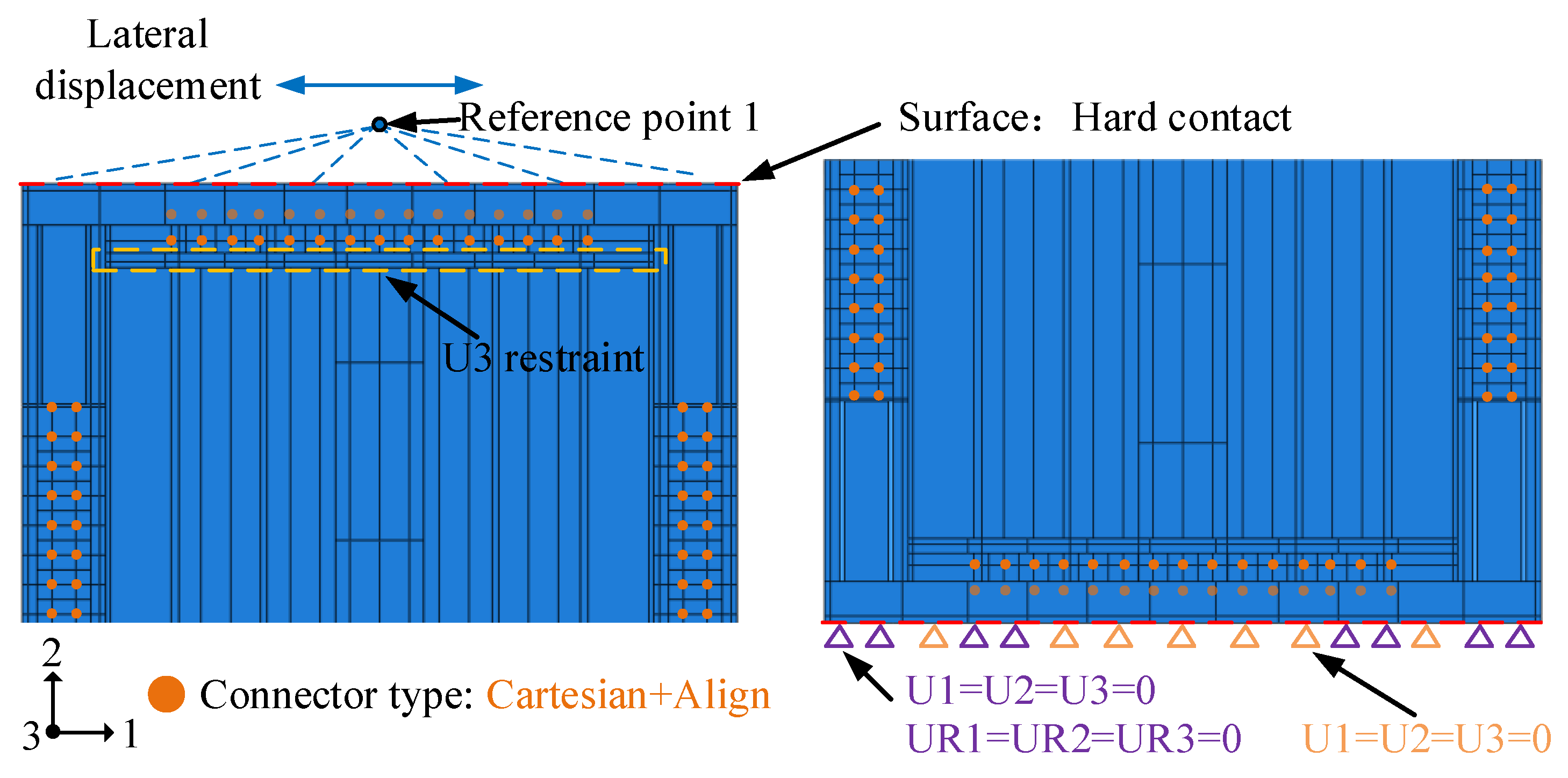

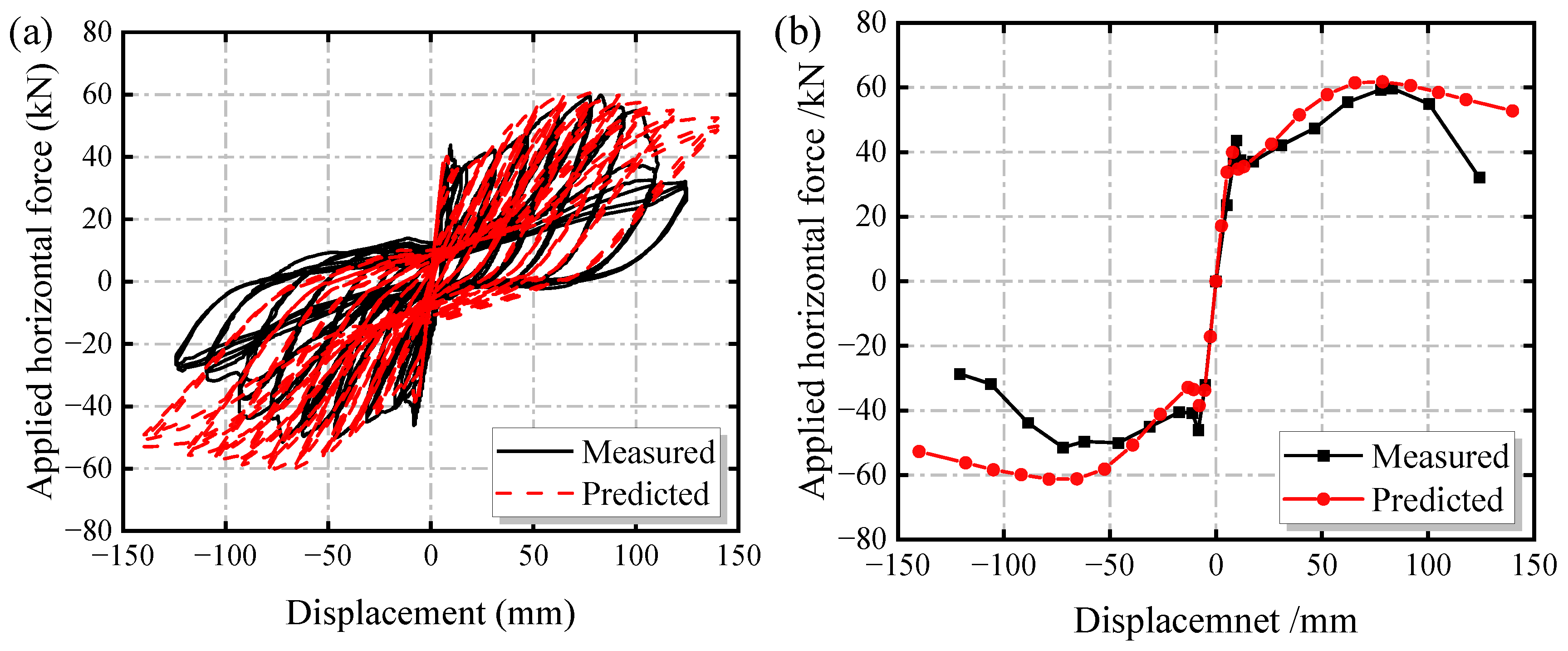

| Component | Steel Strength Grade | Steel Thickness t (mm) | Yield Strength fy (MPa) | Tensile Strength fu (MPa) | fu/fy | Elongation S (%) |
|---|---|---|---|---|---|---|
| Corrugated steel | Q235 | 0.7 | 238 | 320 | 1.34 | 33.67 |
| Steel frame | Q355 | 2.0 | 330 | 433 | 1.31 | 23.72 |
| Specimen Label | Amplitude | Ke (kN/mm) | Δy (mm) | Py (kN) | Δmax (mm) | Pmax (kN) | Δu (mm) | μ (--) | E (J) | Ec (--) |
|---|---|---|---|---|---|---|---|---|---|---|
| SW-1 | Positive | 4.60 | 40.35 | 45.28 | 83.09 | 59.73 | 104.83 | 2.60 | 2.37 | 0.69 |
| Negative | 6.28 | 20.48 | 41.54 | 72.19 | 51.44 | 88.89 | 4.34 | 2.09 | 0.57 | |
| Average | 5.44 | 30.42 | 43.41 | 77.64 | 55.59 | 96.86 | 3.18 | 2.23 | 0.63 | |
| SW-2 | Positive | 5.20 | 28.81 | 47.07 | 77.01 | 59.40 | 105.20 | 3.65 | 2.59 | 0.65 |
| Negative | 5.52 | 32.10 | 39.47 | 89.50 | 51.62 | 120.46 | 3.75 | 2.61 | 0.79 | |
| Average | 5.36 | 30.46 | 43.27 | 83.26 | 55.51 | 112.83 | 3.70 | 2.60 | 0.72 |
| Steel Strength Grade | σ|0 (N/mm2) | Q∞ (N/mm2) | biso | Ckin,1 (N/mm2) | γ1 | Ckin,2 (N/mm2) | γ2 | Ckin,3 (N/mm2) | γ3 | Ckin,4 (N/mm2) | γ4 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q235 | 238 | 21 | 1.2 | 6050 | 175 | 5050 | 120 | 3050 | 25 | 1000 | 35 |
| Q355 | 330 | 21 | 1.2 | 8000 | 175 | 6800 | 120 | 2850 | 35 | 1450 | 30 |
| Connection Object | Constitutive Model | Δ0.2 (mm) | 0.2Pmax (kN) | Ke (kN/mm) | Δy (mm) | Py (kN) | Δmax (mm) | Pmax (kN) |
|---|---|---|---|---|---|---|---|---|
| End stud + Corrugated steel | Ⅰ | 0.511 | 1.136 | 2.226 | 2.553 | 4.376 | 7.371 | 5.682 |
| Beam + Corrugated steel | Ⅱ | 0.047 | 0.464 | 9.910 | 0.214 | 1.013 | 1.168 | 2.319 |
| Specimen Label | Ke (kN/mm) | Δy (mm) | Py (kN) | Δmax (mm) | Pmax (kN) | |
|---|---|---|---|---|---|---|
| SW-B-1 | FE analysis | 5.81 | 33.96 | 47.79 | 78.60 | 61.46 |
| Test | 5.44 | 30.42 | 43.41 | 77.64 | 56.59 | |
| Error (%) | 6.80 | 11.63 | 10.09 | 1.24 | 8.61 | |
| Specimen Label | Screw Spacing (mm) | Yield Displacement (mm) | Yield Load (kN) | Maximum Displacement (mm) | Maximum Load (kN) | Stiffness (kN/mm) | Ductility |
|---|---|---|---|---|---|---|---|
| SW-1-F1 | 50 | 33.96 | 47.79 | 78.60 | 61.46 | 5.81 | 3.50 |
| SW-1-F2 | 75 | 35.76 | 47.35 | 78.74 | 60.19 | 5.40 | 4.13 |
| SW-1-F3 | 100 | 42.11 | 46.76 | 91.87 | 59.74 | 4.95 | 4.21 |
| SW-1-F4 | 125 | 42.39 | 45.60 | 91.90 | 57.96 | 4.71 | 4.71 |
| SW-1-F5 | 150 | 42.50 | 45.54 | 91.92 | 57.11 | 4.12 | 4.89 |
| Sheet Thickness Ratio (ts/tp) | Specimen Label | Height (m) × Width (m) | Stud (mm) | Track (mm) | Sheet (mm) | Remark | |
|---|---|---|---|---|---|---|---|
| ts/tp ≥ 2.5 | 4.00 | SW-1-F6 | 3.0 × 1.2 | 2.0 | 2.0 | 0.5 | The frame thickness is fixed, the sheet thickness is variable. |
| 3.33 | SW-1-F7 | 3.0 × 1.2 | 2.0 | 2.0 | 0.6 | ||
| 2.86 | SW-1-F1 | 3.0 × 1.2 | 2.0 | 2.0 | 0.7 | ||
| 2.50 | SW-1-F8 | 3.0 × 1.2 | 2.0 | 2.0 | 0.8 | ||
| 2.86 | SW-1-F1 | 3.0 × 1.2 | 2.0 | 2.0 | 0.7 | The sheet thickness is fixed, the frame thickness is variable. | |
| 3.57 | SW-1-F9 | 3.0 × 1.2 | 2.5 | 2.5 | 0.7 | ||
| 4.29 | SW-1-F10 | 3.0 × 1.2 | 3.0 | 3.0 | 0.7 | ||
| 1≤ts/tp < 2.5 | 2.22 | SW-1-F11 | 3.0 × 1.2 | 2.0 | 2.0 | 0.9 | The frame thickness is fixed, the sheet thickness is variable. |
| 2.00 | SW-1-F12 | 3.0 × 1.2 | 2.0 | 2.0 | 1.0 | ||
| 1.43 | SW-1-F13 | 3.0 × 1.2 | 2.0 | 2.0 | 1.4 | ||
| 1.33 | SW-1-F14 | 3.0 × 1.2 | 2.0 | 2.0 | 1.5 | ||
| 1.25 | SW-1-F15 | 3.0 × 1.2 | 2.0 | 2.0 | 1.6 | ||
| 1.00 | SW-1-F16 | 3.0 × 1.2 | 2.0 | 2.0 | 2.0 | ||
| 1.00 | SW-1-F17 | 3.0 × 1.2 | 0.7 | 0.7 | 0.7 | The sheet thickness is fixed, the frame thickness is variable. | |
| 1.14 | SW-1-F18 | 3.0 × 1.2 | 0.8 | 0.8 | 0.7 | ||
| 1.29 | SW-1-F19 | 3.0 × 1.2 | 0.9 | 0.9 | 0.7 | ||
| 1.43 | SW-1-F20 | 3.0 × 1.2 | 1.0 | 1.0 | 0.7 | ||
| 1.71 | SW-1-F21 | 3.0 × 1.2 | 1.2 | 1.2 | 0.7 | ||
| 2.14 | SW-1-F22 | 3.0 × 1.2 | 1.5 | 1.5 | 0.7 | ||
| Sheet Thickness Ratio (ts/tp) | Specimen Label | Δy (mm) | Py (kN) | Δmax (mm) | Pmax (kN) | Ke (kN/m) | μ |
|---|---|---|---|---|---|---|---|
| ts/tp > 2.0 | SW-1-F6 | 56.78 | 44.97 | 104.98 | 53.31 | 5.27 | 4.00 |
| SW-1-F7 | 44.70 | 46.40 | 91.87 | 57.81 | 5.40 | 4.03 | |
| SW-1-F1 | 33.96 | 47.79 | 78.60 | 61.73 | 5.81 | 4.17 | |
| SW-1-F8 | 26.23 | 52.41 | 65.62 | 69.26 | 5.93 | 4.99 | |
| SW-1-F11 | 19.01 | 63.42 | 52.46 | 75.35 | 7.59 | 5.40 | |
| SW-1-F22 | 16.24 | 36.81 | 52.50 | 43.23 | 5.69 | 6.10 | |
| SW-1-F1 | 33.96 | 47.79 | 78.60 | 61.73 | 5.81 | 4.03 | |
| SW-1-F9 | 51.18 | 65.77 | 84.82 | 82.26 | 6.40 | 3.50 | |
| SW-1-F10 | 64.09 | 81.82 | 91.88 | 100.82 | 7.62 | 3.17 |
| Specimen Label | Aspect Ratio | Δmax (mm) | Pmax (kN) | Shear Strength (kN/m) | μ |
|---|---|---|---|---|---|
| SW-1-F23 | 1.08 | 78.21 | 137.53 | 49.51 | 4.13 |
| SW-1-F24 | 1.33 | 78.75 | 113.06 | 50.47 | 4.10 |
| SW-1-F25 | 1.74 | 78.73 | 87.14 | 50.49 | 4.14 |
| SW-1-1 | 2.50 | 78.60 | 61.73 | 51.22 | 4.17 |
| SW-1-F26 | 3.00 | 91.94 | 34.00 | 33.66 | 3.78 |
| SW-1-F27 | 3.96 | 118.11 | 19.34 | 25.51 | 2.77 |
| SW-1-F28 | 4.45 | 137.56 | 15.23 | 22.60 | 2.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Bi, Y.; Fan, Y.; Gao, C.; Zhang, X.; Feng, Y.; Zhou, D.; Dong, L. Finite Element Investigation of a Novel Cold-Formed Steel Shear Wall. Buildings 2024, 14, 1691. https://doi.org/10.3390/buildings14061691
Xie Z, Bi Y, Fan Y, Gao C, Zhang X, Feng Y, Zhou D, Dong L. Finite Element Investigation of a Novel Cold-Formed Steel Shear Wall. Buildings. 2024; 14(6):1691. https://doi.org/10.3390/buildings14061691
Chicago/Turabian StyleXie, Zhiqiang, Ye Bi, Ying Fan, Chengwei Gao, Xiangdong Zhang, Yin Feng, Daxing Zhou, and Lei Dong. 2024. "Finite Element Investigation of a Novel Cold-Formed Steel Shear Wall" Buildings 14, no. 6: 1691. https://doi.org/10.3390/buildings14061691
APA StyleXie, Z., Bi, Y., Fan, Y., Gao, C., Zhang, X., Feng, Y., Zhou, D., & Dong, L. (2024). Finite Element Investigation of a Novel Cold-Formed Steel Shear Wall. Buildings, 14(6), 1691. https://doi.org/10.3390/buildings14061691







