Probabilistic Fatigue Crack Growth Prediction for Pipelines with Initial Flaws
Abstract
1. Introduction
2. Fatigue Crack Growth Data and Model
2.1. Data in the Literature
2.2. Fatigue Crack Growth Model
2.3. Stress Intensity Factor
3. Particle Filtering Method
4. Prognosis of One-Dimensional Fatigue Crack Growth and Remaining Service Life
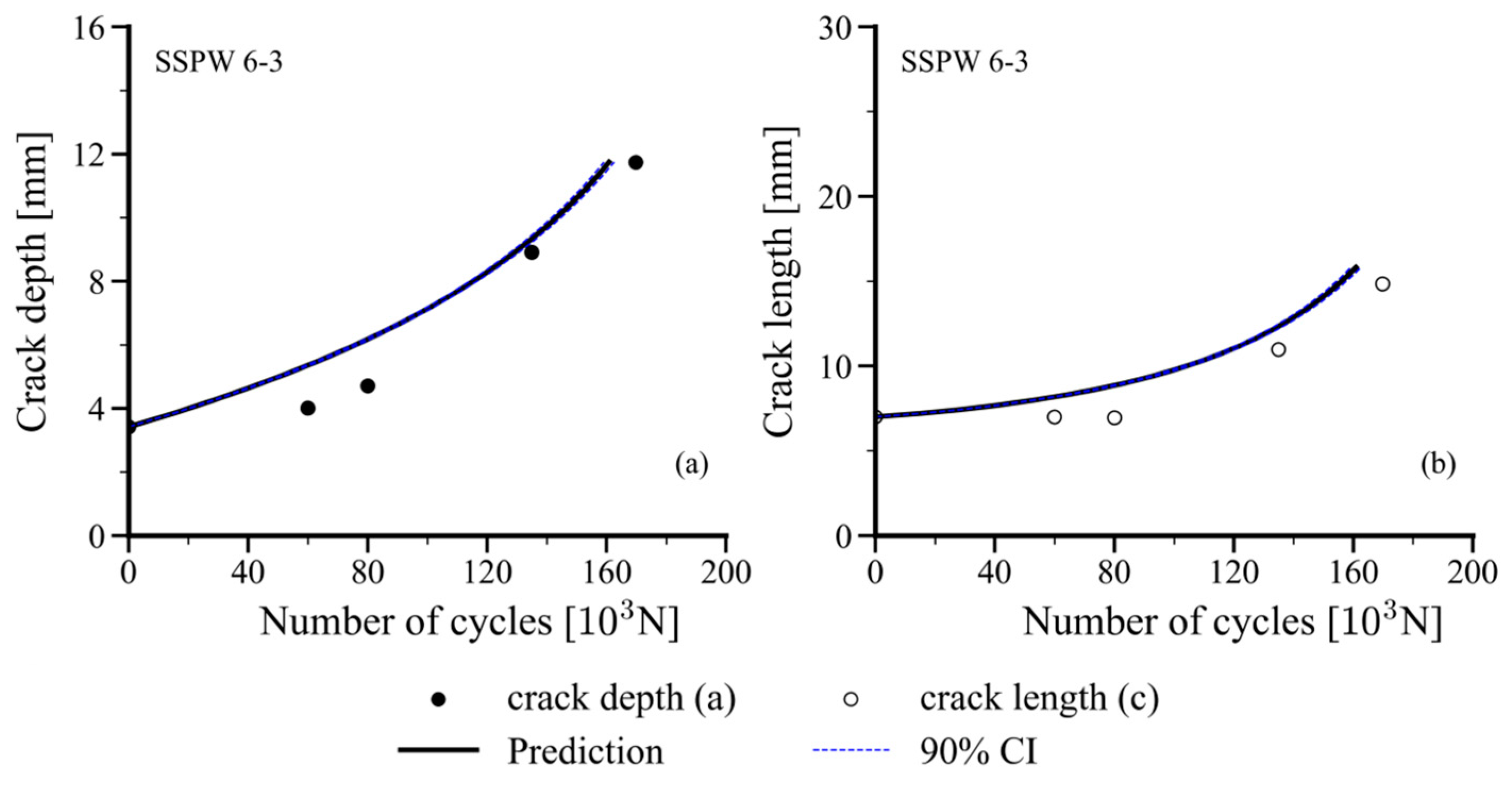
4.1. One-Dimensional Fatigue Crack Growth
4.2. Predicted Remaining Service Life
5. Prognosis of Two-Dimensional Fatigue Crack Growth and Remaining Service Life
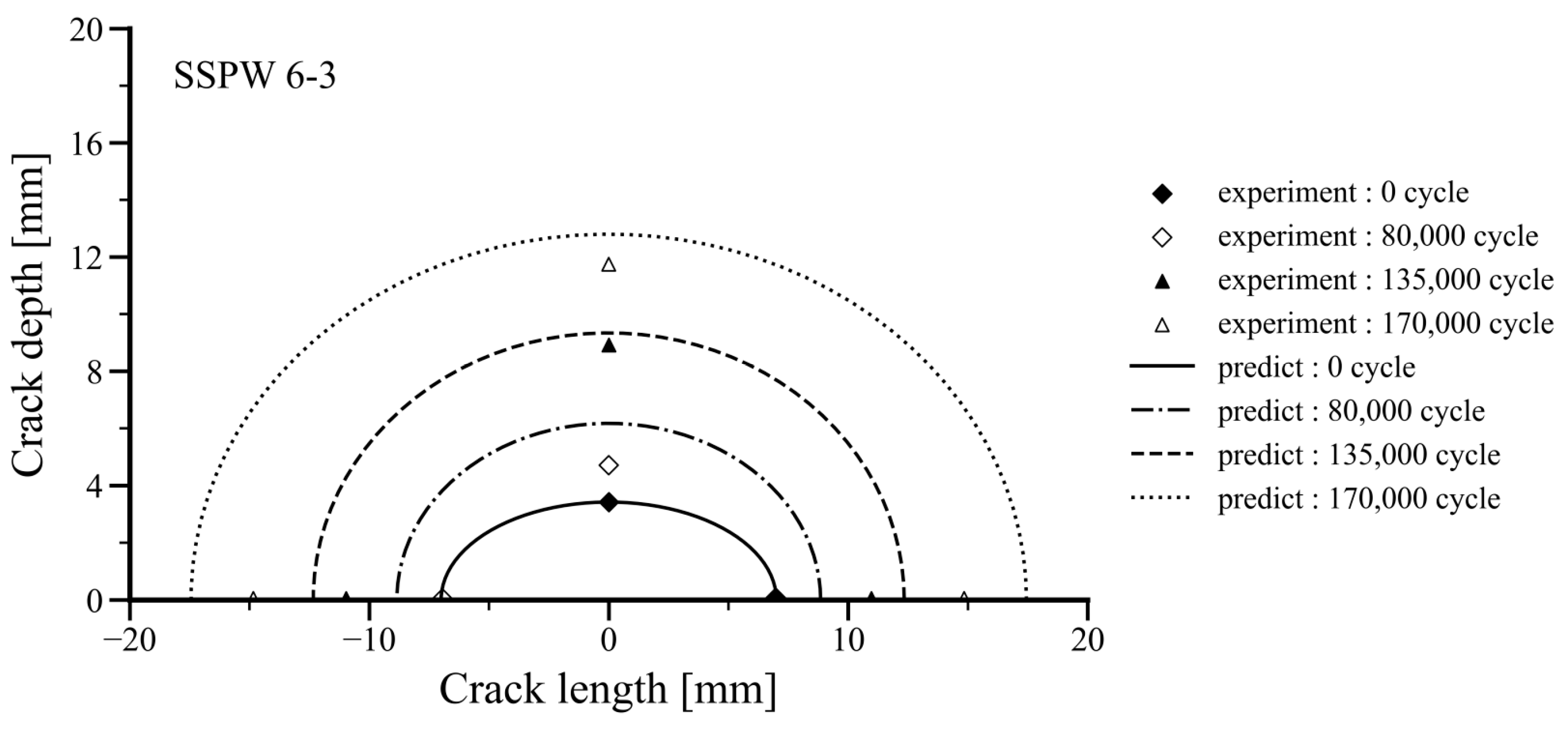
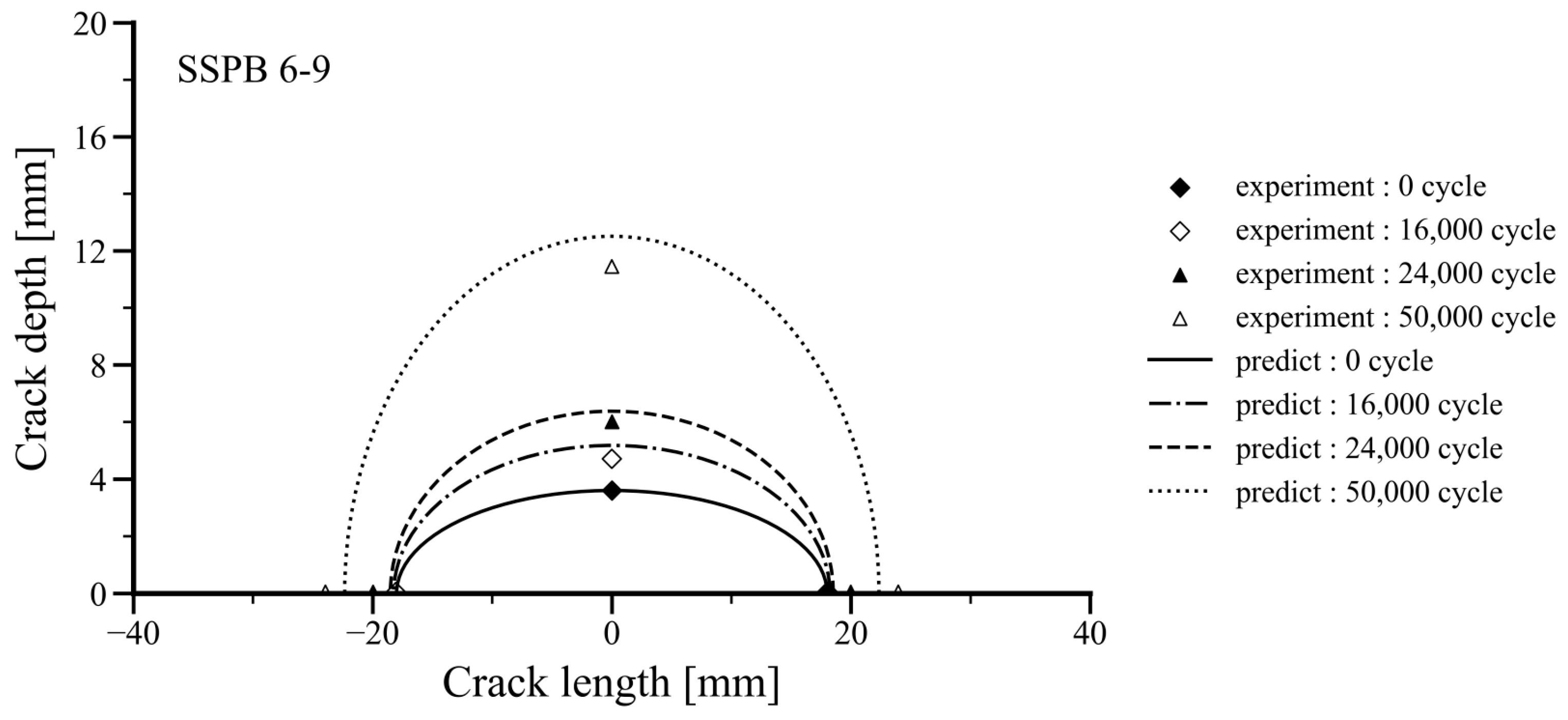
5.1. Two-Dimensional Fatigue Crack Growth
- Randomly generate the initial states with n number of particles.
- For = 1, 2, ⋯, the following are carried out:
- 1.
- Perform the time propagating step to obtain the next step particles using Equations (17) and (18). For Equation (17), the stress intensity factor at the deepest point of the flaw needs to be used, and for Equation (18), the stress intensity factor at the intersection of flaw with free surface needs to be used.
- 2.
- Compute the relative likelihood Equation (22) of each particle, conditioned on the measurement Equation (20).
- 3.
- Resample using the scale the relative likelihood obtained in the previous step as follows:
- 4.
- Generate a set of posterior particles on the basis of the relative likelihood .
- 5.
- Compute the relative likelihood , Equation (24) of each particle, conditioned on the measurement Equation (21).
- 6.
- Resample using the scale the relative likelihood obtained in the previous step as follows:
- 7.
- Generate a set of posterior particles on the basis of the relative likelihood .
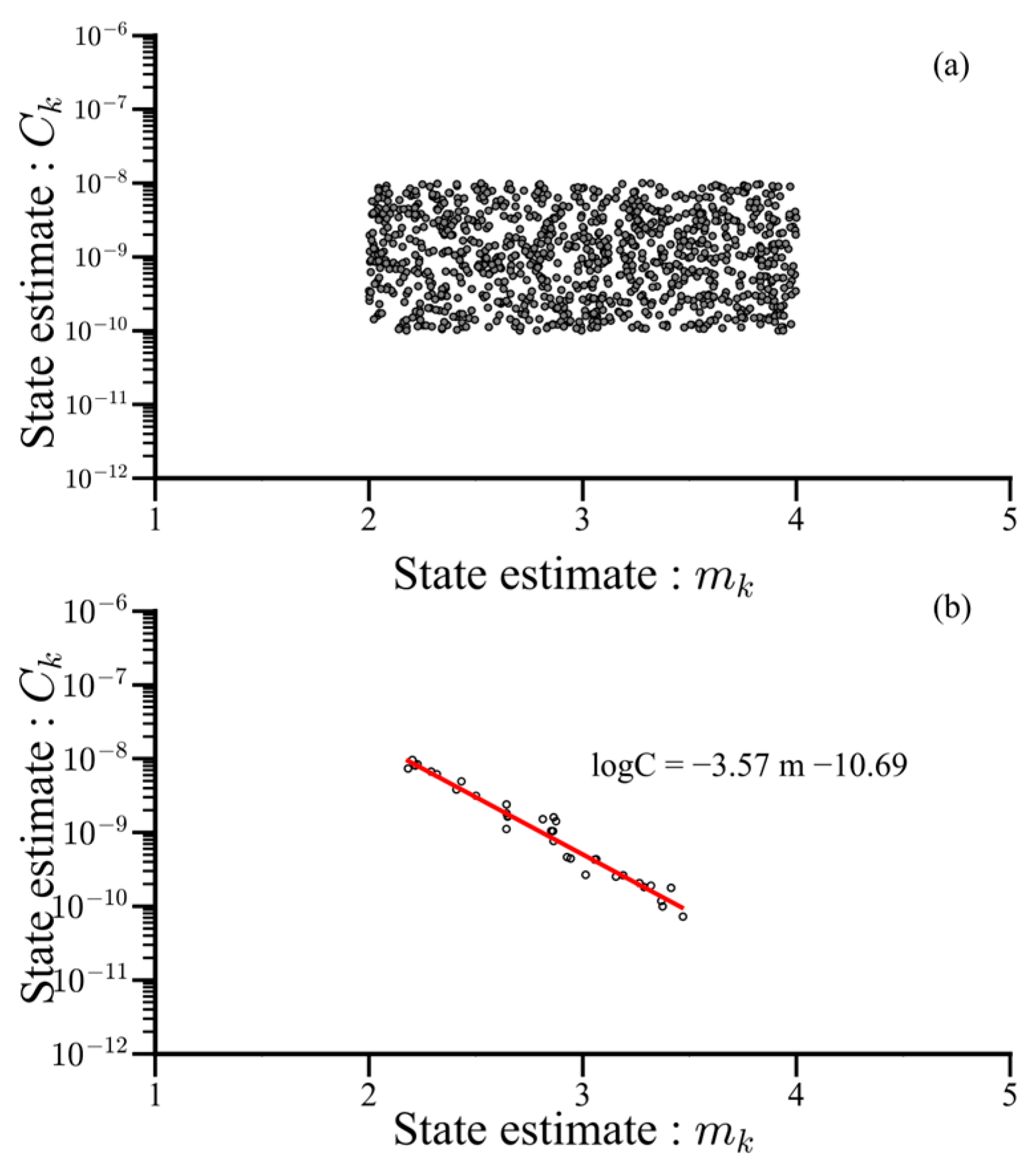
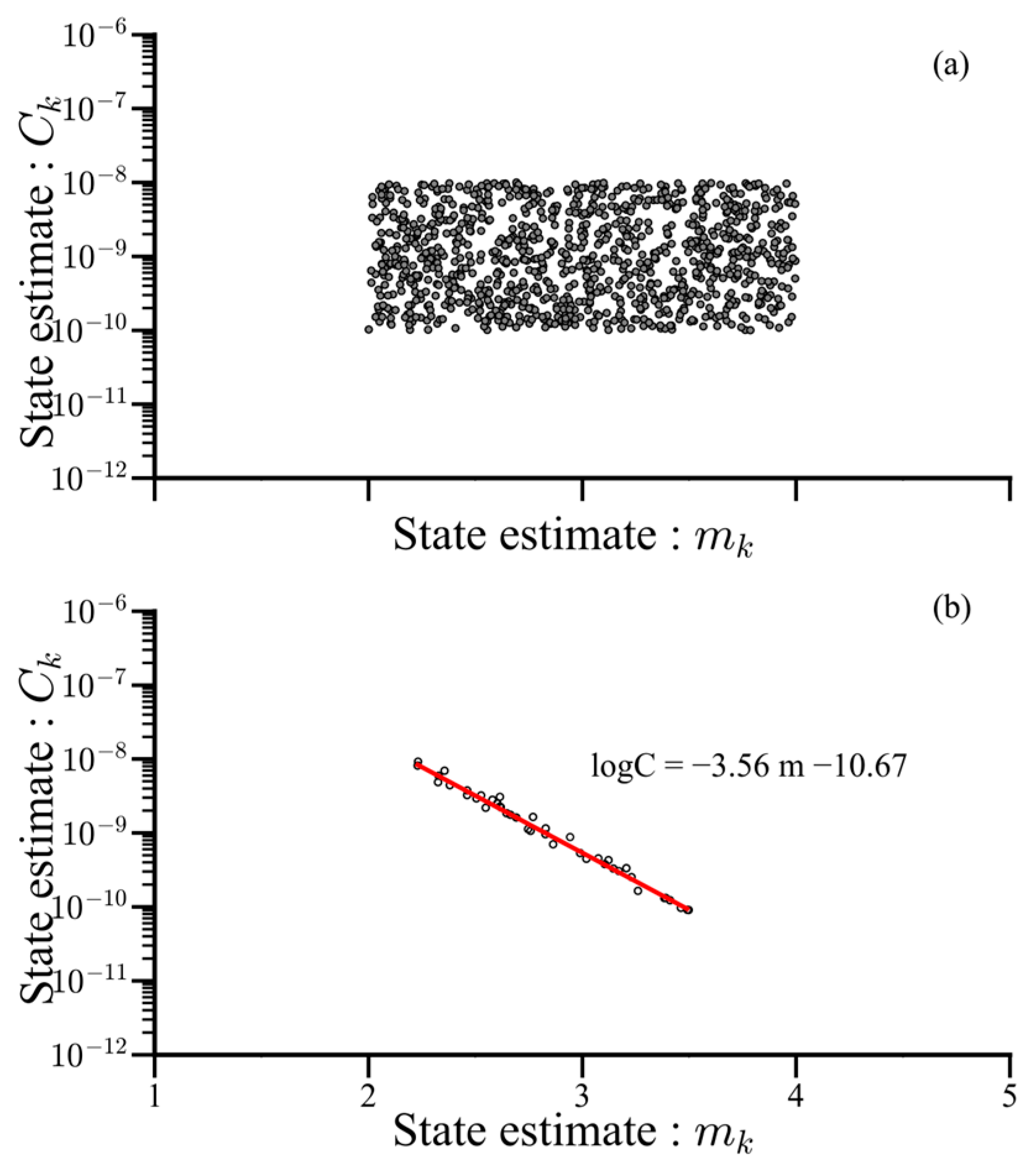
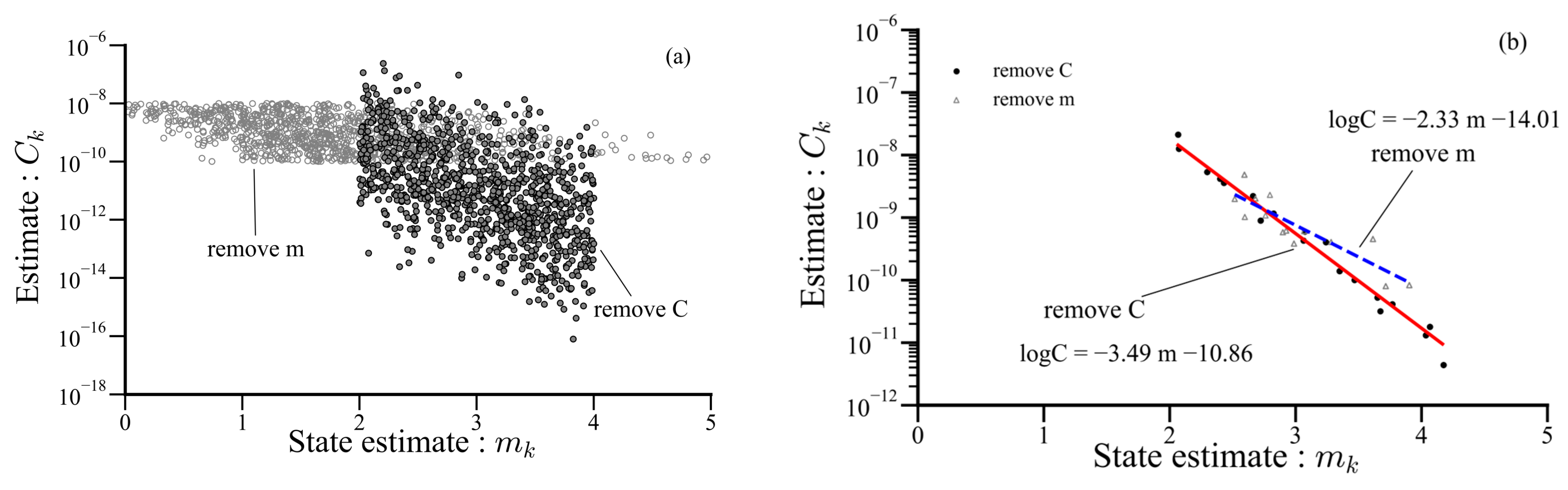
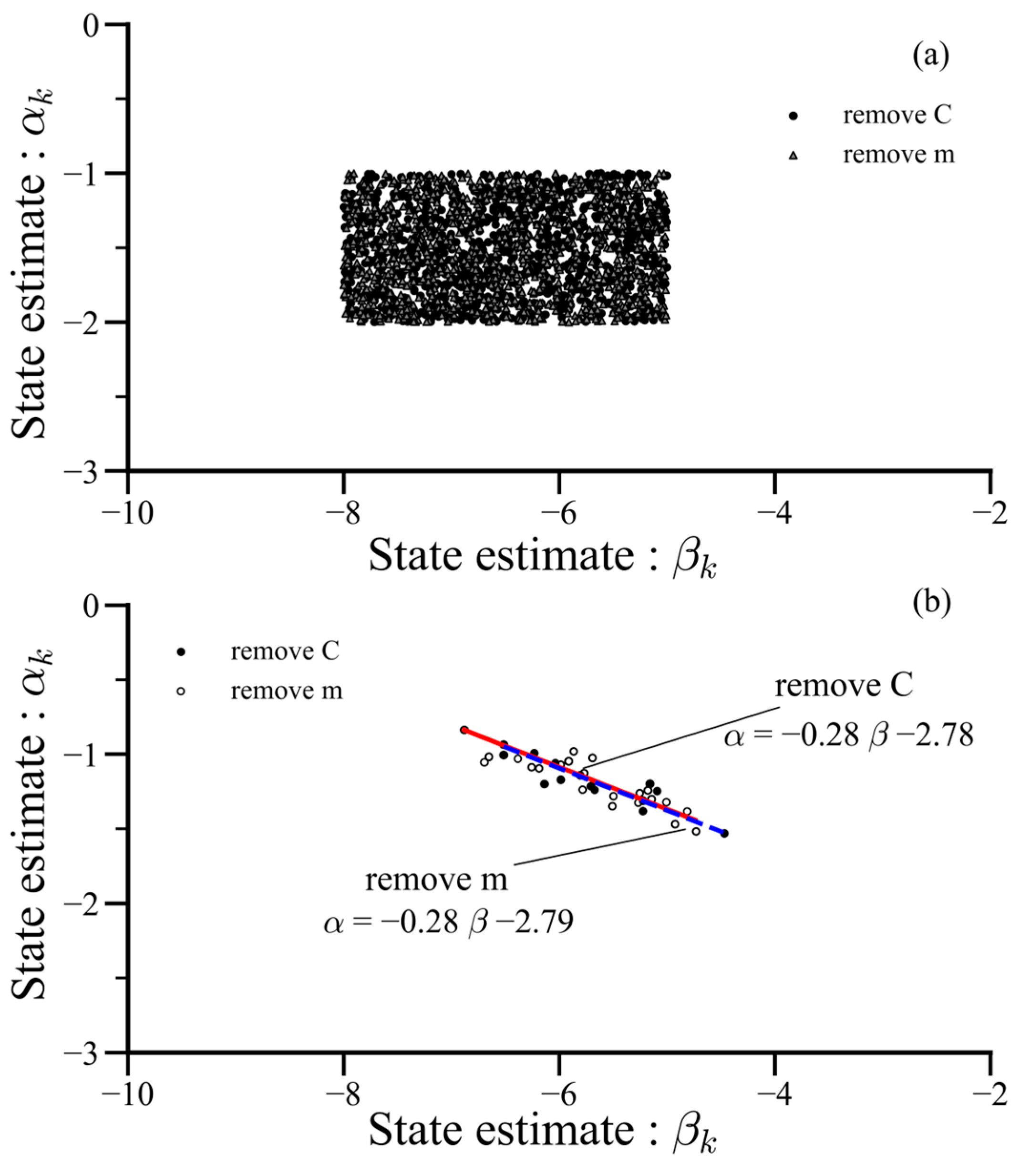
5.2. Pearson Correlation between Paris Parameters
6. Conclusions
- First, with a fixed crack length of the semi-elliptical crack, crack growth was predicted using the particle filtering method with 1000 particles for one-dimensional fatigue crack growth, focusing on crack depth. This evaluation, based on experimental data from previous studies, included various ratios and initial crack depths. The results were consistent with previous tests, indicating an effective prediction of crack growth.
- The remaining service life of each pipe was predicted based on the initial crack depth using the particle filtering method. Additionally, the simulation results showed that the Pearson correlation between the Paris parameters and converged to the expected value range, consistent with previous studies reporting a strong negative correlation. This demonstrates that the particle filtering method can effectively simulate the Pearson correlation for fatigue crack growth in a SA333 Gr.6 carbon steel pipeline, even when the parameters are initially uncorrelated.
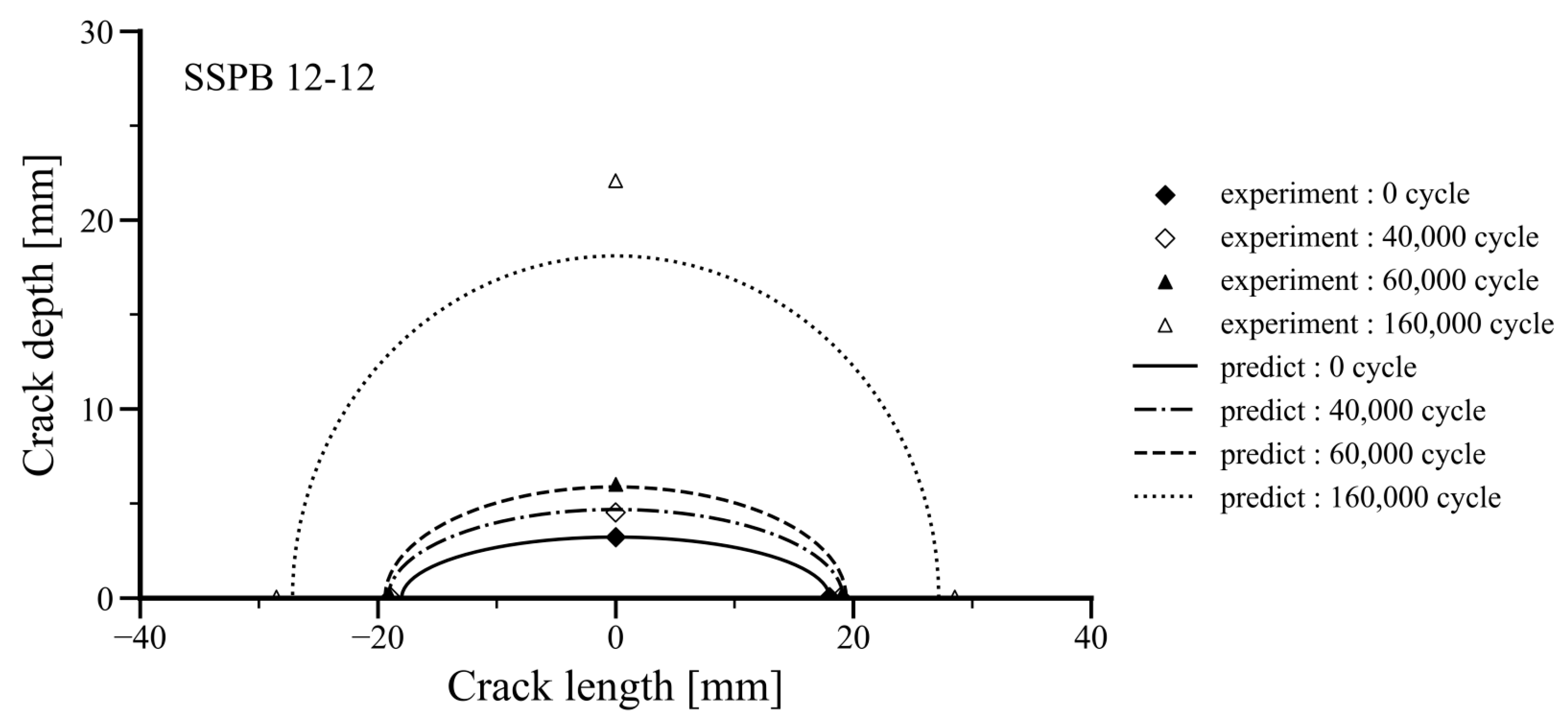
- With a small semi-elliptical surface defect aspect ratio, crack growth occurs in both depth and longitudinal directions. To predict this, the particle filtering method was combined with the finite difference method for two-dimensional fatigue crack growth. The predictions, consistent with previous studies, effectively modeled crack growth. Although initial cycle predictions were slightly larger than test data, they matched closely as the number of cycles increased, demonstrating the effectiveness of the particle filtering method in modeling two-dimensional crack growth.
- In the crack growth model considered in this study, the Pearson correlation between the Paris parameters and was predicted despite not considering their strong correlation initially. By dividing the Paris parameters into two sets of states, and , we obtained fatigue crack growth prediction results similar to those using only and . This indicates that the particle filtering method effectively predicted fatigue crack growth and that the correlation of each variable converged to an expected value range.
- The innovation of this research lies in applying and validating the particle filtering method for predicting fatigue crack growth in pipelines with initial flaws. This probabilistic approach continuously updates predictions with new data, enhancing accuracy and reliability. While we examined the model’s applicability based on existing experimental data, there are limitations in determining failure and critical size for practical applications. These aspects will be addressed in future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ossai, C.I.; Boswell, B.; Davies, I.J. Pipeline failures in corrosive environments–A conceptual analysis of trends and effects. Eng. Fail. Anal. 2015, 53, 36–58. [Google Scholar] [CrossRef]
- Lee, S.-J.; Cho, W.-Y.; Kim, K.-S.; Zi, G.; Yoon, Y.-C. Numerical Evaluation of Compressive Strain Capacity for API X100 Line Pipe. KSCE J. Civ. Eng. 2018, 22, 3039–3051. [Google Scholar] [CrossRef]
- Arora, P.; Singh, P.; Bhasin, V.; Vaze, K.; Ghosh, A.; Pukazhendhi, D.; Gandhi, P.; Raghava, G. Predictions for fatigue crack growth life of cracked pipes and pipe welds using RMS SIF approach and experimental validation. Int. J. Press. Vessels Pip. 2011, 88, 384–394. [Google Scholar] [CrossRef]
- Mittal, R.; Singh, P.; Pukazhendi, D.; Bhasin, V.; Vaze, K.; Ghosh, A. Effect of vibration loading on the fatigue life of part-through notched pipe. Int. J. Press. Vessels Pip. 2011, 88, 415–422. [Google Scholar] [CrossRef]
- Shibata, H. On the basic research of design analysis and testing based on the failure rate for pipings and equipment under earthquake conditions. Nucl. Eng. Des. 1980, 60, 79–84. [Google Scholar] [CrossRef]
- Shimakawa, T.; Takahashi, H.; Doi, H.; Watashi, K.; Asada, Y. Creep-fatigue crack propagation tests and the development of an analytical evaluation method for surface cracked pipe. Nucl. Eng. Des. 1993, 139, 283–292. [Google Scholar] [CrossRef]
- Singh, P.; Vaze, K.; Bhasin, V.; Kushwaha, H.; Gandhi, P.; Murthy, D.R. Crack initiation and growth behaviour of circumferentially cracked pipes under cyclic and monotonic loading. Int. J. Press. Vessels Pip. 2003, 80, 629–640. [Google Scholar] [CrossRef]
- Zhu, L.; Tao, X.; Cengdian, L. Fatigue strength and crack propagation life of in-service high pressure tubular reactor under residual stress. Int. J. Press. Vessels Pip. 1998, 75, 871–877. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Y.; Li, L.; Zhu, L.; Wu, G. Fatigue failure analysis of dented pipeline and simulation calculation. Eng. Fail. Anal. 2020, 113, 104572. [Google Scholar] [CrossRef]
- Baker, M. Delivery Order DTRS56-02-D-70036. Integrity Management Program; Research and Special Programs Administration Office of Pipeline Safety: Washington, DC, USA, 2004. [Google Scholar]
- Vishnuvardhan, S.; Murthy, A.R.; Choudhary, A. A review on pipeline failures, defects in pipelines and their assessment and fatigue life prediction methods. Int. J. Press. Vessels Pip. 2023, 201, 104853. [Google Scholar] [CrossRef]
- Hussain, M.; Zhang, T.; Chaudhry, M.; Jamil, I.; Kausar, S.; Hussain, I. Review of prediction of stress corrosion cracking in gas pipelines using machine learning. Machines 2024, 12, 42. [Google Scholar] [CrossRef]
- Amerincan Petroleum Institute(API), A. 579-1/ASME FFS-1: Fitness-for-Service; American Petroleum Institute: Washington, DC, USA, 2007. [Google Scholar]
- Meresht, E.S.; Farahani, T.S.; Neshati, J. Failure analysis of stress corrosion cracking occurred in a gas transmission steel pipeline. Eng. Fail. Anal. 2011, 18, 963–970. [Google Scholar] [CrossRef]
- Mansor, N.; Abdullah, S.; Ariffin, A. Effect of loading sequences on fatigue crack growth and crack closure in API X65 steel. Mar. Struct. 2019, 65, 181–196. [Google Scholar] [CrossRef]
- Li, L.; Yang, Y.; Xu, Z.; Chen, G.; Chen, X. Fatigue crack growth law of API X80 pipeline steel under various stress ratios based on J-integral. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 1124–1135. [Google Scholar] [CrossRef]
- Mohammadi Esfarjani, S.; Salehi, M. Inspection of aboveground pipeline using vibration responses. J. Pipeline Syst. Eng. Pract. 2020, 11, 04020021. [Google Scholar] [CrossRef]
- Deng, Y.-S.; Li, L.; Yao, Z.-G.; Meng, L.-Q. Stress intensity factors and fatigue crack growth law of cracked submarine special-shaped pipe under earthquake load. Ocean Eng. 2022, 257, 111267. [Google Scholar] [CrossRef]
- Lee, S.-J.; Zi, G.; Mun, S.; Kong, J.S.; Choi, J.-H. Probabilistic prognosis of fatigue crack growth for asphalt concretes. Eng. Fract. Mech. 2015, 141, 212–229. [Google Scholar] [CrossRef]
- Guo, Y.; Shao, Y.; Gao, X.; Li, T.; Zhong, Y.; Luo, X. Corrosion fatigue crack growth of serviced API 5L X56 submarine pipeline. Ocean Eng. 2022, 256, 111502. [Google Scholar] [CrossRef]
- Liu, C.; Li, B.; Cai, Y.; Chen, X. Fatigue crack propagation behaviour of pressurised elbow pipes under cyclic bending. Thin-Walled Struct. 2020, 154, 106882. [Google Scholar] [CrossRef]
- Huang, S.; Peng, L.; Sun, H.; Li, S. Deep learning for magnetic flux leakage detection and evaluation of oil & gas pipelines: A review. Energies 2023, 16, 1372. [Google Scholar] [CrossRef]
- Peng, D.; She, X.; Zheng, Y.; Tang, Y.; Fan, Z.; Hu, G. Research on the 3D Reverse Time Migration Technique for Internal Defects Imaging and Sensor Settings of Pressure Pipelines. Sensors 2023, 23, 8742. [Google Scholar] [CrossRef]
- Parlak, B.O.; Yavasoglu, H.A. A comprehensive analysis of in-line inspection tools and technologies for steel oil and gas pipelines. Sustainability 2023, 15, 2783. [Google Scholar] [CrossRef]
- Lyu, F.; Zhou, X.; Ding, Z.; Qiao, X.; Song, D. Application Research of Ultrasonic-Guided Wave Technology in Pipeline Corrosion Defect Detection: A Review. Coatings 2024, 14, 358. [Google Scholar] [CrossRef]
- BS 7910; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures. The British Standards Institution: London, UK, 2005.
- CSA Z662-11; Oil and Gas Pipeline Systems. CSA Group: Toronto, ON, Canada, 2011.
- OS-F101; Submarine Pipeline Systems. Offshore Standard: Høvik, Norway, 2000.
- Wilkowski, G. Leak-before-break: What does it really mean? J. Press. Vessel Technol. 2000, 122, 267–272. [Google Scholar] [CrossRef]
- Rastogi, R.; Ghosh, S.; Ghosh, A.; Vaze, K.; Singh, P. Fatigue crack growth prediction in nuclear piping using Markov chain Monte Carlo simulation. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 145–156. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Lee, J.H.; Choi, Y.; Ann, H.; Jin, S.Y.; Lee, S.-J.; Kong, J.S. Maintenance cost estimation in PSCI girder bridges using updating probabilistic deterioration model. Sustainability 2019, 11, 6593. [Google Scholar] [CrossRef]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Jeong, M.C.; Lee, S.-J.; Cha, K.; Zi, G.; Kong, J.S. Probabilistic model forecasting for rail wear in seoul metro based on bayesian theory. Eng. Fail. Anal. 2019, 96, 202–210. [Google Scholar] [CrossRef]
- Djuric, P.; Kotecha, J.; Zhang, J.; Huang, Y.; Ghirmai, T.; Bugallo, M.; Miguez, J. Particle filtering. IEEE Signal Proc. Mag. 2003, 20, 19–38. [Google Scholar] [CrossRef]
- Cadini, F.; Zio, E.; Avram, D. Monte Carlo-based filtering for fatigue crack growth estimation. Probabilistic Eng. Mech. 2009, 24, 367–373. [Google Scholar] [CrossRef]
- Zio, E.; Peloni, G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components. Reliab. Eng. Syst. Saf. 2011, 96, 403–409. [Google Scholar] [CrossRef]
- An, D.; Choi, J.-H.; Kim, N.H. Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab. Reliab. Eng. Syst. Saf. 2013, 115, 161–169. [Google Scholar] [CrossRef]
- Wang, C.-W.; Niu, Z.-G.; Jia, H.; Zhang, H.-W. An assessment model of water pipe condition using Bayesian inference. J. Zhejiang Univ.-Sci. A 2010, 11, 495–504. [Google Scholar] [CrossRef]
- Kim, K.; Lee, G.; Park, K.; Park, S.; Lee, W.B. Adaptive approach for estimation of pipeline corrosion defects via Bayesian inference. Reliab. Eng. Syst. Saf. 2021, 216, 107998. [Google Scholar] [CrossRef]
- Niu, X.; He, C.; Zhu, S.-P.; Foti, P.; Berto, F.; Wang, L.; Liao, D.; Wang, Q. Defect sensitivity and fatigue design: Deterministic and probabilistic aspects in AM metallic materials. Prog. Mater. Sci. 2024, 144, 101290. [Google Scholar] [CrossRef]
- He, J.-C.; Zhu, S.-P.; Gao, J.-W.; Liu, R.; Li, W.; Liu, Q.; He, Y.; Wang, Q. Microstructural size effect on the notch fatigue behavior of a Ni-based superalloy using crystal plasticity modelling approach. Int. J. Plast. 2024, 172, 103857. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Keshtegar, B.; Qian, G.; Wang, Q. Probabilistic framework for fatigue life assessment of notched components under size effects. Int. J. Mech. Sci. 2020, 181, 105685. [Google Scholar] [CrossRef]
- Zhou, T.; Jiang, S.; Han, T.; Zhu, S.-P.; Cai, Y. A physically consistent framework for fatigue life prediction using probabilistic physics-informed neural network. Int. J. Fatigue 2023, 166, 107234. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, S.-P.; Luo, C.; Liao, D.; Wang, Q. Physics-guided machine learning frameworks for fatigue life prediction of AM materials. Int. J. Fatigue 2023, 172, 107658. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Gong, J.; Xuan, F.-Z. Machine learning-based fatigue life prediction of metal materials: Perspectives of physics-informed and data-driven hybrid methods. Eng. Fract. Mech. 2023, 284, 109242. [Google Scholar] [CrossRef]
- Benson, J.; Edmonds, D. Relationship between the parameters C and m of Paris' law for fatigue crack growth in a low-alloy steel. Scr. Metall. 1978, 12, 645–647. [Google Scholar] [CrossRef]
- Tanaka, K.; Masuda, C.; Nishijima, S. The generalized relationship between the parameters C and m of Paris’ law for fatigue crack growth. Scr. Metall. 1981, 15, 259–264. [Google Scholar] [CrossRef]
- Cortie, M.; Garrett, G. On the correlation between the C and m in the Paris equation for fatigue crack propagation. Eng. Fract. Mech. 1988, 30, 49–58. [Google Scholar] [CrossRef]
- Cortie, M. The irrepressible relationship between the Paris law parameters. Eng. Fract. Mech. 1991, 40, 681–682. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. Are the Paris’ law parameters dependent on each other? Frat. Integrità Strutt. 2007, 1, 10–16. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Gong, D. The interrelation of the parameters in the Paris equation of fatigue crack growth. Eng. Fract. Mech. 2012, 96, 500–509. [Google Scholar] [CrossRef]
- Ray, S.; Kishen, J.C. Fatigue crack propagation model for plain concrete–An analogy with population growth. Eng. Fract. Mech. 2010, 77, 3418–3433. [Google Scholar] [CrossRef]
- Ciavarella, M.; Paggi, M.; Carpinteri, A. One, no one, and one hundred thousand crack propagation laws: A generalized Barenblatt and Botvina dimensional analysis approach to fatigue crack growth. J. Mech. Phys. Solids 2008, 56, 3416–3432. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. Dimensional analysis and fractal modeling of fatigue crack growth. J. ASTM Int. 2011, 8, 1–13. [Google Scholar] [CrossRef]
- Ray, S.; Kishen, J.C. Fatigue crack propagation model and size effect in concrete using dimensional analysis. Mech. Mater. 2011, 43, 75–86. [Google Scholar] [CrossRef]
- Fathima, K.P.; Kishen, J.C. A thermodynamic framework for fatigue crack growth in concrete. Int. J. Fatigue 2013, 54, 17–24. [Google Scholar] [CrossRef]
- Bergner, F.; Zouhar, G. A new approach to the correlation between the coefficient and the exponent in the power law equation of fatigue crack growth. Int. J. Fatigue 2000, 22, 229–239. [Google Scholar] [CrossRef]
- An, D.; Choi, J.-H.; Kim, N.H. Identification of correlated damage parameters under noise and bias using Bayesian inference. Struct. Health Monit. 2012, 11, 293–303. [Google Scholar] [CrossRef]
- An, D.; Choi, J.; Kim, N.H. A comparison study of methods for parameter estimation in the physics-based prognostics. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Andersson, P.; Bergman, M.; Brickstad, B.; Dahlberg, L.; Nilsson, F.; Sattari-Far, I. A Procedure for Safety Assessment of Components with Cracks-Handbook; Swedish Nuclear Power Inspectorate: Stockholm, Sweden, 1999. [Google Scholar]
- Kitagawa, G. A self-organizing state-space model. J. Am. Stat. Assoc. 1998, 93, 1203–1215. [Google Scholar] [CrossRef]
- Dowd, M.; Joy, R. Estimating behavioral parameters in animal movement models using a state-augmented particle filter. Ecology 2011, 92, 568–575. [Google Scholar] [CrossRef]
- Simon, D. Kalman h-infinity and nonlinear approaches. In Optimal State Estimation; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hickerson, J.; Hertzberg, R. The role of mechanical properties in low-stress fatigue crack propagation. Metall. Mater. Trans. B 1972, 3, 179–189. [Google Scholar] [CrossRef]
- ASTM E399-90; Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 1997.
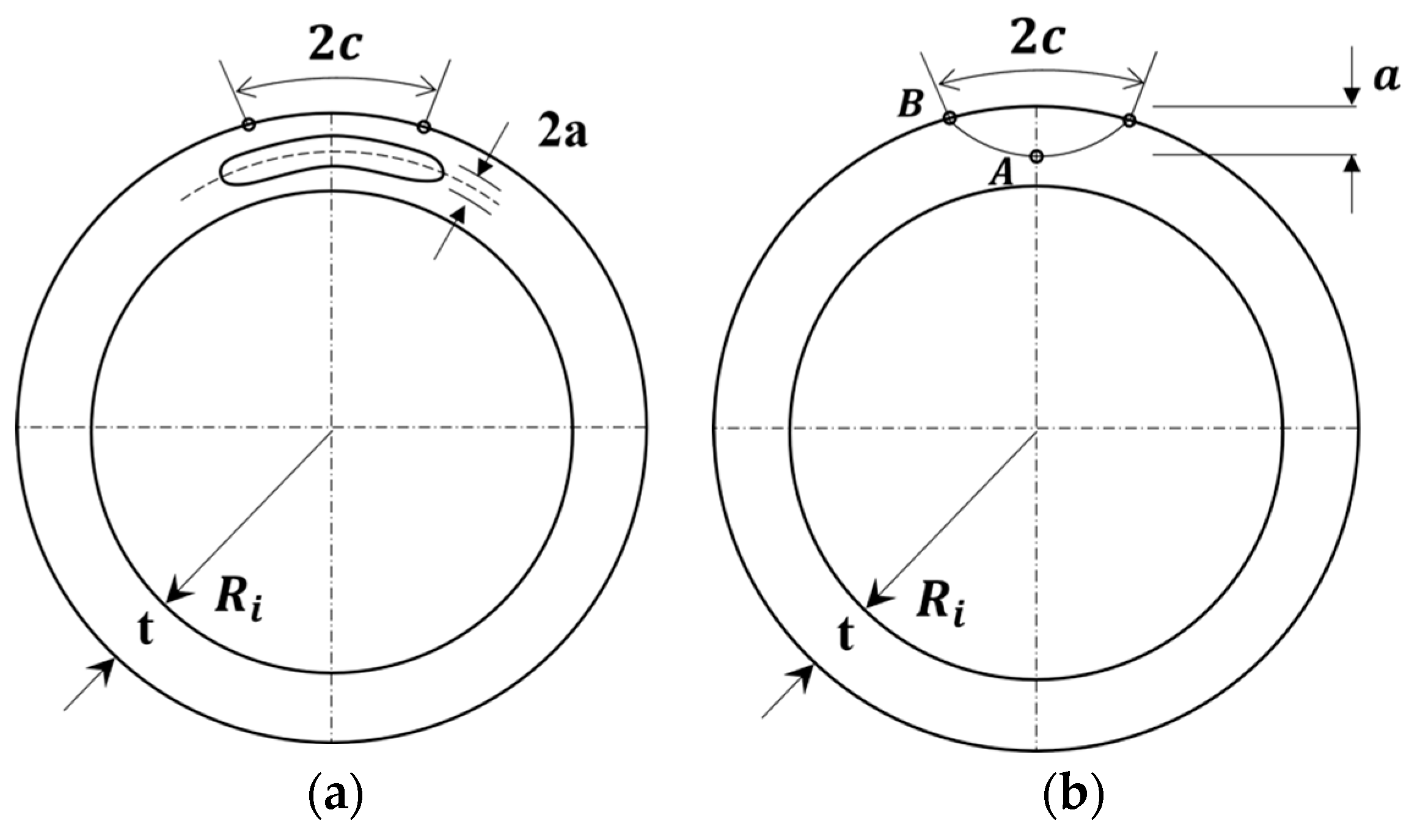

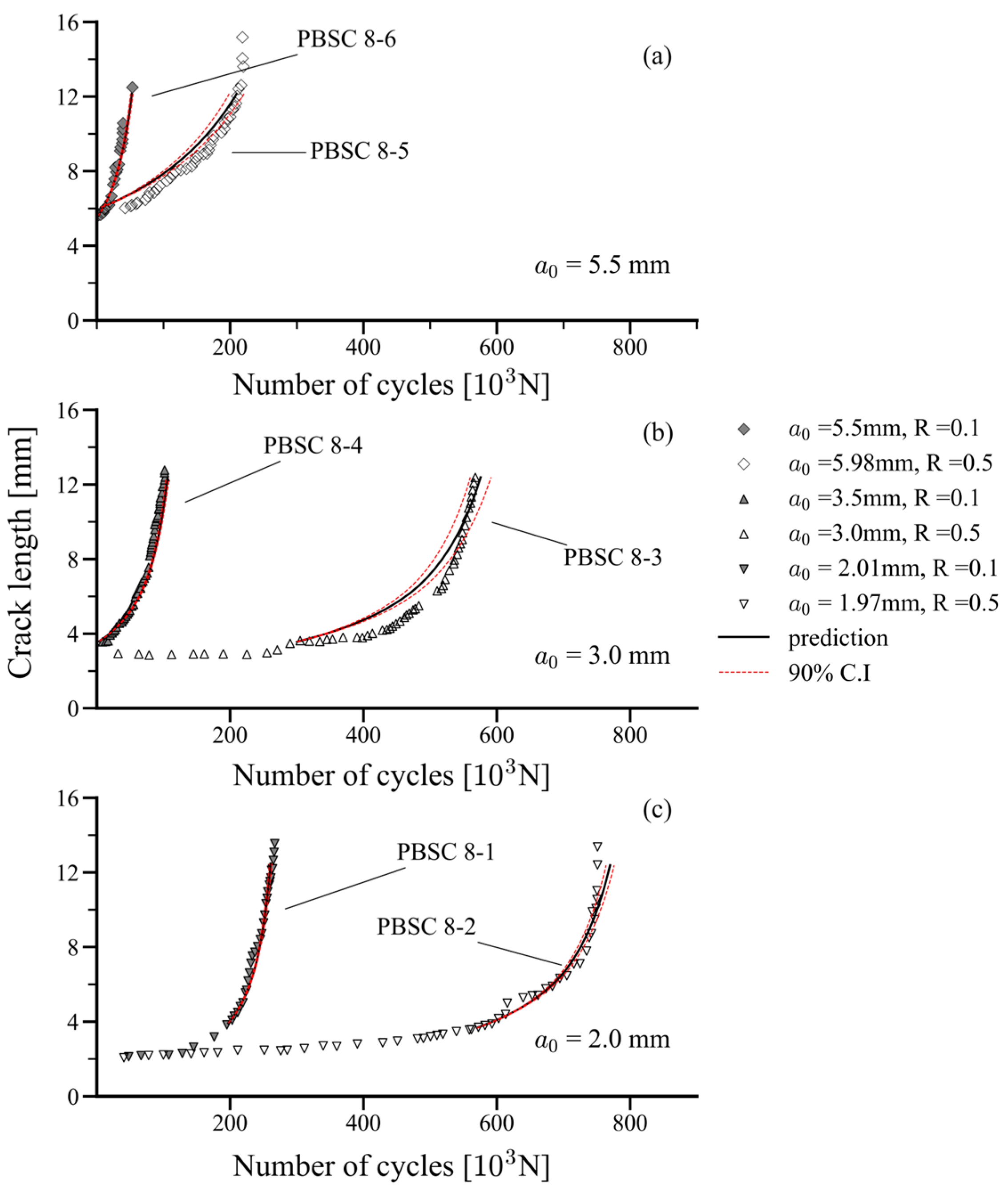
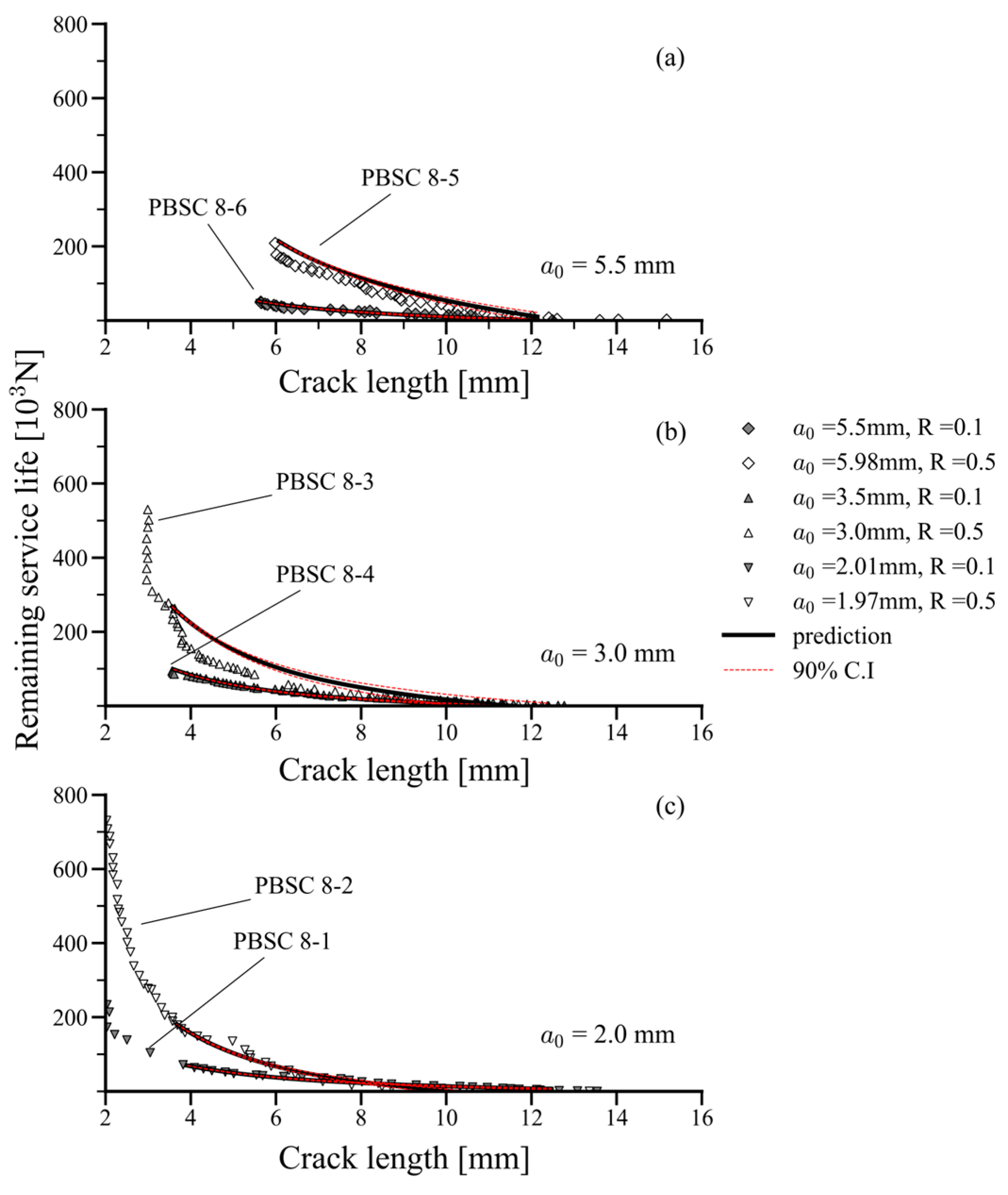









| Source | Specimens | Material | OD [mm] | t [mm] | [mm] | [mm] | Loading | [kN] | [kN] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Arora et al. (2011) [3] | SSPW 6-3 | Stainless steel: GTAW | 170.0 | 14.44 | 3.42 | 14.0 | 4PB | 258 | 25.8 | 0.1 |
| SSPW 6-7 | Stainless steel: GTAW | 170.0 | 15.25 | 3.62 | 44.0 | 4PB | 258 | 25.8 | 0.1 | |
| SSPB 6-9 | Stainless steel: Base | 168.0 | 14.80 | 3.60 | 36.0 | 4PB | 185 | 18.5 | 0.1 | |
| SSPW 12-10 | Stainless steel: GTAW | 324.0 | 28.5 | 10.9 | 123.0 | 4PB | 460 | 50 | 0.1 | |
| SSPB 12-12 | Stainless steel: Base | 324.0 | 28.12 | 3.22 | 38.0 | 4PB | 460 | 46 | 0.1 | |
| Mittal et al. (2011) [4] | Pipe 1 | Stainless steel | 168.0 | 14.3 | 3.58 | 17.88 | 4PB | 308 | 0 | |
| Pipe 2 | Stainless steel | 168.0 | 14.3 | 3.58 | 17.88 | 4PB | 258 | 0 | ||
| Singh et al. (2003) [7] | PSBC 8-1 | Carbon steel | 219.0 | 15.58 | 2.01 | 114.3 | 4PB | 200 | 20 | 0.1 |
| PSBC 8-2 | Carbon steel | 219.0 | 15.38 | 1.97 | 113.4 | 4PB | 250 | 125 | 0.5 | |
| PSBC 8-3 | Carbon steel | 219.0 | 15.12 | 3.00 | 110.0 | 4PB | 200 | 100 | 0.5 | |
| PSBC 8-4 | Carbon steel | 219.0 | 15.38 | 3.50 | 113.0 | 4PB | 160 | 16 | 0.1 | |
| PSBC 8-5 | Carbon steel | 219.0 | 15.17 | 5.98 | 113.8 | 4PB | 200 | 100 | 0.5 | |
| PSBC 8-6 | Carbon steel | 219.0 | 15.13 | 5.50 | 113.2 | 4PB | 160 | 16 | 0.1 | |
| Zhu et al. (1998) [8] | Virgin | Alloy steel | 140.0 | 40.0 | - | - | Pressure | - | - | |
| Autofrettage | AISI4340H II | 140.0 | 40.0 | - | - | Pressure | - | - |
| Source | Specimens | Material | [MPa] | [MPa] | Elongation [%] |
|---|---|---|---|---|---|
| Arora et al. (2011) [3] | SSPW 6-3 | SA312 type 304LN stainless steel: GTAW | 400 | 586 | 57 |
| SSPW 6-7 | SA312 type 304LN stainless steel: GTAW | 400 | 586 | 57 | |
| SSPB 6-9 | SA312 type 304LN stainless steel: Base | 318 | 650 | 67 | |
| SSPW 12-10 | SA312 type 304LN stainless steel: GTAW | 450 | 593 | 42 | |
| SSPB 12-12 | SA312 type 304LN stainless steel: Base | 324 | 660 | 63 | |
| Mittal et al. (2011) [4] | Pipe 1 | SA312 type 304LN stainless steel | 298 | 620 | 69 |
| Pipe 2 | SA312 type 304LN stainless steel | 298 | 620 | 69 | |
| Singh et al. (2003) [7] | PSBC 8-1 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 |
| PSBC 8-2 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 | |
| PSBC 8-3 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 | |
| PSBC 8-4 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 | |
| PSBC 8-5 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 | |
| PSBC 8-6 | SA333 Gr.6 carbon steel | 302 | 450 | 36.7 | |
| Zhu et al. (1998) [8] | Virgin | AISI4340H II alloy steel | 935 | 1045 | 19.6 |
| Autofrettage | AISI4340H II alloy steel | 935 | 1045 | 19.6 |
| Source | Material | ||||
|---|---|---|---|---|---|
| Hickerson and Hertzberg (1972) [65] | Stainless steel, aluminum | −4 | −16 | −14.5 | |
| Benson and Edmonds (1978) [47] | 1/2Cr-1/2Mo-1/4V-0.1C Steel | −1.664 | −1.299 | −4.776 | −3.908 |
| Cortie and Garrett (1988) [49] | 1Cr-1/2Mo Steel | −3.829 | −3.47 | −15.59 | −14.289 |
| Bergner and Zouhar (2000) [58] | Aluminum | −0.99 | −3.96 | ||
| Carpinteri and Paggi (2007) [51] | Steel | −1.777 | −1.742 | −6.119 | |
| Aluminum | −1.544 | −1.371 | −5.602 | ||
| Ciavarella et al. (2008) [54] | Brittle steel | −1.190 | −7.539 | ||
| Ductile steel | −1.507 | −6.770 | |||
| 4340 steel | −4.2 | −7.43 | |||
| ASTM steel [66] | −1.62 | −6.6 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Lee, S.-J. Probabilistic Fatigue Crack Growth Prediction for Pipelines with Initial Flaws. Buildings 2024, 14, 1775. https://doi.org/10.3390/buildings14061775
Choi Y, Lee S-J. Probabilistic Fatigue Crack Growth Prediction for Pipelines with Initial Flaws. Buildings. 2024; 14(6):1775. https://doi.org/10.3390/buildings14061775
Chicago/Turabian StyleChoi, Youngjin, and Seung-Jung Lee. 2024. "Probabilistic Fatigue Crack Growth Prediction for Pipelines with Initial Flaws" Buildings 14, no. 6: 1775. https://doi.org/10.3390/buildings14061775
APA StyleChoi, Y., & Lee, S.-J. (2024). Probabilistic Fatigue Crack Growth Prediction for Pipelines with Initial Flaws. Buildings, 14(6), 1775. https://doi.org/10.3390/buildings14061775





