Mechanical Properties and Energy Damage Evolution Mechanism of Basalt Fiber-Modified Tailing Sand Cementation and Filling Body Mechanics
Abstract
:1. Introduction
2. Experimental Materials and Program
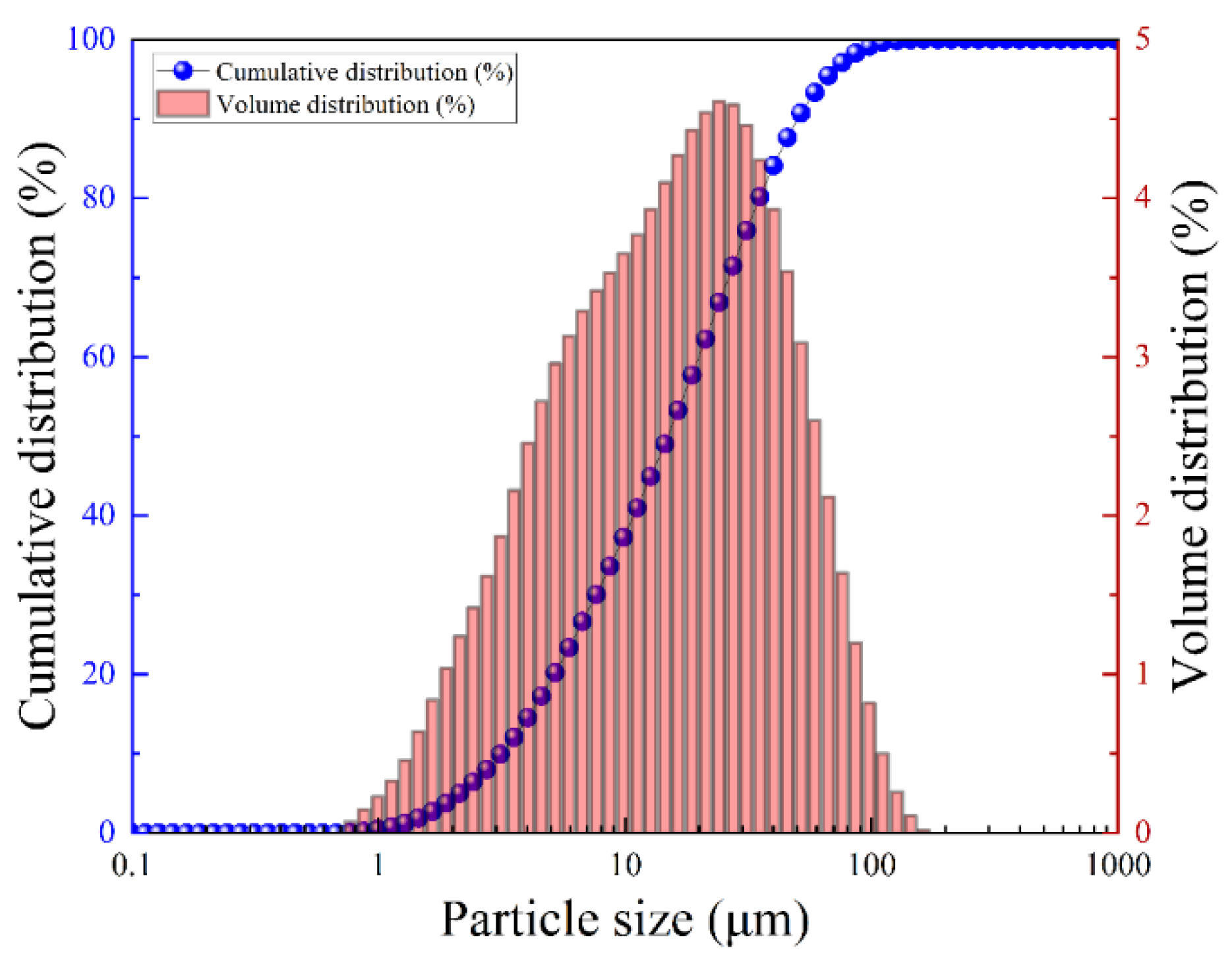
2.1. Experimental Materials
2.2. Experimental Program
2.3. Experimental Methods and Specimen Preparation
3. Experimental Results and Analysis
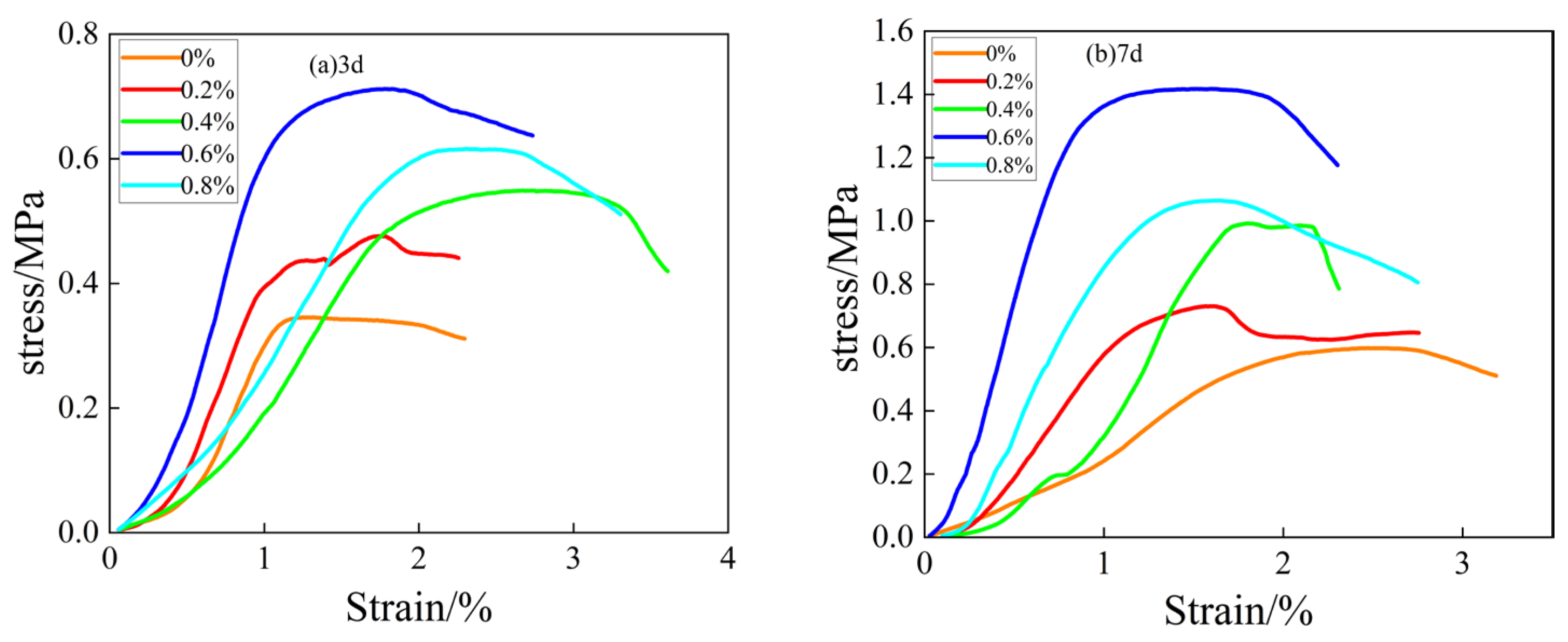
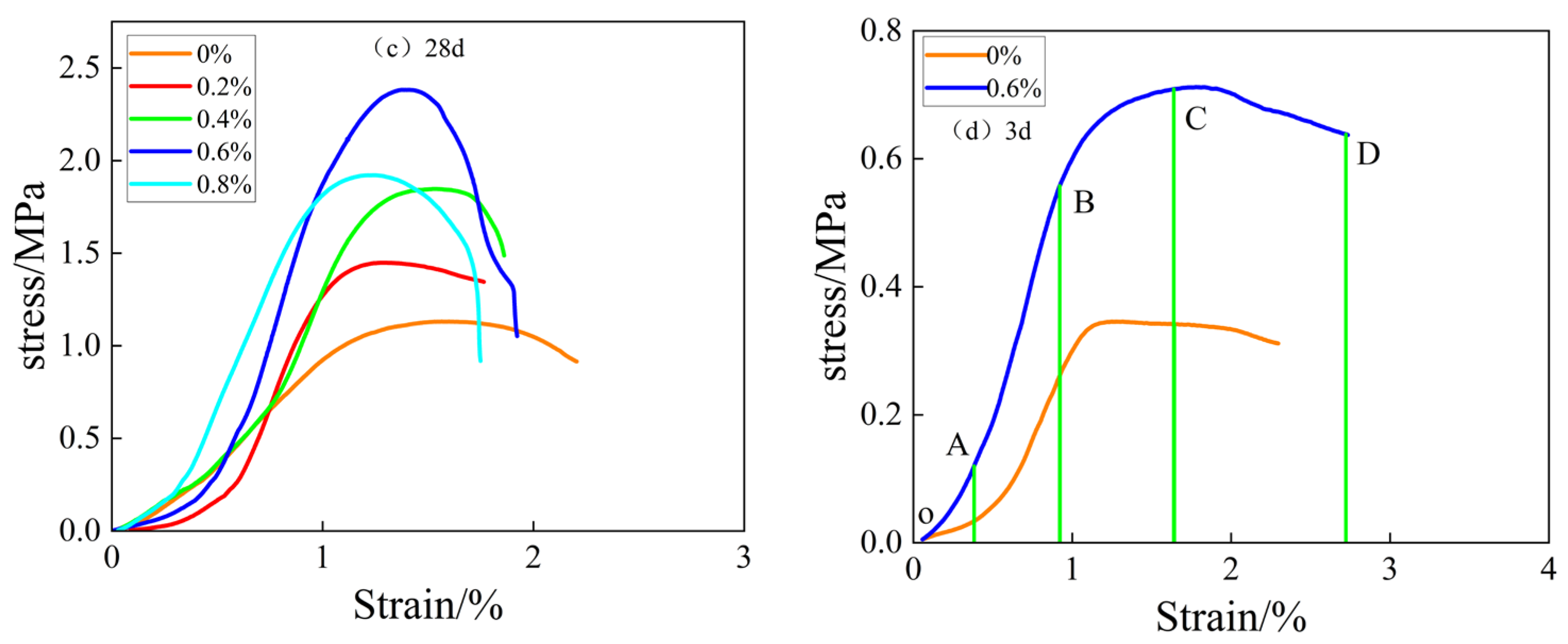
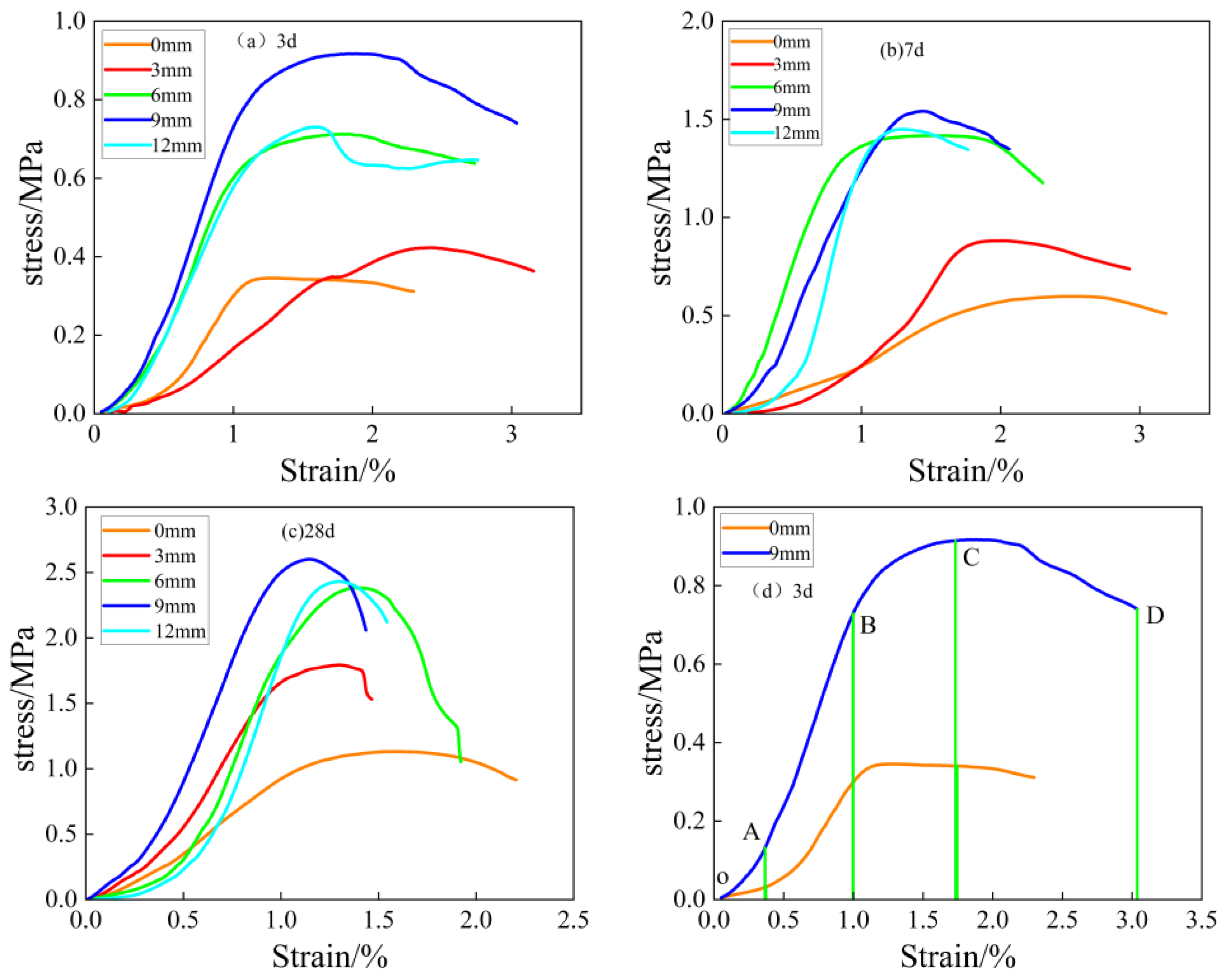
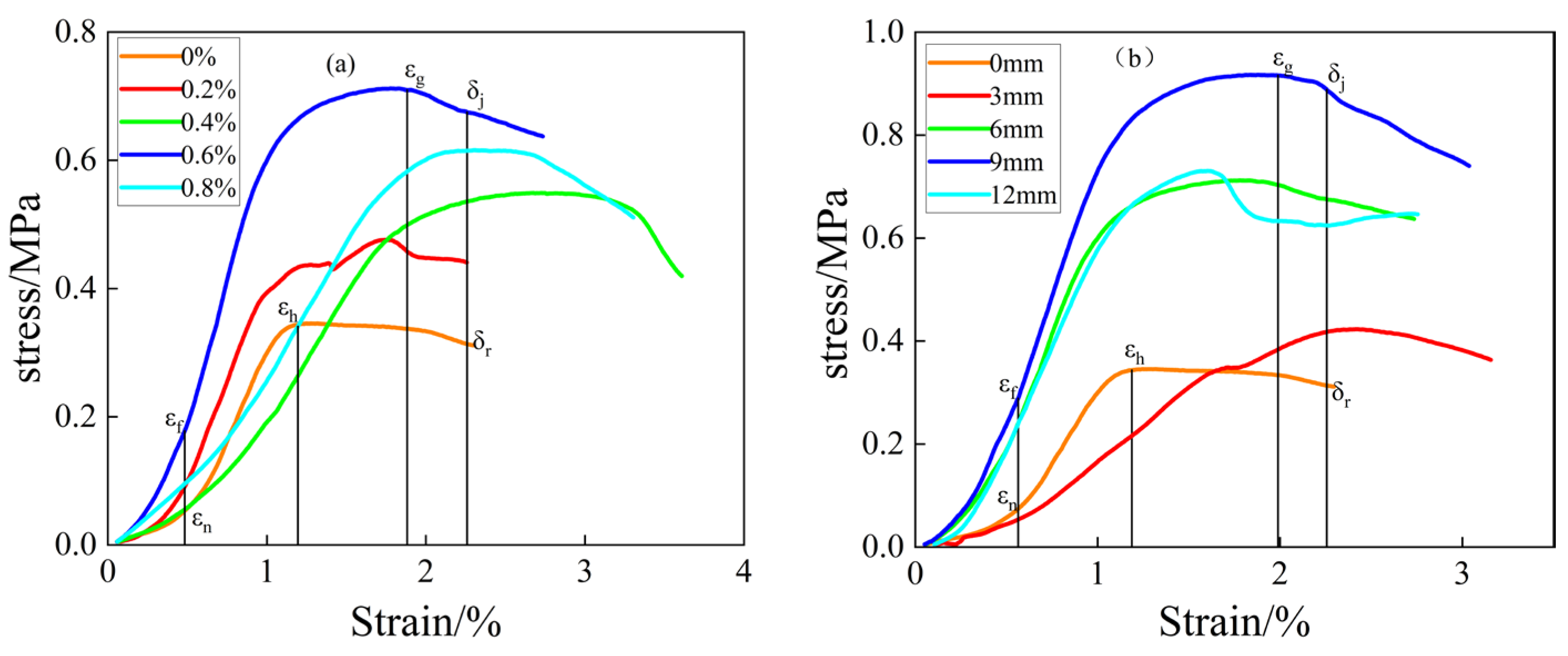
3.1. Morphological Characteristics of the Stress–Strain Curve of the Filling Body
- (1)
- Initial pore compacting stage (OA). At this stage, there are initial pores in the interior of the filling body, and with the increase of external load, the pores are gradually compacted. It can be seen from the Figure that the curves of the specimens without fibers show a more pronounced “concave” shape, whereas the curves of the fibers are less pronounced. The reason for this is that the inclusion of fibers fills the initial pores in the filled specimens, thus making the compaction of the filled bodies less pronounced at this stage;
- (2)
- Linear elastic deformation stage (AB). At this stage, the stress–strain curve of the filling body is approximately straight, and the stress increases approximately linearly with the strain. The inclusion of an appropriate amount of basalt fiber improves the strength of the filling body to a certain extent, further blocking the crack expansion and extension, but the specimen of the filling body at this time has not yet reached the threshold of destruction;
- (3)
- Yield damage stage (BC). At this stage, new cracks are created inside the filling body, the stress growth rate begins to slow down, and the stress–strain curve of the filling body shows a “convex” pattern. The stress value of the filling body at point C is the peak stress, and when the stress value exceeds the peak stress, the filling body enters the post-peak damage stage. It can be found that the strain at peak stress increases with the increase of basalt fiber doping.
- (4)
- Post-peak destruction phase (CD). At this stage, the stress in the filling body shows a tendency to decrease with increasing axial strain, and macroscopic main cracks appear on the surface of the filled body specimen. When the stress value reaches point D, there is overall damage to the filled body specimen, but the stress does not always drop to 0, indicating that the filled body specimen still has a certain residual strength after destruction [27]. At the same time, it shows that the filling body still has a certain bearing capacity after damage [28], and with the prolongation of the age of maintenance as well as the increase of the fiber content and length, its residual stress increases accordingly. The reason for this is that the fibers play a bridging and crack-blocking role inside the filler [29], maintaining the overall stability of the specimen. The compressive strength at a strain of 2.25% (at which time the stress–strain curve tends to flatten) was used as an evaluation criterion for ductility [30], and it was found that the post-peak ductility of the specimens was the best when the fiber doping was 0.6%, and the fiber length was 9 mm.
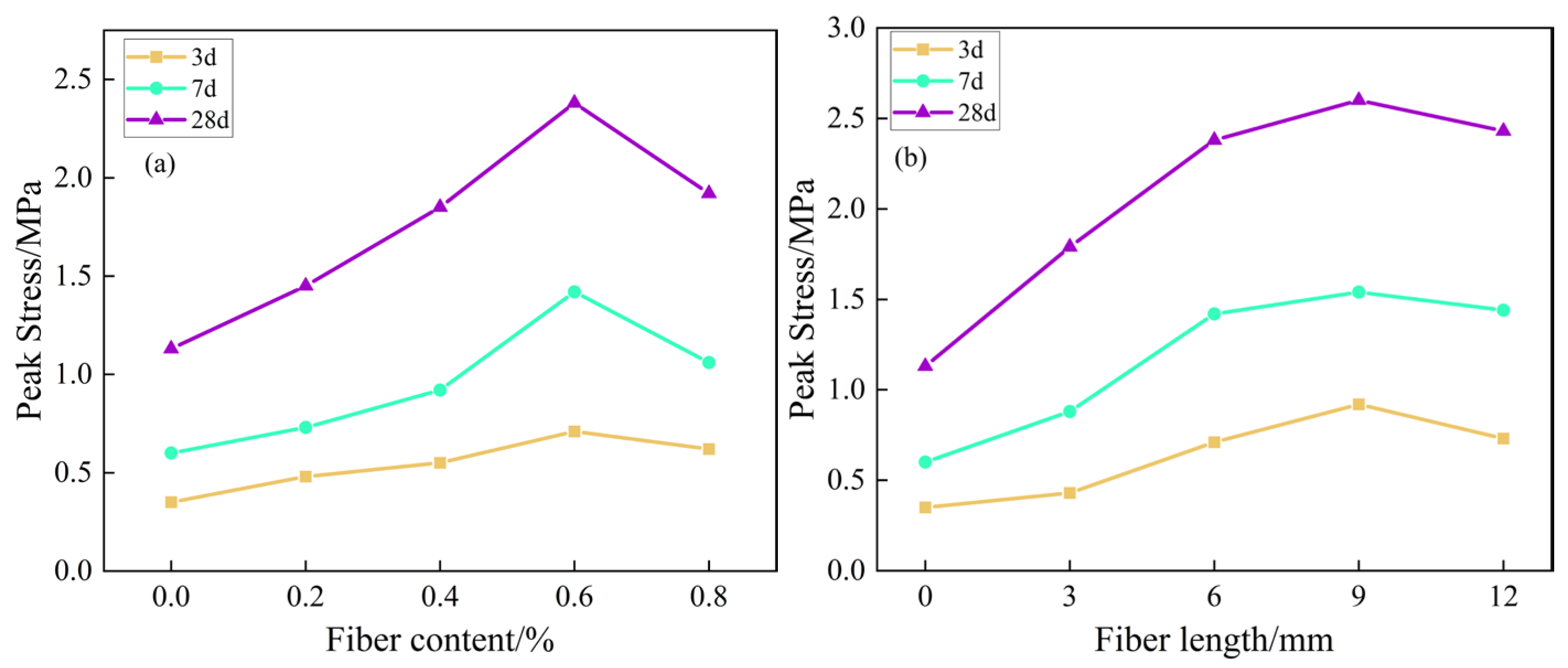
3.2. Effect of Fiber Dosage and Fiber Length on Uniaxial Compressive Strength of Filled Bodies
3.3. Evolution of Deformation Properties of BFCTB Specimens
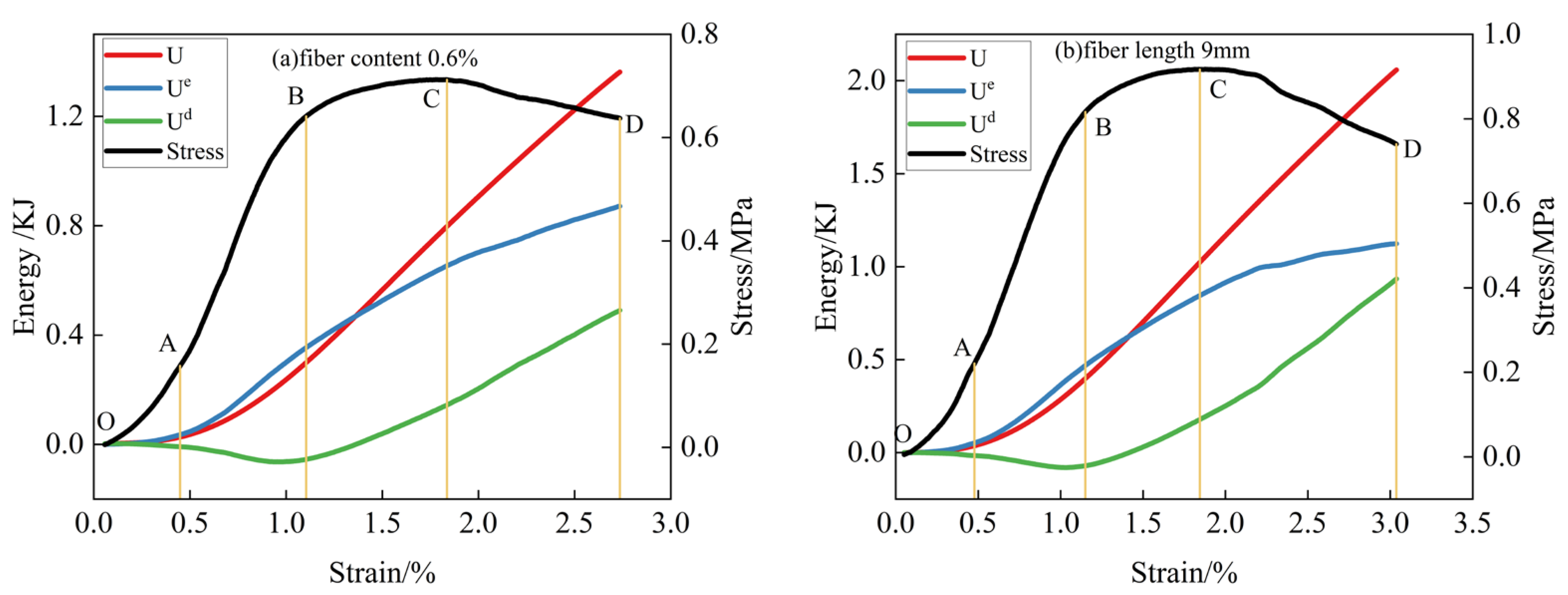
4. Theory of Filling Body Damage and Energy Dissipation
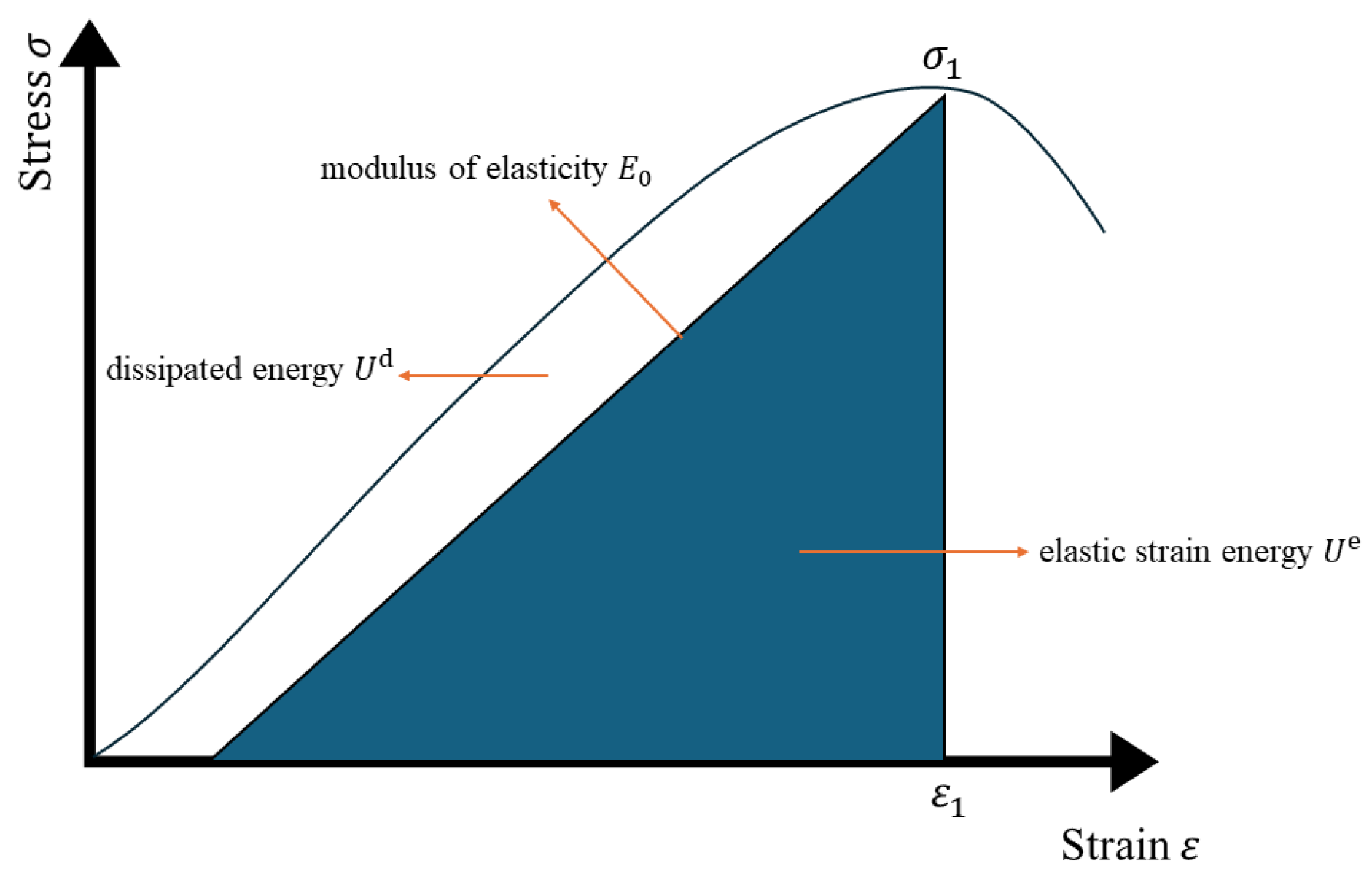
4.1. Principle of Energy Dissipation
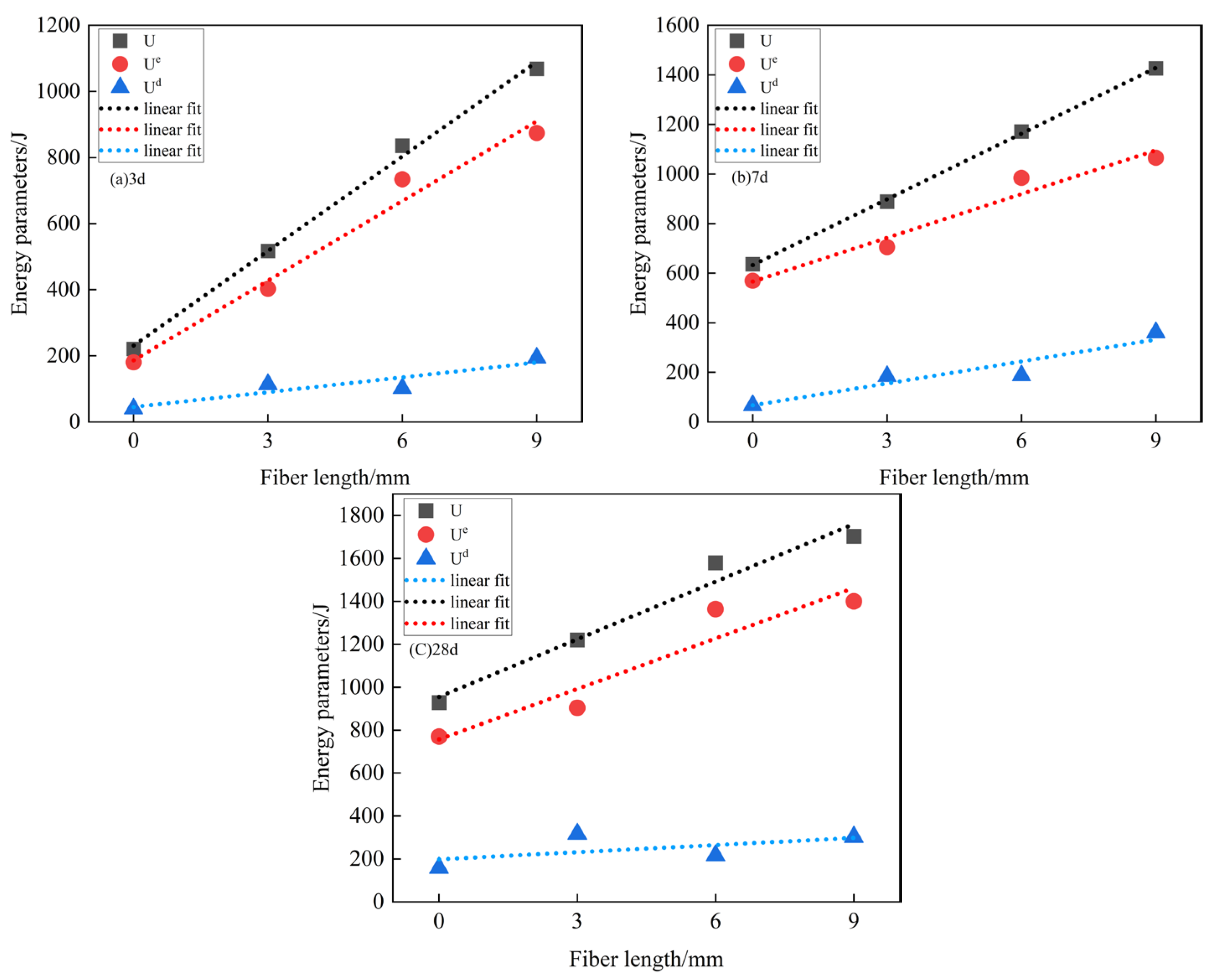
4.2. Characterization of the Variation of Energy Parameters of the Specimen
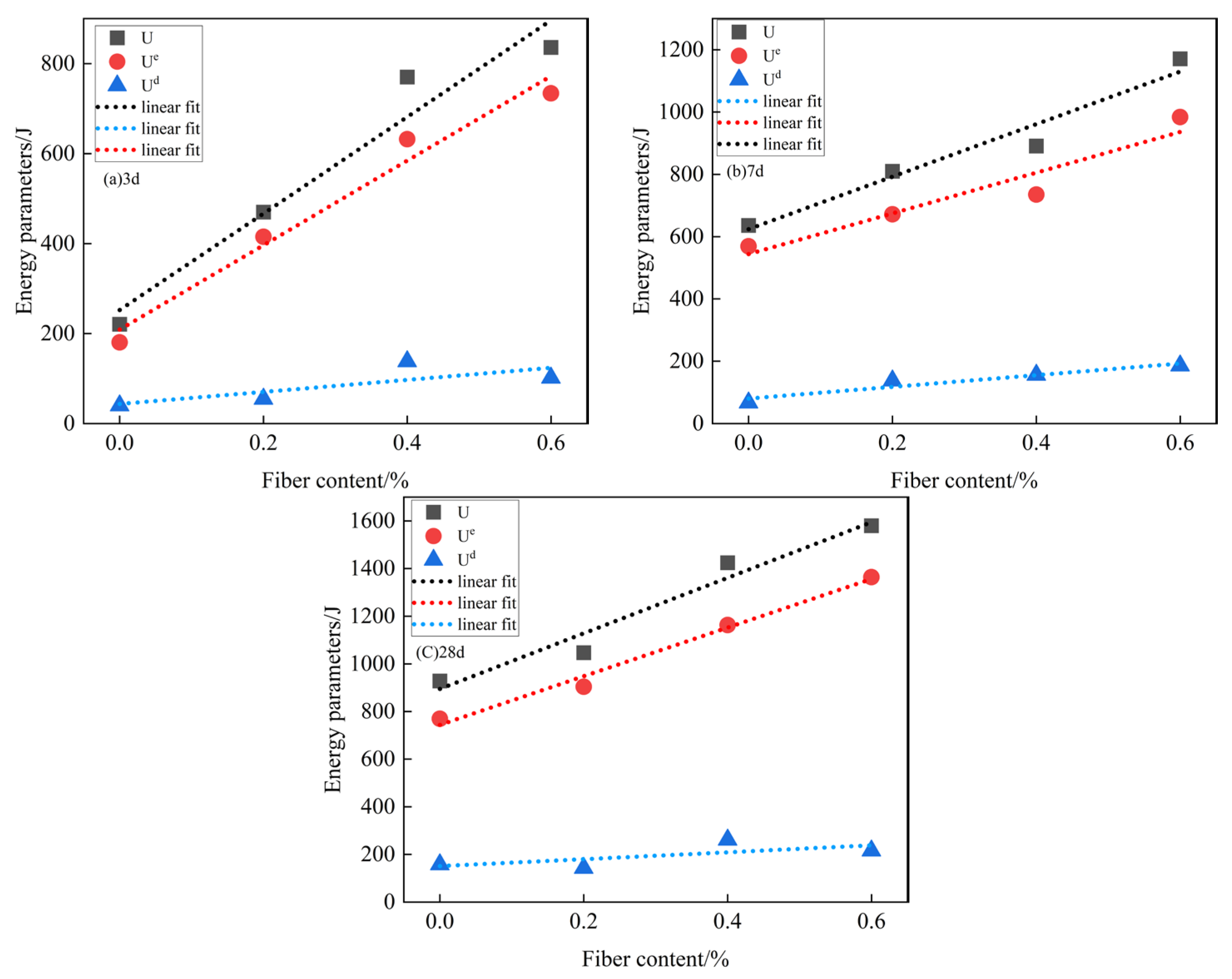
4.3. Evolutionary Law of Energy Distribution for Deformation Damage of BFCTB Specimens under Uniaxial Compression
- (1)
- Initial pore and pore compaction stage (OA). At this stage, the initial pores and cracks inside the filled specimen are gradually compacted, while the energy value inside the specimen is small, and most of the energy will be converted into dissipated energy. Through the table and with the increase of fiber doping to 0.6% and fiber length to 9 mm, the proportion of dissipated energy is decreasing. Therefore, the energy is dominated by dissipated energy, and the total energy is small in the initial compacting stage;
- (2)
- Linear elastic deformation stage (AB). Within this phase, most of the energy absorbed by the filled body specimen is stored as elastic strain energy. And it can be seen from the Figure that the elastic strain energy has an overall linear growth trend, while the dissipated energy inside the specimen at this moment is basically maintained in a constant state. The percentage of elastic strain energy of BFCTB specimens was 80.8%, 82.54%, 86.83%, and 90.4%, as the fiber doping increased from 0% to 0.6% when the age of curing was 3 d. The percentage of elastic strain energy of BFCTB specimens was 80.8%, 82.54%, 86.83%, and 90.4%. As the fiber length grows from 0 mm to 9 mm, the percentage of elastic strain energy of the BFCTB specimen is 78.65%, 84.38%, 87.26%, and 89.83%, respectively. Therefore, in this linear elastic deformation stage, the energy absorbed by the specimen will be stored in the form of elastic strain energy. However, the proportion of elastic strain energy does not reach 100%, indicating that the linear elastic deformation of the specimen is not a fully elastic deformation, and the BFCTB specimen still produces a certain amount of damage in this stage, and this part of the lost energy will be in the form of dissipated energy;
- (3)
- Yield damage stage (BC). At this stage, the elastic strain energy of the BFCTB specimen is increasing, but the slope is slowly decreasing, showing an up-convex trend. At this time, new cracks are generated inside the specimen, and the dissipation energy shows an increasing trend, but the proportion of elastic strain energy is still higher than the dissipation energy. Therefore, the energy absorbed by the BFCTB specimen is still stored in the form of elastic strain energy at this yield damage stage, but the dissipated energy shows an increasing trend at this time;
- (4)
- Post-peak destruction phase (CD). In this stage, the elastic strain energy of the BFCTB specimen shows a decreasing trend, while the slope of the dissipation energy increases, showing a growing trend BFCTB specimen in this stage of the stored elastic strain energy reaches the limit, the specimen is pressurized to produce a macroscopic main crack, and the energy is released with kinetic energy and friction energy, etc., and at the same time the dissipation energy grows rapidly to make the filling body specimen damage is aggravated, thus reducing the load carrying capacity and resistance to deformation damage.
5. Damage Modeling of Cemented Fill with Basalt Fiber-Doped Tailing Sand under Uniaxial Compression
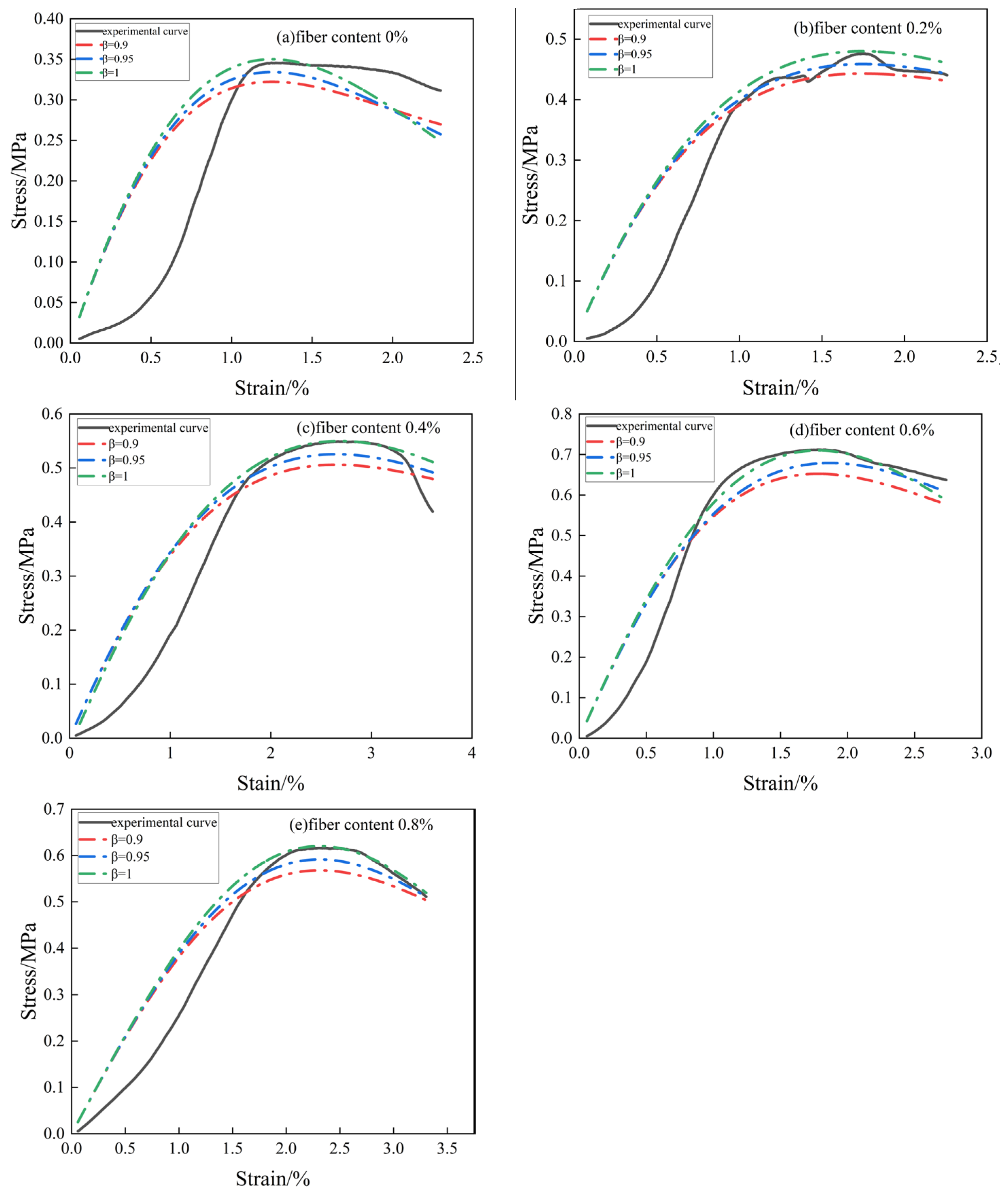
5.1. Establishment of Damage Modeling for BFCTB Specimens under Uniaxial Compression
5.2. Theoretical Model Validation and Discussion
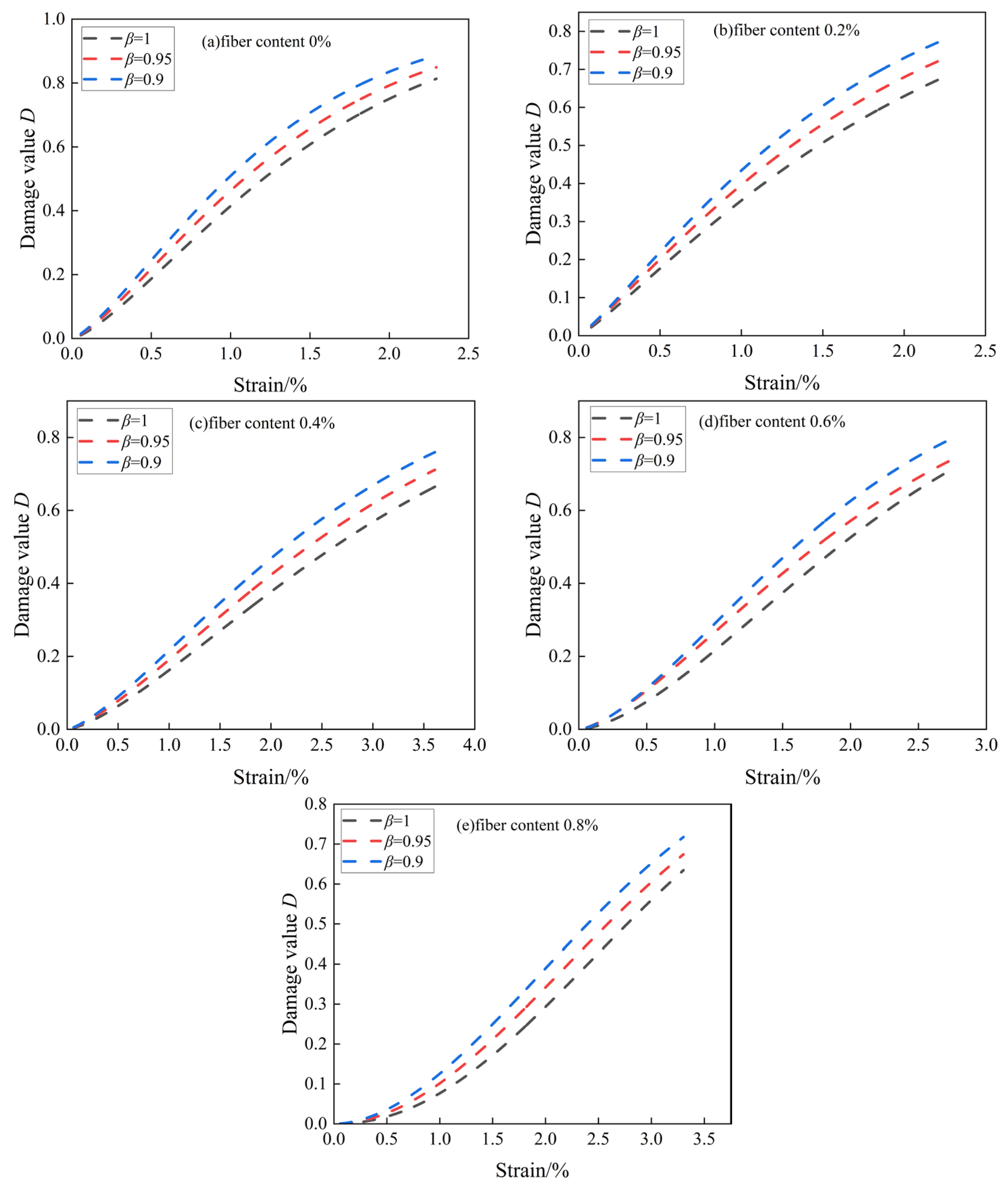
5.3. Compression Damage Evolution of BFCTB Specimens under Uniaxial Compression
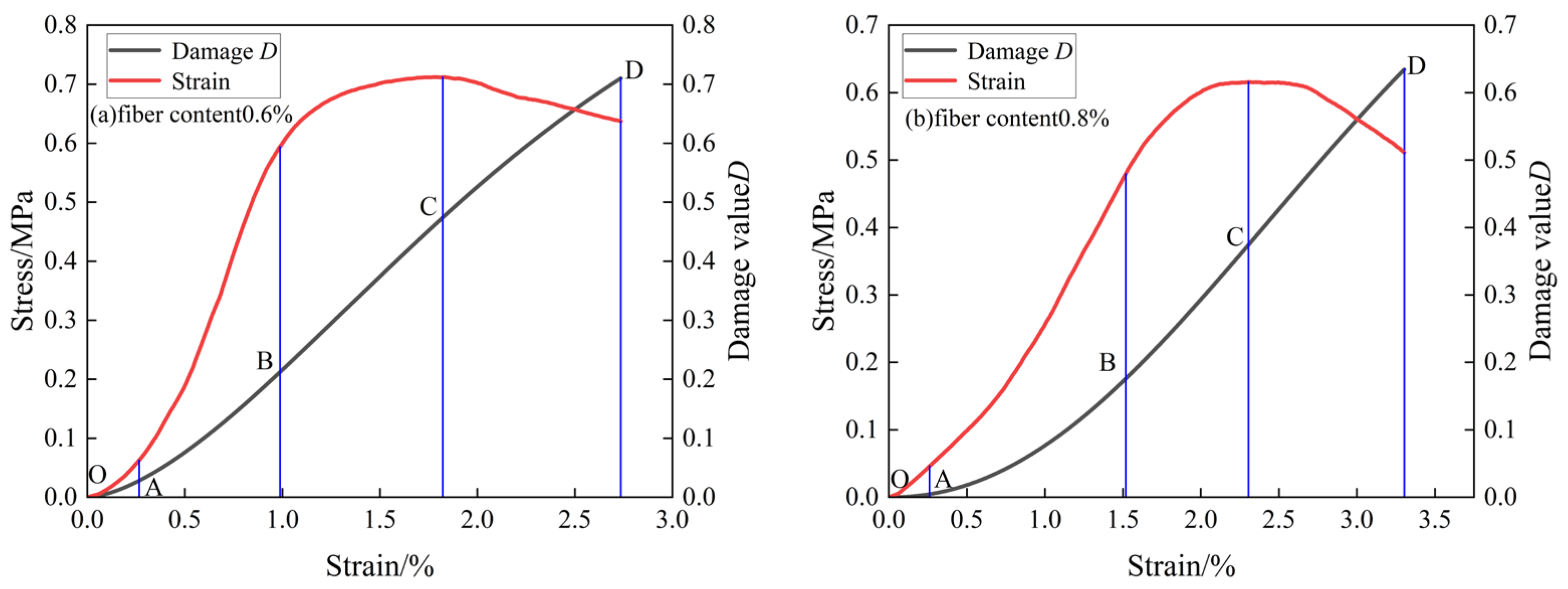
5.4. Characteristics of Compressive Damage Evolution of BFCTB Specimens under Uniaxial Compression
- (1)
- Initial damage stage (OA). At this stage, the damage value of the BFCTB specimen is almost zero, and the specimen is in the stage of pore compaction at this time. The microfractures and cracks inside the BFCTB specimen are compacted, and the slope of the damage evolution curve is zero;
- (2)
- Stable developmental stage of impairment (AB). The damage value of the BFCTB specimen at this stage gradually increases from 0, while the BFTF specimen is in the linear elastic deformation stage, which indicates that damage starts to occur inside the filled body specimen at the linear elastic stage. Moreover, with the increase of axial strain, the damage evolution curve of the BFCTB specimen shows a certain “concave” pattern;
- (3)
- The stage of accelerated damage growth (BC). The damage value of the BFCTB specimen increases rapidly during this phase, and the BFCTB specimen is in the yield damage phase. At this stage, the stress–strain curve of the BFCTB specimen shows a “convex”, while new cracks are created inside the specimen, leading to a rapid increase in the damage value;
- (4)
- Damage destruction phase (CD). The damage values of the BFCTB specimens within this phase show an overall linear increase when the filled body specimens are in the post-peak damage phase. When the damage value of the BFCTB specimen reached an extreme value, the overall damage of the filled body test occurred under uniaxial compression, and the specimen showed that it was also accompanied by the development of macroscopic main cracks and the dislodgement of part of the block. Therefore, when a whole BFCTB specimen is damaged by external load deformation, its damage evolution curve changes characteristics of “gentle-slow growth-fast growth-linear growth”.
6. Conclusions
- (1)
- The stress–strain curves of the filled body specimens with basalt fibers added did not decrease rapidly after the external load exceeded the peak stress, indicating that the incorporation of basalt fibers improved the overall stability and resistance to deformation damage of the filled body specimens;
- (2)
- Uniaxial loading, with the increase of fiber doping and fiber length growth of the compressive strength and toughness index of the filling body (the first crack strain, peak strain, and residual stress), showed a trend of increasing and then decreasing, which indicates that the doping of an appropriate amount of basalt fibers can improve the mechanical properties of the filling body specimens, and the optimal value of fiber doping is 0.6%, and the optimal value of the fiber length is 9 mm;
- (3)
- Under uniaxial loading, with the increase of fiber doping, the total strain energy, elastic strain energy, and dissipation energy of basalt fiber-modified tailing sand cemented filling body at the peak stress showed a trend of increasing and then decreasing and reached the optimal fiber doping of 0.6%. The increase of fiber length on the energy of the filling body specimen is also so, and there is an optimal length of the same; the optimal length of the fiber is 9 mm. In the optimal range, the total strain energy, elastic strain energy, and dissipation energy of the filled body showed a linear growth pattern;
- (4)
- Under uniaxial loading, the fiber doping and fiber length do not significantly affect the change process of energy inside the BFCTB specimen and the conversion process. In the initial pore compaction stage, most of the energy absorbed by the filled body specimen is converted into dissipated energy. In the linear elastic deformation stage and yield stage, the energy inside the filling body is mainly stored in the form of elastic strain energy; in the post-peak damage stage, the stored elastic strain energy inside the filling body reaches the limit, and the dissipated energy grows rapidly, which accelerates the damage–destruction process of the BFTF specimen.
- (5)
- Based on the principle of Lemaitre strain equivalence and Weibull statistical theory to construct the damage constitutive equation, on the basis of the introduction of damage correction coefficient, and finally constructed the damage constitutive equation of basalt fiber doped tailing sand cemented filling body, found that the theoretical curve after the introduction of the damage correction coefficient with the experimental curve of a high degree of consistency, the engineering practice has a certain degree of significance and value of guidance and reference. On this basis, the damage evolution equation is derived, the characteristic law of damage evolution is analyzed, and the damage evolution process is divided into four stages: the initial damage stage (OA), the damage stable development stage (AB), the damage accelerated growth stage (BC), and the damage destruction stage (CD).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, M.Z.; Wang, M.Y.; Xie, J.; Gao, Y.N.; Deng, G.D.; Yang, B.G.; Wang, F.; Hao, H.C.; Xie, H.P. In situ perturbation dynamic behavior of deep coal rock. J. Coal Sci. 2020, 45, 2691–2703. [Google Scholar] [CrossRef]
- Benzaazoua, M.; Fall, M.; Belem, T. A contribution to under-standing the hardening process of cemented pastefill. Miner. Eng. 2004, 17, 141–152. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Stone, D.M. Stability of reinforced cemented backfills. Can. Geotech. J. 1987, 24, 189–197. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Zhou, J.; Chen, Q.; Li, E.; Du, X. Compressive behaviour and microstructural properties of tailings polypropylene fiber-reinforced cemented paste backfill. Constr. Build. Mater. 2018, 190, 211–221. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Yu, X.; Zhou, Y.; Yan, Y.; Wang, J. Early mechanical properties and damage modeling of tailing sand cemented fill under different fiber effects. J. Rock Mech. Eng. 2022, 41, 282–291. [Google Scholar]
- Hou, Y.; Yang, K.; Yin, S.; Yu, X.; Wang, L.; Yang, X. Enhancing the physical properties of cemented ultrafine tailings backfill (CUTB) with fiber and rice husk ash: Performance, mechanisms, and optimization. J. Mater. Res. Technol. 2024, 29, 837–848. [Google Scholar] [CrossRef]
- Yi, X.W.; Ma, G.W.; Fourie, A. Compressive behavior of fiber-reinforced cemented paste backfill. Geotext. Geomembr. 2015, 43, 207–215. [Google Scholar] [CrossRef]
- Cao, S.; Yilmaz, E.; Song, W. Fiber type effect on strength, toughness and microstructure of early age cemented tailings backfill. Constr. Build. Mater. 2019, 223, 44–54. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Xu, M.; Liang, Z.; Ran, L. Study on the energy evolution mechanism of damage in non-through jointed rock mass under uniaxial compression. J. Geotech. Eng. 2019, 41, 639–647. [Google Scholar]
- Cheng, A.-P.; Dai, S.-Y.; Zhang, Y.-S.; Huang, S.-B.; Ye, Z.-Y. Study on the size effect of damage evolution in cemented fillings. J. Rock Mech. Eng. 2019, 38, 3053–3060. [Google Scholar]
- Zhou, Y.; Yan, Y.; Zhao, K.; Yu, X.; Song, Y.; Wang, J.; Suo, T. Study of the effect of loading modes on the acoustic emission fractal and damage characteristics of crmented paste backfill. Constr. Build. Mater. 2021, 277, 122311. [Google Scholar] [CrossRef]
- Liu, Z.X.; Ming, L.; Xiao, S.Y.; Guo, H.Q. Damage failure of cemented backfill and its reasonable match with rock mass. Trans. Nonferrous Met. Soc. China 2015, 25, 954–959. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Dai, T.; Cao, P. Damage modeling of tailing sand cemented fill and matching analysis with rock body. Geotech. Mech. 2006, 27, 1442–1446. [Google Scholar]
- Hou, Y.; Yin, S.; Cao, Y.; Yang, S.; Zhang, M. Uniaxial compressive stress-strain relationship of tailing sand cemented filler and its damage constitutive model. Mater. Rep. 2022, 36, 179–186. [Google Scholar] [CrossRef]
- Zhao, K.; Yu, X.; Zhou, Y.; Wang, Q.; Wang, J.; Hao, J. Energy evolution of brittle granite under different loading rates. Int. J. Rock Mech. Min. Sci. 2020, 132, 104392. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-reinforced polymer composites: Manufacturing, properties, and applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef]
- Fazlnia, A. Origin and magmatic evolution of the Quaternary syn-collision alkali basalts and related rocks from Salmas, northwestern Iran. Lithos 2019, 344, 297–310. [Google Scholar] [CrossRef]
- Chen, J.; Gu, Y.; Yang, Z.; Wang, S. Effects of high temperature treatment on the composition and tensile properties of several basalt fibers. Mater. Eng. 2017, 45, 61–66. [Google Scholar]
- Xiao, J.Z.; Han, N.; Li, Y.; Zhang, Z.; Shah, S.P. Review of Recent Developments in Cement Composites Reinforced with Fibers and Nanomaterials. Front. Struct. Civ. Eng. 2021, 15, 1–19. [Google Scholar] [CrossRef]
- Yan, L.; Chu, F.L.; Tuo, W.Y.; Zhao, X.B.; Wang, Y.; Zhang, P.Q.; Gao, Y.B. Review of Research on Basalt Fibers and Basalt Fiber Reinforced Composites in China(I):Physicochemical and Mechanical Properties. Polym. Polym. Compos. 2021, 29, 1612–1624. [Google Scholar] [CrossRef]
- Ayub, T.; Shafiq, N.; Fadhil Nuruddin, M.; Ullah Khan, S. Mechanical properties of high-strength concrete reinforced with PVA and basalt fibers. In InCIEC 2013: Proceedings of the International Civil and Infrastructure Engineering Conference 2013, Kuching, Malaysia, 22–25 September 2013; Springer: Singapore, 2014. [Google Scholar]
- Borhan, T.M.; Bailey, C.G. Structural behaviour of basalt fiber reinforced glass concrete slabs. Mater. Struct. 2014, 47, 77–87. [Google Scholar] [CrossRef]
- Shaikh, F.; Haque, S. Behaviour of carbon and basalt fibers reinforced fly ash geopolymer at elevated temperatures. Int. J. Concr. Struct. Mater. 2018, 12, 35. [Google Scholar] [CrossRef]
- Sateshkumar, S.K.; Awoyera, P.O.; Kandasamy, T.; Nagaraj, S.; Murugesan, P.; Ponnusamy, B. Impact resistance of high strength chopped basalt fiber-reinforced concrete. Rev. Constr. J. Constr. 2018, 17, 240–249. [Google Scholar]
- Chin, S.C.; Shaaban, I.G.; Rizzuto, J.P.; Khan, S.U.; Mohamed, D.; Roslan, N.I.M.; Aziz, A.A. Predictive models for mechanical properties of hybrid fibers reinforced concrete containing bamboo and basalt fibers. Structures 2024, 61, 106093. [Google Scholar] [CrossRef]
- Yang, X.; Hou, Y.; Yin, S. Mechanical properties and energy distribution evolution characteristics of fiber-reinforced cemented filler with sulfur-containing tailings. J. Cent. South Univ. (Nat. Sci. Ed.) 2022, 53, 4435–4448. [Google Scholar]
- Yin, S.; Cao, Y.; Wu, A. Mechanical and flow properties of glass fiber reinforced cemented filler with sulfur-containing tailings. Mater. Her. 2023, 37, 246–252. [Google Scholar]
- Wu, A.; Wang, J.; Peng, N. Effect of grain composition on coarse aggregate filling slurry segregation. J. Cent. South Univ. (Sci. Technol.) 2016, 47, 3201–3207. [Google Scholar]
- Xue, X.; Gu, Y.; Zhang, X.; Wu, S.; Sun, P.; Cui, J.; Wang, X. Mechanical behavior and microscopic mechanism of fiber reinforced coarse aggregate cemented backfill. Constr. Build. Mater. 2023, 366, 130093. [Google Scholar] [CrossRef]
- Ardanuy, M.; Claramunt, J.; Toledo, F.R.D. Cellulosic fiber reinforced cement-based composites: A review of recent research. Constr. Build. Mater. 2015, 79, 115–128. [Google Scholar] [CrossRef]
- Sukontasukkul, P.; Pongsopha, P.; Chindaprasirt, P.; Songpiriyakij, S. Flexural performance and toughness of hybrid steel and polypropylene fiber reinforced geopolymer. Constr. Build. Mater. 2018, 161, 37–44. [Google Scholar] [CrossRef]
- Xu, F.; Deng, X.; Peng, C.; Zhu, J.; Chen, J. Mix design and flexural toughness of PVA fiber reinforced fly ash-geopolymer composites. Constr. Build. Mater. 2017, 150, 179–189. [Google Scholar] [CrossRef]
- Yan, R.F.; Liu, J.M.; Yin, S.H.; Zou, L.; Kou, Y.Y.; Zhang, P.Q. Effect of polypropylene fiber and coarse aggregate on the ductility and fluidity of cemented tailings backfill. J. Cent. South Univ. 2022, 29, 515–527. [Google Scholar] [CrossRef]
- Peng, R.; Xie, H.; Ju, Y. Analysis of energy dissipation and damage evolution during sandstone stretching. J. Rock Mech. Eng. 2007, 26, 2526. [Google Scholar]
- Xie, H.; Ju, Y.; Li, L. Rock strength and overall damage criterion based on the principle of energy dissipation and release. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Dang, W. Soft-hardening constitutive model of damage in tailing sand cemented fill. J. Shandong Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 31, 36–41. [Google Scholar] [CrossRef]
- Zhao, S.; Su, D.; Wu, W.; Zhang, Y. Uniaxial compression damage modeling of filling body based on Weibull distribution. China Min. Ind. 2017, 26, 106–111. [Google Scholar]
- Xu, W.; Du, J.; Song, W.; Chen, H. Experiment on the mechanism of consolidating backfill body of extra-fine grain unclassified tailings and cementitious materials. Rock Soil Mech. 2013, 34, 2295–2302. [Google Scholar]
- Hou, Y.; Yin, S.; Cao, Y.; Dai, C. Damage characteristics and energy dissipation analysis of tailing sand cemented fill under uniaxial compression with different maintenance ages. J. Cent. South Univ. (Nat. Sci. Ed.) 2020, 51, 1955–1965. [Google Scholar]

| Makings | SiO2 | Cao | Fe2O3 | MgO | Al2O3 | TiO | K2O | MnO | Other |
|---|---|---|---|---|---|---|---|---|---|
| Tailings | 39.31 | 23.34 | 14.26 | 8.34 | 4.06 | 0.39 | 0.35 | 0.1 | 3.32 |
| Clinker | 30.36 | 47.65 | 3.17 | 2.50 | 12.30 | 0.50 | 1.04 | 0.13 | 2.21 |
| Fiber Type | Tensile Strength/MPa | Elastic Modulus/GPa | Elongation/% | Melting Point/°C | Absorbent /% | Proportion /(g/cm3) | Diameter /μm |
|---|---|---|---|---|---|---|---|
| BF | 3000–3500 | 90–110 | 3.2 | 1600 | <0.1 | 2.8–3.3 | 17 |
| Sample | Mass Concentration% | Cement-Sand Ratio | Tailings | Fiber Length/mm | Fiber Content/% |
|---|---|---|---|---|---|
| A0 | 72% | 1:6 | T1 | 0 | 0 |
| A1 | 72% | 1:6 | T1 | 3 mm | 0.6% |
| A2 | 72% | 1:6 | T1 | 6 mm | 0.6% |
| A3 | 72% | 1:6 | T1 | 9 mm | 0.6% |
| A4 | 72% | 1:6 | T1 | 12 mm | 0.6% |
| B1 | 72% | 1:6 | T1 | 6 mm | 0.2% |
| B2 | 72% | 1:6 | T1 | 6 mm | 0.4% |
| B3 | 72% | 1:6 | T1 | 6 mm | 0.6% |
| B4 | 72% | 1:6 | T1 | 6 mm | 0.8% |
| Influence Factor | Groups | Strain of the First Crack/% | E | Strain of Peak Strength/% | K | Stress of Strain 2.25%/MPa | R |
|---|---|---|---|---|---|---|---|
| 0 | 0.40 | 1 | 1.2 | 1 | 0.31 | 1 | |
| 0.2 | 0.42 | 1.05 | 1.72 | 1.42 | 0.44 | 1.42 | |
| Fiber content/% | 0.4 | 0.48 | 1.2 | 1.87 | 1.56 | 0.54 | 1.74 |
| 0.6 | 0.55 | 1.36 | 1.95 | 1.63 | 0.68 | 2.19 | |
| 0.8 | 0.53 | 1.33 | 1.86 | 1.55 | 0.61 | 1.97 | |
| 0 | 0.40 | 1 | 1.2 | 1 | 0.31 | 1 | |
| 3 | 0.43 | 1.08 | 1.70 | 1.42 | 0.42 | 1.35 | |
| Fiber length/mm | 6 | 0.55 | 1.36 | 1.95 | 1.63 | 0.68 | 2.19 |
| 9 | 0.58 | 1.45 | 1.98 | 1.65 | 0.86 | 2.77 | |
| 12 | 0.51 | 1.28 | 1.88 | 1.57 | 0.63 | 2.03 |
| Age of Conservation/d | Fiber Length/mm | Fiber Content/% | |||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 220.5 | 180.4 | 40.1 | 81.8% | 18.2% | |
| 6 | 0.2 | 470 | 415.2 | 54.8 | 88.4% | 11.6% | |
| 3 | 6 | 0.4 | 770 | 631.9 | 138.1 | 82.06% | 17.94% |
| 6 | 0.6 | 835.7 | 734 | 101.7 | 87.83% | 12.17% | |
| 6 | 0.8 | 760 | 616.1 | 143.9 | 81.07% | 18.93% | |
| 0 | 0 | 636.32 | 569.4 | 66.92 | 89.48% | 10.52% | |
| 6 | 0.2 | 809.77 | 672 | 137.77 | 82.99% | 17.01% | |
| 7 | 6 | 0.4 | 891 | 735 | 156 | 82.49% | 17.51% |
| 6 | 0.6 | 1171 | 984 | 187 | 84.03% | 15.97% | |
| 6 | 0.8 | 965.1 | 858.6 | 106.5 | 88.96% | 11.04% | |
| 0 | 0 | 928 | 770 | 158 | 82.97% | 17.03% | |
| 6 | 0.2 | 1047 | 904 | 143 | 86.34% | 13.66% | |
| 28 | 6 | 0.4 | 1424.5 | 1163 | 261.5 | 81.64% | 18.36% |
| 6 | 0.6 | 1579.5 | 1364 | 215.5 | 86.36% | 13.64% | |
| 6 | 0.8 | 1243 | 1090.4 | 153 | 87.69% | 12.31% |
| Age of Conservation/d | Fiber Length/mm | Fiber Content/% | |||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 220.5 | 180.4 | 40.1 | 81.8% | 18.2% | |
| 3 | 0.6 | 517 | 403 | 114 | 77.95% | 22.05% | |
| 3 | 6 | 0.6 | 835.7 | 734 | 101.7 | 87.83% | 12.17% |
| 9 | 0.6 | 1068 | 874 | 194 | 81.84% | 18.16% | |
| 12 | 0.6 | 784 | 630 | 154 | 80.36% | 19.64% | |
| 0 | 0 | 636.32 | 569.4 | 66.92 | 89.48% | 10.52% | |
| 3 | 0.6 | 888.8 | 705 | 183.8 | 79.32% | 20.68% | |
| 7 | 6 | 0.6 | 1171 | 984 | 187 | 84.03% | 15.97% |
| 9 | 0.6 | 1425.9 | 1065 | 360.9 | 74.69% | 25.31% | |
| 12 | 0.6 | 943.2 | 810 | 133.2 | 85.9% | 14.1% | |
| 0 | 0 | 928 | 770 | 158 | 82.97% | 17.03% | |
| 3 | 0.6 | 1220 | 904 | 316 | 74.1% | 25.9% | |
| 28 | 6 | 0.6 | 1579.5 | 1364 | 215.5 | 86.36% | 13.64% |
| 9 | 0.6 | 1702.5 | 1400 | 302.5 | 82.24% | 17.76% | |
| 12 | 0.6 | 1434 | 1090.4 | 344 | 76.01% | 23.99% |
| Fiber Content/% | Peak Stress/MPa | Peak Strain/10−2 | Modulus of Elasticity/MPa | |||
|---|---|---|---|---|---|---|
| 0.90 | 1.289 | 1.342 | ||||
| 0 | 0.35 | 1.25 | 58 | 0.95 | 1.121 | 1.338 |
| 1 | 1 | 1.373 | ||||
| 0.90 | 1.339 | 1.203 | ||||
| 0.2% | 0.48 | 1.75 | 64 | 0.95 | 1.14 | 1.174 |
| 1 | 1 | 1.18 | ||||
| 0.90 | 1.283 | 1.378 | ||||
| 0.4% | 0.55 | 2.65 | 42 | 0.95 | 1.119 | 1.379 |
| 1 | 1 | 1.419 | ||||
| 0.90 | 1.253 | 1.522 | ||||
| 0.6% | 0.71 | 1.78 | 74 | 0.95 | 1.040 | 1.454 |
| 1 | 1 | 1.618 | ||||
| 0.90 | 1.212 | 1.876 | ||||
| 0.8% | 0.62 | 2.31 | 43 | 0.95 | 1.091 | 1.966 |
| 1 | 1 | 2.122 |
| Fiber Content/% | Damage Stress Equation |
|---|---|
| 0 | |
| 0.2 | |
| 0.4 | |
| 0.6 | |
| 0.8 | |
| Fiber Content/% | Damage Evolution Equation |
|---|---|
| 0 | |
| 0.2 | |
| 0.4 | |
| 0.6 | |
| 0.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Zhang, Y. Mechanical Properties and Energy Damage Evolution Mechanism of Basalt Fiber-Modified Tailing Sand Cementation and Filling Body Mechanics. Buildings 2024, 14, 1851. https://doi.org/10.3390/buildings14061851
Chen R, Zhang Y. Mechanical Properties and Energy Damage Evolution Mechanism of Basalt Fiber-Modified Tailing Sand Cementation and Filling Body Mechanics. Buildings. 2024; 14(6):1851. https://doi.org/10.3390/buildings14061851
Chicago/Turabian StyleChen, Rongsen, and Yaoping Zhang. 2024. "Mechanical Properties and Energy Damage Evolution Mechanism of Basalt Fiber-Modified Tailing Sand Cementation and Filling Body Mechanics" Buildings 14, no. 6: 1851. https://doi.org/10.3390/buildings14061851
APA StyleChen, R., & Zhang, Y. (2024). Mechanical Properties and Energy Damage Evolution Mechanism of Basalt Fiber-Modified Tailing Sand Cementation and Filling Body Mechanics. Buildings, 14(6), 1851. https://doi.org/10.3390/buildings14061851





