Characterizing Splitting Failure of Concrete Influenced by Material Heterogeneity Based on Digital Image Processing Techniques
Abstract
1. Introduction
2. Experiments
2.1. Concrete Specimens
2.2. Testing Procedures
3. Numerical Approach
3.1. Splitting Surface Analysis through DIP Techniques
3.2. Establishment of the Numerical Model
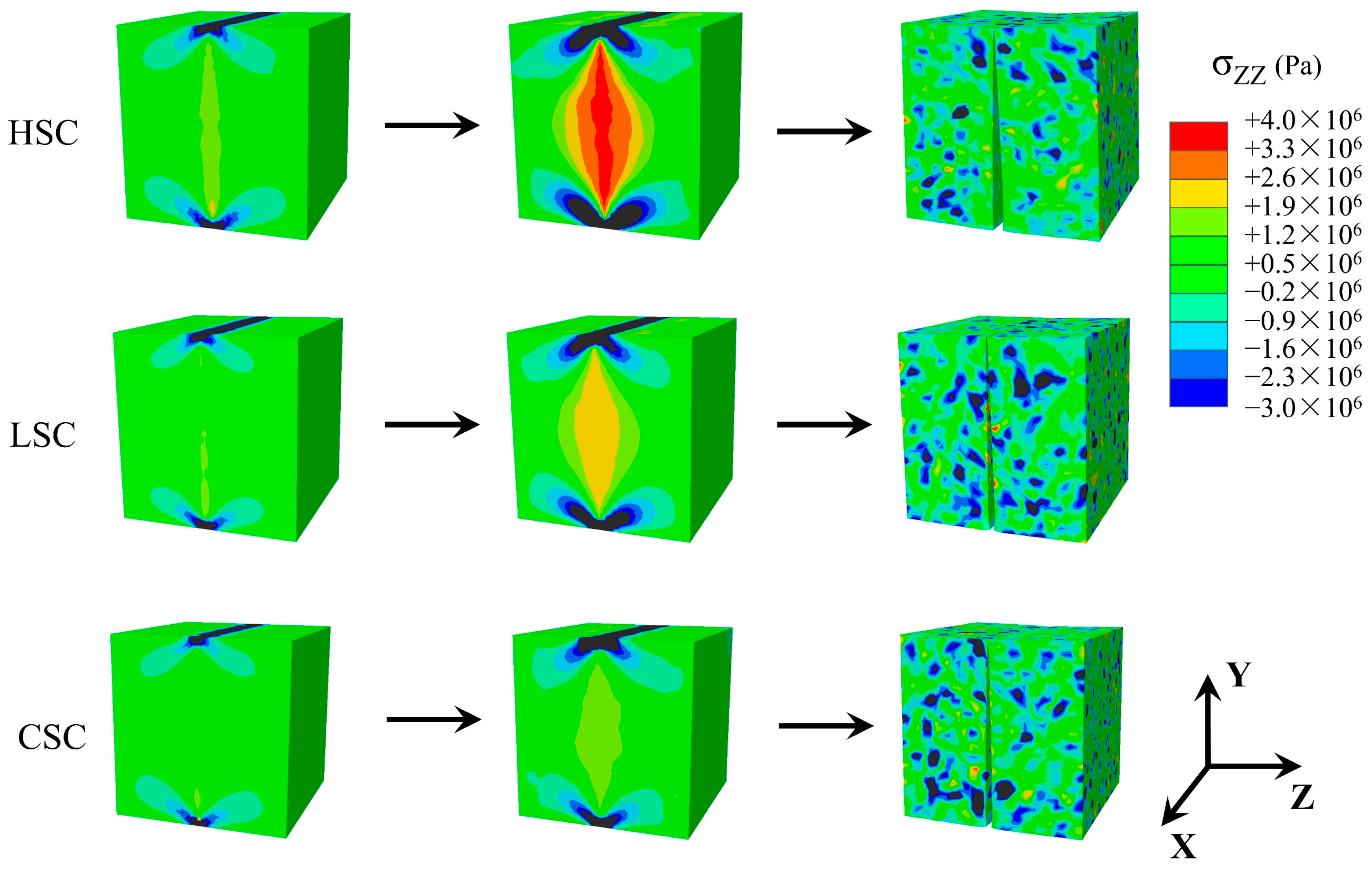
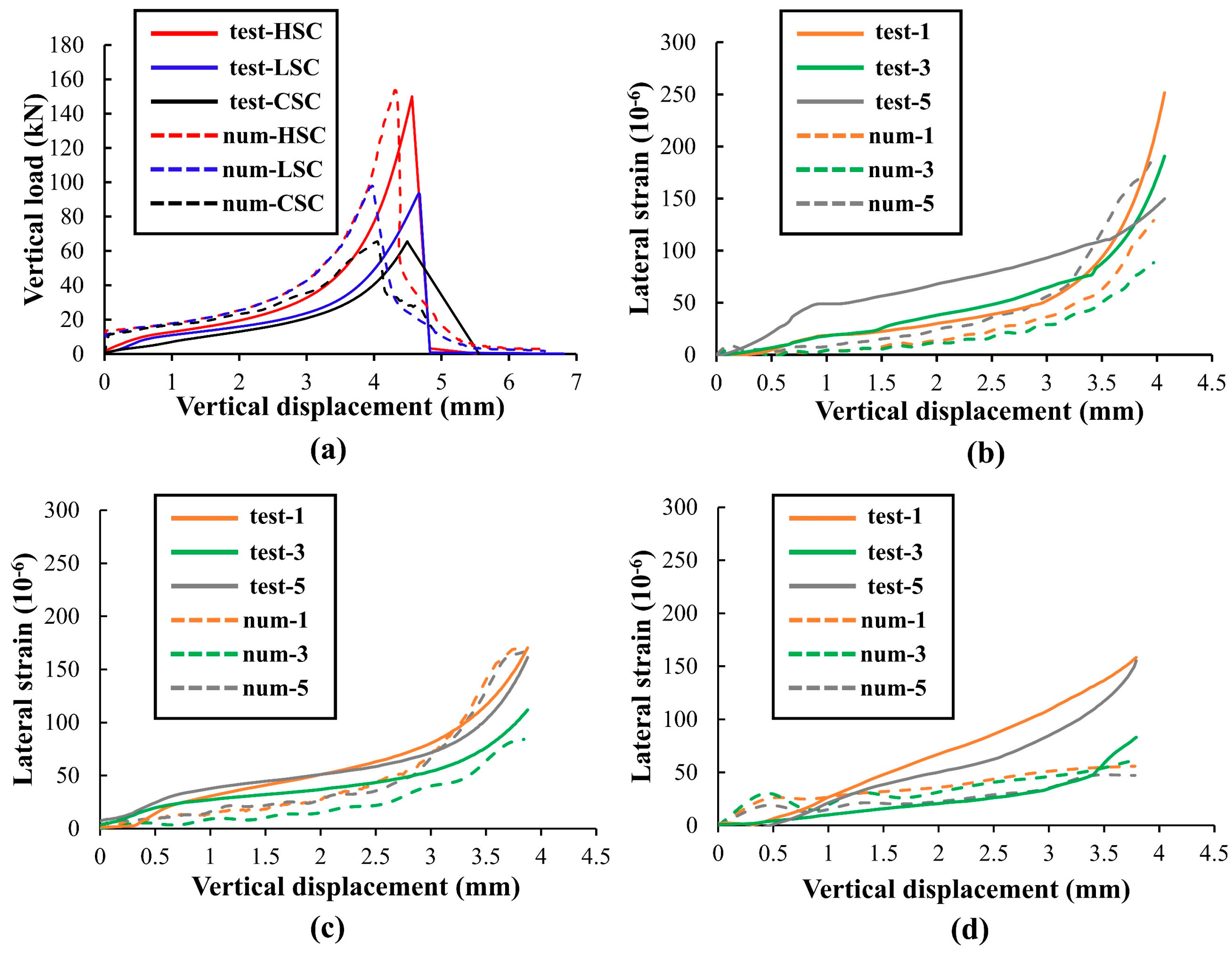
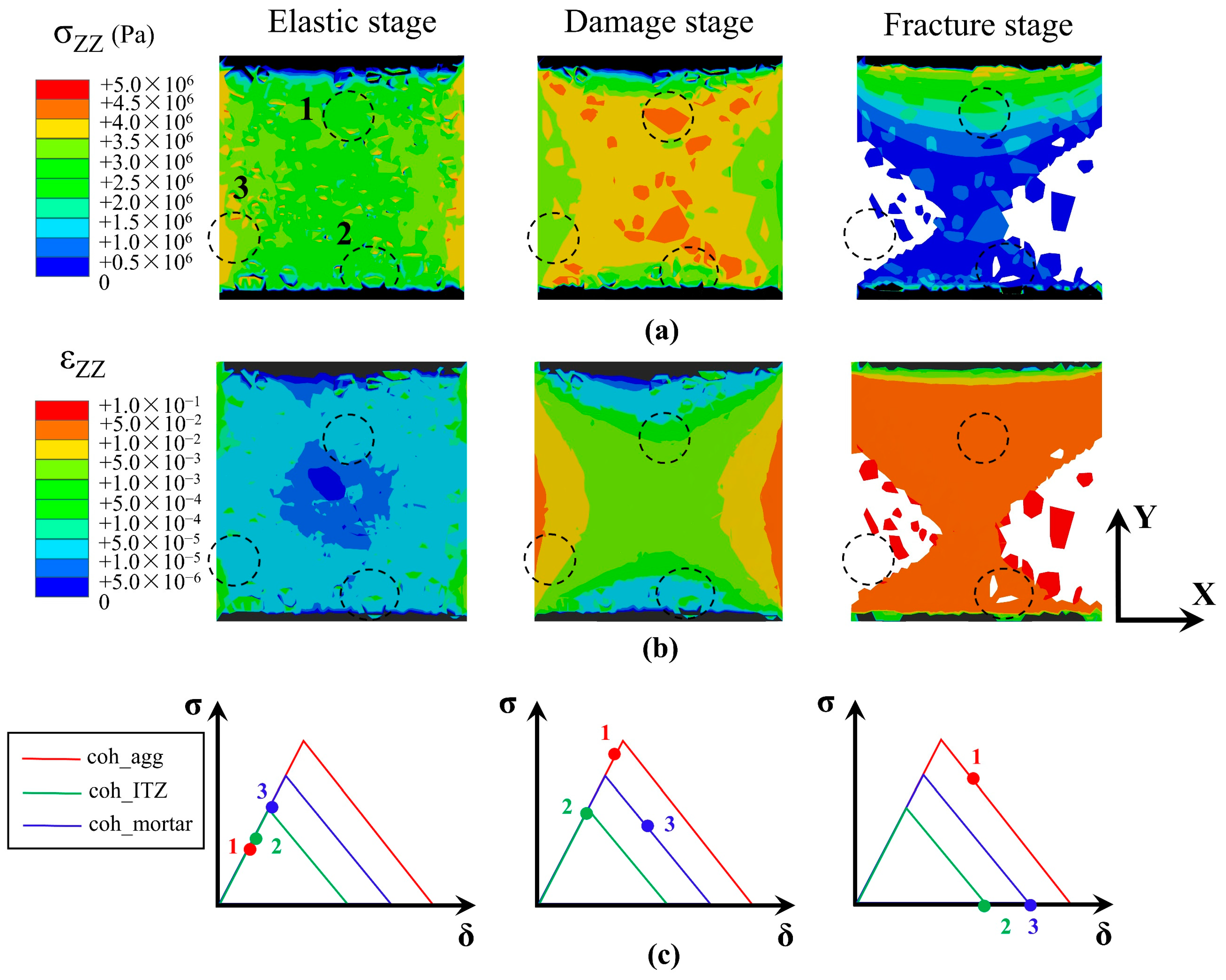
4. Results
4.1. Analysis of Mechanics and Deformation
4.2. Splitting Process
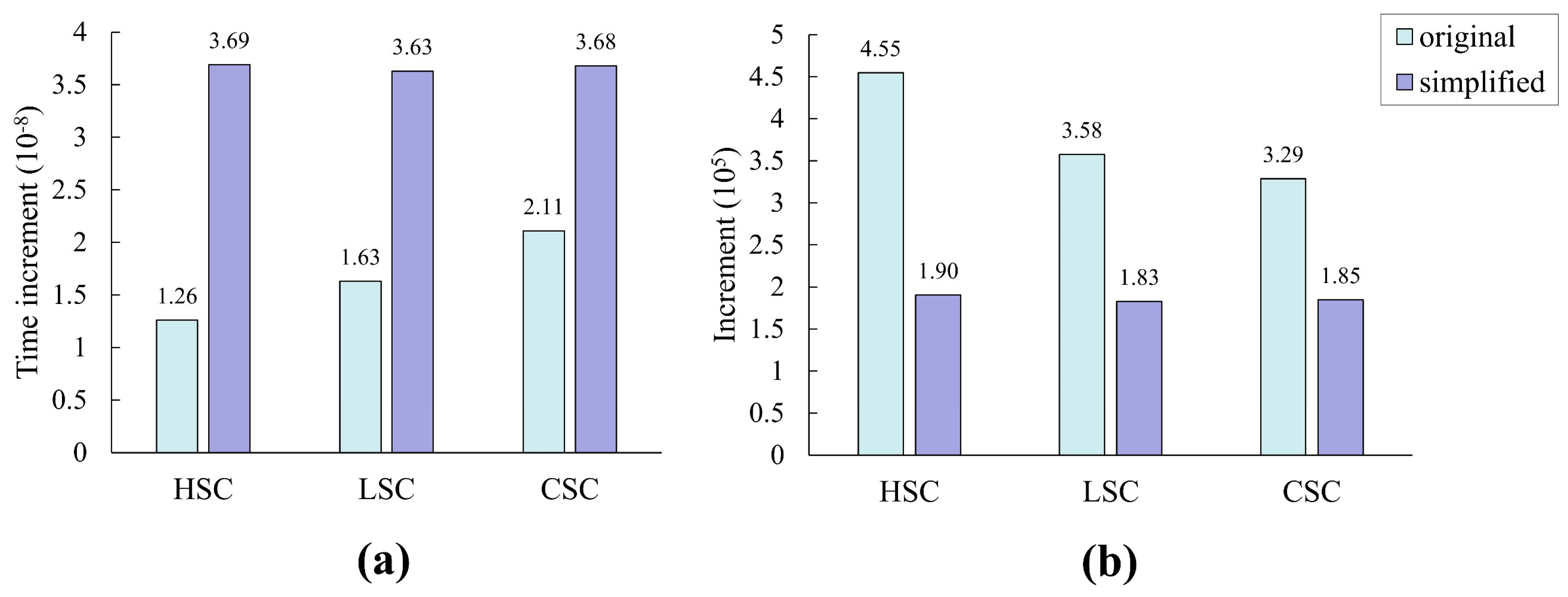
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | |
| DIP | Digital image processing |
| ITZ | Interfacial transition zone |
| CT | Computed tomography |
| HSC | High-strength concrete |
| LSC | Low-strength concrete |
| CSC | Combined-strength concrete |
| FEM | Finite element method |
| CDP | Concrete damaged plasticity |
| coh_agg | Cohesive elements sandwiched by aggregate-aggregate segment |
| coh_ITZ | Cohesive elements sandwiched by aggregate-mortar segment |
| coh_motar | Cohesive elements sandwiched by mortar segment |
| Notation | |
| Tensile splitting strength | |
| Peak axial load | |
| Length of the side of the sample parallel to the loading strip | |
| Height of the specimen | |
| Lower threshold | |
| Upper threshold | |
| Density | |
| Young’s modulus | |
| Poisson’s ratio | |
| Compressive strength | |
| Tensile strength | |
| Dilation angle | |
| Flow potential eccentricity | |
| Initial equibiaxial compressive yield stress | |
| Initial uniaxial compressive yield stress | |
| K | Ratio of the second stress invariant on the tensile meridian to that on the compressive meridian |
| Viscosity parameter | |
| Initial stiffness | |
| Cohesive strength | |
| Fracture energy | |
| Horizontal stress along the Z-direction | |
| Horizontal strain along the Z-direction | |
| Stress | |
| Separation distance of cohesive elements | |
References
- Iskhakov, I.; Ribakov, Y. Structural phenomenon based theoretical model of concrete tensile behavior at different stress-strain conditions. J. Build. Eng. 2021, 33, 101594. [Google Scholar] [CrossRef]
- Cotsovos, D.M.; Pavlović, M.N. Numerical investigation of concrete subjected to high rates of uniaxial tensile loading. Int. J. Impact Eng. 2008, 35, 319–335. [Google Scholar] [CrossRef]
- Vořechovský, M.; Sadílek, V. Computational modeling of size effects in concrete specimens under uniaxial tension. Int. J. Fract. 2008, 154, 27–49. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Silani, M.; Weinberg, K. Fracture studies of Ultra-High Performance Concrete using dynamic Brazilian tests. Theor. Appl. Fract. Mech. 2018, 93, 302–310. [Google Scholar] [CrossRef]
- Abrishambaf, A.; Barros, J.A.O.; Cunha, V.M.C.F. Tensile stress–crack width law for steel fibre reinforced self-compacting concrete obtained from indirect (splitting) tensile tests. Cem. Concr. Compos. 2015, 57, 153–165. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, J.; Yu, H.; Wu, Q.; Da, B. Computer-aided investigation of the tensile behavior of concrete: Relationship between direct and splitting tensile strength. Structures 2023, 55, 453–467. [Google Scholar] [CrossRef]
- Diamond, S. Considerations in image analysis as applied to investigations of the ITZ in concrete. Cem. Concr. Compos. 2001, 23, 171–178. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, R.; Pan, Z.; Zhou, H. Review of Mesoscale geometric models of concrete materials. Buildings 2023, 13, 2428. [Google Scholar] [CrossRef]
- Jin, L.; Liu, M.; Zhang, R.; Du, X. Cracking of cover concrete due to non-uniform corrosion of corner rebar: A 3D meso-scale study. Constr. Build. Mater. 2020, 245, 118449. [Google Scholar] [CrossRef]
- Meng, Z.; Liu, Q.F.; She, W.; Cai, Y.; Yang, J.; Farjad Iqbal, M. Electrochemical deposition method for load-induced crack repair of reinforced concrete structures: A numerical study. Eng. Struct. 2021, 246, 112903. [Google Scholar] [CrossRef]
- Tong, L.Y.; Qin, X.X.; Zhang, M.Z.; Meng, Z.Z.; Meftah, F.; Liu, Q.F. Multi-scale modelling and statistical analysis of heterogeneous characteristics effect on chloride transport properties in concrete. Constr. Build. Mater. 2023, 367, 130096. [Google Scholar] [CrossRef]
- Fang, Q.; Zhang, J.H.; Zhang, Y.D.; Liu, J.C. Mesoscopic investigation of the sand particulate system subjected to intense dynamic loadings. Int. J. Impact Eng. 2016, 89, 62–71. [Google Scholar] [CrossRef]
- Ren, W.Y.; Yang, Z.J.; Sharma, R.; Zhang, C.; Withers, P.J. Two-dimensional X-ray CT image based meso-scale fracture modelling of concrete. Eng. Fract. Mech. 2015, 133, 24–39. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Chen, P.; Liu, X.R.; Du, L.B.; Tan, J.K.; Liang, N.H. Study on the tensile and compressive mechanical properties of multi-scale fiber-reinforced concrete: Laboratory test and mesoscopic numerical simulation. J. Build. Eng. 2024, 86, 108852. [Google Scholar] [CrossRef]
- Bentz, D.P.; Barboczi, E.J. Digital-image-based computer modelling of cement-based materials. In Digital Image Processing: Techniques and Application in Civil Engineering; Frost, J.D., Wright, J.R., Eds.; ASCE: New York, NY, USA, 1993; pp. 44–51. [Google Scholar]
- Bentz, D.P.; Garboczi, E.J.; Jennings, H.M.; Quenard, D.A. Multi-Scale Digital-Image-Based Modelling of Cement-Based Materials. MRS Online Proc. Libr. 1994, 370, 33–41. [Google Scholar] [CrossRef]
- Khormani, M.; Kalat Jaari, V.R. Statistical analysis of the compressive strength of concrete using 2D DIP technology and Finite Element Method. Case Stud. Constr. Mater. 2023, 19, e02461. [Google Scholar] [CrossRef]
- Yu, Q.L.; Liu, H.Y.; Yang, T.H.; Liu, H.L. 3D numerical study on fracture process of concrete with different ITZ properties using X-ray computerized tomography. Int. J. Solids Struct. 2018, 147, 204–222. [Google Scholar] [CrossRef]
- Peng, Y.J.; Ying, L.P.; Kamel, M.M.A.; Wang, Y. Mesoscale fracture analysis of recycled aggregate concrete based on digital image processing technique. Struct. Concr. 2021, 22, E33–E47. [Google Scholar] [CrossRef]
- Yu, J.J.; Li, G.D.; Ren, Z.Y.; Zhang, W.; Tang, J.Q.; Zhang, L.; Si, X.L.; Zhao, Z.M. Mixed-mode I-II mesoscale fracture behavior of concrete determined by the realistic aggregate numerical model. Constr. Build. Mater. 2019, 226, 802–817. [Google Scholar]
- Zhang, S.; Hamed, E.; Song, C.M. Computational modelling of the basic creep of concrete: An image-based meso-scale approach. Eng. Anal. Bound. Elem. 2022, 136, 64–76. [Google Scholar] [CrossRef]
- Cai, K.P.; Wang, G.Q.; Li, W.; Long, W. Numerical simulation of concrete strength based on microstructure and mineral composition analysis using micro-CT and XRD technology. Constr. Build. Mater. 2024, 432, 136505. [Google Scholar] [CrossRef]
- Huang, M.; Li, Y.M. X-ray tomography image-based reconstruction of microstructural finite element mesh models for heterogeneous materials. Comput. Mater. Sci. 2013, 67, 63–72. [Google Scholar] [CrossRef]
- Xue, G.L.; Yilmaz, E.; Song, W.D.; Cao, S. Analysis of internal structure behavior of fiber reinforced cement-tailings matrix composites through X-ray computed tomography. Compos. Part B Eng. 2019, 175, 107091. [Google Scholar] [CrossRef]
- Wen, F.S.; Li, W.C.; Zhou, G.F.; Li, H.J.; Chen, T.; Zhang, K.Q. A simplified numerical simulation of uniaxial compression for polyacrylonitrile fiber reinforced permeable concrete based on CT images. Constr. Build. Mater. 2024, 411, 134319. [Google Scholar] [CrossRef]
- Feng, X.H.; Gong, B.; Tang, C.A.; Zhao, T. Study on the non-linear deformation and failure characteristics of EPS concrete based on CT-scanned structure modelling and cloud computing. Eng. Fract. Mech. 2022, 261, 108214. [Google Scholar] [CrossRef]
- Khormani, M.; Kalat Jaari, V.R.; Aghayan, I.; Ghaderi, S.H.; Ahmadyfard, A. Compressive strength determination of concrete specimens using X-ray computed tomography and finite element method. Constr. Build. Mater. 2020, 256, 119427. [Google Scholar] [CrossRef]
- Meng, Q.X.; Xu, W.Y.; Wang, H.L.; Zhuang, X.Y.; Xie, W.C.; Rabczuk, T. DigiSim—An open source software package for heterogeneous material modeling based on digital image processing. Adv. Eng. Softw. 2020, 148, 102836. [Google Scholar] [CrossRef]
- Mishnaevsky, L.L.; Schmauder, S. Continuum mesomechanical finite element modeling in materials development: A state-Of-The-Art review. Appl. Mech. Rev. 2001, 54, 49–67. [Google Scholar] [CrossRef]
- Shakir, Q.M.; Hanoon, H.K. New models for reinforced concrete precast hybrid deep beams under static loads with curved hybridization. Structures 2023, 54, 1007–1025. [Google Scholar] [CrossRef]
- Shakir, Q.M.; Alliwe, R. Upgrading of deficient disturbed regions in precast RC beams with near surface mounted (NSM) steel bars. J. Mater. Eng. Struct. 2020, 7, 167–184. [Google Scholar]
- GB/T50081-2002; Ministry of Construction of the People’s Republic of China. Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2003. (In Chinese)
- ASTM C 469-2002; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM. International: West Conshohocken, PA, USA, 2002.
- ASTM C 138-2001; Standard Test Method for Unit Weight, Yield, and Air Content (Gravimetric) of Concrete. ASTM. International: West Conshohocken, PA, USA, 2001.
- BS 1881-117; Testing Concrete—Part 117: Method for Determination of Tensile Splitting Strength. British Standards Institution: London, UK, 1983.
- Hammoumi, A.; Moreaud, M.; Jeulin, D.; Jolimaitre, E.; Chevalier, T.; Sorbier, L.; Klotz, M.; Novikov, A. A novel physisorption model based on mathematical morphology operators preserving exact pore morphology and connectivity. Microporous Mesoporous Mater. 2022, 337, 111847. [Google Scholar] [CrossRef]
- Graham, R.L. An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Inf. Process. Lett. 1972, 1, 132–133. [Google Scholar] [CrossRef]
- Wang, T.X.; Wang, Y.; Crocetti, R.; Wålinder, M. Influence of face grain angle, size, and moisture content on the edgewise bending strength and stiffness of birch plywood. Mater. Des. 2022, 223, 111227. [Google Scholar] [CrossRef]
- GB 50010-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Zhao, H.Y.; Wu, Z.H.; Liu, A.; Zhang, L.C. Numerical insights into the effect of ITZ and aggregate strength on concrete properties. Theor. Appl. Fract. Mech. 2022, 120, 103415. [Google Scholar] [CrossRef]
- Kılıç, A.; Atiş, C.D.; Teymen, A.; Karahan, O.; Özcan, F.; Bilim, C.; Özdemir, M. The influence of aggregate type on the strength and abrasion resistance of high strength concrete. Cem. Concr. Compos. 2008, 30, 290–296. [Google Scholar] [CrossRef]
- Zhou, F.P.; Lydon, F.D.; Barr, B.I.G. Effect of coarse aggregate on elastic modulus and compressive strength of high performance concrete. Cem. Concr. Res. 1995, 25, 177–186. [Google Scholar] [CrossRef]
- ABAQUS/CAE User’s Manual; ABAQUS, Inc.: Palo Alto, CA, USA, 2004.
- Zhu, S.S.; Zhou, Z.F.; Xiong, Y. Mesoscale fracture analysis of three-point bending concrete beams based on cohesive zone model. Eng. Fract. Mech. 2024, 296, 109828. [Google Scholar] [CrossRef]
- Viñuela, J.Z.; Torres, M.; Silva, R.G. Cohesive zone modeling in load–unload situations. Int. J. Mech. Sci. 2022, 222, 107205. [Google Scholar] [CrossRef]
- Tang, L.W.; Zhou, W.; Liu, X.H.; Ma, G.; Chen, M.X. Three-dimensional mesoscopic simulation of the dynamic tensile fracture of concrete. Eng. Fract. Mech. 2019, 211, 269–281. [Google Scholar] [CrossRef]
- Huang, Y.J.; Yang, Z.J.; Zhang, H.; Natarajan, S. A phase-field cohesive zone model integrated with cell-based smoothed finite element method for quasi-brittle fracture simulations of concrete at mesoscale. Comput. Methods Appl. Mech. Eng. 2022, 396, 115074. [Google Scholar] [CrossRef]
- Li, Y.; Hao, Z.; Shen, Z.; Fu, P.; Zhang, J. Mesoscopic modeling and simulation of tensile properties of cracked concrete using cohesive model. Case Stud. Constr. Mater. 2023, 18, e02186. [Google Scholar] [CrossRef]
- Naderi, S.; Zhang, M.Z. Meso-scale modelling of static and dynamic tensile fracture of concrete accounting for real-shape aggregates. Cem. Concr. Compos. 2021, 116, 103889. [Google Scholar] [CrossRef]
- Carmona, S.; Aguado, A. New model for the indirect determination of the tensile stress–strain curve of concrete by means of the Brazilian test. Mater. Struct. 2012, 45, 1473–1485. [Google Scholar] [CrossRef]
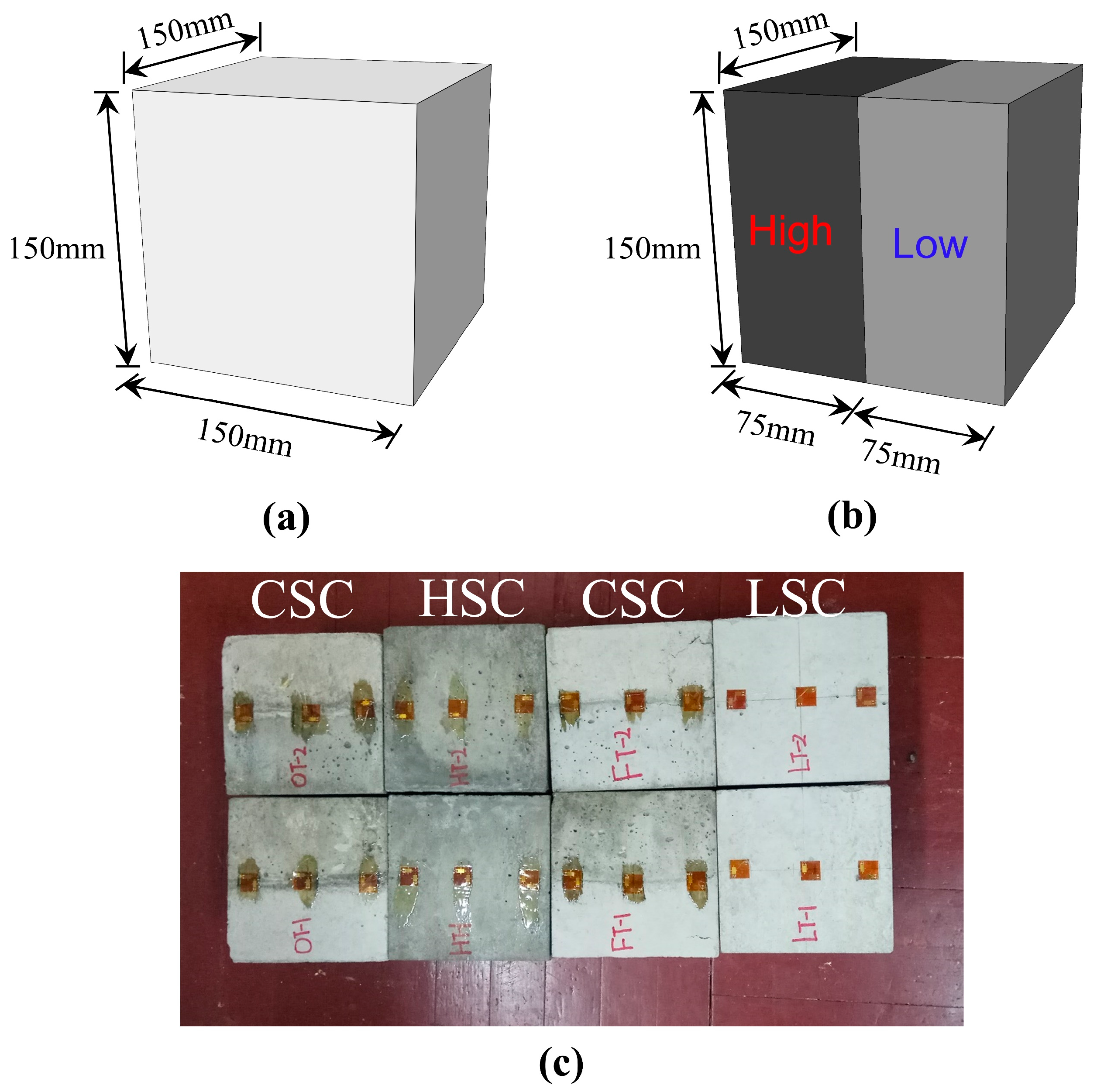


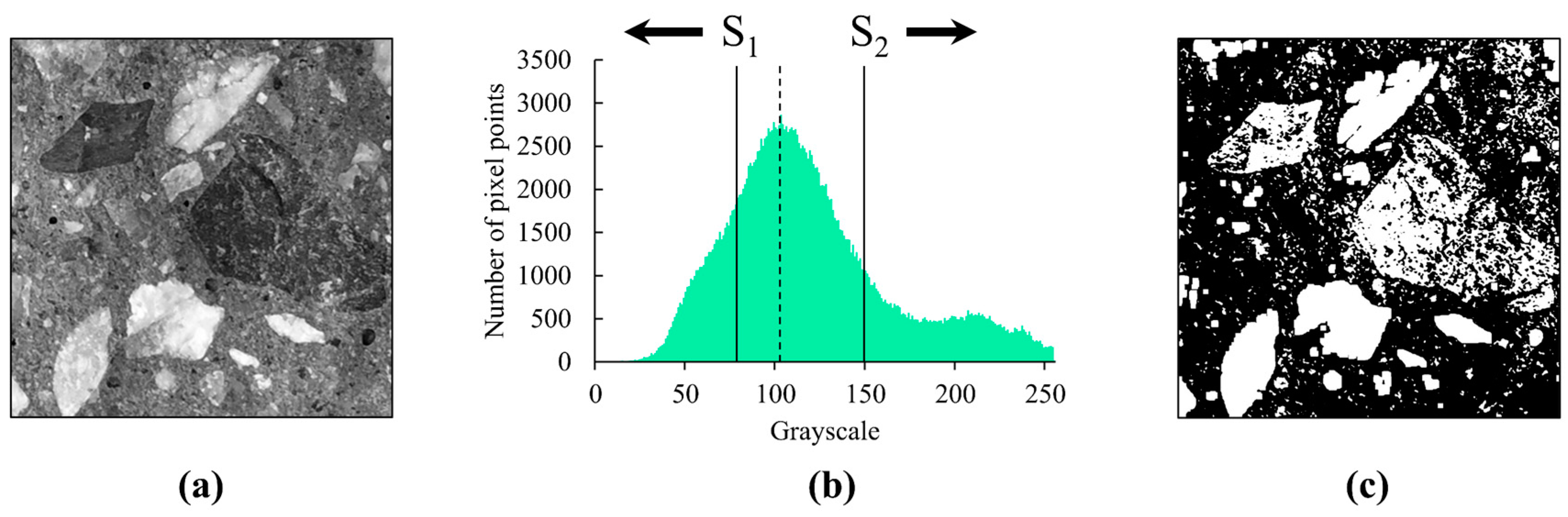
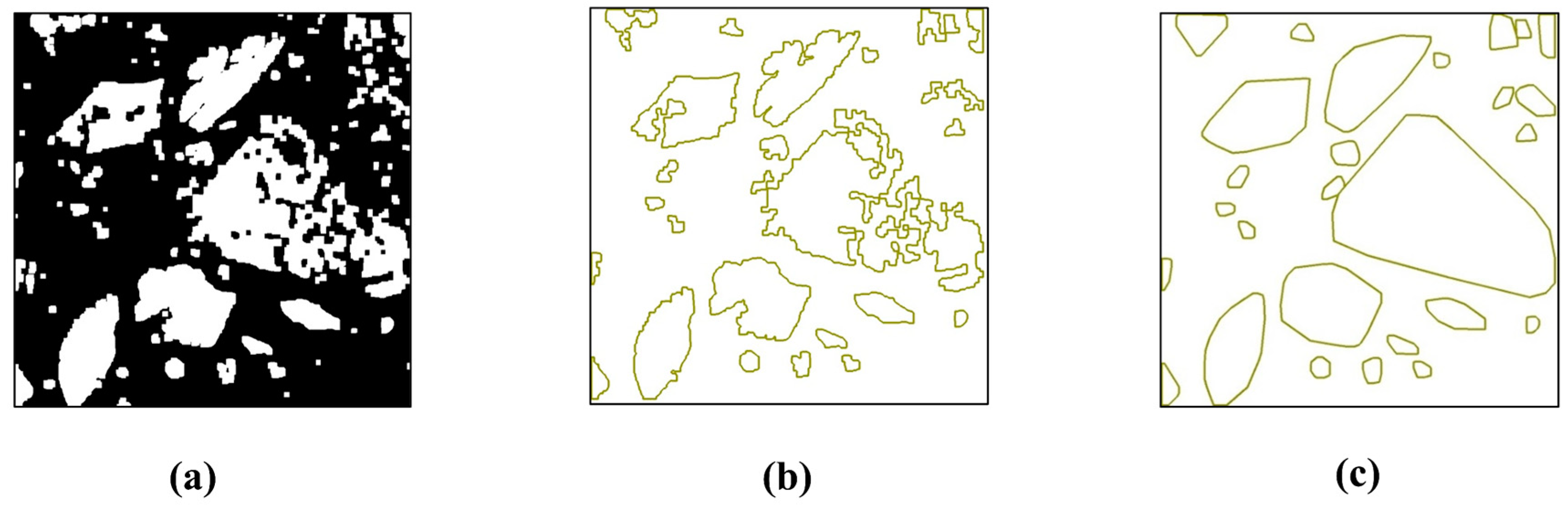

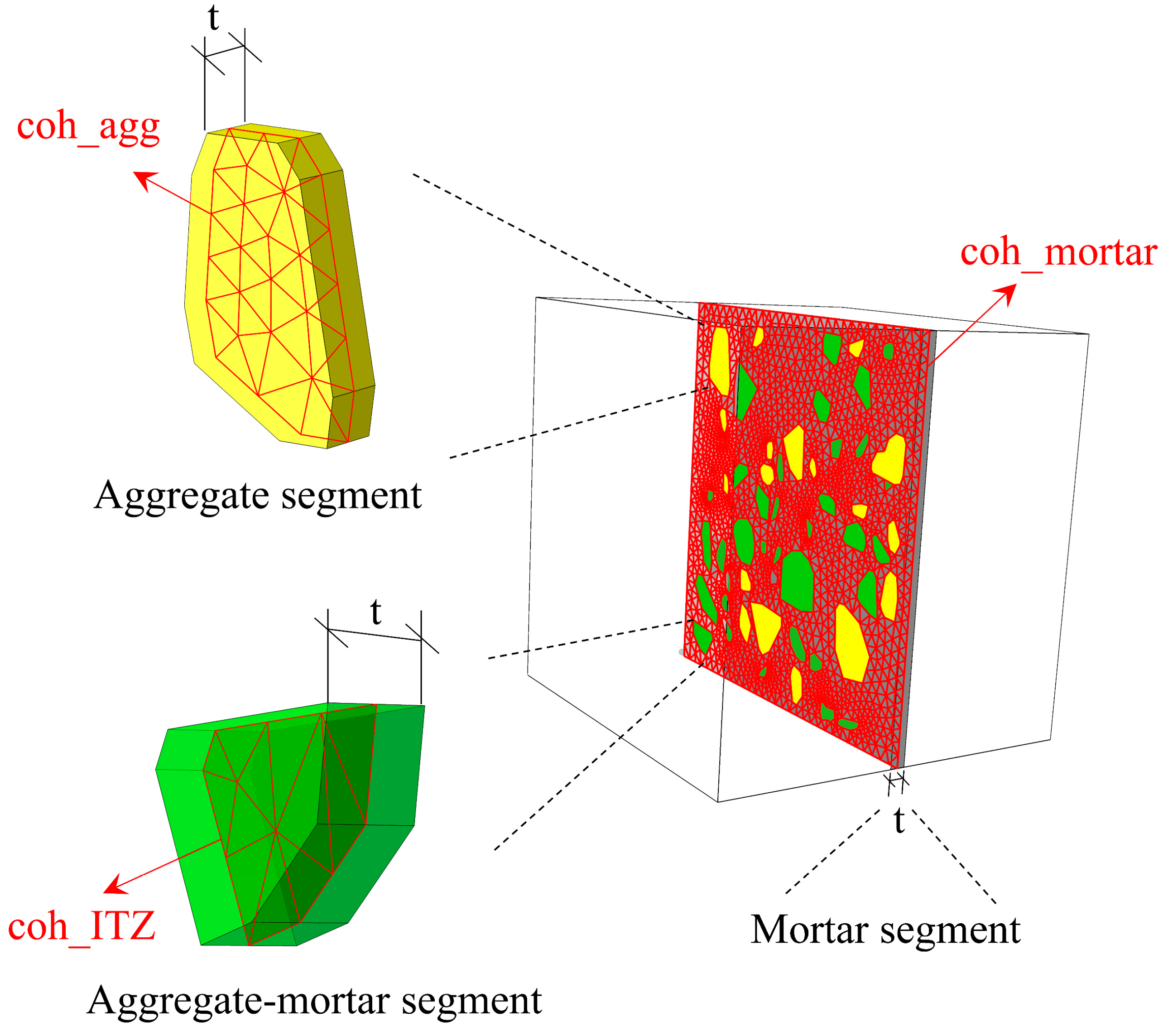

| Mixtures | Cement | Water | Fine Sand | Coarse Aggregate | Limestone Powder | Slag | Admixture |
|---|---|---|---|---|---|---|---|
| HSC | 388 | 145 | 623 | 1081 | 108 | 50 | 13.65 |
| LSC | 227 | 149 | 795 | 1098 | 68 | 44 | 6.4 |
| Sample | Compressive Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Unit Weight (kg/m3) | |
|---|---|---|---|---|---|
| HSC | 1 | 69.1 | 45.2 | 0.14 | 2406 |
| 2 | 65.4 | 44.7 | 0.15 | 2397 | |
| 3 | 70.4 | 47.5 | 0.15 | 2411 | |
| Average | 68.3 | 45.8 | 0.15 | 2405 | |
| LSC | 1 | 36.2 | 39.5 | 0.14 | 2390 |
| 2 | 35.3 | 38.4 | 0.15 | 2381 | |
| 3 | 31.6 | 37.9 | 0.16 | 2370 | |
| Average | 34.4 | 38.6 | 0.15 | 2380 | |
| Segment Region | Density ρ (kg/m3) | Young’s Modulus EC (MPa) | Poisson’s Ratio ν | Compressive Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Aggregate | 3000 | 50,000 | 0.15 | 80 | 4.2 |
| ITZ | 2500 | 35,000 | 0.15 | 53 | 3.5 |
| HSC | 2400 | 45,000 | 0.15 | 70 | 4.1 |
| LSC | 2400 | 38,000 | 0.15 | 36 | 2.6 |
| Strip | 1000 | 5000 | 0.3 | 15 | - |
| φ | ε | fb0/fc0 | K | μ |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.667 | 0.0005 |
| Model | Elements | Density ρ (kg/m3) | Initial Stiffness k0 (MPa/mm) | Cohesive Strength ft (MPa) | Fracture Energy GC (N/mm) |
|---|---|---|---|---|---|
| HSC | coh_mortar | 2400 | 106 | 4 | 0.1 |
| coh_agg | 3000 | 106 | 4.2 | 0.12 | |
| coh_ITZ | 2500 | 106 | 3.5 | 0.075 | |
| LSC | coh_mortar | 2400 | 106 | 2.5 | 0.05 |
| coh_agg | 3000 | 106 | 4.2 | 0.12 | |
| coh_ITZ | 2500 | 106 | 1.8 | 0.025 | |
| CSC | coh_mortar | 2400 | 106 | 1.5 | 0.025 |
| coh_agg | 3000 | 106 | 4.2 | 0.12 | |
| coh_ITZ | 2500 | 106 | 0.8 | 0.01 |
| Sample | Peak Load (kN) | Splitting Tensile Strength (MPa) | Average (MPa) |
|---|---|---|---|
| HSC | 137.313 | 3.885 | 3.949 |
| 150.014 | 4.245 | ||
| 131.344 | 3.716 | ||
| LSC | 93.622 | 2.649 | 2.679 |
| 93.461 | 2.644 | ||
| 96.940 | 2.743 | ||
| CSC | 64.376 | 1.821 | 1.805 |
| 65.572 | 1.855 | ||
| 61.423 | 1.738 |
| Sample | Peak Load (kN) | Splitting Tensile Strength (MPa) | Error (%) | ||
|---|---|---|---|---|---|
| Test | Simulation | Test | Simulation | ||
| HSC | 150.015 | 153.565 | 4.245 | 4.345 | 2.36 |
| LSC | 93.461 | 97.909 | 2.644 | 2.770 | 4.77 |
| CSC | 65.572 | 65.342 | 1.855 | 1.849 | −0.32 |
| Sample | Mortar | Aggregates | ITZs |
|---|---|---|---|
| HSC | 72.5% | 24.8% | 2.7% |
| LSC | 73.7% | 7.3% | 19.0% |
| CSC | 92.6% | 1.9% | 5.5% |
| Sample | Test | Original Model | Simplified Model | ||
|---|---|---|---|---|---|
| (MPa) | (MPa) | Error (%) | (MPa) | Error (%) | |
| HSC | 4.245 | 4.345 | 2.36 | 4.234 | −0.26 |
| LSC | 2.644 | 2.770 | 4.77 | 2.527 | −4.43 |
| CSC | 1.855 | 1.849 | −0.32 | 1.857 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Li, D.; Hu, Z.; Li, X.; Yan, Z.; Li, H.; Liu, J. Characterizing Splitting Failure of Concrete Influenced by Material Heterogeneity Based on Digital Image Processing Techniques. Buildings 2024, 14, 1856. https://doi.org/10.3390/buildings14061856
Lin H, Li D, Hu Z, Li X, Yan Z, Li H, Liu J. Characterizing Splitting Failure of Concrete Influenced by Material Heterogeneity Based on Digital Image Processing Techniques. Buildings. 2024; 14(6):1856. https://doi.org/10.3390/buildings14061856
Chicago/Turabian StyleLin, Houquan, Dong Li, Zheng Hu, Xiang Li, Zhaoxi Yan, Hui Li, and Jiankun Liu. 2024. "Characterizing Splitting Failure of Concrete Influenced by Material Heterogeneity Based on Digital Image Processing Techniques" Buildings 14, no. 6: 1856. https://doi.org/10.3390/buildings14061856
APA StyleLin, H., Li, D., Hu, Z., Li, X., Yan, Z., Li, H., & Liu, J. (2024). Characterizing Splitting Failure of Concrete Influenced by Material Heterogeneity Based on Digital Image Processing Techniques. Buildings, 14(6), 1856. https://doi.org/10.3390/buildings14061856






