Temperature Effect of Composite Girders with Corrugated Steel Webs Considering Local Longitudinal Stiffness of Webs
Abstract
1. Introduction
2. Analysis of the Mechanical Properties of Corrugated Steel Web
3. Effect of Temperature on Composite Box Girder with Corrugated Steel Web
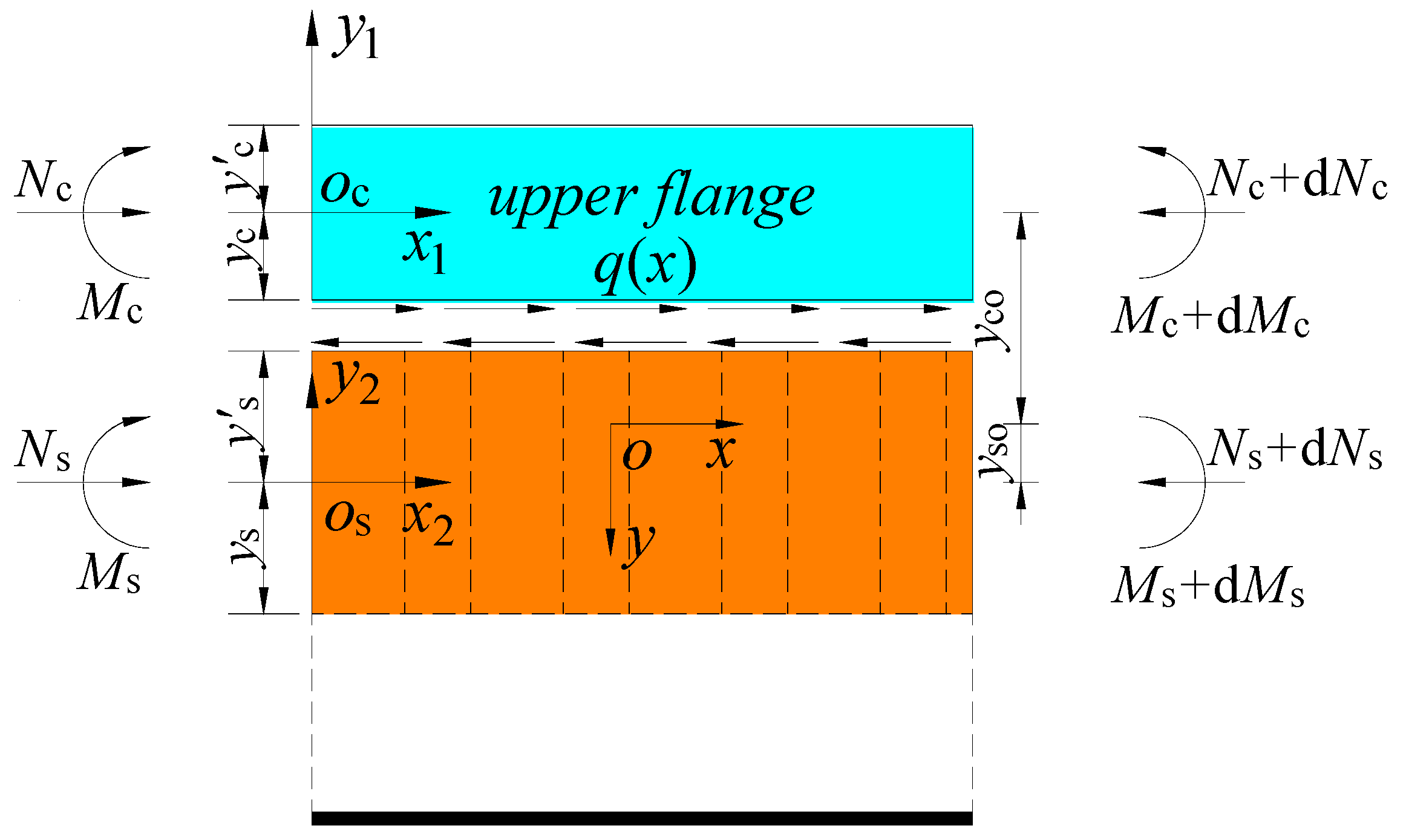
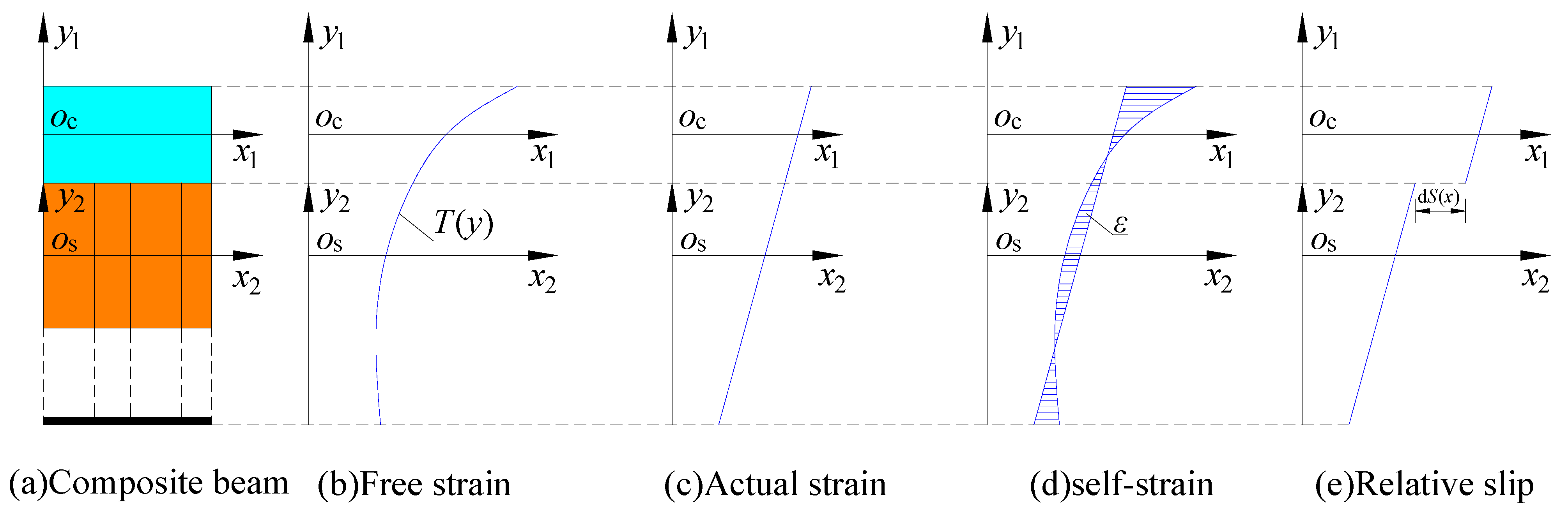
3.1. Basic Assumption
- (1)
- Composite box girders with corrugated steel webs are assumed to have a quasi-flat section,
- (2)
- the composite box girder with a corrugated steel web is in an elastic working state,
- (3)
- the friction between the corrugated steel web and concrete plate interface is not considered. The shear force of the shear nails is directly proportional to the relative slip between the layers,
- (4)
- the shear keys are responsible for bearing all the horizontal shear forces at the interface of the composite box girder with corrugated steel webs, and they vary directly with the interlayer slip,
- (5)
- at the interface of the corrugated steel web composite box girder, there is no longitudinal lifting, and the curvature of the steel beam matches that of the concrete slab.
3.2. Analysis of Temperature Effects
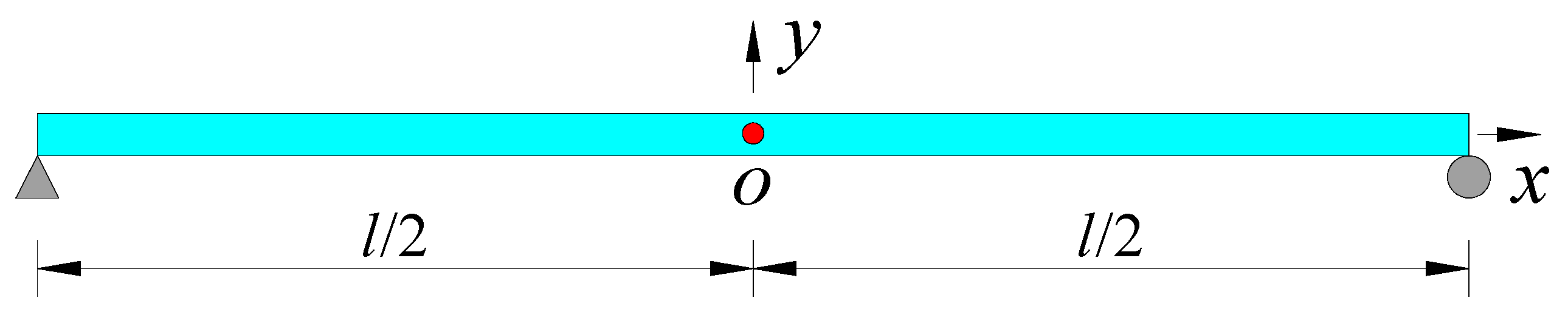
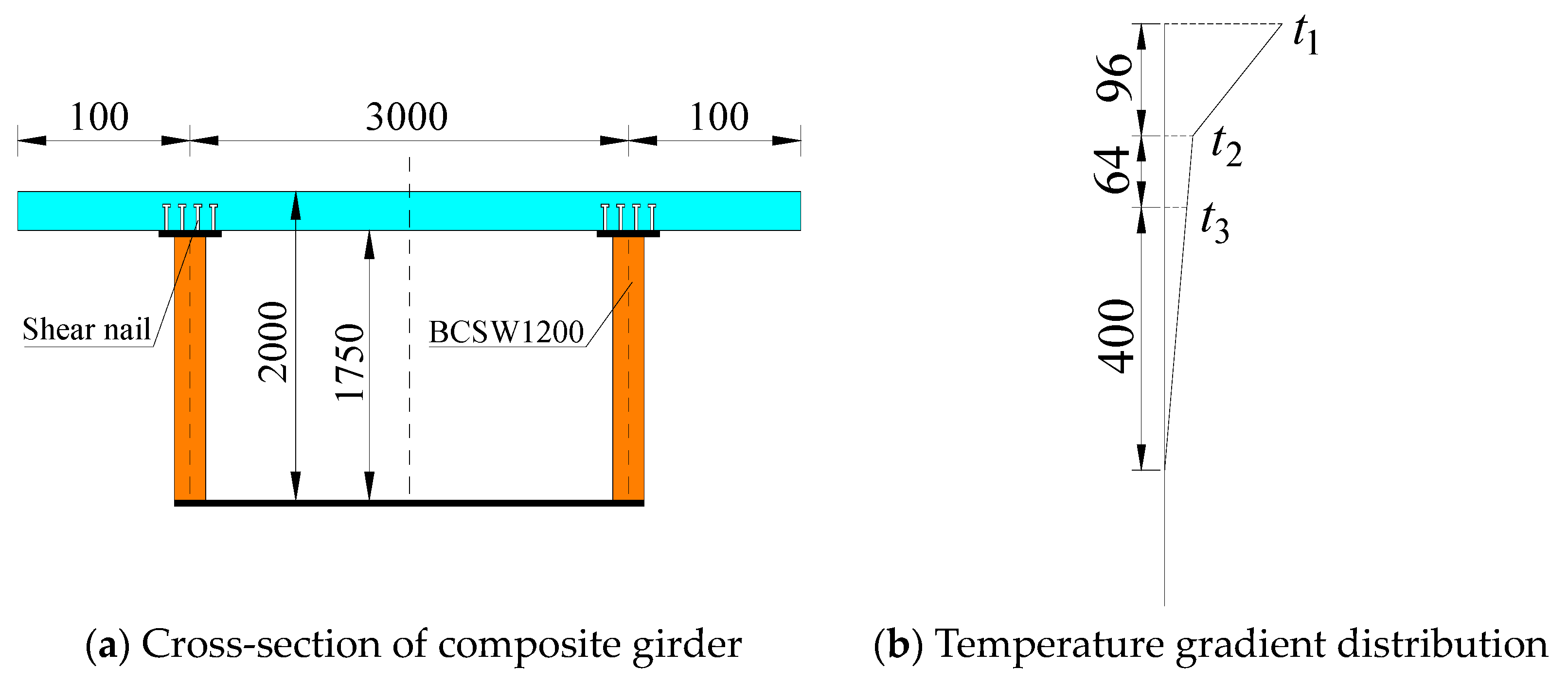
4. Numerical Example
5. Comparative Analysis of Calculation Results
5.1. Determination of the Standard Resistance to Bending
5.2. Investigation of Influencing Factors
5.2.1. Analysis of Glide Stiffness
5.2.2. Analysis of Temperature Differences
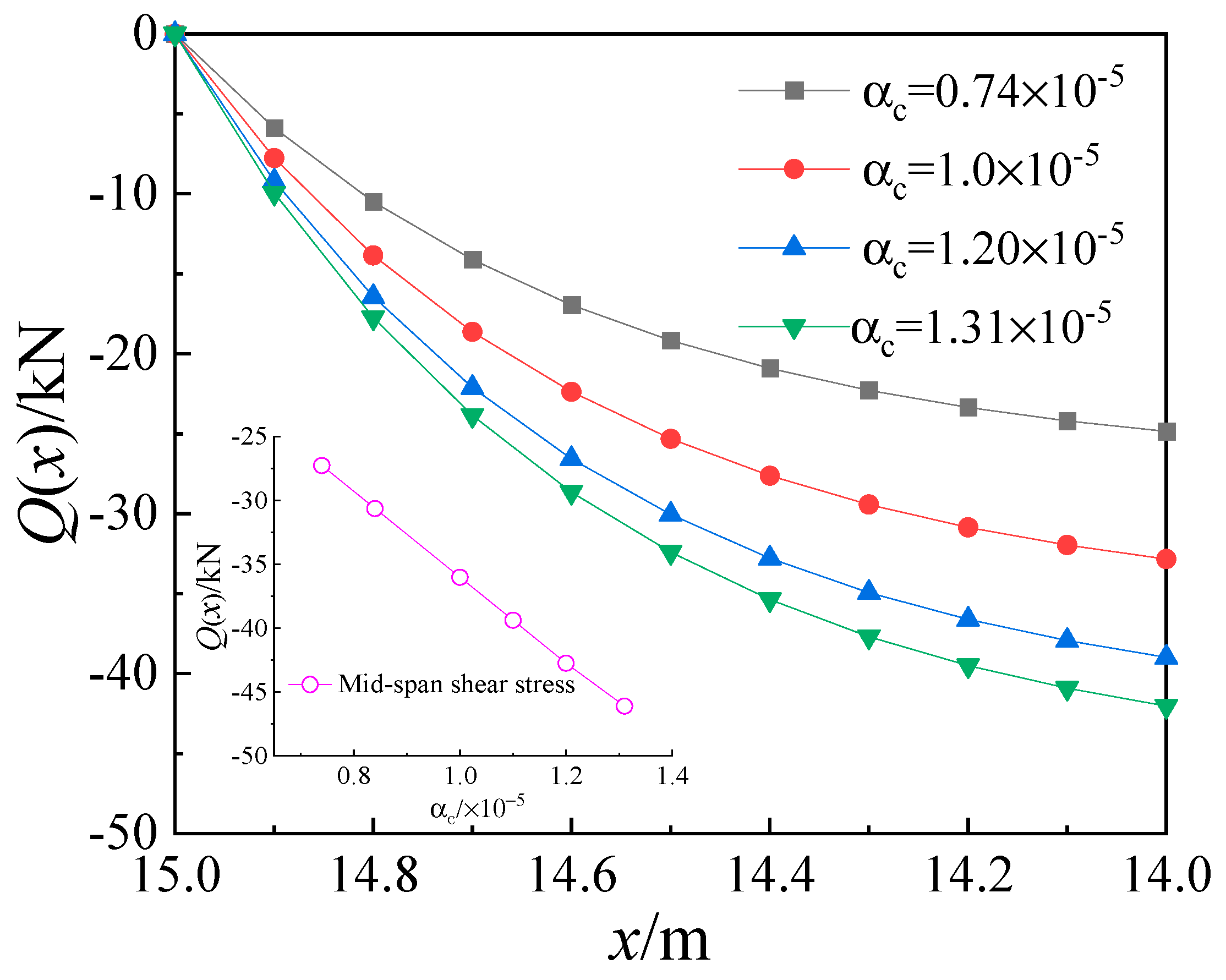
5.2.3. Analysis of the Linear Expansion Coefficient of Concrete
6. Conclusions
- (1)
- Taking into consideration the influence of the local longitudinal stiffness of the web, the calculation method for determining the temperature effect on composite box girders with corrugated steel webs under various temperature gradient modes aligns excellently with the results obtained from the ANSYS finite element analysis. This validates the accuracy of the theoretical derivation.
- (2)
- Considering 10% of the height of the corrugated steel web as the common bending zone improves the accuracy of the calculation results. Taking into account the longitudinal constraints of the web enhances the consistency between the theoretical calculations and the actual stress conditions observed in such bridges.
- (3)
- The distribution of the interfacial shear force and interfacial slip in the composite box girder with corrugated steel webs varies along the longitudinal beam. The highest relative slip occurs at the end of the composite beam, while it is negligible in the middle span. Similarly, the interface shear force is minimal at the beam ends and reaches its maximum value at the mid-span. Therefore, it is advisable to arrange the shear nails segmentally along the length of the composite box girder and reinforce them at the ends.
- (4)
- The accuracy of temperature effect calculations for corrugated steel web composite box girders is influenced by factors such as longitudinal sliding stiffness, temperature difference, and concrete linear expansion coefficient. When computing the temperature effect for such bridges, it is crucial to reasonably select a vertical temperature distribution model, account for the variability of the concrete linear expansion coefficient, and arrange the shear nails in a rational manner.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elgaal, Y.M. Shear strength of beans with corrugated web. J. Struct. Eng. 1996, 122, 90. [Google Scholar]
- Li, H.J.; Ye, J.S.; Wan, S.; Wu, W. Influence of shear Deformation on Deflection of Box Girder with Corrugated Steel Webs. J. Traffic Transp. Eng. 2002, 4, 17–20. (In Chinese) [Google Scholar]
- Zhou, X.F.; Wang, Z.Y.; Liu, Z.F.; Liu, Y.; Jiang, Y.; Gai, W. Study on strength and stress properties of external prestressed composite beams with corrugated steel webs. J. Build. Struct. 2021, 42, 229–238. (In Chinese) [Google Scholar]
- Liu, Y.J.; Liu, J. Review on temperature action and effect of steel-concrete composite girder bridge. J. Traffic Transp. Eng. 2020, 20, 42–59. (In Chinese) [Google Scholar]
- Heckel, R. The Fourth Danube Bridge in Vienna-damage and repair. Dev. Bridge Des. Constr. Process 1971, 588–598. [Google Scholar]
- Dilger, W.H.; Ghali, A.; Chan, M.; Cheung, M.S.; Maes, M.A. Temperature stresses in composite box girder bridges. J. Struct. Eng. 1983, 109, 1460–1478. [Google Scholar] [CrossRef]
- Chen, Y.J.; Ye, M.X. Analyses of responses of composite girders under the action of temperature. China Railw. Sci. 2001, 22, 48–53. (In Chinese) [Google Scholar]
- Zhou, L.; Lu, Y.C.; Li, X.F. Calculation of temperature stress of steel-concrete composite beam. J. Highw. Transp. Res. Dev. 2012, 29, 83–88. (In Chinese) [Google Scholar]
- Zhou, Y.C.; Hu, S.N.; Song, L.; Li, Z. Effect analysis of steel-concrete composite beam caused by sudden change of temperature. J. Traffic Transp. Eng. 2013, 13, 20–26. (In Chinese) [Google Scholar]
- Liu, Y.J.; Liu, J.; Zhang, N.; Lei, X.U. Analytical solution of temperature effects of steel-concrete composite girder. J. Traffic Transp. Eng. 2017, 17, 9–19. (In Chinese) [Google Scholar]
- Qiang, J.T.; Yao, C.; Zhang, F. Study of temperature effect on the composed bridge with corrugated steel webs. Highway 2016, 61, 54–57. (In Chinese) [Google Scholar]
- Dong, X.; Deng, Z.Q.; Li, S.S.; Feng, Z. Research on sun light temperature field and thermal difference effect of long span box girder bridge with corrugated steel webs. Eng. Mech. 2017, 34, 230–238. (In Chinese) [Google Scholar]
- Xu, X.F.; Zhang, F.; Liu, J.Q. Temperature distribution of box girder with corrugated steel webs. J. Chongqing Jiaotong Univ. Nat. Sci. 2018, 37, 1–10. (In Chinese) [Google Scholar]
- Zhao, P.; Ye, J.S. Analysis of transverse temperature effects on the deck of box girder with corrugated steel webs. J. Harbin Eng. Univ. 2019, 40, 974–978. (In Chinese) [Google Scholar]
- Wang, L.; Liu, S.Z.; Ding, W.; Liu, S.; Wu, W. Analysis on temperature effect of new-pattern corrugated steel web composite box girder in dry cold region. Adv. Eng. Sci. 2021, 53, 60–66. (In Chinese) [Google Scholar]
- CJJ/T 272—2017; Technical Standard for Composite Girder Bridges with Corrugated Steel Webs. China Building Industry Press: Beijing, China, 2017. (In Chinese)
- Li, H.J. Experimental Study and Analysis on Torsion and Distortion Corrugated Steel Webs and Composite Deck; SouthEast University: Dhaka, Bangladesh, 2003. (In Chinese) [Google Scholar]
- Zhang, Y.H.; Sun, C.C. Analysis on the torsion effect of box girders with corrugated steel webs considering local longitudinal stiffness of webs. J. Southeast Univ. Nat. Sci. Ed. 2022, 54, 133–140. (In Chinese) [Google Scholar]
- Wang, L.; Liu, S.Z.; Li, Z.Q.; Huang, J.; Ding, W. Temperature Effect of Simply Supported Composite Box Girder with Corrugated Steel Webs and Composite Deck. Adv. Eng. Sci. 2021, 51, 195–201. (In Chinese) [Google Scholar]
- Huang, S.H.; Cai, C.Z.; Zou, Y.F.; He, X.H.; Zhou, T.; Zhu, X. Experimental and numerical investigation on the temperature distribution of composite box-girders with corrugated steel webs. Struct. Control Health Monit. 2022, 29, e3123. [Google Scholar] [CrossRef]
- BS5400; Steel, Concrete and Composite Bridges—Part 2. Specification for Loads. British Standards Institution: London, UK, 1978.
- Neville, A.M. Properties of Concrete; LAP: London, UK, 1995. [Google Scholar]



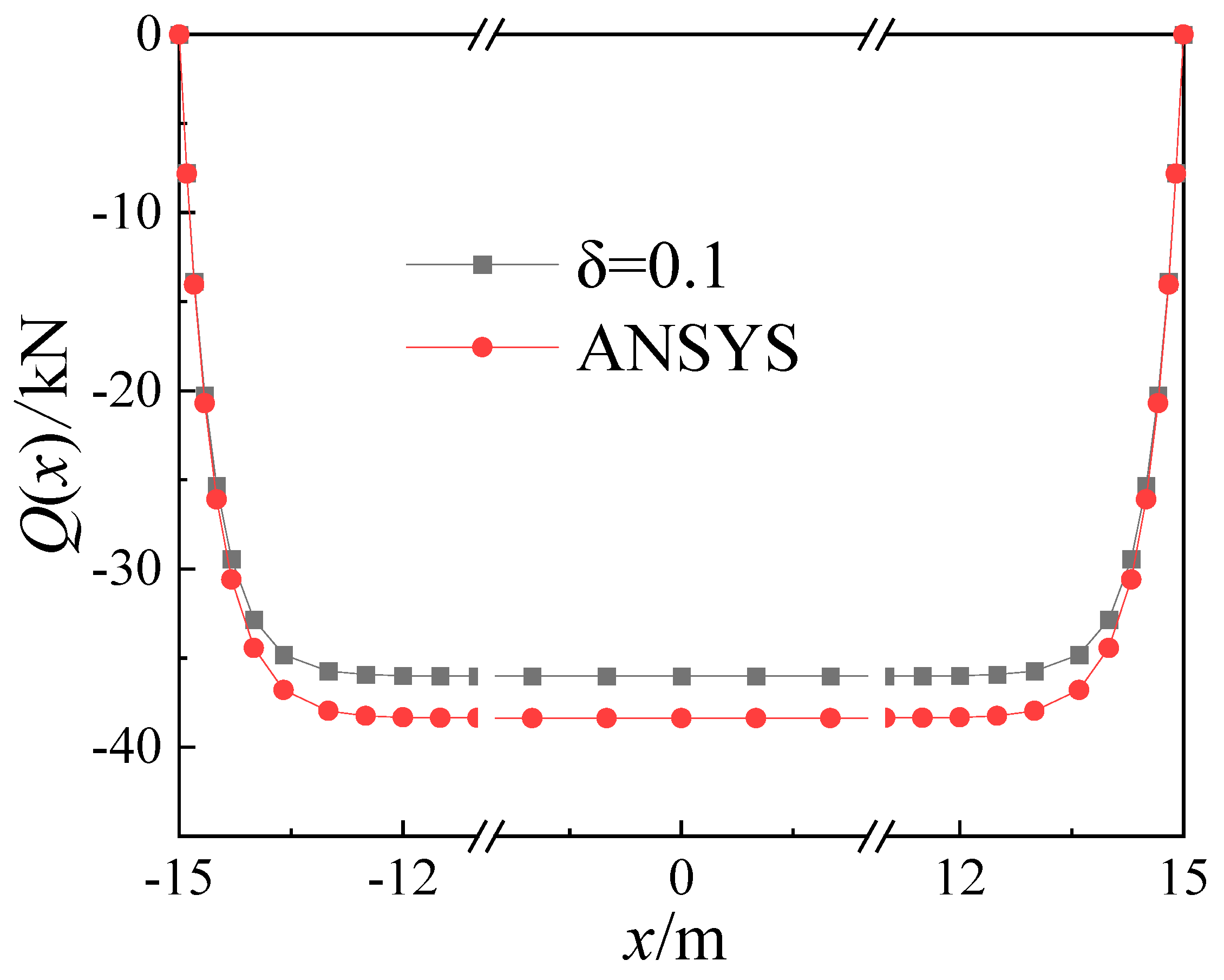
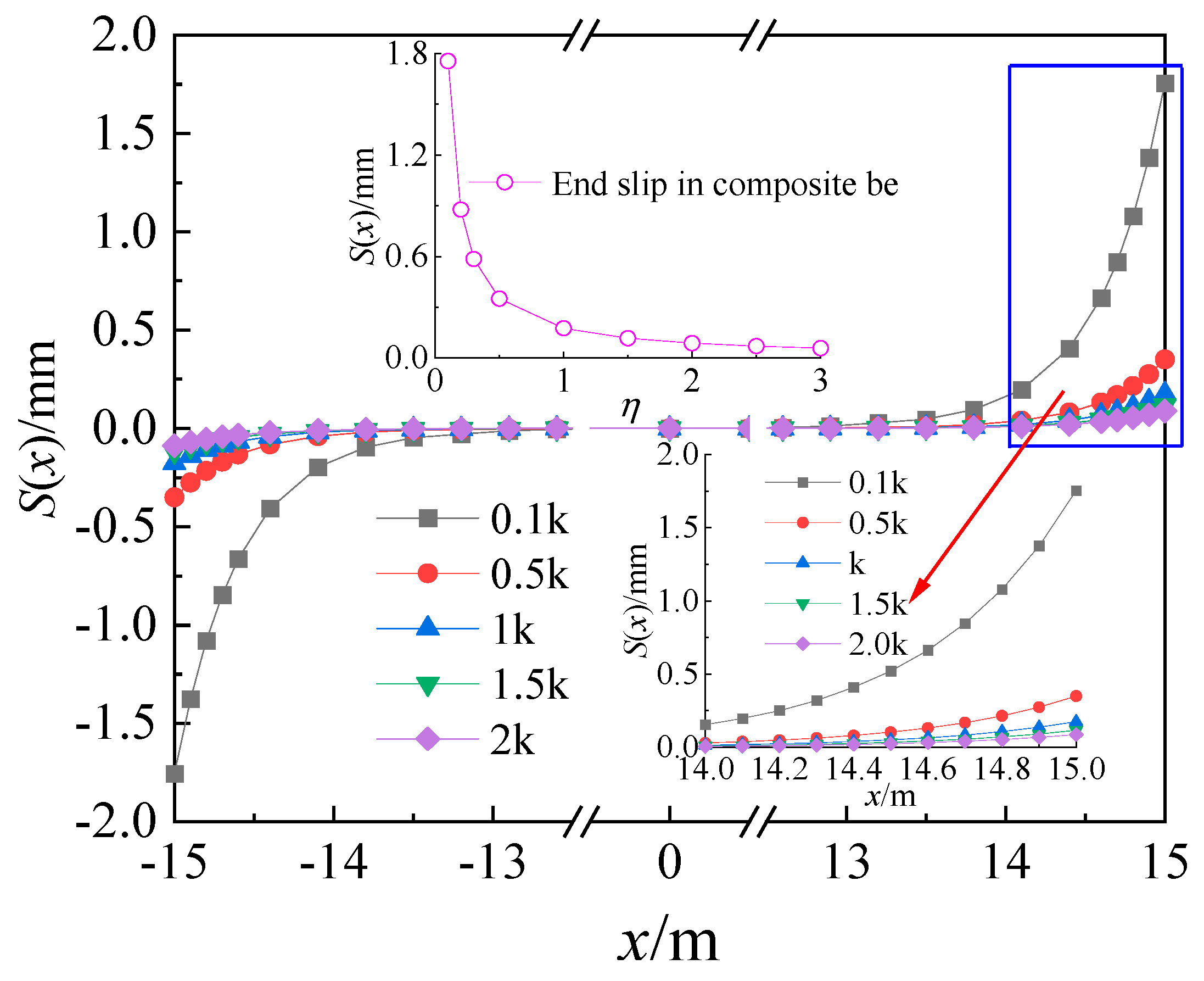
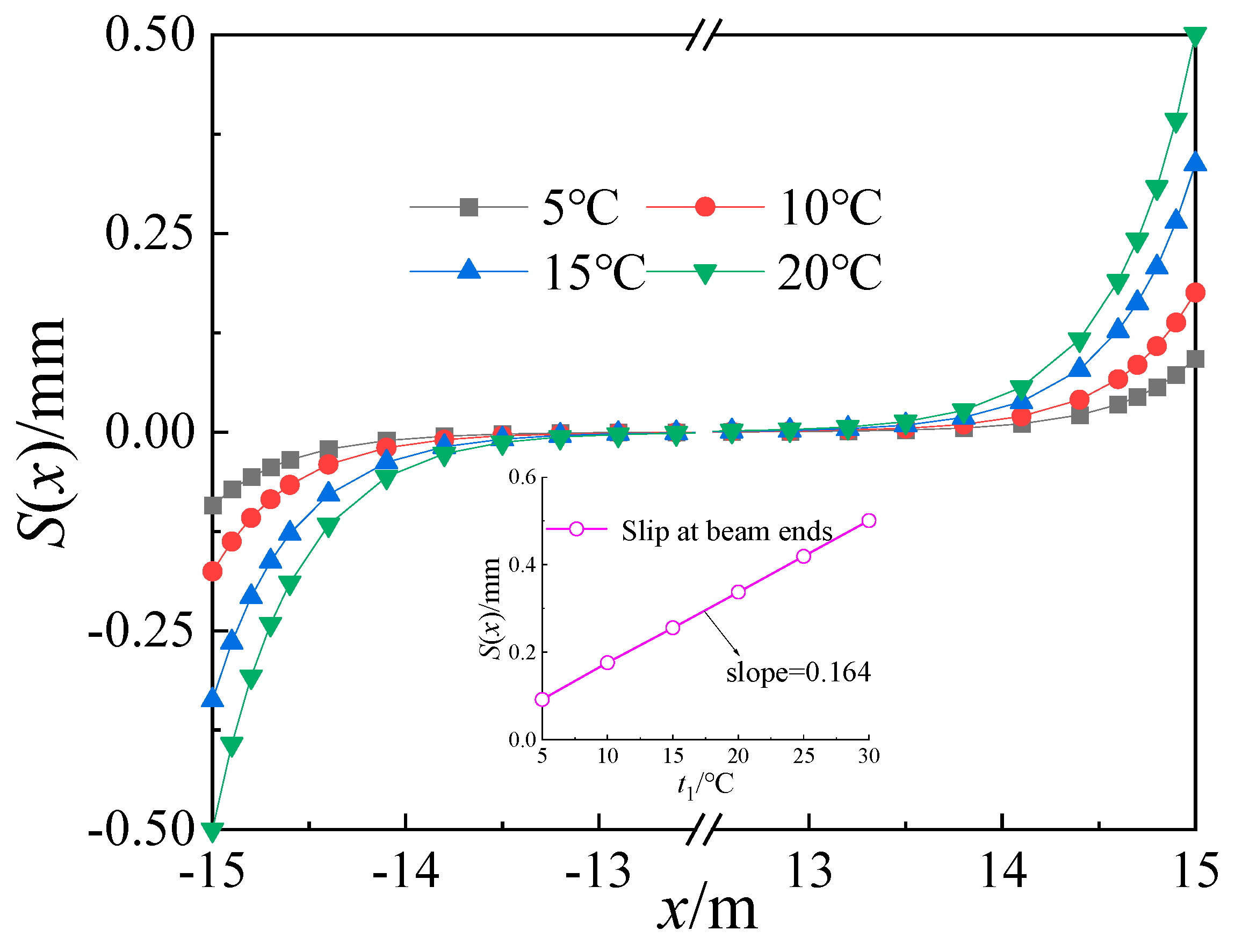

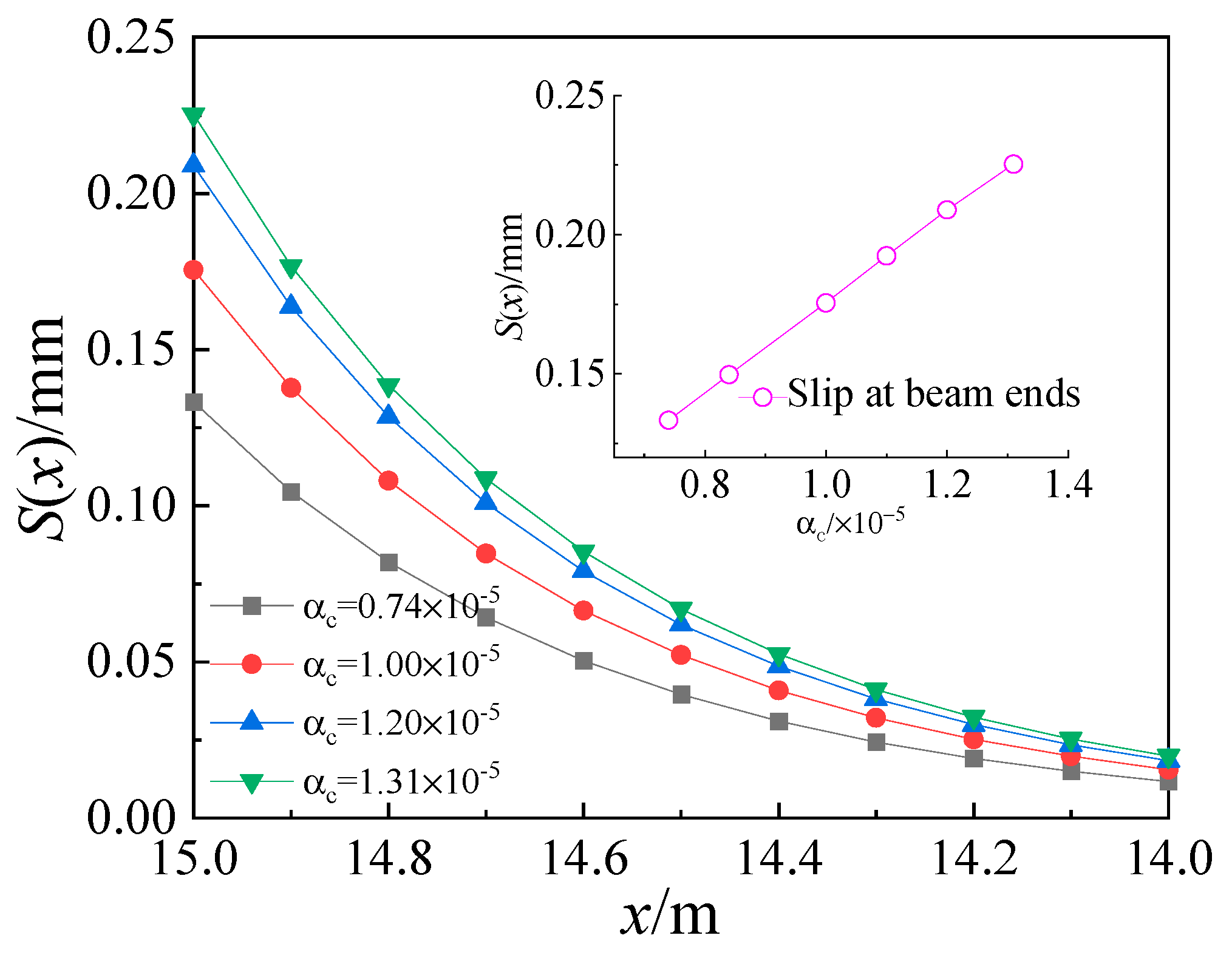
| δ | Mid-Span Shear Force (Q(x)/kN) | The Slipping of the Beam End S(x)/mm |
|---|---|---|
| 0 | −31.476 | 0.1570 |
| 0.05 | −33.319 | 0.1676 |
| 0.10 | −36.011 | 0.1755 |
| 0.15 | −57.058 | 0.2406 |
| 0.20 | −71.441 | 0.3075 |
| ANSYS | −37.843 | 0.1819 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Liu, S.; Wang, F. Temperature Effect of Composite Girders with Corrugated Steel Webs Considering Local Longitudinal Stiffness of Webs. Buildings 2024, 14, 1939. https://doi.org/10.3390/buildings14071939
Cai M, Liu S, Wang F. Temperature Effect of Composite Girders with Corrugated Steel Webs Considering Local Longitudinal Stiffness of Webs. Buildings. 2024; 14(7):1939. https://doi.org/10.3390/buildings14071939
Chicago/Turabian StyleCai, Minghao, Shizhong Liu, and Fangxu Wang. 2024. "Temperature Effect of Composite Girders with Corrugated Steel Webs Considering Local Longitudinal Stiffness of Webs" Buildings 14, no. 7: 1939. https://doi.org/10.3390/buildings14071939
APA StyleCai, M., Liu, S., & Wang, F. (2024). Temperature Effect of Composite Girders with Corrugated Steel Webs Considering Local Longitudinal Stiffness of Webs. Buildings, 14(7), 1939. https://doi.org/10.3390/buildings14071939





