Prestress Force and General Excitation Identification for Plate-like Concrete Bridges
Abstract
:1. Introduction
2. Method
2.1. Motion Equation of Plate-like Bridge
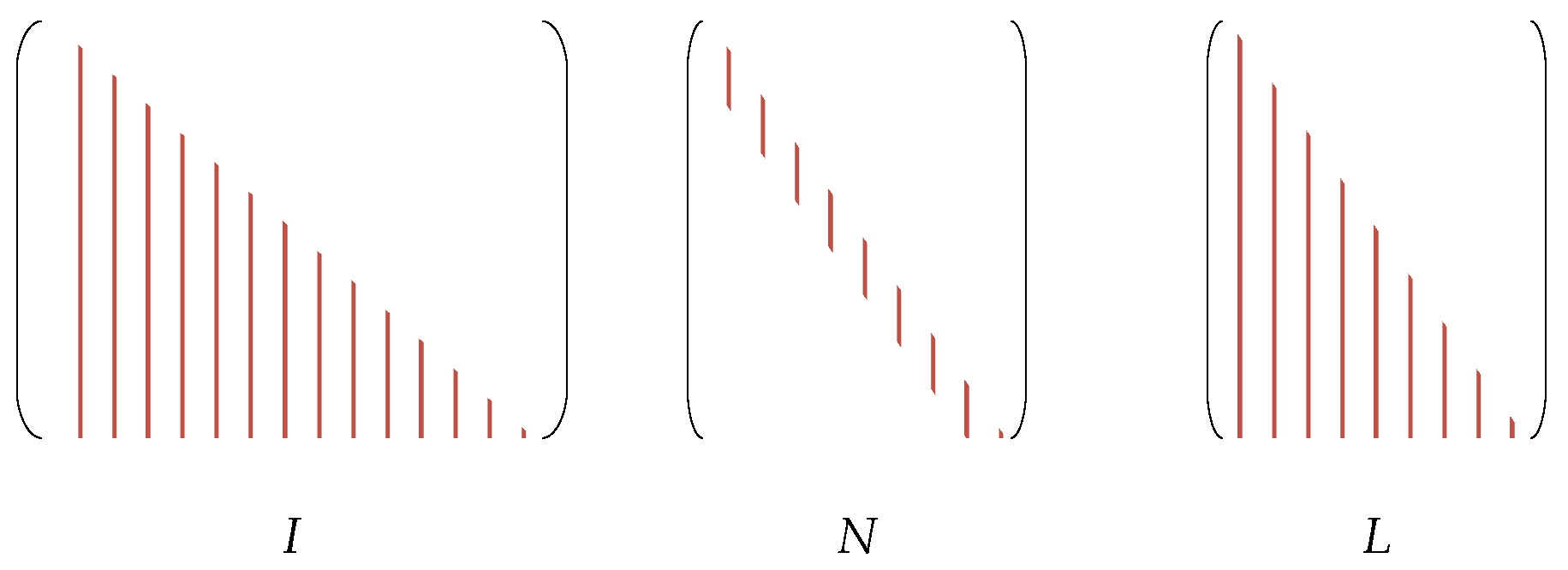
2.2. Excitation Force Identification Method
2.3. Prestress Force Identification Method
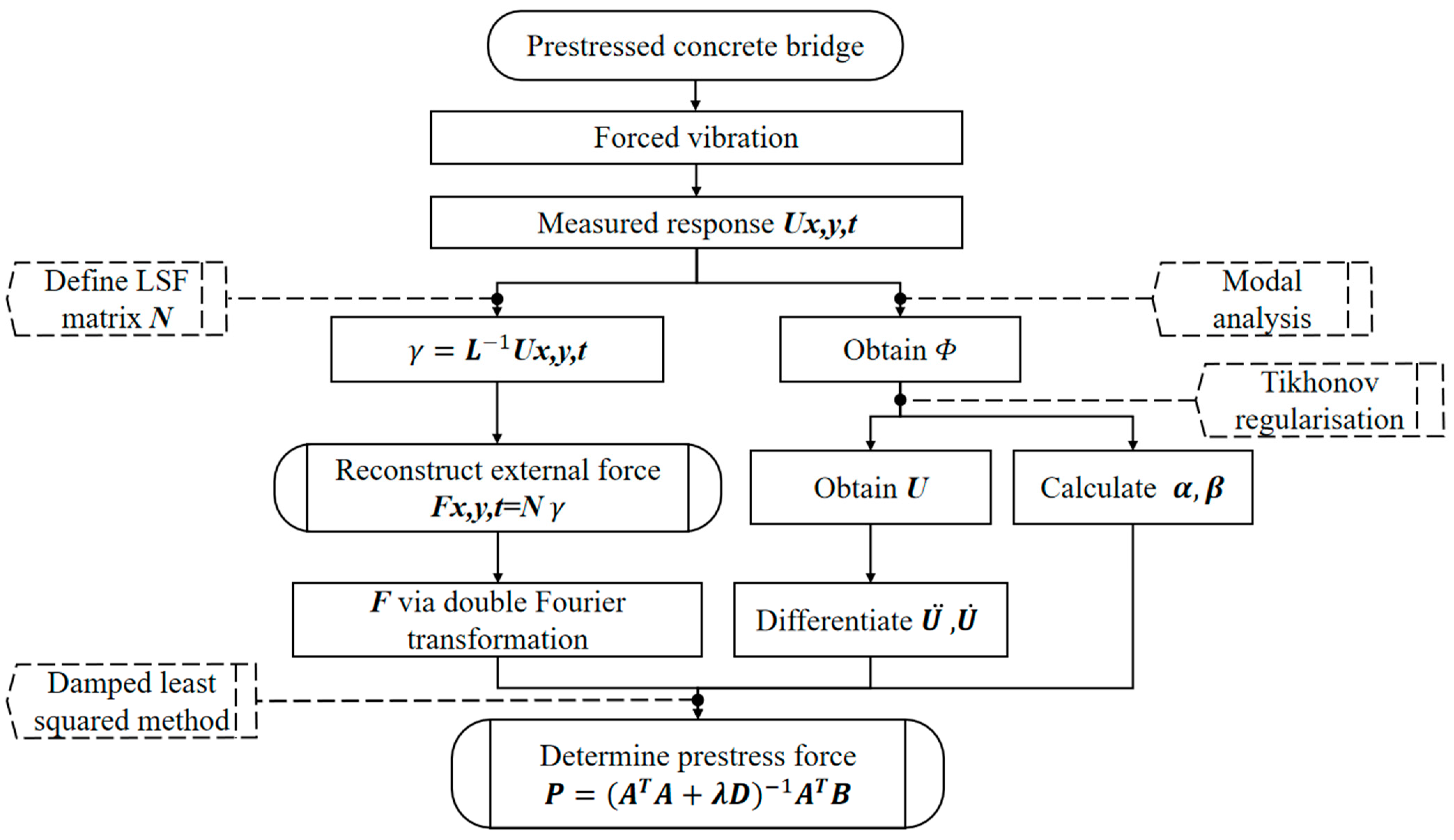
2.4. Two-Step Identification Procedure
- measure the bridge response induced by unknown excitation,
- define the LSF matrix according to the frequency spectrum of ,
- determine the coefficient via the LSF method,
- reconstruct the moving force .
- obtain the mode shape matrix by modal analysis,
- calculate the modal responses using the measured response and shape matrix via Tikhonov regularization,
- transform the determined moving force into image matrix via double Fourier transformation,
- establish the state-space formulation of prestress ,
- identify the prestress P via the least squared method.
3. Results and Discussion
3.1. Numerical Study on Prestressed Plate Subjected to a Moving Load
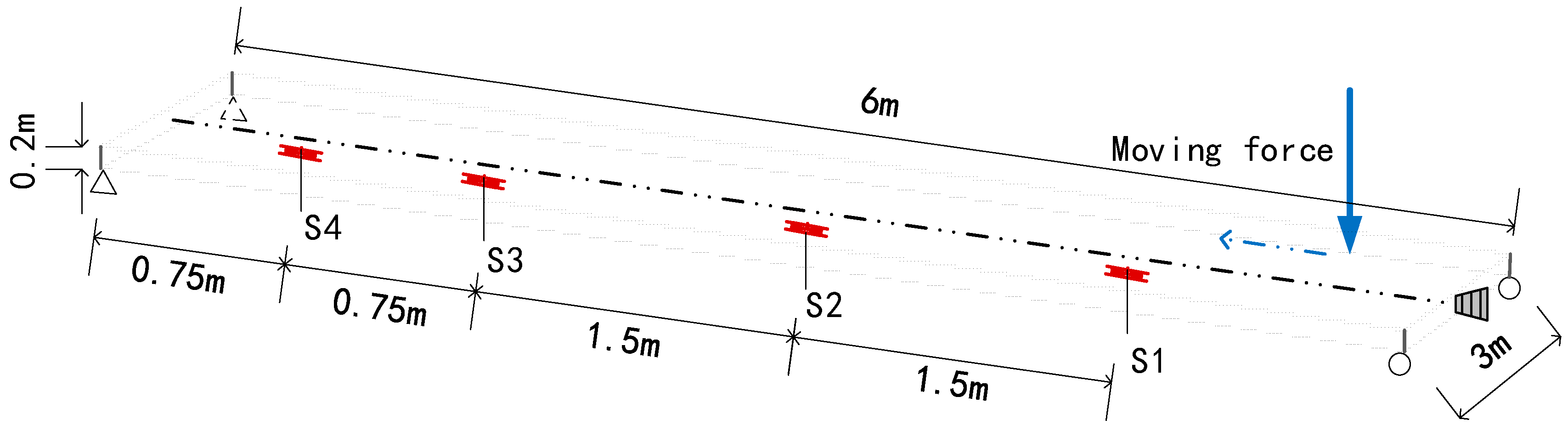
3.1.1. Model Design
3.1.2. Modal Analysis for Numerical Study
3.1.3. Case Setting for Numerical Study
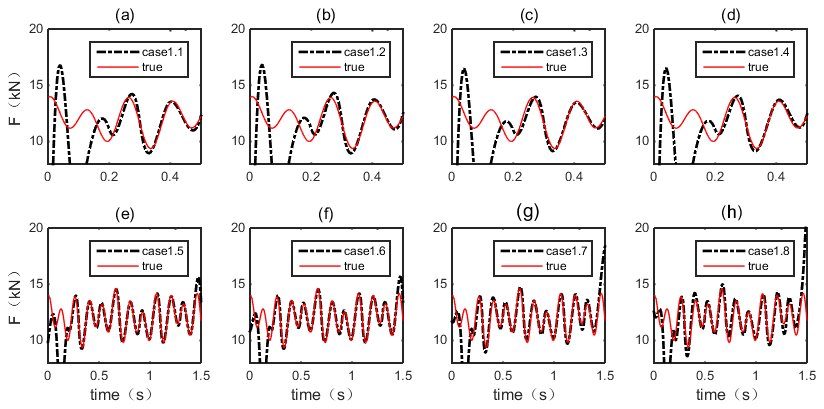
3.1.4. Moving Force Identification Results
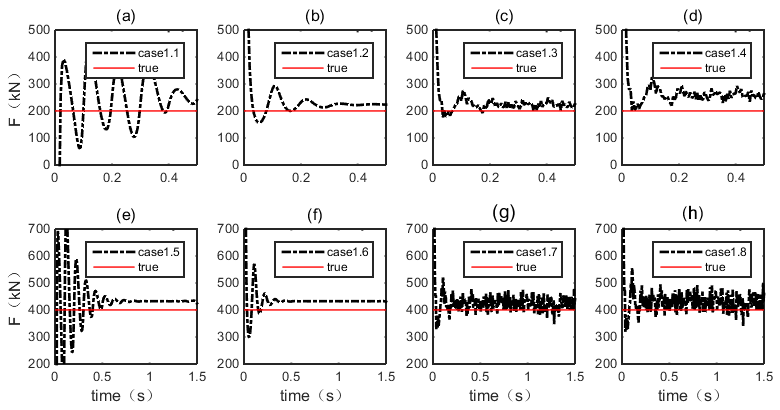
3.1.5. Prestress Force Identification Results
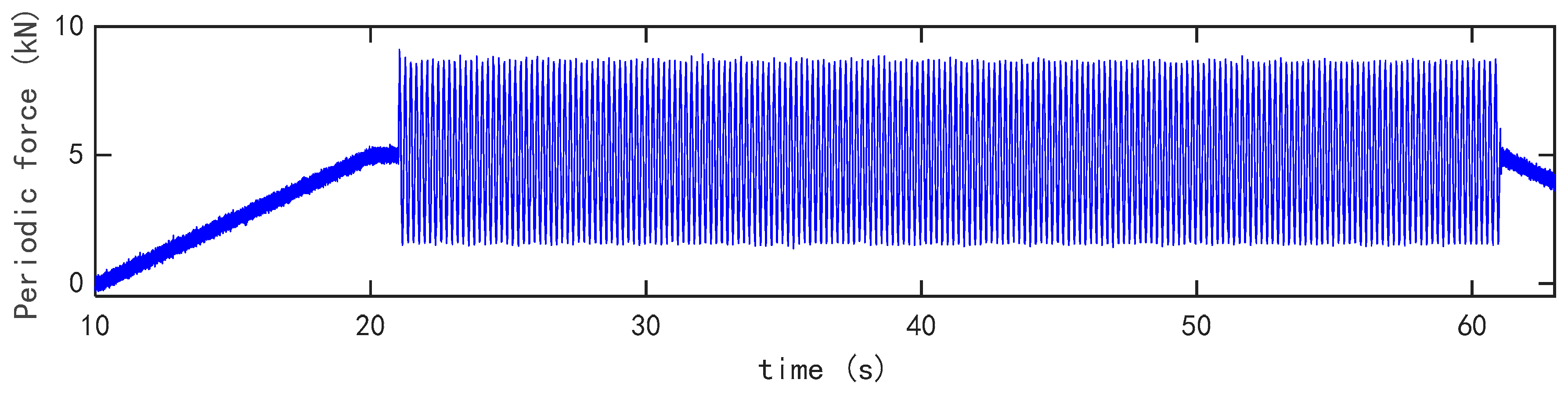
3.2. Experimental Study on Prestressed Box-Girder Subjected to a Periodic Load
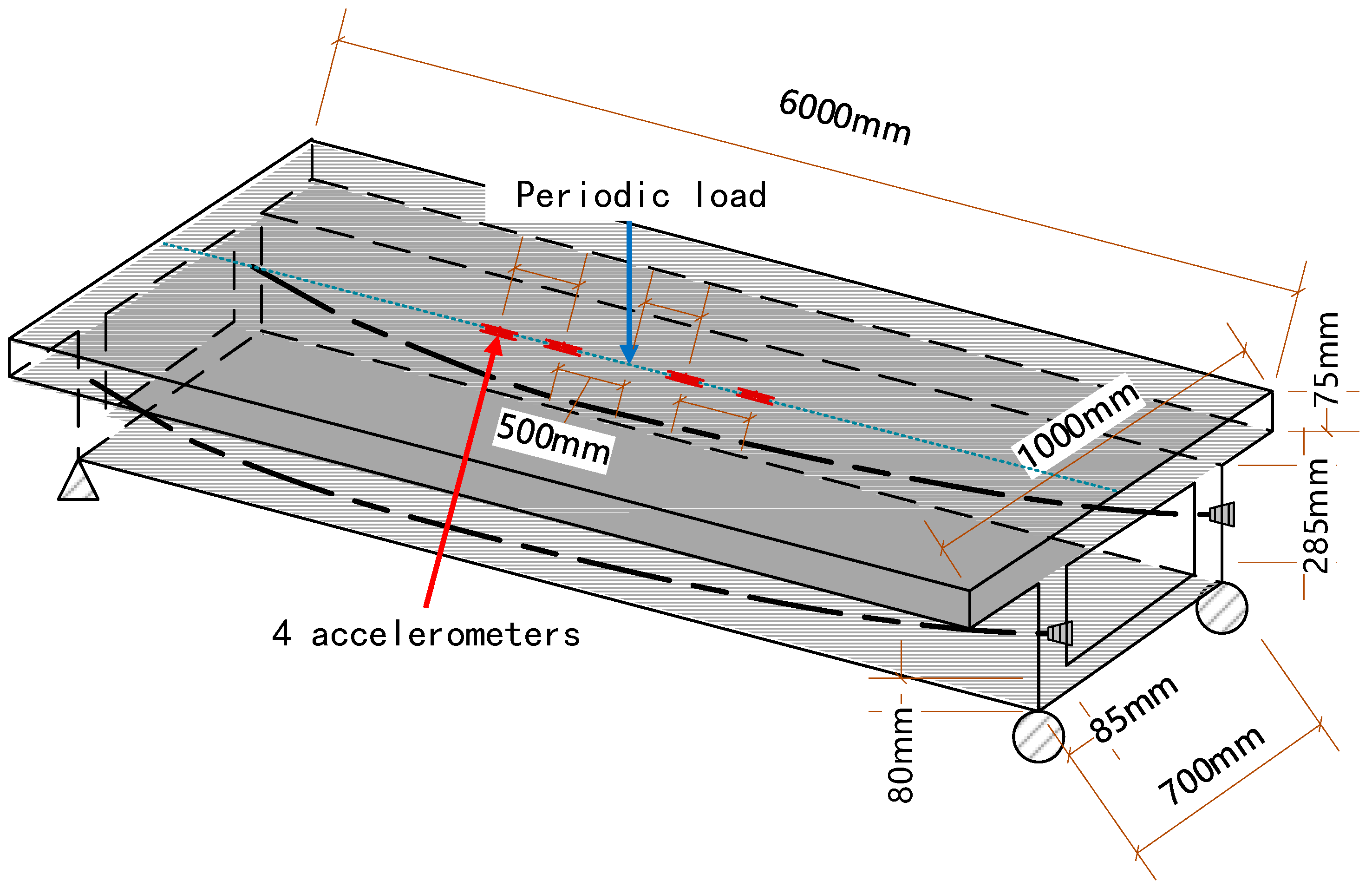
3.2.1. Model Design and Construction
3.2.2. Modal Analysis for Experimental Study
3.2.3. Case Setting for Experimental Study
3.2.4. Identified Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonopera, M.; Chang, K. Novel method for identifying residual prestress force in simply supported concrete girder-bridges. Adv. Struct. Eng. 2021, 24, 3238–3251. [Google Scholar] [CrossRef]
- Kraľovanec, J.; Moravčík, M.; Bujňáková, P.; Jošt, J. Indirect determination of residual prestressing force in post-tensioned concrete beam. Materials 2021, 14, 1338. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Hoang, N.D.; Nguyen, T.H.; Huynh, T.C. Analytical impedance model for piezoelectric-based smart Strand and its feasibility for prestress force prediction. Struct. Control Health Monit. 2022, 29, e3061. [Google Scholar] [CrossRef]
- Bagge, N.; Nilimaa, J.; Elfgren, L. In-situ methods to determine residual prestress forces in concrete bridges. Eng. Struct. 2017, 135, 41–52. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, J.; Zhou, J.; Liao, L.; Xiao, Y.; Tong, K.; Zhang, S. Prestress monitoring for prestress tendons based on the resonance-enhanced magnetoelastic method considering the construction process. Struct. Health Monit. 2024, 23, 958–970. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X. Thoughts on the development of bridge technology in China. Engineering 2019, 5, 1120–1130. [Google Scholar] [CrossRef]
- Noble, D.; Nogal, M.; O’Connor, A.; Pakrashi, V. The effect of prestress force magnitude and eccentricity on the natural bending frequencies of uncracked prestressed concrete beams. J. Sound Vib. 2016, 365, 22–44. [Google Scholar] [CrossRef]
- Ho, D.-D.; Kim, J.-T.; Stubbs, N.; Park, W.-S. Prestress-force estimation in PSC girder using modal parameters and system identification. Adv. Struct. Eng. 2012, 15, 997–1012. [Google Scholar] [CrossRef]
- Li, J.; Miki, T.; Yang, Q.; Mao, M. Experimental Study on Prestressing Force of Corroded Prestressed Concrete Steel Strands. J. Adv. Concr. Technol. 2022, 20, 550–563. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C.; Chen, C.-C.; Sung, Y.-C.; Tullini, N. Prestress force effect on fundamental frequency and deflection shape of PCI beams. Struct. Eng. Mech. Int. J. 2018, 67, 255–265. [Google Scholar]
- Kim, J.T.; Yun, C.B.; Ryu, Y.S.; Cho, H.M. Identification of prestress-loss in PSC beams using modal information. Struct. Eng. Mech. 2004, 17, 467–482. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Dezi, L. Discussion of “Prestress Force Effect on Vibration Frequency of Concrete Bridges” by M. Saiidi, B. Douglas, and S. Feng. J. Struct. Eng. 1996, 122, 458. [Google Scholar] [CrossRef]
- Abdel Jaber, H.; Glisic, B. Monitoring of prestressing forces in prestressed concrete structures—An overview. Struct. Control Health Monit. 2019, 26, e2374. [Google Scholar] [CrossRef]
- Aloisio, A.J.I. Aspects of vibration-based methods for the prestressing estimate in concrete beams with internal bonded or unbonded tendons. Infrastructures 2021, 6, 83. [Google Scholar] [CrossRef]
- Bonopera, M.; Liao, W.-C.; Perceka, W. Experimental-theoretical investigation of the short-term vibration response of uncracked prestressed concrete members under long-age conditions. Structures 2022, 35, 260–273. [Google Scholar] [CrossRef]
- Jaiswal, O.R. Effect of prestressing on the first flexural natural frequency of beams. Struct. Eng. Mech. 2008, 28, 515–524. [Google Scholar] [CrossRef]
- Wang, Y. Research on fundamental frequencies and dynamic characteristics of pre-stressed concrete beams based on experiment and numerical simulation. Mechanika 2017, 23, 552–561. [Google Scholar] [CrossRef]
- Xiang, Z.; Chan, T.H.T.; Thambiratnam, D.P.; Nguyen, A. Prestress and excitation force identification in a prestressed concrete box-girder bridge. Comput. Concr. 2017, 20, 617–625. [Google Scholar] [CrossRef]
- Lu, Z.; Law, S. Identification of prestress force from measured structural responses. Mech. Syst. Signal Process. 2006, 20, 2186–2199. [Google Scholar] [CrossRef]
- Law, S.; Lu, Z. Time domain responses of a prestressed beam and prestress identification. J. Sound Vib. 2005, 288, 1011–1025. [Google Scholar] [CrossRef]
- Xu, J.; Sun, Z. Prestress force identification for eccentrically prestressed concrete beam from beam vibration response. Struct. Longev. 2011, 5, 107–115. [Google Scholar]
- Wang, N.; Can, W.; Wei, S.; Litian, H. Prestress identification method based on actual influence line information of bridge. J. Vib. Eng. 2023, 36, 688–697. [Google Scholar]
- Zhong, H.; Yang, M. Prestress loss identification based on dynamic vehicle responses. J. Eng. Mech. 2018, 144, 04018088. [Google Scholar] [CrossRef]
- Cruz, A.; Vélez, W.; Thomson, P. A novel and robust technique for identifying prestress forces in prestressed concrete beams using generic finite elements and simulated annealing algorithms. J. Appl. Res. Technol. 2021, 19, 250–262. [Google Scholar] [CrossRef]
- Fu, C.C.; Wang, S. Computational Analysis and Design of Bridge Structures; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ji, W.; Deng, L.; Liu, S.Z.; Lin, P.Z. Study of vertical bending vibration behavior of continuous prestressed concrete box girders with corrugated steel webs. Adv. Struct. Eng. 2016, 19, 953–965. [Google Scholar] [CrossRef]
- Jacquelin, E.; Bennani, A.; Hamelin, P. Force reconstruction: Analysis and regularization of a deconvolution problem. J. Sound Vib. 2003, 265, 81–107. [Google Scholar] [CrossRef]
- Hu, W.H.; Tang, D.H.; Teng, J.; Said, S.; Rohrmann, R.G. Structural Health Monitoring of a Prestressed Concrete Bridge Based on Statistical Pattern Recognition of Continuous Dynamic Measurements over 14 years. Sensors 2018, 18, 4117. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lv, Z.; Liu, J. Assessment of prestress force in bridges using structural dynamic responses under moving vehicles. Math. Probl. Eng. 2013, 2013, 435939. [Google Scholar] [CrossRef]
- Dozio, L. On the use of the Trigonometric Ritz method for general vibration analysis of rectangular Kirchhoff plates. Thin-Walled Struct. 2011, 49, 129–144. [Google Scholar] [CrossRef]
- Wang, Z.C.; Ren, W.X. Dynamic Analysis of Prestressed Concrete Box-girders by Using the Beam Segment Finite Element Method. Int. J. Struct. Stab. Dyn. 2011, 11, 379–399. [Google Scholar] [CrossRef]
- Madhavi, N.C.; Sekar, M.; Paramasivam, V. Experimental investigations on the structural behaviour of prestressed concrete box girders using innovative construction technology. J. Struct. Eng. 2006, 33, 171–175. [Google Scholar]
- ACI 318-08; Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2018.
- Loo, Y.C.; Chowdhury, S. Introduction to prestressed concrete. In Reinforced and Prestressed Concrete; Cambridge University Press: Cambridge, UK, 2013; pp. 377–388. [Google Scholar] [CrossRef]
- AS5100; Bridge Design. Standards Australia: Sydney, Australia, 2004.
- Jia, J.; Zhang, L.; Ou, J.; Chen, X. Nondestructive Testing and Health Monitoring Techniques for Structural Effective Prestress. Struct. Control. Health Monit. 2023, 2023, 8940008. [Google Scholar] [CrossRef]
- Chen, Z.; Chan, T.H.T.; Nguyen, A. Moving force identification based on modified preconditioned conjugate gradient method. J. Sound Vib. 2018, 423, 100–117. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, L.; Chen, K.; Qin, X.; Zhang, Q. A time-domain method for load identification using moving weighted least square technique. Comput. Struct. 2020, 234, 106254. [Google Scholar] [CrossRef]
- Zhong, J.; Xiang, Z.; Li, C. Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function. Appl. Sci. 2022, 12, 691. [Google Scholar] [CrossRef]
- Law, S.S.; Wu, S.Q.; Shi, Z.Y. Moving load and prestress identification using wavelet-based method. J. Appl. Mech. -Trans. Asme 2008, 75, 021014. [Google Scholar] [CrossRef]
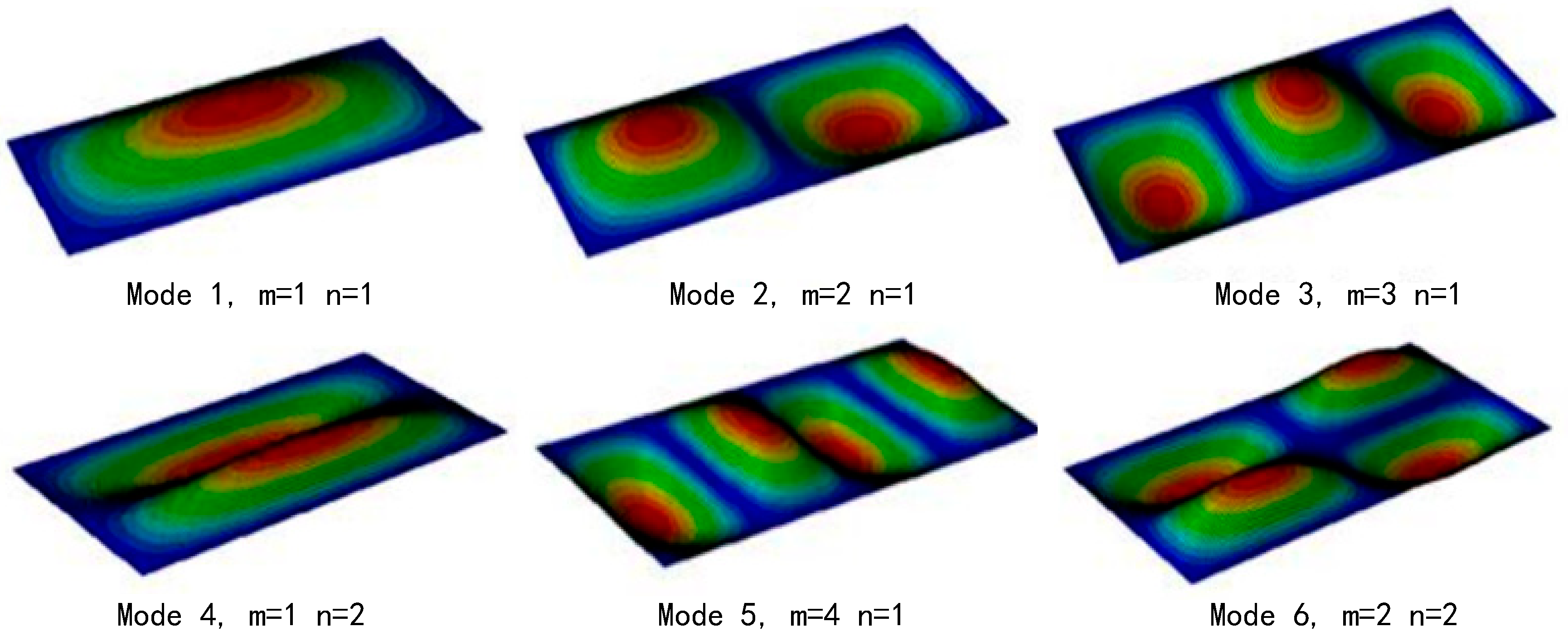


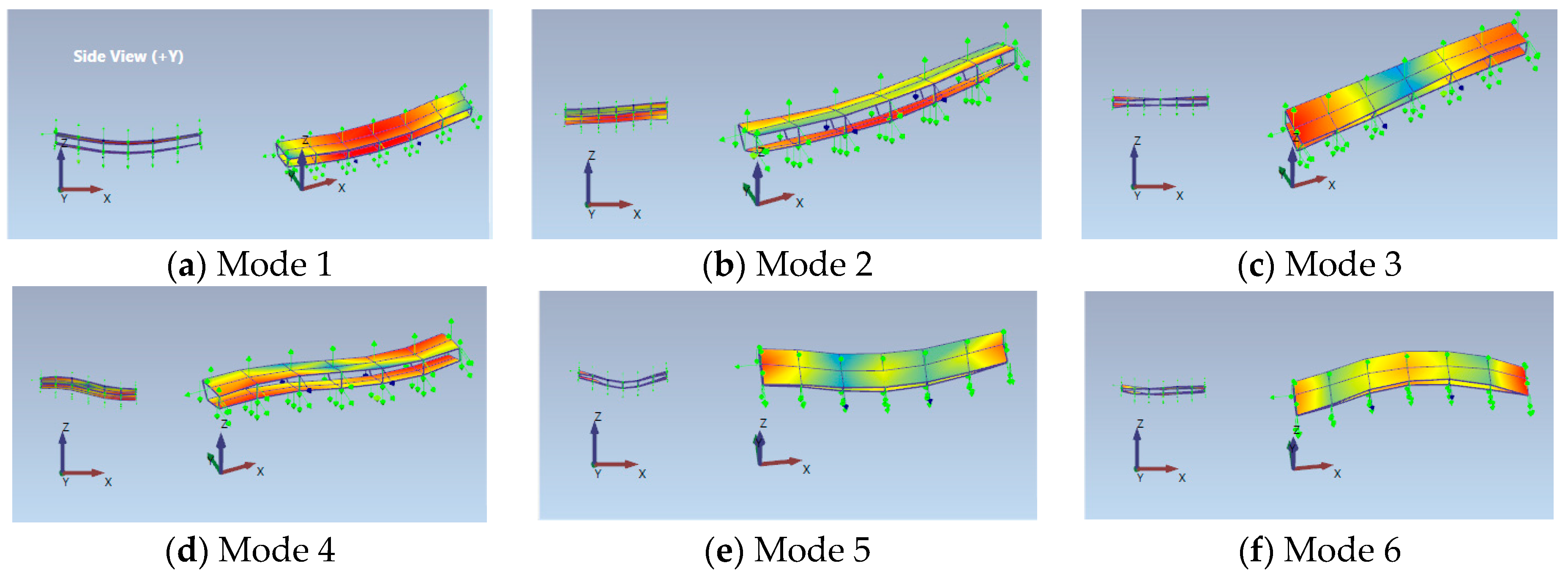


| Mode | Frequency (Hz) | |||
|---|---|---|---|---|
| m | n | No PF | PF = 850 kN | PF = 1200 kN |
| 1 | 1 | 45.45 | 45.32 | 45.24 |
| 2 | 1 | 72.72 | 72.56 | 71.83 |
| 3 | 1 | 118.17 | 117.92 | 116.95 |
| 1 | 2 | 154.53 | 154.60 | 154.32 |
| 4 | 1 | 181.81 | 181.32 | 180.85 |
| 2 | 2 | 181.90 | 181.70 | 181.56 |
| Case No. | PF (kN) | (%) | Vehicle Speed (m/s) | Sensors |
|---|---|---|---|---|
| 1.1 | 850 | 0 | 10 | S2 |
| 1.2 | 850 | 0 | 10 | S1, S2 |
| 1.3 | 850 | 5 | 10 | S1, S2, S3 |
| 1.4 | 850 | 10 | 10 | S1, S2, S3 |
| 1.5 | 1200 | 0 | 4 | S2 |
| 1.6 | 1200 | 0 | 4 | S2, S3 |
| 1.7 | 1200 | 5 | 4 | S1, S2, S3, S4 |
| 1.8 | 1200 | 10 | 4 | S1, S2, S3, S4 |
| Case No. | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 |
| RPE (%) | −16.41 | −15.12 | −16.91 | −17.30 | −5.64 | −5.08 | −5.93 | −7.33 |
| Case No. | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 |
| Regressed | - | 219.08 | 223.10 | 227.98 | 437.76 | 427.32 | 434.52 | 440.72 |
| True | 200 | 200 | 200 | 200 | 400 | 400 | 400 | 400 |
| error | - | 9.54% | 11.55% | 13.99% | 9.44% | 6.83% | 8.63% | 10.18% |
| Longitude (mm) | 0 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| Distance (mm) | 235 | 209 | 184 | 163 | 146 | 134 | 130 |
| Property | Section | ||
|---|---|---|---|
| Top Slab | Web | Bottom Slab | |
| Rebound hammer reading (average) | 42.14 | 44.5 | 47.29 |
| Cylinder compressive strength (without correction) (MPa) | 47.43 | 28.99 | 34.18 |
| Derived strength from Hammer test | 44.2 | 46.5 | 49.5 |
| E value from lab test (GPa) | 47.43 | Not available | Not available |
| Corrected Strength (MPa) | 47.43 | 49.89 | 53.12 |
| Corrected E Value (GPa) | 30.6 | 31.38 | 32.38 |
| Mode | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| PF = 0 kN | 23.451 | 43.980 | 57.893 | 61.857 | 91.521 | 95.874 |
| PF = 171.277 kN | 23.025 (−1.817%) | 43.785 (−0.443%) | 57.768 (−0.216%) | 61.745 (−0.181%) | 89.229 (−2.504%) | 94.720 (−1.204%) |
| PF = 284.009 kN | 22.973 (−2.038%) | 43.502 (−1.087%) | 57.204 (−1.190%) | 61.432 (−0.687%) | 84.864 (−7.274%) | 94.014 (−1.940%) |
| PF = 378.293 kN | 22.902 (−2.341%) | 43.536 (−1.010%) | 57.235 (−1.137%) | 61.414 (−0.716%) | 83.954 (−8.268%) | 91.718 (−4.335%) |
| Case No. | 2.1 | 2.2 | 2.3 | 2.4 |
| PF (kN) | 171.277 | 284.009 | 284.009 | 378.293 |
| Measuring time (s) | 3 (31.5~34.5 s) | 3 (31.5~34.5 s) | 10 (61~71 s) | 10 (31.5~41.5 s) |
| Case No. | 2.1 | 2.2 | 2.3 | 2.4 |
| RPE (%) | 7.09 | 9.12 | 9.64 | 10.43 |
| Case No. | 2.1 | 2.2 | 2.3 | 2.4 |
| Regressed results | 153.16 | 253.39 | 254.45 | 335.44 |
| True | 171.277 | 284.009 | 284.009 | 378.293 |
| RPE (%) | −10.57 | −10.81 | −10.41 | −11.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xiang, Z.; Wang, Y.; Shao, X.; Lu, J. Prestress Force and General Excitation Identification for Plate-like Concrete Bridges. Buildings 2024, 14, 2032. https://doi.org/10.3390/buildings14072032
Wang W, Xiang Z, Wang Y, Shao X, Lu J. Prestress Force and General Excitation Identification for Plate-like Concrete Bridges. Buildings. 2024; 14(7):2032. https://doi.org/10.3390/buildings14072032
Chicago/Turabian StyleWang, Wensen, Ziru Xiang, Yi Wang, Xuejun Shao, and Jieyu Lu. 2024. "Prestress Force and General Excitation Identification for Plate-like Concrete Bridges" Buildings 14, no. 7: 2032. https://doi.org/10.3390/buildings14072032
APA StyleWang, W., Xiang, Z., Wang, Y., Shao, X., & Lu, J. (2024). Prestress Force and General Excitation Identification for Plate-like Concrete Bridges. Buildings, 14(7), 2032. https://doi.org/10.3390/buildings14072032







