Theoretical Analysis of the Plastic Property for Equal Angle Sections Subjected to Axial Force and Biaxial Bending
Abstract
1. Introduction
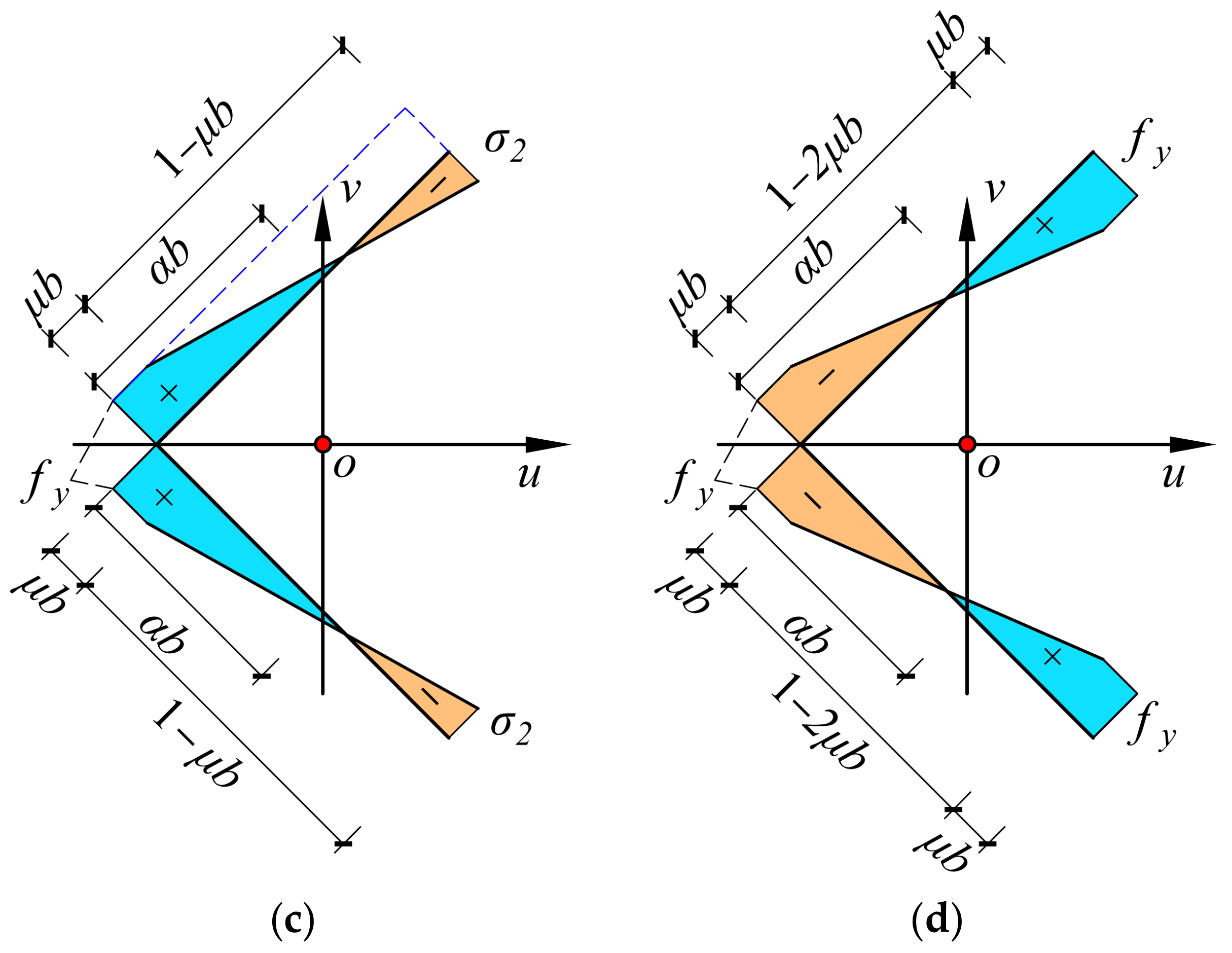
2. Full Plastic Analysis of the Angle Section
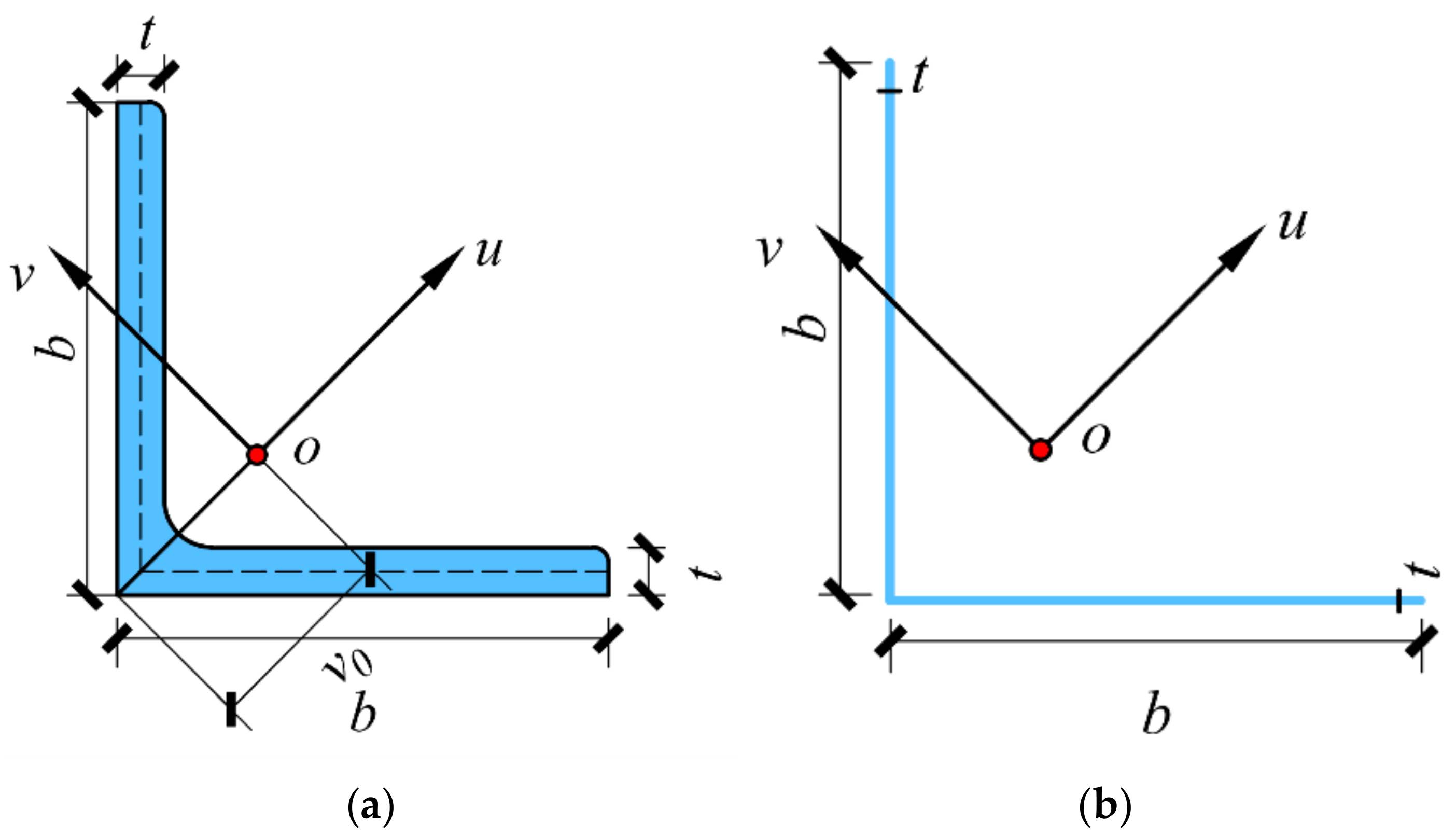
2.1. Cross-Section Simplification
2.2. Full Plastic Analysis
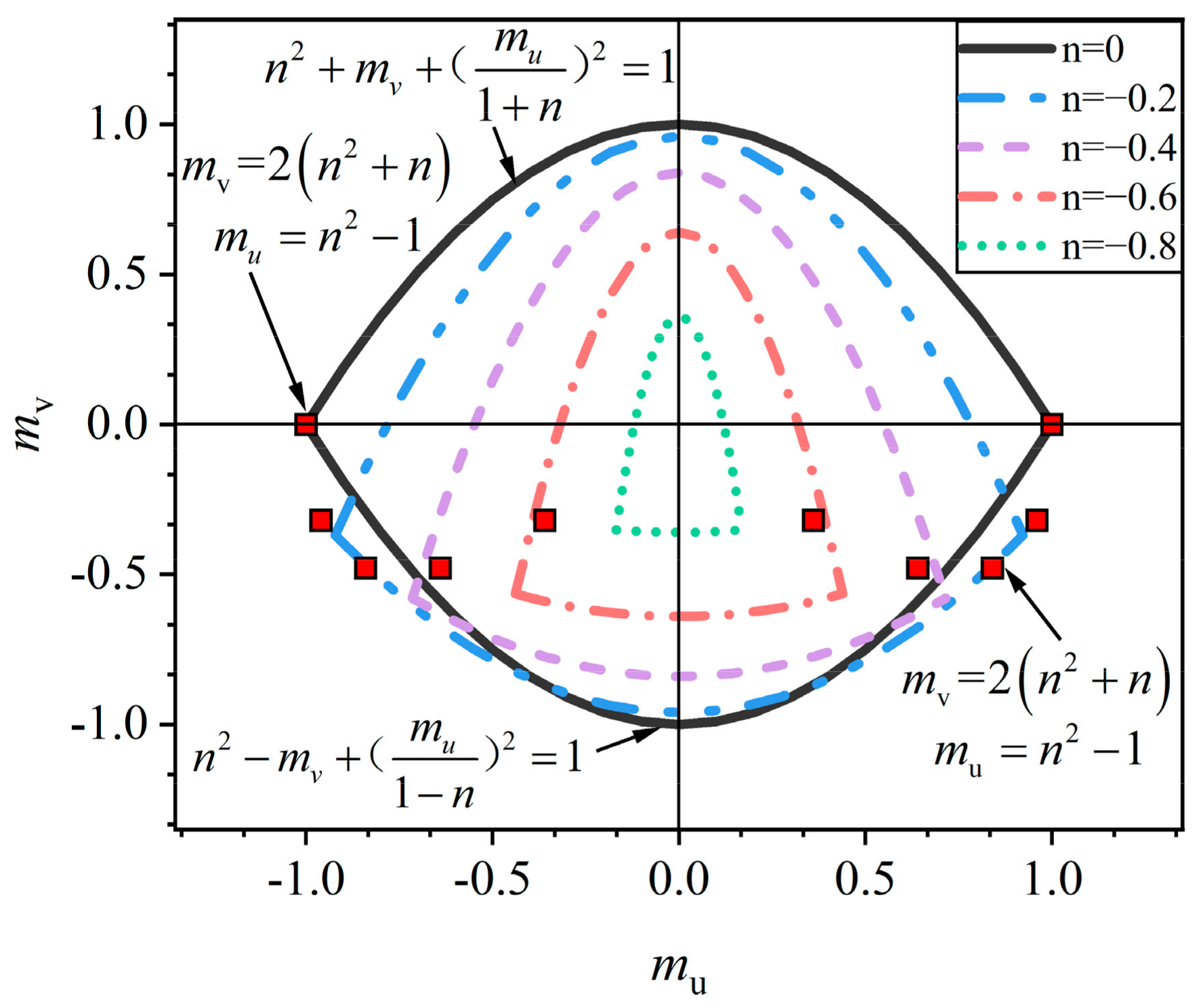
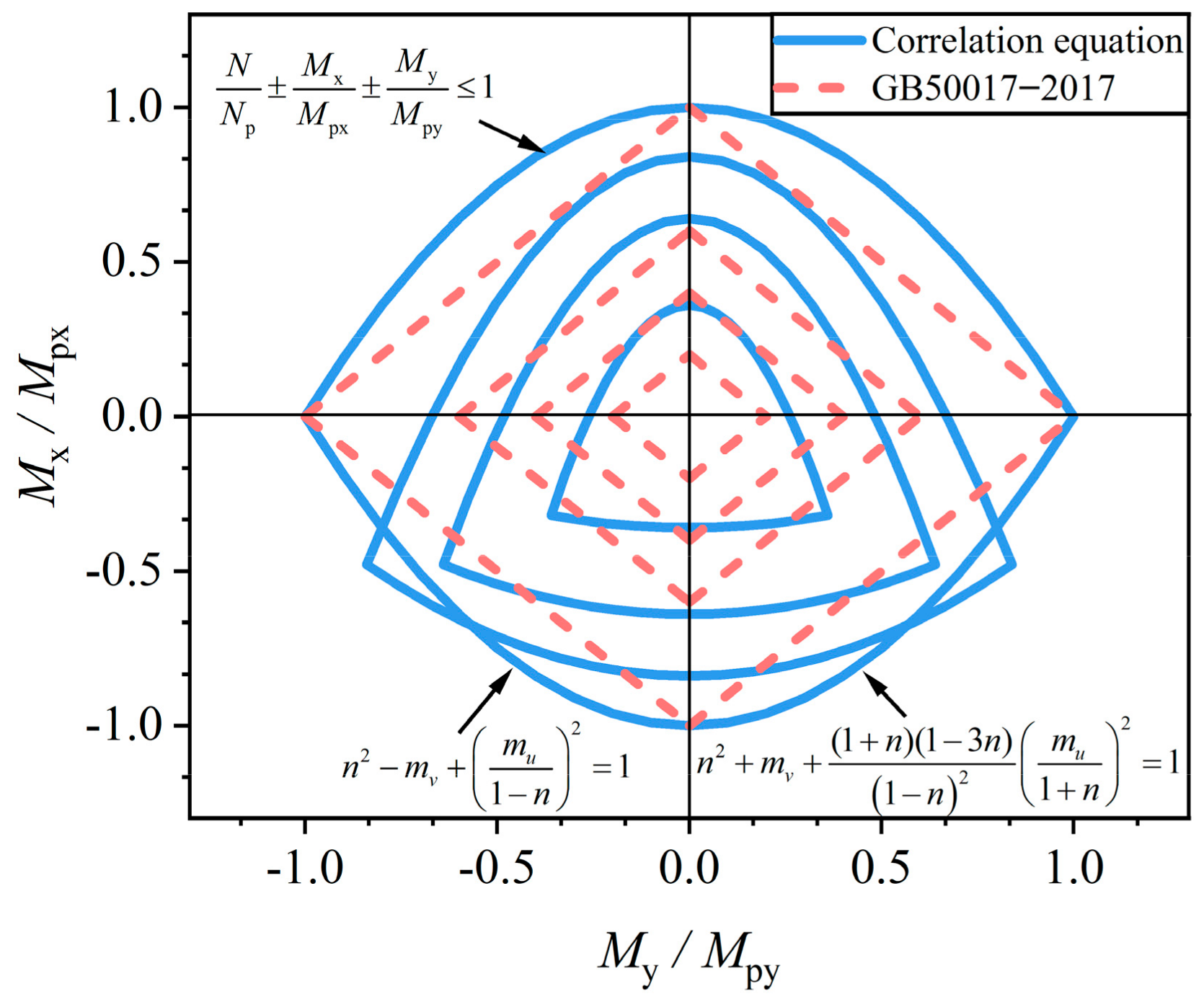
2.3. Full Plastic Correlation Equations
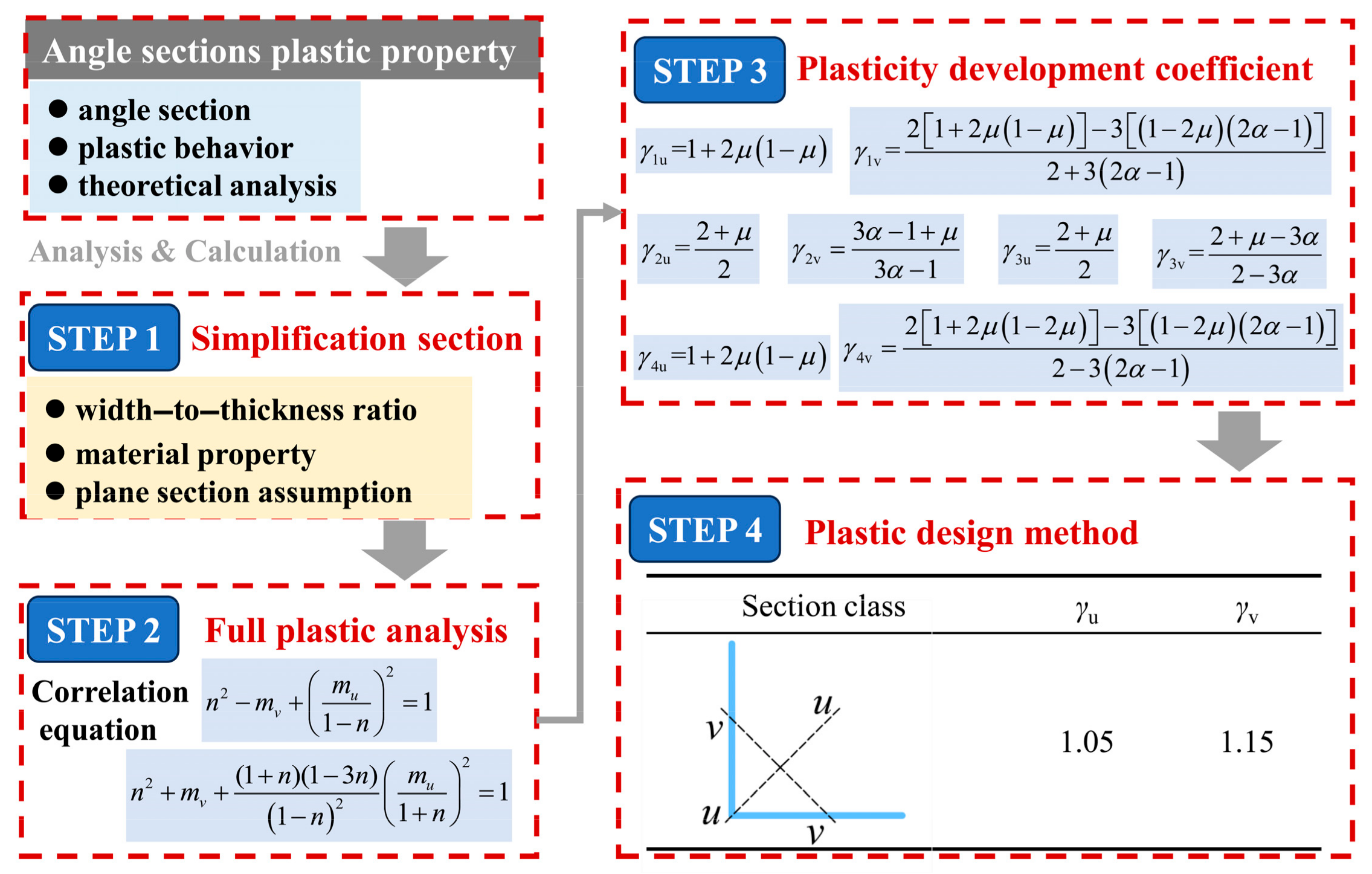
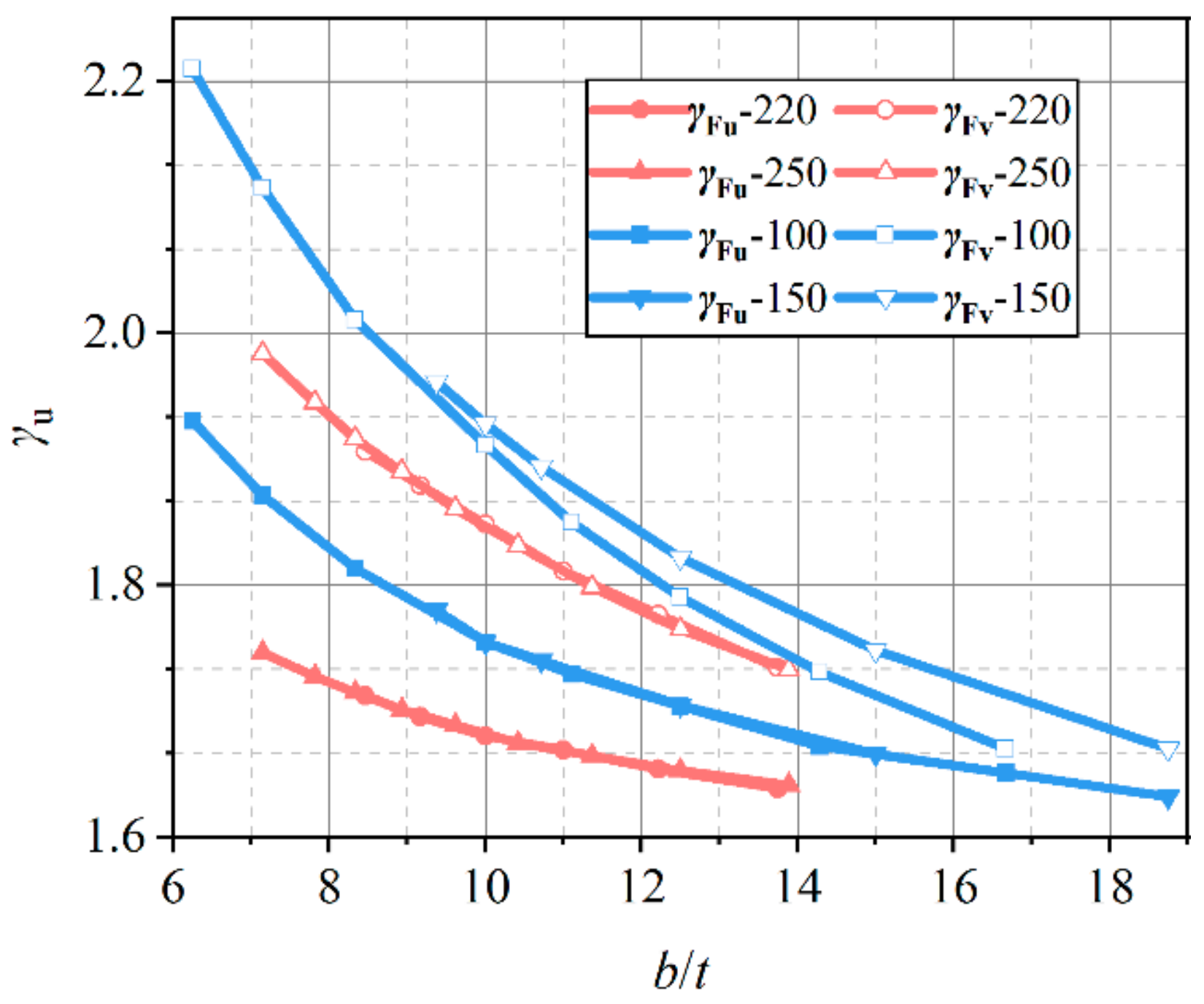
3. Plasticity Development Coefficient
3.1. Section Shape Coefficient
3.2. Plastic Development Coefficient
4. Angle Section Classification Discussion
5. Conclusions
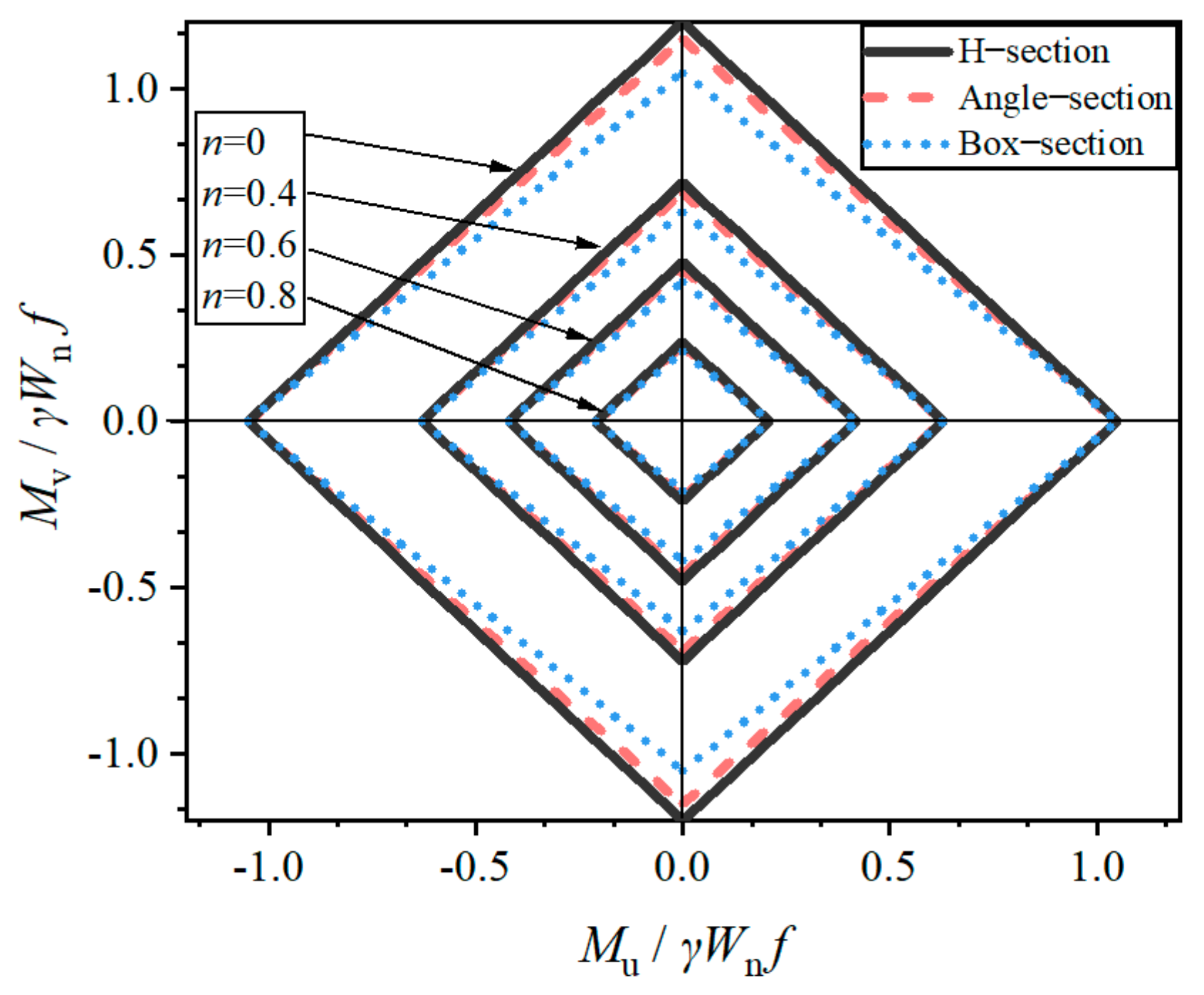
- The axial force and moment full plasticity equation results are nonlinear, whereas the specification design formula follows a linear relationship. Furthermore, the specification design formula is relatively conservative compared with the full plasticity equation. This conservative arises from the fact that the standard employs a linear simplified formula, utilizing the section plastic development coefficient to restrict the section plastic development depth.
- The section shape coefficients are inversely associated with their width-to-thickness ratio; an escalation in this ratio results in a gradual reduction in the section shape coefficients. This implies that angle sections possessing higher width-to-thickness ratios display diminished plasticity. Additionally, the section shape coefficients for large-size angle sections are smaller than those of regular-size sections, signifying that regular-size angle sections exhibit pronounced plasticity.
- The angle sections’ plastic development coefficients are related to plastic development depth. Higher values of development depths are associated with larger values of γu and γv. The plastic development capability of angle sections is also between that of H-sections and box-sections, and they exhibit better plastic development capacity along the weak axis than the strong axis.
- For regular-size and large-size angle sections, the plastic development coefficients for plastic design can be set to the same values. This choice aligns with the steel structure design code GB50017, stipulating that the plastic development depth should be taken as 1/8 of the section height, with strong and weak axes taken as γu = 1.05 and γv = 1.15, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hussain, A.; Liu, Y.P.; Chan, S.L. Finite Element Modeling and Design of Single Angle Member Under Bi-axial Bending. Structures 2018, 16, 373–389. [Google Scholar] [CrossRef]
- Charalampakis, A.; Koumousis, V. Ultimate strength analysis of composite sections under biaxial bending and axial load. Adv. Eng. Softw. 2008, 39, 923–936. [Google Scholar] [CrossRef]
- Vayas, I.; Charalampakis, A.; Koumousis, V. Inelastic resistance of angle sections subjected to biaxial bending and normal forces. Steel Constr. Des. Res. 2009, 2, 138–146. [Google Scholar] [CrossRef]
- Charalampakis, A.E. Full plastic capacity of equal angle sections under biaxial bending and normal force. Eng. Struct. 2011, 33, 2085–2090. [Google Scholar] [CrossRef]
- BS EN 1993-1-1; Eurocode3: Design of Steel Structures: Part 1-1: General Rules and Rules for Buildings. British Standards Institution (BSI): London, Britain, 2005.
- ANSI/AISC 360-16; Specification for Structural steel Buildings, ANSI/AISC 360-10. American Institute of Steel Construction (AISC): Chicago, IL, USA, 2016.
- GB50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Jiang, W.-Q.; Liu, Y.-P.; Chan, S.-L.; Wang, Z.-Q. Direct analysis of an ultrahigh-voltage lattice transmission tower considering joint effects. J. Struct. Eng. 2017, 143, 4017009. [Google Scholar] [CrossRef]
- Cho, S.; Chan, S.L. Second-order analysis and design of angle trusses, Part II: Plastic analysis and design. Eng. Struct. 2008, 30, 626–631. [Google Scholar] [CrossRef]
- Li, B.; Cao, P.; Zhang, D.; Guo, Y. Experimental research on behavior of Q420 dual-angle steel with cruciform section under dynamic compression. J. Vibroeng. 2017, 19, 2031–2042. [Google Scholar] [CrossRef]
- Qu, S.; Zhang, B.; Guo, Y.; Sun, Q.; Wang, Y. Ultimate strength of pinned-end dual-angle cross combined section columns under axial compression. Thin Wall Struct. 2020, 157, 107062. [Google Scholar] [CrossRef]
- Ban, H.Y.; Shi, G.; Shi, Y.J.; Wang, Y.Q. Residual Stress Tests of High-Strength Steel Equal Angles. J. Struct. Eng. 2012, 138, 1446–1454. [Google Scholar] [CrossRef]
- Shi, G.; Zhou, W.J.; Bai, Y.; Liu, Z. Local buckling of steel equal angle members with normal and high strengths. Int. J. Steel Struct. 2014, 14, 447–455. [Google Scholar] [CrossRef]
- Ban, H.Y.; Shi, G.; Shi, Y.J.; Wang, Y.Q. Column Buckling Tests of 420 Mpa High Strength Steel Single Equal Angles. Int. J. Struct. Stab. Dyn. 2013, 13, 1250069. [Google Scholar] [CrossRef]
- Cao, X.L.; Xu, Y.; Hao, J.P. Experimental analysis on ultimate bearing capacity of Q460 high-strength angle members under axial compression. J. Civ. Environ. Eng. 2018, 40, 146–152. [Google Scholar]
- Bezas, M.-Z.; Demonceau, J.-F.; Vayas, I.; Jaspart, J.-P. Experimental and numerical investigations on large angle high strength steel columns. Thin Wall Struct. 2021, 159, 107287. [Google Scholar] [CrossRef]
- Wang, F.; Liang, Y.; Zhao, O.; Young, B. Pin-ended press-braked S960 ultra-high strength steel angle section columns: Testing, numerical modelling and design. Eng. Struct. 2021, 228, 111418. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.; Zhao, O. Flexural-torsional buckling behaviour and resistances of fixed-ended press-braked S690 high strength steel angle section columns. Eng. Struct. 2020, 223, 111180. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.; Liang, Y.; Zhao, O. Press-braked S690 high strength steel equal-leg angle and plain channel section stub columns: Testing, numerical simulation and design. Eng. Struct. 2019, 201, 109764. [Google Scholar] [CrossRef]
- Du, R.Z. Applications of Q420 large section angle steel in UHV power transmission line. Power Syst. Clean Energy 2011, 27, 30–34. [Google Scholar]
- Zhang, Z.F.; Li, Q.H.; Xing, H.J.; Tang, C.J.; Yuan, X. Application Study of 300 mm Large Size Angle Steel in +/− 1100 kV Ultra-high Voltage Tower Transmission Tower. Aer. Adv. Eng. Res. 2016, 30, 1304–1311. [Google Scholar]
- Cao, K.; Guo, Y.J.; Zeng, D.W. Buckling behavior of large-section and 420 MPa high-strength angle steel columns. J. Constr. Steel Res. 2015, 111, 11–20. [Google Scholar] [CrossRef]
- Chen, H.; Zeng, D.; Cao, K.; Guo, Y. Buckling behavior and design of large-section angle steel columns under axial compression. J. Build Eng. 2023, 78, 107578. [Google Scholar] [CrossRef]
- Chen, H.; Chen, H.; Cao, K.; Guo, Y. Study on Axial Compression Stability of Q345 Large-Section Angle Steel Columns. Buildings 2023, 13, 1030. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Y.J.; Chen, H.Y.; Cao, K. Stability of Large-Size and High-Strength Steel Angle Sections Affected by Support Constraint. Int. J. Steel Struct. 2021, 21, 85–99. [Google Scholar] [CrossRef]
- Sun, Y.; Song, D.; Sun, S.; Guo, Y. Behavior of large-size and high-strength steel angle subjected to eccentric load. Structures 2023, 57, 105161. [Google Scholar] [CrossRef]
- de Menezes, A.A.; Vellasco, P.C.d.S.; de Lima, L.R.; da Silva, A.T. Experimental and numerical investigation of austenitic stainless steel hot-rolled angles under compression. J. Constr. Steel Res. 2019, 152, 42–56. [Google Scholar] [CrossRef]
- Liang, Y.; Jeyapragasam, V.V.K.; Zhang, L.; Zhao, O. Flexural-torsional buckling behaviour of fixed-ended hot-rolled austenitic stainless steel equal-leg angle section columns. J. Constr. Steel Res. 2019, 154, 43–54. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Z.; Liang, Y.; Zhao, O. Experimental and numerical investigations of hot-rolled austenitic stainless steel equal-leg angle sections. Thin Wall Struct. 2019, 144, 106225. [Google Scholar] [CrossRef]
- Sarquis, F.R.; de Lima, L.R.; Vellasco, P.C.G.d.S.; Rodrigues, M. Experimental and numerical investigation of hot-rolled stainless steel equal leg angles under compression. Thin Wall Struct. 2020, 151, 106742. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.; Zhao, O. Experimental and numerical investigations of pin-ended hot-rolled stainless steel angle section columns failing by flexural buckling. Thin Wall Struct. 2020, 156, 106977. [Google Scholar] [CrossRef]
- Dobrić, J.; Filipović, A.; Baddoo, N.; Buđevac, D.; Rossi, B. Design criteria for pin-ended hot-rolled and laser-welded stainless steel equal-leg angle columns. Thin Wall Struct. 2021, 167, 108175. [Google Scholar] [CrossRef]
- Filipović, A.; Dobrić, J.; Baddoo, N.; Može, P. Experimental response of hot-rolled stainless steel angle columns. Thin Wall Struct. 2021, 163, 107659. [Google Scholar] [CrossRef]
- Behzadi-Sofiani, B.; Gardner, L.; Wadee, M.A. Testing, numerical analysis and design of stainless steel equal-leg angle section beams. Structures 2022, 37, 977–1001. [Google Scholar] [CrossRef]
- Dobrić, J.; Filipović, A.; Baddoo, N.; Marković, Z.; Buđevac, D. Design procedures for cold-formed stainless steel equal-leg angle columns. Thin Wall Struct. 2021, 159, 107210. [Google Scholar] [CrossRef]
- Dobrić, J.; Filipović, A.; Marković, Z.; Baddoo, N. Structural response to axial testing of cold-formed stainless steel angle columns. Thin Wall Struct. 2020, 156, 106986. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, K.H.; Zhao, O. Experimental and numerical studies of fixed-ended cold-formed stainless steel equal-leg angle section columns. Eng. Struct. 2019, 184, 134–144. [Google Scholar] [CrossRef]
- Evans, S.I.; Xu, F.; Wang, J. Material properties and local stability of WAAM stainless steel equal angle sections. Eng. Struct. 2023, 287, 116160. [Google Scholar] [CrossRef]
- Trahair, N. Biaxial bending of steel angle section beams. J. Struct. Eng. 2004, 130, 554–561. [Google Scholar] [CrossRef]
- Trahair, N. Biaxial bending and torsion of steel equal angle section beams. J. Struct. Eng. 2007, 133, 78–84. [Google Scholar] [CrossRef]
- Aydın, R.; Doğan, M. Elastic, full plastic and lateral torsional buckling analysis of steel single-angle section beams subjected to biaxial bending. J. Constr. Steel Res. 2007, 63, 13–23. [Google Scholar] [CrossRef]
- Liu, Y.; Hui, L.B. Finite element study of steel single angle beam-columns. Eng. Struct. 2010, 32, 2087–2095. [Google Scholar] [CrossRef]
- Aydin, R.; Dogan, M.; Gunaydin, A.; Gokdemir, H.; Kirac, N. Experimental and code based study of beam-column behaviour of equal leg single-angles. J. Constr. Steel Res. 2011, 67, 780–789. [Google Scholar] [CrossRef]
- Chan, S.L.; Liu, Y.P.; Liu, S.W. A New Codified Design Theory of Second-order Direct Analysis for Steel and Composite Structures—From Research to Practice. Structures 2017, 9, 105–111. [Google Scholar] [CrossRef]
- Dinis, P.B.; Camotim, D.; Landesmann, A.; Martins, A.D. Improving the Direct Strength Method prediction of column flexural-torsional failure loads. Thin Wall Struct. 2020, 148, 106461. [Google Scholar] [CrossRef]
- Dinis, P.B.; Camotim, D. A novel DSM-based approach for the rational design of fixed-ended and pin-ended short-to-intermediate thin-walled angle columns. Thin Wall Struct. 2015, 87, 158–182. [Google Scholar] [CrossRef]
- GB/T706-2016; Hot Rolled Section Steel. China Standard Press: Beijing, China, 2016.
- Deng, C.; Zhang, C.; Zhou, J.; Chen, Y. Plate assembly elasto-plastic interactive buckling analyses of H Section steel members under compression and bending. J. Tongji Univ. (Nat. Sci.) 2016, 44, 1307–1315. [Google Scholar] [CrossRef]
- Trahair, N. Moment capacities of steel angle sections. J. Struct. Eng. 2002, 128, 1387–1393. [Google Scholar] [CrossRef]



| Stress State | μ | 0.125 | 0.15 | 0.20 | 0.25 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α | 0.532 | 0.553 | 0.575 | 0.532 | 0.553 | 0.575 | 0.532 | 0.553 | 0.575 | 0.532 | 0.553 | 0.575 | |
| 1 | γ1u | 1.219 | 1.255 | 1.320 | 1.375 | ||||||||
| γ1v | 1.269 | 1.308 | 1.354 | 1.314 | 1.361 | 1.415 | 1.396 | 1.457 | 1.528 | 1.468 | 1.542 | 1.628 | |
| 2 | γ2u | 1.063 | 1.075 | 1.100 | 1.125 | ||||||||
| γ2v | 1.210 | 1.189 | 1.173 | 1.252 | 1.227 | 1.207 | 1.336 | 1.303 | 1.276 | 1.419 | 1.379 | 1.345 | |
| 3 | γ3u | 1.063 | 1.075 | 1.100 | 1.125 | ||||||||
| γ3v | 1.309 | 1.368 | 1.453 | 1.371 | 1.441 | 1.543 | 1.495 | 1.588 | 1.725 | 1.619 | 1.735 | 1.906 | |
| 4 | γ4u | 1.219 | 1.255 | 1.320 | 1.375 | ||||||||
| γ4v | 1.269 | 1.308 | 1.354 | 1.314 | 1.361 | 1.415 | 1.396 | 1.457 | 1.528 | 1.468 | 1.542 | 1.628 | |
| Stress State | μ | 0.125 | 0.15 | 0.20 | 0.25 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α | 0.547 | 0.572 | 0.598 | 0.547 | 0.572 | 0.598 | 0.547 | 0.572 | 0.598 | 0.547 | 0.572 | 0.598 | |
| 1 | γ1u | 1.219 | 1.255 | 1.320 | 1.375 | ||||||||
| γ1v | 1.296 | 1.348 | 1.415 | 1.347 | 1.408 | 1.487 | 1.439 | 1.518 | 1.622 | 1.519 | 1.616 | 1.741 | |
| 2 | γ2u | 1.063 | 1.075 | 1.100 | 1.125 | ||||||||
| γ2v | 1.195 | 1.175 | 1.157 | 1.234 | 1.209 | 1.189 | 1.312 | 1.279 | 1.252 | 1.390 | 1.349 | 1.314 | |
| 3 | γ3u | 1.063 | 1.075 | 1.100 | 1.125 | ||||||||
| γ3v | 1.349 | 1.440 | 1.610 | 1.419 | 1.528 | 1.732 | 1.558 | 1.704 | 1.977 | 1.698 | 1.880 | 2.221 | |
| 4 | γ4u | 1.219 | 1.255 | 1.320 | 1.375 | ||||||||
| γ4v | 1.296 | 1.348 | 1.415 | 1.347 | 1.296 | 1.348 | 1.415 | 1.347 | 1.296 | 1.348 | 1.415 | 1.347 | |
| Axis | Plastic λp | Compact λc | Semi-Compact λy | Slender |
|---|---|---|---|---|
| Strong | 12 | 16 | 26 | >26 |
| L100 × 16, L100 × 14 L100 × 12, L100 × 10 L150 × 16, L150 × 15 | L100 × 9, L100 × 8 L150 × 14, L150 × 12 | L100 × 7, L100 × 6 L150 × 10, L100 × 8 | / | |
| Weak | 10 | 14 | 23 | >23 |
| L100 × 16, L100 × 14 L100 × 12 | L100 × 10, L100 × 9 L150 × 16, L150 × 15 L150 × 14 | L100 × 8, L100 × 7 L100 × 6, L150 × 12 L150 × 10, L100 × 8 | / |
| Axis | Plastic λp | Compact λc | Semi-Compact λy | Slender |
|---|---|---|---|---|
| Strong | 12 | 16 | 26 | >26 |
| L220 × 26, L220 × 24 L220 × 22, L250 × 35 L250 × 32, L250 × 30 L250 × 28, L250 × 26 | L220 × 20, L220 × 18 L250 × 24, L250 × 22 L250 × 20 | L220 × 16 L250 × 18 | / | |
| Weak | 10 | 14 | 23 | >23 |
| L220 × 26, L250 × 35 L250 × 32, L250 × 30 | L220 × 24, L220 × 22 L220 × 20, L250 × 28 L250 × 26, L250 × 24 L250 × 22 | L220 × 16 L220 × 18 L250 × 18 L250 × 20 | / |
| Section Class | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| b/t | 9εk | 11εk | 13εk | 15εk | 20 |
| Angle section | L100 × 16 L100 × 14 | L150 × 16 L100 × 12 | L100 × 10 L150 × 15 L150 × 14 | L100 × 9 L100 × 8 L150 × 12 | L100 × 6 L100 × 7 L150 × 10 L150 × 8 |
| Section Class | Class S1 | Class S2 | Class S3 | Class S4 | Class S5 |
|---|---|---|---|---|---|
| b/t | 9εk | 11εk | 13εk | 15εk | 20 |
| Angle section | L250 × 35 L250 × 32 | L220 × 26 L250 × 30 L250 × 28 | L220 × 24 L220 × 22 L220 × 20 L250 × 26 L250 × 24 | L220 × 18 L250 × 22 L250 × 20 | L220 × 16 L250 × 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Song, D.; Cai, Q.; Liu, Y.; Sun, S.; Yang, Y. Theoretical Analysis of the Plastic Property for Equal Angle Sections Subjected to Axial Force and Biaxial Bending. Buildings 2024, 14, 2153. https://doi.org/10.3390/buildings14072153
Sun Y, Song D, Cai Q, Liu Y, Sun S, Yang Y. Theoretical Analysis of the Plastic Property for Equal Angle Sections Subjected to Axial Force and Biaxial Bending. Buildings. 2024; 14(7):2153. https://doi.org/10.3390/buildings14072153
Chicago/Turabian StyleSun, Yun, Da Song, Qi Cai, Yangbing Liu, Shuxuan Sun, and Yuting Yang. 2024. "Theoretical Analysis of the Plastic Property for Equal Angle Sections Subjected to Axial Force and Biaxial Bending" Buildings 14, no. 7: 2153. https://doi.org/10.3390/buildings14072153
APA StyleSun, Y., Song, D., Cai, Q., Liu, Y., Sun, S., & Yang, Y. (2024). Theoretical Analysis of the Plastic Property for Equal Angle Sections Subjected to Axial Force and Biaxial Bending. Buildings, 14(7), 2153. https://doi.org/10.3390/buildings14072153





