Study on the Hydration Heat Effect and Pipe Cooling System of a Mass Concrete Pile Cap
Abstract
1. Introduction
2. Concrete Parameters and Numerical Modeling
2.1. Physical Thermal Parameters of Concrete
2.2. Numerical Modeling
2.2.1. Fundamental Assumptions
2.2.2. Layout of the Pipe Cooling System
2.2.3. Numerical Model of Cap
3. Field Test Data and Parameter Sensitivity Analysis
3.1. Test Instrument and Measuring Point Layout for Field Test
3.2. Analysis of Field Measurement Data
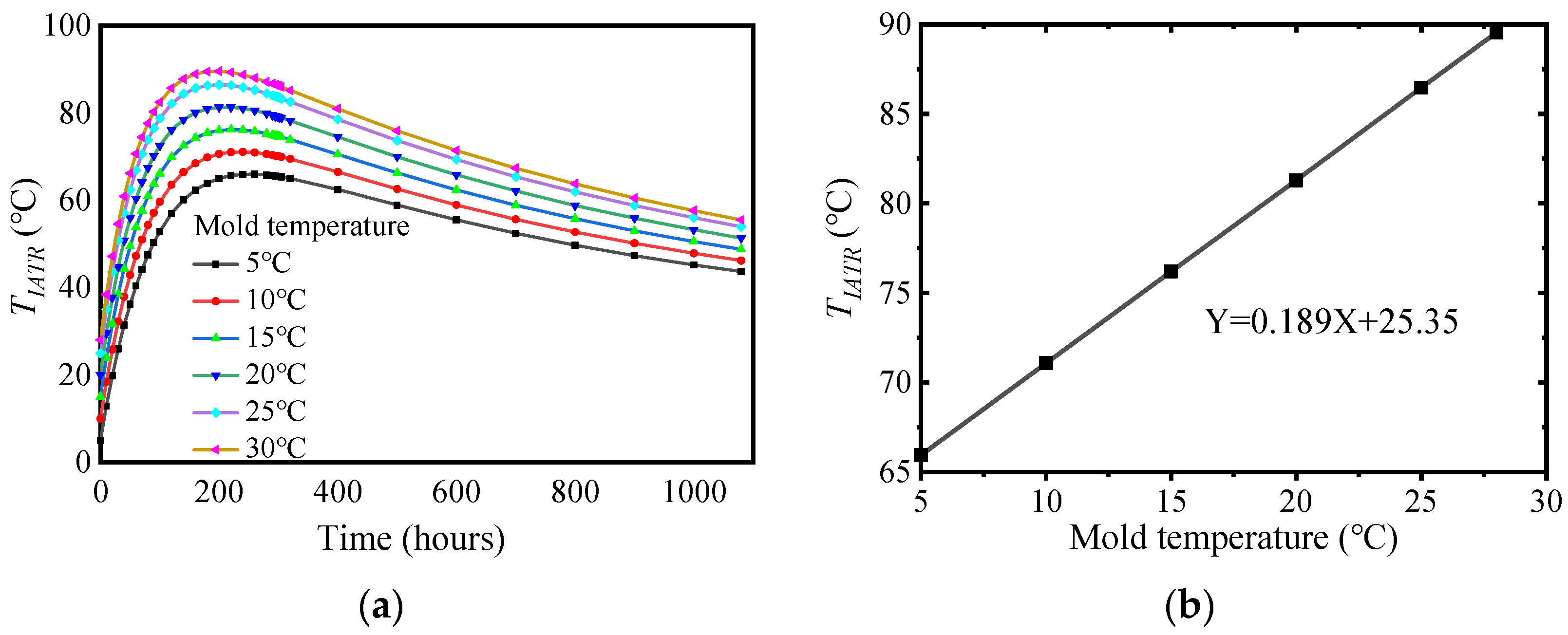
3.3. Influence of Concrete Mold Temperature
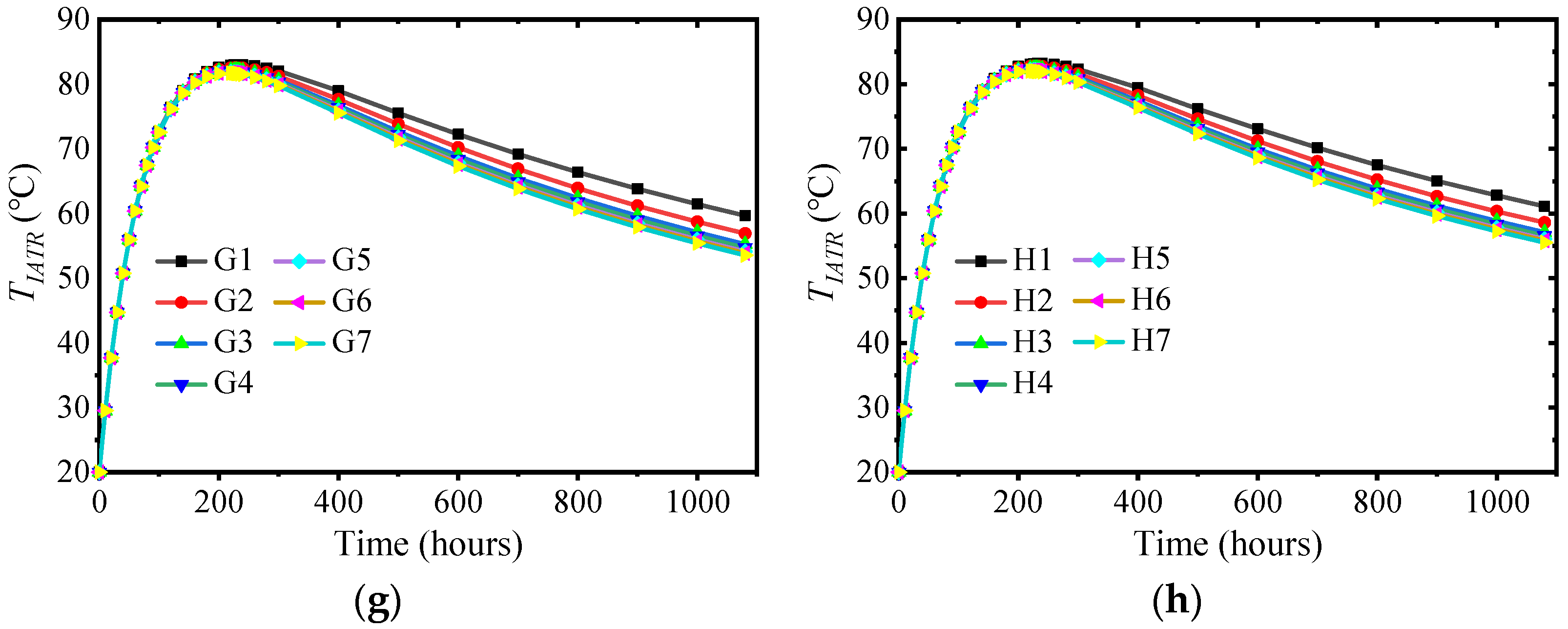
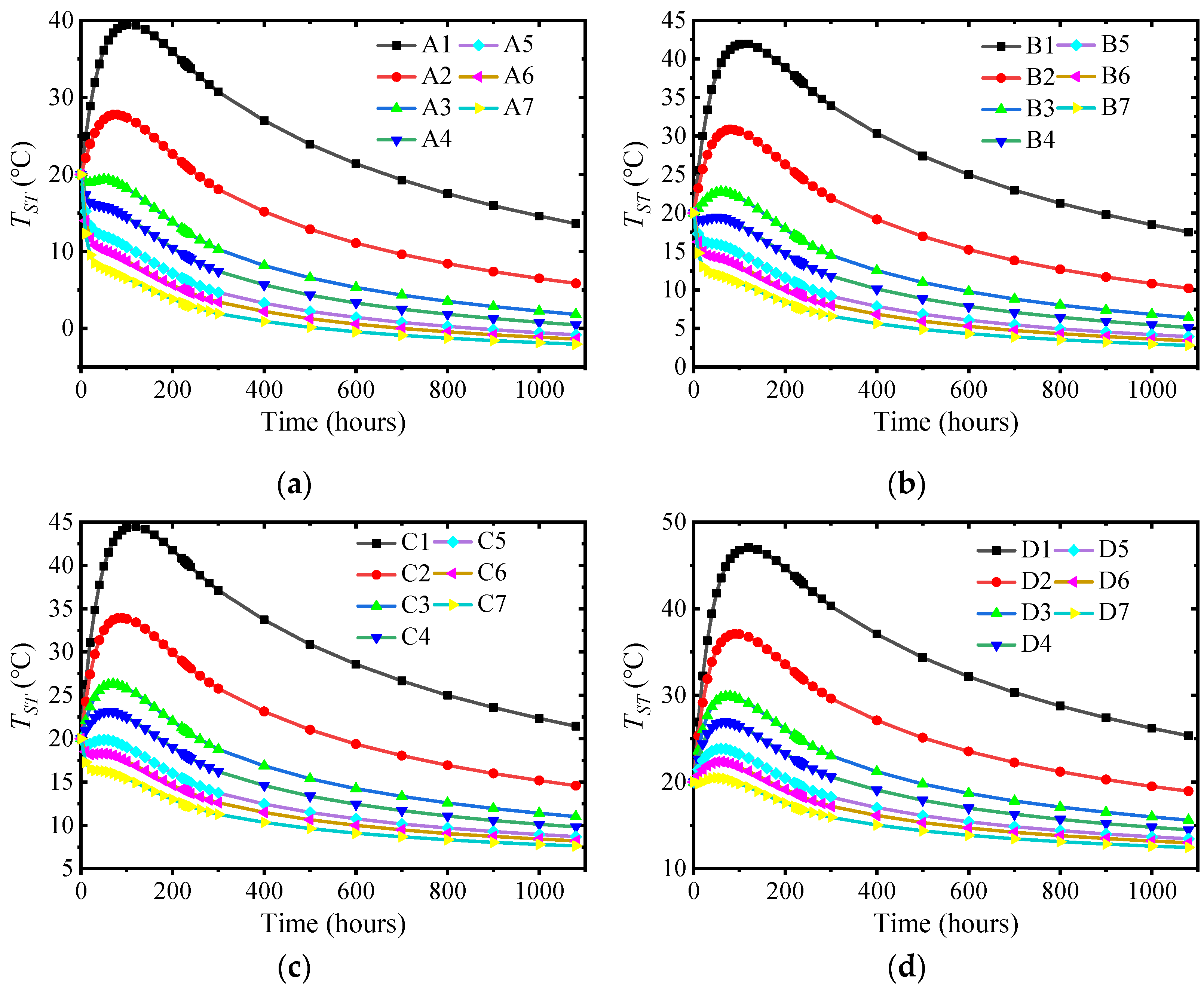
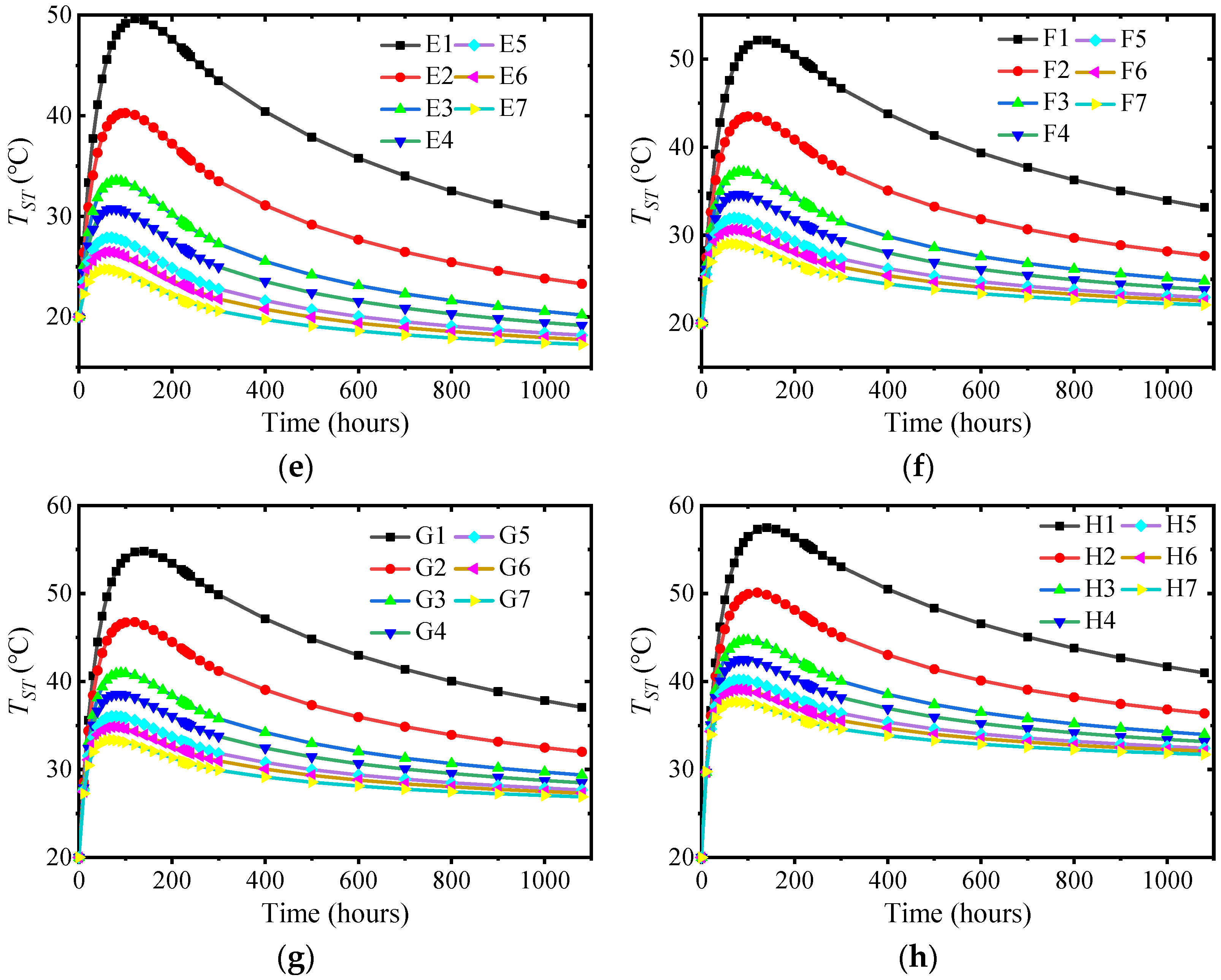
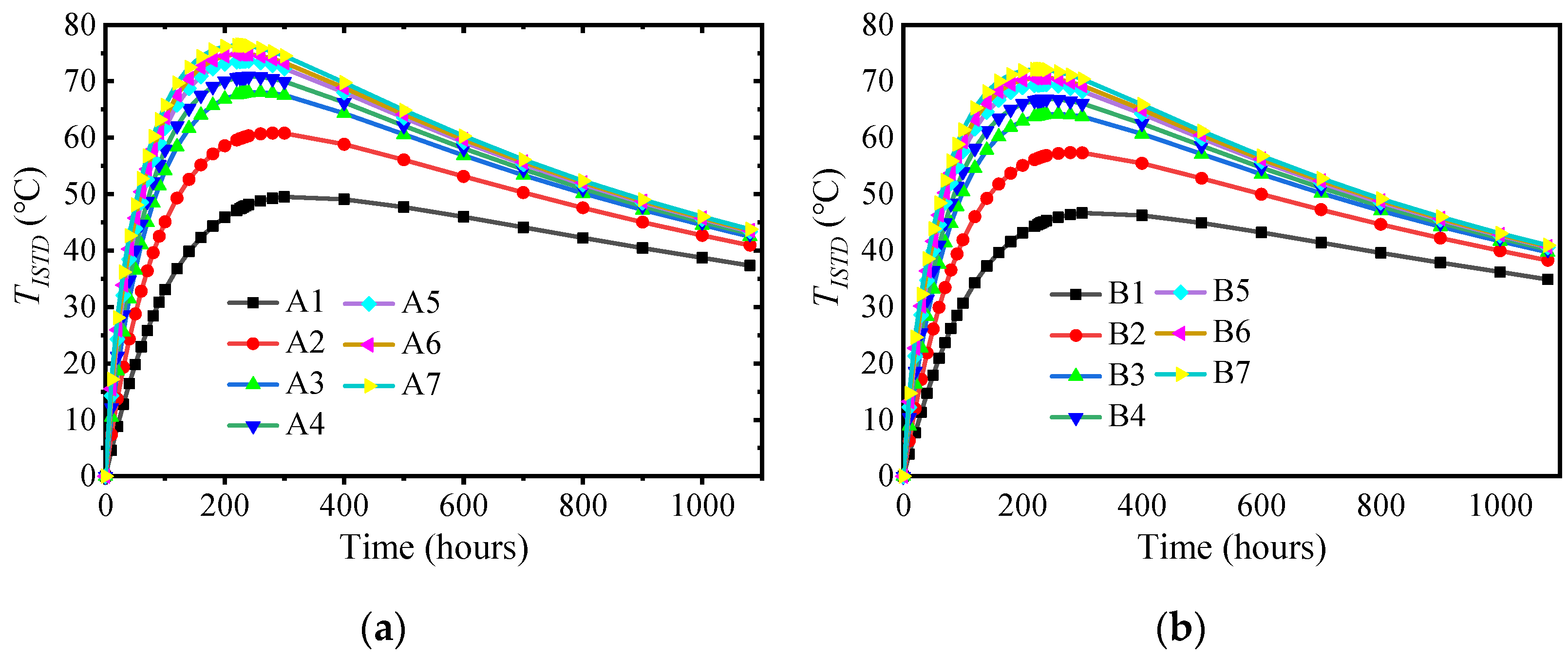
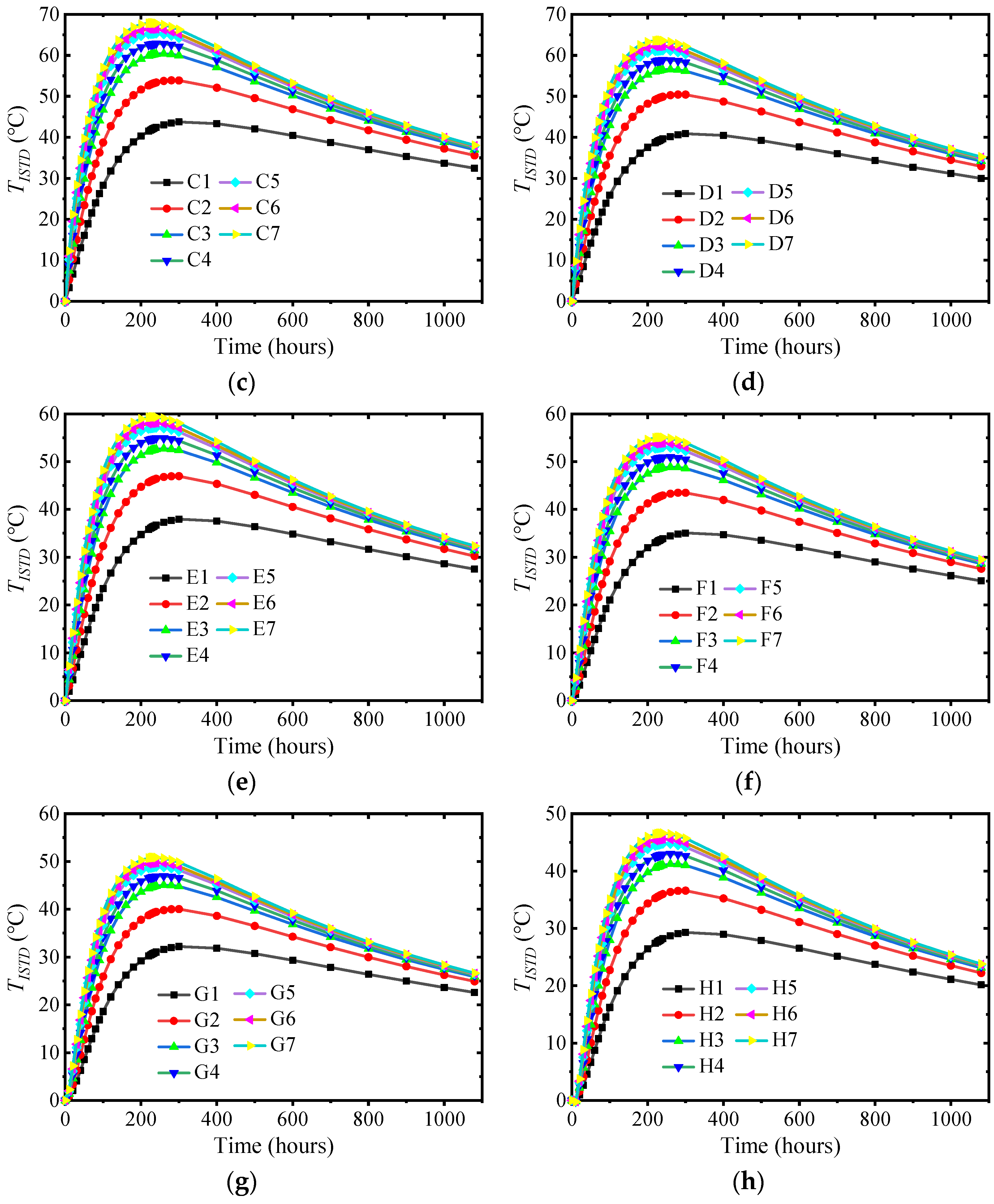
3.4. Influence of Ambient Temperature and Surface Convection Coefficient
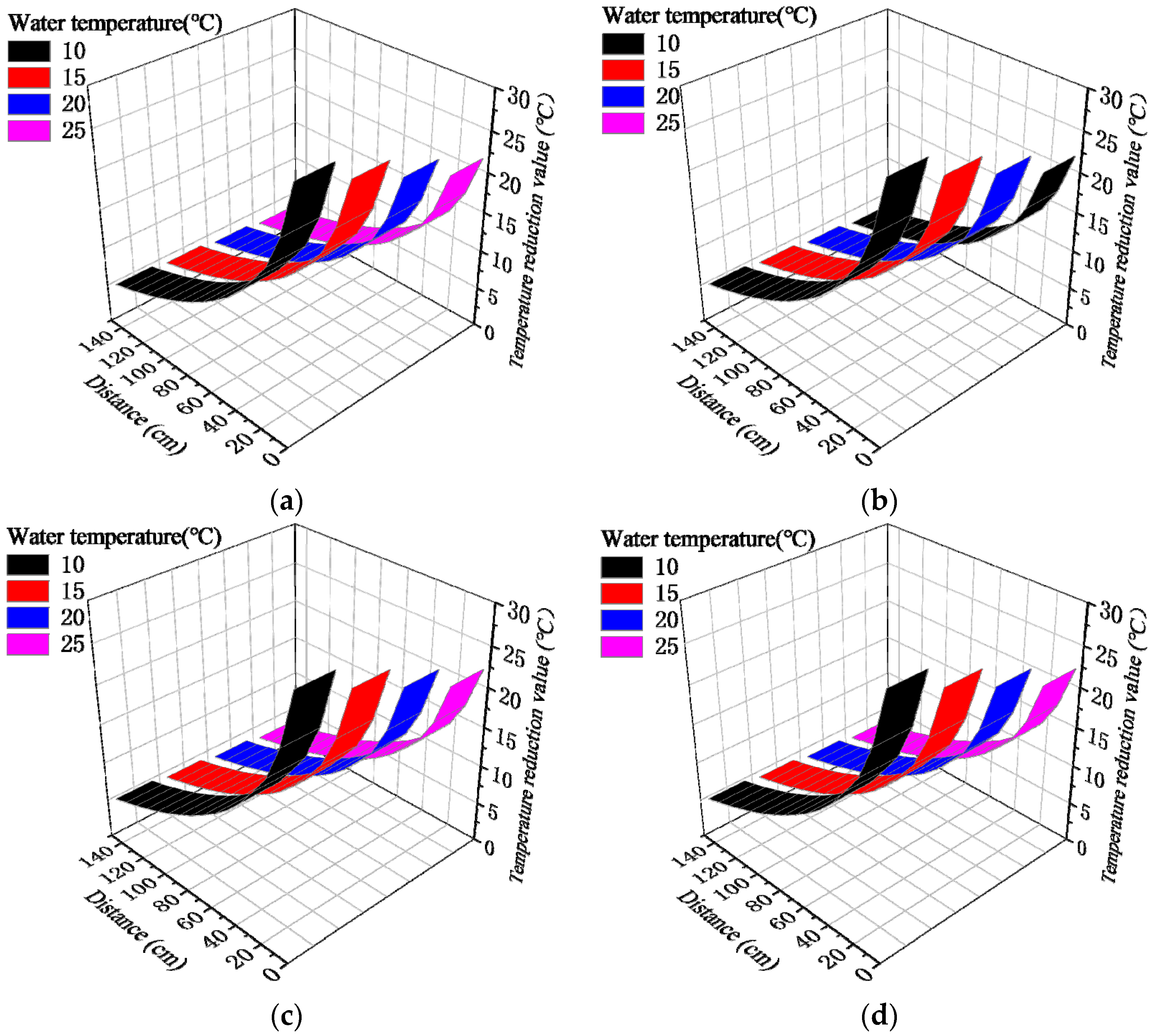
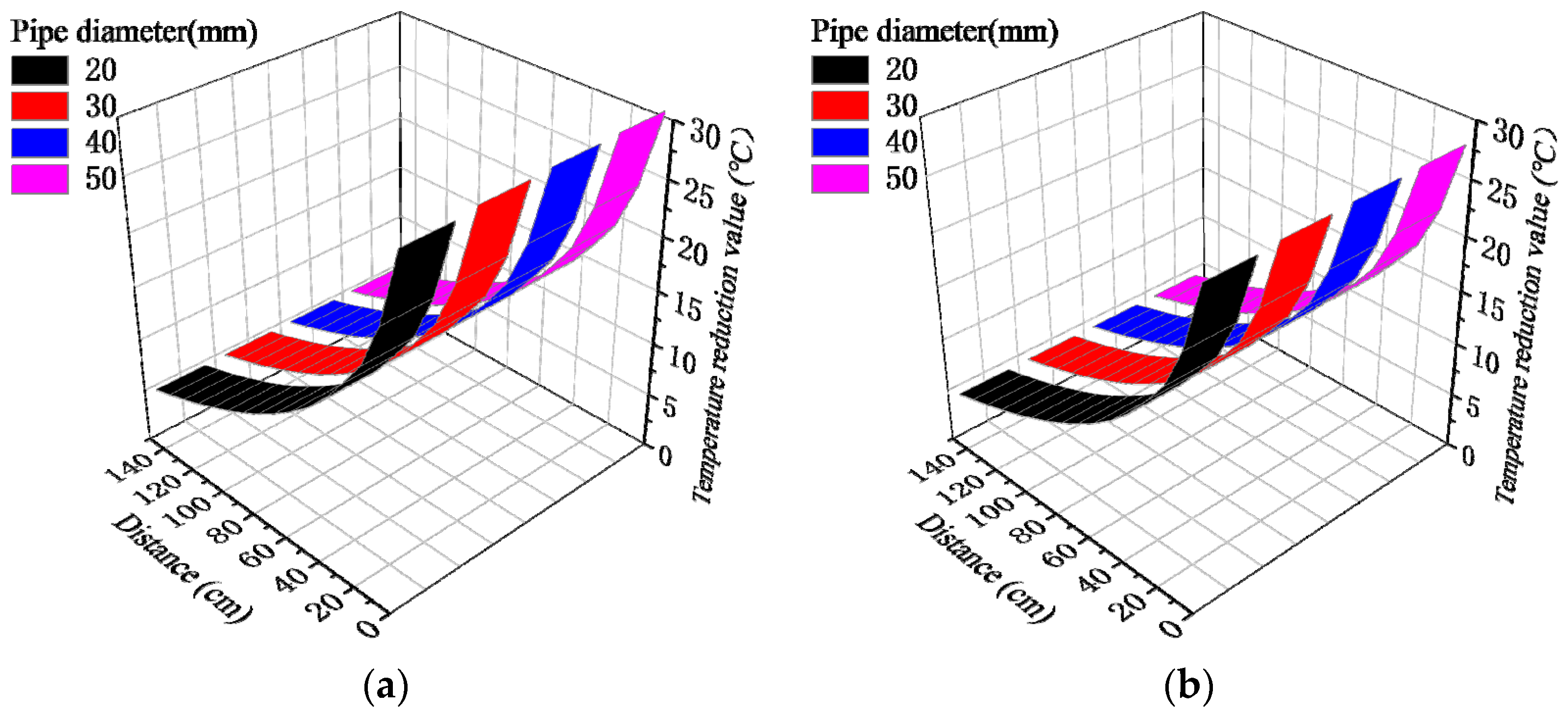
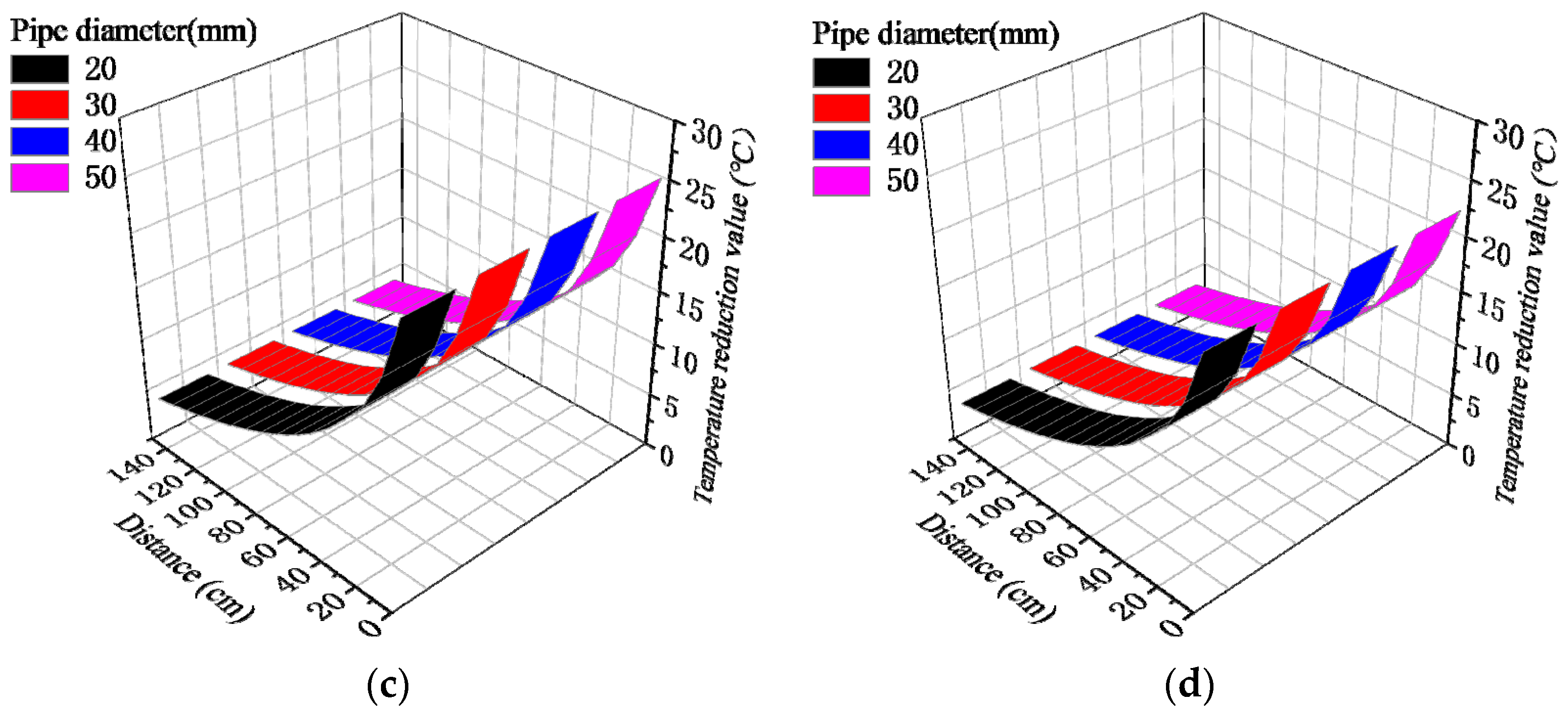
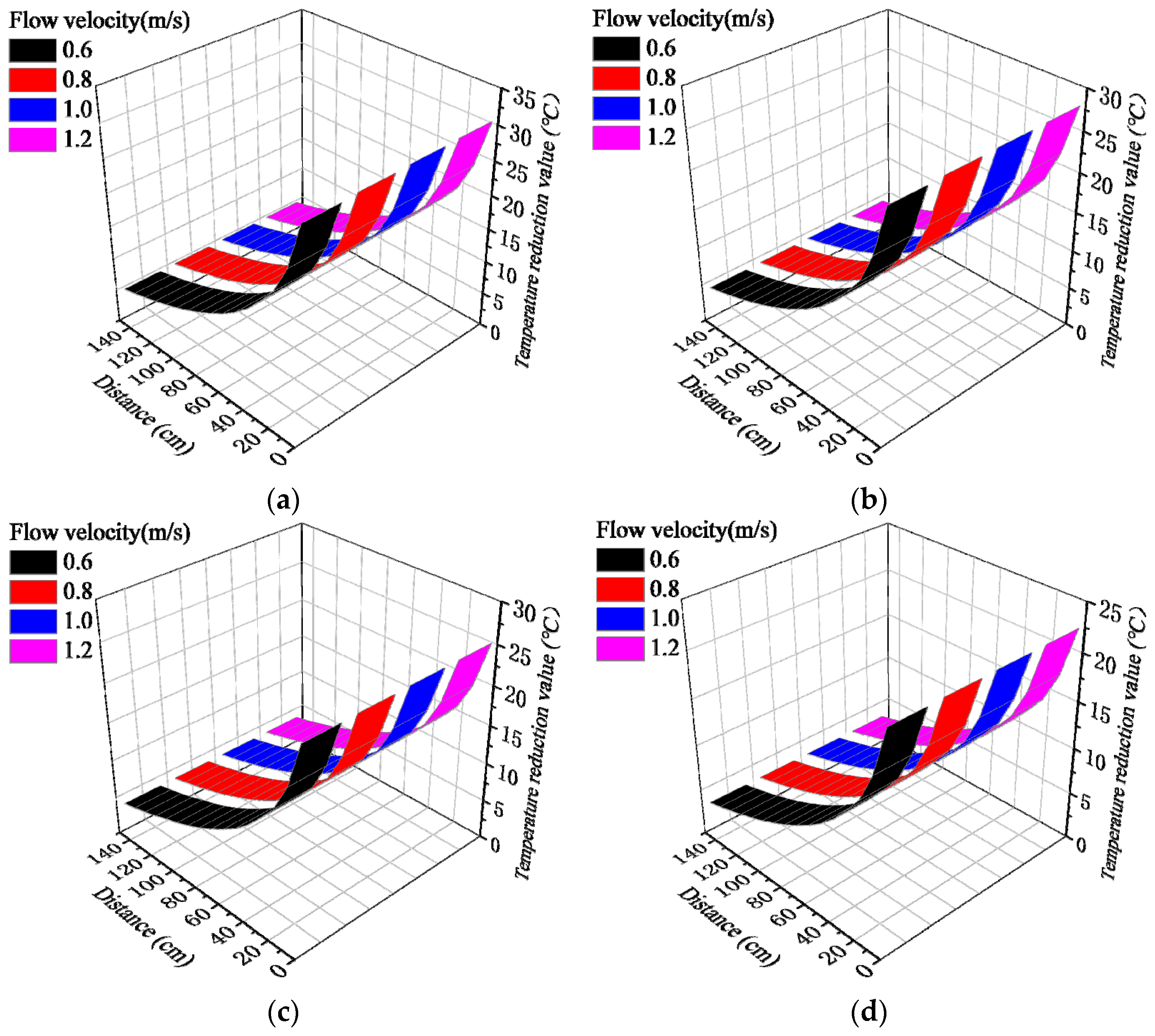
3.5. Influence of Pipe Cooling System Parameters
4. Conclusions
- 1.
- The maximum TIATR of the field measurements was consistent with the numerical results. However, the timing of its occurrence needs to be corrected. The disparity mostly resulted from non-standard insulation, significant fluctuations in the ambient temperature, and the operational stability of the pipe cooling system. The ambient temperature had a significant impact on the observed results of TST and TISTD.
- 2.
- When the mass concrete was naturally cooled without a pipe cooling system, the mold temperature was linearly related to the maximum TIATR, TST, and TISTD. For every 1 °C increase in the mold temperature, the maximum TIATR, TST, and TISTD were increased by approximately 1 °C, 0.2 °C, and 0.94 °C, respectively.
- 3.
- The surface convection coefficient and ambient temperature had minimal impacts on TIATR but significantly influenced TST. Once the structure entered the cooling stage, a higher surface convection coefficient led to a more rapid decrease in the internal temperature. TST decreased at a higher rate when the convection coefficient was smaller and the ambient temperature was larger.
- 4.
- The pipe diameter and water flow velocity of the pipe cooling system had little effect on its effective range and temperature change value. However, reducing the water temperature significantly increased the effective range and the temperature change value. The effective range of the pipe cooling system (where the concrete temperature reduction value exceeds 5 °C) for pipe diameters of 20~50 mm, flow rates of 0.6~1.2 m/s, and water temperatures of 10~25 °C was about 1.2~1.5 m.
5. Further Development
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, N.C.; Yu, M.S.; Yao, X.Y. Intelligent Active Correction Technology and Application of Tower Displacement in Arch Bridge Cable Lifting Construction. Appl. Sci. 2021, 11, 9808. [Google Scholar] [CrossRef]
- Sun, J.P.; Li, J.B.; Jiang, Y.B.; Ma, X.G.; Tan, Z.H.; Zhufu, G.L. Key Construction Technology and Monitoring of Long-Span Steel Box Tied Arch Bridge. Int. J. Steel Struct. 2023, 23, 191–207. [Google Scholar] [CrossRef]
- Bobko, C.P.; Edwards, A.J.; Seracino, R.; Zia, P. Thermal Cracking of Mass Concrete Bridge Footings in Coastal Environments. J. Perform. Constr. Fac. 2015, 29, 04014171. [Google Scholar] [CrossRef]
- ACI Committee 207. Mass Concrete for Dams and Other Massive Structures. J. Proc. 1970, 67, 191–207. [Google Scholar]
- De Schutter, G.; Taerwe, L. Specific heat and thermal diffusivity of hardening concrete. Mag. Concr. Res. 1995, 47, 203–208. [Google Scholar] [CrossRef]
- Liu, B. Concrete Technology; People’s Transportation Publishing House: Beijing, China, 1995; pp. 123–125. (In Chinese) [Google Scholar]
- Code for Construction of Mass Concrete GB5049-2018; China Building Industry Press: Beijing, China, 2018. (In Chinese)
- Hamid, H.; Chorzepa, M.G.; Sullivan, M.; Durham, S.; Kim, S.S. Novelties in Material Development for Massive Concrete Structures: Reduction in Heat of Hydration Observed in Ternary Replacement Mixtures. Infrastructures 2018, 3, 8. [Google Scholar] [CrossRef]
- Pepe, M.; Lima, C.; Martinelli, E. Early-Age Properties of Concrete Based on Numerical Hydration Modelling: A Parametric Analysis. Materials 2020, 13, 2112. [Google Scholar] [CrossRef] [PubMed]
- Cha, S.L.; Jin, S.S. Prediction of thermal stresses in mass concrete structures with experimental and analytical results. Constr. Build. Mater. 2020, 258, 120367. [Google Scholar] [CrossRef]
- Fan, J.S.; Li, B.L.; Liu, C.; Liu, Y.F. An efficient model for simulation of temperature field of steel-concrete composite beam bridges. Structures 2022, 43, 1868–1880. [Google Scholar] [CrossRef]
- Abdel-Raheem, M.; Quintana, O.; Morales, M.; Marroquin-Villa, Y.; Ramos, D.; Hernandez, S. Construction methods used for controlling temperature in mass concrete structure. In Creative Construction Conference 2018, Proceedings of the Creative Construction Conference, Ljubljana, Slovenia, 30 June–3 July 2018; Budapest University of Technology and Economics: Budapest, Hungary, 2018; pp. 139–146. [Google Scholar]
- Abendeh, R.M.; Bani Baker, M. Using steel slag aggregate to strengthen self-compacting concrete durability. Proc. Inst. Civ. Eng. Struct. Build. 2022, 175, 925–939. [Google Scholar] [CrossRef]
- Madi, M.; Refaat, N.; Negm El Din, A.; Ziada, F.; Mazen, M.; Ahmed, S.; Hamza, A.S.; El Nahas, E.; Fathy, A.; Fahmy, E.H.; et al. The impact of mixing water temperature on portland cement concrete quality. In Proceedings of the CSCE Annual Conference, Vancouver, BC, Canada, 31 May–3 June 2017. [Google Scholar]
- Alamayreh, M.I.; Barham, T.; Shaban, N.A.; Olimat, A.N. Design of High Efficiency Aggregate Air Cooling System. In Proceedings of the Second Thermal and Fluids Engineering Conference, Las Vegas, NV, USA, 2–5 April 2017; pp. 2369–2375. [Google Scholar]
- Nguyen, T.C.; Luu, X.B. Reducing temperature difference in mass concrete by surface insulation. Mag. Civ. Eng. 2019, 88, 70–79. [Google Scholar]
- Alamayreh, M.I.; Alahmer, A.; Younes, M.B.; Bazlamit, S.M. Pre-Cooling Concrete System in Massive Concrete Production: Energy Analysis and Refrigerant Replacement. Energies 2022, 15, 1129. [Google Scholar] [CrossRef]
- Xue, S.; Geng, Y.; Li, X.; Li, J.; Song, Y. Song. Stress Development and Crack Monitoring of Massive Concrete Walls with Embedded Air-cooling Pipes. J. Adv. Concr. Technol. 2021, 19, 999–1015. [Google Scholar] [CrossRef]
- Deppo, L.L.; Dates, C.; Fiortto, V. Optimizing the Choice of Quarries for Large Dam Construction. J. Water Power Dam Constr. 1985, 37, 40–44. [Google Scholar]
- Adebar, P.; Zhou, Z. Bearing Strength of Compressive Struts Confined by Plain Concrete. ACI Struct. J. 1993, 90, 534–541. [Google Scholar]
- Aniskin, N.; Nguyen, T.C.; Bui, A.K. The use of ice to cool the concrete mix in the construction of massive structures. In Proceedings of the E3S Web of Conferences, Khabarovsk, Russia, 7–9 September 2021; Volume 264. [Google Scholar]
- Nguyen, T.C.; Nguyen, V.Q.; Aniskin, N.; Phung, B.T.; Hoang, Q.L. Building a nomogram to predict maximum temperature in mass concrete at an early age. In Proceedings of the E3S Web of Conferences, Khabarovsk, Russia, 7–9 September 2021; Volume 263. [Google Scholar]
- Nakane, S.; Saito, H.; Ohike, T. Strength development and microstructure of cement and concrete precooled with liquid nitrogen. In Proceedings of the International Conference on Concrete in Hot Climates, Concrete in Hot Climates, Torquay, UK, 21–25 September 1992. [Google Scholar]
- Harith, I.K.; Hassan, M.S.; Hasan, S.S. Liquid nitrogen effect on the fresh concrete properties in hot weathering concrete. Innov. Infrastruct. Solut. 2022, 7, 127. [Google Scholar] [CrossRef]
- Bamforth, P.B. Early-Age Thermal Crack Control in Concrete; CIRIA Report C660; Construction, Built Environment, Civil Engineering: London, UK, 2007. [Google Scholar]
- Wang, Y.; Liu, F.; Xu, L.; Zhao, H. Effect of elevated temperatures and cooling methods on strength of concrete made with coarse and fine recycled concrete aggregates. Constr. Build. Mater. 2019, 210, 540–547. [Google Scholar] [CrossRef]
- Tasri, A.; Susilawati, A. Effect of cooling water temperature and space between cooling pipes of post-cooling system on temperature and thermal stress in mass concrete. J. Build. Eng. 2019, 24, 100731. [Google Scholar] [CrossRef]
- Ben Jemaa, R.; Mansouri, R.; Boukholda, I.; Bellagi, A. Energy and exergy investigation of R1234ze as R134a replacement in vapor compression chillers. Int. J. Hydrogen Energy 2017, 42, 12877–12887. [Google Scholar] [CrossRef]
- Alabdulkarem, A.; Eldeeb, R.; Hwang, Y.; Aute, V.; Radermacher, R. Testing, simulation and soft-optimization of R410A low-GWP alternatives in heat pump system. Int. J. Refrig. 2015, 60, 106–117. [Google Scholar] [CrossRef]
- Vali, S.S.; Setty, T.P.; Babu, A. Analytical computation of thermodynamic performance parameters of actual vapour compression refrigeration system with R22, R32, R134a, R152a, R290 and R1270. MATEC Web Conf. EDP Sci. 2018, 144, 4009. [Google Scholar] [CrossRef][Green Version]
- Seo, T.S.; Kim, S.S.; Lim, C.K. Experimental study on hydration heat control of mass concrete by vertical pipe cooling method. J. Asian Archit. Build. Eng. 2015, 14, 657–662. [Google Scholar] [CrossRef]
- Lawrence, A.M.; Tia, M.; Ferraro, C.C.; Bergin, M. Effect of early age strength on cracking in mass concrete containing different supplementary cementations materials: Experimental and finite-element investigation. J. Mater. Civ. Eng. 2014, 24, 362–372. [Google Scholar] [CrossRef]
- Huynh, T.P.; Tang, V.L. Prevention of crack formation in massive concrete at an early age by cooling pipe system. Asian J. Civ. Eng. 2019, 20, 1101–1107. [Google Scholar]
- Zhang, T.; Wang, H.; Luo, Y.; Yuan, Y.; Wang, W. Hydration heat control of mass concrete by pipe cooling method and on-site monitoring-based influence analysis of temperature for a steel box arch bridge construction. Materials 2023, 16, 2925. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, G.; Huang, S.; Rao, R.; Hu, C. Experimental and finite element investigations on the temperature field of a massive bridge pier caused by the hydration heat of concrete. Constr. Build. Mater. 2018, 192, 240–252. [Google Scholar] [CrossRef]
- Tasri, A.; Susilawati, A. Effect of material of post-cooling pipes on temperature and thermal stress in mass concrete. Structures 2019, 20, 204–212. [Google Scholar] [CrossRef]
- Yang, J.K.; Lee, Y.; Kim, J.K. Heat Transfer Coefficient in Floe Convention of Pipe-Cooling System in Massive Concrete. J. Adv. Concr. Technol. 2011, 9, 103–114. [Google Scholar] [CrossRef]
- Xiaolong, G.; Chunguang, L.; Yunhong, Q. Study on On-site Monitoring of Hydration Heat of Mass Concrete for Bridge Slab Based on Measured Data. Intell. Autom. Soft Comput. 2019, 25, 775–783. [Google Scholar]
- Zhao, Z. Handbook of High—Rise Building Construction; China Construction Industry Press: Beijing, China, 1997. (In Chinese) [Google Scholar]
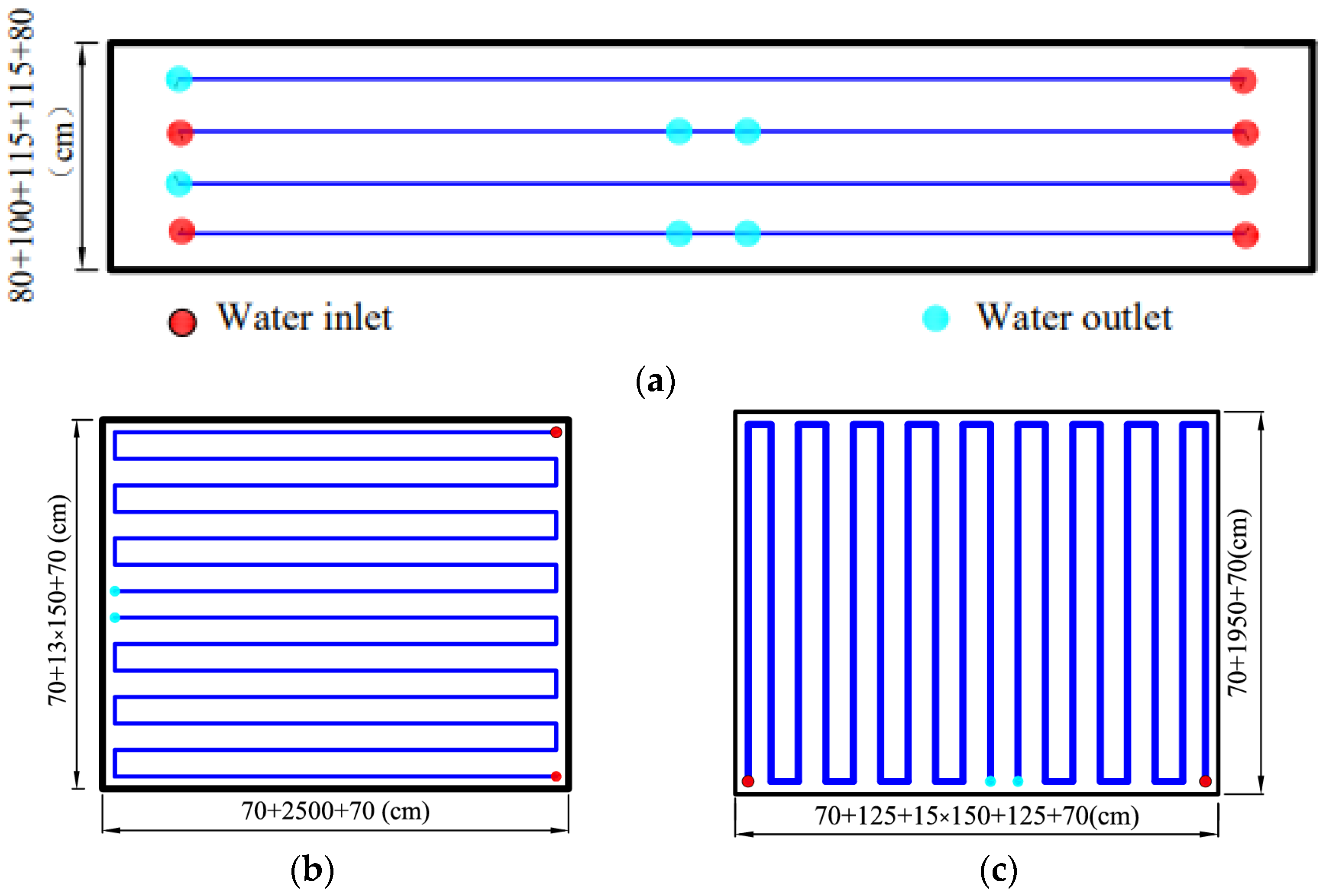
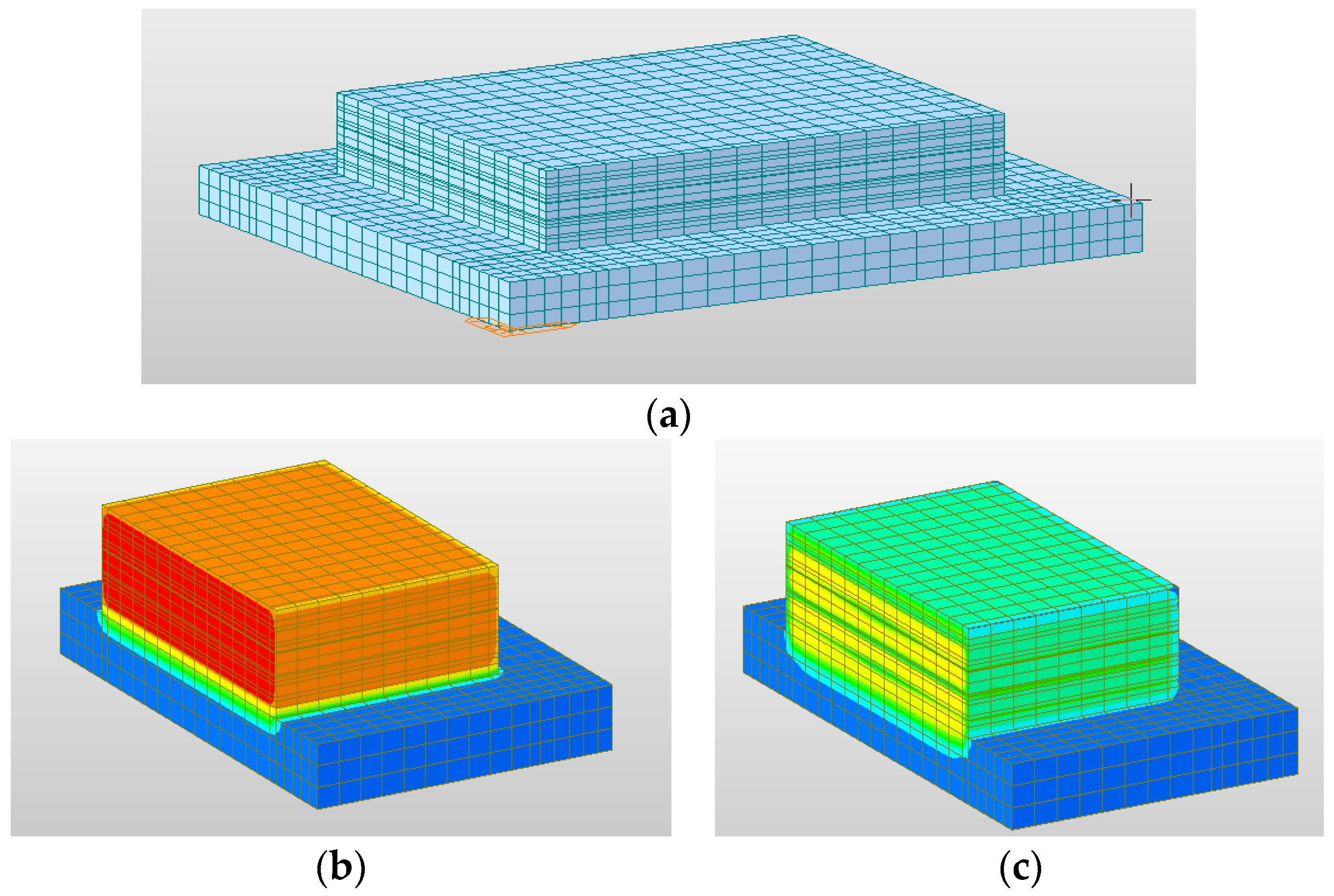





| Concrete Materials | Cement | Sand | Gravel | Water | Fly Ash | Water Reducer |
|---|---|---|---|---|---|---|
| Mix ratio (kg/m3) | 240 | 160 | 779 | 1076 | 145 | 4 |
| Thermal conductivity () | 2.218 | 3.082 | 2.908 | 0.600 | 0.23 | / |
| Specific heat capacity () | 0.536 | 0.745 | 0.708 | 4.187 | 0.92 | / |
| Parameter | 0 | 10% | 20% | 30% | 40% |
|---|---|---|---|---|---|
| Fly ash | 1 | 0.96 | 0.95 | 0.93 | 0.82 |
| Slag powder | 1 | 1 | 0.93 | 0.92 | 0.84 |
| Ambient Temperature | −5 °C | 0 °C | 5 °C | 10 °C | 15 °C | 20 °C | 25 °C | 30 °C |
|---|---|---|---|---|---|---|---|---|
| Surface Convection Coefficient | ||||||||
| 3.275 | A1 | B1 | C1 | D1 | E1 | F1 | G1 | H1 |
| 5.56 | A2 | B2 | C2 | D2 | E2 | F2 | G2 | H2 |
| 8.33 | A3 | B3 | C3 | D3 | E3 | F3 | G3 | H3 |
| 11.11 | A4 | B4 | C4 | D4 | E4 | F4 | G4 | H4 |
| 13.89 | A5 | B5 | C5 | D5 | E5 | F5 | G5 | H5 |
| 16.67 | A6 | B6 | C6 | D6 | E6 | F6 | G6 | H6 |
| 21.279 | A7 | B7 | C7 | D7 | E7 | F7 | G7 | H7 |
| Effective Influence Range (cm)/ Temperature Reduction Value (°C) | Water Temperature (°C) | ||||
|---|---|---|---|---|---|
| 10 | 15 | 20 | 25 | ||
| Effective diameter (mm)/Water flow rate (m/s) | 20/0.6 | 150/30.5–5.0 | 130/27.7–5.4 | 120/24.9–5.3 | 110/22.2–5.2 |
| 20/0.8 | 150/30.7–5.0 | 130/27.9–5.5 | 120/25.1–5.4 | 110/22.3–5.2 | |
| 20/1.0 | 150/30.9–5.0 | 140/28.1–5.0 | 120/25.2–5.4 | 110/22.4–5.2 | |
| 20/1.2 | 150/31.0–5.0 | 140/28.1–5.0 | 120/25.3–5.4 | 110/22.5–5.3 | |
| 30/0.6 | 150/30.8–5.0 | 140/28.0–5.0 | 120/25.2–5.4 | 110/22.4–5.2 | |
| 30/0.8 | 150/31.0–5.0 | 140/28.2–5.0 | 120/25.3–5.4 | 110/22.5–5.3 | |
| 30/1.0 | 150/31.1–5.0 | 140/28.2–5.0 | 120/25.4–5.4 | 110/22.6–5.3 | |
| 30/1.2 | 150/31.1–5.0 | 140/28.3–5.0 | 120/25.5–5.5 | 110/22.6–5.3 | |
| 40/0.6 | 150/31.0–5.0 | 140/28.2–5.0 | 120/25.4–5.5 | 110/22.5–5.3 | |
| 40/0.8 | 150/31.1–5.0 | 140/28.3–5.0 | 120/25.4–5.5 | 110/22.6–5.3 | |
| 40/1.0 | 150/31.2–5.0 | 140/28.3–5.0 | 120/25.5–5.5 | 110/22.7–5.3 | |
| 40/1.2 | 150/31.2–5.0 | 140/28.4–5.0 | 120/25.5–5.5 | 110/22.7–5.3 | |
| 50/0.6 | 150/31.1–5.0 | 140/28.3–5.0 | 120/25.4–5.4 | 110/22.6–5.3 | |
| 50/0.8 | 150/31.2–5.0 | 140/28.4–5.0 | 120/25.5–5.5 | 110/22.7–5.3 | |
| 50/1.0 | 150/31.3–5.0 | 140/28.4–5.0 | 120/25.6–5.5 | 110/22.7–5.3 | |
| 50/1.2 | 150/31.3–5.0 | 140/28.4–5.0 | 120/25.6–5.5 | 110/22.7–5.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Song, Y. Study on the Hydration Heat Effect and Pipe Cooling System of a Mass Concrete Pile Cap. Buildings 2024, 14, 2413. https://doi.org/10.3390/buildings14082413
Wang B, Song Y. Study on the Hydration Heat Effect and Pipe Cooling System of a Mass Concrete Pile Cap. Buildings. 2024; 14(8):2413. https://doi.org/10.3390/buildings14082413
Chicago/Turabian StyleWang, Bo, and Yifan Song. 2024. "Study on the Hydration Heat Effect and Pipe Cooling System of a Mass Concrete Pile Cap" Buildings 14, no. 8: 2413. https://doi.org/10.3390/buildings14082413
APA StyleWang, B., & Song, Y. (2024). Study on the Hydration Heat Effect and Pipe Cooling System of a Mass Concrete Pile Cap. Buildings, 14(8), 2413. https://doi.org/10.3390/buildings14082413





