Drying of a Clayey Ceramic Flat Plate: Simulation Studies Using the Galerkin-Based Integral Method

Abstract

The ceramics sector is crucial to the global economy. This research is devoted to studying the drying process of ceramic parts with arbitrary shapes based on Fick’s second law of diffusion and energy conservation. Herein, the mathematical procedure to obtain the exact solutions of the model equations using the Galerkin-based integral method is provided. In the mathematical modeling are considered constant properties and equilibrium conditions at the surface of the material. Emphasis is given to clay ceramic flat plate. Analytical results of the average moisture content, local temperature, and moisture content and temperature fields within the ceramic parts are presented, followed by an in-depth discussion.

1. Introduction

In the present day, the ceramic industry has presented great developments based on new research and advanced equipment, both developed by specialists, academics, and industrialists. Currently, building ceramics has occupied a prominent place in the world economy, with a share of approximately 1% of GDP in Brazil. With regard to ceramic coatings and sanitary ware in the world, Brazil is one of the main countries, being the third largest producer, the third largest consumer market, and sixth in the export ranking, selling products to more than 110 countries. The production sector represents 6% of the GDP of the construction materials industry [1]. These facts are conditional on the large amount of natural raw materials, renewable energy sources, and the availability of practical technologies.

Traditionally, ceramic material is a non-metallic and inorganic material that presents structure wholly or partially in the crystallized form after firing [2]. Ceramics are composed of different raw materials and have a higher percentage of clay. An important property of the material class is that by addition of water, they acquire great plasticity, allowing them to be easily molded into different shapes. The water added to the dry clay mass covers the surface of the clay particle (forming a thin film around it) and fills the continuous voids, causing the separation of the particles inside.

Clayey ceramic parts can be molded in different forms given origin to new products such as blocks, floor and roof tiles, and common and hollow bricks, which are frequently used in building construction. The manufacturing of clay pieces comprises several stages, including extraction and treatment of raw materials, mechanical conformation, thermal processing (drying and firing), and shipping.

During the mechanical processing, the clay plastic mass is molded into products with different shapes and sizes according to the material composition and application. The next steps are drying and firing. In the drying process, the water added during the molding of the piece is removed by evaporation by using dryers. The idea is to reduce, under severe control, the moisture content of the products to the desired level.

Drying is perhaps the oldest and most common thermal method applied in the ceramics industry and is also one of the most complex and least understood processes. Drying can be classified as natural, artificial, or mixed. Artificial drying can be carried out by equipment such as an oven and dryer. The basic functions of the drying include: (a) the transport of the heat necessary for water evaporation, (b) the removal of the produced water vapor, (c) the reduction in the saturated vapor layer formed on the product surface, and (d) the movement of liquid and/or vapor inside the part. The following steps are frequently encountered during the drying process: adaptation (induction, accommodation, and warming up), exit of colloidal water, formation of voids, and expulsion of interstitial moisture. Then, it becomes clear the complexity of the drying process. Thus, in the drying process, heat and mass transport occur simultaneously, along with dimensional variations, and, when it comes to ceramic materials, the process is not different.

It is important to notice that ceramic clay has water in the constitution of its crystal lattice (bound water), so, during the drying process, the water that has been added in the molding stage (unbound (free) water) can be easily removed, with the temperature ranging from room temperature to 110 °C. However, water that is in the clay crystal lattice will only be removed at higher temperatures (above 400 °C) depending on the type and composition of clay. Further, with the progress of the drying, the clay may contract as the spaces that were occupied by water inside the material become empty after water evaporation.

If moisture is not removed adequately, severe mechanical, thermal, and hydric stresses caused by moisture and temperature gradients within the body can occur, leading to defects such as deformations and cracks or perhaps revealing them. These defects reduce the quality of the product for the next manufacturing step (firing). Therefore, understanding this complex process becomes crucial. The most common defects in clay ceramic parts are deformation, cracks, black hearts, and efflorescence. Furthermore, there may also be a decrease in thermophysical and mechanical properties in fired clay pieces, for example, strength, modulus of elasticity, color, and appearance (discoloration). An in-depth discussion about drying defects in ceramic parts and their effects on the product quality after processing can be found in the published literature [3,4,5,6,7,8,9,10,11,12,13,14,15].

In the present day, the ceramic industry has used the convective drying technique (artificial) for water removal from the parts. In the academy, the study of drying clay materials has been done on the basis of theoretical studies and experiments. Thus, we state that the development of robust and advanced modeling to predict the drying process is already a reality. For predicting mass transfer, a particular reference can be made to the liquid diffusion model, which is based on Fick’s second law of diffusion. This model has been applied to predict the drying of various ceramic parts, such as clay plates [3], roof tiles [4,5,6], and bricks [7,8,9,10,11,12,13,14,15]. In these studies, different mathematical techniques have been used to obtain the analytical (separation of variables and GBI method) or numerical (finite-volume and CFD commercial software, for example Ansys CFX v. 15) solutions of the governing equation.

In this paper, the focus is to develop a theoretical mathematical formulation and its exact solution via the Galerkin-based integral method (GBI method) to predict heat and mass transport inside clay ceramic materials using a 2D approach (flat plate). The innovation of this research lies in the application of the GBI technique to the drying process of clay materials and the theoretical procedure to obtain the exact solution of the diffusion equation.

There are several reasons, motivations, and advantages for the use of the GBI method in linear transient diffusion problems. For examples, (a) it is flexible, powerful, and can be applied to conventional and non-conventional geometric shapes of the material in study; (b) it follows a systematic solution procedure for homogeneous and heterogeneous bodies; (c) for homogeneous body, with regular geometry, multidimensional linear problems in Cartesian coordinates are solved by multiplying one-dimensional solution for most of the boundary condition; (d) it can be applied for homogeneous and nonhomogeneous boundary conditions; (e) it can be applied for orthogonal and non-orthogonal bodies; (f) it can be used to obtain solution of the diffusion equation and to validate numerical results obtained for different methods such as separation of variables, finite-volume, finite-difference, finite-element, and computational fluid dynamic. Thus, applications to different ceramic material compositions and shapes become feasible.

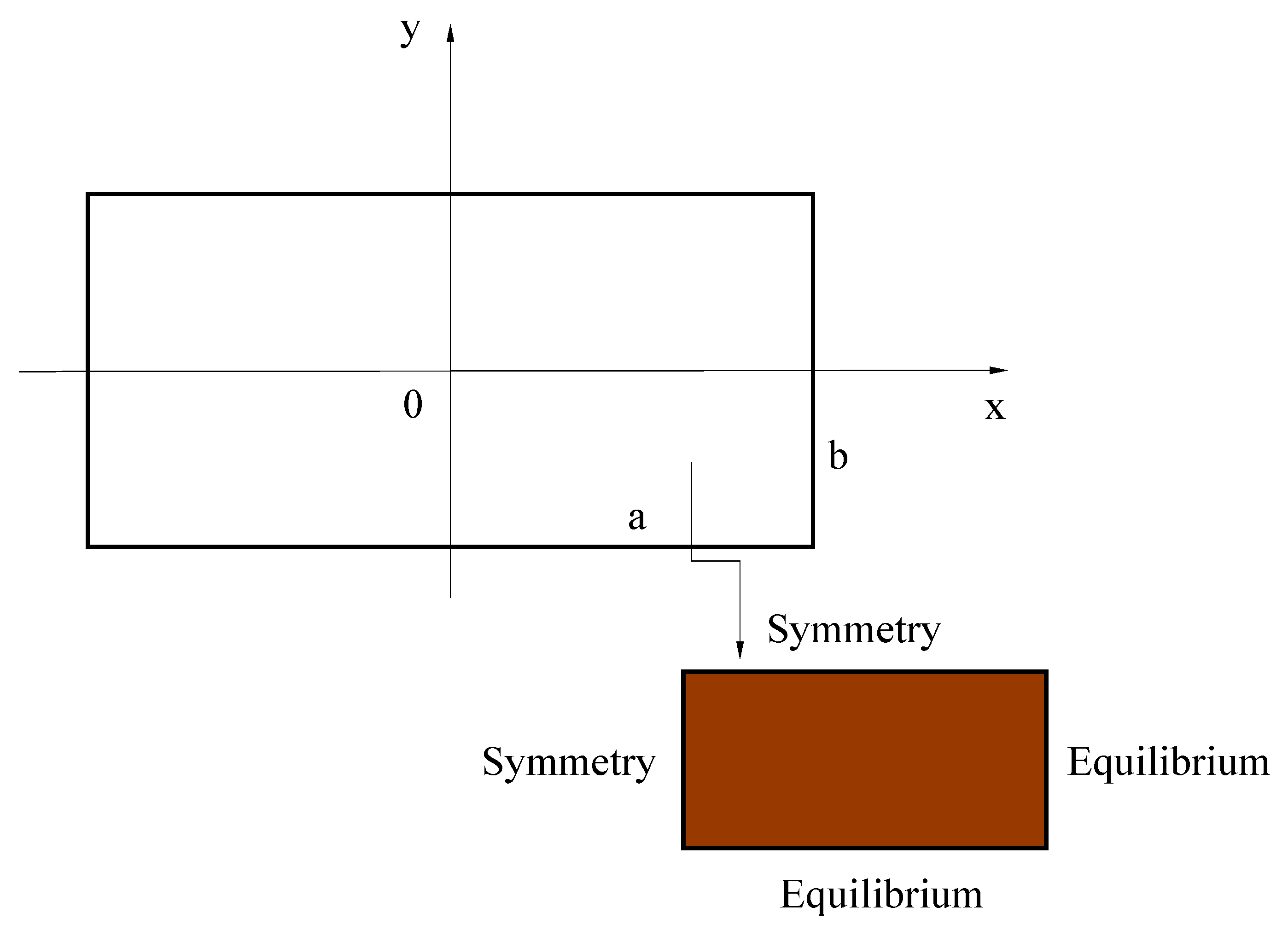
2. Materials and Methods

Heat and mass transport in a porous body can be predicted by considering the classical diffusion equation in its short form, expressed as:

$${\displaystyle \frac{\partial \left(\mathsf{\lambda }\mathsf{\Phi }\right)}{\partial \mathrm{t}}}=\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla \mathsf{\Phi }\right).$$

(1)

where ${\mathsf{\Gamma }}^{\mathsf{\Phi }}$ and $\mathsf{\lambda }$ represent transport properties, $\mathsf{\Phi }$ is the potential variable to be analyzed, and t is the time.

Herein, the exact solution to Equation (1) was obtained, taking into account the following assumptions:

(a)

Solids are homogeneous and isotropic.

(b)

The initial field of the potential $\mathsf{\Phi }$ inside the solid is uniform.

(c)

Process parameters are constant throughout the entire drying process.

(d)

Mass transfer occurs by liquid water diffusion (into the solid) and water evaporation (at the solid surface).

(e)

Heat transfer occurs by heat conduction (into the solid) and convection (at the solid surface).

By assuming that ${\mathsf{\Gamma }}^{\mathsf{\Phi }}$ and $\mathsf{\lambda }$ are constant, the formal solution of Equation (1), which represents the transient distribution of the potential $\mathsf{\Phi }$ inside the solid, can be written [16,17,18] as follows:

$$\mathsf{\Phi }=\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\psi }}_{\mathrm{n}}{\mathrm{e}}^{-{\mathsf{\gamma }}_{\mathrm{n}}\mathrm{t}}+{\mathsf{\Phi }}_{\mathrm{e}},$$

(2)

where ${\mathsf{\Phi }}_{\mathrm{e}}$ is the potential variable at the equilibrium condition, ${\mathsf{\gamma }}_{\mathrm{n}}$ represents the eigenvalues, and C_n is the constant to be obtained according to initial condition specified.

In Equation (2), the parameters C_n,${\mathsf{\gamma }}_{\mathrm{n}}$, and Φ_e are considered constants, and ${\mathsf{\Psi }}_{\mathrm{n}}$ is not a function of time. By substituting Equation (2) into Equation (1), the following expression is obtained:

$$\left.{\displaystyle \frac{\partial }{\partial \mathrm{t}}}\left[\mathsf{\lambda }\sum _{\mathrm{n}=1}^{\mathrm{N}} {\mathrm{C}}_{\mathrm{n}}{\mathsf{\psi }}_{\mathrm{n}}{\mathrm{e}}^{-{\mathsf{\gamma }}_{\mathrm{n}}\mathrm{t}}+{\mathsf{\Phi }}_{\mathrm{e}}\right]=\nabla \cdot \left\{\nabla \left[{\mathsf{\Gamma }}^{\mathsf{\Phi }}\left(\sum _{\mathrm{n}=1}^{\mathrm{N}} {\mathrm{C}}_{\mathrm{n}}{\mathsf{\psi }}_{\mathrm{n}}{\mathrm{e}}^{-{\mathsf{\gamma }}_{\mathrm{n}}\mathrm{t}}+{\mathsf{\Phi }}_{\mathrm{e}}\right)\right)\right]\right\}.$$

(3)

Calculating the derivative of Equation (3), it is possible to obtain the following expression:

$$\mathsf{\lambda }\sum _{\mathrm{n}=1}^{\mathrm{N}} {\mathrm{C}}_{\mathrm{n}}{\mathsf{\psi }}_{\mathrm{n}}\left(-{\mathsf{\gamma }}_{\mathrm{n}}\right){\mathrm{e}}^{-{\mathsf{\gamma }}_{\mathrm{n}}\mathrm{t}}=\sum _{\mathrm{n}=1}^{\mathrm{N}} {\mathrm{C}}_{\mathrm{n}}{\mathrm{e}}^{-{\mathsf{\gamma }}_{\mathrm{n}}\mathrm{t}}\nabla \cdot \nabla \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}{\mathsf{\psi }}_{\mathrm{n}}\right),$$

(4)

or yet:

$$\sum _{\mathrm{n}=1}^{\mathrm{N}} \left[\nabla \cdot \left[{\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathsf{\psi }}_{\mathrm{n}}\right]+\mathsf{\lambda }{\mathsf{\gamma }}_{\mathrm{n}}{\mathsf{\psi }}_{\mathrm{n}}\right]=0.$$

(5)

We notice that function ${\mathsf{\Psi }}_{\mathrm{n}}$ is determined according to the literature [16,17,18] as follows:

$${\mathsf{\psi }}_{\mathrm{n}}=\sum _{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{d}}_{\mathrm{n}\mathrm{j}}{\mathrm{f}}_{\mathrm{j}},$$

(6)

where f_j is a set of basis functions and ${\mathrm{d}}_{\mathrm{n}\mathrm{j}}$ are constants, which must be determined depending on the boundary condition established at the border of the solid.

In continuation of the mathematical formalism, replacing Equation (6) into Equation (5), multiplying both sides of Equation (5) by ${\mathrm{f}}_{\mathrm{i}}\mathrm{d}\mathrm{V}$ and integrating the resulting equation over the volume of the material in study, we obtain [19] the following equation:

$$\sum _{j=1}^N {\mathrm{d}}_{\mathrm{n}i}\left[{\displaystyle \frac{1}{\mathrm{V}}}{\int }_{\mathrm{v}} {\mathrm{f}}_{\mathrm{i}}\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{V}+\lambda {\gamma }_{\mathrm{n}}{\displaystyle \frac{1}{\mathrm{V}}}{\int }_{\mathrm{v}} {\mathrm{f}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{j}}\mathrm{d}\mathrm{V}\right]=0.$$

(7)

In matrix form, we can write Equation (7) as the following equation:

$$\left(\overline{\mathrm{A}}+{\mathsf{\gamma }}_{\mathrm{n}}\overline{\mathrm{B}}\right){\overline{\mathrm{d}}}_{\mathrm{n}}=0,$$

(8)

where $\overline{A}$ and $\overline{B}$ are square matrices of N × N elements, whose elements are determined by the following equations:

$${\mathrm{a}}_{\mathrm{i}\mathrm{j}}=\left[{\displaystyle \frac{1}{\mathrm{v}}}\int {\mathrm{f}}_{\mathrm{i}}\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{v}\right],$$

(9)

$${\mathrm{b}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{1}{\mathrm{V}}}{\int }_{\mathrm{v}} \mathsf{\lambda }{\mathrm{f}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{j}}\mathrm{d}\mathrm{V}.$$

(10)

In Equation (7), the coefficients ${\mathrm{d}}_{\mathrm{n}1},{\mathrm{d}}_{\mathrm{n}2},\dots ,{\mathrm{d}}_{\mathrm{n}\mathrm{N}}$ are elements of vector ${\overline{\mathrm{d}}}_{\mathrm{n}}$ presented in Equation (8). Further, it can be easily verified that matrix $\overline{\mathrm{B}}$ is symmetrical, so ${\mathrm{b}}_{\mathrm{i}\mathrm{j}}={\mathrm{b}}_{\mathrm{j}\mathrm{i}}$. Matrix $\overline{\mathrm{A}}$ is symmetrical as well. Details about the determination of the eigenvalues ${\mathsf{\gamma }}_{\mathrm{n}}$ and the coefficients ${\mathrm{d}}_{\mathrm{n}\mathrm{j}}$ corresponding to each ${\mathsf{\gamma }}_{\mathrm{n}}$ can found in the literature reported in the text.

For determining the transient distribution of Φ inside the body, we consider the initial condition, the body geometry, and the boundary condition. For this, consider the following mathematical identity:

$${\int }_{\mathrm{V}}{\mathrm{f}}_{\mathrm{i}}\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{V}={\int }_{\mathrm{V}}\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}{\mathrm{f}}_{\mathrm{i}}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{V}-{\int }_{\mathrm{V}}{\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{i}}\cdot \nabla {\mathrm{f}}_{\mathrm{j}}\mathrm{d}\mathrm{V}.$$

(11)

Since ${\mathsf{\Gamma }}^{\mathsf{\varphi }}$ is considered to be constant, Equation (11) can be rewritten as follows:

$${\int }_{\mathrm{V}}{\mathrm{f}}_{\mathrm{i}}\nabla ·\left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{V}={\int }_{\mathrm{S}}{\mathsf{\Gamma }}^{\mathsf{\Phi }}{\mathrm{f}}_{\mathrm{i}}\nabla {\mathrm{f}}_{\mathrm{j}}\overrightarrow{\mathrm{n}}·\mathrm{d}\overrightarrow{\mathrm{S}}-{\int }_{\mathrm{V}}{\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{i}}·\nabla {\mathrm{f}}_{\mathrm{j}}\mathrm{d}\mathrm{V},$$

(12)

or yet

$${\int }_{\mathrm{v}} {\mathrm{f}}_{\mathrm{i}}\nabla \cdot \left({\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{j}}\right)\mathrm{d}\mathrm{V}={\int }_{\mathrm{s}} {\mathsf{\Gamma }}^{\mathsf{\Phi }}{\mathrm{f}}_{\mathrm{i}}\left({\displaystyle \frac{\partial {\mathrm{f}}_{\mathrm{j}}}{\partial \mathrm{n}}}\right)\mathrm{d}\mathrm{S}-{\int }_{\mathrm{v}} {\mathsf{\Gamma }}^{\mathsf{\Phi }}\nabla {\mathrm{f}}_{\mathrm{i}}·\nabla {\mathrm{f}}_{\mathrm{j}}\mathrm{d}\mathrm{V}.$$

(13)

In continuation, we consider the boundary condition as follows:

$$-{\mathsf{\Gamma }}^{\mathsf{\Phi }}{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial \overrightarrow{\mathrm{n}}}}=\mathrm{h}\left(\mathsf{\Phi }-{\mathsf{\Phi }}_{\mathrm{e}}\right).$$

(14)

In Equation (14), the variable $\mathrm{h}$ represents the convective transfer coefficient and $\overrightarrow{\mathrm{n}}$ represents the normal vector to the surface. Applying Equation (14) to Equation (13), we have the following equation:

$$-{\mathsf{\Gamma }}^{\mathsf{\Phi }}{\displaystyle \frac{\partial {\mathrm{f}}_{\mathrm{j}}}{\partial \overrightarrow{\mathrm{n}}}}={\mathrm{h}\mathrm{f}}_{\mathrm{j}},$$

(15)

In this research, we consider boundary conditions of the first kind, or the well-known Dirichlet condition (Φ prescribed at the surface). Thus, $\mathrm{h}$→∞ and, consequently, ${\mathrm{f}}_{\mathrm{j}}=0$.

For determining the values of the parameters ${\mathrm{C}}_{\mathrm{n}}$ in Equation (2), the initial condition (t = 0) was used, that is, $\mathsf{\Phi }={\mathsf{\Phi }}_0$. Then, using this value in Equation (2), the following expression is obtained:

$${\mathsf{\Phi }}_0=\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{n}}+{\mathsf{\Phi }}_{\mathrm{e}}.$$

(16)

Multiplying Equation (16) by ${\mathrm{f}}_{\mathrm{i}}\mathrm{d}\mathrm{V}$ and integrating over the volume of the material, we obtain [19] the following equation:

$${\int }_{\mathrm{v}}{\mathrm{f}}_{\mathrm{i}}\left({\mathsf{\Phi }}_0-{\mathsf{\Phi }}_{\mathrm{e}}\right)\mathrm{dV}={\int }_{\mathrm{v}}{\mathrm{f}}_{\mathrm{i}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{n}}\mathrm{dV}.$$

(17)

Equation (17) results in a set of N linear algebraic equations, and the parameters ${\mathrm{C}}_{\mathrm{n}}$ were obtained from the solution of the linear equations system.

In the literature [20,21], it is possible to find several methods in order to select the base functions, that describe the first-kind boundary conditions, ${\mathrm{f}}_{\mathrm{j}}^{\left(1\right)}$, which correspond to the equilibrium boundary condition at the body surface. The base functions of the first kind can be obtained from the first base function, as follows:

$${\mathrm{f}}_1={\mathsf{\phi }}_1{\mathsf{\phi }}_2{\mathsf{\phi }}_{3\dots }{\mathsf{\phi }}_{\mathrm{m}},$$

(18)

where the variable ${\mathsf{\phi }}_{\mathrm{m}}$ describes one of the surfaces of the body in analysis. It should be mentioned that each base function should tend to zero at the boundary of the solid (i.e., ${\mathsf{\phi }}_{\mathrm{m}}=0$), and m is the number of surfaces of the material under analysis. Finally, it should be taken into account that some base functions (not all) can be null at some point in the solid.

It is absolutely necessary that the set of basis functions be linearly independent, that is, no member of the set of basis functions is a linear combination of the other members. Furthermore, the computation of the parameters a_ij and b_ij in Equations (9) and (10) can be easily obtained for single geometries; however, for complex geometries, it becomes a difficult task, frequently requiring symbolic software to carry out the analytical or numerical integrations [18,20].

After the determination of the values of Φ, the average value of the potential Φ within the material can be determined by the following equation:

$$\overline{\mathsf{\Phi }}={\displaystyle \frac{1}{\mathrm{V}}}{\int }_{\mathrm{v}}\mathsf{\Phi }\mathrm{d}\mathrm{V},$$

(19)

where V is the volume of the solid analyzed. The average value parameter is important to give an idea of the potential Φ inside the solid change (in average) just as a function of time. Thus, it becomes possible to verify the transient effect of the other variables in the potential variable and to control the transient history of this parameter in the material.

To predict the transient mass transport within the solid by using Equation (1), we consider λ = 1, Γ^Φ = D (the mass diffusion coefficient), Φ = M (the local moisture content in dry basis), and h = h_m (the convective mass transfer coefficient at the surface), and thus, Fick’s second law of diffusion in the transient state will be as follows:

$${\displaystyle \frac{\partial \mathrm{M}}{\partial \mathrm{t}}}=\nabla \cdot \left(\mathrm{D}\nabla \mathrm{M}\right).$$

(20)

For prediction of the transient heat transfer, it is considered in Equation (1) λ = ρc_p (where ρ is the density and c_p corresponds to the specific heat), Γ^Φ = k (where k is the thermal conductivity), Φ = θ (where Φ is the local temperature), and h = h_c (where h_c is the convective heat transfer coefficient). Thus, the transient heat conduction equation will be as follows:

$${\displaystyle \frac{\partial \mathsf{\theta }}{\partial \mathrm{t}}}=\nabla \cdot \left(\mathsf{\alpha }\nabla \mathrm{M}\right),$$

(21)

where $\mathsf{\alpha }=\mathrm{k}/\left(\mathsf{\rho }{\mathrm{c}}_{\mathrm{p}}\right)$ corresponds to the thermal diffusivity.

This research focuses on the study of drying on a solid flat plate with dimensions R₁ × R₂ (see Figure 1).

For this study, both the symmetry and boundary conditions will be considered, as illustrated in Figure 2. The symmetry condition was established because two situations are occurring in the physical problem in study: one, namely, geometric symmetry due to the shape of the ceramic parts (rectangular plate), and another well-known physical symmetry due to the same boundary condition at the surface of the material (equilibrium condition). In the symmetry boundary condition, there is both no mass flow and no scalar flux across the boundary. Figure 3 illustrates the base functions of the flat plate. For this case, the border of the plate is given by 2a = R₁ and 2b = R₂. Then, the base functions will be specified by ${\mathsf{\phi }}_1=\mathrm{x}-\mathrm{a}=0$, ${\mathsf{\phi }}_2=\mathrm{y}-\mathrm{b}=0$, ${\mathsf{\phi }}_3=\mathrm{x}+\mathrm{a}=0,$ and ${\mathsf{\phi }}_4=\mathrm{y}+\mathrm{b}=0$.

For a 2D problem, the total volume of the flat plate will be given as follows [22,23]:

$$\mathrm{V}=4\left(\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}\mathrm{dzdxdy}\right)=4\mathrm{ab}$$

(22)

For mass transfer, the coefficients ${\mathrm{a}}_{\mathrm{ij}}$ and ${\mathrm{b}}_{\mathrm{ij}}$ of the matrices $\stackrel{\mathrm{-}}{\mathrm{A}}$ e $\stackrel{\mathrm{-}}{\mathrm{B}}$ are given by the following equations:

$${\mathrm{a}}_{\mathrm{ij}}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}\mathrm{D}\nabla {\mathrm{f}}_{\mathrm{i}}\nabla {\mathrm{f}}_{\mathrm{j}}\mathrm{dzdxdy},$$

(23)

and

$${\mathrm{b}}_{\mathrm{ij}}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{j}}\mathrm{dzdxdy},$$

(24)

and for heat transfer, they are given in the following equations:

$${\mathrm{a}}_{\mathrm{ij}}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}\mathrm{k}\nabla {\mathrm{f}}_{\mathrm{i}}\nabla {\mathrm{f}}_{\mathrm{j}}\mathrm{dzdxdy},$$

(25)

$${\mathrm{b}}_{\mathrm{ij}}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathsf{\rho }{\mathrm{c}}_{\mathrm{p}}\mathrm{f}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{j}}\mathrm{dzdxdy}.$$

(26)

The value of the coefficients C_n can be determined as follows:

$$\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\left({\mathsf{\Phi }}_0-{\mathsf{\Phi }}_{\mathrm{e}}\right)\mathrm{dzdxdy}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{n}}\mathrm{dzdxdy}.$$

(27)

Then, for mass transfer, we have the following equation:

$$\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\left({\mathrm{M}}_0-{\mathrm{M}}_{\mathrm{e}}\right)\mathrm{dzdxdy}=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{n}}\mathrm{dzdxdy},$$

(28)

and for heat transfer, we have the following equation:

$$\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\left({\mathsf{\theta }}_0-{\mathsf{\theta }}_{\mathrm{e}}\right)\mathrm{dzdxdy} =\underset{0}{\overset{1}{\int }}\underset{0}{\overset{\mathrm{a}}{\int }}\underset{0}{\overset{\mathrm{b}}{\int }}{\mathrm{f}}_{\mathrm{i}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{n}}\mathrm{dzdxdy}.$$

(29)

According to Figure 3, the base functions f_j for a flat plate are given by the following equation:

$${\mathrm{f}}_{\mathrm{j}}\left(\mathrm{x},\mathrm{y}\right)=\left({\mathrm{x}}^2-{\mathrm{a}}^2\right)\left({\mathrm{y}}^2-{\mathrm{b}}^2\right){\mathrm{x}}^{\mathrm{i}-\mathrm{j}}{\mathrm{y}}^{\mathrm{j}},$$

(30)

being i = 0, 1, 2, 3, 4, 5 and j = 0, 1, 2, 3, 4, 5. In this research, 21 base functions were used.

To validate the mathematical modeling developed in this research, the average moisture content and the average temperature (both in dimensionless form) of the ceramic plate (with dimensions R₁ × R₂) were compared with the results obtained using the exact solution of the mass diffusion equation obtained by the method of separation of variables, as follows [24,25]:

$$\overline{{\mathsf{\Phi }}^{\mathrm{*}}}=\sum _{\mathrm{n}=1}^{\mathrm{\infty }}\sum _{\mathrm{m}=1}^{\mathrm{\infty }}{\mathrm{B}}_{\mathrm{n}}{\mathrm{B}}_{\mathrm{m}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\left({{\mathsf{\beta }}_{\mathrm{n}}}^2+{{\mathsf{\beta }}_{\mathrm{m}}}^2\right){\displaystyle \frac{{\mathsf{\Gamma }}^{\mathsf{\Phi }}}{\mathsf{\lambda }}}\mathrm{t}\right],$$

(31)

where $\overline{{\mathsf{\Phi }}^{\mathrm{*}}}=\overline{(\mathsf{\Phi }-{\mathsf{\Phi }}_{\mathrm{e}})/({\mathsf{\Phi }}_0-{\mathsf{\Phi }}_{\mathrm{e}})}$ and the coefficients ${\mathrm{B}}_{\mathrm{n}}$ and ${\mathrm{B}}_{\mathrm{m}}$ are given by the following equation:

$${\mathrm{B}}_{\mathrm{n}}={\displaystyle \frac{2}{{\left({\mathsf{\beta }}_{\mathrm{n}}{\mathrm{R}}_1\right)}^2}},$$

(32)

$${\mathrm{B}}_{\mathrm{m}}={\displaystyle \frac{2}{{\left({\mathsf{\beta }}_{\mathrm{m}}{\mathrm{R}}_2\right)}^2}},$$

(33)

where the eigenvalues ${\mathsf{\beta }}_{\mathrm{j}}$ are determined by the following equation:

$$\mathrm{c}\mathrm{o}\mathrm{s}\left({\mathsf{\beta }}_{\mathrm{n}}{\mathrm{R}}_1\right)=0,$$

(34)

$$\mathrm{c}\mathrm{o}\mathrm{s}\left({\mathsf{\beta }}_{\mathrm{m}}{\mathrm{R}}_2\right)=0.$$

(35)

In general, dimensions, mass diffusion coefficient, thermal conductivity, specific heat, density, and thermal diffusivity are dependent on the moisture content or temperature, or a combination thereof; however, in most physical situations, variations in these parameters are negligible due to small variations experimentally observed throughout the drying process. Thus, to describe the moisture removal and heating of the ceramic plate, the following thermophysical and geometric parameters established in

Table 1. Geometric and moisture parameters of the ceramic plate for different drying-air conditions.

Air		Ceramic Plate
T (°C)	RH (%)	R1 (mm)	R2 (mm)	M0 (d.b.)	Me (d.b.)
110	2	120	60	0.102	0.0043130
80	6	120	60	0.094	0.000935
60	14	120	60	0.078	0.005395

T—temperature; RH—relative humidity; R₁ and R₂—dimensions of the plate; M₀—initial moisture content; M_e—equilibrium moisture content.

and

Table 2. Thermophysical parameters of the ceramic plate for different drying conditions.

Air		Ceramic Plate
T (°C)	RH (%)	D (m2/s)	α (m2/s)	$\mathsf{\rho }$ (kg/m3)	k (W/m K)	cp (J/kg K)
110	2	6.82 × 10−8	3.11 × 10−7	1920	1.0	1673.51
80	6	5.17 × 10−8	---	---	---	---
60	14	2.89 × 10−8	---	---	---	---

T—temperature; RH—relative humidity; D—diffusion coefficient; α—thermal conductivity; $\mathsf{\rho }$—density; k—thermal conductivity; c_p—specific heat.

were used:

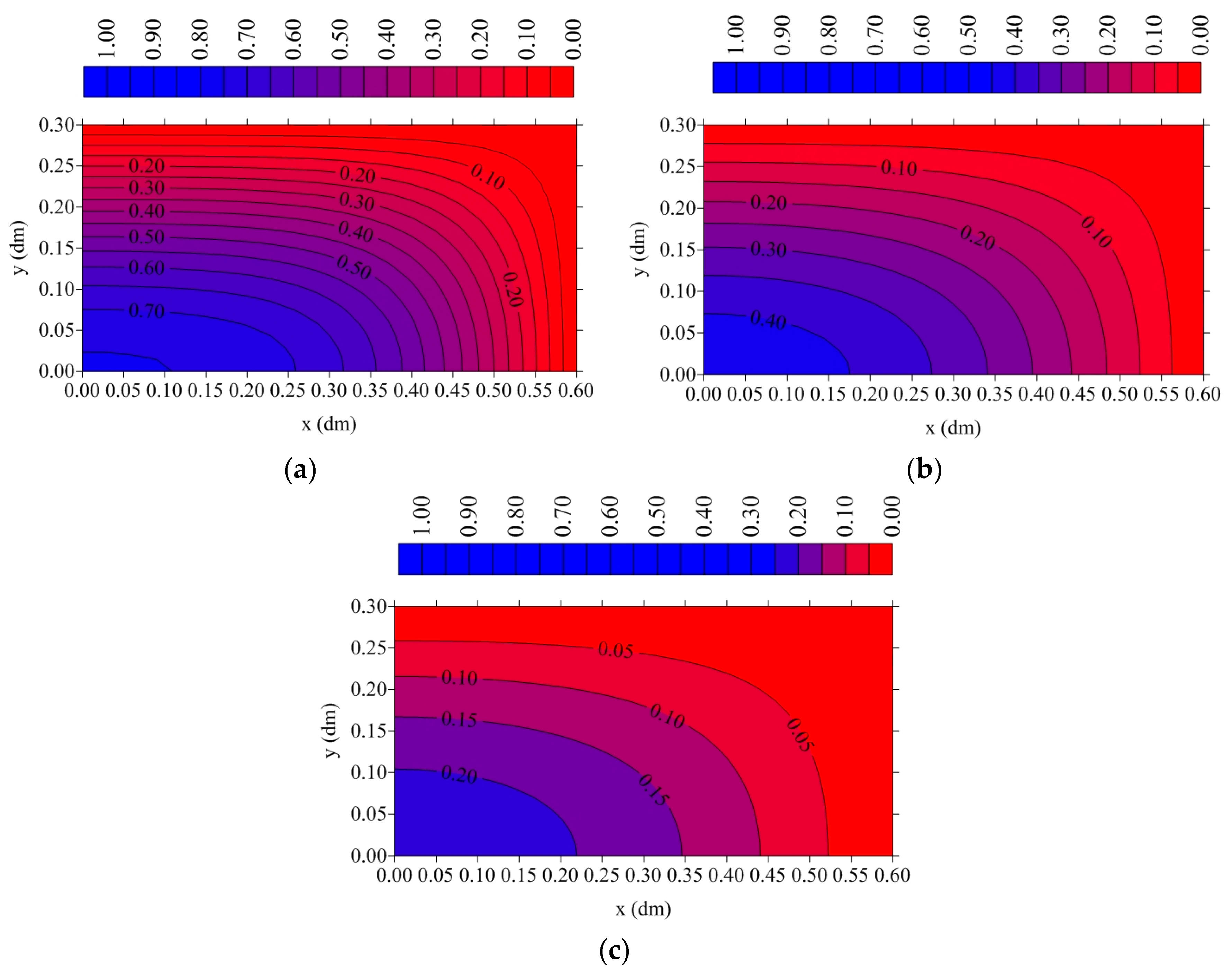
3. Results and Discussions

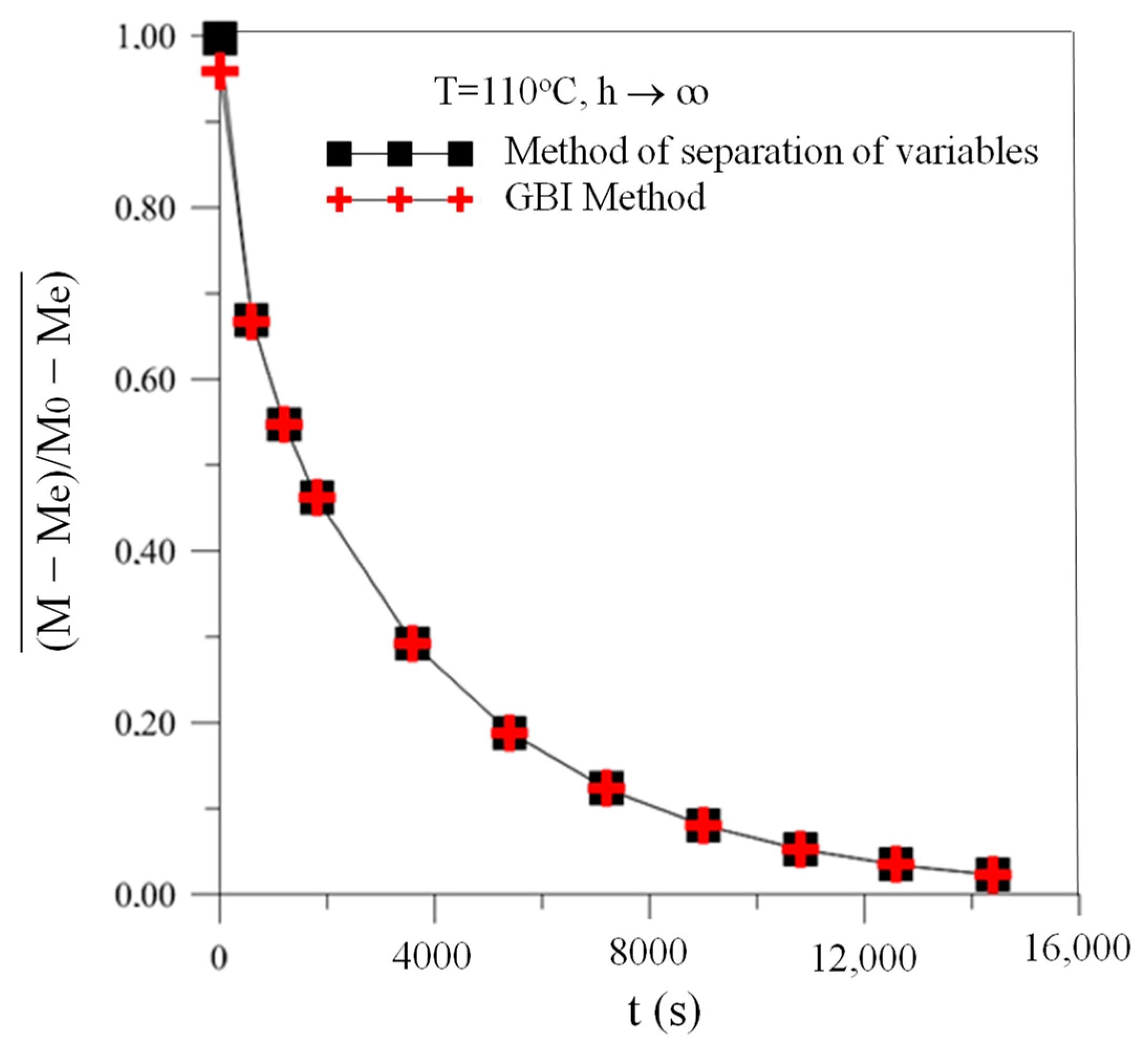
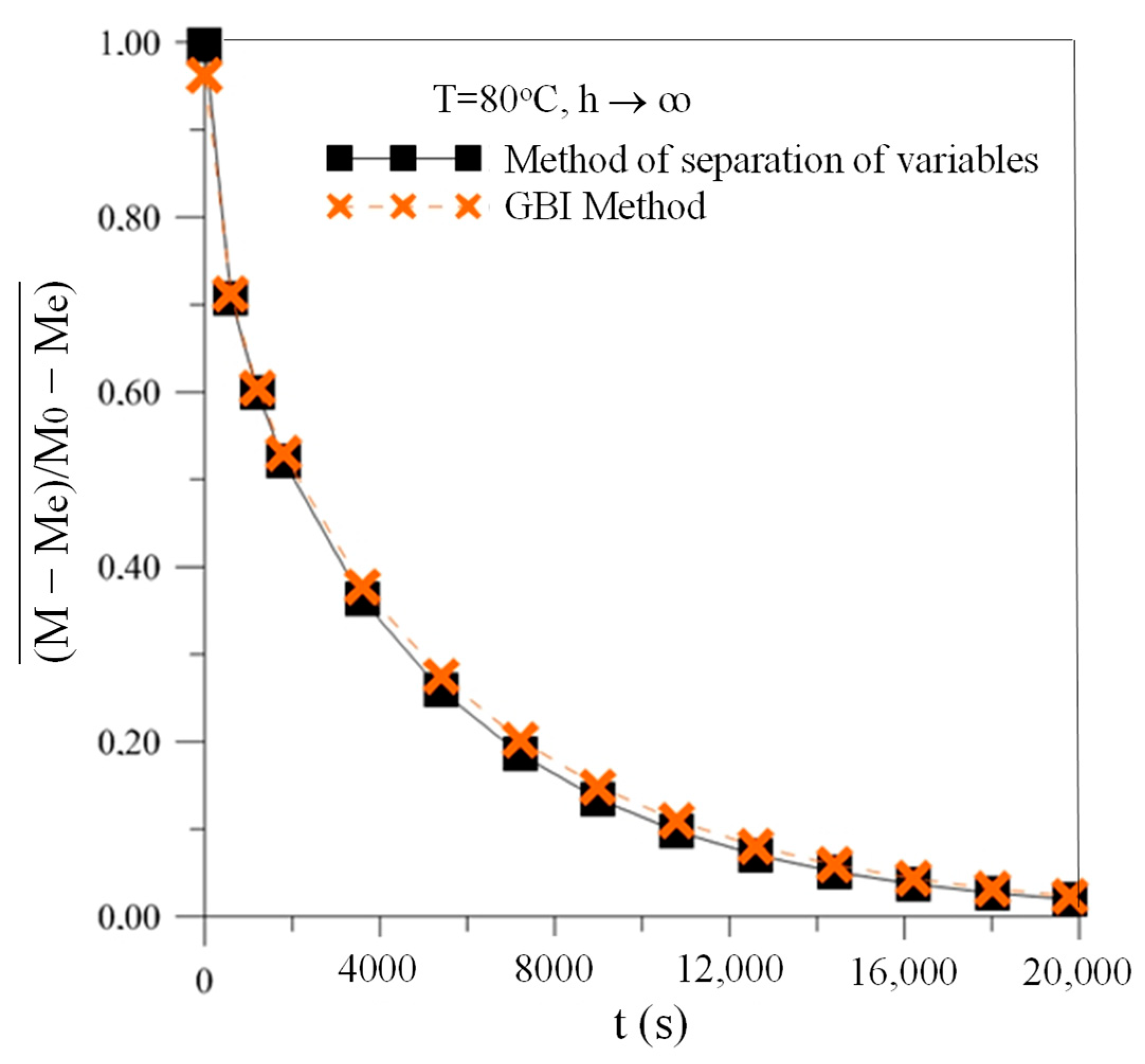
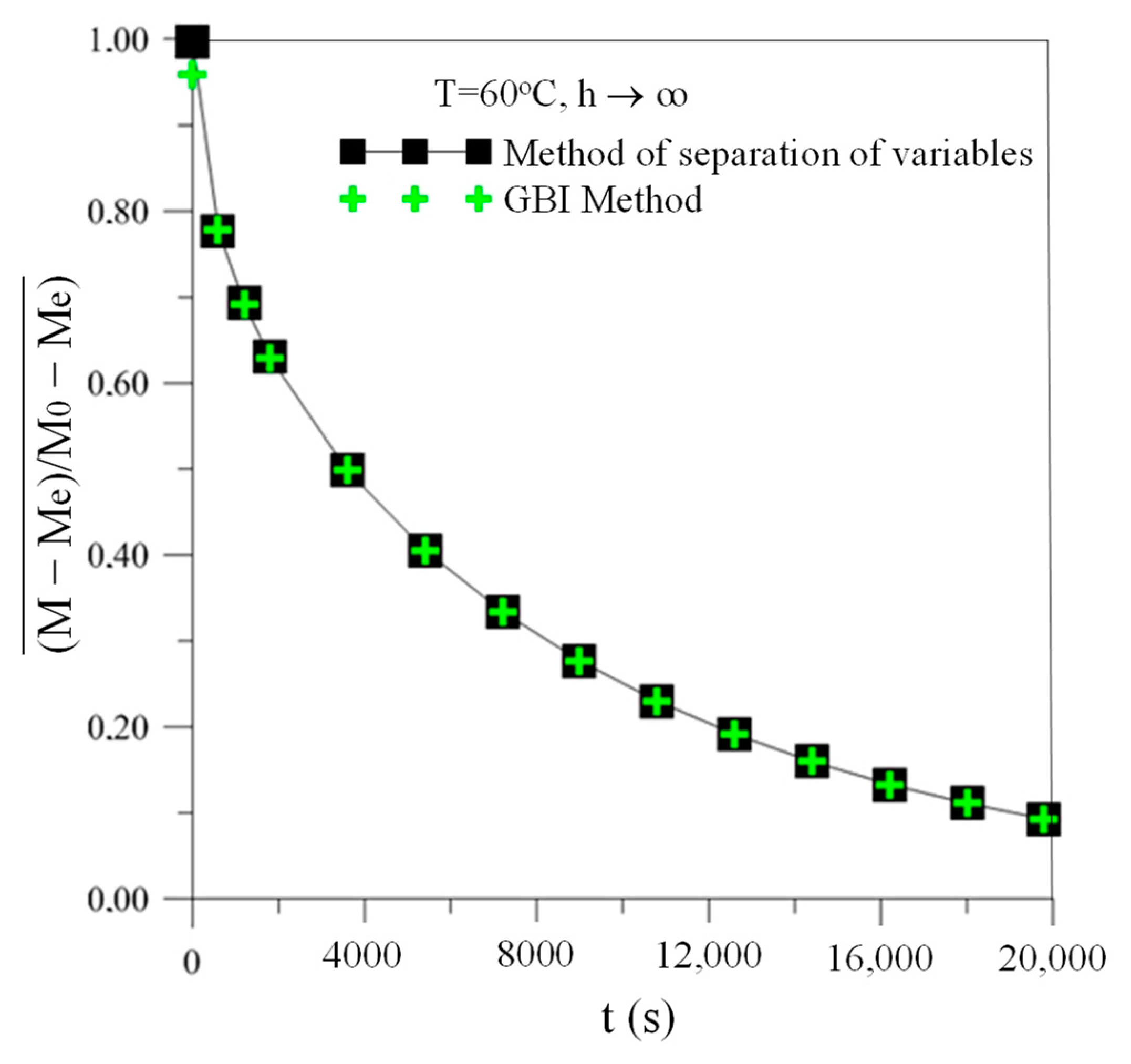
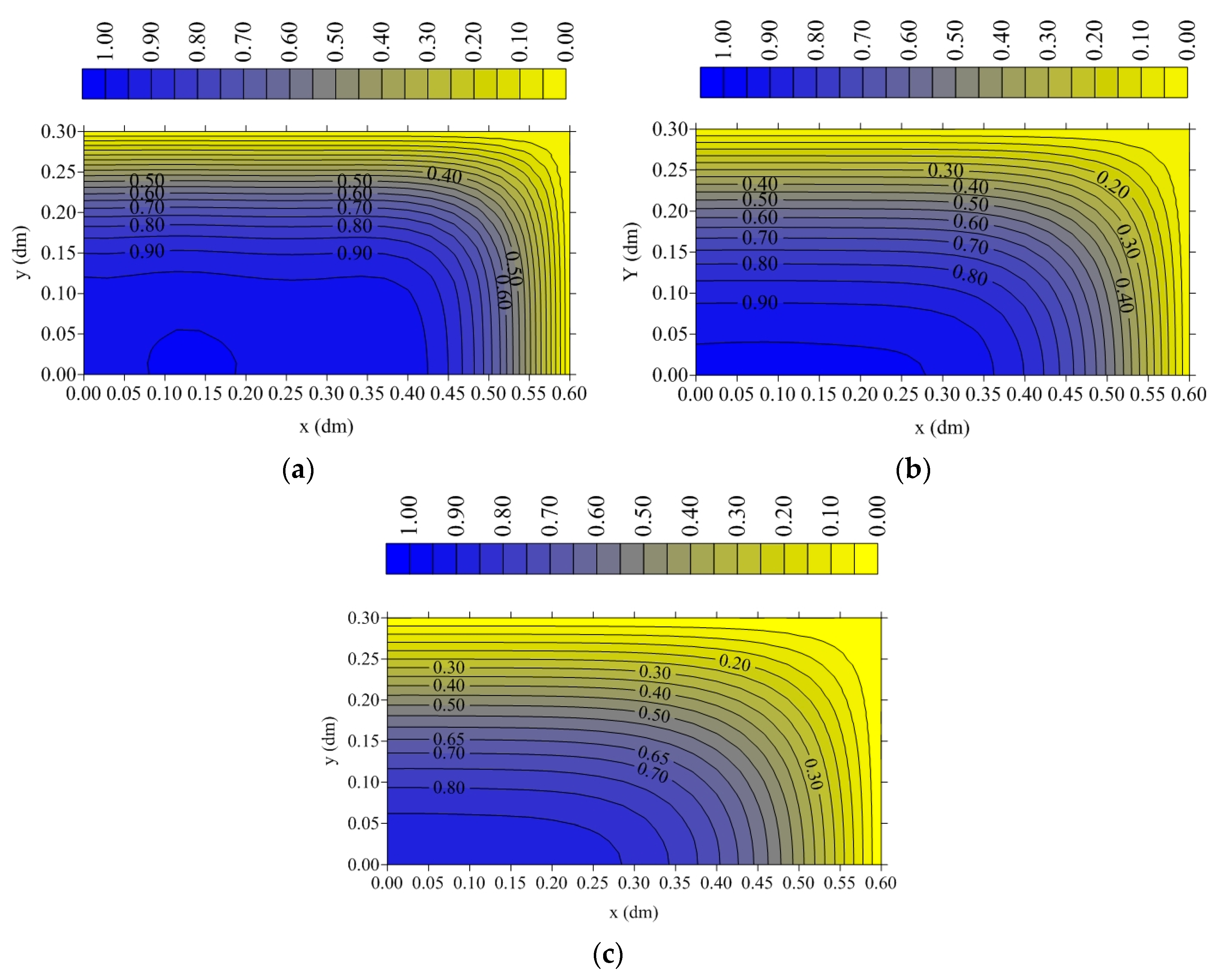
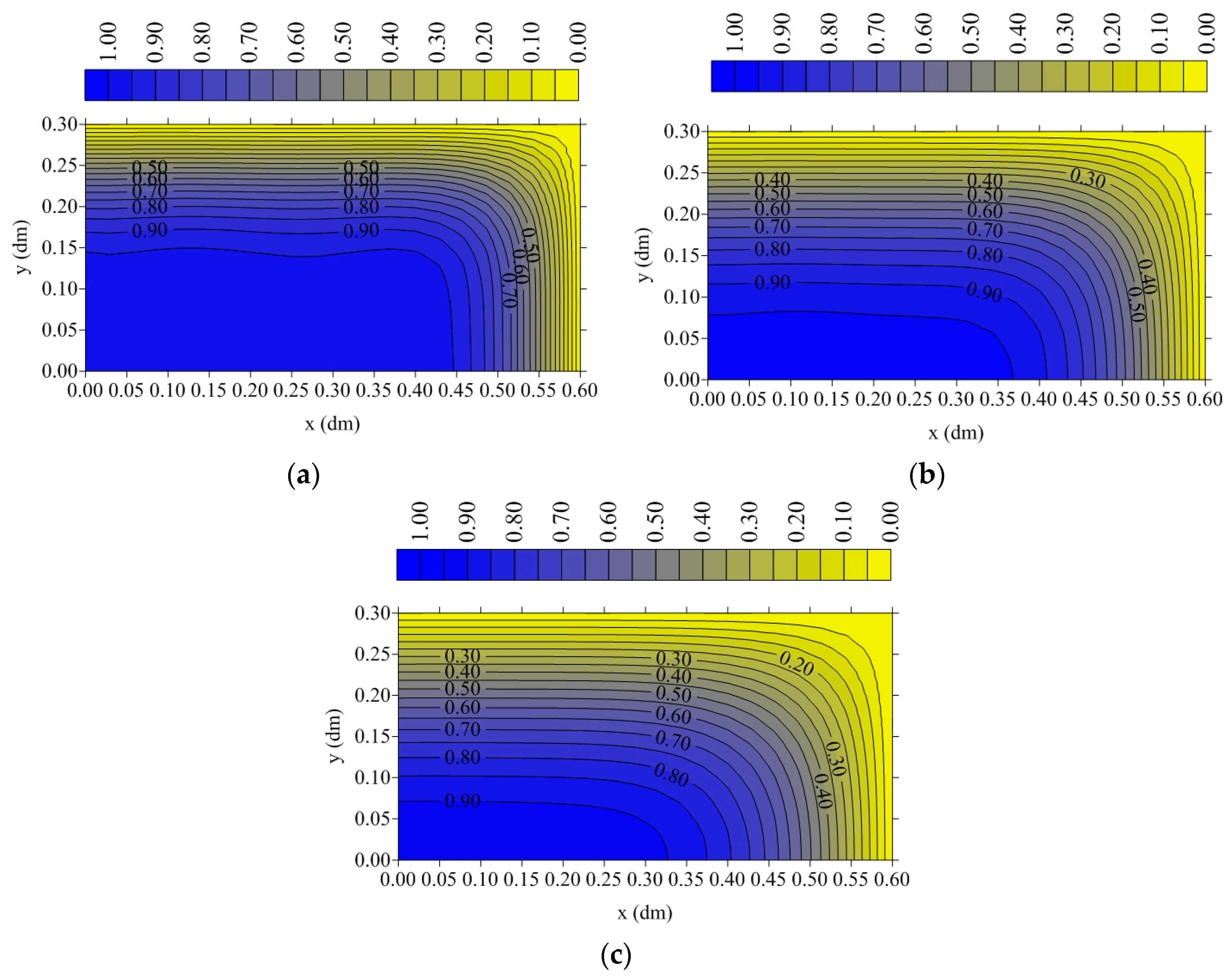
3.1. Moisture Transport

Figure 4, Figure 5 and Figure 6 illustrate the transient history of the average moisture content obtained by the GBI and variable separation methods considering first-kind boundary conditions and constant thermophysical properties for three temperatures: 110, 80, and 60 °C, respectively. Analyzing these figures, an excellent concordance can be clearly seen between the results for average moisture content obtained by the two different methods, thus proving the versatility and effectiveness of the GBI method in predicting the drying phenomenon.

Comparing both Figure 4, Figure 5 and Figure 6, from a physical point of view, it is possible to see that the moisture removal rate is strongly dependent on the air temperature. Thus, the higher the drying-air temperature, the higher the moisture migration rate, and the shorter the final process time until the ceramic slab reaches hygroscopic equilibrium. The explanation for this effect is related to the maximum solubility of water vapor in dry air, which increases with an increase in air temperature and a reduction in relative humidity. Therefore, the air’s ability to absorb water vapor is greater when a higher drying air temperature is used. Further, we can add the main effect of the difference between the partial pressure of water vapor on the surface of the ceramic piece and the partial pressure of water vapor in humid air, which increases with increasing air temperature and decreases with increasing relative humidity in the surrounding air. Both effects contribute to an increase in the moving velocity of water molecules inside the ceramic parts towards the surface and, consequently, to an increase in the velocity of moisture removal.

Figure 7, Figure 8 and Figure 9 show the dimensionless moisture content fields inside the ceramic plate (one-fourth of the physical domain due to the geometric and physical symmetry conditions) at the moments: (a) t = 600 s, (b) t = 1200 s, and (c) t = 1800 s, for temperatures 110, 80, and 60 °C, respectively. Analyzing these figures, it can be seen that the iso-concentration lines follow the shape of the plate and that close to its surface, there are the greatest moisture gradients and, therefore, the greatest loss of moisture over time, due to the fact that they are in direct contact with the drying air. At the top of the ceramic slab, especially at a temperature of 110 °C, there is a more pronounced loss of moisture, making this region more susceptible to drying defects, such as cracks and deformations, which can considerably affect the product quality at the end of the process.

A severe increase in temperature and a decrease in the relative humidity of the drying air may cause susceptible ceramic products to crack, fracture, and deformation. These effects are provoked by the moisture gradient formed due to the different hygroscopic capacities of different layers inside the material. As a result, hydric stresses are created, which, depending on the intensity, can overcome the material’s rupture stress and cause microcracks and failure, which can lead to the material breaking. In addition to the deformation caused by hydric stresses in ceramic products, we can also add the shrinkage induced by drying. A more recent comprehensive study on the drying-induced stress of ceramic pieces has been published in the literature [26].

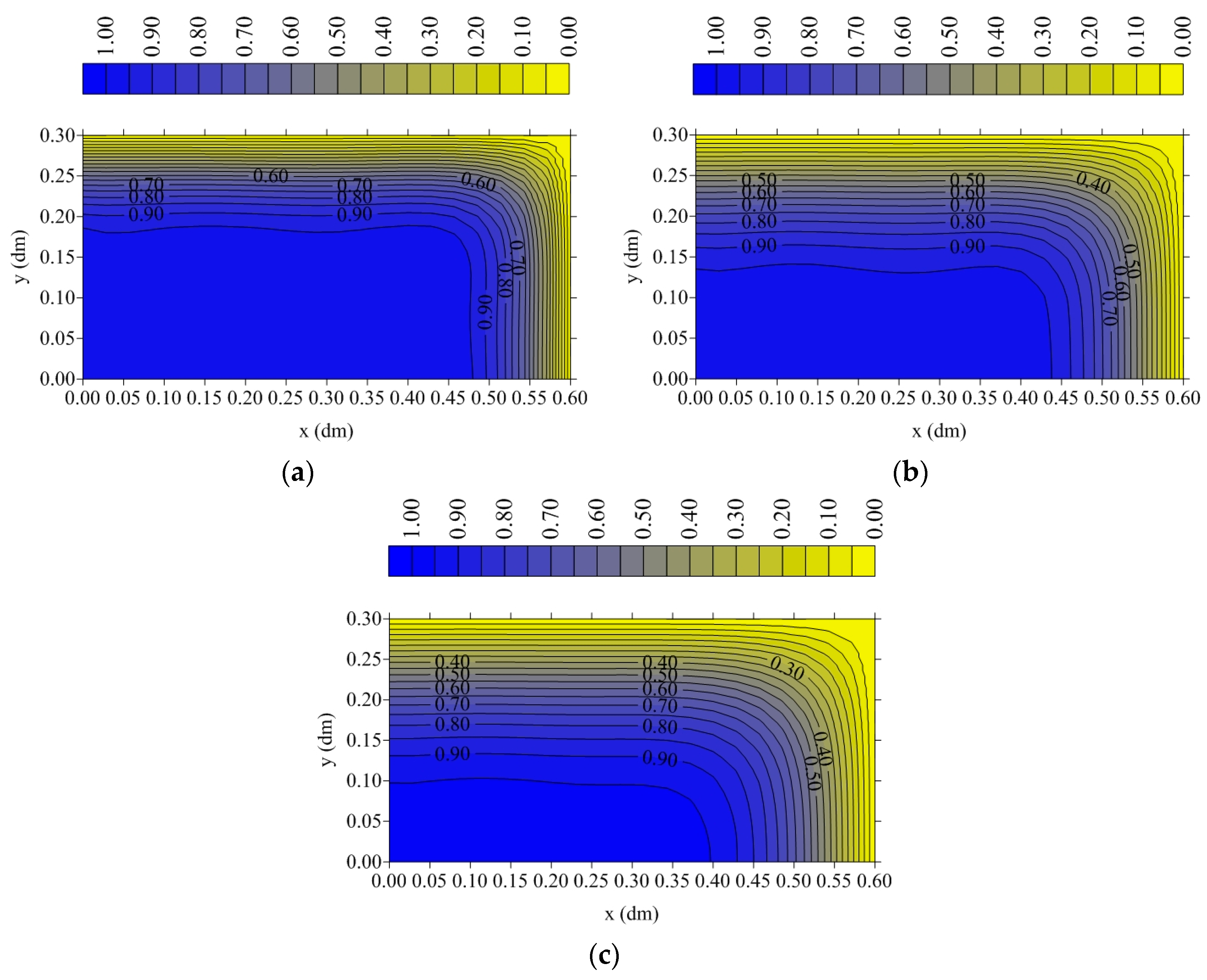
3.2. Heat Transport

Figure 10 illustrates the transient history of the dimensionless average moisture content and the dimensionless average temperature of the ceramic slab being dried at a constant temperature of 110 °C. Using the first-kind boundary condition, it can be seen that the average moisture content of the plate decreases over time, tending towards the equilibrium moisture content. Additionally, its dimensionless average temperature increases more quickly than the moisture content, reaching thermal equilibrium in a much shorter time than that necessary for the ceramic plate to achieve its hydroscopic equilibrium condition. This thermal phenomenon has occurred due to the high thermal diffusivity of the ceramic plate as compared to the mass diffusion coefficient.

According to the predicted results, it was verified that lower air-relative humidity and a higher air temperature lead to an increased drying rate. However, it is important to notice that the drying rate can also be influenced by many other factors, such as the moisture migration mechanism, the shape of the ceramic part, external environment conditions, initial moisture content, dimension variations, and green product porosity.

Volume variations can occur due to the evaporation of water (shrinkage) and heating of the ceramic parts (volumetric expansion). The thermal expansion phenomenon has little effect on the dimensional variation of the ceramic piece because the volumetric expansion coefficient is smaller than the volumetric shrinkage coefficient. It is important to mention that the stresses caused by thermal expansion (heating) are opposite to those caused by volume reduction (moisture loss). Furthermore, by analyzing the figures presented in this paper, it can be easily verified that the drying process occurred during the stage of decreasing drying rate, that is, a condition in which the moisture content is lower than the critical moisture content (the moisture content at which the drying rate begins to reduce and the moisture transition point from a constant drying rate period to a falling drying rate period). During this stage, the heat exchange is no longer compensated by the reduction in water mass, so the product´s temperature increases asymptotically to reach the thermal equilibrium condition. This occurs for the following two reasons: first, when the surface of the piece dries quickly and pores are narrower, the rate of moisture migration reduces to a value lower than the evaporation rate, and second, because the temperature of the ceramic piece is higher than the wet bulb temperature for a fixed drying-air condition, we have a decrease in the partial pressure of water vapor at the surface of the ceramic piece.

Figure 11 shows the dimensionless temperature distribution inside the ceramic slab (one-fourth of the physical domain) subjected to drying at a temperature of 110 °C at drying times of 600 s, 1200 s, and 1800 s. By analyzing the results presented in Figure 11, we can note accentuated heating in the region close to the vertex of the ceramic piece. Thus, this region is more appropriate to generate severe thermal stresses, which can be responsible for provoking several failures in the material after drying.

As a final comment, although this study has emphasized pure clayey material, it can be applied to other materials, for example, those composed of clay mixed with iron tailings [27,28,29]. Moreover, the study proved that the drying process must be carried out slowly and under controlled air conditions (moderate temperature and high relative humidity). This procedure will reduce undesirable cracks and deformations and thus allow the production of a clay product with good postdrying quality and energy savings.

4. Conclusions

In this study, robust mathematical modeling to predict heat transport and moisture migration in porous materials with arbitrary shapes was developed. The GBI method was applied to obtain the exact solution of the governing equations. The formulation was used for predicting the drying process of clay ceramic plates. From the results, the following conclusions can be summarized:

(a)

Both the model and the technique developed herein have great potential, presenting accuracy and efficiency in simulating many practical problems of diffusion such as heating, cooling, wetting, and drying of solids of different shapes. The solution to these different diffusion problems can be realized by changing the potential variables and the basis function related to the body’s shape.

(b)

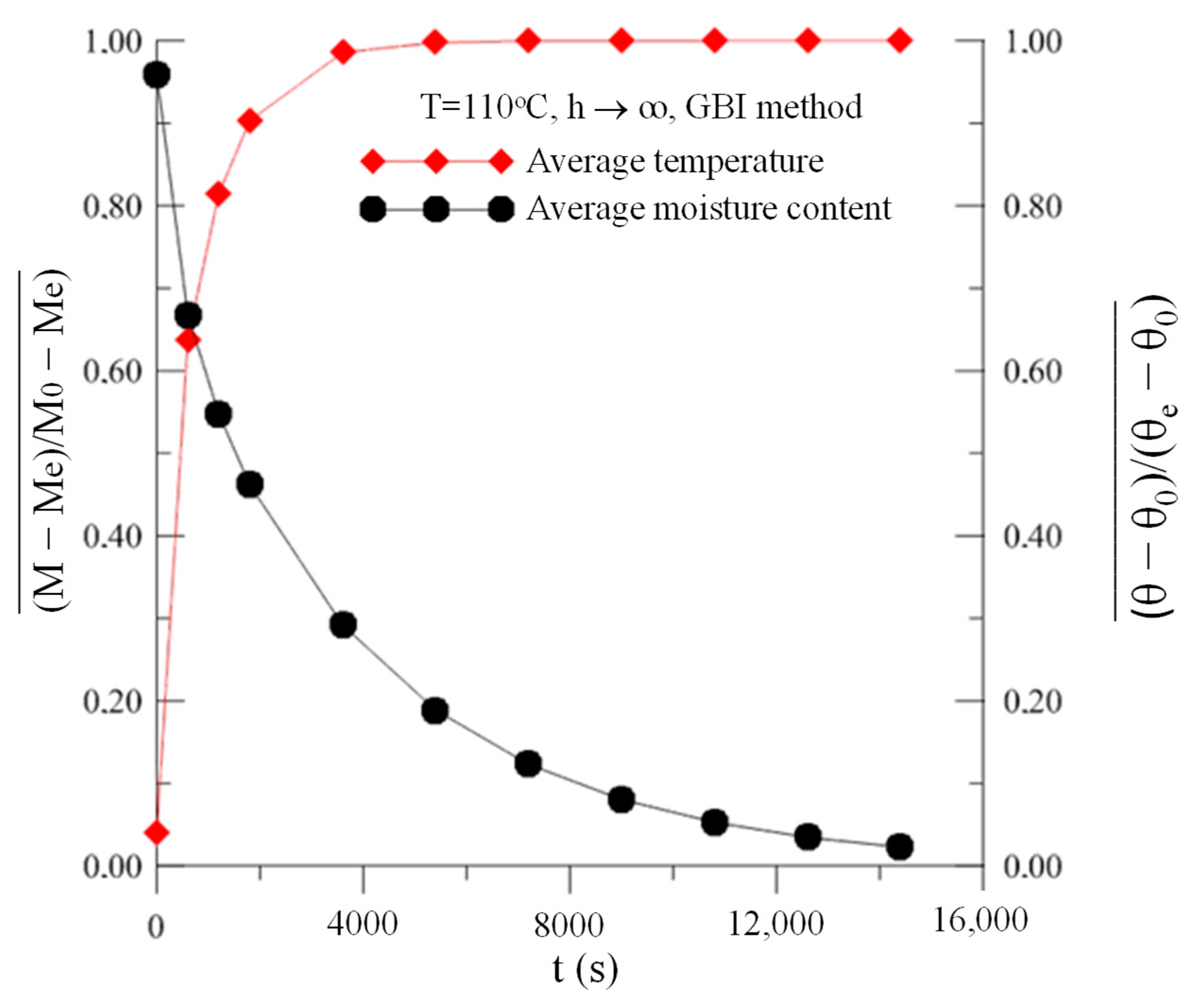
The drying process at higher temperatures and lower relative humidity occurs in a shorter time. For example, at T = 110 °C and RH = 2%, the total drying time reached values close to 15,000 s and the average moisture content was almost zero. However, at T = 60 °C and RH = 14%, the total drying time reached values close to 20,000 s, and the average moisture content was almost 0.1. Thus, it is clear that at 110 °C, the drying rate is higher than at 60 °C. The same analysis can be easily verified at any moment of drying, especially at the beginning of the drying process.

(c)

The highest temperature and moisture gradients in the ceramic parts are found closest to the surface, especially at the edge point, making these regions more susceptible to the highest hydric and thermal stresses, which can provoke drying defects such as deformations, cracks, and fissures that reduce the material’s quality after processing.

This study highlights the ease of applying the methodology to different materials, their nature and composition, and geometric shapes by changing only the base functions when compared with the exact solution (method of separation of variables) of the diffusion problem in conventional geometries such as flat plates, spheres, and cylinders, where it is absolutely necessary to use the diffusion equation written in a coordinate system adequate to a specified geometry. Furthermore, this study has shown that the proposed modeling can be useful for several purposes, such as the detection of the correct estimation of total drying time, reduction in energy consumption, increase in productivity of the dried clay piece, and in-depth understanding of the effect of process variables on product quality.