Mechanical Response and Anti-Reflective Crack Design in New Asphalt Overlays on Existing Asphalt Overlaying Composite Portland Cement Pavement
Abstract
1. Introduction
2. Project
3. Detection and Evaluation
3.1. Pavement Structural Integrity
3.2. Pavement Layer Thickness
3.3. Pavement Bearing Capacity
- Considering the requirement for the minimum parameters in pavement structure assessment and the convenience of structure evaluation, the pavement layer beneath the cement slab was considered as a layer of elastic half-space foundation. The pavement combination of Type B is thus represented as GAC-13C (modified), AC-25C (modified), cement concrete slab, and equivalent subgrade from top to bottom.
- The thickness range and modulus range of the four structural layers were specified, respectively. Subsequently, 5000 sets of theoretical pavement structures were randomly generated. The theoretical deflection basins for each of these pavement structures were then computed using the pavement analysis software KENLAYER.
- A database of defection basin parameters was constructed, which included indices such as the single deflection value, deflection ratio, deflection difference, curvature, shape factor, slope, area, and more. The relationship between these defection basin parameters from the theoretical deflection basins and the modulus of each pavement structural layer was established using a neural network model.
- According to (3), the defection basin parameters of the in situ measured deflection basin were computed, and the four moduli of the structural layer were predicted using the established neural network model. Subsequently, these four modulus values, along with the thickness measurements obtained by GPR, were input into KENLAYER to obtain the calculated modulus deflection basin. When the root mean square error (RMSE) is less than 10%, an acceptable backcalculated modulus combination of pavement structure can be obtained.
- The modulus combinations for each measured deflection basin were statistically analyzed. The mean modulus of each structure layer, along with the representative value at a 95% guarantee rate, are listed in Table 4.
4. Optimization Design of Repaving Structure
4.1. Optimization Principle of Repaving Structure Design
4.2. Thickness Design of Stress-Absorbing Layer
5. Material Design of Stress-Absorbing Layer
5.1. Requirements and Objectives
5.2. Mixture Design of Stress-Absorbing Layer
5.2.1. Raw Materials
5.2.2. Grading Design
5.3. Performance Verification of Stress-Absorption Layer
6. Conclusions
- (1)
- A detection and evaluation system utilizing 3D GPR and FWD was developed to assess the structural integrity and bearing capacity. It accurately measures the layer thickness and modulus, with errors of less than 3%. Transverse cracks in asphalt overlays primarily arise from load-induced grade stresses and slab joint effects.
- (2)
- Additionally repaving with a 10 cm new asphalt layer can reduce temperature stress by 64.1% and fatigue stress by 29.3% at the cement slab bottom, and theoretically extends the service life by 23.1 years. To combat reflective cracking, the reasonable thickness of the stress-absorbing layer ranges from 1.5 cm to 2.0 cm. The optimal design for a Type B pavement repaving asphalt layer consists of a 4 cm SMA-13 for the surface wear layer, a 4 cm AC-16 for the anti-rutting layer, and a 2 cm stress-absorbing layer for anti-reflective cracking.
- (3)
- The ratio of asphalt binder to aggregate is 8.5%, with percentages of 3–5 mm sandstone and 0–3 mm sandstone of 69% and 21.5%, respectively. The impact toughness of the designed stress-absorbing layer was about 1599 N∙mm, which is about 1.05 times and 1.44 times that of the stress-absorbing layer that has been successfully used for four years and the AC-16 asphalt mixture, respectively. This proves that the stress-absorbing layer designed in this paper has excellent stress-absorbing capability.
Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Liao, C.; Xiong, C.; Chen, C.; Wang, Z.; Wu, C.; Li, S.; Li, W.; Xu, X. Research on distresses detection, evaluation and maintenance decision-making for highway pavement in reconstruction and expansion project. Case Stud. Constr. Mater. 2023, 19, e02451. [Google Scholar] [CrossRef]
- Itani, H.; Saad, G.; Chehab, G. The use of geogrid reinforcement for enhancing the performance of concrete overlays: An experimental and numerical assessment. Constr. Build. Mater. 2016, 124, 826–837. [Google Scholar] [CrossRef]
- Deng, H.; Fu, X.; Gao, W.; Ni, T.; Chen, K. Research on New Technology to Control Highway Semi-Rigid Base Asphalt Pavement Cracks. Adv. Eng. Mater. 2011, 194–196, 1632–1638. [Google Scholar]
- Li, S.; Liu, Z.; Chen, X. Application Technology of Thin Asphalt Concrete Overlay on Old Pavement. Adv. Eng. Mater. 2011, 282–283, 124. [Google Scholar]
- Ning, P.; Zhang, J.; Tian, Q. Numerical simulation analysis of the application of cement-mixed pile curtain in an expressway extension project. Int. J. Pavement Eng. 2018, 21, 170–176. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Luo, S. Reflection Crack Analysis of Asphalt Overlay on Cement Concrete Pavement Based on XFEM. Adv. Civ. Eng. 2021, 2021, 1230447. [Google Scholar] [CrossRef]
- Zhao, Z.; Guan, X.; Xiao, F.; Xie, Z.; Xia, P.; Zhou, Q. Applications of asphalt concrete overlay on Portland cement concrete pavement. Constr. Build. Mater. 2020, 264, 120045. [Google Scholar] [CrossRef]
- Jin, T.; Liu, L.; Yang, R.; Sun, L.; Yuan, J. Investigation of interlayer bonding performance between asphalt concrete overlay and Portland cement concrete using inclined shear fatigue test. Constr. Build. Mater. 2023, 400, 132681. [Google Scholar] [CrossRef]
- Naseri, H.; Shokoohi, M.; Jahanbakhsh, H.; Golroo, A.; Gandomi, A.H. Evolutionary and swarm intelligence algorithms on pavement maintenance and rehabilitation planning. Int. J. Pavement Eng. 2022, 23, 4649–4663. [Google Scholar] [CrossRef]
- JTG/T 5142-01—2021; Technical Specifications for Maintenance of Highway Asphalt Pavement. Ministry of Transport of the People’s Republic of China: Beijing, China, 2021.
- JTJ 073.1—2001; Technical Specifications of Cement Concrete Pavement Maintenance for Highway. Ministry of Transport of the People’s Republic of China: Beijing, China, 2001.
- Vyas, V.; Singh, A.P. Modeling asphalt pavement condition using artificial neural networks. Mater. Today 2022, 62, 1671–1676. [Google Scholar] [CrossRef]
- Solatifar, N.; Lavasani, S.M. Development of an artificial neural network model for asphalt pavement deterioration using LTPP data. J. Rehabil. Civ. Eng. 2020, 8, 121–132. [Google Scholar] [CrossRef]
- Hoang, N.-D. An Artificial Intelligence Method for Asphalt Pavement Pothole Detection Using Least Squares Support Vector Machine and Neural Network with Steerable Filter-Based Feature Extraction. Adv. Civ. Eng. 2018, 2018, 7419058. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z. Review of applications of artificial intelligence algorithms in pavement management. J. Transp. Eng. B Pavements 2022, 148, 03122001. [Google Scholar] [CrossRef]
- Peraka, N.S.P.; Biligiri, K.P. Pavement asset management systems and technologies: A review. Autom. Constr. 2020, 119, 103336. [Google Scholar] [CrossRef]
- Thives, L.P.; Pais, J.; Pereira, P.A.A.; Minhoto, M.J.C.; Triches, G. Performance of Asphalt Rubber Mixture Overlays to Mitigate Reflective Cracking. Materials 2022, 15, 2375. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.W.; Doh, Y.S.; Lim, S. Mode I reflection cracking resistance of strengthened asphalt concretes. Constr. Build. Mater. 1999, 13, 243–251. [Google Scholar] [CrossRef]
- Xu, L.; Li, X.; Jiang, F.; Yu, X.; Wang, J.; Xiao, F. Thermosetting characteristics and performances of polyurethane material on airport thin-overlay. Constr. Build. Mater. 2022, 344, 128252. [Google Scholar] [CrossRef]
- Seferoğlu, M.T.; Seferoğlu, A.G.; Çelik, M.; Akpinar, M.V. Investigating the Influence of Joint Reinforcements of Portland Cement Concrete Slabs Under Asphalt Concrete Overlays on Vertical Deflections Using Accelerated Pavement Testing. Transp. Res. Rec. 2022, 2676, 296–305. [Google Scholar] [CrossRef]
- Li, X.; Wen, H. Effects of Preoverlay Pavement Conditions and Preoverlay Repair Methods on the Performance of Asphaltic Concrete Overlays. J. Transp. Eng. 2014, 140, 42–49. [Google Scholar] [CrossRef]
- Habbouche, J. Evaluation of Thin Asphalt Overlays for Pavement Preservation in Nevada. Master’s Thesis, University of Nevada, Reno, NV, USA, 2015. [Google Scholar]
- Das, A.; Bhuyan, M.R.; Khattak, M.J.; Zhang, Q. Mitigating reflective cracking in composite pavements through the use of a ductile concrete interlayer. Constr. Build. Mater. 2020, 259, 120383. [Google Scholar] [CrossRef]
- Dave, E.V.; Buttlar, W.G. Thermal reflective cracking of asphalt concrete overlays. Int. J. Pavement Eng. 2011, 11, 477–488. [Google Scholar] [CrossRef]
- Chen, D.; Won, M. CAM and SMA mixtures to delay reflective cracking on PCC pavements. Constr. Build. Mater. 2015, 96, 226–237. [Google Scholar] [CrossRef]
- Oshone, M.; Dave, E.V.; Sias, J.E. Asphalt mix fracture energy based reflective cracking performance criteria for overlay mix selection and design for pavements in cold climates. Constr. Build. Mater. 2019, 211, 1025–1033. [Google Scholar] [CrossRef]
- Khudoyarov, S.; Kim, N.; Lee, J.-J. Three-dimensional convolutional neural network–based underground object classification using three-dimensional ground penetrating radar data. Struct. Health Monit. 2020, 19, 1884–1893. [Google Scholar] [CrossRef]
- Xiong, X.; Tan, Y.; Hu, J.; Hong, X.; Tang, J. Evaluation of Asphalt Pavement Internal Distresses Using Three-Dimensional Ground-Penetrating Radar. Int. J. Pavement Res. Technol. 2024, 1–12. [Google Scholar] [CrossRef]
- Dong, Z.; Ye, S.; Gao, Y.; Fang, G.; Zhang, X.; Xue, Z.; Zhang, T. Rapid detection methods for asphalt pavement thicknesses and defects by a vehicle-mounted ground penetrating radar (GPR) system. Sensors 2016, 16, 2067. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zheng, J.; Yu, J.; Xiong, C.; Li, W.; Deng, J. Clustering of Asphalt Pavement Maintenance Sections Based on 3D Ground-Penetrating Radar and Principal Component Techniques. Buildings 2023, 13, 1752. [Google Scholar] [CrossRef]
- Vyas, V.; Singh, A.P.; Srivastava, A. Prediction of asphalt pavement condition using FWD deflection basin parameters and artificial neural networks. Road Mater. Pavement Des. 2021, 22, 2748–2766. [Google Scholar] [CrossRef]
- Mehta, Y.; Roque, R. Evaluation of FWD data for determination of layer moduli of pavements. J. Mater. Civ. Eng. 2003, 15, 25–31. [Google Scholar] [CrossRef]
- Kapela, R.; Śniatała, P.; Turkot, A.; Rybarczyk, A.; Pożarycki, A.; Rydzewski, P.; Wyczałek, M.; Błoch, A. Asphalt surfaced pavement cracks detection based on histograms of oriented gradients. In Proceedings of the 2015 22nd International Conference Mixed Design of Integrated Circuits & Systems (MIXDES), Torun, Poland, 25–27 June 2015; pp. 579–584. [Google Scholar]
- Fujita, Y.; Shimada, K.; Ichihara, M.; Hamamoto, Y. A method based on machine learning using hand-crafted features for crack detection from asphalt pavement surface images. In Proceedings of the Thirteenth International Conference on Quality Control by Artificial Vision 2017, Tokyo, Japan, 14 May 2017; pp. 117–124. [Google Scholar]
- Luo, X.; Gu, F.; Zhang, Y.; Lytton, R.L.; Birgisson, B. Kinetics-based aging evaluation of in-service recycled asphalt pavement. J. Clean. Prod. 2018, 200, 934–944. [Google Scholar] [CrossRef]
- Deng, Y.; Luo, X.; Zhang, Y.; Lytton, R.L. Determination of complex modulus gradients of flexible pavements using falling weight deflectometer and artificial intelligence. Mater. Struct. 2020, 53, 100. [Google Scholar] [CrossRef]
- Xiong, C.; Yu, J.; Zhang, X.; Korolev, E.; Svetlana, S.; Chen, B.; Chen, F.; Yang, E. Modulus backcalculation methodology based on full-scale testing road and its rationality and feasibility analysis. Int. J. Pavement Eng. 2022, 24, 2111424. [Google Scholar] [CrossRef]
- Kheradmandi, N.; Modarres, A. Precision of back-calculation analysis and independent parameters-based models in estimating the pavement layers modulus-Field and experimental study. Constr. Build. Mater. 2018, 171, 598–610. [Google Scholar] [CrossRef]
- Zhao, W.; Yang, Q.; Wu, W.; Liu, J. Improving the accuracy of pavement structural quality assessment by correcting numerical hypothetical model of modulus Back-Calculation through GPR. Constr. Build. Mater. 2022, 333, 127422. [Google Scholar] [CrossRef]
- Hong, X.; Tan, W.; Xiong, C.; Qiu, Z.; Yu, J.; Wang, D.; Wei, X.; Li, W.; Wang, Z. A Fast and Non-Destructive Prediction Model for Remaining Life of Rigid Pavement with or without Asphalt Overlay. Buildings 2022, 12, 868. [Google Scholar] [CrossRef]
- JTG D40—2011; Specifications for Design of Highway Cement Concrete Pavement. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- Vestena, P.M.; Schuster, S.L.; Almeida Jr, P.O.B.d.; Faccin, C.; Specht, L.P.; Pereira, D.d.S. Dynamic modulus master curve construction of asphalt mixtures: Error analysis in different models and field scenarios. Constr. Build. Mater. 2021, 301, 124343. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; Zheng, J.; Wu, H. Reflective Crack Propagation and Control in Asphalt Pavement Widening. J. Test. Eval. 2016, 44, 838–846. [Google Scholar] [CrossRef]
- Li, S. Numerical investigation on viscoelastic response of asphalt mixture under tire braking slip. Case Stud. Constr. Mater. 2023, 18, e02009. [Google Scholar] [CrossRef]
- Sun, H.-g. Development of an indoor test method for evaluating the anti-reflection crack performance of asphalt overlay. Case Stud. Constr. Mater. 2023, 19, e02241. [Google Scholar] [CrossRef]
- Ban, H.; Im, S.; Kim, Y.-R.; Jung, J.S. Laboratory tests and finite element simulations to model thermally induced reflective cracking of composite pavements. Int. J. Pavement Eng. 2018, 19, 220–230. [Google Scholar] [CrossRef]
- JTG D50—2017; Design Specification for Asphalt Pavement of Highways. Ministry of Transport of the People’s Republic of China: Beijing, China, 2017.
- Dempsey, B.J. Development and performance of interlayer stress-absorbing composite in asphalt concrete overlays. Transp. Res. Rec. 2002, 1809, 175–183. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Z.; Luo, Y.J. Material Composition Design and Anticracking Performance Evaluation of Asphalt Rubber Stress-Absorbing Membrane Interlayer (AR-SAMI). Adv. Mater. 2018, 2018, 8560604. [Google Scholar] [CrossRef]
- Joumblat, R.; Kassem, H.A.; Al Basiouni Al Masri, Z.; Elkordi, A.; Al-Khateeb, G.; Absi, J. Performance evaluation of hot-mix asphalt with municipal solid waste incineration fly ash using the stress sweep rutting test. Innov. Infrastruct. So. 2023, 8, 261. [Google Scholar] [CrossRef]
- Hassan, H.M.Z.; Wu, K.; Huang, W.; Chen, S.; Zhang, Q.; Xie, J.; Cai, X. Study on the influence of aggregate strength and shape on the performance of asphalt mixture. Constr. Build. Mater. 2021, 294, 123599. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Wang, Y.; Li, Q.; Liu, H. Time-and-Depth-Dependent Model of Chloride Diffusion Coefficient for Concrete Members Considering the Effect of Coarse Aggregate. J. Mater. Civ. Eng. 2018, 30, 04017302. [Google Scholar] [CrossRef]
- Yu, J.; Chen, F.; Deng, W.; Ma, Y.; Yu, H. Design and performance of high-toughness ultra-thin friction course in south China. Constr. Build. Mater. 2020, 246, 118508. [Google Scholar] [CrossRef]

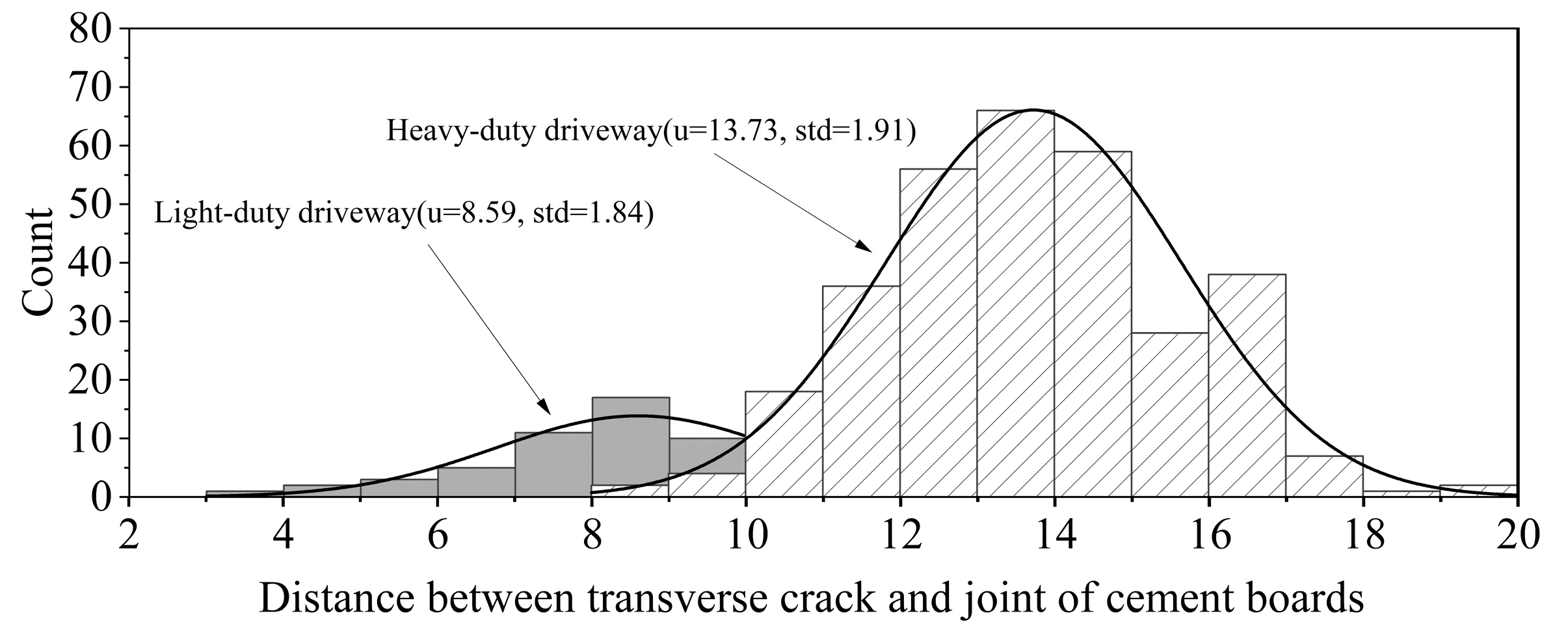
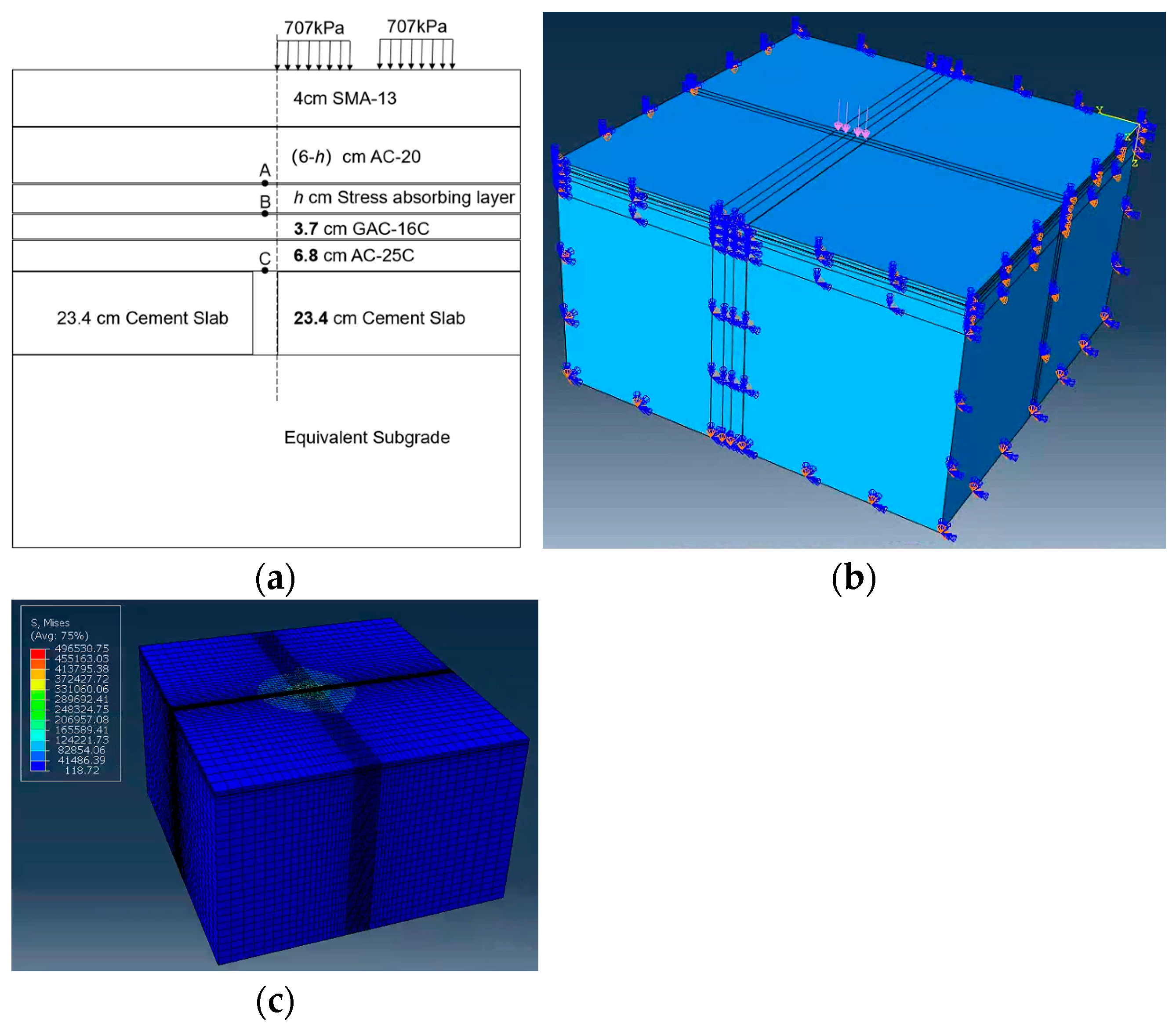
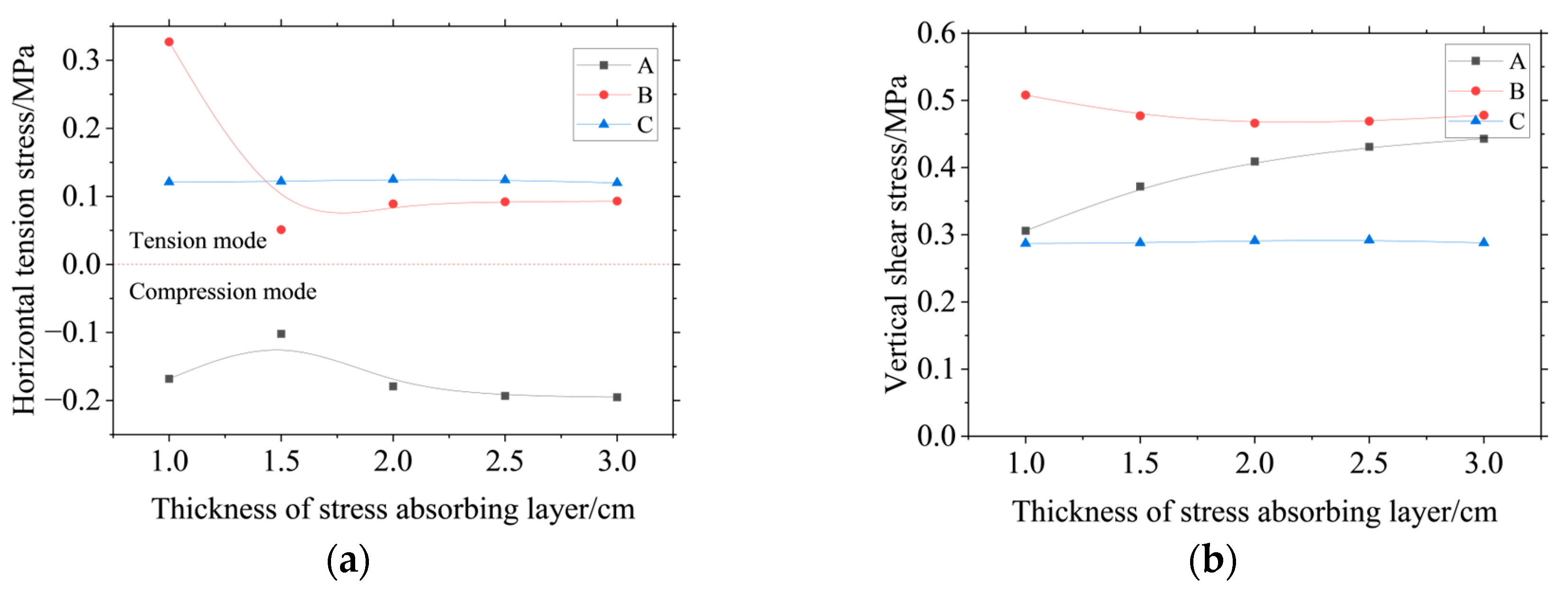

| Construction Time | Structural Layer | Type A | Type B-1 | Type B-2 |
|---|---|---|---|---|
| Major repairs carried out in 2008–2009 | Now top layer | 5 cm GAC-16 (binder modified using SBS) | 5 cm GAC-16C (binder modified using SBS) | 4 cm GAC-13C (binder modified using SBS) |
| Now middle layer | 8 cm AC-20C (binder modified using SBS) | 8 cm AC-25C (binder modified using SBS) | 8 cm AC-25C (binder modified using SBS) | |
| Now lower layer | 9~15 cm ATB-25 | / | 24 cm C20 cement concrete | |
| Built in 1996 | Old top layer | 3~4 cm anti-skid surface | 26 cm C35 cement concrete | 14 cm AC-20 |
| Old middle layer | 5 m AC-20 | / | / | |
| Old lower layer | 6~7 cm AM | / | / | |
| Old base layer | 20~28 cm cement stabilized | 18 cm cement stabilized | 28 cm cement stabilized | |
| Old crush layer | 28~46 cm gravel base | 15 cm gravel base | 28 cm gravel base |
| No. | Structure Type | Proportion |
|---|---|---|
| 1 | B-1 | 72.61% |
| 2 | B-2 | 2.78% |
| 3 | A | 24.61% |
| Structural Layer | Existing Top Asphalt Overlay | Existing Lower Asphalt Overlay | Ratio Greater Than the Design Value | Cement Slab | Ratio Greater Than the Design Value |
|---|---|---|---|---|---|
| Thickness/cm | [3.3, 4.1] | [6.7, 7.2] | / | [21.4, 24.0] | / |
| Representative value (95% guarantee rate) | 3.7 | 6.8 | 38.2% | 23.4 | 0% |
| Structure Layer | Mean Modulus/MPa | 95% Guarantee Representative Modulus/MPa | Representative Indoor Measured Modulus/MPa |
|---|---|---|---|
| 5 cm GAC-16C (modified with SBS) | 6331 | 5803 | / |
| 8 cm AC-25C (modified with SBS) | 5290 | 4467 | / |
| 26 cm C35 Portland cement concrete | 29,138 | 28,645 | 27,913 |
| Equivalent Subgrade | 453 | 364 | / |
| Structure Layer | Fatigue Stress at Bottom of Slab/MPa | Temperature Stress at Bottom of Slab/MPa | Predicted Service Life/Year |
|---|---|---|---|
| Existing pavement | 1.923 | 0.672 | 0.0 |
| Repaving a 10 cm asphalt layer | 1.358 | 0.241 | 23.1 |
| Raw Materials | 3–5 mm | 0–3 mm | Cement | Filler | Asphalt Binder |
|---|---|---|---|---|---|
| Apparent density, g/cm3 | 2.748 | 2.698 | 3.140 | 2.690 | 1.037 |
| Bulk density, g/cm3 | 2.660 | 2.602 | 3.140 | 2.690 | |
| Compact density, g/cm3 | 1.481 |
| Sieve Size/mm | Pass Rate (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| 3–5 | 100 | 91.5 | 3.8 | 1.8 | 0.6 | 0.6 | 0.6 | 0.6 |
| 0–3 | 100 | 100 | 90.2 | 60.3 | 43.4 | 25.2 | 16.8 | 8.8 |
| Filler | 100 | 100 | 100 | 100 | 100 | 100 | 99.5 | 89.5 |
| Cement | 100 | 100 | 100 | 100 | 100 | 99.8 | 99 | 91.2 |
| Pass rate/% | ||||||||
| Sieve size/mm | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| Grade | 100 | 94.1 | 31.5 | 23.7 | 19.2 | 15.3 | 13.5 | 10.8 |
| Test Indicators | Results | Requirements |
|---|---|---|
| Asphalt binder content (%) | 8.5 | / |
| Maximum theoretical relative density | 2.402 | / |
| Measured bulk density | 2.325 | / |
| Void (%) | 3.2 | 3–6 |
| VMA (%) | 19.3 | ≥17 |
| VFA (%) | 83.3 | 75–85 |
| Stability (kN) | 9.5 | ≥8.0 |
| Flow (0.1 mm) | 3.45 | 1.5–4.0 |
| Coefficient of water seepage (ml/min) | 3.7 | ≤200 |
| Residual stability (%) | 93.2 | ≥85 |
| Rutting tested at 60 °C (times/mm) | 5364 | ≥5000 |
| Rutting tested at 70 °C (times/mm) | 3773 | ≥3500 |
| Shear strength of uniaxial penetration (MPa) | 0.514 | 0.466 (max vertical shear stress) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Qiu, Z.; Xiong, C. Mechanical Response and Anti-Reflective Crack Design in New Asphalt Overlays on Existing Asphalt Overlaying Composite Portland Cement Pavement. Buildings 2024, 14, 2702. https://doi.org/10.3390/buildings14092702
Gao J, Qiu Z, Xiong C. Mechanical Response and Anti-Reflective Crack Design in New Asphalt Overlays on Existing Asphalt Overlaying Composite Portland Cement Pavement. Buildings. 2024; 14(9):2702. https://doi.org/10.3390/buildings14092702
Chicago/Turabian StyleGao, Jianping, Zhixiong Qiu, and Chunlong Xiong. 2024. "Mechanical Response and Anti-Reflective Crack Design in New Asphalt Overlays on Existing Asphalt Overlaying Composite Portland Cement Pavement" Buildings 14, no. 9: 2702. https://doi.org/10.3390/buildings14092702
APA StyleGao, J., Qiu, Z., & Xiong, C. (2024). Mechanical Response and Anti-Reflective Crack Design in New Asphalt Overlays on Existing Asphalt Overlaying Composite Portland Cement Pavement. Buildings, 14(9), 2702. https://doi.org/10.3390/buildings14092702






