Coupling Analysis of Safety Influencing Factors in Subway Station Operation under a High-Pressure Gas Pipeline
Abstract
:1. Introduction
2. Literature Review
2.1. Study on the SIFs of High-Pressure Gas Pipelines
2.2. Study on the SIFs of Subway Station Operation
2.3. Study on the Coupling of SIFs between Gas Pipelines and Subway Stations
2.4. Summary of the Current Status of Research
3. Identification and Coupling Model of SIFs of SSOUHP
3.1. Identification of SIFs of SSOUHP
3.1.1. Preliminary Identification of Operational SIFs
3.1.2. Optimization of Operational SIFs
3.2. Coupling Model of SIFs of SSOUHP
3.2.1. Coupling and Coupling Degree Theory
3.2.2. Coupling Model
- Step 1: Build the hierarchical model
- Step 2: Build the pairwise comparison matrix
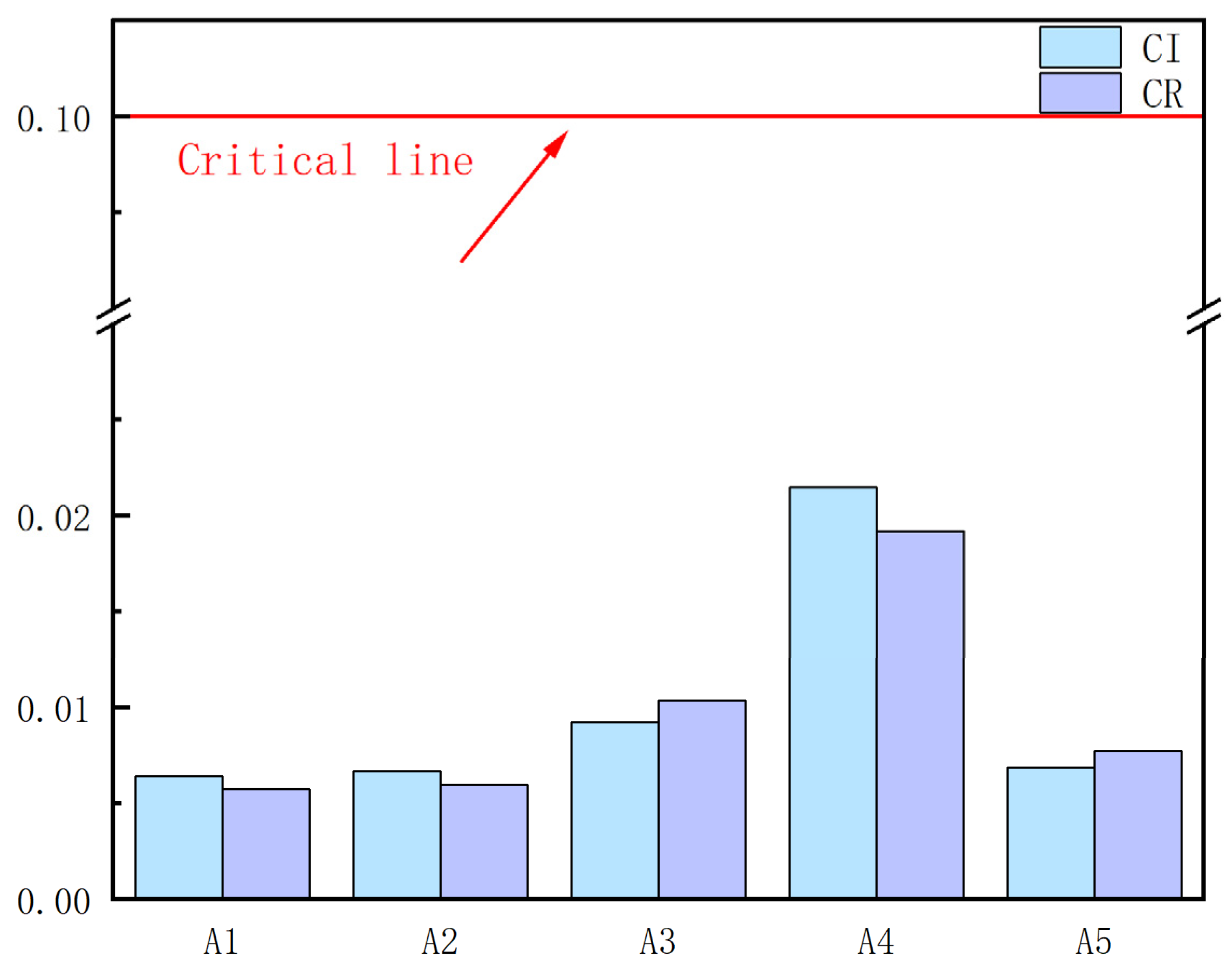
- Step 3: Consistency check
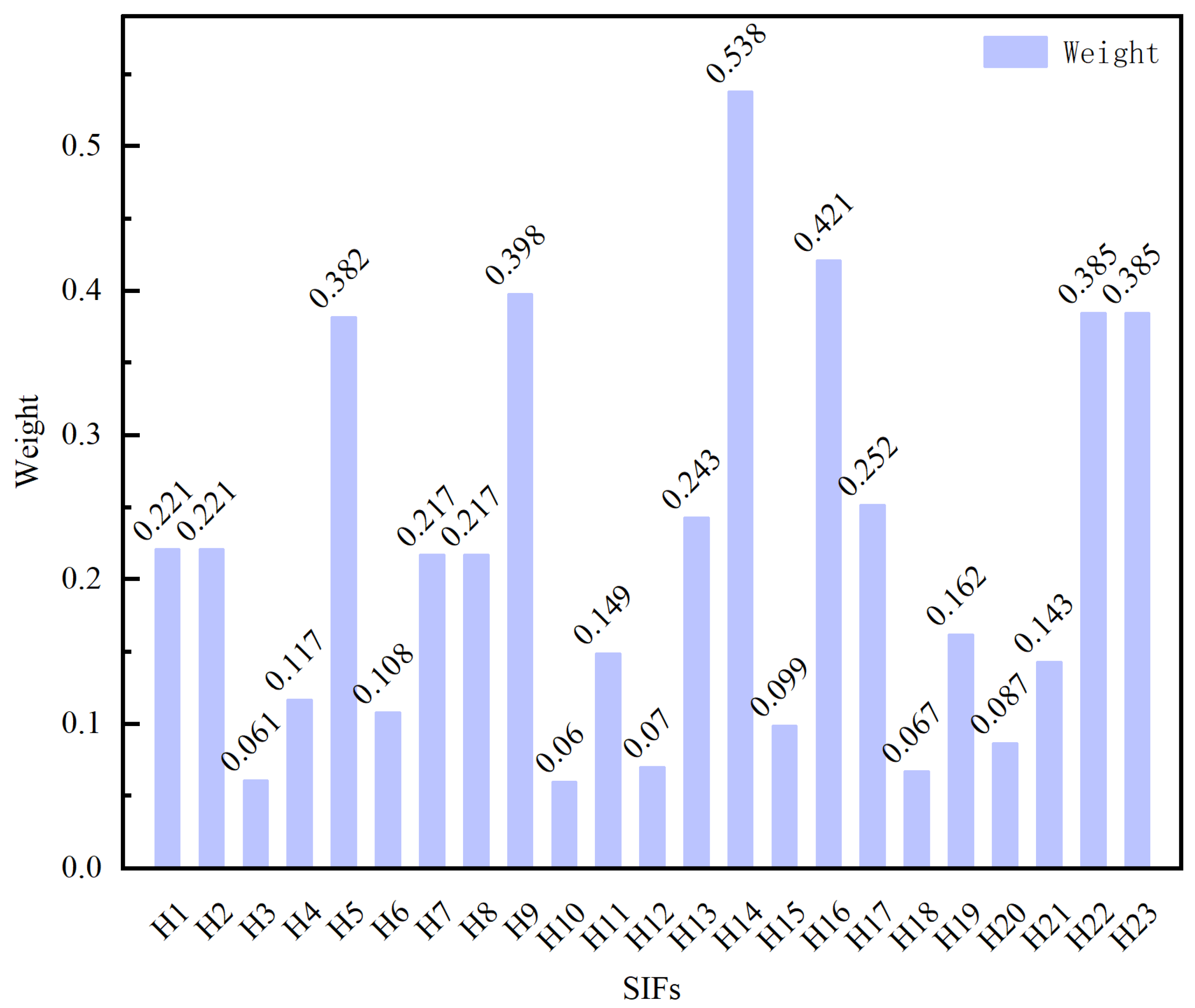
- Step 4: Calculate the criterion weight vector
- Step 5: Calculation of the comprehensive index of SIFs
- Step 6: The construction of the power function
- Step 7: Coupling Degree and Coupling Coordination
4. Case Study and Discussion
4.1. Case Background
4.2. The Construction of Hierarchy Model of SIFs in Case Study
4.3. Case Calculation
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Initial Table of SIFs
| First-Level SIFs | Second-Level SIFs | Source |
| Human factors | Human destruction | [25,65,66,67] |
| Design errors | [25,65] | |
| Misoperation by employees | [23,25,65,66,68] | |
| Staff quality and experience | [10,58,65] | |
| Safety awareness | [10,58,69] | |
| Pipeline factors | Internal corrosion of pipeline | [24,25,58,65] |
| Pipeline characteristics | [25,65,70] | |
| Pipeline manufacturing defects | [25,58,65,67] | |
| Service life | [65] | |
| Operating pressure fluctuation | [25,65,70] | |
| Pipeline equipment condition | [58,65,71] | |
| Station factors | Vibration of subway operation | [71,72] |
| Stray current | [71,73,74] | |
| Settlement and displacement | [73] | |
| Environmental factors | The surrounding environment | [58,75,76] |
| Relative position | [70,73] | |
| Geological conditions | [72,75] | |
| Natural disasters | [23,66,67] | |
| Management factors | Daily operation and maintenance management | [58,77,78] |
| Accident alarm system | [65,75,79] | |
| Safety management practice | [10,58,75,79] | |
| Policy and legal protection | [10,58,65,75] |
References
- The 14th Five-Year Plan: Accelerating the Construction of Urban (Suburban) Railroads and Promoting the Development of Urban Rail Transit in an Orderly Manner. China Metros 2021, 3, 6.
- China Association of Metros. Urban Rail Transit 2022 Annual Statistics and Analysis Report; China Association of Metros: Beijing, China, 2023; pp. 13–15. [Google Scholar]
- Wu, B.; Gao, B.; Suo, X.M.; Liu, W.N.; Shi, Y.X. Study on Influence of Metro Tunnel Excavation on Buried Pipelines. Rock Soil Mech. 2004, 25, 657–662. [Google Scholar]
- Shi, J.H. Revised Calculation and Numerical Analysis on Peck Formula for Safety of Metro Passage with Underneath Crossing Gas Pipeline. J. Saf. Sci. Technol. 2018, 14, 182–186. [Google Scholar]
- Yan, Q.S.; Zhang, Y.N.; Sun, Q.W. Characteristic Study on Gas Blast Loadings in an Urban Utility Tunnel. J. Perform. Constr. Facil. 2020, 34, 04020076. [Google Scholar] [CrossRef]
- Zheng, S.F.; Wen, J. Analysis and Prediction of Subway Settlement Deformation Based on Grey Model. IOP Conf. Ser. Earth Environ. Sci. 2021, 638, 012073. [Google Scholar]
- Li, J.W. Review of Testing and Analysis on Metro-Induced Vibration. Appl. Mech. Mater. 2014, 580–583, 1088–1091. [Google Scholar] [CrossRef]
- Wang, C.T.; Li, W.; Wang, Y.Q. Remaining Lifetime Assessment of Gas Pipelines Subjected to Stray Current Interference Using an Integrated Electric-electrochemical Method. Eng. Fail. Anal. 2021, 127, 105494. [Google Scholar] [CrossRef]
- Luan, X. Safety Risk Assessment of Metro Operation Period Based on AHP and Entropy Weight Method: Taking Nanjing Metro as an Example. Intell. City 2023, 9, 44–47. [Google Scholar]
- Yao, S.Y. Research on Safety Risk Assessment of Metro Station in Integrated Transportation Hub Based on Fuzzy Bayesian Network. Master’s Thesis, South China University of Technology, Guangzhou, China, 2022. [Google Scholar]
- Xiao, X.M.; Wang, Y.H.; Jia, L.M. Safety Assessment Model for Urban Rail Transit Network Operations Based on Complex Network and Entropy Theory. China Saf. Sci. J. 2011, 21, 41–48. [Google Scholar]
- Liu, P.; Li, Q.M.; Bian, J.; Song, L.L.; Hou, X.X. Using Interpretative Structural Modeling to Identify Critical Success Factors for Safety Management in Subway Construction: A China Study. Int. J. Environ. Res. Public Health 2018, 15, 1359. [Google Scholar] [CrossRef]
- Yu, M.Y.; Zhu, L.; Liu, Z.G. Coupling Analysis of Subway Operation Safety Risk Factors Based on N-K Model. Logist. Sci-Tech 2022, 45, 9. [Google Scholar]
- Pan, H.Z.; Gou, J.; Wan, Z.H.; Ren, C.X.; Chen, M.J.; Gou, T.Q.; Luo, Z.H. Research on Coupling Degree Model of Safety Risk System for Tunnel Construction in Subway Shield Zone. Math. Probl. Eng. 2019, 2019, 5783938. [Google Scholar] [CrossRef]
- Wang, F.; Ding, L.Y.; E D Love, P.; J Edwards, D. Modeling Tunnel Construction Risk Dynamics: Addressing the Production Versus Protection Problem. Saf. Sci. 2016, 87, 101–115. [Google Scholar] [CrossRef]
- Wang, J.; Fang, W.N.; Zhang, Y. Identification and Evaluation of Human Error Influential Factors in Subway Scheduling System. China Saf. Sci. J. 2011, 21, 74–79. [Google Scholar]
- Balali, A.; Valipour, A.; Edwards, R.; Moehler, R. Ranking Effective Risks on Human Resources Threats in Natural Gas Supply Projects Using ANP-COPRAS Method: Case study of Shiraz. Reliab. Eng. Syst. Saf. 2021, 208, 107442. [Google Scholar] [CrossRef]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Safety Assessment of Upper Buried Gas Pipeline Under Blasting Vibration of Subway Tunnel: A Case Study in Beijing Subway Line. J. Vibroeng. 2019, 21, 888–900. [Google Scholar] [CrossRef]
- Li, Y.Q.; Liao, Q.; Hao, Z.F.; Yin, X.F.; Liu, B. Influence Factors and Mathematical Modeling of the Security of Underground Gas Conduit Network. J. South China Univ. Technol. (Nat. Sci. Ed.) 2004, 89–93. [Google Scholar]
- Ba, Z.N.; Han, Y.X.; Liang, J.W. Risk Assessment of the Gas Pipeline Corrosion Based on the Improved AHP and Fuzzy Comprehensive Evaluation Method. J. Saf. Environ. 2018, 18, 2103–2109. [Google Scholar]
- Zeng, X.K.; Feng, Y.; Lai, W.Q.; Tang, B.K.; Wu, T.; Fu, X.B.; Huang, X.B.; Zhong, S.C.; Zhong, J.F. Risk Assessment of Urban Gas Pipeline Based on AHP and Entropy Weight Method. J. Saf. Sci. Technol. 2021, 17, 130–135. [Google Scholar]
- Wang, C. Research on Risk Assessment of Urban Gas Pipelines and Management. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2013. [Google Scholar]
- Yang, Z.H.; Can, W.; Hu, S.J. Study on Fuzzy Comprehensive Evaluation System of City Gas Pipeline Based on AHP. J. Saf. Environ. 2013, 13, 257–260. [Google Scholar]
- Bai, Y.P.; Wu, J.S.; Ren, Q.R.; Jiang, Y.; Cai, J.T. A BN-Based Risk Assessment Model of Natural Gas Pipelines Integrating Knowledge Graph and DEMATEL. Process Saf. Environ. Prot. 2023, 171, 640–654. [Google Scholar] [CrossRef]
- Guo, Y.B.; Meng, X.L.; Meng, T.; Wang, D.G.; Liu, S.H. A Novel Method of Risk Assessment Based on Cloud Inference for Natural Gas Pipelines. J. Nat. Gas Sci. Eng. 2016, 30, 421–429. [Google Scholar] [CrossRef]
- Zhang, H.B.; Cheng, W.Y.; Zhou, L.J.; Feng, Q.S.; Zheng, H.L.; Dai, L.S.; Xiang, X.Q.; Cao, T.; Liu, Y. Pipeline Risk Assessment Practice of PetroChina Pipeline Company. Oil Gas Storage Transp. 2012, 31, 96–98. [Google Scholar]
- Liu, J.; Wan, L.T.; Wang, W.Q.; Yang, G.D.; Ma, Q.; Zhou, H.W.; Zhao, H.Y.; Lu, F. Integrated Fuzzy DEMATEL-ISM-NK for Metro Operation Safety Risk Factor Analysis and Multi-Factor Risk Coupling Study. Sustainability 2023, 15, 5898. [Google Scholar] [CrossRef]
- Du, X.L.; Zhang, Y.; Miao, H.Q.; Li, Y.; Zhong, Z.L.; Jiang, L.Z.; Hou, B.W. Indicator System for the Evaluation of Metro System Safe Operation from the Perspective of Resilient Cities. J. Nat. Disasters 2023, 32, 1–13. [Google Scholar]
- Ren, G.; Chen, J.J.; Gao, J.Y.; Wang, Y.; Yuan, C.Q.; Jiang, Q.Y. Safety Assessment of Metro Station Operation Based on Improved Extension and Matter Element Method. Urban Mass Transit 2020, 23, 136–139. [Google Scholar]
- Bai, S.M.; Sun, H.S.; Zhao, Y.C. Study of the Safety Evaluation of Urban Subway Operation Based on Extenics. Adv. Mater. Res. 2014, 919–921, 878–882. [Google Scholar] [CrossRef]
- Xiao, X.M.; Wang, Y.H.; Jia, L.M. Safety Assessment of subway stations Operation Based on Grey Clustering Method. Adv. Mater. Res. 2013, 748–748, 1212–1216. [Google Scholar] [CrossRef]
- Li, J.; Song, R.; Jiang, J.L. Safety evaluation of rail transit based on comprehensive fuzzy evaluation model. J. Transp. Sci. Eng. 2011, 27, 91–95. [Google Scholar]
- Yang, Y.; Cai, Z.; Jiang, N.; Zhou, C.; Li, H. Safety Evaluation of Underground Gas Pipe under Blasting of Subway Connected Aisle: A Case Study. KSCE J. Civ. Eng. 2022, 26, 921–932. [Google Scholar] [CrossRef]
- Fu, B.W.; Jiang, H.Y.; Xu, T.L.; Lin, Y.A. Coupling Analysis on Failure Possibility Factors of Urban Gas Pipeline Based on N-K Model. J. Saf. Sci. Technol. 2018, 14, 145–149. [Google Scholar]
- Wang, M.S. Operation Safety Risk Assessment of Municipal Gas Pipeline Network under Multi Factor Coupling Effect. Master’s Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Xu, H.; Yue, J.C.; Du, M.K.; Jiao, L.D. Analysis of Urban Rail Transit Coupling Operation Risks Based on N-K Model. Urban Mass Transit 2020, 23, 105–108. [Google Scholar]
- Zhao, J.X.; Liu, L.Y.; Wang, F.; Mao, N. The Subway Operation Safety Risk Based on N-K Model Coupling Research. J. Civ. Eng. Manag. 2023, 40, 31–36. [Google Scholar]
- Huang, W.C.; Shuai, B.; Sun, Y. Study on Coupling Risk Formation Mechanism of Railway Dangerous Goods Transportation System Based on N-K Model. J. China Railw. Soc. 2019, 41, 1–9. [Google Scholar]
- Shi, J.R.; Lv, Q.W.; Jin, S.M. Coupling Coordination Analysis of Urban Metro Station Catchment Area Development Based on Urban Multi-Source Data. In Proceedings of the International Conference on Smart Transportation and City Engineering (STCE 2022), Chongqing, China, 25–27 November 2022; Volume 12460, pp. 909–914. [Google Scholar]
- Huang, J.C.; Fang, C.L. Analysis of Coupling Mechanism and Rules Between Urbanization and Eco-Environment. Geogr. Res. 2003, 22, 211–220. [Google Scholar]
- Norgaard, R.B. Economic Indicators of Resource Scarcity: A Critical Essay. J. Environ. Econ. Manag. 1990, 19, 19–25. [Google Scholar] [CrossRef]
- Tao, J.; Xie, Y.; Zhou, H.; Xu, Y.; Zhao, G. Cross-County Characteristics of Water–Ecology–Economy Coupling Coordination in the Wuding River Watershed, China. Land 2022, 11, 2283. [Google Scholar] [CrossRef]
- Wang, R.X.; Chen, J.C.; Li, M.H. Coupling and Coordinating Relationship between Agricultural Eco-Efficiency and Food Security System in China. Int. J. Environ. Res. Public Health 2023, 20, 431. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.R.; Dong, Q.L.; Qian, L.; Fei, H.M.; Wu, J.N. A Study on the Coupling and Coordination between Logistics Industry and Economy in the Background of High-Quality Development. Sustainability 2021, 13, 10360. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, X.Q.; Ran, C.Y.; Shi, V.; Zhou, Y.F. Evaluation of the Sustainable Coupling Coordination of the Logistics Industry and the Manufacturing Industry in the Yangtze River Economic Belt. Sustainability 2021, 13, 5167. [Google Scholar] [CrossRef]
- Cong, X.N. Expression and Mathematical Property of Coupling Model, and Its Misuse in Geographical Science. Econ. Geogr. 2019, 39, 18–25. [Google Scholar]
- Xue, Y.; Liu, Y.L.; Zhang, T.T. Research on Formation Mechanism of Coupled Disaster Risk. J. Nat. Disasters 2013, 22, 44–50. [Google Scholar]
- Vanegas, L.V.; Labib, A.W. Application of New Fuzzy-Weighted Average (NFWA) Method to Engineering Design Evaluation. Int. J. Prod. Res. 2001, 39, 1147–1162. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, W.B.; Xu, C.; Cheng, S.E. An Improved Extension System for Assessing Risk of Water Inrush in Tunnels in Carbonate Karst Terrain. KSCE J. Civ. Eng. 2019, 23, 1147–1162. [Google Scholar] [CrossRef]
- Illingworth, V. The Penguin Dictionary of Physics, 2nd ed.; Penguin Books: London, UK, 1991; p. 544. [Google Scholar]
- Wang, Y.F.; Geng, Q.J.; Si, X.H.; Kan, L.P. Coupling and Coordination Analysis of Urbanization, Economy and Environment of Shandong Province, China. Environ. Dev. Sustain. 2020, 23, 10397–10415. [Google Scholar] [CrossRef]
- Dong, G.L.; Ge, Y.B.; Liu, J.J.; Kong, X.K.; Zhai, R.X. Evaluation of Coupling Relationship between Urbanization and Air Quality Based on Improved Coupling Coordination Degree Model in Shandong Province, China. Ecol. Indic. 2023, 154, 110578. [Google Scholar] [CrossRef]
- Ji, Y.; Sheng, Q.Q.; Zhu, Z.L. Assessment of Ecological Benefits of Urban Green Spaces in Nanjing City, China, Based on the Entropy Method and the Coupling Harmonious Degree Model. Sustainability 2023, 15, 10516. [Google Scholar] [CrossRef]
- Wang, M.; Chen, F.R.; Zhang, D.Q.; Rao, Q.Y.; Li, J.J.; Tan, S.K. Supply–Demand Evaluation of Green Stormwater Infrastructure (GSI) Based on the Model of Coupling Coordination. Int. J. Environ. Res. Public Health 2022, 19, 14742. [Google Scholar] [CrossRef]
- Hou, X.F.; Zhang, D.F.; Fu, L.Y.; Zeng, F.; Wang, Q. Spatio-Temporal Evolution and Influencing Factors of Coupling Coordination Degree between Urban–Rural Integration and Digital Economy. Sustainability 2023, 15, 9718. [Google Scholar] [CrossRef]
- Suo, Q.; Wang, L.Y.; Yao, T.Z.; Wang, Z.H. Promoting Metro Operation Safety by Exploring Metro Operation Accident Network. J. Syst. Sci. Inf. 2021, 9, 455–468. [Google Scholar] [CrossRef]
- Zhang, M. Risk Assessment of Metro Operation Based on G1-EW Combination Weighting Cloud Model. China Saf. Sci. J. 2022, 32, 163–170. [Google Scholar]
- Fang, F. Coupling Analysis and Simulation of Human and Environment Factors in Gas Pipeline Safety Risk. Master’s Thesis, Anhui Jianzhu University, Hefei, China, 2021. [Google Scholar]
- Li, D.N.; Zhao, B.K.; Xu, S.M. Research on Safety Evaluation System of Underground Pipelines Adjacent to Metro Construction Based on Pipelines Properties and Pipe-tunnel Position Relationship. J. Munic. Technol. 2023, 41, 206–215. [Google Scholar]
- Sreenivasan, A.; Ma, S.; Nedungadi, P.; Sreedharan, V.R.; Raman, R.R. Interpretive Structural Modeling: Research Trends, Linkages to Sustainable Development Goals, and Impact of COVID-19. Sustainability 2023, 15, 4195. [Google Scholar] [CrossRef]
- Yan, H.Y.; Zheng, Z.W.; Huang, H.J.; Zhou, X.Y.; Tang, Y.Z.; Hu, P. Risk Coupling Evaluation of Social Stability of Major Engineering Based on N-K Model. Buildings 2022, 12, 702. [Google Scholar] [CrossRef]
- Molloy, G.J.; O’Boyle, C.A. The SHEL Model: A Useful Tool for Analyzing and Teaching the Contribution of Human Factors to Medical Error. Acad. Med. J. Assoc. Am. Med. Coll. 2005, 80, 152–155. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; He, C.L.; Huang, Q.; Luo, J. Coordination Degree of Multimodal Rail Transit Network. J. Jilin Univ. (Eng. Technol. Ed.) 2021, 51, 2040–2050. [Google Scholar]
- Yao, X.H. Analysis on the Current Situation, Internal Coupling and Influencing Factors of the Urban Resilience of China’s Provincial Capital Cities. Master’s Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar]
- Wang, Q.S.; Tan, Y.F.; Qi, H.Y. Mutual Coupling Analysis of Safety Impact Factors of Gas Network. Gas Heat 2010, 30, 22–26. [Google Scholar]
- Zhang, Y.; Lv, S.R.; Wang, W.Q. Risk Analysis of High Pressure Gas Pipeline Leakage Based on Bow-tie Model and IAHP. IOP Conf. Ser. Earth Environ. Sci. 2020, 461, 012079. [Google Scholar] [CrossRef]
- Sheng, K.; Lai, X.L.; Chen, Y.; Jiang, J.C.; Zhou, L. Risk Assessment of Urban Gas Pipeline Based on Different Unknown Measure Functions. Teh. Vjesn. 2021, 28, 1605–1614. [Google Scholar]
- Li, J.; Zhang, H.; Han, Y.S.; Wang, B.D. Study on Failure of Third-Party Damage for Urban Gas Pipeline Based on Fuzzy Comprehensive Evaluation. PLoS ONE 2017, 11, e0166472. [Google Scholar] [CrossRef]
- Han, W.; Qian, Z.X.; Wang, J.W. A Safety Risk Evaluation Index System of Subway Projects Based on the Analytic Hierarchy Process. J. Phys. Conf. Ser. 2020, 1676, 012134. [Google Scholar]
- Gao, B.L.; Xi, R.J. Safety Risk Assessment for Adjacent Underground Pipelines in Metro Construction. Mod. Tunn. Technol. 2016, 53, 118–123. [Google Scholar]
- Wu, B.B.; Qiu, P.Y.; Shi, J.H.; Liu, J.J. Analysis on the Interaction Between Subway and Gas Pipeline. J. Saf. Sci. Technol. 2021, 17, 64–67. [Google Scholar]
- Zou, B.P.; Sun, D.; Mu, J.D.; Xu, Z.P. Comprehensive Risk Evaluation in the Long-Term Operation of Urban Subway Based on Multiple Indices. Math. Probl. Eng. 2021, 2021, 5521630. [Google Scholar] [CrossRef]
- Yao, X.J.; Zhang, W.; Wu, Z.Z.; Lu, Q.C.; Xia, D.L. Safety Protection Standards for Oil and Gas Pipelines Adjacent to A Subway. Oil Gas Storage Transp. 2018, 37, 1380–1384. [Google Scholar]
- Saeed, R.A.; Michael, I.; Mohammad, D.; Masoud, S.; Hojjat, S.; Ashkan, R. Investigation on corrosion rate and a novel corrosion criterion for gas pipelines affected by dynamic stray current. J. Nat. Gas Sci. Eng. 2015, 26, 453–460. [Google Scholar]
- Wu, Q.T. Resilience Evaluation and Promotion of Urban Metro Network. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2022. [Google Scholar]
- Hu, Y.W. Research on Reliability of Safety Management System for Subway Shield Construction. Master’s Thesis, China Three Gorges University, Yichang, China, 2020. [Google Scholar]
- Long, Y.T. Study on the Risk Evaluation of Operation and Maintenance of X Integrated Pipeline Corridor Project in F City Based on Cloud Model. Master’s Thesis, Jiangxi University of Science and Technology, Ganzhou, China, 2022. [Google Scholar]
- Pan, K.; Wang, H.D.; Shi, J.Y. Application of Multi-level Extensible Method to Urban Subway Operation Safety Evaluation. J. China Railw. Soc. 2011, 33, 14–19. [Google Scholar]
- Jiang, T.T.; Yao, C.Q.; Tong, Z.J. Safety Evaluation of Deep Foundation Pit Construction in subway stationss Based on Game Theory-Extenics Theory. J. North China Inst. Sci. Technol. 2023, 20, 103–110. [Google Scholar]

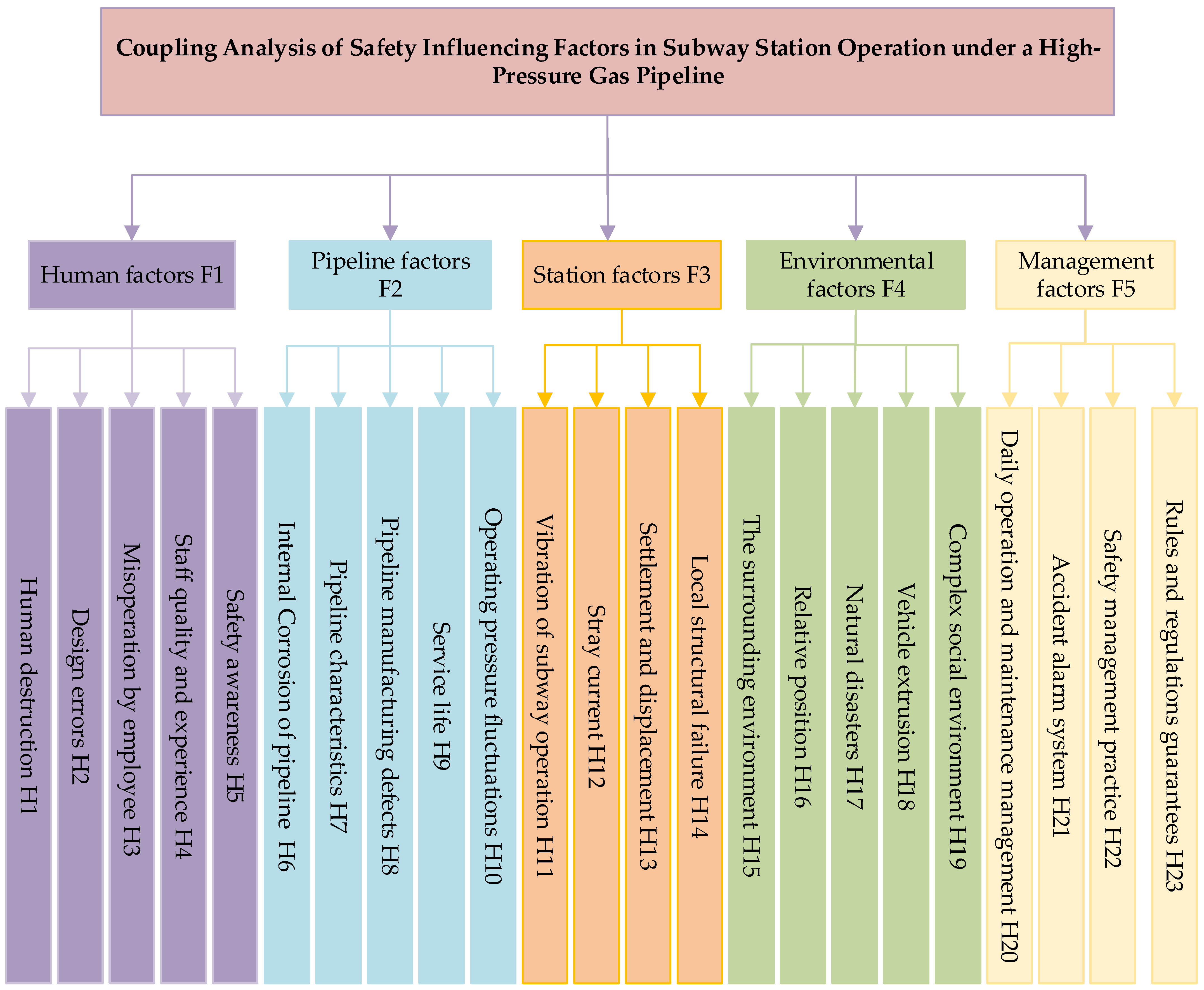
| First-Level SIFs | Second-Level SIFs | Interpretation |
|---|---|---|
| Human factors | Human destruction | Damage caused by third-party construction, terrorist attacks, etc. |
| Design errors | The design rationality, material selection, safety factor design, and other potential errors caused by the experience and qualification of the designers of the special design scheme. | |
| Misoperation by employees | Daily operational errors in pipeline or station caused by employees’ lack of concentration, misunderstanding, work pressure, etc. | |
| Staff quality and experience | Including staff mental health, basic quality, responsibility, experience of similar projects, and regular training sessions. | |
| Safety awareness | Daily operation and maintenance staff education, training, safety awareness, safety attitude, safety knowledge popularization, and so on. | |
| Pipeline factors | Internal corrosion of pipeline | The interaction between the inner wall of the pipeline and the impurities contained in the transported gas causes an accidental explosion accident caused by gas leakage after pipeline corrosion. |
| Pipeline characteristics | Mainly the thickness of the pipeline, material, the likelihood of gas leakage after destruction, etc. | |
| Pipeline manufacturing defects | Accidental explosion caused by gas leakage caused by pipeline damage, small cracks, wrinkle bending, welding defects, or insufficient strength. | |
| Service life | Mainly due to disrepair and fatigue damage appearing after a long time of use. | |
| Operating pressure fluctuation | When the pipeline pressure is high, it will aggravate an accidental explosion caused by gas. | |
| Station factors | Operation vibration | Fatigue damage to gas pipelines caused by the continuous cyclic action of vibration generated in subway operation. |
| Stray current | Subway operation has some current leakage to form stray currents, which can cause galvanic corrosion on the pipeline. | |
| Settlement and displacement | The effect on the overall system of settlement and displacement generated by the main structure of the subway station during the operational phase. | |
| Local structural failure | Impact on the overall system after failure of the main structure such as beams, slabs, and columns in the subway station due to abnormal factors. | |
| Environmental factors | The surrounding environment | In underground engineering, the safety risks brought by changes in geological conditions cannot be ignored. Its complexity and diversity pose a potential threat to the safe operation of subway stations and high-pressure gas pipelines. |
| Relative position | The clear distance between the bottom of the high-pressure gas pipeline and the roof of the subway station. | |
| Natural disasters | Mainly the impact of natural disasters such as earthquakes, high temperatures, rainstorms, floods, and soil settlement on high-pressure gas pipelines and subway stations. | |
| Vehicle squeeze | The gas pipeline is laid under the road, and the long-term extrusion of vehicles will aggravate the wear of the pipeline. When the pipeline reaches its limit, the pipeline damage will cause an accidental gas leakage. | |
| Complex social environment | Mainly refers to the public safety awareness of the social group, the popularization of safety knowledge, the ability to prevent security, and the ability to report problems in time. | |
| Management factors | Daily operation and maintenance management | Configuration, installation and maintenance of software and hardware for the entire system of gas pipelines and subway stations. |
| Accident alarm system | Monitoring of the status of gas pipelines and subway stations, and whether problems can be alarmed in a timely manner, and information transmission and sharing. | |
| Safety management practice | Including the preparation of emergency plans, emergency equipment configuration, accident management, etc. | |
| Rules and regulations guarantee | Whether the safety regulations and responsibility system are sound, whether the safety responsibility system is clear, and the implementation and supervision of responsibilities. |
| Single-Factor Coupling | Two-Factor Coupling | Multi-Factor Coupling | ||
|---|---|---|---|---|
| Three-Factor Coupling | Four-Factor Coupling | Five-Factor Coupling | ||
| Human–Human | Human–Pipeline | Human–Pipeline–Station | Human–Pipeline–Station–Environment | Human–Pipeline–Station–Environment–Management |
| Human–Pipeline | Human–Pipeline–Environment | |||
| Pipeline–Pipeline | Human–Environment | Human–Pipeline–Management | Human–Pipeline–Station–Management | |
| Human–Management | Human–Station–Environment | |||
| Station–Station | Pipeline–Station | Human–Station–Management | Human–Pipeline–Environment–Management | |
| Pipeline–Environment | Human–Environment–Management | |||
| Environment–Environment | Pipeline–Management | Pipeline–Station–Environment | Human–Station–Environment–Management | |
| Station–Environment | Pipeline–Station–Management | |||
| Management–Management | Station–Management | Pipeline–Environment–Management | Pipeline–Station–Environment–Management | |
| Environment–Management | Station–Environment–Management | |||
| Scale | Meaning |
|---|---|
| 1 | Both factors are equally important. |
| 3 | Factor i is slightly more important than factor j. |
| 5 | Factor i is more important than factor j. |
| 7 | Factor i is significantly more important than factor j. |
| 9 | Factor i is extremely important compared to factor j. |
| 2, 4, 6, 8 | Scale between two neighboring levels of importance. |
| Count backwards | The importance of factor i relative to j is aij, and the importance of j relative to i is aji = 1/aij. |
| Order | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| RI value | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 |
| Coupling Coordination Degree Interval | Degree of Coordination | Coordinated Contrast Type |
|---|---|---|
| [0.0~0.1] | Dysfunctional recession | Extreme disorder |
| (0.1~0.2] | Severe disorder | |
| (0.2~0.3] | Moderate disorder | |
| (0.3~0.4] | Mild disorder | |
| (0.4~0.5] | Transitional coordination | Critical coordination |
| (0.5~0.6] | Barely coordination | |
| (0.6~0.7] | Junior coordination | |
| (0.7~0.8] | Coordination development | Moderate coordination |
| (0.8~0.9] | Good coordination | |
| (0.9~1.0] | High-quality coordination |
| αij | β1j | ||
|---|---|---|---|
| α1j | 1.917 | β1j | 0.306 |
| α2j | 1.999 | β2j | 0.302 |
| α3j | 2.214 | β3j | 0.288 |
| α4j | 2.139 | β4j | 0.338 |
| α5j | 1.548 | β5j | 0.351 |
| U1 | U2 | U3 | U4 | U5 | |
|---|---|---|---|---|---|
| Value | 0.621 | 0.615 | 0.653 | 0.606 | 0.796 |
| Factors Set | T | D | Coupling Coordination Type | ||
|---|---|---|---|---|---|
| Single-factor | F1F1 | 1.000 | 0.788 | moderate coordination | |
| F2F2 | 1.000 | 0.784 | moderate coordination | ||
| F3F3 | 1.000 | 0.808 | good coordination | ||
| F4F4 | 1.000 | 0.778 | moderate coordination | ||
| F5F5 | 1.000 | 0.892 | good coordination | ||
| Two-factor | F1F2 | 1.000 | 0.786 | moderate coordination | |
| F1F3 | 1.000 | 0.798 | moderate coordination | ||
| F1F4 | 1.000 | 0.783 | moderate coordination | ||
| F1F5 | 0.992 | 0.839 | good coordination | ||
| F2F3 | 1.000 | 0.796 | moderate coordination | ||
| F2F4 | 1.000 | 0.781 | good coordination | ||
| F2F5 | 0.992 | 0.836 | moderate coordination | ||
| F3F4 | 0.999 | 0.793 | good coordination | ||
| F3F5 | 0.995 | 0.849 | moderate coordination | ||
| F4F5 | 0.991 | 0.833 | good coordination | ||
| Multi-factor | Three-factor | F1F2F3 | 1.000 | 0.793 | moderate coordination |
| F1F2F4 | 1.000 | 0.783 | moderate coordination | ||
| F1F2F5 | 0.993 | 0.820 | good coordination | ||
| F1F3F4 | 1.000 | 0.791 | moderate coordination | ||
| F1F3F5 | 0.994 | 0.828 | good coordination | ||
| F1F4F5 | 0.992 | 0.818 | good coordination | ||
| F2F3F4 | 0.999 | 0.790 | moderate coordination | ||
| F2F3F5 | 0.994 | 0.826 | good coordination | ||
| F2F4F5 | 0.992 | 0.816 | good coordination | ||
| F3F4F5 | 0.993 | 0.824 | good coordination | ||
| Four-factor | F1F2F3F4 | 1.000 | 0.790 | moderate coordination | |
| F1F2F3F5 | 0.994 | 0.817 | good coordination | ||
| F1F2F4F5 | 0.993 | 0.809 | good coordination | ||
| F1F3F4F5 | 0.994 | 0.816 | good coordination | ||
| F2F3F4F5 | 0.994 | 0.814 | good coordination | ||
| Five-factor | F1F2F3F4F5 | 0.995 | 0.809 | good coordination | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Weng, Y.; Cheng, J.; Li, H.; Guo, J.; Li, L. Coupling Analysis of Safety Influencing Factors in Subway Station Operation under a High-Pressure Gas Pipeline. Buildings 2024, 14, 2727. https://doi.org/10.3390/buildings14092727
Yan W, Weng Y, Cheng J, Li H, Guo J, Li L. Coupling Analysis of Safety Influencing Factors in Subway Station Operation under a High-Pressure Gas Pipeline. Buildings. 2024; 14(9):2727. https://doi.org/10.3390/buildings14092727
Chicago/Turabian StyleYan, Wenrong, Yingkang Weng, Jianhua Cheng, Hujun Li, Jiaqi Guo, and Linyu Li. 2024. "Coupling Analysis of Safety Influencing Factors in Subway Station Operation under a High-Pressure Gas Pipeline" Buildings 14, no. 9: 2727. https://doi.org/10.3390/buildings14092727
APA StyleYan, W., Weng, Y., Cheng, J., Li, H., Guo, J., & Li, L. (2024). Coupling Analysis of Safety Influencing Factors in Subway Station Operation under a High-Pressure Gas Pipeline. Buildings, 14(9), 2727. https://doi.org/10.3390/buildings14092727






