Comparative Study of Optimal Flat Double-Layer Space Structures with Diverse Geometries through Genetic Algorithm
Abstract
:1. Introduction
2. Methodology
2.1. Double-Layer Space Structure
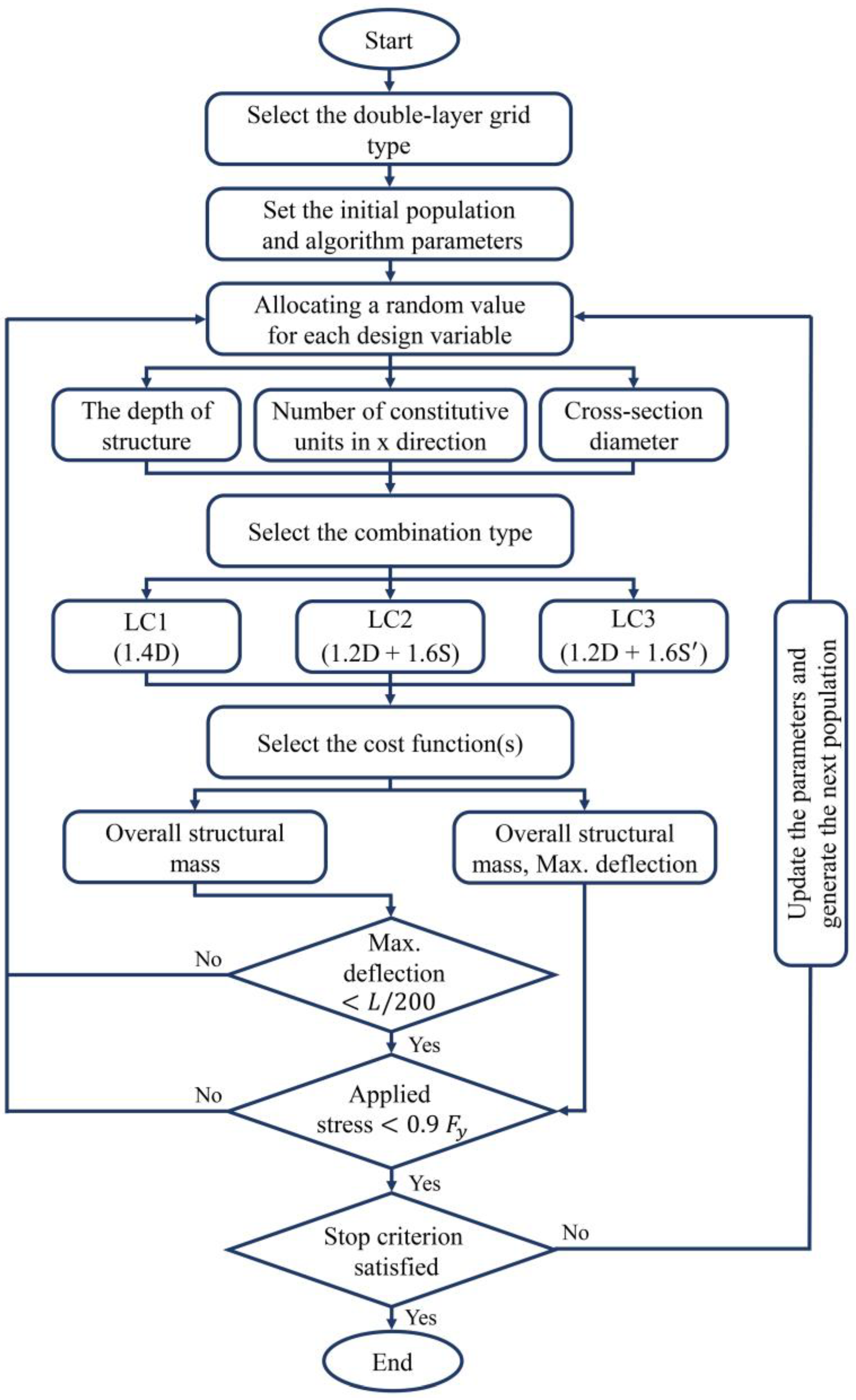
2.2. Optimization Process
2.2.1. Cost Function
2.2.2. Constraints
2.2.3. Genetic Algorithm
3. Numerical Simulations
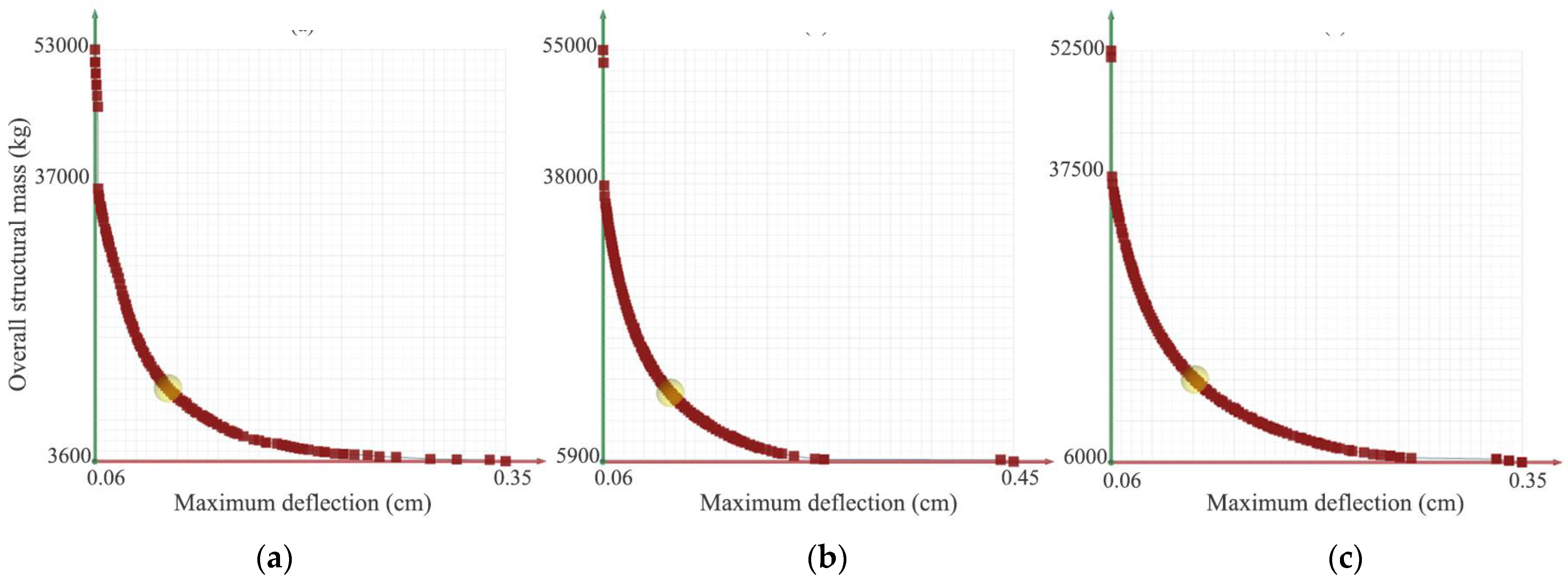
4. Results and Discussion
5. Conclusions
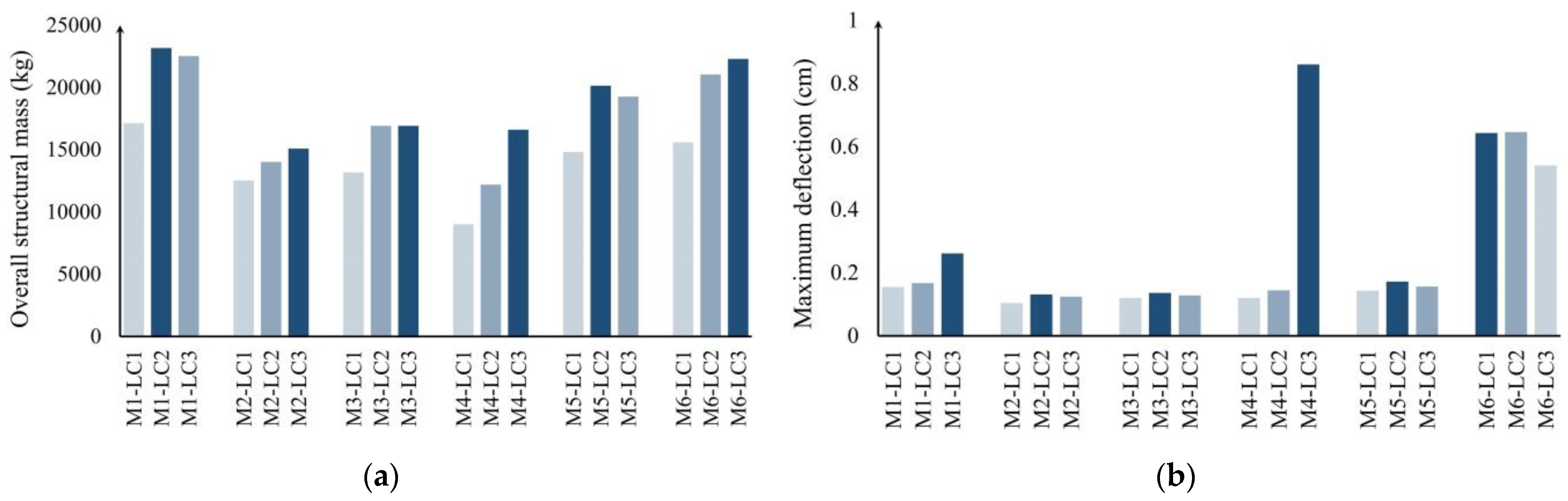
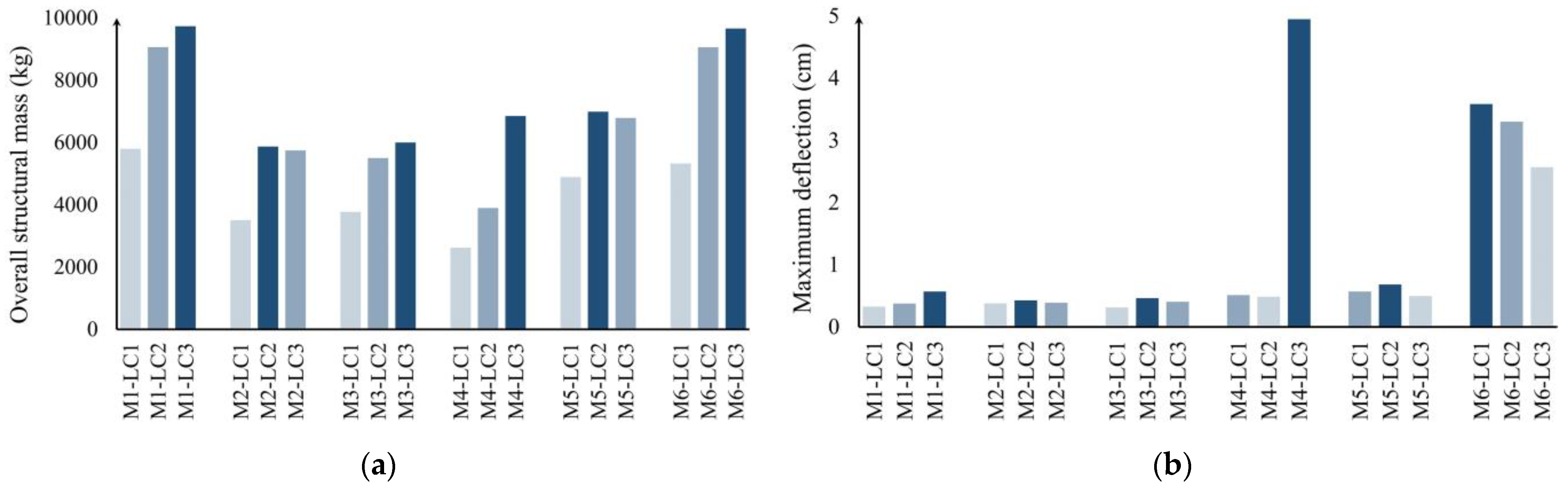
- The superiority of the semi-octahedron configuration over the square grid configuration in minimizing both structural mass and maximum deflection is clearly demonstrated. Specifically, the multi-objective optimization results show that the semi-octahedron configuration achieves an overall structural mass of approximately 15,093 kg and a maximum deflection of 0.124 cm. In contrast, under the single-objective optimization process, the overall structural mass is reduced to 5873 kg, with a corresponding maximum deflection of 0.428 cm.
- The critical load combination affecting optimization results varies depending on the pattern of constitutive units.
- Increasing the number of constitutive units, structural depth, and cross-section diameter leads to an increase in structural mass. However, the rate of increase is more sensitive to the number of constitutive units and cross-section diameter than to structural depth.
- Unlike structural depth and cross-section diameter, an increase in the number of constitutive units results in higher maximum deflection.
- The effects of the number of constitutive units and cross-section diameter on structural deflection are highly dependent on the selected type of double-layer grid.
- Based on the analysis of all models, it was found that selecting a structural depth within the range of 1 m to 1.5 m and choosing a cross-section diameter between 6 cm and 7 cm result in optimal structural deflection. These quantitative insights provide a clear direction for designers in selecting the most effective configuration and design parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chilton, J. Space Grid Structures, 1st ed.; Routledge: London, England, 2007. [Google Scholar]
- Austern, G.; Capeluto, I.G.; Grobman, Y.J. Rationalization methods in computer aided fabrication: A critical review. Autom. Constr. 2018, 90, 281–293. [Google Scholar] [CrossRef]
- Fujita, S.; Ohsaki, M. Shape optimization of free-form shells using invariants of parametric surface. Int. J. Space Struct. 2010, 25, 143–157. [Google Scholar] [CrossRef]
- Wang, H.; Pellis, D.; Rist, F.; Pottmann, H.; Müller, C. Discrete geodesic parallel coordinates. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Shahbazi, Y.; Ghofrani, M.; Pedrammehr, S. Aesthetic Assessment of Free-Form Space Structures Using Machine Learning Based on the Expert’s Experiences. Buildings 2023, 13, 2508. [Google Scholar] [CrossRef]
- Gasii, G.M. The flat double-layer grid-cable steel-concrete composite structure. In Proceedings of the METNET Annual Seminar, Castellon, Spain, 11–12 October 2016. [Google Scholar]
- Behnejad, S.A.; Parke, G.A. Half a century with the Space Structures Research Centre of the University of Surrey. Int. J. Space Struct. 2019, 29, 205–214. [Google Scholar] [CrossRef]
- Mostafavian, S.A.; Davoodi, M.R.; Amiri, J.V. Ball joint behavior in a double layer grid by dynamic model updating. J. Constr. Steel Res. 2012, 76, 28–38. [Google Scholar] [CrossRef]
- Arekar, V.A.; Patil, Y.D.; Patil, H.S. Development of a new connector for double layer space grids. J. Sci. Perspect. 2016, 8, 525–528. [Google Scholar] [CrossRef]
- Maalek, S.; Maalek, R.; Maalek, B. Intrinsic properties of composite double layer grid superstructures. Infrastructures 2023, 8, 129. [Google Scholar] [CrossRef]
- Sutjiadi, H.Y.; Charleson, A.W. Structural design and analysis of vertical double-layer space structures in super-tall buildings. Struct. Des. Tall Build. 2014, 23, 512–525. [Google Scholar] [CrossRef]
- Liu, H.; Gao, H.; Chen, Z. Research on reinforcing method for welded hollow spherical joints. J. Constr. Steel Res. 2021, 182, 106685. [Google Scholar] [CrossRef]
- Kozich, M.; Wald, F. Resistance of circular hollow section branch plate joints made from high strength steel. Thin-Walled Struct. 2022, 176, 109345. [Google Scholar] [CrossRef]
- Zuo, W.; Chang, H.; Li, Z.; An, A.; Xia, J.; Yu, T. Experimental investigation on compressive behavior of corroded thin-walled CHS T-joints with grout-filled GFRP tube repairing. Thin-Walled Struct. 2022, 175, 109222. [Google Scholar] [CrossRef]
- Tian, L.M.; Jin, B.B.; Li, L. Axial compressive mechanical behaviors of a double-layer member. J. Struct. Eng. 2023, 149, 04023110. [Google Scholar] [CrossRef]
- Tian, L.M.; Wei, J.P.; Huang, Q.X.; Ju, J.W. Collapse-resistant performance of long-span single-layer spatial grid structures subjected to equivalent sudden joint loads. J. Struct. Eng. 2021, 147, 04020309. [Google Scholar] [CrossRef]
- Lee, H.G.; Makowski, Z.S. Study of Factors Affecting Stress Distribution in Double-Layer Grids of The Souare-And-Diagonal Type. Archit. Sci. Rev. 1977, 20, 90–102. [Google Scholar] [CrossRef]
- Stefańska, A.; Rokicki, W. Architectural Design Optimisation in Reticulated Free-Form Canopies. Buildings 2022, 12, 1068. [Google Scholar] [CrossRef]
- Yavan, F.; Maalek, R.; Toğan, V. Structural Optimization of Trusses in Building Information Modeling (BIM) Projects Using Visual Programming, Evolutionary Algorithms, and Life Cycle Assessment (LCA) Tools. Buildings 2024, 14, 1532. [Google Scholar] [CrossRef]
- Schling, E.; Barthel, R. Repetitive structures. In Impact: Design With All Senses. In Proceedings of the Design Modelling Symposium, Berlin, Germany, 29 August 2020. [Google Scholar]
- Li, P.; Zhao, X.; Ding, D.; Li, X.; Zhao, Y.; Ke, L.; Zhang, X.; Jian, B. Optimization Design for Steel Trusses Based on a Genetic Algorithm. Buildings 2023, 13, 1496. [Google Scholar] [CrossRef]
- Salajegheh, E.; Mashayekhi, M.; Khatibinia, M.; Kaykha, M. Optimum shape design of space structures by genetic algorithm. Int. J. Space Struct. 2009, 24, 45–57. [Google Scholar] [CrossRef]
- Lee, T.U.; Liu, Y.; Xie, Y.M. Dividing a sphere hierarchically into a large number of spherical pentagons using equal area or equal length optimization. Comput. Aided Des. 2022, 148, 103259. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, T.U.; Rezaee Javan, A.; Xie, Y.M. Extending Goldberg’s method to parametrize and control the geometry of Goldberg polyhedra. R. Soc. Open Sci. 2022, 9, 220675. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Xie, Y.M. Reducing the number of different members in truss layout optimization. Struct. Multidiscip. Optim. 2023, 66, 52. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, T.U.; Koronaki, A.; Pietroni, N.; Xie, Y.M. Reducing the number of different nodes in space frame structures through clustering and optimization. Eng. Struct. 2023, 284, 116016. [Google Scholar] [CrossRef]
- Agerskov, H. Optimum geometry design of double-layer space trusses. J. Struct. Eng. 1986, 112, 1454–1463. [Google Scholar] [CrossRef]
- Grigorian, M. Performance control for efficient design of double-layer grids under uniform loading. Int. J. Adv. Struct. 2014, 6, 52. [Google Scholar] [CrossRef]
- Surzhan, Y.; Rapina, K.; Rapina, T. Parameters rationalization for flat double-layer grid spatial structure (STiSK system). In Proceedings of the MATEC Web of Conferences, Sibiu, Romania, 7–9 June 2017; EDP Sciences: Lisses, Franch, 2017; Volume 116, p. 02033. [Google Scholar] [CrossRef]
- Alpatov, V. Search for the Optimal Shape of Metal Spatial (space) Structures. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 753, p. 022050. [Google Scholar] [CrossRef]
- Alpatov, V. Numerical studies of the nodal connections of metal spatial frames. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 463, p. 032103. [Google Scholar] [CrossRef]
- Botsch, M.; Kobbelt, L.; Pauly, M.; Alliez, P.; Lévy, B. Polygon Mesh Processing, 1st ed.; CRC Press: Delhi, India, 2010. [Google Scholar]
- Liu, Y.; Xu, W.; Wang, J.; Zhu, L.; Guo, B.; Chen, F.; Wang, G. General planar quadrilateral mesh design using conjugate direction field. ACM Trans. Graph. 2011, 30, 1–10. [Google Scholar] [CrossRef]
- Pluta, K.; Edelstein, M.; Vaxman, A.; Ben-Chen, M. PH-CPF: Planar hexagonal meshing using coordinate power fields. ACM Trans. Graph. 2021, 40, 156. [Google Scholar] [CrossRef]
- Jiang, C.; Tang, C.; Vaxman, A.; Wonka, P.; Pottmann, H. Polyhedral patterns. ACM Trans. Graph. 2015, 34, 1–12. [Google Scholar] [CrossRef]
- Engel, H. Structure Systems, 4th ed.; Deutsche Verlags-Anstalt: Munich, Germany, 1977. [Google Scholar]
- Iranian National Building Codes Compilation Office. Iranian National Building Codes Compilation Office. Iranian National Building Code, Part 10. In Steel Building Design; Ministry of Housing and Urban Development (MHUD): Tehran, Iran, 2022. [Google Scholar]
- Goldberg, D.E. Genetic Algorithm in Search, Optimization and Machine Learning, 1st ed.; Addition-Wesley Professional: Boston, MA, USA, 2010. [Google Scholar]
- Iranian National Building Codes Compilation Office. Iranian National Building Codes Compilation Office. Iranian National Building Code, Part 6. In Minimum Design Loads for Buildings and Other Structures; Ministry of Housing and Urban Development (MHUD): Tehran, Iran, 2019. [Google Scholar]
- Maalek, S.; Nooshin, H.; Dianat, N.; Abedi, K.; Heristchian, M.; Chenaghlou, M.R. Code of Practice for Skeletal Steel Space Structures; Management and Planning Organization of Iran: Tehran, Iran, 2011. [Google Scholar]
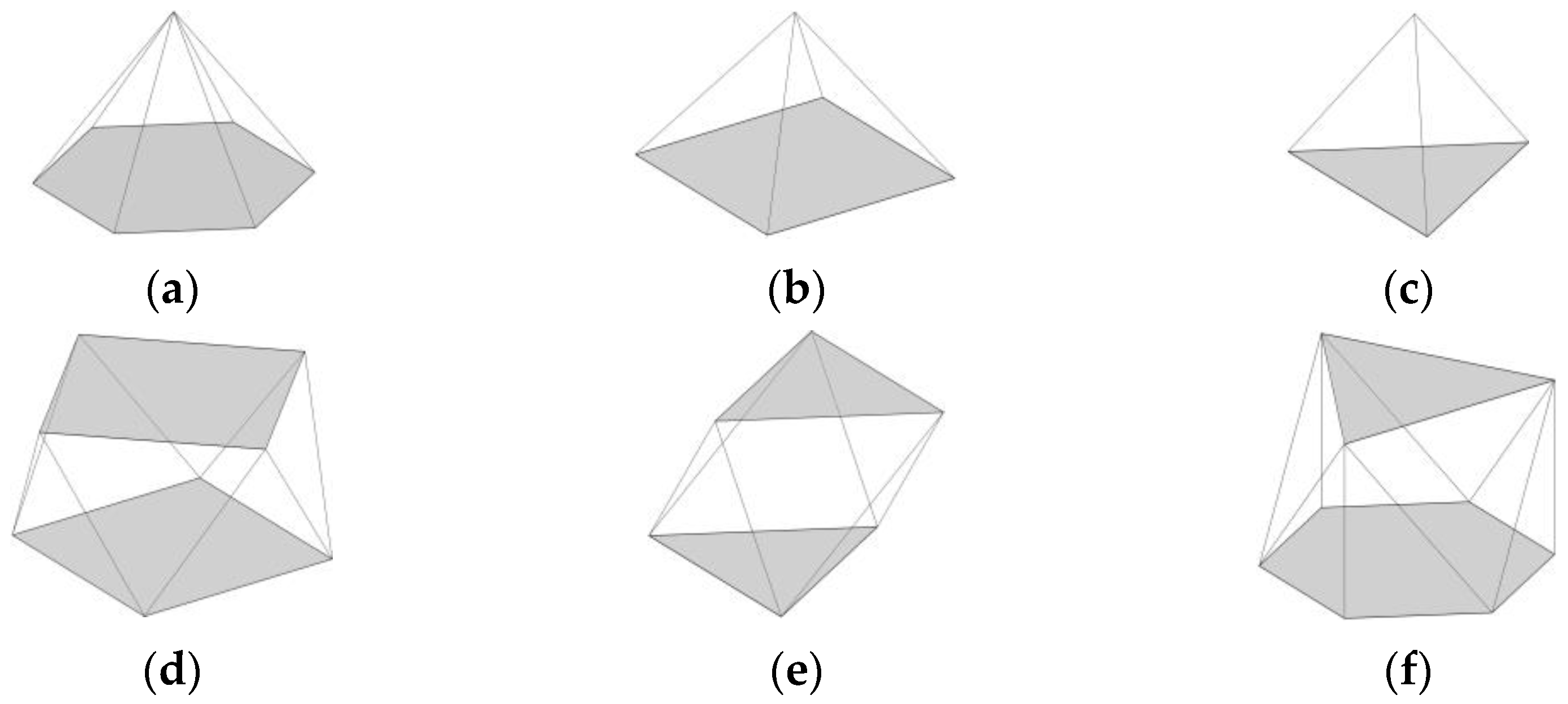
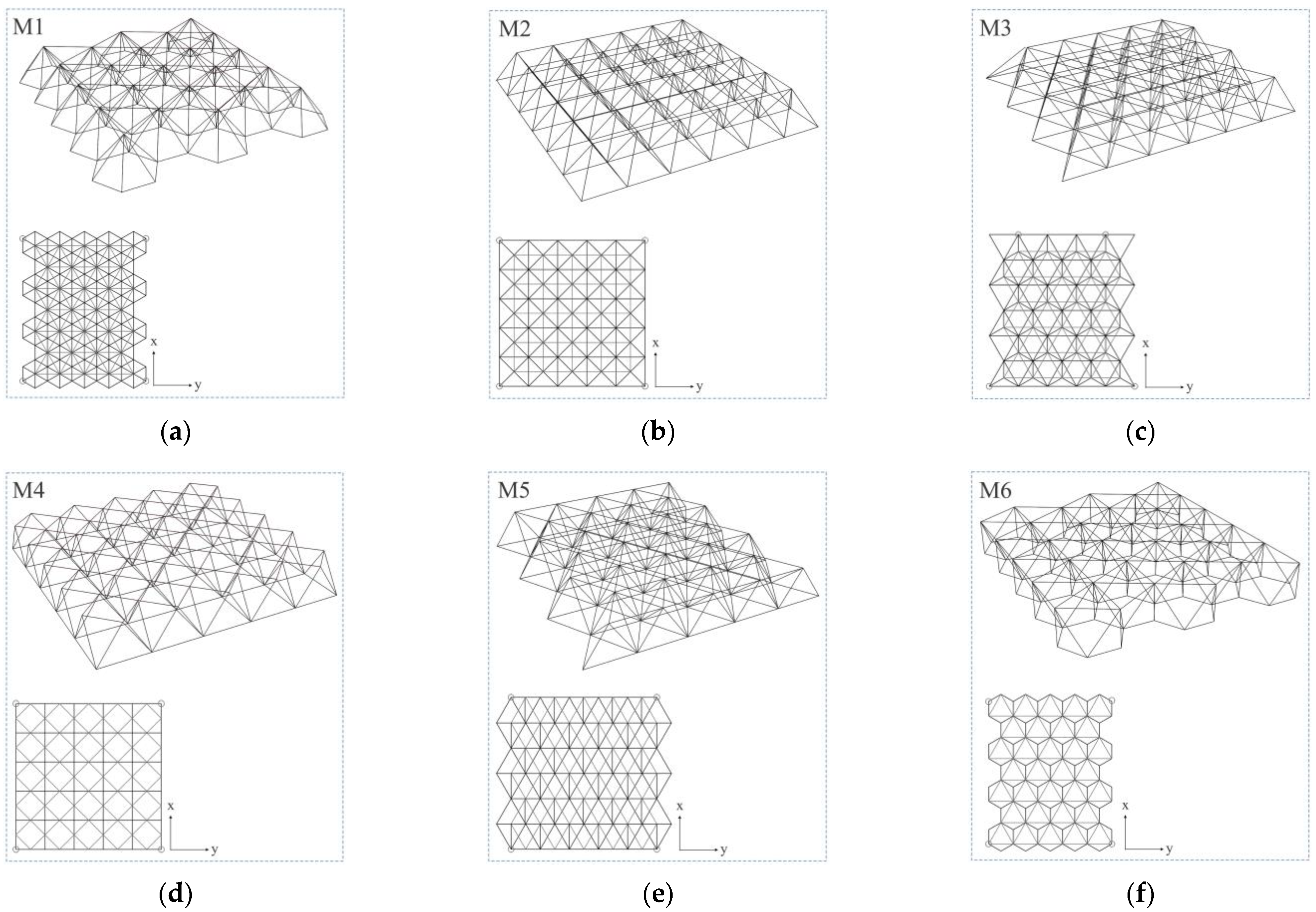
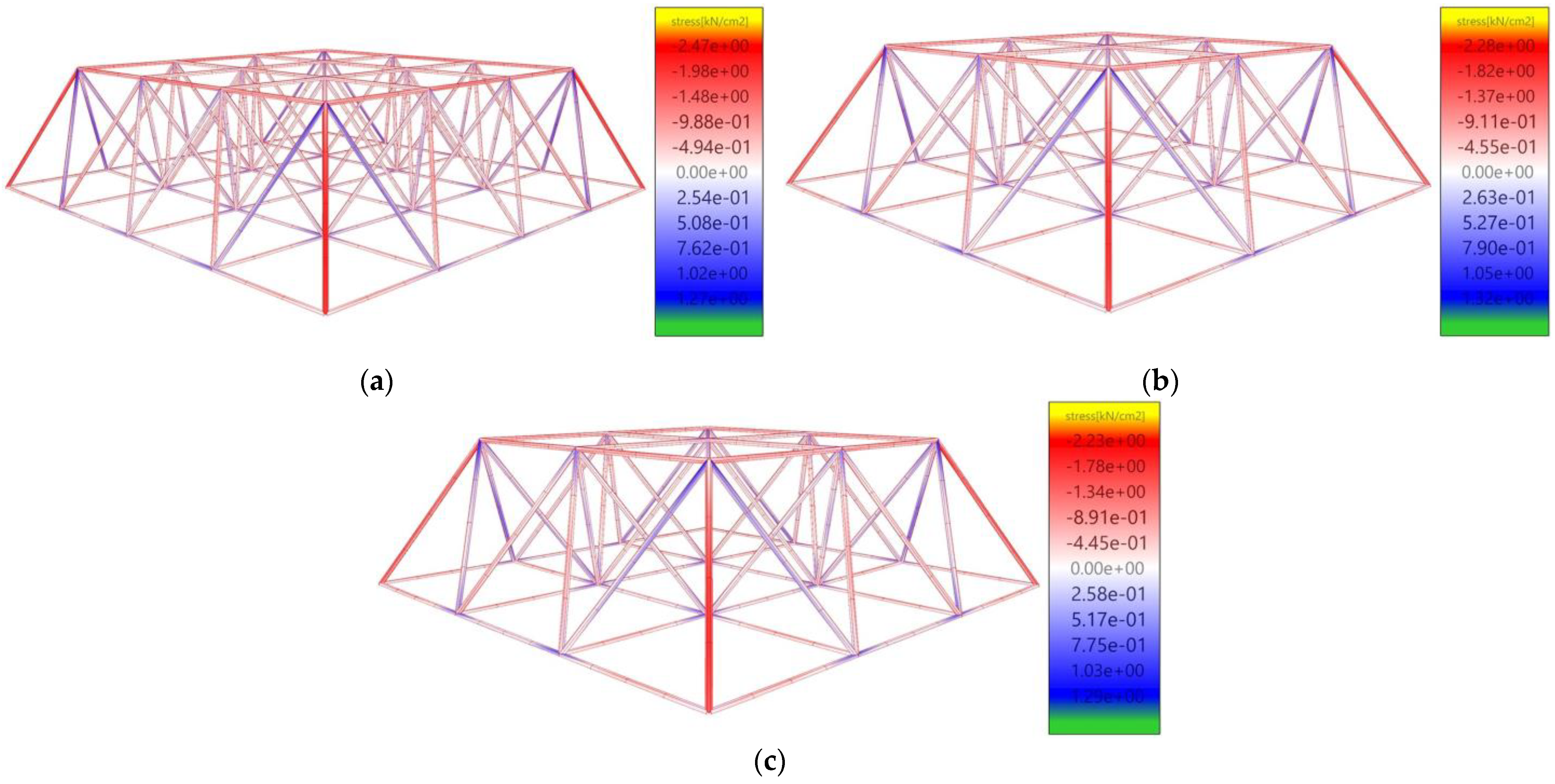

| Design Variable | Symbol | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Cross-section diameter | d | cm | 3 | 15 |
| No. of constitutive units | n | - | 3 | 10 |
| Depth | D | m | 0.5 | 4 |
| Model | Load Combination | Span (m) | Design Variable | Cost Function | |||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | n | d (cm) | D (m) | Structural Mass (kg) | Max. Deflection (cm) | |||
| x | y | ||||||||
| M1 | LC1 | 10 | 10.39 | 3 | 4 | 8.4 | 2.9 | 17,130 | 0.155 |
| 10 | 6.92 | 3 | 3 | 8.5 | 2.7 | 12,308 | 0.115 | ||
| LC2 | 10 | 10.39 | 3 | 4 | 9.7 | 3 | 23,160 | 0.167 | |
| 10 | 6.92 | 3 | 3 | 9.3 | 3 | 15,362 | 0.119 | ||
| LC3 | 10 | 10.39 | 3 | 4 | 9.5 | 3.1 | 22,522 | 0.261 | |
| 10 | 6.92 | 3 | 3 | 9.4 | 3 | 15,694 | 0.159 | ||
| M2 | LC1 | 10 | 10 | 4 | 4 | 7.5 | 2.6 | 12,527 | 0.104 |
| LC2 | 10 | 10 | 3 | 3 | 9.4 | 3 | 14,019 | 0.131 | |
| LC3 | 10 | 10 | 3 | 3 | 9.7 | 3.1 | 15,093 | 0.124 | |
| M3 | LC1 | 10 | 10.39 | 4 | 6 | 6.4 | 2.4 | 13,175 | 0.12 |
| 10 | 6.92 | 4 | 4 | 6.4 | 2.2 | 8489 | 0.076 | ||
| LC2 | 10 | 10.39 | 4 | 6 | 7.2 | 2.5 | 16,909 | 0.136 | |
| 10 | 6.92 | 4 | 4 | 6.9 | 2.3 | 10,008 | 0.087 | ||
| LC3 | 10 | 10.39 | 4 | 6 | 7.2 | 2.5 | 16,909 | 0.128 | |
| 10 | 6.92 | 4 | 4 | 7 | 2.1 | 10,012 | 0.08 | ||
| M4 | LC1 | 10 | 10 | 4 | 4 | 5.6 | 2.9 | 9005 | 0.12 |
| LC2 | 10 | 10 | 3 | 3 | 7.6 | 3.3 | 12,190 | 0.144 | |
| LC3 | 10 | 10 | 3 | 3 | 8.5 | 4 | 16,608 | 0.86 | |
| M5 | LC1 | 10 | 10.39 | 4 | 6 | 6.1 | 2.3 | 14,819 | 0.143 |
| 10 | 6.92 | 4 | 4 | 6.2 | 2 | 10,051 | 0.093 | ||
| LC2 | 10 | 10.39 | 4 | 6 | 7 | 2.5 | 20,137 | 0.172 | |
| 10 | 6.92 | 4 | 4 | 7.1 | 2.1 | 13,395 | 0.107 | ||
| LC3 | 10 | 10.39 | 4 | 6 | 6.9 | 2.4 | 19,262 | 0.156 | |
| 10 | 6.92 | 4 | 4 | 7.3 | 2.1 | 14,160 | 0.098 | ||
| M6 | LC1 | 10 | 10.39 | 3 | 4 | 6.9 | 4.5 | 15,591 | 0.643 |
| 10 | 6.92 | 3 | 3 | 6.7 | 4.2 | 10,755 | 0.785 | ||
| LC2 | 10 | 10.39 | 3 | 4 | 8.2 | 4.1 | 21,029 | 0.646 | |
| 10 | 6.92 | 3 | 3 | 8.1 | 4.2 | 15,719 | 0.715 | ||
| LC3 | 10 | 10.39 | 3 | 4 | 8.7 | 3.6 | 22,300 | 0.54 | |
| 10 | 6.92 | 3 | 3 | 7.8 | 3.9 | 14,066 | 0.729 | ||
| Model | Load Combination | Span | Design Variable | Cost Function | |||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | n | d (cm) | D (m) | Structural Mass (kg) | Max. Deflection (cm) | |||
| x | y | ||||||||
| M1 | LC1 | 10 | 10.39 | 3 | 4 | 5.2 | 2 | 5800 | 0.327 |
| 10 | 6.92 | 3 | 3 | 4.7 | 2.1 | 3462 | 0.294 | ||
| LC2 | 10 | 10.39 | 3 | 4 | 6.5 | 2 | 9063 | 0.377 | |
| 10 | 6.92 | 3 | 3 | 6 | 2.1 | 5642 | 0.277 | ||
| LC3 | 10 | 10.39 | 3 | 4 | 6.6 | 2.3 | 9734 | 0.569 | |
| 10 | 6.92 | 3 | 3 | 6.1 | 2.3 | 5995 | 0.38 | ||
| M2 | LC1 | 10 | 10 | 3 | 3 | 5.1 | 1.4 | 3506 | 0.378 |
| LC2 | 10 | 10 | 3 | 3 | 6.6 | 1.4 | 5873 | 0.428 | |
| LC3 | 10 | 10 | 3 | 3 | 6.5 | 1.5 | 5745 | 0.389 | |
| M3 | LC1 | 10 | 10.39 | 4 | 6 | 3.7 | 1.3 | 3771 | 0.313 |
| 10 | 6.92 | 4 | 4 | 3.9 | 0.7 | 2578 | 0.387 | ||
| LC2 | 10 | 10.39 | 4 | 6 | 4.5 | 1.2 | 5504 | 0.462 | |
| 10 | 6.92 | 4 | 4 | 4 | 1.2 | 2879 | 0.294 | ||
| LC3 | 10 | 10.39 | 4 | 6 | 4.7 | 1.2 | 6004 | 0.404 | |
| 10 | 6.92 | 4 | 4 | 4.1 | 1.2 | 3025 | 0.268 | ||
| M4 | LC1 | 10 | 10 | 3 | 3 | 4 | 1.3 | 2627 | 0.512 |
| LC2 | 10 | 10 | 3 | 3 | 4.7 | 1.9 | 3897 | 0.484 | |
| LC3 | 10 | 10 | 3 | 3 | 5.7 | 3.3 | 6856 | 4.95 | |
| M5 | LC1 | 10 | 10.39 | 4 | 6 | 3.9 | 0.9 | 4890 | 0.57 |
| 10 | 6.92 | 4 | 4 | 4 | 0.7 | 3446 | 0.424 | ||
| LC2 | 10 | 10.39 | 4 | 6 | 4.6 | 1.1 | 6991 | 0.682 | |
| 10 | 6.92 | 4 | 4 | 4.2 | 1.2 | 4064 | 0.348 | ||
| LC3 | 10 | 10.39 | 4 | 6 | 4.5 | 1.2 | 6788 | 0.496 | |
| 10 | 6.92 | 4 | 4 | 4.1 | 1.3 | 3932 | 0.29 | ||
| M6 | LC1 | 10 | 10.39 | 3 | 4 | 4.8 | 1.7 | 5326 | 3.585 |
| 10 | 6.92 | 3 | 3 | 4.3 | 2.2 | 3441 | 4.398 | ||
| LC2 | 10 | 10.39 | 3 | 4 | 6.3 | 1.6 | 9060 | 3.301 | |
| 10 | 6.92 | 3 | 3 | 5.7 | 2.4 | 6208 | 3.534 | ||
| LC3 | 10 | 10.39 | 3 | 4 | 6.3 | 2.1 | 9661 | 2.569 | |
| 10 | 6.92 | 3 | 3 | 5.6 | 2.2 | 5836 | 3.629 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahbazi, Y.; Abdkarimi, M.; Ahmadnejad, F.; Mokhtari Kashavar, M.; Fotouhi, M.; Pedrammehr, S. Comparative Study of Optimal Flat Double-Layer Space Structures with Diverse Geometries through Genetic Algorithm. Buildings 2024, 14, 2816. https://doi.org/10.3390/buildings14092816
Shahbazi Y, Abdkarimi M, Ahmadnejad F, Mokhtari Kashavar M, Fotouhi M, Pedrammehr S. Comparative Study of Optimal Flat Double-Layer Space Structures with Diverse Geometries through Genetic Algorithm. Buildings. 2024; 14(9):2816. https://doi.org/10.3390/buildings14092816
Chicago/Turabian StyleShahbazi, Yaser, Mahsa Abdkarimi, Farhad Ahmadnejad, Mohsen Mokhtari Kashavar, Mohammad Fotouhi, and Siamak Pedrammehr. 2024. "Comparative Study of Optimal Flat Double-Layer Space Structures with Diverse Geometries through Genetic Algorithm" Buildings 14, no. 9: 2816. https://doi.org/10.3390/buildings14092816






