Energy-Saving Optimization of HVAC Systems Using an Ant Lion Optimizer with Enhancements
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. The Overview of This Paper
2. Methodology
2.1. Standard Ant Lion Optimizer
- (1)
- Initialize Population
- (2)
- Random Walk
- (3)
- Hunting Behavior
2.2. Ant Lion Optimizer with Enhancements
2.2.1. The Levy Flight of the Ant Mechanism
2.2.2. The Adaptive Elite Guidance Mechanism
2.2.3. Dynamic Cauchy Variation Mechanism
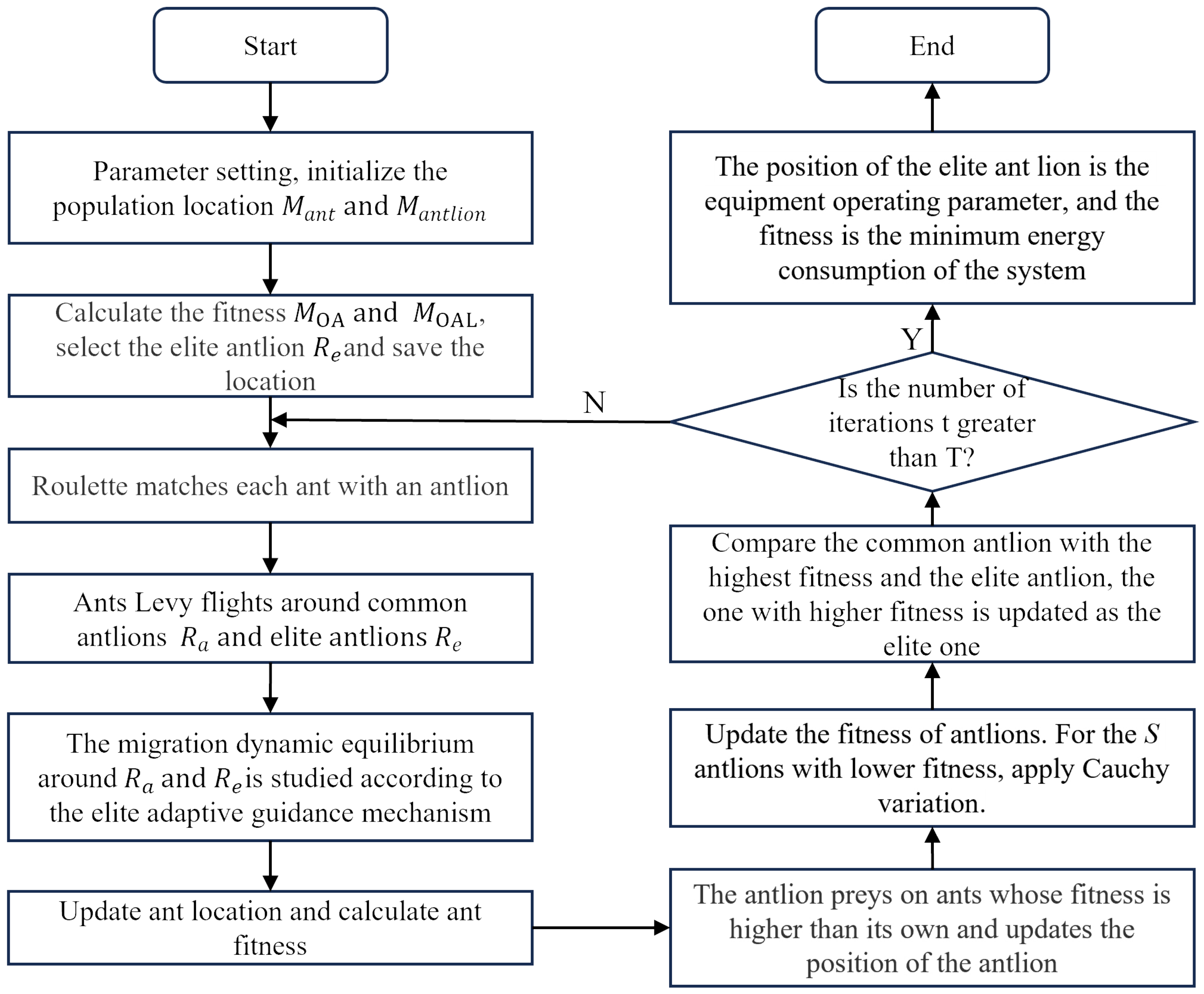
2.2.4. Algorithm Flow
- (a)
- Initialize the positions of the ant and antlion populations, and .
- (b)
- Calculate the fitness of the ants and antlions, and , select the elite antlion , and save its position.
- (c)
- Use the roulette wheel to select the antlion around which each ant will walk.
- (d)
- The ants perform Levy flights around and .
- (e)
- Dynamically balance the walks around and according to the adaptive elite strategy.
- (f)
- Update the positions of the ants and calculate their fitness .
- (g)
- The ants fall into traps, and the antlions prey on the ants, updating their positions according to Equation (8).
- (h)
- Update the fitness of the antlions and apply the Cauchy mutation to the antlions with the lowest fitness.
- (i)
- Compare the fitness of the best antlion with the elite antlion, and if the former is better, update the elite antlion .
3. Case Study
3.1. System Background
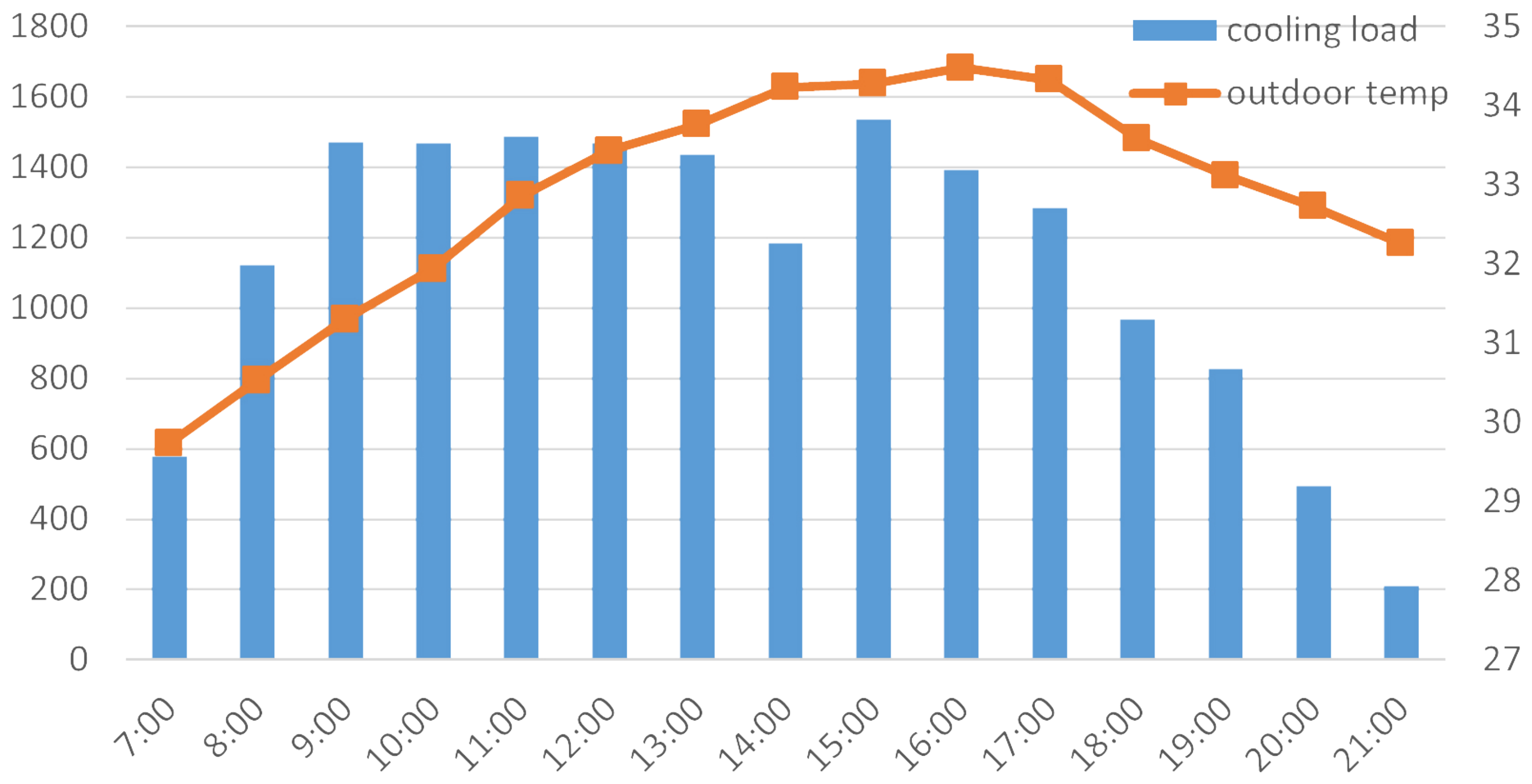
3.2. Data Description
3.3. System Modeling
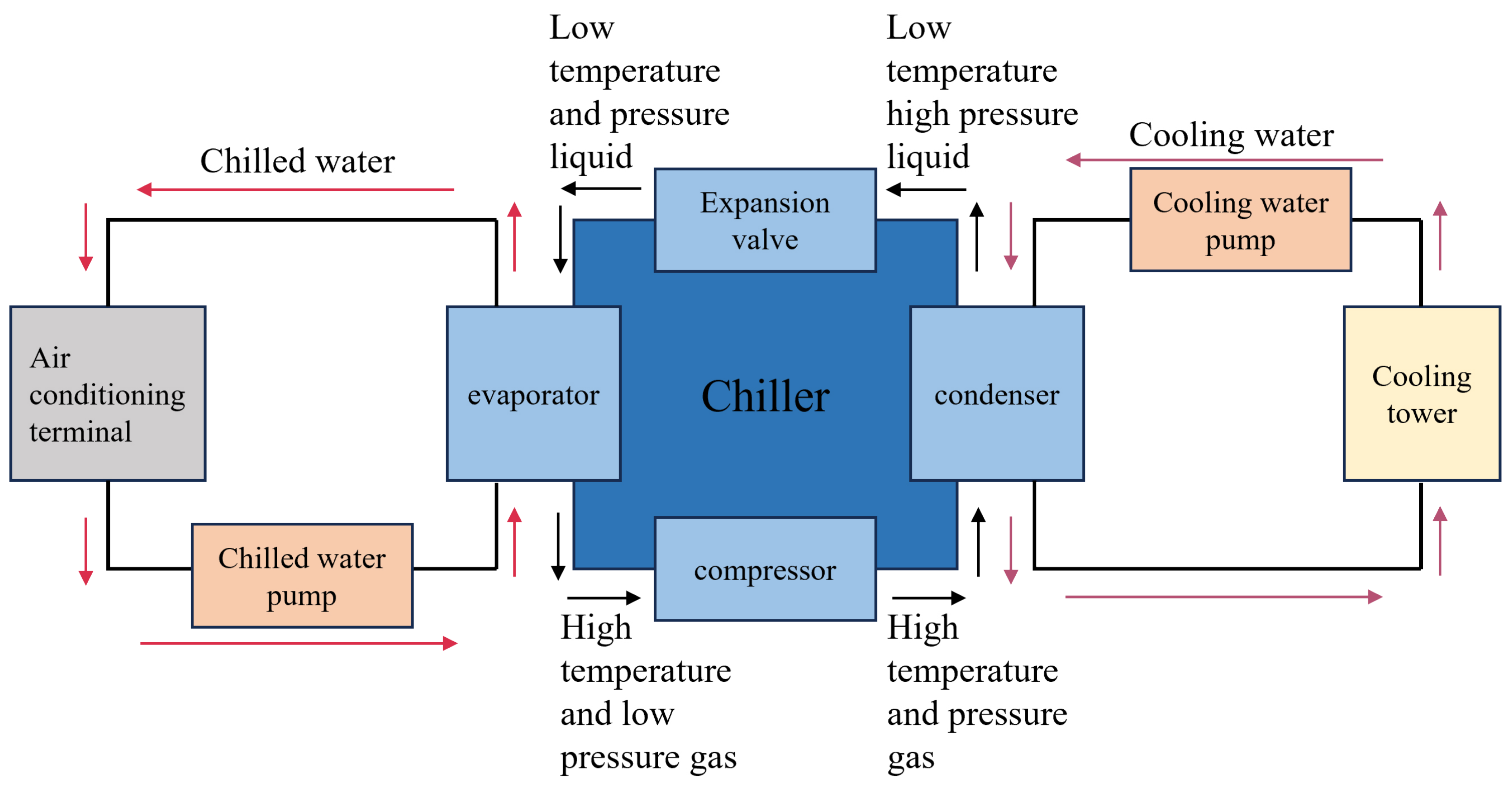
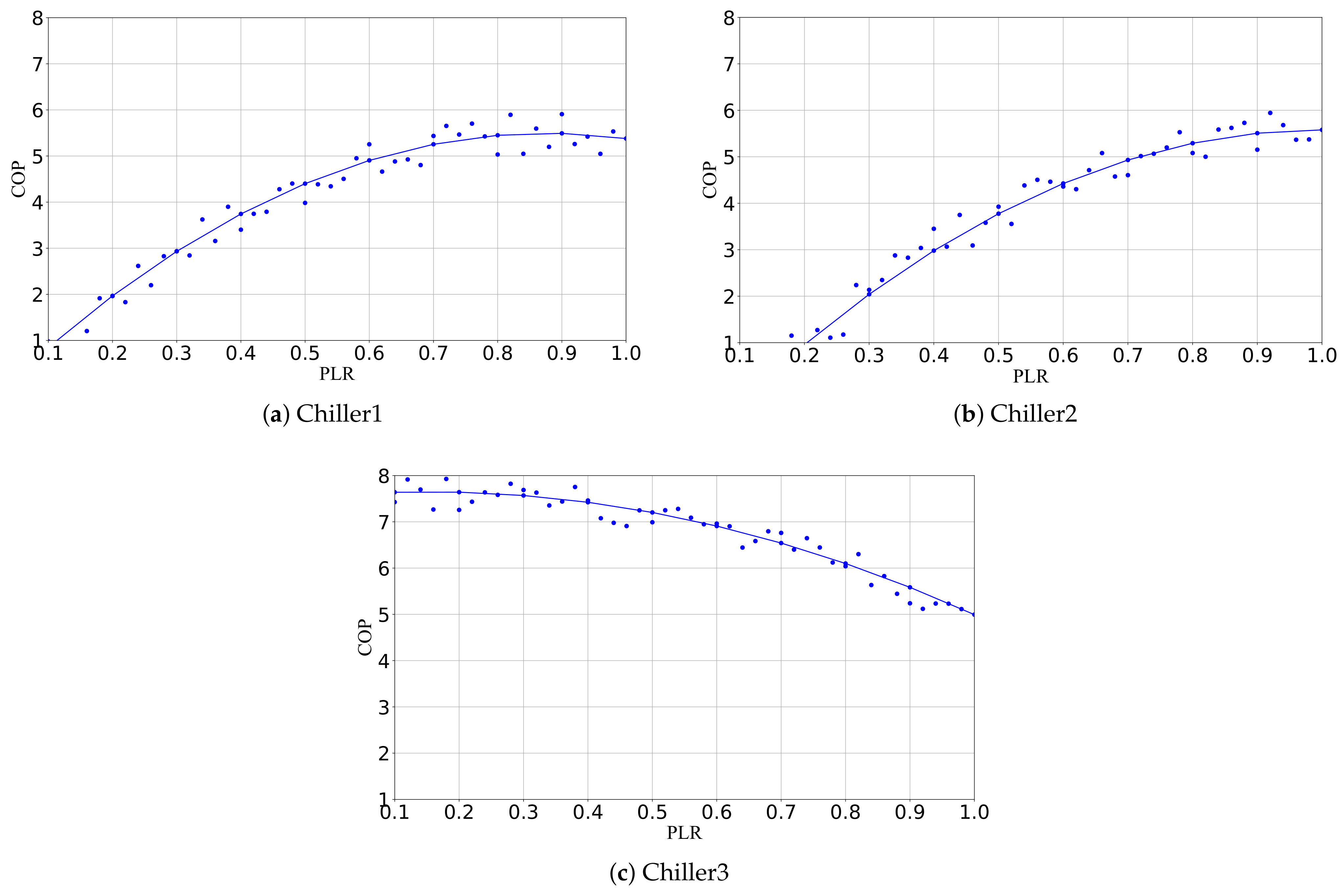
3.3.1. Model for Chiller
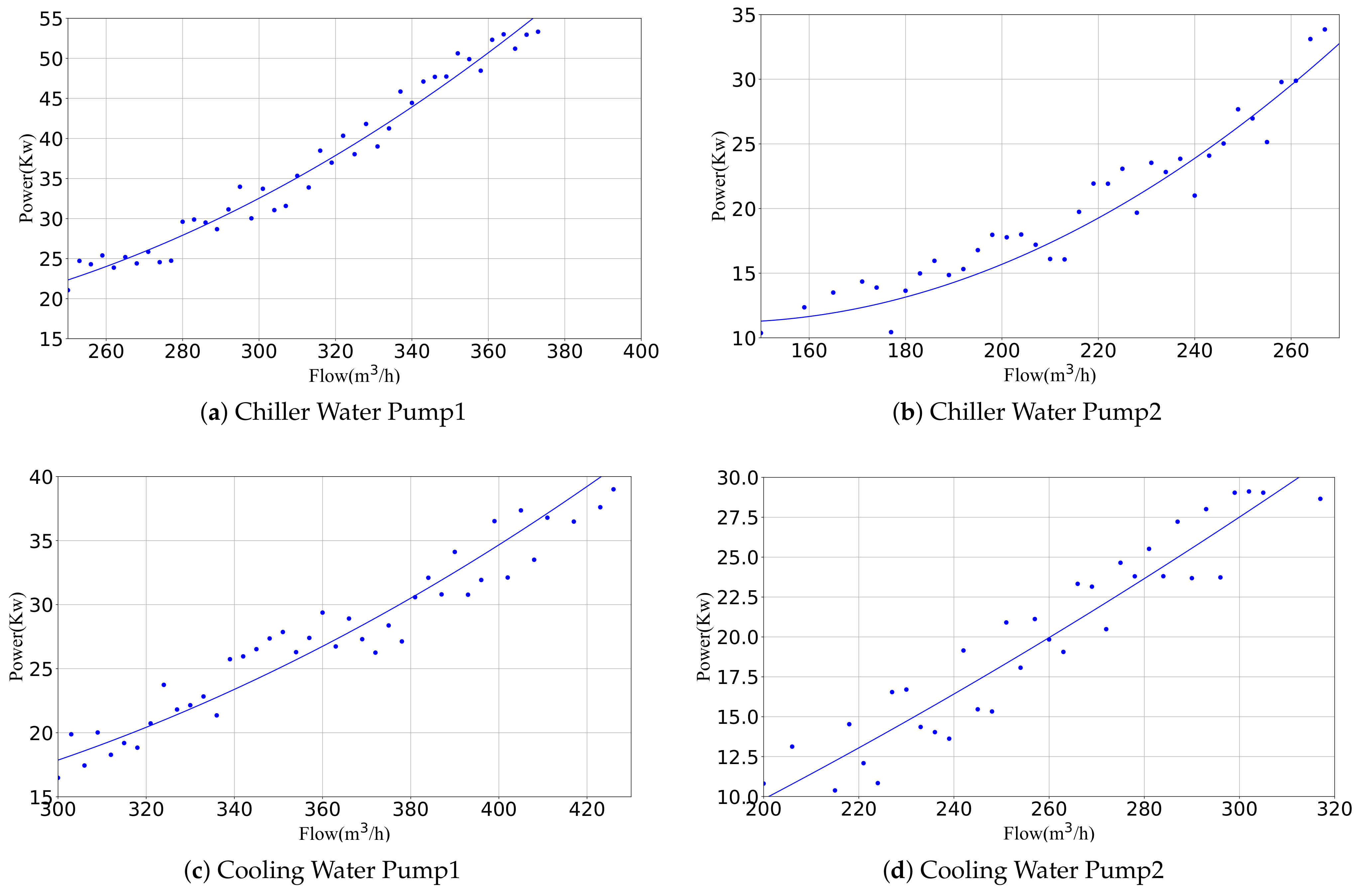
3.3.2. Model for Cooling/Chilled Water Pump
3.3.3. Model for Cooling Tower
3.3.4. System Energy Consumption Model
4. Experiment
4.1. Experimental Setting
4.1.1. Hyperparameters
4.1.2. Evaluation Metrics
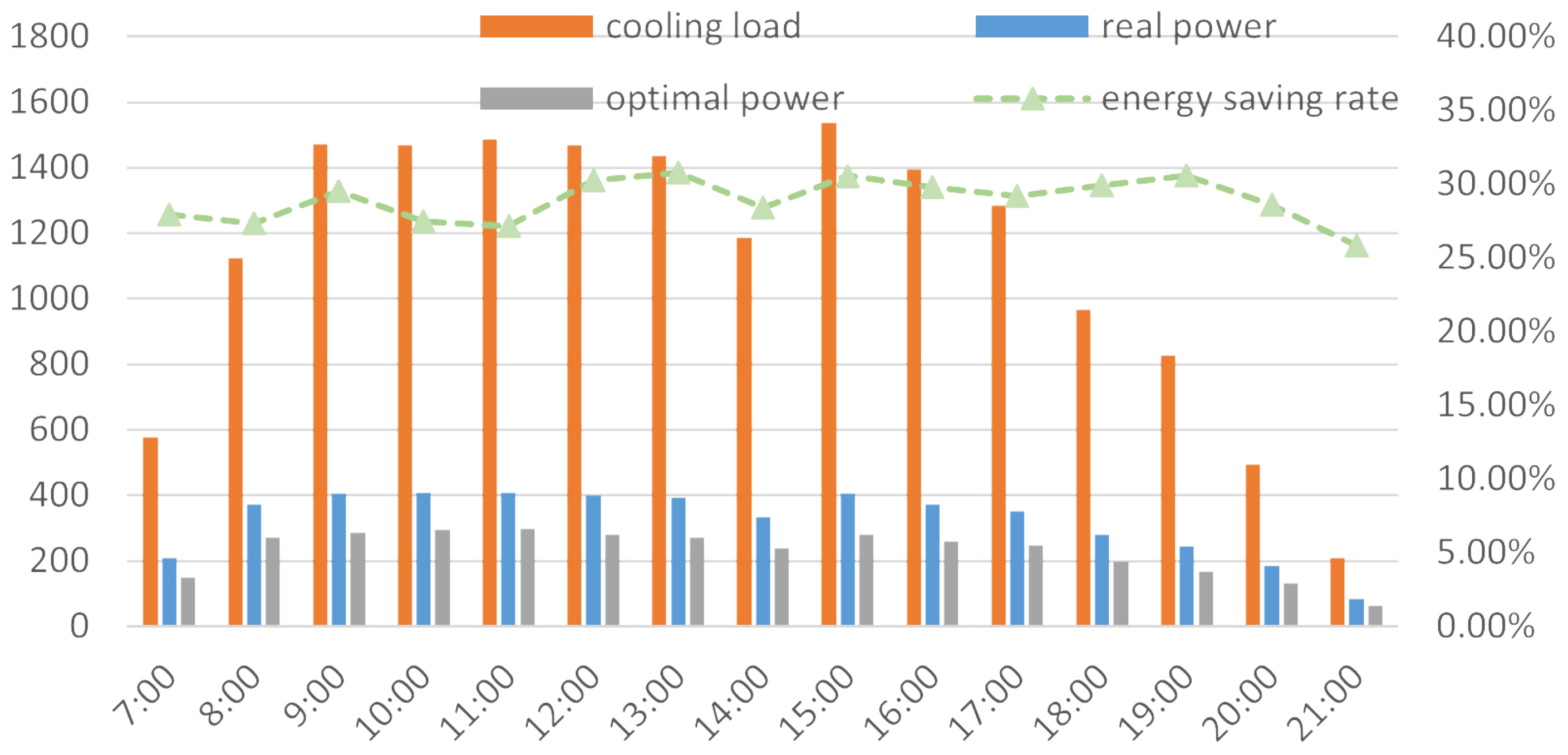
4.2. Comparison of Energy-Saving Optimization Results
4.3. Typical Day Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- China Association of Building Energy Efficiency. China Building Energy Consumption and Carbon Emissions Research Report (2022). Constr. Archit. 2023, 2, 57–69. [Google Scholar]
- Miao, Y.; Yao, Y.; Hong, X.; Xiong, L.; Zhang, F.; Chen, W. Research on optimal control of HVAC system using swarm intelligence algorithms. Build. Environ. 2023, 241, 110467. [Google Scholar] [CrossRef]
- Farahnak, M.; Farzaneh-Gord, M.; Deymi-Dashtebayaz, M.; Dashti, F. Optimal sizing of power generation unit capacity in ICE-driven CCHP systems for various residential building sizes. Appl. Energy 2015, 158, 203–219. [Google Scholar] [CrossRef]
- Kohlenbach, P.; Ziegler, F. A dynamic simulation model for transient absorption chiller performance. Part I: The model. Int. J. Refrig. 2008, 31, 217–225. [Google Scholar] [CrossRef]
- Wemhoff, A.; Frank, M. Predictions of energy savings in HVAC systems by lumped models. Energy Build. 2010, 42, 1807–1814. [Google Scholar] [CrossRef]
- Vakiloroaya, V.; Samali, B.; Madadnia, J.; Ha, Q. Component-wise optimization for a commercial central cooling plant. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 2769–2774. [Google Scholar]
- Park, M.H.; Shin, E.G.; Lee, H.R.; Suh, I.S. Dynamic model and control algorithm of HVAC system for OLEV® application. In Proceedings of the ICCAS 2010, Gyeonggi-do, Republic of Korea, 27–30 October 2010; pp. 1312–1317. [Google Scholar]
- Terzi, E.; Fagiano, L.; Farina, M.; Scattolini, R. Structured modelling from data and optimal control of the cooling system of a large business center. J. Build. Eng. 2020, 28, 101043. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Yao, Y.; Lian, Z.; Hou, Z.; Zhou, X. Optimal operation of a large cooling system based on an empirical model. Appl. Therm. Eng. 2004, 24, 2303–2321. [Google Scholar] [CrossRef]
- Lu, L.; Cai, W.; Xie, L.; Li, S.; Soh, Y.C. HVAC system optimization—In-building section. Energy Build. 2005, 37, 11–22. [Google Scholar] [CrossRef]
- Xiaomei, F.; Qifei, J.; Zheng, Z. Analysis on Energy-saving of Year-round Operation Conditions with Variable Flow Cooling Water System. Build. Sci. 2010, 26, 80–84. [Google Scholar]
- Yang, C.; Gunay, B.; Shi, Z.; Shen, W. Machine learning-based prognostics for central heating and cooling plant equipment health monitoring. IEEE Trans. Autom. Sci. Eng. 2020, 18, 346–355. [Google Scholar] [CrossRef]
- Krinidis, S.; Tsolakis, A.; Katsolas, I.; Ioannidis, D.; Tzovaras, D. Multi-criteria HVAC control optimization. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Barrett, E.; Linder, S. Autonomous hvac control, a reinforcement learning approach. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2015, Porto, Portugal, 7–11 September 2015; Proceedings, Part III 15. Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–19. [Google Scholar]
- Afroz, Z.; Shafiullah, G.; Urmee, T.; Shoeb, M.; Higgins, G. Predictive modelling and optimization of HVAC systems using neural network and particle swarm optimization algorithm. Build. Environ. 2022, 209, 108681. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Rahkar Farshi, T. Battle royale optimization algorithm. Neural Comput. Appl. 2021, 33, 1139–1157. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Baghalzadeh Shishehgarkhaneh, M. Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar] [CrossRef]
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. Expert Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Trojovskỳ, P.; Dehghani, M. Walrus optimization algorithm: A new bio-inspired metaheuristic algorithm. Preprint 2022. [Google Scholar] [CrossRef]
- Amali, D.; Dinakaran, M. Wildebeest herd optimization: A new global optimization algorithm inspired by wildebeest herding behaviour. J. Intell. Fuzzy Syst. 2019, 37, 8063–8076. [Google Scholar] [CrossRef]
- Terzi, E.; Cataldo, A.; Lorusso, P.; Scattolini, R. Modelling and predictive control of a recirculating cooling water system for an industrial plant. J. Process Control 2018, 68, 205–217. [Google Scholar] [CrossRef]
- Saxena, P.; Kothari, A. Ant lion optimization algorithm to control side lobe level and null depths in linear antenna arrays. AEU-Int. J. Electron. Commun. 2016, 70, 1339–1349. [Google Scholar] [CrossRef]
- Reynolds, A. Liberating Lévy walk research from the shackles of optimal foraging. Phys. Life Rev. 2015, 14, 59–83. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Jensi, R.; Jiji, G.W. An enhanced particle swarm optimization with levy flight for global optimization. Appl. Soft Comput. 2016, 43, 248–261. [Google Scholar] [CrossRef]
- Han, X.M.; Qiu, B.; Liu, Q.M.; Zhou, L.Y.; Wang, L.M. Fruit fly optimization algorithm based on Cauchy mutation. Microelectron. Comput. 2017, 34, 26–30. [Google Scholar]
- Tashtoush, B.; Molhim, M.; Al-Rousan, M. Dynamic model of an HVAC system for control analysis. Energy 2005, 30, 1729–1745. [Google Scholar] [CrossRef]
- Wijaya, T.K.; Alhamid, M.I.; Saito, K.; Nasruddin, N. Dynamic optimization of chilled water pump operation to reduce HVAC energy consumption. Therm. Sci. Eng. Prog. 2022, 36, 101512. [Google Scholar] [CrossRef]




| Problem Type | Method Type | References | Limitations |
|---|---|---|---|
| System Energy Consumption Modeling | mechanistic modeling | [4,5,6,7] | Requires extensive domain-specific expertise, time, and high technical costs. |
| data-driven modeling | [8,9] | Requires large amounts of data and computational resources, and is difficult to transfer to new application scenarios. | |
| HVAC System Optimization Methods | Traditional Methods | [10,11,12] | Difficult for traditional optimization algorithms based on expert experience to handle the high complexity and strong coupling of internal factors in HVAC systems. |
| Machine Learning | [13,14,15,16] | High computational resource demand, large deviations in system operation data, and data quality is hard to meet requirements. | |
| Swarm intelligence optimization | [2,17,18,19,20,21,22,23,24,25] | The structure of the algorithm is complex, the parameters are large, and a large number of random individuals increase the invalid calculation and reduce the efficiency of the algorithm. |
| Equipment Type | Parameters | Quantity |
|---|---|---|
| Chiller1 | Rated cooling capacity 1934 kW, rated power 336 kw | 1 |
| Chiller2 | Rated cooling capacity 1135 kW, rated power 261 kw | 1 |
| Chiller3 | Rated cooling capacity 353.5 kW, rated power 74 kw | 1 |
| Chilled water pump | Rated flow 80 m3/h, rated power 15 kw | 1 |
| Chilled water pump | Rated flow 200 m3/h, rated power 30 kw | 2 |
| Chilled water pump | Rated flow 400 m3/h, rated power 55 kw | 2 |
| Cooling water pump | Rated flow 250 m3/h, rated power 30 kw | 2 |
| Cooling water pump | Rated flow 450 m3/h, rated power 45 kw | 2 |
| Cooling Tower | Rated flow 250 m3/h, rated power 7.5 kw | 4 |
| Algorithm | Parameter | Function | Value |
|---|---|---|---|
| BRO [19] | threshold | dead threshold | 3 |
| DMOA [20] | n_baby_sitter | number of babysitters | 3 |
| peep | define vocalization coeff | 2 | |
| GSKA [22] | pb | percent of the best | 0.1 |
| kr | knowledge ratio | 0.7 | |
| HBO [23] | degree | the degree level in corporate rank hierarchy | 2 |
| WHO [25] | n_explore_step | number of exploration step | 3 |
| n_exploit_step | number of exploitation step | 3 | |
| eta | learning rate the | 0.15 | |
| probability of wildebeest | |||
| p_hi | move to another position | 0.9 | |
| based on herd instinct | |||
| local_alpha | control local movement | 0.9 | |
| local_beta | control local movement | 0.3 | |
| global_alpha | control global movement | 0.2 | |
| global_beta | control global movement | 0.8 | |
| delta_w | dist to worst | 2.0 | |
| delta_c | dist to best | 2.0 |
| Case | Temperature | Humidity | Result | CHW Pump | CW Pump | Cooling Tower | Chiller | System |
|---|---|---|---|---|---|---|---|---|
| High | 34.28 | 35.78 | Actual Predicted Error | 27.62 | 20.40 | 10.28 | 156.00 | 214.28 |
| 27.48 | 22.55 | 12.97 | 139.60 | 201.60 | ||||
| 0.36% | 10.39% | 16.73% | 10.51% | 5.92% | ||||
| Medium | 30.53 | 54.22 | Actual Predicted Error | 28.77 | 26.13 | 4.21 | 51.75 | 110.87 |
| 27.74 | 24.02 | 4.60 | 55.64 | 112.00 | ||||
| 3.60% | 8.10% | 9.38% | 7.51% | 1.02% | ||||
| Low | 32.26 | 43.18 | Actual Predicted Error | 6.62 | 10.11 | 1.78 | 19.52 | 38.03 |
| 6.27 | 9.84 | 1.74 | 22.74 | 40.60 | ||||
| 5.26 | 2.62 | 2.32 | 16.50 | 6.74 | ||||
| - | - | - | Mean Error | 3.07% | 7.00% | 9.48% | 11.51% | 4.56% |
| Case | Result | ALO [17] | ARO [18] | BRO [19] | DMOA [20] | EVO [21] | GSKA [22] | HBO [23] | WaOA [24] | WHO [25] | ALOE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| High | ART (s) | 272 | 531 | 281 | 654 | 290 | 467 | 286 | 613 | 2111 | 348 |
| (%) | 19.90 | 16.51 | 14.66 | 8.14 | 7.33 | 16.74 | 4.31 | 15.57 | 7.69 | 28.16 | |
| VESR (%) | 0.004 | 0.239 | 0.097 | 0.175 | 0.189 | 0.076 | 0.014 | 0.258 | 0.017 | 0.000 | |
| Medium | ART (s) | 286 | 549 | 268 | 713 | 384 | 307 | 288 | 560 | 2246 | 327 |
| (%) | 15.12 | 9.62 | 11.51 | 8.93 | 17.52 | 27.91 | 8.93 | 21.30 | 20.79 | 28.26 | |
| VESR (%) | 0.178 | 0.809 | 0.006 | 0.846 | 0.197 | 0.277 | 0.232 | 0.307 | 1.137 | 0.000 | |
| Low | ART (s) | 255 | 457 | 285 | 605 | 421 | 283 | 273 | 573 | 2336 | 341 |
| (%) | 19.11 | 19.31 | 18.28 | 22.04 | 18.40 | 22.83 | 17.49 | 15.49 | 18.97 | 24.85 | |
| VESR (%) | 0.061 | 0.009 | 0.520 | 0.079 | 0.004 | 0.104 | 0.020 | 0.160 | 0.264 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Guo, Y.; Huang, W.; Jin, J.; Zou, M.; Zhu, Z. Energy-Saving Optimization of HVAC Systems Using an Ant Lion Optimizer with Enhancements. Buildings 2024, 14, 2842. https://doi.org/10.3390/buildings14092842
Hu B, Guo Y, Huang W, Jin J, Zou M, Zhu Z. Energy-Saving Optimization of HVAC Systems Using an Ant Lion Optimizer with Enhancements. Buildings. 2024; 14(9):2842. https://doi.org/10.3390/buildings14092842
Chicago/Turabian StyleHu, Bin, Yuhu Guo, Wenjun Huang, Jianxiang Jin, Mingxuan Zou, and Zhikun Zhu. 2024. "Energy-Saving Optimization of HVAC Systems Using an Ant Lion Optimizer with Enhancements" Buildings 14, no. 9: 2842. https://doi.org/10.3390/buildings14092842
APA StyleHu, B., Guo, Y., Huang, W., Jin, J., Zou, M., & Zhu, Z. (2024). Energy-Saving Optimization of HVAC Systems Using an Ant Lion Optimizer with Enhancements. Buildings, 14(9), 2842. https://doi.org/10.3390/buildings14092842






