Consideration of Different Soil Properties and Roughness in Shear Characteristics of Concrete–Soil Interface
Abstract
:1. Introduction
2. Interface Shear Experiment
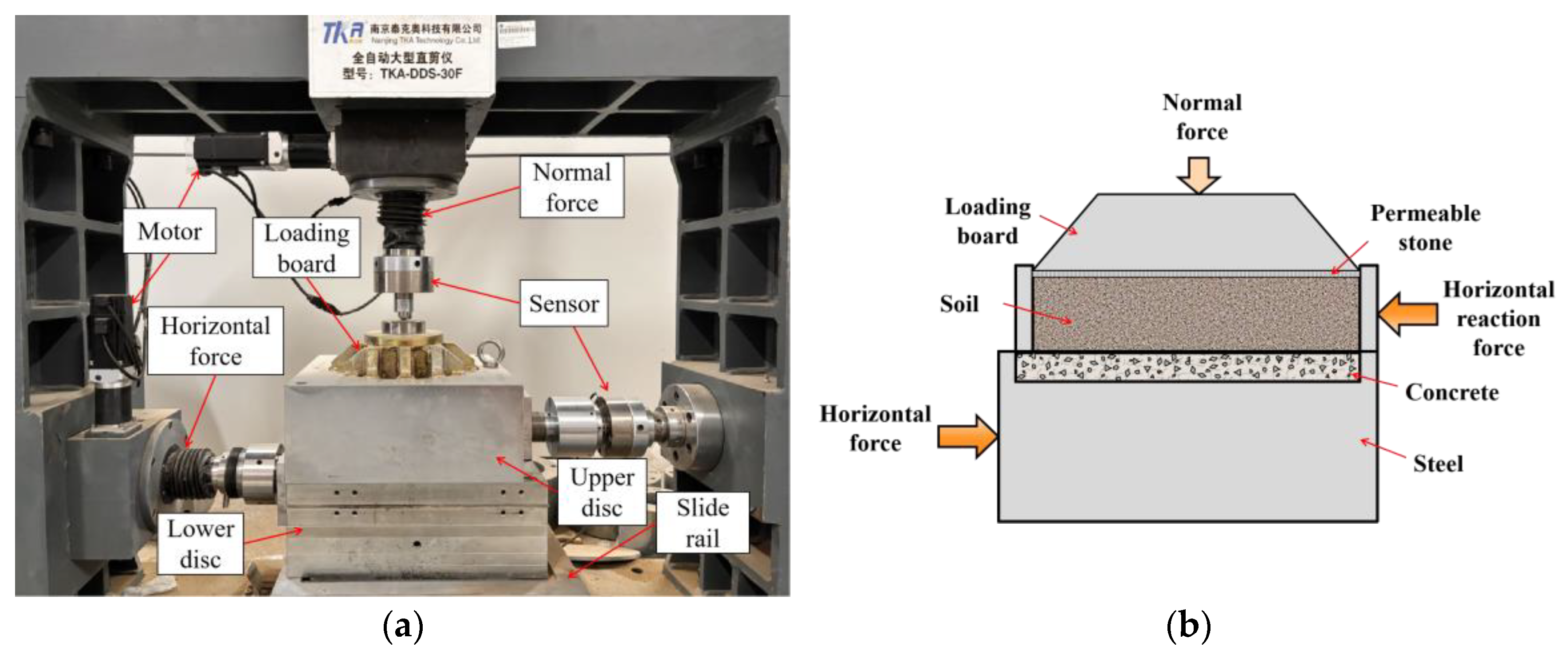
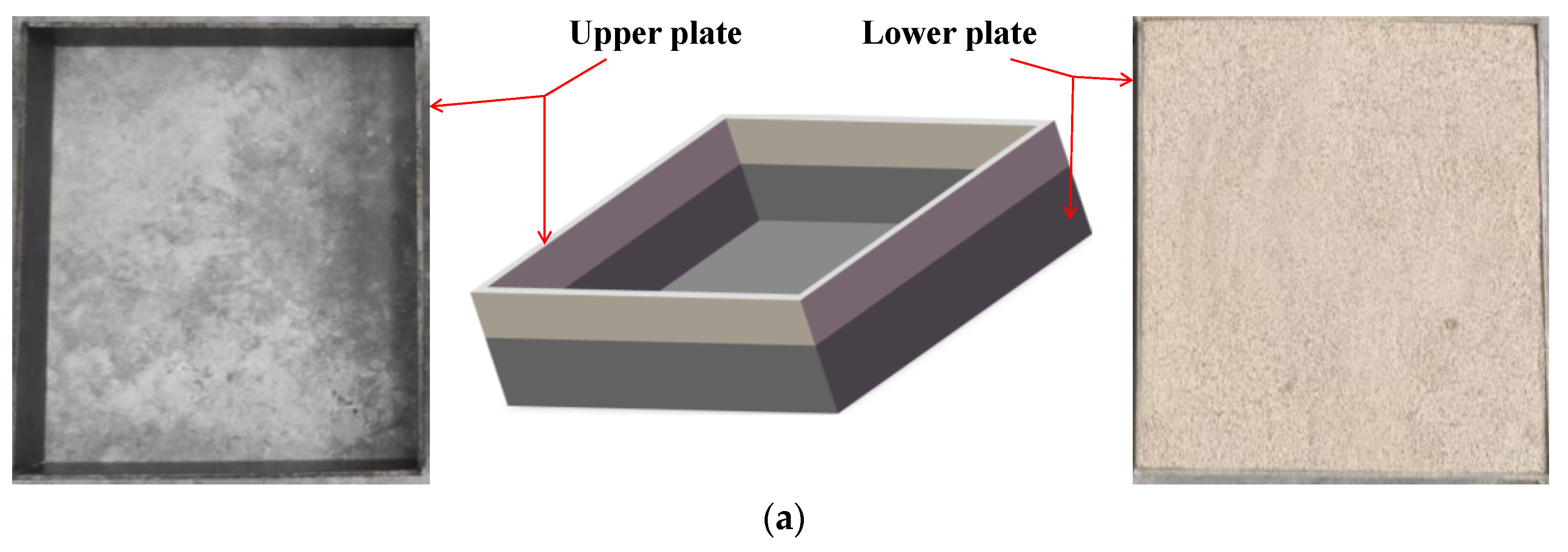
2.1. Experiment Apparatus and Materials
2.2. Evaluation and Calculation of Roughness
2.3. Experiment Method
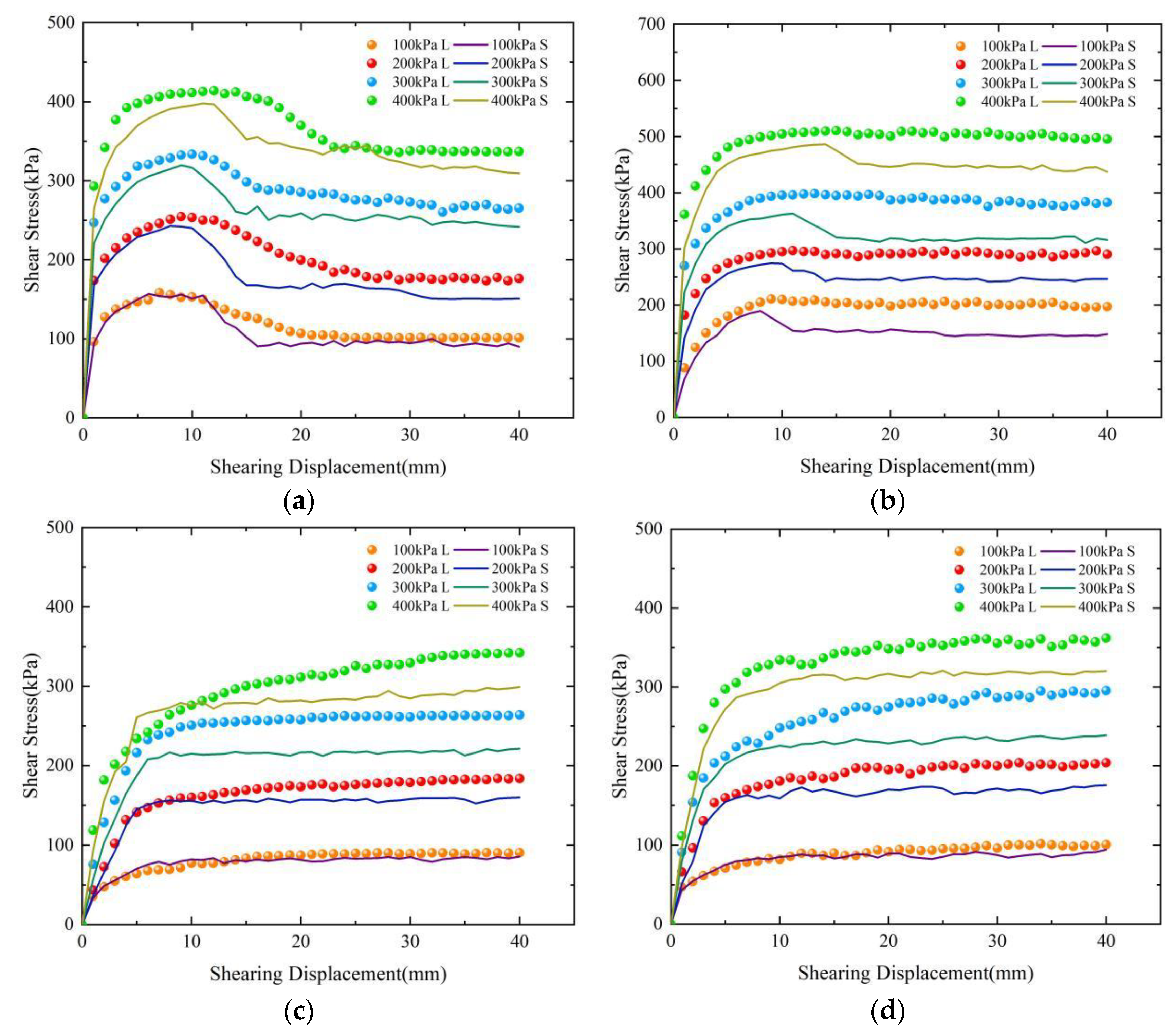
3. Influence of Soil Properties on Interfacial Shear Properties
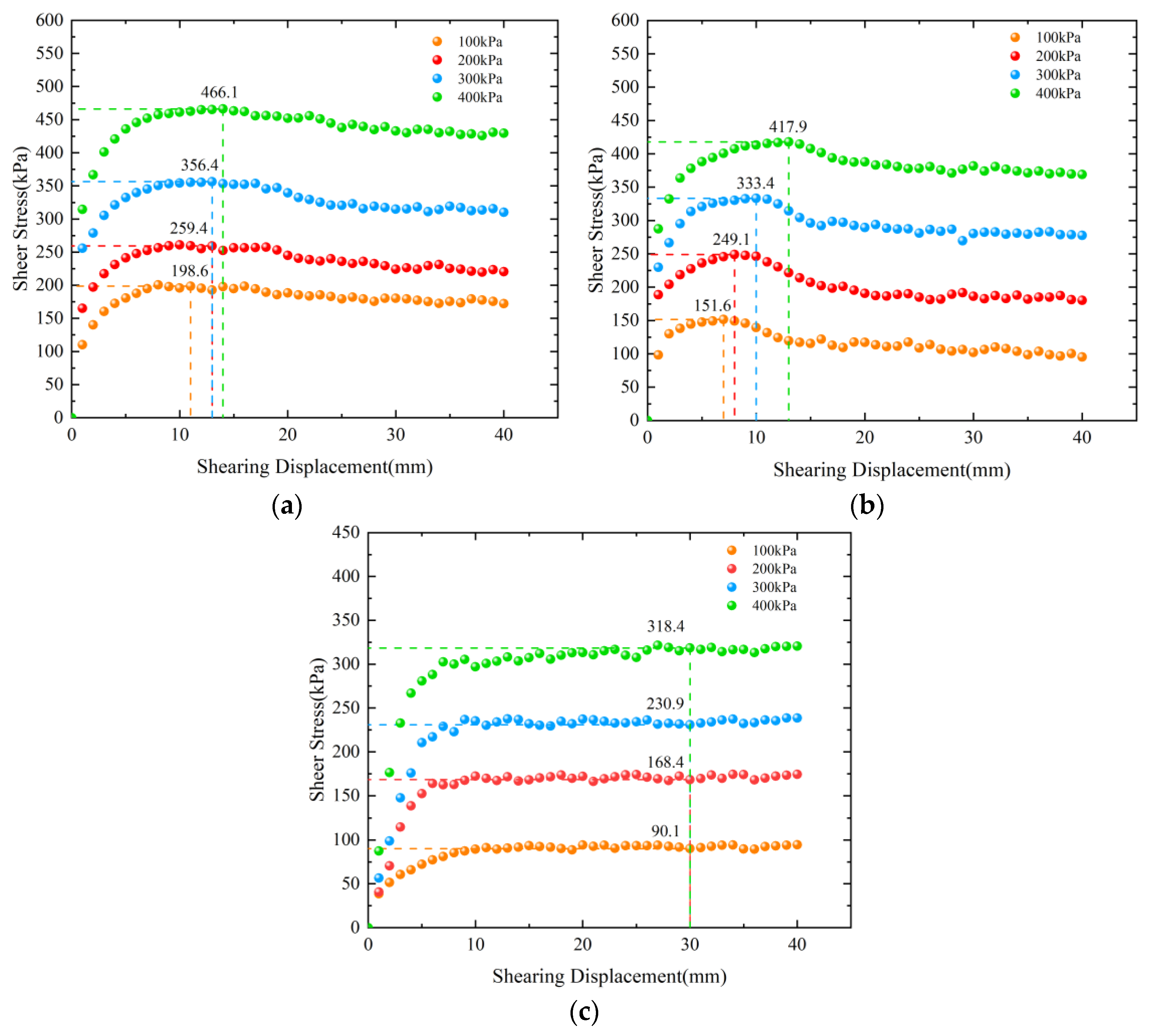
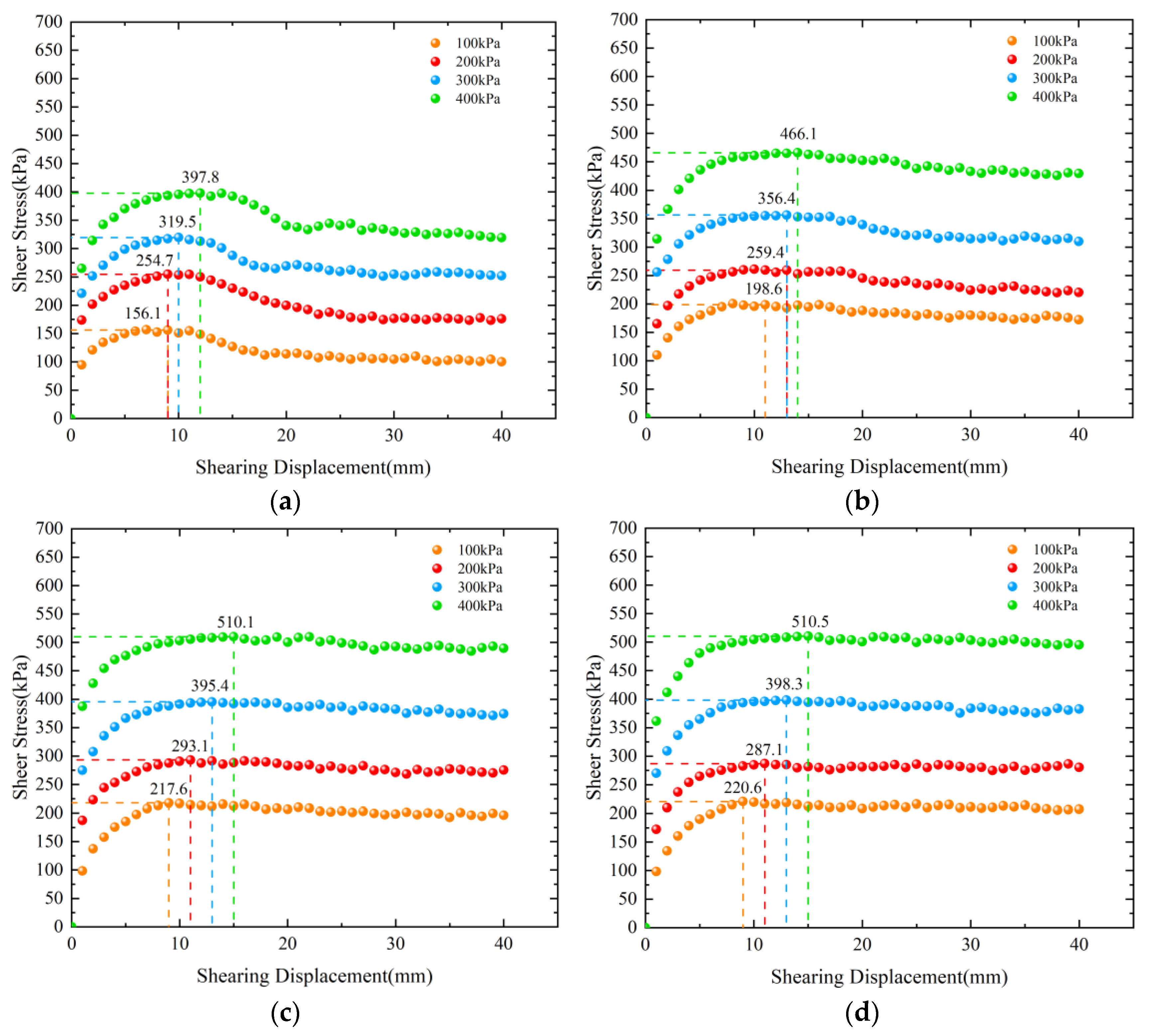
3.1. Influence of Soil Properties on the Peak Value of Shear Stress
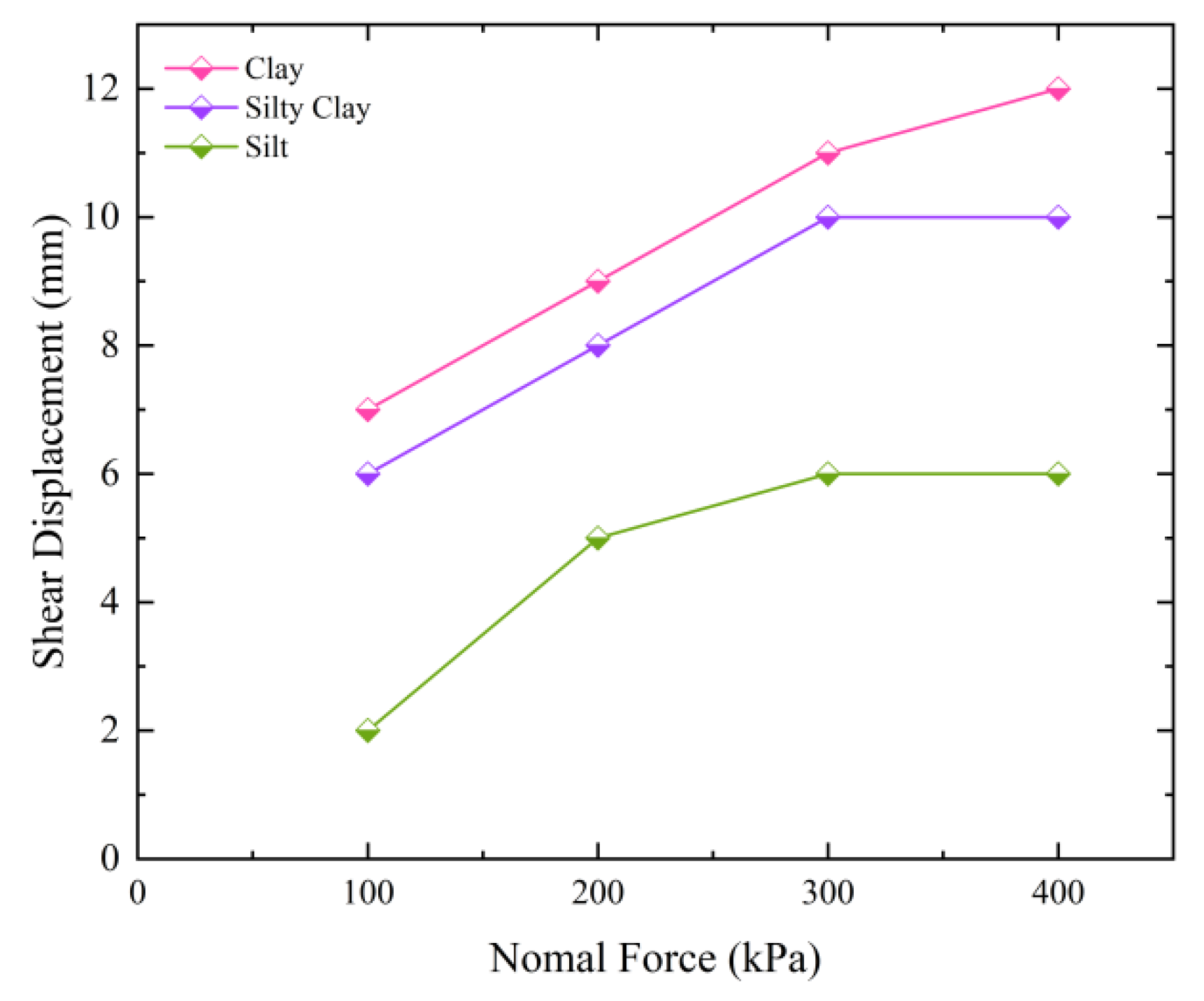
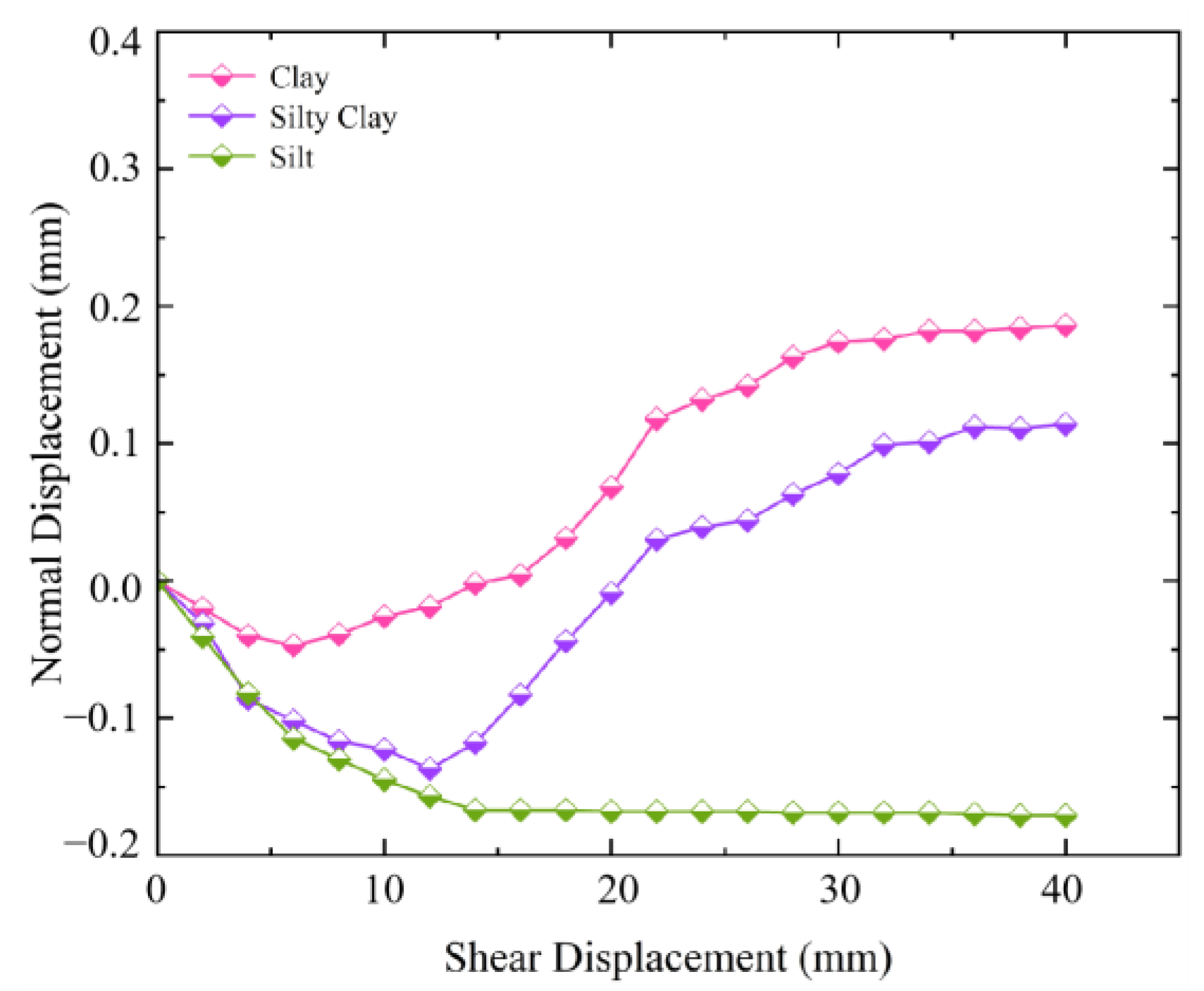
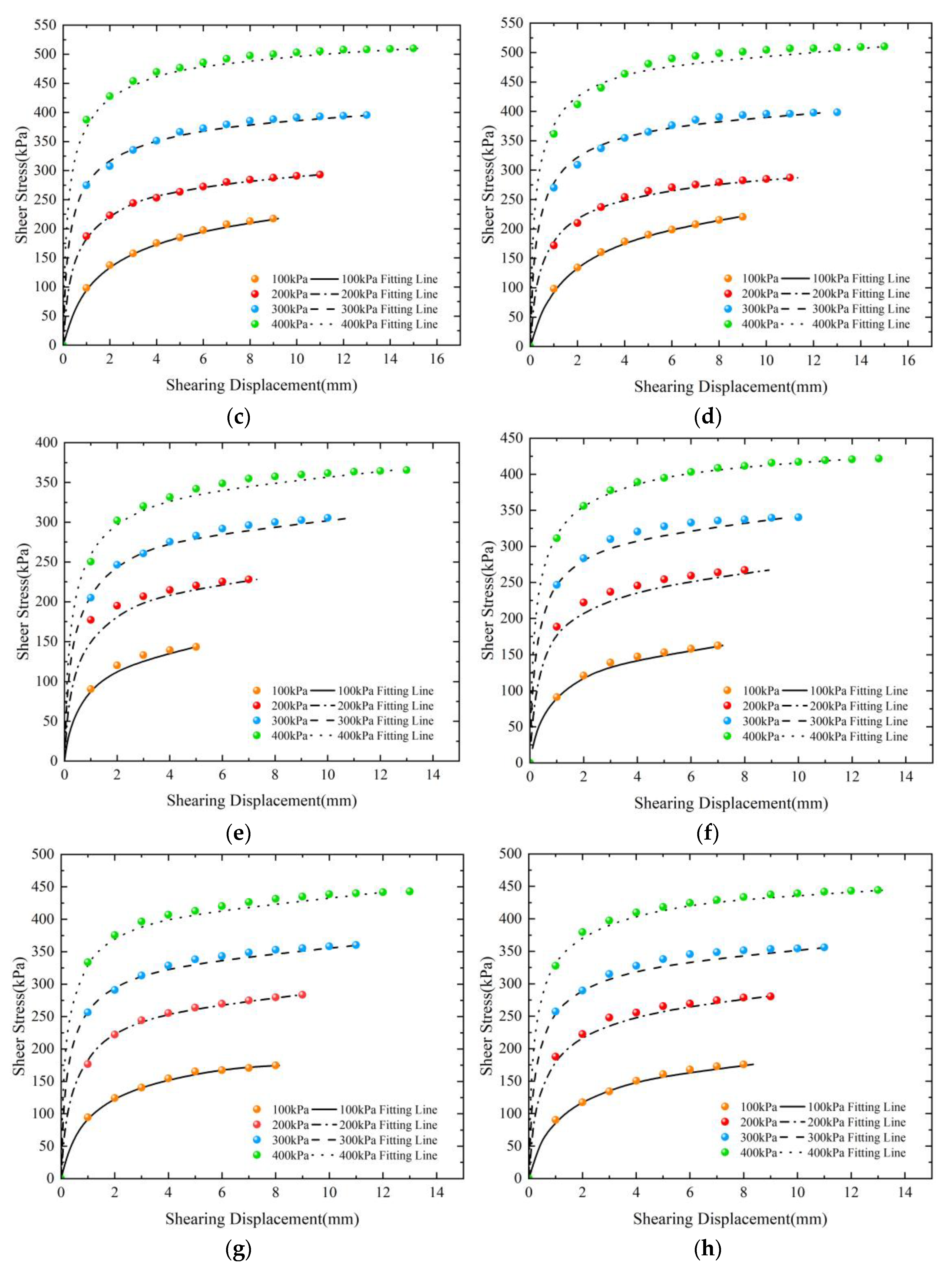
3.2. Influence of Soil Properties on the Relationship between Shear Stress and Displacement
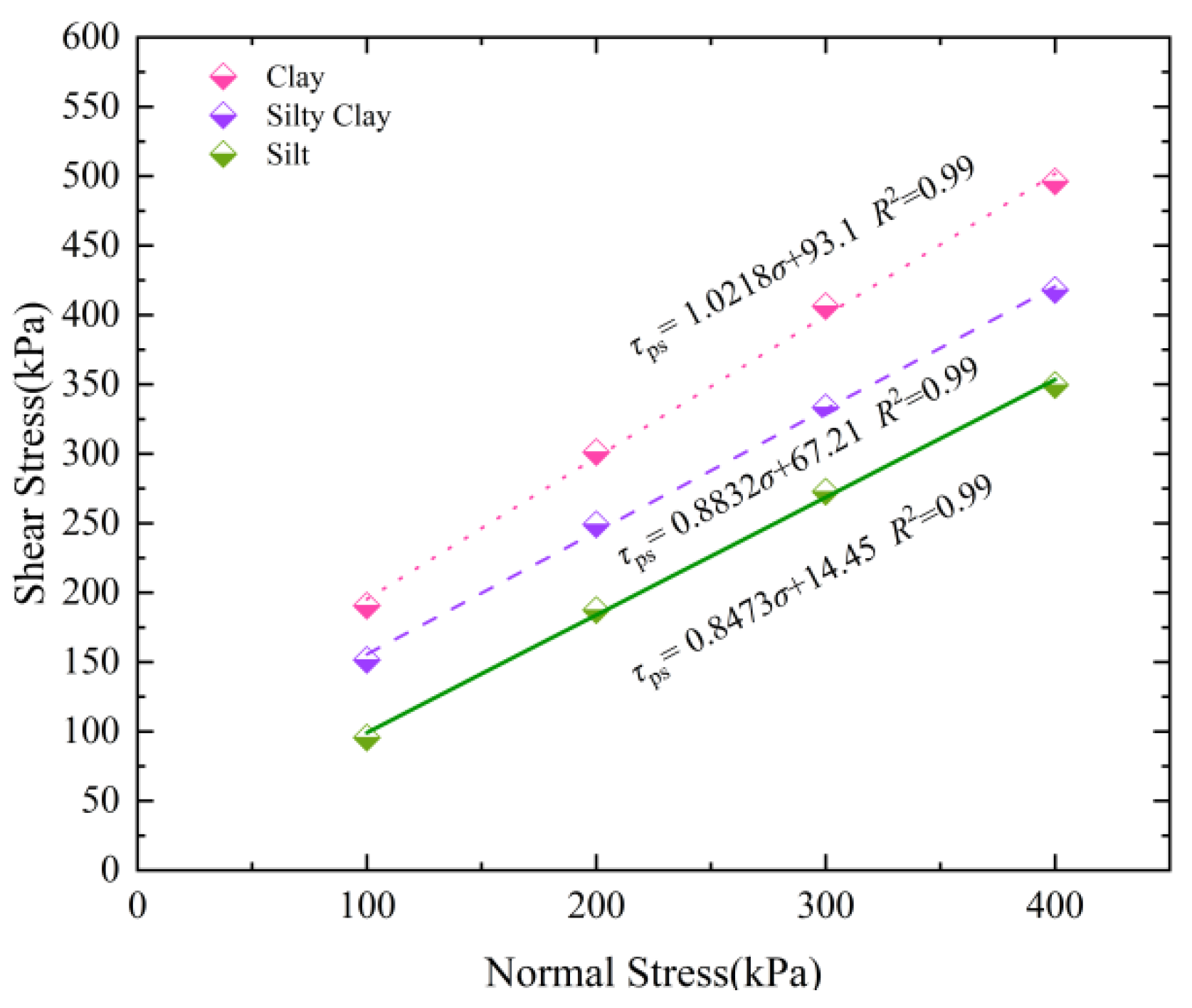
3.3. Influence of Soil Properties on Shear Strength Indexes
4. Influence of Roughness on Interfacial Shear Experiments
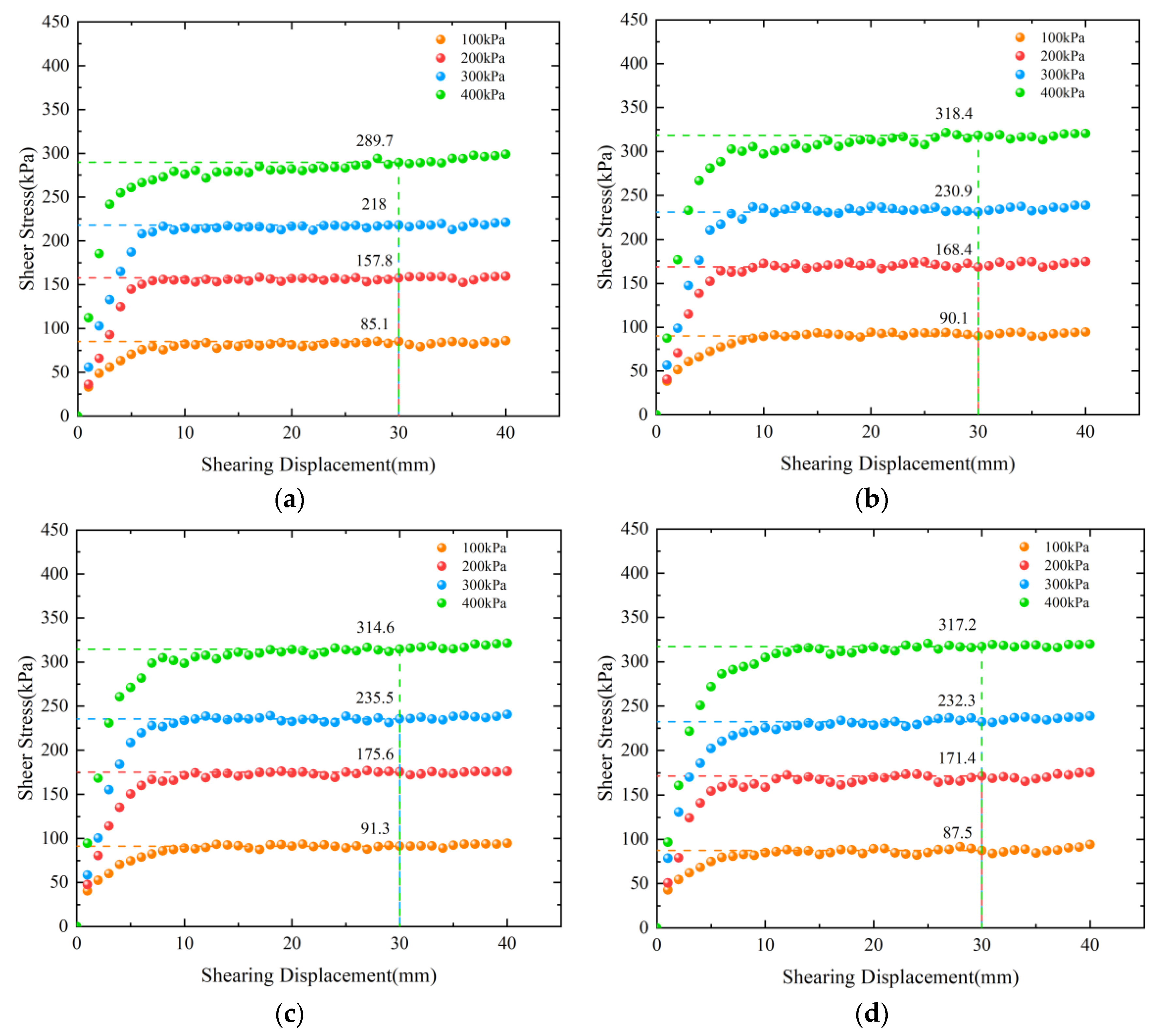
4.1. Influence of Roughness on the Interfacial Shear Experiment
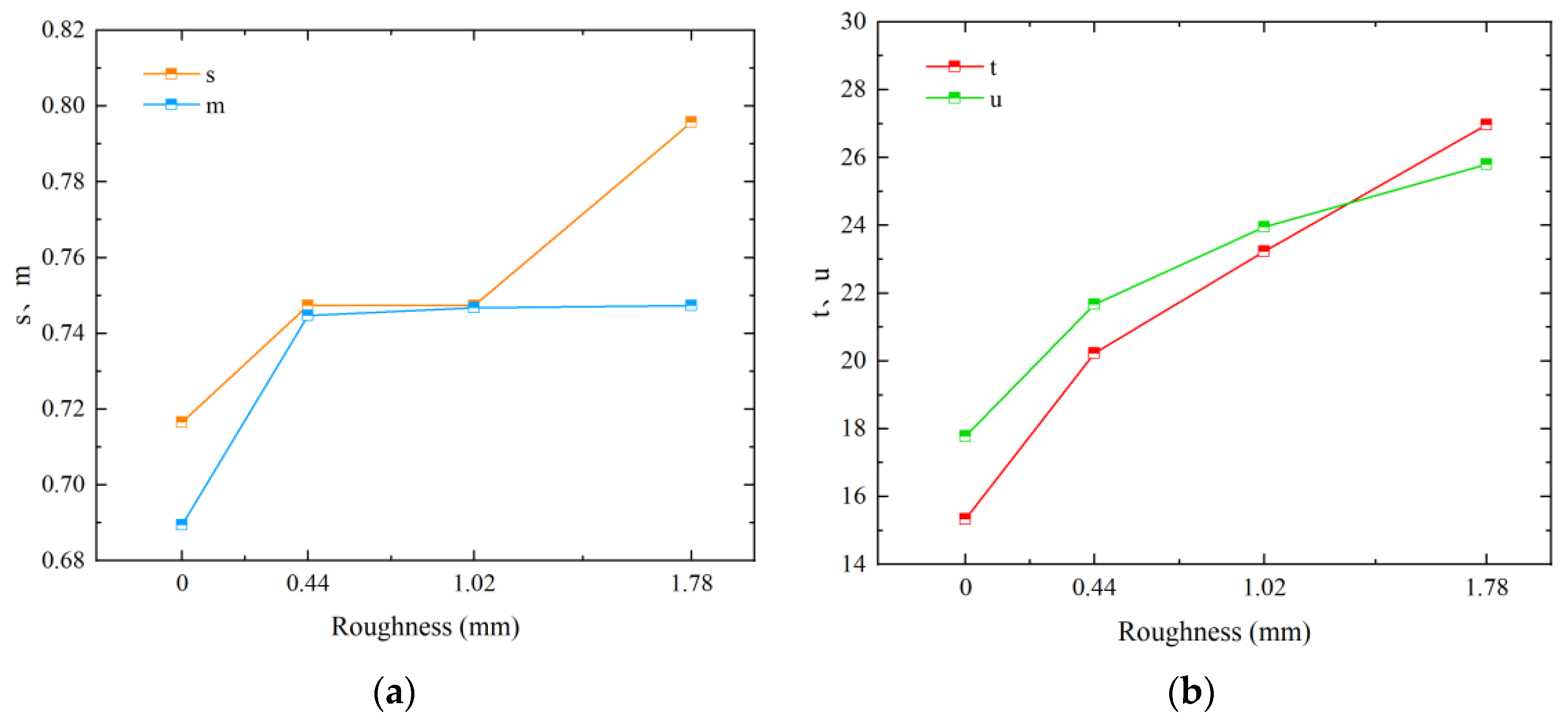
4.2. Influence of Roughness on Shear Strength Indexes
5. Numerical Simulation
5.1. Concrete and Soil Shear Modeling
5.2. Parameter Calibration and Model Validation
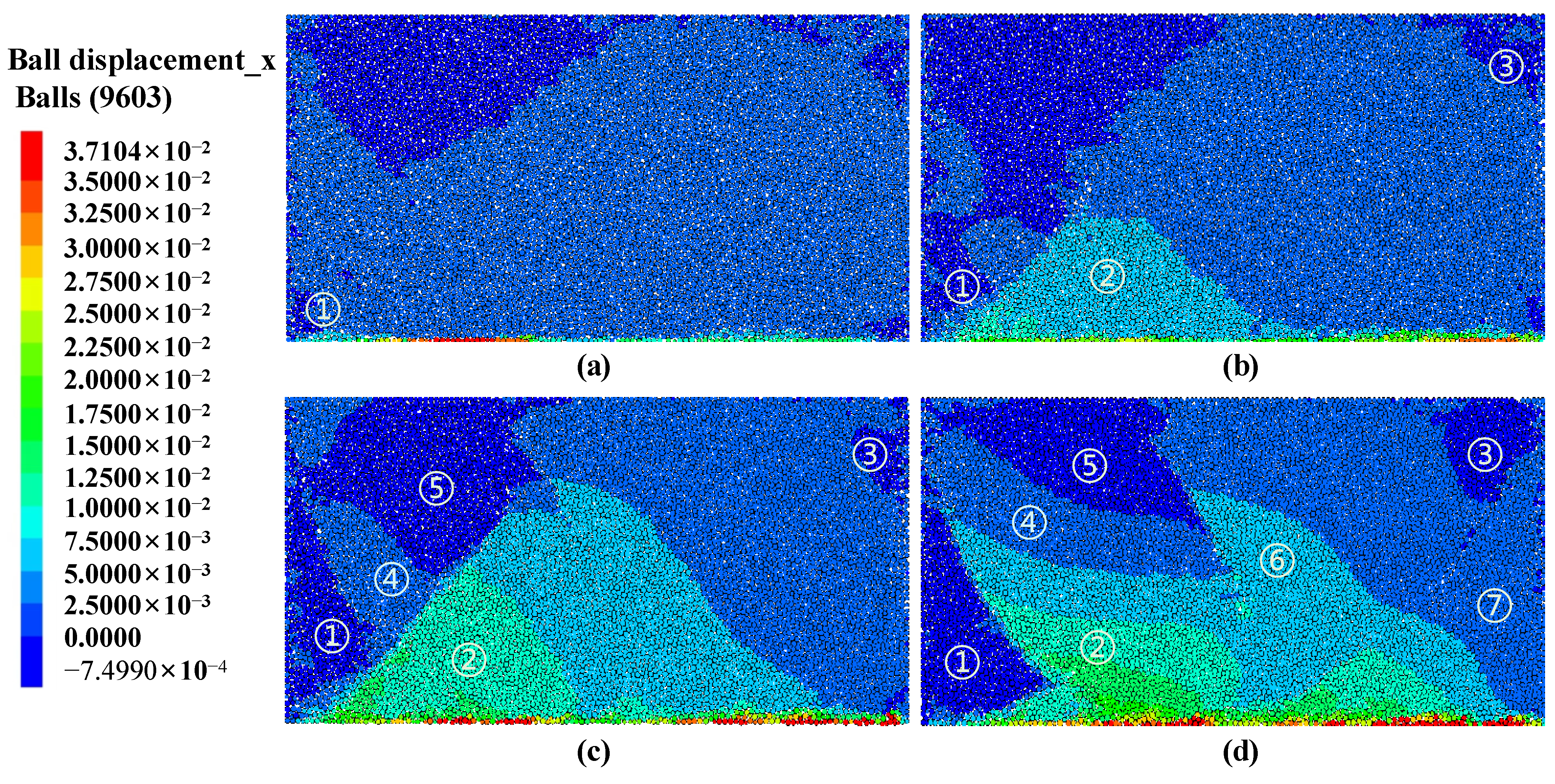
5.3. Clay Displacement Analysis
5.4. Displacement Analysis of Silt
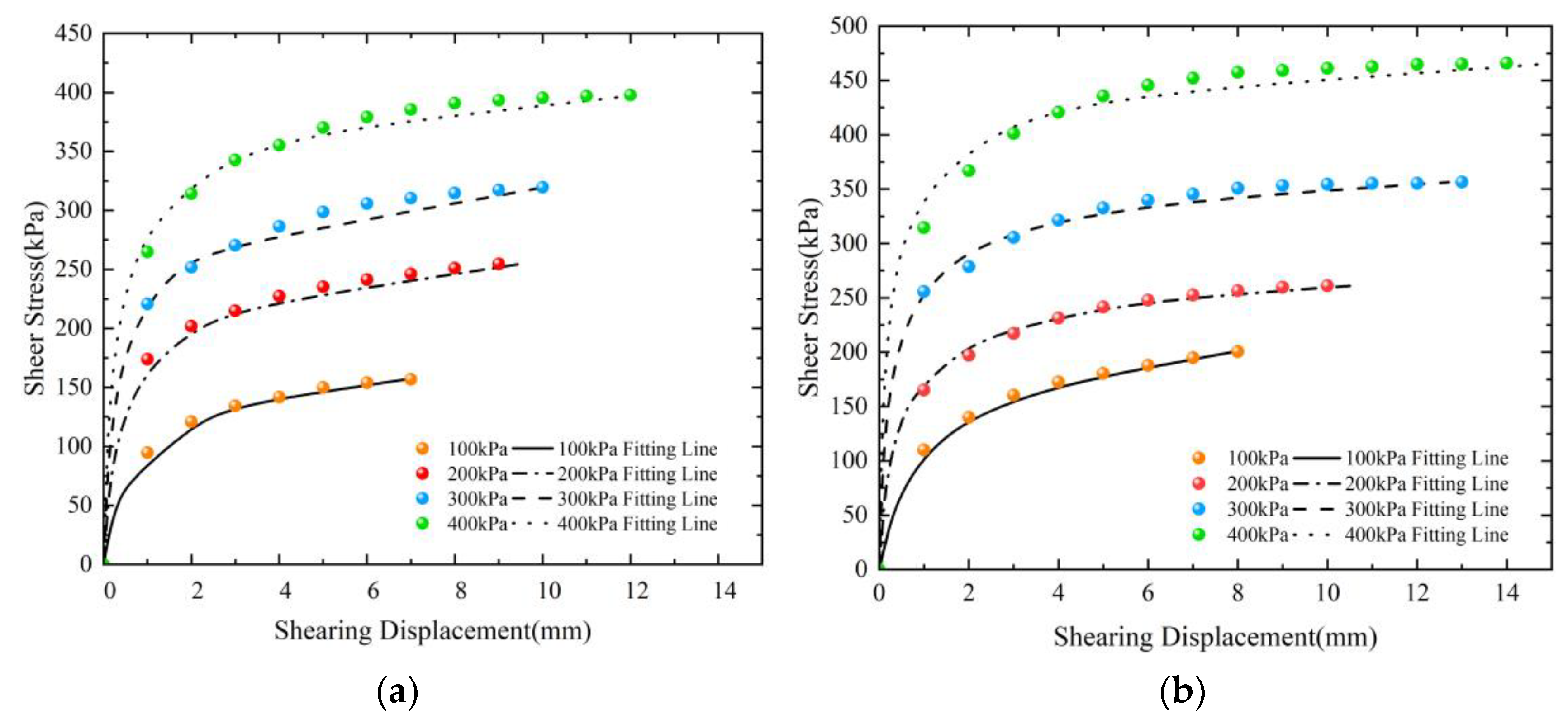
6. Constitutive Model
6.1. Fitting before Peak Strain Softening
6.2. Strain Hardening Fitting
7. Discussion
8. Conclusions
- (1)
- When subjected to the same level of roughness, the shear stress–displacement curves of clay and silty clay demonstrate strain softening, whereas silt exhibits strain hardening. As the normal stress increases, the displacement required for the peak shear strength of the three soils increases. During the shear process, the clay and silty clay exhibit shear expansion deformation, while the silt displays shear contraction deformation.
- (2)
- During the shear process, clay particles form aggregates of varying sizes to resist shear, resulting in the formation of multiple shear bands with the increase in normal stress. Silt particles resist shear through interfacial friction generated by shear, and when the bottom particles are displaced, occlusion force is generated between the particles to resist shear. The magnitude of this occlusion force is directly proportional to the normal stress, and the displacement of particles is directly proportional to the magnitude of the occlusion force.
- (3)
- The hyperbolic model put forth by Clough and Duncan was fitted to obtain model equations that are suitable for strain softening prior to the peak and strain hardening. Additionally, an intrinsic model of strain hardening under the influence of roughness was proposed, and it yielded favorable fitting results.
- (4)
- Future work will focus on addressing the limitations identified in this study. Tests under CNS and CV conditions will be conducted to gain a more comprehensive understanding of interfacial shear behavior. Efforts will be made to improve the matching of simulated and actual concrete slabs in terms of roughness. Moreover, the model after the shear peak under strain-softening conditions will be explored to enhance the theoretical analysis. This will contribute to a more in-depth understanding of interfacial shear behavior and provide more accurate guidance for practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.Y.; Wen, Y.F.; Zhu, B.Z.; Yu, Y.Z. A Review of Developments in Geotechnical Structures and Slope Engineering—Mechanisms of Action and Numerical Simulation Methods. China Civ. Eng. J. 2016, 49, 1–15+35. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Zhao, Z.; Jin, X. Research on Bearing Difference between Single-Pile Composite Foundation Field Test and Group-Pile Composite Foundation of High-Rise Buildings. Buildings 2023, 13, 2127. [Google Scholar] [CrossRef]
- Boulon, M. Basic features of soil structure interface behaviour. Comput. Geotech. 1989, 7, 115–131. [Google Scholar] [CrossRef]
- Hu, L.M. Study on Mechanical Characteristies of Soil-Structure Interface and Its Application; D. Tsinghua University: Beijing, China, 2000. [Google Scholar]
- Yin, Z.Z.; Zhu, H.; Xu, G.H. Deformation of soil-structure material contact surface and its mathematical simulation. Chin. J. Geotech. Eng. 1994, 3, 14–22. [Google Scholar]
- Zhang, G.; Zhang, J.M. Experimental study of monotonic mechanical properties of coarse-grained soils in contact with structural surfaces. Chin. J. Geotech. Eng. 2004, 1, 21–25. [Google Scholar]
- Wang, G.; Zhang, X.P.; Jiang, Y.J.; Li, B.; Wu, X.Z.; Huang, N. Meso-mechanism research on shear failure of rock joint based on particle discrete element method. J. Cent. South Univ. 2015, 46, 1442–1453. [Google Scholar]
- Feligha, M.; Hammoud, F.; Belachia, M.; Nouaouria, M.S. Experimental Investigation of Frictional Behavior Between Cohesive Soils and Solid Materials Using Direct Shear Apparatus. Geotech. Geol. Eng. 2016, 34, 567–578. [Google Scholar] [CrossRef]
- Han, F.; Ganju, E.; Salgado, R.; Prezzi, M. Effects of Interface Roughness, Particle Geometry, and Gradation on the Sand-Steel Interface Friction Angle. J. Geotech. Geoenviron. Eng. 2018, 144, 12. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Zhang, M.; Bai, X. Effect of Roughness on Shear Characteristics of the Interface between Silty Clay and Concrete. Adv. Civ. Eng. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Zhang, M.; Sang, S.; Wang, Y.; Bai, X. Factors Influencing the Mechanical Characteristics of a Pile–Soil Interface in Clay Soil. Front. Earth Sci. 2020, 7, 364. [Google Scholar] [CrossRef]
- Zhou, J.J.; Yu, J.L.; Gong, X.; Naggar, M.H.E.; Zhang, R. The effect of cemented soil strength on the frictional capacity of precast concrete pile-cemented soil interface. Acta Geotech. 2020, 15, 3271–3282. [Google Scholar] [CrossRef]
- Gu, M.; Han, J.; Zhao, M. Three-Dimensional DEM Analysis of Axially Loaded Geogrid-Encased Stone Column in Clay Bed. Int. J. Geomech. 2020, 20, 04019180. [Google Scholar] [CrossRef]
- Ding, L.N.; Chai, J.N.; Qin, Y.; Xu, Z.G. A study of the correction of the formula for the peak shear strength of joints. Chin. J. Appl. Mech. 2021, 2, 811–817. [Google Scholar] [CrossRef]
- Li, D.; Shi, C.; Ruan, H.; Li, B.Y. Shear Characteristics of Soil—Concrete Structure Interaction Interfaces. Appl. Sci. 2022, 12, 9145. [Google Scholar] [CrossRef]
- Jin, J.X.; Yuan, S.H.; Liang, B. Visualized test study on shear characteristics of friction pile-sand-soil interface. J. Exp. Mech. 2022, 37, 551–559. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, J.; Wang, R.; Zhang, Q.; Zhang, Q.; Li, J.; Zuo, S. Study on Cyclic Shear Properties of Siliceous Sand–Steel Interface under Different Normal Loading Conditions. Buildings 2023, 13, 2241. [Google Scholar] [CrossRef]
- Jia, J.; Wei, H.; Yang, D.; Wu, Y. The Impact of Freeze–Thaw Cycles on the Shear and Microstructural Characteristics of Compacted Silty Clay. Buildings 2023, 13, 2308. [Google Scholar] [CrossRef]
- Lin, C.; Wang, G.; Guan, C.; Feng, D.; Zhang, F. Experimental study on the shear characteristics of different pile-soil interfaces and the influencing factors. Cold Reg. Sci. Technol. 2023, 206, 103739. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, D.M.; Nguyen, T.; Thanh, C.P. Interface Shear Strength Behavior of Cement-Treated Soil under Consolidated Drained Conditions. Buildings 2023, 13, 1626. [Google Scholar] [CrossRef]
- Santos, D.B.; Sousa, P.F.D.; Cavalcante, A.L.B. Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios. Sustainability 2024, 16, 1394. [Google Scholar] [CrossRef]
- Amorosi, A.; Kavvadas, M. A constitutive model for structured soils. Géotechnique 2000, 50, 263–273. [Google Scholar] [CrossRef]
- Savvides, A.A.; Papadrakakis, M. A computational study on the uncertainty quantification of failure of clays with a modified Cam-Clay yield criterion. SN Appl. Sci. 2021, 3, 659. [Google Scholar] [CrossRef]
- Liu, F.C.; Shang, S.P.; Wang, H.D. Study df Shaer Properties of Silty Clay-Concrete Interface by Simple Shear Tests. Chin. J. Rock Mech. Eng. 2011, 30, 1720–2728. [Google Scholar]
- Cheng, H.; Zeng, G.D.; Zhou, M.; Wang, X.; Zhang, J.S.; Wang, J. Peak Shear Strength Model for Clay-concrete Interface Considering Roughness. Adv. Eng. Sci. 2021, 53, 168–177. [Google Scholar] [CrossRef]
- Chen, X.B.; Zhang, J.S.; Xiao, Y.; Li, J. Effect of roughness on shear behavior of red clay–concrete interface in large-scale direct shear tests. Can. Geotech. J. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Li, S.Y.; Wang, C.; You, T.T.; Liu, X.Y.; Zhao, Y.C. A universal soil–water characteristic curve model based on the particle size distribution and fractal theory. J. Hydrol. 2023, 622, 129691. [Google Scholar] [CrossRef]
- Taha, A.; Fall, M. Shear Behavior of Sensitive Marine Clay-Concrete Interfaces. J. Geotech. Geoenviron. Eng. 2013, 139, 644–650. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, X.B.; Zhang, J.S.; Li, J.; Zhang, B. Experimental Study on Residual Strength Characteristics of Red Viscous Concrete-Clay Structures at Contact Surfaces. J. Cent. South Univ. 2017, 48, 2458–2464. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H. Influential Factors of Friction Between Steel and Dry Sands. Soils Found. 1986, 26, 33–46. [Google Scholar] [CrossRef]
- Martinez, A.; Frost, J.D. The influence of surface roughness form on the strength of sand–structure interfaces. Géotech. Lett. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Mehrotra, B.K.M.P. Modelling of particle stratification in jigs by the discrete element method. Miner. Eng. 1998, 11, 511–522. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Wu, K.J. Exploring Mesoscopic Deformation Mechanism of Sand in Direct ShearTest by Numerical Simulation Using Discrete Element Method. J. Yangtze River Sci. Res. Inst. 2017, 34, 8. [Google Scholar] [CrossRef]
- Gu, M.; Han, J.; Zhao, M. Three-Dimensional Discrete-Element Method Analysis of Stresses and Deformations of a Single Geogrid-Encased Stone Column. Int. J. Geomech. 2017, 17, 04017070. [Google Scholar] [CrossRef]
- Clough, G.W.; Duncan, J.M. Finite element analyses of retaining wall behavior. J. Soil Mech. Found. Eng. 1971, 97, 1657–1673. [Google Scholar] [CrossRef]
- Gao, D.H.; Xing, Y.C.; Guo, M.X.; Zhang, A.J.; Wang, X.T.; Ma, B.H. Modified hyperbola model of interface between unsaturated remolded loess and concrete. J. Jilin Univ. 2020, 50, 156–164. [Google Scholar] [CrossRef]



| Soil | Relative Density g/cm3 | Density g/cm3 | Dry Density g/cm3 | Porosity | Liquid Limit % | Plastic Limit % | Plasticity Index | Cu | Cc |
|---|---|---|---|---|---|---|---|---|---|
| Clay | 2.73 | 1.91 | 1.48 | 0.832 | 38.9 | 20.2 | 18.7 | 3.19 | 0.82 |
| Silty Clay | 2.72 | 1.83 | 1.48 | 0.885 | 28.9 | 17.3 | 11.6 | 2.73 | 0.95 |
| Silt | 2.69 | 1.87 | 1.48 | 0.763 | 19.5 | 12.5 | 7.0 | 2.36 | 0.93 |
| Concrete Number | Sand Size Distribution (mm) | Maximum Surface Height (mm) | Sand Filling Volume (mm3) | R (mm) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | <1.18 | 0.32 | 44.8 | 0.44 |
| 2 | 2.36–1.18 | 0.97 | 103.7 | 1.02 |
| 3 | 4.75–2.36 | 1.81 | 181.6 | 1.78 |
| Soil | Normal Stiffness (N/m) | Tangential Stiffness (N/m) | Normal Bond Strength (N) | Tangential Bond Strength (N) | Coefficient of Friction |
|---|---|---|---|---|---|
| Clay | 6 × 106 | 5 × 106 | 9 × 103 | 9 × 103 | 0.3 |
| Silt | 2 × 106 | 1 × 106 | 4 × 103 | 4 × 103 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ni, Z.; Hou, F.; Li, W.; Bing, L. Consideration of Different Soil Properties and Roughness in Shear Characteristics of Concrete–Soil Interface. Buildings 2024, 14, 2889. https://doi.org/10.3390/buildings14092889
Wang S, Ni Z, Hou F, Li W, Bing L. Consideration of Different Soil Properties and Roughness in Shear Characteristics of Concrete–Soil Interface. Buildings. 2024; 14(9):2889. https://doi.org/10.3390/buildings14092889
Chicago/Turabian StyleWang, Shihao, Zhenqiang Ni, Fengzhan Hou, Wenlan Li, and Long Bing. 2024. "Consideration of Different Soil Properties and Roughness in Shear Characteristics of Concrete–Soil Interface" Buildings 14, no. 9: 2889. https://doi.org/10.3390/buildings14092889
APA StyleWang, S., Ni, Z., Hou, F., Li, W., & Bing, L. (2024). Consideration of Different Soil Properties and Roughness in Shear Characteristics of Concrete–Soil Interface. Buildings, 14(9), 2889. https://doi.org/10.3390/buildings14092889





