Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory
Abstract
1. Introduction
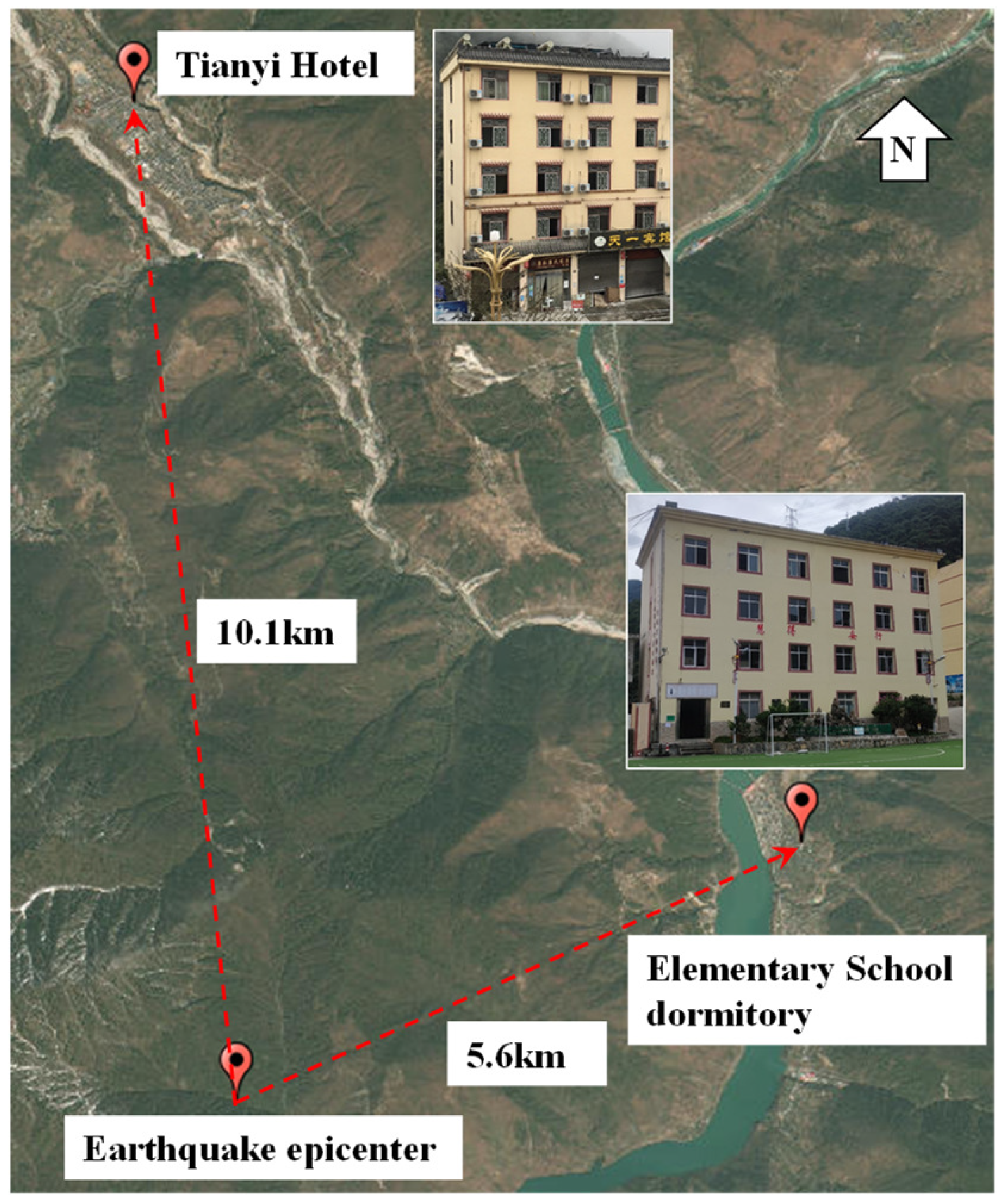
2. Seismic Damage Investigation
2.1. Tianyi Hotel
2.2. Beitou Village Central Elementary School Dormitory
3. Structural Elastoplastic Dynamic Time–History Analysis
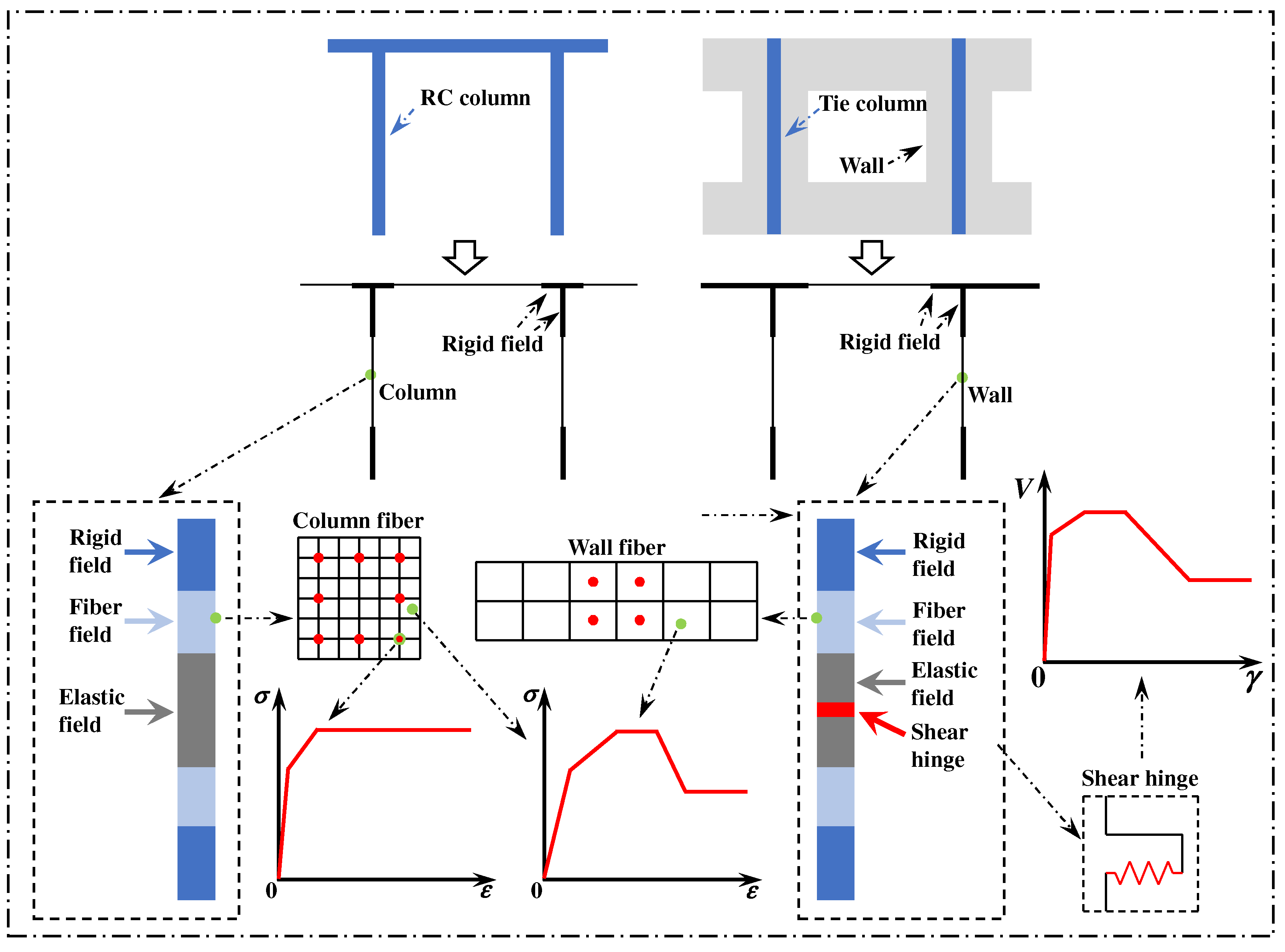
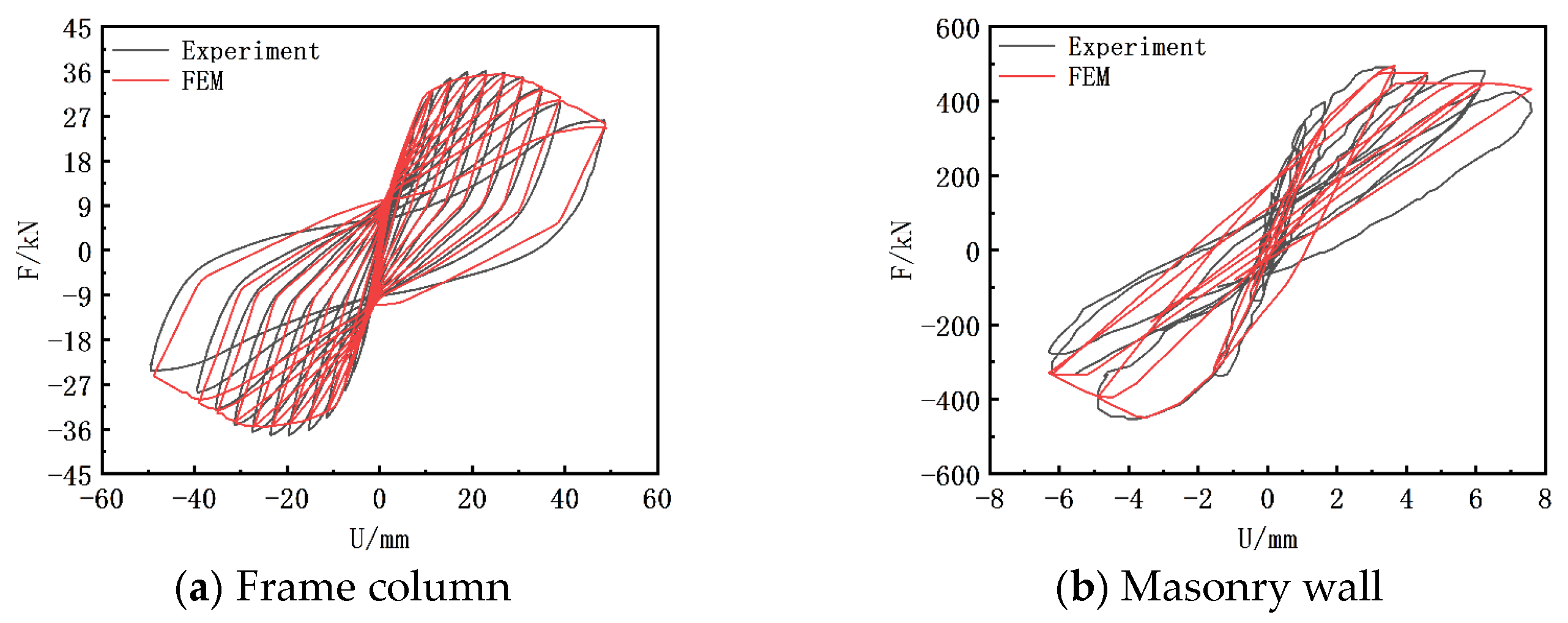
3.1. Modeling Method and Model Validation
3.2. Model Establishment and Seismic Input
3.3. Structural Characteristics
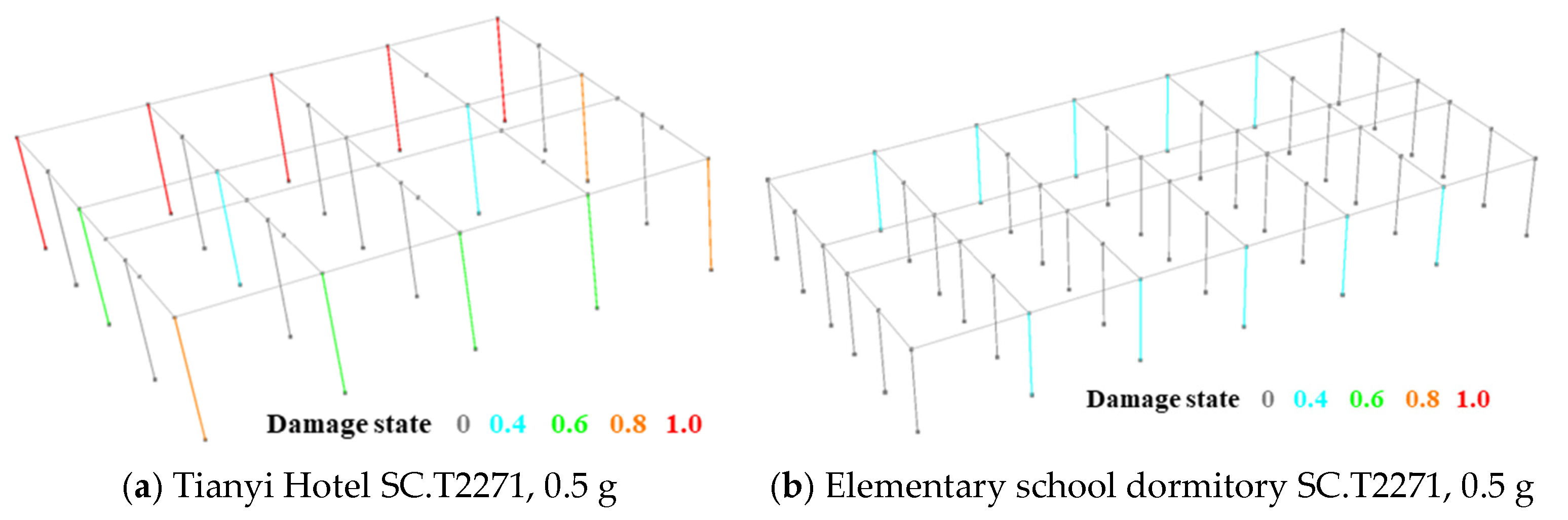
3.4. Model Plastic State
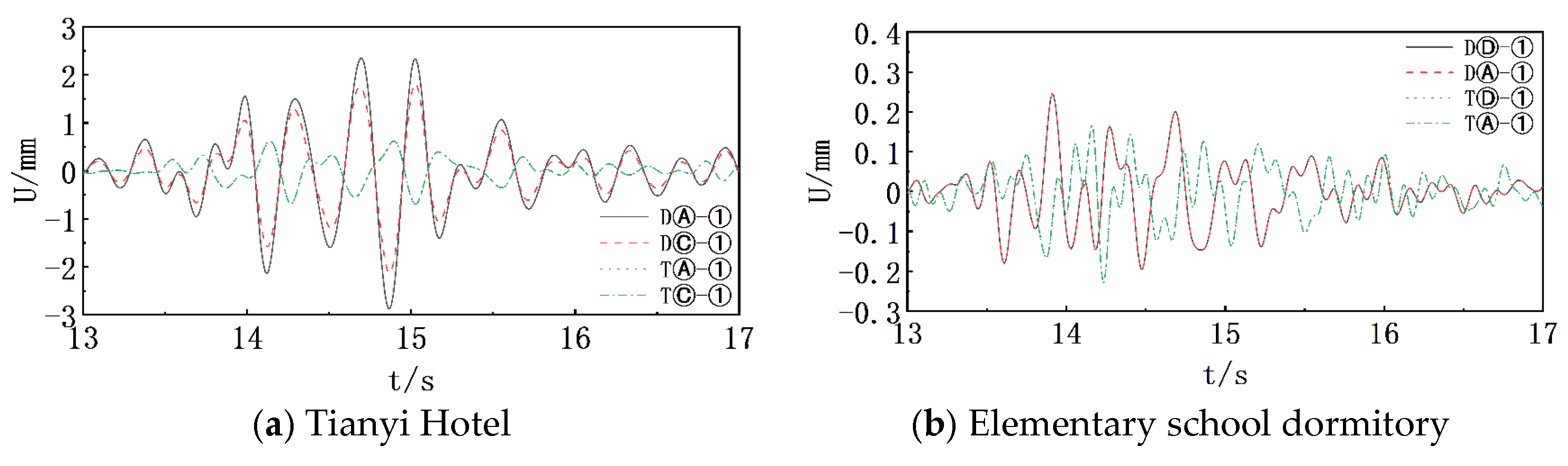
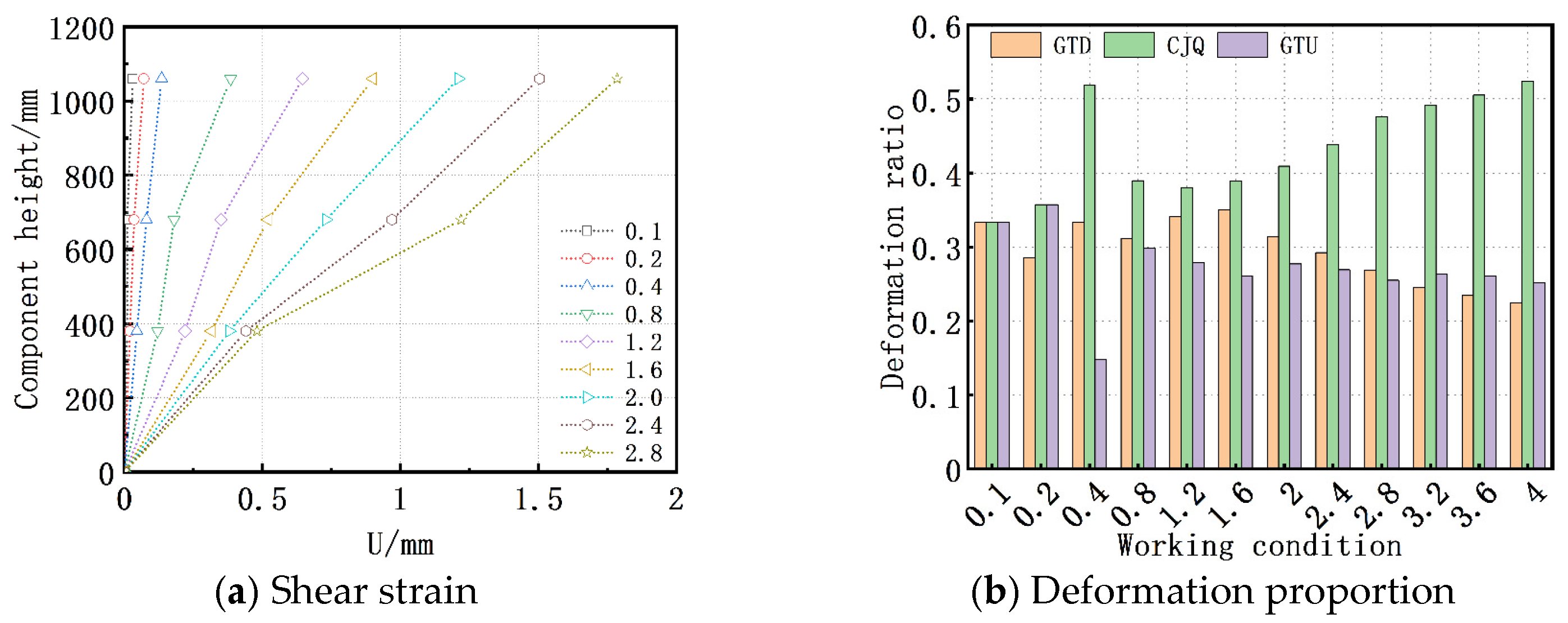
3.5. Displacement Response
3.6. Base Shear Response
4. “Deformation Saturation” Theory Discussion and Validation
4.1. Model Parameters
4.2. Material Testing
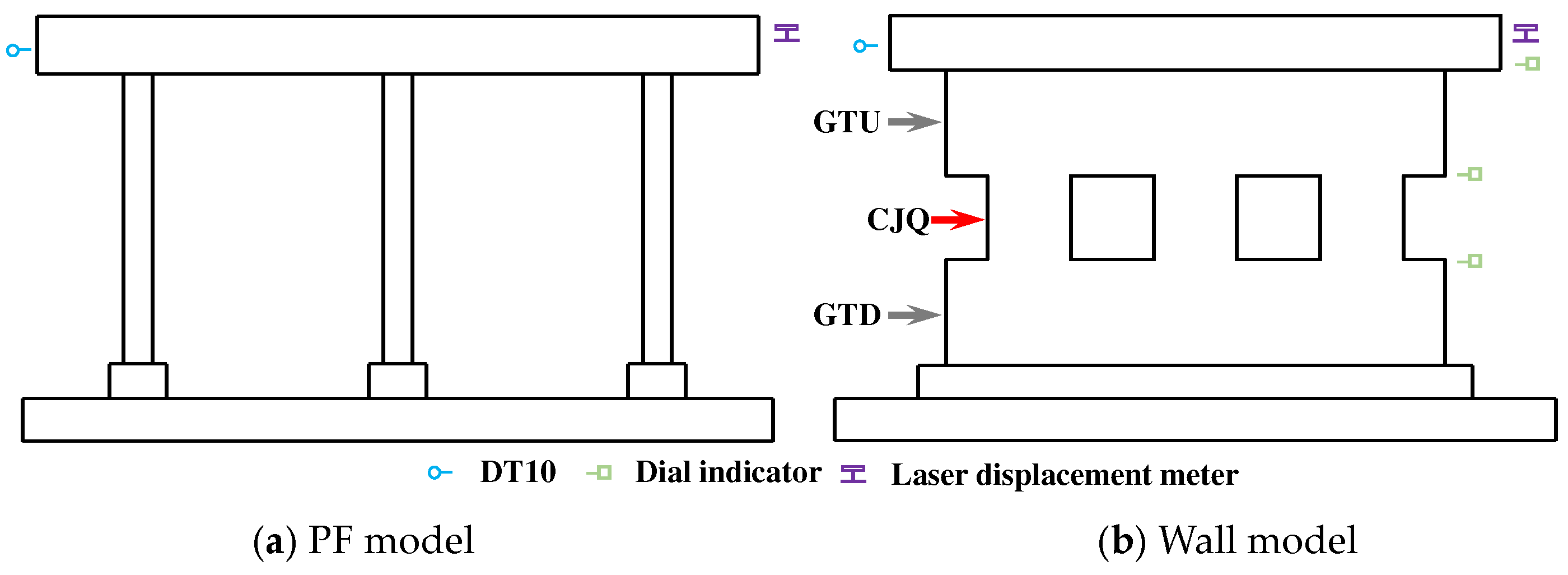
4.3. Experimental Loading and Measurement
4.4. Damage Modes
4.4.1. PF Model
4.4.2. Wall Model
4.5. Force–Displacement Relationship
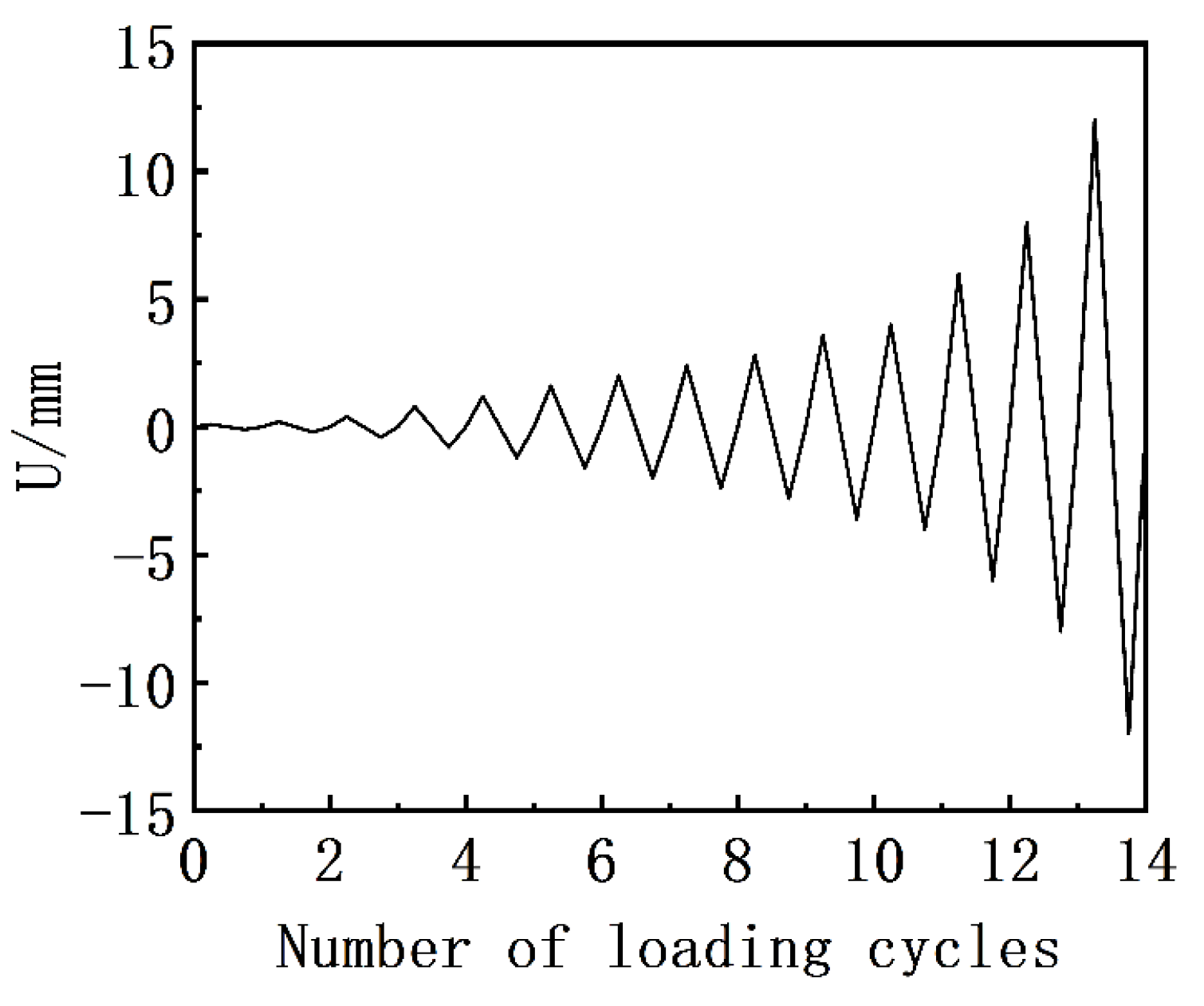
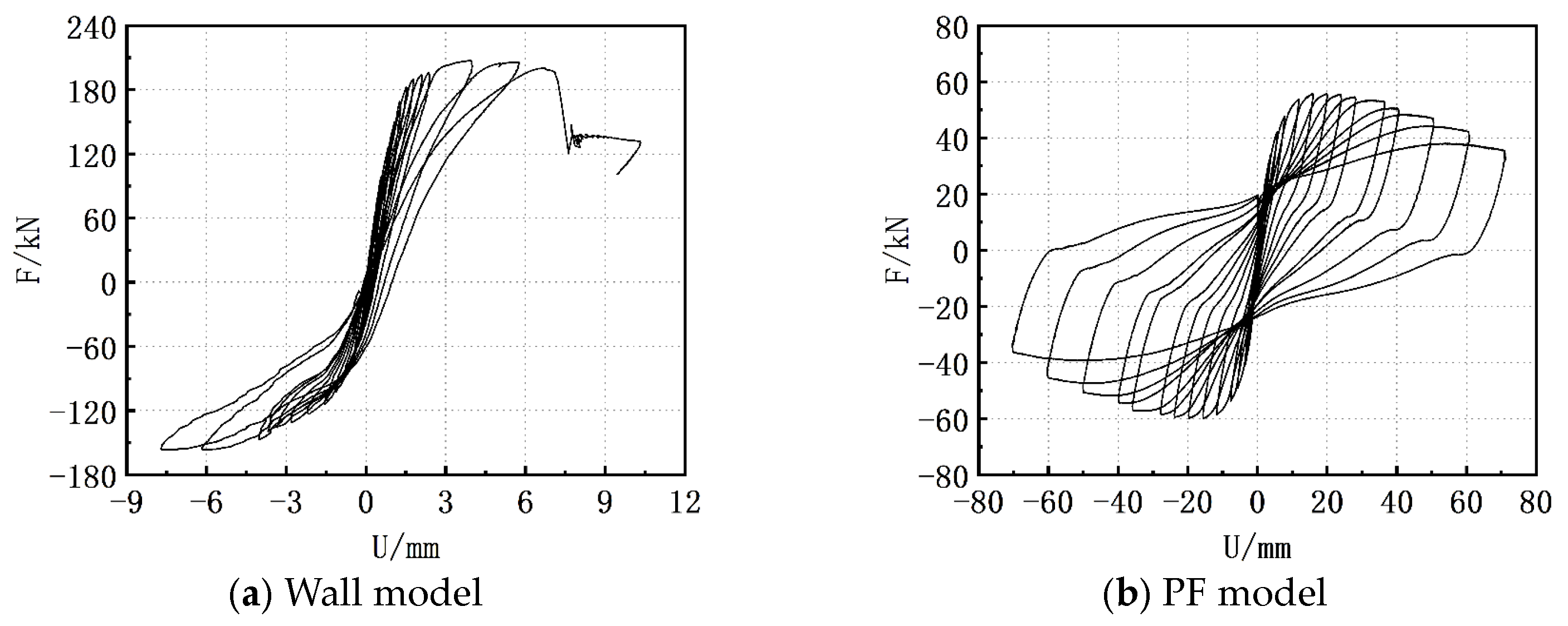
4.5.1. Hysteresis Curve
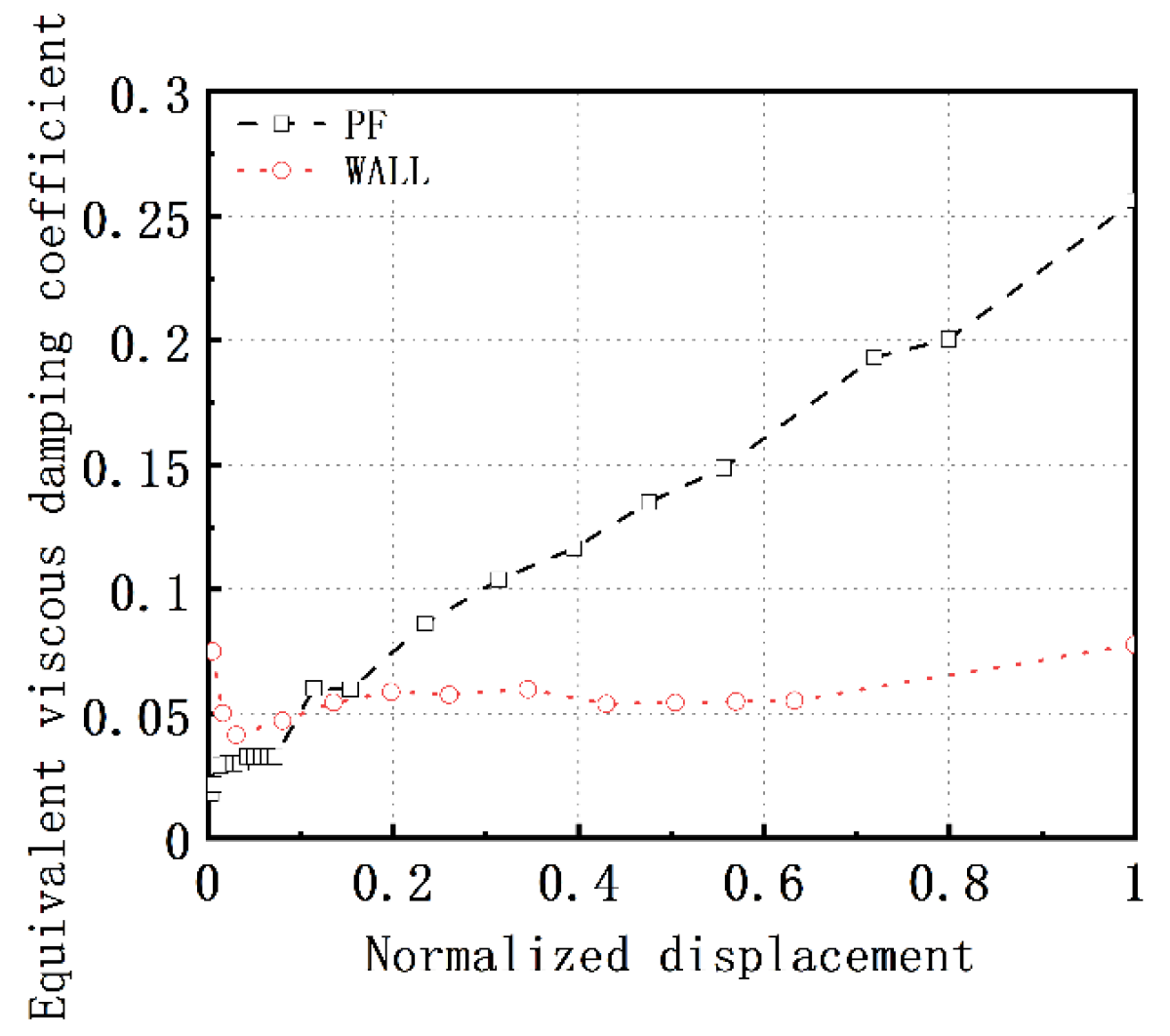
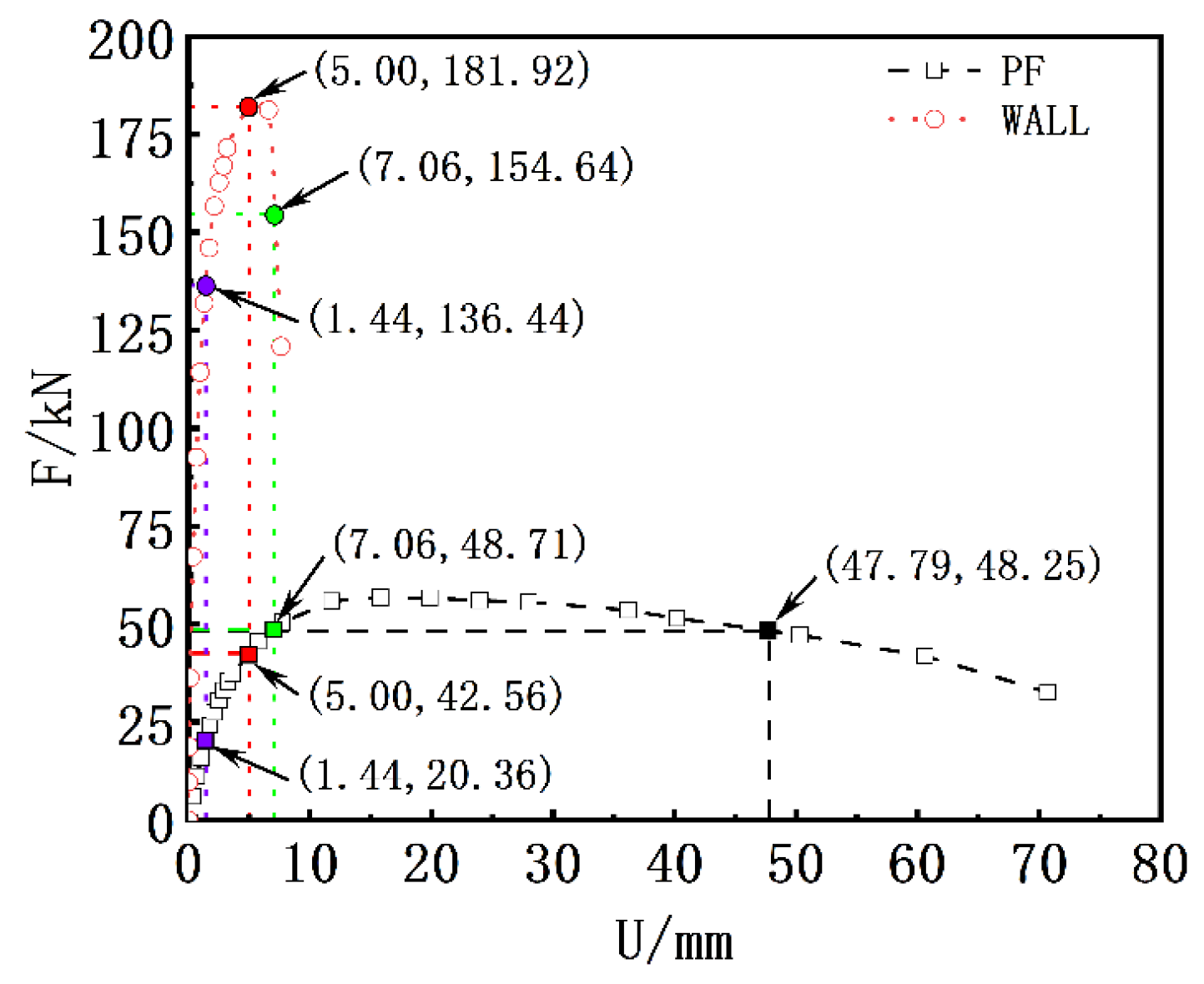
4.5.2. Skeleton Curve Analysis
5. Discussion on “Asymmetry” and “Symmetry” Characteristics
6. Conclusions
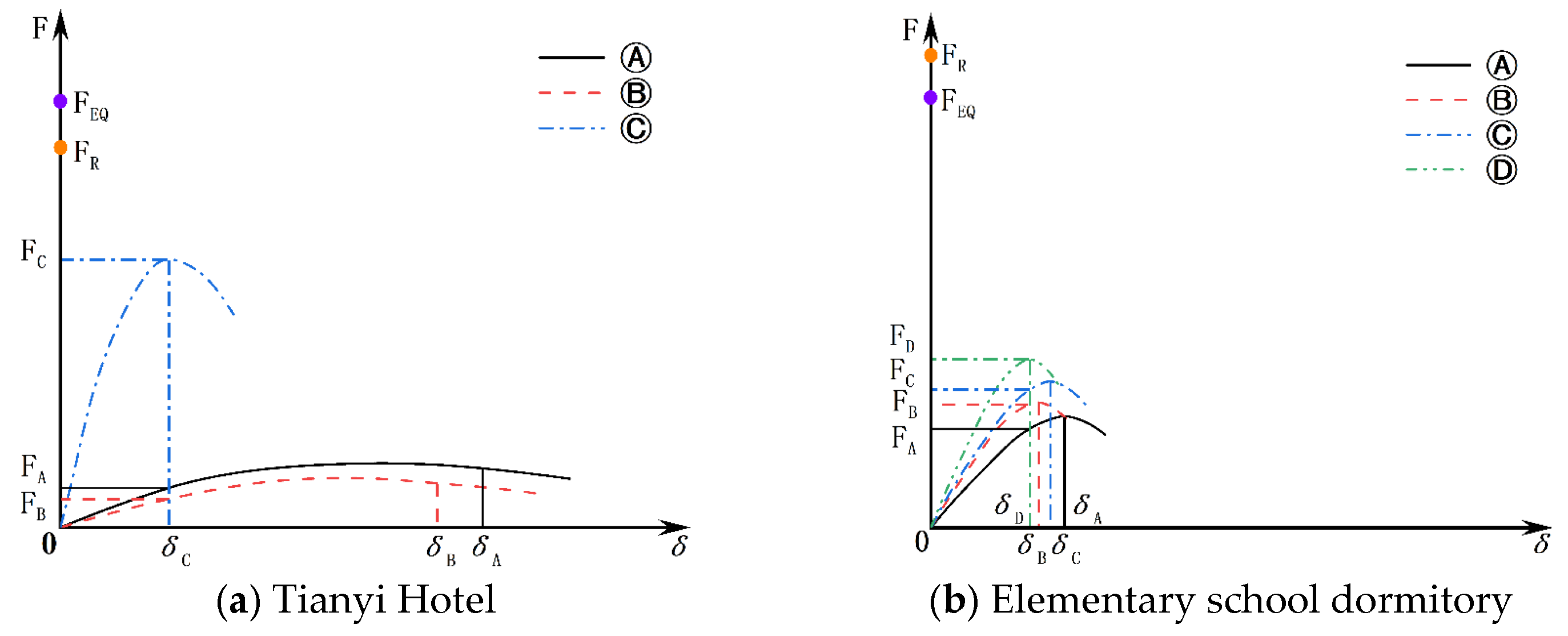
- Structures previously thought to have poor seismic performance exhibited good behavior after the earthquake. Seismic damage investigations revealed that the y-direction load-bearing components of Tianyi Hotel suffered more severe damage than those in the x-direction, with the Ⓒ axis components being the most severely damaged, putting the building at risk of collapse. In contrast, the elementary school dormitory, which is composed entirely of masonry walls, including y-direction walls with varying degrees of openings, showed poor component deformation, leading to shear damage, yet no significant damage was observed in the dormitory. The numerical analysis results show that Tianyi Hotel has a minimum shear force ratio of 2.2:1.0:11.8 among its axes, while the elementary school dormitory has a maximum shear force ratio of 2.1:1.0:1.1:2.0, indicating significant differences in lateral stiffness due to varied constructions, leading to “force concentration” phenomena.
- Both the damage sites and numerical analyses reveal the presence of multiple fully masonry transverse walls, with the x-direction stiffness being greater than the y-direction stiffness. This configuration causes the structure to primarily move towards the x-direction, forming the basis for the “deformation saturation” theory. Due to differences in functionality and construction methods, various structural axes exhibit different structural configurations. These configurations possess distinct shear force–displacement curves, leading to a mixture of vertical load-bearing components with different constitutive properties on the same floor. This phenomenon contributes to “deformation saturation” and can cause structural failure or even collapse.
- Open-window walled components have a high load-bearing capacity but poor ultimate deformation and ductility. The deformation of the walls between windows accounts for about 50% of the total deformation and hence the concentration of earthquake damage in these areas. Conversely, concrete columns exhibit better ultimate deformation and ductility, demonstrating a strong energy absorption capability, although their load-bearing capacity is lower than that of walls. When both types of structural components coexist on the same floor, the wall components are likely to sustain damage first, leading to structural collapse. Meanwhile, the concrete columns do not reach their limit displacement, and their excellent ductility is not fully utilized. Therefore, the key to building damage and even collapse lies in the brittle components with poor deformation. Defining the minimum deformation of the least-deformed component as the structure’s deformation saturation point is crucial for assessing the building’s seismic resilience. This approach highlights the importance of considering both strength and ductility in structural design to prevent premature failure in certain components, while others remain largely unutilized.
- When the constitutive properties of vertical load-bearing components on the same floor are similar, lateral shifts are less likely to reach the collapse trigger point of the structure, meaning the structural resistance is greater than the seismic forces it experiences. While the “deformation saturation” theory offers a reasonable explanation for the behavior of the two buildings discussed, further investigation and analysis of other structures are required to gain a more comprehensive understanding of the collapse mechanisms and to validate the applicability of this theory more broadly.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paulay, T. Developments in the seismic design of reinforced concrete frames in New Zealand. Can. J. Civ. Eng. 1981, 8, 91–113. [Google Scholar] [CrossRef]
- Ivanović, S.; Trifunac, M.; Novikova, E.; Gladkov, A.; Todorovska, M. Ambient vibration tests of a seven-story reinforced concrete building in Van Nuys, California, damaged by the 1994 Northridge earthquake. Soil Dyn. Earthq. Eng. 2000, 19, 391–411. [Google Scholar] [CrossRef]
- Civil and Structural Groups of Tsing Hua University; Xi’nan Jiao Tong University; BeiJing Jiao Tong University. Analysis on seismic damage of buildings in the wen chuan earthquake. J. Build. Struct. 2008, 29, 1–9. [Google Scholar]
- Varum, H.; Furtado, A.; Rodrigues, H.; Dias-Oliveira, J.; Vila-Pouca, N.; Arêde, A. Seismic performance of the infill masonry walls and ambient vibration tests after the Ghorka 2015, Nepal earthquake. Bull. Earthq. Eng. 2017, 15, 1185–1212. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Park, R. Improving the resistance of structures to earthquakes. Bull. N. Z. Soc. Earthq. Eng. 2001, 34, 1–39. [Google Scholar] [CrossRef][Green Version]
- Halder, L.; Dutta, S.C.; Sharma, R.P.; Bhattacharya, S. Lessons learnt from post-earthquake damage study of Northeast India and Nepal during last ten years: 2021 Assam earthquake, 2020 Mizoram earthquake, 2017 Ambasa earthquake, 2016 Manipur earthquake, 2015 Nepal earthquake, and 2011 Sikkim earthquake. Soil Dyn. Earthq. Eng. 2021, 151, 106990. [Google Scholar] [CrossRef]
- Ye, L.P.; Qu, Z.; Ma, Q.L.; Lin, X.C.; Lu, X.; Pan, P. Study on ensuring the strong column-weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake. Build. Struct. 2008, 38, 52–59+67. [Google Scholar]
- Sudarsana, I.K.; Budiwati, I.A.M.; Aditya, P.W. Effect of Column to Beam Strength Ratio on Performance of Reinforced Concrete Frames. In Proceedings of the 1st International Conference on Engineering Technology and Industrial Application, Surakarta, Indonesia, 4 December 2014. [Google Scholar]
- Haselton, C.B.; Liel, A.B.; Deierlein, G.G.; Dean, B.S.; Chou, J.H. Seismic collapse safety of reinforced concrete buildings. I: Assessment of ductile moment frames. J. Struct. Eng. 2011, 137, 481–491. [Google Scholar] [CrossRef]
- Liel, A.B.; Haselton, C.B.; Deierlein, G.G. Seismic collapse safety of reinforced concrete buildings. II: Comparative assessment of nonductile and ductile moment frames. J. Struct. Eng. 2011, 137, 492–502. [Google Scholar] [CrossRef]
- Chaker, A.A.; Cherifati, A. Influence of masonry infill panels on the vibration and stiffness characteristics of R/C frame buildings. Earthq. Eng. Struct. Dyn. 2015, 28, 1061–1065. [Google Scholar] [CrossRef]
- Xu, J.G.; Cao, X.Y.; Shi, J.Z. A comparative study of the novel externally-attached precast SRC braced-frames for seismic retrofitting under near-field spectrum-compatible non-stationary stochastic earthquake. Structures 2023, 50, 200–214. [Google Scholar] [CrossRef]
- Xu, J.G.; Cao, X.Y.; Wu, G. Seismic collapse and reparability performance of reinforced concrete frames retrofitted with external PBSPC BRBF sub-frame in near-fault regions. J. Build. Eng. 2023, 64, 105716. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.; Liao, W.; Zhang, L.; Qin, X. Building damages in Deyang city by the 2008 Wenchuan earthquake. Geod. Geodyn. 2011, 2, 59–63. [Google Scholar]
- Penna, A.; Morandi, P.; Rota, M.; Manzini, C.F.; Da Porto, F.; Magenes, G. Performance of masonry buildings during the Emilia 2012 earthquake. Bull. Earthq. Eng. 2014, 12, 2255–2273. [Google Scholar] [CrossRef]
- Mistler, M.; Butenweg, C.; Meskouris, K. Modelling methods of historic masonry buildings under seismic excitation. J. Seismol. 2006, 10, 497–510. [Google Scholar] [CrossRef]
- Nakagawa, T.; Narafu, T.; Imai, H.; Hanazato, T.; Ali, Q.; Minowa, C. Collapse behavior of a brick masonry house using a shaking table and numerical simulation based on the extended distinct element method. Bull. Earthq. Eng. 2012, 10, 269–283. [Google Scholar] [CrossRef]
- Parisi, F.; Augenti, N. Seismic capacity of irregular unreinforced masonry walls with openings. Earthq. Eng. Struct. Dyn. 2013, 42, 101–121. [Google Scholar] [CrossRef]
- Kallioras, S.; Graziotti, F.; Penna, A. Numerical assessment of the dynamic response of a URM terraced house exposed to induced seismicity. Bull. Earthq. Eng. 2019, 17, 1521–1552. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016.
- Piroglu, F.; Ozakgul, K. Site investigation of masonry buildings damaged during the 23 October and 9 November 2011 Van Earthquakes in Turkey. Nat. Hazards Earth Syst. Sci. 2013, 13, 689–708. [Google Scholar] [CrossRef]
- Medeiros, P.; Vasconcelos, G.; Lourenço, P.B.; Gouveia, J. Numerical modelling of non-confined and confined masonry walls. Constr. Build. Mater. 2013, 41, 968–976. [Google Scholar] [CrossRef]
- Qamaruddin, M.; Chandra, B.; Arya, A. Dynamic testing of brick building models. Proc. Inst. Civ. Eng. Part Res. Theory 2015, 77, 353–365. [Google Scholar] [CrossRef]
- Benedetti, D.; Carydis, P.; Pezzoli, P. Shaking table tests on 24 simple masonry buildings. Earthq. Eng. Struct. Dyn. 1998, 27, 67–90. [Google Scholar] [CrossRef]
- Bhalkikar, A.; Kumar, R.P. A comparative study of different rapid visual survey methods used for seismic assessment of existing buildings. Structures 2021, 29, 1847–1860. [Google Scholar] [CrossRef]
- Kassem, M.M.; Beddu, S.; Ooi, J.H.; Tan, C.G.; Mohamad El-Maissi, A.; Mohamed Nazri, F. Assessment of seismic building vulnerability using rapid visual screening method through web-based application for Malaysia. Buildings 2021, 11, 485. [Google Scholar] [CrossRef]
- Mertol, H.C.; Tunç, G.; Akış, T.; Kantekin, Y.; Aydın, İ.C. Investigation of RC Buildings after 6 February 2023, Kahramanmaraş, Türkiye Earthquakes. Buildings 2023, 13, 1789. [Google Scholar] [CrossRef]
- Aykanat, B.; Ertürk, E.; Altunışık, A.C.; Aslan, M.E. Field Investigation on Reinforced Concrete and Masonry Buildings Damages after 23 November 2022 Gölyaka (Düzce) Earthquake. J. Earthq. Tsunami 2023, 17, 1793–4311. [Google Scholar] [CrossRef]
- Işık, E.; Hadzima-Nyarko, M.; Radu, D.; Bulajić, B. Study on Effectiveness of Regional Risk Prioritisation in Reinforced Concrete Structures after Earthquakes. Appl. Sci. 2024, 14, 6992. [Google Scholar] [CrossRef]
- Huang, S.N.; Yuan, Y.F.; Meng, Q.L. Study on seismic resistance of rural houses based on earthquake damage to buildings in Yushu earthquake. World Earthq. Eng. 2011, 27, 77–82. [Google Scholar]
- Zhe, Q.; Zhong, J.; Sun, J. Seismic damage to masonry structures in M7.0 Lushan earthquake. Earthq. Eng. Eng. Dyn. 2013, 33, 27–35. [Google Scholar]
- Zhang, L.; Zhu, B.; Tao, Z.; Chen, X. Field Investigation and Failure Characteristics of Buildings Damaged by the 7.0-Magnitude Earthquake in Jiuzhaigou. China Earthq. Eng. J. 2019, 41, 1053–1059. [Google Scholar]
- Ye, L.; Li, Y.; Peng, P. Seismic damages of building structures of Xuankou Middle School in Yingxiu Town. Build. Struct. 2009, 39, 54–57. [Google Scholar]
- Mei, Y. A Study on the Aseismic Capacity of ‘Qiuzhi Building’ with Masonry Structure in Bailu Middle School; Institute of Engineering Mechanics, China Earthquake Administration: Harbin, China, 2012.
- Guo, X. Application of deformation saturation theory in the seismic damage analysis of Luding, Sichuan Ms6.8 Earthquake in 2022. J. Inst. Disaster Prev. 2022, 24, 1–10. [Google Scholar]
- Federal Emergency Management Agency (FEMA). NEHRP Guidelines for the Seismic Rehabilitation of Buildings; FEMA 273; FEMA: Washington, DC, USA, 1997.
- GB 50010−2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Scott, A.; Park, R.; Priestley, M.J.M. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. J. Am. Concr. Inst. 1982, 79, 13–27. [Google Scholar]
- Peruch, M.; Spacone, E.; Camata, G. Nonlinear analysis of masonry structures using fiber-section line elements. Earthq. Eng. Struct. Dyn. 2019, 48, 1345–1364. [Google Scholar] [CrossRef]
- Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonry walls. In Proceedings of the 2nd International Brick & Block Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1971; British Ceramic Research Association: Stoke-on-Trent, UK, 1971; pp. 149–156. [Google Scholar]
- Anthoine, A.; Magonette, G.; Magenes, G. Shear-compression testing and analysis of brick masonry walls. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1995; Central Institute for Meteorology and Geodynamics: Vienna, Austria, 1995; pp. 1657–1662. [Google Scholar]
- Shabani, A.; Kioumarsi, M. A novel macroelement for seismic analysis of unreinforced masonry buildings based on MVLEM in OpenSees—ScienceDirect. J. Build. Eng. 2022, 49, 104019. [Google Scholar] [CrossRef]
- Lata, A.; Xun, G.; Ruofan, L.; Xiaoyao, D.; Bideng, L. Experimental study on the seismic performance of RC frames considering the cast sequence of infilled walls and columns. Structures 2022, 44, 186–199. [Google Scholar] [CrossRef]
- Sun, M.; Liu, W. Experimental study on seismic behavior for porous masonry. Earthq. Resist. Eng. Retrofit. 2004, 31–34. [Google Scholar] [CrossRef]
- GB 50009−2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Park, R. State of the art report ductility evaluation from laboratory and analytical testing. In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]





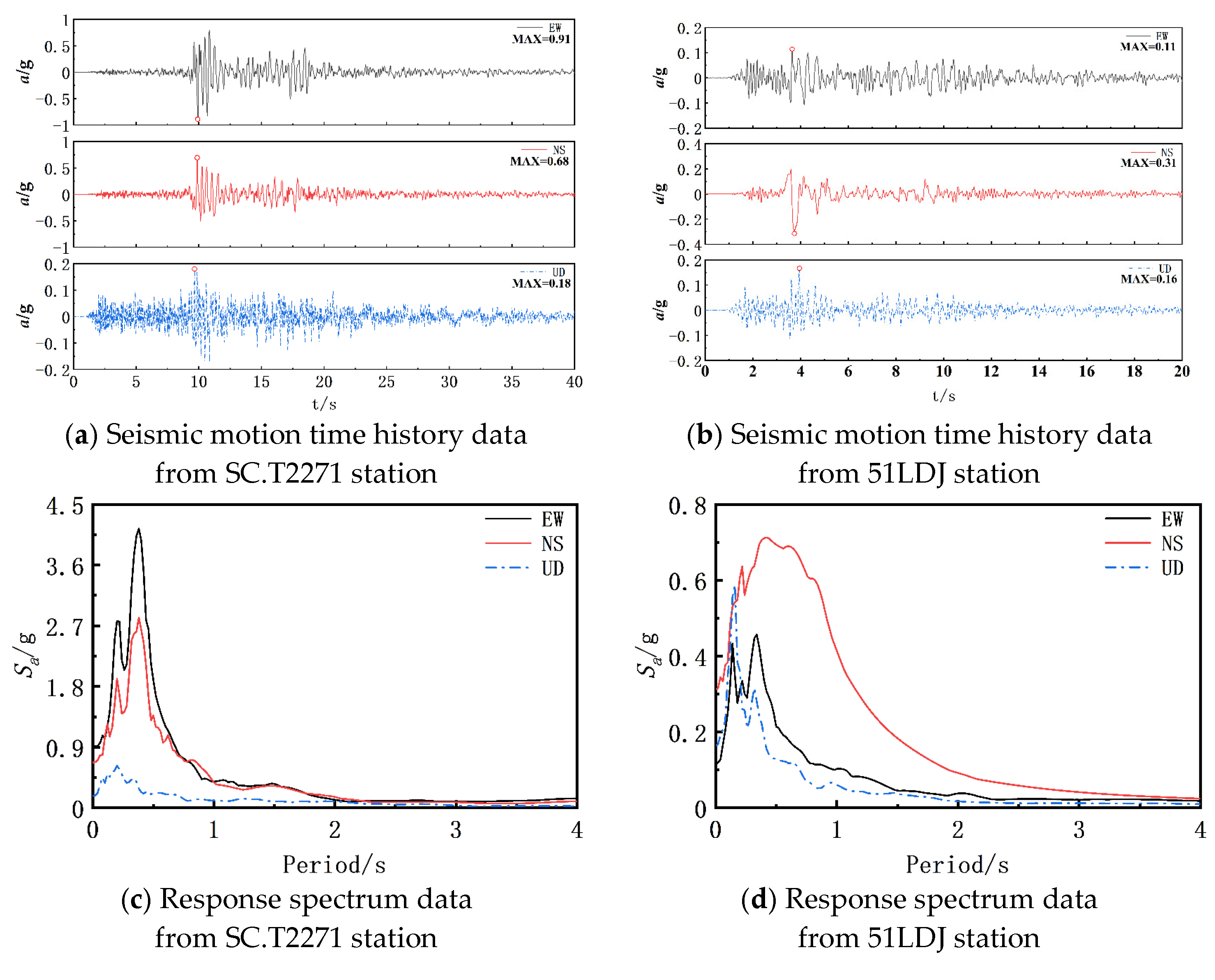






| Serial Number | Station Code | Epicentral Distance/km | PGA/g | Duration/s | |||
|---|---|---|---|---|---|---|---|
| EW | NS | UD | Record | After Clipping | |||
| 1 | SC.T2271 | - | 0.91 | 0.68 | 0.18 | 120 | 46 |
| 2 | 51LDJ | 16.20 | 0.11 | 0.31 | 0.16 | 139 | 29 |
| Calculation Model | Mode Number | Mode Shape | Natural Period/s |
|---|---|---|---|
| Tianyi Hotel | 1 | x-direction motion | 0.2741 |
| 2 | y-direction motion | 0.1776 | |
| 3 | z-rotation | 0.1573 | |
| Elementary school dormitory | 1 | x-direction motion | 0.1360 |
| 2 | y-direction motion | 0.1128 | |
| 3 | z-rotation | 0.0998 |
| Model | Working Conditions/g | Time/s | Uy/mm | Ux/mm | Ratio | |||
|---|---|---|---|---|---|---|---|---|
| N1 | N2 | N1 | N2 | |||||
| Tianyi Hotel | SC.T2271 | 0.1 | 14.87 | 0.55 | 0.55 | −2.87 | −2.13 | 1.0:1.0:5.2:3.9 |
| 0.5 | 14.16 | 1.98 | 1.98 | −13.33 | −13.19 | 1.0:1.0:6.7:6.7 | ||
| 51LDJ | 0.1 | 4.12 | −0.33 | −0.33 | 2.02 | 1.42 | 1.0:1.0:6.1:4.3 | |
| 0.5 | 4.13 | −1.49 | −1.49 | 12.03 | 10.18 | 1.0:1.0:8.1:6.8 | ||
| Elementary school dormitory | SC.T2271 | 0.1 | 13.91 | −0.12 | −0.12 | 0.23 | 0.23 | 1.0:1.0:1.9:1.9 |
| 0.5 | 13.92 | −0.18 | −0.18 | 1.35 | 1.35 | 1.0:1.0:7.5:7.5 | ||
| 1.0 | 13.93 | −0.51 | −0.51 | 4.63 | 4.62 | 1.0:1.0:9.1:9.1 | ||
| 51LDJ | 0.1 | 4.15 | 0.02 | 0.02 | −0.43 | −0.43 | 1.0:1.0:21.5:21.5 | |
| 0.5 | 4.15 | 0.04 | 0.04 | −0.83 | −0.83 | 1.0:1.0:20.8:20.8 | ||
| 1.0 | 4.16 | 0.07 | 0.07 | −2.49 | −2.49 | 1.0:1.0:35.6:35.6 | ||
| Model | Working Conditions/g | Time/s | F(×103)/kN | Ratio | ||||
|---|---|---|---|---|---|---|---|---|
| Ⓐ | Ⓑ | Ⓒ | Ⓓ | |||||
| Tianyi Hotel | SC.T2271 | 0.1 | 14.87 | −0.15 | −0.07 | −1.34 | - | 2.1:1.0:19.1 |
| 0.5 | 14.16 | −0.45 | −0.21 | −2.79 | - | 2.1:1.0:13.3 | ||
| 51LDJ | 0.1 | 4.12 | 0.11 | 0.05 | 0.90 | - | 2.2:1.0:18.0 | |
| 0.5 | 4.13 | 0.50 | 0.23 | 2.71 | - | 2.2:1.0:11.8 | ||
| Elementary school dormitory | SC.T2271 | 0.1 | 13.91 | 0.42 | 0.20 | 0.21 | 0.39 | 2.1:1.0:1.1:2.0 |
| 0.5 | 13.92 | 1.94 | 1.13 | 1.20 | 1.80 | 1.7:1.0:1.1:1.6 | ||
| 1.0 | 13.93 | 2.57 | 1.81 | 1.82 | 2.38 | 1.4:1.0:1.0:1.3 | ||
| 51LDJ | 0.1 | 4.15 | −0.73 | −0.34 | −0.36 | −0.68 | 2.1:1.0:1.1:2.0 | |
| 0.5 | 4.15 | −2.56 | −1.79 | −1.80 | −2.37 | 1.4:1.0:1.0:1.3 | ||
| 1.0 | 4.16 | −3.05 | −2.14 | −2.20 | −2.80 | 1.4:1.0:1.0:1.3 | ||
| Model | fcu | Ec | fy,c | fu,c | Es | fy,b | fu,b | fy,s | fu,s |
|---|---|---|---|---|---|---|---|---|---|
| PF | 17.64 | 20,492 | 150 | 260 | 197,000 | 474 | 636 | 160 | 201 |
| WALL | - | - | - |
| Model | Pcr/kN | Δcr/mm | Py/kN | Δy/mm | Pmax/kN | Δmax/mm | Pu/kN | Δu/mm | η1 | η2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Wall | 162.69 | 2.55 | 136.44 | 1.44 | 181.92 | 5.00 | 154.64 | 7.06 | - | - |
| PF | 45.54 | 5.76 | 42.56 | 5.00 | 56.75 | 15.80 | 48.23 | 47.79 | 10% | 75% |
| No. | Category | Buildings | Combination | Type | Status |
|---|---|---|---|---|---|
| 1 | I | No. 7, group 1, Detuo Town | PF + wall | Asymmetry | Damaged |
| 2 | II | Former Minya Konka school dormitory | Wall + wall | Symmetry | Undamaged |
| 3 | III | A frame under construction | PF + PF | Undamaged |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Guo, X.; A, L.; Luo, R.; Yan, C. Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory. Buildings 2024, 14, 2887. https://doi.org/10.3390/buildings14092887
Dong X, Guo X, A L, Luo R, Yan C. Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory. Buildings. 2024; 14(9):2887. https://doi.org/10.3390/buildings14092887
Chicago/Turabian StyleDong, Xiaoyao, Xun Guo, Lata A, Ruofan Luo, and Cheng Yan. 2024. "Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory" Buildings 14, no. 9: 2887. https://doi.org/10.3390/buildings14092887
APA StyleDong, X., Guo, X., A, L., Luo, R., & Yan, C. (2024). Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory. Buildings, 14(9), 2887. https://doi.org/10.3390/buildings14092887






