Flexural Behavior of Wet Joints with Contact U-Bars
Abstract
:1. Introduction
2. Experimental Section
2.1. General
2.2. Specimens Design
2.3. Material Property
2.4. Test Setup
3. Test Results and Comments
3.1. Bearing Capacity
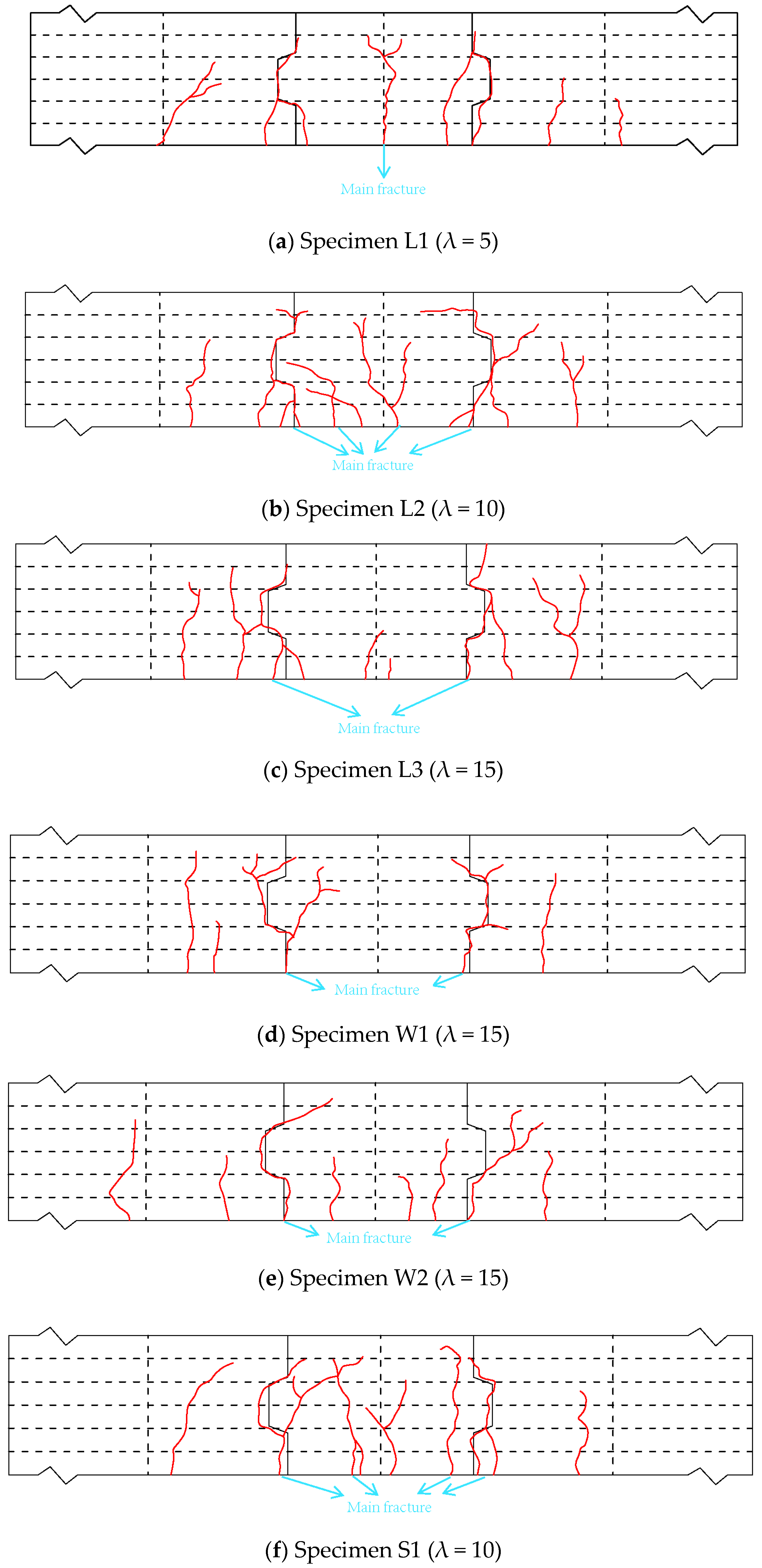
3.2. Cracking and Failure Conditions
3.2.1. Specimen λ = 5
3.2.2. Specimen λ = 10
3.2.3. Specimen λ = 15
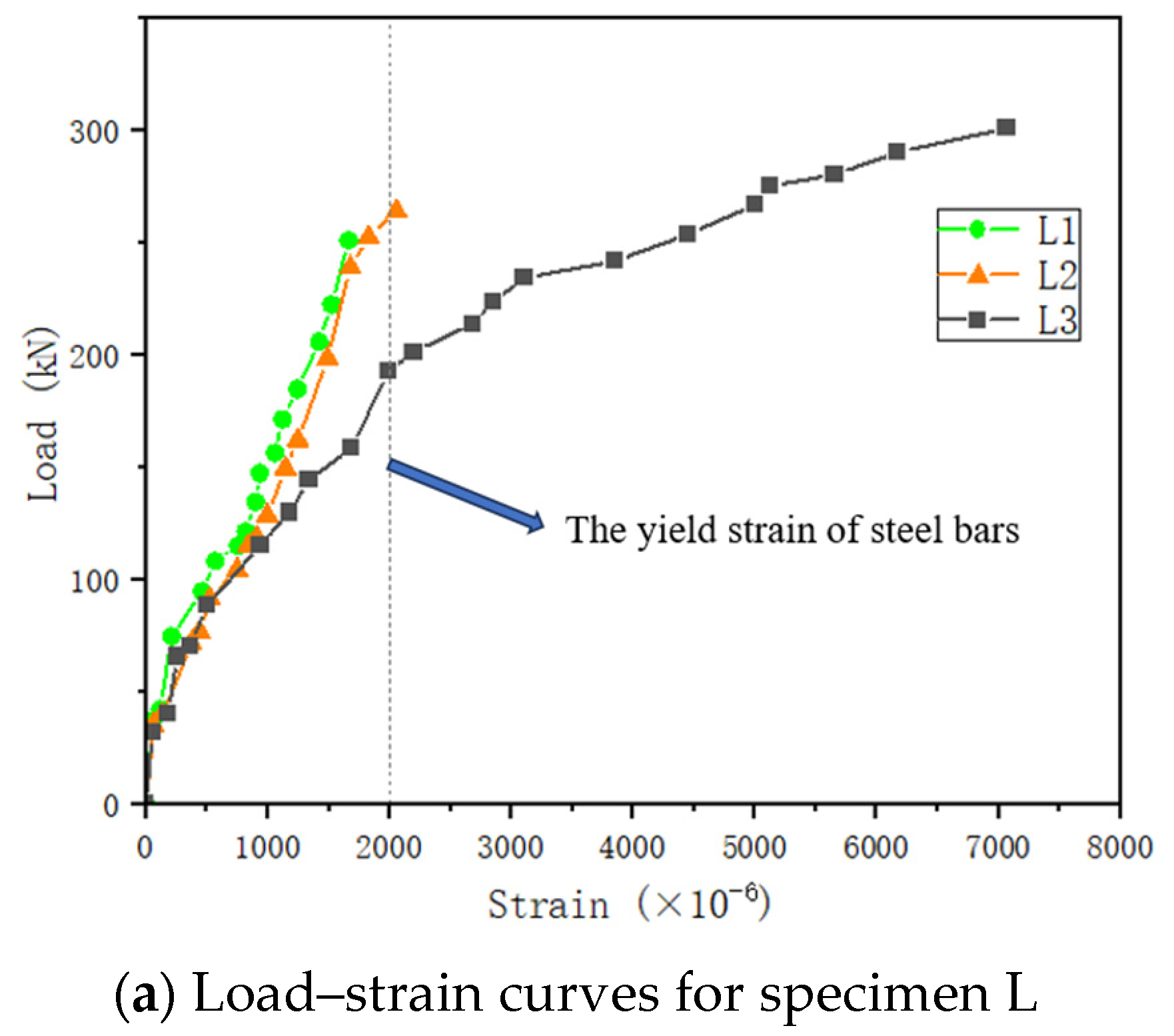
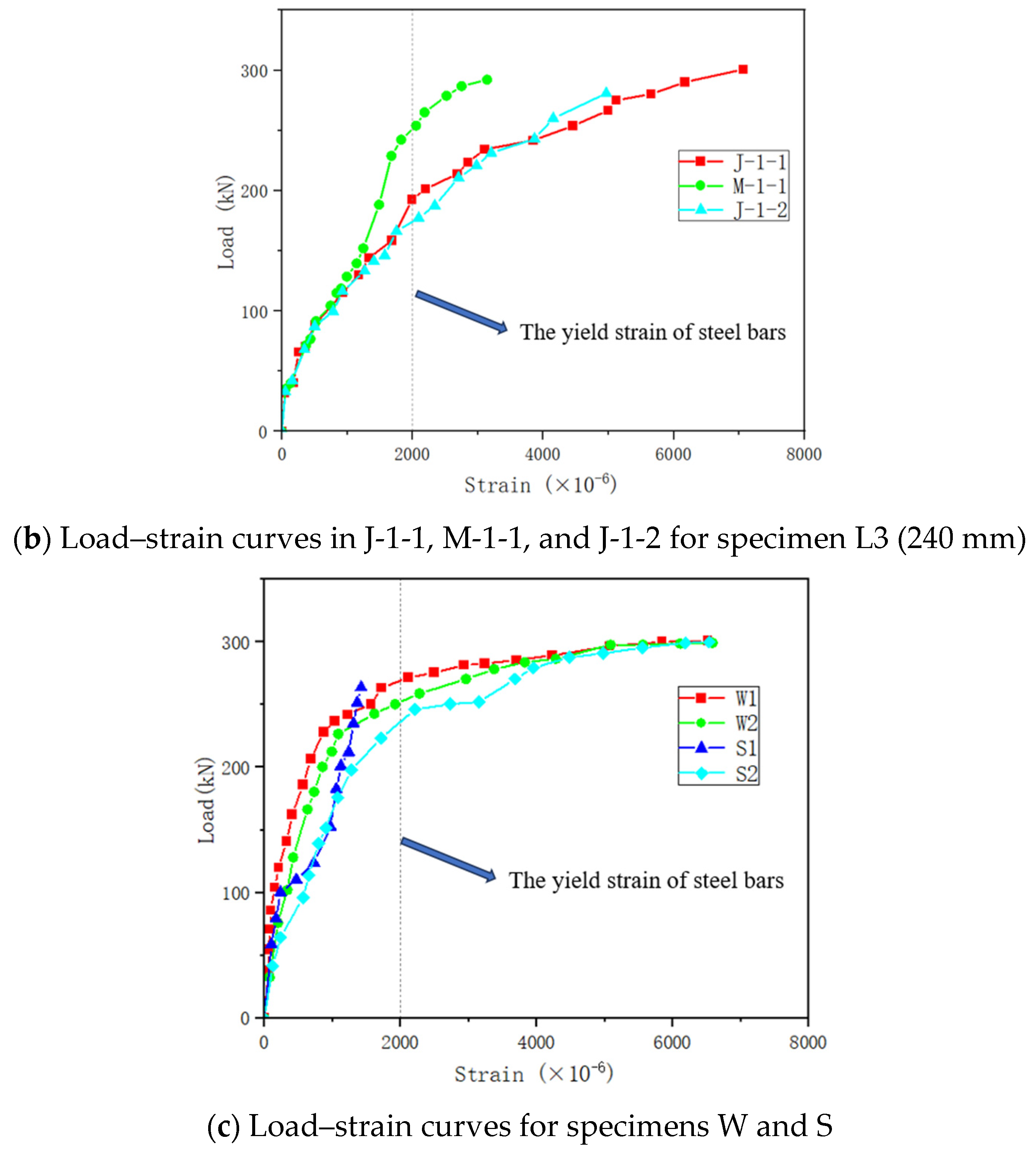
3.3. Strain
4. Finite Element Analysis
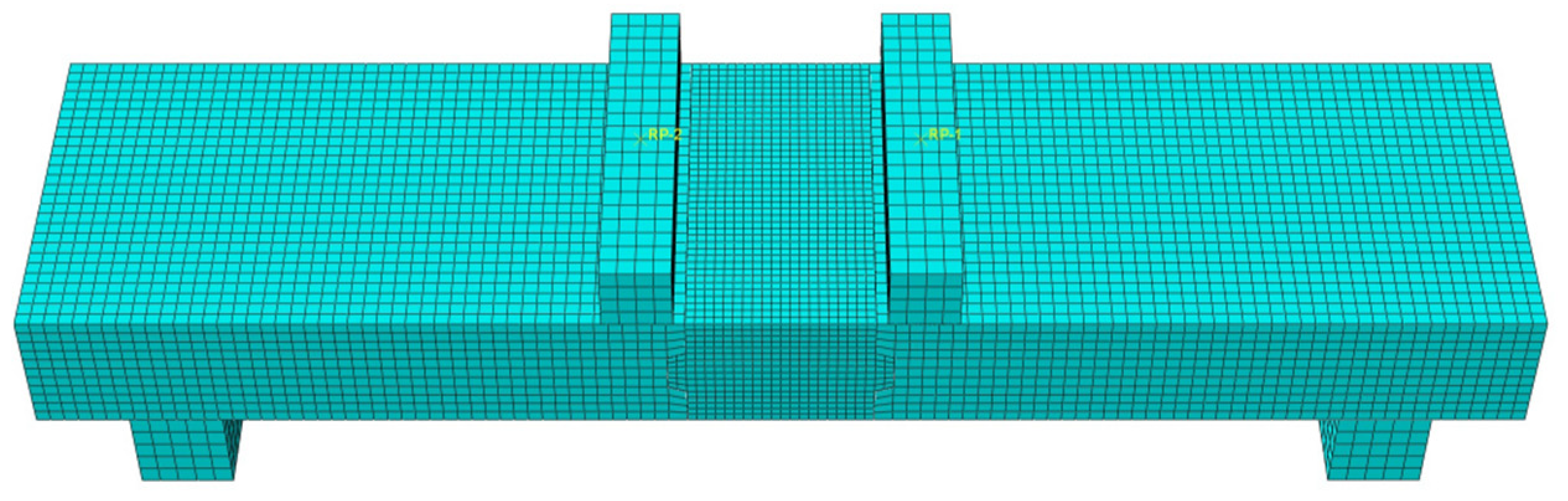
4.1. Modelling and Meshing
4.2. Boundary Conditions and Load
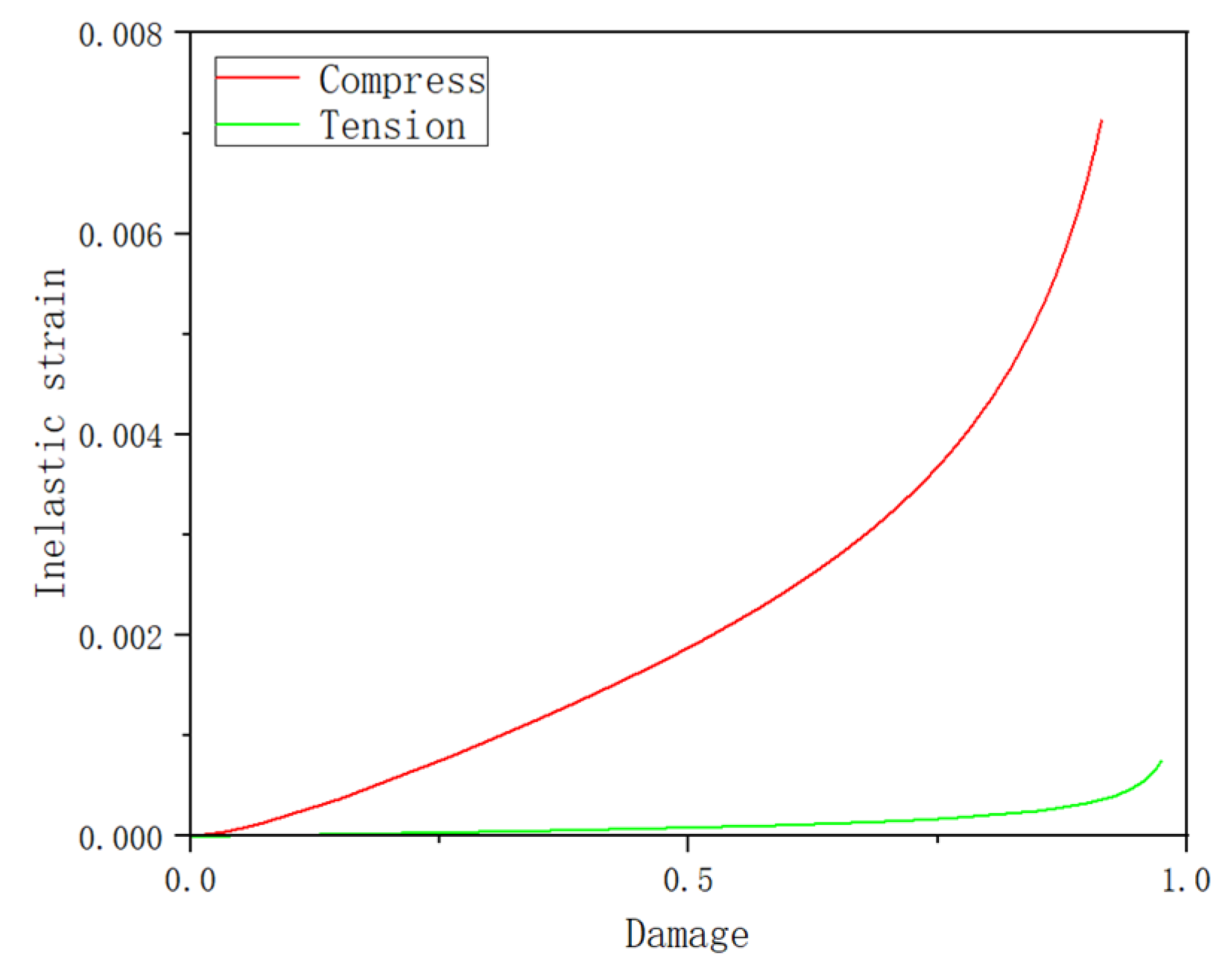
4.3. Material Constitutive Model and Parameters
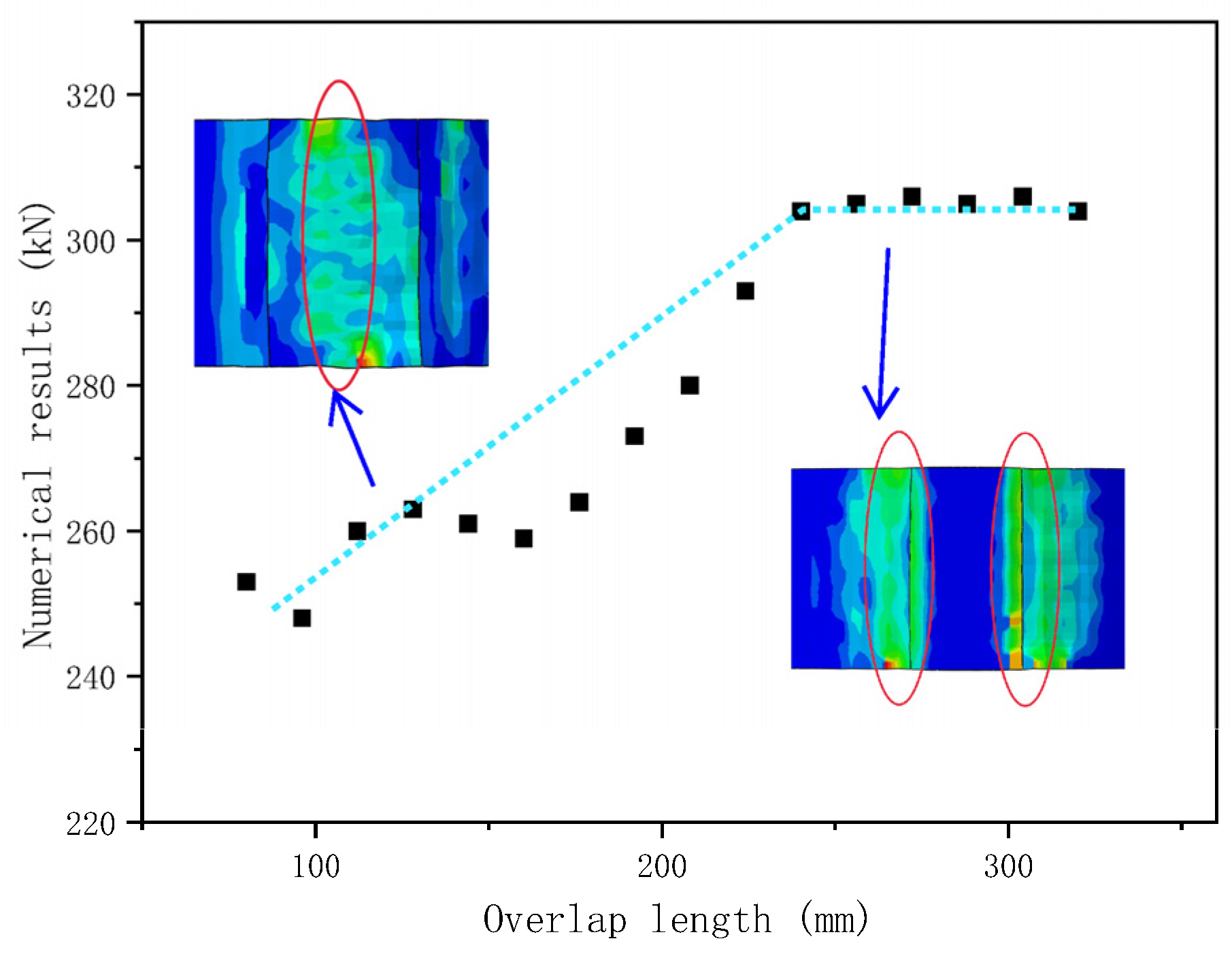
4.4. Finite Element Analysis Results
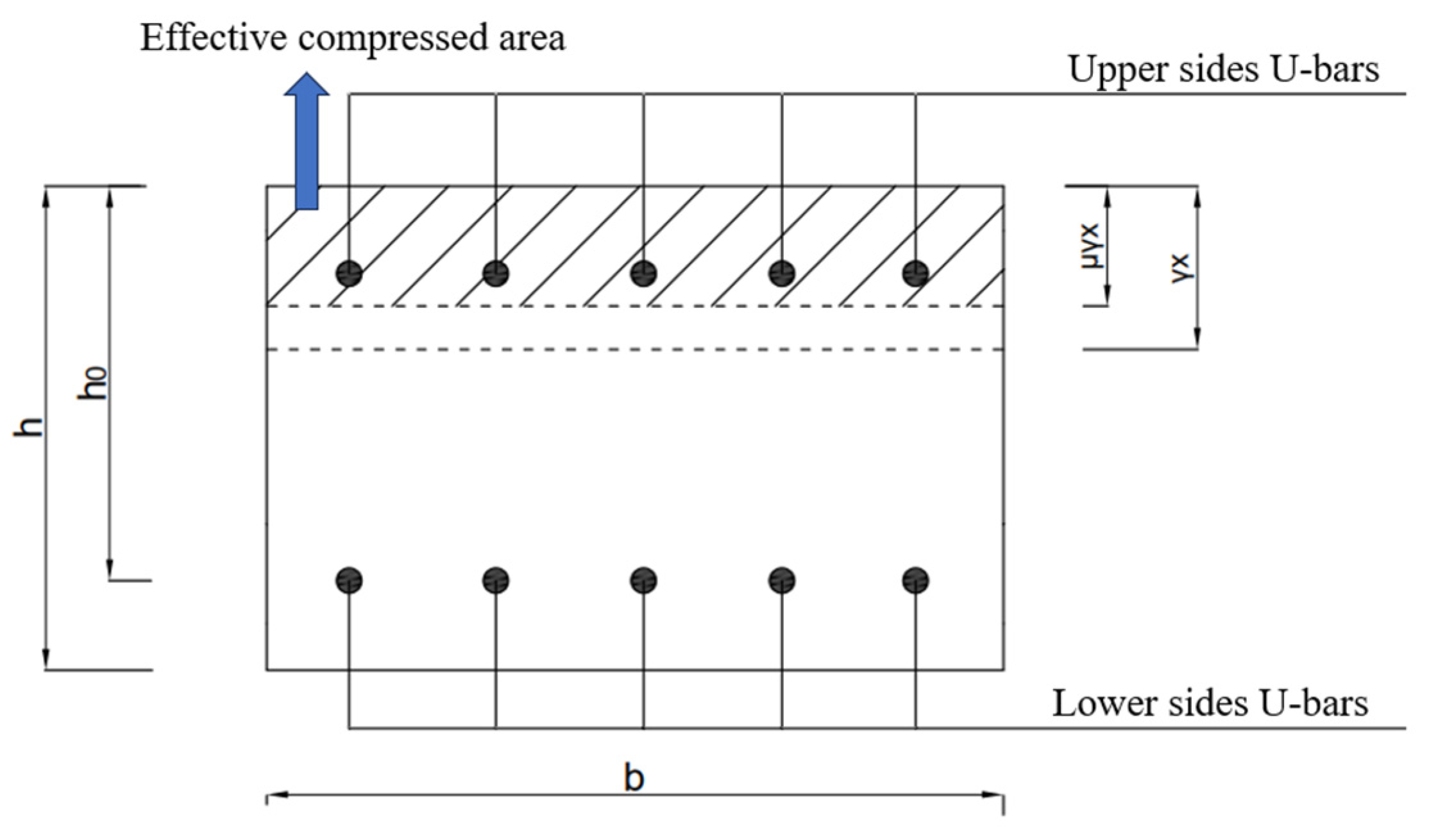
5. Analysis of Ultimate Bending Capacity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leonhardt, F.; Walther, R.; Dieterle, H. Empirical Tests for Determination of Ultimate Strength of U-Bar Splices. Dtsch. Aussch. Stahlbeton 1973, 1–22. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-0015728280&origin=inward&txGid=87b1a6f9858bdbab7511b5d14d53c742 (accessed on 12 February 2025).
- Di, J.; Han, B.; Qin, F. Investigation of U-bar joints between precast bridge decks loaded in combined bending and shear. Structures 2020, 27, 37–45. [Google Scholar] [CrossRef]
- Jørgensen, H.B. Strength of Loop Connections Between Precast Concrete Elements. Ph.D. Thesis, Department of Technology and Innovation, SDU Civil and Architectural Engineering, Jinan, China, 2014. [Google Scholar]
- Zalesov, A.S.; Kirillov, A.P.; Rubin, O.D.; Sleznev, S.V. Calculation of the strength and design of welding loops and linear anchor joints in combined precast-in situ reinforced concrete members. Hydrotech. Constr. 1989, 23, 120–124. [Google Scholar] [CrossRef]
- Zhu, P.; Ma, Z.J.; French, C.E. Fatigue Evaluation of Longitudinal U-Bar Joint Details for Accelerated Bridge Construction. J. Bridge Eng. 2012, 17, 201–210. [Google Scholar] [CrossRef]
- Li, L.; Jiang, Z. Flexural behavior and strut-and-tie model of joints with headed bar details connecting precast members. Perspect. Sci. 2016, 7, 253–260. [Google Scholar] [CrossRef]
- Han, B.; Zuo, Z.; Di, J.; Qin, F. Flexural behavior of improved joint details connecting pre-cast bridge decks. Eng. Struct. 2021, 245, 112948. [Google Scholar] [CrossRef]
- Ou, Y.-C.; Sutejo, H.; Huang, J.-L.; Yen, S.-I. Seismic Performance of Reinforced Concrete Beams with Proposed Lap-Spliced Intermediate Hoops. J. Struct. Eng. 2024, 150, 04023239. [Google Scholar] [CrossRef]
- Ma, Z.J.; Lewis, S.; Cao, Q.; He, Z.; Burdette, E.G.; French, C.E.W. Transverse Joint Details with Tight Bend Diameter U-Bars for Accelerated Bridge Construction. J. Struct. Eng. 2012, 138, 697–707. [Google Scholar] [CrossRef]
- Huang, D.; Nie, X.; Zeng, J.; Jiang, Y. Experimental and numerical analysis on flexural behavior of improved U-bar joint details for accelerated bridge construction. Eng. Struct. 2023, 289, 116328. [Google Scholar] [CrossRef]
- Chapman, C.E. Behavior of Precast Bridge Deck Joints with Small Bend Diameter Ubars. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2010. [Google Scholar]
- Shi, X.; Zhong, Y.; Ma, H.; Hu, K.; Xie, P.; Zeng, C. Numerical analysis on tensile capacity of loop connections. Eng. Struct. 2021, 246, 113022. [Google Scholar] [CrossRef]
- Villalba-Herrero, S.; Casas, J.R. New structural joint by rebar looping applied to staged box girder bridge construction. Static tests. Struct. Concr. J. FIB 2016, 17, 824–835. [Google Scholar] [CrossRef]
- Asemi, K.; Salehi, M.; Akhlaghi, M. Three dimensional graded finite element elasticity shear buckling analysis of FGM annular sector plates. Aerosp. Sci. Technol. 2015, 43, 1–13. [Google Scholar] [CrossRef]
- Yao, J.; Luo, J.; Ren, D.; Nagai, K. Mesoscopic simulation of interface and loop connections of precast concrete structures by 3D RBSM. Structures 2024, 70, 107749. [Google Scholar] [CrossRef]
- Andersen, M.E.M.; Poulsen, P.N.; Olesen, J.F. Finite-Element Limit Analysis for Solid Modeling of Reinforced Concrete. J. Struct. Eng. 2021, 147, 04021051. [Google Scholar] [CrossRef]
- Savino, V.; Lanzoni, L.; Tarantino, A.; Viviani, M. A cohesive FE model for simulating the cracking/debonding pattern of composite NSC-HPFRC/UHPFRC members. Constr. Build. Mater. 2020, 258, 119516. [Google Scholar] [CrossRef]
- Ooi, E.T.; Yang, Z.J. Modelling crack propagation in reinforced concrete using a hybrid finite element–scaled boundary finite element method. Eng. Fract. Mech. 2011, 78, 252–273. [Google Scholar] [CrossRef]
- Sørensen, J.H.; Hoang, L.C.; Olesen, J.F.; Fischer, G. Tensile capacity of loop connections grouted with concrete or mortar. Mag. Concr. Res. 2017, 69, 892–904. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. John Wiley & Sons: Hoboken, NJ, USA, 2010.
- Franz, G.; Timm, G. Tests on the flexural behavior of slab with hook and loop connection. Dtsch. Aussch. Stahlbeton 1973, 23–54. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-0015744285&origin=inward&txGid=92762a32103e97ed60e89f58ab31b275 (accessed on 12 February 2025).
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. ACI (American Concrete Institute): Indianapolis, IN, USA, 2019.

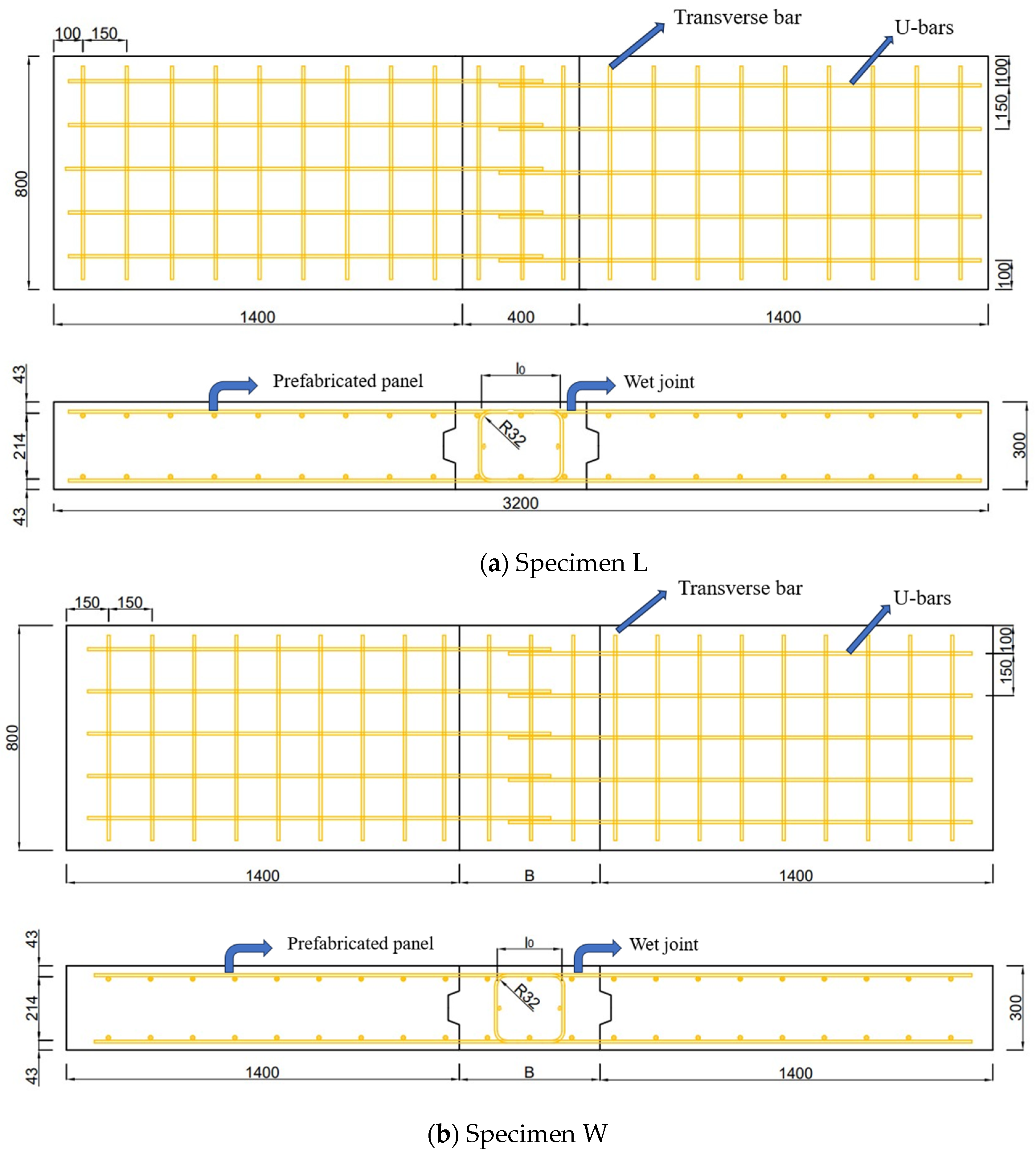
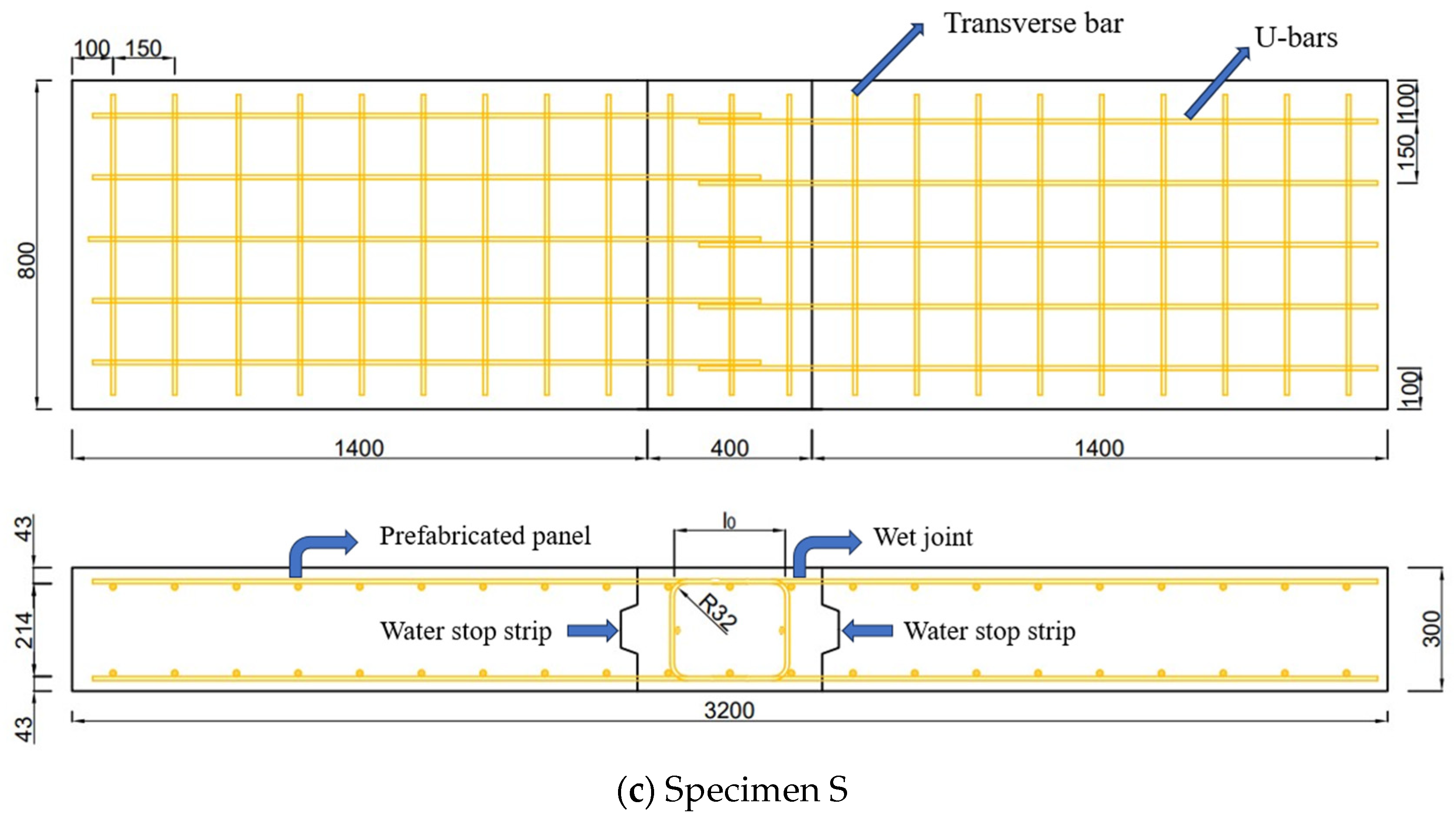

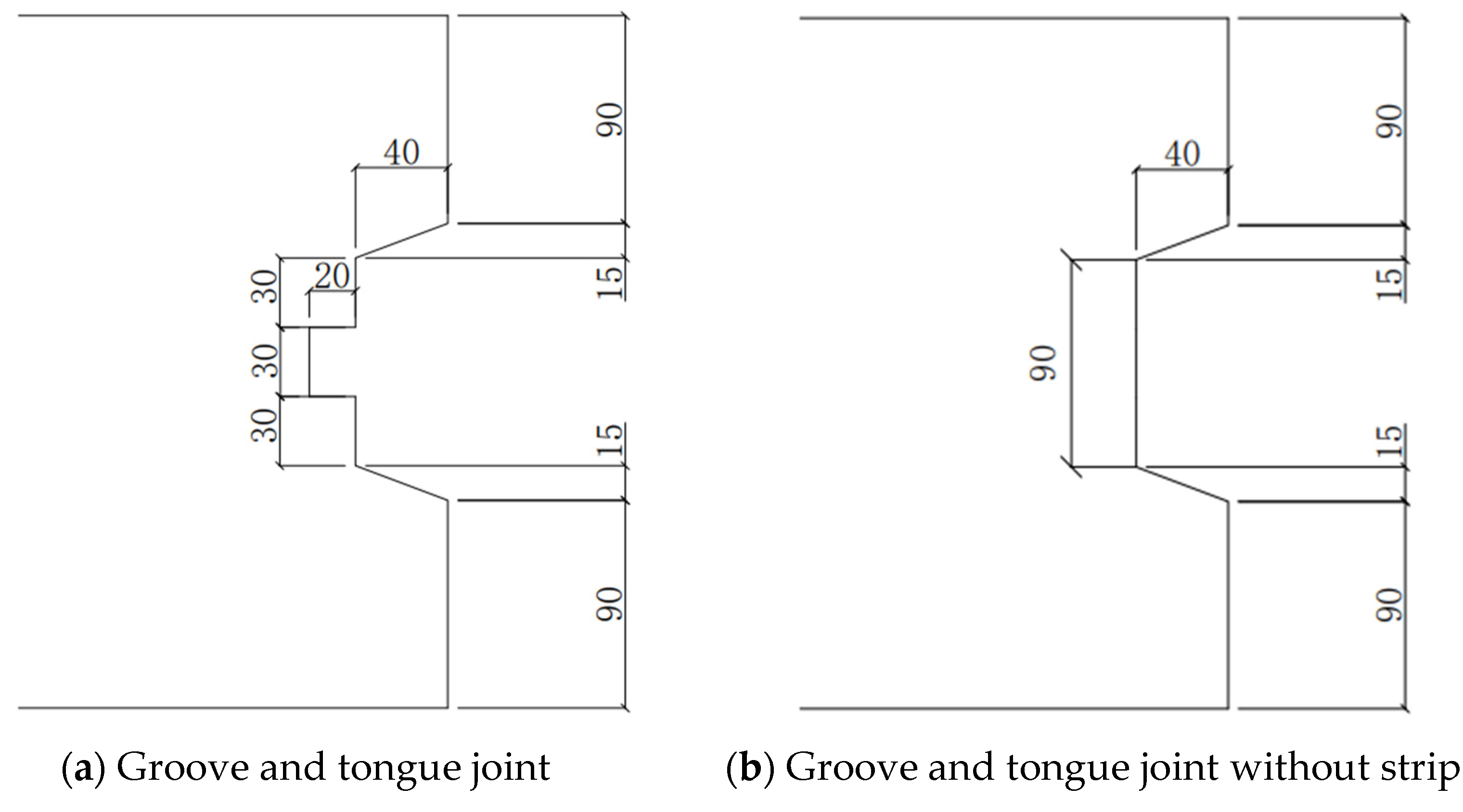

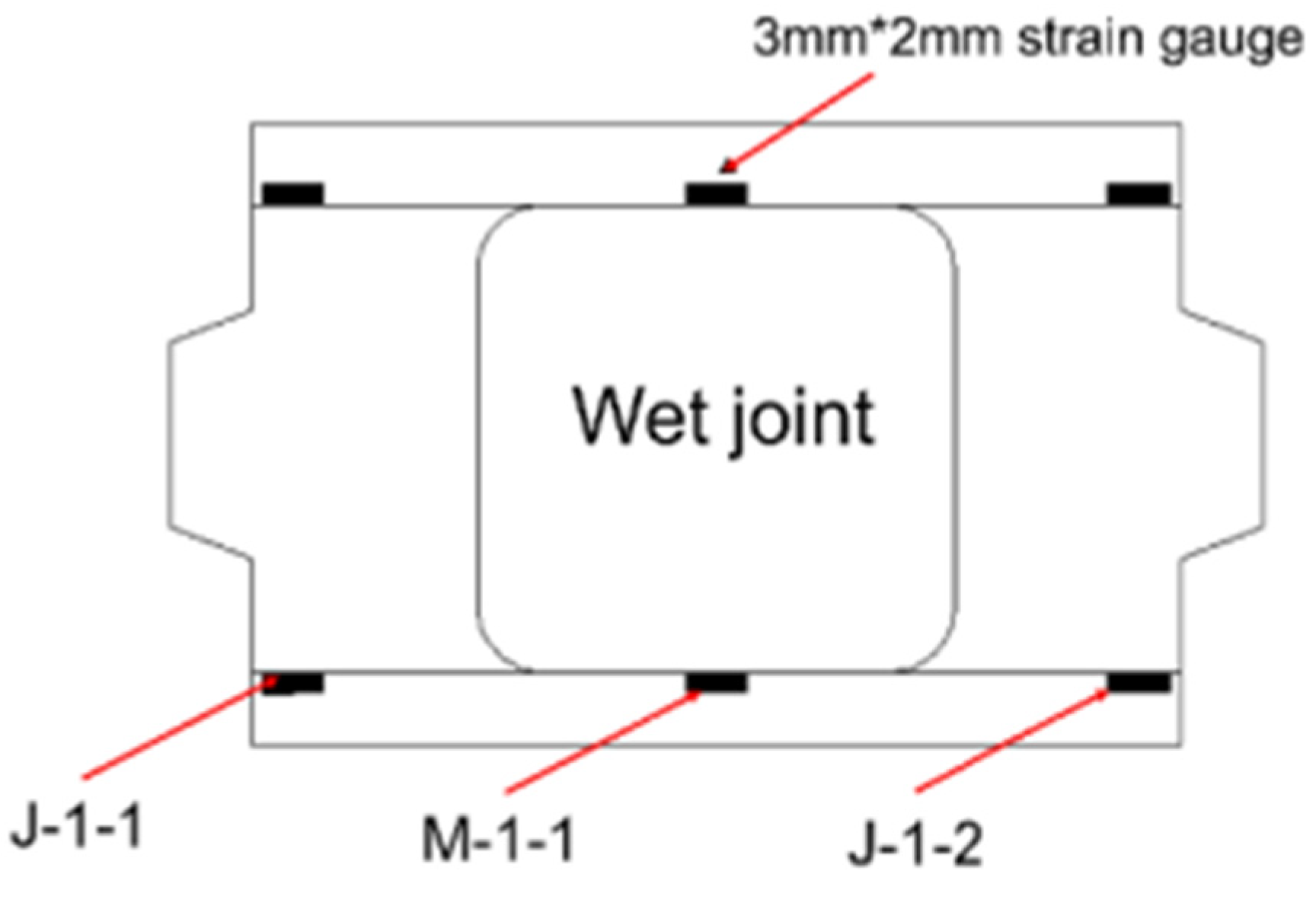
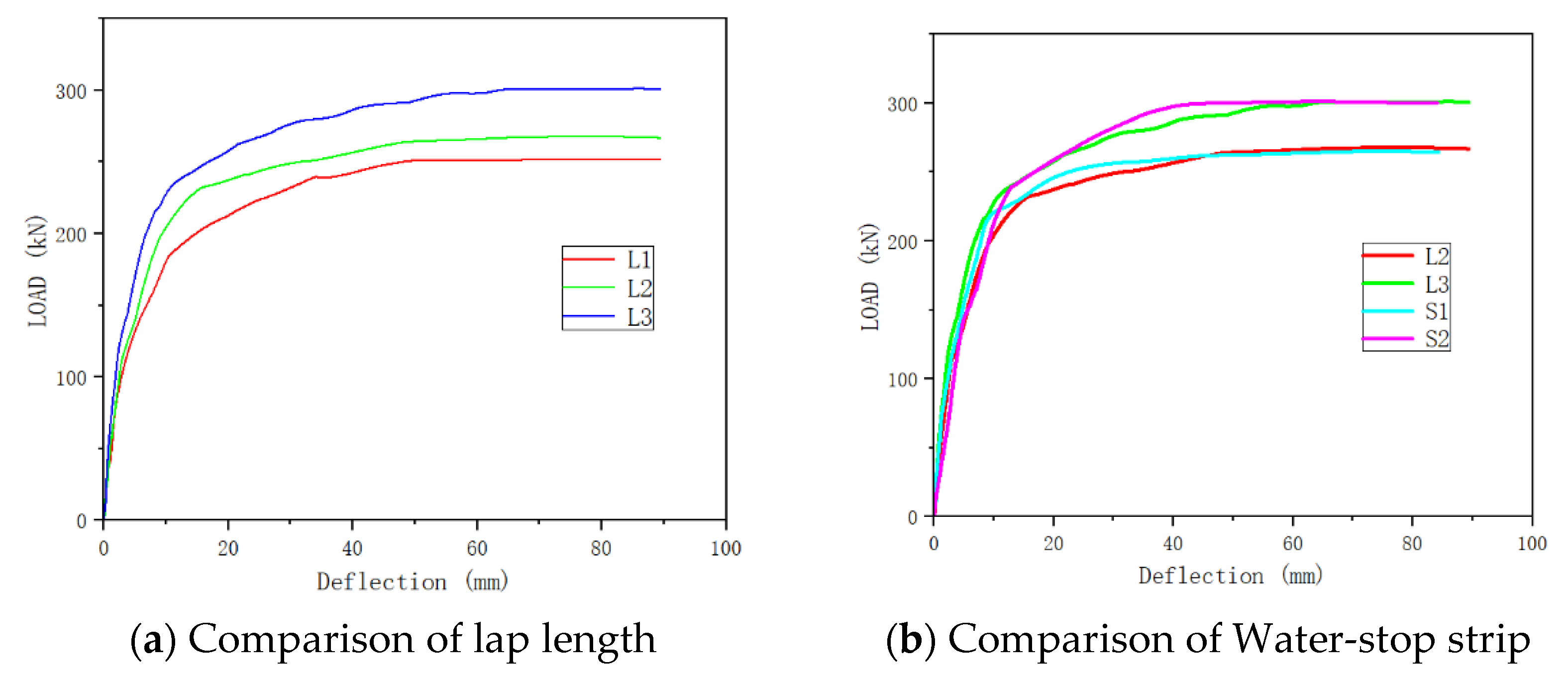
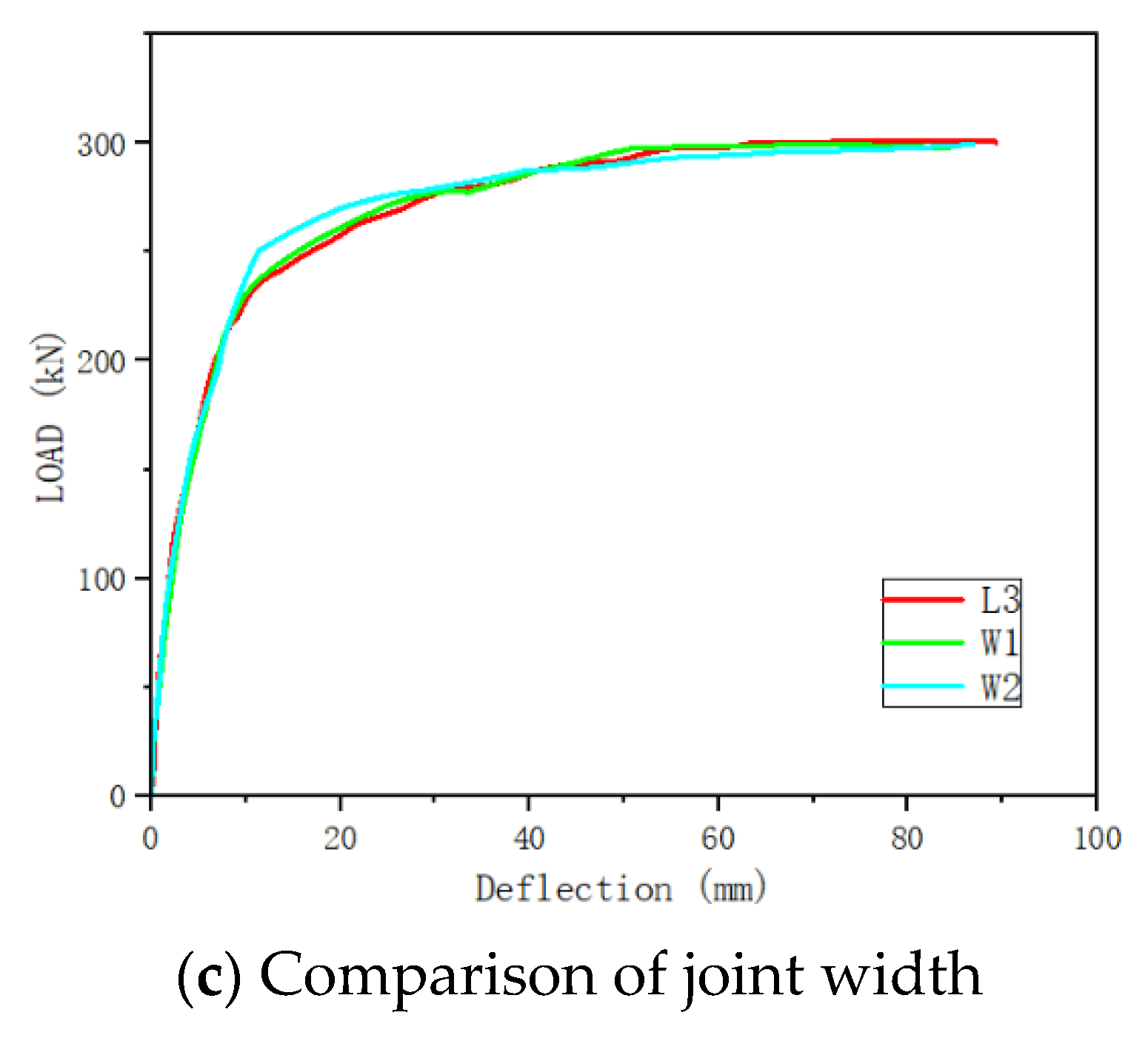










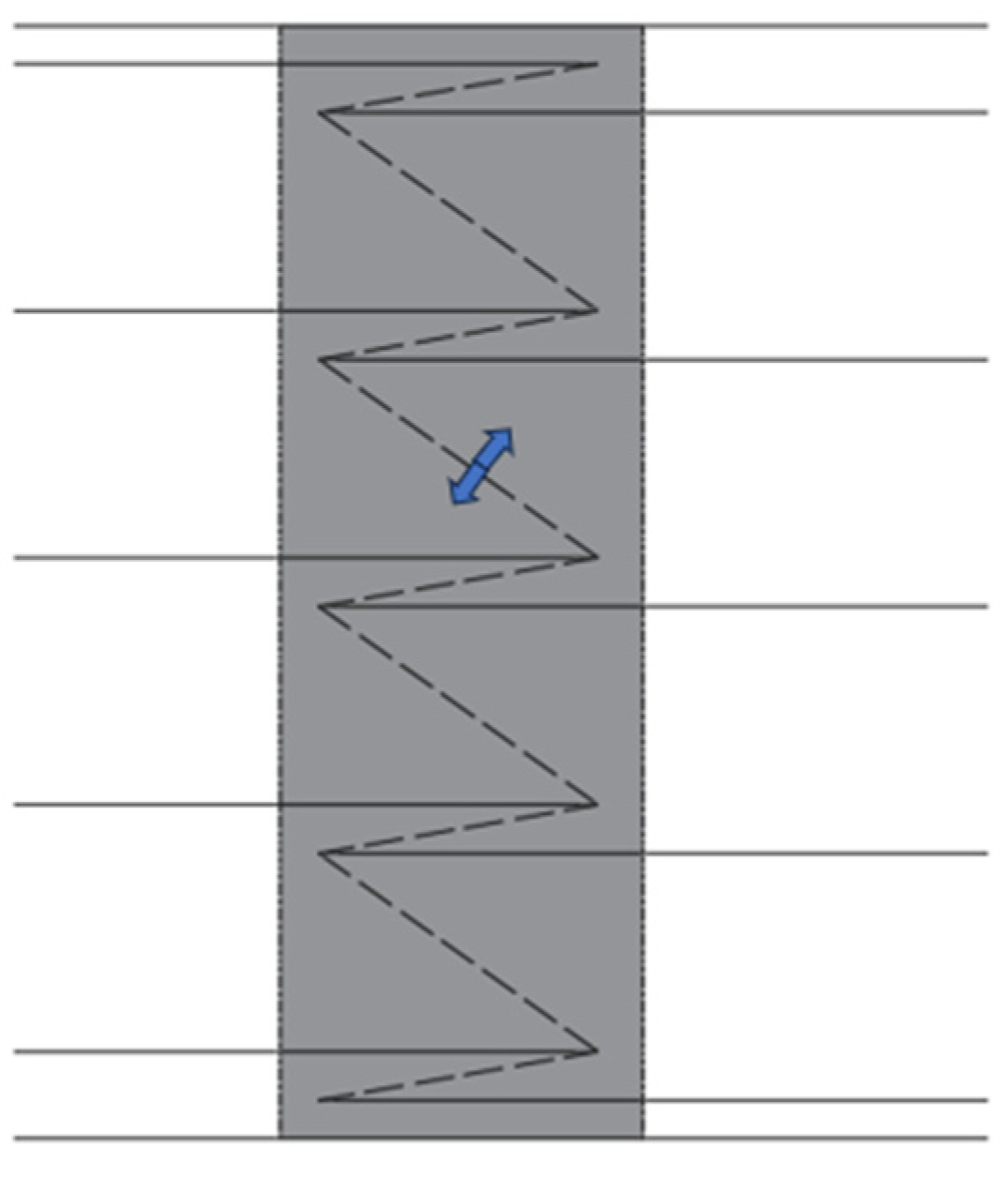
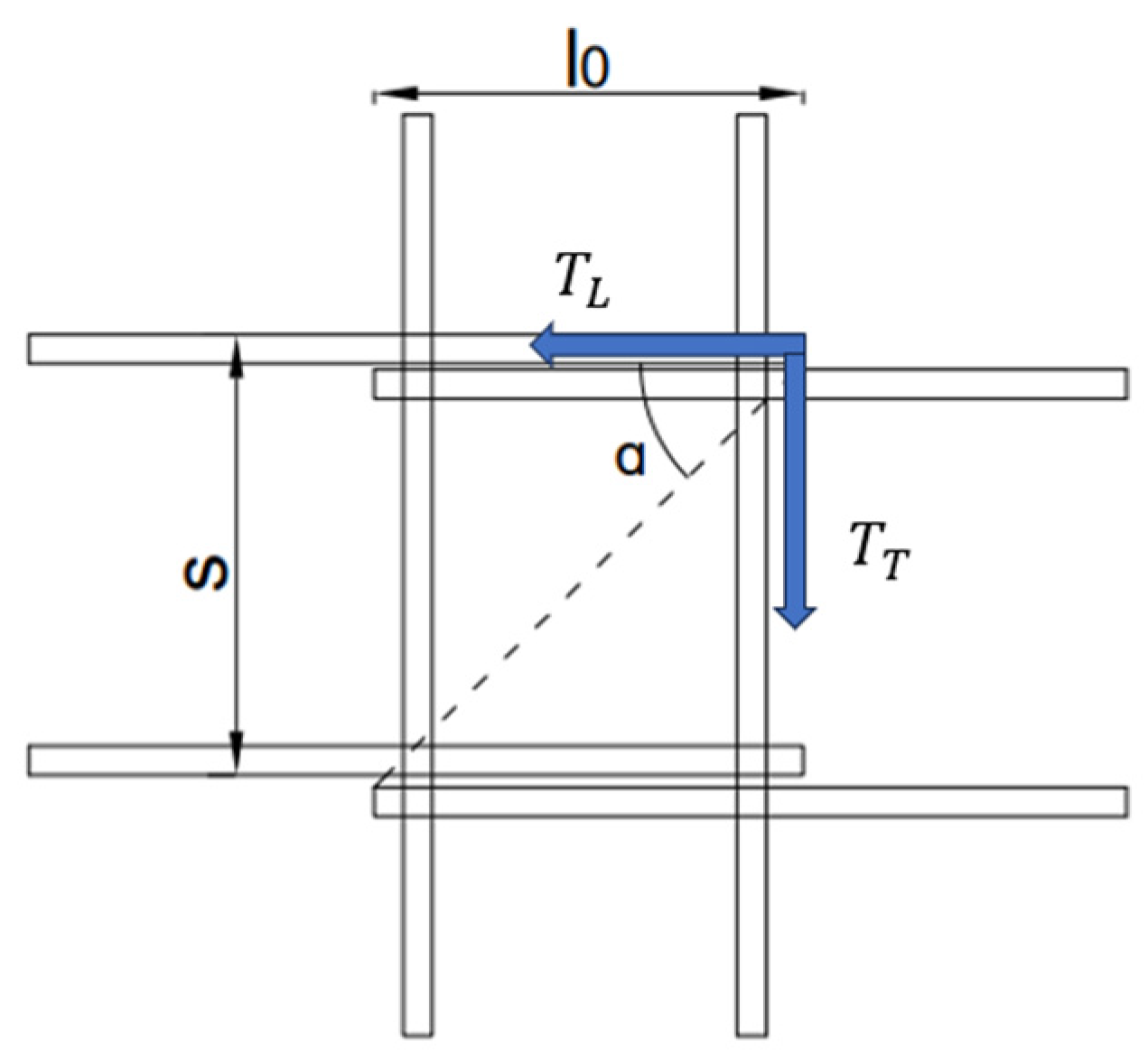
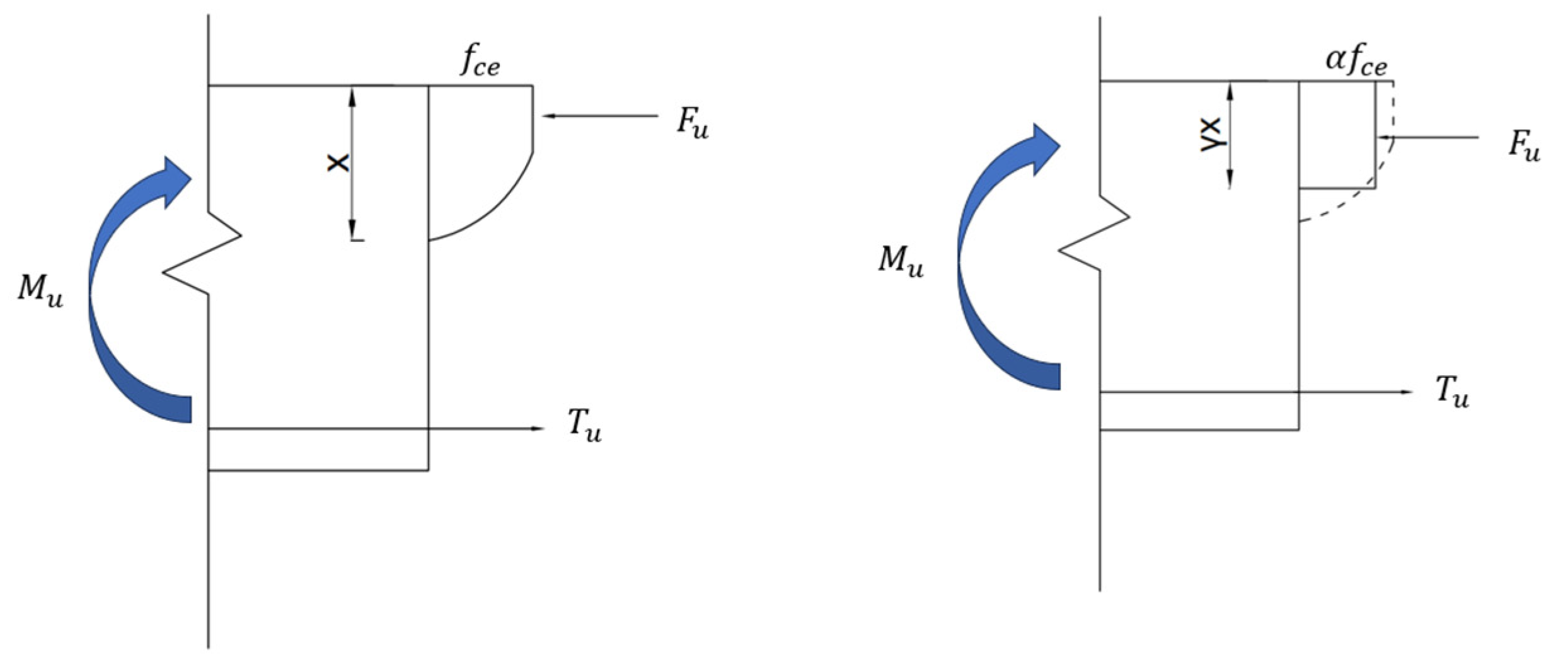
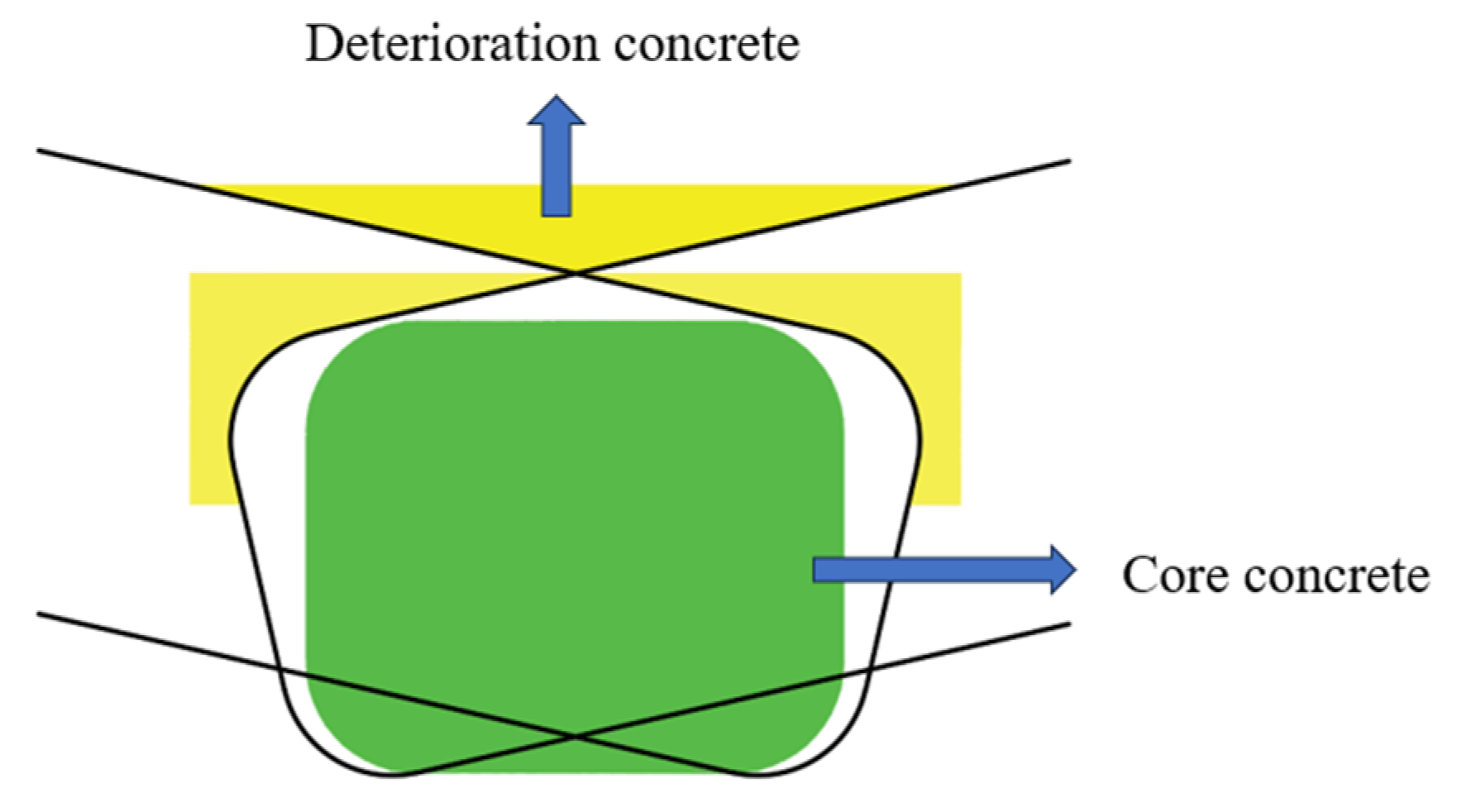
| Specimen | Overlap Length | Wet Joint Width/B (mm) | Water Stop Strips | λ (Ratio of Overlap Length to Diameter) |
|---|---|---|---|---|
| L1 | 80 | 400 | No | 5 |
| L2 | 160 | 400 | No | 10 |
| L3 | 240 | 400 | No | 15 |
| W1 | 240 | 300 | No | 10 |
| W2 | 240 | 500 | No | 15 |
| S1 | 160 | 400 | Yes | 10 |
| S2 | 240 | 400 | Yes | 15 |
| No. | Young’s Modulus | Yield Strength | Ultimate Strength |
|---|---|---|---|
| d12-1 | 207 | 438 | 572 |
| d12-2 | 204 | 430 | 568 |
| d12-3 | 210 | 435 | 562 |
| Average | 207 | 434 | 567 |
| d16-1 | 205 | 422 | 590 |
| d16-2 | 203 | 419 | 588 |
| d16-3 | 200 | 428 | 592 |
| Average | 203 | 423 | 590 |
| Parameters | Value |
|---|---|
| Young’s modulus (C30) | 30,612 MPa |
| Young’s modulus (C35) | 31,533 MPa |
| Poisson’s ratio | 0.2 |
| Dilation angle | 30 |
| Eccentricity | 0.1 |
| Ratio of initial biaxial compressive yield stress to initial uniaxial compressive yield stress | 1.16 |
| Ratio of the concrete strength under biaxial compression to the concrete strength under triaxial compression | 0.66667 |
| Viscosity parameter | 0.001 |
| Specimen | Experimental Results | Numerical Results | Difference (%) |
|---|---|---|---|
| L1 | 250 | 253 | 1.2 |
| L2 | 264 | 259 | −2.0 |
| L3 | 301 | 304 | 1.1 |
| W1 | 298 | 289 | −3.0 |
| W2 | 301 | 298 | −1.1 |
| S1 | 263 | 267 | 1.5 |
| S2 | 299 | 302 | 1.0 |
| Specimen | Experimental Results | Theoretical Result | Difference (%) | |
|---|---|---|---|---|
| Own | L1 | 125 | 122 | −2.4 |
| L2 | 132 | 127 | −3.8 | |
| L3 | 150 | 153 | 2.0 | |
| W1 | 149 | 153 | 2.7 | |
| W2 | 150 | 153 | 2.0 | |
| S1 | 131 | 127 | −3.1 | |
| S2 | 148 | 153 | 3.4 | |
| Han | LU | 195 | 198 | 1.5 |
| LUS | 188 | 198 | 5.4 | |
| LUT | 205 | 198 | −3.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Hu, S.; Li, M.; Rong, B. Flexural Behavior of Wet Joints with Contact U-Bars. Buildings 2025, 15, 855. https://doi.org/10.3390/buildings15060855
Wu Y, Hu S, Li M, Rong B. Flexural Behavior of Wet Joints with Contact U-Bars. Buildings. 2025; 15(6):855. https://doi.org/10.3390/buildings15060855
Chicago/Turabian StyleWu, Yuancong, Songtao Hu, Meng Li, and Bin Rong. 2025. "Flexural Behavior of Wet Joints with Contact U-Bars" Buildings 15, no. 6: 855. https://doi.org/10.3390/buildings15060855
APA StyleWu, Y., Hu, S., Li, M., & Rong, B. (2025). Flexural Behavior of Wet Joints with Contact U-Bars. Buildings, 15(6), 855. https://doi.org/10.3390/buildings15060855





