Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios
Abstract
1. Introduction
2. Experimental Program
2.1. Test Specimens
2.2. Material Properties
2.3. Test Setup and Instrumentation
3. Experimental Results and Discussion
3.1. Failure Modes and Crack Patterns
3.2. Load–Deflection Relationship
3.3. Flexural Capacity and Ductility
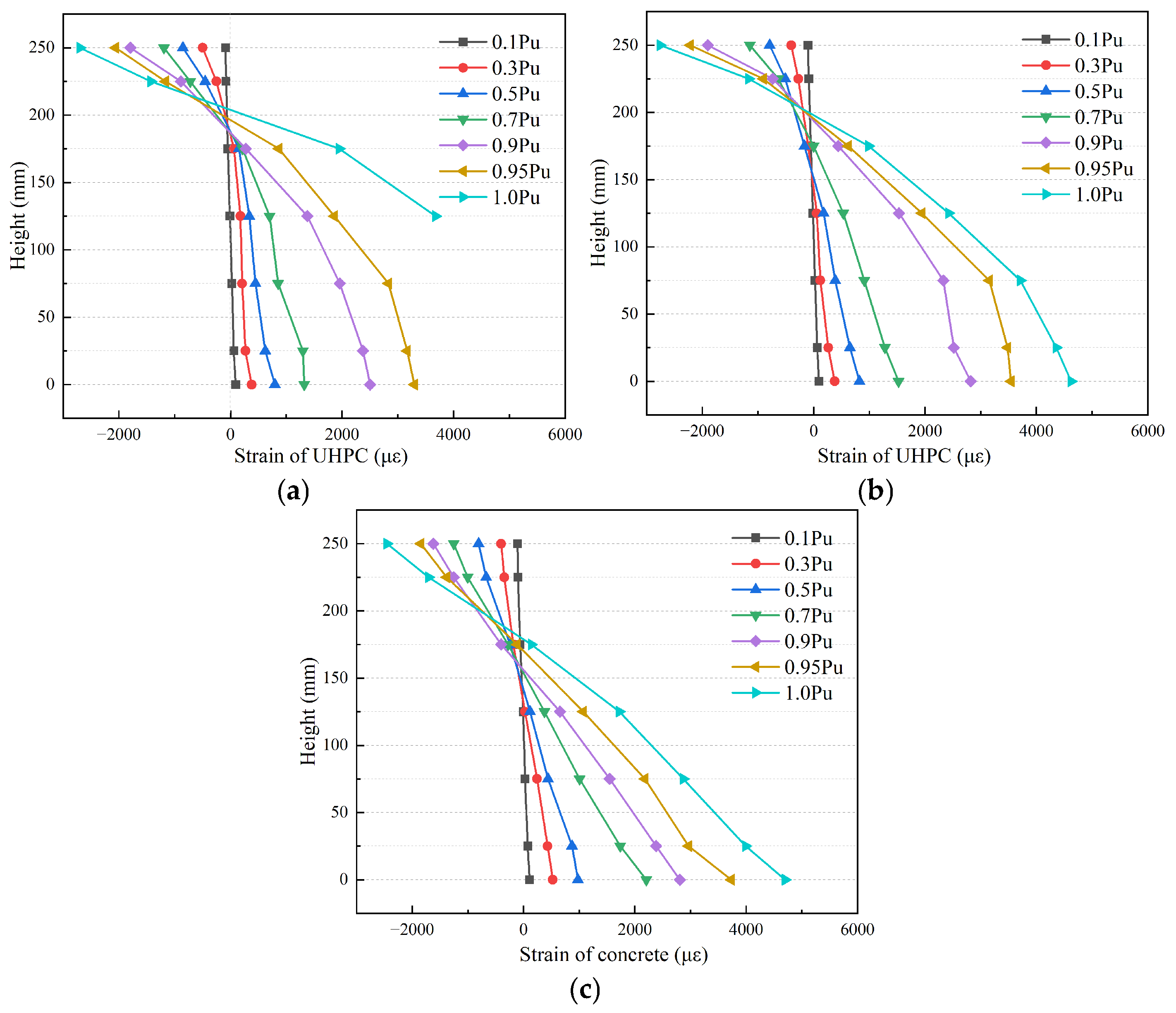
3.4. UHPC Strain of Mid-Span Section
4. Theoretical Analysis of Flexural Capacity
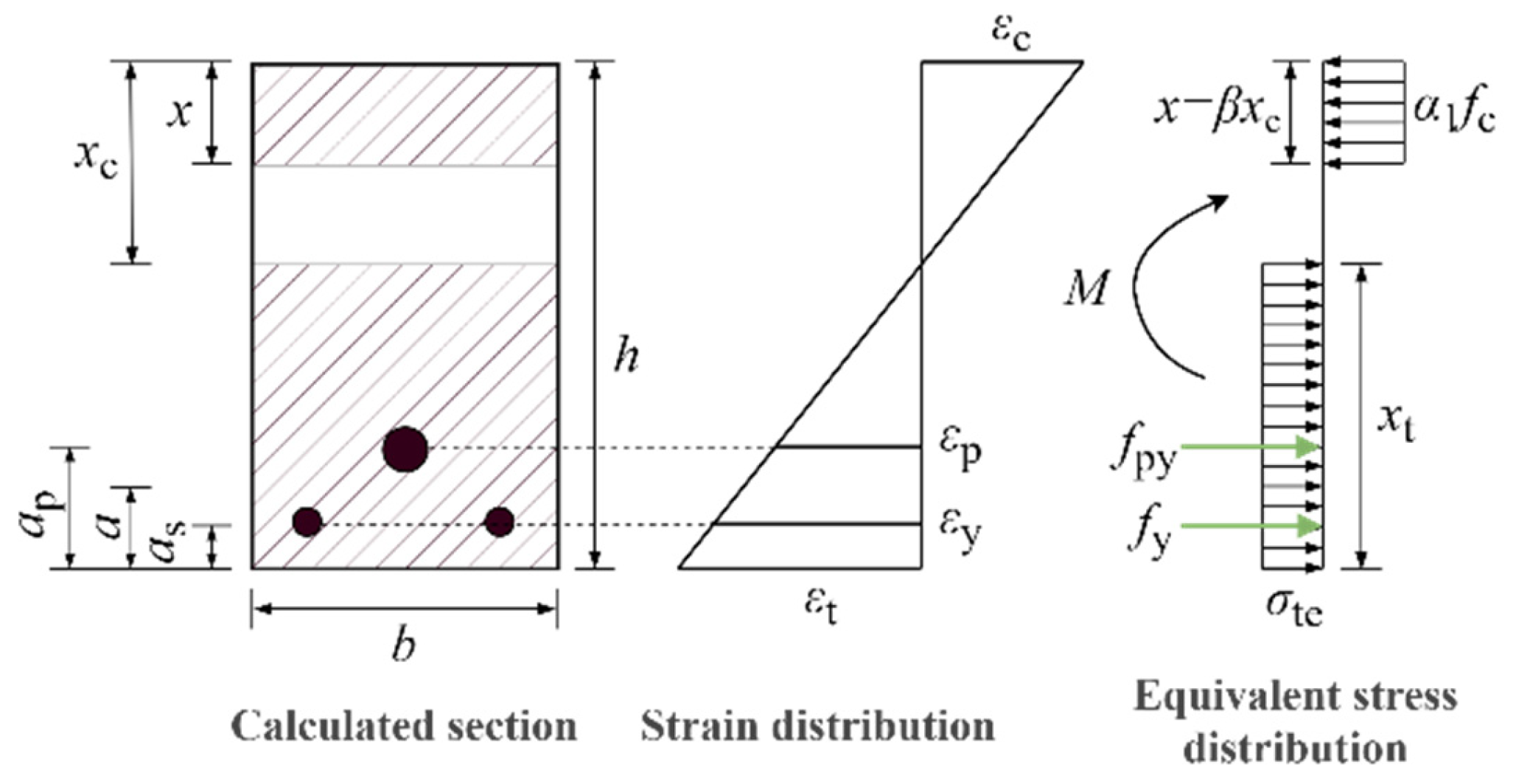
4.1. Basic Assumptions
4.2. Calculation of Prestressing Losses
4.3. Calculation of Cracking Moment
4.4. Calculation of Ultimate Moment
5. Conclusions
- (1)
- The RBPU beams in this experiment exhibited typical flexural failure modes. Compared to that of conventional prestressed concrete beams, the crack distribution was more uniform, which can be attributed to the retard-bonded prestressed technology and the bridging effect of steel fibers in UHPC. Additionally, compared to conventional concrete beams, the phenomena of concrete spalling and bulging at the late loading stage were relatively mild, and there was no significant drop in load.
- (2)
- As the reinforcement ratio was increased from 1.28% to 2.10%, the cracking load saw an 11.22% increase, suggesting that higher reinforcement ratios can improve crack resistance. Additionally, the ultimate load capacity and ductility coefficient grew by 53.04% and 39.34%, respectively, under the same conditions. This indicates that increasing the reinforcement ratio enhances both the load-bearing capacity and ductility of the component.
- (3)
- Taking into account the bridging effect of steel fibers in UHPC, the plastic influence coefficient γ for the section’s moment resistance was adjusted. Post-modification, the computed cracking moment values aligned closely with the experimental data. Likewise, the calculated ultimate moment values demonstrated strong agreement with the experimental findings.
- (4)
- While this study investigates the flexural behavior of retard-bonded prestressed UHPC (RBPU) beams with varying reinforcement ratios, there are certain limitations that warrant further exploration in the following aspects:
- (i)
- A parametric influence analysis of RBPU beams: experimental studies should be conducted to examine the effects of critical parameters such as prestressing levels and steel fiber volume content on the flexural performance of RBPU beams;
- (ii)
- High-precision numerical modeling: refined finite-element models should be developed to elucidate the underlying mechanisms of flexural behavior in RBPU beams.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, X.L.; Shen, S.Y.; Wan, Y.; Qin, S.W. Experimental Study on Bond Behavior of Steel Bar Embedded in Thin UHPC. J. Build. Eng. 2024, 86, 108865. [Google Scholar] [CrossRef]
- Shao, Y.; Hung, C.C.; Billington, S.L. Gradual Crushing of Steel Reinforced HPFRCC Beams: Experiments and Simulations. J. Struct. Eng. 2021, 147, 04021114. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. A Comparison of Existing Analytical Methods to Predict the Flexural Capacity of Ultra High Performance Concrete (UHPC) Beams. Constr. Build. Mater. 2018, 172, 10–18. [Google Scholar] [CrossRef]
- Krahl, P.A.; Carrazedo, R.; El Debs, M.K. Mechanical Damage Evolution in UHPFRC: Experimental and Numerical Investigation. Eng. Struct. 2018, 170, 63–77. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, R.; Sushant, S.; Ashour, A.; Fu, S.; Qiu, L.; Zhang, Z.; Ge, W. Experimental Investigation on Flexural Performance of UHPC Beams Reinforced with Steel-FRP Bars. Arch. Civ. Mech. Eng. 2024, 24, 132. [Google Scholar] [CrossRef]
- Hung, C.; El-Tawil, S.; Chao, S. A Review of Developments and Challenges for UHPC in Structural Engineering: Behavior, Analysis, and Design. J. Struct. Eng. 2021, 147, 03121001. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.; Lee, G. Application of Ultra-High Performance Concrete in Bridge Engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Li, D.B.; Li, W.L. Development of retard-bonded prestressed technique in China. Build. Sci. 2022, 38, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, X.; Jiang, F.; Liu, F.; Yin, Y.; Jin, H. Effect of Aging and Temperature on the Viscosity of the Adhesive Used for Retard-Bonded Prestressed Systems. J. Test. Eval. 2019, 47, 1848–1863. [Google Scholar] [CrossRef]
- Xu, J.Q.; Zhang, W.; Chen, S.Z. Design and analysis of slowly-bonded prestressed structure of Ganzhou West Railway Station. Build. Sci. 2020, 50, 132–137. [Google Scholar] [CrossRef]
- Song, X.F.; Li, J.A.; Zhu, S.W.; Zhu, S. Construction of Retard-bonded Prestressed in the Shuangliao Station. Build. Sci. 2011, 27, 167–168+171. [Google Scholar] [CrossRef]
- Pham, H.D.; Khuc, T.; Nguyen, T.; Cu, H.; Le, D.B.; Trinh, T.P. Investigation of Flexural Behavior of a Prestressed Girder for Bridges Using Nonproprietary UHPC. Adv. Concr. Constr. 2020, 10, 71–79. [Google Scholar] [CrossRef]
- Chen, L.; Graybeal, B.A. Modeling Structural Performance of Ultrahigh Performance Concrete I-Girders. J. Bridge Eng. 2012, 17, 754–764. [Google Scholar] [CrossRef]
- Steinberg, E. Structural Reliability of Prestressed UHPC Flexure Models for Bridge Girders. J. Bridge Eng. 2010, 15, 65–72. [Google Scholar] [CrossRef]
- Bahmani, H.; Mostafaei, H.; Santos, P.; Fallah Chamasemani, N. Enhancing the Mechanical Properties of Ultra-High-Performance Concrete (UHPC) Through Silica Sand Replacement with Steel Slag. Buildings 2024, 14, 3520. [Google Scholar] [CrossRef]
- Tian, X.; Fang, Z.; Shao, Y. Flexural Behavior and Design of Prestressed Ultra-High Performance Concrete (UHPC) Beams: Failure Mode and Ductility 2024. arXiv 2024, arXiv:2411.01113. [Google Scholar]
- El-Helou, R.G.; Graybeal, B.A. Flexural Behavior and Design of Ultrahigh-Performance Concrete Beams. J. Struct. Eng. 2022, 148, 04022013. [Google Scholar] [CrossRef]
- Sun, X.; Ma, Y.; Jiang, F.; Fan, X.; Wu, H. Bending Resistance Mechanism of Prestressed Ultra-High Performance Concrete—Reinforced Concrete Beam Based on a Full-Scale Experiment. Adv. Struct. Eng. 2024, 27, 1746–1761. [Google Scholar] [CrossRef]
- Sim, C.; Tadros, M.; Gee, D.; Asaad, M. Flexural Design of Precast, Prestressed Ultra-High-Performance Concrete Members. PCI J. 2020, 65, 35–61. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Fan, X.; Ye, M.; Shao, X.; Yi, L. Experimental and Numerical Investigation on the Flexural Behavior of a Large-Scale Prestressed UHPC T-Shaped Girder. Eng. Struct. 2022, 272, 115027. [Google Scholar] [CrossRef]
- Leutbecher, T.; Heck, L.; Metje, K.; Riedel, P. Flexural design of UHPC girders with mixed reinforcement. Beton-Stahlbetonbau 2022, 117, 863–877. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B.S. Flexural Strength of Large-Scale Ultra High Performance Concrete Prestressed T-Beams. Can. J. Civ. Eng. 2011, 38, 1185–1195. [Google Scholar] [CrossRef]
- Deng, Z.; Li, Q.; Tuladhar, R.; Shi, F. Flexural Performance of Prestressed UHPC Beams with Different Prestressing Degrees and Levels. Comput. Concr. 2024, 34, 379–391. [Google Scholar] [CrossRef]
- Dogu, M.; Menkulasi, F. Moment-Curvature-Deformation Response of Post-Tensioned Ultra-High-Performance Concrete Beams. ACI Struct. J. 2022, 119, 301–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, S.; Zhu, Y.; Hussein, H.H.; Shao, X. Experimental Validation of Damaged Reinforced Concrete Beam Strengthened by Pretensioned Prestressed Ultra-High-Performance Concrete Layer. Eng. Struct. 2022, 260, 114251. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, S.; Liu, Y.; Fan, W.; Shao, X. Flexural Behavior of Damaged RC Beams Strengthened with Prestressed UHPC Layer. Eng. Struct. 2023, 283, 115806. [Google Scholar] [CrossRef]
- Li, W.; Ji, W.; An, M.; Zhu, L.; Wang, J. Flexural Performance of Composite Prestressed UHPC-NC T-Girders. J. Bridge Eng. 2020, 25, 04020064. [Google Scholar] [CrossRef]
- Mohebbi, A.; Graybeal, B. Prestress Loss Model for Ultra-High Performance Concrete. Eng. Struct. 2022, 252, 113645. [Google Scholar] [CrossRef]
- John, E.E.; Ruiz, E.D.; Floyd, R.W.; Hale, W.M. Transfer and Development Lengths and Prestress Losses in Ultra-High-Performance Concrete Beams. Transp. Res. Rec. 2011, 2251, 76–81. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, J.; Yang, H.; Liang, Z.; Li, W. Flexural Behavior of Externally Prestressed Steel-UHPC-NC Composite Beams in Negative Moment Regions. SSRN, 2025; preprint. [Google Scholar] [CrossRef]
- Feng, J.; Shao, X.; Qiu, M.; Li, H.; Gao, X.; Huang, Z. Reliability Evaluation of Flexural Capacity Design Provision for UHPC Beams Reinforced with Steel Rebars/Prestressing Tendons. Eng. Struct. 2024, 300, 117160. [Google Scholar] [CrossRef]
- Cao, G.H.; Hu, J.X.; Xiao, M.; Zhang, K. Ultimate Bearing Capacity Test of Retard-Bonded Prestressed Concrete T-Beams. Appl. Mech. Mater. 2013, 256, 769–774. [Google Scholar] [CrossRef]
- Cao, G.; Zhang, W.; Hu, J.; Zhang, K. Experimental Study on the Long-Term Behaviour of RBPC T-Beams. Int. J. Civ. Eng. 2018, 16, 887–895. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, X.; He, P.; Wang, L.; Chen, Z. Experimental Study and Finite Element Analysis on Stress Transfer Mechanism of Retard-Bonded Prestressed Concrete Beams. In Proceedings of the 2020 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Vientiane, Laos, 11–12 January 2020; pp. 288–293. [Google Scholar]
- Xiong, X.; He, L.; Bao, L. Experimental Study on Flexural Behavior of Full-Scale Retard-Bonded Prestressed UHPC Variable Section Cantilever Beams. Eng. Struct. 2023, 284, 115943. [Google Scholar] [CrossRef]
- T/CECS 864-2021; Standard for Test Method of Ultra-High Performance Concrete. China Architecture & Building Press: Beijing, China, 2021.
- GB/T 228.1-2021; Metallic Materials: Tensile Testing. Standards Press of China: Beijing, China, 2021.
- GB/T 21839-2019; Test Methods of Steel for Prestressing Concrete. Standards Press of China: Beijing, China, 2019.
- GB/T 50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- Gao, X.; Wang, M.; Guo, J.; Li, H. Flexural Behaviors of a Novel Precast Hollow UHPC Composite Beam Reinforced with Inverted T-Shaped Steel: Experimental Investigation and Theoretical Analysis. J. Build. Eng. 2024, 86, 108893. [Google Scholar] [CrossRef]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L. Mechanical Behavior of Concrete-Filled Square Steel Tube with FRP-Confined Concrete Core Subjected to Axial Compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Impact of UHPC Tensile Behavior on Steel Reinforced UHPC Flexural Behavior. J. Struct. Eng. 2022, 148, 04021244. [Google Scholar] [CrossRef]
- JGJ 387-2017; Technical Specification for Concrete Structures Prestressed with Retard-Bonded Tendons. China Architecture & Building Press: Beijing, China, 2017.
- JGJ 369-2016; Code for Design of Prestressed Concrete Structures. China Architecture & Building Press: Beijing, China, 2016.
- SIA 2052; Recommendation: Ultra-high Performance Fiber Reinforced Cement-based Composites (UHPFRC) Construction Material, Dimensioning and Application. MCS-EPFL: Lausanne, Switzerland, 2017.
- T/CCPA 35-2022; Specification for Design of Ultra-High Performance Concrete Structures. China Building Material Council: Beijing, China, 2022.
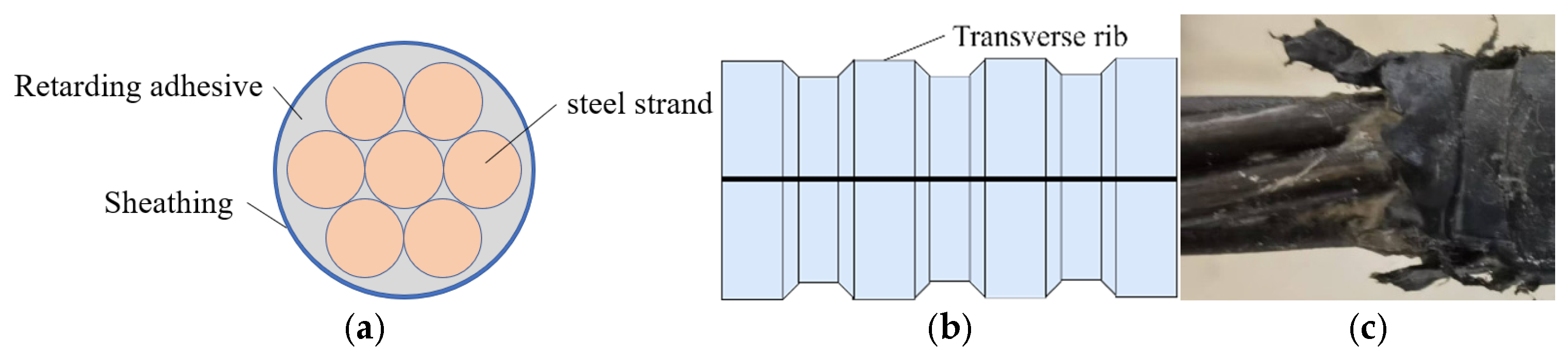
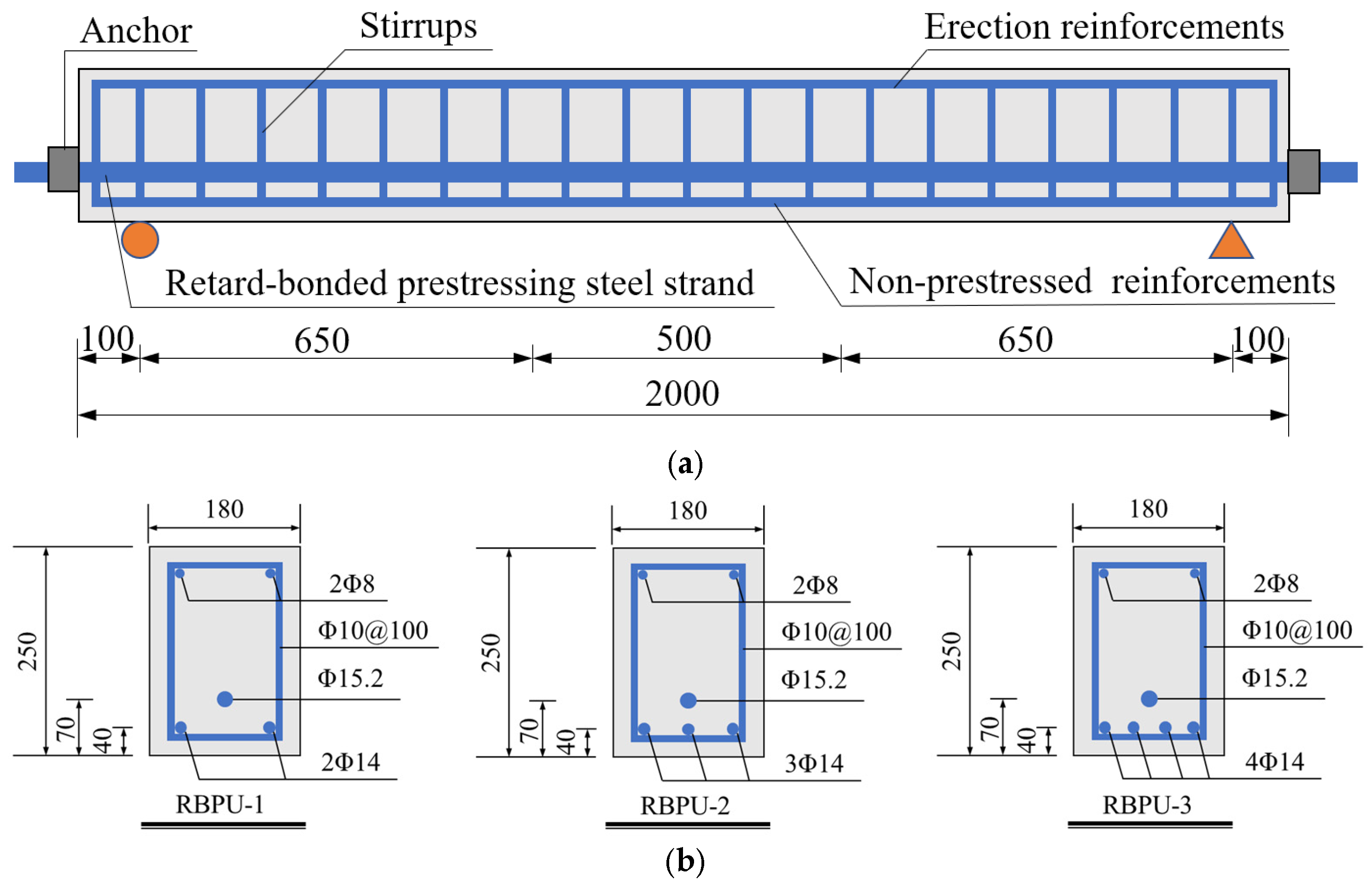

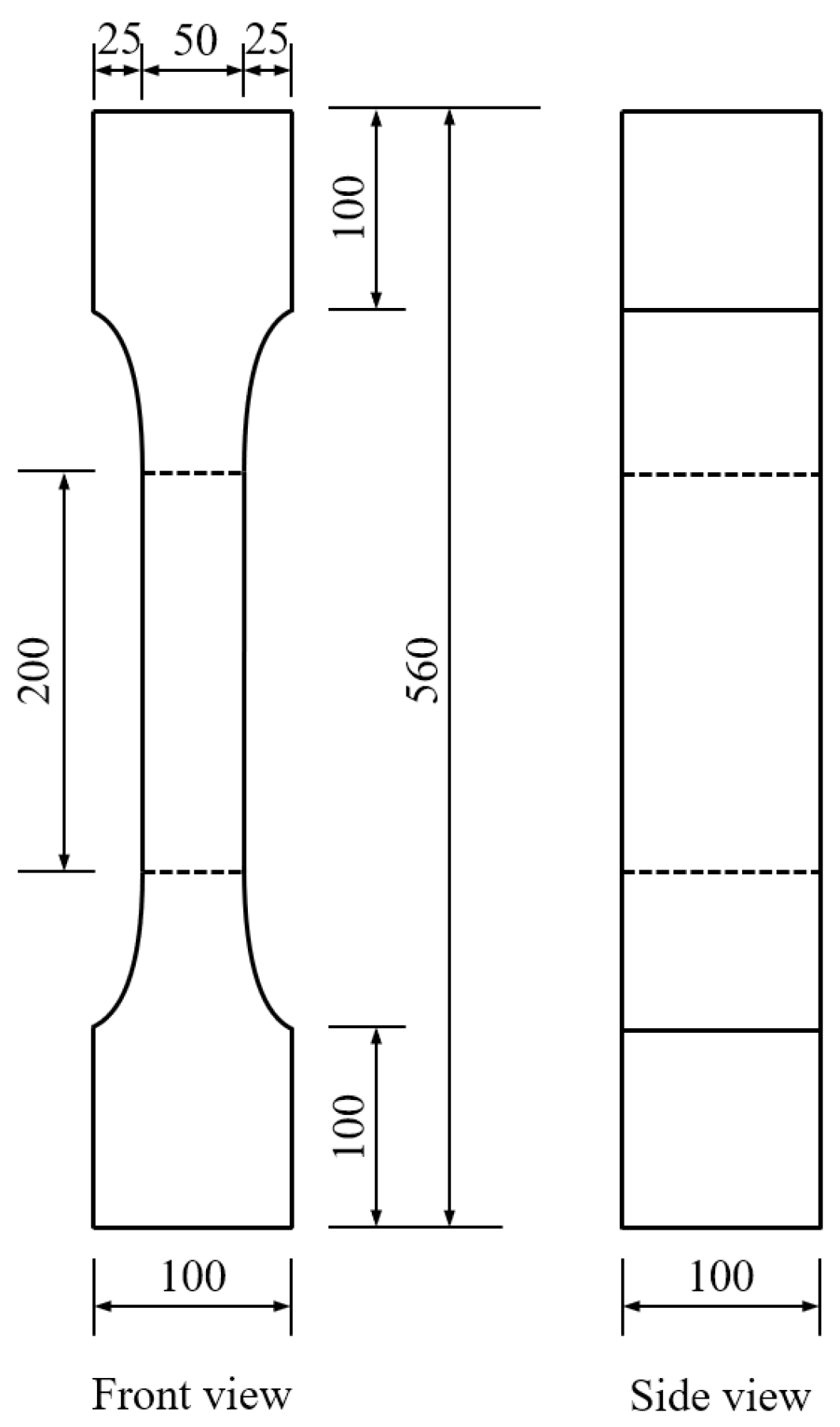
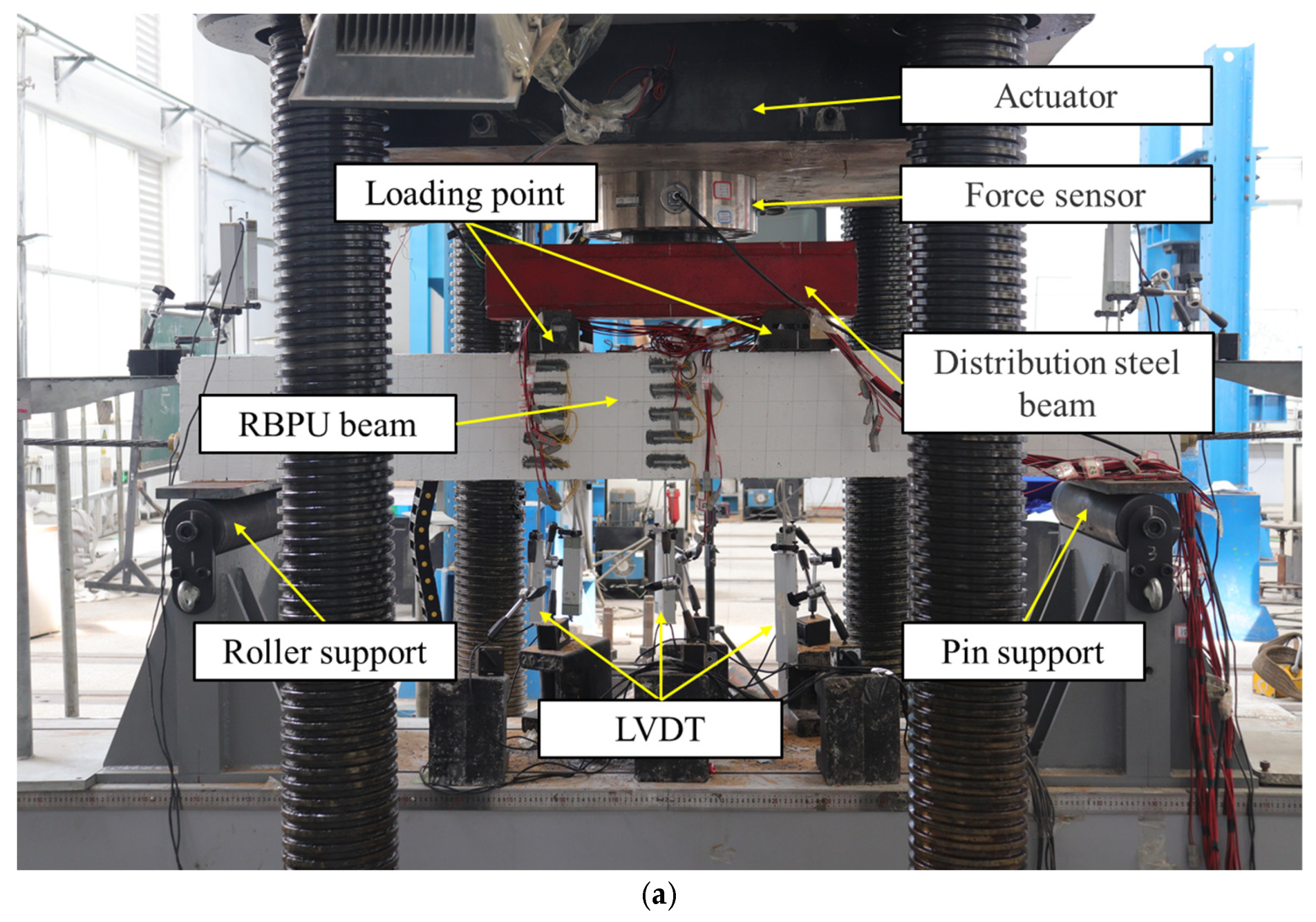
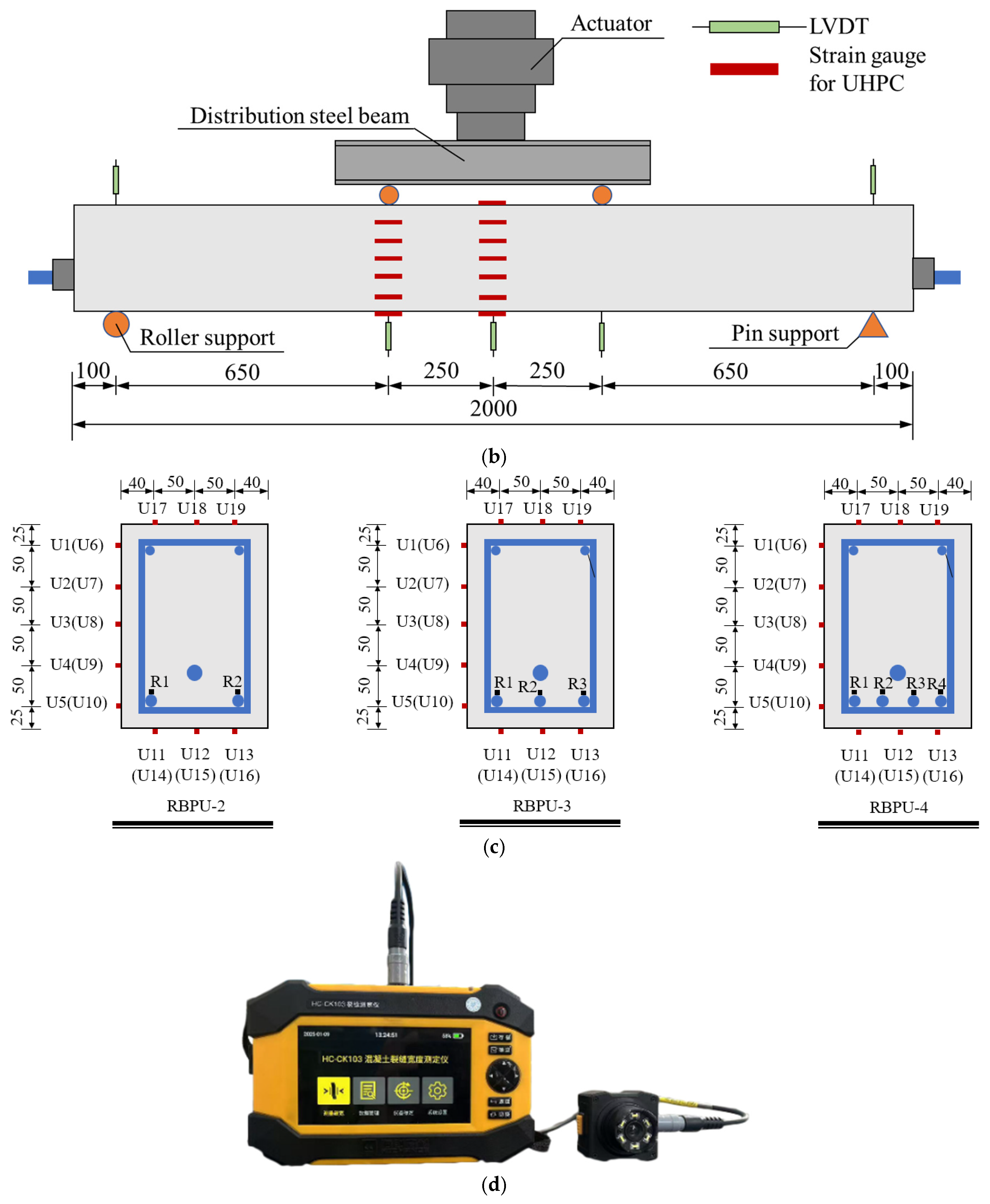



| Specimen | Dimensions (mm) | Non-Prestressed Reinforcements | Stirrups | Number of Steel Strands | Prestressing Level (%) | (MPa) |
|---|---|---|---|---|---|---|
| RBPU-1 | 2000 × 180 × 250 | 2Φ14 | Φ10@100 | 1 | 55 | 1023 |
| RBPU-2 | 3Φ14 | |||||
| RBPU-3 | 4Φ14 |
| Cement | Silica Fume | Grinding Quartz Powder | Silica Sand | Water | Superplasticizer |
|---|---|---|---|---|---|
| 745 | 223.5 | 223.5 | 998.3 | 179.0 | 13.1 |
| fcu (MPa) | fc (MPa) | ft (MPa) | Ec (GPa) |
|---|---|---|---|
| 121.6 | 94.2 | 6.9 | 43.0 |
| Type | Grade | Nominal Diameter | fy (MPa) | fu (MPa) | Ec (GPa) |
|---|---|---|---|---|---|
| Erection reinforcements | HRB400 | 8 | 448.6 | 635.2 | 204.5 |
| Stirrups | HRB400 | 10 | 445.2 | 625.4 | 205.4 |
| Non-prestressed reinforcements | HRB400 | 14 | 490.4 | 668.8 | 205.3 |
| Steel strands | 1860 | 15.2 | 1771.3 | 1970.1 | 196.7 |
| Specimen | Pcr (kN) | δcr (mm) | Py (kN) | δy (mm) | Pp (kN) | δp (mm) | Pu (kN) | δu (mm) | μ |
|---|---|---|---|---|---|---|---|---|---|
| RBPU-1 | 90.0 | 1.22 | 250.6 | 7.6 | 285.6 | 35.68 | 272.1 | 46.45 | 6.1 |
| RBPU-2 | 95.4 | 1.26 | 279.6 | 8.21 | 355.8 | 40.51 | 336.7 | 59.01 | 7.2 |
| RBPU-3 | 100.1 | 1.42 | 371.2 | 8.65 | 437.1 | 50.49 | 411.8 | 73.56 | 8.5 |
| Specimens | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| RBPU-1 | 491.75 | 6.14 | 497.89 | 6.39 | 53.10 | 59.49 | 557.37 | 465.63 | 2.01 |
| RBPU-2 | 491.75 | 6.14 | 497.89 | 6.39 | 50.72 | 57.11 | 555.00 | 468.00 | 1.87 |
| RBPU-3 | 491.75 | 6.14 | 497.89 | 6.39 | 48.53 | 54.92 | 552.80 | 470.20 | 1.71 |
| Specimen | (kN · m) | (MPa) | ft (MPa) | αcr |
|---|---|---|---|---|
| SB80-2 [22] | 57.72 | 3.69 | 4.3 | 1.067 |
| SB90-2 [22] | 58.15 | 4.28 | 4.3 | 0.999 |
| SB95-2 [22] | 63.68 | 4.58 | 4.3 | 0.890 |
| SB90-3 [22] | 81.03 | 6.4 | 4.3 | 1.062 |
| RBPU-1 | 40.51 | 2.01 | 6.9 | 1.198 |
| RBPU-2 | 42.95 | 1.87 | 6.9 | 1.258 |
| RBPU-3 | 45.04 | 1.71 | 6.9 | 1.306 |
| Average value | - | - | - | 1.131 |
| Coefficient of variation | - | - | - | 0.131 |
| Specimen | (kN · m) | (kN · m) | (kN · m) | (kN · m) | ||
|---|---|---|---|---|---|---|
| RBPU-1 | 38.56 | 40.51 | 1.066 | 99.16 | 92.82 | 0.936 |
| RBPU-2 | 39.13 | 42.95 | 1.114 | 112.20 | 115.64 | 1.031 |
| RBPU-3 | 39.65 | 45.04 | 1.153 | 125.02 | 142.06 | 1.136 |
| Average value | - | - | 1.111 | - | - | 1.034 |
| Coefficient of variation | - | - | 0.039 | - | - | 0.097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Wu, D.; Wang, J.; Wang, S.; Zhao, B.; Tang, X. Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios. Buildings 2025, 15, 887. https://doi.org/10.3390/buildings15060887
Du L, Wu D, Wang J, Wang S, Zhao B, Tang X. Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios. Buildings. 2025; 15(6):887. https://doi.org/10.3390/buildings15060887
Chicago/Turabian StyleDu, Lingfeng, Dongchang Wu, Jun Wang, Shaowei Wang, Boyi Zhao, and Xiufeng Tang. 2025. "Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios" Buildings 15, no. 6: 887. https://doi.org/10.3390/buildings15060887
APA StyleDu, L., Wu, D., Wang, J., Wang, S., Zhao, B., & Tang, X. (2025). Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios. Buildings, 15(6), 887. https://doi.org/10.3390/buildings15060887





