A Novel Vulnerability Evaluation Model of a Public Service Building Based on Structural Equation Modeling and Matter-Element Extension
Abstract
:1. Introduction
2. Materials and Methods
2.1. Establishment of Vulnerability Assessment Index System
- (1)
- Lifecycle Coverage: Dimensions were chosen to address vulnerabilities across the entire project lifecycle (design, construction, and operation). For instance, the technical system ensures robustness during construction, while the funding system addresses operational stability.
- (2)
- Literature Validation: Key dimensions were derived from prior studies on PSB risks. For example, the contract system importance aligns with Yuan et al. [4], who emphasized contractual clarity in PPP projects.
- (3)
- Expert Consensus: A Delphi survey with 20 PSB experts validated the relevance of dimensions. For example, the organizational management system was prioritized due to its role in mitigating coordination failures.
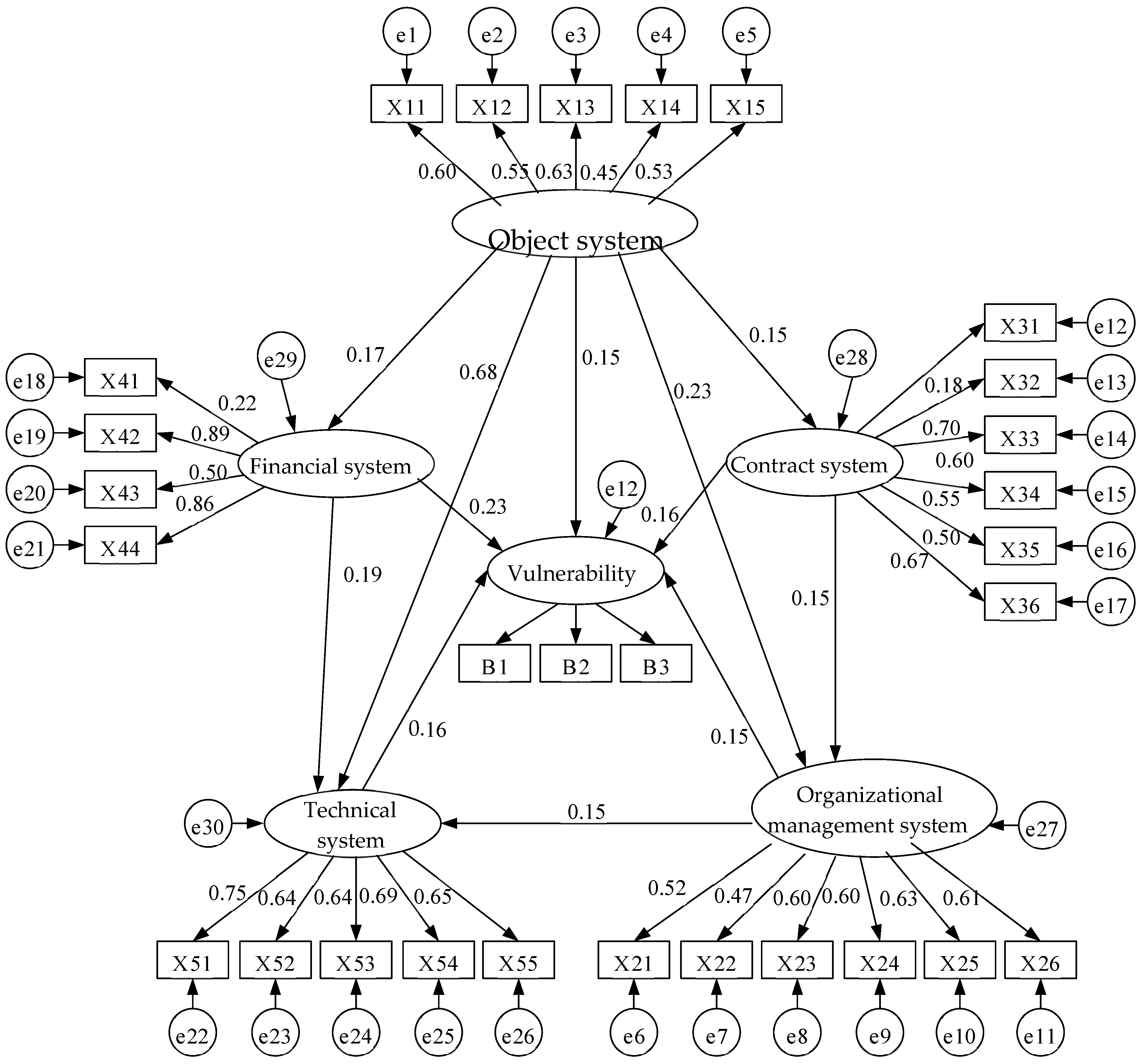
2.2. Vulnerability Analysis of PSBs Using SEM
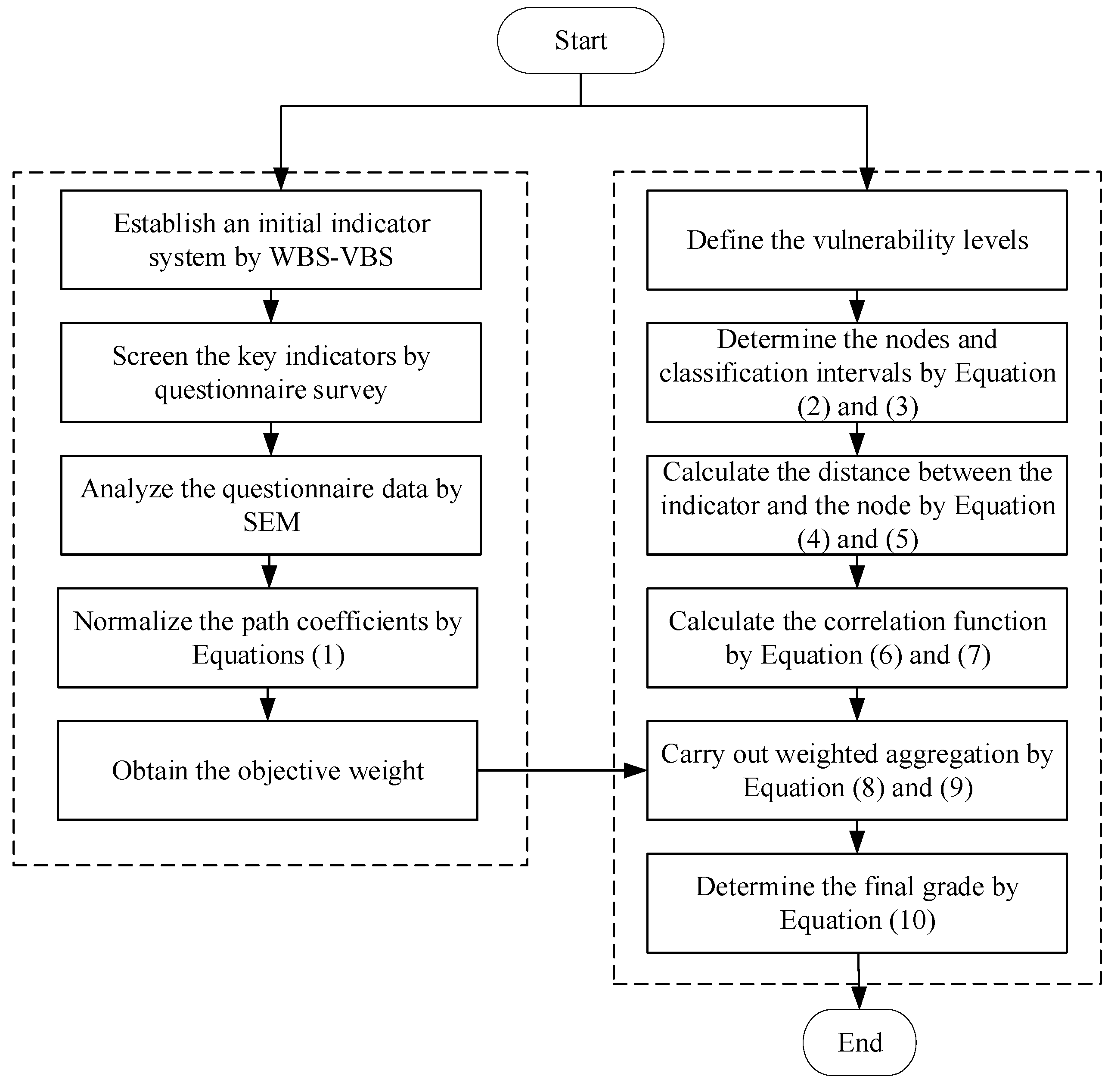
2.3. Vulnerability Evaluation Model for PSBs Based on MEE
- (1)
- Find the distance between the score and the nodal region [33]:
- (2)
- Find the distance between the score and the classes [33]:
- (3)
- The correlation function is defined as follows [33]:
- (1)
- Calculating the vulnerability levels of the indicators
- (2)
- Determine the evaluation level
2.4. Implementation of the Proposed Framework
3. Case Study
3.1. Project Overview and Data Collection
3.2. Calculating the Indicator Weights Based on the Path Coefficient
3.3. Vulnerability Assessment by the MEE
4. Discussion
4.1. Discussion of Weight Calculation Results
4.2. Discussion on the Results of Vulnerability Assessment
Analysis of Calculation Results of Vulnerability Evaluation
5. Conclusions
- (1)
- This paper established a WBS-VBS framework for a PSB and conducted a case study of the Qianjiang Vocational Education Center relocation. A questionnaire survey was used to obtain data for creating a vulnerability evaluation index system. SEM was used to perform a quantitative analysis of the factors influencing vulnerability. Objective weights were obtained by normalizing the path coefficients between variables.
- (2)
- The MEE method was used to determine the vulnerability levels of the PSBs. Correlation functions were established to determine the classes and nodes and derive the projects’ vulnerability level.
- (3)
- The case study results indicated a vulnerability level of III (low vulnerability), which was consistent with the project’s actual operational conditions. This finding underscores the necessity for adaptive management strategies tailored to systemic interdependencies identified in the model.
- (1)
- This manuscript analyzes the vulnerability of public service buildings by taking an educational public service building as an example. However, different types of public service buildings may have different limitations. In the future, more case studies are required to verify the research findings of this paper and promote more efficient public service provisions by various public service buildings globally.
- (2)
- Vulnerability is an inherent attribute of the public service building system. The failure of public service buildings is caused by the combined effect of external risk factors and their own vulnerability. In the future, the interaction mechanism between external risk factors and self-vulnerability can be analyzed in more detail to summarize more management strategies worthy of engineering guidance for the public service building system.
- (3)
- Future research should generalize this framework to diverse PSB types and integrate machine learning to automate data-driven vulnerability updates. Beyond academia, this approach can guide policymakers in formulating standardized risk assessment protocols for public infrastructure, ensuring long-term service continuity. Additionally, the model’s adaptability to different cultural and economic contexts could enhance global resilience in public service delivery.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, T.; Song, R.; Jin, C.Z. Risk Identification and Analysis of National Wetland Park Public-private Partnership Project Based on Grey Correlation Model. J. Ecol. Rural Environ. 2023, 39, 429–435. [Google Scholar]
- Erdem, T.D.; Birgonul, Z.; Bilgin, G.; Akcay, E.C. Exploring the Critical Risk Factors of Public–Private Partnership City Hospital Projects in Turkey. Buildings 2024, 14, 498. [Google Scholar] [CrossRef]
- Zhao, H.; Yu, G.; Cheng, X. Risk management of hydrogenation station PPP project based on 3D framework-A case study in China. PLoS ONE 2023, 18, e0293348. [Google Scholar] [CrossRef]
- Yuan, J.F.; Li, X.; Chen, K.W.; Skibniewski, M.J. Modelling residual value risk through ontology to address vulnerability of PPP project system. Adv. Eng. Inform. 2018, 38, 776–793. [Google Scholar] [CrossRef]
- Kim, Y.-J. Public–private Partnerships for Urban Projects: A Korean Case of Partnership Failure. Int. J. Public Adm. 2022, 45, 499–510. [Google Scholar] [CrossRef]
- Mhamed, B.; Omar, A. When the institutional context thwarts public-private partnerships: The role of political factors in the failure of PPPs. J. Infrastruct. Policy Dev. 2023, 7, 1937. [Google Scholar] [CrossRef]
- Urbina, O.; Sousa, H.S.; Fekete, A.; Matos, J.C.; Teixeira, E. Spatial Vulnerability Assessment of Critical Infrastructure Based on Fire Risk through GIS Systems—Case Study: Historic City Center of Guimarães, Portugal. Appl. Sci. 2023, 13, 8881. [Google Scholar] [CrossRef]
- M’Cleod, L.; Vecsler, R.; Shi, Y.; Levitskaya, E.; Kulkarni, S.; Malinchik, S.; Sobolevsky, S. Vulnerability of Transportation Networks: The New York City Subway System under Simultaneous Disruptive Events. In Proceedings of the 6th Annual International Young Scientists Conference on HPC and Computational Science (YSC), Kotka, Finland, 1–3 November 2017; pp. 42–50. [Google Scholar]
- Yang, X.; Liu, S.; Jia, C.; Liu, Y.; Yu, C. Vulnerability assessment and management planning for the ecological environment in urban wetlands. J. Environ. Manag. 2021, 298, 113540. [Google Scholar] [CrossRef]
- Nam, W.-H.; Choi, J.-Y.; Hong, E.-M. Irrigation vulnerability assessment on agricultural water supply risk for adaptive management of climate change in South Korea. Agric. Water Manag. 2015, 152, 173–187. [Google Scholar] [CrossRef]
- Borzì, I. Vulnerability assessment of water supply infrastructures through multiple indicator methodology. J. Water Clim. Change 2023, 14, 3967–3984. [Google Scholar] [CrossRef]
- David, E.-E.R.; Mauricio, L.-B.; Gerardo, M.; Carlos, O.-G.J. Selection of software agile practices using Analytic hierarchy process. Heliyon. 2024, 10, e22948. [Google Scholar]
- Na, S.; Cailin, L.; Baoyun, G.; Xiaokai, S.; Yukai, Y.; Yue, W. Urban flooding risk assessment based on FAHP–EWM combination weighting: A case study of Beijing. Geomat. Nat. Hazards Risk 2023, 14, 2240943. [Google Scholar]
- Zhong, J.; Li, Z.; Zhang, D.; Yang, J.; Zhu, J. An evaluation framework for urban ecological compensation priority in China based on meta-analysis and fuzzy comprehensive evaluation. Ecol. Indic. 2024, 158, 111284. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Cavallaro, F.; Hezam, I.M.; Lakshmi, J. An Integrated Intuitionistic Fuzzy Closeness Coefficient-Based OCRA Method for Sustainable Urban Transportation Options Selection. Axioms 2023, 12, 144. [Google Scholar] [CrossRef]
- Brotcorne, L.; Guajardo, M.; Ribeiro, C.C.; Speranza, M.G. Tutorials and Reviews in Operations Research. Int. Trans. Oper. Res. 2023, 30, 2707–2708. [Google Scholar] [CrossRef]
- Wang, J. Construction of Risk Evaluation Index System for Power Grid Engineering Cost by Applying WBS-RBS and Membership Degree Methods. Math. Probl. Eng. 2020, 2020, 6217872. [Google Scholar] [CrossRef]
- Afieroho, U.E.; Li, Y.K.; Han, Y.L.; Soomro, M.A.; Radujkovic, M. Transformational Community Engagement in Urban Infrastructure Public-Private Partnerships: A Governmentality Approach to Create Social Value. Buildings 2023, 13, 1225. [Google Scholar] [CrossRef]
- Bogovac, J.; Lugaric, T.R.; Dodig, D. Public-private partnership in Croatia—Students’ attitudes. Ekon. Misao Praksa-Econ. Thought Pract. 2021, 30, 121–144. [Google Scholar] [CrossRef]
- Cruz, C.O.; Marques, R.C. Revisiting the Portuguese experience with public-private partnerships. Afr. J. Bus. Manag. 2011, 5, 4023–4032. [Google Scholar]
- Ghasemi, M.; Amini-Rarani, M.; Zadeh, N.S.; Karimi, S. Role of Public-Private Partnerships in Primary Healthcare Services Worldwide: A Scoping Review. Health Scope 2022, 11, e129176. [Google Scholar] [CrossRef]
- Hadiuzzaman, M.; Farazi, N.P.; Hossain, S.; Barua, S.; Rahman, F. Structural equation approach to investigate trip-chaining and mode choice relationships in the context of developing countries. Transp. Plan. Technol. 2019, 42, 391–415. [Google Scholar] [CrossRef]
- Gim, T.-H.T. SEM application to the household travel survey on weekends versus weekdays: The case of Seoul, South Korea. Eur. Transp. Res. Rev. 2018, 10, 11. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, X.; Zhou, Y.; Xue, Q. Influencing Mechanism of Potential Factors on Passengers’ Long-Distance Travel Mode Choices Based on Structural Equation Modeling. Sustainability 2017, 9, 1943. [Google Scholar] [CrossRef]
- Hodge, G.A.; Greve, C. On Public-Private Partnership Performance: A Contemporary Review. Public Work Manag. Policy 2017, 22, 55–78. [Google Scholar] [CrossRef]
- Klunko, N.S.; Lobanova, A.E. Interaction System of the State and Business in the Regime of Public-Private Partnership in the Pharmaceutical Complex of the Russian Federation. J. Pharm. Res. Int. 2021, 33, 16–22. [Google Scholar] [CrossRef]
- Krumm, T.; Mause, K. Public-private partnerships as object of political sciences. Polit. Vierteljahresschr. 2009, 50, 105–129. [Google Scholar] [CrossRef]
- Tariq, S.; Zhang, X.Q.; Leung, R.H.M. An analytical review of failed water public-private partnerships in developing countries. Proc. Inst. Civ. Eng.-Manag. Procure. Law 2019, 172, 60–69. [Google Scholar] [CrossRef]
- Wang, H.M.; Xiong, W.; Wu, G.D.; Zhu, D.J. Public-private partnership in Public Administration discipline: A literature review. Public Manag. Rev. 2018, 20, 293–316. [Google Scholar] [CrossRef]
- Zuvela, A.; Dragija, M.S.; Jelincic, D.A. Partnerships in Heritage Governance and Management: Review Study of Public-Civil, Public-Private and Public-Private-Community Partnerships. Heritage 2023, 6, 6862–6880. [Google Scholar] [CrossRef]
- Wu, H.; Wang, J. Assessment of Waterlogging Risk in the Deep Foundation Pit Projects Based on Projection Pursuit Model. Adv. Civ. Eng. 2020, 2020, 2569531. [Google Scholar] [CrossRef]
- Xiao, Q.; He, R.; Ma, C.; Zhang, W. Evaluation of urban taxi-carpooling matching schemes based on entropy weight fuzzy matter-element. Appl. Soft Comput. 2019, 81, 105493. [Google Scholar] [CrossRef]
- Tang, J.; Wang, C. Comprehensive Evaluation of Safety Risk of Air Traffic Management System Based on Matter Element Model: Take the Air Traffic Management Unit of a Coastal City in China as an Example. J. Coast. Res. 2020, 104, 328–332. [Google Scholar] [CrossRef]
- Liu, S.F.; Yang, Y.J.; Xie, N.M.; Forrest, J. New progress of Grey System Theory in the new millennium. Grey Syst.-Theory Appl. 2016, 6, 2–31. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]

| Primary Indices | Secondary Indices | References |
|---|---|---|
| Object system: | Rationality of project scale: | [1,2] |
| Total investment ratio of the government: | [1,2,3] | |
| Features of public services: | [1,4] | |
| The substitutability of the project: | [1,5,6] | |
| Availability of land for the project: | [2,6] | |
| Organization management system: | Rationality of organizational structure: | [1,3,4] |
| Rationality of management decisions: | [18] | |
| Stakeholder partnership: | [3,4,5,6] | |
| Information sharing degree: | [5,6] | |
| Degree of risk sharing: | [1,3,4] | |
| Experience of stakeholders in developing PSBs projects: | [1,2,3,4] | |
| Contract system: | Completeness of construction contract: | [4,6] |
| Completeness of operation contract: | [1,6] | |
| Performance bond ratio: | [3,5,6] | |
| Rationality of equity change restrictions: | [1,2,5] | |
| Rationality of early termination compensation: | [19] | |
| Rationality of distribution of rights and obligations: | [2,6] | |
| Funding system: | Capital cost rate: | [5,6] |
| Applicability of financing model: | [1,3,4] | |
| Applicability of payment mechanism: | [20] | |
| Capital risk level: | [4,5,6] | |
| Technical system: | Technical and economic rationality of the scheme: | [21] |
| Accuracy of bill of quantities: | [1,2,3,4] | |
| Quality of preliminary work: | [1,4,6] | |
| Rationality of construction organization design: | [1,3,4] | |
| Operation and maintenance complexity: | [2,4,5,6] |
| Absolute Fitting INDEX | Incremental Fitting Index | Reduced Fitting Index | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CMIN/DF | RMR | RMSEA | GFI | NFI | TLI | CFI | PGFI | PNFI | PCFI |
| <2 | <0.05 | <0.05 | >0.90 | >0.90 | >0.90 | >0.90 | >0.50 | >0.50 | >0.50 |
| 1.109 | 0.024 | 0.022 | 0.923 | 0.913 | 0.988 | 0.990 | 0.725 | 0.778 | 0.853 |
| Passed | Passed | Passed | Passed | Passed | Passed | Passed | Passed | Passed | Passed |
| Factors Affecting Vulnerability | Utility Value | Factors Affecting Vulnerability | Utility Value |
|---|---|---|---|
| 0.60 | 0.60 | ||
| 0.55 | 0.55 | ||
| 0.63 | 0.50 | ||
| 0.45 | 0.67 | ||
| 0.53 | 0.22 | ||
| 0.52 | 0.69 | ||
| 0.47 | 0.50 | ||
| 0.60 | 0.86 | ||
| 0.60 | 0.75 | ||
| 0.63 | 0.64 | ||
| 0.61 | 0.64 | ||
| 0.18 | 0.69 | ||
| 0.70 | 0.65 |
| Path | Direct Influence | Indirect Influence | Comprehensive Influence | Rank |
|---|---|---|---|---|
| Object system Vulnerability | 0.149 | 0.244 | 0.393 | 1 |
| Organizational management system Vulnerability | 0.145 | 0.029 | 0.174 | 4 |
| Contract system Vulnerability | 0.163 | 0.026 | 0.189 | 3 |
| Financial system Vulnerability | 0.226 | 0.03 | 0.256 | 2 |
| Technical system Vulnerability | 0.156 | 0 | 0.156 | 5 |
| Vulnerability Classification | Definition | Value Range |
|---|---|---|
| Ⅰ | The vulnerability is high and unacceptable. | |
| Ⅱ | The vulnerability is moderate and must be improved. | |
| Ⅲ | The vulnerability is low and acceptable. | |
| Ⅳ | The vulnerability is extremely low and acceptable. |
| Index | Calculation Method |
|---|---|
| Obtain the project management data, consisting of 8 million data points, accounting for 10% of the project capital. | |
| Shared information/total information = 341 files/731 files = 0.466. | |
| Th performance bond ratio during the operation period is 3%. | |
| The fund occupation fee/net fund raising is 6.49%. | |
| Correct bill of quantities/all bills of quantities = 13,596.55 (ten thousand yuan)/17,596.55 (ten thousand yuan) = 0.7727. | |
| Actual operation and maintenance costs/planned operation and maintenance costs = 3451.42 (ten thousand yuan/year)/25,502,800 yuan/year = 1.353. |
| Indicator | I | II | III | IV |
|---|---|---|---|---|
| Secondary Indicators | Scores | Secondary Indicators | Scores |
| 91.25 | 3% | ||
| 10% | 71.05 | ||
| 84.30 | 67.35 | ||
| 87.55 | 92.85 | ||
| 84.95 | 6.49% | ||
| 78.30 | 88.60 | ||
| 73.75 | 81.70 | ||
| 80.75 | 79.25 | ||
| 0.466 | 85.55 | ||
| 72.35 | 0.7727 | ||
| 83.60 | 74.90 | ||
| 90.10 | 84.75 | ||
| 78.45 | 1.353 |
| Primary Indicators | Comprehensive Influence | Comprehensive Weight |
|---|---|---|
| 0.393 | 0.336 | |
| 0.174 | 0.149 | |
| 0.189 | 0.162 | |
| 0.256 | 0.219 | |
| 0.156 | 0.134 |
| Indicators | Weight | Comprehensive Weight | Rank | Indicators | Weight | Comprehensive Weight | Rank |
|---|---|---|---|---|---|---|---|
| 0.217 | 0.0729 | 3 | 0.188 | 0.0305 | 11 | ||
| 0.199 | 0.0669 | 4 | 0.172 | 0.0279 | 13 | ||
| 0.228 | 0.0766 | 2 | 0.156 | 0.0253 | 22 | ||
| 0.163 | 0.0548 | 7 | 0.209 | 0.0339 | 10 | ||
| 0.192 | 0.0645 | 6 | 0.097 | 0.0212 | 24 | ||
| 0.152 | 0.0226 | 23 | 0.304 | 0.0666 | 5 | ||
| 0.137 | 0.0204 | 25 | 0.220 | 0.0482 | 8 | ||
| 0.175 | 0.0261 | 17 | 0.379 | 0.0830 | 1 | ||
| 0.175 | 0.0261 | 18 | 0.223 | 0.0299 | 12 | ||
| 0.184 | 0.0274 | 15 | 0.190 | 0.0255 | 20 | ||
| 0.178 | 0.0265 | 16 | 0.190 | 0.0255 | 21 | ||
| 0.056 | 0.0091 | 26 | 0.205 | 0.0275 | 14 | ||
| 0.219 | 0.0355 | 9 | 0.193 | 0.0259 | 19 |
| Indicator | Nodes | Class Ⅰ | Class Ⅱ | Class Ⅲ | Class Ⅳ |
|---|---|---|---|---|---|
| 16.25 | −16.25 | 43.75 | 58.75 | 73.75 | |
| 24.90 | 23.90 | 24.70 | 24.80 | 24.85 | |
| 9.30 | −9.30 | 50.70 | 65.70 | 80.70 | |
| 12.55 | −12.55 | 47.45 | 62.45 | 77.45 | |
| 9.95 | −9.95 | 50.05 | 65.05 | 80.05 | |
| 3.30 | −3.30 | 56.70 | 71.70 | 86.70 | |
| −1.25 | 1.25 | 61.25 | 76.25 | 91.25 | |
| 5.75 | −5.75 | 54.25 | 69.25 | 84.25 | |
| 24.53 | 23.53 | 23.78 | 24.03 | 24.28 | |
| −2.65 | 2.65 | 62.65 | 77.65 | 92.65 | |
| 8.60 | −8.60 | 51.40 | 66.40 | 81.40 | |
| 15.10 | −15.10 | 44.90 | 59.90 | 74.90 | |
| 3.45 | −3.45 | 56.55 | 71.55 | 86.55 | |
| 24.97 | 24.87 | 24.94 | 24.95 | 24.96 | |
| −3.95 | 3.95 | 63.95 | 78.95 | 93.95 | |
| −7.65 | 7.65 | 67.65 | 82.65 | 97.65 | |
| 17.85 | −17.85 | 42.15 | 57.15 | 72.15 | |
| 24.94 | 23.94 | 24.74 | 24.84 | 24.89 | |
| 13.60 | −13.60 | 46.40 | 61.40 | 76.40 | |
| 6.70 | −6.70 | 53.30 | 68.30 | 83.30 | |
| 4.25 | −4.25 | 55.75 | 70.75 | 85.75 | |
| 10.55 | −10.55 | 49.45 | 64.45 | 79.45 | |
| 24.23 | 23.23 | 23.33 | 23.43 | 23.53 | |
| −0.10 | 0.10 | 60.10 | 75.10 | 90.10 | |
| 9.75 | −9.75 | 50.25 | 65.25 | 80.25 | |
| 23.65 | 21.65 | 22.45 | 22.55 | 22.65 |
| System Dimension | Primary Indicators | Correlation Coefficients | Vulnerability Level |
|---|---|---|---|
| [0.217, 0.199, 0.228, 0.163, 0.192] | [−0.656, −0.450, 0.373, −0.159] | Ⅲ | |
| [0.152, 0.137, 0.175, 0.175, 0.184, 0.178] | [−0.484, −0.174, 0.255, −0.321] | Ⅲ | |
| [0.056, 0.219, 0.188, 0.172, 0.156, 0.209] | [−0.480, −0.172, −0.021, −0.139] | Ⅲ | |
| [0.097, 0.304, 0.22, 0.379] | [−0.600, −0.359, 0.233, −0.128] | Ⅲ | |
| [0.223, 0.19, 0.19, 0.205, 0.193] | [−0.591, −0.345, 0.351, −0.237] | Ⅲ |
| Index | Group 1 | Group 2 | Group 3 | Group 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Weight | Sort | Weight | Sort | Weight | Sort | Weight | Sort | |
| 0.0881 | 1 | 0.0954 | 1 | 0.0815 | 3 | 0.0896 | 3 | |
| 0.0578 | 7 | 0.0233 | 22 | 0.0675 | 5 | 0.0681 | 4 | |
| 0.0779 | 2 | 0.0341 | 10 | 0.1582 | 1 | 0.1829 | 1 | |
| 0.0195 | 23 | 0.0244 | 21 | 0.0125 | 18 | 0.0103 | 19 | |
| 0.0208 | 21 | 0.0914 | 2 | 0.0519 | 7 | 0.0505 | 8 | |
| 0.0210 | 20 | 0.0261 | 18 | 0.0411 | 11 | 0.0316 | 12 | |
| 0.0189 | 24 | 0.0200 | 24 | 0.0406 | 12 | 0.0282 | 14 | |
| 0.0254 | 17 | 0.0256 | 20 | 0.1215 | 2 | 0.1077 | 2 | |
| 0.0246 | 18 | 0.0356 | 9 | 0.0134 | 16 | 0.0119 | 18 | |
| 0.0089 | 26 | 0.0322 | 12 | 0.0497 | 8 | 0.0009 | 26 | |
| 0.0200 | 22 | 0.0659 | 5 | 0.0481 | 9 | 0.0135 | 17 | |
| 0.0216 | 19 | 0.0073 | 26 | 0.0166 | 15 | 0.0024 | 25 | |
| 0.0776 | 3 | 0.0256 | 19 | 0.0681 | 4 | 0.0615 | 6 | |
| 0.0664 | 5 | 0.0282 | 16 | 0.0452 | 10 | 0.0309 | 13 | |
| 0.0439 | 8 | 0.0295 | 14 | 0.0554 | 6 | 0.0083 | 22 | |
| 0.0686 | 4 | 0.0228 | 23 | 0.0325 | 13 | 0.0091 | 21 | |
| 0.0331 | 12 | 0.0306 | 13 | 0.0085 | 23 | 0.0028 | 24 | |
| 0.0131 | 25 | 0.0198 | 25 | 0.0118 | 19 | 0.0097 | 20 | |
| 0.0411 | 10 | 0.0532 | 6 | 0.0041 | 25 | 0.0162 | 16 | |
| 0.0414 | 9 | 0.0814 | 3 | 0.0109 | 21 | 0.0035 | 23 | |
| 0.0613 | 6 | 0.0663 | 4 | 0.0182 | 14 | 0.0434 | 10 | |
| 0.0330 | 13 | 0.0357 | 8 | 0.0037 | 26 | 0.0188 | 15 | |
| 0.0255 | 16 | 0.0276 | 17 | 0.0129 | 17 | 0.0656 | 5 | |
| 0.0341 | 11 | 0.0370 | 7 | 0.0086 | 22 | 0.0435 | 9 | |
| 0.0299 | 14 | 0.0323 | 11 | 0.0114 | 20 | 0.0576 | 7 | |
| 0.0265 | 15 | 0.0287 | 15 | 0.0063 | 24 | 0.0318 | 11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Zhang, J.; Wang, X.; Peng, C. A Novel Vulnerability Evaluation Model of a Public Service Building Based on Structural Equation Modeling and Matter-Element Extension. Buildings 2025, 15, 948. https://doi.org/10.3390/buildings15060948
Peng H, Zhang J, Wang X, Peng C. A Novel Vulnerability Evaluation Model of a Public Service Building Based on Structural Equation Modeling and Matter-Element Extension. Buildings. 2025; 15(6):948. https://doi.org/10.3390/buildings15060948
Chicago/Turabian StylePeng, Hao, Jin Zhang, Xinyu Wang, and Chenyang Peng. 2025. "A Novel Vulnerability Evaluation Model of a Public Service Building Based on Structural Equation Modeling and Matter-Element Extension" Buildings 15, no. 6: 948. https://doi.org/10.3390/buildings15060948
APA StylePeng, H., Zhang, J., Wang, X., & Peng, C. (2025). A Novel Vulnerability Evaluation Model of a Public Service Building Based on Structural Equation Modeling and Matter-Element Extension. Buildings, 15(6), 948. https://doi.org/10.3390/buildings15060948






