A Load Estimation Method Based on Surface Crack Distribution Images of Reinforced Concrete Beams
Abstract
1. Introduction
2. Methodology
2.1. Basic Framework
2.2. Image Segmentation
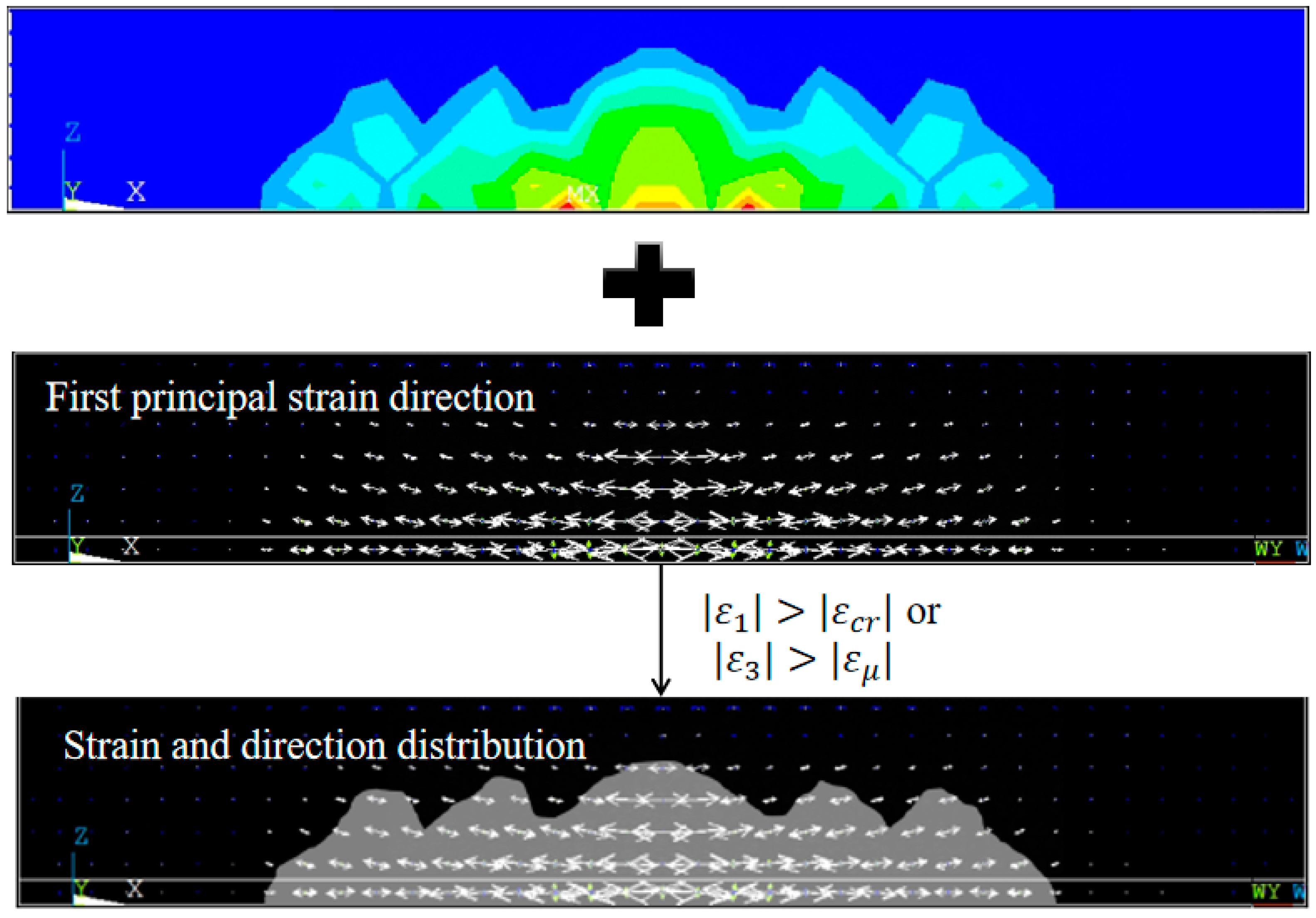
2.3. Load Evaluation Model Based on Crack Image
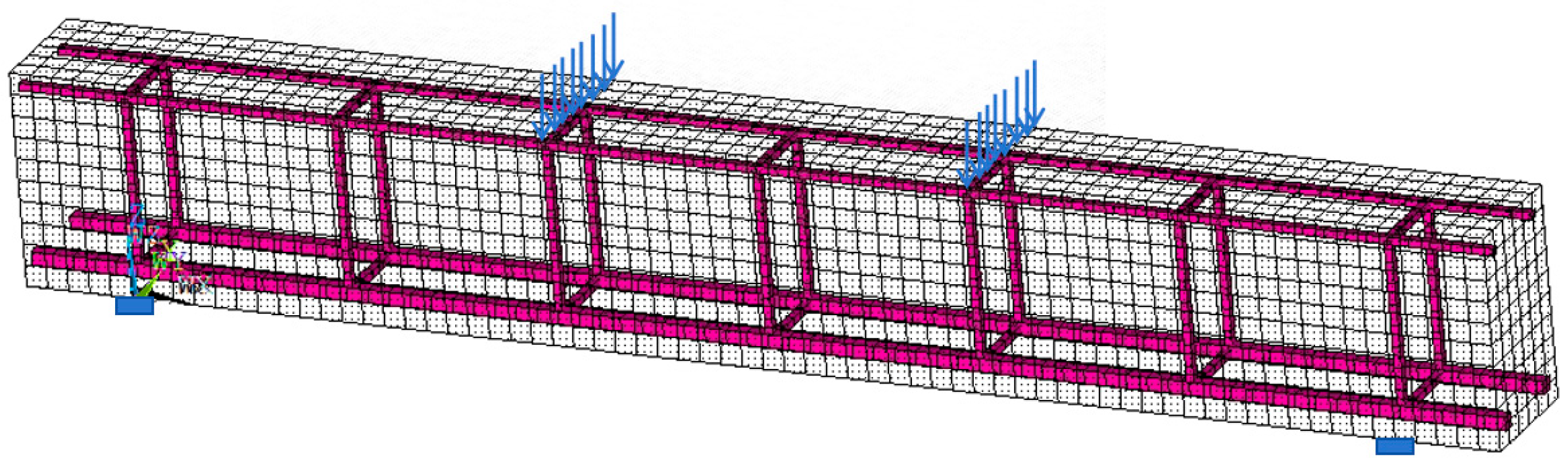
2.3.1. Finite Element-Based Structural Strain Distribution Calculation
2.3.2. Image-Based Correlation Evaluation Model
3. Experiment and Analysis
3.1. Data Sources
3.2. Load Identification Results
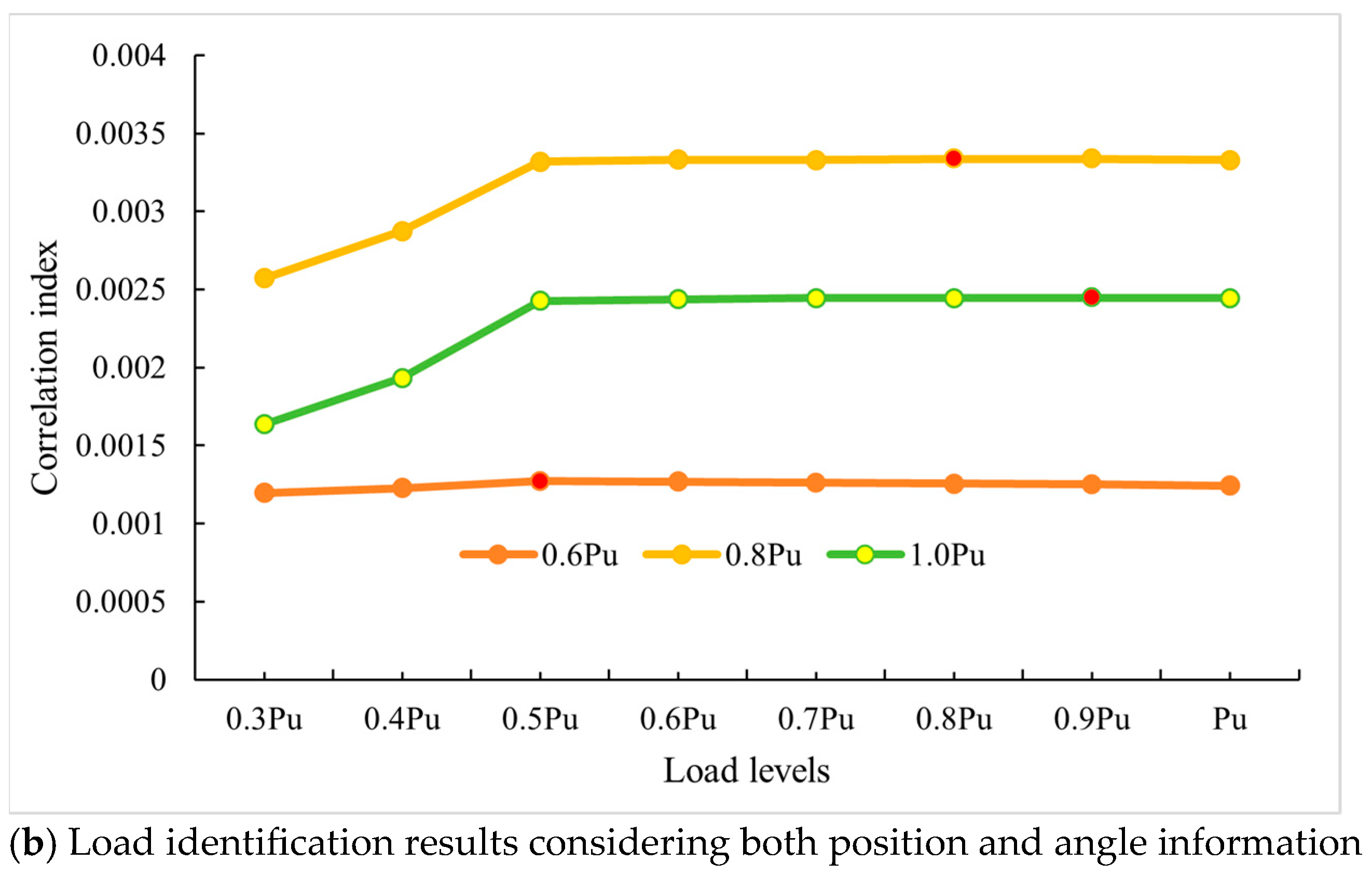
3.2.1. Analysis of the Impact of Positional and Angular Information on Load Identification Results
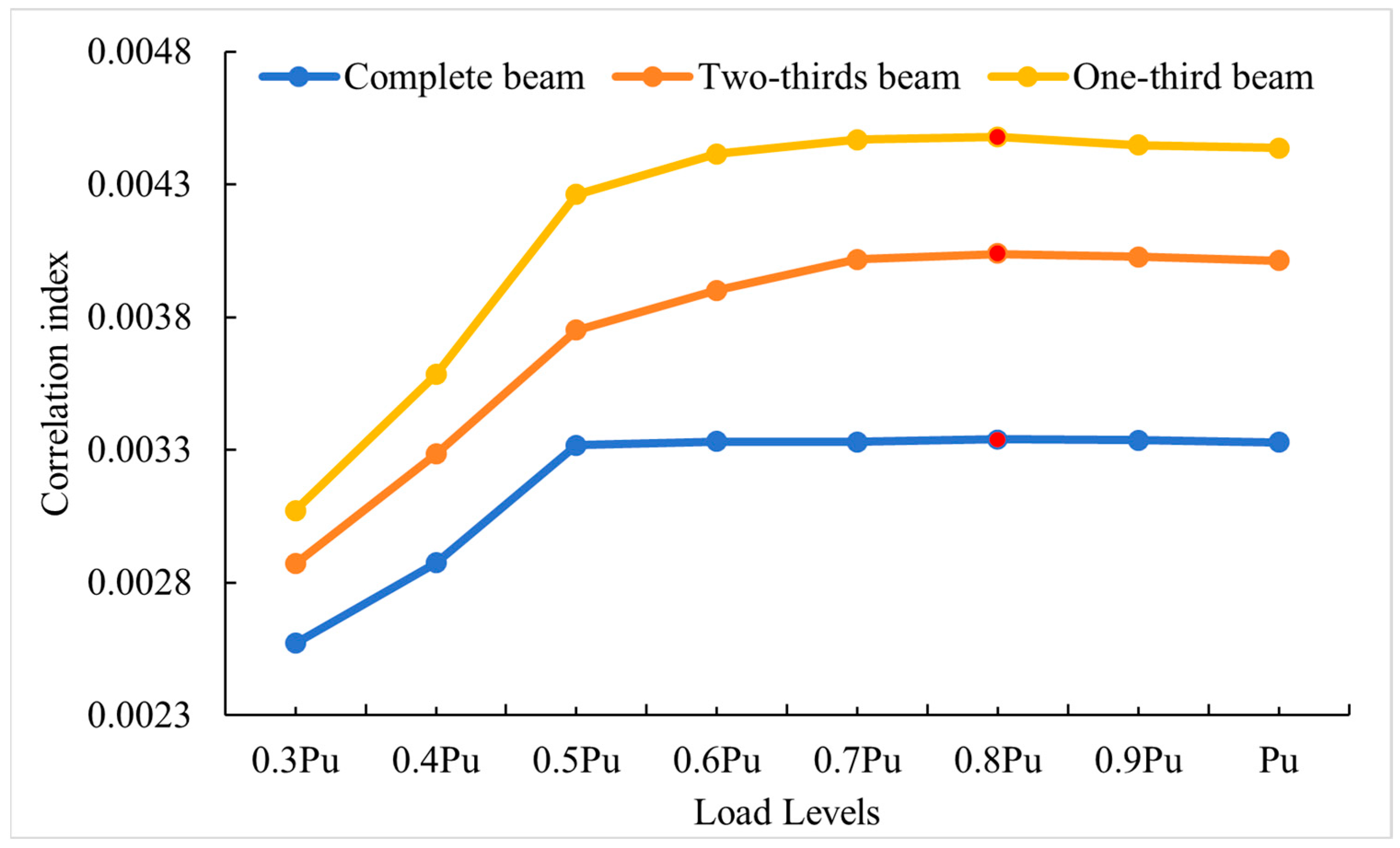
3.2.2. Analysis of the Impact of Incomplete Information on Load Identification Results
3.2.3. Load Identification Analysis of Crack Image Sample Set
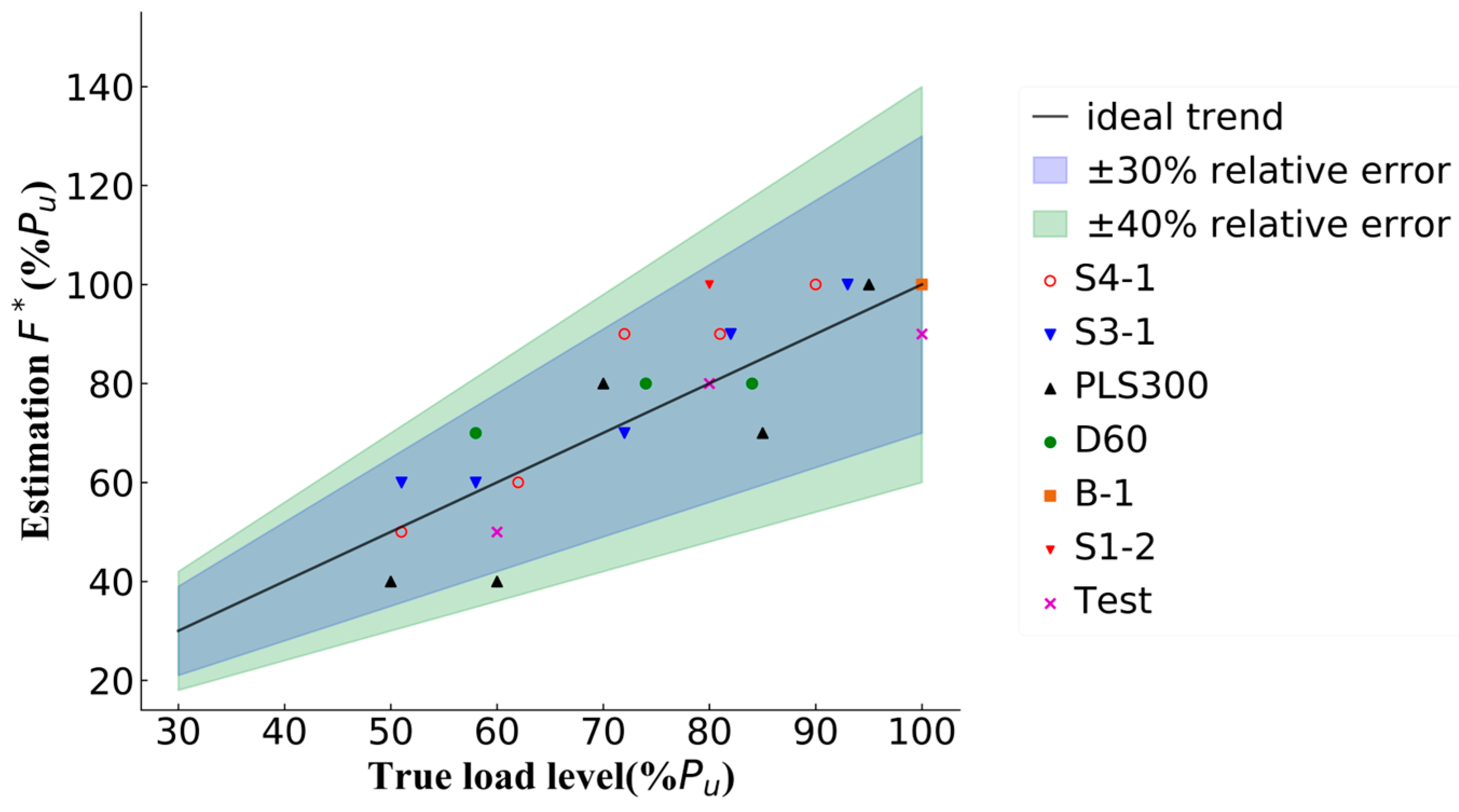
3.3. Structural Damage Estimation
4. Conclusions
- Load evaluation and damage analysis based on surface crack images can achieve non-destructive, real-time, and efficient monitoring. By utilizing automated image processing techniques, manual intervention is reduced, improving detection accuracy and safety.
- By comparing the location and angle information between the crack images and the finite element stress–strain field, a correlation model between the two is established. The load level corresponding to the maximum correlation coefficient is selected as the final identified load. The average error of load identification is only 10.98%, achieving the goal of rapid and quantitative load assessment.
- The load obtained from the crack image provides sufficient prior conditions for assessing the structural damage state. Therefore, the structural damage state is evaluated using structural damage factors.
- The load and damage identification method proposed in this paper exhibits strong generality and is not dependent on specific structural forms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. In Proceedings of the Computer Science—Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Liu, D.; Cui, Y.; Tan, W.; Chen, Y. SG-Net: Spatial granularity network for one-stage video instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9816–9825. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Davoudi, R.; Miller, G.R.; Kutz, J.N. Structural load estimation using machine vision and surface crack patterns for shear-critical RC beams and slabs. J. Comput. Civ. Eng. 2018, 32, 04018024. [Google Scholar] [CrossRef]
- Zhang, W.-X.; Liu, X.-L.; Luo, B.; Li, M.-G. Quick assessment of loading capacity of bridge by cracking characteristics. J. Northeast. Univ. (Nat. Sci.) 2008, 29, 1346. [Google Scholar]
- Li, K.; Cao, G.; Yang, L. Experimental study on assessment of mechanical performance of prestressed concrete continuous box girder under different cracking conditions. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 3475–3483. [Google Scholar]
- Xu, G.; Yue, Q.; Liu, X. Identification of historical maximum load on concrete beams based on crack and deformation response using knowledge-embedded machine learning algorithms. Eng. Struct. 2024, 314, 118376. [Google Scholar] [CrossRef]
- Davoudi, R. A Machine Learning and Computer Vision Framework for Damage Characterization and Structural Behavior Prediction. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2019. [Google Scholar]
- Davoudi, R.; Miller, G.R.; Calvi, P.; Kutz, J.N. Computer vision–based damage and stress state estimation for reinforced concrete and steel fiber–reinforced concrete panels. Struct. Health Monit. 2020, 19, 1645–1665. [Google Scholar] [CrossRef]
- Davoudi, R.; Miller, G.R.; Kutz, J.N. Data-driven vision-based inspection for reinforced concrete beams and slabs: Quantitative damage and load estimation. Autom. Constr. 2018, 96, 292–309. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Y.J.; Wu, G.Y.; Wu, H.; Ding, H.; Yu, J.; Wan, R. A Correlation analysis-based structural load estimation method for RC beams using machine vision and numerical simulation. Buildings 2024, 15, 207. [Google Scholar] [CrossRef]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. In Proceedings of the Computer Science—Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 379–387. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Zhang, T.Y.; Suen, C.Y. A fast parallel algorithm for thinning digital patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Lü, H.E.; Wang, P.S.P. A comment on “a fast parallel algorithm for thinning digital patterns”. Commun. ACM 1986, 29, 239–242. [Google Scholar] [CrossRef]
- Wu, R.-Y.; Tsai, W.-H. A new one-pass parallel thinning algorithm for binary images. Pattern Recognit. Lett. 1992, 13, 715–723. [Google Scholar] [CrossRef]
- Nguyen, N.H. U-net based skeletonization and bag of tricks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 2105–2109. [Google Scholar]
- GB 55008-2021; General Code for Concrete Structures. Ministry of Housing and Urban Rural Development of the People’s Republic of China: Beijing, China, 2021.
- Gribniak, V.; Pérez Caldentey, A.; Kaklauskas, G.; Rimkus, A.; Sokolov, A. Effect of arrangement of tensile reinforcement on flexural stiffness and cracking. Eng. Struct. 2016, 124, 418–428. [Google Scholar] [CrossRef]
- Korol, E.; Tejchman, J.; Mróz, Z. Experimental and numerical assessment of size effect in geometrically similar slender concrete beams with basalt reinforcement. Eng. Struct. 2017, 141, 272–291. [Google Scholar] [CrossRef]
- Yan, W. Impact Factors Analysis on the Crack Width of Reinforced Concrete Beams. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2010. [Google Scholar]
- Yang, C. Research on Crack Width of Concrete Beam Reinforced with 600 MPa Steel Bars. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2017. [Google Scholar]
- Quach, P.T. Understanding and Safely Predicting the Shear Response of Large-Scale Reinforced Concrete Structures. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2016. [Google Scholar]




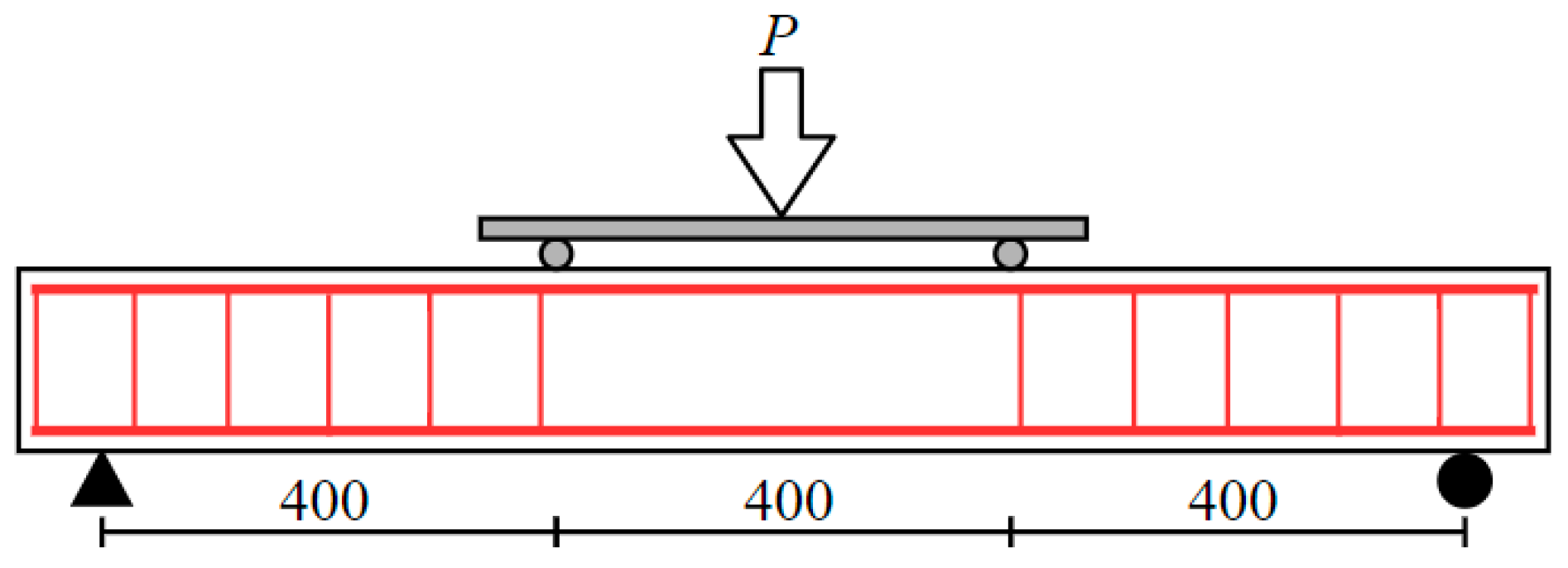





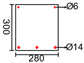
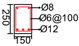
| Beam Number | Recorded Load | (mm) | (mm) | (mm) | (%) | (MPa) | (GPa) | (GPa) | (MPa) | (kN) |
|---|---|---|---|---|---|---|---|---|---|---|
| Test | 1400 | 120 | 200 | 1.28 | 11.9 | 28 | 200 | 360 | 78.37 | |
| S1-2 [20] | 3280 | 284 | 300 | 1.0 | 49.4 | 33.03 | 210.5 | 632.3 | 224 | |
| B-1 [23] | 3500 | 200 | 400 | 0.7 | 43.8 | 27.84 | 200 | 712.58 | 226 | |
| S3-1 [22] | 2000 | 150 | 250 | 1.06 | 34.2 | 31.64 | 200 | 525 | 82.94 | |
| S4-1 [22] | 2000 | 150 | 250 | 1.41 | 34.2 | 31.64 | 200 | 525 | 111.4 | |
| D60 [21] | 4200 | 250 | 664 | 0.74 | 55 | 50 | 50 | 1100 | 169.6 | |
| PLS300 [24] | 1800 | 175 | 300 | 0.65 | 44.8 | 36.3 | 185 | 457.7 | 95 | |
| Test | S1-2 | B1 | Beam S3-1 | Beam S4-1 | PLS300 | D60 |
|---|---|---|---|---|---|---|
 |  |  |  | 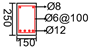 |  | 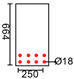 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Zhang, C.; Zhao, Y.; Yu, J. A Load Estimation Method Based on Surface Crack Distribution Images of Reinforced Concrete Beams. Buildings 2025, 15, 922. https://doi.org/10.3390/buildings15060922
Ding H, Zhang C, Zhao Y, Yu J. A Load Estimation Method Based on Surface Crack Distribution Images of Reinforced Concrete Beams. Buildings. 2025; 15(6):922. https://doi.org/10.3390/buildings15060922
Chicago/Turabian StyleDing, Hongli, Chun Zhang, Yinjie Zhao, and Jian Yu. 2025. "A Load Estimation Method Based on Surface Crack Distribution Images of Reinforced Concrete Beams" Buildings 15, no. 6: 922. https://doi.org/10.3390/buildings15060922
APA StyleDing, H., Zhang, C., Zhao, Y., & Yu, J. (2025). A Load Estimation Method Based on Surface Crack Distribution Images of Reinforced Concrete Beams. Buildings, 15(6), 922. https://doi.org/10.3390/buildings15060922






