Assessing Train-Induced Building Vibrations in a Subway Transfer Station and Potential Control Strategies
Abstract
:1. Introduction
2. Indoor Vibration Evaluation
2.1. Domestic Standard
2.2. Evaluation Indicator
3. Prediction Methods for Over-Track Building Vibrations
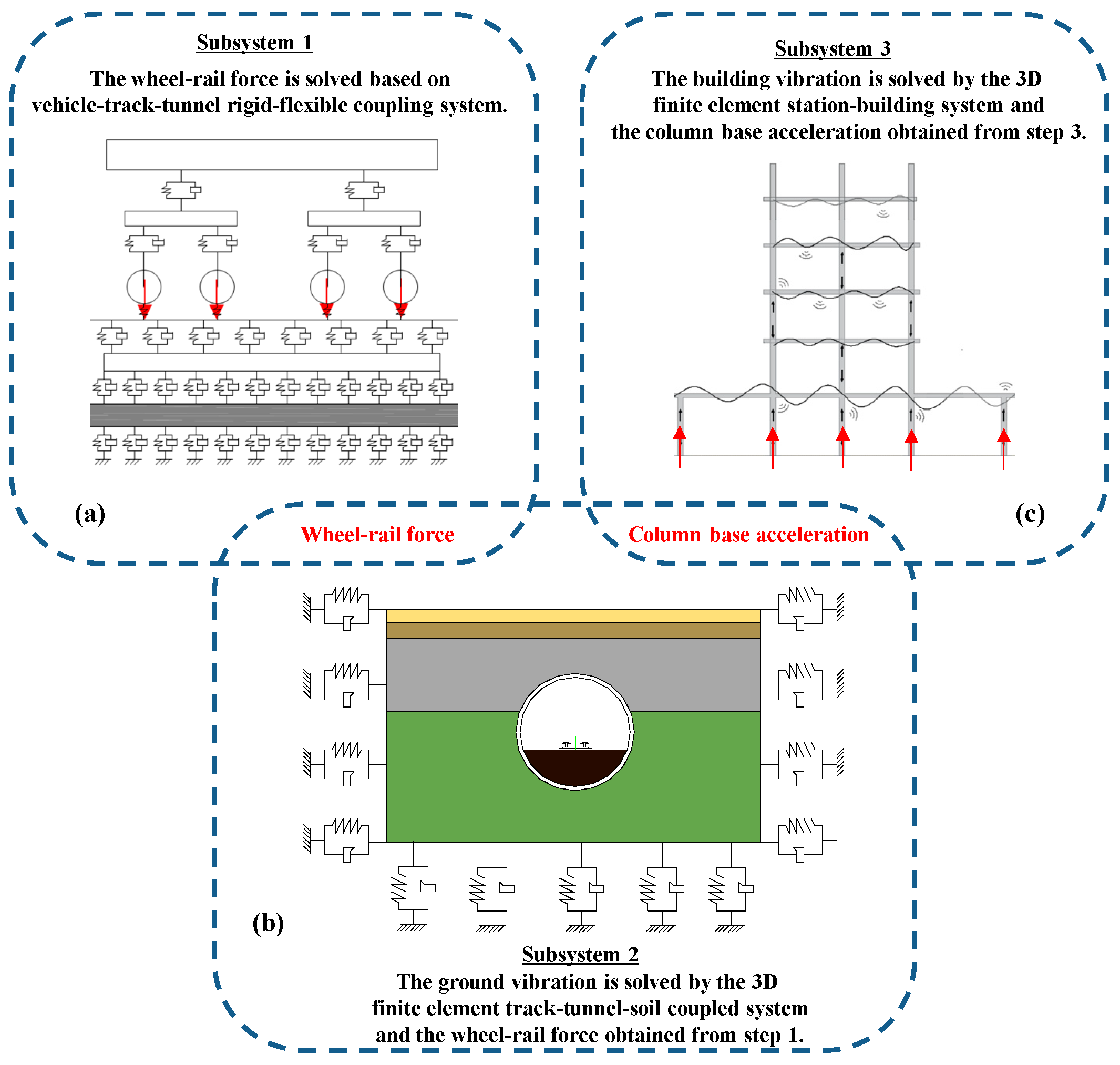
3.1. Simulation of Vibration Generation and Propagation
- Utilizing the principles of the finite element analysis and dynamics of multi-body systems, a coupling model comprising the vehicle, track, and tunnel is developed. The vehicle model is represented as a rigid multi-body system consisting of 42 degrees of freedom, including a car body, two bogie frames, and four wheelsets, amounting to seven rigid body components in total. An analysis of the fixed track is conducted, resulting in the development of a flexible track–tunnel model that accounts for the elasticity of the rail, the resilience of fasteners, and the deformation of the track slab, along with the tunnel and its elastic supports. The Timoshenko beam model serves as the standard for the rail, maintaining an interval of 0.6 m. The slabs of the track and the tunnel structure are represented as solid components, the fasteners are depicted as linear spring–damper systems, and the elastic support provided by the soil is modeled as a uniformly distributed viscoelastic element with a stiffness of 60 MPa/m.
- A 3D finite element subsystem is created for the track–tunnel–soil system; this model comprises the rail, fasteners, track slabs, tunnel, and soil. It stretches vertically for 80 m along the line, with a width of 100 m oriented perpendicular to the central line, and features a soil layer depth of 60 m. The mesh size for the rail beam elements is set at 0.1 m, while the grid for the solid elements of both the track slab and tunnel is configured at 0.5 m. The solid element mesh for the soil is categorized into three distinct regions; the central section features a grid size of 0.5 m, oriented perpendicular to both sides along the 0.8 m line, while the lower section has a grid size of 1.0 m. This finite element model is composed of 1260560 elements and has a total of 1341516 nodes.
- The validation of the vehicle–track–tunnel–soil coupled numerical model is achieved through the analysis of ground vibration measurements. The simulation results align closely with the gathered experimental findings regarding both temporal and spectral characteristics.
3.2. Simulation of Vibration Reception
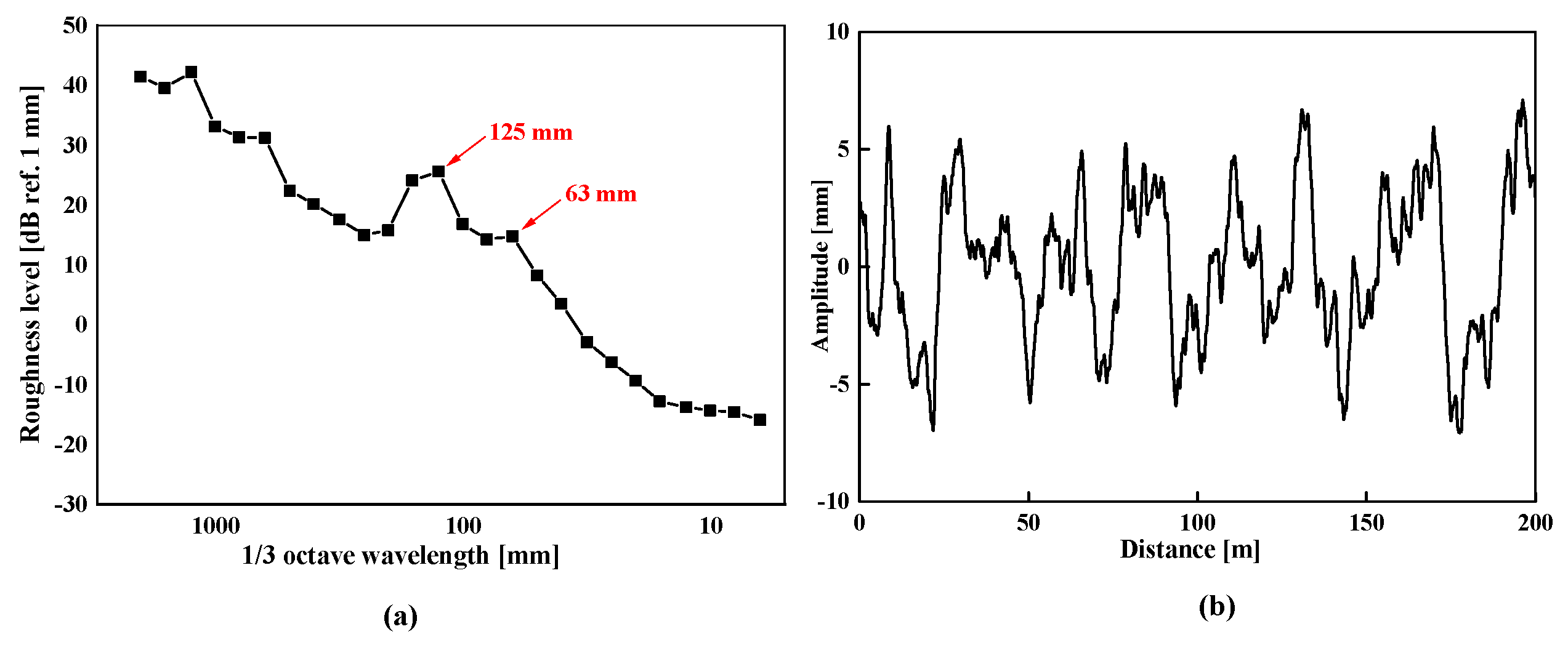
3.3. Track Irregularity
3.4. Column Base Dynamic Load
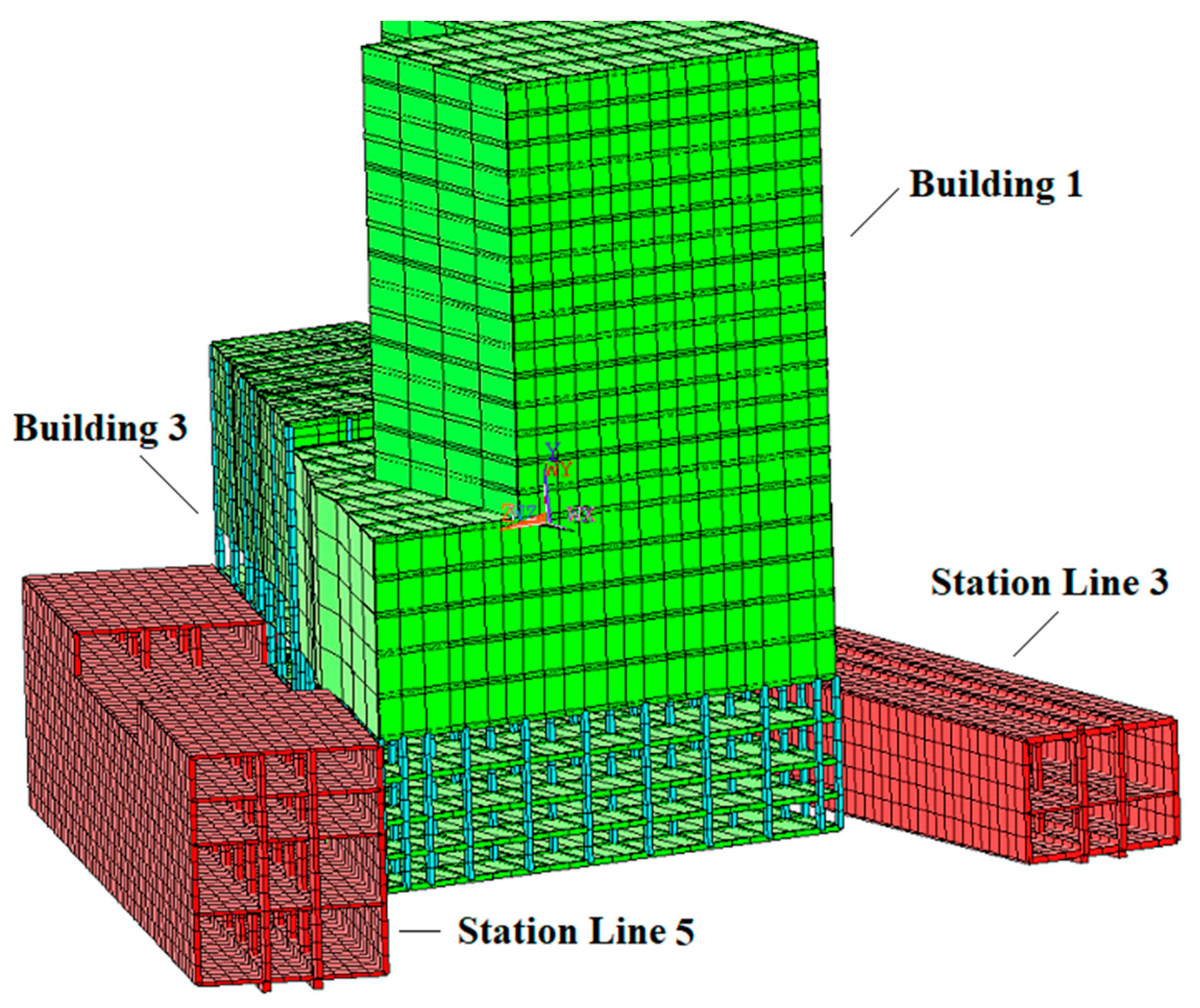
4. Case Study of Over-Track Buildings in a Subway Transfer Station
4.1. General Description
4.2. Dynamic Parameters
4.3. Analysis of Numerical Results
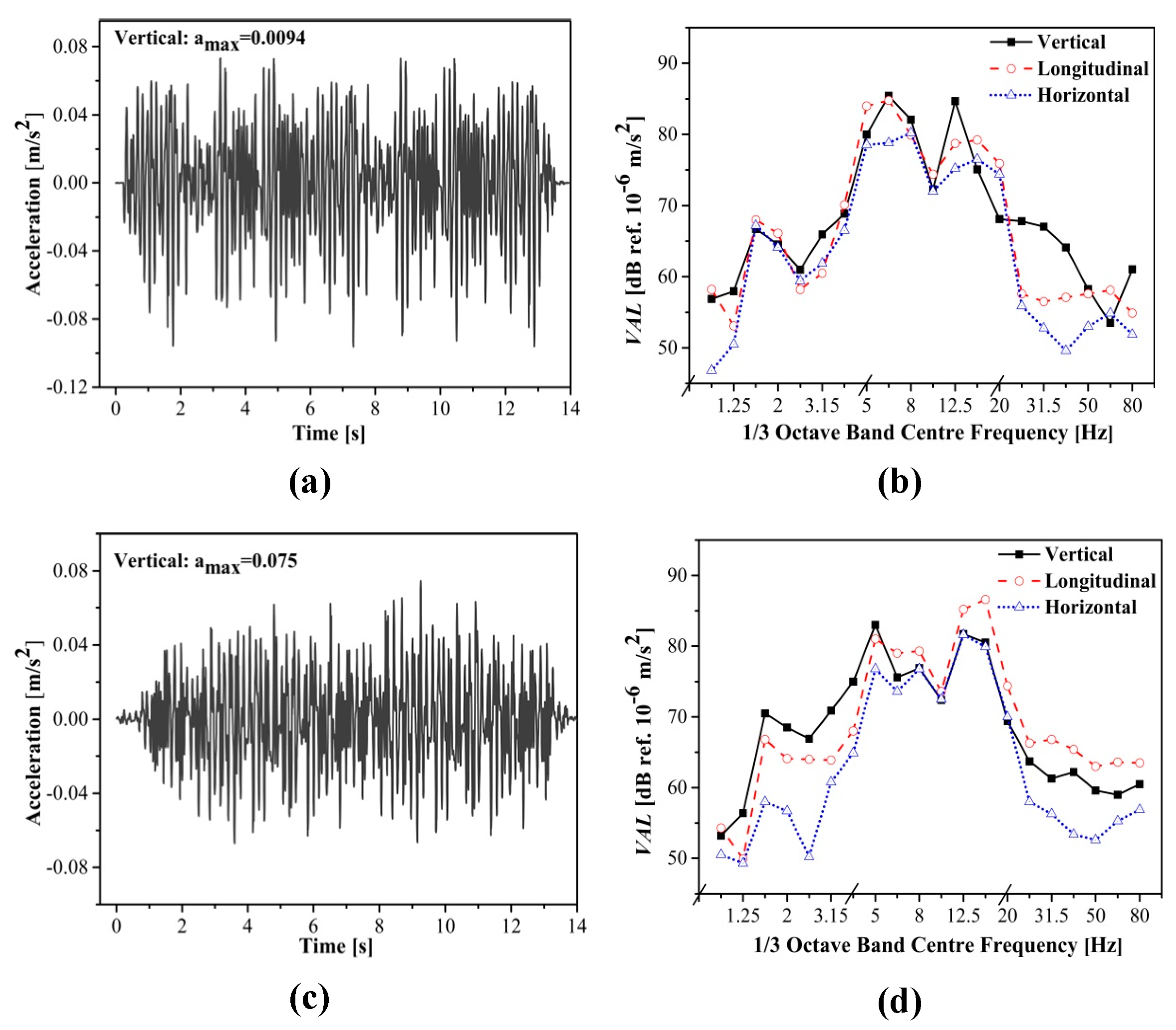
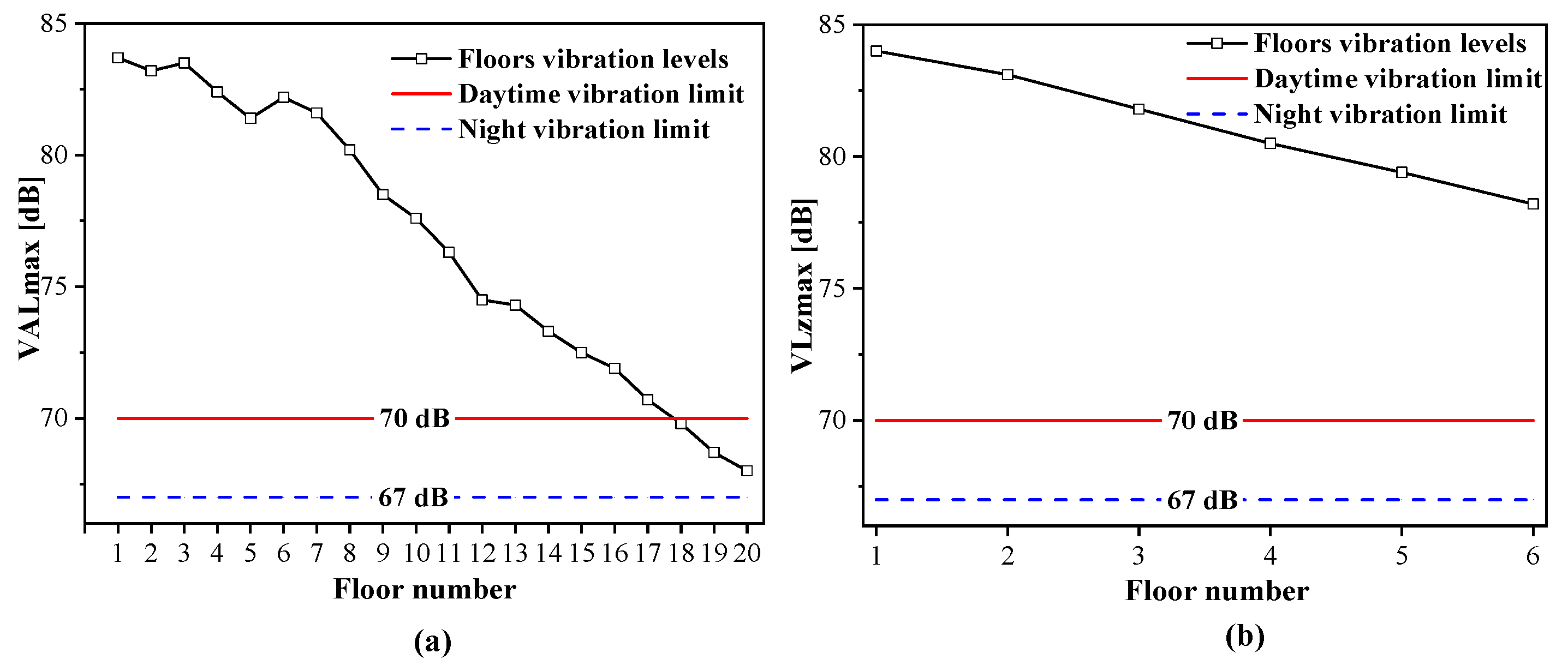
4.3.1. Building Foundation Response
4.3.2. Indoor Vibration Assessment
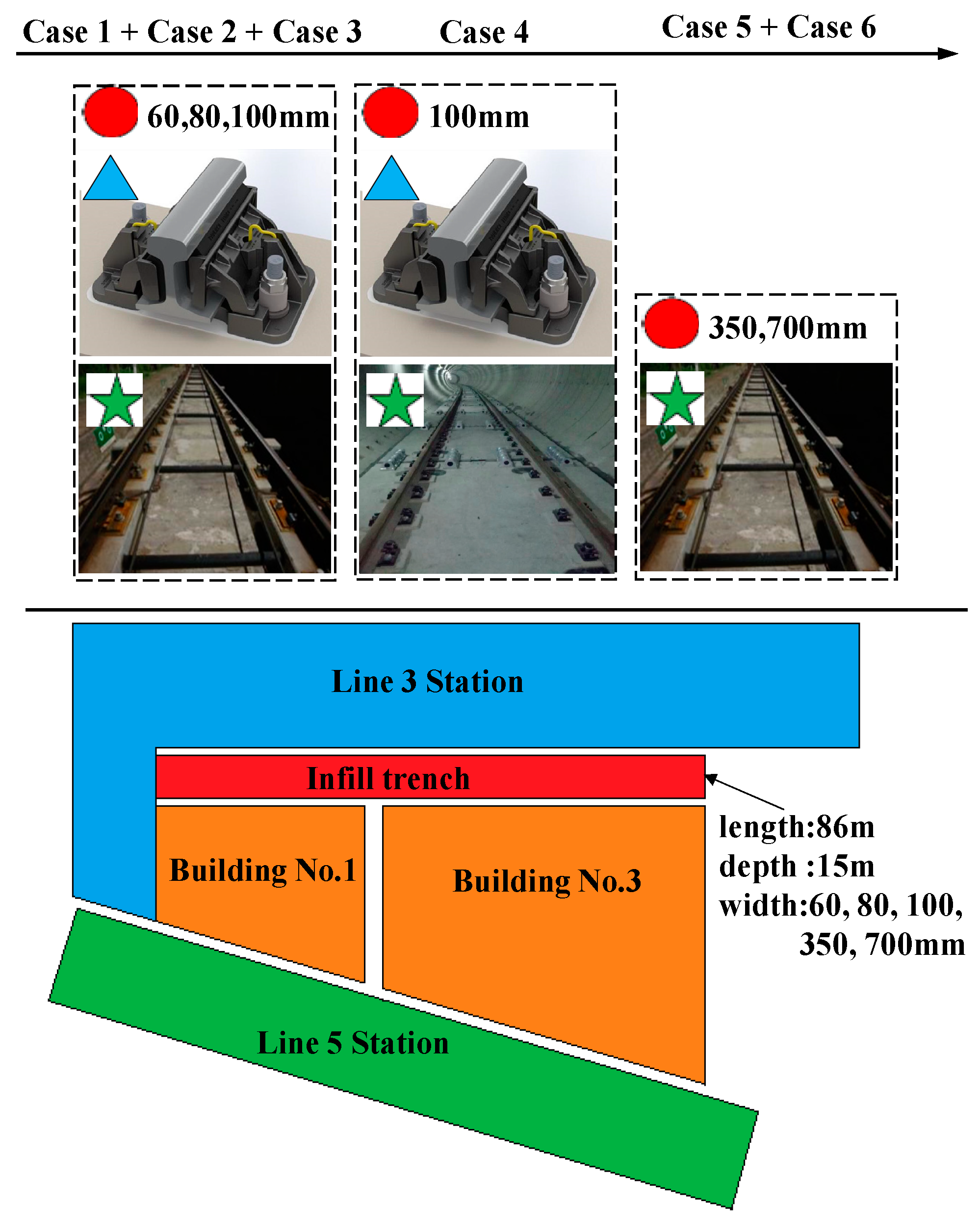
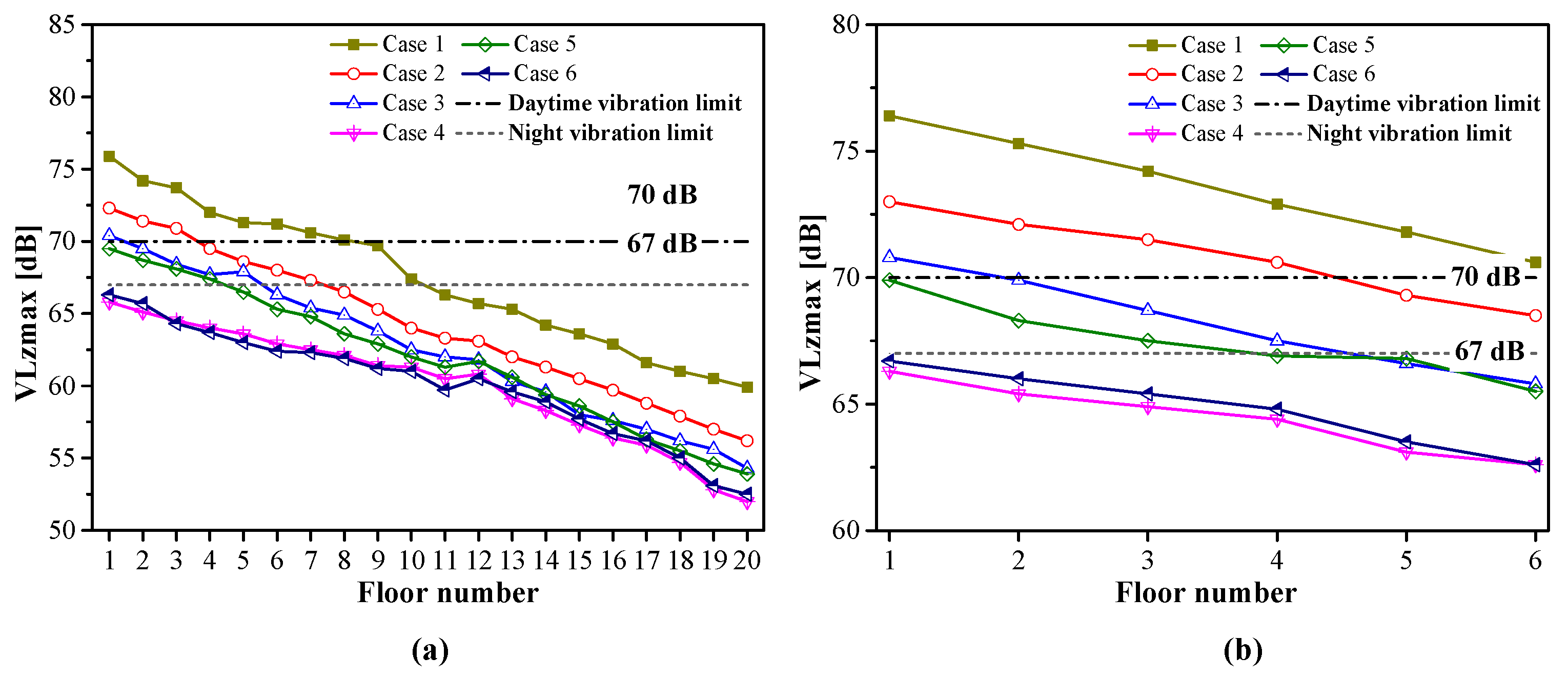
5. Vibration Mitigation by Comprehensive Control Strategies
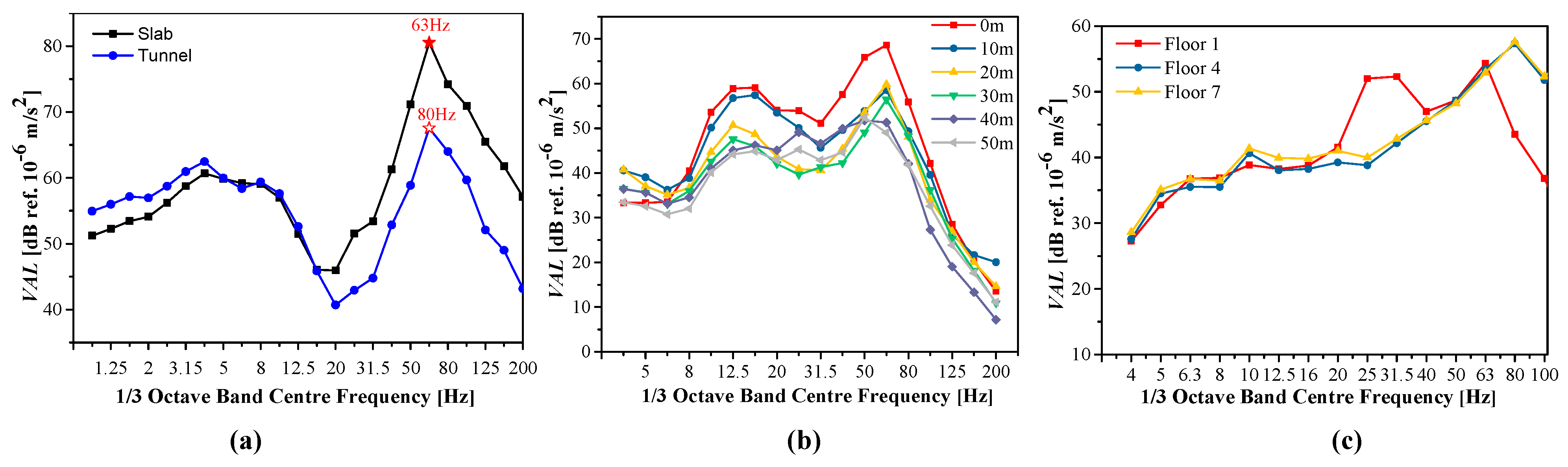
6. In-Site Test Measurement
6.1. Test Scheme
6.2. Analysis of Test Results
7. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Takemiya, H.; Goda, K. Prediction of ground vibration induced by high-speed train operation. In Proceedings of the 5th International Conference on Sound and Vibration, University of Adelaide South Australia, Adelaide, Australia, 15–18 December 1997; Volume 5, pp. 2681–2688. [Google Scholar]
- François, S.; Schevenels, M.; Galvín, P.; Lombaert, G.; Degrande, G. A 2.5D coupled FE-BE methodology for the dynamic interaction between longitudinally invariant structures and a layered halfspace. Comput. Methods Appl. Mech. Eng. 2010, 199, 1536–1548. [Google Scholar]
- Cao, Y.; Xia, H.; Lombaert, G. Solution of moving-load-induced soil vibrations based on the Betti–Rayleigh Dynamic Reciprocal Theorem. Soil Dyn. Earthq. Eng. 2010, 30, 470–480. [Google Scholar] [CrossRef]
- Gupta, S.; Liu, W.; Degrande, G.; Lombaer, G.; Liu, W. Prediction of vibrations induced by underground railway traffic in Beijing. J. Sound Vib. 2006, 310, 608–630. [Google Scholar]
- Fiala, P.; Degrande, G.; Augusztinovicz, F. Numerical modelling of ground-borne noise and vibration in buildings due to surface rail traffic. J. Sound Vib. 2007, 301, 718–738. [Google Scholar] [CrossRef]
- Thompson, D.; Kouroussis, G.; Ntotsios, E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles. Veh. Syst. Dyn. 2019, 57, 936–983. [Google Scholar] [CrossRef]
- Celebi, E. Three-dimensional modelling of train-track and sub-soil analysis for surface vibrations due to moving loads. Appl. Math. Comput. 2006, 179, 209–230. [Google Scholar] [CrossRef]
- Wang, L.; Wang, P.; Wei, K.; Dollevoet, R.; Li, Z. Ground vibration induced by high speed trains on an embankment with pile-board foundation: Modelling and validation with in situ tests. Transp. Geotech. 2022, 34, 100734. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liang, X.; Hung, H.H.; Wu, Y.l. Comparative study of 2D and 2.5D responses of long underground tunnels to moving train loads. Soil Dyn. Earthq. Eng. 2017, 97, 86–100. [Google Scholar]
- Yang, Y.B.; Liu, S.J.; Chen, W.; Tan, Q.; Wu, Y.T. Half-space response to trains moving along curved paths by 2.5D finite/infinite element approach. Soil Dyn. Earthq. Eng. 2021, 145, 106740. [Google Scholar]
- Yang, Y.; Hung, H.; Chang, D. Train-induced wave propagation in layered soils using finite/infinite element simulation. Dyn. Earthq. Eng. 2003, 23, 263–278. [Google Scholar] [CrossRef]
- Jones, S.; Hunt, H. Predicting surface vibration from underground railways through inhomogeneous soil. J. Sound Vib. 2012, 331, 2055–2069. [Google Scholar] [CrossRef]
- Xia, H.; Chen, J.; Wei, P.; Xia, C.; De Roeck, G.; Degrande, G. Experimental investigation of railway train-induced vibrations of surrounding ground and a nearby multi-story building. Earthq. Eng. Eng. Vib. 2009, 8, 137–148. [Google Scholar] [CrossRef]
- Kouroussis, G.; Conti, C.; Verlinden, O. Experimental study of ground vibrations induced by Brussels IC/IR trains in their neighbourhood. Mech. Ind. 2013, 14, 99–105. [Google Scholar]
- Zou, C.; Wang, Y.; Wang, P.; Guo, J. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.; Wang, Y.; Moore, J.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
- GB10071; Measurement Method of Environmental Vibration of Urban Area. Ministry of Ecology and Environment: Beijing, China, 1988.
- GB/T 50355; Standard of Limit and Measurement Method of Vibration in the Room of Residential Buildings. Ministry of construction: Beijing, China, 2018.
- TB/T 3152; Measurement of Railway Environmental Vibration. China Academy of Railway Sciences Corporation Limited: Beijing, China, 2007.
- JGJ/T 170; Standard for Limit and Measuring Method of Building Vibration and Secondary Noise Caused by Urban Rail Transit. Ministry of Housing and Urban-Rural Development: Beijing, China, 2009.
- ISO2631/1; Mechanical vibration and shock: Evaluation of human exposure to whole-body vibration—Part 1: General requirements. International Organization for Standardization: Geneva, Switzerland, 1997.
- Xing, M.; Zhao, C.; Wang, P.; Lu, J.; Yi, Q. A Numerical Analysis of Ground Vibration Induced by Typical Rail Corrugation of Underground Subway. Shock. Vib. 2019, 2019, 8406813. [Google Scholar]


| Element | Parameter | Unit | Value |
|---|---|---|---|
| Vehicle | Mass of car body | kg | 39,000 |
| Mass of bogie | kg | 3600 | |
| Mass of wheel set | kg | 1600 | |
| Mass moment of inertia of car body | kg·m2 | 1,400,000 | |
| Mass moment of inertia of car bogie | kg·m2 | 1760 | |
| Vertical stiffness of primary suspension | kN/mm | 1.7 | |
| Vertical damping of primary suspension | kN·s/m | 60 | |
| Vertical stiffness of primary suspension | kN/mm | 0.45 | |
| Vertical damping of primary suspension | kN·s/m | 60 | |
| Track | Fastener support spacing | m | 0.625 |
| Fastener stiffness | kN/mm | 35 | |
| Fastener damping | kN·s/m | 20 | |
| Slab length × width × thickness | M × m × m | 5.6 × 2.5 × 0.4 | |
| Slab density | kg/m3 | 2500 | |
| Slab Young’s modulus | GPa | 35 | |
| Building | Density | kg/m3 | 2500 |
| Young’s modulus | GPa | 32.5 | |
| Poisson’s ratio | - | 0.4 | |
| Damping ratio | - | 0.05 |
| Metro | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| Line 3 | Vanguard fasteners + Isolation trench 60mm wide | Vanguard fasteners + Isolation trench 80mm wide | Vanguard fasteners + Isolation trench 100mm wide | Vanguard fasteners + Isolation trench 100mm wide | Infill trench 350 mm wide | Infill trench 700 mm wide |
| Line 5 | Ladder track | Ladder track | Ladder track | Steel spring | Ladder track | Ladder track |
| Steel-Spring Floating Slab Track | Ladder-Type Track | ||||
|---|---|---|---|---|---|
| Structure Parts | Parameters | Value | Structure Parts | Parameters | Value |
| Floating slab | Young’s modulus (GPa) | 3.50 | Ladder sleeper | Young’s modulus (GPa) | 3.50 |
| Length (m) | 0.25 | Length (m) | 6.15 | ||
| Width (m) | 3.0 | Width (m) | 0.46 | ||
| Height (m) | 0.35 | Height (m) | 0.175 | ||
| Density (kg/m) | 2500 | Density (kg/m) | 2500 | ||
| Steel spring | Vertical stiffness (N/m) | 6 × 106 | Filled steel stub | Poisson’s ratio | 0.3 |
| Vertical damping (N·s/m) | 17,000 | Young’s modulus (GPa) | 21 | ||
| Shear hinge | Shear stiffness (N/m) | 5 × 109 | Density (kg/m) | 2808 | |
| Fastener | Vertical stiffness (N/m) | 4 × 107 | Damping material under sleeper | Vertical stiffness (N/m) | 1.5 × 107 |
| Vertical damping (N·s/m) | 9.8 × 104 | Vertical damping (N·s/m) | 10,000 | ||
| Setup | Site | Point | PPA (m/s2) | VLzmax (dB) | VALmax (dB) |
|---|---|---|---|---|---|
| Setup A | Slab | O1 | 1.29 | 98.4 | — |
| Tunnel | O2 | 0.106 | 79.5 | ||
| Setup B | 0 m | P1 | 0.081 | 71.64 | — |
| 10 m | P2 | 0.050 | 64.27 | ||
| 20 m | P3 | 0.037 | 61.98 | ||
| 30 m | P4 | 0.024 | 58.91 | ||
| 40 m | P5 | 0.019 | 58.19 | ||
| 50 m | P6 | 0.016 | 56.80 | ||
| Setup A | Floor 1 | Q1 | 0.012 | — | 56.0 |
| Floor 4 | Q2 | 0.006 | 53.9 | ||
| Floor 7 | Q3 | 0.002 | 53.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, M.; Zhu, J.; Chen, D. Assessing Train-Induced Building Vibrations in a Subway Transfer Station and Potential Control Strategies. Buildings 2025, 15, 1024. https://doi.org/10.3390/buildings15071024
Xing M, Zhu J, Chen D. Assessing Train-Induced Building Vibrations in a Subway Transfer Station and Potential Control Strategies. Buildings. 2025; 15(7):1024. https://doi.org/10.3390/buildings15071024
Chicago/Turabian StyleXing, Mengting, Juxiang Zhu, and Dingqing Chen. 2025. "Assessing Train-Induced Building Vibrations in a Subway Transfer Station and Potential Control Strategies" Buildings 15, no. 7: 1024. https://doi.org/10.3390/buildings15071024
APA StyleXing, M., Zhu, J., & Chen, D. (2025). Assessing Train-Induced Building Vibrations in a Subway Transfer Station and Potential Control Strategies. Buildings, 15(7), 1024. https://doi.org/10.3390/buildings15071024








