The Effect of Wind Speed on Structural Along-Wind Response of a Lighting Pole According to TS498 and Eurocode 1
Abstract
:1. Introduction
2. Materials and Methods
2.1. General Properties of Lighting Pole
2.2. TS498
2.3. Eurocode 1
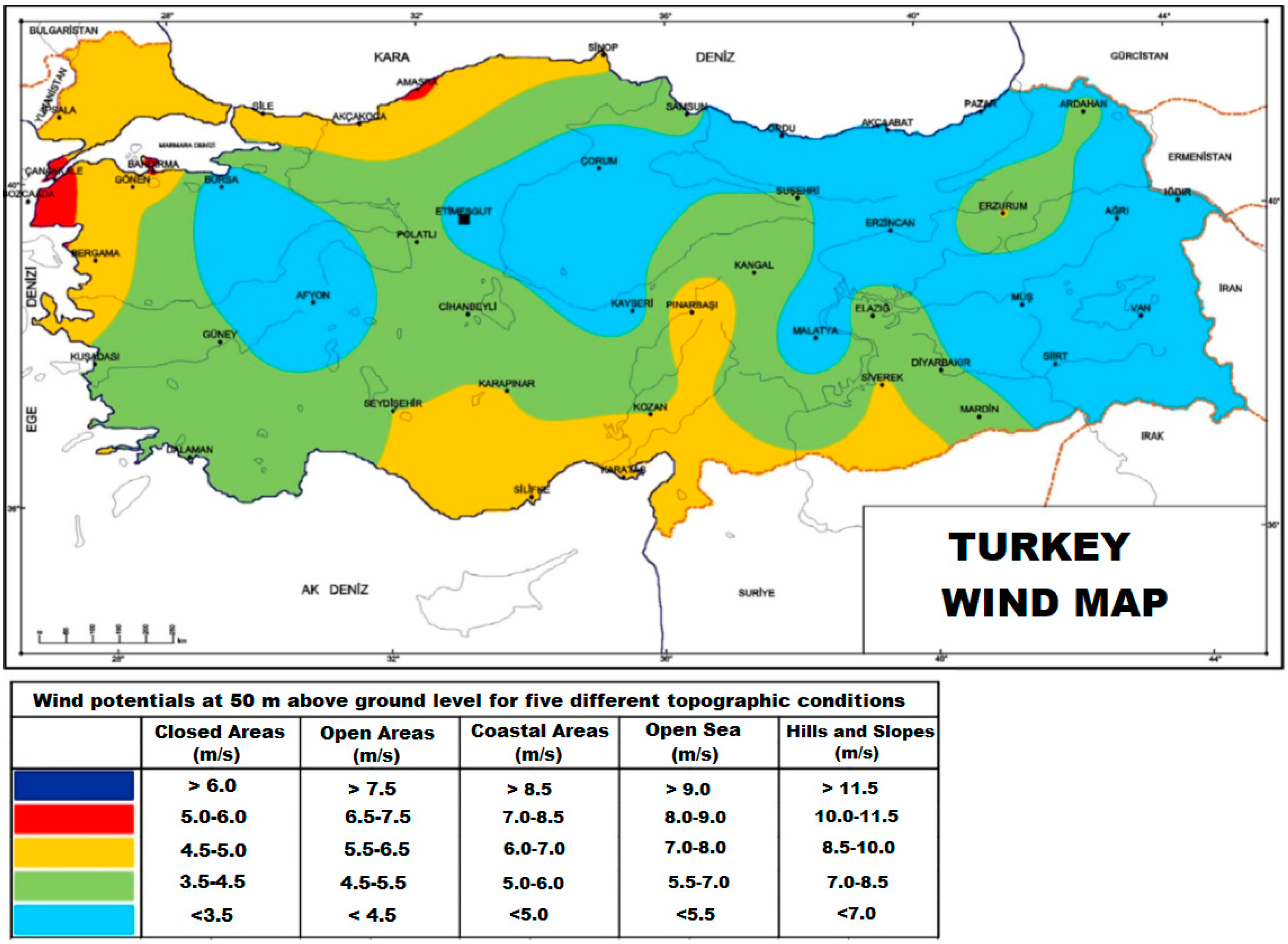
2.4. Türkiye Wind Map
3. Results
3.1. Wind Load Calculations According to TS498
3.2. Wind Load Calculations According to Eurocode 1
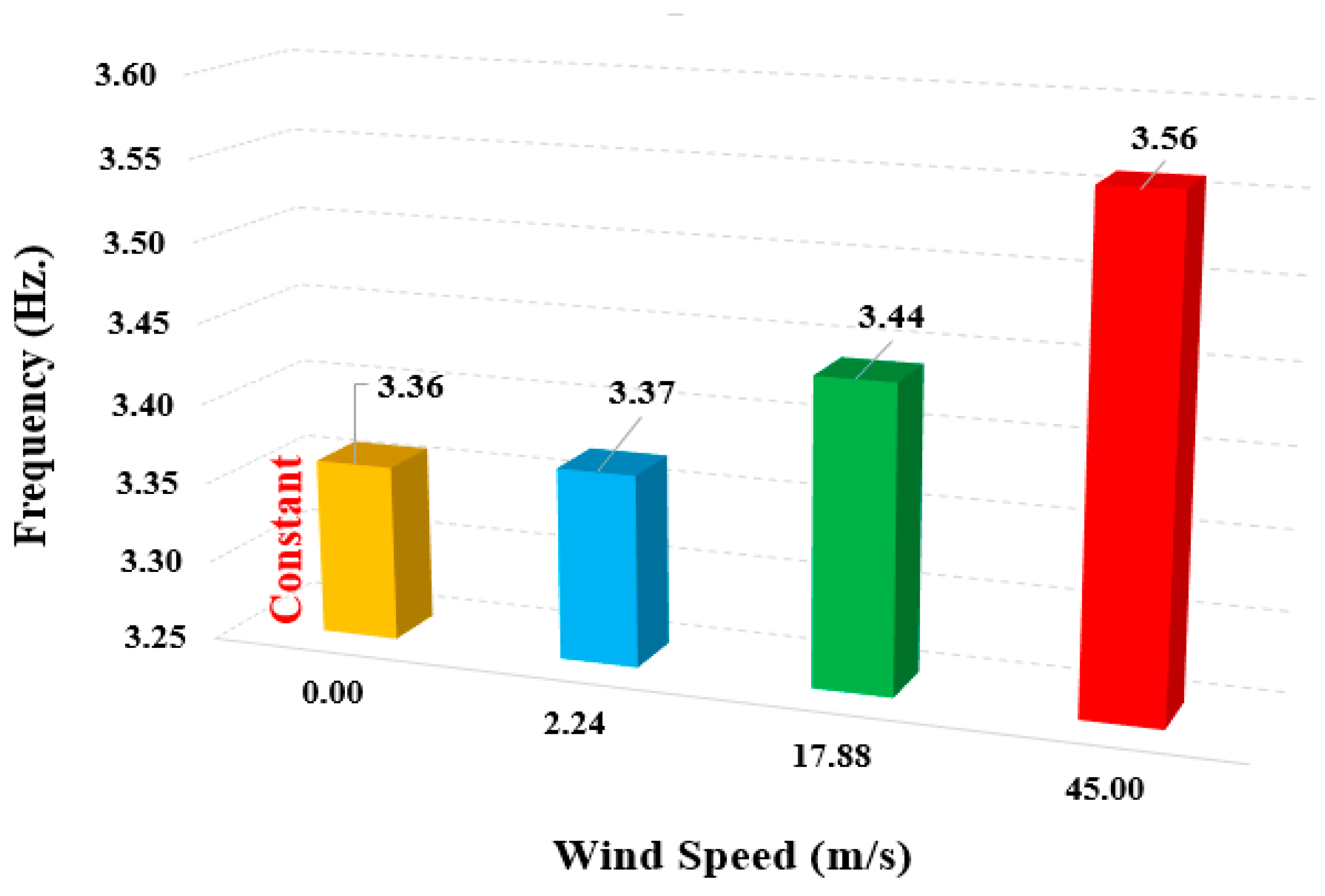
3.2.1. Constant First Mode Frequency with Wind Speed
3.2.2. Variable First Mode Frequency with Wind Speed
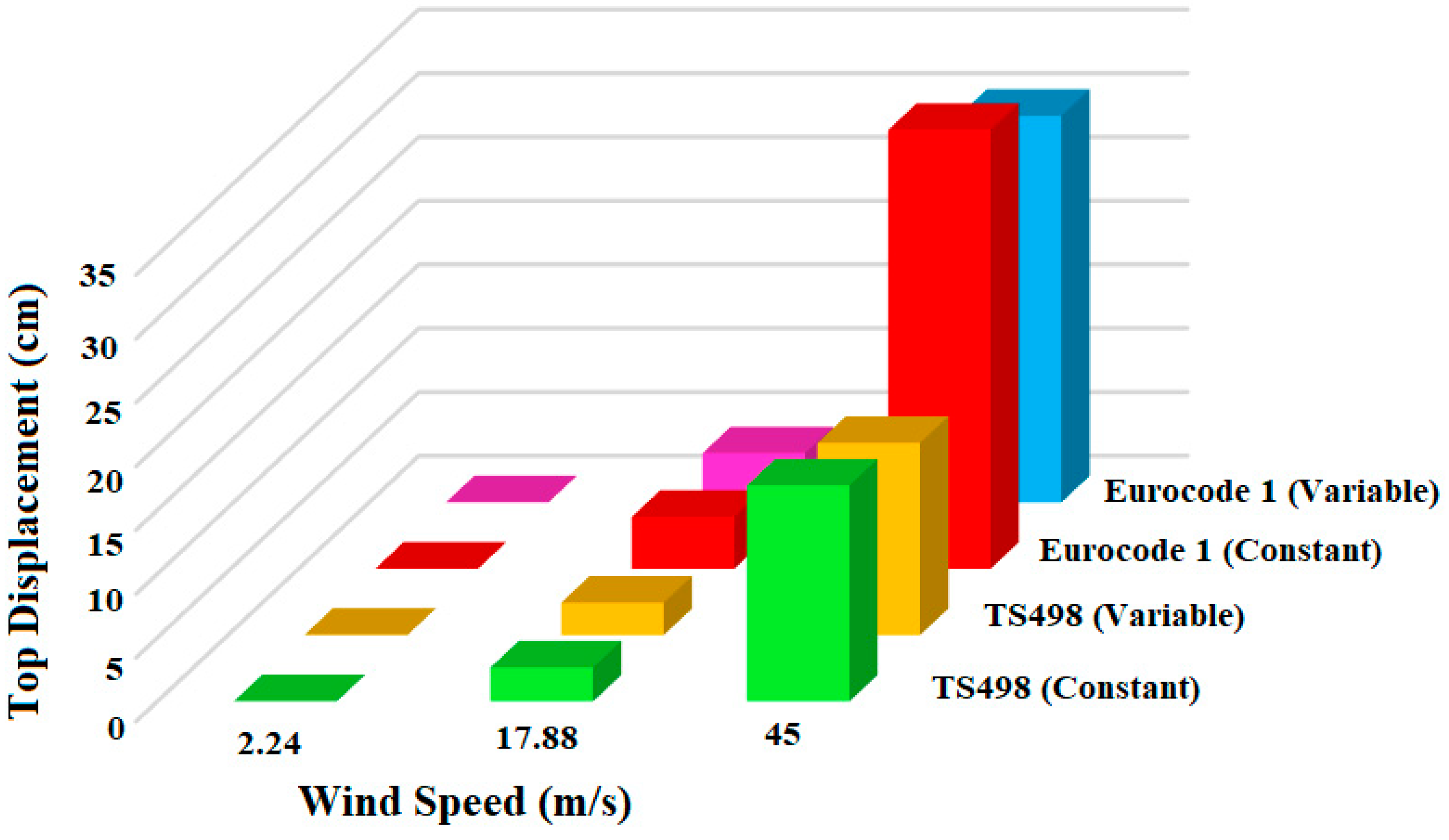
3.3. Comparison of Wind Loads
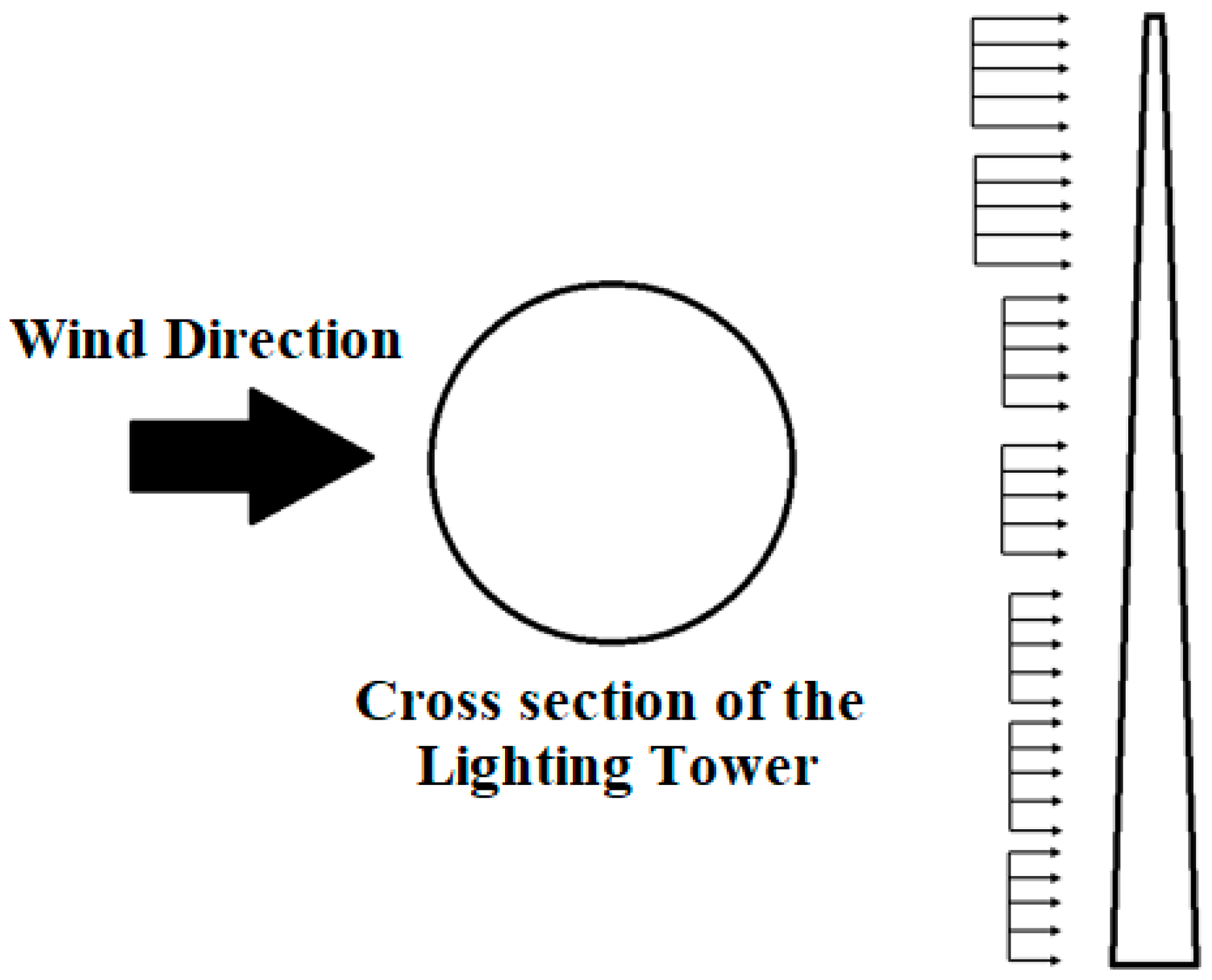
3.4. Application of Wind Loads to Lighting Pole
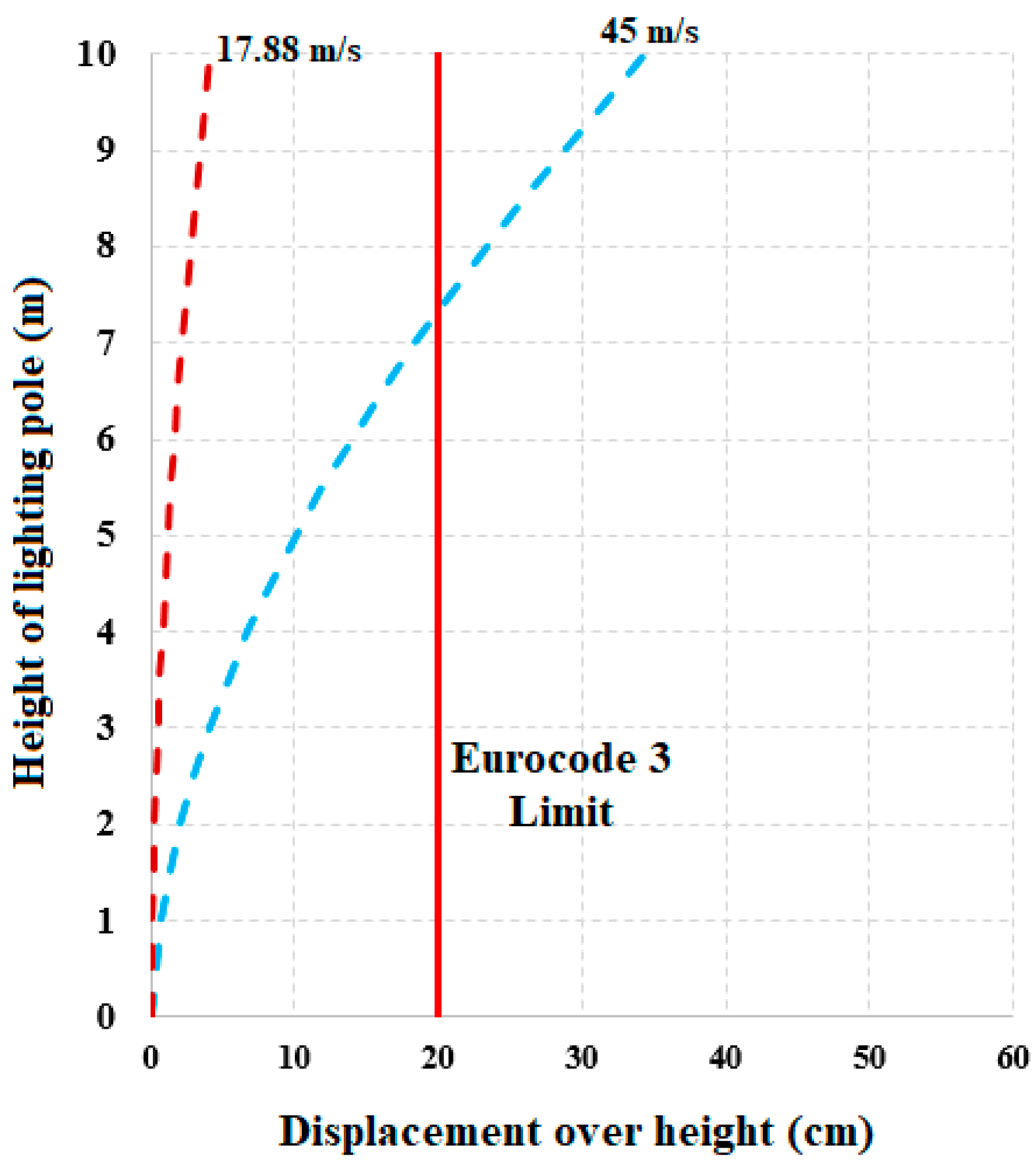
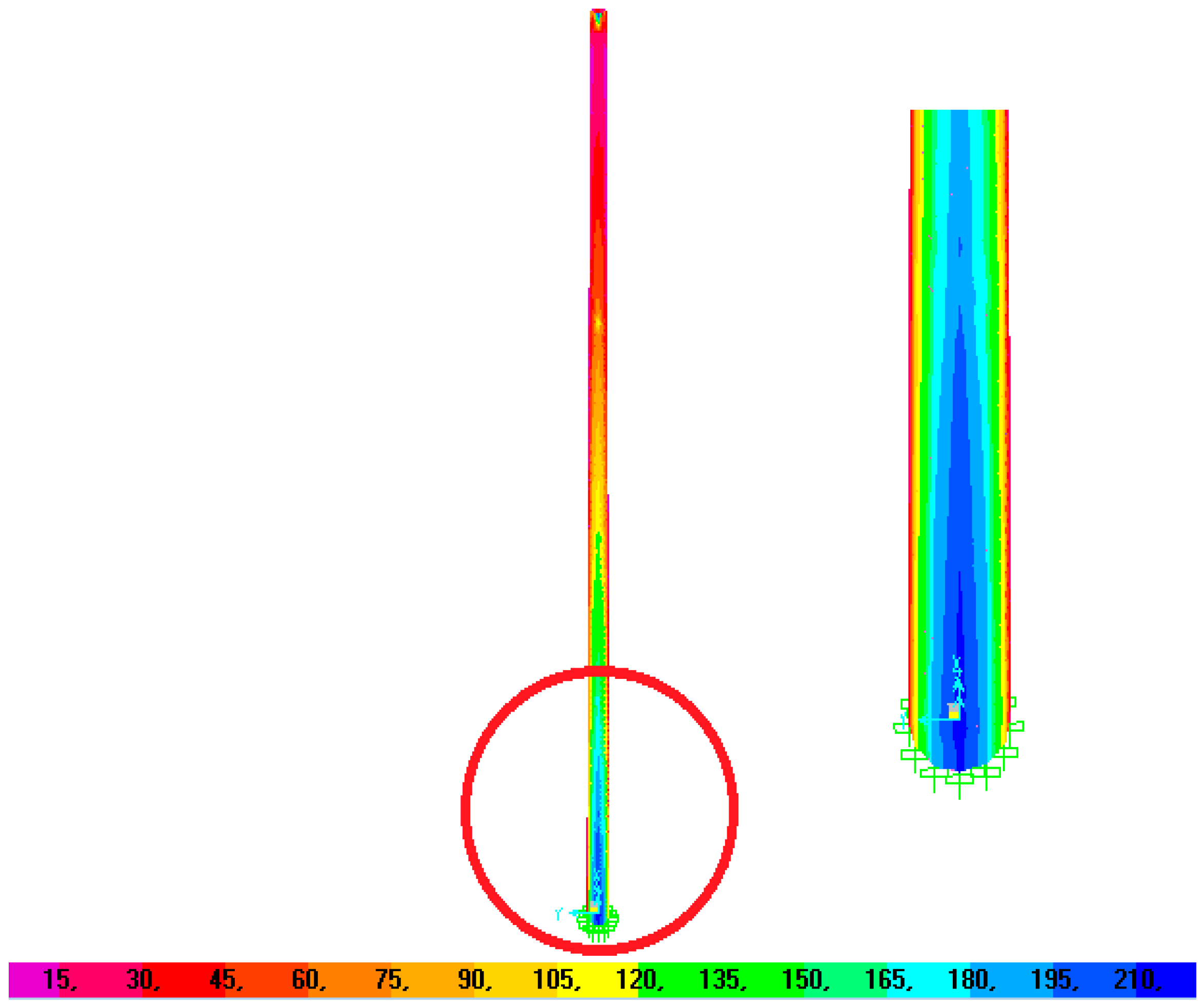
3.5. Structural Analysis Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Light Poles and Pole Lights Buyers Guide. Available online: https://www.ledlightexpert.com/light-poles-and-pole-lights_ep1 (accessed on 21 January 2025).
- OMS Lighting and Pole Private Limited. Available online: https://www.omslighting.in/ (accessed on 21 January 2025).
- Breaking: College Football Stadium Ravaged by 100 mph Winds over the Weekend. Available online: https://www.totalprosports.com/ncaa/tulsa-chapman-football-stadium-100mph-winds/ (accessed on 21 January 2025).
- Zhang, M.; Li, T.; Wang, Y.; Chen, Y.; Zhao, G. Wind-Induced Vibration and Vibration Suppression of High-Mast Light Poles with Spiral Helical Strakes. Buildings 2023, 13, 907. [Google Scholar] [CrossRef]
- Holmes, J.D. Codification of Wind Loads on Wind-sensitive Structures. Int. J. Space Struct. 2009, 24, 87–95. [Google Scholar] [CrossRef]
- Stochino, F.; Attoli, A.; Serra, M.; Napoli, A.; Meloni, D.; Mistretta, F. Structural Identification from Operational Modal Analysis: The Case of Steel Structures. Buildings 2023, 13, 548. [Google Scholar] [CrossRef]
- Yilmaz, Z.; Okur, F.Y.; Günaydin, M.; Altunişik, A.C. Enhanced Modal Participation Ratio-Based Structural Damage Identification: A New Filtering Approach Using Modal Assurance Criteria. Buildings 2023, 13, 2467. [Google Scholar] [CrossRef]
- Tuhta, S. (Ed.) Determination of Wind Speed Effect on Dynamic Parameters of Full-Scale Lighting Pole by OMA. In Analytical and Operational Modal Analysis Applications in Composite Structures, 1st ed.; Nobel Academic Publishing: Ankara, Türkiye, 2022; pp. 49–67. [Google Scholar]
- Repetto, M.P.; Solari, G. Wind-induced fatigue collapse of real slender structures. Eng. Struct. 2010, 32, 3888–3898. [Google Scholar] [CrossRef]
- Pagnini, L.C.; Solari, G. Damping measurements of steel poles and tubular towers. Eng. Struct. 2001, 23, 1085–1095. [Google Scholar] [CrossRef]
- Repetto, M.P.; Solari, G. Dynamic alongwind fatigue of slender vertical structures. Eng. Struct. 2001, 23, 1622–1633. [Google Scholar] [CrossRef]
- Caracoglia, L.; Jones, N.P. Numerical and experimental study of vibration mitigation for highway light poles. Eng. Struct. 2007, 29, 821–831. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, X.; Wang, L.; Cai, C.S.; Yan, H.; Hu, P. Experimental investigation of the vortex-induced vibration of tapered light poles. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104555. [Google Scholar] [CrossRef]
- Mengistu, M.T.; Orlando, A.; Repetto, M.P. Wind and structural response monitoring of a lighting pole for the study of downburst effects on structures. J. Wind Eng. Ind. Aerodyn. 2023, 240, 105447. [Google Scholar] [CrossRef]
- Piccardo, G.; Solari, G. Closed form prediction of 3-D wind-excited response of slender structures. J. Wind Eng. Ind. Aerodyn. 1998, 74, 697–708. [Google Scholar] [CrossRef]
- Romanic, D.; Shoji, H.; Hangan, H. Experimental investigation of surface pressures, velocities, and dynamic structural analysis of tornadic winds on a luminary pole. J. Fluids Struct. 2023, 116, 103794. [Google Scholar] [CrossRef]
- Gonçalves, E.S.; Gonçalves, J.; Rosse, H.; Costa, J.; Jorge, L.; Gonçalves, J.A.; Coelho, J.P.; Ribeiro, J.E. Static analysis of a lamppost according to Eurocode EN-40. Procedia Struct. Integr. 2024, 54, 83–90. [Google Scholar] [CrossRef]
- Karaca, Z.; Öztürk, H.T.; Türkeli, E. Wind loads for stadium lighting towers according to Eurocode 1. Chall. J. Struct. Mech. 2016, 2, 226–233. [Google Scholar] [CrossRef]
- Erkmen, B. Vibration Behavior of Industrial Towers under Wind Vortexes. In Proceedings of the 6th Steel Structures Symposium, Eskişehir, Türkiye, 15–17 October 2015. (In Turkish). [Google Scholar]
- Devi, S.; Govindaraju, L. A study on wind induced vibration on lighting poles. Int. J. Res. Eng. Technol. 2014, 3, 172–178. [Google Scholar]
- Dilawer, S.I.; Junaidi, M.A.R.; Mehdi, D.S.N.; Ahmed, G.M.S. Design analysis and commissioning of high mast lighting poles. IOSR J. Mech. Civ. Eng. 2013, 8, 40–46. [Google Scholar]
- Dong, X.; Lian, J.; Wang, H.; Yu, T.; Zhao, Y. Structural vibration monitoring and operational modal analysis of offshore wind turbine structure. Ocean Eng. 2018, 150, 280–297. [Google Scholar] [CrossRef]
- Wilson, E.L. SAP 2000: Integrated Finite Element Analysis and Design of Structures; Computers & Structures: Berkeley, CA, USA, 2000. [Google Scholar]
- TS 498 (1997); Design Loads for Buildings. Turkish Standards Institute: Ankara, Türkiye, 1997. (In Turkish)
- EN 1991-1-4 (2005); Eurocode 1: Actions on Structures—General Actions—Part1-4: Wind Actions. Comite Europeen De Normalisation: Brussels, Belgium, 2005.
- General Directorate of Meteorology, Türkiye Wind Map. Available online: https://www.mgm.gov.tr/genel/ruzgar-atlasi.aspx (accessed on 11 April 2024).
- Lowest and Highest Values Recorded in Türkiye and the World. Available online: https://www.mgm.gov.tr/genel/sss.aspx?s=sicaklikenleri2 (accessed on 11 April 2024).
- EN 1993-3-2 (2006); Eurocode 3: Design of Steel Structures—Part 3-2: Towers, Masts and Chimneys-Chimneys. Comite Europeen De Normalisation: Brussels, Belgium, 2006.
- Choi, H.; Roda, A.; Najm, H. Fatigue Life Evaluation of High-Mast Lighting Tower (HMLT) and Aluminum Poles for Traffic Signals and Luminaires (Technical Report); Center for Advanced Infrastructure and Transportation: Piscataway, NJ, USA, 2016. [Google Scholar]



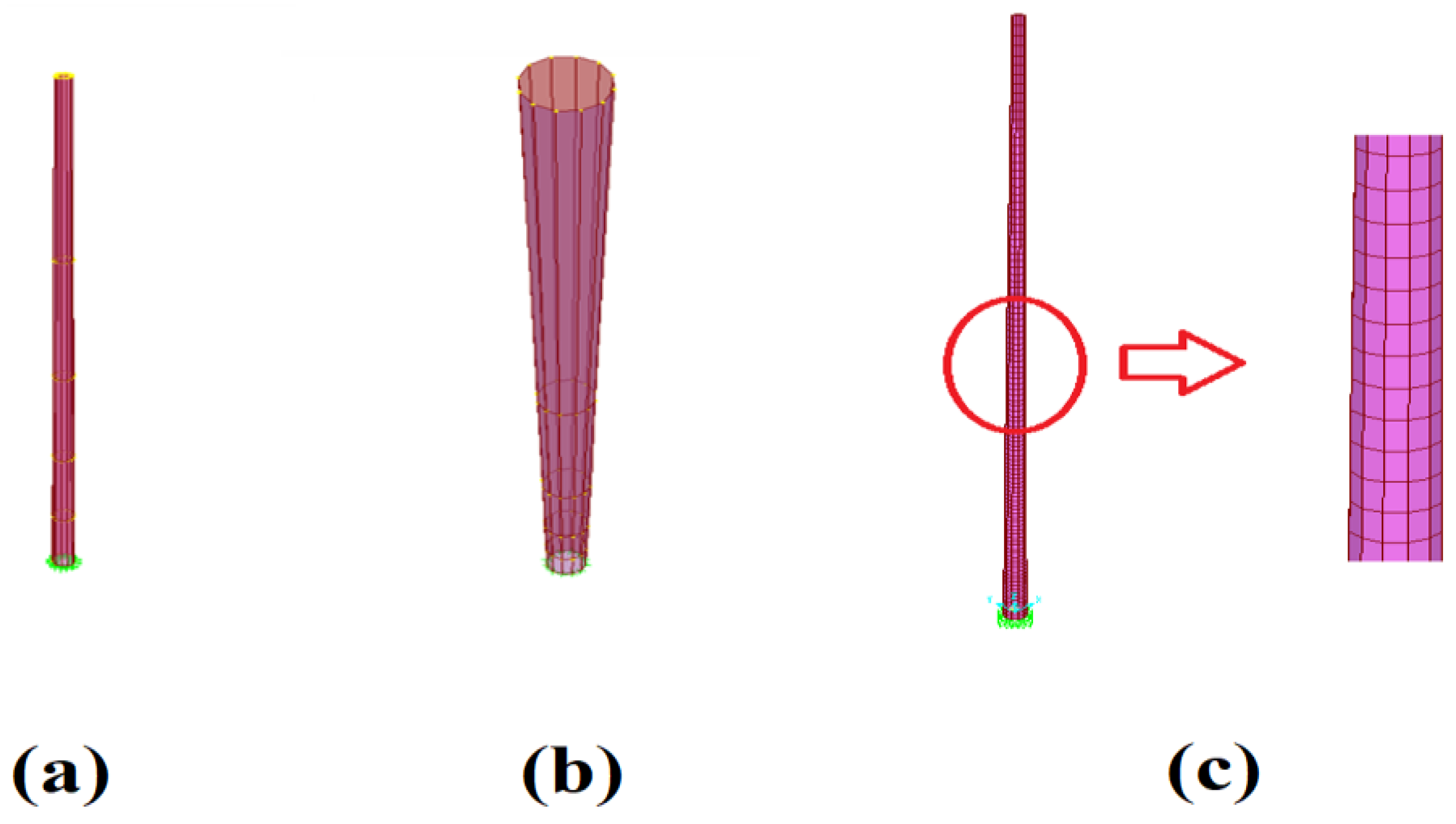

| Section No | Height from Ground (m) | Outer Diameter (m) | V0 (m/s) | Vb,0 (m/s) | q | A | W (kN) | W (kN/m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 2.24 | 1.80 | 0.002015 | 0.56 | 0.001805 | 0.000903 |
| 2 | 2.00–4.00 | 0.26 | 2.24 | 1.99 | 0.002468 | 0.48 | 0.001895 | 0.000948 |
| 3 | 4.00–6.00 | 0.22 | 2.24 | 2.10 | 0.002753 | 0.40 | 0.001762 | 0.000881 |
| 4 | 6.00–8.00 | 0.18 | 2.24 | 2.18 | 0.002966 | 0.32 | 0.001519 | 0.000759 |
| 5 | 8.00–10.00 | 0.14 | 2.24 | 2.24 | 0.003136 | 0.24 | 0.001204 | 0.000602 |
| Section No | Height from Ground (m) | Outer Diameter (m) | V0 (m/s) | Vb,0 (m/s) | q | A | W (kN) | W (kN/m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 17.88 | 14.33 | 0.13 | 0.56 | 0.115035 | 0.057517 |
| 2 | 2.00–4.00 | 0.26 | 17.88 | 15.86 | 0.16 | 0.48 | 0.120744 | 0.060372 |
| 3 | 4.00–6.00 | 0.22 | 17.88 | 16.75 | 0.18 | 0.40 | 0.112279 | 0.056140 |
| 4 | 6.00–8.00 | 0.18 | 17.88 | 17.39 | 0.19 | 0.32 | 0.096751 | 0.048376 |
| 5 | 8.00–10.00 | 0.14 | 17.88 | 17.88 | 0.20 | 0.24 | 0.076727 | 0.038363 |
| Section No | Height from Ground (m) | Outer Diameter (m) | V0 (m/s) | Vb,0 (m/s) | q | A | W (kN) | W (kN/m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 45.00 | 36.07 | 0.81 | 0.56 | 0.728650 | 0.364325 |
| 2 | 2.00–4.00 | 0.26 | 45.00 | 39.92 | 1.00 | 0.48 | 0.764811 | 0.382405 |
| 3 | 4.00–6.00 | 0.22 | 45.00 | 42.17 | 1.11 | 0.40 | 0.711195 | 0.355597 |
| 4 | 6.00–8.00 | 0.18 | 45.00 | 43.76 | 1.20 | 0.32 | 0.612839 | 0.306420 |
| 5 | 8.00–10.00 | 0.14 | 45.00 | 45.00 | 1.27 | 0.24 | 0.486000 | 0.243000 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 1.80 | 1.63 | 0.17 | 47.59 | 0.01 | 3.65 | 0.40 | 0.92 | 0.37 | 0.03182 | 1.02 | 0.56 | 0.00039 |
| 2 | 2.00–4.00 | 0.26 | 1.99 | 2.23 | 0.14 | 47.59 | 0.01 | 6.14 | 0.38 | 0.92 | 0.35 | 0.03182 | 1.02 | 0.48 | 0.00052 |
| 3 | 4.00–6.00 | 0.22 | 2.10 | 2.49 | 0.13 | 47.59 | 0.01 | 7.44 | 0.35 | 0.92 | 0.32 | 0.03182 | 1.02 | 0.40 | 0.00049 |
| 4 | 6.00–8.00 | 0.18 | 2.18 | 2.68 | 0.13 | 47.59 | 0.01 | 8.48 | 0.30 | 0.92 | 0.28 | 0.03182 | 1.02 | 0.32 | 0.00038 |
| 5 | 8.00–10.00 | 0.14 | 2.24 | 2.84 | 0.12 | 47.59 | 0.01 | 9.36 | 0.22 | 0.92 | 0.20 | 0.03182 | 1.02 | 0.24 | 0.00023 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 14.33 | 12.99 | 0.17 | 5.96 | 0.03 | 232.60 | 0.75 | 0.92 | 0.69 | 0.87747 | 1.25 | 0.56 | 0.05606 |
| 2 | 2.00–4.00 | 0.26 | 15.86 | 17.81 | 0.14 | 5.96 | 0.03 | 390.98 | 0.75 | 0.92 | 0.69 | 0.87747 | 1.25 | 0.48 | 0.08076 |
| 3 | 4.00–6.00 | 0.22 | 16.75 | 19.87 | 0.13 | 5.96 | 0.03 | 474.04 | 0.75 | 0.92 | 0.69 | 0.87747 | 1.25 | 0.40 | 0.08157 |
| 4 | 6.00–8.00 | 0.18 | 17.39 | 21.40 | 0.13 | 5.96 | 0.03 | 540.37 | 0.74 | 0.92 | 0.69 | 0.87747 | 1.25 | 0.32 | 0.07436 |
| 5 | 8.00–10.00 | 0.14 | 17.88 | 22.63 | 0.12 | 5.96 | 0.03 | 596.34 | 0.74 | 0.92 | 0.68 | 0.87747 | 1.25 | 0.24 | 0.06151 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 36.07 | 32.70 | 0.17 | 2.37 | 0.06 | 1.473.30 | 0.82 | 0.92 | 0.75 | 2.33905 | 1.51 | 0.56 | 0.46813 |
| 2 | 2.00–4.00 | 0.26 | 39.92 | 44.82 | 0.14 | 2.37 | 0.06 | 2.476.55 | 0.82 | 0.92 | 0.76 | 2.33905 | 1.51 | 0.48 | 0.67619 |
| 3 | 4.00–6.00 | 0.22 | 42.17 | 50.01 | 0.13 | 2.37 | 0.06 | 3.002.63 | 0.82 | 0.92 | 0.76 | 2.33905 | 1.51 | 0.40 | 0.68539 |
| 4 | 6.00–8.00 | 0.18 | 43.76 | 53.87 | 0.13 | 2.37 | 0.06 | 3.422.77 | 0.83 | 0.92 | 0.76 | 2.33905 | 1.51 | 0.32 | 0.62776 |
| 5 | 8.00–10.00 | 0.14 | 45.00 | 56.96 | 0.12 | 2.37 | 0.06 | 3.777.30 | 0.83 | 0.92 | 0.77 | 2.33905 | 1.51 | 0.24 | 0.52298 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 1.80 | 1.63 | 0.17 | 47.73 | 0.01 | 3.65 | 0.40 | 0.92 | 0.37 | 0.03164 | 1.02 | 0.56 | 0.00039 |
| 2 | 2.00–4.00 | 0.26 | 1.99 | 2.23 | 0.14 | 47.73 | 0.01 | 6.14 | 0.38 | 0.92 | 0.35 | 0.03164 | 1.02 | 0.48 | 0.00052 |
| 3 | 4.00–6.00 | 0.22 | 2.10 | 2.49 | 0.13 | 47.73 | 0.01 | 7.44 | 0.35 | 0.92 | 0.32 | 0.03164 | 1.02 | 0.40 | 0.00049 |
| 4 | 6.00–8.00 | 0.18 | 2.18 | 2.68 | 0.13 | 47.73 | 0.01 | 8.48 | 0.30 | 0.92 | 0.28 | 0.03164 | 1.02 | 0.32 | 0.00038 |
| 5 | 8.00–10.00 | 0.14 | 2.24 | 2.84 | 0.12 | 47.73 | 0.01 | 9.36 | 0.22 | 0.92 | 0.20 | 0.03164 | 1.02 | 0.24 | 0.00023 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 14.33 | 12.99 | 0.17 | 6.10 | 0.03 | 232.60 | 0.75 | 0.92 | 0.69 | 0.85113 | 1.25 | 0.56 | 0.05587 |
| 2 | 2.00–4.00 | 0.26 | 15.86 | 17.81 | 0.14 | 6.10 | 0.03 | 390.98 | 0.75 | 0.92 | 0.69 | 0.85113 | 1.25 | 0.48 | 0.08048 |
| 3 | 4.00–6.00 | 0.22 | 16.75 | 19.87 | 0.13 | 6.10 | 0.03 | 474.04 | 0.75 | 0.92 | 0.69 | 0.85113 | 1.25 | 0.40 | 0.08129 |
| 4 | 6.00–8.00 | 0.18 | 17.39 | 21.40 | 0.13 | 6.10 | 0.03 | 540.37 | 0.74 | 0.92 | 0.69 | 0.85113 | 1.25 | 0.32 | 0.07410 |
| 5 | 8.00–10.00 | 0.14 | 17.88 | 22.63 | 0.12 | 6.10 | 0.03 | 596.34 | 0.74 | 0.92 | 0.68 | 0.85113 | 1.25 | 0.24 | 0.06130 |
| Section No | Height from Ground (m) | Outer Diameter (m) | Vb (m/s) | Vm(z) (m/s) | Iv(z) | C | F | qp(z) (kg/m.s2) | Cf,0 | ψλ | Cf | R2 | cscd | Aref | Fw (kN/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0–2.00 | 0.30 | 36.07 | 32.70 | 0.17 | 2.51 | 0.06 | 1.473.30 | 0.82 | 0.92 | 0.75 | 2.22329 | 1.49 | 0.56 | 0.46378 |
| 2 | 2.00–4.00 | 0.26 | 39.92 | 44.82 | 0.14 | 2.51 | 0.06 | 2.476.55 | 0.82 | 0.92 | 0.76 | 2.22329 | 1.49 | 0.48 | 0.66990 |
| 3 | 4.00–6.00 | 0.22 | 42.17 | 50.01 | 0.13 | 2.51 | 0.06 | 3.002.63 | 0.82 | 0.92 | 0.76 | 2.22329 | 1.49 | 0.40 | 0.67902 |
| 4 | 6.00–8.00 | 0.18 | 43.76 | 53.87 | 0.13 | 2.51 | 0.06 | 3.422.77 | 0.83 | 0.92 | 0.76 | 2.22329 | 1.49 | 0.32 | 0.62193 |
| 5 | 8.00–10.00 | 0.14 | 45.00 | 56.96 | 0.12 | 2.51 | 0.06 | 3.777.30 | 0.83 | 0.92 | 0.77 | 2.22329 | 1.49 | 0.24 | 0.51812 |
| Section No | Height from Ground (m) | W (kN/m) TS 498 | Fw (kN/m) (Constant) Eurocode 1 | Fw (kN/m) (Variable) Eurocode 1 |
|---|---|---|---|---|
| 1 | 0–2.00 | 0.00090300 | 0.00038556 | 0.00038555 |
| 2 | 2.00–4.00 | 0.00094800 | 0.00052427 | 0.00052426 |
| 3 | 4.00–6.00 | 0.00088100 | 0.00048590 | 0.00048589 |
| 4 | 6.00–8.00 | 0.00075900 | 0.00038245 | 0.00038244 |
| 5 | 8.00–10.00 | 0.00060200 | 0.00022723 | 0.00022722 |
| Section No | Height from Ground (m) | W (kN/m) TS 498 | Fw (kN/m) (Constant) Eurocode 1 | Fw (kN/m) (Variable) Eurocode 1 |
|---|---|---|---|---|
| 1 | 0–2.00 | 0.05752 | 0.05606 | 0.05587 |
| 2 | 2.00–4.00 | 0.06037 | 0.08076 | 0.08048 |
| 3 | 4.00–6.00 | 0.05614 | 0.08157 | 0.08129 |
| 4 | 6.00–8.00 | 0.04838 | 0.07436 | 0.07410 |
| 5 | 8.00–10.00 | 0.03836 | 0.06151 | 0.06130 |
| Section No | Height from Ground (m) | W (kN/m) TS 498 | Fw (kN/m) (Constant) Eurocode 1 | Fw (kN/m) (Variable) Eurocode 1 |
|---|---|---|---|---|
| 1 | 0–2.00 | 0.36433 | 0.46813 | 0.46378 |
| 2 | 2.00–4.00 | 0.38241 | 0.67619 | 0.66990 |
| 3 | 4.00–6.00 | 0.35560 | 0.68539 | 0.67902 |
| 4 | 6.00–8.00 | 0.30642 | 0.62776 | 0.62193 |
| 5 | 8.00–10.00 | 0.24300 | 0.52298 | 0.51812 |
| TS498 | Eurocode 1 | |||||
|---|---|---|---|---|---|---|
| Wind Speed (m/s) | Displacement (cm) (First Mode Frequency Constant) | Displacement (cm) (First Mode Frequency Variable) | Difference (%) | Displacement (cm) (First Mode Frequency Constant) | Displacement (cm) (First Mode Frequency Variable) | Difference (%) |
| 2.24 | 0.0420 | 0.0417 | 0.71 | 0.0194 | 0.0193 | 0.52 |
| 17.88 | 2.67 | 2.5412 | 4.82 | 4.0679 | 3.8525 | 5.30 |
| 45 | 16.94 | 15.06 | 11.10 | 34.39 | 30.3 | 11.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Türkeli, E.; Cokli, D. The Effect of Wind Speed on Structural Along-Wind Response of a Lighting Pole According to TS498 and Eurocode 1. Buildings 2025, 15, 1085. https://doi.org/10.3390/buildings15071085
Türkeli E, Cokli D. The Effect of Wind Speed on Structural Along-Wind Response of a Lighting Pole According to TS498 and Eurocode 1. Buildings. 2025; 15(7):1085. https://doi.org/10.3390/buildings15071085
Chicago/Turabian StyleTürkeli, Erdem, and Deniz Cokli. 2025. "The Effect of Wind Speed on Structural Along-Wind Response of a Lighting Pole According to TS498 and Eurocode 1" Buildings 15, no. 7: 1085. https://doi.org/10.3390/buildings15071085
APA StyleTürkeli, E., & Cokli, D. (2025). The Effect of Wind Speed on Structural Along-Wind Response of a Lighting Pole According to TS498 and Eurocode 1. Buildings, 15(7), 1085. https://doi.org/10.3390/buildings15071085







