An Enhanced Load-Transfer Model for Pile-Supported Embankments Incorporating Slip Between Pile and Soil
Abstract
:1. Introduction
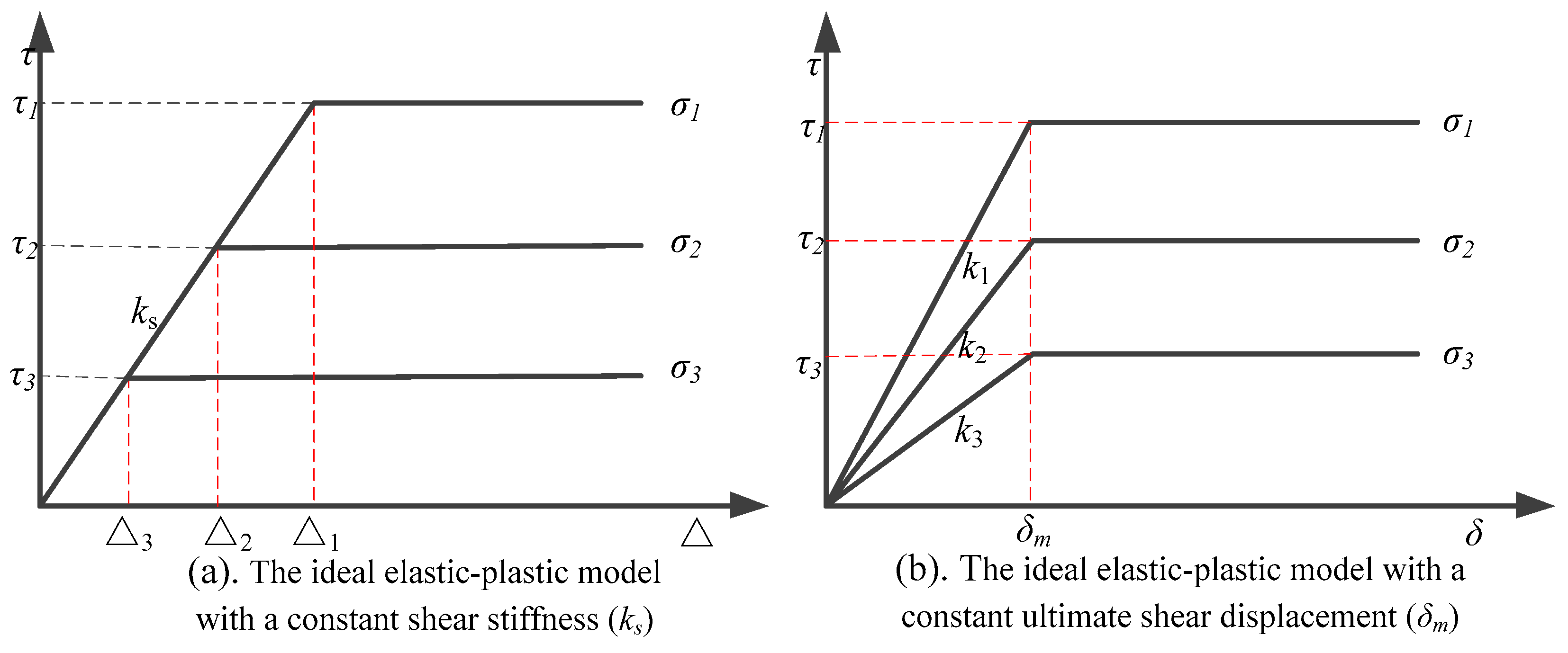
2. Improved Ideal Elastic-Plastic Model
3. Mathematical Model
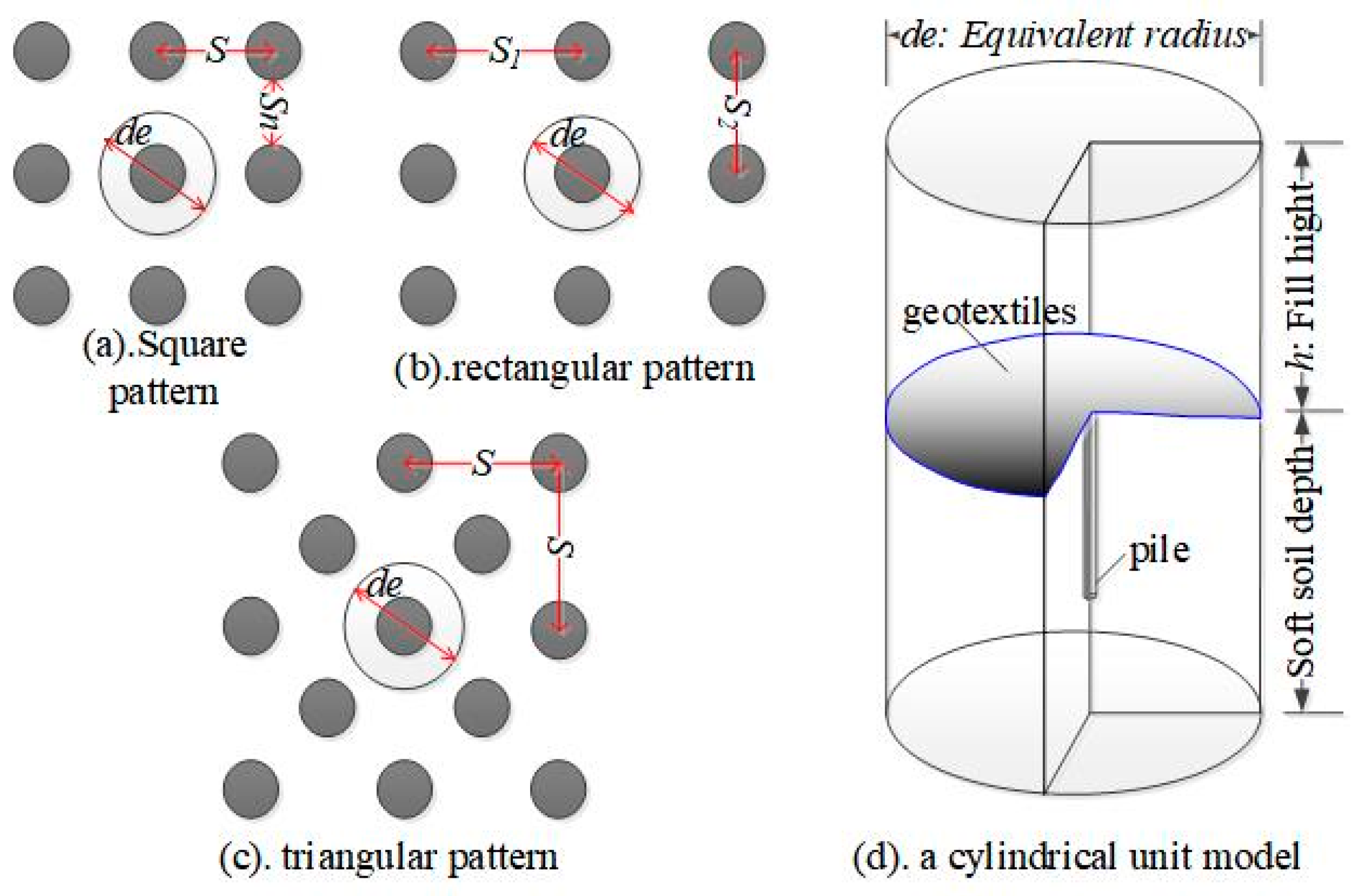
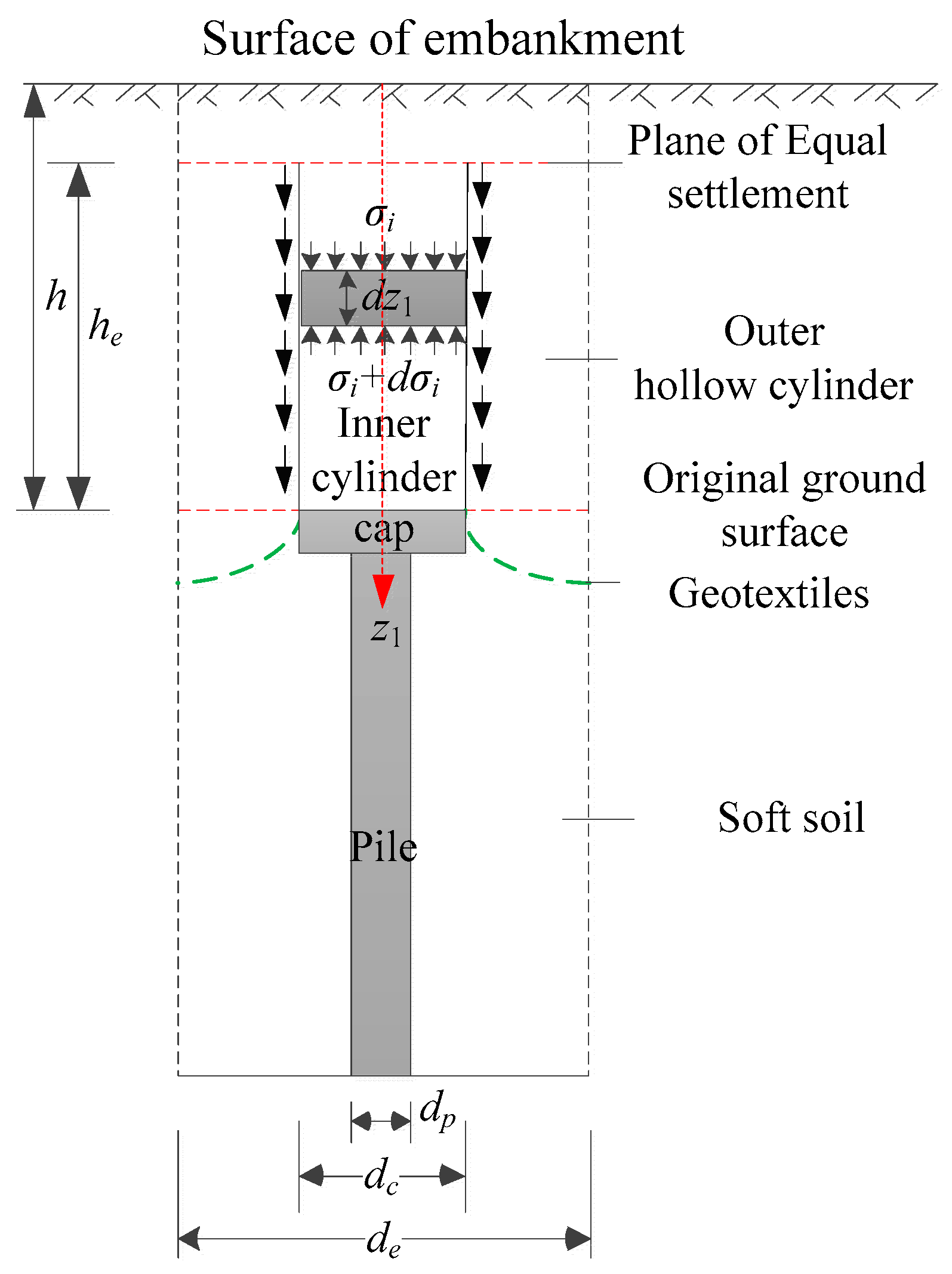
3.1. Analytical Model
3.2. Load Transfer in the Embankment
- The fill material is assumed to be homogeneous, isotropic, and non-cohesive. This means that the material properties are uniform throughout the volume and do not vary with direction. The material is characterized by the internal friction angle φe, the unit weight γe, and Young’s modulus Ee.
- It is assumed that the pile, soil, and embankment fill experience vertical compression only, with any lateral deformations being neglected. This assumption is made to focus on the primary load transfer mechanism in the system, which is vertical compression due to the weight of the embankment and applied loads.
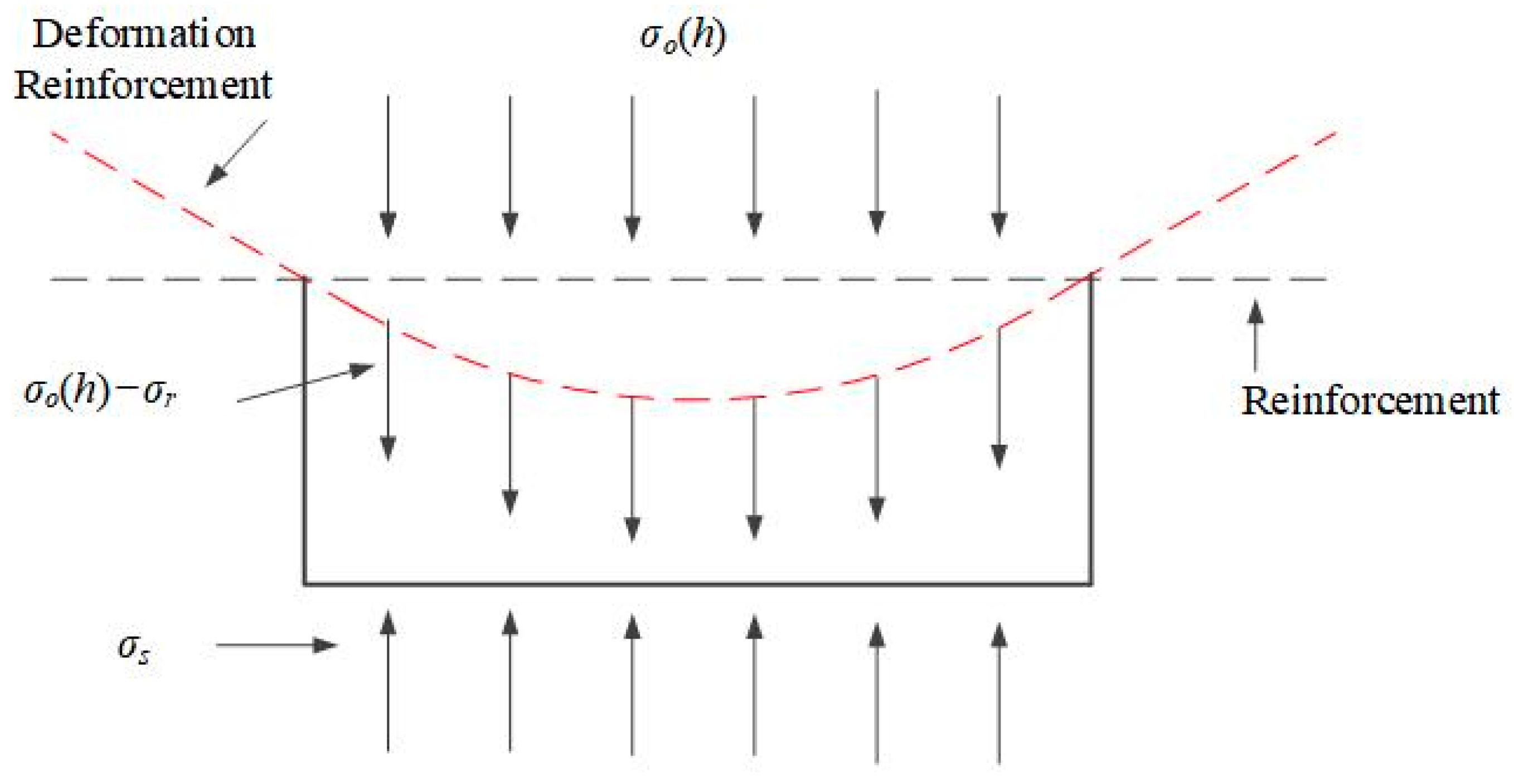
3.3. Load Transfer Within Tensile Reinforcement
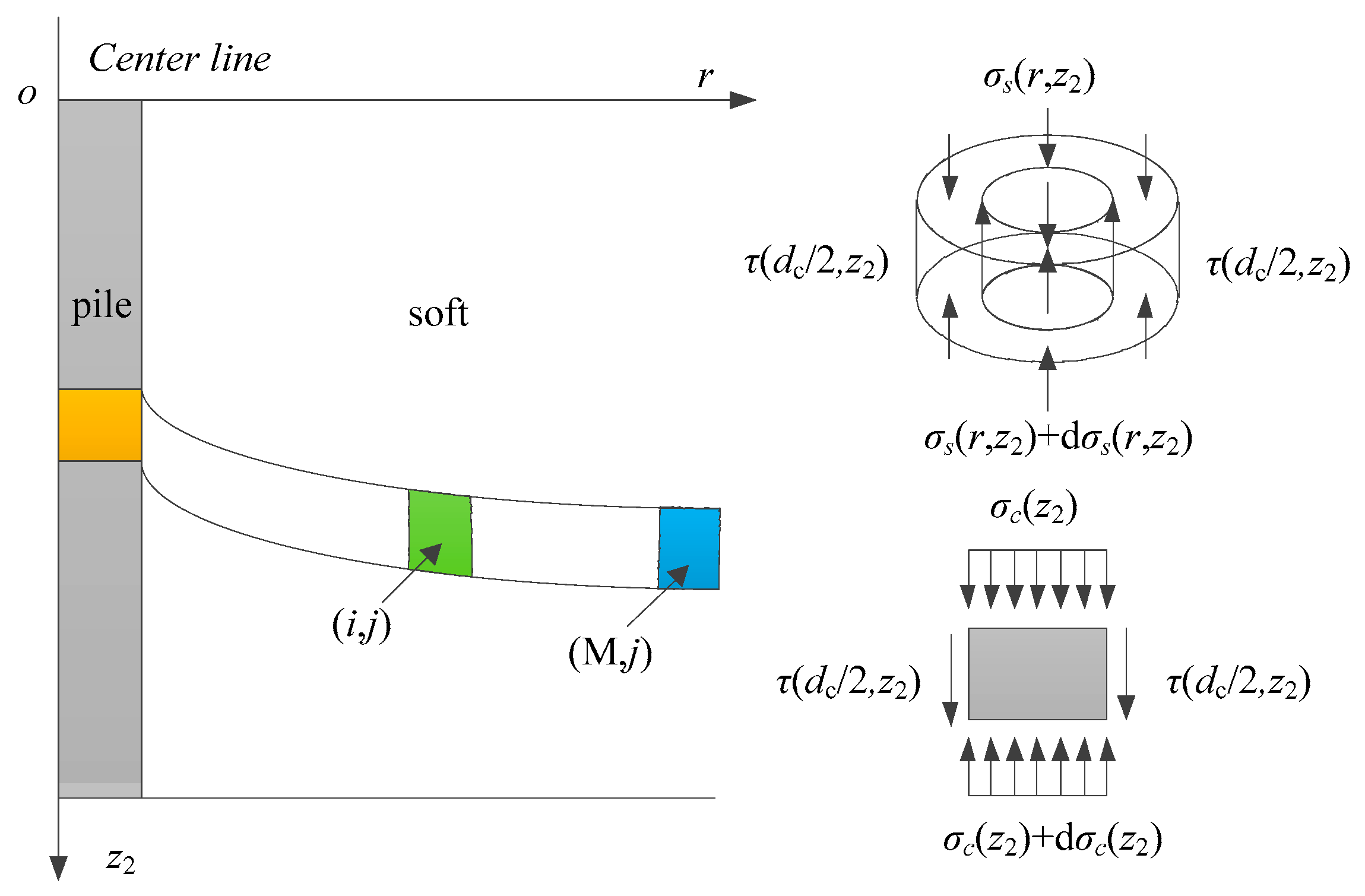
3.4. Load Transfer Within Reinforced Areas
3.5. Solution
4. Determining the Calculation Parameters
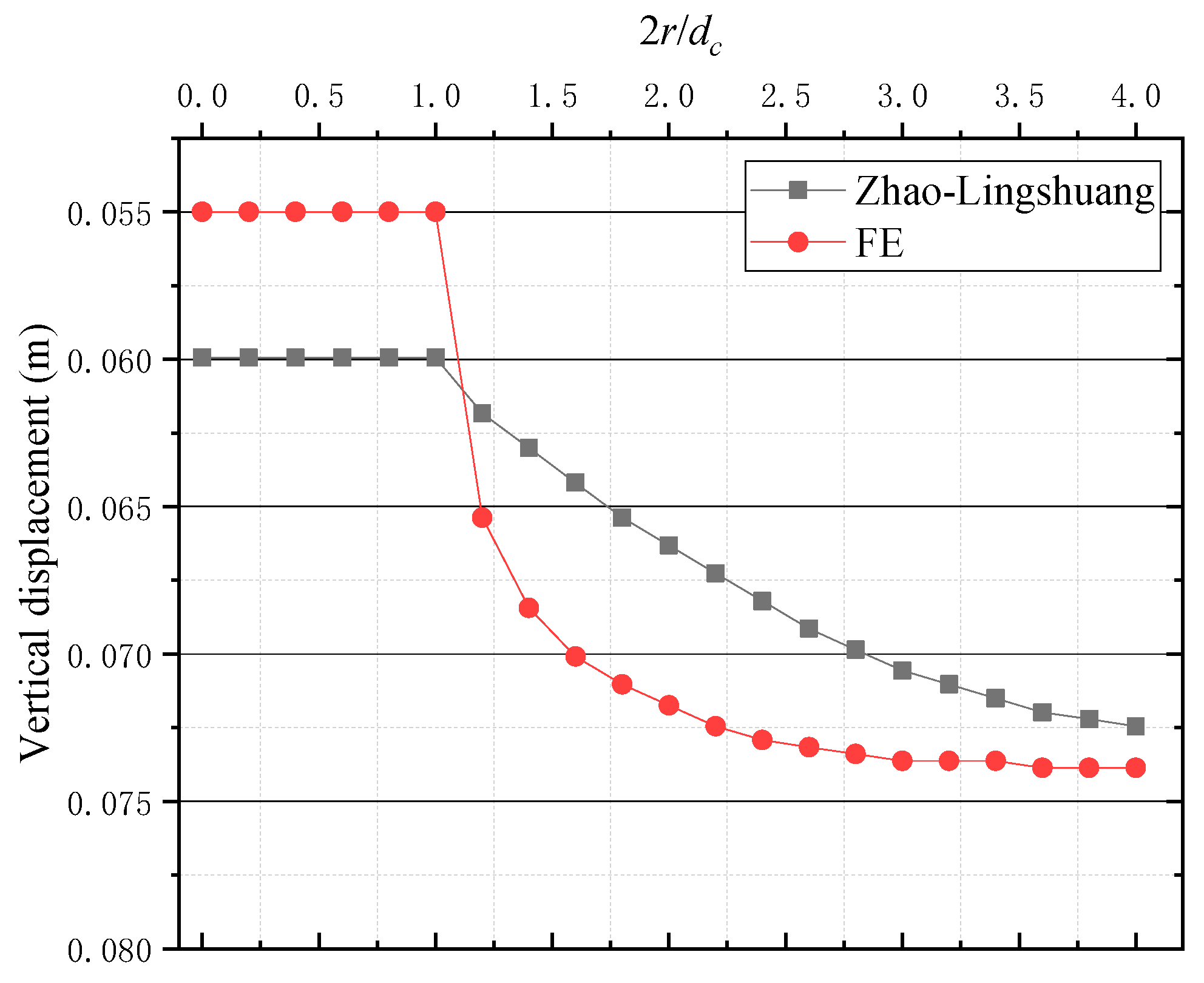
5. Validation
Comparison with the Finite Difference Element (FDE) Model
6. Conclusions
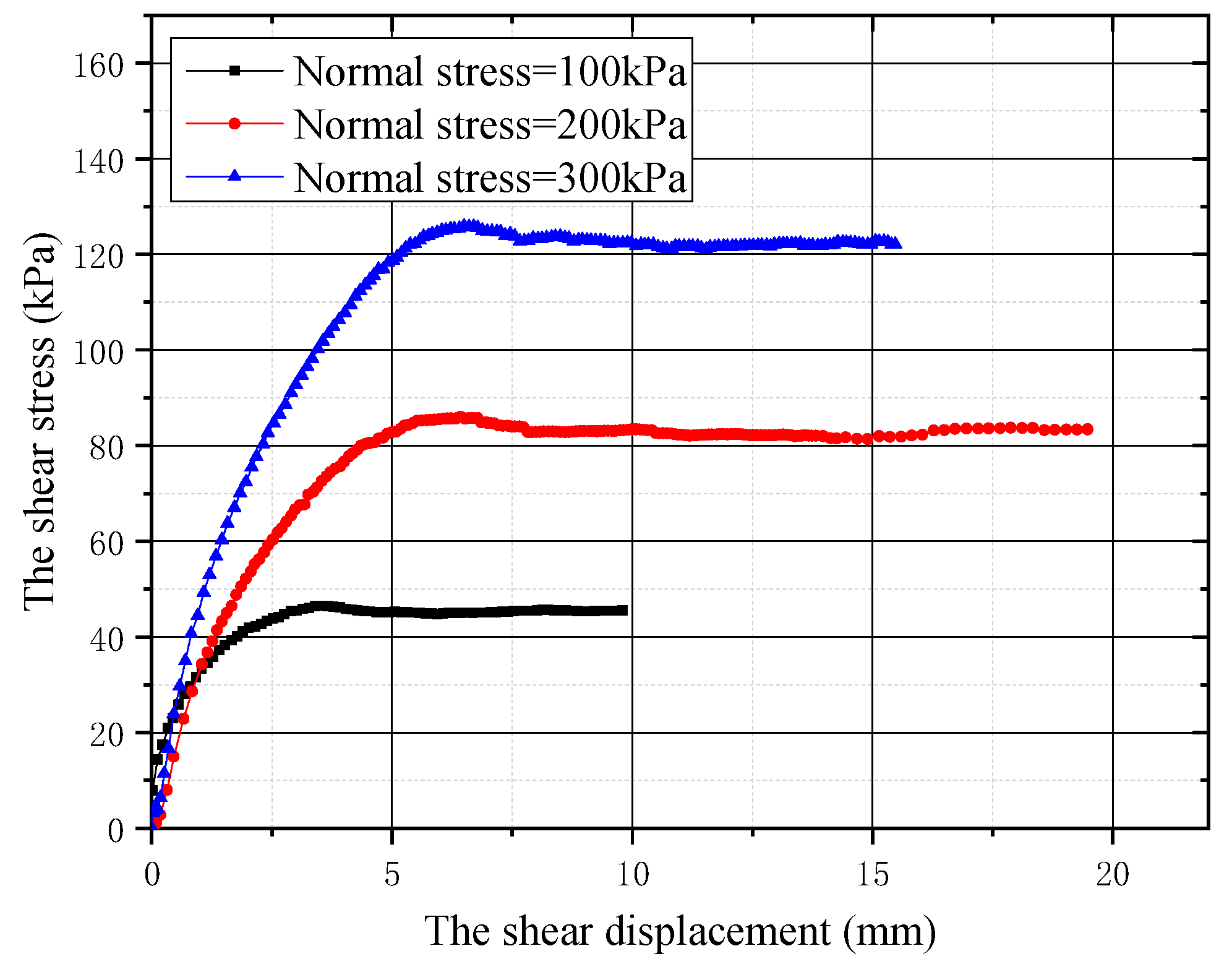
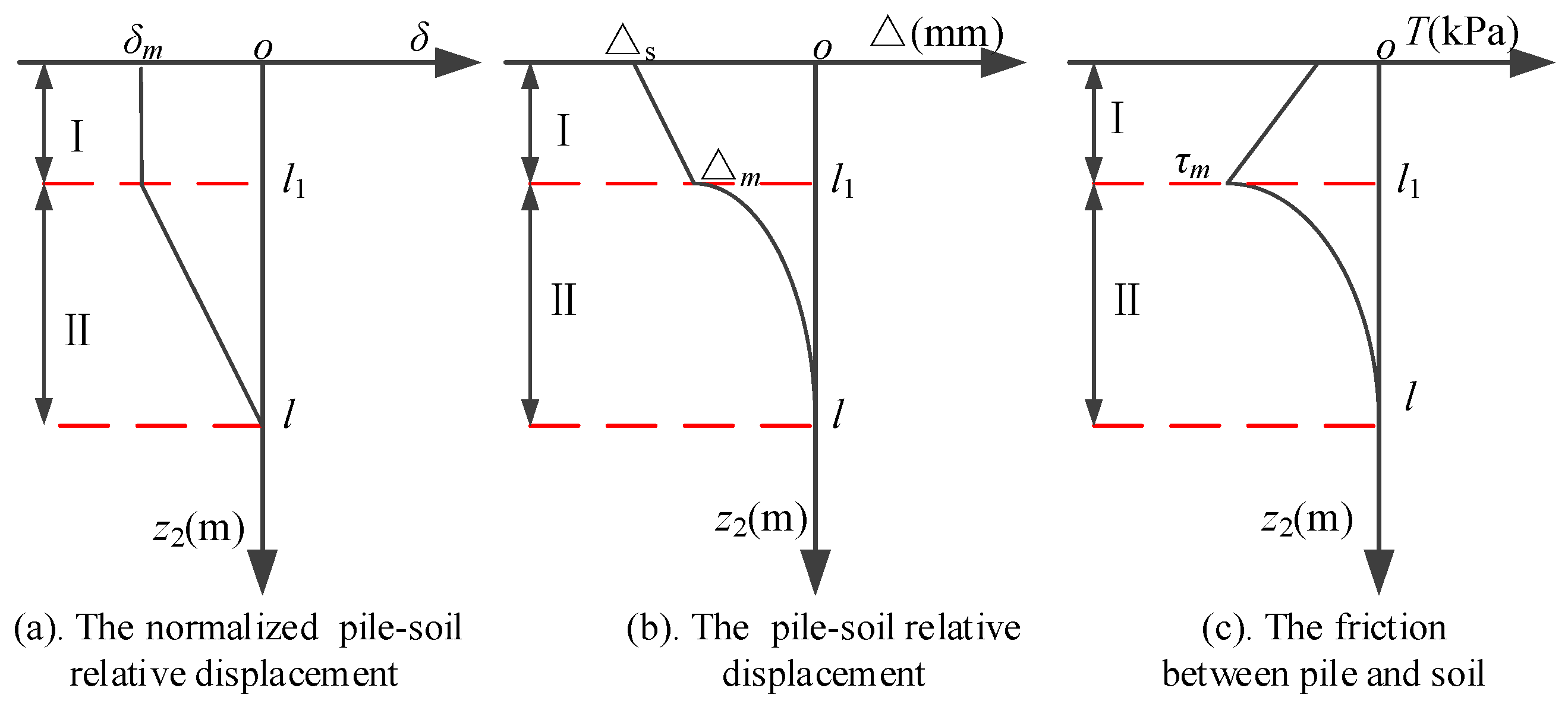
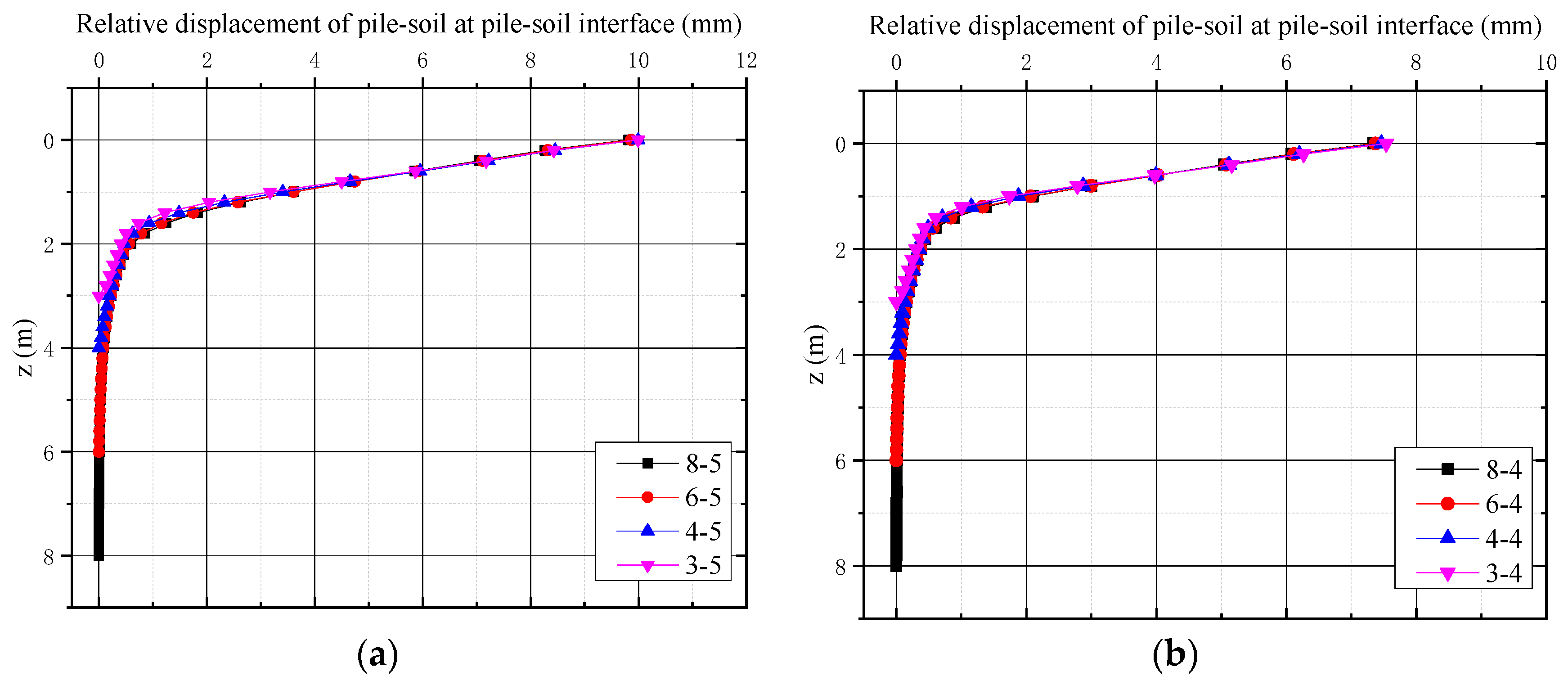
- According to experimental data and numerical results, relative slippage at the pile–soil contact surface is a significant phenomenon under the load of the embankment and should not be overlooked in theoretical calculations.
- The relative displacement between the pile and soil initially exhibits a linear relationship with depth and later follows a quadratic function as the depth increases.
- When determining the ultimate shear stress between the soil and structure, the improved ideal elastic-plastic model, assuming a constant ultimate shear displacement regardless of normal stress, proves to be more appropriate compared to the ideal elastic-plastic model assuming a constant shear stiffness regardless of normal stress, as supported by experimental findings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abusharar, S.W.; Zheng, J.-J.; Chen, B.-G.; Yin, J.-H. A simplified method for analysis of a piled embankment reinforced with geosynthetics. Geotext. Geomembr. 2009, 27, 39–52. [Google Scholar] [CrossRef]
- Ikbarieh, A.; Izadifar, M.; Abu-Farsakh, M.Y.; Voyiadjis, G.Z. A parametric study of embankment supported by geosynthetic reinforced load transfer platform and timber piles tip on sand. Transp. Geotech. 2023, 38, 100901. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Zhou, S.; Lin, W.; Chen, Y.H.; Zhao, M.H. Numerical multi-span segmented trapdoor test with viscoelastic boundary for soil arching within pile-supported embankment under cyclic loading. Int. J. Numer. Anal. Methods Geomech. 2023, 48, 28–54. [Google Scholar]
- Wu, G.; Zhao, M.; Zhang, C. Experimental Investigation on the Evolution of Soil Arching in Cohesive Soils Using a DIC Technique. Int. J. Geomech. 2024, 24, 04023270. [Google Scholar]
- Zhuang, Y.; Wang, K.Y.; Liu, H.L. A simplified model to analyze the reinforced piled embankments. Geotext. Geomembr. 2014, 42, 154–165. [Google Scholar] [CrossRef]
- Diao, Y.; Guo, Y.; Jia, Z.; Zheng, G.; Pan, W.; Shang, D.; Zhang, Y. A simplified method for investigating the bending behavior of piles supporting embankments on soft ground. Front. Struct. Civ. Eng. 2023, 17, 1021–1032. [Google Scholar]
- Ma, L.; Shen, S.; Luo, C.; Xu, Y. Field Evaluation on the Strength Increase of Marine Clay under Staged Construction of Embankment. Mar. Georesources Geotechnol. 2011, 29, 317–332. [Google Scholar]
- Zhang, C.; Zhao, M.; Zhao, H.; Zhou, S. Simplified Model of Column-Supported Embankment to Account for Nonuniform Deformations of Soils. J. Eng. Mech. 2020, 146, 04020060. [Google Scholar]
- Zhang, N.; Shen, S.L.; Wu, H.N.; Chai, J.C.; Xu, Y.S.; Yin, Z.Y. Evaluation of effect of basal geotextile reinforcement under embankment loading on soft marine deposits. Geotext. Geomembr. 2015, 43, 506–514. [Google Scholar] [CrossRef]
- Indraratna, B. Recent Advances in Vertical Drains and Vacuum Preloading for Soft Ground Stabilisation. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–21 September 2017; International Society for Soil Mechanics and Geotechnical Engineering: London, UK, 2017; pp. 141–166. [Google Scholar]
- Le, G.L.; Bergado, D.T.; Nguyen, T.N.T. Soft Ground Improved by Prefabricated Vertical Drains with Vacuum and Thermal Preloading. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering (ICSMGE), Paris, France, 19–20 February 2018. [Google Scholar]
- Georgiannou, N.V.; Konstadinou, M.; Triantafyllos, P. Sand Behavior under Stress States Involving Principal Stress Rotation. J. Geotech. Geoenviron. Eng. 2018, 144, 04018028. [Google Scholar] [CrossRef]
- Wang, T.; Wang, P.; Yin, Z.-Y.; Zhang, F.; Xu, C. DEM-DFM Modeling Suffusion of Granular Soils under Triaxial Compression. Int. J. Geomech. 2025, 25, 2. [Google Scholar]
- Song, S.; Wang, P.; Yin, Z. Micromechanical modeling of hollow cylinder torsional shear test on sand using discrete element method. J. Rock Mech. Geotech. Eng. 2024, 16, 5193–5208. [Google Scholar] [CrossRef]
- Lai, H.J.; Zheng, J.J.; Zhang, R.J.; Cui, M.J. Classification and characteristics of soil arching structures in pile-supported embankments. Comput. Geotech. 2018, 98, 153–171. [Google Scholar] [CrossRef]
- Lu, W.; Miao, L. A simplified 2-D evaluation method of the arching effect for geosynthetic-reinforced and pile-supported embankments. Comput. Geotech. 2015, 65, 97–103. [Google Scholar] [CrossRef]
- Terzaghi, B.K. Theoretical Soil Mechanics; John Wiley & Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Guido, V.A.; Kneuppel, J.D.; Sweeney, M.A. Plate loading test on geogrid reinforced earth slabs. In Proceedings of the Geosynthetics ‘87, New Orleans, LA, USA, 24–25 February 1987; IFAI: Roseville, MN, USA, 1987; pp. 216–225. [Google Scholar]
- Collin, J.G. Column supported embankment design considerations. In Proceedings of the 52th Annual Geotechnical Engineering Conference, Falcon Heights, MN, USA, 27 February 2004; pp. 51–78. [Google Scholar]
- Hewlett, W.J.; Randolph, M.F. Analysis of piled embankments. Ground Eng. 1988, 21, 12–18. [Google Scholar]
- Kempfert, H.G.; Stadel, M.; Zaeske, D. Design of geosynthetic-reinforced bearing layers over piles. Bautechnik 1997, 74, 818–825. [Google Scholar]
- Van Eekelen, S.J.M.; Bezuijen, A.; van Tol, A.F. An analytical model for arching in piled embankments. Geotext. Geomembr. 2013, 39, 78–102. [Google Scholar] [CrossRef]
- Chen, R.P.; Chen, Y.M.; Han, J.; Xu, Z.Z. A theoretical solution for pile-supported embankments on soft soils under one-dimensional compression. Can. Geotech. J. 2008, 45, 611–623. [Google Scholar] [CrossRef]
- Stewart, M.E.; Filz, G.M. Influence of clay compressibility on geosynthetic loads in bridging layers for column-supported embankments. In Proceedings of the GeoFrontiers 2005, Austin, TX, USA, 24–26 January 2005; pp. 1–14. [Google Scholar]
- Naughton, P.J.; Kempton, G.T. Comparison of analytical and numerical analysis design methods for piled embankments. In Proceedings of the GeoFrontiers 2005, Austin, TX, USA, 24–26 January 2005; pp. 1–10. [Google Scholar]
- Ellis, E.; Aslam, R. Arching in piled embankments: Comparison of centrifuge tests and predictive methods—Part 2 of 2. Ground Eng. 2009, 42, 28–31. [Google Scholar]
- Han, J.; Wang, F.; Al-Naddaf, M.; Xu, C. Progressive Development of Two-Dimensional Soil Arching with Displacement. Int. J. Geomech. 2017, 17, 04017112. [Google Scholar] [CrossRef]
- Rui, R.; Han, J.; van Eekelen SJ, M.; Wan, Y. Experimental Investigation of Soil-Arching Development in Unreinforced and Geosynthetic-Reinforced Pile-Supported Embankments. J. Geotech. Geoenviron. Eng. 2019, 145, 04018103. [Google Scholar] [CrossRef]
- Alamgir, M.; Miura, N.; Poorooshasbh, H.B.; Madhav, M.R. Deformation analysis of soft ground reinforced by columnar inclusions. Comput. Geotech. 1996, 18, 267–290. [Google Scholar]
- Zhao, L.-S.; Zhou, W.-H.; Yuen, K.-V. A simplified axisymmetric model for column supported embankment systems. Comput. Geotech. 2017, 92, 96–107. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, S.K.; Choa, V. Arching in Piled Embankments. J. Geotech. Eng. 1992, 120, 1917–1938. [Google Scholar]
- Deb, K. A mathematical model to study the soil arching effect in stone column-supported embankment resting on soft foundation soil. Appl. Math. Model. 2010, 34, 3871–3883. [Google Scholar]
- BS 8006:2010; British Standard Code of Practice for Strengthened, Reinforced Soils and Other Fills. British Standards Institution: London, UK, 2010.
- GGS (German Geotechnical Society). Recommendation for Design and Analysis of Earth Structures Using Geosynthetic Reinforcements, EBGEO; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Indraratna, B.; Basack, S.; Rujikiatkamjorn, C. Numerical solution of stone column–improved soft soil considering arching. J. Geotech. Geoenviron. Eng. 2013, 139, 377–394. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, M.; Hu, Y.; Zhao, H.; Chen, B. Semi-analytical solutions for geosynthetic-reinforced and pile-supported embankment. Comput. Geotech. 2012, 44, 167–175. [Google Scholar] [CrossRef]
- Deb, K.; Mohapatra, S.R. Analysis of stone column-supported geosynthetic-reinforced embankments. Appl. Math. Model. 2013, 37, 2943–2960. [Google Scholar] [CrossRef]
- Shi, P. Pile Foundation Engineering Manual; China Communications Press: Beijing, China, 2008; pp. 178–194. [Google Scholar]
- Kezdi, A. Bearing capacity of piles and pile groups. In Proceedings of the IV ICSMFE, London, UK, 12–24 August 1957; pp. 46–51. [Google Scholar]
- Richard, R.M.; Abbott, B.J. Versatile Elastic-Plastic Stress-Strain Formula. J. Eng. Mech. Div. 1975, 101, 511–515. [Google Scholar]
- Kraft, L.M.; Richard, P.R.; Takaaki, K. Theoretical t-z Curves. J. Geotech. Eng. Div. 1981, 107, 1543–1561. [Google Scholar]
- Heydinger, A.G. Recommendations: Load-Transfer Criteria for Piles in Clay; Dept of Civil Engineering, University of Toledo: Toledo, OH, USA, 1987. [Google Scholar]
- Coombs, W.M.; Crouch, R.S.; Heaney, C.E. Observations on Mohr-Coulomb plasticity under plane strain. J. Eng. Mech. 2013, 139, 1218–1228. [Google Scholar] [CrossRef]
- Xu, X.; Dai, Z. Numerical implementation of a modified Mohr–Coulomb model and its application in slope stability analysis. J. Mod. Transp. 2017, 25, 40–51. [Google Scholar]
- Zvi, G.; Gellert, M.; Eitan, R. Analysis of arching pressures in ideal elastic soil. J. Soil Mech. Found. Div. 1970, 96, 1357–1372. [Google Scholar]
- Wu, G.; Zhao, M.; Zhao, H.; Xiao, Y. Effect of eccentric load on the undrained bearing capacity of strip footings above voids. Int. J. Geomech. 2020, 20, 04020078. [Google Scholar] [CrossRef]
- Wu, G.; Zhao, H.; Zhao, M.; Zhu, Z. Stochastic analysis of dual tunnels in spatially random soil. Comput. Geotech. 2021, 129, 103861. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, R.; Zhao, M.; Zhou, S. Undrained stability analysis of eccentrically loaded strip footing lying on layered slope by finite element limit analysis. Comput. Geotech. 2020, 123, 103600. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, G. Seismic Stability of Dual Tunnels in Cohesive–Frictional Soil Subjected to Surcharge Loading. Appl. Sci. 2022, 12, 2779. [Google Scholar] [CrossRef]
- Randolph, M.F.; Wroth, C.P. Analysis of deformation of vertically loaded piles. J. Geotech. Eng. Div. 1978, 104, 1465–1488. [Google Scholar] [CrossRef]
- Reddy, E.S.; Chapman, D.N.; Sastry, V.V.R.N. Direct Shear Interface Test for Shaft Capacity of Piles in Sand. Geotech. Test. J. 2000, 23, 199–205. [Google Scholar] [CrossRef]
- Gómez, J.E.; Filz, G.M.; Ebeling, R.M.; Dove, J.E. Sand-to-Concrete Interface Response to Complex Load Paths in a Large Displacement Shear Box. Geotech. Test. J. 2008, 31, 358–369. [Google Scholar] [CrossRef]
- Borges, J.L.; Marques, D.O. Geosynthetic-reinforced and jet grout column-supported embankments on soft soils: Numerical analysis and parametric study. Comput. Geotech. 2011, 38, 883–896. [Google Scholar] [CrossRef]
- Wong, K.S.; Teh, C.I. Negative Skin Friction on Piles in Layered Soil Deposits. J. Geotech. Eng. 1995, 121, 457–465. [Google Scholar]
- Zhang, J.; Cui, X.; Huang, D.; Jin, Q.; Lou, J.; Tang, W. Numerical Simulation of Consolidation Settlement of Pervious Concrete Pile Composite Foundation under Road Embankment. Int. J. Geomech. 2016, 16, 1. [Google Scholar] [CrossRef]
- Wang, F.; Han, J.; Miao, L.-C.; Bhandari, A. Numerical Analysis of Embankments Supported by Geosynthetics over Drilled Shafts in Karst Terrains. Geosynth. Int. 2009, 16, 408–419. [Google Scholar] [CrossRef]
- Han, J.; Gabr, M.A. Numerical Analysis of Geosynthetic-Reinforced and Pile-Supported Earth Platforms over Soft Soil. J. Geotech. Geoenviron. Eng. 2002, 128, 44–53. [Google Scholar] [CrossRef]



| Analytical Method | Considering Soil Arching | Considering Pile–Soil Interaction |
|---|---|---|
| H&R (1988) [20] | Yes | No |
| Low et al. (1994) [31] | Yes | No |
| Chen et al. (2008) [23] | Yes | Yes |
| Abusharar et al. (2009) [1] | Yes | No |
| Deb (2010) [32] | Yes | No |
| BSI (2010) [33] | Yes | No |
| GGS (2010) [34] | Yes | No |
| Indraratna et al. (2013) [35] | Yes | No |
| Zhang et al. (2012) [36] | No | No |
| Deb and Mohapatra (2013) [37] | Yes | No |
| Van Eekelen et al. (2013) [22] | Yes | No |
| Zhuang et al. (2014) [5] | Yes | No |
| Lu and Miao (2015) [16] | Yes | No |
| Zhao Lin-Shuang (2017) [30] | Yes | Yes |
| Embankment | h = 5 m, γe = 20 kN/m3, Ee = 30 MPa, υe = 0.35, φe = 25° |
|---|---|
| Soft soil | γs = 16.8 kN/m3, Es = 2.06 MPa, υs = 0.35, φs = 9°, c = 10 kPa |
| pile | γp = 25 kN/m3, Ep = 20,000 MPa, υc = 0.15, d = 0.38 m, S = 1.8 m |
| Project | Embankment Height (5 m) | Embankment Height (4 m) | Average | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Pile: 8 m | Pile: 6 m | Pile: 4 m | Pile: 3 m | Pile: 8 m | Pile: 6 m | Pile: 4 m | Pile: 3 m | ||
| δm | 0.00572 | 0.00581 | 0.00609 | 0.00628 | 0.00525 | 0.00532 | 0.00527 | 0.00581 | 0.00600 |
| The Pile–Soil Stress Ratios | The Height of Equal Settlement Plane | |||
|---|---|---|---|---|
| FLAC | Proposed model | FLAC | Proposed model | |
| Case of l = 6, h = 4 | 5.525 | 5.602 | 1.36 | 1.192 |
| Case of l = 6, h = 4 | 5.947 | 6.024 | 1.4 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Tan, Y.; Huang, C.; Liu, Y.; Yue, S.; Wu, G. An Enhanced Load-Transfer Model for Pile-Supported Embankments Incorporating Slip Between Pile and Soil. Buildings 2025, 15, 1086. https://doi.org/10.3390/buildings15071086
Zhang C, Tan Y, Huang C, Liu Y, Yue S, Wu G. An Enhanced Load-Transfer Model for Pile-Supported Embankments Incorporating Slip Between Pile and Soil. Buildings. 2025; 15(7):1086. https://doi.org/10.3390/buildings15071086
Chicago/Turabian StyleZhang, Chengfu, Yongjie Tan, Chaoguang Huang, Yufei Liu, Shao Yue, and Gaoqiao Wu. 2025. "An Enhanced Load-Transfer Model for Pile-Supported Embankments Incorporating Slip Between Pile and Soil" Buildings 15, no. 7: 1086. https://doi.org/10.3390/buildings15071086
APA StyleZhang, C., Tan, Y., Huang, C., Liu, Y., Yue, S., & Wu, G. (2025). An Enhanced Load-Transfer Model for Pile-Supported Embankments Incorporating Slip Between Pile and Soil. Buildings, 15(7), 1086. https://doi.org/10.3390/buildings15071086





