Effect of Local Strengthening on the Overall Seismic Performance of Reinforced Concrete Frame Structures
Abstract
:1. Introduction
2. Engineering Background
2.1. Structural Parameters of the Project
2.2. Strengthening and Retrofitting Scheme
2.3. Mechanical Properties of Strengthened Materials
3. Finite Element Modeling Procedure
3.1. Description of the RC Frame Model
3.2. Material Model
3.3. Loading Conditions
4. Results and Discussion
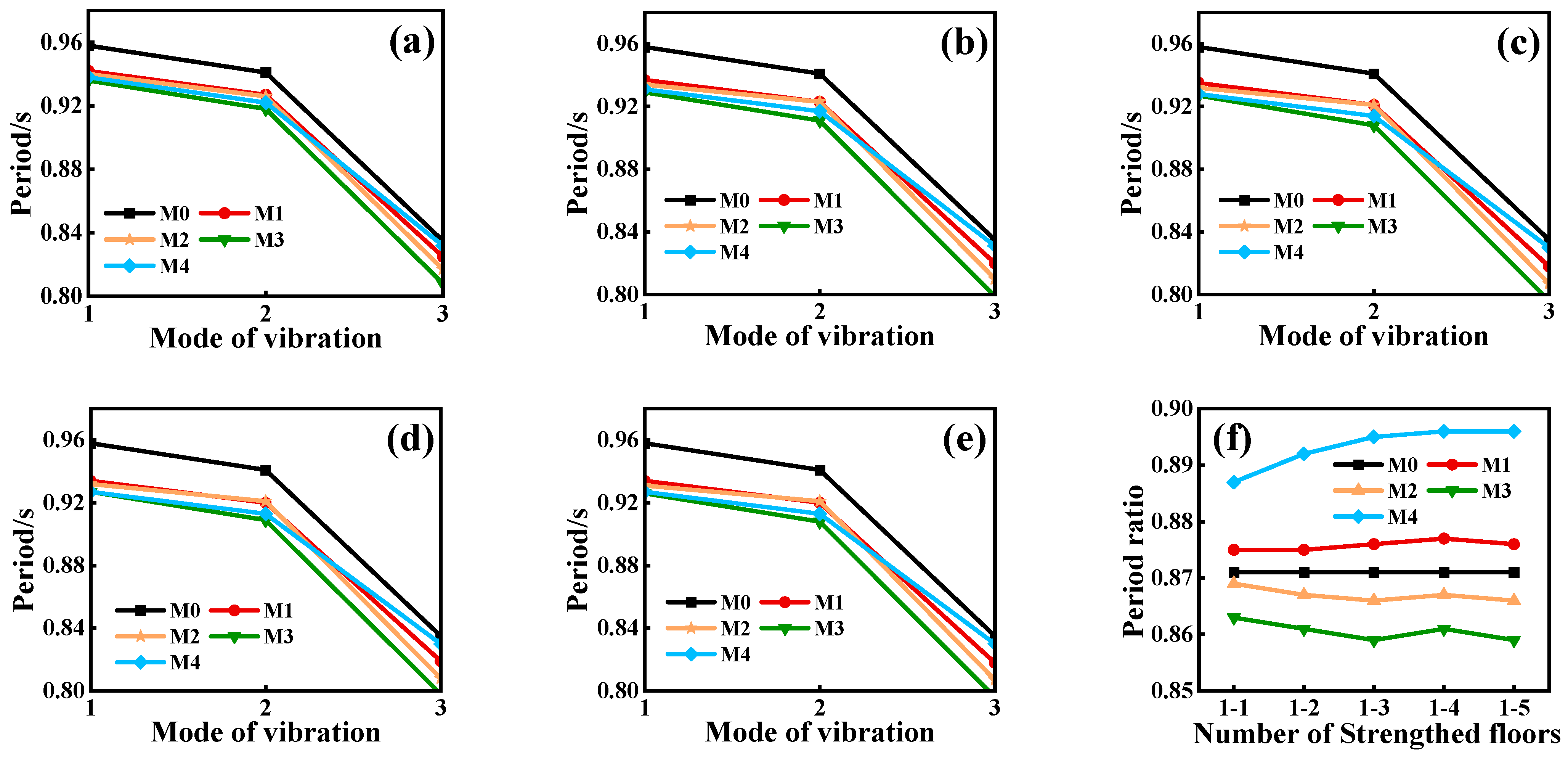
4.1. Mode of Vibration
4.2. Period
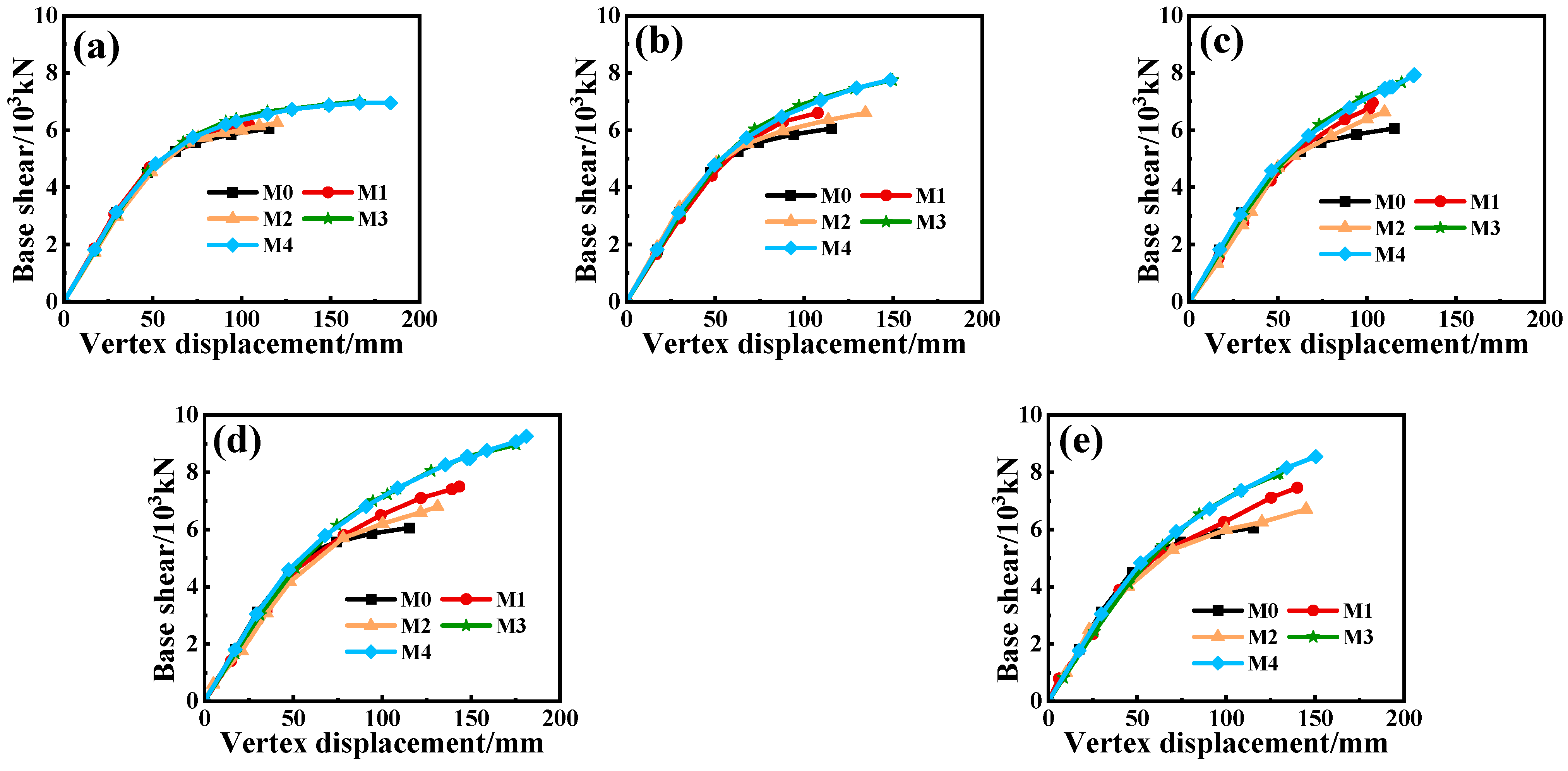
4.3. Base Shear vs. Vertex Displacement
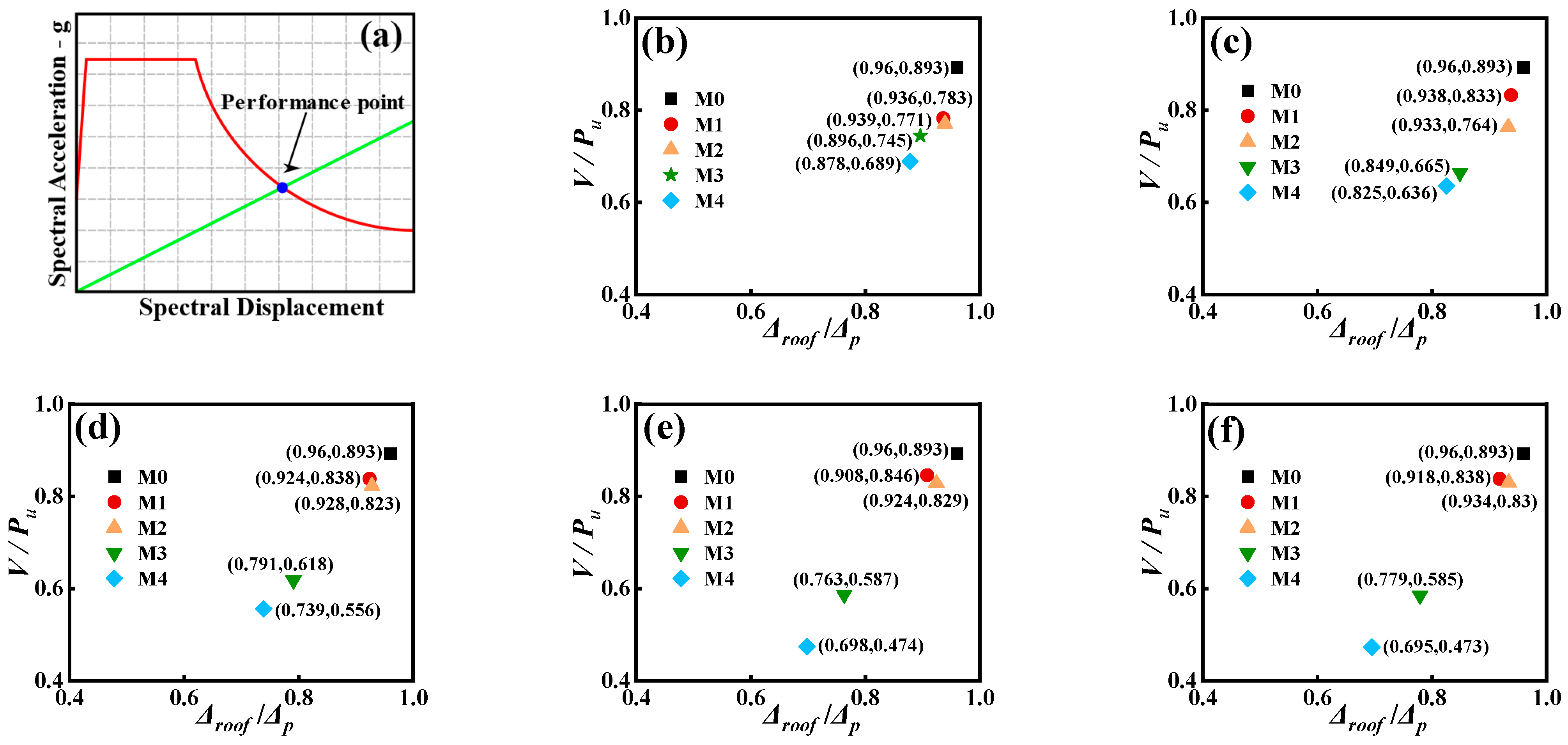
4.4. Performance Point
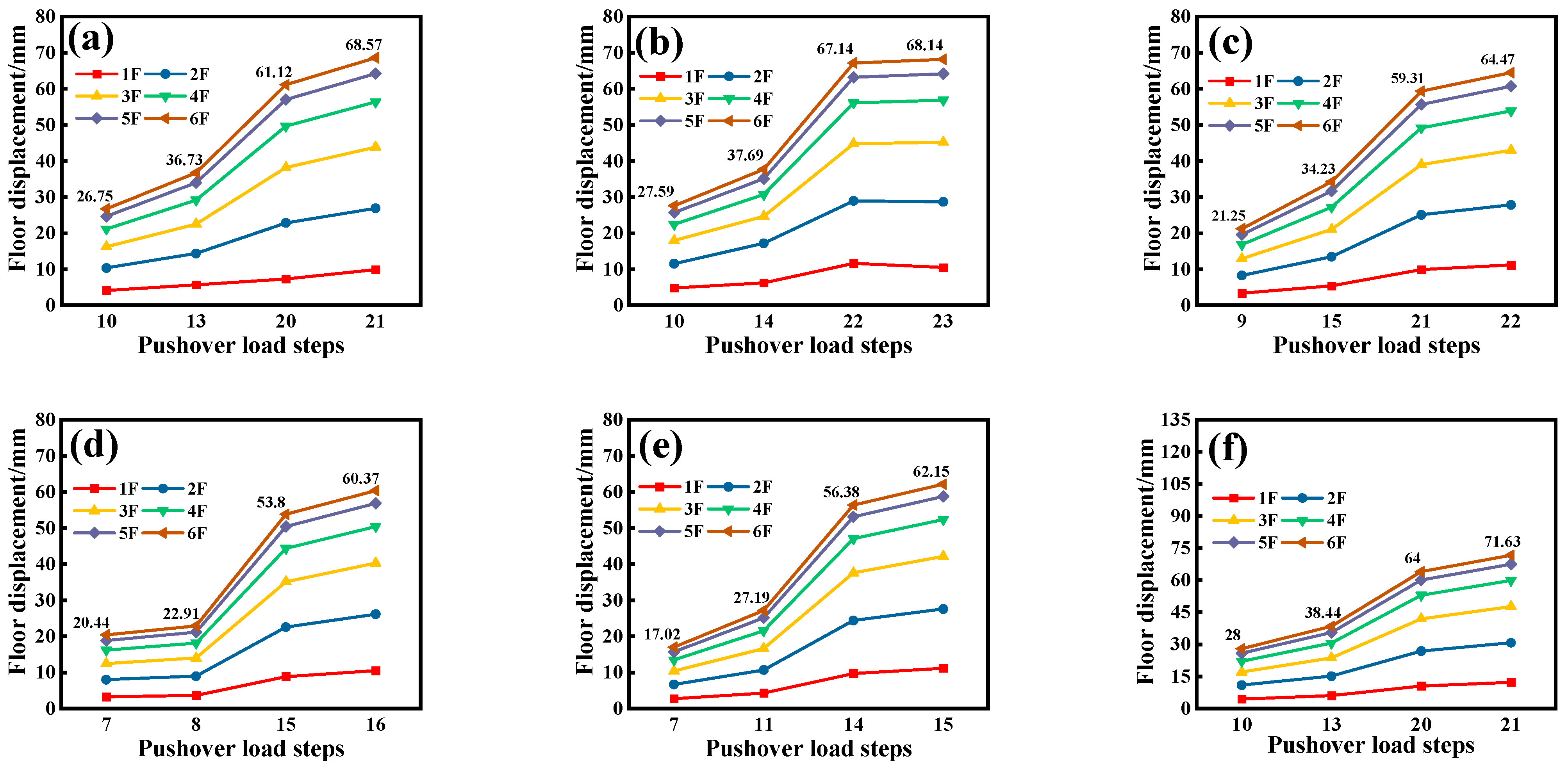
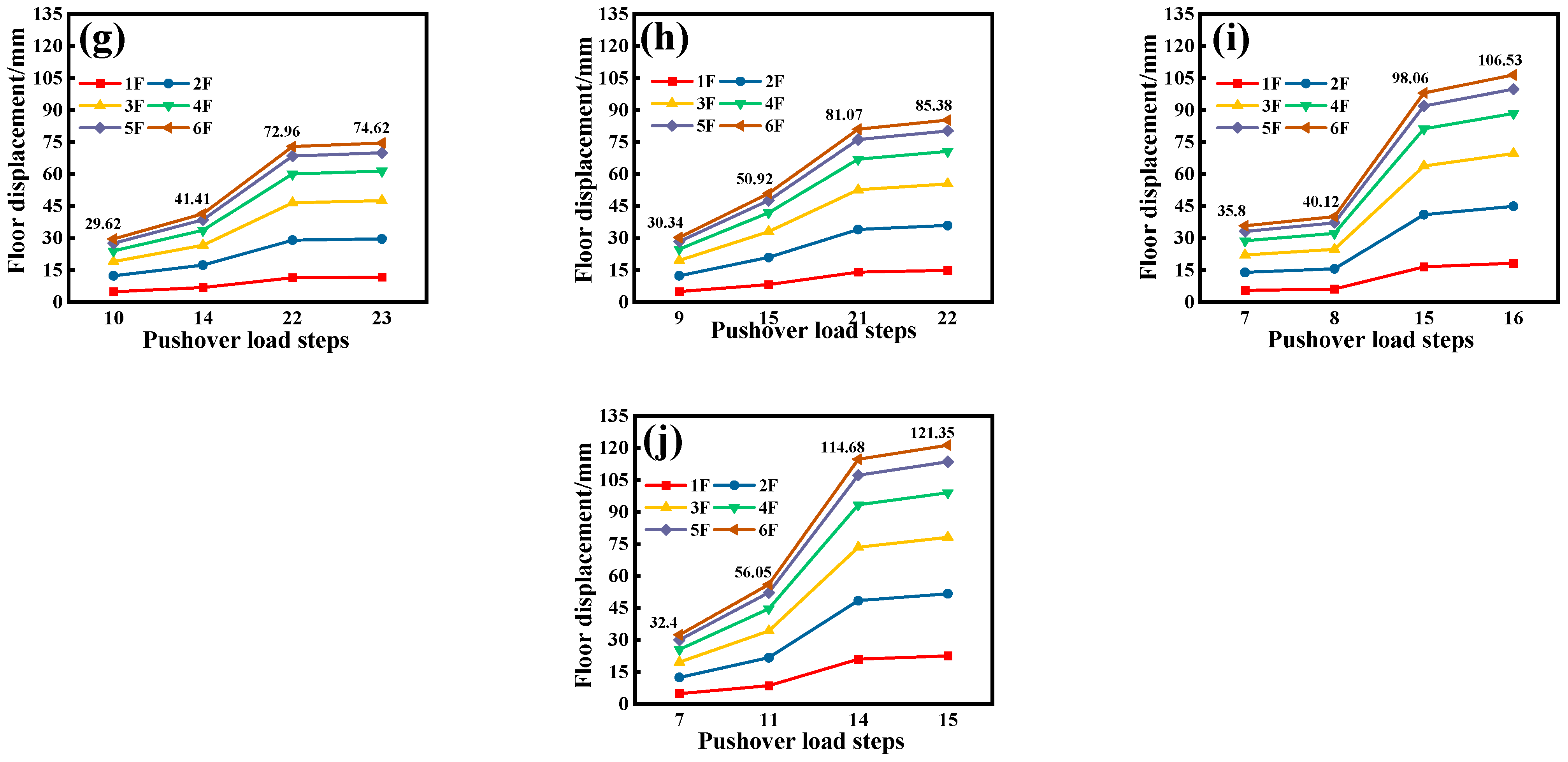
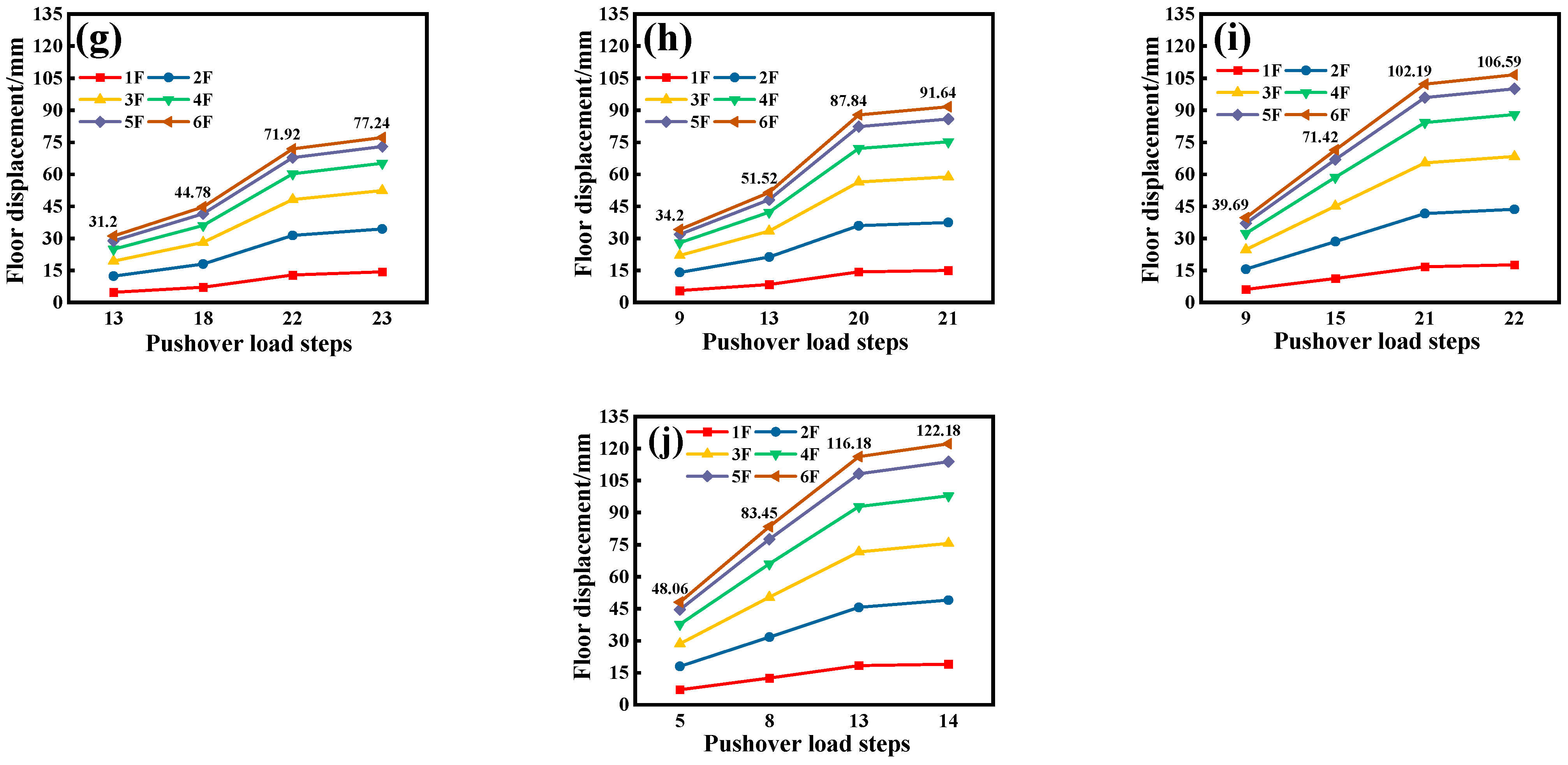
4.5. Floor Displacement
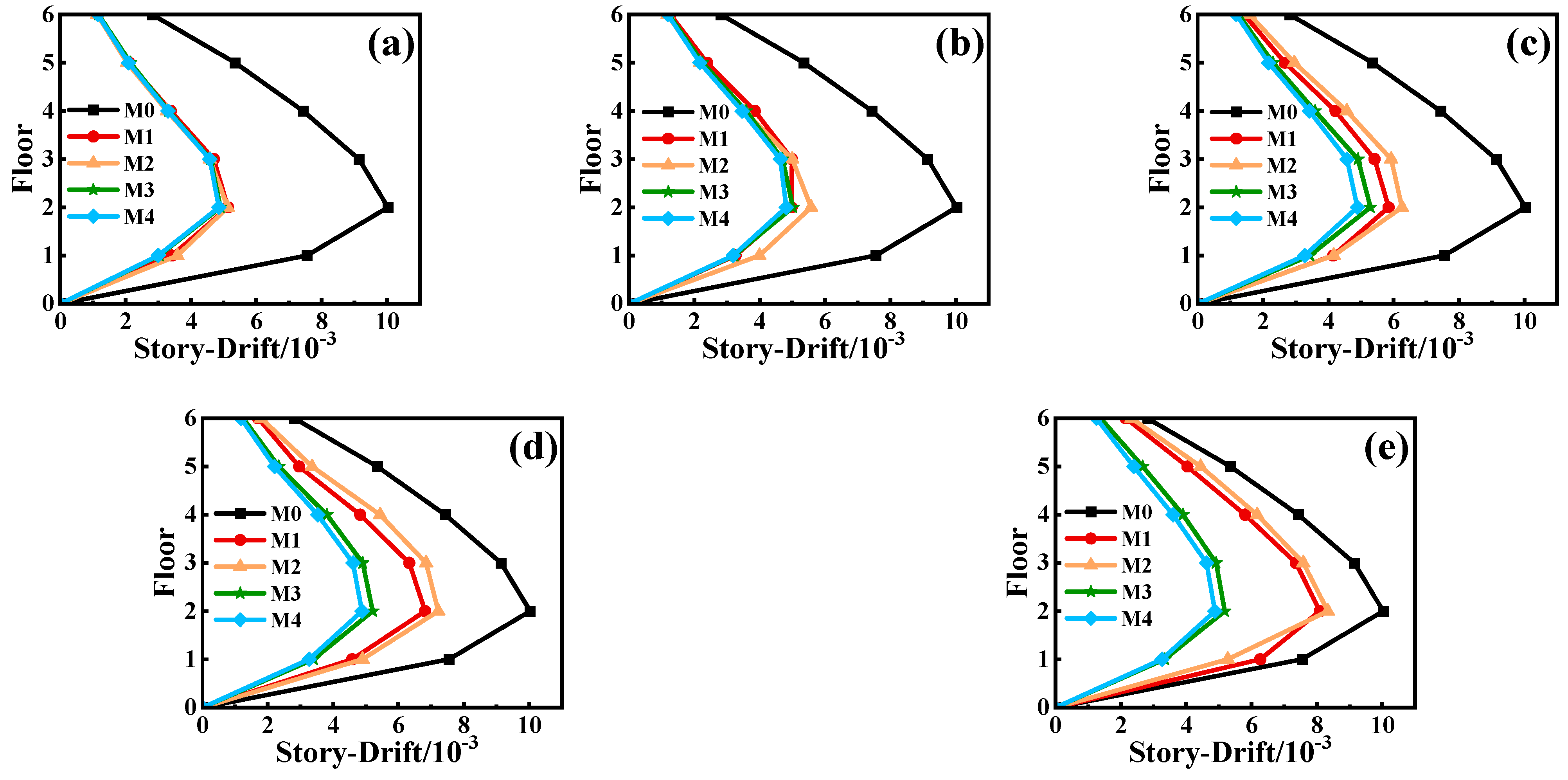
4.6. Inter-Story Drift Ratio
5. Conclusions
- All strengthened structures exhibit a shorter fundamental period, indicating that local strengthening effectively enhances the overall stiffness. Quadrangle symmetric strengthening (M3) best improves the torsional stiffness, whereas middle symmetric strengthening (M4) more effectively enhances the lateral stiffness. However, asymmetric strengthening schemes (M1 and M2) yield uneven stiffness distributions, potentially inducing localized vibrations and torsional effects.
- Symmetric strengthening more effectively improves the lateral stiffness and shear capacity of the structure compared to asymmetric strengthening. Notably, middle symmetric strengthening (M4) increases the lateral load-bearing capacity by 53.6% compared to the original structure.
- The pushover analysis shows that symmetric strengthening provides greater lateral stiffness and seismic performance reserves. With more strengthened stories, the adverse effects in asymmetric schemes intensify, while the symmetric performance improves steadily.
- Asymmetric strengthening results in significant stiffness variations, causing torsional effects and larger displacement differences. Increasing the number of strengthened stories sharply elevates the inter-story drift ratios, posing safety risks. Conversely, symmetric strengthening promotes a uniform stiffness distribution, ensuring better deformation coordination and structural integrity. Thus, symmetric strengthening is recommended in high-seismic regions. Asymmetric strengthening is suitable for localized strengthening but requires displacement monitoring and additional torsional control measures.
6. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, F.A.; Khan, S.; Khan, W. Seismic performance of RC-ECC composite frame by eliminating shear reinforcement in beam-column joint: Shake table tests. Adv. Struct. Eng. 2022, 25, 2966–2980. [Google Scholar] [CrossRef]
- Yuan, F.; Hu, R. Flexural behaviour of ECC and ECC–concrete composite beams reinforced with hybrid FRP and steel bars. Adv. Struct. Eng. 2021, 24, 3171–3183. [Google Scholar] [CrossRef]
- Dautaj, A.; Kadiri, Q.V.; Kabashi, N. Experimental study on the contribution of masonry infill in the behavior of RC frame under seismic loading. Eng. Struct. 2018, 165, 27–37. [Google Scholar] [CrossRef]
- Bikçe, M.; Emsen, E.; Erdem, M.M.; Bayrak, O.F. An investigation on behavior of RC frames with non-interacting infill wall. Eng. Struct. 2021, 245, 112920. [Google Scholar] [CrossRef]
- Alhusban, M.; Parvin, A. Local Strengthening of Reinforced Concrete Frames Using Textile Reinforced Mortar Jackets under Gravity and Cyclic Loadings. Pract. Period. Struct. Des. Constr. 2023, 28, 04023050. [Google Scholar] [CrossRef]
- Alcocer, S.M. RC frame connections rehabilitated by jacketing. J. Struct. Eng.—ASCE 1993, 119, 1413–1431. [Google Scholar] [CrossRef]
- Guo, H. The Reliability of Enlarging the Cross-Section in Reinforcing the Frame Construction Buildings. Adv. Mater. Res. 2011, 189–193, 4365–4369. [Google Scholar] [CrossRef]
- Cheong, H.K.; MacAlevey, N. Experimental behavior of jacketed reinforced concrete beams. J. Struct. Eng.—ASCE 2000, 126, 692–699. [Google Scholar] [CrossRef]
- Zhao, D.P.; Li, K.; Fan, J.J.; Wang, Y.; Zhu, J.T. Shear behavior of RC beams strengthened with high-strength steel strand mesh reinforced ECC: Shear capacity, cracking and deformation. Eng. Struct. 2024, 298, 117081. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, S.; Li, K.; Fan, J.; Zhou, X.; Liang, Y. Effect of residual strains in damaged RC beam after unloading on the flexural and shear behaviours of SSS-ECC repaired beams. Eng. Struct. 2025, 332, 120144. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Abdalla, J.A.; Hawileh, R.A.; Qin, F.; Xu, X. Flexural behavior of reinforced concrete beams externally strengthened with ECC and FRP grid reinforcement. Constr. Build. Mater. 2024, 446, 137964. [Google Scholar] [CrossRef]
- Attari, N.; Amziane, S.; Chemrouk, M. Flexural strengthening of concrete beams using CFRP, GFRP and hybrid FRP sheets. Constr. Build. Mater. 2012, 37, 746–757. [Google Scholar] [CrossRef]
- Zhao, D.P.; Li, K.; Zhu, J.T.; Fan, J.J.; Yuan, F.G. Shear Performance of RC Beams Strengthened with Steel Strand Wire Mesh-Reinforced Engineered Cementitious Composites under Cyclic Loading. J. Compos. Constr. 2024, 28, 04024058. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Asgarkhani, N.; Yoo, D.-Y. Machine-learning methods for estimating compressive strength of high-performance alkali-activated concrete. Eng. Appl. Artif. Intell. 2024, 136, 109053. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Bagherzadeh, F.; Mieloszyk, M.; Yoo, D.-Y. Chained machine learning model for predicting load capacity and ductility of steel fiber–reinforced concrete beams. Comput.—Aided Civ. Infrastruct. Eng. 2024, 39, 3573–3594. [Google Scholar] [CrossRef]
- Arslan, G.; Sevuk, F.; Ekiz, I. Steel plate contribution to load-carrying capacity of retrofitted RC beams. Constr. Build. Mater. 2008, 22, 143–153. [Google Scholar] [CrossRef]
- Ciampa, E.; Ceroni, F.; De Angelis, A.; Pecce, M.R. Bond tests on concrete elements externally bonded with steel plates and assessment of bond strength models. Eng. Struct. 2023, 296, 116835. [Google Scholar] [CrossRef]
- Zhang, G.H.; Song, C.Z.; Han, X.H.; Lu, B. Research on the development of low-temperature-resistant fast-curing structural adhesive and steel plate strengthening concrete beam flexural test. Civ. Eng. J.—Staveb. Obz. 2024, 33, 78–91. [Google Scholar] [CrossRef]
- Tang, F.; Yao, Y.; Yang, S. Corrosion mechanism and resistance of g-C3N5@PDA nanosheets modified epoxy-coated carbon steel. Prog. Org. Coat. 2025, 200, 109048. [Google Scholar] [CrossRef]
- Tena-Colunga, A.; Godínez-Domínguez, E.A.; Hernández-Ramírez, H. Seismic retrofit and strengthening of buildings. Observations from the 2017 Puebla-Morelos earthquake in Mexico City. J. Build. Eng. 2022, 47, 103916. [Google Scholar] [CrossRef]
- Ren, H.M.; Zhang, F.W.; Mao, C.X.; Fan, Q.Q.; Lu, Z. Numerical and experimental analysis in seismic performance of post-earthquake reinforced concrete frame retrofitted with ECC. Adv. Struct. Eng. 2024, 27, 3–16. [Google Scholar] [CrossRef]
- Baran, M. Comparison of seismic performances of reinforced concrete frames strengthened by different techniques. Lat. Am. J. Solids Struct. 2021, 18, e350. [Google Scholar] [CrossRef]
- Sadeq, S.F.; Muhammad, B.R.; Al-zuheriy, A.J. Seismic behaviour of rc building located in erbil, Iraq and strengthening by using steel frame sections precast bolt-connected steel-plate reinforced concrete. IOP Conf. Ser. Earth Environ. Sci. 2022, 961, 012012. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, S.; Li, Q. Influence of Local Members Strengthening on Overall Performance of Reinforced Concrete Frame Structure. J. Disaster Prev. Mitig. Eng. 2013, 33, 140–146. [Google Scholar]
- GB 55021-2021; General Code for Assessment and Rehabilitation of Existing Buildings. China Architecture and Architecture Press: Beijing, China, 2021.
- GB/T228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. China Architecture and Architecture Press: Beijing, China, 2021.
- JG/T 271-2019; Structural Adhesives for Strengthening Structures with Steel Plate. China Architecture and Building Press: Beijing, China, 2019.
- Paul, G.; Agarwal, P. Experimental verification of seismic evaluation of RC frame building designed as per previous is codes before and after retrofitting by using steel bracing. Asian J. Civ. Eng. 2012, 13, 165–179. Available online: https://sid.ir/paper/298922/en (accessed on 14 April 2025).
- Moehle, J. Seismic Design of the Reinforced Concrete Buildings; McGraw Hill Professional: New York, NY, USA, 2014. [Google Scholar]
- Aboualam, M.O.; Maree, A.F.; Maksoud, A.M.A.; Tork, B.S. Monorail guideway structures performance under seismic loads. Structures 2024, 70, 107793. [Google Scholar] [CrossRef]
- Romero, M.; Museros, P. Learning Structural Analysis with K’NEX and SAP2000: A Practical Experience in Spain. Comput. Civ. Build. Eng. 2000, 2000, 1141–1147. [Google Scholar] [CrossRef]
- ASTM C109/C109M-16a; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50-mm] Cube Specimens). ASTM International: West Conshohocken, PA, USA, 2016.
- Qin, F.; Zhang, Z.; Yin, Z.; Di, J.; Xu, L.; Xu, X. Use of high strength, high ductility engineered cementitious composites (ECC) to enhance the flexural performance of reinforced concrete beams. J. Build. Eng. 2020, 32, 101746. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture and Architecture Press: Beijing, China, 2012.
- GB/T50011-2010; Code for Seismic Design of Buildings. China Architecture and Architecture Press: Beijing, China, 2024.
- JGJ3-2010; Technical Specification for Concrete Structures of Tall Building. China Architecture and Building Press: Beijing, China, 2010.
- Applied Technology Council. Seismic Evaluation and Retrofit of Concrete Buildings, Report No. SSC 96-01: ATC-40 1; California Seismic Safety Commission: West Sacramento, CA, USA, 1996. [Google Scholar]
- GB 55002-2021; General Code for Seismic Precaution of Buildings and Municipal Engineering. China Architecture and Architecture Press: Beijing, China, 2021.
- Yurdakul, Ö.; Vnenk, P.; Routil, L.; Culek, B.; Avşar, Ö. Post-damage recovery of substandard RC columns by CFRPs. Eng. Struct. 2024, 306, 117806. [Google Scholar] [CrossRef]

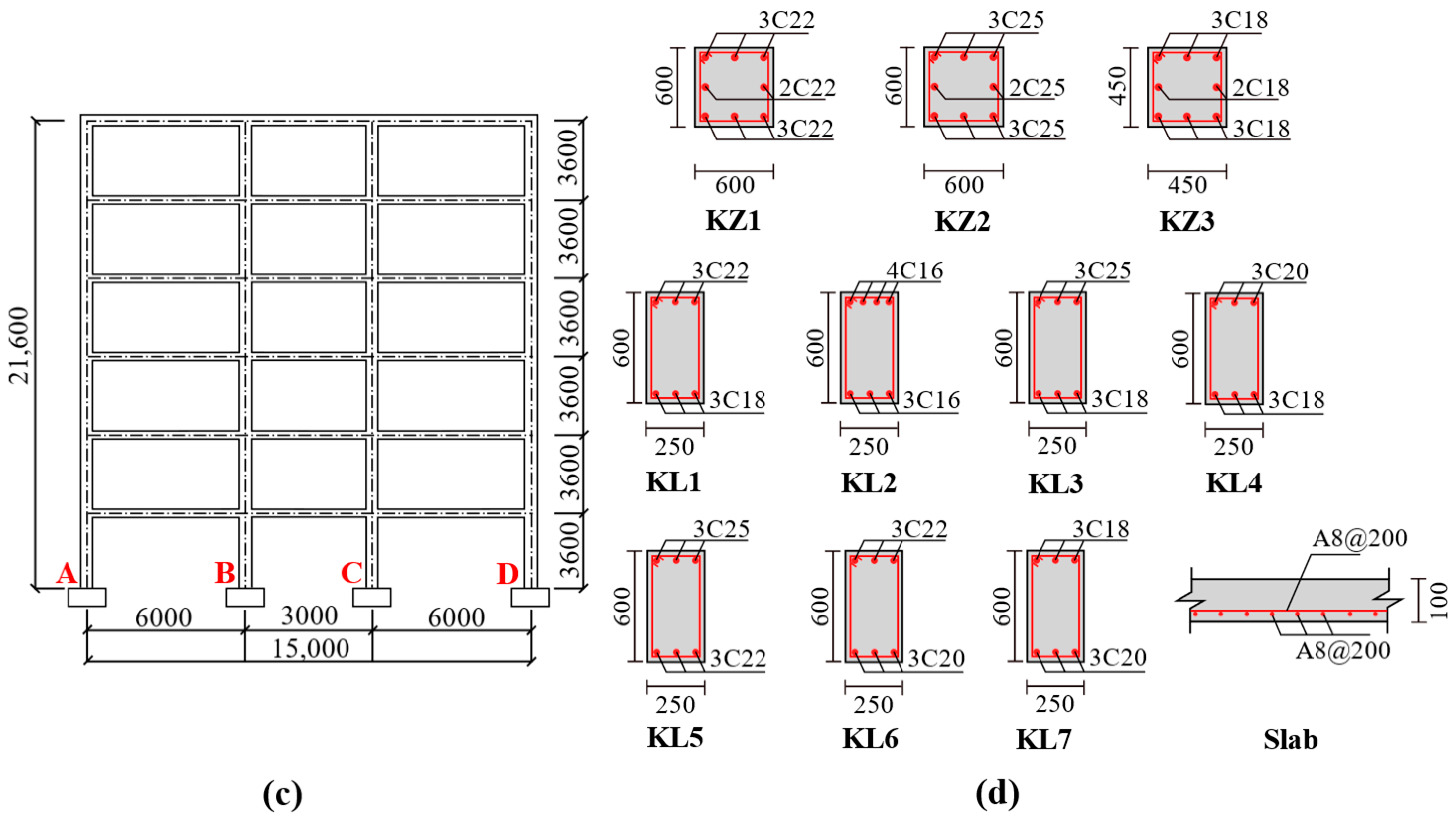
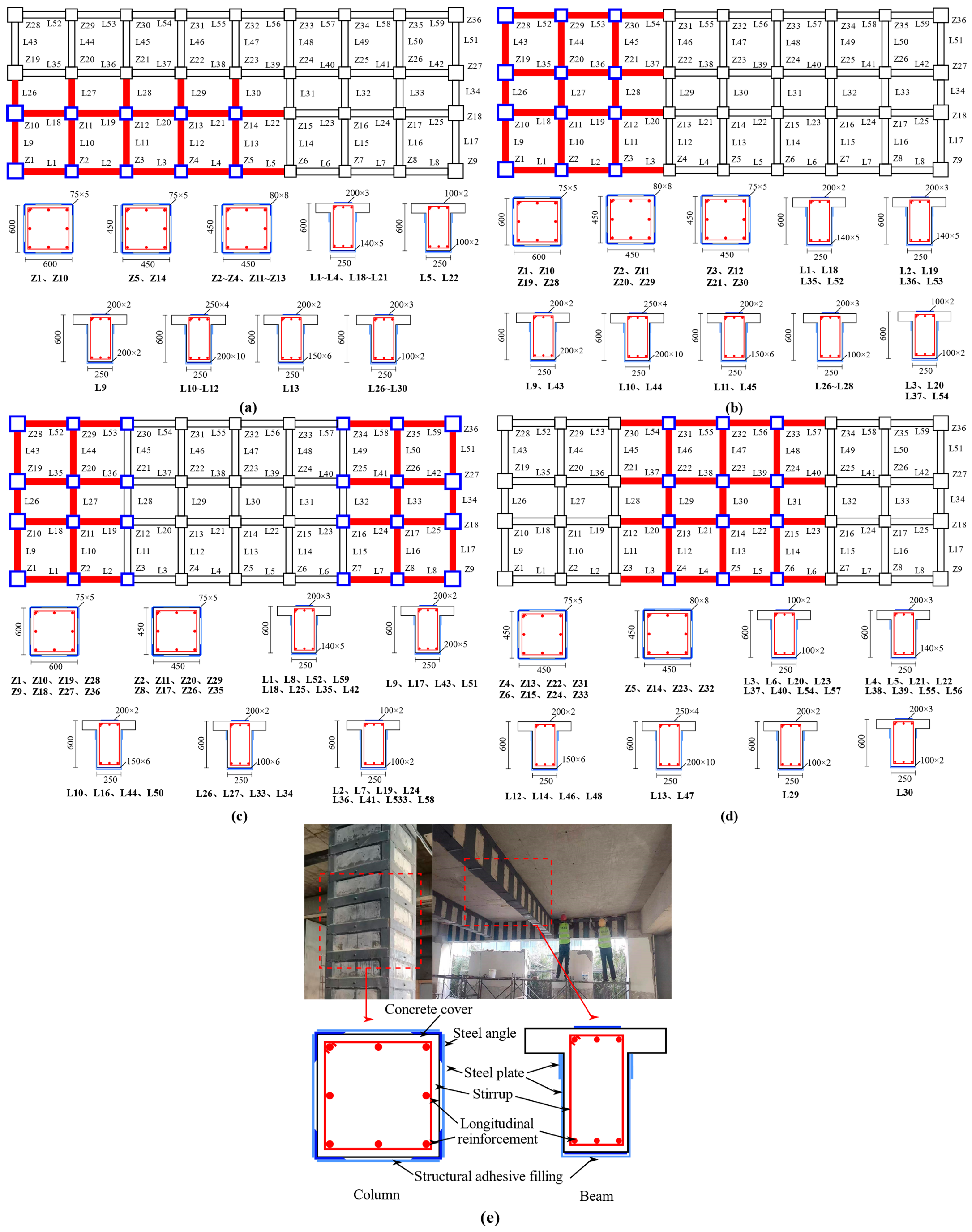

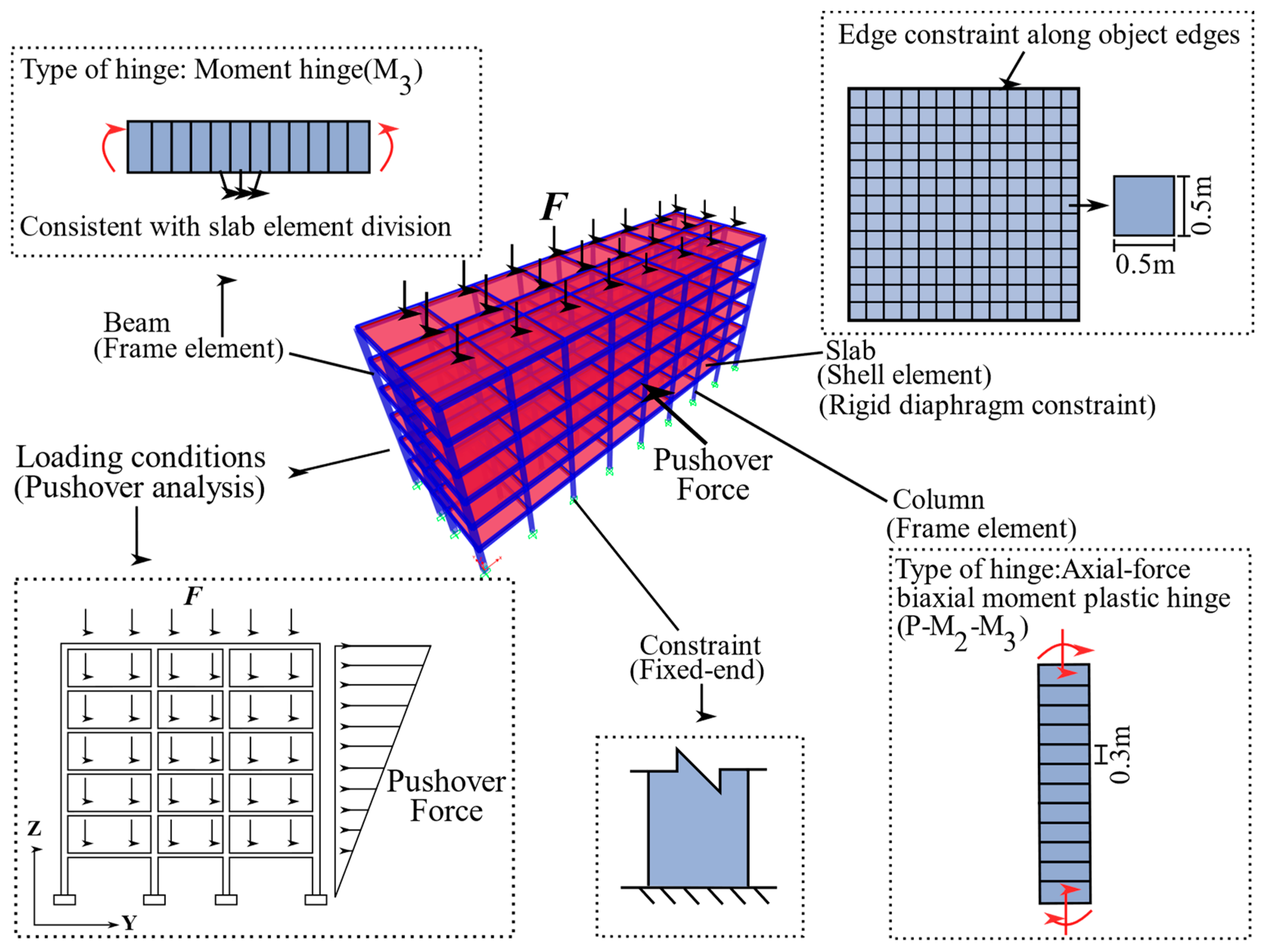
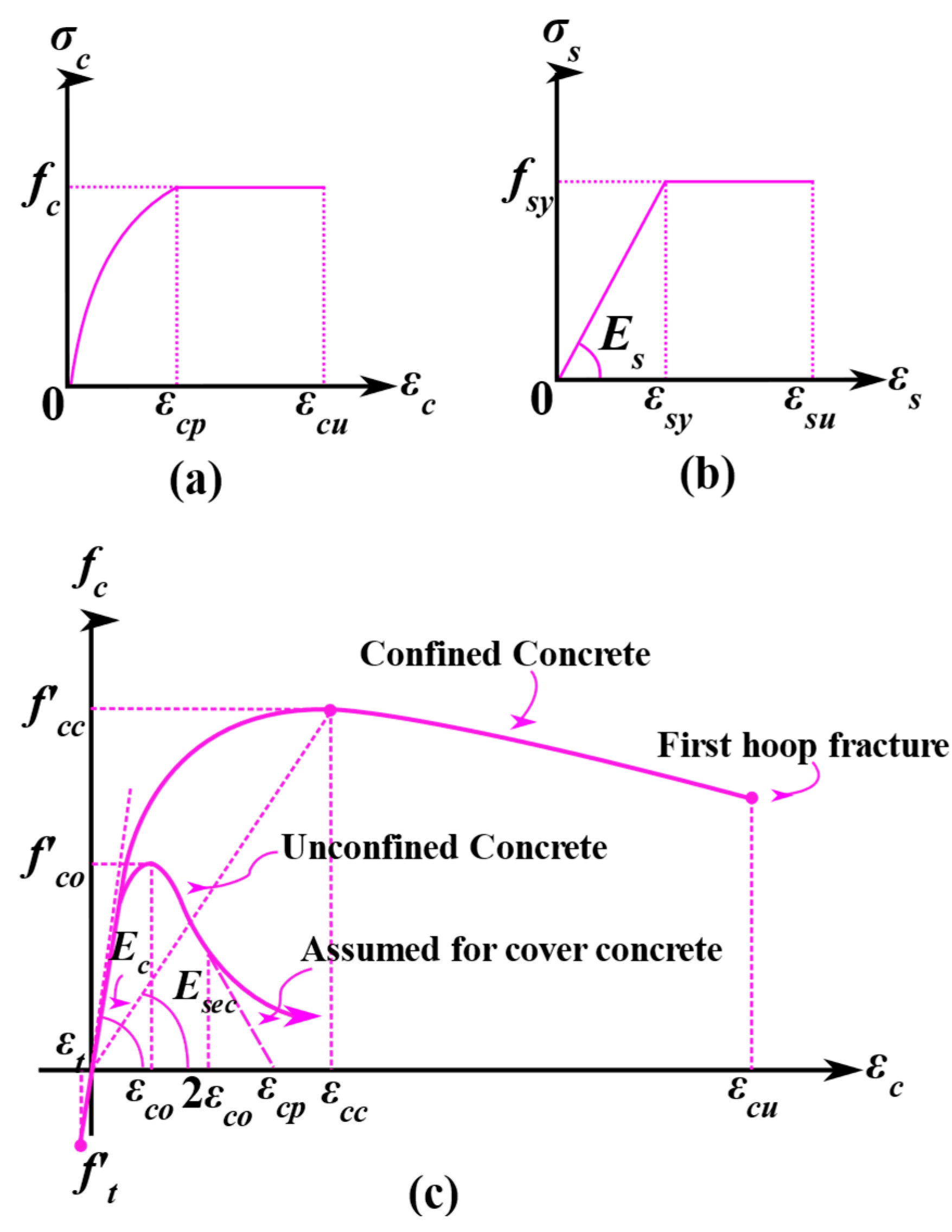



| Number | Strengthening Position | Strengthening Level |
|---|---|---|
| M1 | single-corner asymmetric | 1, 1~2, 1~3, 1~4, 1~5 |
| M2 | single-end asymmetric | 1, 1~2, 1~3, 1~4, 1~5 |
| M3 | quadrangle symmetric | 1, 1~2, 1~3, 1~4, 1~5 |
| M4 | central symmetric | 1, 1~2, 1~3, 1~4, 1~5 |
| Material | Compressive Strength (MPa) | Yield Strength (MPa) | Tensile Strength (MPa) | Shear Strength (MPa) | Bending Strength (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg | Cov | Avg | Cov | Avg | Cov | Avg | Cov | Avg | Cov | ||
| Steel plate | 2 mm | — | — | 411.7 | 0.006 | 510.0 | 0.002 | — | — | — | — |
| 3 mm | — | — | 423.7 | 0.001 | 511.0 | 0.002 | — | — | — | — | |
| 4 mm | — | — | 417.3 | 0.001 | 531.3 | 0.002 | — | — | — | — | |
| 5 mm | — | — | 425.7 | 0.002 | 513.3 | 0.002 | — | — | — | — | |
| 6 mm | — | — | 404.3 | 0.002 | 525.0 | 0.002 | — | — | — | — | |
| 8 mm | — | — | 446.7 | 0.002 | 543.7 | 0.002 | — | — | — | — | |
| 10 mm | — | — | 447.7 | 0.004 | 523.0 | 0.003 | — | — | — | — | |
| Adhesive | — | 80.7 | — | — | — | 54.4 | — | 25.2 | — | 75.8 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Li, C.; Zhao, D.; Li, Q.; Du, H. Effect of Local Strengthening on the Overall Seismic Performance of Reinforced Concrete Frame Structures. Buildings 2025, 15, 1326. https://doi.org/10.3390/buildings15081326
Zhao G, Li C, Zhao D, Li Q, Du H. Effect of Local Strengthening on the Overall Seismic Performance of Reinforced Concrete Frame Structures. Buildings. 2025; 15(8):1326. https://doi.org/10.3390/buildings15081326
Chicago/Turabian StyleZhao, Gengqi, Chenbo Li, Dapeng Zhao, Qing Li, and Huiying Du. 2025. "Effect of Local Strengthening on the Overall Seismic Performance of Reinforced Concrete Frame Structures" Buildings 15, no. 8: 1326. https://doi.org/10.3390/buildings15081326
APA StyleZhao, G., Li, C., Zhao, D., Li, Q., & Du, H. (2025). Effect of Local Strengthening on the Overall Seismic Performance of Reinforced Concrete Frame Structures. Buildings, 15(8), 1326. https://doi.org/10.3390/buildings15081326





