The Influence of Various Tensile and Shear Reinforcement Configurations on the Ultimate Capacity and Failure Mechanisms of Reinforced Concrete Beams
Abstract
:1. Introduction
2. Experimental Program
2.1. Beam Configuration and Test Variables
2.2. Materials Properties
2.3. Test Setup and Instrumentation
2.4. Experimental Results
2.4.1. Failure Mode and Load Capacity
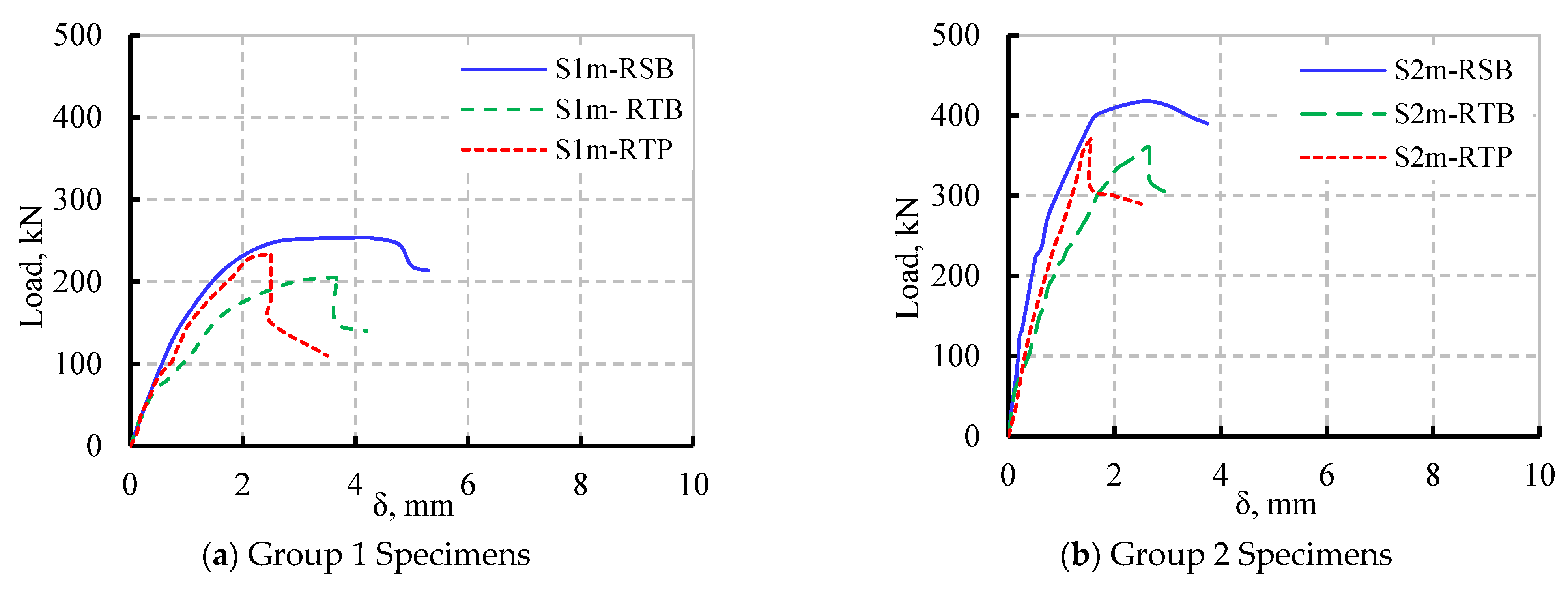
2.4.2. Load Deflection Curve
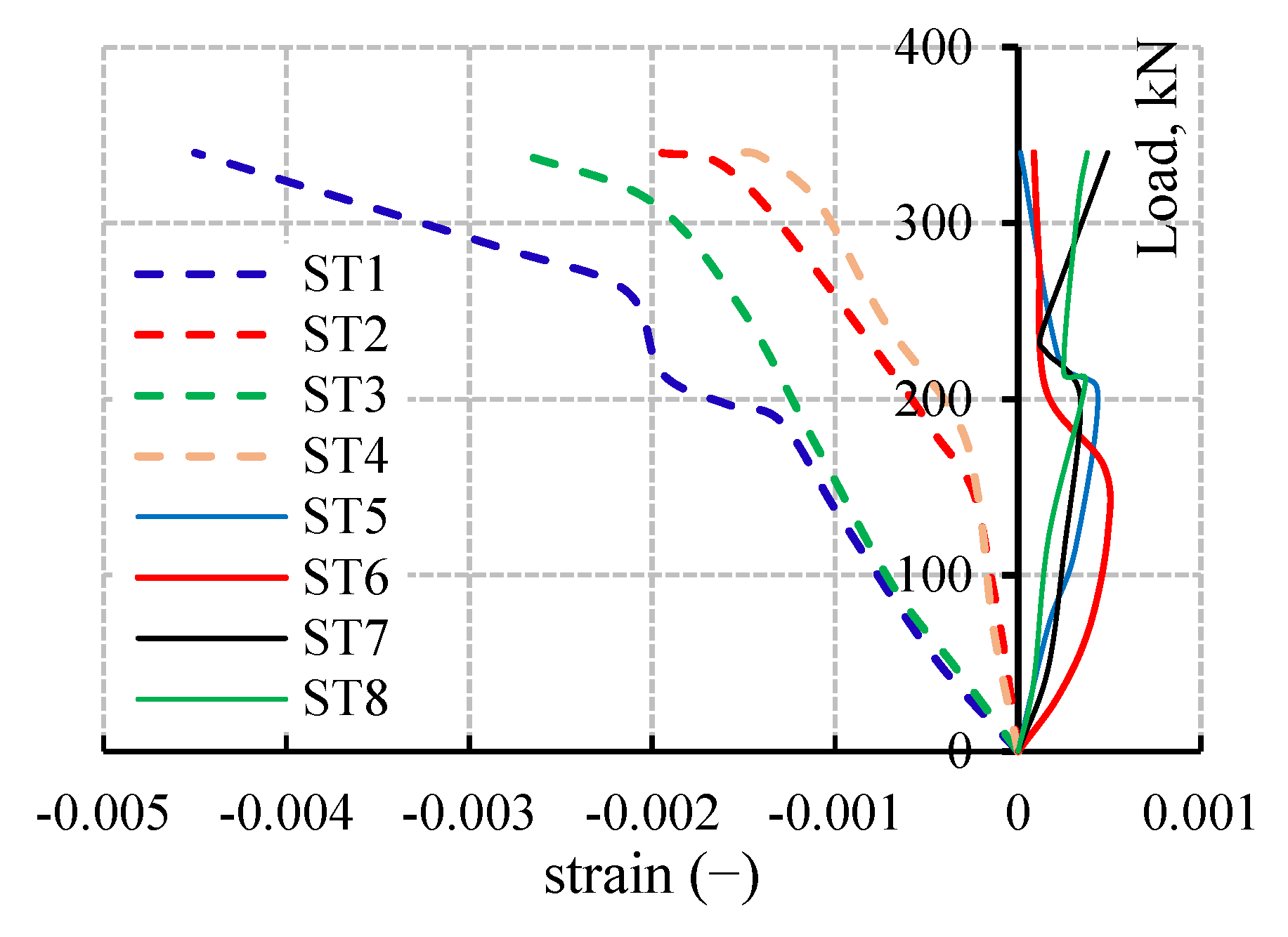
2.4.3. Strain Gauge Results
3. Analytical Analysis
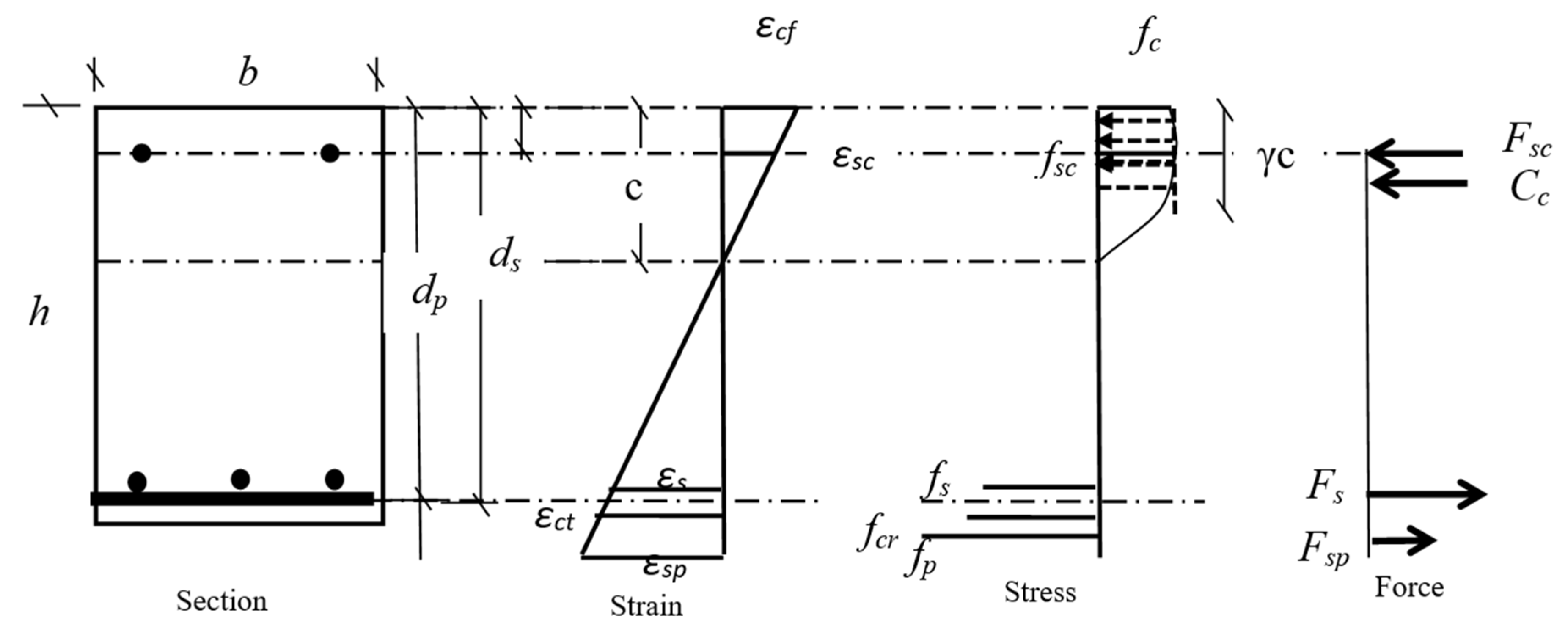
3.1. Flexural Capacity
3.2. Shear Capacity
3.3. Analytical Results
4. Numerical Analysis
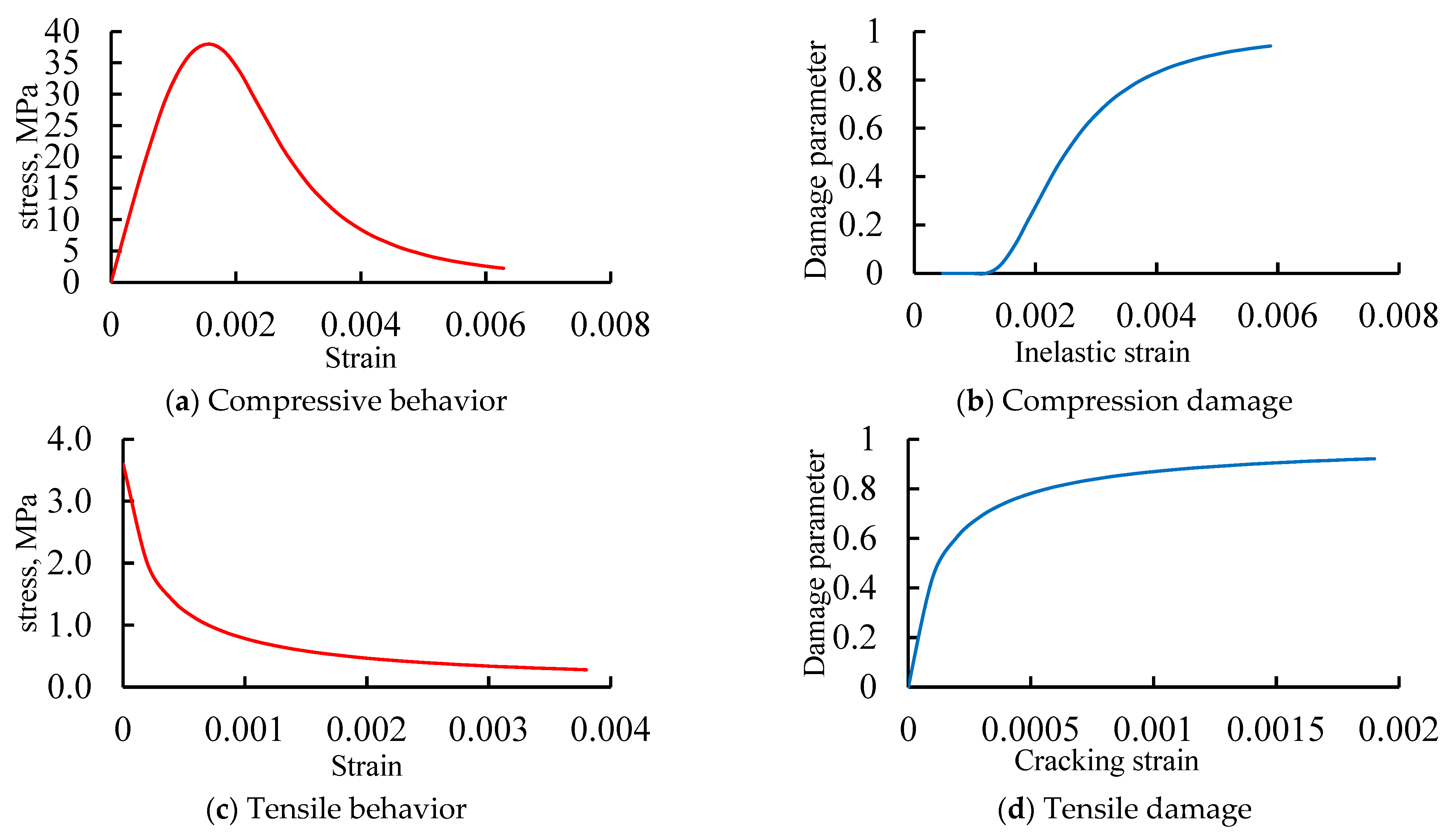
4.1. Program and the Constitutive Parameters
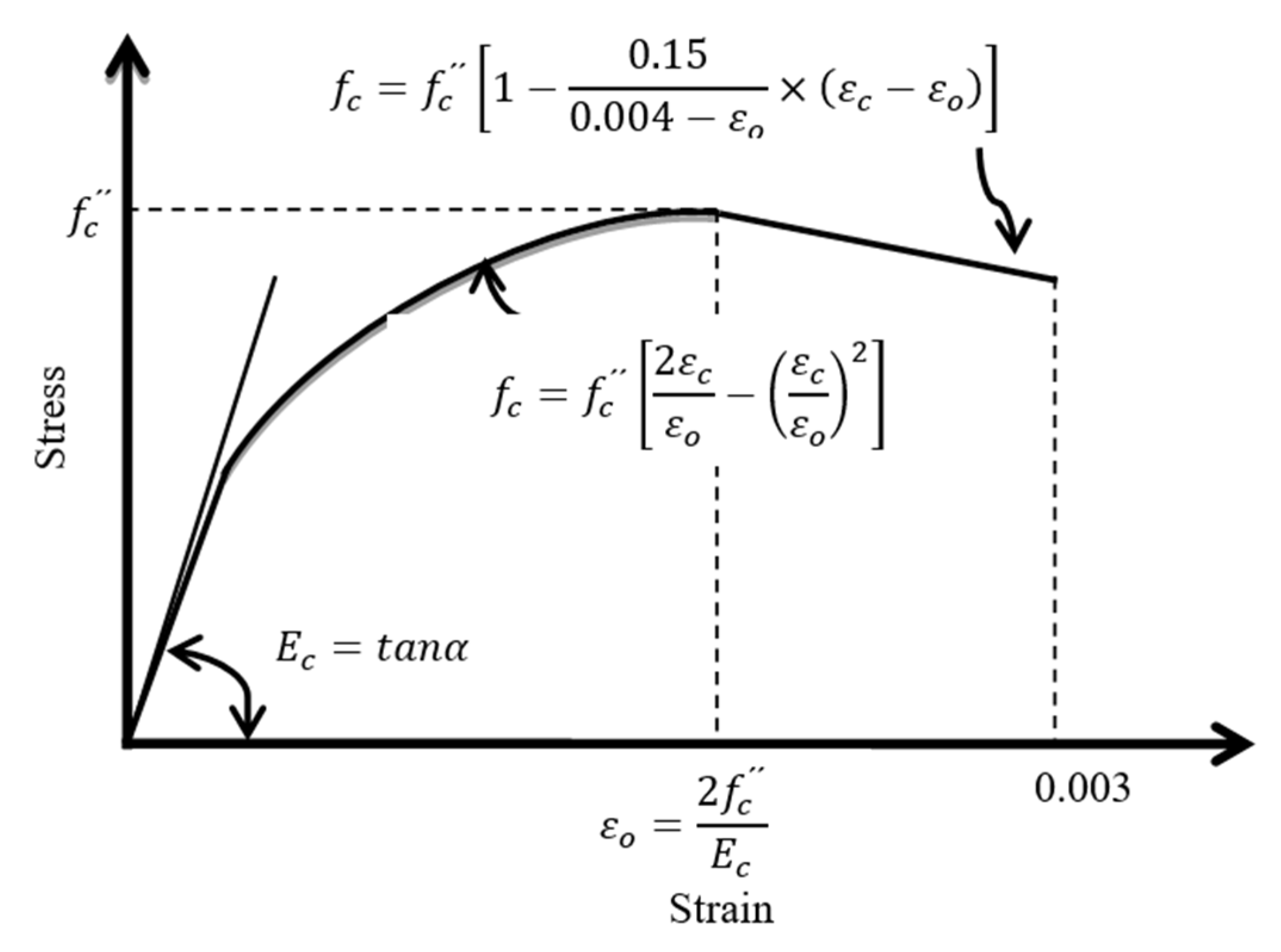
4.2. Materials and Sensitivity Analysis
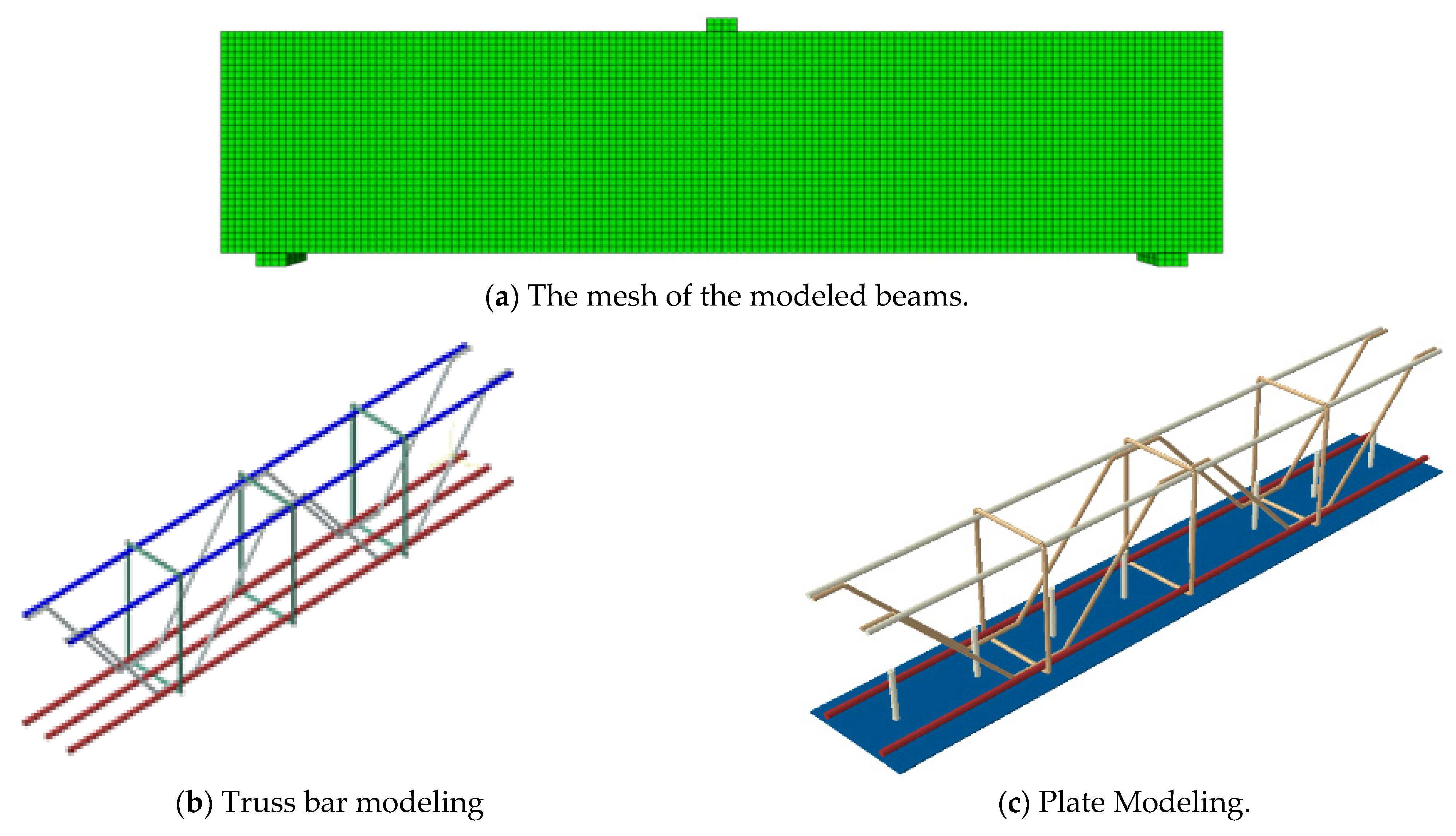
4.3. Model Built-Up and Boundary Conditions
4.4. FE Model Validation
4.5. Parametric Study
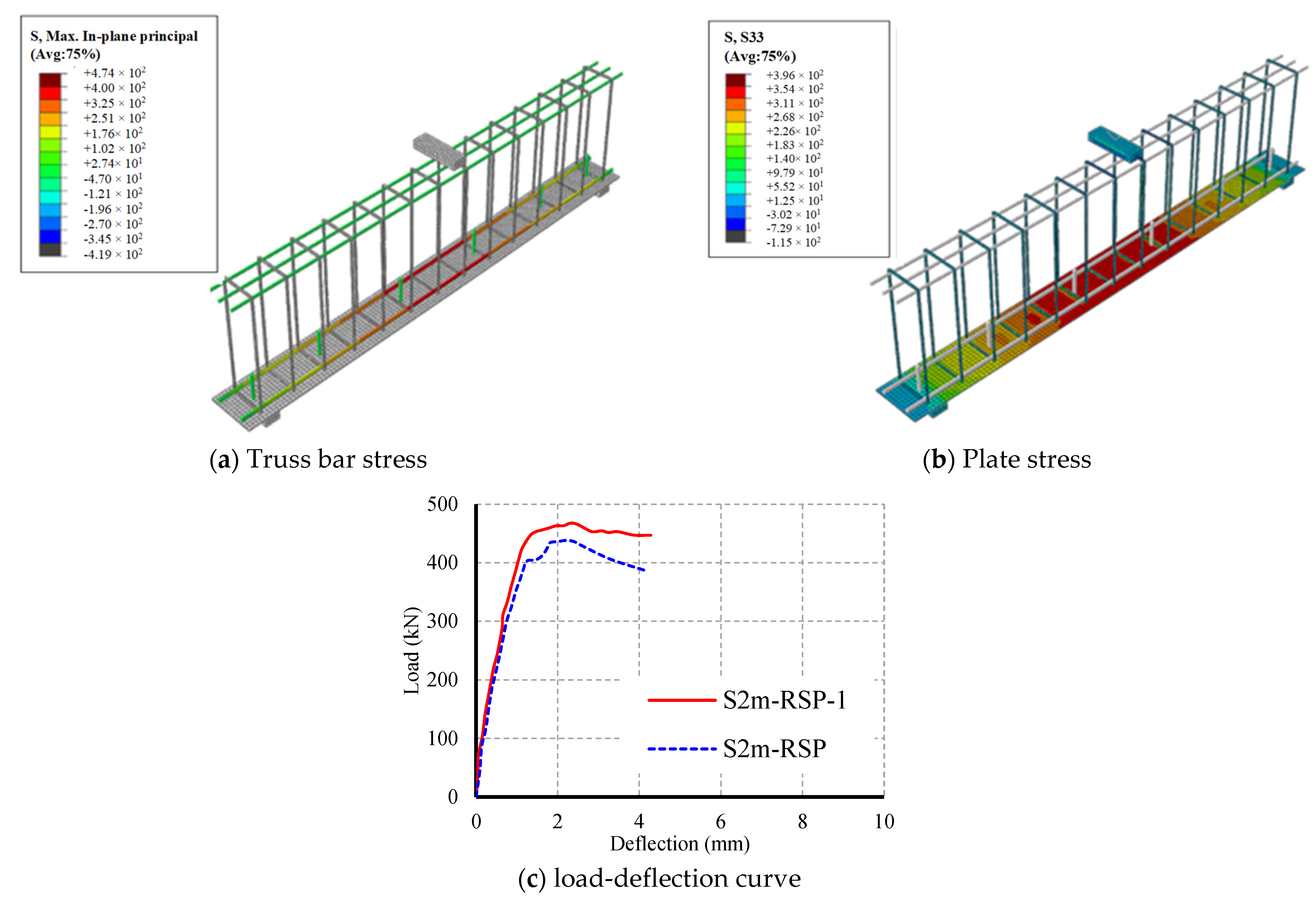
4.6. Results of the Parametric Study
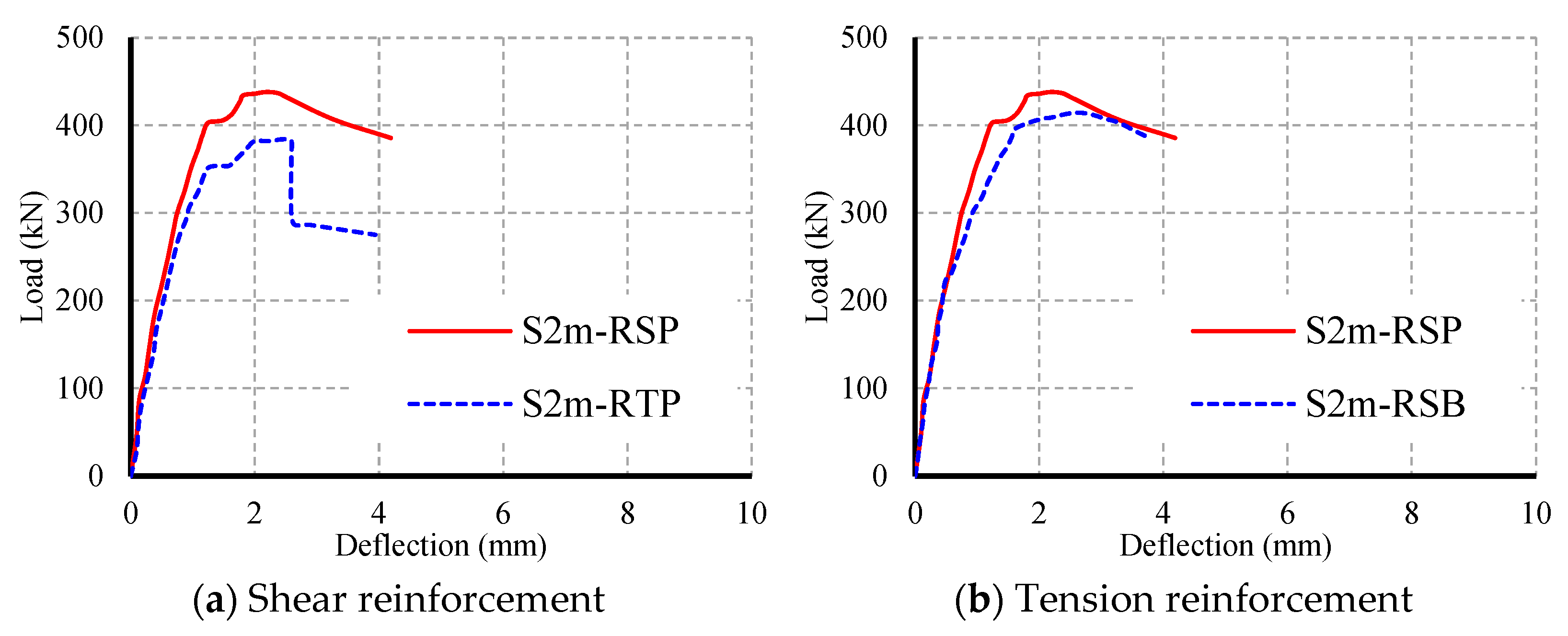
4.6.1. Evaluating the Impact of Truss Bars and Stirrups
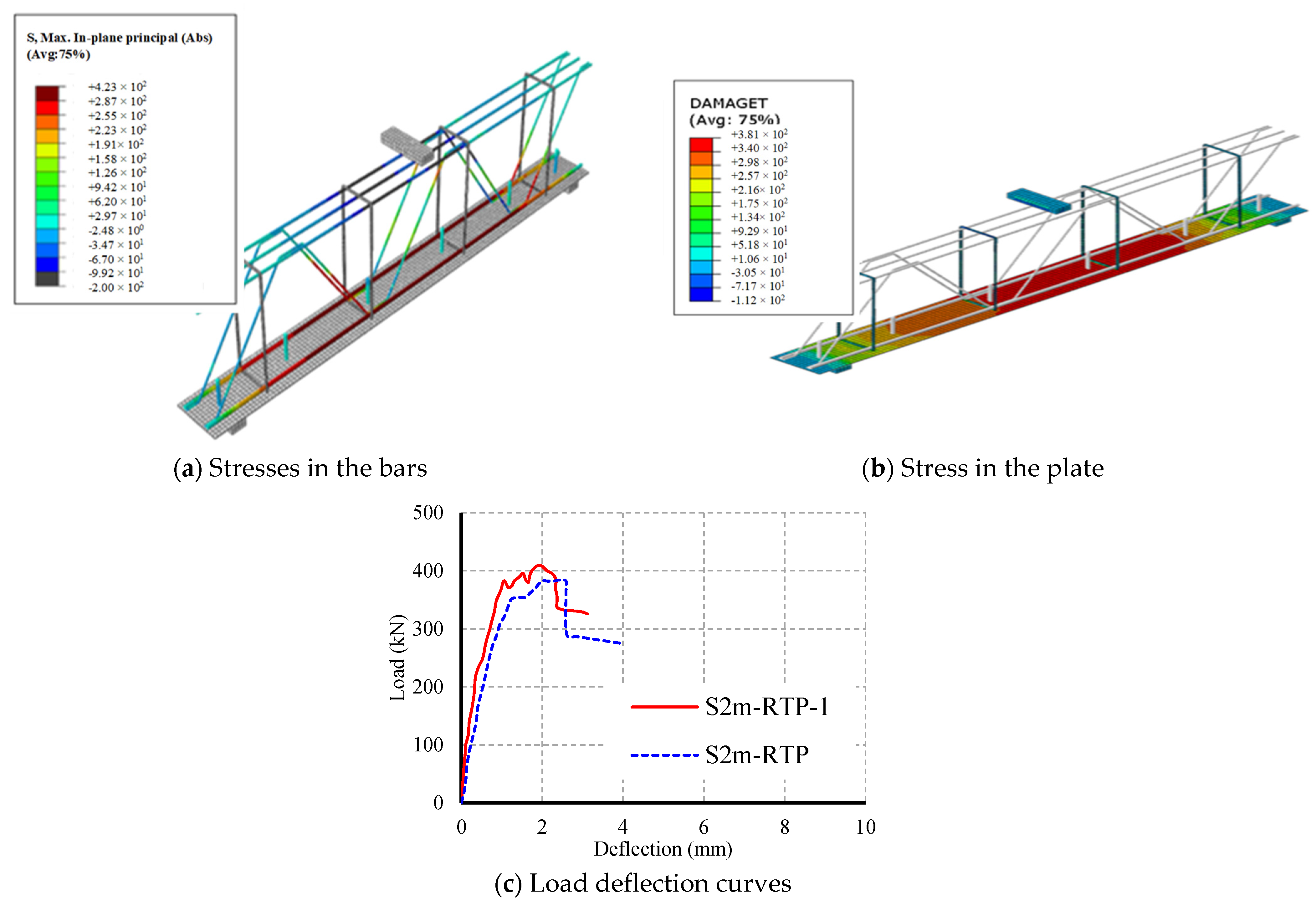
4.6.2. Assessing the Influence of Yielding in Steel Plate
5. Conclusions
- The shear span-to-depth ratio decreased the capacity of the beam but increased related to its control ones when the failure was shear, and the tensile reinforcement kept the ratio constant. Conversely, the tensile reinforcement showed an insignificant effect on enhanced beam shear capacity when the beams had the same shear configuration.
- The concrete beam reinforced with a steel plate and stirrups had the highest load-carrying capacity when compared to the conventional concrete beams. Moreover, both beams with the steel plate and truss shear bar, as well as beams reinforced with tension steel bars and truss shear bars, exhibited the same failure mode, i.e., shear failure mode.
- The beam had truss shear reinforcement of about 51.1% compared to stirrups, which could attain 87% of its capacity. As the truss shear reinforcement had the advantages of easier formation and support compared to stirrups, it is recommended to use the same shear steel area of the stirrups to form the truss.
- The beam reinforced with a steel plate and stirrups exhibited slightly greater capacity than those reinforced with bars and stirrups (5% increase), although the yield stress of the steel plate was 20% lower than that of the bars. Increasing the plate yield from 420 to 520 MPa improved the beam’s stiffness, while the ultimate capacity experienced a 6% increase.
- The truss configuration was not better at resisting the shear flow through the total shear span with the same efficiency, so it is recommended to extend this study in the future to study the effect of the truss shear reinforcement configuration, such as the N shape truss, on the beam shear capacity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Subedi, N.; Baglin, P. Plate Reinforced Concrete Beams: Experimental Work. Eng. Struct. 1999, 21, 232–254. [Google Scholar] [CrossRef]
- Subedi, N. Reinforced Concrete Beams with Plate Reinforcement for Shear. Proc. Inst. Civ. Eng. 1989, 87, 377–399. [Google Scholar] [CrossRef]
- Lam, W.; Su, R.; Pam, H. Experimental Study on Embedded Steel Plate Composite Coupling Beams. J. Struct. Eng. 2005, 131, 1294–1302. [Google Scholar] [CrossRef]
- Su, R.; Lam, W.; Pam, H. Experimental Study of Plate-reinforced Composite Deep Coupling Beams. Struct. Des. Tall Spec. Build. 2009, 18, 235–257. [Google Scholar] [CrossRef]
- Lam, W.; Li, L.; Su, R.; Pam, H. Behaviour of Plate Anchorage in Plate-Reinforced Composite Coupling Beams. Sci. World J. 2013, 2013, 190430. [Google Scholar] [CrossRef] [PubMed]
- BS8110-2:1985; Structural Use of Concrete: Code of Practice for Special Circumstances. Part 2: Code of Practice for Special Circumstances 3. BSI: London, UK, 1985.
- Hamoda, A.; Eltaly, B.; Sera, R.; Liang, Q. Behavior of Reinforced Concrete Stair Slabs Strengthened with Steel Plates and near Surface Mounted Steel Bars. Eng. Struct. 2023, 292, 116514. [Google Scholar] [CrossRef]
- Adhikary, B.; Mutsuyoshi, H. Numerical Simulation of Steel-Plate Strengthened Concrete Beam by a Non-Linear Finite Element Method Model. Constr. Build. Mater. 2002, 16, 291–301. [Google Scholar] [CrossRef]
- Arslan, G.; Sevuk, F.; Ekiz, I. Steel Plate Contribution to Load-Carrying Capacity of Retrofitted RC Beams. Constr. Build. Mater. 2008, 22, 143–153. [Google Scholar] [CrossRef]
- Rakgate, S.; Dundu, M. Effectiveness of Surface Preparation on the Capacity of Plated Reinforced Concrete Beams. Structures 2018, 14, 348–357. [Google Scholar] [CrossRef]
- Atea, R. A Case Study of Flexural Performance of Reinforced Concrete Beams Bonded with Steel Plates with Different Thickness. J. Mater. Res. Technol. 2019, 8, 22–32. [Google Scholar] [CrossRef]
- Braconi, A.; Elamary, A.; Salvatore, W. Seismic Behaviour of Beam-to-Column Partial-Strength Joints for Steel–Concrete Composite Frames. J. Constr. Steel Res. 2010, 66, 1431–1444. [Google Scholar] [CrossRef]
- Elamary, A.; Ahmed, M.; Mohmoud, A. Flexural Behaviour and Capacity of Reinforced Concrete–Steel Composite Beams with Corrugated Web and Top Steel Flange. Eng. Struct. 2017, 135, 136–148. [Google Scholar] [CrossRef]
- Alharthi, Y.; Sharaky, I.; Elamary, A.; Al-Sharef, A.; Al-Salmi, A.; Al-Sufyani, A.; Al-Osaimi, O.; Al-Mufti, A. Flexural Behavior and Capacity of Composite Concrete-Steel Beams Using Various Shear Connectors. Arab. J. Sci. Eng. 2023, 48, 5587–5601. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, C.; Peng, J.; Li, H.; Dong, Y.; Cai, C. Theory-Informed Deep Neural Network-Based Time-Dependent Flexural Reliability Assessment of Corroded PC Structures. Eng. Struct. 2025, 329, 119819. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Peng, J.; Dong, Y. Machine Learning-Based Probabilistic Prediction Model for Chloride Concentration in the Interfacial Zone of Precast and Cast-in-Place Concrete Structures. Structures 2025, 72, 108224. [Google Scholar] [CrossRef]
- Elamary, A.; Sharaky, I.; Alharthi, Y.; Rashed, A. Optimizing Shear Capacity Prediction of Steel Beams with Machine Learning Techniques. Arab. J. Sci. Eng. 2024, 49, 4685–4709. [Google Scholar] [CrossRef]
- Elamary, A.; Mohamed, M.; Sharaky, I.; Mohamed, A.; Alharthi, Y.; Ali, M. Utilizing Artificial Intelligence Approaches to Determine the Shear Strength of Steel Beams with Flat Webs. Metals 2023, 13, 232. [Google Scholar] [CrossRef]
- Sharaky, I.; Torres, L.; Sallam, H. Experimental and Analytical Investigation into the Flexural Performance of RC Beams with Partially and Fully Bonded NSM FRP Bars/Strips. Compos. Struct. 2015, 122, 113–126. [Google Scholar] [CrossRef]
- Alharthi, Y.; Emara, M.; Elamary, A.; Sharaky, I. Flexural Response and Load Capacity of Reinforced Concrete Beams Strengthened with Reinforced Mortar Layer. Eng. Struct. 2021, 245, 112884. [Google Scholar] [CrossRef]
- 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019; ISBN 9781641950565.
- EN 1993-1-5; Eurocode 3—Design of Steel Structures—Part. 1–5: Plated Structural Elements. JRC Scientific and Technical Reports; European Committee for Standardization: Brussels, Belgium, 2006; pp. 1–53.
- Aci 440R-07; Report on Fiber-Reinforced Polymer (FRP) Reinforcement for Concrete Structures. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2007.
- ASTM C39/C39M-18; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2018.
- Carmona, S.; Aguado, A. New Model for the Indirect Determination of the Tensile Stress–Strain Curve of Concrete by Means of the Brazilian Test. Mater. Struct. 2012, 45, 1473–1485. [Google Scholar] [CrossRef]
- Gunes, O.; Buyukozturk, O.; Karaca, E. A Fracture-Based Model for FRP Debonding in Strengthened Beams. Eng. Fract. Mech. 2009, 76, 1897–1909. [Google Scholar] [CrossRef]
- DS Simulia. ABAQUS Theory Manual, User Manual and Example Manual; Version 6.7; Hibbitt Karlsson and Sorenson Inc.: Providence, RI, USA, 2010. [Google Scholar]
- Carreira, D.; Chu, K. Stress-Strain Relationship for Plain Concrete in Compression. ACI J. Proc. 1985, 82, 797–804. [Google Scholar] [CrossRef]
- Barros, J.; Lourenço, L.; Soltanzadeh, F.; Taheri, M. Steel Fibre Reinforced Concrete for Elements Failing in Bending and in Shear. Adv. Concr. Constr. 2013, 1, 1–27. [Google Scholar] [CrossRef]
- Ahmed, S.; Sharaky, I.; Ibrahim, Y.; Abdo, A. Flexural Response of GFRP RC Beams Strengthened with Side and Bottom NSM GFRP Bars. Case Stud. Constr. Mater. 2023, 18, e01858. [Google Scholar] [CrossRef]
- Seleem, M.; Megahed, F.; Badawy, A.; Sharaky, I. Performance of NSM and EB Methods on the Flexural Capacity of the RC Beams Strengthened with Reinforced HSC Layers. Structures 2023, 56, 104950. [Google Scholar] [CrossRef]
- Sharaky, I.; Elamary, A.; Alharthi, Y. Experimental and Numerical Investigation on the Flexural Performance of RC Slabs Strengthened with EB/NSM CFRP Reinforcement and Bonded Reinforced HSC Layers. Eng. Struct. 2023, 289, 116338. [Google Scholar] [CrossRef]
- Abdo, A.; Sharaky, I.; Ahmed, S. Shear Performance of Reinforced Concrete Beams Strengthened in Shear Using NSM Bars and Reinforced HSC Layers. Struct. Concr. 2023, 24, 7295–7313. [Google Scholar] [CrossRef]
- El-Mandouh, M.; Elsamak, G.; Rageh, B.; Hamoda, A.; Abdelazeem, F. Experimental and Numerical Investigation of One-Way Reinforced Concrete Slabs Using Various Strengthening Systems. Case Stud. Constr. Mater. 2023, 18, e01691. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Hamoda, A.; Emara, M.; Abdelazeem, F.; Ahmed, M. Experimental and Numerical Analysis of RC Beams Strengthened with ECC and Stainless Steel Strips. Mag. Concr. Res. 2023, 75, 251–270. [Google Scholar] [CrossRef]
- Jahani, Y.; Baena, M.; Barris, C.; Torres, L.; Sena-Cruz, J. Effect of Fatigue Loading on Flexural Performance of NSM CFRP-Strengthened RC Beams under Different Service Temperatures. Eng. Struct. 2022, 273, 115119. [Google Scholar] [CrossRef]
- Ahmed, M.; Sheikh, M.; Hadi, M.; Liang, Q. Numerical Modeling of Self-Compacting Concrete Columns Longitudinally Reinforced with Steel Tubes under Axial Loading. Eng. Struct. 2022, 270, 114913. [Google Scholar] [CrossRef]
- Hamoda, A.; Ahmed, M.; Sennah, K. Experimental and Numerical Investigations of the Effectiveness of Engineered Cementitious Composites and Stainless Steel Plates in Shear Strengthening of Reinforced Concrete Beams. Struct. Concr. 2023, 24, 2778–2799. [Google Scholar] [CrossRef]
- Elsamak, G.; Salama, M.; Hamoda, A. Behavior of Precast Segmental Beams Made of High-Strength Concrete and Ultra-High Performance Fiber Concrete Connected by Shear Keys Technique. Arab. J. Sci. Eng. 2023, 48, 4907–4923. [Google Scholar] [CrossRef]
- Yuan, F.; Wei, W.; Hu, R. Shear Strengthening of Reinforced Concrete Beams with High-Strength Steel Wire and Engineered Cementitious Composites. Adv. Struct. Eng. 2022, 25, 158–170. [Google Scholar] [CrossRef]
- Sharaky, I.; Baena, M.; Barris, C.; Sallam, H.; Torres, L. Effect of Axial Stiffness of NSM FRP Reinforcement and Concrete Cover Confinement on Flexural Behaviour of Strengthened RC Beams: Experimental and Numerical Study. Eng. Struct. 2018, 173, 987–1001. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Ci, J.; Kong, L.; Ahmed, M.; Liang, Q.; Hamoda, A.; Chen, S.; Wu, C. Experimental and Numerical Studies of Axially Loaded Square Concrete-encased Concrete-filled Large-diameter Steel Tubular Short Columns. Struct. Concr. 2022, 23, 2748–2769. [Google Scholar] [CrossRef]
- Ci, J.; Ahmed, M.; Liang, Q.; Chen, S.; Chen, W.; Sennah, K.; Hamoda, A. Experimental and Numerical Investigations into the Behavior of Circular Concrete-Filled Double Steel Tubular Slender Columns. Eng. Struct. 2022, 267, 114644. [Google Scholar] [CrossRef]
- Ayough, P.; Ibrahim, Z.; Sulong, N.; Hsiao, P.; Elchalakani, M. Numerical Analysis of Square Concrete-Filled Double Skin Steel Tubular Columns with Rubberized Concrete. Structures 2021, 32, 1026–1047. [Google Scholar] [CrossRef]
- Yu, K.; Wang, Y.; Yu, J.; Xu, S. A Strain-Hardening Cementitious Composites with the Tensile Capacity up to 8%. Constr. Build. Mater. 2017, 137, 410–419. [Google Scholar] [CrossRef]










| Specimen | B × t (mm) | Shear Reinforcement | Bottom Steel | Top Steel | Shear Studs | ρ % |
|---|---|---|---|---|---|---|
| S1m-RSB | 200 × 300 | 7ϕ8/m’ | 3ϕ12 | 2ϕ10 | - | 0.57 |
| S1m-RTB | 200 × 300 | 2ϕ8/m’ + T | 3ϕ12 | 2ϕ10 | - | 0.57 |
| S1m-RTP | 200 × 300 | 2ϕ8/m’ + T | 2ϕ10 + SP | 2ϕ10 | Φ14@400 | 0.58 |
| S2m-RSB | 200 × 500 | 7ϕ8/m’ | 5ϕ14 | 3ϕ10 | - | 0.77 |
| S2m-RTB | 200 × 500 | 2ϕ8/m’ + T | 5ϕ14 | 3ϕ10 | - | 0.77 |
| S2m-RTP | 200 × 500 | 2ϕ8/m’ + T | 2ϕ14 + SP | 3ϕ10 | Φ14@400 | 0.76 |
| Steel Reinforcement | fy, MPa | fu, MPa | E GPa | Elongation % |
|---|---|---|---|---|
| 8 mm bars | 430 | 540 | 205 | 12 |
| 10 mm bars | 530 | 620 | 210 | 10 |
| 12 mm bars | 560 | 640 | 210 | 8 |
| 14 mm bars | 520 | 620 | 210 | 10 |
| 3 mm plate | 250 | 400 | 200 | 16 |
| Specimen ID | Pu (kN) | Pu/PCB × 100 (%) | δu (mm) | Failure Mode |
|---|---|---|---|---|
| S1m-RSB | 254 | - | 5.0 | Flexural |
| S1m-RTB | 205 | 81 | 3.5 | Shear |
| S1m-RTP | 234 | 92 | 2.5 | Shear |
| S2m-RSB | 417 | - | 3.5 | Flexural |
| S2m-RTB | 361 | 87 | 2.3 | Shear |
| S2m-RTP | 370 | 88 | 1.8 | Shear |
| (MPa) | |||
| β | 0.85 | 0.65 |
| Specimen ID | Experimental Results | Analytical Results | Pu,th/Pu,Exp. × 100 (%) | ||||
|---|---|---|---|---|---|---|---|
| Pu,Exp., kN | FM | Psh, kN | Pflex., kN | Pu,th | FM | ||
| S1m-RSB | 254 | Flexural | 284 | 256 | 256 | Flexural | 100.8 |
| S1m-RTB | 205 | Shear | 219 | 256 | 256 | Shear | 124.9 |
| S1m-RTP | 234 | Shear | 227 | 276 | 276 | Shear | 117.9 |
| S2m-RSB | 417 | Flexural | 486 | 419 | 419 | Flexural | 100.5 |
| S2m-RTB | 361 | Shear | 371 | 419 | 371 | Shear | 102.8 |
| S2m-RTP | 370 | Shear | 373 | 382 | 373 | Shear | 100.8 |
| Average | 107.9 | ||||||
| Standard deviation | 9.8 | ||||||
| Specimen | Experimental Results | FE Results | Pu,FE/Pu,Exp. × 100 | ||
|---|---|---|---|---|---|
| ID | Pu,Exp., kN | FM | Pu,FE, kN | FM | (%) |
| S1m-RSB | 254 | Flexural | 275.2 | Flexural | 108.3 |
| S1m-RTB | 205 | Shear | 216.9 | Shear | 105.8 |
| S1m-RTP | 234 | Shear | 252.3 | Shear | 107.8 |
| S2m-RSB | 417 | Flexural | 439.4 | Flexural | 105.4 |
| S2m-RTB | 361 | Shear | 372 | Shear | 103.0 |
| S2m-RTP | 370 | Shear | 383 | Shear | 103.5 |
| Average | 105.7 | ||||
| Standard deviation | 2.0 | ||||
| Beam ID | Internal Reinforcement | Shear Reinforcement | fy,P MPa | fy,B MPa | Variable |
|---|---|---|---|---|---|
| S2m-RTP | Plate + 2ϕ14 | Truss | 420 | 520 | Reference |
| S2m-RSP | Plate + 2ϕ14 | Stirrups 7ϕ8//m | 420 | 520 | Shear reinforcement |
| S2m-RSB | 5ϕ14 | Stirrups 7ϕ8//m | - | 520 | Tension reinforcement |
| S2m-RTP-1 | Plate + 2ϕ14 | Truss | 520 | 520 | Plate yield strength |
| S2m-RSP-1 | Plate + 2ϕ14 | Stirrups 7ϕ8//m | 520 | 520 | fy,P and Shear reinforcement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elamary, A.S.; Sharaky, I.A.; Alharthi, F.M.; El-Zohairy, A.; Mostafa, M.M.A. The Influence of Various Tensile and Shear Reinforcement Configurations on the Ultimate Capacity and Failure Mechanisms of Reinforced Concrete Beams. Buildings 2025, 15, 1396. https://doi.org/10.3390/buildings15091396
Elamary AS, Sharaky IA, Alharthi FM, El-Zohairy A, Mostafa MMA. The Influence of Various Tensile and Shear Reinforcement Configurations on the Ultimate Capacity and Failure Mechanisms of Reinforced Concrete Beams. Buildings. 2025; 15(9):1396. https://doi.org/10.3390/buildings15091396
Chicago/Turabian StyleElamary, Ahmed S., Ibrahim A. Sharaky, Fahad M. Alharthi, Ayman El-Zohairy, and Mostafa M. A. Mostafa. 2025. "The Influence of Various Tensile and Shear Reinforcement Configurations on the Ultimate Capacity and Failure Mechanisms of Reinforced Concrete Beams" Buildings 15, no. 9: 1396. https://doi.org/10.3390/buildings15091396
APA StyleElamary, A. S., Sharaky, I. A., Alharthi, F. M., El-Zohairy, A., & Mostafa, M. M. A. (2025). The Influence of Various Tensile and Shear Reinforcement Configurations on the Ultimate Capacity and Failure Mechanisms of Reinforced Concrete Beams. Buildings, 15(9), 1396. https://doi.org/10.3390/buildings15091396







