A Modified Method for Calculating the Uplift Capacity of Micropiles Considering the Correction of the Critical Embedment Depth
Abstract
1. Introduction
2. The Model Tests
2.1. The Model Piles
2.2. The Soil Sample
2.3. The Loading System
3. Results and Discussions
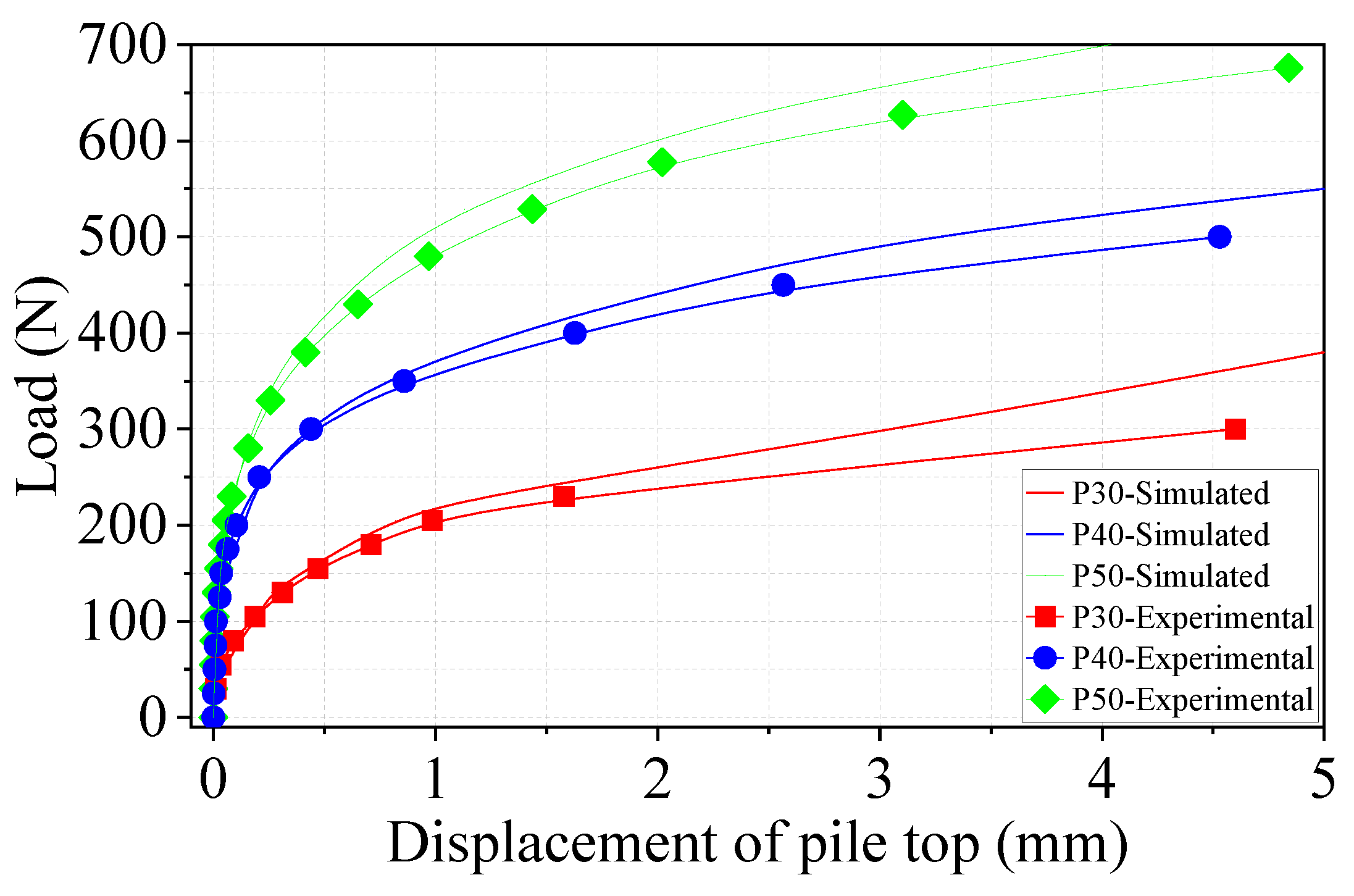
3.1. The Bearing Capacity
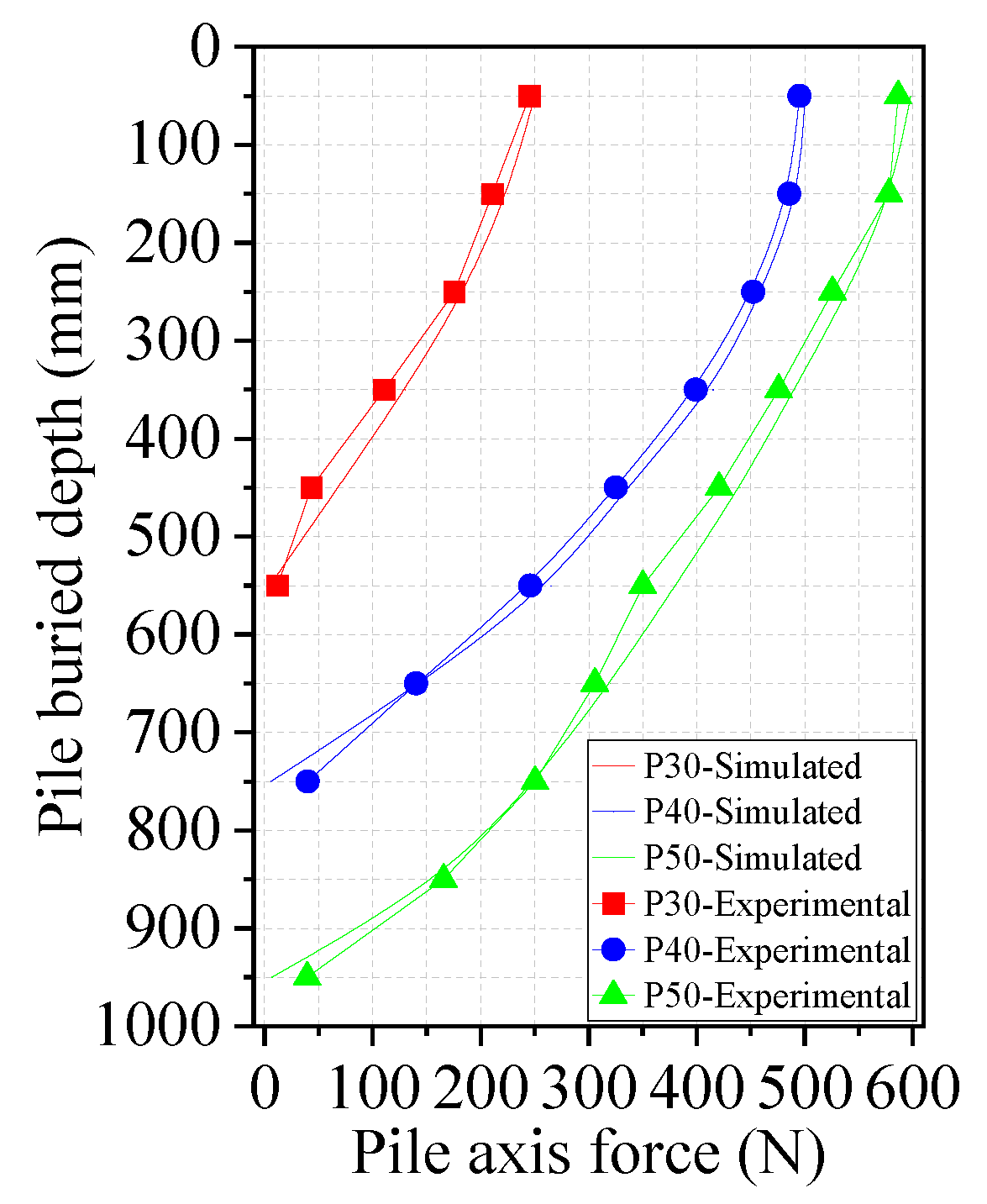
3.2. The Axial Force of the Piles
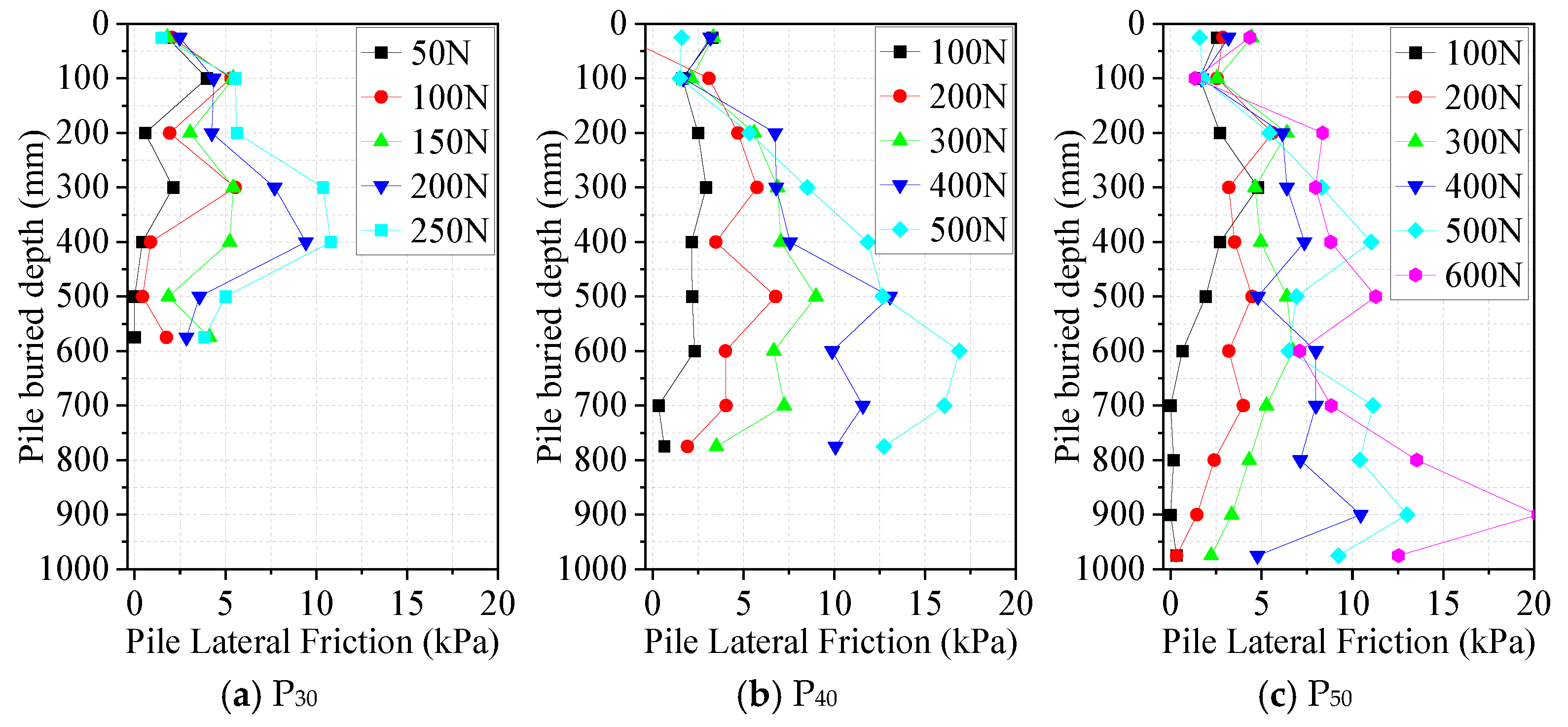
3.3. The Side Friction Resistance
4. Prediction of the Ultimate Uplift Capacity
4.1. The Available Prediction Models and Improvements
- (1)
- The standard model [33]
- (2)
- The truncated cone model
- (3)
- Meyerhof’s model [17]
- (4)
- Das’s model [18]
- (5)
- Chattopadhyay’s model [19]
- (6)
- Shanker’s model [20]
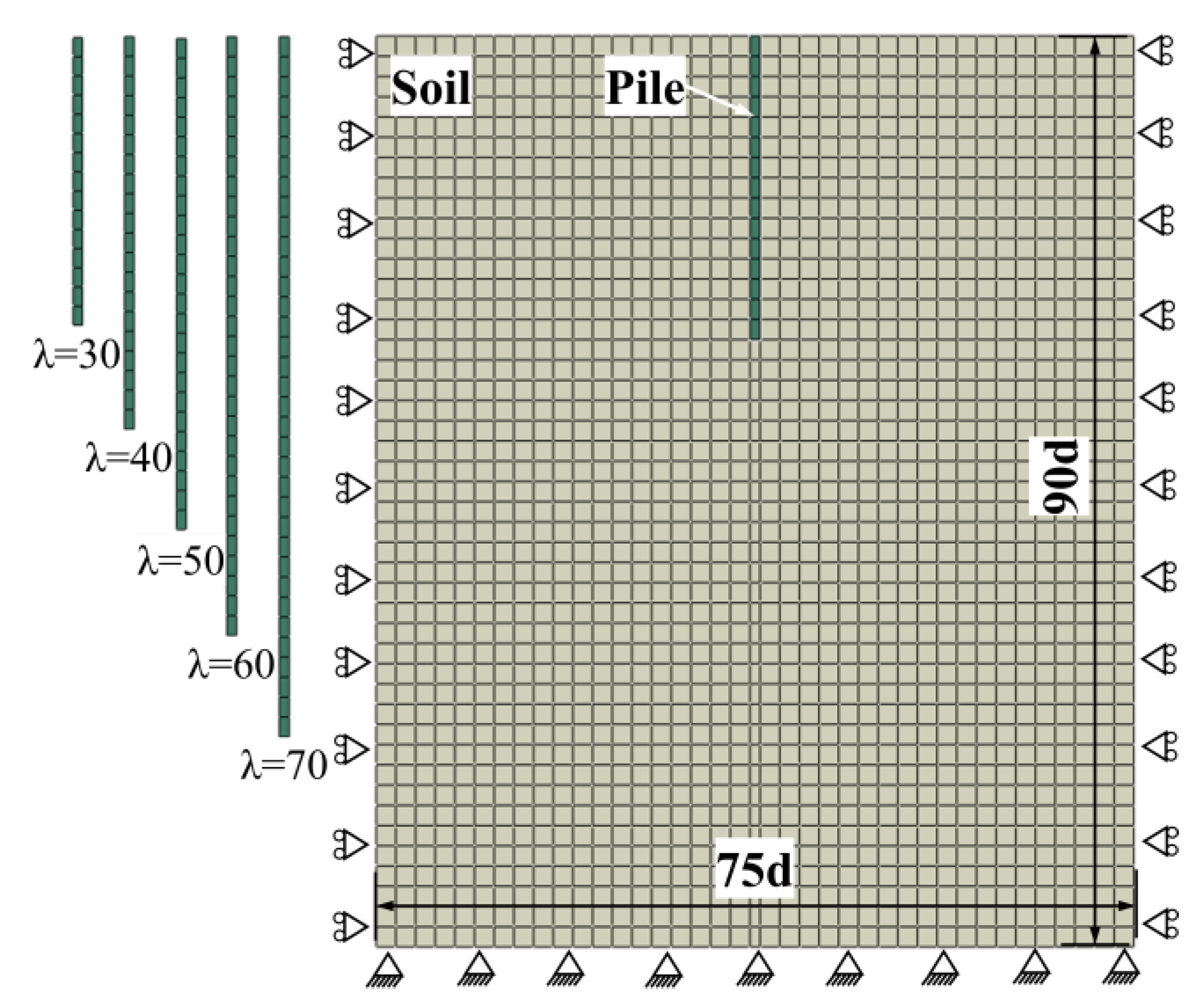
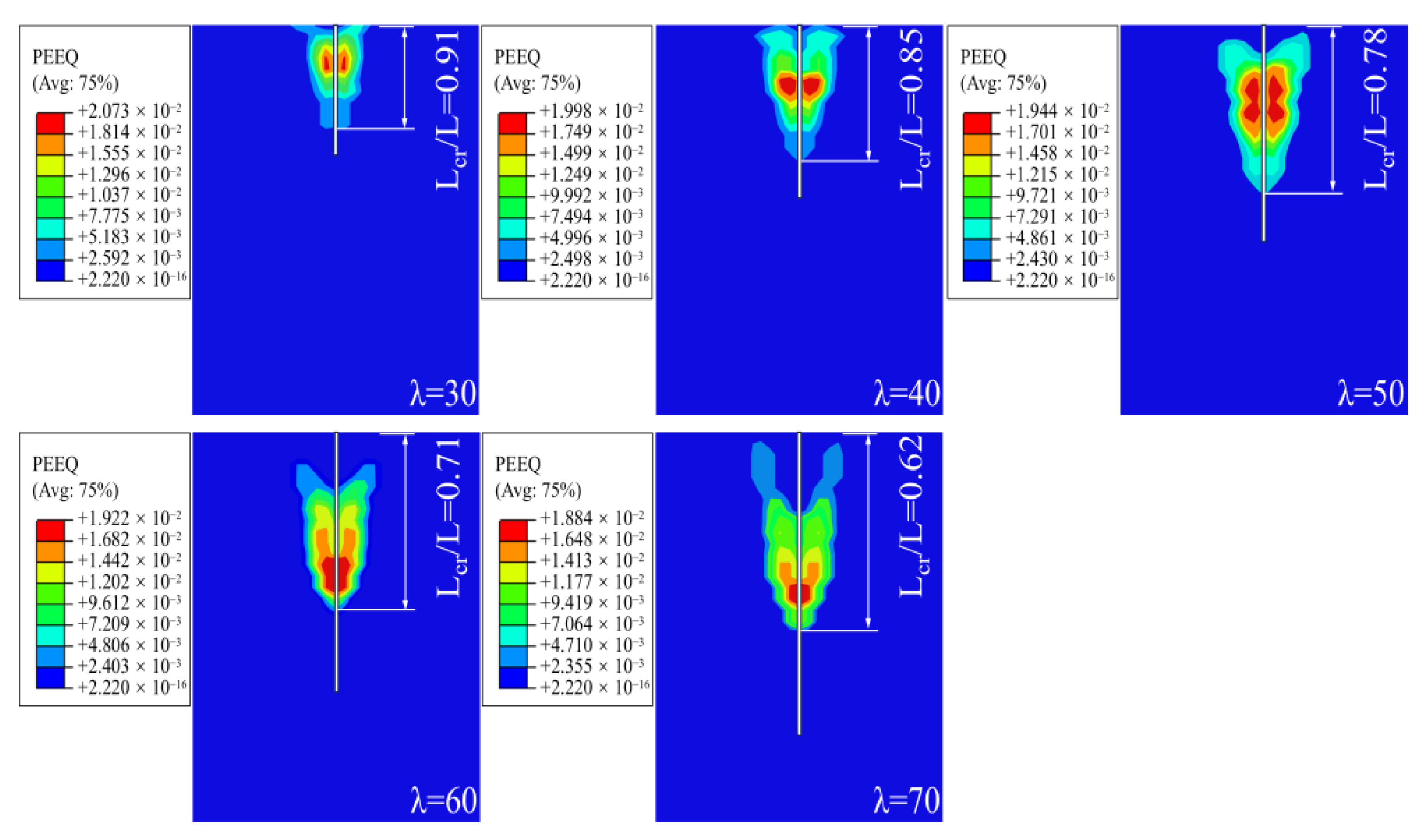
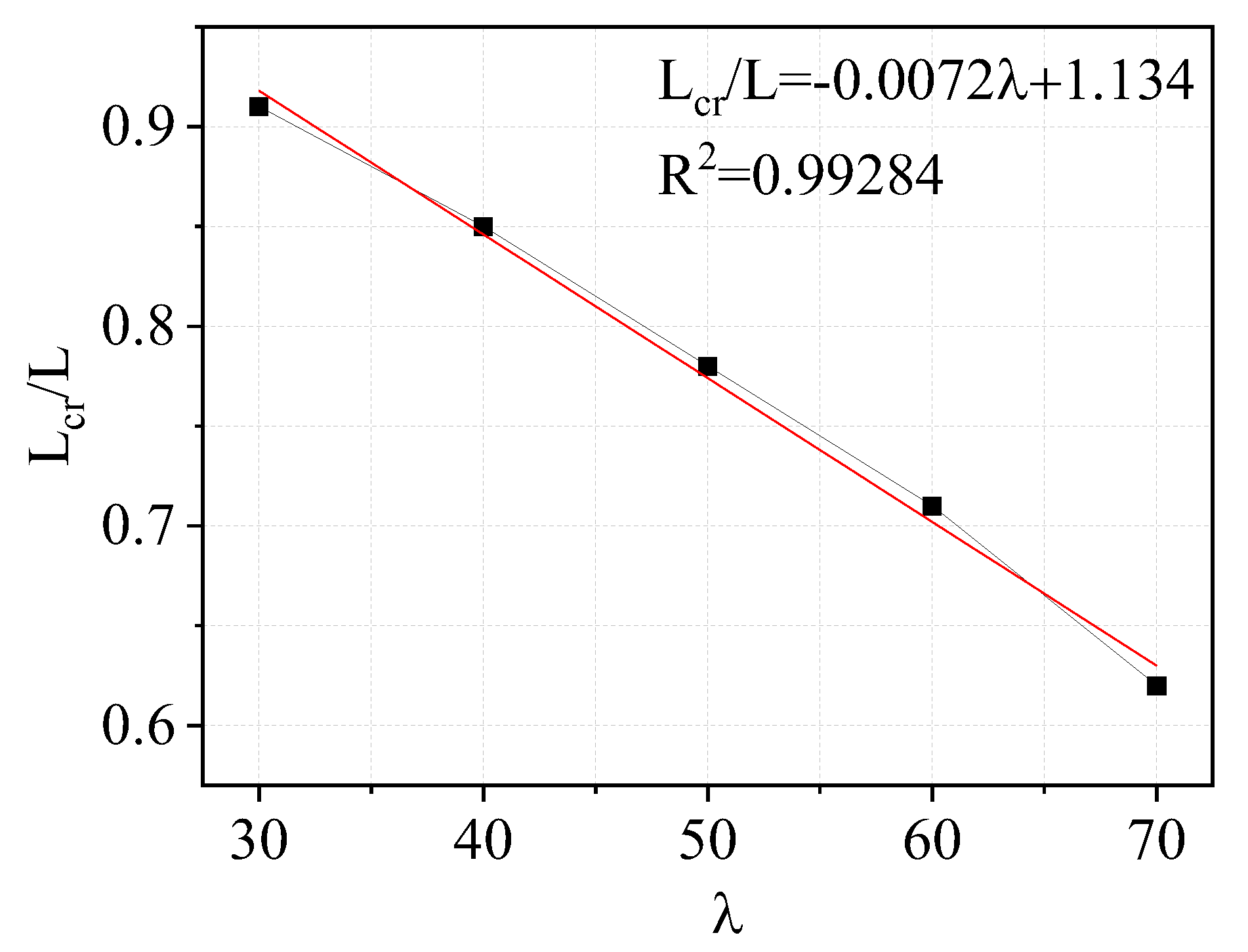
4.2. The Determination of Lcr for Micropiles with Different Values
4.2.1. The Finite Element Model
4.2.2. Validation of the Numerical Model
4.3. Validation of the Improved Model
5. Conclusions
- (1)
- As the slenderness ratio increases, the ultimate uplift capacity of a pile gradually increases, but the rate of increase decreases progressively. The load distribution of the micropiles varies with their slenderness ratios, showing that as the slenderness ratio increases, the embedment effect and range of the surrounding soil at the lower part of the pile become more significant, and the critical embedment depth of the micropile shifts further away from the tip of the pile.
- (2)
- The improved model is suitable for predicting the uplift capacity of micropiles. Validation through case studies demonstrates that this method provides accurate predictions, with errors below 12%.
- (3)
- The improved model is easy to use without a complex analysis and is suitable for the rapid design of micropiles in engineering. It is recommended in practical projects to first calculate Lcr using Equation (14) based on the preliminarily designed . Subsequently, Pnu should be calculated via Equation (15), compared with the design value, and an appropriate selected to optimize the design of the micropile size.
- (4)
- The current model does not encompass specific soil conditions (e.g., expansive soil and collapsible loess). Future research will incorporate in situ testing and specialized soil analyses to expand the model’s applicability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruce, D.A.; Dimillio, A.F.; Juran, I. Introduction to Micropiles: An International Perspective; Kentucky Geotechnical Special Publication, ASCE: Louisville, KY, USA, 1995; pp. 1–26. [Google Scholar]
- Hwang, T.H.; Kim, K.H.; Shin, J.H. Experimental and numerical study on lateral resistance of micropile in sand. KSCE J. Civ. Eng. 2023, 27, 3740–3752. [Google Scholar] [CrossRef]
- Kyung, D.; Lee, J. Uplift load-carrying capacity of single and group micropiles installed with inclined conditions. J. Geotech. Geoenviron. Eng. 2017, 143, 04017031. [Google Scholar] [CrossRef]
- Wang, H.J. Research on micropile foundation of transmission tower on soft soil area. In Proceedings of the 2016 5th International Conference on Civil, Architectural and Hydraulic Engineering (ICCAHE 2016), Zhuhai, China, 30–31 July 2016; Beijing China Atlantis Press: Beijing, China, 2016; pp. 574–579. [Google Scholar]
- Yu, X.; Wang, X. Research on the Design of Miniature Pile Foundation for Transmission Line. E3S Web Conf. EDP Sci. 2019, 136, 02022. [Google Scholar] [CrossRef]
- Emirler, B.; Tolun, M.; Yildiz, A. Investigation on determining uplift capacity and failure mechanism of the pile groups in sand. Ocean Eng. 2020, 218, 108145. [Google Scholar] [CrossRef]
- Elsawwaf, A.; El Sawwaf, M.; Farouk, A.; Aamer, F.; El Naggar, H. Restoration of tilted buildings via micropile underpinning: A case study of a multistory building supported by a raft foundation. Buildings 2023, 13, 422. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; El Naggar, M.H.; Wu, W. Seismic response of pile group embedded in unsaturated soil considering the coupling of kinematic and inertia pile-pile interactions. Comput. Geotech. 2025, 178, 106937. [Google Scholar] [CrossRef]
- Li, L.; Yan, N.; Liu, Z.; Wu, W.; Jiang, G.; Chen, L.; Liu, H. Investigation on the cyclic laterally-loaded response of pile-bucket foundation with grouted connection. Mar. Struct. 2025, 103, 103808. [Google Scholar] [CrossRef]
- Borthakur, N.; Dey, A.K. Evaluation of group capacity of micro-pile in soft clayey soil from experimental analysis using SVM-based prediction model. Int. J. Geomech. 2020, 20, 04020008. [Google Scholar] [CrossRef]
- Li, H.; Ren, G. Horizontal and uplift bearing characteristics of a cast-in-place micropile group foundation in a plateau mountainous area. Sustainability 2023, 15, 13554. [Google Scholar] [CrossRef]
- Tsukada, Y.; Miura, K.; Tsubokawa, Y.; Otani, Y.; You, G.-L. Mechanism of bearing capacity of spread footings reinforced with micropiles. Soils Found. 2006, 46, 367–376. [Google Scholar] [CrossRef]
- Jang, Y.E.; Kim, B.; Wang, C.; Han, J.-T. Prediction of vertical bearing capacity of waveform micropile. Géotech. Lett. 2019, 9, 198–204. [Google Scholar] [CrossRef]
- Elsawwaf, A.; Nazir, A.; Azzam, W. The effect of combined loading on the behavior of micropiled rafts installed with inclined condition. Environ. Sci. Pollut. Res. 2022, 29, 81321–81336. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.I.L.; Kim, M.Y.; Hwang, T.H. Reinforcement effect of micropile and bearing characteristics of micropiled raft according to the cohesion of soil and stiffness of pile. Geomech. Eng. 2024, 37, 511–525. [Google Scholar]
- Kishida, H. Stress distribution by model piles in sand. Soils Found. 1963, 4, 1–23. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Uplift resistance of inclined anchors and piles. In Proceedings of the 8th International Conference on Soil Mechanics and Foundation Engineering, Moscow, Russia, 6–11 August 1973; Volume 2, pp. 167–172. [Google Scholar]
- Das, B.M. A procedure for estimation of uplift capacity of rough piles. Soils Found. 1983, 23, 122–126. [Google Scholar] [CrossRef]
- Chattopadhyay, B.C.; Pise, P.J. Uplift capacity of piles in sand. J. Geotech. Eng. 1986, 112, 888–904. [Google Scholar] [CrossRef]
- Shanker, K.; Basudhar, P.K.; Patra, N.R. Uplift capacity of single piles: Predictions and performance. Geotech. Geol. Eng. 2007, 25, 151–161. [Google Scholar] [CrossRef]
- Shelke, A.; Patra, N.R. Effect of arching on uplift capacity of pile groups in sand. Int. J. Geomech. 2008, 8, 347–354. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, R.; Liu, S.; Li, X.-M. Estimation of uplift capacity of a single pile embedded in sand considering arching effect. Int. J. Geomech. 2018, 18, 06018021. [Google Scholar] [CrossRef]
- Grindheim, B.; Trinh, N.; Li, C.C.; Høien, A.H. Investigating Load Arches and the Uplift Capacity of Rock Anchors: A Numerical Approach. Rock Mech. Rock Eng. 2024, 57, 7313–7342. [Google Scholar] [CrossRef]
- Deshmukh, V.B.; Dewaikar, D.M.; Choudhury, D. Computations of uplift capacity of pile anchors in cohesionless soil. Acta Geotech. 2010, 5, 87–94. [Google Scholar] [CrossRef]
- Chattopadyay, B.C. Uplift capacity of pile groups. In Proceedings of the 13thICSMFE, New Delhi, India, 5–10 January 1994; pp. 539–542. [Google Scholar]
- Hong, W.P.; Chim, N. Prediction of uplift capacity of a micropile embedded in soil. KSCE J. Civ. Eng. 2015, 19, 116–126. [Google Scholar] [CrossRef]
- Iai, S. Similitude for shaking table tests on soil-structure-fluid model in 1g gravitational field. Soils Found. 1989, 29, 105–118. [Google Scholar] [CrossRef]
- FHWA. Micropile Design and Construction Reference Manual for NHI Course 132078; Federal Highway Administration, United States Department of Transportation: Washington, DC, USA, 2005.
- Miura, K.; Tsukada, Y.; Tsubokawa, Y.; Ishito, M.; Nishimura, N.; Ohtani, Y.; You, G.L. Bearing capacity during the earthquake of the spread footing reinforced with micropiles. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Japan, 30 January–4 February 2000. [Google Scholar]
- ASTM D3080/D3080M-11; Standard Test Method for Direct Shear Test of Soils Under Consolidated Drained Conditions. ASTM: West Conshohocken, PA, USA, 2014.
- Da Silva, L.S.; Simões, R.; Gervásio, H. Design of Steel Structures: Eurocode 3: Design of Steel Structures, Part 1-1: General Rules and Rules for Buildings; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- American Petroleum Institute. API RP 2GEO: Recommended Practice for Geotechnical and Foundation Design Considerations, 2nd ed.; API Publishing Services: Washington, DC, USA, 2021. [Google Scholar]
- Johnson, S.M.; Kavanagh, C.T. The Design of Foundations for Buildings; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Hong, Y.; He, B.; Wang, L.Z.; Wang, Z.; Ng, C.W.W.; Masín, D. Cyclic lateral response failure mechanisms of semi-rigid pile in soft clay: Centrifuge tests numerical modelling. Can. Geotech. J. 2017, 54, 806–824. [Google Scholar] [CrossRef]
- Siddamal, U.V. Behavior of Pile Group Under Uplift Loads. Master’s Thesis, Indian Institute of Technology, Ghana City, India, 1989. [Google Scholar]
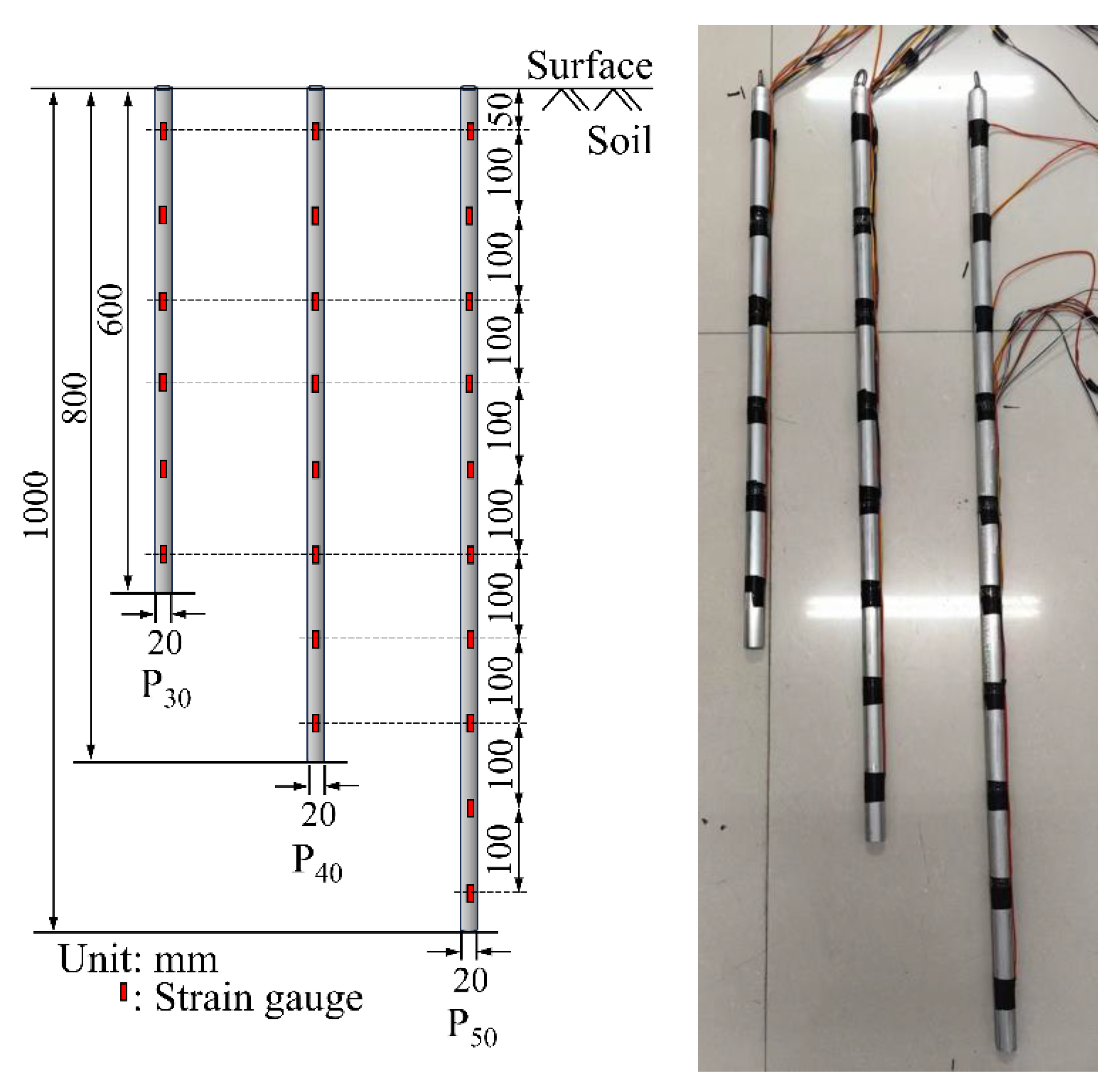
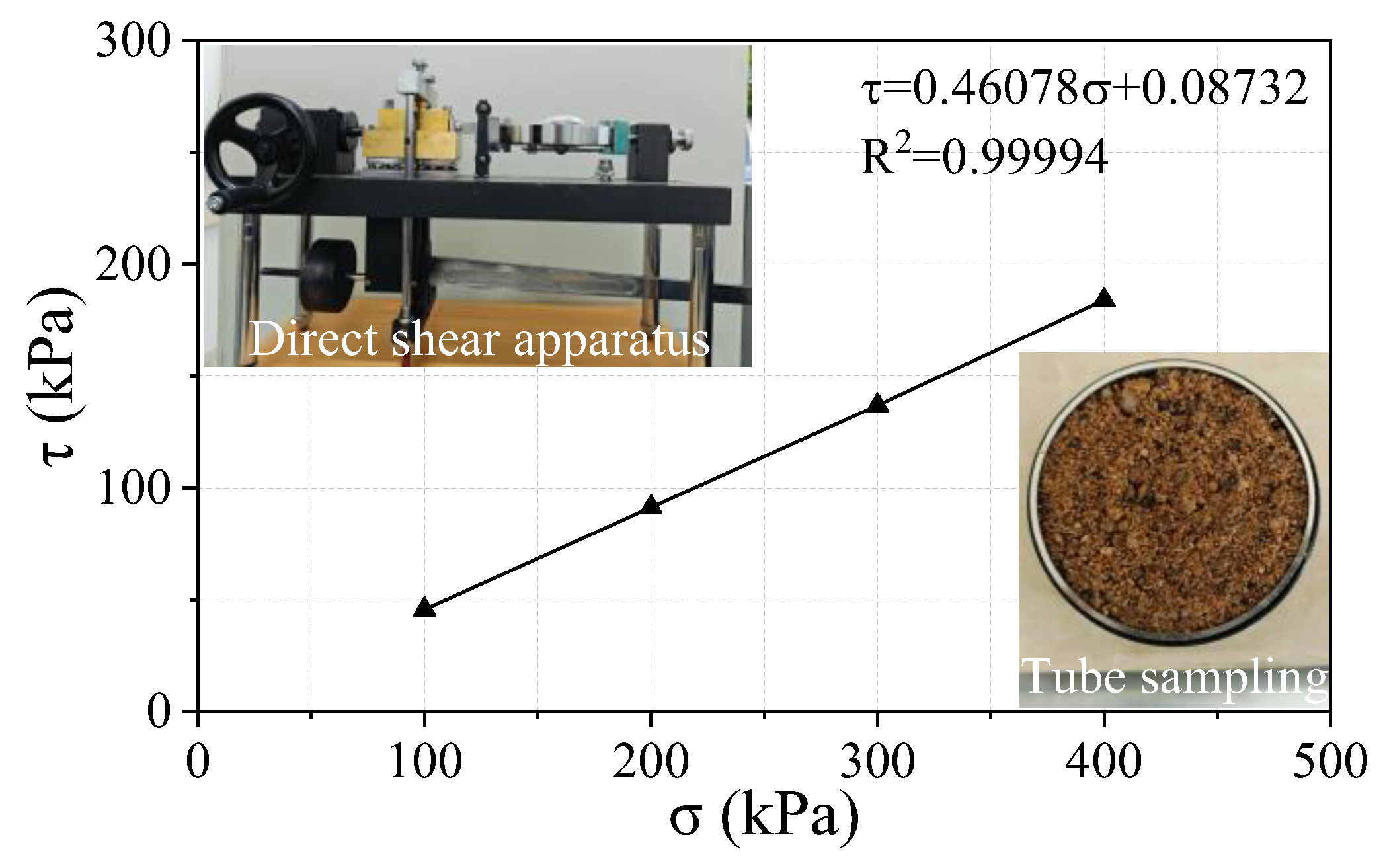
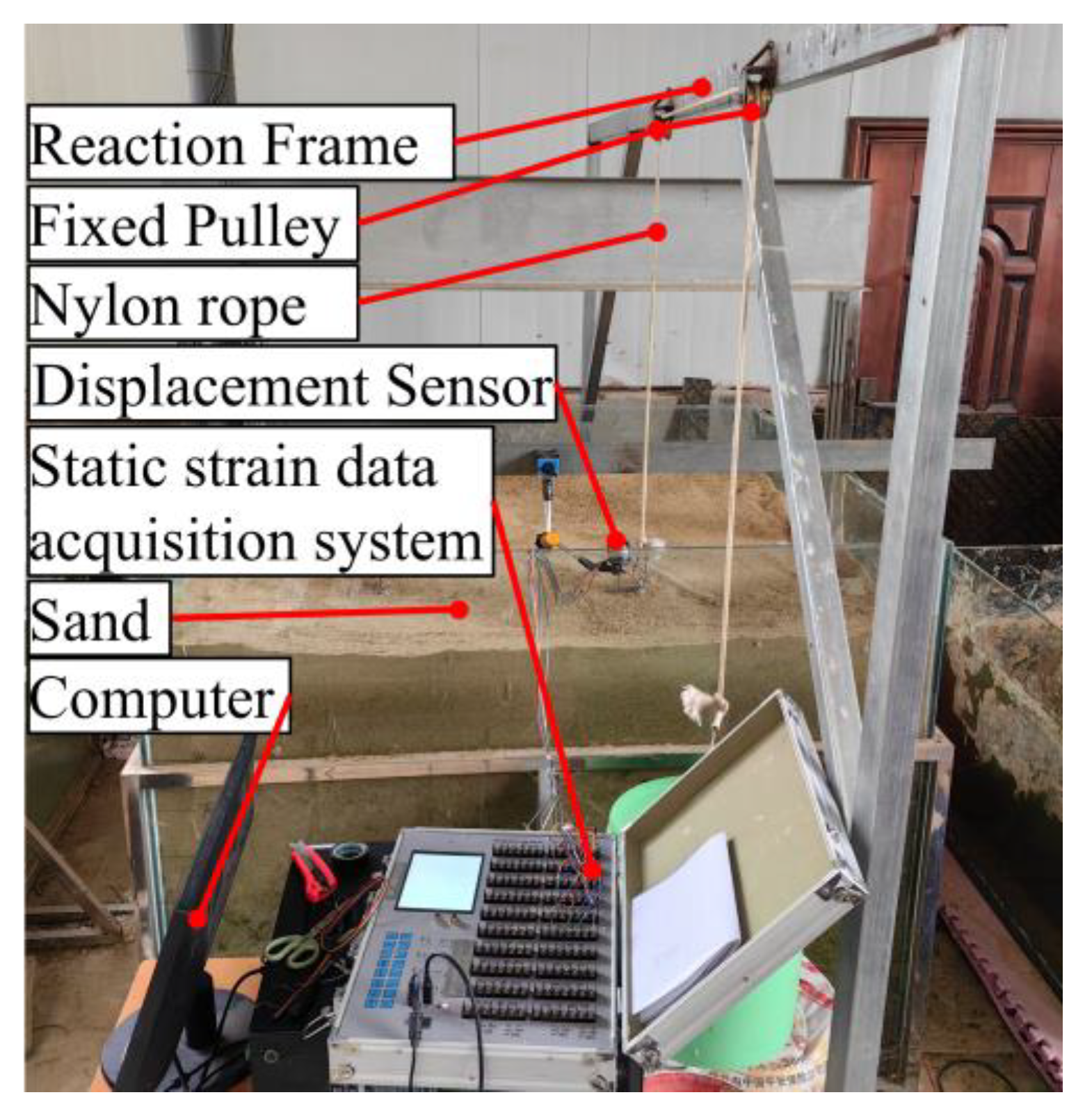

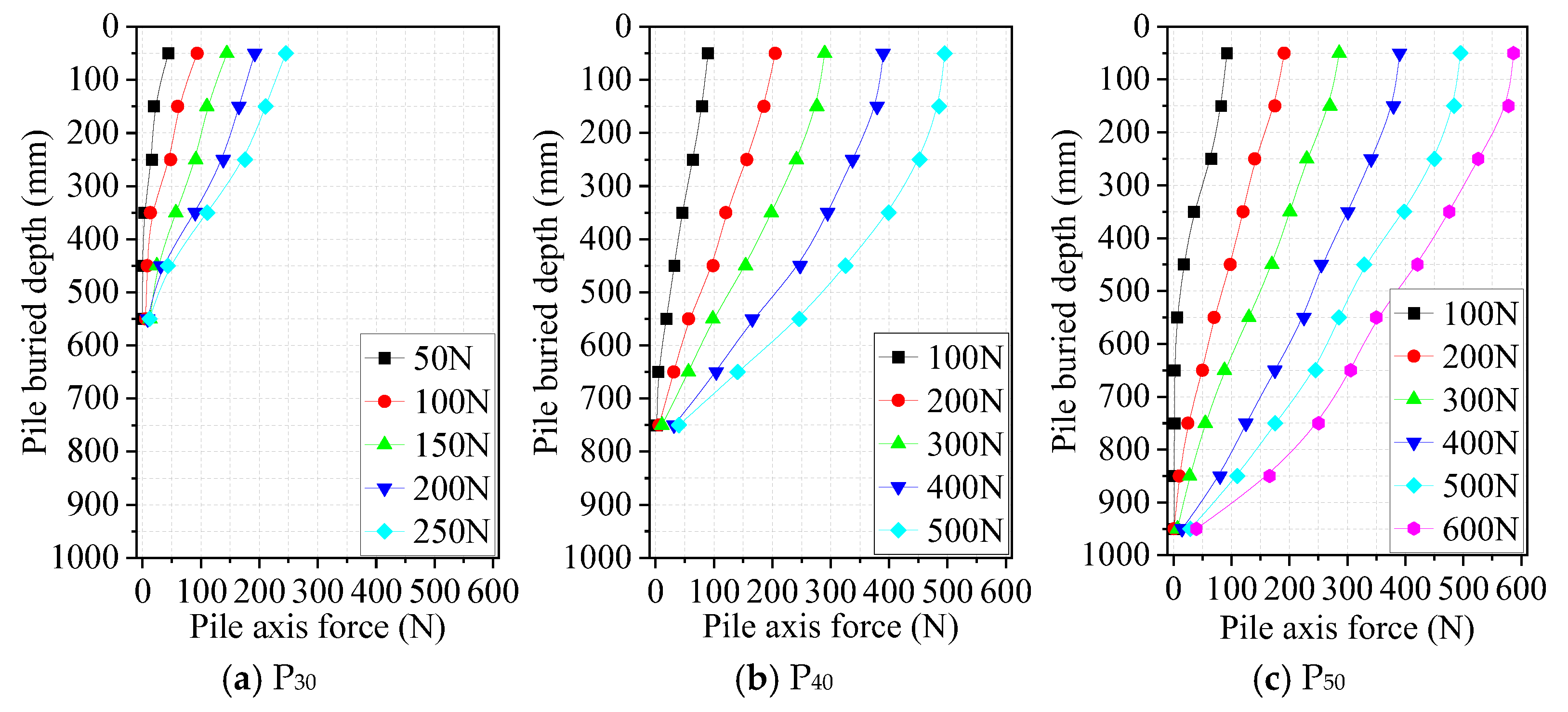

| Unit | ρ (kg/m3) | E (MPa) | v | φ (°) | Cohesion c (kPa) |
|---|---|---|---|---|---|
| Micropile | 2.7 | 70,000 | 0.33 | - | - |
| Soil mass | 1.9 | 5.0 | 0.3 | 25 | 1 |
| Data Sources | Expt. Parameters | Expt. Results (N) | Model [33] | Truncated Cone Model | Model [17] | Model [18] | Model [19] | Model [20] | Improved Model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kN/m3) | (°) | (°) | d (m) | (N) | Error (%) | (N) | Error (%) | (N) | Error (%) | (N) | Error (%) | (N) | Error (%) | (N) | Error (%) | (N) | Error (%) | |||
| Siddamal [35] | 16.1 | 40.5 | 23 | 0.02 | 40 | 441.6 | 48.17 | −89.1 | 1174.9 | 166.1 | 316.04 | −28.4 | 206.4 | −53.3 | 194.2 | −56 | 401.5 | −9.08 | 485.5 | 9.94 |
| Chattopadhyay [19] | 17.0 | 40 | 25 | 0.019 | 31.57 | 130 | 30.36 | 76.6 | 509.4 | −291.8 | 228 | −75.38 | 165 | −26.9 | 165 | −26.9 | 197.0 | −51.5 | 124.1 | −4.5 |
| Shanker [20] | 15.8 | 38 | 26 | 0.02 | 30 | 181.6 | 42.6 | 76.5 | 423.5 | −133.0 | 266.5 | −46.8 | 169 | 6.9 | 127.2 | 30.0 | 178.0 | 2.0 | 160.5 | 11.6 |
| 40 | 363 | 75.8 | 79.1 | 1004.0 | −176.6 | 468 | −28.9 | 239 | 34.2 | 165 | 54.5 | 391.0 | −7.71 | 404.5 | 11.4 | |||||
| 15.4 | 34 | 22 | 0.02 | 30 | 108.6 | 39.5 | 63.6 | 325.0 | −199.7 | 150 | −38 | 50.6 | 53.4 | 54.7 | 49.6 | 143.0 | −31.6 | 121.1 | 11.5 | |
| 40 | 242.4 | 70.22 | 71.0 | 771.5 | −218.3 | 267 | −10.1 | 68.3 | 71.8 | 80 | 67.0 | 311.0 | −28.3 | 214 | −11.7 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, L.; Zheng, Y.; Zhou, Y.; Wu, D.; Wang, W.; Guo, Z.; Xu, Z. A Modified Method for Calculating the Uplift Capacity of Micropiles Considering the Correction of the Critical Embedment Depth. Buildings 2025, 15, 1486. https://doi.org/10.3390/buildings15091486
Bao L, Zheng Y, Zhou Y, Wu D, Wang W, Guo Z, Xu Z. A Modified Method for Calculating the Uplift Capacity of Micropiles Considering the Correction of the Critical Embedment Depth. Buildings. 2025; 15(9):1486. https://doi.org/10.3390/buildings15091486
Chicago/Turabian StyleBao, Linli, Yuesong Zheng, Yi Zhou, Dongya Wu, Wenhao Wang, Zhaoxiang Guo, and Zhijun Xu. 2025. "A Modified Method for Calculating the Uplift Capacity of Micropiles Considering the Correction of the Critical Embedment Depth" Buildings 15, no. 9: 1486. https://doi.org/10.3390/buildings15091486
APA StyleBao, L., Zheng, Y., Zhou, Y., Wu, D., Wang, W., Guo, Z., & Xu, Z. (2025). A Modified Method for Calculating the Uplift Capacity of Micropiles Considering the Correction of the Critical Embedment Depth. Buildings, 15(9), 1486. https://doi.org/10.3390/buildings15091486






