A Non-Linear Continuous-Time Generalized Predictive Control for a Planar Cable-Driven Parallel Robot
Abstract
:1. Introduction
2. Robot Structure and Modeling
3. The Proposed NCGCP Controller Design
4. Stability Analysis
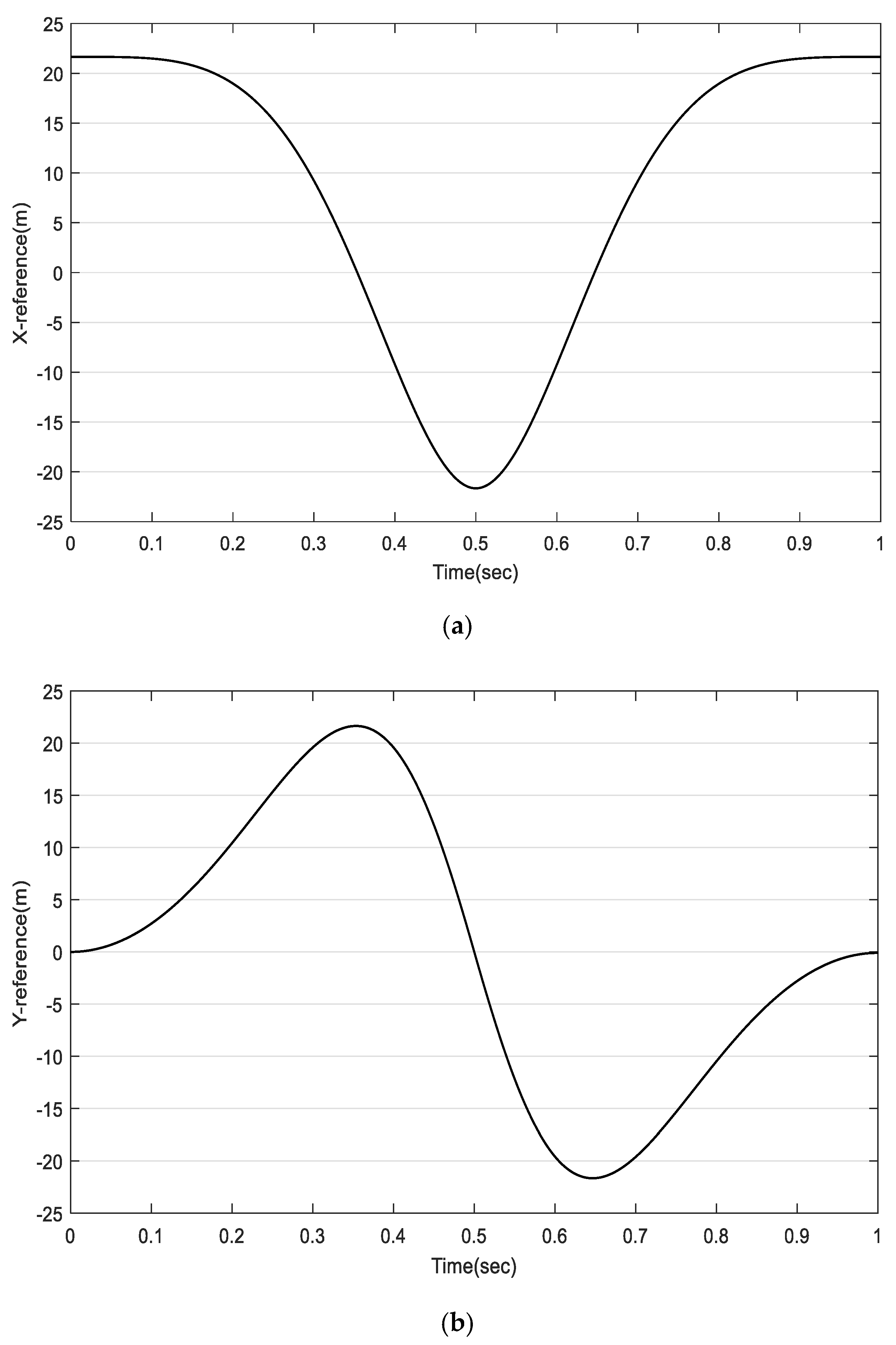
5. Simulation Results
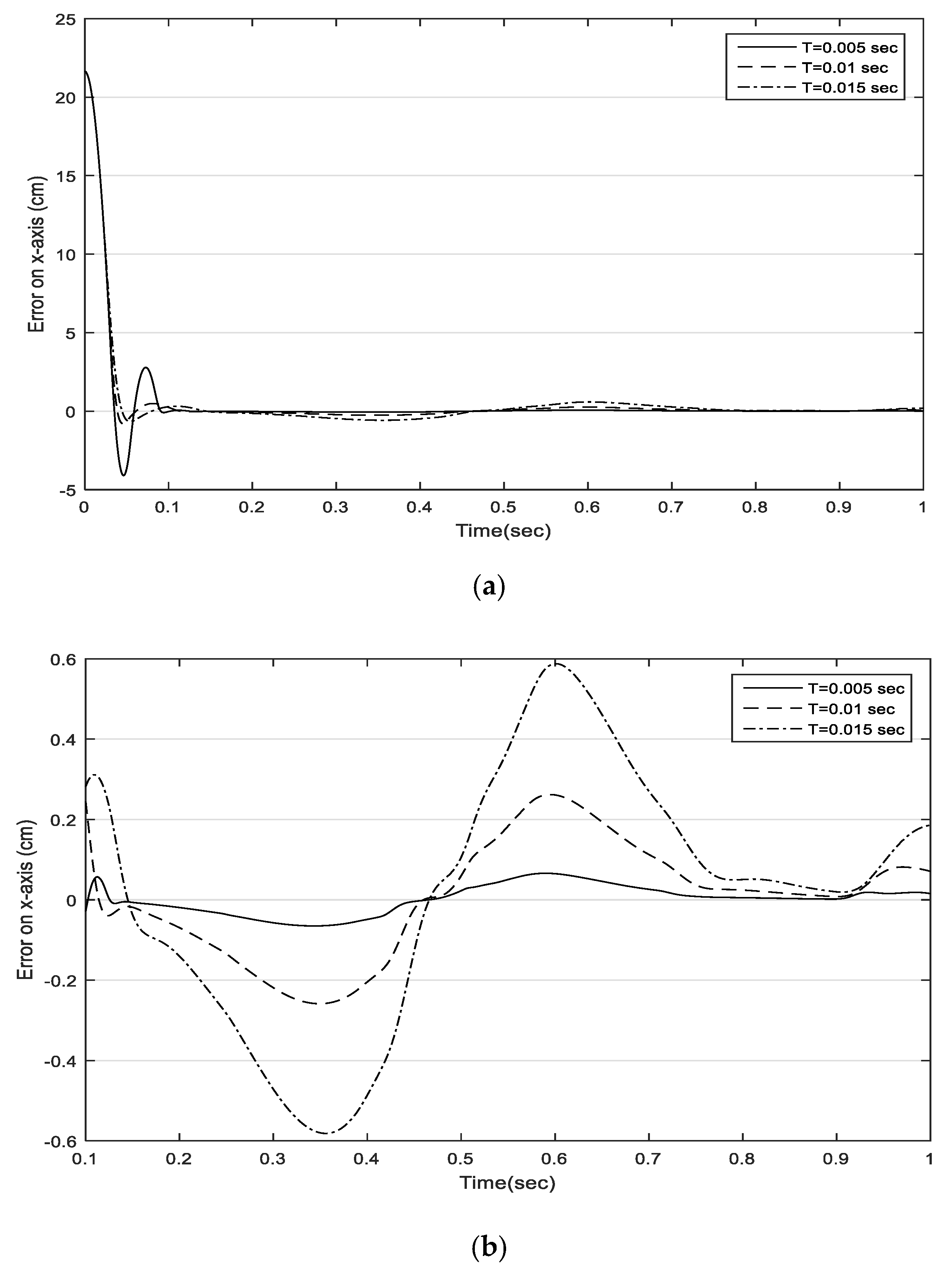
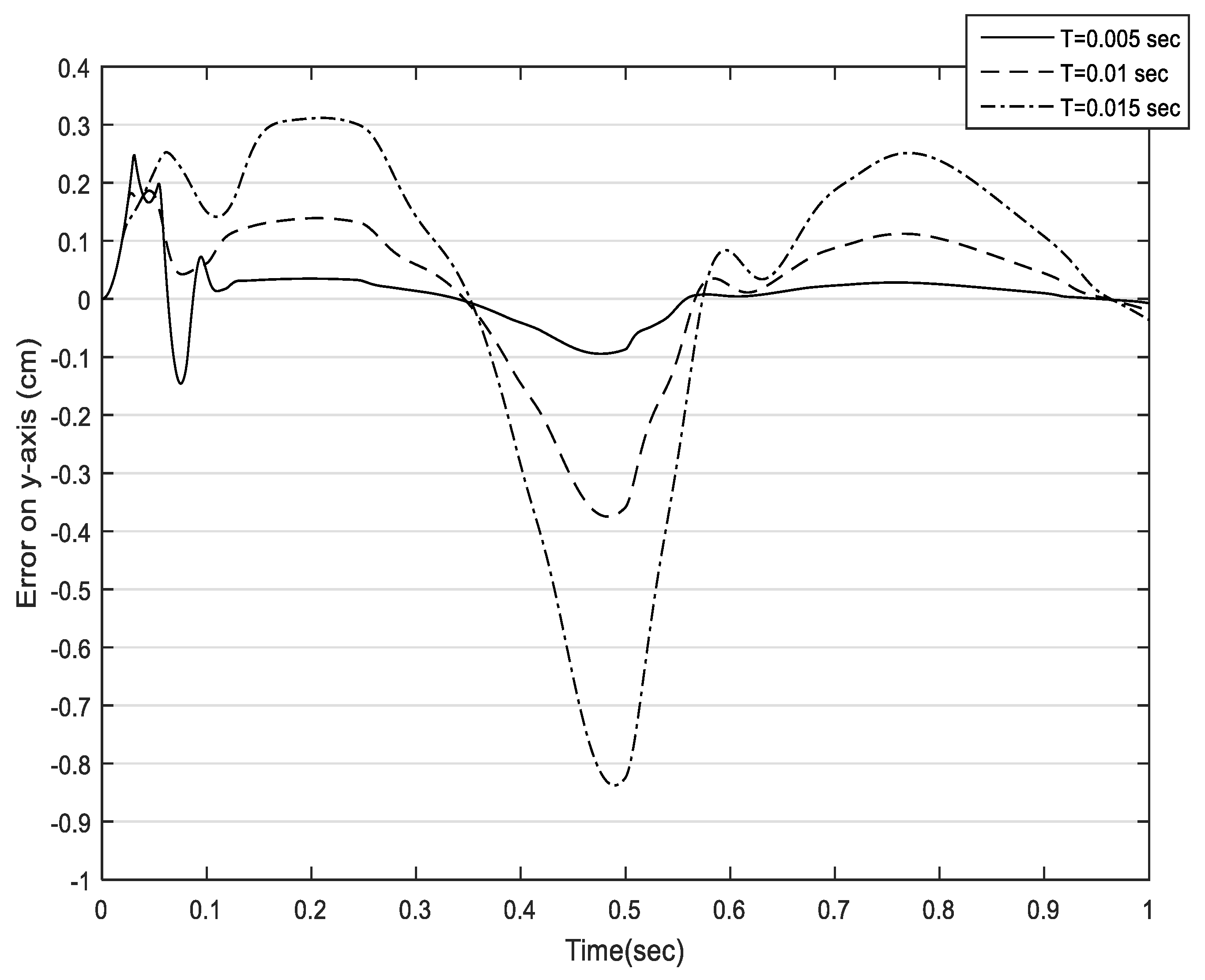
- Phase 1: Influence of the prediction horizon on NCGPC tracking performances.
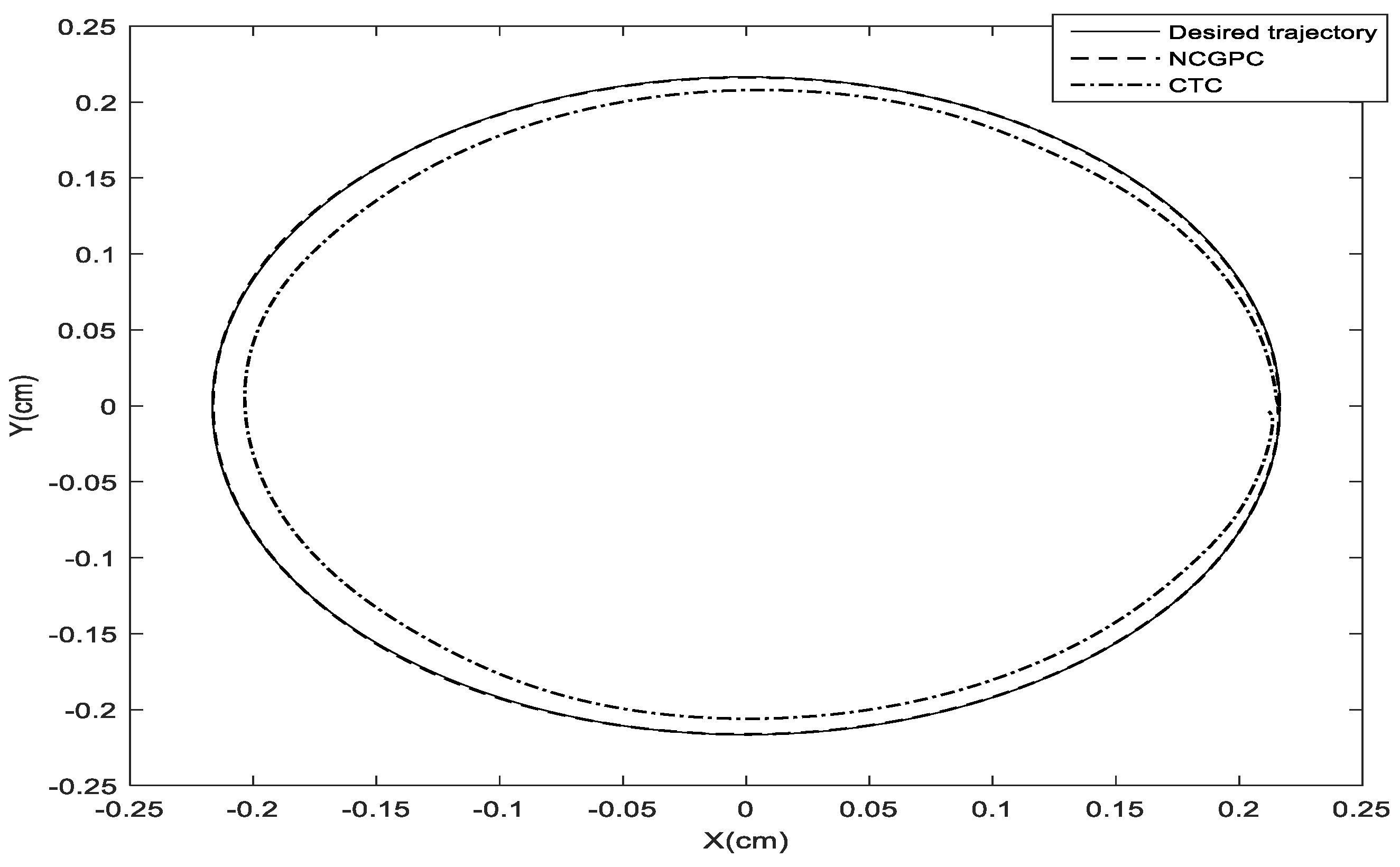
- Phase 2: Comparison between NCGPC and CTC based on tracking errors.
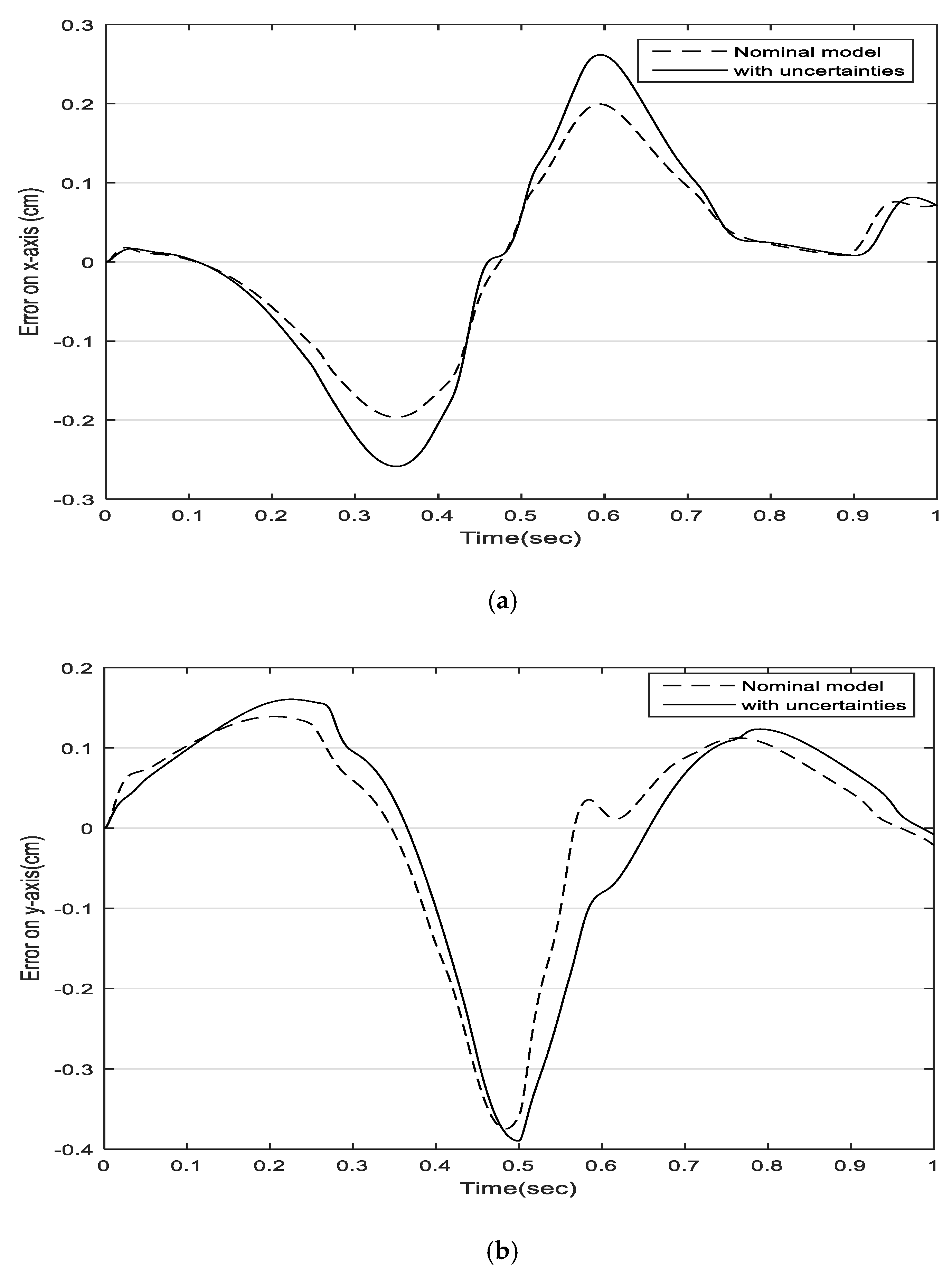
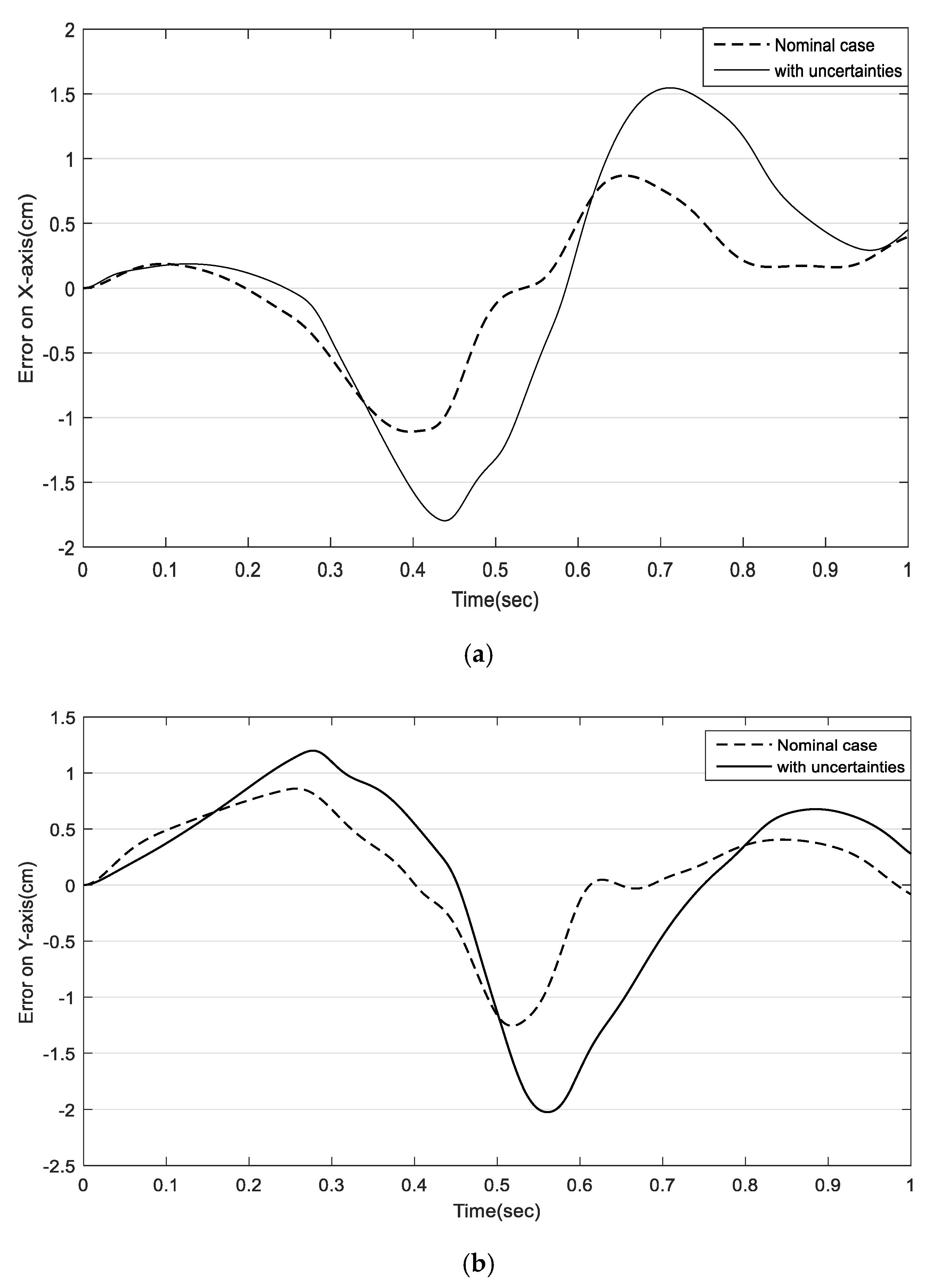
- Phase 3: Robustness test of payload and parameter uncertainties for both NCGPC and CTC.
5.1. Influence of the Prediction Horizon on NCGPC Tracking Performances
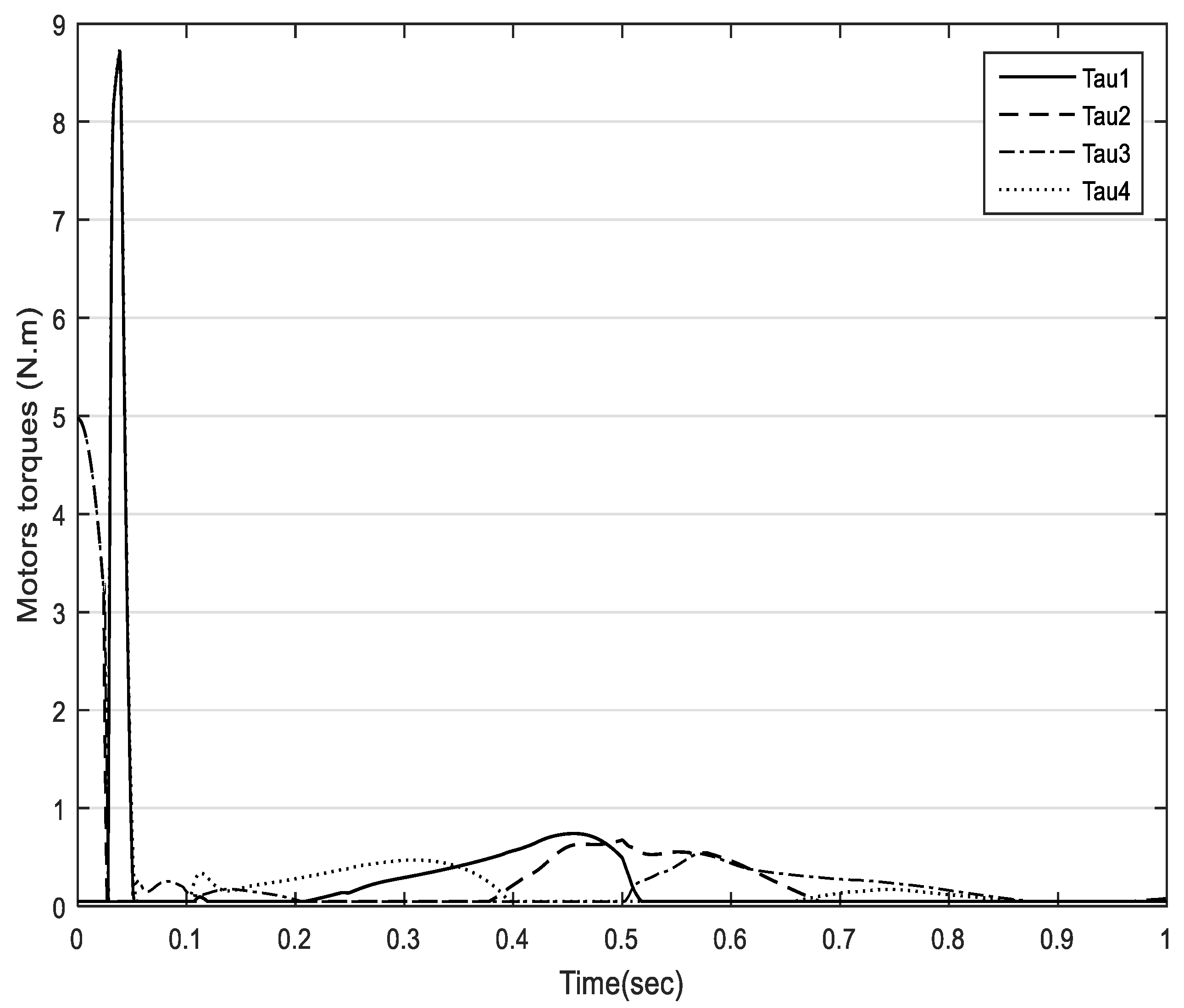
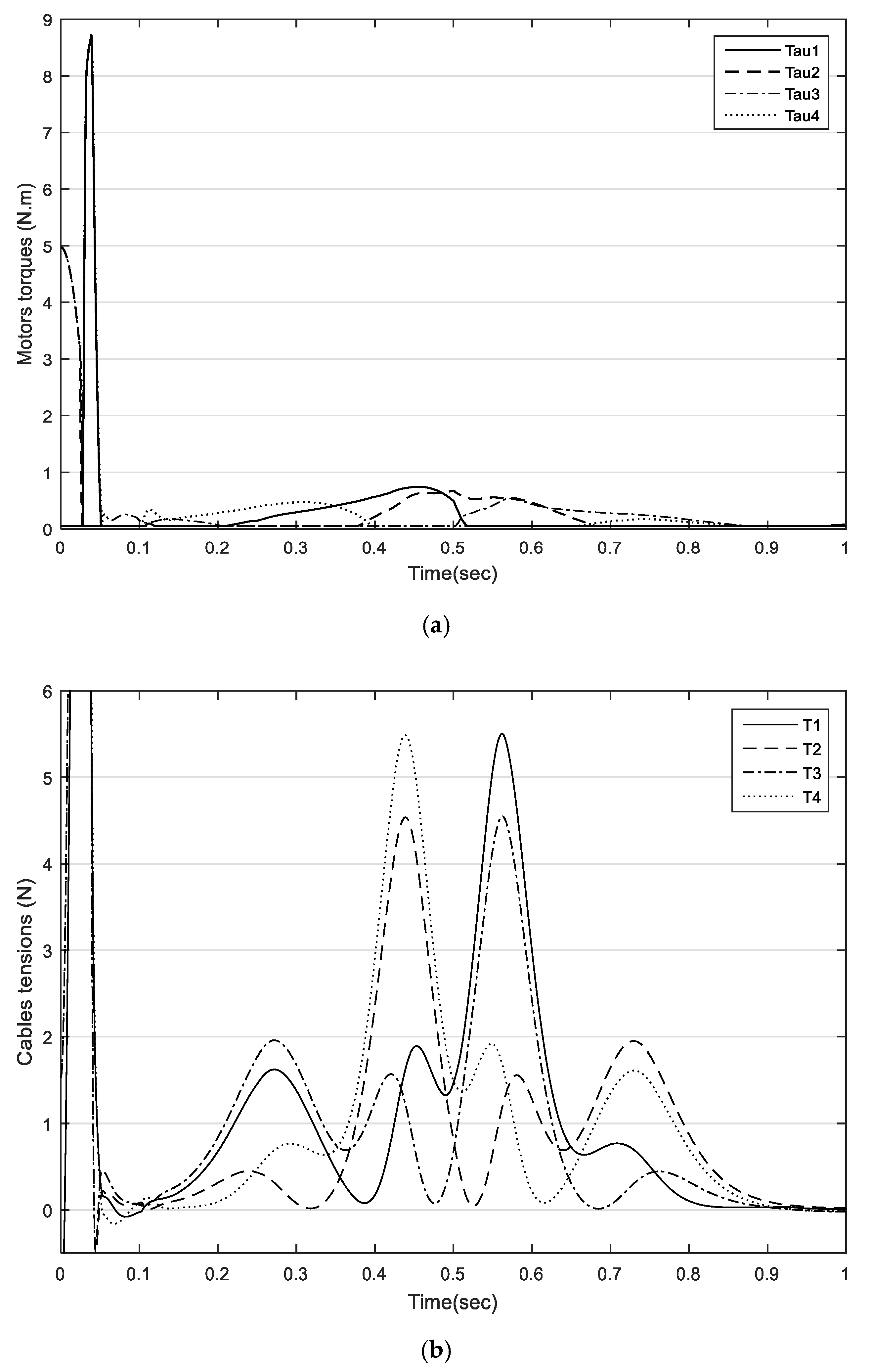
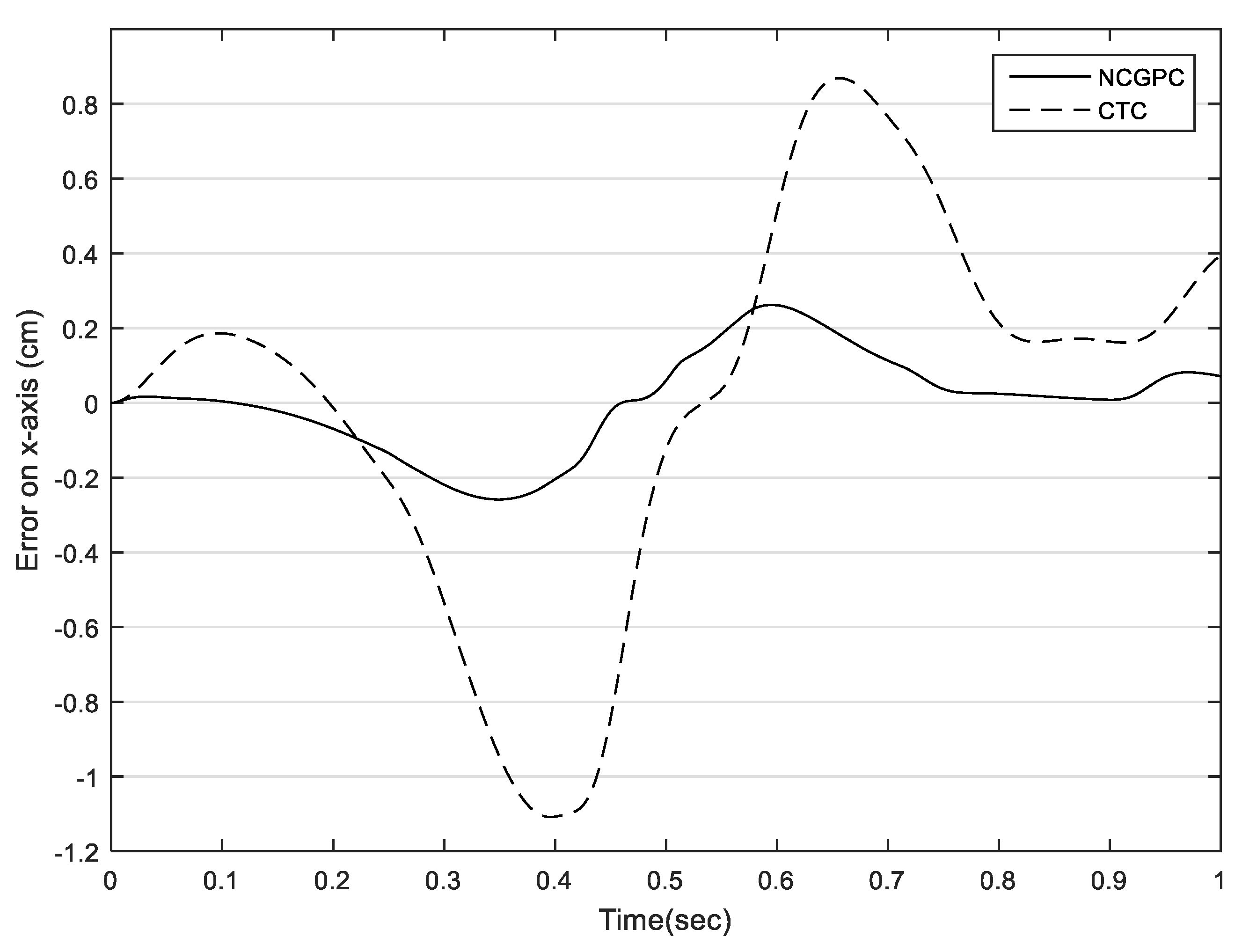
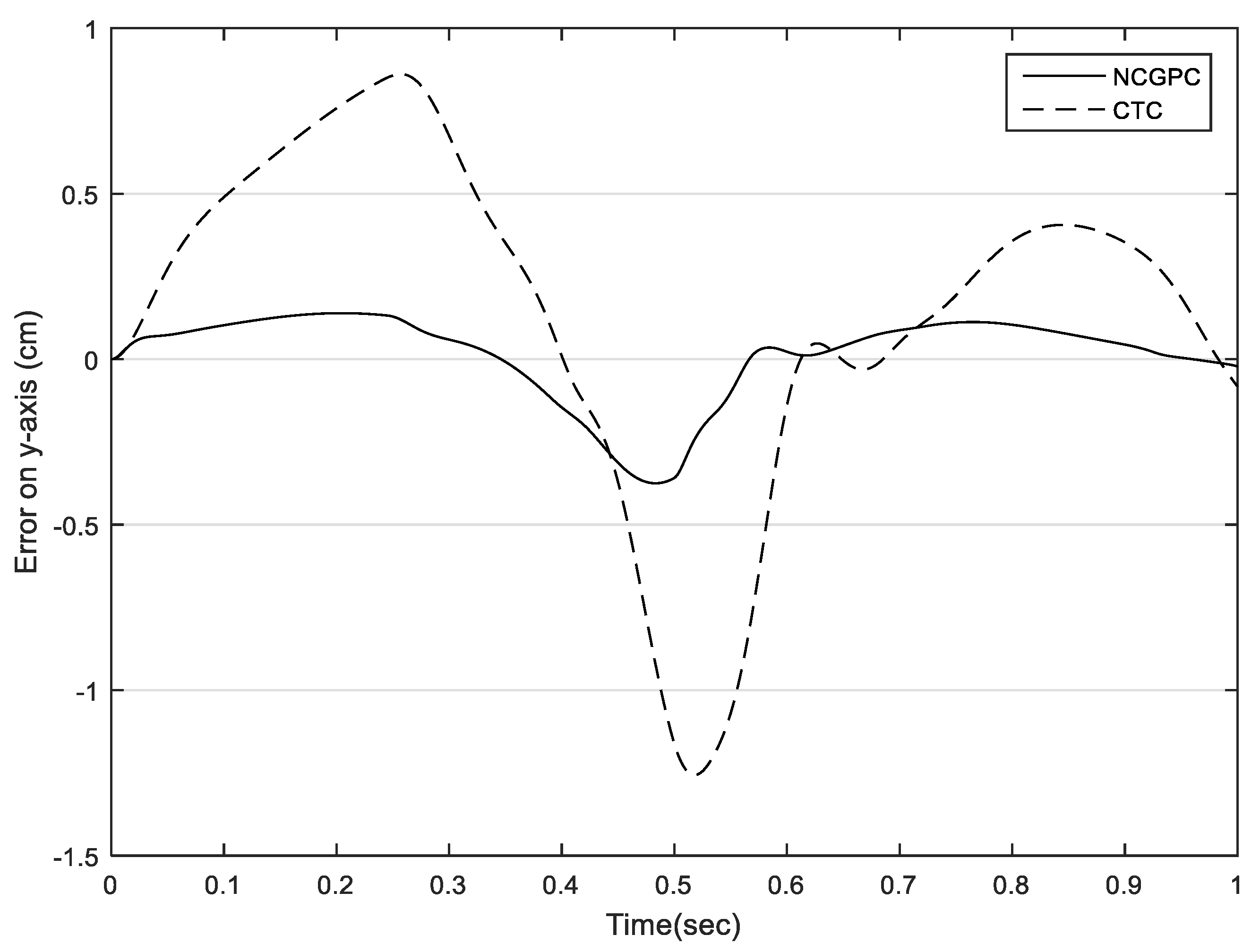
5.2. Comparison between NCGPC and CTC Based on Tracking Errors
5.3. Robustness Test of Payload and Parameter Uncertainties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Albus, J.; Bostelman, R.; Dagalakis, N. The NIST RoBoCrane. J. Res. Natl. Inst. Stand. Technol. 1992, 94, 373–384. [Google Scholar] [CrossRef] [PubMed]
- Tang, X. An Overview of the Development for Cable-Driven Parallel Manipulator. Adv. Mech. Eng. 2014, 6, 823028. [Google Scholar]
- Pinto, A.M.; Moreira, E.; Lima, J.; Sousa, J.P.; Costa, P. A cable-driven robot for architectural constructions: A visual-guided approach for motion control and path-planning. Auton. Robots 2017, 41, 1487–1499. [Google Scholar] [CrossRef]
- Morizono, T.; Kurahashi, K.; Kawamura, S. Realization of a Virtual Sports Training System with Parallel Wire Mechanism. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 21–27 April 1997; Volume 4, pp. 3025–3030. [Google Scholar]
- Reddy, M.V.; Praneet, N.C.; Ananthasuresh, G.K. Planar Cable-Driven Robots with Enhanced Orientability. In Cable-Driven Parallel Robots Mechanisms and Machine Science 74; Springer Nature: Cham, Switzerland, 2019; pp. 3–12. [Google Scholar]
- Korayem, M.; Yousefzadeh, M.; Tourajizadeh, H. Optimal Control of a Wheeled Mobile Cable-Driven Parallel Robot ICaSbot with Viscoelastic Cables. Robotica 2020, 38, 1513–1537. [Google Scholar] [CrossRef]
- Wei, H.; Qiu, Y.; Sheng, Y. On the Cable Pseudo-Drag Problem of Cable-Driven Parallel Camera Robots at High Speeds. Robotica 2019, 37, 1695–1709. [Google Scholar]
- Hwang, S.; Bak, J.; Yoon, J.; Park, J. Oscillation Reduction and Frequency Analysis of Under-Constrained Cable-Driven Parallel Robot with Three Cables. Robotica 2020, 38, 375–395. [Google Scholar] [CrossRef]
- Laroche, E.; Chellal, R.; Cuvillon, L.; Gangloff, J. A preliminary study for H∞ control of parallel cable-driven manipulators. Cable Driven Parallel Robot. Mech. Mach. Sci. 2013, 12, 353–369. [Google Scholar]
- Khosravi, M.A.; Taghirad, H.D. Dynamic analysis and control of cable driven robots with elastic cables. Trans. Can. Soc. Mech. Eng. 2011, 35, 543–558. [Google Scholar] [CrossRef] [Green Version]
- Korayem, M.H.; Tourajizadeh, H.; Taherifar, M.; Korayem, A.H. Optimal feedback linearization control of a flexible cable robot. Lat. Am. Appl. Res. 2014, 44, 259–265. [Google Scholar]
- Li, B.; Yan, L.; Gerada, C. The Novel Singular-Perturbation-Based Adaptive Control with σ-Modification for Cable Driven System. Actuators 2021, 10, 45. [Google Scholar] [CrossRef]
- Fernández, J.D.; Yu, B.; Bargsten, V.; Zipper, M.; Sprengel, H. Design, Modelling and Control of Novel Series-Elastic Actuators for Industrial Robots. Actuators 2020, 9, 6. [Google Scholar]
- Deng, E.; Tadesse, Y. A Soft 3D-Printed Robotic Hand Actuated by Coiled SMA. Actuators 2021, 10, 6. [Google Scholar] [CrossRef]
- Laribi, A.; Carbone, G.; Zeghloul, S. On the Optimal Design of Cable Driven Parallel Robot with a Prescribed Workspace for Upper Limb Rehabilitation Tasks. J. Bionic Eng. 2019, 16, 503–513. [Google Scholar] [CrossRef]
- Inel, F.; Menssouri, Z.; Carbone, G.; Ceccarelli, M. Dynamic Modeling and Simulation of Sliding Mode Control for a Cable Driven Parallel Robot. In New Advances in Mechanism and Machine Science; Springer: Cham, Switzerland, 2018; Volume 57, pp. 413–426. [Google Scholar]
- Carbone, G.; Gherman, B.; Ulinici, I.; Vaida, C.; Pisla, D. Design issues for an inherently safe robotic rehabilitation device. In New Advances in Mechanism and Machine Science; Springer: Cham, Switzerland, 2018; Volume 49, pp. 1025–1032. [Google Scholar]
- Tang, X.Q.; Shao, Z.F. Trajectory generation and tracking control of a multi-level hybrid support manipulator in FAST. Mechatronics 2013, 23, 1113–1122. [Google Scholar] [CrossRef]
- Li, M.; Wu, H.; Wang, Y.; Handroos, H.; Carbone, G. Modified Levenberg-Marquardt algorithm for backpropagation neural network training in dynamic model identification of mechanical systems. J. Dyn. Syst. Meas. Control Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Poignet, P.; Gautier, M. Nonlinear model predictive control of a robot manipulator. In Proceedings of the 6th International Workshop on Advanced Motion Control. Proceedings (Cat. No.00TH8494), Nagoya, Japan, 30 March–1 April 2000; pp. 401–406. [Google Scholar] [CrossRef]
- Chen, W.H. Predictive Control of General Non-linear Systems Using Approximation. IEEE Proc. Control Theory Appl. 2004, 151, 137–144. [Google Scholar] [CrossRef] [Green Version]
- Hedjar, R.; Toumi, R.; Boucher, P.; Dumur, D. Finite Horizon Non-linear Predictive Control by the Taylor Approximation Application to Robot Tracking Trajectory. Int. J. Appl. Math. Comput. Sci. 2005, 15, 527–540. [Google Scholar]
- Zhao, L.; Li, Q.; Liu, B.; Cheng, H. Trajectory tracking control of a one degree of freedom manipulator based on a switched sliding mode controller with a novel extended state observer framework. IEEE Trans. Syst. Man Cybernet. Syst. 2019, 49, 1110–1118. [Google Scholar] [CrossRef]
- Dabo, M.; Chafouk, H.; Langlois, N. Unconstrained NCGPC with a Guaranteed Closed-Loop Stability: Case of Non-linear SISO Systems with the Relative Degree Greater than Four. In Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 15–18 December 2009; pp. 1980–1985. [Google Scholar]
- Siller-Alcalá, I.I.; Liceaga-Castro, J.U. Continuous Time Generalized Predictive Control from a Classical Control Perspective. WSEAS Trans. Syst. Control 2018, 13, 447–452. [Google Scholar]
- Carbone, G.; Aróstegui Cavero, C.; Ceccarelli, M.; Altuzarra, O. A study of feasibility for a limb exercising device. In New Advances in Mechanism and Machine Science; Springer: Cham, Switzerland, 2018; Volume 47, pp. 11–21. [Google Scholar]
- Errouissi, R.; Ouhrouche, M.; Chen, W.-H. Robust Non-linear Generalized Predictive Control of a Permanent Magnet Synchronous Motor with an Anti-Windup Compensator. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Bari, Italy, 4–7 July 2010; pp. 3184–3189. [Google Scholar]
- Krid, M.; Benamar, F.; Lenain, R. A New Explicit Dynamic Path Tracking Controller Using Generalized Predictive Control. Int. J. Control Automat. Syst. 2017, 15, 303–314. [Google Scholar]
- Siller-Alcalá, I.I.; Liceaga-Castro, J.U.; Alcántara-Ramírez, R.; Jaimes-Ponce, J. Non-linear Control of a Single-Link Flexible Joint Manipulator via Predictive Control. WSEAS Trans. Syst. Control 2016, 11, 371–375. [Google Scholar]
- Wang, H.; Li, S.; Lan, Q.; Zhao, Z.; Zhou, X. Continuous terminal sliding mode control with extended state observer for PMSM speed regulation system. Trans. Inst. Meas. Control 2017, 39, 1195–1204. [Google Scholar] [CrossRef]
- Piao, J.; Kim, E.; Choi, H.; Moon, C.; Choi, E.; Park, J.; Kim, C.-S. Indirect Force Control of a Cable-Driven Parallel Robot Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements. Sensors 2019, 19, 2520. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Jung, J.; Ko, S.Y.; Choi, E.; Park, J.-O.; Kim, C.-S. Geometric Parameter Calibration for a Cable-Driven Parallel Robot Based on a Single One-Dimensional Laser Distance Sensor Measurement and Experimental Modeling. Sensors 2018, 18, 2392. [Google Scholar]
- Piao, J.; Jin, X.; Jung, J.; Choi, E.; Park, J.-O.; Kim, C.-S. Open-loop position control of a polymer cable–driven parallel robot via a viscoelastic cable model for high payload workspaces. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Cafolla, D.; Russo, M.; Carbone, G. CUBE, a Cable-driven Device for Limb Rehabilitation. J. Bionic Eng. 2019, 16, 493–494. [Google Scholar] [CrossRef]
- Kumar, R.; Mukherjee, S. Enhanced Dynamic Capability of Cable-Driven Parallel Manipulators by Reconfiguration. Robotica 2021, 1–9. [Google Scholar] [CrossRef]
- Mu, Z.; Liu, T.; Xu, W.; Lou, Y.; Liang, B. Dynamic feedforward control of spatial cable-driven hyper-redundant manipulators for on-orbit servicing. Robotica 2019, 37, 18–38. [Google Scholar] [CrossRef]
- Yao, S.; Ceccarelli, M.; Carbone, G.; Dong, Z. Grasp configuration planning for a low-cost and easy-operation under actuated three-fingered robot hand. Mech. Mach. Theory 2018, 129, 51–69. [Google Scholar] [CrossRef]
- Gherman, B.; Birlescu, I.; Plitea, N.; Carbone, G.; Tarnita, D.; Pisla, D. On the singularity-free workspace of a parallel robot for lower-limb rehabilitation. Proc. Roman. Acad. Series A Math. Phys. Techn. Sci. Inform. Sci. 2019, 20, 383–391. [Google Scholar]
- Boschetti, G.; Carbone, G.; Passarini, C. Cable failure operation strategy for a rehabilitation cable-driven robot. Robotics 2019, 8, 17. [Google Scholar] [CrossRef] [Green Version]
- Hernández-Martínez, E.E.; Ceccarelli, M.; Carbone, G.; López-Cajún, C.S.; Jáuregui-Correa, J.C. Characterization of a cable-based parallel mechanism for measurement purposes. Mech. Based Design Struct. Mach. 2010, 38, 25–49. [Google Scholar] [CrossRef]
- Tucan, P.; Vaida, C.; Ulinici, I.; Banica, A.; Burz, A.; Pop, N.; Birlescu, I.; Gherman, B.; Plitea, N.; Antal, T.; et al. Optimization of the ASPIRE Spherical Parallel Rehabilitation Robot Based on Its Clinical Evaluation. Int. J. Environ. Res. Public Health 2021, 18, 3281. [Google Scholar] [CrossRef]
- Vaida, C.; Birlescu, I.; Pisla, A.; Ulinici, I.; Tarnita, D.; Carbone, G.; Pisla, D. Systematic design of a parallel robotic system for lower limb rehabilitation. IEEE Access 2020, 8, 34522–34537. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Carbone, G.; Ottaviano, E. Multi criteria optimum design of manipulators. Bull. Polish Acad. Sci. Techn. Sci. 2019, 53, 9–18. [Google Scholar]
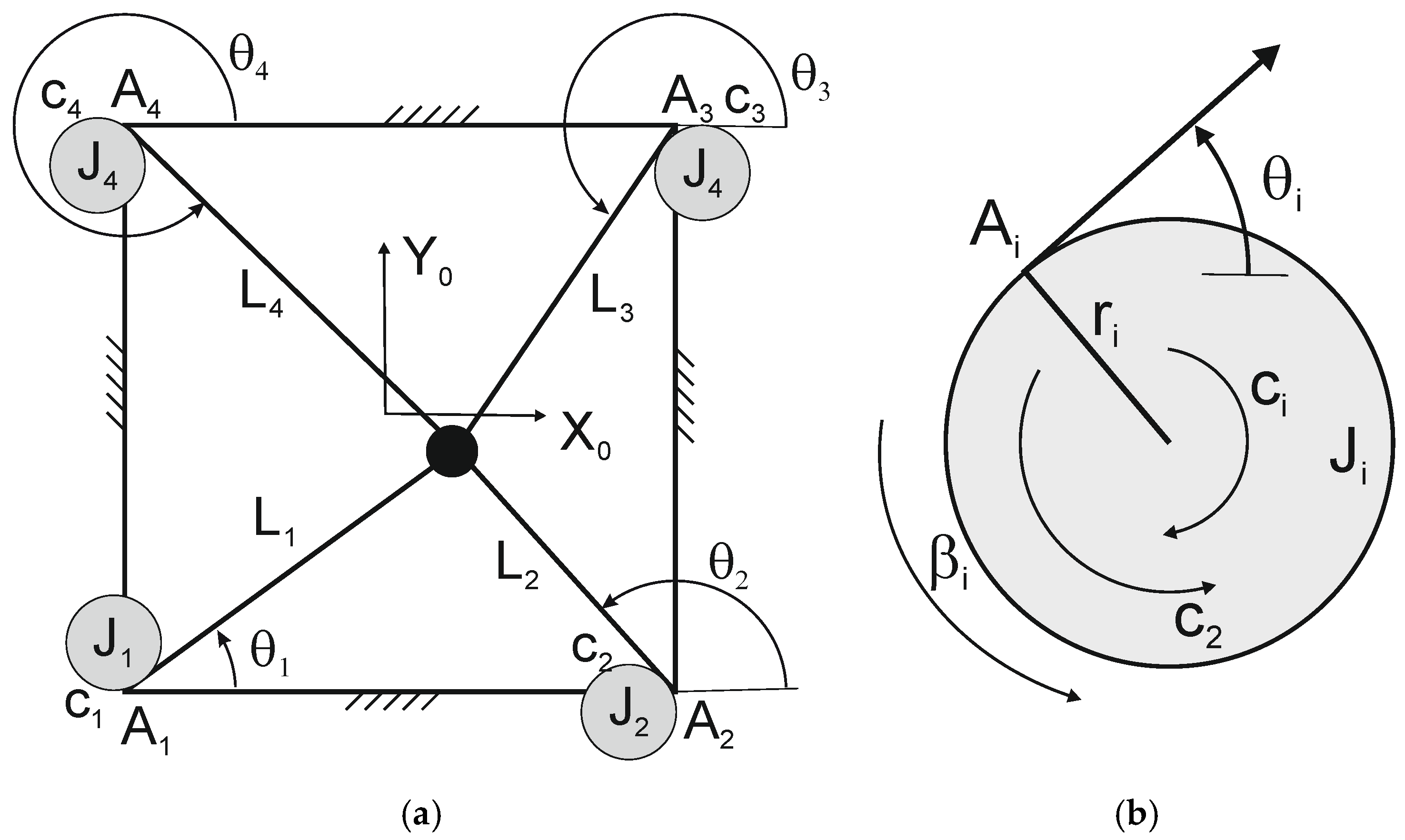



| Parameters | Nomenclature |
|---|---|
| Attachment points of the driving cables to the motorized pulleys. | |
| Cables angles with respect to the x-axis. | |
| The lengths of the workspace side. | |
| End-effector’s x-coordinate. | |
| End-effector’s y-coordinate. | |
| End-effector’s mass. | |
| Motors torques. | |
| Rotational inertia of shaft-pulley system. | |
| Motors shafts viscous damping coefficients. | |
| Pulleys’ rotation angles. | |
| Pulleys radius. |
| Parameters | Nomenclature |
|---|---|
| x | the states vector |
| U | control vector |
| y | output vector |
| F(x) and h(x) | smooth vector fields |
| y (t + T) | future reference |
| e (t + T) | future tracking error vector |
| yr (t + T) | quadratic performance |
| the last row of the matrix | |
| is the last element of | |
| is the gain vector | |
| ρi | relative degree |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| (−32.5;0) cm | 65 cm | ||
| (32.5;0) cm | 0.01 kg | ||
| (32.5;32.5) cm | 0.0008 kg m2 | ||
| (−32.5;32.5) cm | 0.01 Nms |
| Parameters | Uncertainties |
|---|---|
| +5% | |
| 5% | |
| +10% | |
| Payload: | +20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inel, F.; Medjbouri, A.; Carbone, G. A Non-Linear Continuous-Time Generalized Predictive Control for a Planar Cable-Driven Parallel Robot. Actuators 2021, 10, 97. https://doi.org/10.3390/act10050097
Inel F, Medjbouri A, Carbone G. A Non-Linear Continuous-Time Generalized Predictive Control for a Planar Cable-Driven Parallel Robot. Actuators. 2021; 10(5):97. https://doi.org/10.3390/act10050097
Chicago/Turabian StyleInel, Fouad, Ali Medjbouri, and Giuseppe Carbone. 2021. "A Non-Linear Continuous-Time Generalized Predictive Control for a Planar Cable-Driven Parallel Robot" Actuators 10, no. 5: 97. https://doi.org/10.3390/act10050097
APA StyleInel, F., Medjbouri, A., & Carbone, G. (2021). A Non-Linear Continuous-Time Generalized Predictive Control for a Planar Cable-Driven Parallel Robot. Actuators, 10(5), 97. https://doi.org/10.3390/act10050097







