Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams
Abstract
1. Introduction
2. Design and Analysis of the Compliant End-Effector
2.1. Mechanical Design of the Compliant End-Effector
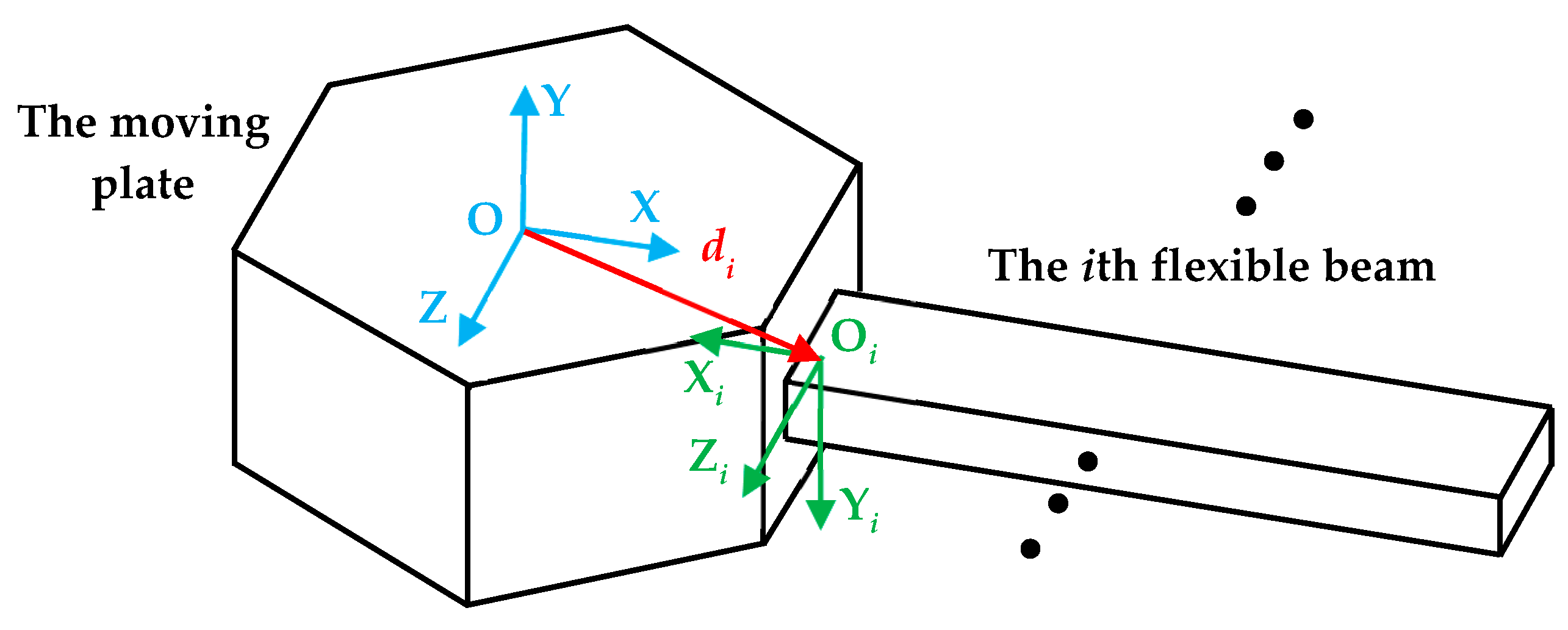
2.2. Analytical Modeling of the Compliant End-Effector
3. Finite Element Analysis and Verification
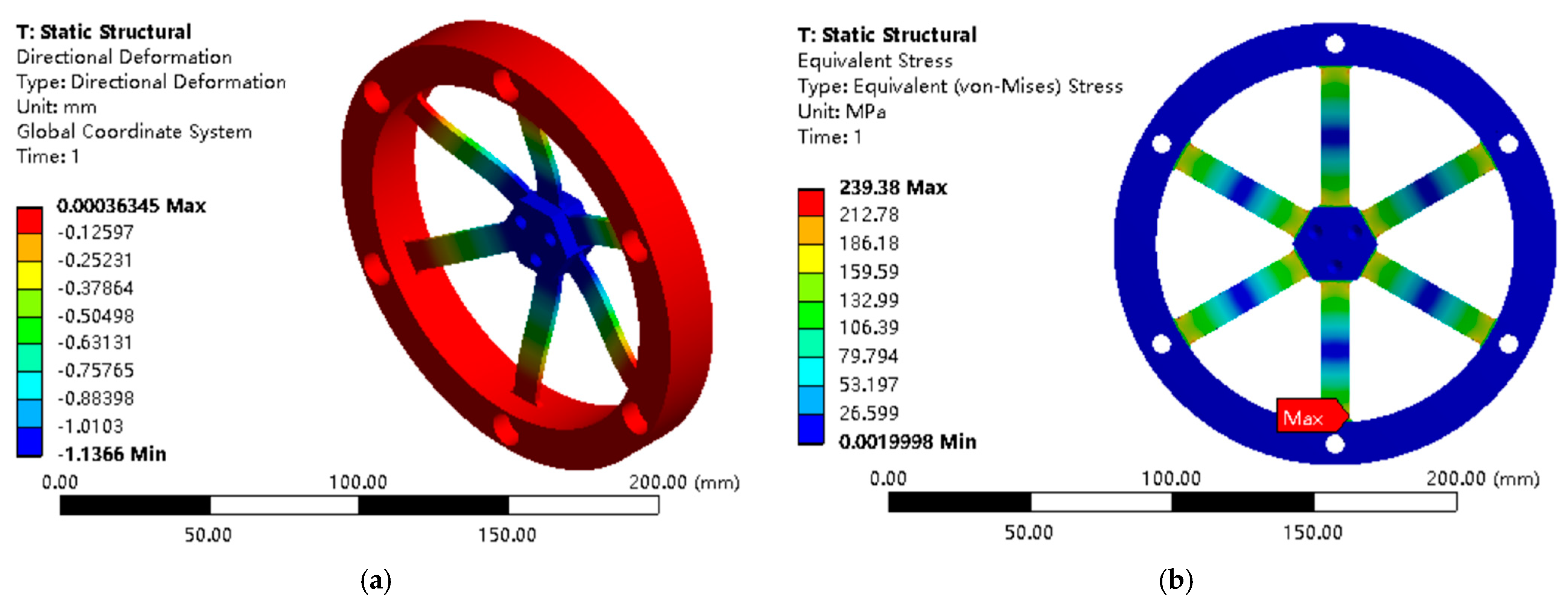
3.1. Static Analysis Validation
3.2. Dynamic Analysis Validation
4. Prototype Fabrication and Experimental Test
4.1. Experimental Setup
4.2. Test of Equivalent Stiffness
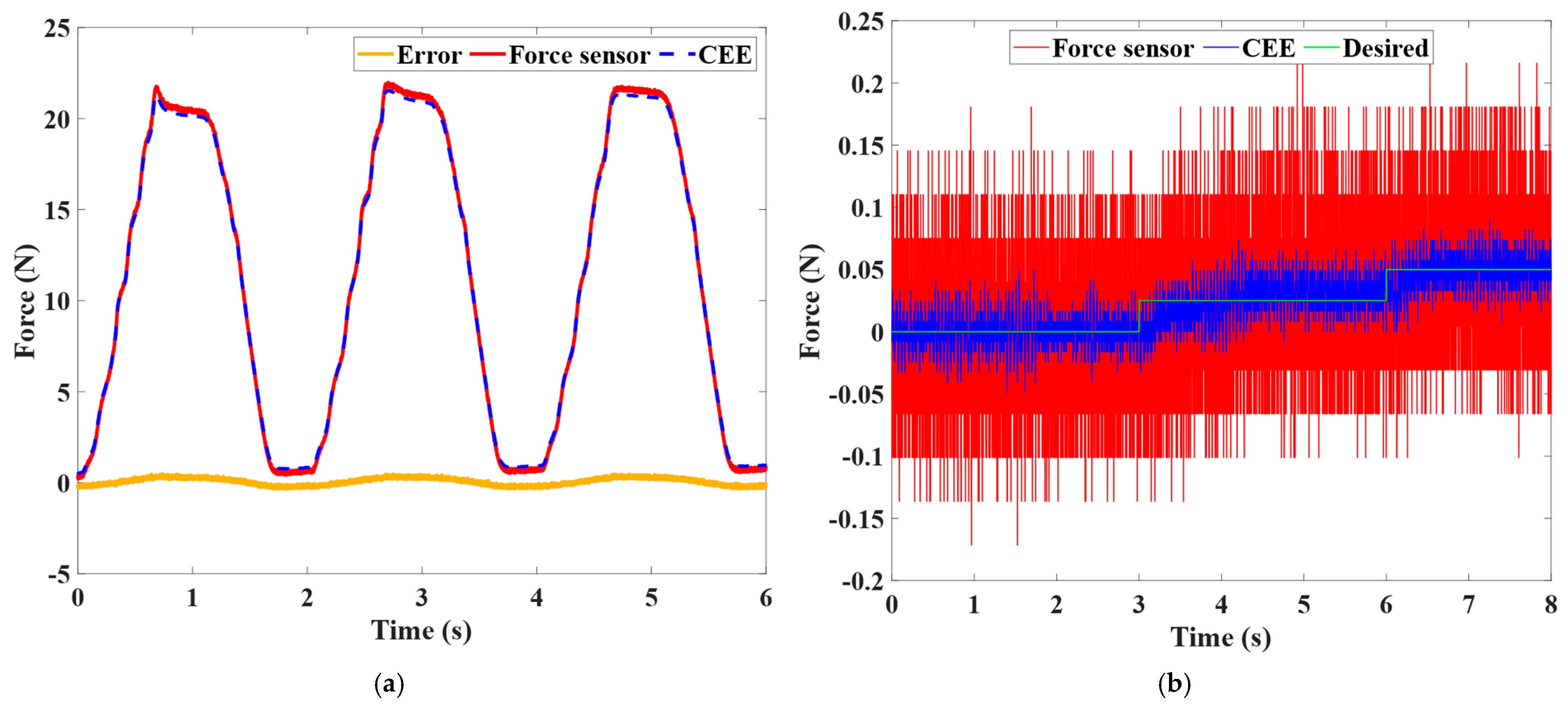
4.3. Test of Contact Force Sensing
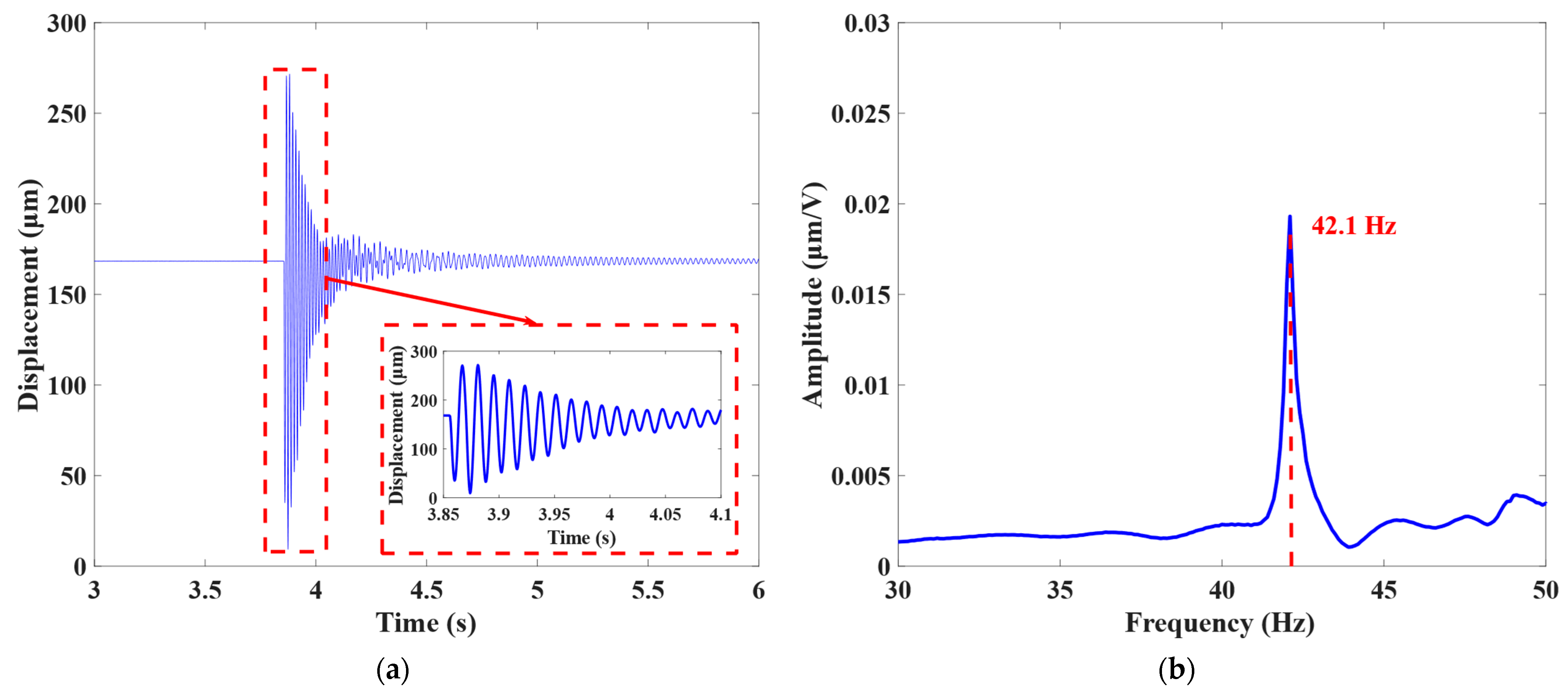
4.4. Test of Natural Frequency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammad, A.E.K.; Hong, J.; Wang, D. Design of a force-controlled end-effector with low-inertia effect for robotic polishing using macro-mini robot approach. Robot. Comput.-Integr. Manuf. 2018, 49, 54–65. [Google Scholar] [CrossRef]
- Mohammad, A.E.K.; Wang, D. Electrochemical mechanical polishing technology: Recent developments and future research and industrial needs. Int. J. Adv. Manuf. Technol. 2016, 86, 1909–1924. [Google Scholar] [CrossRef]
- Tao, B.; Zhao, X.; Ding, H. Mobile-robotic machining for large complex components: A review study. Sci. China Technol. Sci. 2019, 62, 1388–1400. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Wang, W.; Xu, M. Effect of pad wear on tool influence function in robotic polishing of large optics. Int. J. Adv. Manuf. Technol. 2019, 102, 2521–2530. [Google Scholar] [CrossRef]
- Tsai, M.J.; Huang, J.F.; Kao, W.L. Robotic polishing of precision molds with uniform material removal control. Int. J. Mach. Tools Manuf. 2009, 49, 885–895. [Google Scholar] [CrossRef]
- Liao, L.; Xi, F.; Liu, K. Modeling and control of automated polishing/deburring process using a dual-purpose compliant toolhead. Int. J. Mach. Tools Manuf. 2008, 48, 1454–1463. [Google Scholar] [CrossRef]
- Liu, C.; Chen, C.C.A.; Huang, J. The polishing of molds and dies using a compliance tool holder mechanism. J. Mater. Process. Technol. 2005, 166, 230–236. [Google Scholar] [CrossRef]
- Cheng, F.; Qi, Z.; Lei, Z.; Hong, Z. Development of the Polishing Tool System Based on the Pneumatic Force Servo. In Proceedings of the 2017 2nd International Conference on Advanced Robotics and Mechatronics (ICARM), Hefei and Tai’an, China, 27–31 August 2017; pp. 126–131. [Google Scholar]
- Li, J.; Guan, Y.; Chen, H.; Wang, B.; Zhang, T.; Liu, X.; Hong, J.; Wang, D.; Zhang, H. A High-Bandwidth End-Effector With Active Force Control for Robotic Polishing. IEEE Access 2020, 8, 169122–169135. [Google Scholar] [CrossRef]
- Tang, J.; Wang, T.; Yan, Z.Q.; Wang, L.W. Design and Analysis of the End-Effector of the Flexible Polishing Robot. Key Eng. Mater. 2016, 693, 58–63. [Google Scholar] [CrossRef]
- Tian-Soon, S.; Ang, M.H., Jr.; Kah-Bin, L. A compliant end-effector coupling for vertical assembly: Design and evaluation. Robot. Comput.-Integr. Manuf. 1997, 13, 21–27, 29–30. [Google Scholar] [CrossRef]
- Lopes, A.; Almeida, F. A force–impedance controlled industrial robot using an active robotic auxiliary device. Robot. Comput.-Integr. Manuf. 2008, 24, 299–309. [Google Scholar] [CrossRef]
- Kim, J.-D.; Noh, I.-H. Magnetic polishing of three dimensional die and mold surfaces. Int. J. Adv. Manuf. Technol. 2007, 33, 18–23. [Google Scholar] [CrossRef]
- Wahrburg, A.; Bos, J.; Listmann, K.D.; Dai, F.; Matthias, B.; Ding, H. Motor-Current-Based Estimation of Cartesian Contact Forces and Torques for Robotic Manipulators and Its Application to Force Control. IEEE Trans. Autom. Sci. Eng. 2018, 15, 879–886. [Google Scholar] [CrossRef]
- Ott, C.; Albu-Schaffer, A.; Kugi, A.; Hirzinger, G. On the Passivity-Based Impedance Control of Flexible Joint Robots. IEEE Trans. Robot. 2008, 24, 416–429. [Google Scholar] [CrossRef]
- Tian, F.; Lv, C.; Li, Z.; Liu, G. Modeling and control of robotic automatic polishing for curved surfaces. CIRP J. Manuf. Sci. Technol. 2016, 14, 55–64. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, H.; Li, D.; Chen, L.; Tan, C.; Ding, H. Contact force control and vibration suppression in robotic polishing with a smart end effector. Robot. Comput.-Integr. Manuf. 2019, 57, 391–403. [Google Scholar] [CrossRef]
- Du, H.; Sun, Y.; Feng, D.; Xu, J. Automatic robotic polishing on titanium alloy parts with compliant force/position control. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1180–1192. [Google Scholar] [CrossRef]
- Wu, X.; Huang, Z.; Wan, Y.; Liu, H.; Chen, X. A Novel Force-Controlled Spherical Polishing Tool Combined With Self-Rotation and Co-Rotation Motion. IEEE Access 2020, 8, 108191–108200. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, X.; Shirinzadeh, B.; Tian, Y.; Zhang, D. Closed-Form Modeling and Analysis of an XY Flexure-Based Nano-Manipulator. Chin. J. Mech. Eng. 2018, 31, 7. [Google Scholar] [CrossRef]
- He, S.; Tang, H.; Zhu, Z.; Zhang, P.; Xu, Y.; Chen, X. A Novel Flexure Piezomotor With Minimized Backward and Nonlinear Motion Effect. IEEE Trans. Ind. Electron. 2022, 69, 652–662. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Y.; Deng, J.; Gao, X.; Cheng, J. A compact inchworm piezoelectric actuator with high speed: Design, modeling, and experimental evaluation. Mech. Syst. Signal Process. 2023, 184, 109704. [Google Scholar] [CrossRef]
- Wang, F.; Huo, Z.; Liang, C.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. A Novel Actuator-Internal Micro/Nano Positioning Stage With an Arch-Shape Bridge-Type Amplifier. IEEE Trans. Ind. Electron. 2019, 66, 9161–9172. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, X.; Huang, W.-W.; Li, L.; Hu, C.; Zhang, X.; Zhu, L. Intelligent Tracking Error Prediction and Feedforward Compensation for Nanopositioning Stages with High-bandwidth Control. IEEE Trans. Ind. Inform. 2022, 1–10. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Li, Y. Configuration design and experimental verification of a variable constant-force compliant mechanism. Robotica 2022, 40, 3463–3475. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. Design of a new passive end-effector based on constant-force mechanism for robotic polishing. Robot. Comput. -Integr. Manuf. 2022, 74, 102278. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, J.; Li, Y. Design of a spatial constant-force end-effector for polishing/deburring operations. Int. J. Adv. Manuf. Technol. 2021, 116, 3507–3515. [Google Scholar] [CrossRef]
- Lai, L.; Zhu, Z. Design, modeling and testing of a novel flexure-based displacement amplification mechanism. Sens. Actuators A Phys. 2017, 266, 122–129. [Google Scholar] [CrossRef]





| Parameter | l (mm) | b (mm) | t (mm) | θ (rad) |
|---|---|---|---|---|
| Value | 50 | 10 | 2 | π/3 |
| i | dxi (mm) | dzi (mm) | θi (rad) |
|---|---|---|---|
| 1 | 12.99 | 0 | 0 |
| 2 | 6.50 | −11.25 | π/3 |
| 3 | −6.50 | −11.25 | 2π/3 |
| 4 | −12.99 | 0 | π |
| 5 | −6.50 | 11.25 | 4π/3 |
| 6 | 6.50 | 11.25 | 5π/3 |
| Load | No Load (0 N) | Flange Only (13.82 N) | Flange + Plastic Tool (20.68 N) | Flange + Aluminum Tool (22.83 N) |
|---|---|---|---|---|
| Anal. (Hz) | 498.84 | 77.32 | 58.48 | 55.65 |
| FEA (Hz) | 501.93 | 68.87 | 56.48 | 53.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Wu, H.; Li, Z.; Sun, N.; Sun, L. Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams. Actuators 2022, 11, 284. https://doi.org/10.3390/act11100284
Qin Y, Wu H, Li Z, Sun N, Sun L. Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams. Actuators. 2022; 11(10):284. https://doi.org/10.3390/act11100284
Chicago/Turabian StyleQin, Yanding, Haitao Wu, Zhiyuan Li, Ning Sun, and Lei Sun. 2022. "Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams" Actuators 11, no. 10: 284. https://doi.org/10.3390/act11100284
APA StyleQin, Y., Wu, H., Li, Z., Sun, N., & Sun, L. (2022). Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams. Actuators, 11(10), 284. https://doi.org/10.3390/act11100284










