A Soft Self-Stable Actuator and Its Energy-Efficient Grasping
Abstract
:1. Introduction
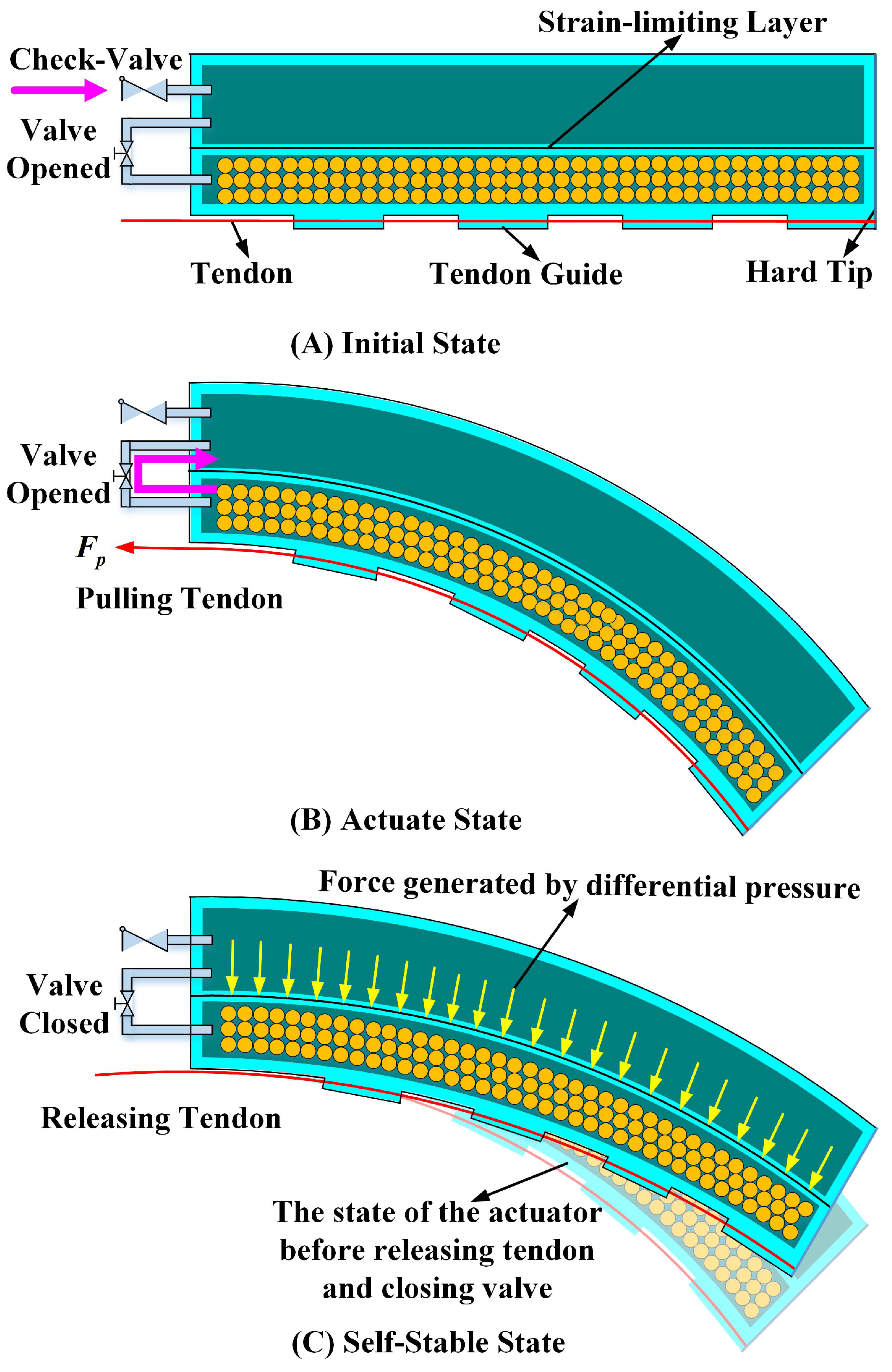
2. Actuator Structure
3. Modeling
- The radial expansion of the actuator is ignored contributing to the constrain fibers;
- The friction between the tendon and the actuator is ignored;
- The elongation of the tendon is ignored, and the tension force along the tendon direction is equal everywhere;
- The tendon is pulled with uniform velocity during the bending period.
3.1. Pressure Variation
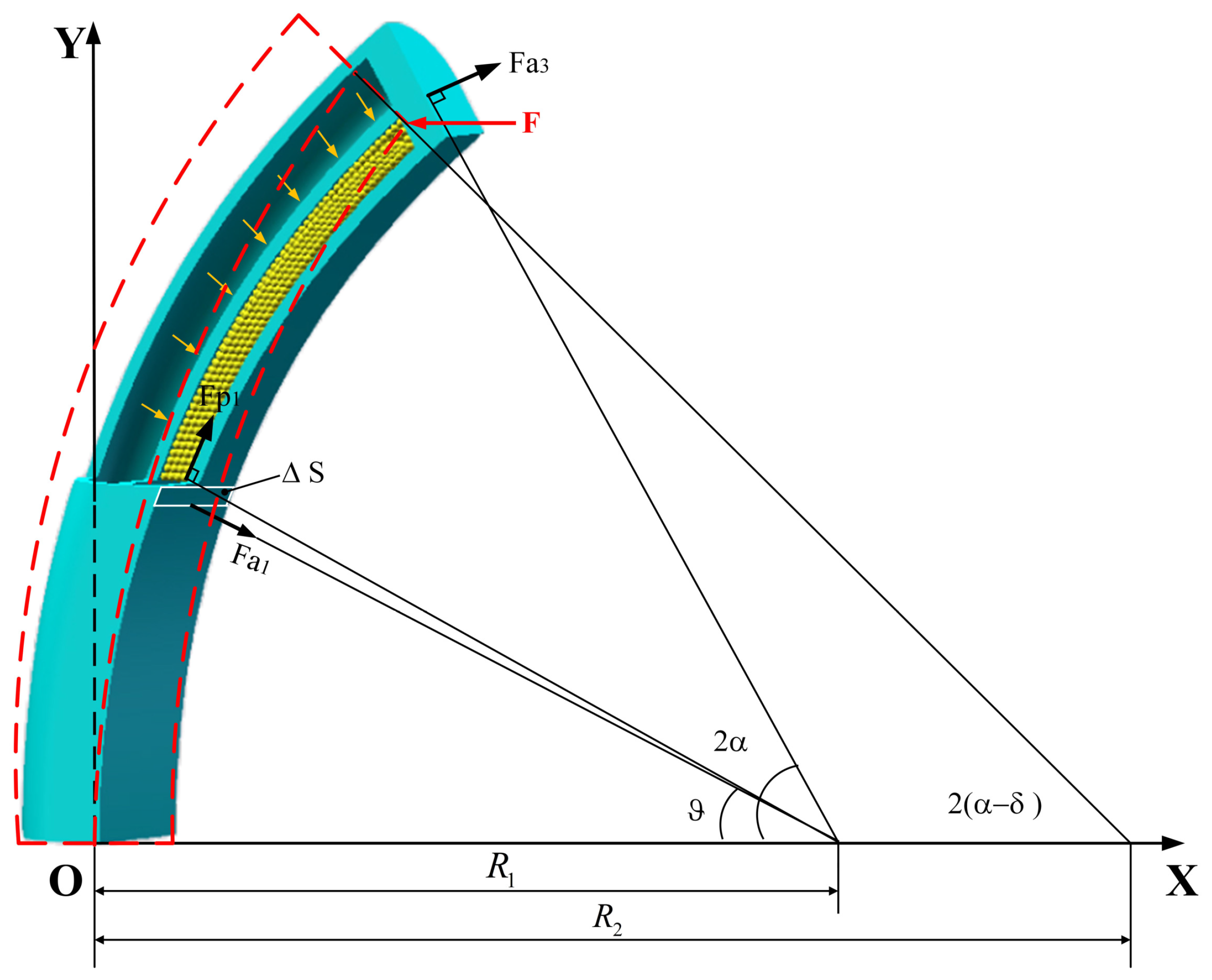
3.2. Torque Analysis
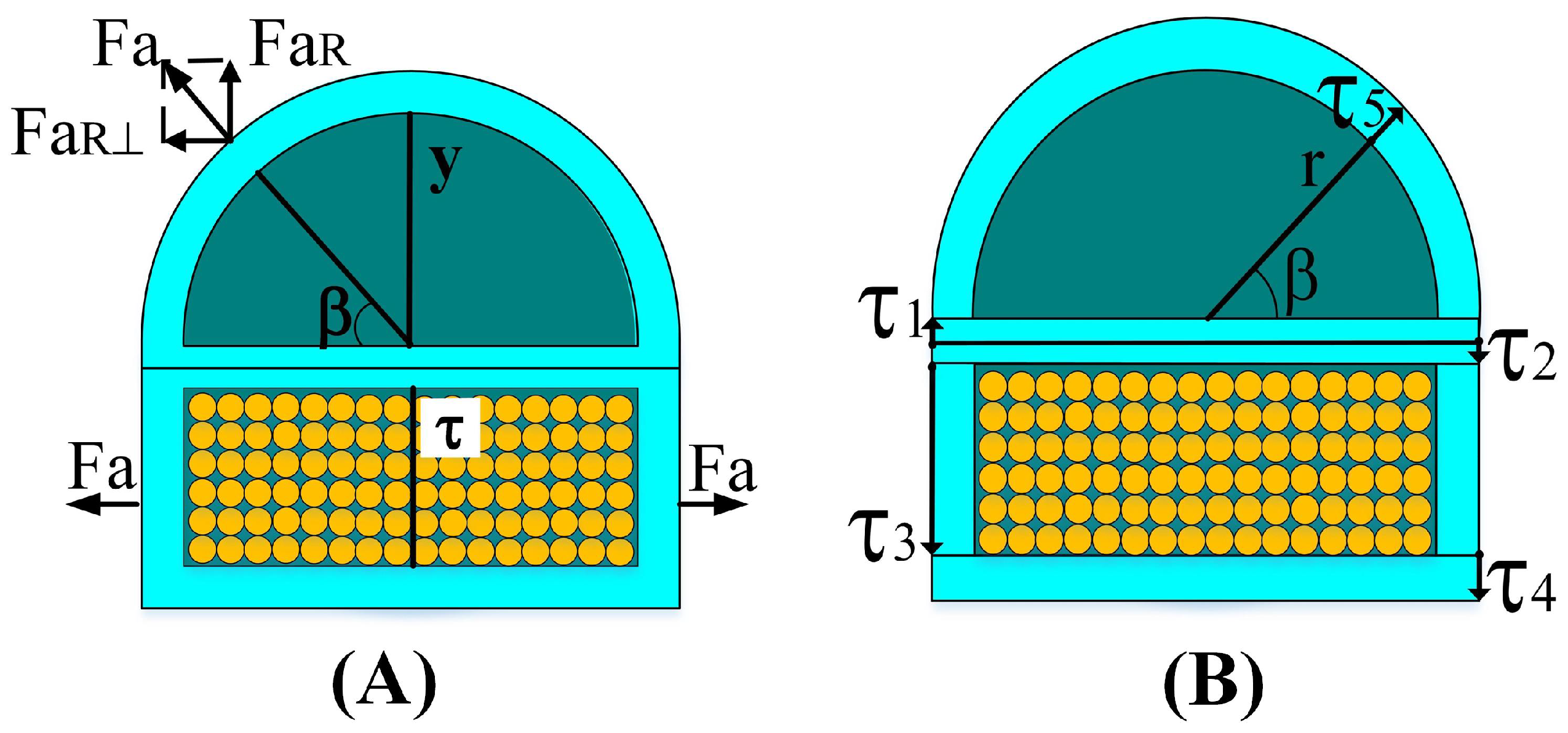
3.2.1. Torque of Particle Jamming
3.2.2. Torque of Air Pressure
3.2.3. Torque of Elastic Stress
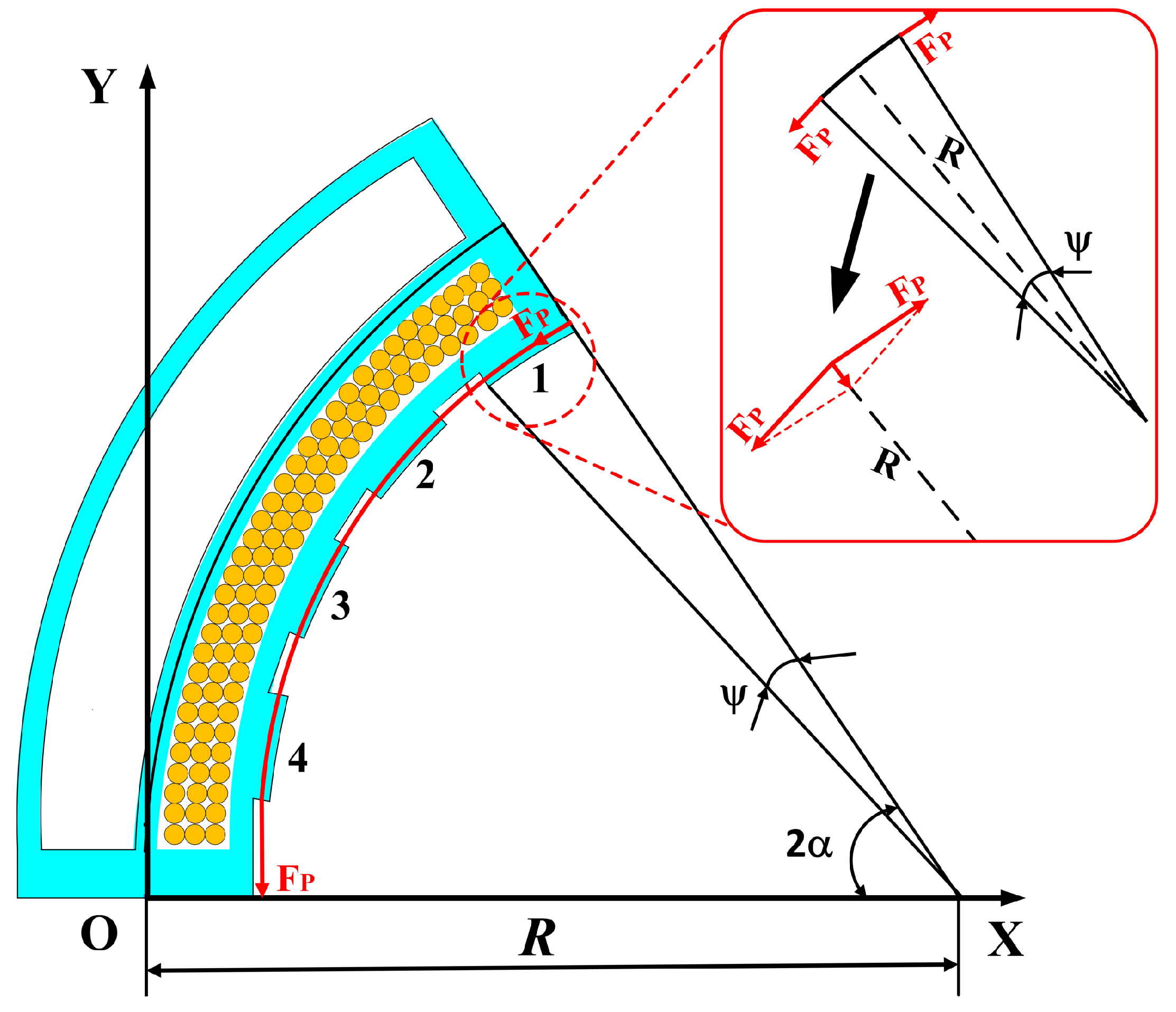
3.3. Torque Equilibrium of the Actuator
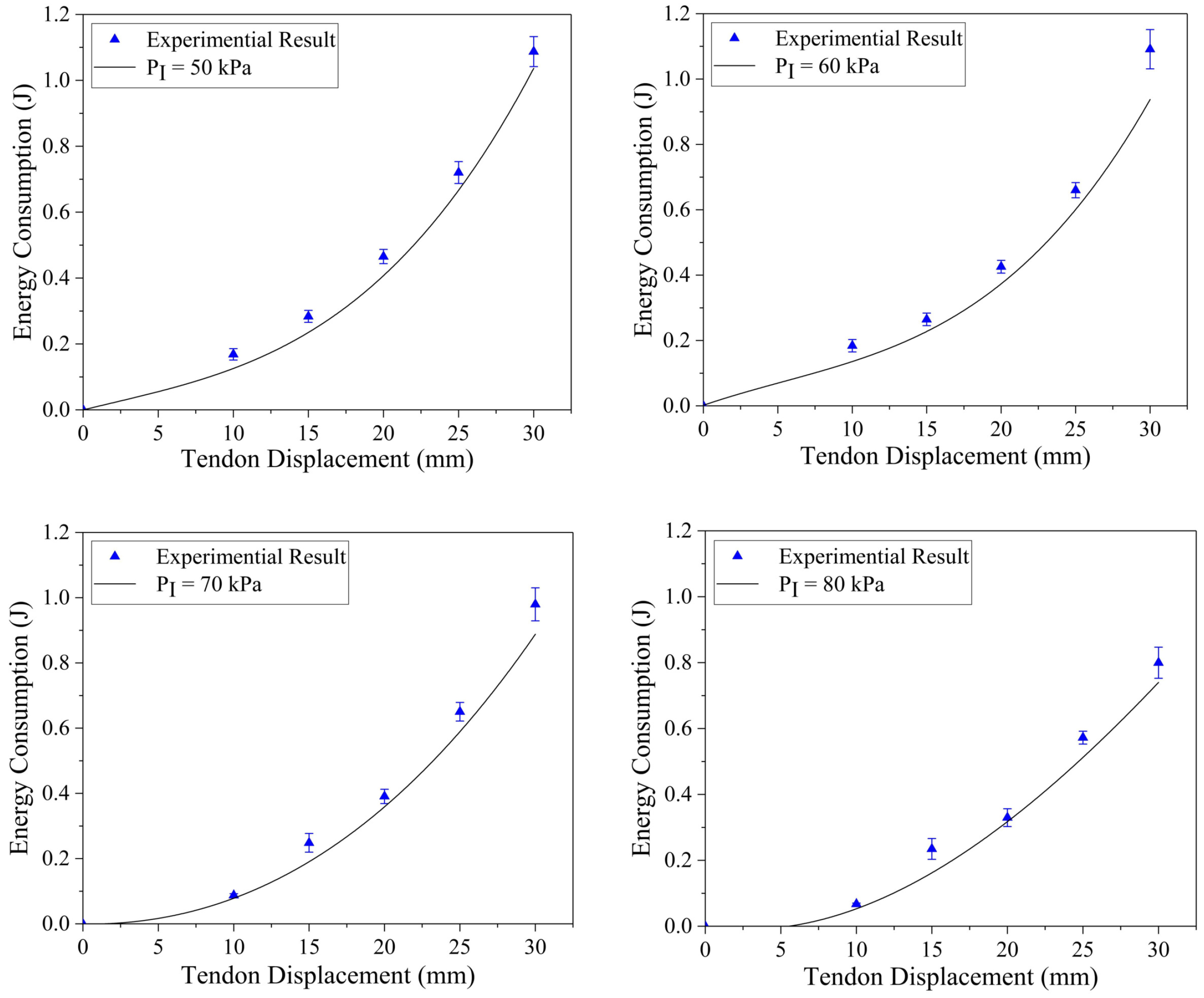
3.4. Analysis of Energy Consumption
4. Experiments
4.1. Experimental Environment
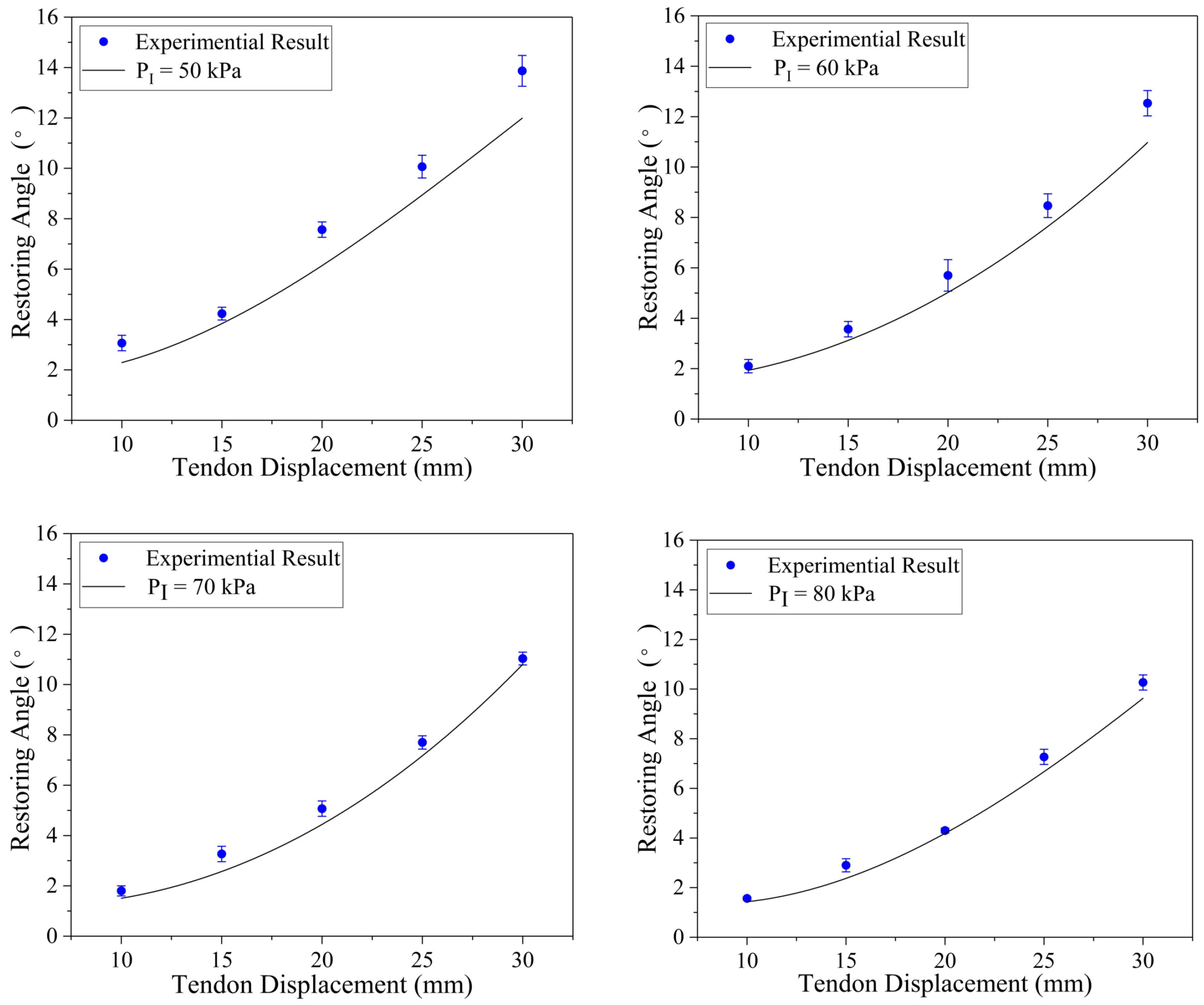
4.2. Model Verification
4.3. Influence Factors
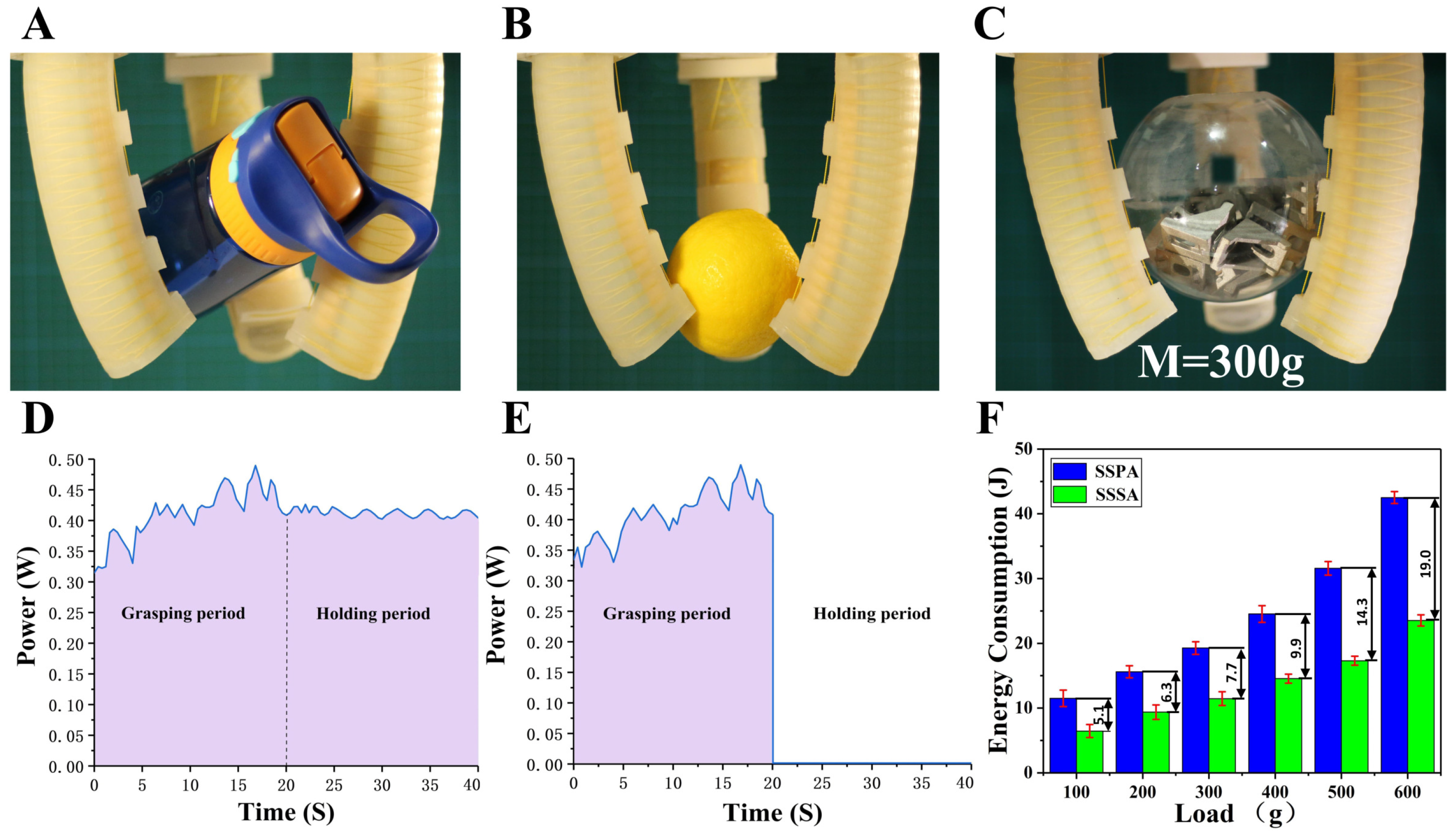
4.4. Grasping Demonstration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ni, X.; Liao, C.; Li, Y.; Zhang, Z.; Sun, M.; Chai, H.; Wu, H.; Jiang, S. Experimental study of multi-stable morphing structures actuated by pneumatic actuation. Int. J. Adv. Manuf. Technol. 2020, 108, 1203–1216. [Google Scholar] [CrossRef]
- Zhao, Y.; Shan, Y.; Zhang, J.; Guo, K.; Qi, L.; Han, L.; Yu, H. A soft continuum robot, with a large variable-stiffness range, based on jamming. Bioinspir. Biomim. 2019, 14, 066007. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, S.G.; Delaney, G.W.; Howard, D. A Review of Jamming Actuation in Soft Robotics. Actuators 2020, 9, 104. [Google Scholar] [CrossRef]
- Wang, X.; Khara, A.; Chen, C. A soft pneumatic bistable reinforced actuator bioinspired by Venus Flytrap with enhanced grasping capability. Bioinspir. Biomim. 2020, 15, 056017. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Hou, N.; Dinjens, P.J.D.; Wang, R.; Dong, C.; Xie, G. A Thermoplastic Elastomer Belt Based Robotic Gripper. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 9275–9280. [Google Scholar]
- Chen, Y.; Chung, H.; Chen, B. A lobster-inspired articulated shaft for minimally invasive surgery. Robot. Auton. Syst. 2020, 131, 103599. [Google Scholar] [CrossRef]
- Chen, R.; Yuan, Z.; Guo, J.; Bai, L.; Zhu, X.; Liu, F.; Pu, H.; Xin, L.; Peng, Y.; Luo, J. Legless soft robots capable of rapid, continuous, and steered jumping. Nat. Commun. 2021, 12, 7028. [Google Scholar] [CrossRef]
- Li, H.; Yao, J.; Zhou, P.; Zhao, W.; Xu, Y.; Zhao, Y. Design and modeling of a high-load soft robotic gripper inspired by biological winding. Bioinspir. Biomim. 2020, 15, 026006. [Google Scholar] [CrossRef]
- Bilancia, P.; Berselli, G. Design and testing of a monolithic compliant constant force mechanism. Smart Mater. Struct. 2020, 29, 044001. [Google Scholar] [CrossRef]
- Chen, R.; Wu, L.; Sun, Y.; Chen, J.Q.; Guo, J.L. Variable stiffness soft pneumatic grippers augmented with active vacuum adhesion. Smart Mater. Struct. 2020, 29, 105028. [Google Scholar] [CrossRef]
- Bishop-Moser, J.; Krishnan, G.; Kim, C. Design of soft robotic actuators using fluid-filled fiber-reinforced elastomeric enclosures in parallel combinations. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 4264–4269. [Google Scholar]
- Yi, J.; Chen, X.; Song, C. Customizable three-dimensional-printed origami soft robotic joint with effective behavior shaping for safe interactions. IEEE Trans. Robot. 2018, 35, 114–123. [Google Scholar] [CrossRef]
- Obiajulu, S.C.; Roche, E.T.; Pigula, F.A. Soft pneumatic artificial muscles with low threshold pressures for a cardiac compression device. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013; Volume 55935, p. V06AT07A009. [Google Scholar]
- Gafford, J.; Ding, Y.; Harris, A. Shape deposition manufacturing of a soft, atraumatic, deployable surgical grasper. ASME. J. Med. Devices 2014, 8, 030927. [Google Scholar] [CrossRef] [Green Version]
- Keplinger, C.; Li, T.; Baumgartner, R. Harnessing snap-through instability in soft dielectrics to achieve giant voltage-triggered deformation. Soft Matter 2012, 8, 285–288. [Google Scholar] [CrossRef]
- Mac Murray, B.C.; An, X. Poroelastic foams for simple fabrication of complex soft robots. Adv. Mater. 2015, 27, 6334–6340. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, X.J.; Dong, X.; Zhou, J.; Zhao, H. Enhancing the Universality of a Pneumatic Gripper via Continuously Adjustable Initial Grasp Postures. IEEE Trans. Robot. 2021, 37, 1604–1618. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, J.; Zhao, J. A Gas–Ribbon-Hybrid Actuated Soft Finger with Active Variable Stiffness. Soft Robot. 2021. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Yang, Y.; Chen, M.Z. A variable stiffness gripper based on differential drive particle jamming. Bioinspir. Biomim. 2019, 14, 036009. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, Y.; Kan, Z.; Zeng, J.; Wang, M.Y. Hybrid Jamming for Bioinspired Soft Robotic Fingers. Soft Robot 2019, 7, 292–308. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wu, X.; Zhang, J.; Du, Y. A Pneumatic Novel Combined Soft Robotic Gripper with High Load Capacity and Large Grasping Range. Actuators 2022, 11, 3. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Yang, Y.; Li, Y. A soft robotic spine with tunable stiffness based on integrated ball joint and particle jamming. Mechatronics 2016, 33, 84–92. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Yang, Y. Passive particle jamming and its stiffening of soft robotic grippers. IEEE Trans. Robot. 2017, 33, 446–455. [Google Scholar] [CrossRef]
- Tolley, M.T.; Shepherd, R.F.; Mosadegh, B. A resilient, untethered soft robot. Soft Robot 2014, 1, 213–223. [Google Scholar] [CrossRef]
- Mitsuda, T.; Otsuka, S. Active bending mechanism employing granular jamming and vacuum-controlled adaptable gripper. IEEE Robot. Autom. Lett. 2021, 6, 3041–3048. [Google Scholar] [CrossRef]
- Lee, G.; Hong, G.Y.; Choi, Y. Tendon-driven Compliant Prosthetic Wrist Consisting of Three Rows Based on the Concept of Tensegrity Structure. IEEE Robot. Autom. Lett. 2021, 6, 3956–3963. [Google Scholar] [CrossRef]
- Fang, B.; Sun, F.; Wu, L.; Liu, F.; Wang, X.; Huang, H.; Huang, W.; Liu, H.; Wen, L. Multimode Grasping Soft Gripper Achieved by Layer Jamming Structure and Tendon-Driven Mechanism. Soft Robot. 2021. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Hyodo, K.; Ogane, D. On tendon-driven robotic mechanisms with redundant tendons. Int. J. Robot. Res 1998, 17, 561–571. [Google Scholar] [CrossRef]
- Shirafuji, S.; Ikemoto, S.; Hosoda, K. Development of a tendon-driven robotic finger for an anthropomorphic robotic hand. Int. J. Robot. Res. 2014, 33, 677–693. [Google Scholar] [CrossRef]
- Shiva, A.; Stilli, A.; Noh, Y. Tendon-based stiffening for a pneumatically actuated soft manipulator. IEEE Robot. Autom. Lett. 2016, 1, 632–637. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wu, L.; Fang, B. Layer jamming-based soft robotic hand with variable stiffness for compliant and effective grasping. Cogn. Comput. Syst. 2020, 2, 44–49. [Google Scholar] [CrossRef]
- Yang, G.Z.; Bellingham, J.; Dupont, P.E. The grand challenges of Science Robotics. Sci. Robot. 2018, 3, eaar7650. [Google Scholar] [CrossRef]
- Marchese, A.D.; Onal, C.D. Soft robot actuators using energy-efficient valves controlled by electropermanent magnets. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 756–761. [Google Scholar]
- Ren, T.; Li, Y.; Xu, M. A novel tendon-driven soft actuator with self-pumping property. Soft Robot. 2020, 7, 130–139. [Google Scholar] [CrossRef]
- Loepfe, M.; Schumacher, C.M.; Stark, W.J. Design, performance and reinforcement of bearing-free soft silicone combustion-driven pumps. Ind. Eng. Chem. Res. 2014, 53, 12519–12526. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Ren, T. Precharged pneumatic soft actuators and their applications to untethered soft robots. Soft Robot. 2018, 5, 567–575. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Liu, X.; Chen, X. Design and simulation analysis of a soft manipulator based on honeycomb pneumatic networks. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 350–356. [Google Scholar]
- Yoshimura, Y. On the Mechanism of Buckling of a Circular Cylindrical Shell under Axial Compression; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1955.
- Li, X.; Lan, Y.; Jiang, P.; Cao, H.; Zhou, J. An Efficient Computation for Energy Optimization of Robot Trajectory. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Jiang, P.; Huang, S.; Xiang, J.; Chen, M.Z. A unified approach for second-order control of the manipulator with joint physical constraints. J. Mech. Robot. 2017, 9, 041009. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Li, Y. Pre-charged pneumatic soft gripper with closed-loop control. IEEE Robot. Autom. Lett. 2019, 4, 1402–1408. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T. Modeling of soft fiber-reinforced bending actuators. IEEE Trans. Robot 2015, 31, 778–789. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Polygerinos, P.; Overvelde, J.T. Interaction forces of soft fiber reinforced bending actuators. IEEE ASME Trans. Mechatron. 2016, 22, 717–727. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Jiang, P.; Li, X.; Bai, L.; Liu, F.; Chen, R. A Soft Self-Stable Actuator and Its Energy-Efficient Grasping. Actuators 2022, 11, 107. https://doi.org/10.3390/act11040107
Luo J, Jiang P, Li X, Bai L, Liu F, Chen R. A Soft Self-Stable Actuator and Its Energy-Efficient Grasping. Actuators. 2022; 11(4):107. https://doi.org/10.3390/act11040107
Chicago/Turabian StyleLuo, Ji, Pei Jiang, Xiaobin Li, Long Bai, Fuqiang Liu, and Rui Chen. 2022. "A Soft Self-Stable Actuator and Its Energy-Efficient Grasping" Actuators 11, no. 4: 107. https://doi.org/10.3390/act11040107
APA StyleLuo, J., Jiang, P., Li, X., Bai, L., Liu, F., & Chen, R. (2022). A Soft Self-Stable Actuator and Its Energy-Efficient Grasping. Actuators, 11(4), 107. https://doi.org/10.3390/act11040107







