Double Redundancy Electro-Hydrostatic Actuator Fault Diagnosis Method Based on Progressive Fault Diagnosis Method
Abstract
:1. Introduction
2. Methods
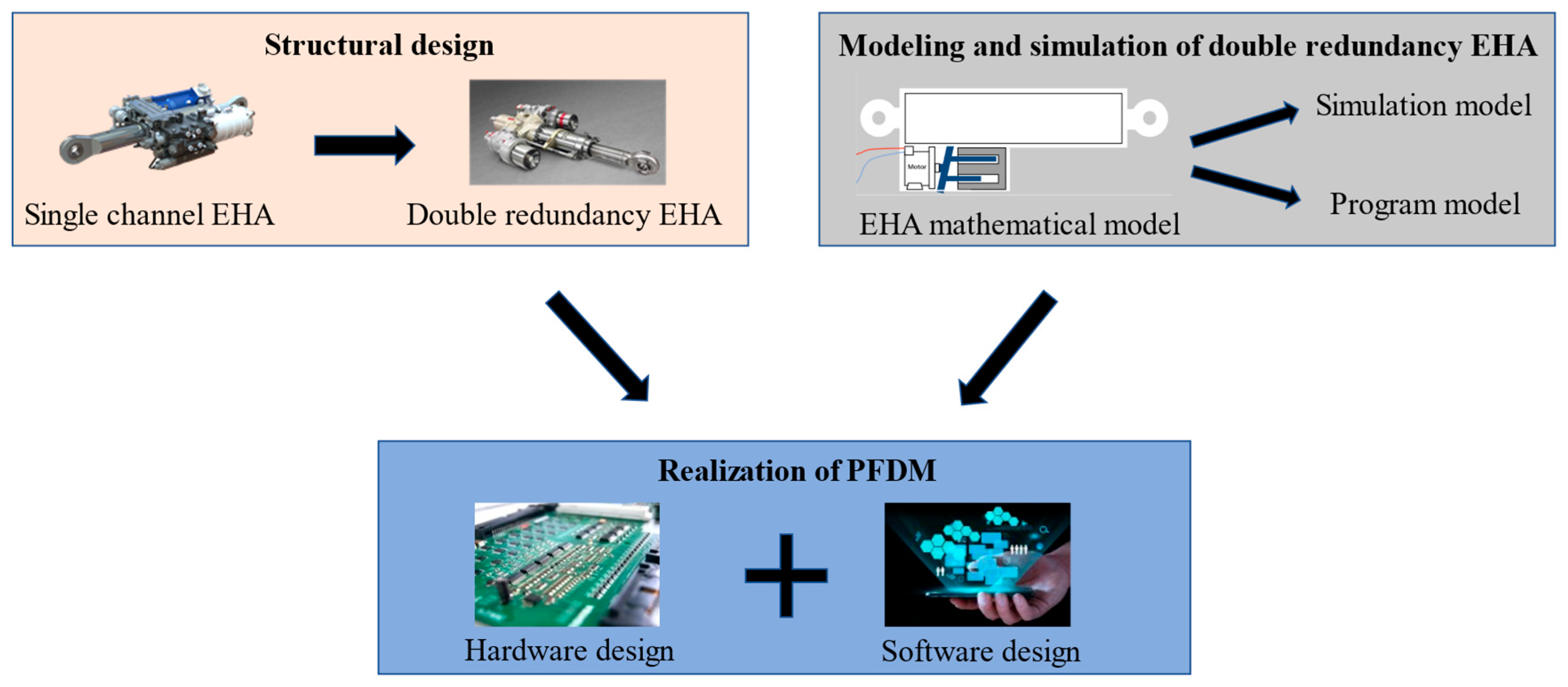
2.1. Structural Design and Sensor Layout of Double Redundancy EHA
2.2. Common Fault Types and Judgment Scheme
2.2.1. Fault Type of Double Redundancy EHA System
2.2.2. Fault Diagnosis Based on Threshold
- (1)
- Driver overcurrent fault
- (2)
- Driver overvoltage and undervoltage fault
- (3)
- Abnormal drive heating fault
- (4)
- Abnormal pump heating fault
2.2.3. Fault Diagnosis Based on Logical Judgment
- (1)
- Redundant displacement sensor and motor speed sensor fault
- (2)
- Driver phase failure
- (3)
- Motor immobility fault
- (4)
- Oil pump stuck fault
2.2.4. Fault Diagnosis Based on Double Redundancy EHA Analytical Model
- (1)
- Motor winding open circuit fault
- (2)
- Motor winding short circuit fault
- (3)
- Abnormal pump output pressure
- (4)
- Pump, hydraulic cylinder leakage fault
- (5)
- The hydraulic cylinder is stuck and creeping
2.3. Mathematical Model of Double Redundancy EHA System
2.3.1. Mathematical Model of Permanent Magnet Synchronous Motor (PMSM)
- The back electromotive force of the motor is sinusoidal in space.
- The stator windings are symmetrically distributed.
- The effects of core saturation, eddy current, hysteresis, and core loss are not considered.
2.3.2. Mathematical Model of Hydraulic Pump
2.3.3. Mathematical Model of Hydraulic Cylinder
2.4. Establishment and Verification of Double Redundancy EHA Model
2.4.1. Main Parameters of Double Redundancy EHA System
2.4.2. Simulation of double redundancy EHA system
2.4.3. Establishment of Model in C Language
2.4.4. Sensor Fault Diagnosis Based on Kalman Filter
3. Experimental Results of Physical Prototype
3.1. Realization of PFDM
3.2. Fault Experiment Based on Threshold
3.3. Fault Experiment Based on Logical Judgment
3.4. Fault Experiment Based on Double Redundancy EHA Mathematical Model
3.5. Fault Isolation and System Reconfiguration
4. Conclusions
- It overcomes the limitation of other fault diagnosis methods with fewer programs and easier on-line diagnosis.
- It does not depend on specific equipment and is easier to update and maintain. The state variables of the model can be updated in real time according to the parameter changes of the actual system, so as to make the fault diagnosis results more accurate.
- PFDM has more faults than other common diagnosis methods. It can distinguish and locate faults that are difficult to judge in the system more accurately, and has strong engineering applicability.
- PFDM is combined with the traditional actuator modeling and simulation method, which has stronger reliability.
- Combined with redundancy technology, it can accurately locate sensor faults and diagnose faults accurately.
- PFDM can separate sensor faults from double redundancy EHA system faults, avoiding the disadvantage of traditional data analysis methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Wang, M.; Yang, R.; Fu, Y.; Zhu, D. Adaptive damping variable sliding mode control for an electrohydrostatic actuator. Actuators 2021, 10, 83. [Google Scholar] [CrossRef]
- David, E.B. An assessment of developing dual use electric actuation technologies for military aircraft and commercial application. In Proceedings of the IECEC-97 Proceedings of the Thirty-Second Intersociety Energy Conversion Engineering Conference (Cat. No.97CH6203), Honolulu, HI, USA, 27 July–1 August 1997; pp. 716–721. [Google Scholar]
- Zhang, H.F.; Xie, J.; Guan, W.L.; Zhang, L. Modeling and simulation of EHA system based on fuzzy adaptive PID control. In Proceedings of the 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; pp. 750–753. [Google Scholar]
- Yu, B.; Wu, S.; Jiao, Z.; Shang, Y. Multi-objective optimization design of an electrohydrostatic actuator based on a particle swarm optimization algorithm and an analytic hierarchy process. Energies 2018, 11, 2426. [Google Scholar] [CrossRef]
- Liu, X.X.; Zhang, W.G.; Li, G.W. Redundancy design technology of fly by wire flight control system. J. Aircr. design. Commun. 2006, 1, 35–38. (In Chinese) [Google Scholar]
- Zhao, J.Y.; Hu, J.; Yao, J.Y.; Zhou, H.B.; Wang, J.L.; Cao, M.M. EHA fault diagnosis and fault tolerant control based on adaptive neural network robust observer. J. Beijing Univ. Aeronaut. Astronaut. 2022, 1–16. (In Chinese) [Google Scholar] [CrossRef]
- Philippe, G. Oscillatory failure case detection in the A380 electrical flight control system by analytical redundancy. Control Eng. Pract. 2010, 18, 1110–1119. [Google Scholar]
- Chi, C.Z.; Zhang, W.G.; Liu, X.X. A method for comprehensive diagnosis of sensors of flight control system using analytical redundancy. In Proceedings of the 2010 International Conference on Electrical and Control Engineering, Washington, DC, USA, 25–27 June 2010; pp. 4892–4895. [Google Scholar]
- Stephen, C.J.; Gavin, D.J.; David, D. Flight test experience with an electromechanical actuator on the F-18 Systems Research Aircraft. In Proceedings of the 19th Digital Avionics Systems Conference. Proceedings (Cat. No.00CH37126), Philadelphia, PA, USA, 7–13 October 2000; Volume 1, p. 2E3/1-2E310. [Google Scholar]
- Navarro, R. Performance of an Electro-Hydrostatic Actuator on the F-18 Systems Research Aircraft; National Aeronautics and Space Administration, Dryden Flight Research Center: Edwards, CA, USA, 1997. [Google Scholar]
- Liu, H.; Peng, S.; Jiang, B. Fault detection, diagnosis, and fault tolerant control with flight applications. J. Frankl. Inst. 2013, 350, 2371–2372. [Google Scholar] [CrossRef]
- Isermann, R.; Balle, P. Trends in the application of model-based fault diagnosis of technical processes. Control Eng. Pract. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Wlamir, V.; Luiz, R.; Takashi, Y. Electro hydraulic servovalve health monitoring using fading extended Kalman filter. In Proceedings of the 2015 IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, 22–25 June 2015; pp. 1–6. [Google Scholar]
- Gao, Z.; Cecati, C.; Steven, X.D. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Yu, Y.; Denchai, W.; Yu, D. A review of fault detection and diagnosis methodologies on air-handling units. Energy Build. 2014, 82, 550–562. [Google Scholar] [CrossRef]
- Davor, L.; Vladimir, K. Fault diagnosis of a hydraulic actuator using neural network. In Proceedings of the IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; pp. 108–111. [Google Scholar]
- Andrea, M.; Giovanni, J. Prognostic and health management system for fly-by-wire electro-hydraulic servo actuators for detection and tracking of actuator faults. Procedia CIRP 2017, 59, 116–121. [Google Scholar]
- Arellano-Espitia, F.; Delgado-Prieto, M.; Martinez-Viol, V.; Saucedo-Dorantes, J.J.; Osornio-Rios, R.A. Deep-learning-based methodology for fault diagnosis in electromechanical systems. Sensors 2020, 20, 3949. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Yao, X.; Zhang, H. Echo state networks based data-driven adaptive fault tolerant control with its application to electromechanical system. IEEE/ASME Trans. Mechatron. 2018, 23, 1372–1382. [Google Scholar] [CrossRef]
- Wang, J.; Miao, J.; Wang, J.; Yang, F.; Tsui, K.L.; Miao, Q. Fault diagnosis of electrohydraulic actuator based on multiple source signals: An experimental investigation. Neurocomputing 2020, 417, 224–238. [Google Scholar] [CrossRef]
- Chinniah, Y. Fault Detection in the Electrohydraulic Actuator Using Extended Kalman Filter; University of Saskatchewan: Saskatoon, SK, Canada, 2004. [Google Scholar]
- Chinniah, Y.; Burton, R.; Habibi, S. Failure monitoring in a high performance hydrostatic actuation system using the extended Kalman filter. Mechatronics 2006, 16, 643–653. [Google Scholar] [CrossRef]
- Chinniah, Y.; Burton, R.; Habibi, S.; Sampson, E. Identification of the nonlinear friction characteristics in a hydraulic actuator using the extended Kalman filter. Trans. Can. Soc. Mech. Eng. 2008, 32, 121–136. [Google Scholar] [CrossRef]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-based fault diagnosis for aerospace systems: A survey. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1329–1360. [Google Scholar] [CrossRef]
- Isermann, R. Model-based fault-detection and diagnosis—Status and applications. IFAC Proc. Vol. 2005, 37, 46–60. [Google Scholar] [CrossRef]
- Dai, X.W.; Gao, Z.W. From model, signal to knowledge: A data-driven perspective of fault detection and diagnosis. IEEE Trans. Ind. Inform. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Li, K.; Lv, Z.; Lu, K.; Yu, P. Thermal-hydraulic Modeling and Simulation of the Hydraulic System based on the Electro-hydrostatic Actuator. Procedia Eng. 2014, 80, 272–281. [Google Scholar] [CrossRef] [Green Version]
- Wiegand, C. F-35 Air Vehicle Technology Overview. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, Georgia, 25–29 June 2018. [Google Scholar]
- Lei, Z.F.; Qin, L.J.; Wu, X.D.; Jin, W.; Wang, C.X. Research on fault diagnosis method of electro-hydrostatic actuator. Shock. Vib. 2021, 2021, 6688420. [Google Scholar]
- Wang, Y.Y.; Chen, H.J.; Yang, X.G.; Sun, Q.; Qiao, T.T.; Zhang, K. Fault diagnosis method of underwater control module hydraulic system based on decision tree. Mar. Eng. 2022, 44, 154–164. (In Chinese) [Google Scholar]
- Fu, Y.L.; Wang, L.J.; Qi, H.T.; Liu, H.S. Fault diagnosis and management of electro-hydrostatic actuator. Mach. Tools Hydraul. 2010, 38, 120–124. (In Chinese) [Google Scholar]
- Cai, Z.N. Analysis of fault types and diagnosis Countermeasures in mechanical hydraulic system. Value Eng. 2018, 37, 158–159. (In Chinese) [Google Scholar]
- Li, Q.Z. Talking about fault types and diagnosis Countermeasures in mechanical hydraulic system. Sci. Technol. Inf. 2016, 14, 116–117. (In Chinese) [Google Scholar]
- Li, Y.; Zhou, J.M. Simulation of electric-hydrostatic actuator driven by permanent magnet synchronous motor. J. Nanchang Hangkong Univ. (Nat. Sci.) 2014, 28, 38–44. (In Chinese) [Google Scholar]
- Kamalaselvan, A.; Prakash, S.L. Modeling simulation and analysis of closed loop speed control of PMSM drive system. In Proceedings of the 2014 International Conference on Circuits, Power and Computing Technologies, Nagercoil, India, 20–21 March 2014; pp. 692–697. [Google Scholar]
- Xia, L.Q.; Zhu, M.J.; Hu, Y.X.; Yang, Y.K. Modeling and simulation analysis of EHA actuator. Mach. Tools Hydraul. 2021, 49, 136–142. (In Chinese) [Google Scholar]
- Ge, Y.W.; Zhu, W.L.; Liu, J.H.; Deng, W.X.; Yao, J.Y. Refined Modeling and Characteristic Analysis of Electro-hydrostatic Actuator. J. Mech. Eng. 2021, 57, 66–73. (In Chinese) [Google Scholar]





















| Sensor Name | Quantity | Layout Location |
|---|---|---|
| Temperature sensor | 6 | Driver circuit board and hydraulic pump inlet and outlet |
| Current sensor | 5 | Permanent magnet synchronous motor and power bus circuit |
| Pressure sensor | 3 | At the booster oil tank and in the oil inlet and outlet of hydraulic cylinder |
| Displacement sensor | 2 | Both ends of hydraulic cylinder |
| Booster tank pressure sensor | 1 | In booster tank |
| Speed sensor | 2 | Permanent magnet synchronous motor |
| Voltage sensor | 1 | power bus circuit |
| Fault Type | ||
|---|---|---|
| Electrical system failure | Driver failure | Driver phase failure (Fault code 1) |
| Driver overcurrent fault (Fault code 2) | ||
| Driver overvoltage fault (Fault code 3) | ||
| Driver undervoltage fault (Fault code 4) | ||
| Abnormal drive heating fault (Fault code 5) | ||
| Motor failure | Motor immobility fault (Fault code 6) | |
| Motor winding open circuit fault (Fault code 7) | ||
| Motor winding short circuit fault (Fault code 8) | ||
| Sensor failure | Motor winding current sensor fault (Fault code 9) | |
| Motor speed sensor fault (Fault code 10) | ||
| Displacement sensor 1 and 2 fault (Fault code 11 and 12) | ||
| Booster tank pressure sensor fault (Fault code 13) | ||
| Cylinder chamber pressure sensor fault (Fault code 14) | ||
| Temperature sensor fault (Fault code 15) | ||
| Hydraulic system failure | Hydraulic pump failure | Abnormal pump output pressure fault (Fault code 16) |
| Oil pump stuck fault (Fault code 17) | ||
| Pump leakage fault (Fault code 18) | ||
| Abnormal pump heating fault (Fault code 19) | ||
| Hydraulic cylinder failure | Hydraulic cylinder stuck fault (Fault code 20) | |
| Hydraulic cylinder leakage fault (Fault code 21) | ||
| Hydraulic cylinder creeping fault (Fault code 22) | ||
| Parameter Name/Unit | Parameter Value |
|---|---|
| Motor winding resistance | 0.15 |
| Equivalent inductance of motor /H | 0.8 × 10−3 |
| Equivalent inductance of motor /H | 0.8 × 10−3 |
| Total moment of inertia of motor and pump /kg·m2 | 58 × 10−6 |
| Damping coefficient of motor and hydraulic pump /N·m·s·rad−1 | 5.969 × 10−4 |
| Total inertia mass converted from piston and load to piston /kg | 51 |
| Permanent magnet flux linkage /Wb | 0.0467 |
| Theoretical displacement of pump /m3·rad−1 | 2.374 × 10−7 |
| Number of pole pairs | 2 |
| The sum of the volume of the oil inlet pipeline and the left chamber of the hydraulic cylinder when the piston is at the midpoint of the stroke /m3 | 7.370 × 10−5 |
| The sum of the volume of the oil inlet pipeline and the right chamber of the hydraulic cylinder when the piston is at the midpoint of the stroke /m3 | 7.370 × 10−5 |
| Internal leakage coefficient of pump /m3·Pa·s−1 | 7.733 × 10−12 |
| Leakage coefficient in hydraulic cylinder /m3·Pa·s−1 | 2.383 × 10−12 |
| Pump outlet volume /m3 | 0.85 × 10−6 |
| Pump inlet volume /m3 | 0.85 × 10−6 |
| Effective bulk modulus of system /Pa | 1.47 × 109 |
| Load spring stiffness /N·m−1 | 8.89 × 105 |
| Effective area of symmetrical hydraulic cylinder /m2 | 1.256 × 10−3 |
| Viscous damping coefficient /N·s·m−1 | 50 |
| Maximum output torque of PMSM/N·m | 9 |
| Rated power of PMSM/KW | 7.5 |
| Different Working Conditions/N/m | Actual Test Data/rpm | Simulation Result/rpm | Difference |
|---|---|---|---|
| No load | 20,400 | 20,405 | 0.0245% |
| 1.8 | 19,100 | 18,582 | 2.71% |
| 2.5 | 17,800 | 18,002 | 1.13% |
| 3.5 | 16,000 | 16,565 | 3.53% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, H.-T.; Zhao, D.-A.; Liu, D.; Liu, X. Double Redundancy Electro-Hydrostatic Actuator Fault Diagnosis Method Based on Progressive Fault Diagnosis Method. Actuators 2022, 11, 264. https://doi.org/10.3390/act11090264
Qi H-T, Zhao D-A, Liu D, Liu X. Double Redundancy Electro-Hydrostatic Actuator Fault Diagnosis Method Based on Progressive Fault Diagnosis Method. Actuators. 2022; 11(9):264. https://doi.org/10.3390/act11090264
Chicago/Turabian StyleQi, Hai-Tao, Dong-Ao Zhao, Duo Liu, and Xu Liu. 2022. "Double Redundancy Electro-Hydrostatic Actuator Fault Diagnosis Method Based on Progressive Fault Diagnosis Method" Actuators 11, no. 9: 264. https://doi.org/10.3390/act11090264
APA StyleQi, H.-T., Zhao, D.-A., Liu, D., & Liu, X. (2022). Double Redundancy Electro-Hydrostatic Actuator Fault Diagnosis Method Based on Progressive Fault Diagnosis Method. Actuators, 11(9), 264. https://doi.org/10.3390/act11090264






