Target Tracking of Snake Robot with Double-Sine Serpentine Gait Based on Adaptive Sliding Mode Control
Abstract
:1. Introduction
2. Model Description
2.1. The Parameters of Snake Robot
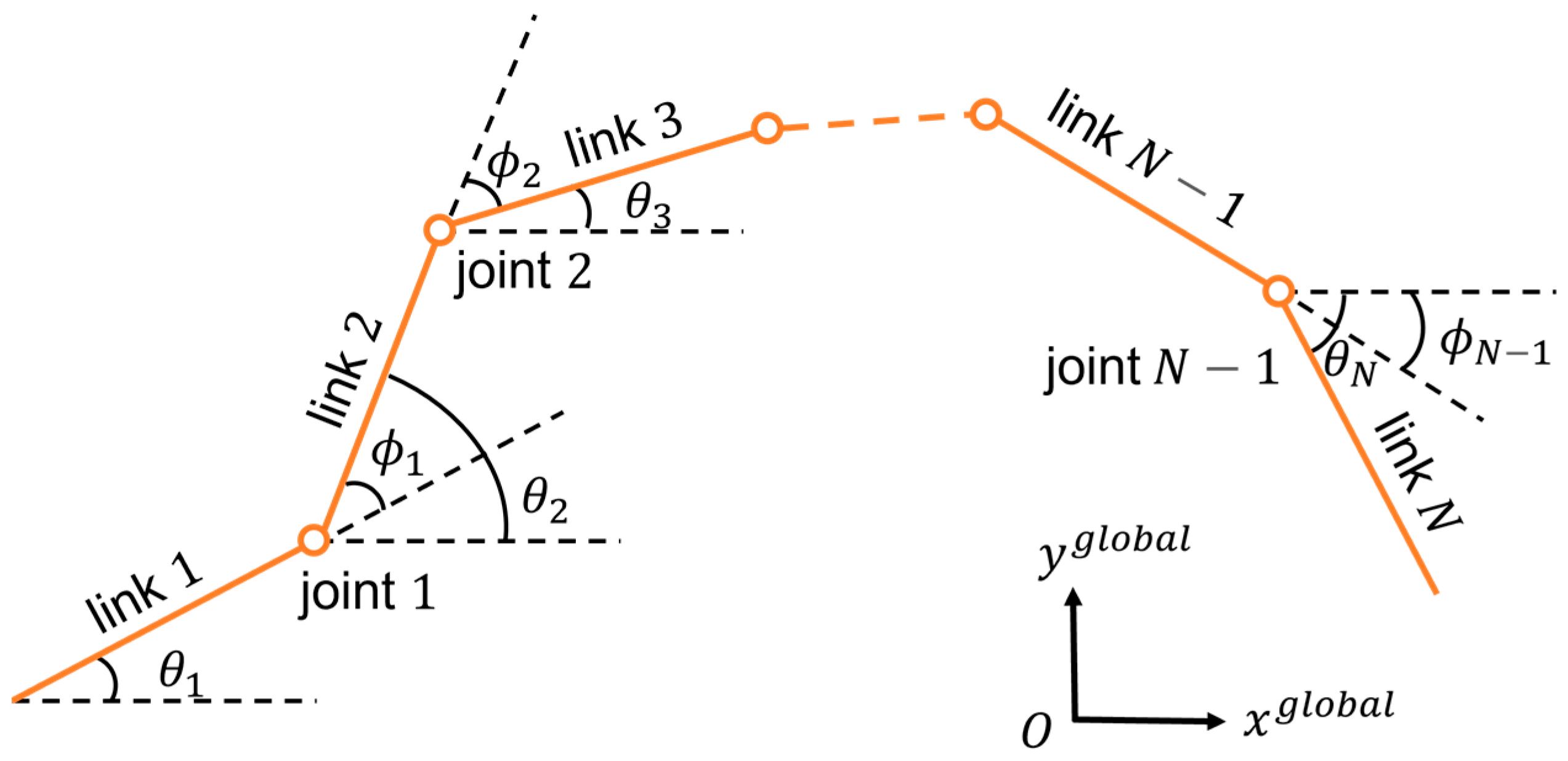
2.2. Definition of Snake Robot Kinematics
2.3. Kinematic Model of Snake Robot
3. Gait Analysis
3.1. Traditional Serpentine Gait
3.2. Omega Turn
3.3. Double-Sine Serpentine Gait
4. Controller Design
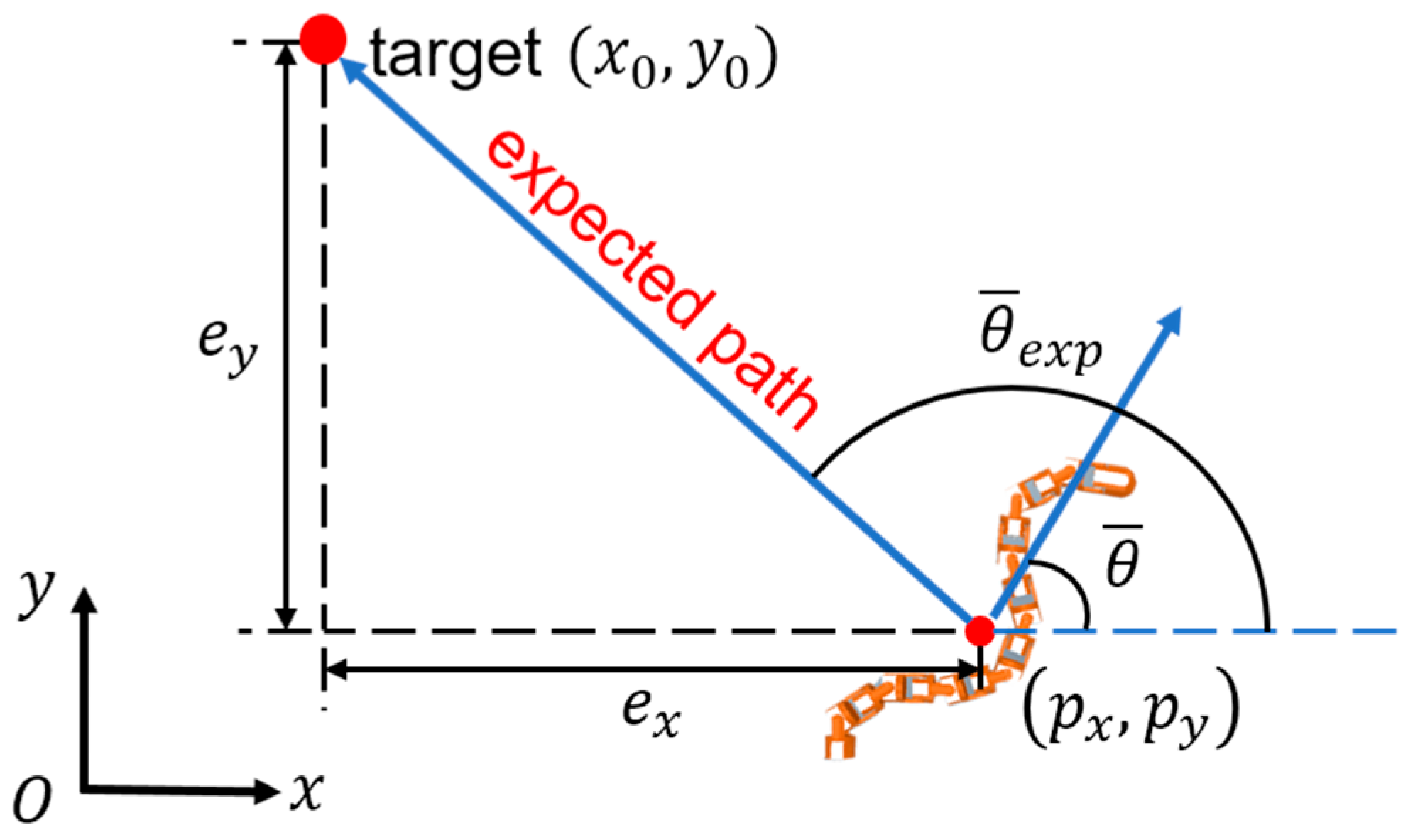
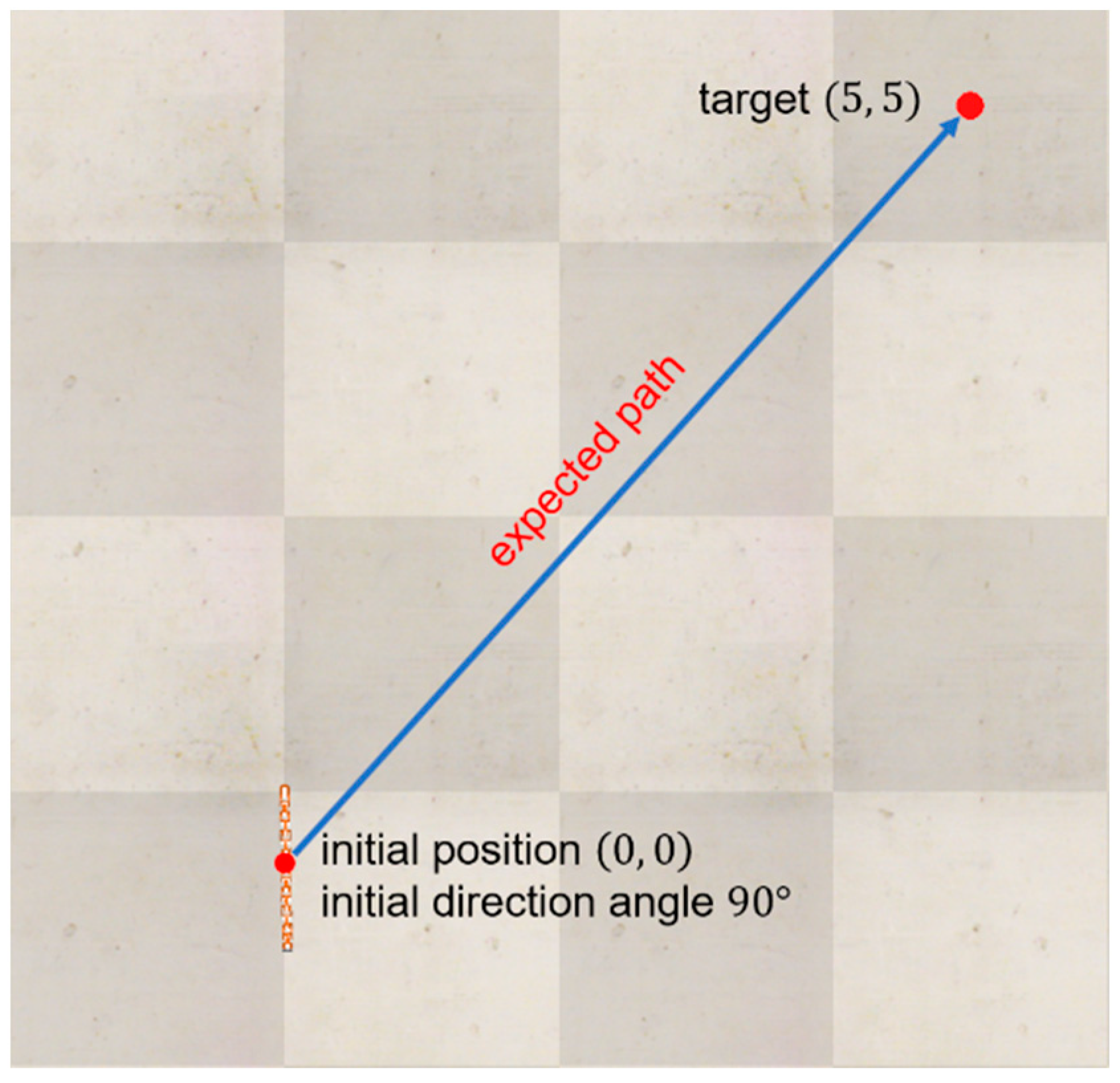
4.1. Control Objectives
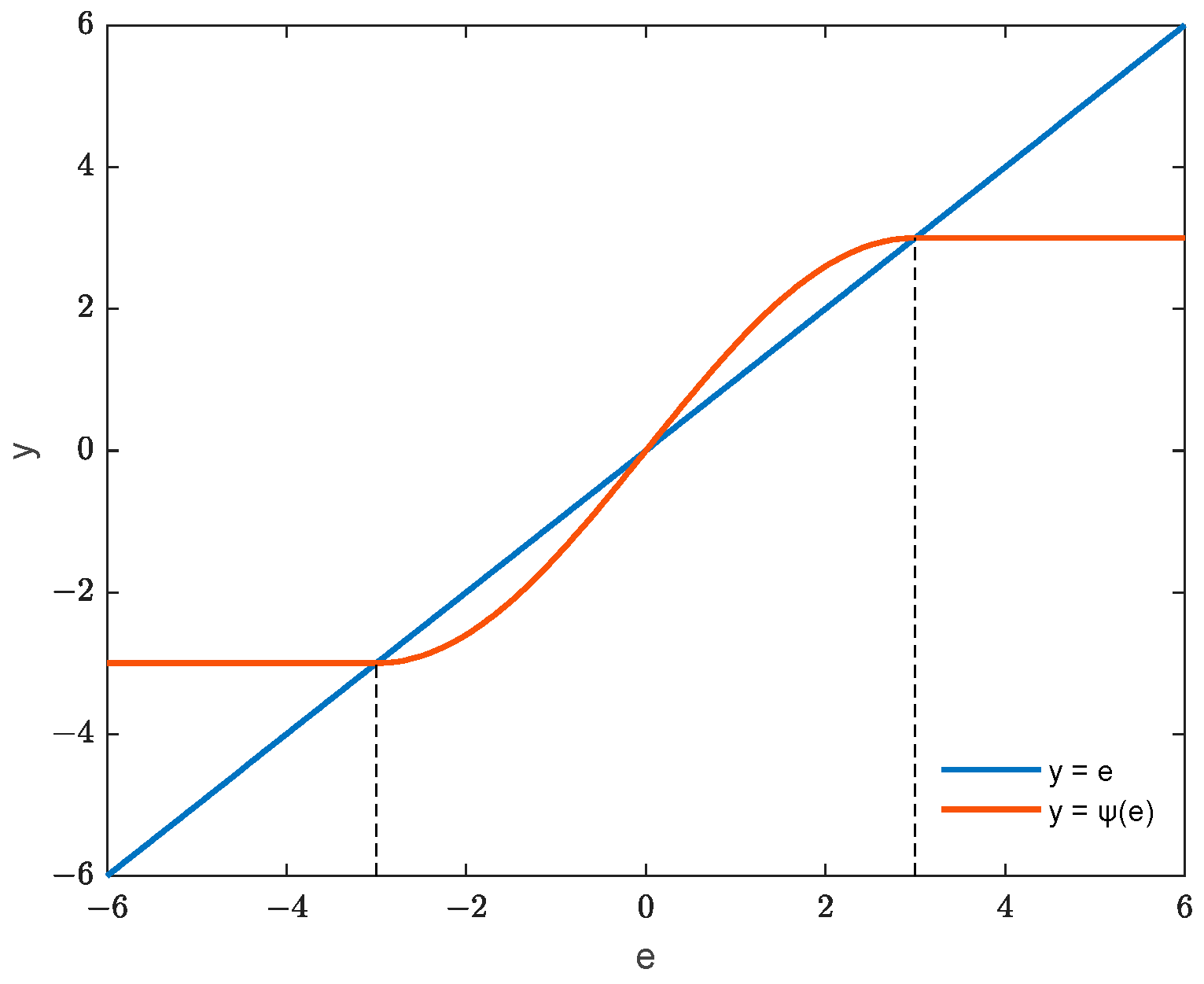
4.2. Sliding Mode Controller Design
4.3. Controller Stability Analysis
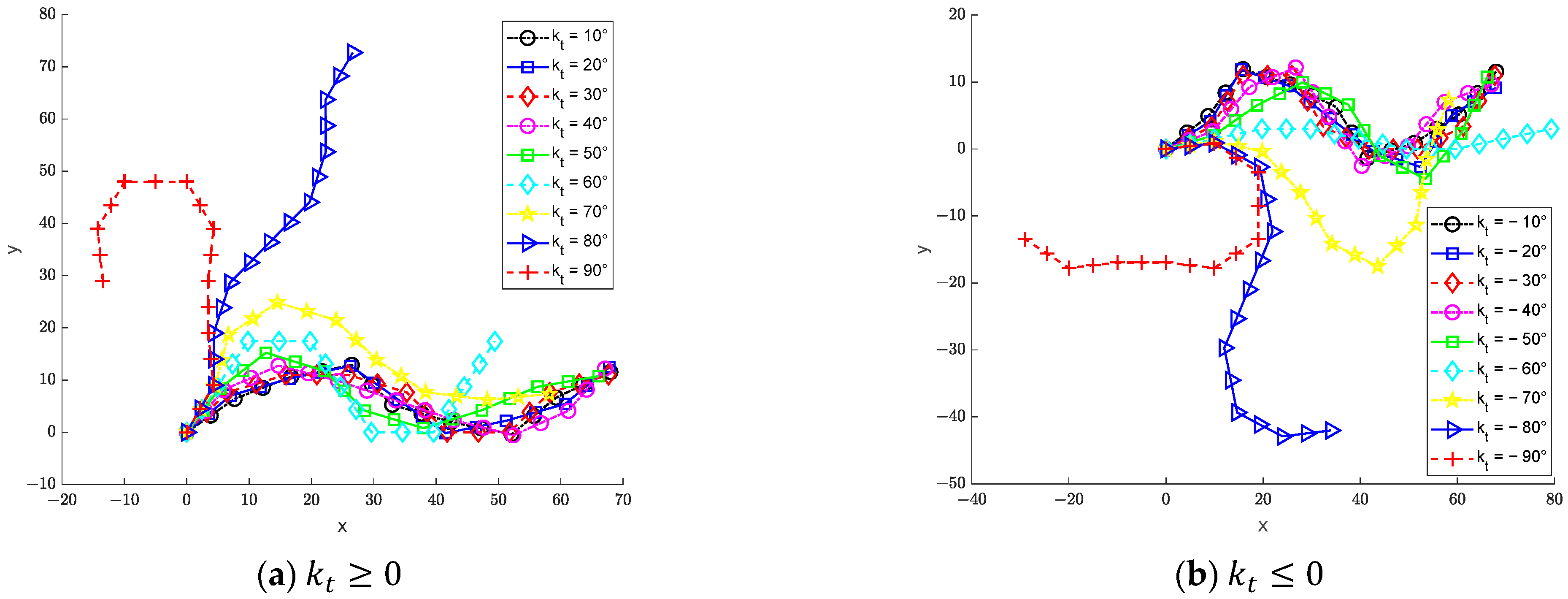
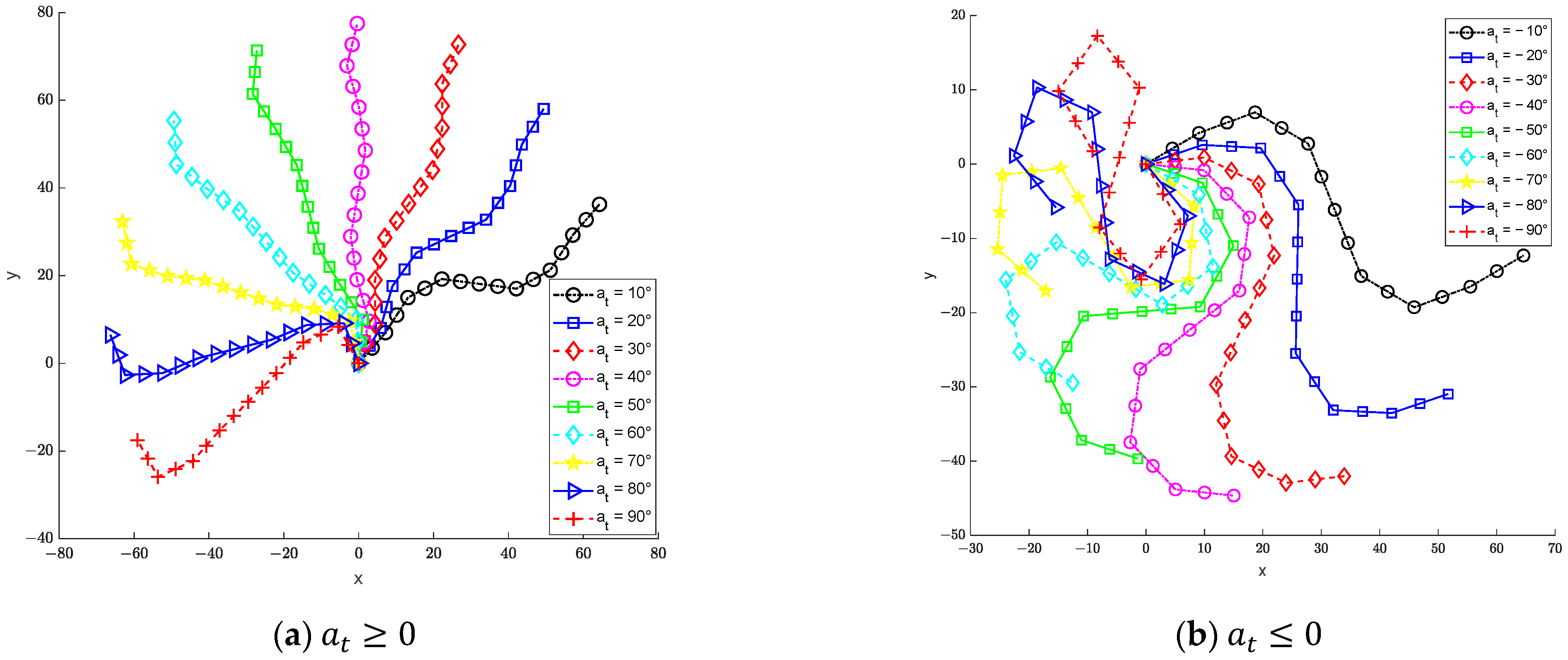
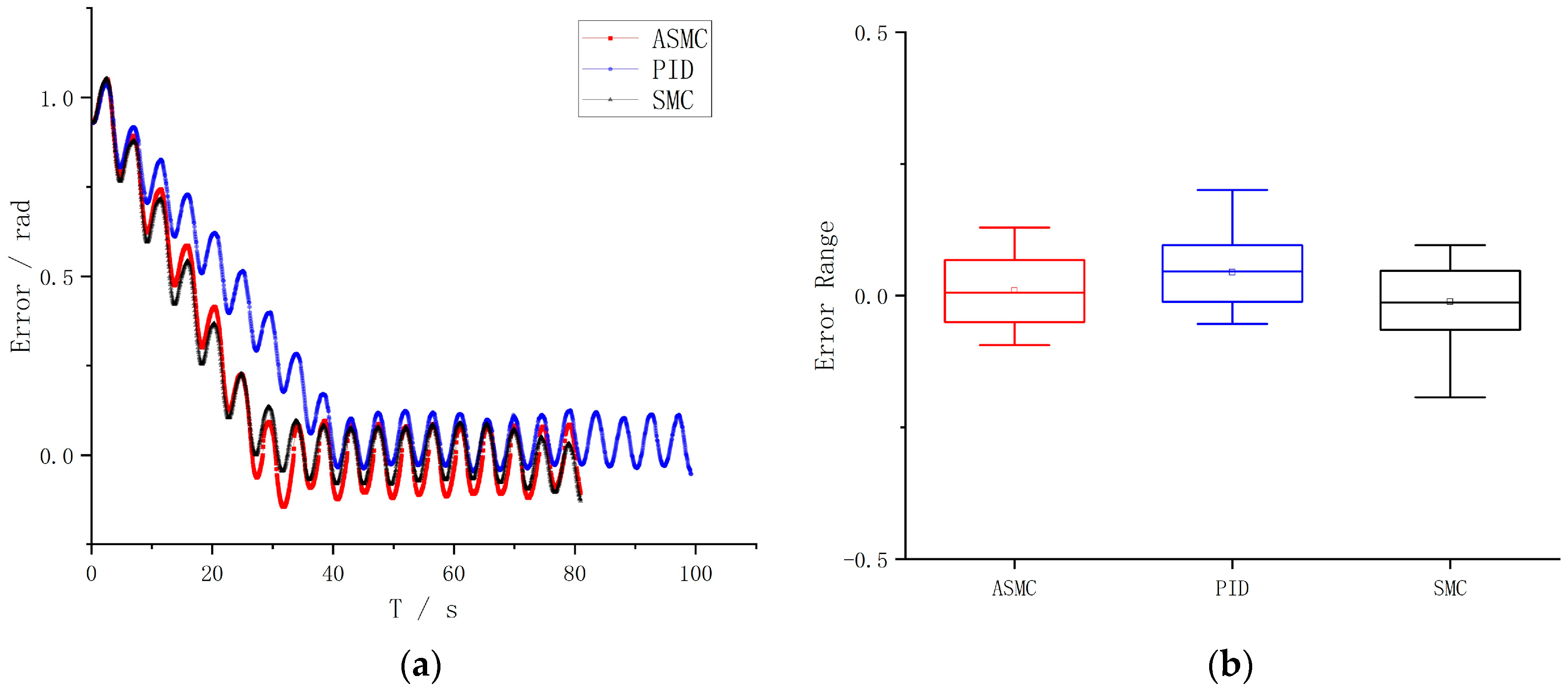
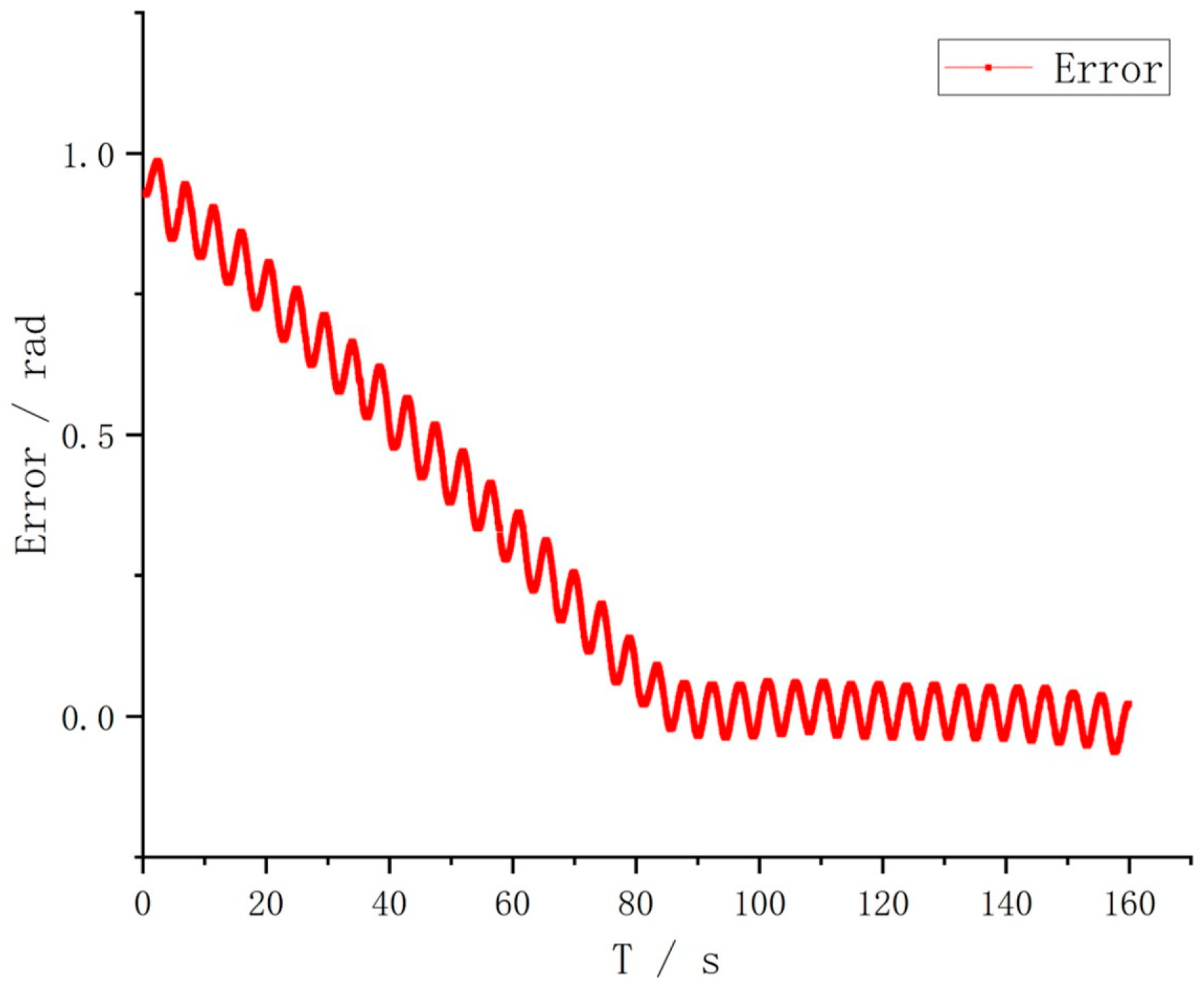
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Zheng, L.; Lü, D.; Wang, J.; Wang, S.; Su, H.; Wang, Z.; Ren, L. The snake-inspired robots: A review. Assem. Autom. 2022, 42, 567–583. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Wang, J.; Fei, Y.; Du, Q. An obstacle-avoiding and stiffness-tunable modular bionic soft robot. Robotica 2020, 40, 2651–2665. [Google Scholar] [CrossRef]
- Li, D.; Deng, H.; Pan, Z.; Xiu, Y. Collaborative obstacle avoidance algorithm of multiple bionic snake robots in fluid based on IB-LBM. ISA Trans. 2022, 122, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Qiao, H. Muscle-synergies-based neuromuscular control for motion learning and generalization of a musculoskeletal system. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3993–4006. [Google Scholar] [CrossRef]
- Bhandari, G.; Raj, R.; Pathak, P.; Yang, J. Robust control of a planar snake robot based on interval type-2 Takagi–Sugeno fuzzy control using genetic algorithm. Eng. Appl. Artif. Intell. 2022, 116, 105437. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, F.; Shi, S. Design and full-link trajectory tracking control of underwater snake robot with vector thrusters under strong time-varying disturbances. Ocean. Eng. 2022, 266, 113012. [Google Scholar] [CrossRef]
- Mahdi, H. Dynamics and computed-muscle-force control of a planar muscle-driven snake robot. Actuators 2022, 11, 194. [Google Scholar]
- Virgala, I.; Kelemen, M.; Prada, E.; Sukop, M.; Kot, T.; Bobovský, Z.; Varga, M.; Ferenčík, P. A snake robot for locomotion in a pipe using trapezium-like travelling wave. Mech. Mach. Theory 2021, 158, 104221. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, P.; Li, F.; Wang, K.; Shui, L.; Chen, X. On the snake-like lateral un-dulatory locomotion in terrestrial, aquatic and sand environments. J. Mech. Phys. Solids 2021, 157, 104629. [Google Scholar] [CrossRef]
- Liu, X.; Lin, G.; Wei, W. Adaptive transition gait planning of snake robot based on polynomial interpolation method. Actuators 2022, 11, 222. [Google Scholar] [CrossRef]
- Bae, J.; Kim, M.; Song, B.; Yang, J.; Kim, D.; Jin, M.; Yun, D. Review of the latest research on snake robots focusing on the structure, motion and control method. Int. J. Control Autom. Syst. 2022, 20, 3393–3409. [Google Scholar] [CrossRef]
- Qin, G.; Wu, H.; Cheng, Y.; Pan, H.; Zhao, W.; Shi, S.; Song, Y.; Ji, A. Adaptive trajectory control of an under-actuated snake robot. Appl. Math. Model. 2022, 106, 756–769. [Google Scholar] [CrossRef]
- Han, S.; Chon, S.; Kim, J.; Seo, J.; Shin, D.G.; Park, S.; Kim, J.T.; Kim, J.; Jin, M.; Cho, J. Snake Robot Gripper Module for Search and Rescue in Narrow Spaces. IEEE Robot. Autom. Lett. 2022, 7, 1667–1673. [Google Scholar] [CrossRef]
- Baysal, Y.; Altas, I. Modelling and simulation of a wheel-less snake robot. In Proceedings of the 2020 7th International Conference on Electrical and Electronics Engineering (ICEEE), Antalya, Turkey, 14–16 April 2020; pp. 285–289. [Google Scholar]
- Huang, Z.; Ma, S.; Lin, Z.; Zhu, K.; Wang, P.; Ahmed, R.; Ren, C.; Marvi, H. Impact of caudal fin geometry on the swimming performance of a snake-like robot. Ocean. Eng. 2022, 245, 110372. [Google Scholar] [CrossRef]
- Gray, J. The mechanism of locomotion in snakes. J. Exp. Biol. 1946, 23, 101–120. [Google Scholar] [CrossRef] [PubMed]
- Mori, M.; Hirose, S. Locomotion of 3D snake-like robots–shifting and rolling control of active cord mechanism ACM-R3. J. Robot. Mechatron. 2006, 18, 521–528. [Google Scholar] [CrossRef]
- Hirose, S. Biologically Inspired Robots: Snake-Like Locomotors and Manipulators; Oxford University Press: London, UK, 1993. [Google Scholar]
- Ye, C.; Ma, S.; Li, B.; Wang, Y. Turning and side motion of snake-like robot. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ’04. 2004, New Orleans, LA, USA, 26 April–1 May 2004; pp. 5075–5080. [Google Scholar]
- Ye, C.; Ma, S.; Li, B.; Wang, Y. Study on turning and sidewise motion of a snake-like robot. Chin. J. Mech. Eng. 2004, 40, 119–123, 128. [Google Scholar] [CrossRef]
- Dai, J.; Faraji, H.; Gong, C.; Hatton, R.; Goldman, D.; Choset, H. Geometric swimming on a granular surface. In Proceedings of the Robotics: Science and Systems 2016, Ann Arbor, MI, USA, 18–22 June 2016. [Google Scholar]
- Wang, T.; Chong, B.; Deng, Y.; Fu, R.; Choset, H.; Goldman, D. Generalized omega turn gait enables agile limbless robot turning in complex environments. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 1–7. [Google Scholar]
- Wang, T.; Chong, B.; Diaz, K.; Whitman, J.; Lu, H.; Travers, M.; Goldman, D.; Choset, H. The omega turn: A biologically-inspired turning strategy for elongated limbless robots. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7766–7771. [Google Scholar]
- Liu, X.; Onal, C.; Fu, J. Reinforcement learning of a CPG-regulated locomotion controller for a soft snake robot. arXiv 2022, arXiv:2207.04899. [Google Scholar]
- Takemori, T.; Tanaka, M.; Matsuno, F. Adaptive helical rolling of a snake robot to a straight pipe with irregular cross-sectional shape. IEEE Trans. Robot. 2022, 1–15. [Google Scholar] [CrossRef]
- Jiang, Z.; Otto, R.; Bing, Z.; Huang, K.; Knoll, A. Target tracking control of a wheel-less snake robot based on a supervised multi-layered SNN. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7124–7130. [Google Scholar]
- Liljebäck, P.; Pettersen, K.; Stavdahl, Ø.; Gravdahl, J.T. Snake Robots Modelling, Mechatronics, and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Liljebäck, P.; Pettersen, K. Waypoint guidance control of snake robots. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 937–944. [Google Scholar]
- Kelasidi, E.; Liljebäck, P.; Pettersen, K.; Gravdahl, J. Integral line-of-sight guidance for path following control of underwater snake robots: Theory and experiments. IEEE Trans. Robot. 2017, 33, 610–628. [Google Scholar] [CrossRef] [Green Version]
- Ariizumi, R.; Takahashi, R.; Tanaka, M.; Asai, T. Head-trajectory-tracking control of a snake robot and its robustness under actuator failure. IEEE Trans. Control Syst. Technol. 2019, 27, 2589–2597. [Google Scholar] [CrossRef]
- Zhang, D.; Li, B.; Chang, J. Path following method for snake robot based on the angle symmetry adjustment. Robot 2019, 41, 788–794, 833. [Google Scholar]
- Zhang, D. A path tracking method for the snake robot based on the path edge guidance strategy. Robot 2021, 43, 36–43. [Google Scholar]
- Xiao, W. Design and Research of Advanced Gaits on Snake Robot. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. [Google Scholar]
- Cao, Z.; Zhang, D.; Zhou, M. Direction control and adaptive path following of 3-D snake-like robot motion. IEEE Trans. Cybern. 2022, 52, 10980–10987. [Google Scholar] [CrossRef]
- Wang, C.; Peng, Y.; Li, D.; Pan, Z.; Deng, H.; Li, D.; Li, B. Turning strategy of snake-like robot based on serpenoid curve under cloud assisted smart conditions. Clust. Comput. 2019, 22, 13041–13053. [Google Scholar] [CrossRef]
- Craig, J. Introduction to Robotics: Mechanics and Control, 4th ed.; China Machine Press: Beijing, China, 2018. [Google Scholar]
- Wei, W.; Li, Y.; Liao, Z.; Zhang, J. Kinematics modeling of snake-like robot based on screw theory. J. South China Univ. Technol. Nat. Sci. Ed. 2019, 47, 1–8. [Google Scholar]
- Wei, W.; Li, Y.; Gao, Y.; Xu, J. Safe climbing of snake-like robot based on screw and envelope theory. J. South China Univ. Technol. Nat. Sci. Ed. 2019, 47, 13–23. [Google Scholar]
- Tursynbek, I.; Shintemirov, A. Modeling and Simulation of Spherical Parallel Manipulators in CoppeliaSim (V-REP) Robot Simulator Software. In Proceedings of the 2020 International Conference Nonlinearity, Information and Robotics (NIR), Innopolis, Russia, 3–6 December 2020; pp. 1–6. [Google Scholar]
- Liu, J. Sliding Mode Control Design and Matlab Simulation: The Basic Theory and Design Method, 4th ed.; Tsinghua University Press: Beijing, China, 2019. [Google Scholar]
- Li, P.; Zheng, Z. Sliding mode control approach with nonlinear integrator. Control Theory Appl. 2011, 28, 421–426. [Google Scholar]
- Li, T. Nonlinear integral sliding mode control method based on new reaching law. Control Eng. China 2019, 26, 2031–2035. [Google Scholar]
- Yue, C.; Qian, L.; Chen, L.; Tian, L.; Yang, H. Adaptive control for artillery chain driving powder based on double power reaching law. J. Southeast Univ. Nat. Sci. Ed. 2017, 47, 1135–1140. [Google Scholar]







| Symbol | Description | Vector |
|---|---|---|
| The total number of joints | ||
| The joint index | ||
| The length of a link | ||
| The forward direction angle of snake robot | ||
| The expected direction angle of snake robot | ||
| Angle between the link and the global -axis | ||
| Angle of joint | ||
| The center point of joint | ||
| The unit vector in the direction of the rotation axis of joint | ||
| The twist of joint | ||
| Global coordinates of the center of mass of snake robot |
| Items | Description |
|---|---|
| Mass | 1.5 kg |
| Length | |
| Diameter | 0.05 m |
| Sensing | Angle sensor, Vision sensor, Proximity sensor |
| Number of modules | 17 |
| Number of joints | 16 |
| Connection mode between modules | Orthogonal connection |
| Pose Matrix | Calculated Data | Actual Data | |
|---|---|---|---|
| Time | |||
| 2.20 s | |||
| 3.70 s | |||
| 12.95 s | |||
| 29.75 s | |||
| 50.05 s | |||
| Gait | Double-Sine Serpentine Gait | Traditional Serpentine Gait | |
|---|---|---|---|
| Turning Time | |||
| Turning Time | 11.15 s | 39.55 s | |
| Turning Time | 16.85 s | 52.95 s | |
| Turning Time | 22.15 s | 89.70 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wei, W.; Liu, X.; Han, S. Target Tracking of Snake Robot with Double-Sine Serpentine Gait Based on Adaptive Sliding Mode Control. Actuators 2023, 12, 38. https://doi.org/10.3390/act12010038
Liu Z, Wei W, Liu X, Han S. Target Tracking of Snake Robot with Double-Sine Serpentine Gait Based on Adaptive Sliding Mode Control. Actuators. 2023; 12(1):38. https://doi.org/10.3390/act12010038
Chicago/Turabian StyleLiu, Zhifan, Wu Wei, Xiongding Liu, and Siwei Han. 2023. "Target Tracking of Snake Robot with Double-Sine Serpentine Gait Based on Adaptive Sliding Mode Control" Actuators 12, no. 1: 38. https://doi.org/10.3390/act12010038
APA StyleLiu, Z., Wei, W., Liu, X., & Han, S. (2023). Target Tracking of Snake Robot with Double-Sine Serpentine Gait Based on Adaptive Sliding Mode Control. Actuators, 12(1), 38. https://doi.org/10.3390/act12010038






